Optimization of Passive Envelop Energy Efficient Measures for Office Buildings in Different Climate Regions of China Based on Modified Sensitivity Analysis
Abstract
:1. Introduction
2. Methodology
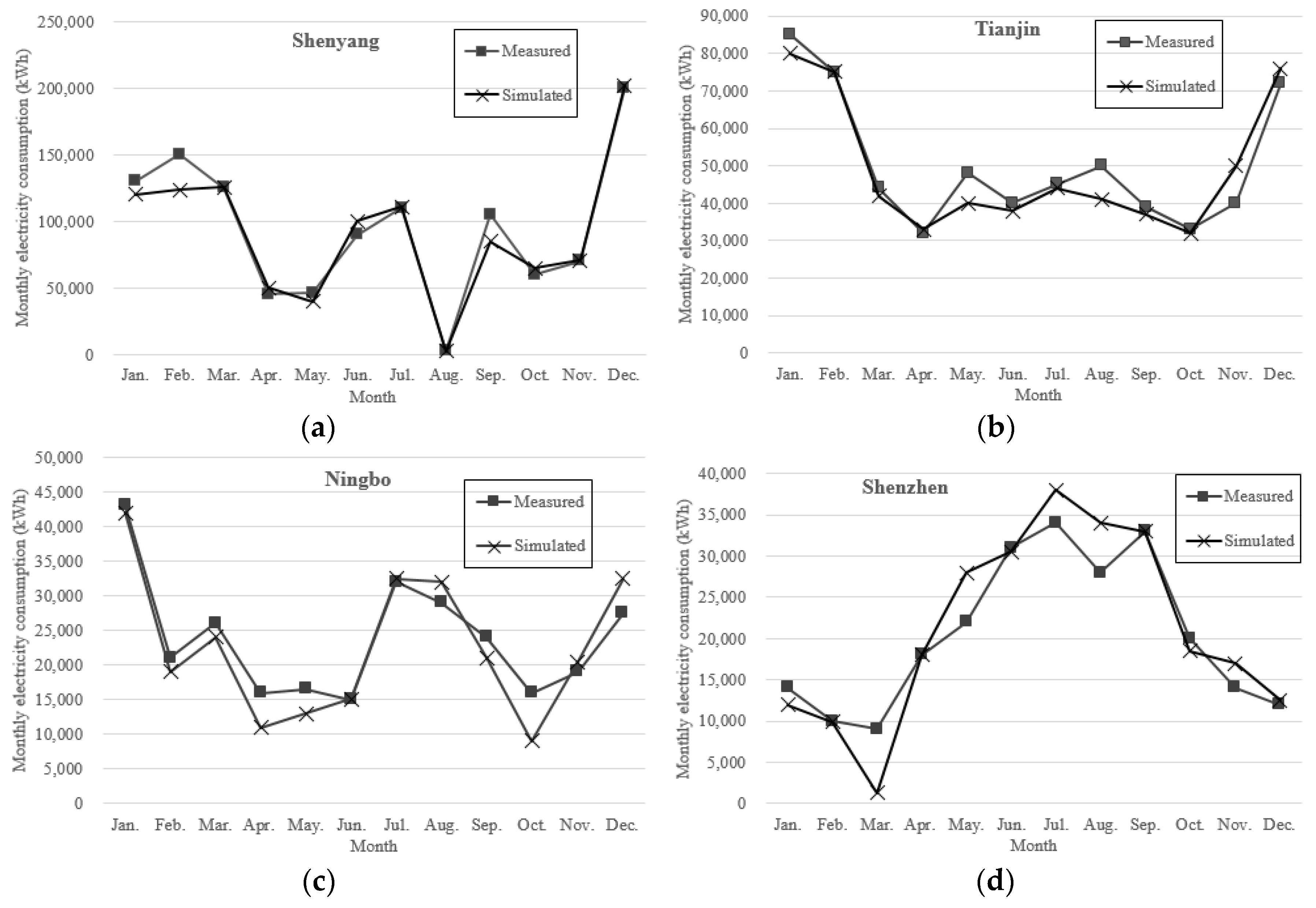
2.1. Building Energy Consumption Simulation and Verification
2.2. Modified Sensitivity Analysis
3. Results
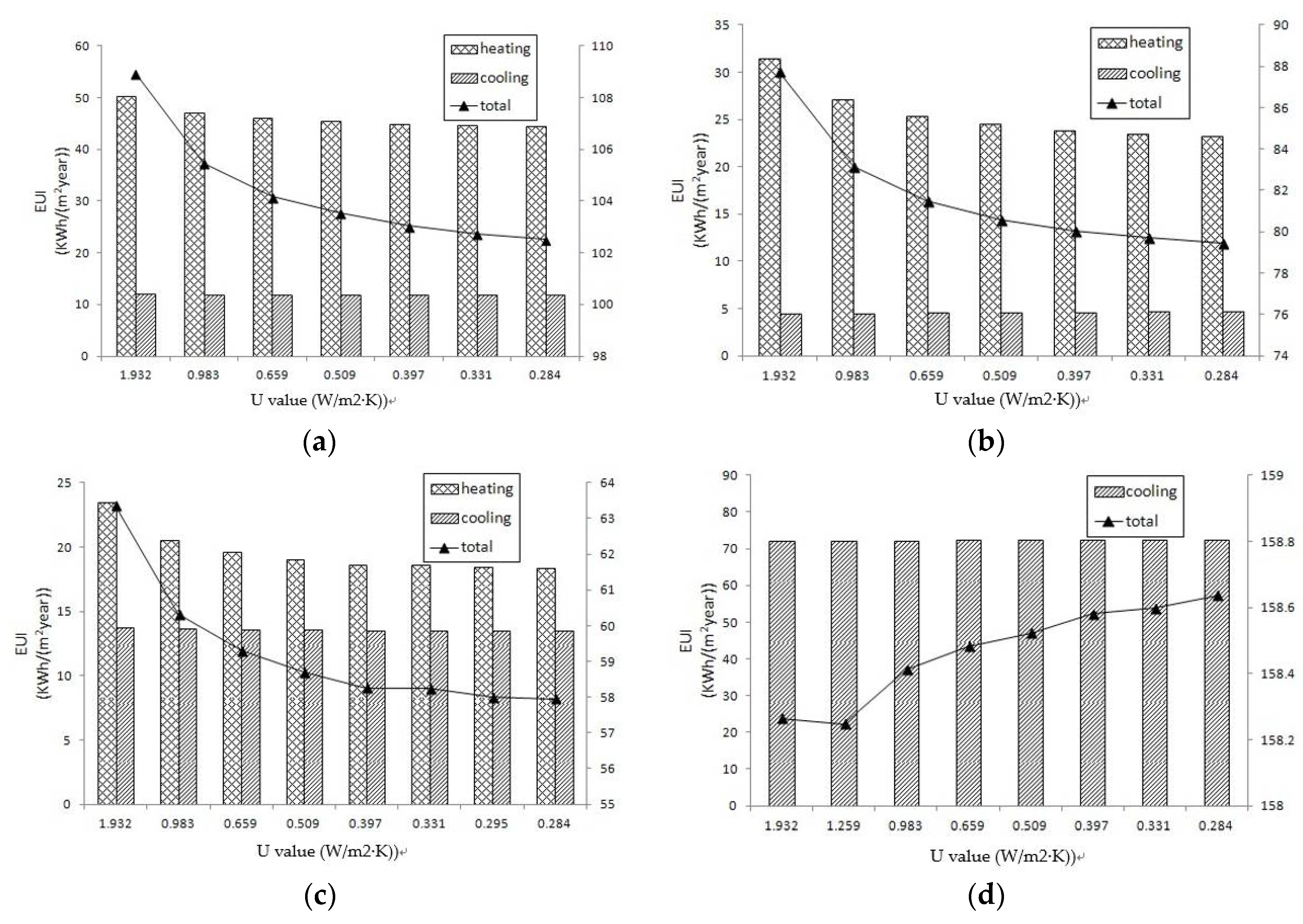
3.1. Exterior Wall Thermal Insulations
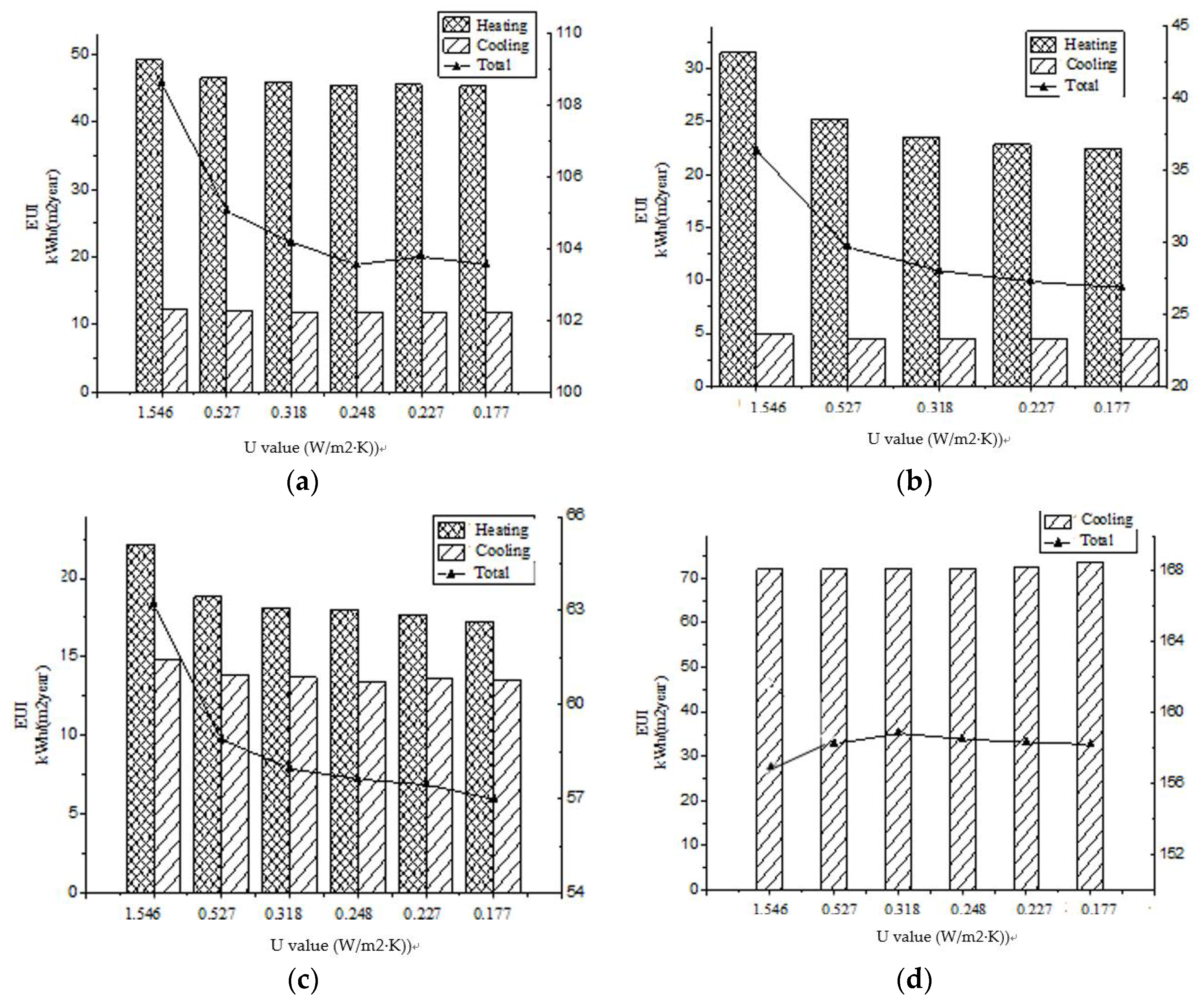
3.2. Roof Thermal Insulation
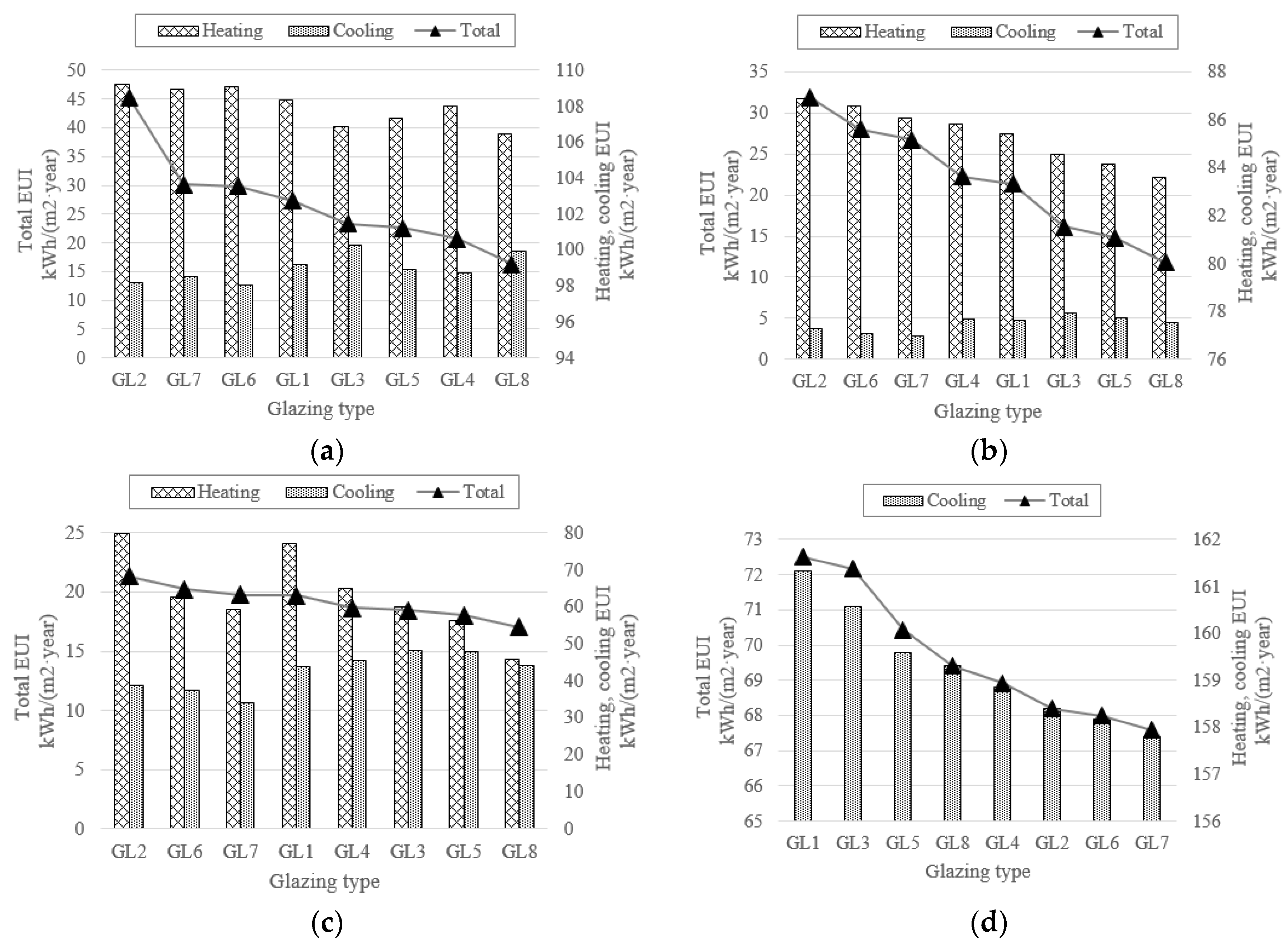
3.3. Glazing of Exterior Windows
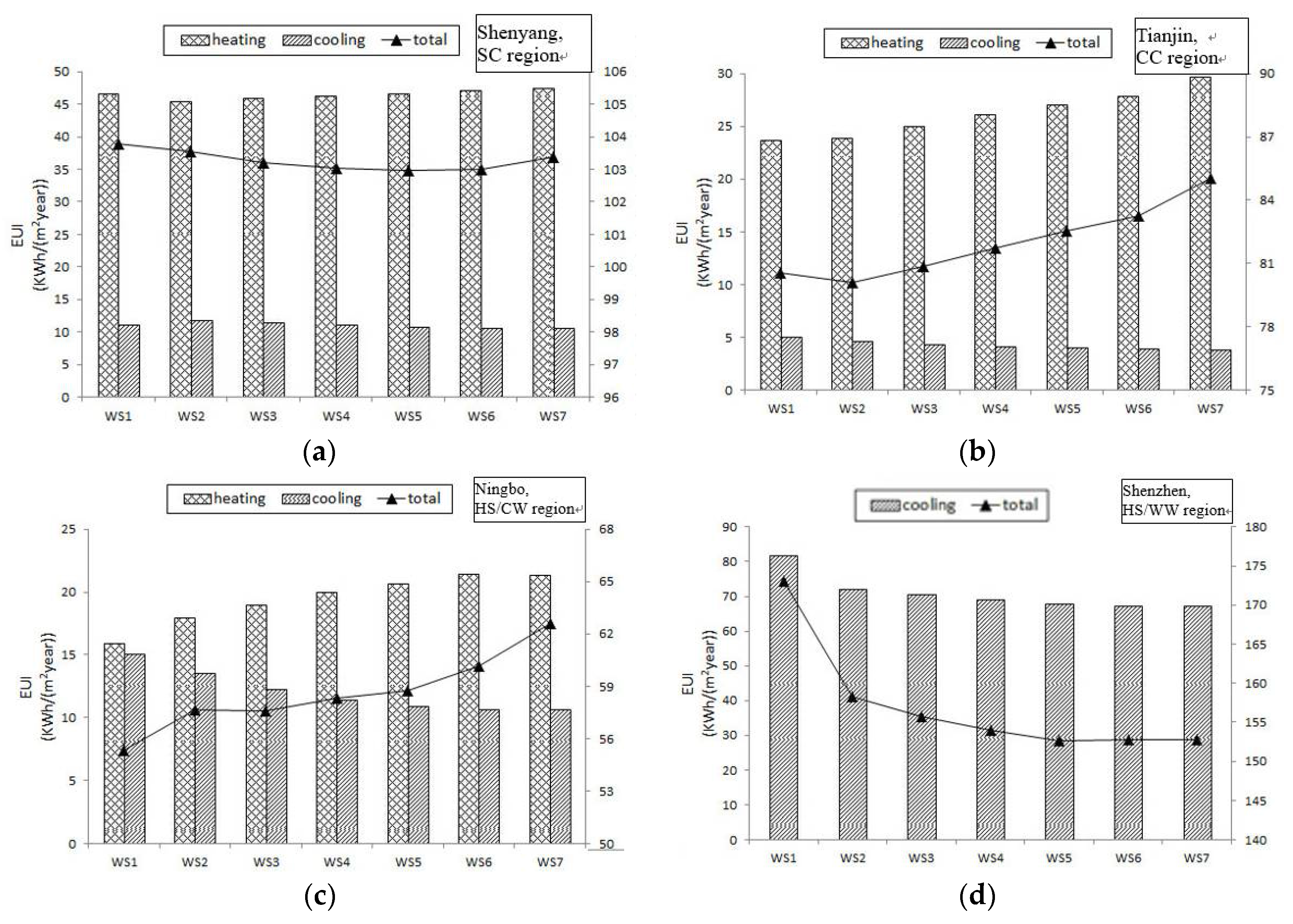
3.4. Shading System
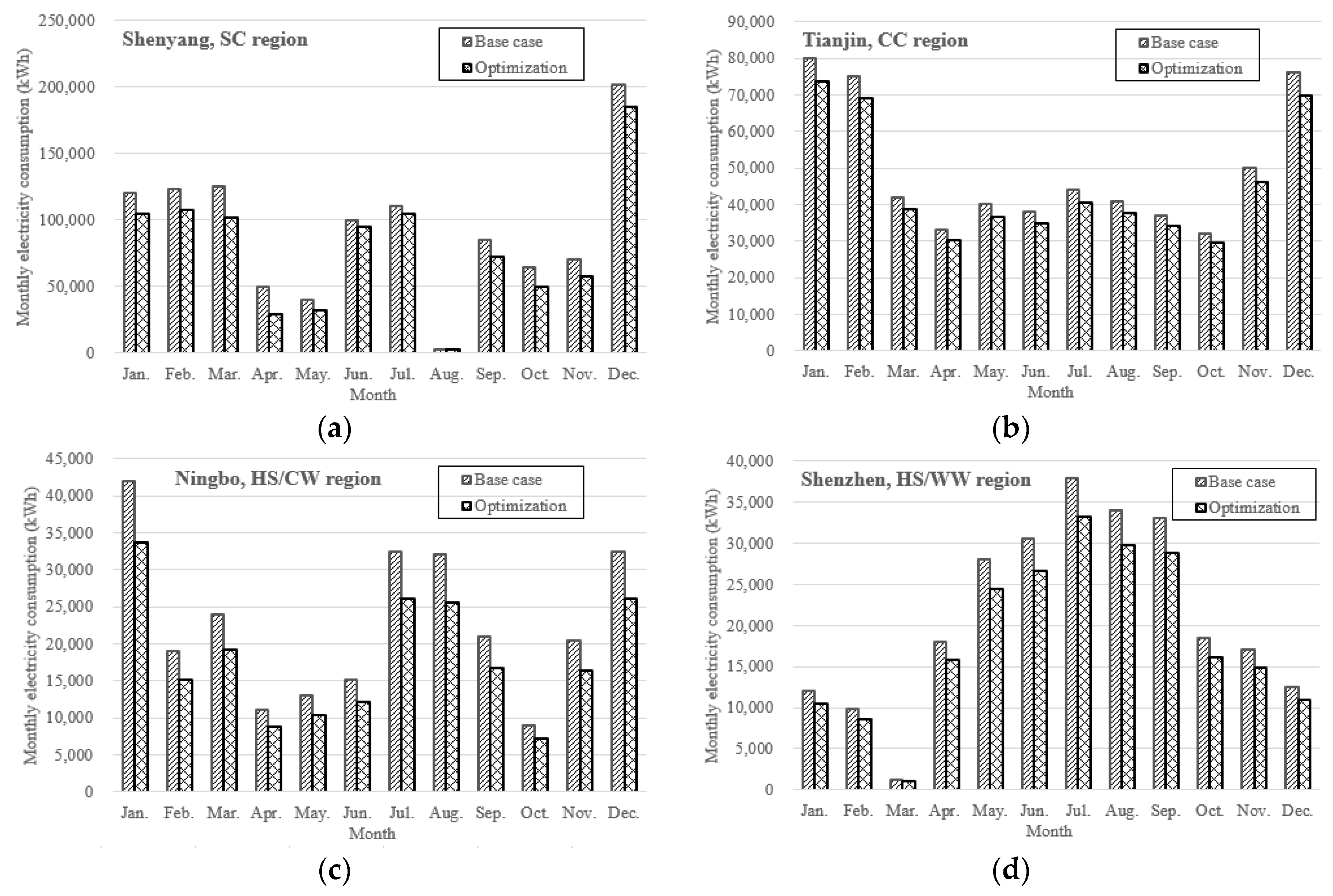
4. Priority Ranking and Optimum Energy Efficiency Strategy of PEEEMS
- Buildings in SC region: Exterior wall insulation > roof insulation > glazing; Shading is not recommended.
- Buildings in CC region: Roof insulation > exterior wall insulation > glazing > shading system.
- Buildings in HS/CW region: Glazing > roof insulation > exterior wall insulation > shading system.
- Buildings in HS/WW region: Shading system > glazing. Insulation is not recommended.
5. Discussion
5.1. Theoretical Economic Benefits
5.2. Indoor Thermal Comfort
5.3. Other Passive Building Energy Efficient Measures
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hasan, O.A.; Defer, D.; Shahrour, I. A simplified building thermal model for the optimization of energy consumption: Use of a random number generator. Energy Build. 2014, 82, 322–329. [Google Scholar] [CrossRef]
- Liu, L.; Zhao, J.; Liu, X.; Wang, Z. Energy consumption comparison analysis of high energy efficiency office buildings in typical climate zones of China and U.S. based on correction model. Energy 2014, 65, 221–232. [Google Scholar] [CrossRef]
- Hopfe, C.; McLeod, R. The Passivhaus Designer’s Manual: A Technical Guide to Low and Zero Energy Buildings; Routledge: Lindon, UK, 2015; pp. 1–2. [Google Scholar]
- Voss, K.; Herkel, S.; Pfafferott, J.; Lohnert, G.; Wagner, A. Energy efficient office buildings with passive cooling—Results and experiences from a research and demonstration programme. Sol. Energy 2007, 81, 424–434. [Google Scholar] [CrossRef]
- Gou, Z.; Lau, S.Y. Contextualizing green building rating systems: Case study of Hong Kong. Habitat Int. 2014, 44, 282–289. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, M.; Jin, W.; Xia-Bauer, C. Managing energy efficiency of buildings in China: A survey of energy performance contracting (EPC) in building sector. Energy Policy 2018, 114, 13–21. [Google Scholar] [CrossRef]
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China (MOHURD); General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China(AQSIQ). Design Standard for Energy Efficiency of Public Buildings (GB50189-2005); China Architecture & Building Press: Beijing, China, 2005; pp. 5–12. [Google Scholar]
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China (MOHURD); General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China(AQSIQ). Design Standard for Energy Efficiency of Public Buildings (GB50189-2015); China Architecture & Building Press: Beijing, China, 2015; pp. 8–13. [Google Scholar]
- Geng, G.; Wang, Z.; Zhao, J.; Zhu, N. Suitability assessment of building energy saving technologies for office buildings in cold areas of China based on an assessment framework. Energy Convers. Manag. 2015, 103, 650–664. [Google Scholar] [CrossRef]
- Lu, S.; Wang, R.; Zheng, S. Passive Optimization Design Based on Particle Swarm Optimization in Rural Buildings of the Hot Summer and Warm Winter Zone of China. Sustainability 2017, 9, 2288. [Google Scholar] [CrossRef]
- Lu, S.; Tang, X.; Ji, L.; Tu, D. Research on Energy-Saving Optimization for the Performance Parameters of Rural-Building Shape and Envelope by TRNSYS-GenOpt in Hot Summer and Cold Winter Zone of China. Sustainability 2017, 9, 294. [Google Scholar] [CrossRef]
- Zhou, S.; Zhao, J. Optimum combinations of building envelop energy-saving technologies for office buildings in different climatic regions of China. Energ. Build. 2013, 57, 103–109. [Google Scholar] [CrossRef]
- Wang, Z.; Ding, Y.; Geng, G.; Zhu, N. Analysis of energy efficiency retrofit schemes for heating, ventilating and air-conditioning systems in existing office buildings based on the modified bin method. Energy Convers. Manag. 2014, 77, 233–242. [Google Scholar] [CrossRef]
- Østergård, T.; Jensen, R.L.; Maagaar, S.E. Early Building Design: Informed decision-making by exploring multidimensional design space using sensitivity analysis. Energy Build. 2017, 142, 8–22. [Google Scholar] [CrossRef]
- Yang, L.; Lam, J.C.; Tsang, C.L. Energy performance of building envelopes in different climate zones in China. Appl. Energy 2008, 85, 800–817. [Google Scholar] [CrossRef]
- Yu, J.; Yang, C.; Tian, L. Low-energy envelope design of residential building in hot summer and cold winter zone in China. Energy Build. 2008, 40, 1536–1546. [Google Scholar] [CrossRef]
- Moon, D.; Sagisaka, M.; Tahara, K.; Tsukahara, K. Progress towards Sustainable Production: Environmental, Economic, and Social Assessments of the Cellulose Nanofiber Production Process. Sustainability 2017, 9, 2368. [Google Scholar] [CrossRef]
- Ghione, A.; Noel, B.; Vinai, P.; Demazière, C. Uncertainty and sensitivity analysis for the simulation of a station blackout scenario in the Jules Horowitz Reactor. Ann. Nucl. Energy 2017, 104, 28–41. [Google Scholar] [CrossRef]
- Shirvan, K.M.; Soroush Mirzakhanlari, S.; Mamourian, M.; Hamdeh, N.A. Numerical investigation and sensitivity analysis of effective parameters to obtain potential maximum power output: A case study on Zanjan prototype solar chimney power plant. Energy Convers. Manag. 2017, 136, 350–360. [Google Scholar] [CrossRef]
- Lam, C.; Wan, K.; Yang, L. Sensitivity analysis and energy conservation measures implications. Energy Convers. Manag. 2008, 49, 3170–3177. [Google Scholar] [CrossRef]
- Aranda, J.; Zabalza, I.; Conserva, A.; Millán, G. Analysis of Energy Efficiency Measures and Retrofitting Solutions for Social Housing Buildings in Spain as a Way to Mitigate Energy Poverty. Sustainability 2017, 9, 1869. [Google Scholar] [CrossRef]
- Stutterecker, W.; Blumel, E. Energy plus standard in buildings constructed by housing associations. Energy 2012, 48, 56–65. [Google Scholar] [CrossRef]
- Arima, Y.; Ooka, R.; Kikumoto, H. Proposal of typical and design weather year for building energy simulation. Energy Build. 2017, 139, 517–524. [Google Scholar] [CrossRef]
- ASHRAE. Measurement of Energy and Demand Savings; ASHRAE Guideline 14-2002; American Society of Heating, Refrigerating and Air-Conditioning Engineers Inc.: Atlanta, GA, USA, 2012. [Google Scholar]
- Zhang, A.; Bokel, R.; Dobbelsteen, A.; Sun, Y.; Huang, Q.; Zhang, Q. The Effect of Geometry Parameters on Energy and Thermal Performance of School Buildings in Cold Climates of China. Sustainability 2017, 9, 1708. [Google Scholar] [CrossRef]
- Ministry of Housing and Urban-Rural Development. Design Standard for Energy Efficiency of Public Buildings (GB 50189-2005); China Architecture & Building Press: Beijing, China, 2005; pp. 4–14. [Google Scholar]
- Tian, W.; Song, J.; Li, Z.; Wilde, P. Bootstrap techniques for sensitivity analysis and model selection in building thermal performance analysis. Appl. Energy 2014, 135, 320–328. [Google Scholar] [CrossRef]
- Xiao, S.; Lu, Z.; Xu, L. Multivariate sensitivity analysis based on the direction of eigen space through principal component analysis. Reliab. Eng. Syst. Saf. 2017, 165, 1–10. [Google Scholar] [CrossRef]
- Shao, Q.; Younes, A.; Fahs, M.; Mara, T.A. Bayesian sparse polynomial chaos expansion for global sensitivity analysis. Comput. Methods Appl. Mech. Eng. 2017, 318, 474–496. [Google Scholar] [CrossRef]
- Lammoglia, S.; Makowski, D.; Moeys, J.; Justes, E.; Barriuso, E.; Mamy, L. Sensitivity analysis of the STICS-MACRO model to identify cropping practices reducing pesticides losses. Sci. Total Environ. 2017, 580, 117–129. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez, G.C.; Andres, A.; Munoz, F.; Lopez, J.; Zhang, Y. Uncertainties and sensitivity analysis in building energy simulation using macroparameters. Energy Build. 2013, 67, 79–87. [Google Scholar] [CrossRef]
- Sanchez, D.G.; Lacarriere, B.; Musy, M.; Bourges, B. Application of sensitivity analysis in building energy simulations: Combining first-and second-order elementary effects methods. Energy Build. 2014, 68, 741–750. [Google Scholar] [CrossRef]
- O’Neill, Z.; Niu, F. Uncertainty and sensitivity analysis of spatio-temporal occupant behaviors on residential building energy usage utilizing Karhunen-Loève expansion. Build. Environ. 2017, 115, 157–172. [Google Scholar] [CrossRef]
- Fang, Z.; Li, N.; Li, B.; Luo, G.; Huang, Y. The effect of building envelope insulation on cooling energy consumption in summer. Energy Build. 2014, 77, 197–205. [Google Scholar] [CrossRef]
- Reda, F.; Tuominen, P.; Hedman, Å.; Ibrahim, M.G.E. Low-energy residential buildings in New Borg El Arab: Simulation and survey based energy assessment. Energy Build. 2015, 93, 65–82. [Google Scholar] [CrossRef]
- Zhang, N.; Smith, S.; Bulatov, I.; Klemes, J. Sustaining high energy efficiency in existing processes with advanced process integration technology. Appl. Energy 2013, 101, 26–32. [Google Scholar] [CrossRef]
- Laurent, M.; Fariborz, H. Multiobjective optimization of building design using TRNSYS simulations, genetic algorithm, and Artificial Neural Network. Build. Environ. 2010, 45, 739–746. [Google Scholar]
- Dhaka, S.; Mathur, J.; Garg, V. Combined effect of energy efficiency measures and thermal adaptation on air conditioned building in warm climatic conditions of India. Energy Build. 2012, 55, 351–360. [Google Scholar] [CrossRef]
- Yao, J.; Zhu, N. Evaluation of indoor thermal environmental, energy and daylighting performance of thermotropic windows. Build. Environ. 2012, 49, 283–290. [Google Scholar] [CrossRef]
- Sadeghi, S.A.; Karava, P.; Konstantzos, I.; Tzempelikos, A. Occupant interactions with shading and lighting systems using different control interfaces: A pilot field study. Build. Environ. 2016, 97, 177–195. [Google Scholar] [CrossRef]
- Salvalai, G.; Pfafferott, J.; Sesana, M.M. Assessing energy and thermal comfort of different low-energy cooling concepts for non-residential buildings. Energy Convers. Manag. 2013, 76, 332–341. [Google Scholar] [CrossRef]
- Pfafferott, J.; Herkel, S.; Wambsganß, M. Design, monitoring and evaluation of a low energy office building with passive cooling by night ventilation. Energy Build. 2004, 36, 455–465. [Google Scholar] [CrossRef]
- Xie, X.; Gou, Z. Building performance simulation as an early intervention or late verification in architectural design: Same performance outcome but different design solutions. J. Green Build. 2017, 12, 45–61. [Google Scholar] [CrossRef]
- Friess, W.A.; Rakhshan, K. A review of passive envelope measures for improved building energy efficiency in the UAE. Renew. Sustain. Energy Rev. 2017, 72, 485–496. [Google Scholar] [CrossRef]
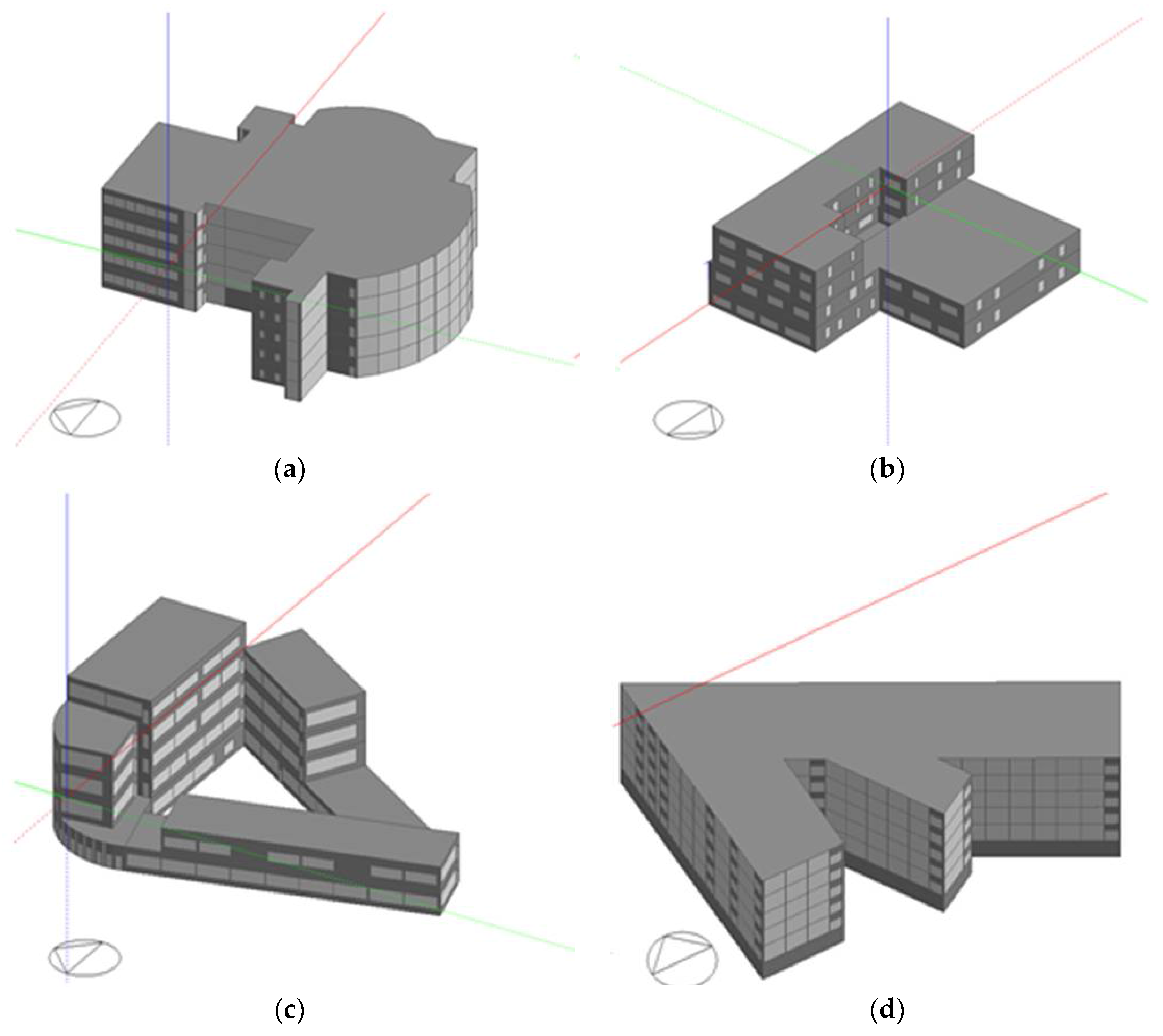
| Name | Indexes | Typical City | |
|---|---|---|---|
| Leading Index | Auxiliary Index | ||
| Severe cold (SC) regions | Average temperature of the coldest month ≤ −10 °C | HDD ≥ 145 °C·day | Shenyang |
| Cold (CC) regions | −10 °C <Average temperature of the coldest month ≤ 0 °C | 90 °C·day ≤ HDD ≤ 45 °C·day | Tianjin |
| Hot summer and cold winter (HS/CW) regions | −10 °C < Average temperature of the coldest month ≤ 0 °C; 25 °C ≤ Average temperature of the hottest month ≤ 30 °C | HDD ≤ 90 °C·day; 40 °C·day ≤ CDD ≤ 110 °C·day | Ningbo |
| Hot summer and warm winter (HS/WW) regions | Average temperature of the coldest month > 10 °C; 25 °C < Average temperature of the hottest month ≤ 29 °C | 100 °C·day ≤ CDD ≤ 200 °C·day | Shenzhen |
| Temperate regions (not discussed) | 0 °C <Average temperature of the coldest month ≤ 13 °C; 18 °C ≤ Average temperature of the hottest month ≤ 25 °C | HDD ≤ 90 °C·day | Sanya |
| Location | Shenyang | Tianjin | Ningbo | Shenzhen |
|---|---|---|---|---|
| Climate parameters of typical meteorological year | ||||
| Climate region | Severe cold region | Cold region | Hot summer and cold winter region | Hot summer and warm winter region |
| Average temperature of the coldest month (Jan.) | −11.5 °C | −2.4 °C | 3.7 °C | 16.2 °C |
| Average temperature of the warmest month (Jul.) | 24.5 °C | 26.1 °C | 27.8 °C | 29.8 °C |
| HDD18 (°C·day) | 4062 | 2738 | 981 | 272 |
| CDD26 (°C·day) | 486 | 566 | 1650 | 2141 |
| Building information | ||||
| Gross floor area (m2) | 10,997.38 | 7525 | 4760 | 16,600 |
| Building type | Office | Office | Office | Office |
| Building height (m) | 19.8 | 23.85 | 20.2 | 20.5 |
| Number of floors | 5 | 6 | 5 | 5 |
| Floor height (m) | 3.9 | 3.5 | 3.5 | 3.9 |
| Building operation information | ||||
| Working time | 8:00–17:00 | 9:00–18:00 | 9:00–18:00 | 9:00–17:30 |
| Occupant density of working zone (people/m2) | 0.08 | 0.125 | 0.15 | 0.25 |
| Commonly occupant number | Around 650 | Around 400 | Around 300 | Around 700 |
| Indoor equipment power density (W/m2) | 6.2 | 20 | 6 | 20 |
| Lighting density (W/m2) | 3.8 | 9 | 4 | 5.2 |
| Envelop form and thermal parameters | ||||
| Exterior wall | ||||
| Form | EPS | EPS | EPS | EPS |
| EPS layer thickness (mm) | 60 | 80 | 115 | 10 |
| U value of the exterior walls (W/m2·K) | 0.51 | 0.39 | 0.295 | 1.26 |
| Roof | ||||
| Form | EPS | EPS | EPS | EPS |
| EPS layer thickness (mm) | 135 | 70 | 135 | 30 |
| U value of the roof (W/m2·K) | 0.25 | 0.42 | 0.248 | 0.67 |
| Exterior window | ||||
| Glazing type | Double layers, reflective + Clear 6 mm/13 mm air | Double layers, electrochromism +Clear 6 mm/13 mm Air | Double layers, low-E + 3 mm/6 mm air | Double layers, reflective + Clear 6 mm/13 mm air |
| Solar heat gain coefficient (SHGC) | 0.176 | 0.6 | 0.687 | 0.176 |
| U value of the windows (W/m2·K) | 2.2 | 1.72 | 2.58 | 2.2 |
| Ratio of window to wall (%) | 20 | 25 | 50 | 90 |
| Shading | Interior shading of diffusing blinds, no exterior shading | Interior shading of diffusing blinds, no exterior shading | Interior shading of diffusing blinds, exterior shading of 0.5 m overhanging board | Interior shading of diffusing blinds, exterior shading of 1.0 m louver |
| Indoor design parameters | ||||
| Indoor temperature in summer (°C) | 26 | 26 | 26 | 26 |
| Indoor relative humidity in summer (%) | 55 | 55 | 60 | 60 |
| Indoor temperature in winter (°C) | 20 | 20 | 20 | 20 |
| Indoor relative humidity in winter (%) | 35 | 35 | 35 | 35 |
| Design fresh air volume (m3/person/h) | 30 | 30 | 30 | 30 |
| Heating and cooling information | ||||
| Cooling supply period | 1 June–30 September | 1 June–30 September | 1 June–30 September | 1 April–1 November |
| Heating supply period | 1 November–31 March | 15 November–15 March | 1 December–15 February | none |
| Heating and cooling unit type | Ground source heat pump (GSHP) | GSHP | VAV system | Electrical air-handling unit |
| Design systematic COP | 5.3 | 4.5 | 3.3. | 2.5 |
| Total energy consumption | ||||
| Annual energy consumption (kWh) | 1,099,123 | 612,427.38 | 283,124.8 | 2,544,400 |
| Annual EUI (kWh/ (m2·a)) | 99.94 | 81.37 | 59.48 | 153.27 |
| Criteria | ASHRAE | Shenyang | Tianjin | Ningbo | Shenzhen |
|---|---|---|---|---|---|
| NMBE (%) | ±5 | 2.84 | 1.84 | 3.40 | −3.54 |
| CVRMSE (%) | ±15 | 12.04 | 9.11 | 12.16 | 11.16 |
| Insulation Layer Thickness (mm) | U-Value (W/(m2·K)) | HVAC EUI (kWh/(m2·a)) | Total EUI (kWh/(m2·a)) | Sensitivity Coefficient to Total EUI |
|---|---|---|---|---|
| Building in Shenyang (SC region) | ||||
| 0 | 1.932 | 62.27 | 108.92 | 0.018550 |
| 20 | 0.983 | 58.96 | 105.47 | 0.019911 |
| 40 | 0.659 | 57.73 | 104.17 | 0.020317 |
| 60 (base case) | 0.509 | 57.17 | 103.55 | - |
| 80 | 0.397 | 56.67 | 103.04 | 0.022383 |
| 100 | 0.331 | 56.39 | 102.74 | 0.022368 |
| 120 | 0.284 | 56.19 | 102.52 | 0.022502 |
| Average | - | - | - | 0.022326 |
| Building in Tianjin (CC region) | ||||
| 0 | 1.932 | 35.84 | 87.73 | 0.024403 |
| 20 | 0.983 | 31.50 | 83.17 | 0.025967 |
| 40 | 0.659 | 29.86 | 81.48 | 0.026585 |
| 60 | 0.509 | 29.00 | 80.59 | 0.026656 |
| 80 (base case) | 0.397 | 28.43 | 80.01 | - |
| 100 | 0.331 | 28.11 | 79.70 | 0.026274 |
| 120 | 0.284 | 27.85 | 79.42 | 0.027102 |
| Average | - | - | - | 0.026709 |
| Building in Ningbo (HS/CW region) | ||||
| 0 | 1.932 | 37.19 | 63.35 | 0.016619 |
| 20 | 0.983 | 34.16 | 60.32 | 0.017150 |
| 40 | 0.659 | 33.14 | 59.30 | 0.018168 |
| 60 | 0.509 | 32.53 | 58.69 | 0.017485 |
| 80 | 0.397 | 32.10 | 58.26 | 0.012814 |
| 100 | 0.331 | 32.08 | 58.24 | 0.034515 |
| 115 (base case) | 0.295 | 31.91 | 58.00 | - |
| 120 | 0.284 | 31.79 | 57.95 | 0.020410 |
| Average | - | - | - | 0.019594 |
| Building in Shenzhen (HS/WW region) | ||||
| 0 | 1.932 | 72.01 | 158.26 | 0.000201 |
| 10 (base case) | 1.259 | 72.02 | 158.25 | - |
| 20 | 0.983 | 72.16 | 158.41 | −0.004760 |
| 40 | 0.659 | 72.23 | 158.48 | −0.003110 |
| 60 | 0.509 | 72.26 | 158.52 | −0.002860 |
| 80 | 0.397 | 72.31 | 158.58 | −0.003070 |
| 100 | 0.331 | 72.32 | 158.60 | −0.003000 |
| 120 | 0.284 | 72.35 | 158.64 | −0.003170 |
| Average | - | - | - | −0.002820 |
| Insulation Layer Thickness (mm) | U-Value (W/(m2·K)) | HVAC EUI (kWh/(m2·a)) | Total EUI (kWh/(m2·a)) | Sensitivity Coefficient to Total EUI |
|---|---|---|---|---|
| Building in Shenyang (SC region) | ||||
| 0 | 1.546 | 61.51 | 106.31 | 0.009355 |
| 50 | 0.527 | 58.50 | 105.05 | 0.012876 |
| 100 | 0.318 | 57.73 | 103.78 | 0.007896 |
| 135 (base case) | 0.248 | 57.39 | 103.55 | - |
| 150 | 0.227 | 57.27 | 102.98 | 0.065007 |
| 200 | 0.177 | 57.18 | 101.55 | 0.101196 |
| Average | - | - | - | 0.039261 |
| Building in Tianjin (CC region) | ||||
| 0 | 1.546 | 35.34 | 85.71 | 0.040538 |
| 50 | 0.527 | 32.64 | 83.12 | 0.054323 |
| 70 (base case) | 0.42 | 30.43 | 81.12 | - |
| 100 | 0.318 | 29.06 | 79.34 | 0.034660 |
| 150 | 0.227 | 28.26 | 78.52 | 0.040559 |
| 200 | 0.177 | 27.84 | 78.06 | 0.042139 |
| Average | - | - | - | 0.042444 |
| Building in Ningbo (HS/CW region) | ||||
| 0 | 1.546 | 36.97 | 63.20 | 0.018469 |
| 50 | 0.527 | 32.66 | 58.89 | 0.019419 |
| 100 | 0.318 | 31.73 | 57.95 | 0.020028 |
| 135 (base case) | 0.248 | 31.40 | 57.63 | - |
| 150 | 0.227 | 31.22 | 57.45 | 0.036803 |
| 200 | 0.177 | 30.76 | 56.98 | 0.039084 |
| Average | - | - | - | 0.026761 |
| Building in Shenzhen (HS/WW region) | ||||
| 0 | 1.546 | 71.94 | 156.66 | 0.016534 |
| 30 (base case) | 0.671 | 72.02 | 158.25 | - |
| 50 | 0.527 | 72.16 | 158.83 | −0.017160 |
| 100 | 0.318 | 72.24 | 158.52 | −0.003180 |
| 150 | 0.227 | 72.36 | 158.33 | −0.000810 |
| 200 | 0.177 | 73.68 | 158.22 | 0.000271 |
| Average | - | - | - | −0.000870 |
| No. | Layer | Specification | SHGC | U-Value (W/m2·K) | Visible Transmittance | Total EUI (kWh/(m2·a)) | |||
|---|---|---|---|---|---|---|---|---|---|
| Shenyang | Tianjin | Ningbo | Shenzhen | ||||||
| GL1 | Single | Clear | 0.810 | 6.121 | 0.898 | 102.76 | 83.32 | 63.10 | 159.31 |
| GL2 | Single | Reflective | 0.235 | 5.005 | 0.080 | 108.50 | 86.93 | 68.35 | 175.65 |
| GL3 | Single | Low-E | 0.710 | 4.233 | 0.811 | 101.46 | 81.53 | 59.06 | 160.07 |
| GL4 | Double | Green 6 mm/6 mm Air | 0.490 | 3.157 | 0.664 | 100.64 | 83.63 | 59.72 | 155.94 |
| GL5 | Double | Low-E+Clear 3 mm/6 mm Air | 0.687 | 2.577 | 0.769 | 101.22 | 81.09 | 57.63 (base case) | 158.40 |
| GL6 | Double | Reflective+Clear 6 mm/13 mm Air | 0.176 | 2.208 | 0.073 | 103.55 (base case) | 85.59 | 64.74 | 158.25 (base case) |
| GL7 | Double | Electrochromism +Clear 6 mm/13 mm Air | 0.155 | 1.772 | 0.752 | 103.66 | 85.18 (base case) | 63.21 | 158.03 |
| GL8 | Triple | Low-E+Clear+Clear 3 mm/13 mm Air | 0.574 | 1.270 | 0.698 | 99.22 | 80.04 | 54.48 | 157.01 |
| Case Building | Building in Shenyang | Building in Tianjin | Building in Ningbo | Building in Shenzhen | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Glazing Parameter | U-Value | SHGC | Visible Transmittance | U-Value | SHGC | Visible Transmittance | U-Value | SHGC | Visible Transmittance | U-Value | SHGC | Visible Transmittance |
| Correlation coefficient R2 | 0.943 | 0.963 | 0.972 | 0.903 | ||||||||
| Standard weight | 1.116 | −0.561 | 0.169 | 0.841 | −0.858 | −0.137 | 0.875 | −0.635 | −0.247 | −0.037 | −0.888 | −0.345 |
| Significance coefficient | 0.001 | 0.005 | 0.192 | 0.001 | 0.000 | 0.193 | 0.000 | 0.001 | 0.031 | 0.865 | 0.007 | 0.139 |
| Significant level | *** | *** | * | *** | *** | * | *** | *** | ** | * | *** | * |
| No. | U-Value (W/(m2·K)) | SHGC | Total EUI (kWh/(m2·a)) | Sensitivity Coefficient to Total EUI (U Value) | Sensitivity Coefficient to Total EUI (SHGC) | Weighted Sensitivity Coefficient to Total EUI |
|---|---|---|---|---|---|---|
| Building in Shenyang (SC region) | ||||||
| GL5 | 2.577 | 0.687 | 101.22 | −0.134210 | −0.089853 | −0.119371 |
| GL4 | 3.157 | 0.490 | 100.64 | −0.065400 | −0.080502 | −0.070452 |
| GL3 | 4.233 | 0.710 | 101.46 | −0.021960 | −0.083099 | −0.042413 |
| GL1 | 6.121 | 0.810 | 102.76 | −0.004290 | −0.035381 | −0.014691 |
| GL7 | 1.772 | 0.155 | 103.66 | −0.00566 | 0.000935 | −0.003454 |
| GL6 (base case) | 2.208 | 0.176 | 103.55 | - | - | - |
| GL8 | 1.270 | 0.574 | 99.22 | 0.098368 | −0.142327 | 0.017849 |
| GL2 | 5.005 | 0.235 | 108.50 | 0.037802 | 0.060916 | 0.045534 |
| Average | −0.013620 | −0.052759 | −0.026714 | |||
| Building in Tianjin (CC region) | ||||||
| GL5 | 2.577 | 0.687 | 81.09 | −0.105640 | −0.223553 | −0.165186 |
| GL3 | 4.233 | 0.710 | 81.53 | −0.030840 | −0.205070 | −0.118827 |
| GL8 | 1.270 | 0.574 | 80.04 | 0.105335 | −0.237813 | −0.067956 |
| GL1 | 6.121 | 0.810 | 83.32 | −0.00886 | −0.116659 | −0.063299 |
| GL4 | 3.157 | 0.490 | 83.63 | −0.023260 | −0.058591 | −0.041102 |
| GL7 (base case) | 1.772 | 0.155 | 85.18 | - | - | - |
| GL6 | 2.208 | 0.176 | 85.59 | 0.019511 | 0.005439 | 0.012405 |
| GL2 | 5.005 | 0.235 | 86.93 | 0.011293 | 0.030521 | 0.021003 |
| Average | −0.004640 | −0.100716 | −0.060423 | |||
| Building in Ningbo (HS/CW region) | ||||||
| GL6 | 2.208 | 0.176 | 64.74 | −0.862110 | 0.028135 | −0.487735 |
| GL7 | 1.772 | 0.155 | 63.21 | −0.310460 | 0.019917 | −0.171527 |
| GL5 (base case) | 2.577 | 0.687 | 57.63 | - | - | - |
| GL3 | 4.233 | 0.710 | 59.06 | 0.038679 | 0.025023 | 0.032936 |
| GL8 | 1.270 | 0.574 | 54.48 | 0.107770 | −0.048309 | 0.042134 |
| GL1 | 6.121 | 0.810 | 63.10 | 0.069086 | 0.102208 | 0.083015 |
| GL4 | 3.157 | 0.490 | 59.72 | 0.161360 | 0.024961 | 0.104000 |
| GL2 | 5.005 | 0.235 | 68.35 | 0.197405 | 0.053650 | 0.136952 |
| Average | −0.085470 | 0.025698 | −0.037175 | |||
| No. | SHGC | Total EUI (kWh/(m2·a)) | Sensitivity Coefficient to Total EUI (SHGC) | Weighted Sensitivity Coefficient to Total EUI |
|---|---|---|---|---|
| GL1 | 0.81 | 161.63 | 0.005805 | 0.005805 |
| GL3 | 0.71 | 161.37 | 0.006372 | 0.006372 |
| GL4 | 0.49 | 158.94 | 0.002933 | 0.002933 |
| GL2 | 0.235 | 158.4 | 0.002825 | 0.002825 |
| GL8 | 0.574 | 159.31 | 0.002442 | 0.002442 |
| GL5 | 0.687 | 160.07 | 0.001916 | 0.001916 |
| GL7 | 0.155 | 157.94 | 0.001645 | 0.016450 |
| GL6 (base case) | 0.176 | 158.25 | - | - |
| Average | 0.005821 | 0.005821 | ||
| No. | Interior Shading | Exterior Shading | SD | OSC | Total EUI (kWh/(m2·a)) | Sensitivity Coefficient to Total EUI |
|---|---|---|---|---|---|---|
| Building in Shenyang (SC region) | ||||||
| WS1 | No shading | No shading | 0.90 | 0.52 | 103.80 | −0.029607 |
| WS2 (base case) | Diffusing blinds | No shading | 0.89 | 0.46 | 103.58 | - |
| WS3 | Diffusing blinds | 0.5 m Overhanging board | 0.84 | 0.44 | 103.20 | −0.007712 |
| WS4 | Diffusing blinds | 1.0 m Overhanging board | 0.72 | 0.38 | 103.05 | −0.019442 |
| WS5 | Diffusing blinds | 1.5 m Overhanging board | 0.65 | 0.34 | 102.96 | −0.013560 |
| WS6 | Diffusing blinds | 2.0 m Overhanging board | 0.61 | 0.32 | 103.00 | −0.013058 |
| WS7 | Diffusing blinds | 1.0 m Louver | 0.19 | 0.10 | 103.36 | −0.005902 |
| Average | - | - | - | −0.014880 | ||
| Building in Tianjin (CC region) | ||||||
| WS1 | No shading | No shading | 0.90 | 0.52 | 80.58 | 0.054403 |
| WS2 (base case) | Diffusing blinds | No shading | 0.89 | 0.46 | 80.01 | - |
| WS3 | Diffusing blinds | 0.5 m Overhanging board | 0.84 | 0.44 | 80.59 | −0.144210 |
| WS4 | Diffusing blinds | 1.0 m Overhanging board | 0.72 | 0.38 | 81.39 | −0.093719 |
| WS5 | Diffusing blinds | 1.5 m Overhanging board | 0.65 | 0.34 | 82.15 | −0.098753 |
| WS6 | Diffusing blinds | 2.0 m Overhanging board | 0.61 | 0.32 | 82.84 | −0.113813 |
| WS7 | Diffusing blinds | 1.0 m Louver | 0.19 | 0.10 | 84.62 | −0.073341 |
| Average | - | - | - | −0.078239 | ||
| Building in Ningbo (HS/CW region) | ||||||
| WS1 | No shading | No shading | 0.90 | 0.52 | 58.34 | 0.079200 |
| WS2 | Diffusing blinds | No shading | 0.89 | 0.46 | 57.98 | 0.213512 |
| WS3 (base case) | Diffusing blinds | 0.5 m Overhanging board | 0.86 | 0.45 | 57.63 | - |
| WS4 | Diffusing blinds | 1.0 m Overhanging board | 0.76 | 0.39 | 57.30 | 0.045906 |
| WS5 | Diffusing blinds | 1.5 m Overhanging board | 0.69 | 0.36 | 56.78 | 0.071568 |
| WS6 | Diffusing blinds | 2.0 m Overhanging board | 0.65 | 0.34 | 56.13 | 0.104850 |
| WS7 | Diffusing blinds | 1.0 m Louver | 0.19 | 0.10 | 55.59 | 0.045357 |
| Average | - | - | - | 0.093399 | ||
| Building in Shenzhen (HS/WW region) | ||||||
| WS1 | No shading | No shading | 0.90 | 0.42 | 173.00 | 0.031529 |
| WS2 | Diffusing blinds | No shading | 0.89 | 0.36 | 158.25 | 0.009887 |
| WS3 | Diffusing blinds | 0.5 m Overhanging board | 0.87 | 0.35 | 155.76 | 0.005545 |
| WS4 | Diffusing blinds | 1.0 m Overhanging board | 0.77 | 0.30 | 153.99 | 0.002643 |
| WS5 | Diffusing blinds | 1.5 m Overhanging board | 0.71 | 0.27 | 153.27 | 0.001224 |
| WS6 | Diffusing blinds | 2.0 m Overhanging board | 0.67 | 0.25 | 152.81 | 0.000105 |
| WS7 (base case) | Diffusing blinds | 1.0 m Louver | 0.19 | 0.14 | 152.77 | - |
| Average | - | - | - | 0.008489 | ||
| PEEEM | Index | Building in Shenyang, SC Region | Building in Tianjin, CC Region | Building in Ningbo, HS/CW Region | Building in Shenzhen, HS/WW Region |
|---|---|---|---|---|---|
| Exterior wall | Type | 120 mm EPS | 120 mm EPS | 100 mm EPS | No exterior wall insulation |
| U-value (W/(m2·K)) | 0.284 | 0.284 | 0.331 | 1.932 | |
| Energy efficiency rate (%) | 5.88 | 9.47 | - | - | |
| Sensitivity coefficient | 0.022502 | 0.027102 | 0.034515 | 0.000201 | |
| Roof | Type | 200 mm EPS | 200 mm EPS | 200 mm EPS | 30 mm EPS |
| U-value (W/(m2·K)) | 0.177 | 0.177 | 0.177 | 0.671 | |
| Energy efficiency rate (%) | 7.03 | 34.84 | 16.8 | - | |
| Sensitivity coefficient | 0.101196 | 0.042139 | 0.039084 | - | |
| Glazing | Type | Double layers, low-E + Clear 3 mm/6 mm Air | Double layers, low-E + Clear 3 mm/6 mm Air | Double layers, low-E + Clear 3 mm/6 mm Air /or low-E | Double layers, low-E + Clear 3 mm/6 mm Air |
| U-value (W/(m2·K)) | 0.687 | 0.687 | 0.574/4.233 | 0.687 | |
| SHGC | 4.233 | 4.233 | 1.270/0.710 | 4.233 | |
| Visible transmittance | 0.769 | 0.769 | 0.698/0.811 | 0.769 | |
| Sensitivity coefficient (U-value) | −0.134210 | −0.105640 | −/0.038679 | - | |
| Sensitivity coefficient (SHGC) | −0.089853 | −0.223553 | −/0.025023 | −0.507640 | |
| Weighted sensitivity coefficient | −0.119371 | −0.165186 | −/0.032936 | −0.507640 | |
| Shading | Type | No shading | Diffusing blinds of interior shading | Diffusing blinds, 2.0 m overhanging board | Diffusing blinds, 1.0 m louver |
| OSC | 0.52 | 0.46 | 0.34 | 0.25 | |
| Sensitivity coefficient | −0.029607 | - | 0.104850 | - | |
| Total energy efficiency rate (%) | 9.44 | 7.75 | 20.87 | 13.27 | |
| PEEEMs | Thermal Performance Property | Buildings in SC Region | Buildings in CC Region | Buildings in HS/CW Region | Buildings in HS/WW Region |
|---|---|---|---|---|---|
| Exterior walls | U-value (W/(m2·K)) | ≤0.331 | ≤0.331 | ≤0.331 | - |
| Roof | U-value (W/(m2·K)) | ≤0.318 | ≤0.318 | ≤0.318 | - |
| Glazing type | U-value (W/(m2·K)) | ≤2.577 | ≤2.577 | ≤4.233 | - |
| SHGC | ≤0.687 | ≤0.687 | Around 0.7 | ≤0.687 | |
| Shading system | OSC | - | - | ≤0.35 | ≤0.35 |
| Building | Building in Shenyang | Building in Tianjin | Building in Ningbo | Building in Shenzhen |
|---|---|---|---|---|
| Energy consumption of initial strategy (kWh/m2) | 103.55 | 80.01 | 57.63 | 158.25 |
| Energy consumption of optimum strategy (kWh/m2) | 93.77 | 73.81 | 45.60 | 137.24 |
| Energy-saving rate (%) | 9.44 | 7.75 | 20.87 | 13.27 |
| Average electricity price (RMB/kWh) | 0.8068 | 0.9925 | 0.8929 | 0.8512 |
| Incremental investment (RMB/m2) | 8.70 | 4.24 | 15.60 | 1.87 |
| Insulation of exterior walls (RMB per insulation area) | 45 | 30 | 0 | 0 |
| Insulation of roof (RMB per insulation area) | 0 | 0 | 65 | 0 |
| Glazing of exterior windows (RMB per window area) | 30 | 30 | 0 | 30 |
| Shading (RMB per shading material area) | 0 | 0 | 40 | 0 |
| Theoretical payback period (year) | 1.10 | 0.69 | 1.45 | 0.10 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Zhao, J. Optimization of Passive Envelop Energy Efficient Measures for Office Buildings in Different Climate Regions of China Based on Modified Sensitivity Analysis. Sustainability 2018, 10, 907. https://doi.org/10.3390/su10040907
Wang Z, Zhao J. Optimization of Passive Envelop Energy Efficient Measures for Office Buildings in Different Climate Regions of China Based on Modified Sensitivity Analysis. Sustainability. 2018; 10(4):907. https://doi.org/10.3390/su10040907
Chicago/Turabian StyleWang, Zhaoxia, and Jing Zhao. 2018. "Optimization of Passive Envelop Energy Efficient Measures for Office Buildings in Different Climate Regions of China Based on Modified Sensitivity Analysis" Sustainability 10, no. 4: 907. https://doi.org/10.3390/su10040907
APA StyleWang, Z., & Zhao, J. (2018). Optimization of Passive Envelop Energy Efficient Measures for Office Buildings in Different Climate Regions of China Based on Modified Sensitivity Analysis. Sustainability, 10(4), 907. https://doi.org/10.3390/su10040907






