Carbon Emission Reduction with Regard to Retailer’s Fairness Concern and Subsidies
Abstract
:1. Introduction
- How has the carbon emission reduction rate of green products changed with regard to the subsidy and fairness concern?
- How has the government subsidy types (fixed subsidy and discount subsidy) affected the manufacturer’s and retailer’s strategies?
- How has the fairness concern affected the manufacturer’s and retailer’s profits when there is a government subsidy?
2. Literature Review
2.1. CEA and Government Policies
2.2. Supply Chain and Fairness Concern
3. Problem Assumptions and Benchmark Model
3.1. Problem Assumptions
3.2. Benchmark Model
4. Retailer’s Fairness Concern and Government Subsidy
4.1. Fairness Concern
- (i)
- When , then the retailer's profit increases with ; and when , then the retailer's profit decreases with ;
- (ii)
- The optimal manufacturer’s profit decreases with .
4.2. Fairness Concern and Government Subsidy
4.2.1. F-Type Subsidy
- (i)
- The optimal carbon emission reduction rate of the green product, wholesale price, and retail price increase with CEA;
- (ii)
- The manufacturer’s and retailer’s profits increase with CEA.
- (i)
- The optimal carbon emission reduction rate, optimal wholesale price, and retail price decrease with ;
- (ii)
- The manufacturer’s profit decreases with ;
- (iii)
- the retailer’s profit increases with when and decreases when .
- (i)
- The optimal carbon emission reduction rate, wholesale price, and retail price increase with the fixed subsidy ;
- (ii)
- The manufacturer’s and retailer’s profits increase with the fixed subsidy .
4.2.2. D-Type Subsidy
- (i)
- The optimal carbon emission reduction rate of green products, wholesale price, and retail price increase with CEA;
- (ii)
- The manufacturer’s and retailer’s profits increase with CEA.
- (i)
- The optimal carbon emission reduction rate, optimal wholesale price, and retail price decrease with ;
- (ii)
- The manufacturer’s profit decreases with ;
- (iii)
- the retailer’s profit increases with when and decreases when .
- (i)
- The optimal carbon emission reduction rate, wholesale price, and retail price increase with the subsidy coefficient ;
- (ii)
- The manufacturer’s and retailer’s profits increase with government subsidy coefficient .
5. Numerical Examples
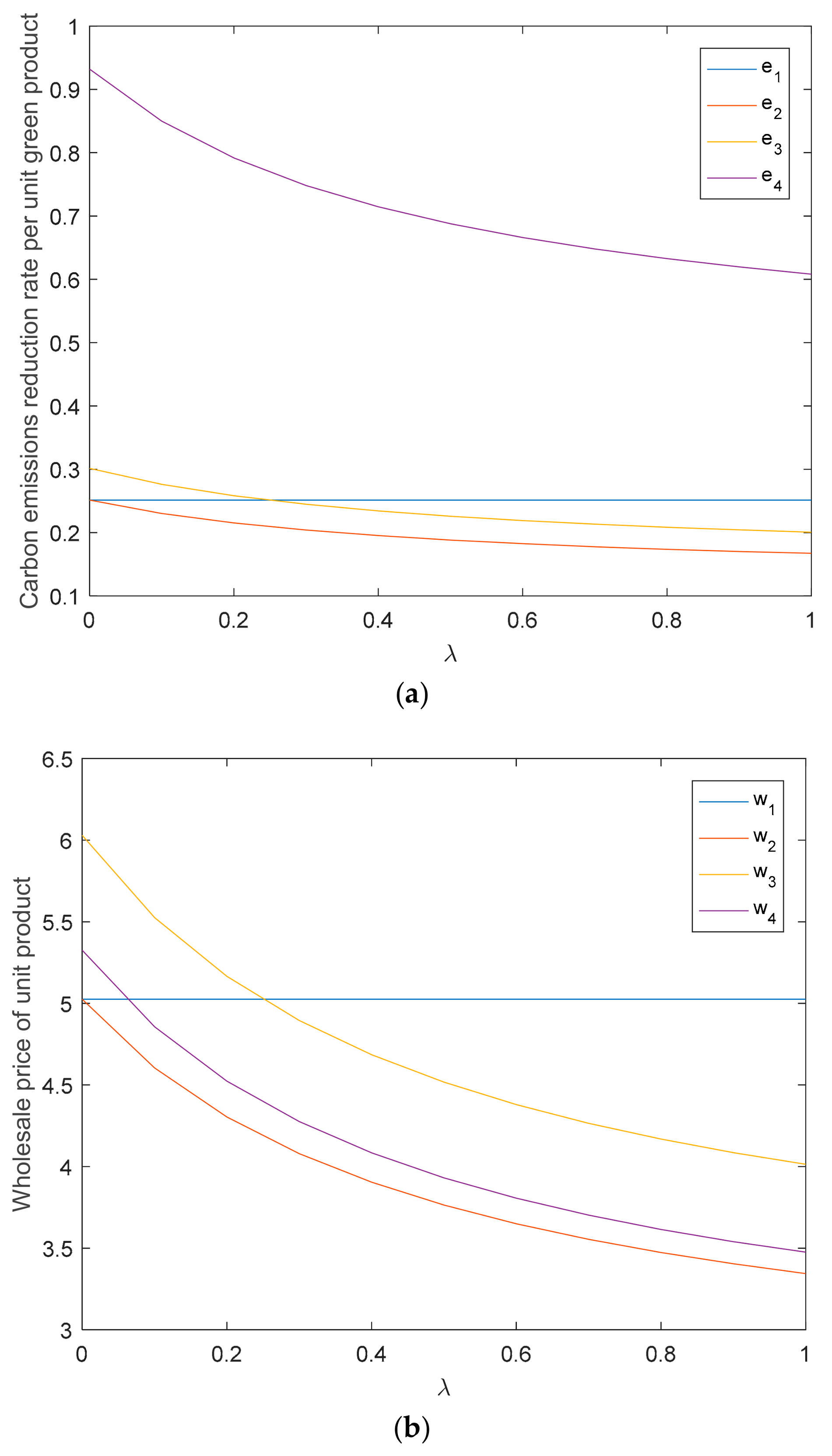
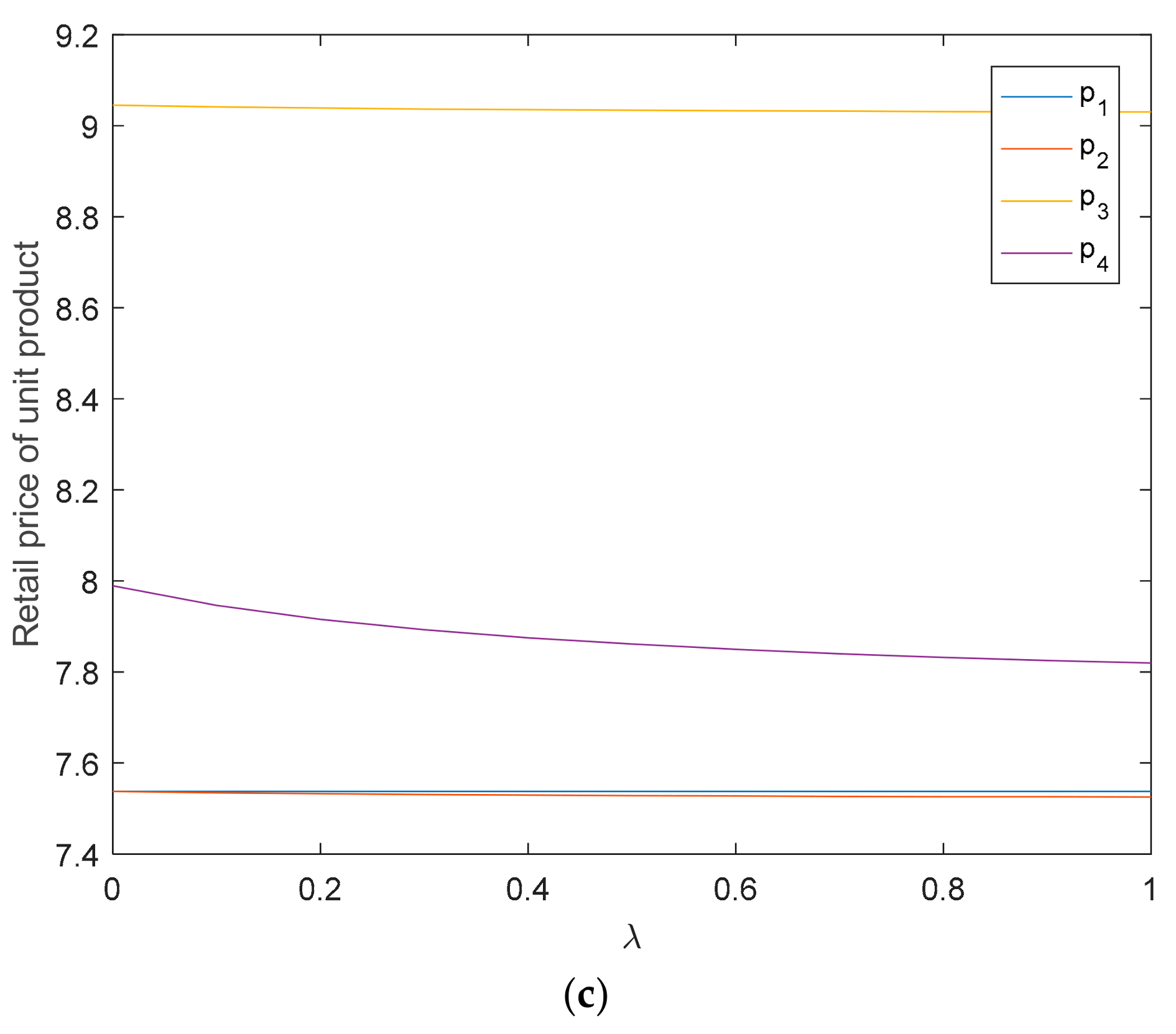
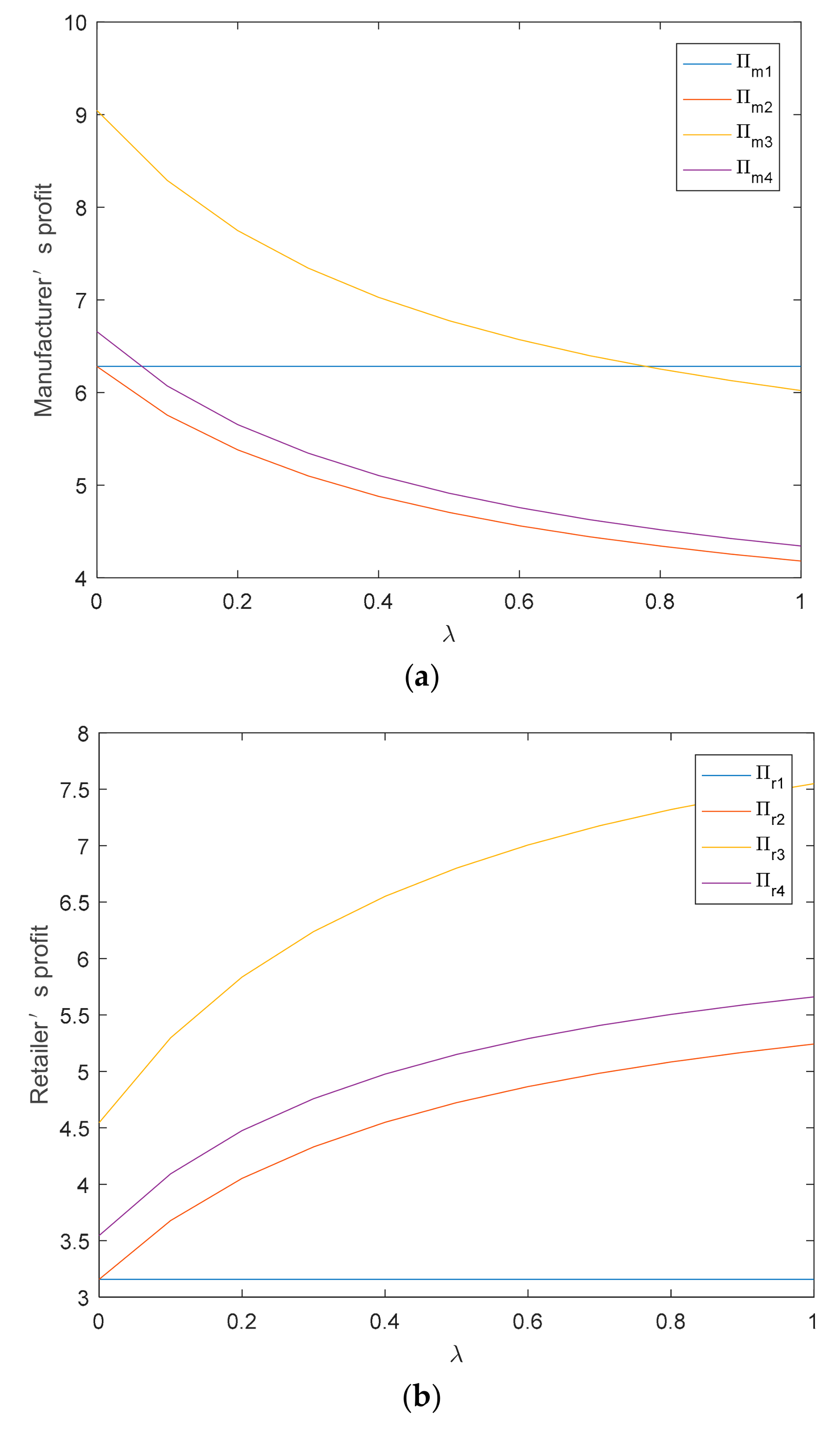
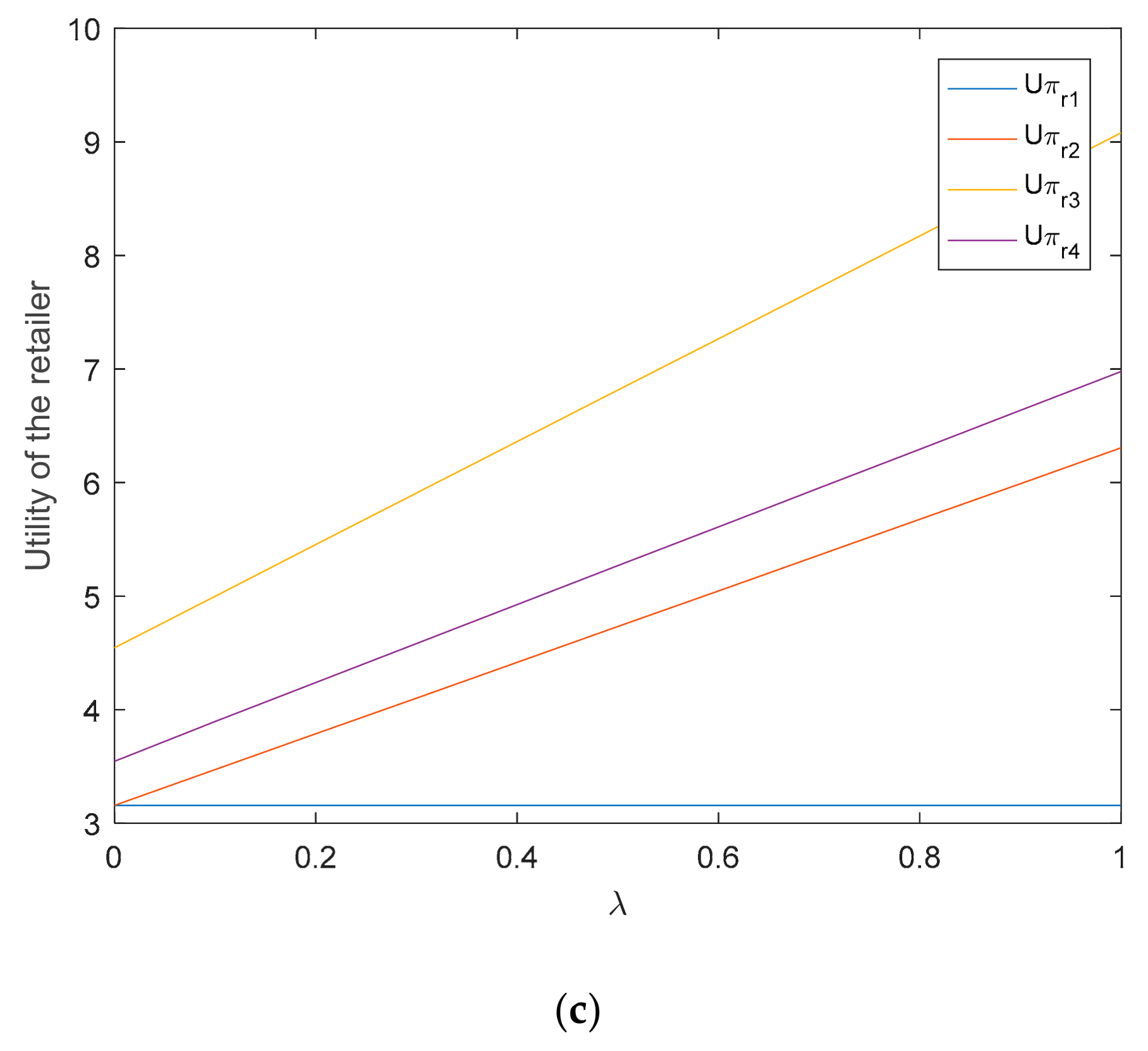
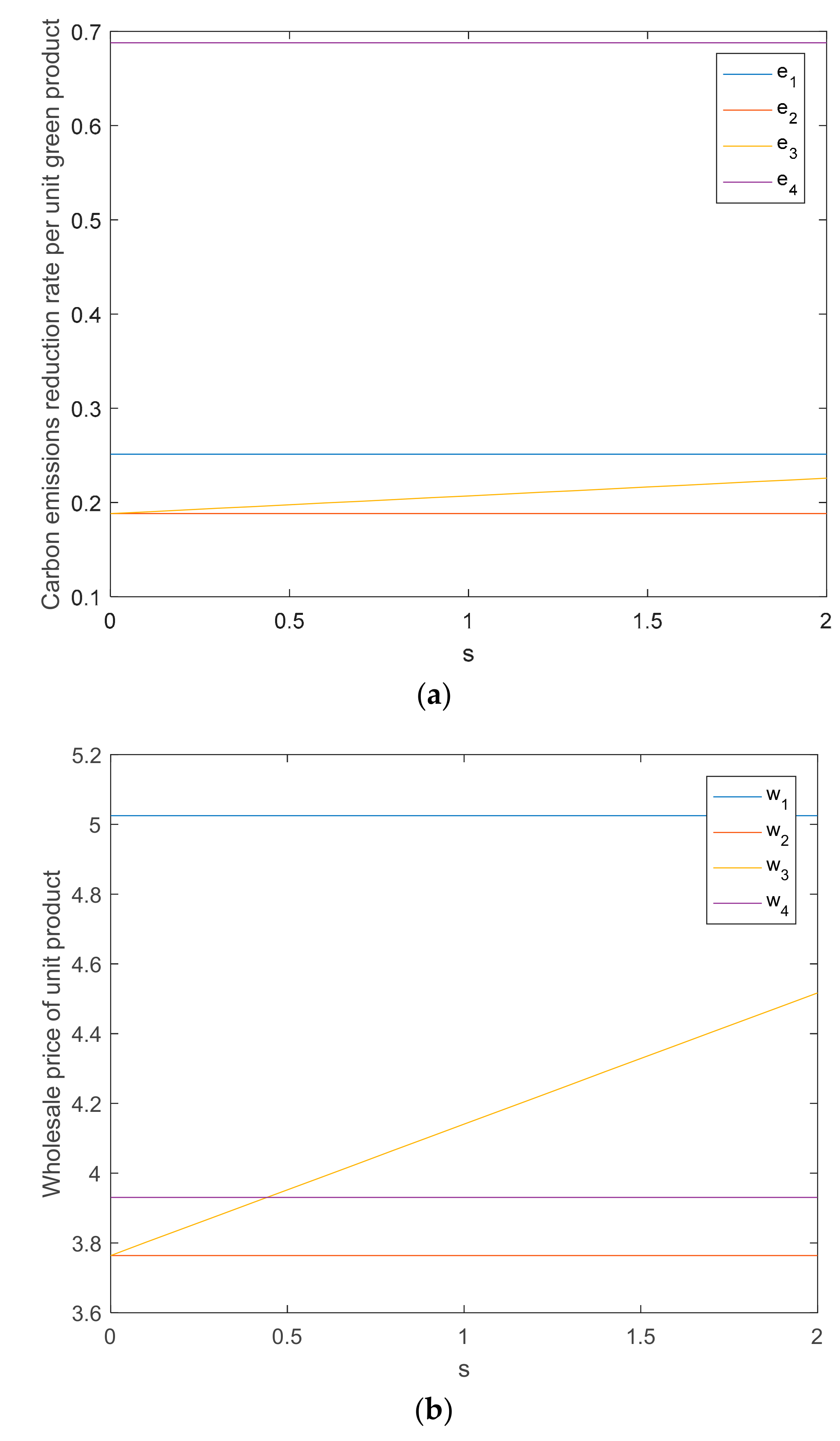
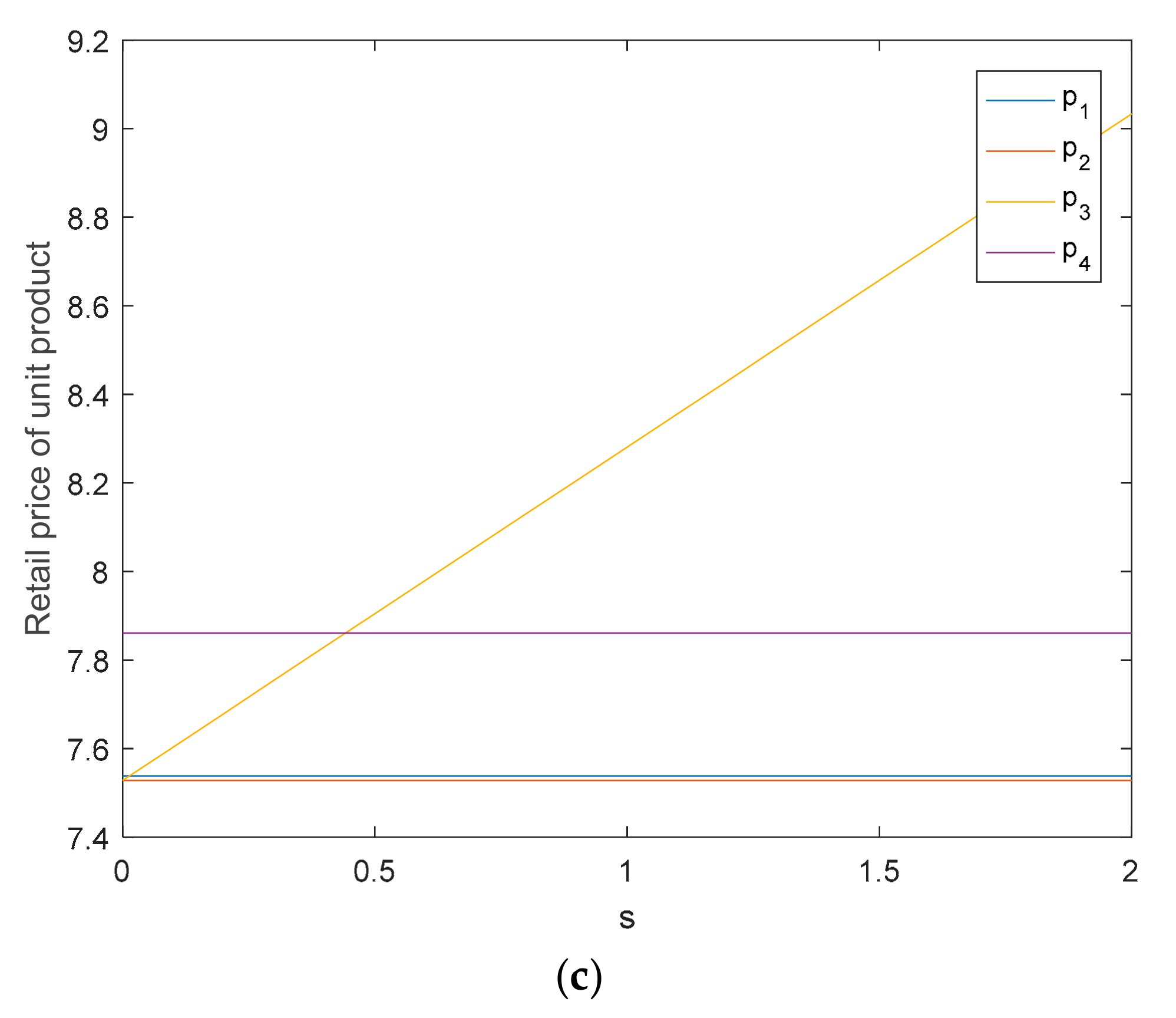
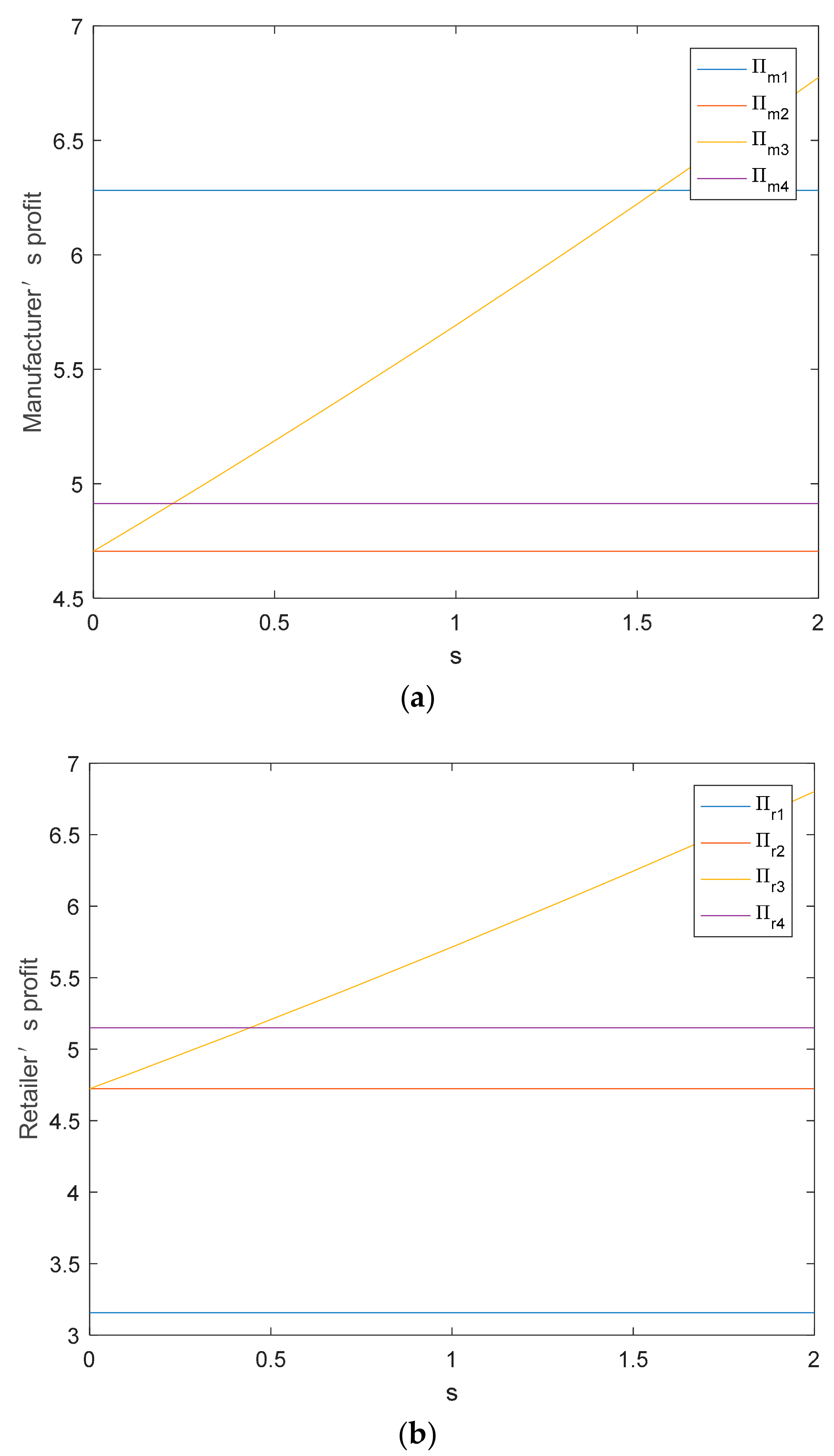
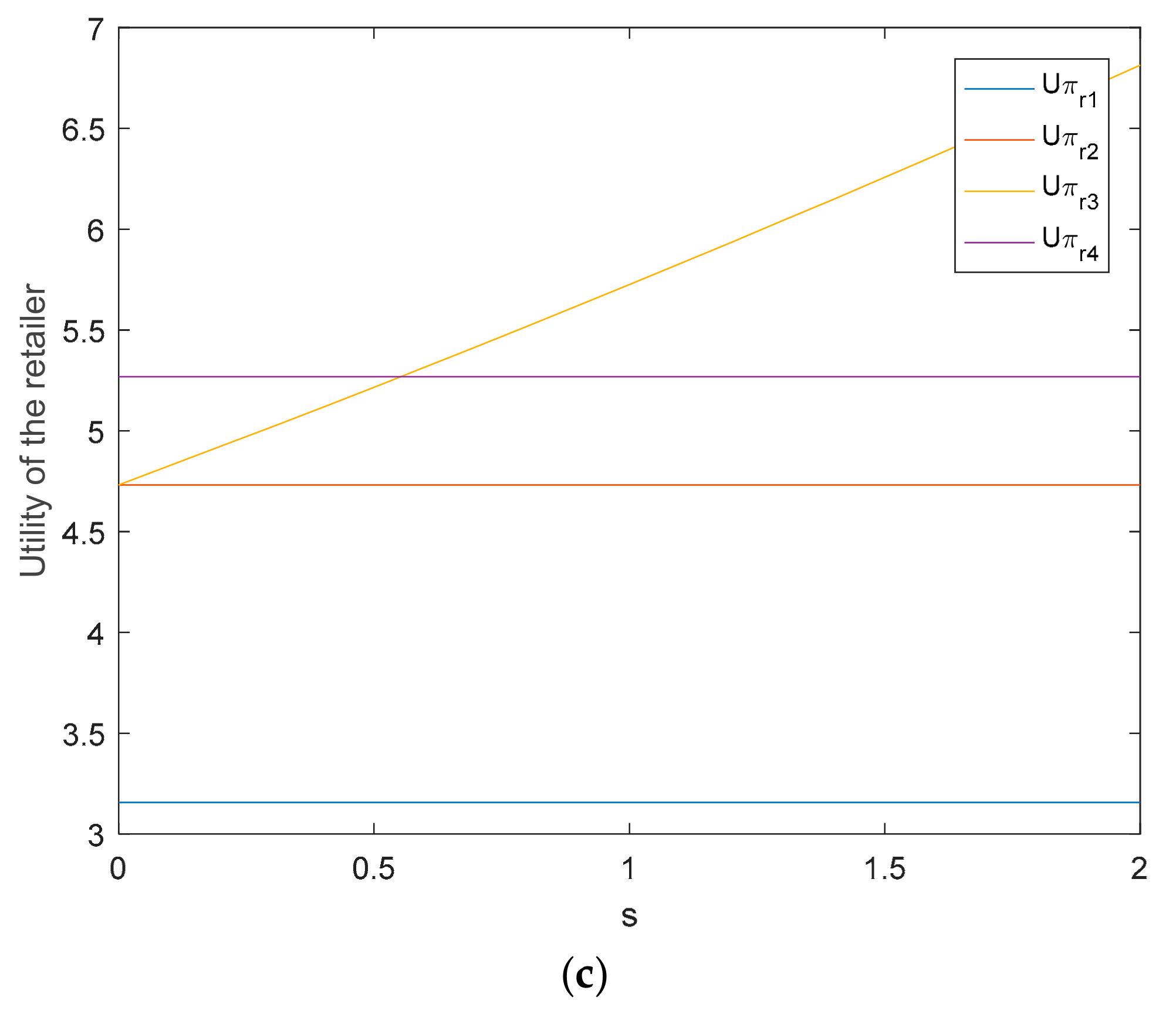
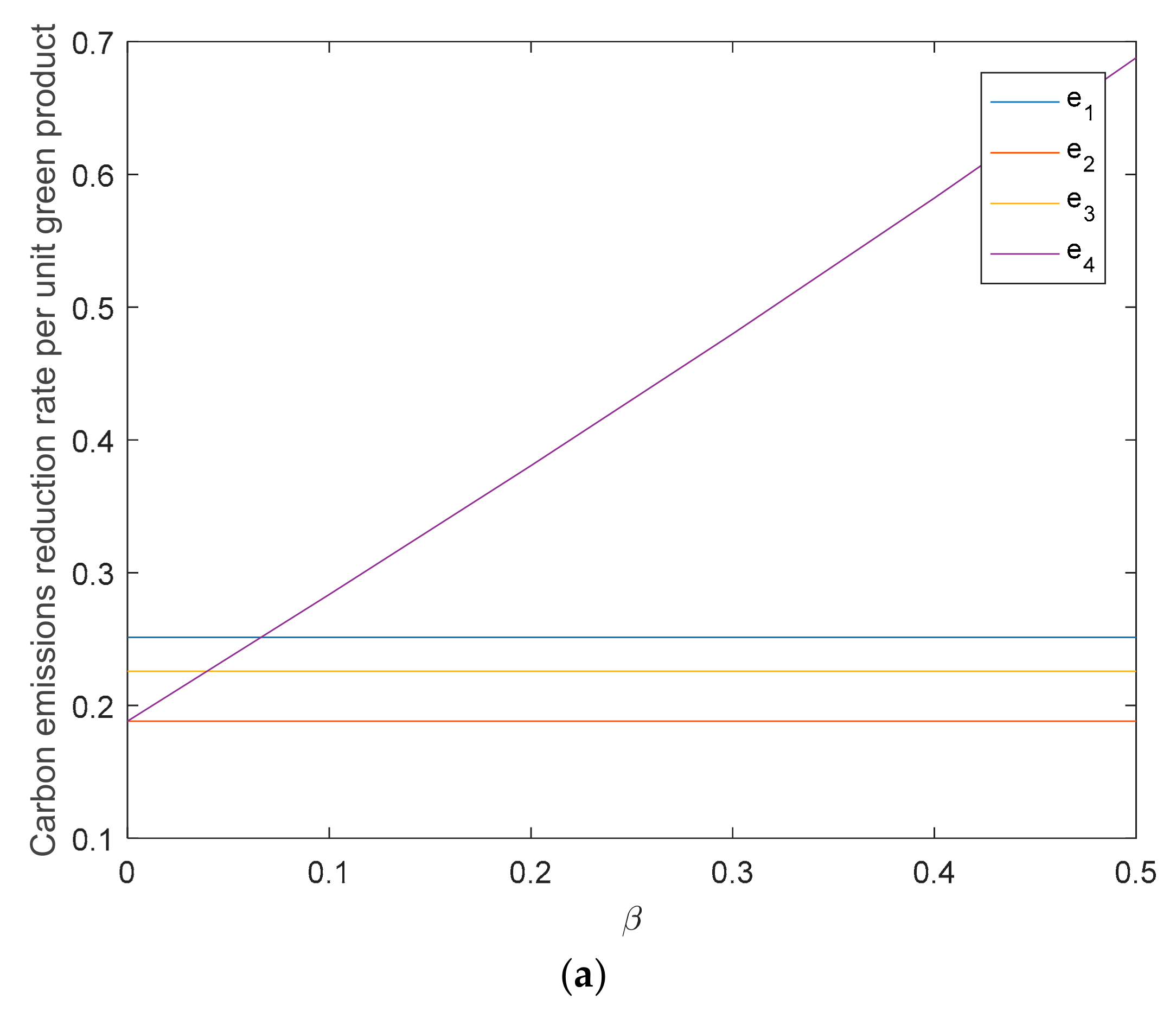
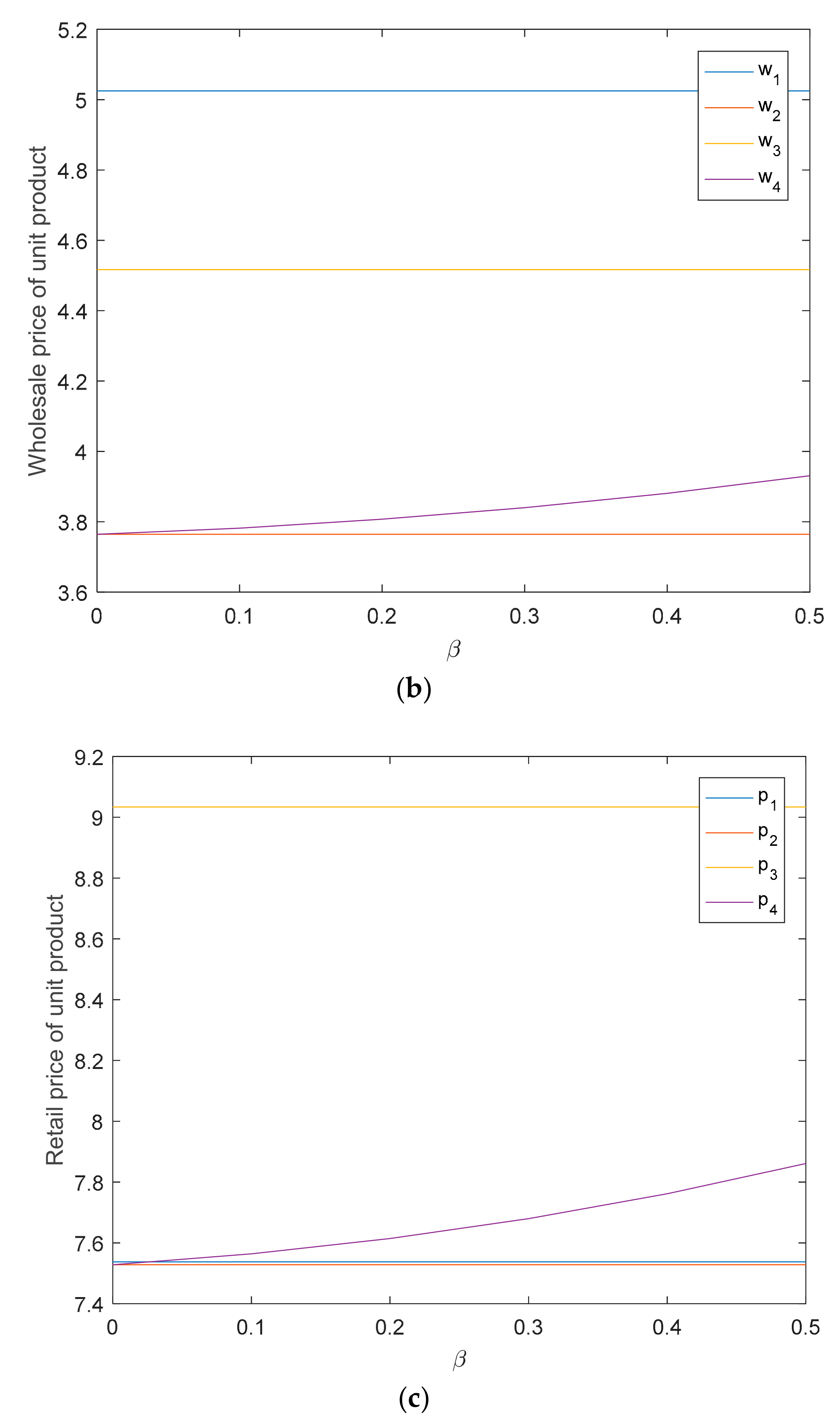
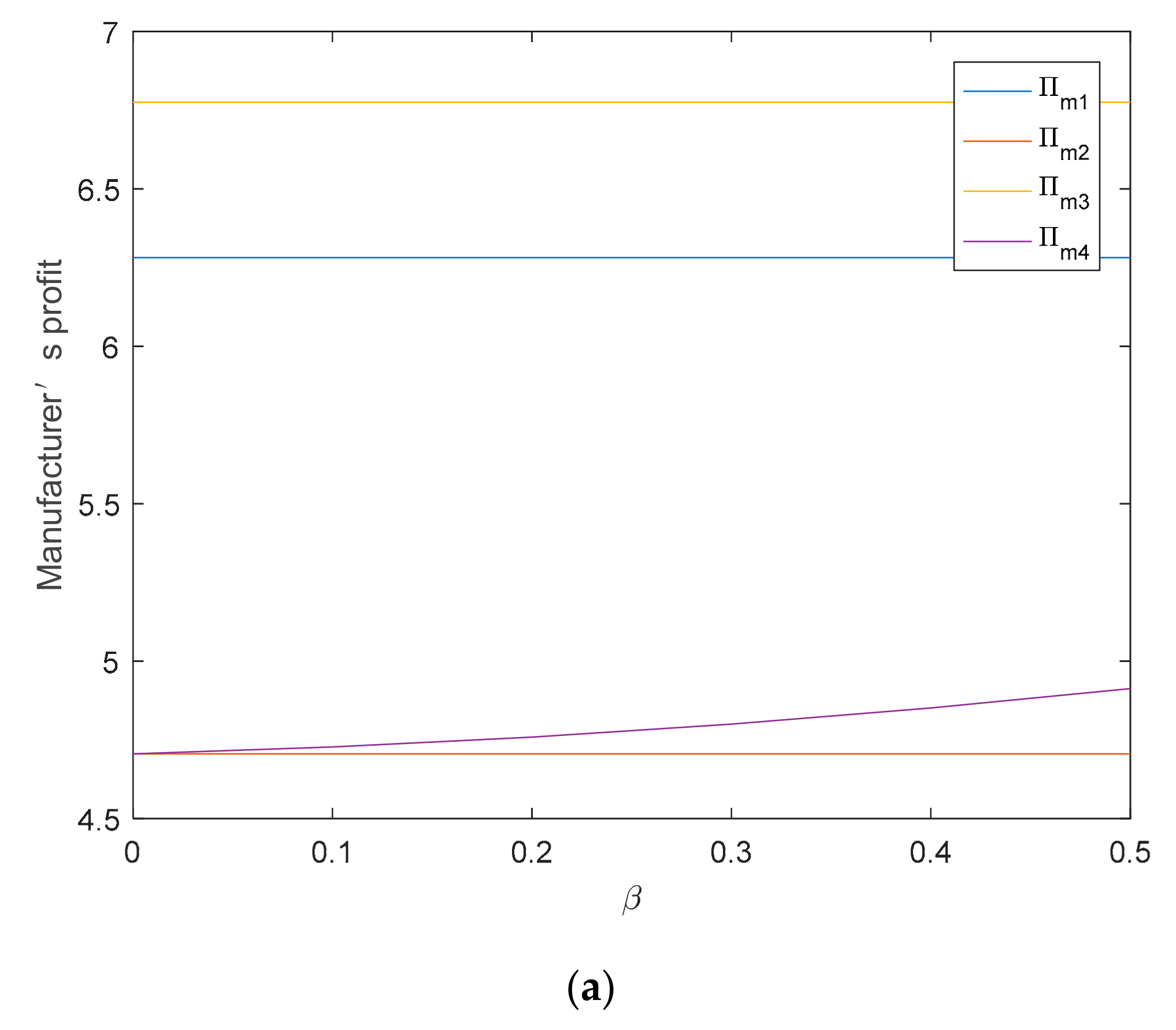
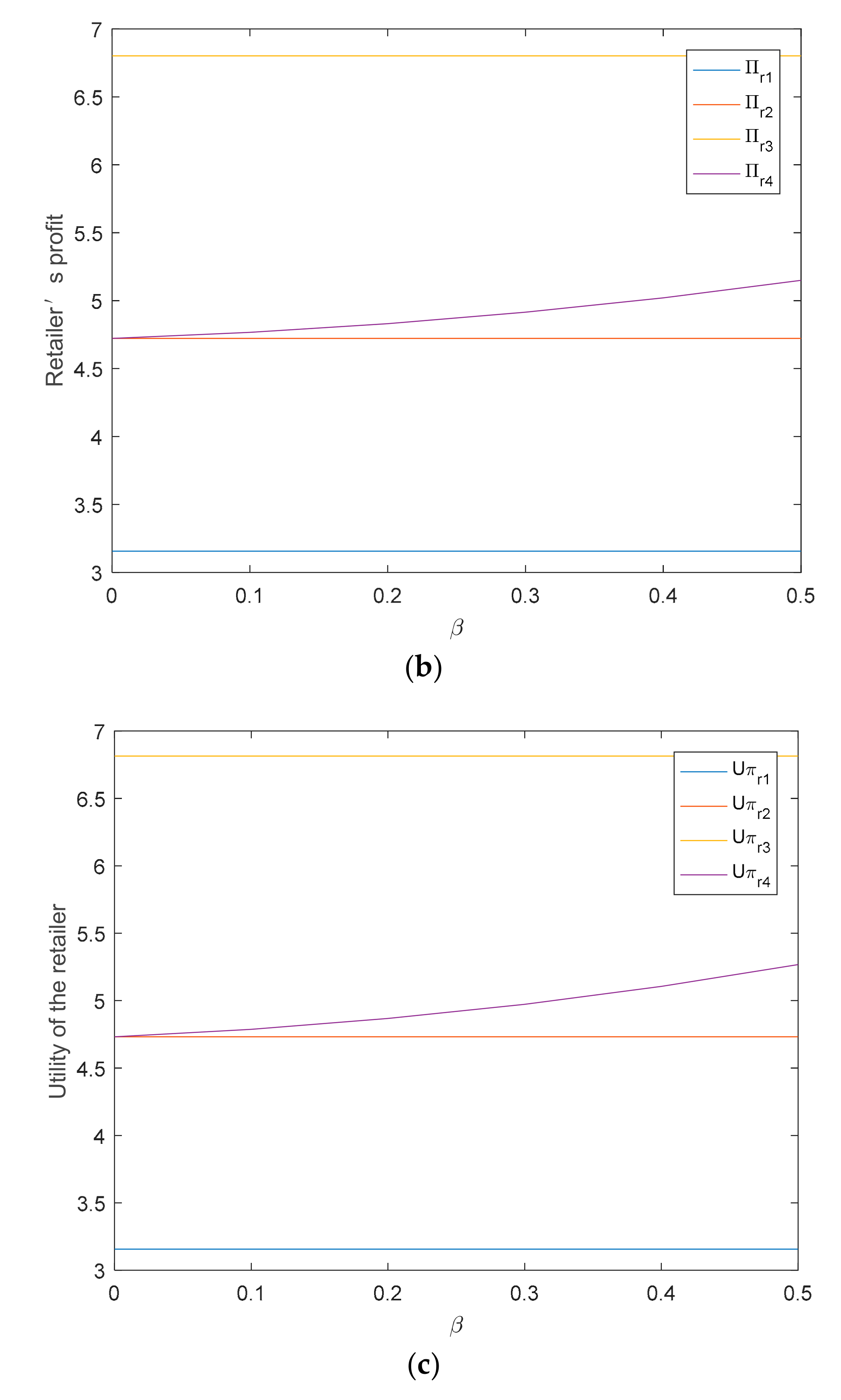
5.1. The Impact of Retailer’s Fairness Concern on Supply Chain
5.2. The Impact of Fixed Subsidy on Supply Chain
5.3. The Impact of D-Type Subsidy Coefficient on Supply Chain
6. Discussion and Conclusions
6.1. Managerial Implications
6.2. Limitations and Future Research
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
- (i)
- and ;
- (ii)
- . □
References
- Chitra, K. In search of the green consumers: A perceptual study. J. Serv. Res. 2007, 7, 173–191. [Google Scholar]
- Zhang, L.; Wang, J.; You, J. Consumer environmental awareness and channel coordination with two substitutable products. Eur. J. Oper. Res. 2015, 241, 63–73. [Google Scholar] [CrossRef]
- Chen, C. Design for the environment: A quality-based model for green product development. Manag. Sci. 2001, 47, 250–263. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, X.; He, P. New Product Design Strategies with Subsidy Policies. J. Syst. Sci. Syst. Eng. 2012, 21, 356–371. [Google Scholar] [CrossRef]
- Luo, Z.; Chen, X.; Wang, X. The role of co-opetition in low carbon manufacturing. Eur. J. Oper. Res. 2016, 253, 392–403. [Google Scholar] [CrossRef]
- Cohen, M.C.; Lobel, R.; Perakis, G. The impact of demand uncertainty on consumer subsidies for green technology adoption. Manag. Sci. 2016, 62, 1235–1258. [Google Scholar] [CrossRef]
- Diamond, D. The impact of government incentives for hybrid-electric vehicles: Evidence from US states. Energy Policy 2008, 37, 972–983. [Google Scholar] [CrossRef]
- Lobel, R.; Perakis, G. Consumer Choice Model for Forecasting Demand And Designing Incentives for Solar Technology; Working Paper; Massachusetts Institute of Technology (MIT): Cambridge, MA, USA, 2011. [Google Scholar]
- Clark, A.E.; Oswald, A.J. Satisfaction and comparison income. J. Public Econ. 2000, 61, 359–381. [Google Scholar] [CrossRef]
- Dahl, G.B.; Løken, K.V.; Mogstad, M. Peer Effects in Program Participation. Soc. Sci. Electron. Publ. 2013, 104, 2049–2074. [Google Scholar]
- Nie, T.; Du, S. Dual-fairness supply chain with quantity discount contracts. Eur. J. Oper. Res. 2017, 258, 491–500. [Google Scholar] [CrossRef]
- Du, S.; Du, C.; Liang, L.; Liu, T.Z. Supply chain coordination considering fairness concerns. J. Manag. Sci. China 2010, 13, 41–48. [Google Scholar]
- Zhou, W.; Huang, W. Contract designs for energy-saving product development in a monopoly. Eur. J. Oper. Res. 2016, 250, 902–913. [Google Scholar] [CrossRef]
- Qiu, G. Influence of Fairness Concern on Decision-making of Manufacturers and Retailers under the Background of Government’s Subsidy. J. Nanchang Hangkong Univ. (Soc. Sci.) 2013, 1, 45–52. [Google Scholar]
- Amacher, G.S.; Koskela, E.; Ollikainen, M. Environmental quality competition and eco-labeling. J. Environ. Econ. Manag. 2004, 47, 284–306. [Google Scholar] [CrossRef]
- Liu, Z.; Anderson, T.D.; Cruz, J.M. Consumer environmental awareness and competition in two-stage supply chains. Eur. J. Oper. Res. 2012, 218, 602–613. [Google Scholar] [CrossRef]
- Xu, L.; Wang, C. Sustainable manufacturing in a closed-loop supply chain considering emission reduction and remanufacturing. Resour. Conserv. Recycl. 2018, 131, 297–304. [Google Scholar] [CrossRef]
- Bansal, S.; Gangopadhyay, S. Tax/subsidy policies in the presence of environmentally aware consumers. J. Environ. Econ. Manag. 2003, 45, 333–355. [Google Scholar] [CrossRef]
- Yu, Y.; Han, X.; Hu, G. Optimal production for manufacturers considering consumer environmental awareness and green subsidies. Int. J. Prod. Econ. 2016, 182, 397–408. [Google Scholar] [CrossRef]
- Liu, D.; Wang, S.K.; Liu, J.C. Optimum Subsidy to Promote Electric Boiler Investment to Accommodate Wind Power. Sustainability 2017, 9, 874. [Google Scholar] [CrossRef]
- Zheng, X.; Lin, H.; Liu, Z. Manufacturing Decisions and Government Subsidies for Electric Vehicles in China: A Maximal Social Welfare Perspective. Sustainability 2018, 10, 672. [Google Scholar] [CrossRef]
- Oestreich, A.M.; Tsiakas, I. Carbon emissions and stock returns: Evidence from the EU Emissions Trading Scheme. J. Bank. Financ. 2015, 58, 294–308. [Google Scholar] [CrossRef]
- Martin, R.; Wagner, U.; Muuls, M. The Impact of the European Union Emissions Trading Scheme on Regulated Firms: What Is the Evidence after Ten Years? Review of Environmental Economics and Policy. 2016, 10, 129–148. [Google Scholar] [CrossRef]
- Liu, Q.; Zhang, C.; Bing, N.; Zhou, Y.; Shi, P. Supply chain two part Tariff Contract with Fairness Preference and Carbon Emissions. Chin. J. Manag. Sci. 2016, 10, 60–68. [Google Scholar]
- Zhang, L.; Wang, J. Coordination of the Traditional and the Online Channels for a Short-life-cycle Product. Eur. J. Oper. Res. 2016, 258, 639–651. [Google Scholar] [CrossRef]
- Sun, J.; Xiao, Z. The impact of government portfolio regulation on dual channel low carbon supply chain decision making. East China Econ. Manag. 2017, 9, 180–184. [Google Scholar]
- Fehr, E.; Schmidt, K.M. A theory of fairness, competition, and cooperation. Q. J. Econ. 1999, 114, 817–868. [Google Scholar] [CrossRef]
- Cui, T.H.; Raju, J.S.; Zhang, Z.J. Fairness and channel coordination. Manag. Sci. 2007, 53, 1303–1314. [Google Scholar] [CrossRef]
- Caliskan-Demirag, O.; Chen, Y.F.; Li, J. Channel coordination under fairness concerns and nonlinear demand. Eur. J. Oper. Res. 2010, 207, 1321–1326. [Google Scholar] [CrossRef]
- Du, S.; Nie, T.; Chu, C.; Yu, Y. Newsvendor model for a dyadic supply chain with Nash bargaining fairness concerns. Int. J. Prod. Res. 2014, 52, 5070–5085. [Google Scholar] [CrossRef]
- Chen, J.; Zhao, X.; Shen, Z.J. Risk Mitigation Benefit from Backup Suppliers in the Presence of the Horizontal Fairness Concern. Decis. Sci. 2015, 46, 663–696. [Google Scholar] [CrossRef]
- Li, Q.H.; Li, B. Dual-channel supply chain equilibrium problems regarding retail services and fairness concerns. Appl. Math. Model. 2016, 40, 7349–7367. [Google Scholar] [CrossRef]
- Jiang, H.; Shao, X.; Zhang, X.; Bao, J. A Study of the Allocation of Carbon Emission Permits among the Provinces of China Based on Fairness and Efficiency. Sustainability 2017, 9, 2122. [Google Scholar] [CrossRef]
- Cheng, F.; Shao, S.; Xu, L.; Sun, L. Optimal Strategy of Government Subsidized Initiative Carbon Reduction. China Pop. Res. Environ. 2015, 7, 32–39. [Google Scholar]
- Zhao, J.; Lin, J. Pricing models of closed-loop supply chain under different subsidy policies. J. Ind. Eng./Eng. Manag. 2017, 1, 85–92. [Google Scholar]
- Carlson, D.K. Public Priorities: Environment vs. Economic Growth. 2005. Available online: http://www.gallup.com/poll/15820/public-priorities-environmentvs-economic-growth.aspx (accessed on 12 April 2005).
- Laroche, M.; Bergeron, J.; Barbaro-Forleo, G. Targeting consumers who are willing to pay more for environmentally-friendly products. J. Consum. Mark. 2001, 18, 503–520. [Google Scholar] [CrossRef]
- Zhu, W.; He, Y. Green product design in supply chains under competition. Eur. J. Oper. Res. 2017, 258, 165–180. [Google Scholar] [CrossRef]
| Author | CEA | Product’s Environmental Quality | Supply Chain Coordination Contract | Subsidy | Fairness Concern |
|---|---|---|---|---|---|
| Zhang et al. (2015) [2] | √ | √ | √ | ||
| Zhou and Huang (2016) [13] | √ | √ | √ | √ | |
| Sun and Xiao(2017) [26] | √ | √ | |||
| Cheng et al. (2015) [34] | √ | √ | |||
| Zhao and Lin (2017) [35] | √ | √ | |||
| Qiu (2013) [14] | √ | √ | |||
| Du et al. (2010) [12] | √ | √ | |||
| This paper | √ | √ | √ | √ |
| Parameters | The Meanings of the Parameters |
| Basic demand of the green product | |
| The demand sensitivity coefficient to price | |
| Consumer environmental awareness | |
| Retailer’s equity concern coefficient | |
| Subsidy for one unit product in F-type | |
| Subsidy coefficient in D-type | |
| The cost coefficient of the environmental quality | |
| Retailer's profit and manufacturer's profit | |
| Utility of the retailer | |
| Utility of the the manufacturer | |
| Decision variables | The Meanings of the Decision Variables |
| Carbon emission reduction rate per unit of green product | |
| Wholesale price of unit product | |
| Retail price of unit product |
| Models | |||
|---|---|---|---|
| N | |||
| F | |||
| F-F | |||
| F-D |
| Models | |||
|---|---|---|---|
| N | |||
| F | |||
| F-F | |||
| F-D |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Xue, B.; Liu, X. Carbon Emission Reduction with Regard to Retailer’s Fairness Concern and Subsidies. Sustainability 2018, 10, 1209. https://doi.org/10.3390/su10041209
Zhang L, Xue B, Liu X. Carbon Emission Reduction with Regard to Retailer’s Fairness Concern and Subsidies. Sustainability. 2018; 10(4):1209. https://doi.org/10.3390/su10041209
Chicago/Turabian StyleZhang, Linghong, Bowen Xue, and Xiyu Liu. 2018. "Carbon Emission Reduction with Regard to Retailer’s Fairness Concern and Subsidies" Sustainability 10, no. 4: 1209. https://doi.org/10.3390/su10041209
APA StyleZhang, L., Xue, B., & Liu, X. (2018). Carbon Emission Reduction with Regard to Retailer’s Fairness Concern and Subsidies. Sustainability, 10(4), 1209. https://doi.org/10.3390/su10041209




