A Self-Scrutinized Backoff Mechanism for IEEE 802.11ax in 5G Unlicensed Networks
Abstract
:1. Introduction
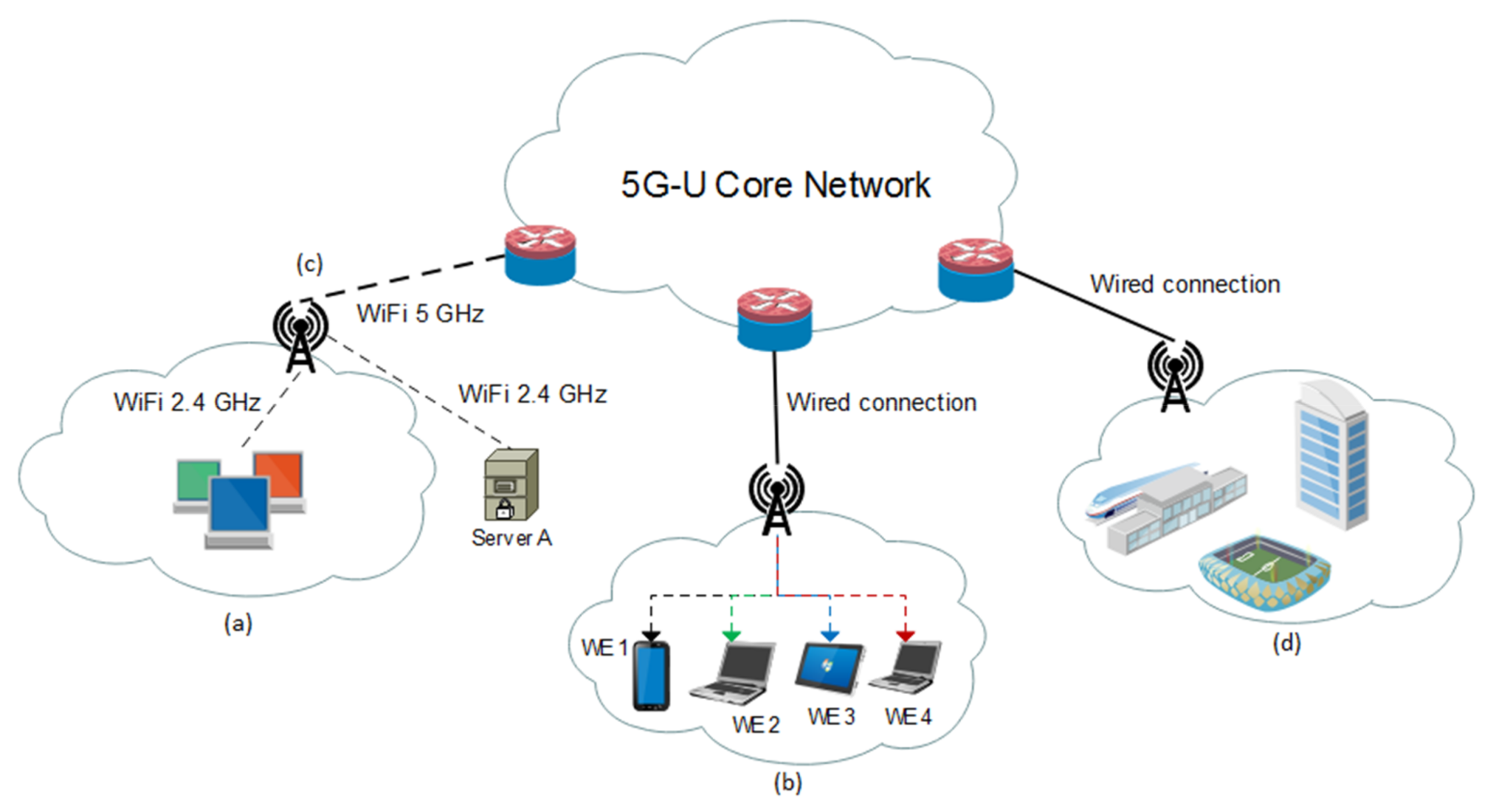
2. IEEE 802.11ax Use Cases in Fifth-Generation Radio Access Network on Unlicensed Bands (5G-U)
2.1. Gigabit Ethernet Connection Replacement
2.2. Improved Network Capacity Using Multi-User Multiple-Input and Multiple-Output (MU-MIMO)
2.3. High-Efficiency Wireless (HEW) as a Backhaul for Local Area Network (LAN)
2.4. Support for Highly Dense Scenarios
3. A Self-Scrutinized Backoff Mechanism for HEW
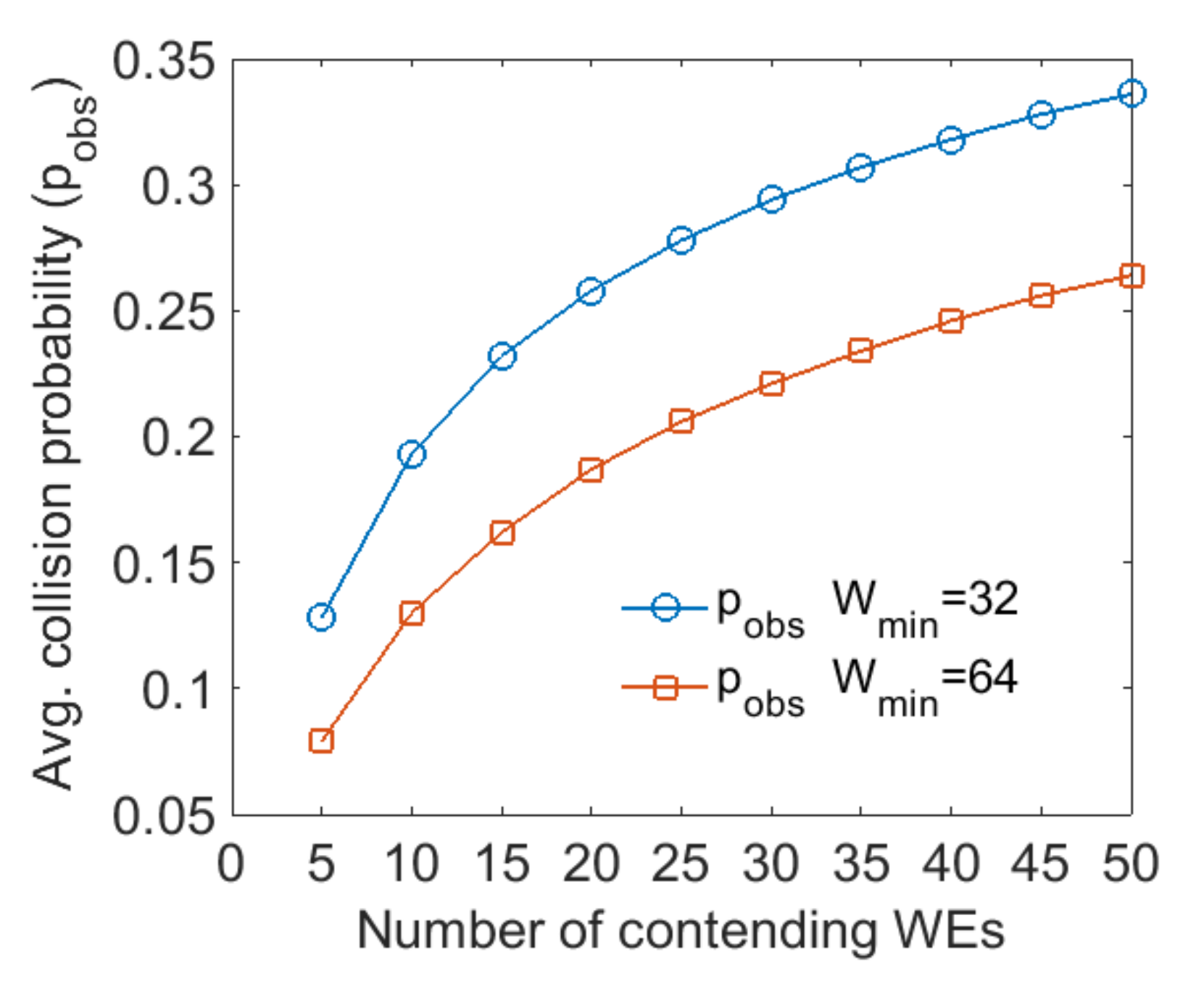
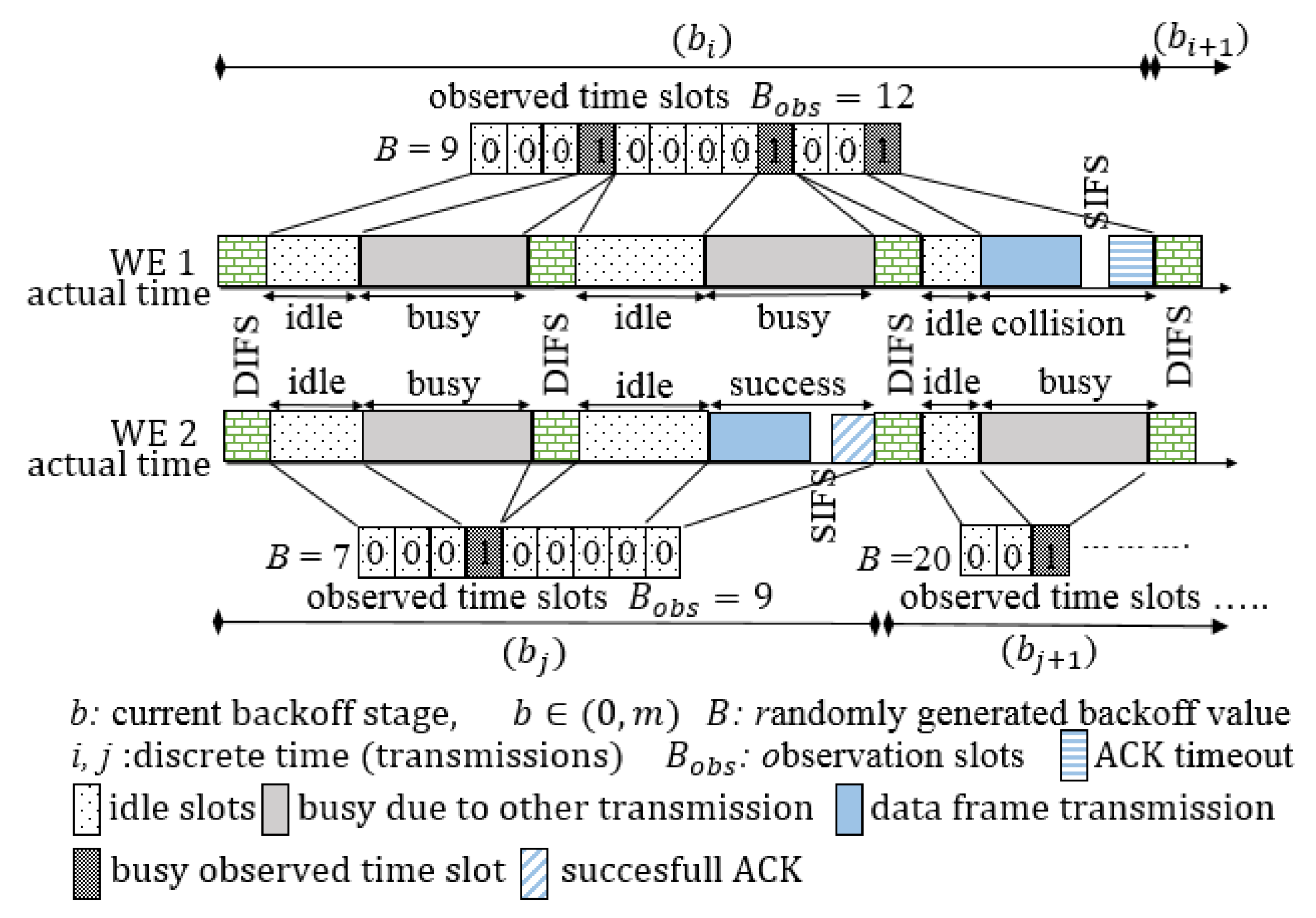
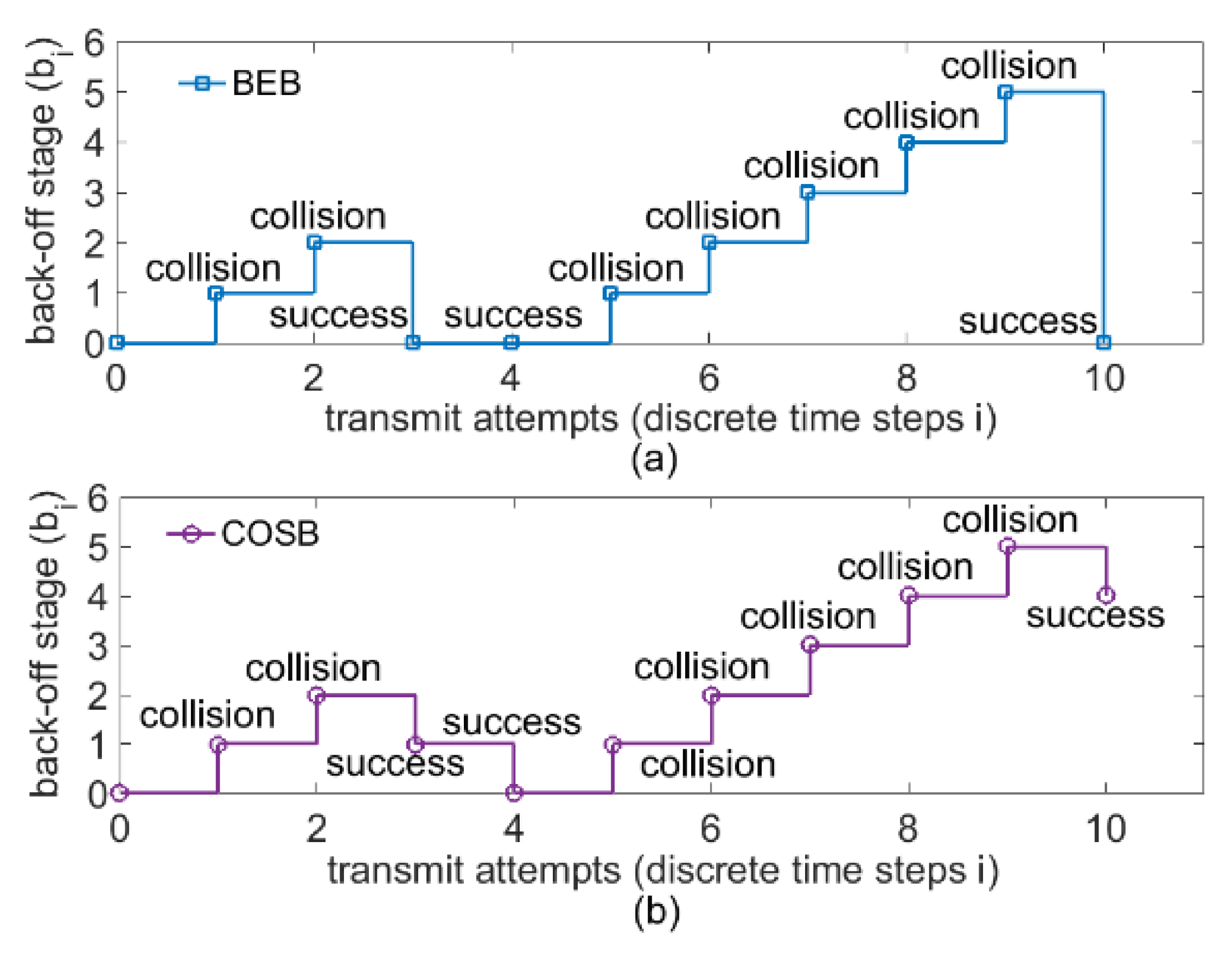
3.1. Problem Statement
3.2. Channel Observation-Based Scaled Backoff (COSB)
4. Analytical Model
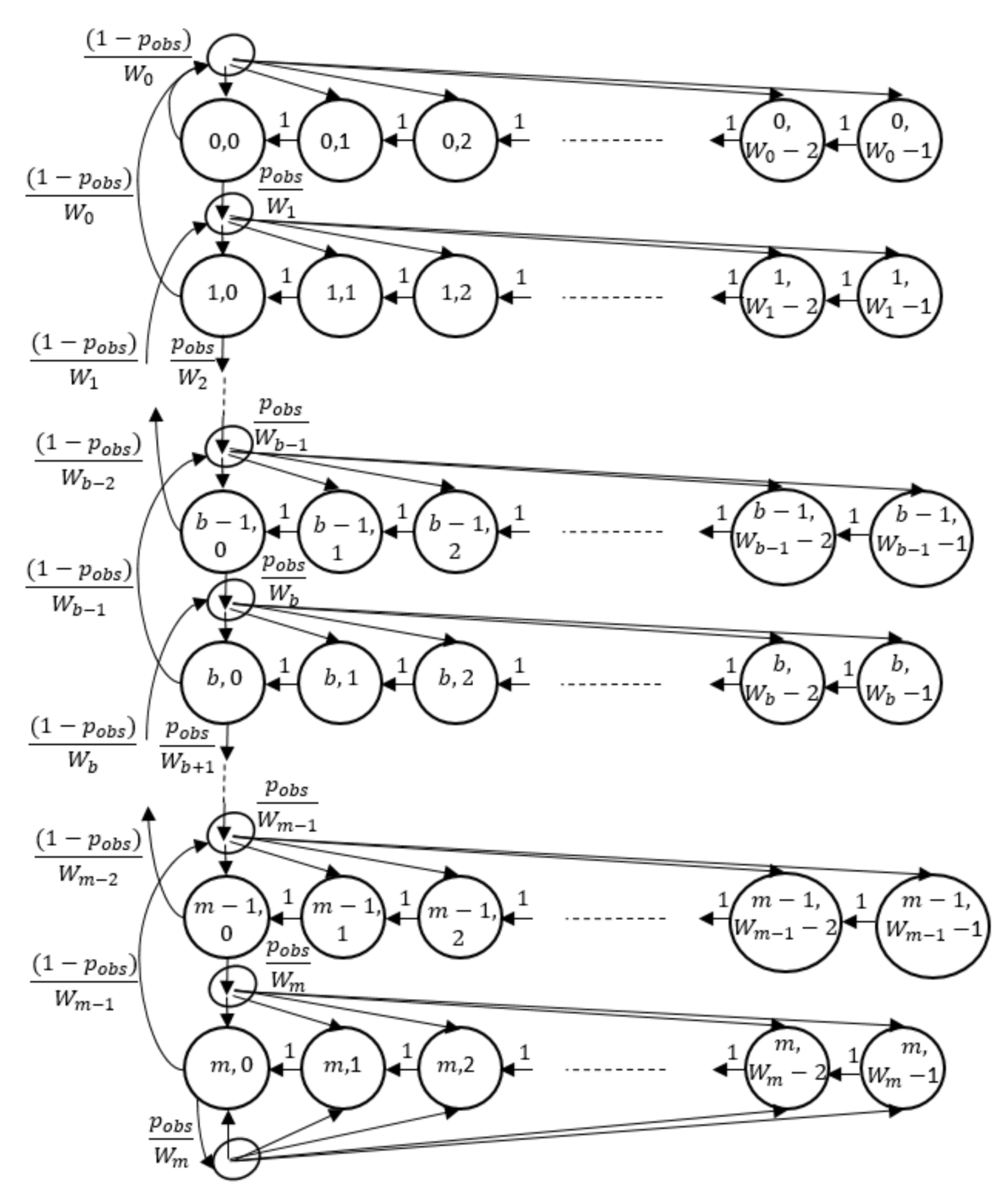
4.1. Recursive Discrete-Time Markove Chain (R-DTMC) Model
4.2. Normalized Throughput
4.3. Average Delay
5. Performance Evaluation
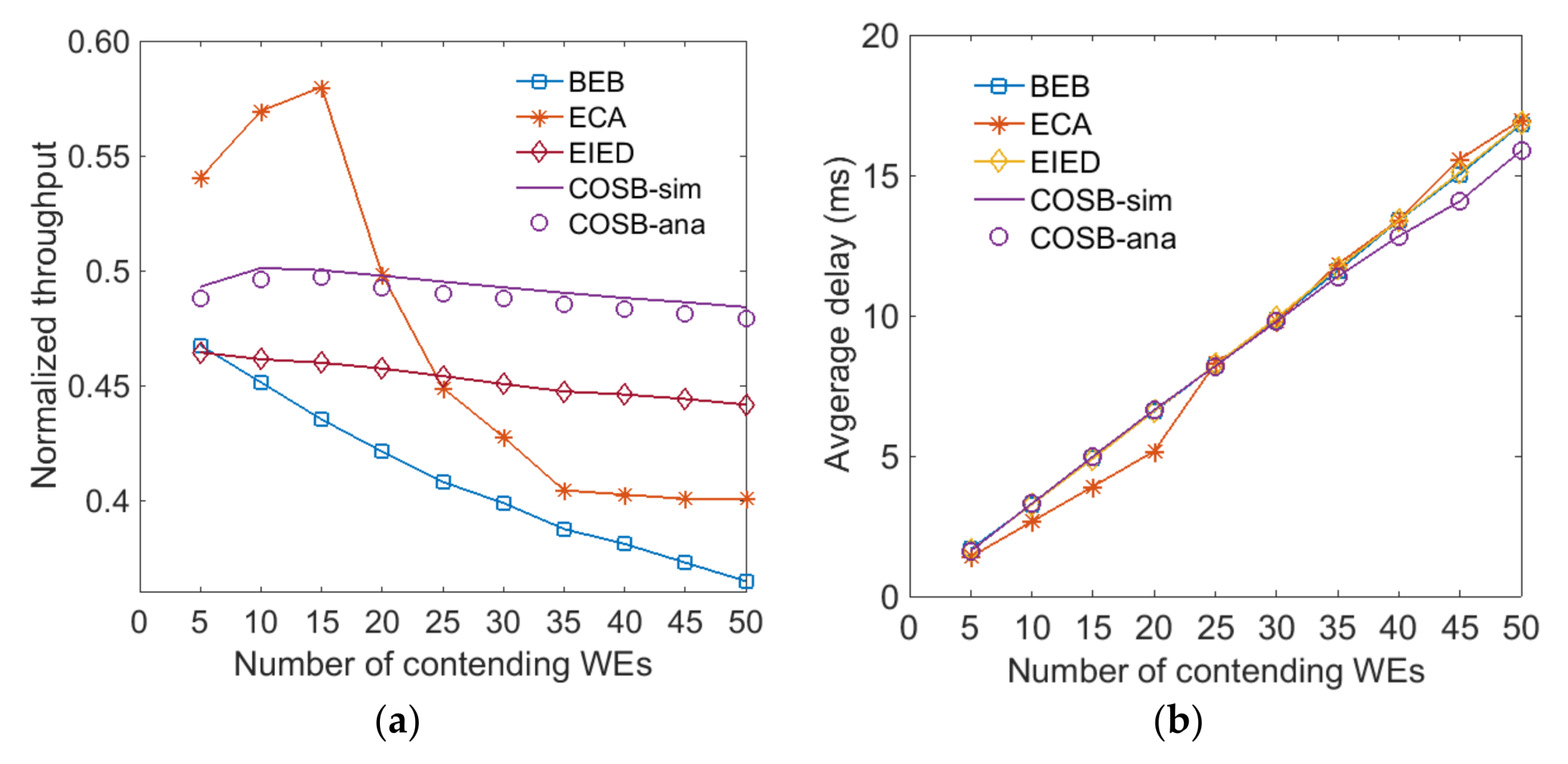
5.1. Normalized Throughput and Average Delay
5.2. Maximum Approximate Saturation Throughput
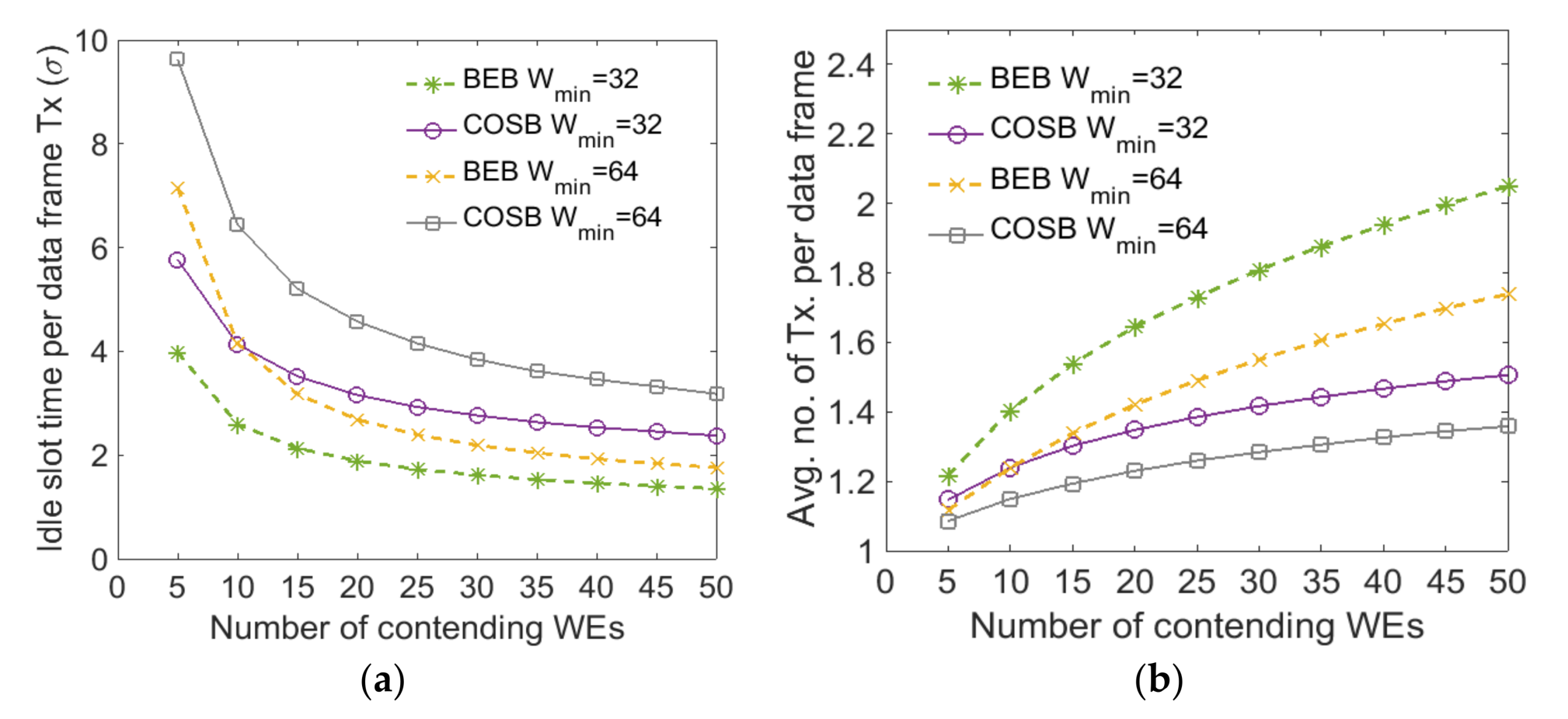
5.3. Average Channel Utilization Per Data Frame Transmission
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Al-Dulaimi, A.; Al-Rubaye, S.; Ni, Q.; Sousa, E. 5G Communications Race: Pursuit of More Capacity Triggers LTE in Unlicensed Band. IEEE Veh. Technol. Mag. 2015, 10, 43–51. [Google Scholar] [CrossRef]
- Bajracharya, R.; Shrestha, R.; Zikria, Y.B.; Kim, S.W. LTE in the unlicensed spectrum: A survey. IETE Tech. Rev. 2018, 35, 78–90. [Google Scholar] [CrossRef]
- Bellalta, B. IEEE 802.11ax: High-efficiency WLANs. IEEE Wireless Communications. 2016, 23, 38–46. [Google Scholar] [CrossRef]
- Ali, R.; Shahin, N.; Kim, Y.T.; Kim, B.; Kim, S.W. Channel Observation-based Scaled Backoff Mechanism for High Efficiency WLANs. Electron. Lett. 2018. [Google Scholar] [CrossRef]
- Ali, R.; Kim, S.W.; Kim, B.; Park, Y. Design of MAC Layer Resource Allocation Schemes for IEEE 802.11ax: Future Directions. IETE Tech. Rev. 2018, 35, 28–52. [Google Scholar] [CrossRef]
- IEEE Standard for Information Technology. Part 11: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications. ANSI/IEEE Std 802.11 2007, i-513. [Google Scholar] [CrossRef]
- Kosek-Szott, K.; Gozdecki, J.; Loziak, K.; Natkaniec, M.; Prasnal, L.; Szott, S.; Wagrowski, M. Coexistence Issues in Future WiFi Networks. IEEE Netw. 2017, 31, 86–95. [Google Scholar] [CrossRef]
- Ali, R.; Zikria, Y.B.; Amin, F.; Kim, B.; Kim, S.W. I-DTMC: An Integrated-Discrete Time Markov Chain Model for Performance Analysis in Future WLANs. In Proceedings of the 2017 IEEE 42nd Conference on Local Computer Networks Workshops, Singapore, 9–12 October 2017. [Google Scholar]
- Bianchi, G. Performance analysis of the IEEE 802.11 distributed coordination function. IEEE J. Sel. Areas Commun. 2000, 18, 535–547. [Google Scholar] [CrossRef]
- Chatzimisios, P.; Boucouvalas, A.C.; Vitsas, V. Packet delay analysis of IEEE 802.11 MAC protocol. Electron. Lett. 2003, 39, 1358–1359. [Google Scholar] [CrossRef]
- The Network Simulator-ns-3. Available online: https://www.nsnam.org/ (accessed on 01 March 2018).
- Sanabria-Russo, L.; Faridi, A.; Bellalta, B.; Barcelo, J.; Oliver, M. Future Evolution of CSMA Protocols for the IEEE 802.11 Standard. In Proceedings of the 2013 IEEE International Conference on Communications Workshops, Budapest, Hungary, 9–13 June 2013. [Google Scholar]
- Ye, C.; Li, Y.; Reznik, A. Performance Analysis of Exponential Increase Exponential Decrease Back-Off Algorithm. In Proceedings of the 2010 IEEE Global Telecommunications Conference (GLOBECOM), Miami, FL, USA, 6–10 December 2010. [Google Scholar]
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Operating Frequency | 5 GHz | Physical rate of channel | 54 Mbps |
| Bandwidth | 20 MHz | MAC header | 24 Bytes |
| MAC payload | 1024 Bytes | PHY header | 20 s |
| Acknowledgment (ACK) | 14 Bytes + PHY header | Transmission range | 10 meters |
| 32 | 1024 | ||
| 32 | 9 s | ||
| SIFS | 16 s | DIFS | 60 s |
| Propagation delay () | 1 s | Max. backoff stages (m) | 6 |
| WEs (n) | Max. Approx. Throughput | COSB | BEB |
|---|---|---|---|
| 5 | 0.510 ( = 0.0573) | 0.493 ( = 0.034) | 0.468 ( = 0.048) |
| 10 | 0.502 ( = 0.0287) | 0.501 ( = 0.024) | 0.452 ( = 0.037) |
| 20 | 0.498 ( = 0.0143) | 0.498 ( = 0.016) | 0.421 ( = 0.026) |
| 30 | 0.497 ( = 0.0095) | 0.493 ( = 0.012) | 0.401 ( = 0.020) |
| 40 | 0.497 ( = 0.0072) | 0.488 ( = 0.010) | 0.381 ( = 0.017) |
| 50 | 0.497 ( = 0.0057) | 0.484 ( = 0.008) | 0.365 ( = 0.015) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, R.; Shahin, N.; Bajracharya, R.; Kim, B.-S.; Kim, S.W. A Self-Scrutinized Backoff Mechanism for IEEE 802.11ax in 5G Unlicensed Networks. Sustainability 2018, 10, 1201. https://doi.org/10.3390/su10041201
Ali R, Shahin N, Bajracharya R, Kim B-S, Kim SW. A Self-Scrutinized Backoff Mechanism for IEEE 802.11ax in 5G Unlicensed Networks. Sustainability. 2018; 10(4):1201. https://doi.org/10.3390/su10041201
Chicago/Turabian StyleAli, Rashid, Nurullah Shahin, Rojeena Bajracharya, Byung-Seo Kim, and Sung Won Kim. 2018. "A Self-Scrutinized Backoff Mechanism for IEEE 802.11ax in 5G Unlicensed Networks" Sustainability 10, no. 4: 1201. https://doi.org/10.3390/su10041201
APA StyleAli, R., Shahin, N., Bajracharya, R., Kim, B.-S., & Kim, S. W. (2018). A Self-Scrutinized Backoff Mechanism for IEEE 802.11ax in 5G Unlicensed Networks. Sustainability, 10(4), 1201. https://doi.org/10.3390/su10041201








