Estimating Emissions from Regional Freight Delivery under Different Urban Development Scenarios
Abstract
1. Introduction
2. Literature Review
3. Model Formulation
3.1. Ring-Sweep Algorithm Review
3.2. Regional Freight Distribution and Collection Modeling
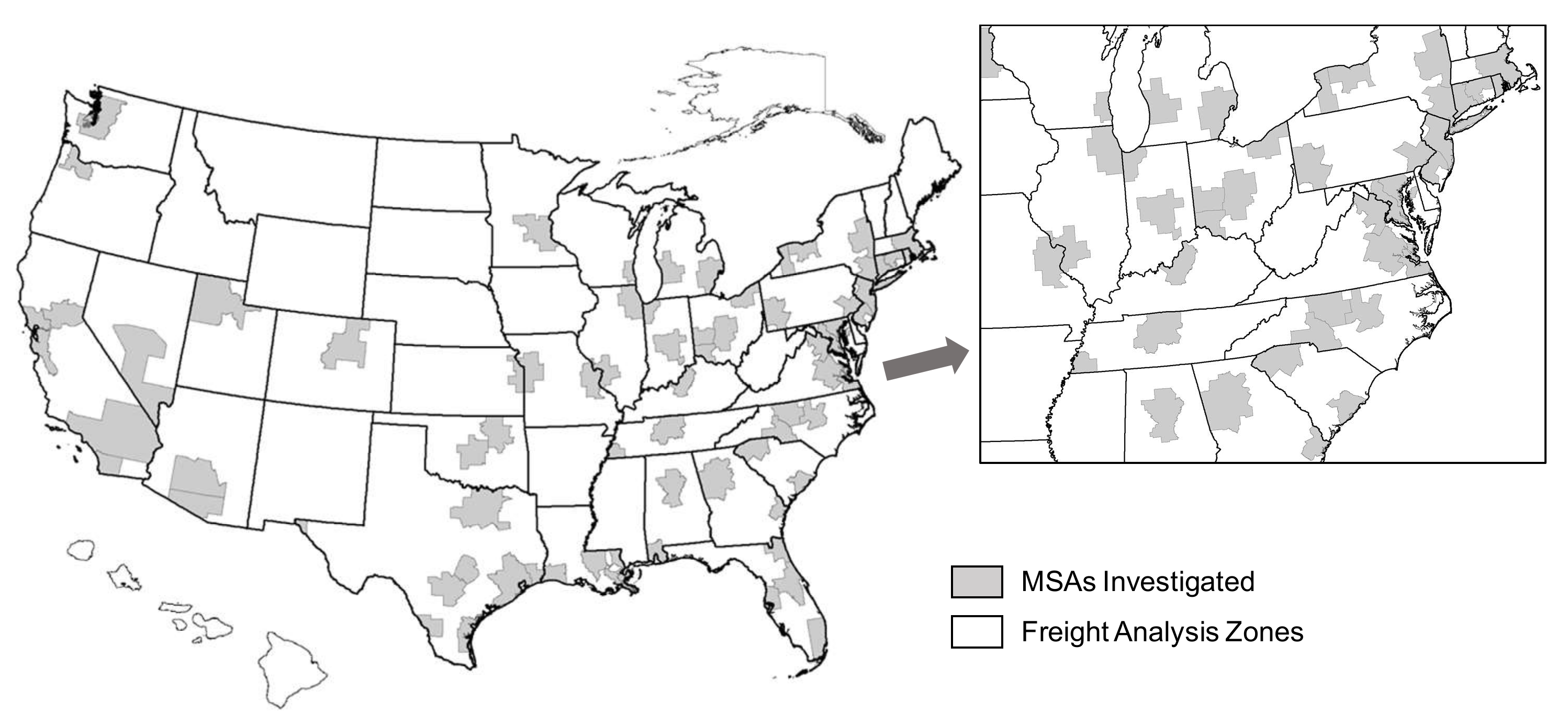
4. Case Study
4.1. Data Preparation and Assumptions
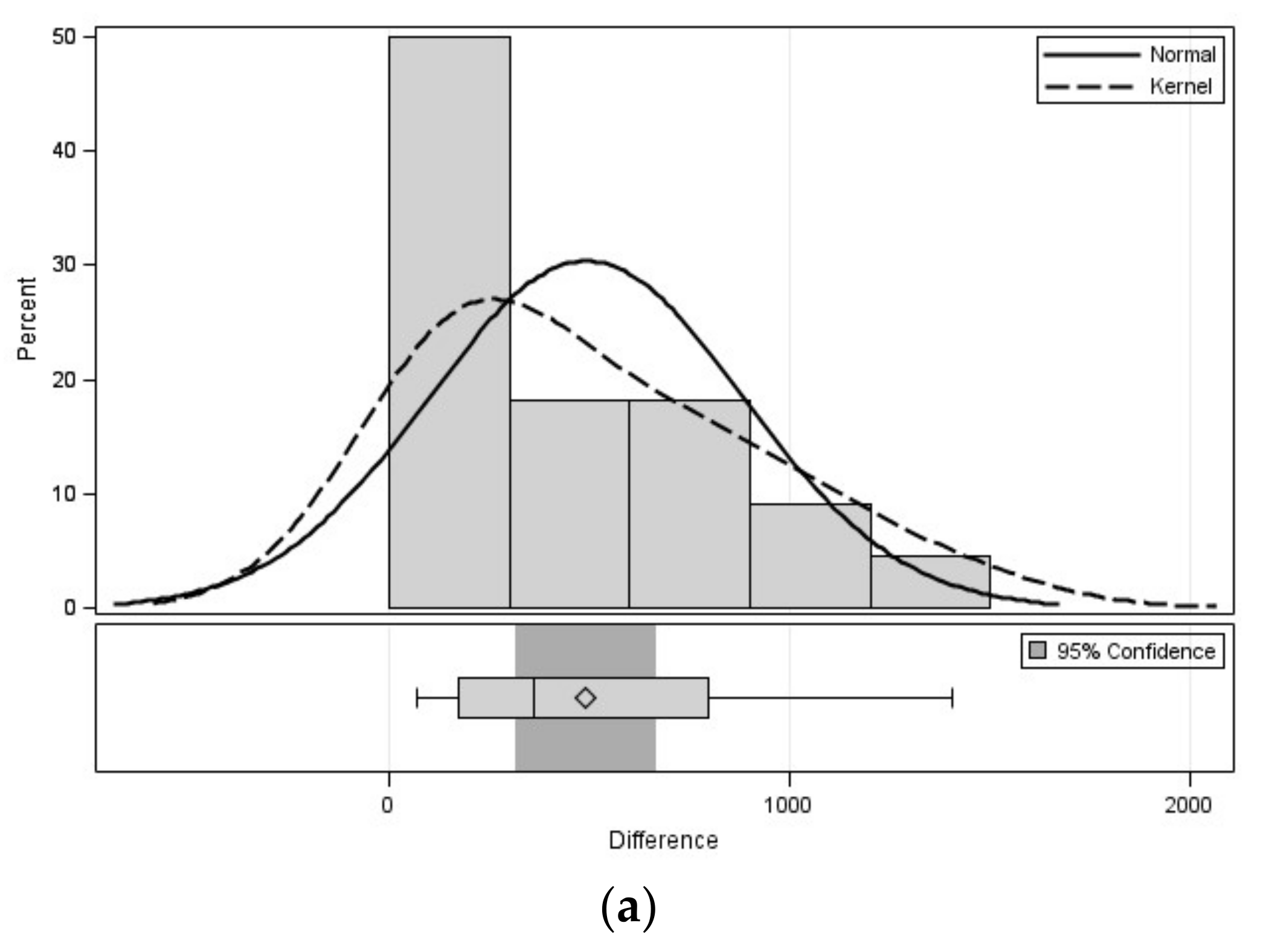
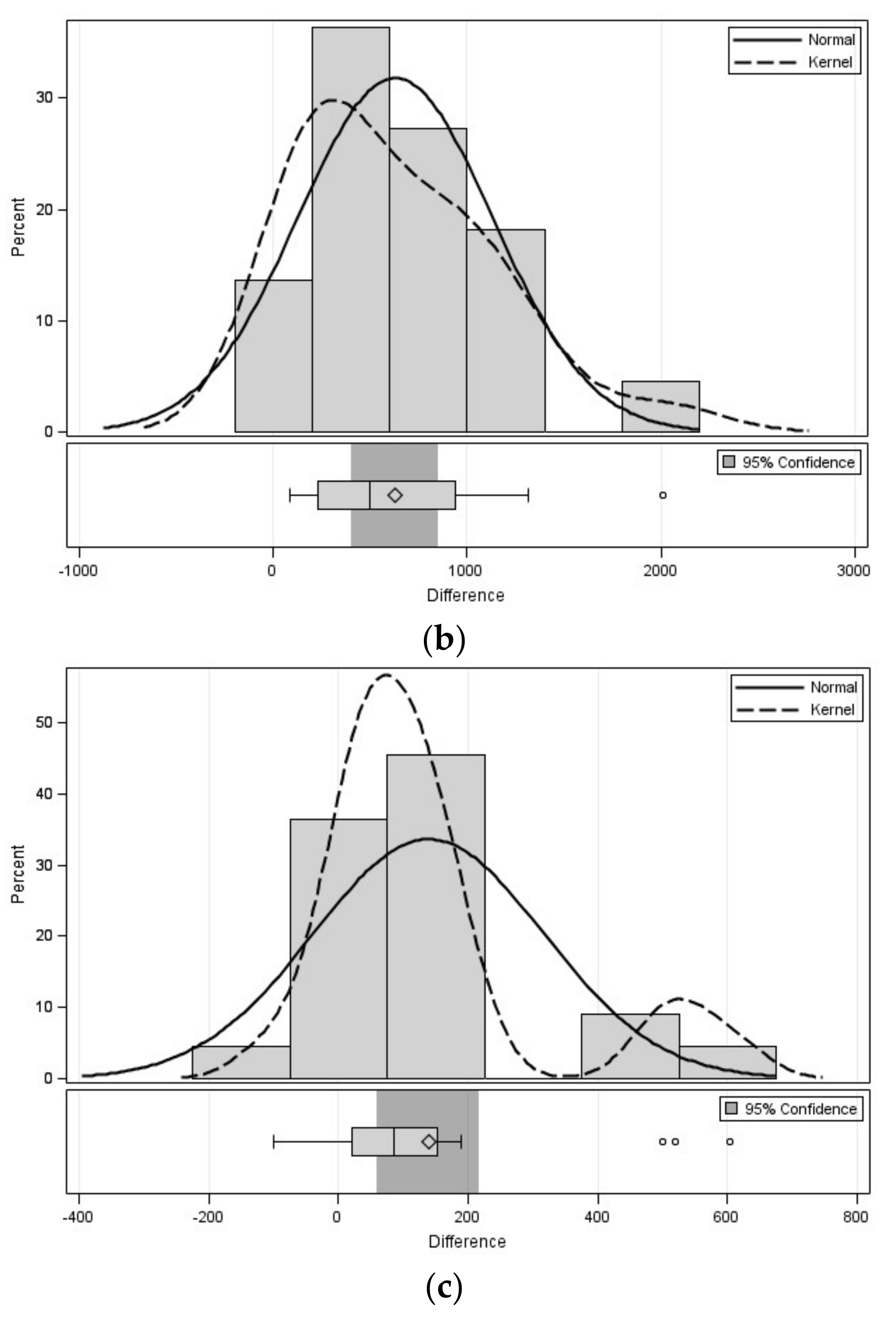
4.2. Results and Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Organisation for Economic Co-operation and Development (OECD). Delivering the Goods: 21st Century Challenges to Urban Goods Transport; OECD: Paris, France, 2003. [Google Scholar]
- Figliozzi, M.A. The impacts of congestion on time-definitive urban freight distribution networks CO2 emission levels: Results from a case study in Portland, Oregon. Transp. Res. Part C 2011, 19, 766–778. [Google Scholar] [CrossRef]
- Russo, F.; Comi, A. Urban freight transport planning towards green goals: Synthetic environmental evidence from tested results. Sustainability 2016, 8, 381. [Google Scholar] [CrossRef]
- Bassok, A.; Johnson, C.; Kitchen, M.; Maskin, R.; Overby, K.; Carlson, D.; Goodchild, A.; McCormack, E.; Wygonik, E. NCFRP Report 24: Smart Growth and Urban Goods Movement; Transportation Research Board of the National Academies: Washington, DC, USA, 2013. [Google Scholar]
- Newell, G.F.; Daganzo, C.F. Design of multiple-vehicle delivery tours—I a ring-radial network. Transp. Res. Part B 1986, 20, 345–364. [Google Scholar] [CrossRef]
- Dantzig, G.B.; Ramser, J.H. The truck dispatching problem. Manag. Sci. 1959, 6, 80–91. [Google Scholar] [CrossRef]
- Solomon, M.M. Algorithms for the vehicle routing and scheduling problems with time window constraints. Oper. Res. 1987, 35, 254–265. [Google Scholar] [CrossRef]
- Potvin, J.Y.; Rousseau, J.M. A parallel route building algorithm for the vehicle routing and scheduling problem with time windows. Eur. J. Oper. Res. 1993, 66, 331–340. [Google Scholar] [CrossRef]
- Thompson, P.M.; Psaraftis, H.N. Cyclic transfer algorithms for multivehicle routing and scheduling problems. Oper. Res. 1993, 41, 935–946. [Google Scholar] [CrossRef]
- Potvin, J.Y.; Rousseau, J.M. An exchange heuristic for routing problems with time windows. J. Oper. Res. Soc. 1995, 46, 1433–1446. [Google Scholar] [CrossRef]
- Taillard, E.; Badeau, P.; Gendreau, M.; Guertin, F.; Potvin, J.Y. A tabu search heuristic for the vehicle routing problem with soft time windows. Transp. Sci. 1997, 31, 170–186. [Google Scholar] [CrossRef]
- Tan, K.C.; Chew, Y.H.; Lee, L.H. A hybrid multiobjective evolutionary algorithm for solving vehicle routing problem with time windows. Comput. Optim. Appl. 2006, 34, 115–151. [Google Scholar] [CrossRef]
- Kallehauge, B. Formulations and exact algorithms for the vehicle routing problem with time windows. Comput. Oper. Res. 2008, 35, 2307–2330. [Google Scholar] [CrossRef]
- Toth, P.; Vigo, D. The Vehicle Routing Problem; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2002. [Google Scholar]
- Xu, H.; Chen, Z.L.; Rajagopal, S.; Arunapuram, S. Solving a practical pickup and delivery problem. Transp. Sci. 2003, 37, 347–364. [Google Scholar] [CrossRef]
- Lin, C.K.Y. A vehicle routing problem with pickup and delivery time windows, and coordination of transportable resources. Comput. Oper. Res. 2011, 38, 1596–1609. [Google Scholar] [CrossRef]
- Vidal, T.; Crainic, T.G.; Gendreau, M.; Prins, C. Heuristics for multi-attribute vehicle routing problems: A survey and synthesis. Eur. J. Oper. Res. 2013, 231, 1–21. [Google Scholar] [CrossRef]
- Daganzo, C.F. The length of tours in zones of different shapes. Transp. Res. Part B 1984, 18, 135–145. [Google Scholar] [CrossRef]
- Daganzo, C.F. The distance traveled to visit N points with a maximum of C stops per vehicle: An analytic model and an application. Transp. Sci. 1984, 18, 331–350. [Google Scholar] [CrossRef]
- Newell, G.F.; Daganzo, C.F. Design of multiple-vehicle delivery tours-II other metrics. Transp. Res. Part B 1986, 20, 365–376. [Google Scholar] [CrossRef]
- Ouyang, Y. Design of vehicle routing zones for large-scale distribution systems. Transp. Res. Part B 2007, 41, 1079–1093. [Google Scholar] [CrossRef]
- Ouyang, Y.; Daganzo, C.F. Discretization and validation of the continuum approximation scheme for terminal system design. Transp. Sci. 2006, 40, 89–98. [Google Scholar] [CrossRef]
- Holguín-Veras, J.; Thorson, E.; Wang, Q.; Xu, N.; González-Calderón, C.; Sánchez-Díaz, I.; Mitchell, J. Urban freight tour models: State of the art and practice. In Freight Transport Modelling; Ben-Akiva, M., Meersman, H., van de Voorde, E., Eds.; Emerald Group Publishing Limited: Bingley, UK, 2013; pp. 335–351. ISBN 978-1-78190-285-1. [Google Scholar]
- Nuzzolo, A.; Comi, A. Tactical and operational city logistics: Freight vehicle flow modelling. In Freight Transport Modelling; Ben-Akiva, M., Meersman, H., Van de Voorde, E., Eds.; Emerald Group Publishing Limited: Bingley, UK, 2013; pp. 433–451. ISBN 978-1-78190-285-1. [Google Scholar]
- Hwang, T.; Ouyang, Y. Urban freight truck routing under stochastic congestion and emission considerations. Sustainability 2015, 7, 6610–6625. [Google Scholar] [CrossRef]
- Crainic, T.G.; Perboli, G.; Mancini, S.; Tadei, R. Two-echelon vehicle routing problem: A satellite location analysis. Procedia Soc. Behav. Sci. 2010, 2, 5944–5955. [Google Scholar] [CrossRef]
- Perboli, G.; Tadei, R.; Vigo, D. The two-echelon capacitated vehicle routing problem: Models and math-based heuristics. Transp. Sci. 2011, 45, 364–380. [Google Scholar] [CrossRef]
- Crainic, T.G.; Perboli, G.; Rosano, M. Simulation of intermodal freight transportation systems: A taxonomy. Eur. J. Oper. Res. 2017. [Google Scholar] [CrossRef]
- Federal Highway Administration, US Department of Transportation, Freight Analysis Framework (FAF). Available online: http://www.ops.fhwa.dot.gov/freight/freight_analysis/faf/ (accessed on 19 December 2011).
- Lee, S. The Role of Urban Spatial Structure in Reducing VMT and GHG Emissions. Ph.D. Thesis, University of Illinois at Urbana-Champaign, Urbana, IL, USA, 2015. [Google Scholar]
- Elhorst, J.P. Dynamic models in space and time. Geogr. Anal. 2001, 33, 119–140. [Google Scholar] [CrossRef]
- Hwang, T. Freight Demand Modeling and Logistics Planning for Assessment of Freight Systems’ Environmental Impacts. Ph.D. Thesis, University of Illinois at Urbana-Champaign, Urbana, IL, USA, 2014. [Google Scholar]
- Fisher-Vanden, K.; Schu, K.; Sue Wing, I.; Calvin, K. Decomposing the impact of alternative technology sets on future carbon emissions growth. Energy Econ. 2012, 34, S359–S365. [Google Scholar] [CrossRef]
- Alam, M.; Rajamanickam, G. Development of Truck Payload Equivalent Factor; Federal Highway Administration, US Department of Transportation: Washington, DC, USA, 2007. [Google Scholar]
- Davis, S.C.; Diegel, S.W.; Boundy, R.G. Transportation Energy Data Book, 31 ed.; US Department of Energy: Washington, DC, USA, 2012. [Google Scholar]
- Stone, B.; Mednick, A.C.; Holloway, T.; Spak, S.N. Is compact growth good for air quality? J. Am. Plan. Assoc. 2007, 73, 404–418. [Google Scholar] [CrossRef]
- Transport Research Laboratory. Project Report SE/491/98: Methodology for Calculating Transport Emissions and Energy Consumption; Transport Research Laboratory: Crowthorne, UK, 1999. [Google Scholar]
- Perboli, G.; Musso, S.; Rosano, M.; Tadei, R.; Godel, M. Synchro-modality and slow steaming: New business perspectives in freight transportation. Sustainability 2017, 9, 1843. [Google Scholar] [CrossRef]
- Nature News: South Korea Cracks Down on Dirty Air. Available online: https://www.nature.com/news/south-korea-cracks-down-on-dirty-air-1.22448 (accessed on 29 December 2017).

| (a) MSA | (b) | (c) | (d) Total Number of Employers | (e) Employment Density (# emp/sqml) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Scenario | DCBD | 2010 | 2020 | 2030 | 2040 | 2050 | 2010 | 2020 | 2030 | 2040 | 2050 | |
| Atlanta | 1 | 3 | 328,300 | 349,474 | 362,889 | 374,372 | 383,460 | 11,617 | 12,366 | 12,841 | 13,247 | 13,569 |
| 6 | 538,336 | 583,925 | 613,019 | 638,024 | 657,878 | 4762 | 5166 | 5423 | 5644 | 5820 | ||
| 9 | 810,257 | 887,933 | 937,660 | 980,462 | 1,014,494 | 3186 | 3491 | 3687 | 3855 | 3989 | ||
| 2 | 3 | 367,829 | 444,817 | 496,818 | 542,820 | 580,137 | 13,016 | 15,740 | 17,580 | 19,208 | 20,529 | |
| 6 | 588,253 | 705,080 | 783,944 | 853,721 | 910,339 | 5204 | 6237 | 6935 | 7552 | 8053 | ||
| 9 | 865,562 | 1,021,932 | 1,126,477 | 1,218,513 | 1,292,924 | 3403 | 4018 | 4429 | 4791 | 5083 | ||
| 3 | 3 | 426,352 | 589,958 | 658,156 | 678,477 | 646,046 | 15,087 | 20,876 | 23,289 | 24,008 | 22,861 | |
| 6 | 686,339 | 973,424 | 1,188,407 | 1,388,267 | 1,556,274 | 6072 | 8611 | 10,513 | 12,281 | 13,767 | ||
| 9 | 951,096 | 1,256,260 | 1,480,259 | 1,686,834 | 1,859,622 | 3739 | 4939 | 5820 | 6632 | 7312 | ||
| Boston | 1 | 3 | 544,170 | 548,477 | 522,083 | 498,015 | 470,746 | 19,256 | 19,408 | 18,474 | 17,623 | 16,658 |
| 6 | 733,460 | 739,884 | 704,952 | 673,070 | 636,919 | 6488 | 6545 | 6236 | 5954 | 5634 | ||
| 9 | 936,928 | 945,527 | 901,301 | 860,921 | 815,120 | 3684 | 3718 | 3544 | 3385 | 3205 | ||
| 2 | 3 | 572,925 | 589,092 | 571,391 | 555,019 | 536,215 | 20,273 | 20,845 | 20,219 | 19,640 | 18,974 | |
| 6 | 761,858 | 779,962 | 753,680 | 729,447 | 701,699 | 6740 | 6900 | 6667 | 6453 | 6208 | ||
| 9 | 963,439 | 982,925 | 946,938 | 913,842 | 876,030 | 3788 | 3865 | 3723 | 3593 | 3444 | ||
| 3 | 3 | 593,708 | 618,720 | 604,880 | 592,045 | 577,281 | 21,009 | 21,894 | 21,404 | 20,950 | 20,427 | |
| 6 | 781,009 | 807,273 | 784,553 | 763,592 | 739,589 | 6909 | 7141 | 6940 | 6755 | 6543 | ||
| 9 | 981,404 | 1,008,558 | 976,057 | 946,144 | 911,983 | 3859 | 3965 | 3838 | 3720 | 3586 | ||
| Cleveland | 1 | 3 | 188,218 | 186,454 | 182,791 | 179,558 | 176,260 | 6660 | 6598 | 6468 | 6354 | 6237 |
| 6 | 308,921 | 306,123 | 300,295 | 295,153 | 289,907 | 2733 | 2708 | 2657 | 2611 | 2565 | ||
| 9 | 459,488 | 455,381 | 446,826 | 439,273 | 431,570 | 1807 | 1790 | 1757 | 1727 | 1697 | ||
| 2 | 3 | 188,403 | 187,052 | 184,232 | 181,727 | 179,170 | 6667 | 6619 | 6519 | 6431 | 6340 | |
| 6 | 309,149 | 306,846 | 302,045 | 297,779 | 293,428 | 2735 | 2714 | 2672 | 2634 | 2596 | ||
| 9 | 459,697 | 456,095 | 448,600 | 441,948 | 435,167 | 1807 | 1793 | 1764 | 1738 | 1711 | ||
| 3 | 3 | 188,568 | 187,422 | 185,035 | 182,913 | 180,747 | 6673 | 6632 | 6548 | 6473 | 6396 | |
| 6 | 309,269 | 307,102 | 302,609 | 298,616 | 294,537 | 2736 | 2717 | 2677 | 2642 | 2606 | ||
| 9 | 459,803 | 456,323 | 449,094 | 442,678 | 436,137 | 1808 | 1794 | 1766 | 1740 | 1715 | ||
| Dallas | 1 | 3 | 221,022 | 232,142 | 239,793 | 246,398 | 251,647 | 7821 | 8215 | 8485 | 8719 | 8905 |
| 6 | 468,259 | 504,205 | 529,136 | 550,761 | 568,007 | 4142 | 4460 | 4681 | 4872 | 5025 | ||
| 9 | 740,872 | 810,539 | 859,366 | 901,988 | 936,176 | 2913 | 3187 | 3379 | 3546 | 3681 | ||
| 2 | 3 | 223,109 | 256,603 | 280,606 | 301,836 | 319,024 | 7895 | 9080 | 9929 | 10,681 | 11,289 | |
| 6 | 471,382 | 540,858 | 590,444 | 634,164 | 669,472 | 4170 | 4785 | 5223 | 5610 | 5922 | ||
| 9 | 745,615 | 866,639 | 955,805 | 1,036,285 | 1,102,671 | 2932 | 3407 | 3758 | 4074 | 4335 | ||
| 3 | 3 | 231,068 | 306,652 | 368,326 | 403,977 | 402,803 | 8177 | 10,851 | 13,033 | 14,295 | 14,253 | |
| 6 | 483,298 | 685,995 | 863,376 | 1,038,421 | 1,191,599 | 4275 | 6069 | 7638 | 9186 | 10,541 | ||
| 9 | 756,542 | 999,235 | 1,201,957 | 1,397,199 | 1,565,329 | 2975 | 3929 | 4726 | 5493 | 6154 | ||
| (a) MSA | (b) | (c) Total Travel Distance (103 m Per Day) | (d) Freight Shipment (103 ton-mile Per Day) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Scenario | 2010 | 2020 | 2030 | 2040 | 2050 | 2010 | % | 2020 | % | 2030 | % | 2040 | % | 2050 | % | |
| Atlanta | 1 | 1818 | 2579 | 3417 | 4390 | 5488 | 3636 | 7.3 | 5157 | 38.4 | 6834 | 47.0 | 8780 | 53.7 | 10,976 | 57.8 |
| 2 | 1723 | 2063 | 2641 | 3312 | 4082 | 3445 | 1.6 | 4126 | 10.7 | 5282 | 13.7 | 6624 | 16.0 | 8164 | 17.4 | |
| 3 | 1695 | 1863 | 2324 | 2856 | 3478 | 3390 | 3726 | 4648 | 5712 | 6955 | ||||||
| Boston | 1 | 551 | 664 | 780 | 909 | 1053 | 1102 | 4.5 | 1328 | 11.3 | 1560 | 12.3 | 1819 | 13.4 | 2106 | 14.4 |
| 2 | 535 | 622 | 727 | 844 | 972 | 1069 | 1.4 | 1244 | 4.2 | 1454 | 4.7 | 1687 | 5.2 | 1944 | 5.6 | |
| 3 | 527 | 597 | 695 | 802 | 920 | 1054 | 1193 | 1389 | 1604 | 1841 | ||||||
| Cleveland | 1 | 554 | 661 | 781 | 916 | 1072 | 1109 | 5.8 | 1,323 | 7.8 | 1,562 | 8.3 | 1,832 | 8.6 | 2,143 | 8.7 |
| 2 | 529 | 624 | 734 | 860 | 1005 | 1058 | 1.0 | 1,247 | 1.6 | 1,469 | 1.8 | 1,719 | 1.9 | 2,009 | 1.9 | |
| 3 | 524 | 614 | 721 | 844 | 986 | 1048 | 1,227 | 1,443 | 1,687 | 1,971 | ||||||
| Dallas | 1 | 949 | 1414 | 1897 | 2462 | 3112 | 1897 | 2.9 | 2828 | 28.5 | 3793 | 35.5 | 4924 | 40.3 | 6223 | 43.2 |
| 2 | 925 | 1142 | 1471 | 1861 | 2318 | 1850 | 0.3 | 2283 | 3.8 | 2942 | 5.1 | 3722 | 6.1 | 4635 | 6.7 | |
| 3 | 922 | 1100 | 1400 | 1754 | 2173 | 1844 | 2200 | 2799 | 3509 | 4346 | ||||||
| Denver | 1 | 603 | 825 | 1070 | 1359 | 1696 | 1206 | 1.1 | 1649 | 14.4 | 2141 | 16.6 | 2718 | 18.4 | 3392 | 20.1 |
| 2 | 598 | 763 | 979 | 1231 | 1523 | 1197 | 0.3 | 1525 | 5.8 | 1958 | 6.6 | 2462 | 7.3 | 3047 | 7.9 | |
| 3 | 597 | 721 | 918 | 1147 | 1412 | 1193 | 1442 | 1837 | 2295 | 2825 | ||||||
| Detroit | 1 | 1249 | 1500 | 1781 | 2084 | 2409 | 2498 | 5.7 | 3000 | 7.4 | 3563 | 8.2 | 4168 | 9.0 | 4819 | 10.1 |
| 2 | 1196 | 1413 | 1665 | 1931 | 2211 | 2391 | 1.2 | 2826 | 1.2 | 3330 | 1.1 | 3862 | 1.0 | 4422 | 1.0 | |
| 3 | 1182 | 1397 | 1647 | 1911 | 2189 | 2363 | 2793 | 3294 | 3822 | 4378 | ||||||
| Houston | 1 | 1793 | 2452 | 3067 | 3776 | 4591 | 3586 | 1.4 | 4904 | 28.3 | 6135 | 28.6 | 7553 | 29.5 | 9182 | 31.2 |
| 2 | 1776 | 2174 | 2715 | 3330 | 4020 | 3552 | 0.4 | 4349 | 13.8 | 5430 | 13.8 | 6660 | 14.1 | 8041 | 14.9 | |
| 3 | 1768 | 1911 | 2385 | 2917 | 3500 | 3537 | 3821 | 4771 | 5834 | 7000 | ||||||
| Los Angeles | 1 | 1707 | 2240 | 2762 | 3364 | 4042 | 3414 | 3.9 | 4480 | 14.9 | 5525 | 16.3 | 6729 | 18.0 | 8085 | 19.7 |
| 2 | 1658 | 2030 | 2483 | 2996 | 3567 | 3317 | 1.0 | 4060 | 4.2 | 4966 | 4.6 | 5993 | 5.1 | 7134 | 5.6 | |
| 3 | 1642 | 1949 | 2374 | 2851 | 3377 | 3284 | 3898 | 4749 | 5702 | 6754 | ||||||
| Miami | 1 | 1622 | 2448 | 3321 | 4359 | 5554 | 3243 | 0.9 | 4896 | 3.0 | 6642 | 3.6 | 8718 | 4.0 | 11,108 | 4.3 |
| 2 | 1616 | 2386 | 3216 | 4197 | 5326 | 3231 | 0.5 | 4772 | 0.4 | 6432 | 0.3 | 8394 | 0.1 | 10,653 | 0.0 | |
| 3 | 1608 | 2376 | 3207 | 4192 | 5324 | 3215 | 4752 | 6414 | 8383 | 10,648 | ||||||
| Minneapolis | 1 | 1412 | 1874 | 2307 | 2786 | 3295 | 2824 | 2.7 | 3747 | 26.0 | 4614 | 29.4 | 5573 | 33.1 | 6589 | 37.0 |
| 2 | 1379 | 1518 | 1826 | 2152 | 2481 | 2757 | 0.2 | 3036 | 2.1 | 3652 | 2.5 | 4305 | 2.8 | 4962 | 3.1 | |
| 3 | 1375 | 1487 | 1782 | 2093 | 2406 | 2751 | 2973 | 3564 | 4187 | 4812 | ||||||
| Phoenix | 1 | 440 | 598 | 750 | 976 | 1282 | 879 | 0.2 | 1197 | 19.8 | 1500 | 20.7 | 1953 | 21.6 | 2565 | 22.2 |
| 2 | 439 | 521 | 649 | 841 | 1100 | 877 | 0.0 | 1042 | 4.3 | 1299 | 4.5 | 1681 | 4.7 | 2200 | 4.9 | |
| 3 | 439 | 500 | 621 | 803 | 1049 | 877 | 999 | 1243 | 1605 | 2098 | ||||||
| Pittsburgh | 1 | 880 | 1019 | 1155 | 1317 | 1518 | 1760 | 3.1 | 2038 | 16.9 | 2310 | 18.2 | 2634 | 19.6 | 3035 | 21.0 |
| 2 | 869 | 960 | 1082 | 1227 | 1406 | 1738 | 1.8 | 1919 | 10.1 | 2164 | 10.7 | 2453 | 11.4 | 2811 | 12.1 | |
| 3 | 854 | 872 | 977 | 1101 | 1254 | 1708 | 1743 | 1954 | 2203 | 2508 | ||||||
| Portland | 1 | 528 | 699 | 853 | 1025 | 1222 | 1057 | 0.4 | 1398 | 18.4 | 1707 | 18.8 | 2051 | 19.5 | 2444 | 20.6 |
| 2 | 527 | 627 | 763 | 915 | 1085 | 1055 | 0.2 | 1253 | 6.1 | 1527 | 6.3 | 1829 | 6.6 | 2170 | 7.1 | |
| 3 | 526 | 591 | 718 | 858 | 1013 | 1052 | 1181 | 1437 | 1716 | 2027 | ||||||
| San Diego | 1 | 939 | 1263 | 1546 | 1878 | 2253 | 1878 | 3.3 | 2526 | 32.6 | 3093 | 35.2 | 3756 | 37.7 | 4506 | 40.1 |
| 2 | 914 | 995 | 1196 | 1428 | 1685 | 1828 | 0.6 | 1991 | 4.5 | 2392 | 4.6 | 2855 | 4.7 | 3371 | 4.8 | |
| 3 | 909 | 952 | 1143 | 1363 | 1608 | 1818 | 1904 | 2287 | 2727 | 3216 | ||||||
| San Francisco | 1 | 830 | 1014 | 1220 | 1468 | 1749 | 1661 | 4.3 | 2029 | 6.6 | 2439 | 7.2 | 2935 | 8.0 | 3498 | 8.8 |
| 2 | 800 | 960 | 1147 | 1371 | 1622 | 1600 | 0.5 | 1919 | 0.8 | 2294 | 0.8 | 2742 | 0.9 | 3243 | 0.9 | |
| 3 | 796 | 952 | 1138 | 1359 | 1608 | 1593 | 1903 | 2275 | 2718 | 3215 | ||||||
| Seattle | 1 | 516 | 731 | 934 | 1171 | 1454 | 1032 | 3.7 | 1462 | 27.3 | 1868 | 31.1 | 2343 | 34.1 | 2907 | 36.3 |
| 2 | 500 | 614 | 768 | 948 | 1161 | 1000 | 0.4 | 1228 | 6.9 | 1537 | 7.8 | 1895 | 8.5 | 2322 | 8.9 | |
| 3 | 498 | 574 | 712 | 873 | 1066 | 995 | 1148 | 1425 | 1747 | 2133 | ||||||
| Tampa | 1 | 1175 | 1581 | 2043 | 2609 | 3288 | 2351 | 6.1 | 3162 | 26.5 | 4086 | 37.2 | 5218 | 49.6 | 6576 | 62.0 |
| 2 | 1137 | 1395 | 1727 | 2105 | 2531 | 2273 | 2.6 | 2789 | 11.5 | 3454 | 16.0 | 4210 | 20.7 | 5062 | 24.7 | |
| 3 | 1107 | 1250 | 1489 | 1744 | 2030 | 2215 | 2501 | 2978 | 3488 | 4059 | ||||||
| Chicago | 1 | 2858 | 3594 | 4373 | 5261 | 6258 | 5715 | 6.0 | 7189 | 15.3 | 8746 | 16.9 | 10,522 | 18.4 | 12,516 | 19.5 |
| 2 | 2708 | 3172 | 3817 | 4548 | 5369 | 5415 | 0.4 | 6344 | 1.8 | 7634 | 2.1 | 9096 | 2.3 | 10,738 | 2.5 | |
| 3 | 2696 | 3117 | 3739 | 4444 | 5237 | 5391 | 6234 | 7479 | 8888 | 10,474 | ||||||
| Philadelphia | 1 | 2039 | 2563 | 3108 | 3741 | 4490 | 4079 | 3.2 | 5127 | 14.1 | 6216 | 14.6 | 7481 | 15.2 | 8980 | 15.7 |
| 2 | 1993 | 2342 | 2831 | 3397 | 4066 | 3987 | 0.8 | 4684 | 4.2 | 5661 | 4.4 | 6793 | 4.6 | 8132 | 4.8 | |
| 3 | 1977 | 2247 | 2711 | 3247 | 3881 | 3954 | 4494 | 5423 | 6495 | 7762 | ||||||
| St. Louis | 1 | 1151 | 1424 | 1664 | 1933 | 2231 | 2301 | 1.9 | 2848 | 11.5 | 3327 | 12.1 | 3865 | 12.7 | 4461 | 13.4 |
| 2 | 1130 | 1287 | 1494 | 1723 | 1974 | 2261 | 0.1 | 2575 | 0.8 | 2988 | 0.7 | 3446 | 0.5 | 3947 | 0.4 | |
| 3 | 1129 | 1277 | 1484 | 1714 | 1967 | 2258 | 2554 | 2968 | 3428 | 3933 | ||||||
| New York | 1 | 2807 | 3756 | 4727 | 5847 | 7151 | 5614 | 4.1 | 7513 | 17.0 | 9455 | 19.4 | 11,695 | 21.3 | 14,301 | 22.6 |
| 2 | 2712 | 3278 | 4050 | 4933 | 5963 | 5424 | 0.5 | 6557 | 2.1 | 8101 | 2.3 | 9866 | 2.3 | 11,927 | 2.2 | |
| 3 | 2697 | 3210 | 3960 | 4821 | 5833 | 5395 | 6421 | 7920 | 9642 | 11,666 | ||||||
| Washington, D.C. | 1 | 1626 | 2256 | 2832 | 3498 | 4256 | 3251 | 0.9 | 4512 | 24.0 | 5663 | 25.5 | 6996 | 26.9 | 8512 | 28.3 |
| 2 | 1607 | 1773 | 2196 | 2678 | 3219 | 3214 | −0.2 | 3546 | −2.5 | 4392 | −2.7 | 5356 | −2.8 | 6439 | −3.0 | |
| 3 | 1611 | 1819 | 2257 | 2756 | 3318 | 3222 | 3,639 | 4,514 | 5512 | 6635 | ||||||
| (a) MSA | (b) | (c) Total Distance to the Assigned Terminals (103 Mile) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Scenario | 2010 | % | 2020 | % | 2030 | % | 2040 | % | 2050 | % | |
| Atlanta | 1 | 28,765 | 5.5 | 46,200 | 28.6 | 50,599 | 35.0 | 54,009 | 40.0 | 56,155 | 43.1 |
| 2 | 27,801 | 2.0 | 40,198 | 11.9 | 43,152 | 15.2 | 45,420 | 17.7 | 46,853 | 19.4 | |
| 3 | 27,266 | 35,926 | 37,473 | 38,576 | 39,246 | ||||||
| Boston | 1 | 20,670 | 5.1 | 24,131 | 12.8 | 23,929 | 14.1 | 23,660 | 15.5 | 23,127 | 16.8 |
| 2 | 20,221 | 2.8 | 23,032 | 7.7 | 22,759 | 8.5 | 22,412 | 9.4 | 21,831 | 10.2 | |
| 3 | 19,665 | 21,390 | 20,978 | 20,481 | 19,804 | ||||||
| Cleveland | 1 | 13,461 | 3.7 | 13,896 | 5.0 | 13,866 | 5.4 | 13,810 | 5.6 | 13,719 | 5.8 |
| 2 | 13,225 | 1.9 | 13,589 | 2.7 | 13,542 | 3.0 | 13,475 | 3.1 | 13,380 | 3.2 | |
| 3 | 12,979 | 13,228 | 13,153 | 13,071 | 12,971 | ||||||
| Dallas | 1 | 25,625 | 1.8 | 39,375 | 17.2 | 42,971 | 21.6 | 45,471 | 24.8 | 46,780 | 26.9 |
| 2 | 25,266 | 0.4 | 34,892 | 3.9 | 37,265 | 5.5 | 38,910 | 6.8 | 39,734 | 7.8 | |
| 3 | 25,168 | 33,595 | 35,326 | 36,426 | 36,872 | ||||||
| (a) MSA | (b) | (c) CO2 (103 kg per day) | (a) | (b) | (c) CO2 (103 kg per day) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Scenario | 2010 | 2020 | 2030 | 2040 | 2050 | MSA | Scenario | 2010 | 2020 | 2030 | 2040 | 2050 | |
| Atlanta | 1 | 1304 | 1849 | 2450 | 3148 | 3936 | Pittsburgh | 1 | 631 | 731 | 828 | 944 | 1088 |
| 2 | 1235 | 1479 | 1894 | 2375 | 2927 | 2 | 623 | 688 | 776 | 880 | 1008 | ||
| 3 | 1215 | 1336 | 1666 | 2048 | 2494 | 3 | 612 | 625 | 701 | 790 | 899 | ||
| Boston | 1 | 395 | 476 | 559 | 652 | 755 | Portland | 1 | 379 | 501 | 612 | 735 | 876 |
| 2 | 383 | 446 | 521 | 605 | 697 | 2 | 378 | 449 | 547 | 656 | 778 | ||
| 3 | 378 | 428 | 498 | 575 | 660 | 3 | 377 | 423 | 515 | 615 | 727 | ||
| Cleveland | 1 | 398 | 474 | 560 | 657 | 768 | San Diego | 1 | 673 | 906 | 1109 | 1347 | 1616 |
| 2 | 379 | 447 | 527 | 616 | 720 | 2 | 656 | 714 | 858 | 1024 | 1209 | ||
| 3 | 376 | 440 | 517 | 605 | 707 | 3 | 652 | 683 | 820 | 978 | 1153 | ||
| Dallas | 1 | 680 | 1014 | 1360 | 1765 | 2231 | San Francisco | 1 | 596 | 727 | 875 | 1052 | 1254 |
| 2 | 663 | 819 | 1055 | 1335 | 1662 | 2 | 574 | 688 | 823 | 983 | 1163 | ||
| 3 | 661 | 789 | 1004 | 1258 | 1558 | 3 | 571 | 682 | 816 | 975 | 1153 | ||
| Denver | 1 | 432 | 591 | 768 | 975 | 1216 | Seattle | 1 | 370 | 524 | 670 | 840 | 1042 |
| 2 | 429 | 547 | 702 | 883 | 1092 | 2 | 358 | 440 | 551 | 680 | 833 | ||
| 3 | 428 | 517 | 658 | 823 | 1013 | 3 | 357 | 412 | 511 | 626 | 765 | ||
| Detroit | 1 | 896 | 1076 | 1277 | 1494 | 1728 | Tampa | 1 | 843 | 1134 | 1465 | 1871 | 2358 |
| 2 | 857 | 1013 | 1194 | 1385 | 1585 | 2 | 815 | 1000 | 1238 | 1509 | 1815 | ||
| 3 | 847 | 1001 | 1181 | 1371 | 1570 | 3 | 794 | 897 | 1068 | 1251 | 1455 | ||
| Houston | 1 | 1286 | 1758 | 2200 | 2708 | 3292 | Chicago | 1 | 2049 | 2578 | 3136 | 3773 | 4488 |
| 2 | 1274 | 1559 | 1947 | 2388 | 2883 | 2 | 1942 | 2275 | 2737 | 3261 | 3850 | ||
| 3 | 1268 | 1370 | 1711 | 2092 | 2510 | 3 | 1933 | 2235 | 2682 | 3187 | 3756 | ||
| Los Angeles | 1 | 1224 | 1606 | 1981 | 2413 | 2899 | Phila- delphia | 1 | 1462 | 1838 | 2229 | 2682 | 3220 |
| 2 | 1189 | 1456 | 1781 | 2149 | 2558 | 2 | 1429 | 1679 | 2030 | 2436 | 2916 | ||
| 3 | 1178 | 1398 | 1703 | 2044 | 2422 | 3 | 1418 | 1611 | 1944 | 2329 | 2783 | ||
| Miami | 1 | 1163 | 1756 | 2381 | 3126 | 3983 | St. Louis | 1 | 825 | 1021 | 1193 | 1386 | 1600 |
| 2 | 1159 | 1711 | 2306 | 3010 | 3819 | 2 | 811 | 923 | 1071 | 1236 | 1415 | ||
| 3 | 1153 | 1704 | 2300 | 3006 | 3818 | 3 | 810 | 916 | 1064 | 1229 | 1410 | ||
| Minnea- polis | 1 | 1012 | 1344 | 1654 | 1998 | 2363 | New York | 1 | 2013 | 2694 | 3390 | 4193 | 5128 |
| 2 | 989 | 1088 | 1310 | 1543 | 1779 | 2 | 1945 | 2351 | 2905 | 3537 | 4276 | ||
| 3 | 986 | 1066 | 1278 | 1501 | 1725 | 3 | 1934 | 2302 | 2840 | 3457 | 4183 | ||
| Phoenix | 1 | 315 | 429 | 538 | 700 | 920 | Washington, D.C. | 1 | 1166 | 1618 | 2031 | 2509 | 3052 |
| 2 | 315 | 374 | 466 | 603 | 789 | 2 | 1152 | 1272 | 1575 | 1920 | 2309 | ||
| 3 | 315 | 358 | 446 | 576 | 752 | 3 | 1155 | 1305 | 1618 | 1976 | 2379 | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.; Hwang, T. Estimating Emissions from Regional Freight Delivery under Different Urban Development Scenarios. Sustainability 2018, 10, 1188. https://doi.org/10.3390/su10041188
Lee S, Hwang T. Estimating Emissions from Regional Freight Delivery under Different Urban Development Scenarios. Sustainability. 2018; 10(4):1188. https://doi.org/10.3390/su10041188
Chicago/Turabian StyleLee, Sungwon, and Taesung Hwang. 2018. "Estimating Emissions from Regional Freight Delivery under Different Urban Development Scenarios" Sustainability 10, no. 4: 1188. https://doi.org/10.3390/su10041188
APA StyleLee, S., & Hwang, T. (2018). Estimating Emissions from Regional Freight Delivery under Different Urban Development Scenarios. Sustainability, 10(4), 1188. https://doi.org/10.3390/su10041188




