Optimal Quality Strategy and Matching Service on Crowdfunding Platforms

Abstract

This paper develops a crowdfunding platform model incorporating quality and a matching service from the perspective of a two-sided market. It aims to explore the impact of different factors on the optimal quality threshold and matching service in a context of crowdfunding from the perspective of a two-sided market. We discuss the impact of different factors on the optimal quality threshold and matching service. Two important influential factors are under consideration, simultaneously. One is the quality threshold of admission and the other is the matching efficiency on crowdfunding platforms. This paper develops a two-sided market model incorporating quality, a matching service, and the characters of crowdfunding campaigns. After attempting to solve the model by derivative method, this paper identifies the mechanism of how the parameters influence the optimal quality threshold and matching service. Additionally, it compares the platform profits in scenarios with and without an exclusion policy. The results demonstrate that excluding low-quality projects is profitable when funder preference for project quality is substantial enough. Crowdfunding platform managers would be unwise to admit the quality threshold of the crowdfunding project and charge entrance fees when the parameter of funder preference for project quality is small.

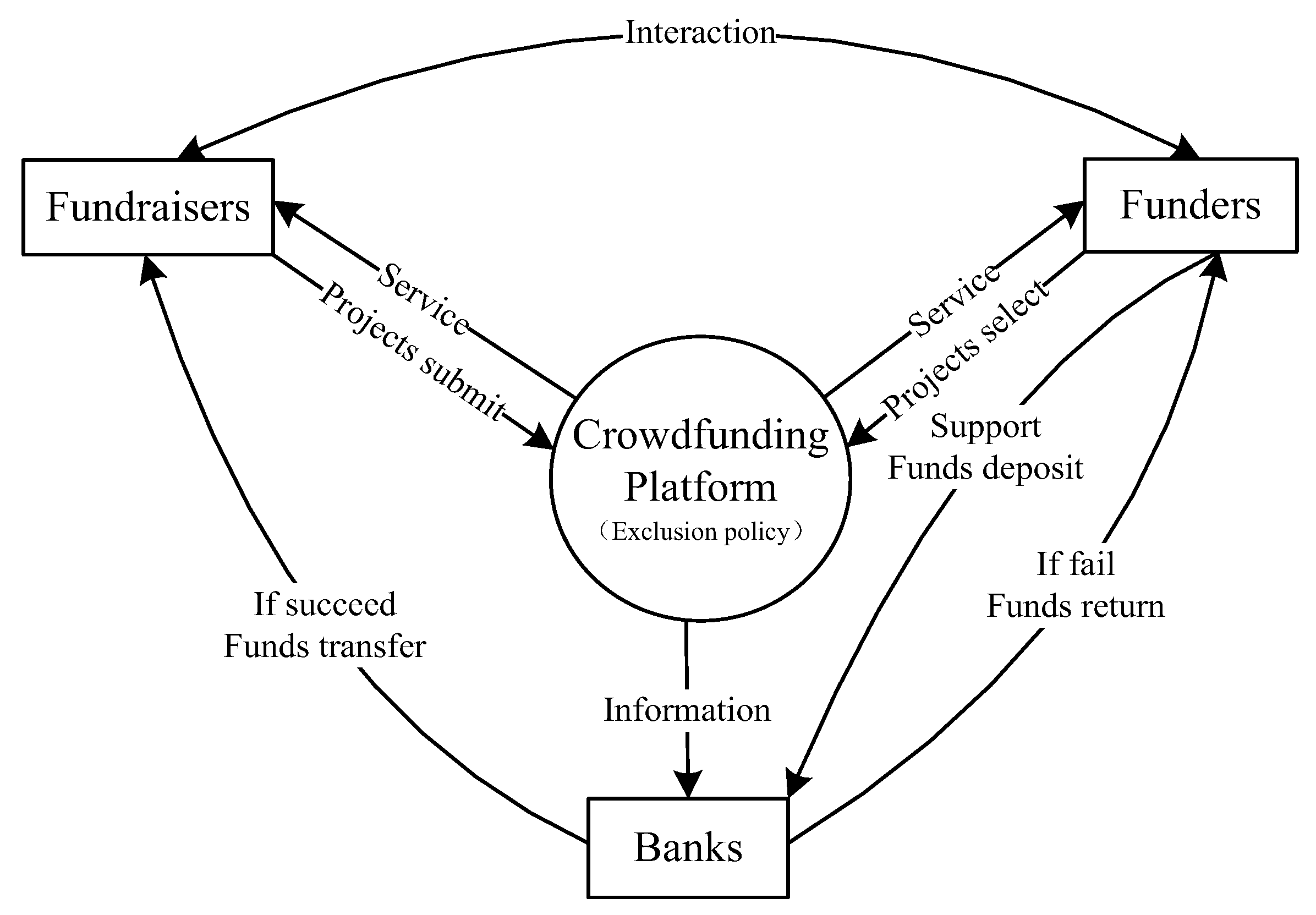
1. Introduction

Crowdfunding has been rapidly expanding as a new method of financing ventures in many countries, and it is an efficient way to fund innovative projects. It allows an entrepreneur to raise funds from the public in the form of an open call, which mostly occurs on the crowdfunding platform and provides financial support for people and organizations who do not have easy access to banks, angel investors, and venture capitalists. Massolutions released the “2015CF Crowdfunding Industry Report” in 2016, which reported crowdfunding’s tremendous growth. Global crowdfunding was a $6.1 billion market in 2013, and this figure grew 167% in 2014 to $16.2 billion. In 2015, it doubled its market share again, and it is now estimated at $34.4 billion. Because of its easily accessible and convenient features, the crowdfunding market grows rapidly. As the world’s largest crowdfunding platform, Kickstarter has enabled more than 110,000 projects to receive over $2.8 billion in funding over the past 7 years.

A crowdfunding platform is a typical two-sided market [1,2]. Crowdfunding platforms link fundraisers to funders, and they promote the success of fundraising activities. Therefore, crowdfunding platforms have the general characteristics of two-sided markets. For example, two-sided platform markets link two distinct groups, allowing one group to benefit from the other group. In the case of crowdfunding platforms, funders benefit from the number of crowdfunding projects, and fundraisers also benefit from the number of funders. Moreover, fundraisers and funders both exert positive cross-group network effects on the other side. In addition, crowdfunding platform markets have unique features. Crowdfunding platforms follow different investment models. The “All-or-Nothing” (AON) model implies that the fundraiser only receives the pledged amount if the target investment is reached. If the goal is not reached, the funds are returned to funders [3]. Most of the crowdfunding platforms choose this model, including Kickstarter. In other words, when a crowdfunding platform chooses the AON model, its crowdfunding campaigns have a possibility of success. The success rate also influences platform profits directly. A high success rate means a higher expected revenue for crowdfunding platforms. Project quality is linked to crowdfunding success, and projects with a higher quality level are more likely to be funded [3]. Therefore, crowdfunding platform managers will conduct due diligence regarding the project and restrict access to the platform for some fundraisers. Non-price governance rules are important parts of many real-world two-sided platforms, such as Microsoft, Sony, and Apple. All of these companies restrict access to some game developers and even exclude certain developers. Excluding some low-quality projects is one of the most common two-sided platform market rules for increasing the average quality of projects. Because a project requires more than one funder to reach its funding target, crowdfunding platforms also provide a one-to-many matching service for the two sides of a market. A proper match can enhance the performance of an organization [4]. A crowdfunding platform has a large number of campaigns, and good matching technology not only helps funders to find campaigns that better meet their needs but also promotes campaigns to help them reach their targeted funds. A high-level matching service makes the arrangement of funders and fundraisers more efficient, but it also raises the cost. A matching service is an important competency for crowdfunding platform markets.

Most research to date into two-sided markets focuses on two-sided pricing strategies [5,6,7]. Some recent papers study non-price strategies, including quality strategy and matching service. Damiano and Li [8] indicate the effect of quality on two-sided markets. Hagiu [9] analyzes the exclusion strategy when considering the preference for quality. Many articles mention that a crowdfunding platform is a typical two-sided market; however, few studies examine crowdfunding platforms from the perspective of a two-sided market. To the best of my knowledge, most papers on crowdfunding platforms study the determinants of funders’ investment intentions, the fraudulent behavior of founders, donor behavior in crowdfunding for non-profits, and some empirical research [10,11,12,13]. In addition, some scholars study the exclusion policy in two-sided markets, but no articles study the choice between quality and quantity on the crowdfunding platform.

This paper focuses on project quality and the matching service on crowdfunding platforms from the perspective of a two-sided market. Project quality is an important factor for funders participating in crowdfunding campaigns. A matching service, the matching technology of crowdfunding platforms, is also part of the first-party content. Crowdfunding platforms can charge higher fees resulting from an increasing number of successful projects. However, if the exclusion strategy and matching service are costly, platform profits will be damaged. Therefore, platform managers need to identify the optimal quality threshold of admission and the optimal matching service level to ensure a profit-maximizing crowdfunding platform.

Our model builds on Hagiu’s work but extends it in three ways. Hagiu’s model does not allow payments from agents on one side to the other side. Our model incorporates payments from fundraisers to funders. A matching service can impact funder utility and platform profits. Our model also includes the matching service of crowdfunding platforms, which is not reflected in Hagiu’s model. Moreover, our model assumes a specific distribution for project quality, which is not presented in Hagiu’s work.

Although some scholars study the quality threshold in two-sided markets and farmers’ markets, little theoretical work has been done on the crowdfunding platform market. Additionally, this paper studies the quality strategy and matching service on crowdfunding platforms. It contributes to the literature by extending the theory of two-sided markets to crowdfunding platform markets. Hagiu’s work builds a general model studying the choice of exclusion for a two-sided platform to maximize profits. However, the model does not incorporate the possibility of a campaign. Zheng and Kaiser [14] study farmers’ markets, but they do not consider the possibility of platform investment. We provide an analysis to model crowdfunding platforms from a two-sided market perspective. The model considers characteristics of crowdfunding platforms, such as the possibility of campaign success or the platform revenue based on a percentage of the funds for all successful campaigns.

Besides, our research also contributes to the incorporation of funder preference for quality and matching service into two-sided market rules. Additionally, our results might also be of interest to crowdfunding platform managers. Although high-quality projects will attract more funders, they may not bring high profits. This paper provides some suggestions for platform managers when they screen projects.

Additionally, the study of crowdfunding platforms also makes a contribution to boosting sustainable development. On the one hand, a crowdfunding project is not released in the market. To some extent, it can be seen as an informational mechanism that could receive evaluation and feedback from the crowd [15]. In other words, if a crowdfunding project violates the idea of sustainable development, it will be resisted by the crowdfunding platform and the crowd before reaching the market. On the other hand, the lack of funding is regarded as one of central obstacles that hinder sustainable development, while crowdfunding, as an alternative means to traditional financing, mitigates small and medium-sized enterprises' plight in financing [1,2]. Crowdfunding is also a new type of sharing economy that is being experimented with around the globe [16]. The development of crowdfunding platforms provides a beneficial and strong opportunity for sustainable economic development. This paper discusses the factors that determine the optimal quality threshold of admission and matching service on crowdfunding platforms. We find it is profitable to exclude low-quality projects when funder preference for project quality is substantial enough. Crowdfunding platform managers should not exclude low-quality crowdfunding projects and charge entrance fees when funder preference for project quality is small. The optimal exclusion strategy and the optimal matching service are related to the parameters of network externalities.

The remainder of this paper is organized as follows. Section 2 reviews the literature. Section 3 shows the two-sided crowdfunding model. We then analyze the optimal levels of matching service and exclusion on two-sided crowdfunding platforms in Section 4. Section 5 discusses and concludes the research limitations and future research directions.

2. Literature Review

Research on two-sided markets starts the study of two-sided pricing strategies [5,6,17]. Some scholars are currently studying the price strategy further. Reisinger [18] studies platforms competing in two-part tariffs that are abstracted from fixed costs per agent and transaction costs, which demonstrates that the equilibrium stays unique with the heterogeneity vanishing. Bardey et al. [19] show some specific properties of price structures when the network externality satisfies a homogeneity condition. Hagiu [20] provides a model that includes consumers’ taste for variety and producer competition, and the findings show that charging variable fees to producers helps relieve the contradiction of producer innovation incentives and platform holdup problems. Besides, Valconcelos [21] studies the exclusionary pricing in two-sided markets and finds that exclusionary pricing is beneficial and not anti-competitive in two-sided markets, while constraining prices not to be below marginal costs may give rise to inefficient social welfare. In recent years, the literature on two-sided markets has also become focused on non-price characteristics, like policy analysis and social effects. Alex and Christiaan [22] add cost asymmetries to Armstrong’s two-sided market model and improve interpretation of the Armstrong model for policy analysis. In recent years, there are scholars paying more attention to the non-price characteristics of two-sided market. Hagiu and Hałaburda [23] find that market power influences the effect of different levels of information on two-sided platform profits. In other words, a monopoly platform prefers facing more informed participants, while a competition platform has the opposite preference. Maruyama and Zennyo [24] analyze the unilateral choices of application compatibility by platforms and find that asymmetric equilibriums exist when one platform chooses incompatibility while the other chooses opposition. Another thing that is worth mentioning is that there are more and more studies focusing on different markets in the two-sided platform context. Wang S. et al. [25] study the effect of price adjustments regulation on competition in taxi-hailing markets under the O2O era. Frishammar et al. [26] focus on the two-sided markets of shopping malls and propose a strategy typology to help managers of shopping malls use omnichannel digitalization strategies to manage the transition to an increasingly digital world. Moreover, although the number of participants is important in many platform markets, participants also relate to the identities of other participants on the same platform. For example, in job search, real estate, and dating two-sided markets, participants have heterogeneous qualities, and the external network effect differs not only in the size of the network pool but also in its quality. In two-sided markets, it is common that each side may care about the number of participants on the other side as well as their quality [27]. However, the quality of participants is still the kind of field that needs to be explored further. Damiano and Li [8] introduce price competition that incorporates the effect of the quality and the number of users. In two-sided markets, each side may care about the number of participants on the other side as well as their quality [27]. In two-sided markets, Damiano and Li [8] introduce price competition that considers the effect of the quality and the number of users. Chen Y et al. explore the fundraisers’ joint decisions with regard to green crowdfunding products of different quality levels that can sufficiently satisfy consumer preferences [28]. Hagiu [9] builds a general model studying the choice of exclusion for a two-sided platform to maximize profits. Zheng and Kaiser [14] incorporate the payments from consumers to farmers and consumer preference for variety based on Hagiu’s model.

Crowdfunding platforms match fundraisers and potential funders over the internet, creating a two-sided market [29,30,31]. As an intermediary of funders and fundraisers, a crowdfunding platform provides the information and matching service between the two sides of a market. With the spread of networks, crowdfunding platforms have been attracting more and more attention from governments, regulators, and the media. Some scholars have studied crowdfunding platforms from different perspectives. Crowdfunding platforms have different business models, including those that are equity based, lending based, reward based, and donation based. Reward-based and donation-based crowdfunding platforms are particularly important types [32]. This paper studies reward-based crowdfunding campaigns. Arta Dollani et al. [33] made the ongoing project “School for Cultural Heritage through Map Exploitation” and research it as a case study. Wang N. et al. [34] illustrate the effect of the interaction between fundraisers and funders on crowdfunding success by using 959 projects from Dreamore in China. Yu et al. [35] propose the strong relationship between successful crowdfunding projects and angle investment and this effect has been increasing over time. Besides, other scholars pay attention to the development of crowdfunding platforms. Zvilichovsky et al. [36] study the dynamic funding network on crowdfunding platforms and find that campaigns initiated by fundraisers who have previously backed others will attract more funders and generate more money. Belleflamme et al. lay out key characteristics of the quickly developing crowdfunding sector and explore the economic forces that can explain the operation of these platforms. Siering et al. [12] propose deception detection support mechanisms to address internet fraud on crowdfunding platforms and analyze the effect of dynamic communication and different types of cues for identifying fraudulent behavior. Da Cruz [15] examines the informational mechanism role of crowdfunding and proposes. Additionally, signals of project quality have significant positive effects on funder investment decisions in the Chinese crowdfunding context [37]. Capital flow is the guarantee of the normal operation of crowdfunding platforms. To be specific, crowdfunding platforms generally have three revenue sources. First, platforms earn interest on the money that is invested in a given campaign because funders transfer money at the moment they invest and this money is passed on to the fundraisers only when the campaign is successful. Platforms tend to hold the fund for a several days or months. In this regard, the crowdfunding platform can earn interest on the funds. Second, some crowdfunding platforms charge for some additional services, such as add-ons for previous projects and project support. Third, many crowdfunding platforms charge a transaction fee to fundraisers based on a percent of the funds for all successful campaigns [32], and this kind of revenue is regarded as a primary source of profit for platform businesses [38].

In two-sided markets, the number of participants on one side of the platform market depends on their expectations concerning the other side of the market because of the cross-group network effect. In order to make one side more attractive to the other, some platforms supply first-party content, such as market information, website links, and other added value services for participants [39]. Network externalities exist whenever the matching quality improves as long as more alternatives become available [40]. Matching refers to the bilateral nature of exchange in two-sided markets [41]. Caillaud and Jullien [42] established a simple pairwise matching model and indicate probable matches with information technology in two-sided markets. Kim [43] refers to the matching service as matching technology, which includes search engine technology, big data technology, and metadata technology. Li et al. [44] argue that matching is a basic mechanism that influences the expectation of participants and further affects the number of platform participants, users’ utility, content providers’ profit, monopolistic media platforms’ profit, and social welfare.

Closely related to our work, Hagiu [9] builds a general model studying the choice between quality and quantity for a profit-maximizing two-sided platform. This article studies a similar problem but incorporating a matching service and crowdfunding characteristics into the general model. Zheng and Kaiser [14] incorporate the payments from consumers to farmers and consumer preference over variety based on Hagiu’s model, but the farmers’ market is somewhat different from the crowdfunding market because of the success rate and matching technology on the crowdfunding platform. Furthermore, the crowdfunding platform market is different from general two-sided markets because the project quality is not only an important factor driving funders to participate in campaigns but also closely related to the possibility of success of the projects. Thus, the quality of projects is a decisive factor in crowdfunding platform profits. The platform can charge greater service fees if the success rate is high rather than low. Additionally, a high matching service means that funders and fundraisers can find each other efficiently. On the crowdfunding platform, both project quality and matching service are notably involved with participants’ utility and platform profits. This paper mainly studies the optimal quality threshold of admission and the optimal matching service for a profit-maximizing monopoly crowdfunding platform. This paper discusses the “All or Nothing” crowdfunding platform model and assumes that both funders and fundraisers are from a single home.

3. A Two-Sided Crowdfunding Model with Quality and Matching Service

3.1. Model Set Up

Consider a two-sided crowdfunding market that maximizes profits. We assume the crowdfunding platform is a monopoly in which fundraisers are allowed to sponsor their projects on one platform and funders are allowed to invest in projects on one platform. In addition, the model allows that funders value both project quality and quantity, whereas fundraisers only value the number of funders. There are n₁ fundraisers and n₂ funders in the crowdfunding platform market. Normalize the mass of fundraisers and funders to unity. A fundraiser obtains a utility λα₁n₂ from the funders’ participation. A funder obtains a utility α(λ,$\overline{q_k}$), from the quality and quantity of the fundraiser side. The matching service λ reflects the crowdfunding platform’s matching technology, for example, search engine technology, big data technology, and metadata technology. Using these technologies, platforms provide their users with projects that better meet their needs, allowing each side of the platform to form a positive feedback loop [43]. A perfect matching service (λ = 1) means no funder and no fundraiser fail to find their favorite projects or investors. Without loss of generality, we also assume that funders and fundraisers are charged entrance fees for participating in the crowdfunding. Each fundraiser pays p₁ to the platform market and each funder pays p₂ to the platform market.

Let q_k denote the quality of project k and be uniformly distributed on [0, $\overline{{\theta }_q}$]. Jones [45] analyzes the effects of approximately 75 major software quality factors on the quality level of software applications and demonstrates that a multifaceted approach to achieving high levels of software quality is a good tool for achieving project success. The projects that are allowed to be initiated on the crowdfunding platform may not succeed in reaching the target amount because of their low quality. If the target is not reached, the campaign fails and no money flows from funders to the fundraiser. To promote the success rate of crowdfunding projects, the crowdfunding platform market sets a quality threshold q_L. We indicate the success possibility of the campaign as $\overline{q_k}$, that is, the average project quality in the market. Making use of the quality distribution, the average quality of projects can be expressed as $\overline{q_k}=\frac{q_L+\overline{{\theta }_q}}{2}$.

Each funder is assumed to invest β in each project. Each project receives an average investment βn₂ in the crowdfunding platform market. $\overline{q_k}\beta n_2$ is the expected investment amount that each fundraiser receives from funders, as they receive no revenue when the project fails to fund. Similarly, $\overline{q_k}\beta n_1$ is the amount that each funder is expected to invest in all projects. Once the project reaches its target amount, the investment from funders will be transferred to the project initiator and the platform will charge δ percent of the amount raised.

Given the specifications above, fundraiser k’s utility and funder m’s utility are specified as follows:

$$u_k=\lambda {\alpha }_1{n}_2+\overline{q_k}\beta n_2-\delta \overline{q_k}\beta n_2-p_1-{\theta }_k$$

(1)

$$u_m=V+\alpha \left(\lambda ,\overline{q_k}\right)n_1-\overline{q_k}\beta n_1-p_2-{\theta }_m$$

(2)

where V is the standalone utility derived by funders from joining the crowdfunding platform (e.g., a way of looking for novel products or spending leisure time). θ_k is a fundraiser-specific horizontal parameter that reflects the opportunity cost of fundraisers, uniformly distributed on [0, $\overline{{\theta }_1}$], such as differentiations in costs, time costs, and transportation costs. θ_m is a funder-specific horizontal parameter that can be seen as the opportunity cost of funders, similar to the definition of θ_k, uniformly distributed on [0, $\overline{{\theta }_2}$].

3.2. Demand and Profit on a Crowdfunding Platform

We suppose that the crowdfunding platform market manager is clearly aware of the quality of the projects submitted by fundraisers. To ensure that the market can exclude some fundraisers, we assume that many fundraisers expect to join the market and fundraisers’ marginal costs of submitting the project are zero. Fundraisers initiate projects on a crowdfunding platform and funders invest projects through the platform. All of the money raised by the funders will be held by banks. In the AON model, fundraisers will keep nothing unless the goal is reached; if the goal is not reached, the investment will return to funders. During the project lifetime, platforms give advice and offer services such as due diligence and consulting. The revenue of a crowdfunding platform contains two parts. One is the revenue from participant entrance, and the other is based on a certain percent of the funds for all successful campaigns. Figure 1 displays the relationship between a crowdfunding platform, funders, and fundraisers.

From the uniform distributions of q_k and θ_k, the fundraiser’s number can be expressed as

$$\begin{array}{l}{n}_1=\mathrm{Prob}\lfloor {\theta }_1\le \left(\lambda {\alpha }_1+\overline{q_k}\beta -\delta \overline{q_k}\beta \right)n_2-p_1\rfloor \mathrm{Prob}\left[q_k\ge q_L\right]\\ =\frac{\left(\lambda {\alpha }_1+\overline{q_k}\beta -\delta \overline{q_k}\beta \right)n_2-p_1}{\overline{{\theta }_1}}{\displaystyle \underset{q_L}{\overset{\overline{{\theta }_q}}{\int }}\frac{1}{\overline{{\theta }_q}}dq}\\ =\frac{\left(\lambda {\alpha }_1+\overline{q_k}\beta -\delta \overline{q_k}\beta \right)n_2-p_1}{\overline{{\theta }_1}}\times \left(1-\frac{q_L}{\overline{{\theta }_q}}\right)\end{array}$$

(3)

If there are no constraints on project quality threshold in the crowdfunding text, all of the fundraisers paying for the entry will participate in the crowdfunding platform. While because of the exclusion policy, as shown in Equation (3), only a portion of $1-\frac{q_L}{\overline{{\theta }_q}}$ fundraisers are allowed to sponsor projects among those who are willing to pay the entrance fee to enter. From the Equation (3), it is obvious that the fundraiser’s number is negatively related to the quality threshold q_L.

$\alpha \left(\lambda ,\overline{q_k}\right)$ increases with λ and $\overline{q_k}$. We refer to α₂ as the parameters of the funder network effect, depending on the size of fundraisers, and α₃ as funder preference for quality. Both α₂ and α₃ are positive. Without the loss of generality, the expression is given as $\alpha \left(\lambda ,\overline{q_k}\right)={\alpha }_2\lambda +{\alpha }_3\overline{q_k}$. Because θ_m is uniformly distributed on [0, $\overline{{\theta }_2}$], we can deduce the funder demand equation:

$$n_2=\frac{V+\left(\lambda {\alpha }_2+{\alpha }_3\frac{q_L+\overline{{\theta }_q}}{2}-\frac{q_L+\overline{{\theta }_q}}{2}\beta \right)n_1-p_2}{\overline{{\theta }_2}}$$

(4)

Making use of Equations (3) and (4), we obtain the inverse demand functions for the fundraiser and funder sides, and then express the inverse demand functions as follows:

$$p_1=\left(\lambda {\alpha }_1+\frac{q_L+\overline{{\theta }_q}}{2}\beta -\delta \frac{q_L+\overline{{\theta }_q}}{2}\beta \right)n_2-\frac{\overline{{\theta }_1}{n}_1}{\left(1-\frac{q_L}{\overline{{\theta }_q}}\right)}$$

(5)

$$p_2=V+\left(\lambda {\alpha }_2+{\alpha }_3\frac{q_L+\overline{{\theta }_q}}{2}-\frac{q_L+\overline{{\theta }_q}}{2}\beta \right)n_1-\overline{{\theta }_2}{n}_2$$

(6)

Although people have easy access to crowdfunding projects on different crowdfunding platforms, it does not automatically mean that there is no cost entering into the crowdfunding market. Specifically, for the fundraisers, they are likely to spend money in choosing a satisfactory crowdfunding platform to initiate a project or advertise a project. For the funders, they also need to pay for additional services in order to take advantage of information. Accordingly, the cost that fundraisers and funders have to pay is a kind of revenue for crowdfunding platforms. In this study, we assume the sources of revenues in a crowdfunding platform context are entrance fees and transaction fees. The cost of a crowdfunding platform market contains three parts: the matching-related cost, the quality-related cost, and the platform market cost, which has nothing to do with the quality and matching service. The entire cost is (f₀ + f₁λ² + f₂$\overline{q_k}$)n₁n₂, where item n₁n₂ is the size of the platform market and the f₀, f₁, f₂ parameters are all positive. The f₁λ² is the matching-related cost per fundraiser per funder, and f₂$\overline{q_k}$ is the quality-related cost per fundraiser per funder. The cost of the matching service is higher when the size of the crowdfunding platform market is greater because of the increased investment in hardware and software. Referring to [39], we express the costs of the matching service by λ². The profit of the crowdfunding platform market is expressed as follows

$$\pi =n_1{p}_1+n_2{p}_2+\delta \overline{q_k}\beta n_1{n}_2-\left(f_0+f_1{\lambda }^2+f_2\overline{q_k}\right)n_1{n}_2$$

(7)

By taking the first-order conditions for profit maximization, we obtain four functions as follows:

$$\frac{\partial \pi }{\partial n_1}=\left[\lambda \left({\alpha }_1+{\alpha }_2\right)+\frac{\left({\alpha }_3-f_2\right)\left(q_L+\overline{{\theta }_q}\right)}{2}-f_0-f_1{\lambda }^2\right]n_2-\frac{2\overline{{\theta }_1}}{1-\frac{q_L}{\overline{{\theta }_q}}}$$

(8)

$$\frac{\partial \pi }{\partial n_2}=V+\left[\lambda \left({\alpha }_1+{\alpha }_2\right)+\frac{\left({\alpha }_3-f_2\right)\left(q_L+\overline{{\theta }_q}\right)}{2}-f_0-f_1{\lambda }^2\right]n_1-2\overline{{\theta }_2}{n}_2$$

(9)

$$\frac{\partial \pi }{\partial \lambda }=\left({\alpha }_1+{\alpha }_2-2f_1\lambda \right)n_1{n}_2$$

(10)

$$\frac{\partial \pi }{\partial q_L}=-\frac{\overline{{\theta }_1}\overline{{\theta }_q}{n}_1^2}{{\left(\overline{{\theta }_q}-q_L\right)}^2}+\frac{{\alpha }_3-f_2}{2}{n}_1{n}_2$$

(11)

If funders have no preference for project quality (α₃ = 0, f₂ = 0), the platform profits decrease with the optimal quality threshold of admission under the condition $-\frac{\overline{{\theta }_1}\overline{{\theta }_q}{n}_1^2}{{\left(\overline{{\theta }_q}-q_L\right)}^2}<0$. When funders do not care about project quality, there is no incentive for platform managers to exclude any project.

4. Optimal Levels of Matching Service and Exclusion

4.1. Parameter Analysis

The item (α₃ − f₂) stands for net utility that fundraisers get from the increased quality threshold. Throughout this article, we assume $\left({\alpha }_3-f_2\right)>0$, ${\left({\alpha }_1+{\alpha }_2\right)}^2-4f_0{f}_1>0$ to make the result more generalizable. We make these first-order partial derivative conditions of Equations (8)–(11) zero. By making these first-order partial derivative conditions zero, we conclude that the optimal matching service and the optimal quality threshold are

$${\lambda }^{*}=\frac{{\alpha }_1+{\alpha }_2}{2f_1}$$

(12)

$${q_L}^{*}=\frac{\overline{{\theta }_q}}{3}-\frac{{\left({\alpha }_1+{\alpha }_2\right)}^2-4f_0{f}_1}{6f_1\left({\alpha }_3-f_2\right)}$$

(13)

Proposition 1.

The optimal matching service level of a crowdfunding platform market increases with the parameter of the fundraiser network effect α₁ and the parameter of the funder network effect α₂, and decreases with the parameter of matching-related cost f₁.

Proof. 

α₁, α₂ and f₁ are all positive, so it is straightforward to see that λ increases with α₁, α₂ and decreases with f₁.

A crowdfunding platform provides a one-to-many matching service for the two sides. The increase in α₁ and α₂ reflects fundraisers’ valuation of the size of funders, and funders’ valuation of the size of fundraisers increases. Crowdfunding platform managers can enhance matching technology to attract more funders and fundraisers and match them efficiently. However, if promoting the matching service is costly, then the platform market has less incentive to promote the matching service.

Proposition 2.

The optimal quality threshold of admission q_L of the crowdfunding platform market decreases with the parameter of the fundraiser network effect α₁, the parameter of the funder network effect α₂, and the parameter of quality-related cost; it increases with the parameter related to project quality α₃.

Proof. 

By differentiating the first-order condition (13) with respect to α₁, α₂, and α₃, we obtain

$$\frac{\partial q_L^{*}}{\partial {\alpha }_1}=-\frac{{\alpha }_1+{\alpha }_2}{3f_1\left({\alpha }_3-f_2\right)}$$

$$\frac{\partial q_L^{*}}{\partial {\alpha }_2}=-\frac{{\alpha }_1+{\alpha }_2}{3f_1\left({\alpha }_3-f_2\right)}$$

$$\frac{\partial q_L^{*}}{\partial {\alpha }_3}=\frac{{\left({\alpha }_1+{\alpha }_2\right)}^2-4f_0{f}_1}{6f_1{\left({\alpha }_3-f_2\right)}^2}$$

(14)

Given ${\left({\alpha }_1+{\alpha }_2\right)}^2-4f_0{f}_1>0$ and $\left({\alpha }_3-f_2\right)>0$, we are able to obtain $\partial q_L^{*}/\partial {\alpha }_1<0$, $\partial q_L^{*}/\partial {\alpha }_2<0$ and $\partial q_L^{*}/\partial {\alpha }_3>0$.

The parameters α₁ and α₂ have a negative effect on q_L^*; however, α₃ has positive effect on q_L^*. If funders add more value to the number of fundraisers, then an additional fundraiser admitted to the market will have a higher utility. Attracting more funders to the market can generate more revenue. Because funders value the number of fundraisers, one way to attract more funders is to lower the quality threshold. When funders have a higher preference for quality, the project quality matters more to funders, spurring the crowdfunding platform to establish a higher quality threshold of admission to increase average project quality in the market.

Proposition 3.

The optimal quality threshold of admission for a crowdfunding platform market increases with the parameter of project quality spread $\overline{{\theta }_q}$, the platform market cost f₀, and the parameter of matching-related cost f₁; it decreases with the parameter of quality-related cost f₂.

Proof. 

By differentiating the first-order condition (13) with respect to $\overline{{\theta }_q}$, f₁, f₂, f₃, we obtain

$$\frac{\partial q_L^{*}}{\partial \overline{{\theta }_q}}=\frac{1}{3},\frac{\partial q_L^{*}}{\partial f_0}>0,\frac{\partial q_L^{*}}{\partial f_1}>0,\frac{\partial q_L^{*}}{\partial f_2}<0$$

(15)

which reflects that the parameters of project quality spread and the platform market cost have a positive relationship with the optimal quality threshold of admission q_L^*. The parameter of quality-related cost f₂ has a negative effect on the optimal quality threshold of admission q_L^*. A higher $\overline{{\theta }_q}$ means that fundraisers have greater differentiation in the quality dimension. It is only a proportion of $\left(1-\frac{q_L}{\overline{{\theta }_q}}\right)$ fundraisers that are actually allowed to enter the market as the exclusion policy. When the admission threshold increases with the project quality spread, the proportion of $\left(1-\frac{q_L}{\overline{{\theta }_q}}\right)$ may remain unchanged. In this sense, a higher $\overline{{\theta }_q}$ allows a higher quality threshold of admission for a crowdfunding platform market.

The parameter of the platform market cost has a positive effect on the quality threshold. A higher f₀ and f₁ mean higher operating costs regardless of the quality threshold of admission. The market managers have an incentive to control costs. Lowering the quality threshold can decrease the average quality, and thus the platform market costs related to project average quality will decrease.

Proposition 4.

The maximum optimal quality threshold of admission for a crowdfunding platform market is $\frac{\overline{{\theta }_q}}{3}$; the parameter of funder preference for quality α₃ has to be sufficiently large compared to the parameters of fundraiser network effect α₁ and funder network effect α₂. Only when the condition ${\alpha }_3>\frac{{\left({\alpha }_1+{\alpha }_2\right)}^2-4f_0{f}_1}{2f_1\overline{{\theta }_q}}+f_2$ is satisfied can the platform market exclude the positive number of fundraisers.

Proof. 

Given Equation (13), when the condition q_L > 0 is established, we can obtain ${\alpha }_3>\frac{{\left({\alpha }_1+{\alpha }_2\right)}^2-4f_0{f}_1}{2f_1\overline{{\theta }_q}}+f_2$. q_L = 0 means all fundraisers who are willing to pay access fees are allowed to access the platform. The platform excludes some fundraisers of low quality when the condition q_L > 0 is established. It happens that only when α₃ is large enough will the crowdfunding platform market establish an exclusion policy.

Because of the assumption $\left({\alpha }_3-f_2\right)>0$ and ${\left({\alpha }_1+{\alpha }_2\right)}^2-4f_0{f}_1>0$, the maximum optimal quality threshold of admission for a crowdfunding platform market is $\frac{\overline{{\theta }_q}}{3}$. Proposition 4 indicates that only when α₃ is sufficiently large will the platform manager establish an exclusion policy. Although funder preference for project quality provides the crowdfunding platform market an incentive to exclude some fundraisers, this type of motivation does not necessarily result in the platform excluding fundraisers of low project quality. When the funder preference for quality is not high enough, the platform market might decide not to implement an exclusion policy.

Table 1. How the parameters affect the optimal quality threshold, matching service, and demand.

Parameters of		Variables
		qL *	λ *	n1 *	n2 *
Fundraiser network effect	α1	+	+	+	+
Funder network effect	α2	+	+	+	+
Funder preference for quality	α3	−	0	+ *	+ *
Platform market cost	f0	+	0	−	−
Platform market cost related to matching service	f1	0	−	−	−
Platform market cost related to quality	f2	−	0	− *	− *
Project quality spread	$\overline{{\theta }_q}$	+	0	+ *	+ *
Fundraiser cost differentiation	$\overline{{\theta }_1}$	0	0	0	0
Funder cost differentiation	$\overline{{\theta }_2}$	0	0	0	0
Funder stand-alone utility	V	0	0	+	+

Note. * The sign is obtained under the condition that q_L > 0; the signs with a superscript “*” are discussed under the condition that the quality threshold of admission is positive.

reveals how the optimal quality threshold, the optimal matching service, and the optimal demand of fundraisers and funders change based on the 10 exogenous parameters. These results are summarized in Proposition 5.

Proposition 5.

The optimal demand of fundraisers and funders increases with the project quality spread $\overline{{\theta }_q}$, funder standalone utility V, the parameters of fundraisers network effect α₁, and funders network effect α₂; it decreases with platform market cost f₀, platform market cost related to matching service f₁, and platform market cost related to quality f₂. Funder preference for quality α₃ increases the demand of funders and decreases the demand of fundraisers.

Proof. 

Making use of the solutions to the optimal quality threshold of admission for crowdfunding platform market q_L^* and the optimal matching service λ^*, plugging Equation (11) into Equation (9), we obtain the optimal fundraiser demand and the funder demand.

$${n_1}^{*}=\frac{6V{f}_1{\left[4\overline{{\theta }_q}{f}_1\left({\alpha }_3-f_2\right)+{\left({\alpha }_1+{\alpha }_2\right)}^2-4f_0{f}_1\right]}^2}{864\overline{{\theta }_1}\overline{{\theta }_2}\overline{{\theta }_q}{f}_1^3\left({\alpha }_3-f_2\right)-{\left[4\overline{{\theta }_q}{f}_1\left({\alpha }_3-f_2\right)+{\left({\alpha }_1+{\alpha }_2\right)}^2-4f_0{f}_1\right]}^3}$$

(16)

$${n_2}^{*}=\frac{432V\overline{{\theta }_1}\overline{{\theta }_q}{f}_1^3\left({\alpha }_3-f_2\right)}{864\overline{{\theta }_1}\overline{{\theta }_2}\overline{{\theta }_q}{f}_1^3\left({\alpha }_3-f_2\right)-{\left[4\overline{{\theta }_q}{f}_1\left({\alpha }_3-f_2\right)+{\left({\alpha }_1+{\alpha }_2\right)}^2-4f_0{f}_1\right]}^3}$$

(17)

For the purpose of brevity, let $A=4\overline{{\theta }_q}{f}_1\left({\alpha }_3-f_2\right)$ and $B={\left({\alpha }_1+{\alpha }_2\right)}^2-4f_0{f}_1$; therefore,

$${n_1}^{*}=\frac{6V{f}_1{\left(A+B\right)}^2}{216\overline{{\theta }_1}\overline{{\theta }_2}{f}_1^{2}A-{\left(A+B\right)}^3}$$

(18)

$${n_2}^{*}=\frac{108V\overline{{\theta }_1}{f}_1^{2}A}{216\overline{{\theta }_1}\overline{{\theta }_2}{f}_1^{2}A-{\left(A+B\right)}^3}$$

(19)

By differentiating the first-order condition (18), in (19), we obtain

$$\frac{\partial {n_1}^{*}}{\partial {\alpha }_1}=\frac{12V{f}_{1}A\left({\alpha }_1+{\alpha }_2\right)\left[532\overline{{\theta }_1}\overline{{\theta }_2}{f}_1^{2}A+{\left(A+B\right)}^3\right]}{{\left[216\overline{{\theta }_1}\overline{{\theta }_2}{f}_1^{2}A-{\left(A+B\right)}^3\right]}^2},$$

$$\frac{\partial {n_1}^{*}}{\partial {\alpha }_2}=\frac{12V{f}_{1}A\left({\alpha }_1+{\alpha }_2\right)\left[532\overline{{\theta }_1}\overline{{\theta }_2}{f}_1^{2}A+{\left(A+B\right)}^3\right]}{{\left[216\overline{{\theta }_1}\overline{{\theta }_2}{f}_1^{2}A-{\left(A+B\right)}^3\right]}^2}$$

$$\frac{\partial {n_1}^{*}}{\partial {\alpha }_3}=\frac{24V{f}_1^2\overline{{\theta }_q}\left(A+B\right)\left[216\overline{{\theta }_1}\overline{{\theta }_2}\left(A-B\right)+{\left(A+B\right)}^3\right]}{{\left[216\overline{{\theta }_1}\overline{{\theta }_2}{f}_1^{2}A-{\left(A+B\right)}^3\right]}^2}$$

$$\frac{\partial {n_2}^{*}}{\partial {\alpha }_1}=\frac{648V\overline{{\theta }_1}{f_1}^{2}A{\left({\alpha }_1+{\alpha }_2\right)}^2{\left(A+B\right)}^2}{{\left[216\overline{{\theta }_1}\overline{{\theta }_2}{f}_1^{2}A-{\left(A+B\right)}^3\right]}^2}$$

$$\frac{\partial {n_2}^{*}}{\partial {\alpha }_2}=\frac{648V\overline{{\theta }_1}{f_1}^{2}A{\left({\alpha }_1+{\alpha }_2\right)}^2{\left(A+B\right)}^2}{{\left[216\overline{{\theta }_1}\overline{{\theta }_2}{f}_1^{2}A-{\left(A+B\right)}^3\right]}^2}$$

$$\frac{\partial {n_2}^{*}}{\partial {\alpha }_3}=\frac{432V\overline{{\theta }_1}\overline{{\theta }_q}{f_1}^3\left(2A-B\right){\left(A+B\right)}^2}{{\left[216\overline{{\theta }_1}\overline{{\theta }_2}{f}_1^{2}A-{\left(A+B\right)}^3\right]}^2}$$

(20)

Note all the above were derived by requiring the condition that q_L > 0 holds. q_L > 0, and equivalently, A − B > 0. Thus, we obtain

$$\frac{\partial {n_1}^{*}}{\partial {\alpha }_1}>0,\frac{\partial {n_1}^{*}}{\partial {\alpha }_2}>0,\frac{\partial {n_1}^{*}}{\partial {\alpha }_3}>0,\frac{\partial {n_2}^{*}}{\partial {\alpha }_1}>0,\frac{\partial {n_2}^{*}}{\partial {\alpha }_2}>0,\frac{\partial {n_2}^{*}}{\partial {\alpha }_3}>0$$

(21)

which reflects parameters of fundraiser network effect α₁, funder network effect α₂, and funder preference for quality α₃, all of which have a positive effect on funder demand. The parameters of fundraiser network effect α₁ and funder network effect α₂ have a positive effect on fundraiser demand. Because the proportion of $\left(1-\frac{q_L}{\overline{{\theta }_q}}\right)$ fundraisers actually allowed to enter the market increases with the parameter of fundraiser quality spread $\overline{{\theta }_q}$, a larger quality spread $\overline{{\theta }_q}$ increases the optimal fundraiser demand. In contrast, the cost parameters of platform market cost f₀, platform market cost related to matching service f₁, and platform market cost related to quality f₂ decrease demand. This result is not surprising: a higher cost per fundraiser per funder provides the crowdfunding platform market with an incentive to restrict the number of fundraisers and funders.

Finally, the parameters of fundraiser cost differentiation and funder cost differentiation decrease the optimal demand of fundraiser and funder, whereas they have no effect on the optimal quality threshold of admission q_L^* and the optimal matching service λ^*. The parameter of funder standalone utility enhances the demand of fundraiser and funder but does not affect the optimal quality threshold q_L^* or the optimal matching service λ^*.

Proposition 6.

The exclusion strategy is optimal when the number of fundraisers n₂ is large enough relative to the number of funders n₂. In addition, when the project quality spread $\overline{{\theta }_q}$ is larger or the parameter of funder preference for quality α₃ is higher, the exclusion strategy is also optimal.

Proof. 

We assume profit is π₀ when the crowdfunding platform has no exclusion policy, and profit is π when the crowdfunding platform has established the project quality of admission. q_L = 0 means that all fundraisers who are willing to pay access fees are allowed to access the platform. q_L > 0 means that the platform excludes some low-quality fundraisers. If there is no quality threshold (q_L = 0), the optimal fundraiser demand and the funder demand are

$$n_1=\frac{\left(\lambda {\alpha }_1+\overline{q_k}\beta -\delta \overline{q_k}\beta \right)n_2-p_1}{{\theta }_1}$$

(22)

$$n_2=\frac{V+\left(\lambda {\alpha }_2+{\alpha }_3\overline{q_k}-\overline{q_k}\beta \right)n_1-p_2}{{\theta }_2}$$

(23)

Making use of Equations (21) and (22), we obtain the inverse demand function as the following:

$$p_1=\left(\lambda {\alpha }_1+\overline{q_k}\beta -\delta \overline{q_k}\beta \right)n_2-\overline{{\theta }_1}{n}_1$$

(24)

$$p_2=V+\left(\lambda {\alpha }_2+{\alpha }_3\overline{q_k}-\overline{q_k}\beta \right)n_1-\overline{{\theta }_2}{n}_2$$

(25)

Market profits with no exclusion can be expressed as

$$\begin{array}{l}{\pi }_0=n_1{p}_1+n_2{p}_2+\delta \overline{q_k}\beta n_1{n}_2-\left(f_0+f_1{\lambda }^2+f_2\overline{q_k}\right)n_1{n}_2\\ =\left[\left(\lambda {\alpha }_1+\frac{\overline{{\theta }_q}}{2}\beta -\delta \frac{\overline{{\theta }_q}}{2}\beta \right)n_2-\overline{{\theta }_1}{n}_1\right]n_1+\left[V+\left(\lambda {\alpha }_2+{\alpha }_3\frac{\overline{{\theta }_q}}{2}-\frac{\overline{{\theta }_q}}{2}\beta \right)n_1-\overline{{\theta }_2}{n}_2\right]n_2\\ +\delta \frac{\overline{{\theta }_q}}{2}\beta n_1{n}_2-\left(f_0+f_1{\lambda }^2+f_2\frac{\overline{{\theta }_q}}{2}\right)n_1{n}_2\end{array}$$

(26)

To obtain the condition of exclusion, we make ${\pi }_0<\pi$. Then, we derive

$$\frac{n_2}{n_1}<\frac{4\overline{{\theta }_q}{\alpha }_3{f}_1\left({\alpha }_3-f_2\right)+{\alpha }_3{\left({\alpha }_1+{\alpha }_2\right)}^2-4f_0{f}_1{\alpha }_3}{12f_1\left({\alpha }_3-f_2\right)}$$

(27)

The result reveals that the larger the project quality spread, the easier it is to meet the inequation. Thus, the exclusion regime is optimal either when the number of fundraisers is large enough relative to the number of funders or when the funder preference for project quality is higher.

4.2. Simulation Results

In this part, we present the simulation results for the two-sided market. The condition of ${\alpha }_3>\frac{{\left({\alpha }_1+{\alpha }_2\right)}^2-4f_0{f}_1}{2f_1\overline{{\theta }_q}}+f_2$ provides us with a positive quality threshold of admission is 3.5. Without loss of generality, we assign the proportion that platforms charge from all the raised money as 3%. Thus we change the parameter of funder preference over quality from 3.4 to 5 and other parameters are assigned in

Table 2. The numerical values used for the 10 parameters.

${\alpha }_1$	${\alpha }_2$	${\alpha }_3$	$f_0$	$f_1$	$f_2$	$\overline{{\theta }_1}$	$\overline{{\theta }_2}$	$\overline{{\theta }_q}$	$V$
1	1	Changing from 3.4 to 5	0.5	0.5	0.5	3	3	1	4

.

The parameter α₃ represents the strength of funder preference over project quality. We use a numerical example to show how the key parameter exerts influence on the optimal quality threshold, the price, the demand, and the matching service. From Figure 2, we find the optimal quality threshold increases with the funder preference over project quality under the condition of ${\alpha }_3>\frac{{\left({\alpha }_1+{\alpha }_2\right)}^2-4f_0{f}_1}{2f_1\overline{{\theta }_q}}+f_2$. The amount of fundraisers decreases by 0.1% when the parameter changes from 3.4 to 5. This means when the platform set up the quality threshold, the size of fundraisers changes slightly even though the funder preference over project quality is increasingly strengthening. From Figure 3, it can be seen that a higher α₃ increases funder demand. The size of funders increases from 53.3 to 54%. Increased numbers of funders in turn increases the willingness of fundraisers to enter the crowdfunding platform market. Figure 4 shows that a higher α₃ leads to the crowdfunding platform market exclude more projects and more fundraisers, while the two forces finally make negative correlation between the parameter α₃ and the demand of fundraisers.

5. Discussion and Conclusions

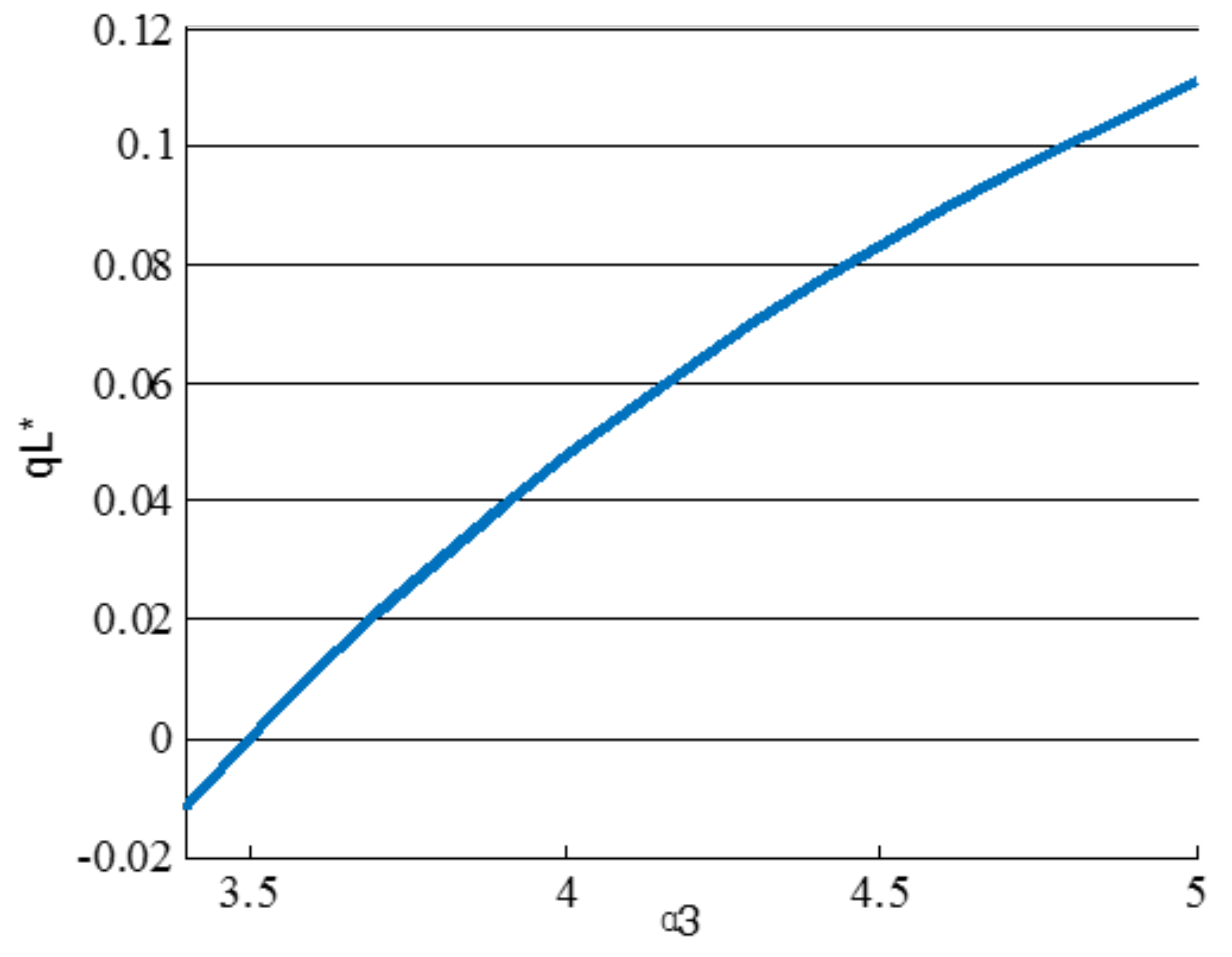
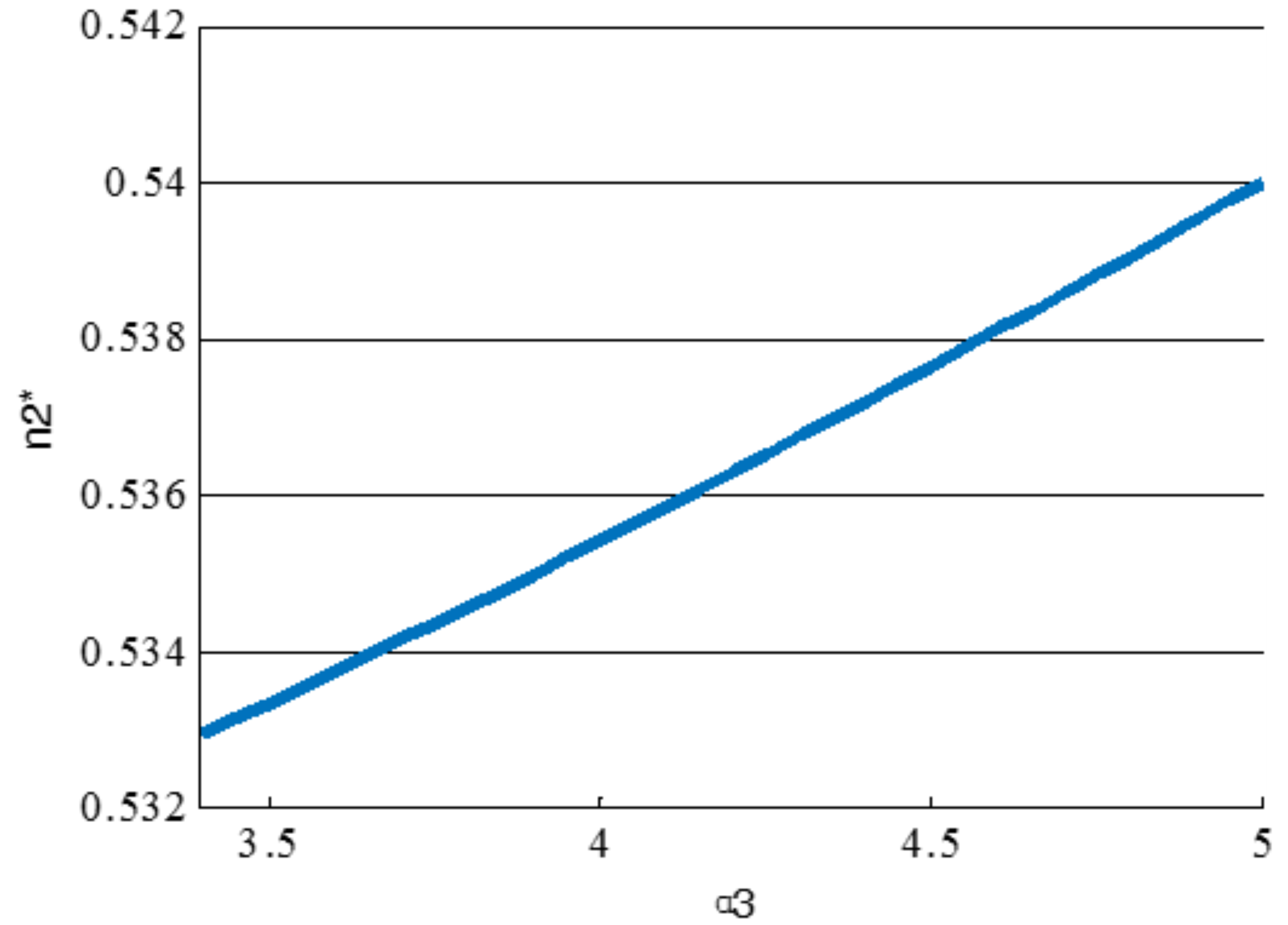
We develop a two-sided model of crowdfunding platform markets in which fundraisers value the quantity of funders, and funders value both the quantity and quality of fundraisers’ projects in the market. Funder preference for fundraisers’ projects provides an incentive for the platform to exclude some low-quality projects. To the best of our knowledge, this paper is the first to analyze quality choice and matching services on crowdfunding platforms. The results show that a higher parameter of funder preference over quality contributes to the crowdfunding platform market, excluding some projects and fundraisers. In another respect, with the average quality of projects increasing, more funders will be attracted to sign up on the crowdfunding platform, further appealing to even more fundraisers. Consequently, the two forces finally result in a positive correlation between the parameter of funder preference over quality and the size of fundraisers when the funder preference over quality is large enough.

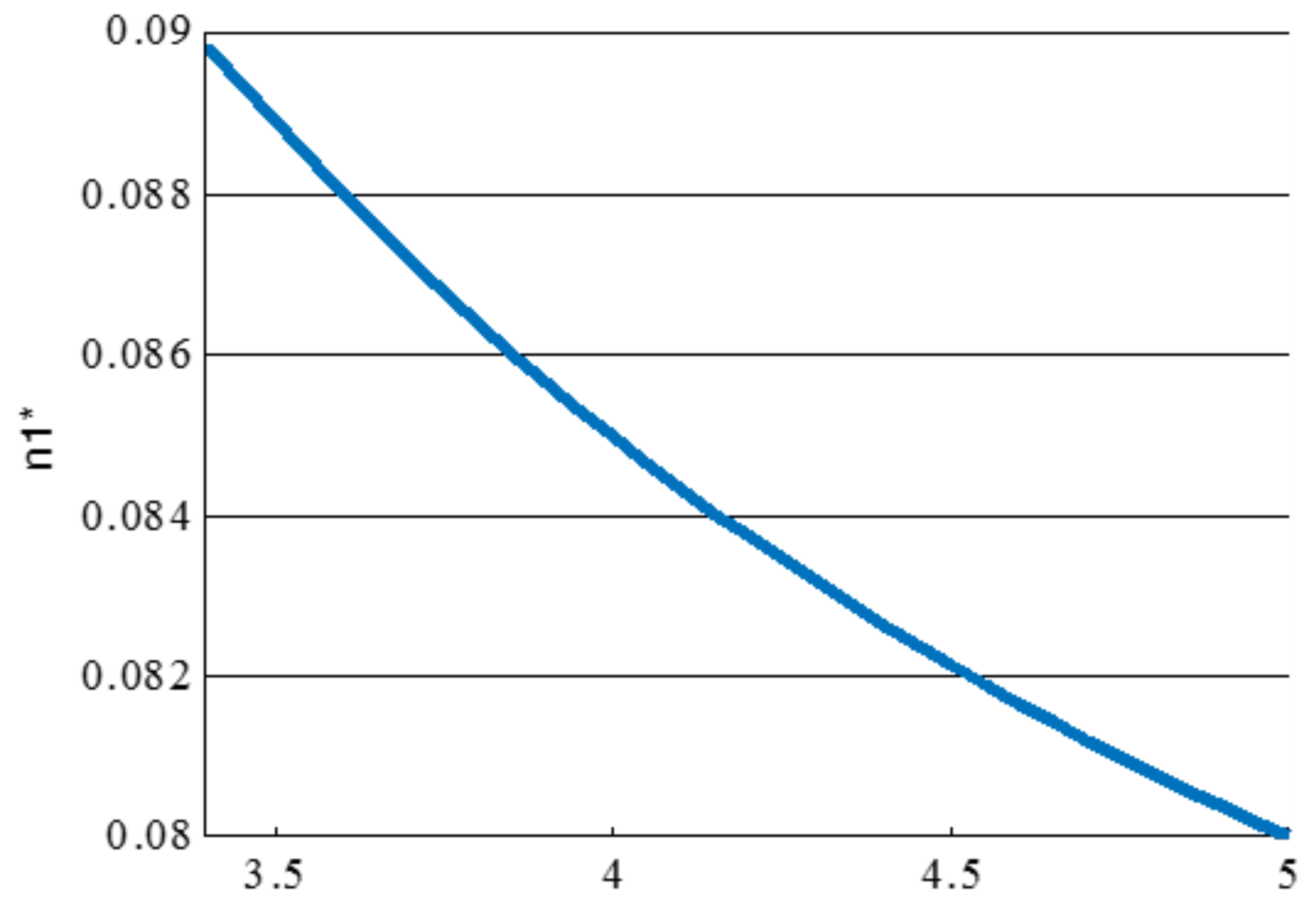
Furthermore, the paper reveals that platform profits in scenarios with an exclusion policy are higher than in scenarios without an exclusion policy under the condition of low preference for project quality. On the one hand, when funder preference for project quality is small, it is unprofitable to exclude low-quality projects. One of the reasons is that censoring crowdfunding projects is costly. If the platform does not get better revenue from the exclusion policy, there is no motivation to screen the low-quality projects. This usually happens at the early stage of crowdfunding when most people do not get clearly on the emerging financing mechanism and they are likely to fund a project at the state of curiosity. Then, with the spread of news with regard to successful crowdfunding projects, people start to realize the important role that crowdfunding is able to play in their life. At this stage, they probably pay more attention to the market value and practical use. They start to distinguish different levels of crowdfunding project quality by making use of all kinds of information, like comments, the reputation of crowdfunding platforms, and professional knowledge. When the funder shows great interest in the quality, platform managers will be also motivated to struggle to judge every project quality because high average quality is positively related to the whole success rate of a crowdfunding. High success rate is also one of the important criteria for funders to estimate the reputation of a crowdfunding platform. On the other hand, if there are too many fundraisers and few funders, it is likely to be a big challenge for fundraisers to reach their goals because of the small number of potential investors. This situation is also closely related to the profit of the crowdfunding platform. That means once a project fails, crowdfunding platforms will not charge a percentage of the funds’ transaction fee to fundraisers. Moreover, considering the large number of fundraisers, it would cause congestion on the internet, and therefore increases the cost burdens of crowdfunding platforms. So it is wise to constrain the participating fundraisers. In doing so, exclusion strategy is optimal when the number of fundraisers is much larger than the number of funders.

In addition, the results of this paper provide some valuable insights into how to maximise the crowdfunding platform profits. When crowdfunding platforms take measures to admit the quality threshold of crowdfunding projects, the optimal quality threshold is one-third of all quality spread. Nevertheless, high average quality is associated with the success rate of crowdfunding projects, while it does not inevitably raise platform profits because screening all projects is the kind of thing that calls for much effort. Although it is somewhat difficult to grasp the project quality of fundraisers, there are methods to assess it. Founders’ track records, prior experience, and the characteristics of the founding team are helpful for venture capitalists to distinguish unsuccessful projects from successful projects. Specifically, on the one hand, according to Colgren [46], crowdfunding is the union of big data, cloud technologies, and social media. The advances in science and technology expand the reach of platforms’ ability to distinguish different levels of crowdfunding projects. One the other hand, the quality of entrepreneurial team information, including the ratio of full-time staff, staff numbers, and enterprise business age, significantly contribute to platform managers uncovering the quality of crowdfunding projects [47]. Besides, according to Bi et al. [37], larger introduction word counts and video counts make funders feel the project has higher quality, and these kinds of signals of quality will exert a positive influence on funder investment decisions. Thus, to avoid the misdiagnosis of crowdfunding platform, the fundraisers are also expected to show their ideas and projects carefully and in detail.

Our results are subject to limitations. We analyze the optimal quality threshold and matching service of a monopoly crowdfunding platform in theory, while the studies of a complete crowdfunding platform also deserve further exploration. This research can be extended in several directions. First, future research can examine the optimal quality threshold and matching service by using a quantitative approach. Second, the social effect is also an interesting topic for a crowdfunding platform. Researchers can analyze how to increase people’s awareness of how they participate in public affairs.