1. Introduction
The building sector is one of the primary energy consumers. Studies show that more than 38% of primary energy and 76% of electrical energy are consumed in buildings in the United States. The energy consumption can be reduced by up to 15–40% with the use of the home energy management system (HEMS) [
1]. Within the HEMS, the smart meter is a critical element to measure the energy consumption of the household in real time. Energy consumption data are fed into the HEMS for analysis with others for controlling and optimizing the energy usage. Most existing HEMSs monitor the household-level electricity usage and therefore lack detailed knowledge on the energy consumption at appliance-level. More smart meters need to be plugged into the appliances to collected fine-grained electricity data, posing higher initial cost for the homeowners. Instead of installing multiple appliance-level meters, NILM uses the aggregate energy consumption data from the household-level smart meter and desegregates it to the appliance-level data. It is acknowledged as an efficient solution for monitoring individual electrical appliance without extra sub-meters.
Appliance-level energy consumption data can benefit different stakeholders. (1) For consumers, the appliance-level energy consumption provides them insight on the detailed energy consumption to realize the opportunities for energy saving through behavior intervention. For example, in real-time market, the electricity price may be low during some period of the day. People may use appliances with high-level energy consumption during this period. With knowledge of where the electrical energy goes, measures can also be taken to reduce energy consumption for appliances with high consumption level. Other services can also be provided such as fault detection of electrical appliances and recommendation of energy-saving appliances. (2) For electrical industry, the implementation of NILM provides an assessment of end-uses and the time of these usages in the buildings, which could play an important role in demand side management and penetration of renewable energy sources. In an electrical system, to ensure the satisfaction of demand, the power generators usually need to provide expensive reserve services. Demand side management is proposed to reduce the reserve service level by demand prediction and demand scheduling. Appliance-level load curves are valuable in demand prediction and scheduling. Prior studies [
2,
3,
4] pointed out that the analysis and sound understanding of demand profile on smaller consumer level could provide reasonably accurate information for predicting peak and average demand and demand shifting. Besides, NILM can also increase the penetration of renewable sources by maintaining the cost and revenue balance in micro-grid [
5]. Due to the fluctuations induced by wind speed variability or passing cloud, the main drawback of renewable energy resources such as wind or solar power plants is that they introduce large voltage fluctuations and supply uncertainty into distribution network [
6,
7,
8]. Many solutions are proposed to eliminate this problem including prediction models of wind speed or solar irradiation and storage system optimization [
9]. However, the literature has paid little attention to demand-side which also contains significant variability. The understanding of demand behavior in appliance-level may help reduce the load uncertainty and benefit the size determination of storage battery in micro-grid. This will benefit the system maintenance and cost control. For building sector, NILM can make a difference for human behavior inference in private homes which can be used for health and safety monitoring for the elderly and building occupancy inference. The inference of human behavior through energy consumption data will also benefit the energy reduction of lighting, space heating and cooling system in buildings [
10].
As shown in [
11,
12,
13,
14], the existing implementation of NILM can be classified into two categories: optimization methods and pattern recognition methods.
In the implementation using optimization method, the NILM problem can be formulated as a combinatorial optimization problem or a single source separation problem, since the aggregate household-level electricity consumption data comprise the electricity consumptions of different appliances. The optimization approach seeks the best appliances combination to minimize the sum of squares of the residuals between estimated signal and real signal. The solution to the optimization problem tells which appliances are on in the household at a specific time. Typical algorithms to solve this type of optimization problem include Hidden Markov model (HMM) and its extensions [
15,
16,
17,
18], discriminative sparse coding [
19] and tensor factorization [
20]. Kolter and colleagues used the additive and difference formulations of Factorial Hidden Markov Model (FHMM) for energy disaggregation task by exploiting the additive structure of the FHMM and maximum a posteriori approximate inference algorithm [
21]. They stated that, through approximate inference, the proposed method is computationally efficient and free of local optimal. Based on Kolter’s work, Bonfigli and his colleagues extended the feature dimension from one (active power) to two (active and reactive power) [
18], leading proposed solution to outperform the original Additive Factorial Approximate Map algorithm based on one dimension only. The discriminative sparse coding and tensor factorization methods consider NILM as single source separation problem. Both methods assume that the appliances’ energy usage is always nonnegative, neglecting the existence of distributed photovoltaic and wind power systems. In fact, Dinesh has considered the solar power influx which consumes negative active power [
22]. Nevertheless, Dinesh and colleagues utilized a subspace component power level matching algorithm which needs optimization over every subspace component and poses high computational requirement. These optimization methods are mainly unsupervised, and all of them used low-resolution power features (≤1 Hz). The most significant limitation of these methods is that they need to build a model beforehand for every appliance or source, making the methods unreliable when unknown appliances appear. The second limitation is that it is an NP-hard (non-deterministic polynomial-time hard) problem because of the exponentially increasing number of combinations of appliance states [
23].
The NILM can also be considered as a pattern recognition problem. The objective is to recognize the state-transiting appliance one by one using pattern recognition algorithms (e.g., clustering techniques and classification algorithms). Typical approaches include event-based algorithms [
11,
24,
25] and deep learning (DNN) based algorithms [
13,
26]. Kelly et al. adapted three deep neural network architectures in their NILM approach: (1) a long short-term memory (LSTM) recurrent neural network; (2) denoising autoencoders; and (3) a neural network trained to estimate the start time, the end time and the average power demand of each appliance activation [
26]. However, Kelly’s approach does not perform well when appliances outside the training set are included in the house. Lukas and Yang utilized LSTM network to developed an energy disaggregation approach in 2015 [
13] and later improved it by combining the HMM with DNN together to extract single target load in 2016, in which multiple important appliances can be identified by using multiple neural networks [
27]. Recently, Bonfigli and colleagues treated the NILM problem as a noise reduction problem and proposed an encoder-decoder deep convolution network, in which multiple neural networks were trained to meet the NILM requirement. Previous studies [
13,
26,
27] showed that deep learning based algorithms can handle with situations where complex and variable appliances exist. These algorithms cater for appliances with complex and apparent operation patterns, such as washing machines, dish-washers, fridges, etc. However, they are unsuitable for simple ON/OFF or multi-state appliances such as lamps or hairdryers because fewer features can be learned from their energy consumption patterns and they are limited for lack of training data. Therefore, integration of different algorithms is imperative because they can identify different types of appliance.
Apparently, the optimization method needs to identify all kinds of the appliance operating on the power network every timestamp while the pattern recognition approach only needs to make event detection and classification at specific timestamp when the network changes state. The former method poses higher requirements on computational capability of smart meters which is not practical.
NILM algorithms can also be categorized into supervised one and unsupervised one according to what data they use [
28]. Supervised algorithms not only need the aggregate house-level data but also a massive volume of appliance-level data while unsupervised algorithms (e.g., HMM) only need the aggregate house-level data. Although supervised methods require prior knowledge about appliances and involve an intensive training process, they do not require the one-time manual appliance naming intervention when applied to real life. While unsupervised methods do not need a large training dataset, they require one-time appliance naming which can be more intrusive to the users [
24]. In addition, the accuracy of unsupervised methods is usually lower than the supervised methods. Apparently, the supervised algorithm is more advanced and practical for generalizing the patterns of appliances of the same type and can minimize the interference to users. Therefore, many NILM implementations use supervised methods [
13,
23,
27,
29]. Recently, semi-supervised methods have been proposed by researchers to make the tradeoff [
28,
30,
31]. Liu et al. [
30] proposed a similarity metric between aggregate signals of a few sampled homes and other out-of-sample homes. The proposed similarity metric allows them to train the supervised models on a few houses and generalize these models to some unmodeled homes. This implementation is a typical case semi-supervised models.
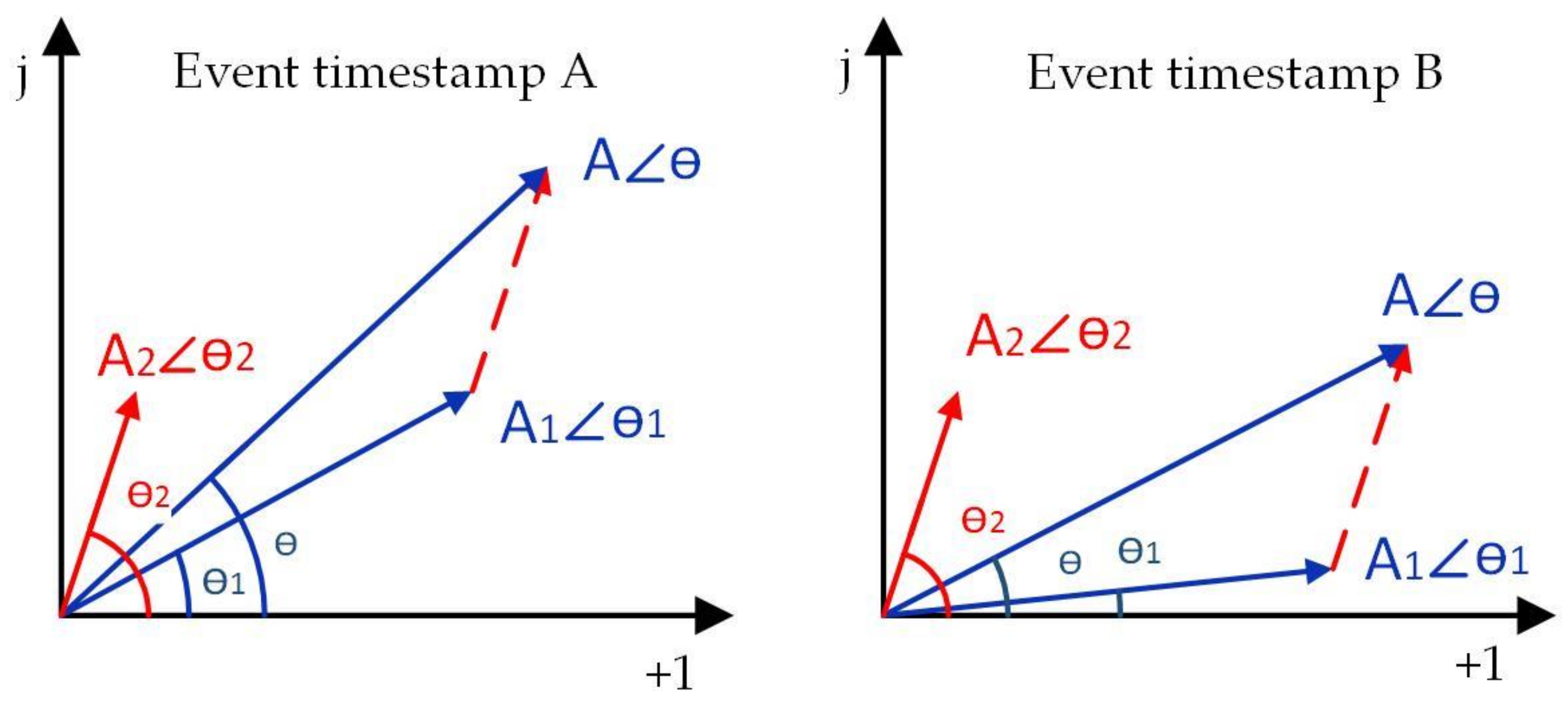
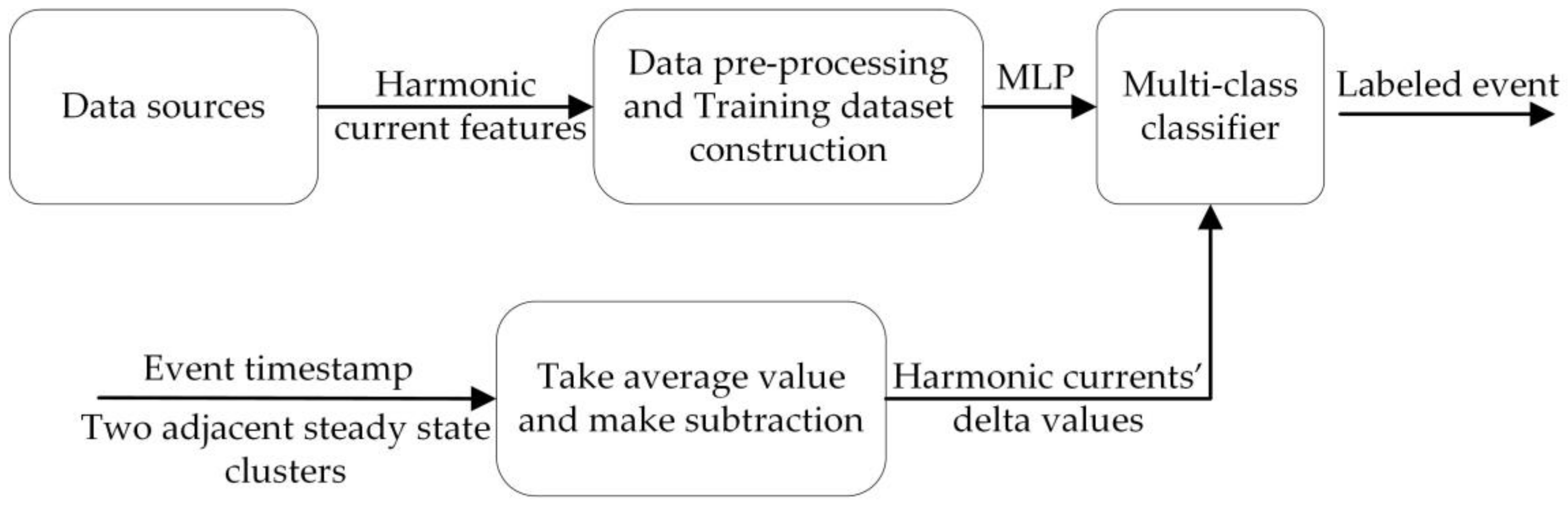
In this context, a supervised event-based NILM approach was proposed using harmonic current features, which have a good additive property. The additive property of feature refers to the property that when appliances are connected or disconnected to the power network, the corresponding feature of the network will increase or decrease by an amount equal to that produced by these appliances working individually. This property should hold independent of power network states. Hart [
24] stated that steady-state features are additive while transient features are not. However, no substantial proof was provided. Since then, little attention has been given to features’ additive property except for Liang and colleagues in 2010 [
11]. The features’ additive property is important for the event-based NILM system, as it guarantees that the appliance features stay unchanged in different power network states and the features can be extracted by subtracting the baseline data from the live data. Therefore, harmonic current features are verified first regarding its perfect additive property in
Section 2. For event-based NILM systems, effective and efficient event detection algorithms still need to be researched and concluded. Besides, NILM systems using harmonic features may work well for non-linear appliances but have not been well researched and commented using the real-life dataset to our best knowledge. Therefore, this paper focuses on the following three objectives: (1) verify that harmonic based features have a good additive property independent of practical power network states; (2) find which event detection algorithm has the best performance in NILM; and (3) demonstrate which types of appliance can be identified accurately by harmonic features based NILM system.
The remainder of this paper is organized as follows.
Section 2 provides a brief background work of event-based NILM including event identification algorithms and summarizes the features used in NILM. Then, the additive property of several features is tested by experiments.
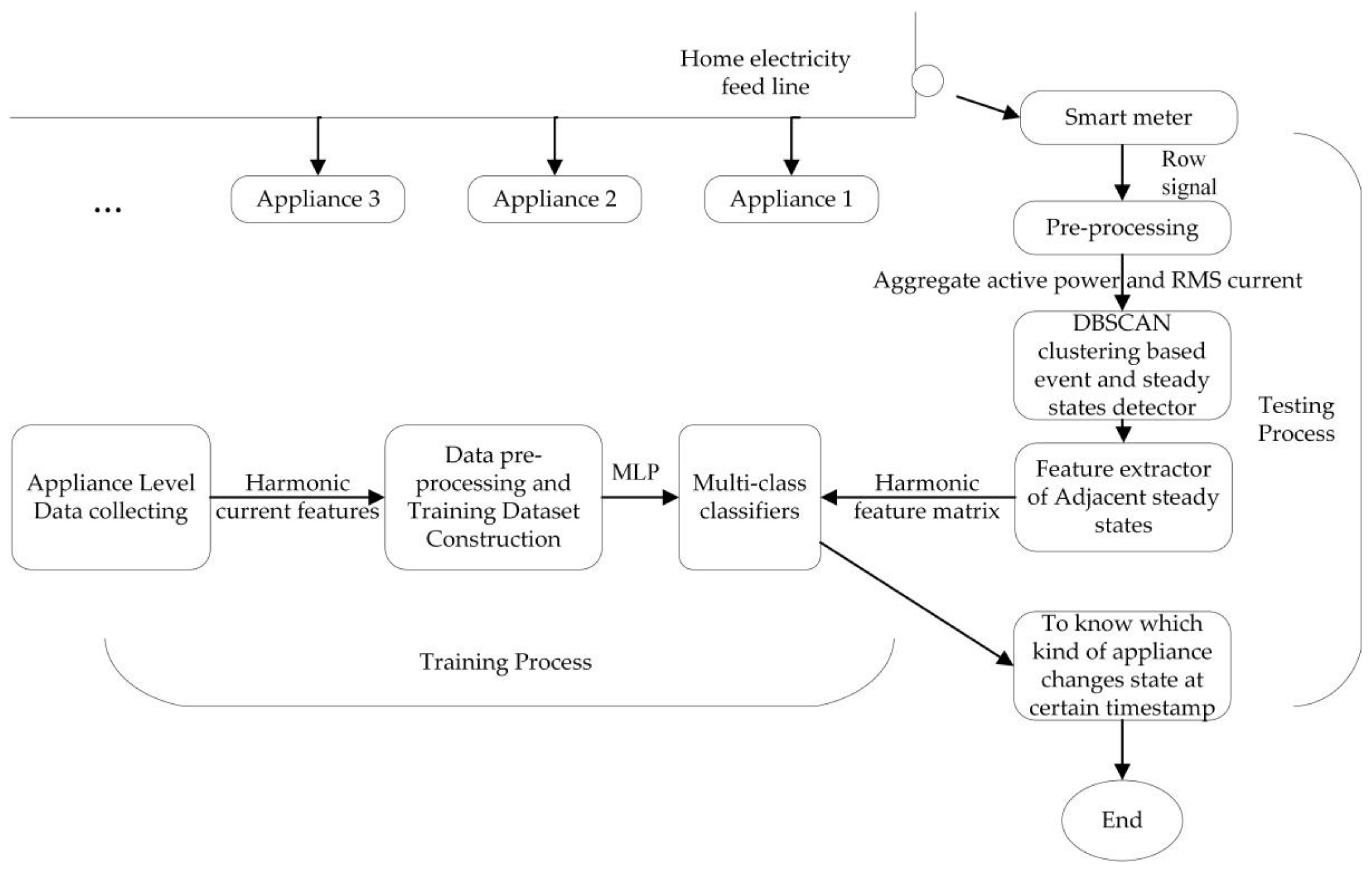
Section 3 describes the framework of the proposed approach, followed by the details of the two components in the framework: event detection model and classification model.
Section 4 describes the two data sources and the evaluation metrics.
Section 5 analyzes and discusses the performance of the proposed event detection model and classification model, which is followed by a laboratory validation of the whole approach.
Section 6 concludes the paper and envisions the future work.
5. Results and Discussion
5.1. Event Detection on BLUED
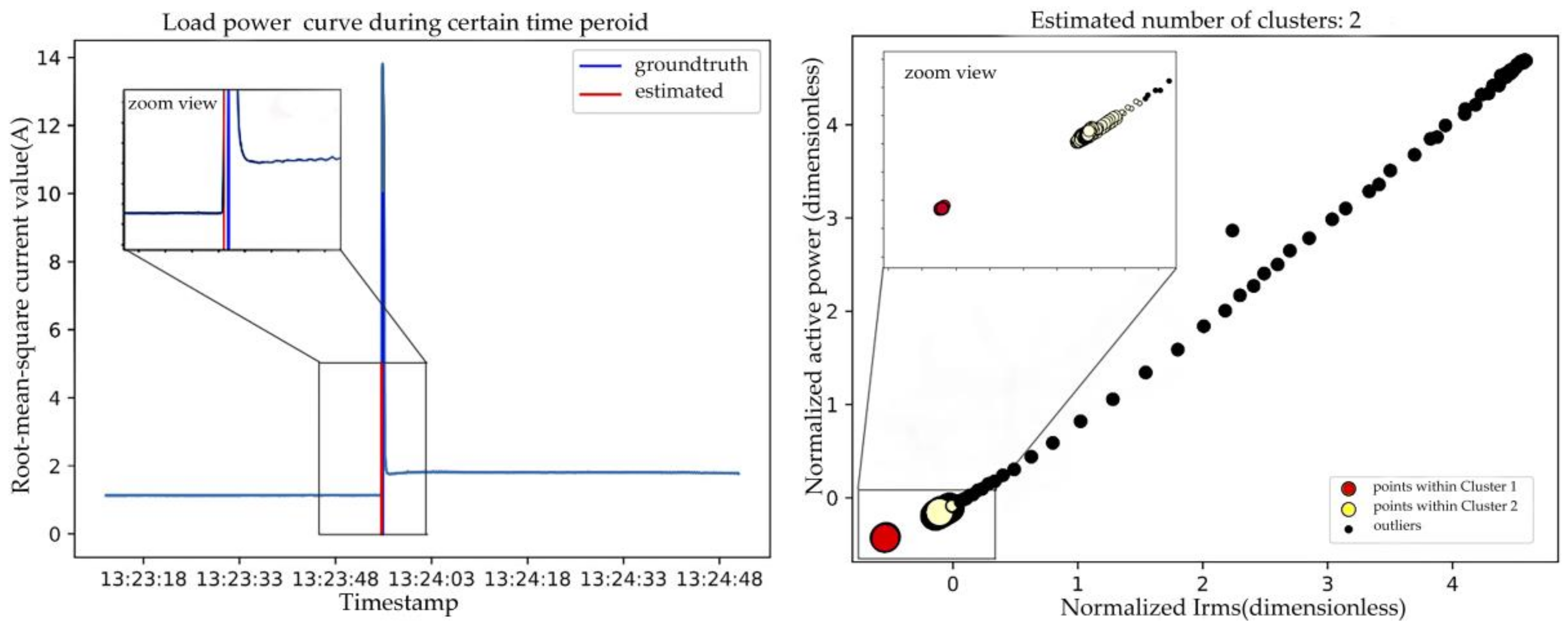
This section presents the performance of proposed DBSCAN clustering-based event detector and makes a comparison with other three event detectors over BLUED dataset. A python evaluation toolbox for sound event detection
sed_eval is introduced to compare the estimated events list with the reference events list [
55]. The other three detectors give no information about how reference events and estimated events are compared and this may lead to vagueness in algorithm comparison and reproduction.
sed_eval is an evaluation toolbox designed in 2016 for polyphonic sound event detection and it can be applied to NILM field directly without much revising. In
sed_eval, a tolerance between reference events and estimated events
collar needs to be specified. It means that, if the estimated event is located within the
collar radius of reference event, it is considered as true positive. In this paper, the authors set
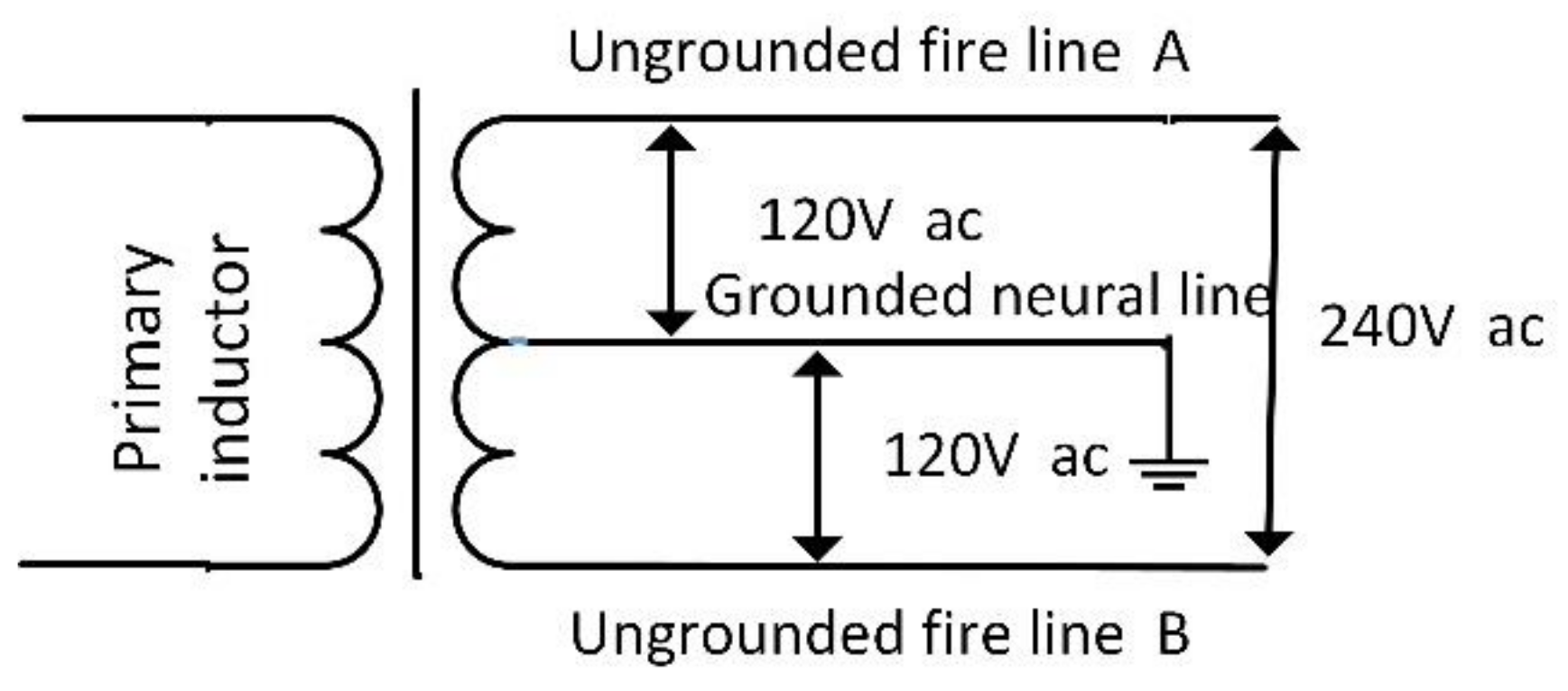
collar as 3.0 s. It is worth noting that BLUED dataset is constructed in America, where there are three electricity feed lines for ordinary houses: two firewires and one neutral line. As
Figure 9 shows, the two firewires have 120 V amplitude of voltage and they are named as Phase A and Phase B. Usually, small 120 V-rated appliances are connected between one firewire and one neutral while larger 240 V-rated appliances such as heaters and air conditioners are connected between two firewires. Therefore, the BLUED event ground truth and estimated result are both compared in Phase A and Phase B.
Main metrics have been given in
Table 4 and
Table 5 except
Score. According to Equation (11), the
Score value of proposed event detector is:
In
Table 4 and
Table 5, the three other detectors have no definition of TN, FPR, and AUC except threshold filtering event detector [
11] without specifying how they are generated. Except for GLR detector, the two other event detectors, threshold filtering detector and bucketing clustering detector, only give parts of the final metrics and no intermediate statistics are given. Therefore, a comprehensive comparison cannot be conducted. First, the authors note that the total number of reference events and system estimated events is different. The reason is that different ways are used to make a comparison between reference events list and estimated events list. Some events are merged because there are some repeatedly labeled timestamps on one event both in reference events list and system estimated events list. The merge time interval is set as 1.2 s, which means if two events in reference or estimated events list are so near with less than 1.2 s time interval, the last event was discarded.
As for performance, in Phase A, DBSCAN clustering based detector outperforms GLR detector in each metric. It also outperforms Threshold filtering detector in terms of TPR (98.70% and 94%, respectively). Compared with Bucketing clustering detector, it has better performance in TPP (98.70%) while worse performance in FPP (0.71%). Threshold filtering event detector has the worst result and clustering-based event detectors have better performance than the other two (TPP for DBSCAN clustering event detector is 98.70% and for bucketing clustering, it is 98.5%). In Phase B, DBSCAN detector has higher TPR and TPP (87.85%) but it has many false positive (FP) events. Compared to Phase A, all the detectors have worse performance in Phase B. The main reason is that more events exist in Phase B and they distribute more intensively.
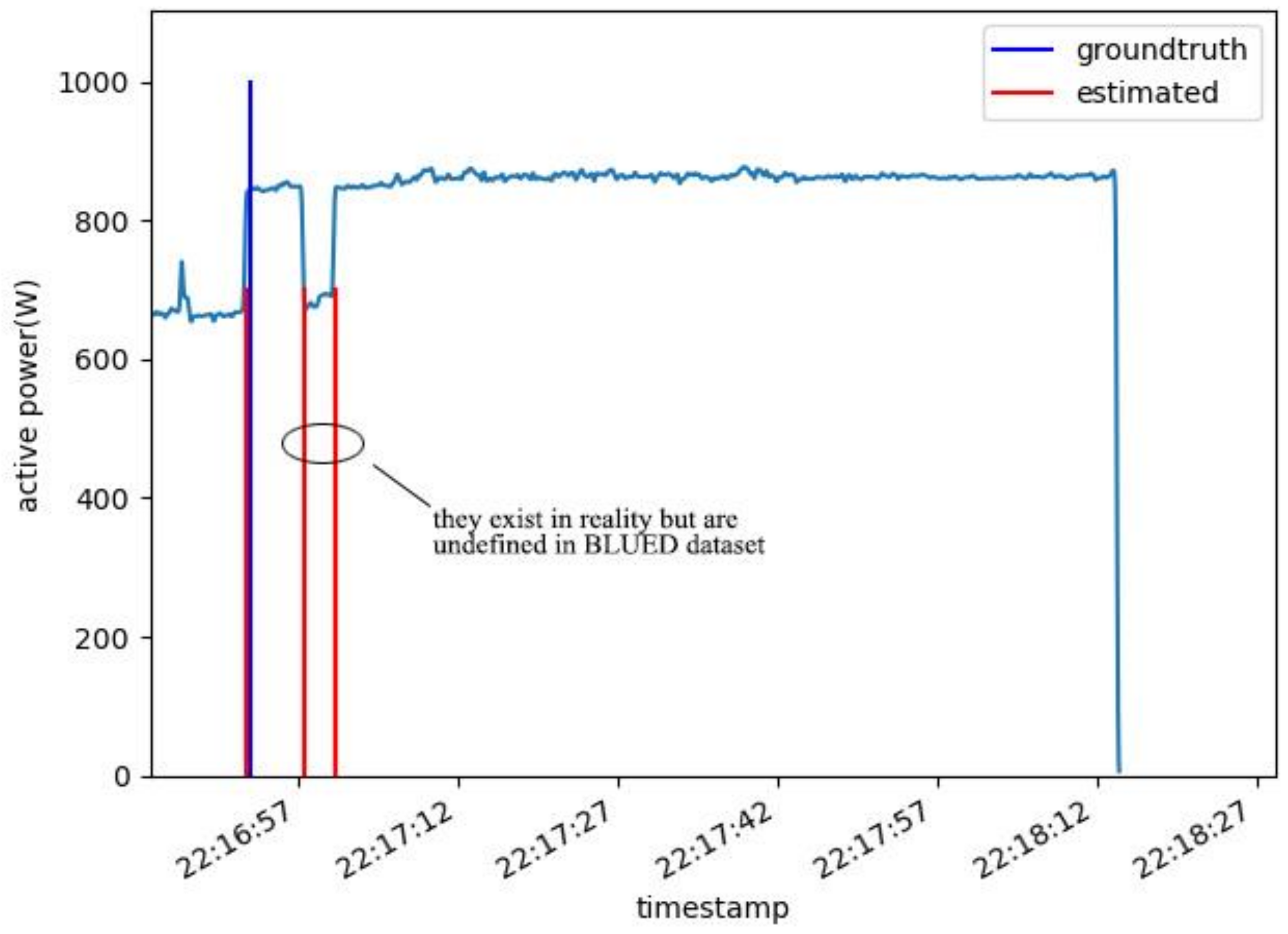
To find out why DBSCAN clustering detector generates so many false positive events in Phase B, plots was made near these FP events and the reason is found as ground truth did not label some undefined events. According to BLUED releasers, they defined an event to be any change in power consumption great than 30 watts and lasting at least 5 s [
50]. However, Phase B contains many events undefined and labeled in BLUED dataset while our DBSCAN clustering detector model can detect them sensitively as
Figure 10 illustrates. It seems that the given ground truth is not so ground true and the “false positive” events detected by our model exist in reality. This may be another important reason DBSCAN clustering approach has higher FP and why all event detectors have worse performance. Anyway, looking at performance in Phase A and Phase B, the authors can still conclude clustering based event detectors may suit better for step change point and adjacent steady states detection.
To get a high performance over BLUED dataset, an intensive work on parameter determination was done. It is difficult to quantify the process of parameter determination. Instead, the parameters are mainly determined according to experiment feedbacks and qualitative analysis mentioned before. Since the BLUED data volume is huge, parameter search over the whole dataset is time-consuming and impossible. To solve this problem, several sub-files are selected to do parameters search and parameters are finally determined according to the performance of these sub-files. Then, these parameters are generalized to other data files. Therefore, the parameters determined are local optimal parameters but not globally optimal. In fact, DBSCAN clustering methods have been proved to be sensitive to parameters in practice and another drawback is that they are incapable to handle data having clusters with different densities since the parameters remain constant during the process [
26]. That is the why pre-processing and post-processing are required in the implementation. To overcome these drawbacks, some other new or revised density-based clustering methods have been proposed such as density-based clustering based on hierarchical density estimates (HDBSCAN) and ordering points to identify the clustering structure (OPTICS). In the future, the authors may consider using these revised algorithms to do event detection, as no filtering block, easier parameter determination, and better performance are expected.
5.2. Event Classification on PLAID
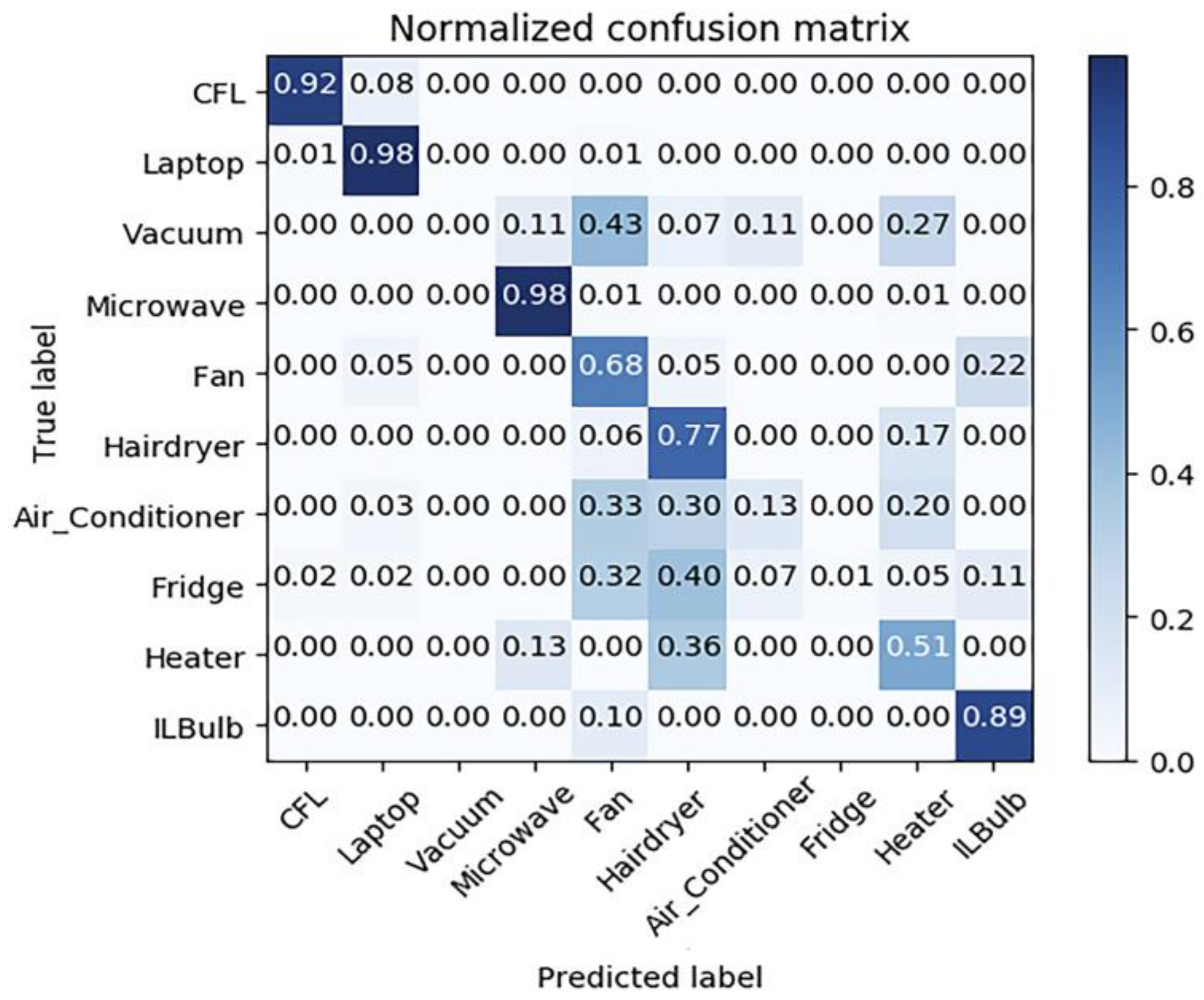
The data in the PLAID dataset are all appliance level data containing 11 appliances with on–off states: compact fluorescent lamp, laptop, vacuum, microwave, fan, hairdryer, air conditioner, fridge, heater, incandescent lightbulb, and washing machine. Since washing machine has variable current waveforms in practice and is not stable during operation, the authors discard washing machine from consideration. Harmonic decomposition is conducted over each record to construct experimental dataset from PLAID. Then, it is split into a training dataset and a testing dataset with a ratio of 3:1 to test the performance of harmonic-based classification over real-life data and the result is given by a normalized confusion matrix (
Figure 11).
As illustrated in
Figure 11, the MLP classifier using harmonic features has good performance over specific appliances including compact fluorescent lamp, laptop, microwave and relatively high performance over fan, hairdryer, heater, and lightbulb. This is within expectation since harmonic features based NILM suits for identifying non-linear loads.
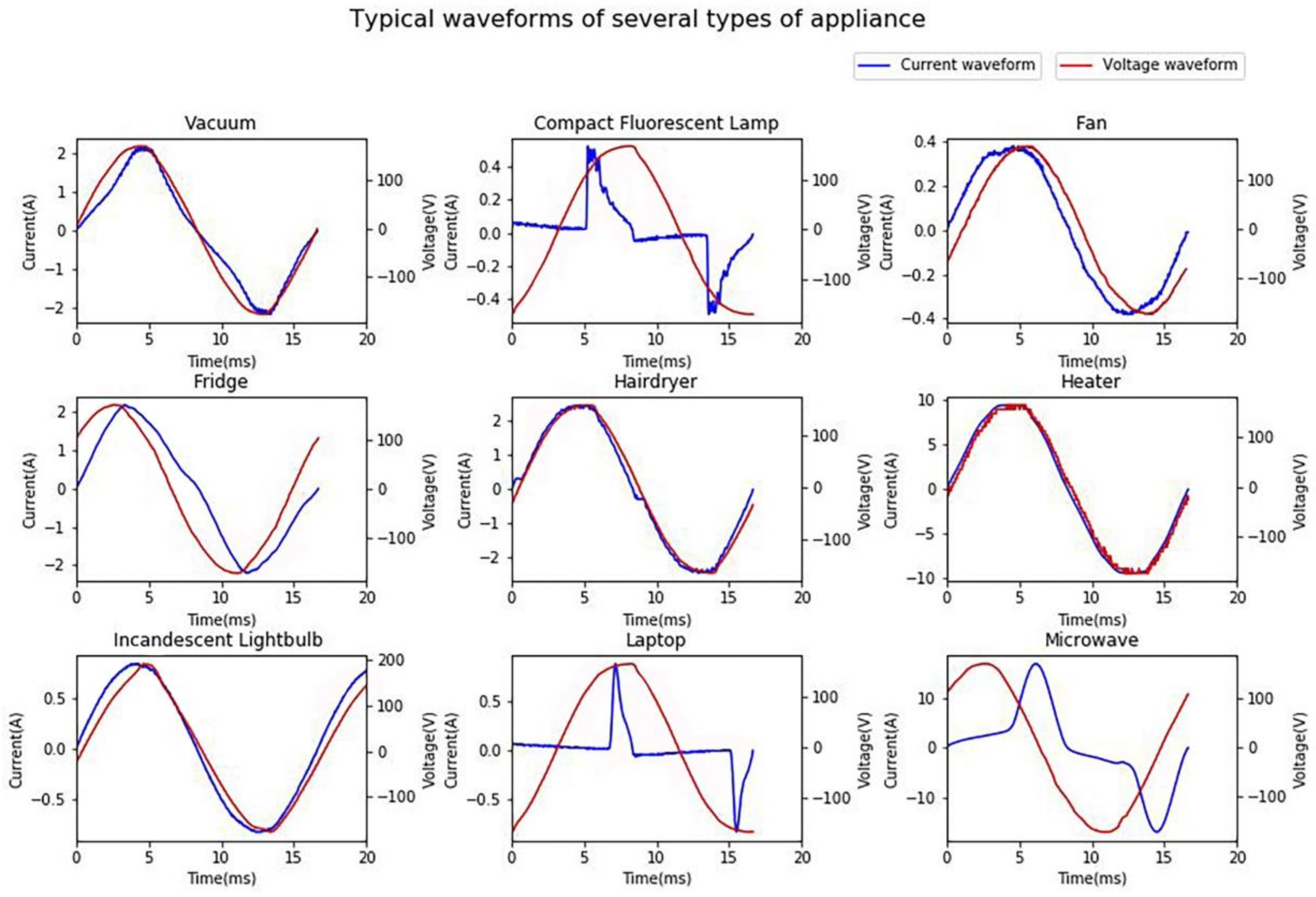
Figure 12 shows the typical current waveforms of each type of appliances. Obviously, the waveforms of compact fluorescent lamp, laptop, and microwave distort dramatically and thus they are typical non-linear loads. It is observed that fan and bulb have similar current waveforms and hairdryer and heater have similar waveforms except for their amplitudes. It can be confirmed by confusion matrix. It is suggested by
Figure 11 that 68% of fans are correctly classified and 22% of fans are misclassified as lightbulbs while 89% of lightbulbs are correctly classified and 10% of lightbulbs are misclassified as fans. Overall, 77% of hairdryers are correctly classified and 17% of hairdryers are misclassified as heaters while 51% of heaters are correctly classified and 36% of heaters are misclassified as hairdryers. Note that, in the PLAID dataset, all hairdryers work in the full-wave state, unlike hairdryers in laboratory experiment, which could work in the half-wave state. Besides, all the voltage waveforms are nearly identical, which means the assumption holds that network voltage is constant.
The current distortion level can also be quantified. Current total harmonic distortion rate (THD) is defined as a metric measuring the current harmonic distortion degree in power network which can be calculated by Equation (12). The minimum of
is 0 when the signals are total sine and the maximum can exceed 1 when energy spreads over the entire spectrum. The higher the current total harmonic distortion rate is, the larger the harmonic current is and the more obvious are the non-linear properties the load generates.
Table 6 shows the average current total harmonic distortion rate of different appliance types in PLAID. It is observed that three types of the appliances with highest distortion rate are compact fluorescent lamp (123.1%), laptop (132.3%), microwave (43.3%) and three types of the appliance with lowest distortion rate are lightbulb, heater and fan. Combined with confusion matrix, the authors conclude that classifiers using steady-state harmonic features could identify typical non-linear loads well and some totally resistive loads with relatively high performance.
where
denotes RMS amplitude of the
hth harmonic component of current for appliance
k, and
denotes the total number of instance records for appliance
.
denotes the harmonic distortion rate of one instance of appliance
k.
denotes the average current total harmonic distortion rate for appliance
.
Finally, the result is compared with other algorithms tested on the PLAID dataset using accuracy calculated by Equation (13). Gao et al. [
41] concludes the classification accuracy over PLAID dataset of five classifiers using different features such as current, active/reactive power, harmonic, U-I image, etc. For algorithms using individual feature, the best classifier is random forest using U-I image with an accuracy of 81.75%. When all features are combined, the accuracy is improved to 86.03%. Alcalá claims that the PQD-PCA classification algorithm outperforms the best classifier in the literature [
41] with an accuracy of 88% [
23]. However, one drawback of the PLAID dataset is that it only contains appliance instance data for training and does not contain aggregated data for testing. Therefore, although PQD-PCA algorithm outperforms other methods, it may decrease dramatically when applied to aggregated signals for the sake of lousy additive property mentioned in
Section 2. Although the MLP classifier using harmonic current features only have an accuracy of 75.38%, it is still valuable because it can identify some non-linear appliances accurately and harmonic features make it more practical on its excellent additive property.
5.3. Laboratory Validation by Combinational Experiments
In this part, a training dataset and an MLP classifier are constructed to validate the proposed approach in the laboratory. As mentioned in
Section 3.2, gird search and K-fold cross-validation are conducted to make classifier selection and prevent overfitting. As suggested by
Table 7 and
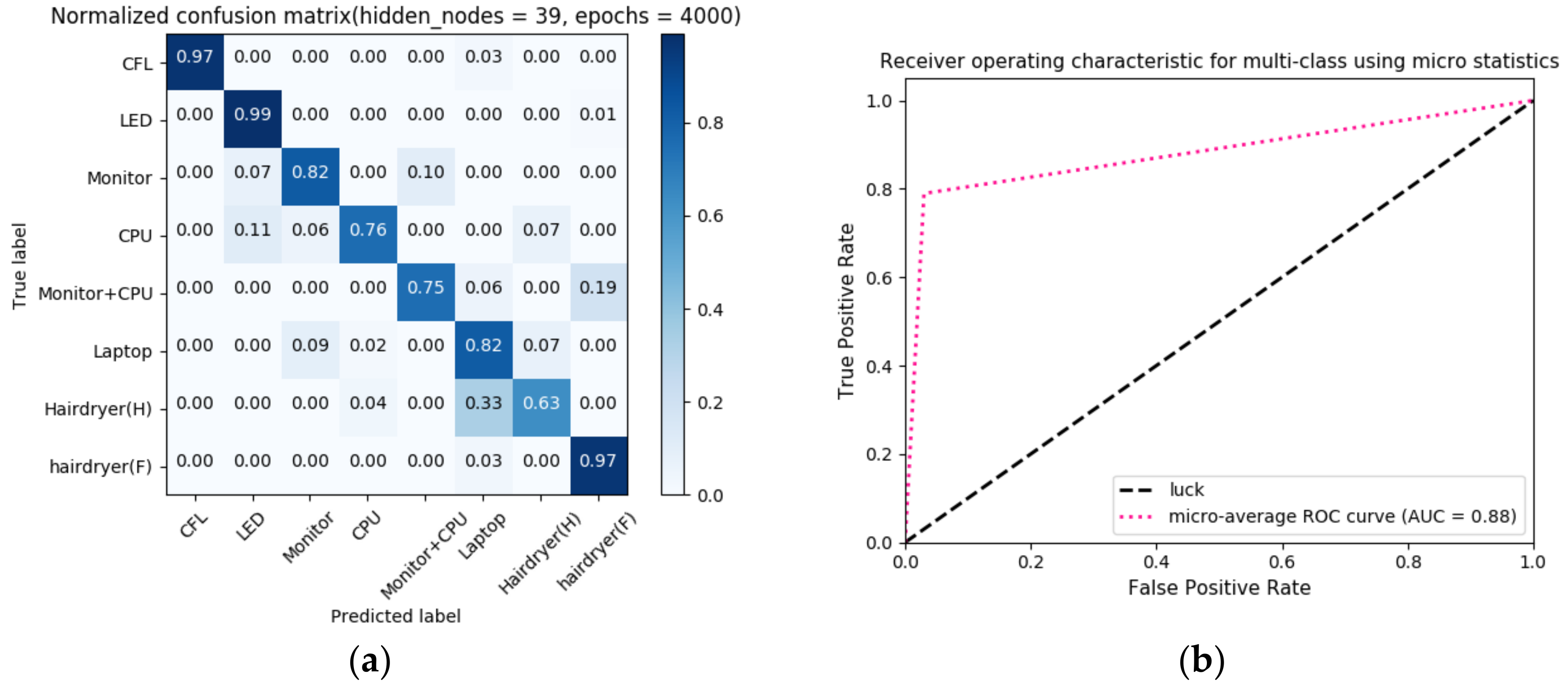
Table 8, two parameters are searched: hidden layer nodes number and epochs number. With fixed epochs number of 3000, the classifier with 39 hidden layer nodes has the better performance. With fixed nodes number of 39, the classifier with 4000 epochs has better performance. The selected classifier has 39 hidden layer nodes and 4000 epochs.
Using the above parameters, the K-fold cross-validation visible results of the final classifier are shown in
Figure 13.
The eight types of event belong to different non-linear loads except for hairdryer with full waveforms which is nearly sine. It can be seen in
Figure 13a that the MLP classifier using harmonic current features has a good performance in identifying some typical non-linear loads such as compact fluorescent lamp (97%), LED (99%), monitor (82%) and laptop (82%) and typical resistive loads such as hairdryer with full waveforms (97%).
Figure 13b represents the ROC curve for multi-class classification evaluation. The slope at the beginning of curve is steep which means the classifier can have a relatively TPR with a low FPR. The selected classifiers have an AUC up to 88%.
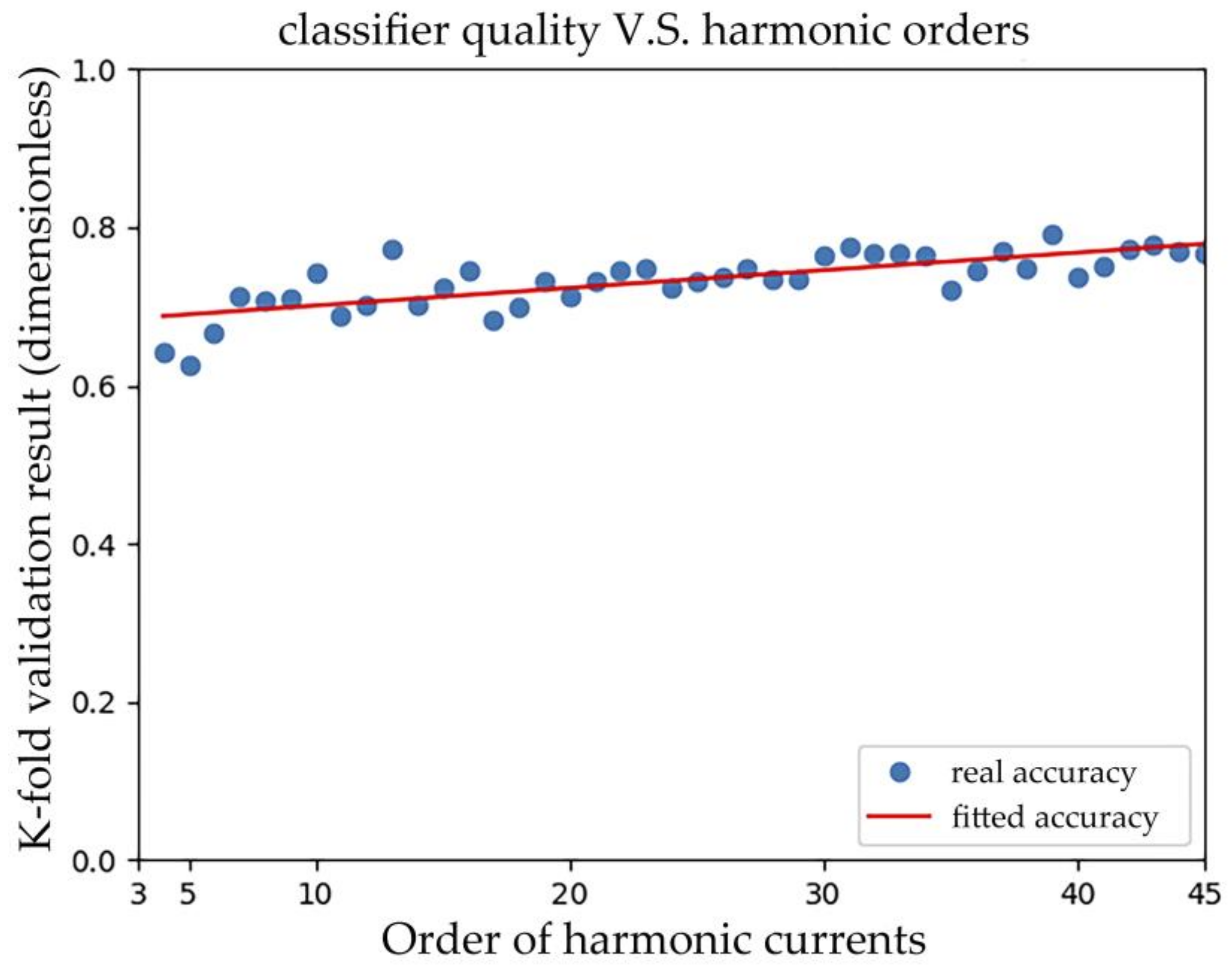
The orders of harmonic currents used in the feature vector are expected to influence the performance of classifiers. The more orders of harmonic currents included means more information are transferred and utilized. In
Figure 14, the accuracy of classifiers increases slightly and linearly with the orders of harmonic currents used. According to the Nyquist Sampling Theorem, the sampling frequency should be at least twice the highest frequency contained in the signal. This implies that compromise can be made between hardware requirement and classification performance in practice. For example, if four orders of harmonic currents are considered, assuming the fundamental frequency is 50 Hz, the least sampling frequency would be 400 Hz.
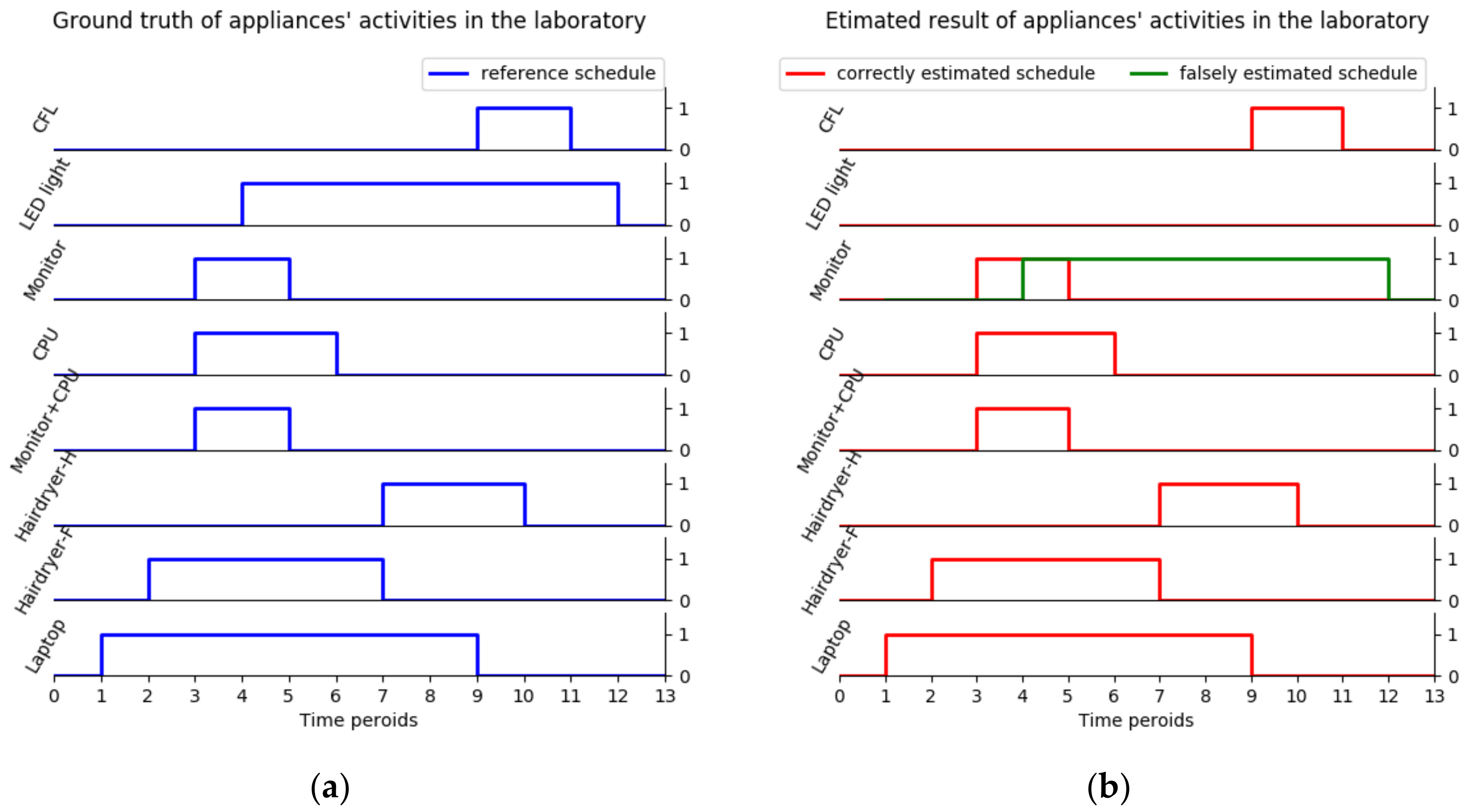
To validate the proposed approach, several appliance types in
Table 2 are chosen to do a combinational experiment in the laboratory and these appliances are not first measured in a training process. In this combinational experiment, twelve appliance transitions represent twelve events. As
Figure 15a shows, an appliance on–off experimental schedule is made to obtain the events ground truth. Then, the aggregate experimental data through CW500 are obtained, and event detection, feature extraction, and event classification are performed, as illustrated in
Figure 3. The validation result (
Figure 15b) shows that 10 of the events are predicted correctly, which is a relatively high performance, while the other two LED light events are mislabeled as monitor.
To make it more convincing, several extra combinational experiments are conducted. The final testing contains 90 total events with 100% event detection accuracy and 89.34% event classification accuracy in the laboratory. The authors conclude that the testing result not only validates the additive property of harmonic current features again but also confirms the proposed approach can correctly detect all the events and correctly classify most of the events in the laboratory.
5.4. Computational Complexity and Response Latency of Proposed Approach
Finally, the computational complexity of proposed approach is evaluated by both Big O notation and laboratory experiment as shown in
Table 9. Note that all the programs run on python platform on a computer with Windows 10 Home system and Intel Core i7-6700K CPU.
The time and space complexity of MLP classifier with three layers is and , respectively, where N is the nodes number. The time complexity of DBSCAN clustering reduces to ) from when optimized by using k-dimensional trees. The space complexity of DBSCAN clustering is , where N is the number of input points. Fortunately, the application of DBSCAN clustering in event detection has no time and space complexity concerns since it is conducted in a sliding window and only needs limited points to create clusters. Experiment is also conducted to evaluate the computational complexity. The trained MLP classifier contains 2 non-linear layers, 39 nodes for hidden layer and 8 nodes for output layer, for a total of 47 neurons. The training set contains 651 records with size of 445 KB and 10-fold cross-validation is conducted. The total training time consumed is 2.35 s including data preparation. The RMA space consumed is less than 1 MB. The average time of feature extraction and classification for one event is 6.7 ms and 33 μs, respectively. An aggregated energy consumption curve over 30 min with 1811 points is clustered by sliding windowed DBSCAN algorithm with step length of 10 points and window length of 60. The time consumed for total and each clustering are 1.45 s and 8 ms, respectively. The RMA space taken up can be neglected.
The response latency of proposed approach is analyzed. The training of MLP classifier is offline and will not affect the real-time response. Therefore, time latency of the whole approach is dominated by DBSCAN clustering event detection block. The event detection latency of DBSCAN clustering block depends on the preprocessing time, sliding window length and data resolution. Preprocessing aims to prepare data for DBSCAN input such as calculation of active power and RMS current. In BLUED dataset, the window length is 300 points and data resolution is 60 points per second. The latency without considering preprocessing is 2.5 s. In the laboratory, the apparatus captures one record of the harmonics, active power and RMS current every second. The window length is smaller with 60 points and data resolution is one point per second. The latency neglecting preprocessing time is 30 s.
Therefore, the computational complexity of proposed approach is low. The response latency is related to the data resolution and sliding window length. The value can be reduced by narrowing the window length and increasing data resolution. Although the experiments in this paper are conducted on offline historical data, the designed approach can realize online identification with acceptable latency.
6. Conclusion and Future Works
In this paper, a supervised event-based NILM framework is proposed and validated using both public dataset and laboratory experiment. The experiment shows that harmonic current features’ additive property is independent of power network states, which is suitable for event-based NILM. A novel DBSCAN clustering-based approach is proposed to implement the high accuracy event detection, which outperformed the other three event detectors on BLUED—a public dataset. The results indicated that the clustering-based event detection method has better performance than other existing approaches on the detection of events and adjacent steady states. In addition, an MLP classifier using harmonic features is trained on the PLAID dataset and the results show that harmonic features based method has superior performance in identifying non-linear loads and some totally resistive loads. To validate the integrated NILM approach, a training dataset was built using YOKOGAWA CW500 power quality analyzer to collect the data on multiple appliances. The dataset from the lab validated that harmonic current features are effective and efficient for identifying typical non-linear loads.
The authors fully acknowledge the limitation of the proposed approach. This approach only considers non-linear appliances with on/off and multi-state appliances. Although there are many non-linear loads in buildings, some other appliances with little current distortion such as vacuum, air conditioner and fridge cannot be distinguished by steady-state harmonic features based methods. Besides, since this method needs to extract features from adjacent steady states, it cannot distinguish variable appliances without steady states.
In the future, the limitations mentioned above should be considered seriously. For example, some appliances are complex and variable during operation while event-based NILM is best used for the event with adjacent steady states. In this case, methods without detecting events and drafting hand-engineering features may work better such as deep neural network models. Moreover, different algorithms based on different features may be effective for certain types of appliances. Therefore, integrating complementary NILM models together is necessary and feasible.