Measuring Rice Farmer’s Pesticide Overuse Practice and the Determinants: A Statistical Analysis Based on Data Collected in Jiangsu and Anhui Provinces of China
Abstract
:1. Introduction
2. Literature Review
2.1. Comprehensive Rationality and Prospect Theory
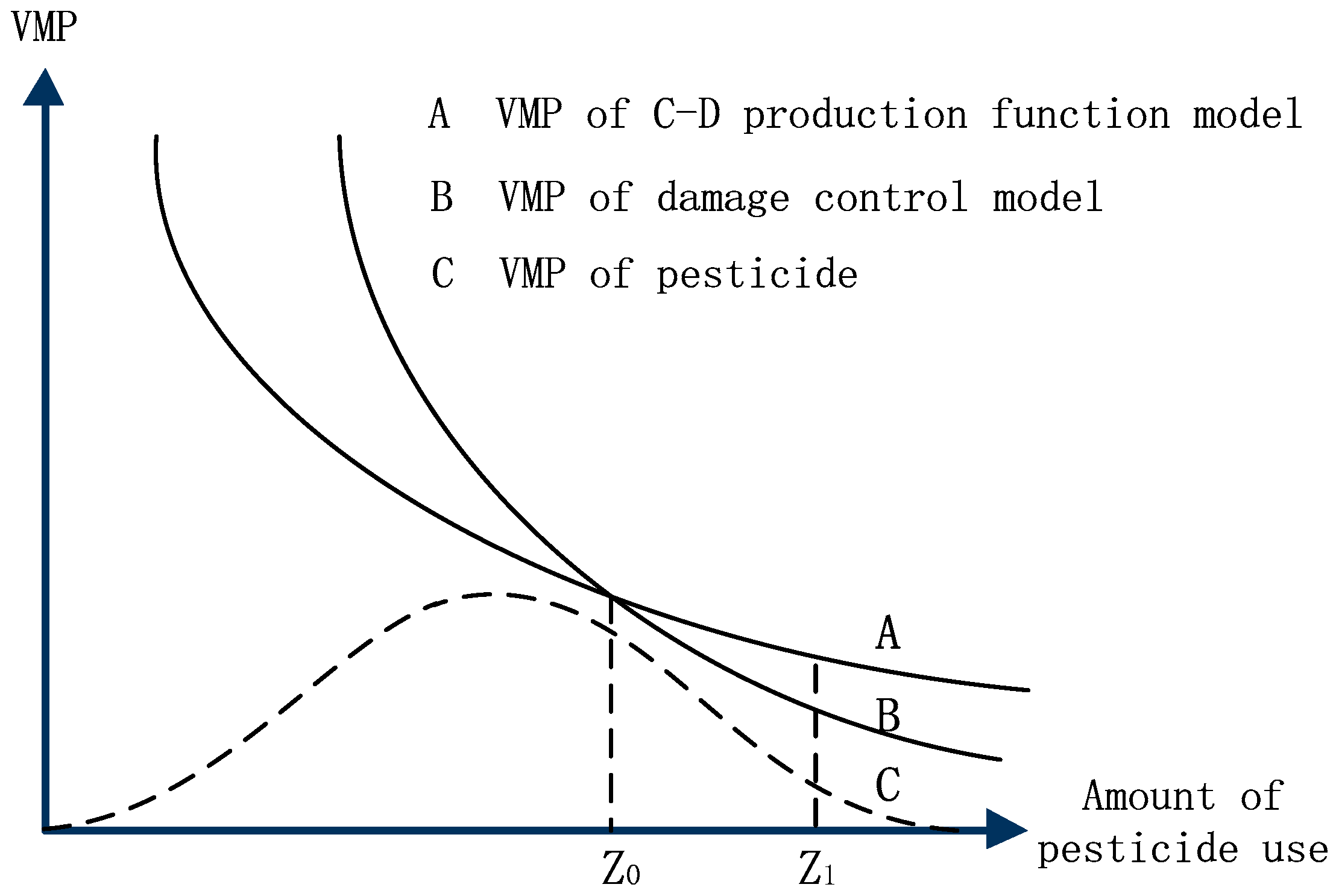
2.2. Measuring Marginal Productivity of Pesticides and Determining Overuse
2.3. Factors Attributing to Pesticide Application
3. Materials and Methods
3.1. Case Selection
3.2. Data Collection
3.3. Estimated Marginal Productivity of Pesticides
3.3.1. Model Framework for Marginal Productivity of Pesticides
3.3.2. Regression Model of Marginal Productivity of Pesticide
3.4. Regression Model of Drivers to Pesticide Overuse
4. Results and Discussion
4.1. Descriptive Statistics of the Survey
4.2. Analysis of Marginal Productivity of Pesticides
4.2.1. Results
4.2.2. Discussion
4.3. Estimation of Factors Inducing Pesticide Overuse
4.3.1. Results
4.3.2. Discussion
5. Conclusions and Policy Implications
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Liu, C.J.; Men, W.J.; Liu, Y.J.; Zhang, H. The pollution of pesticides in soils and its bio-remediation. Syst. Sci. Compr. Stud. Agric. 2002, 18, 291–292. [Google Scholar]
- Mi, J.W.; Huang, J.K.; Chen, R.J.; Liu, E.M. Risk aversion and pesticide application behavior of Cotton farmers in China. Chin. Rural Econ. 2012, 7, 60–71. (In Chinese) [Google Scholar]
- Wang, C.W.; Gu, H.Y. The market vs. the government: What forces affect the selection of amount of pesticide used by China’s vegetable grower? Manag. World 2013, 29, 50–66. [Google Scholar]
- Schultz, T.W. Transforming Traditional Agriculture; Yale University Press: New Haven, CT, USA, 1964. [Google Scholar]
- Kahneman, D.; Tversky, A. Prospect theory: An analysis of decision under risk. Econometrica 1979, 47, 263–291. [Google Scholar] [CrossRef]
- World Resource Institute (WRI). World Resource 1998/1999; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Chambers, R.G.; Lichtenberg, E. Simple econometrics of pesticide productivity. Am. J. Agric. Econ. 1994, 76, 407–417. [Google Scholar] [CrossRef]
- Ajayi, O.O. Pesticide Use Practices, Productivity and Farmers’ Health: The Case of Cotton-Rice Systems in Côte d’Ivoire, West Africa; Pesticide Policy Project; University of Hanover: Hanover, Germany, 2000. [Google Scholar]
- Headley, J.C. Estimating the productivity of agricultural pesticides. Am. J. Agric. Econ. 1968, 50, 13–23. [Google Scholar] [CrossRef]
- Campbell, H.F. Estimating the marginal productivity of agricultural pesticides: The case of tree-fruit farms in the Okanagan Valley. Can. J. Agric. Econ. 1976, 24, 23–30. [Google Scholar] [CrossRef]
- Carlson, G.A. Long-run productivity of insecticides. Am. J. Agric. Econ. 1977, 59, 543–548. [Google Scholar] [CrossRef]
- Fernandez-Cornejo, J.; Jans, S.; Smith, M. The economic impact of pesticide use in US agriculture. In Proceedings of the NAREA Meeting, Atlantic City, NJ, USA, 7–9 June 1996. [Google Scholar]
- Babcock, B.A.; Lichtenberg, E.; Zilberman, D. Impact of damage control and quality of output: Estimating pest control effectiveness. Am. J. Agric. Econ. 1992, 74, 163–172. [Google Scholar] [CrossRef]
- Lichtenberg, E.; Zilberman, D. The econometrics of damage control: Why specification matters. Am. J. Agric. Econ. 1986, 68, 261–273. [Google Scholar] [CrossRef]
- Huang, J.; Qiao, F.; Zhang, L.; Rozelle, S. Farm Pesticide, Rice Production, and Human Health; International Development Research Centre: Ottawa, ON, Canada, 2000. [Google Scholar]
- Huang, J.; Hu, R.; Rozelle, S.; Qiao, F.; Pray, C.E. Transgenic varieties and productivity of smallholder cotton farmers in China. Aust. J. Agric. Resour. Econ. 2002, 46, 367–387. [Google Scholar] [CrossRef]
- Jha, R.K.; Regmi, A.P. Productivity of Pesticides in Vegetable Farming in Nepa; SANDEE Working Paper No. 43-09; SANDEE: Kathmandu, Nepal, 2009. [Google Scholar]
- Gong, J.H.; Huang, M.S.; Ma, Y.S.; Sun, J. Cultural background, Eco-environment awareness and pesticide application behavior of farmers. J. Ecol. Rural Environ. 2016, 32, 546–551. [Google Scholar]
- Abhilash, P.C.; Singh, N. Pesticide use and application: An Indian scenario. J. Hazard. Mater. 2009, 165, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Stadlinger, N.; Mmochi, A.J.; Dobo, S.; Gyllbäck, E.; Kumblad, L. Pesticide use among smallholder rice farmers in Tanzania. Environ. Dev. Sustain. 2011, 13, 641–656. [Google Scholar] [CrossRef]
- Zhao, J.X.; Zhang, Z.G. Analysis of Factors Influencing Farmers’ Safe Production of Agricultural Products. Stat. Res. 2007, 24, 90–92. [Google Scholar]
- Jia, X.L.; Dong, H.R.; Qi, L.L.; Wang, J.P. Study on using pesticide behavior of the vegetable growers—In Hebei province. Issues For. Econ. 2011, 31, 266–270. [Google Scholar]
- Hashemi, S.M.; Hosseini, S.M.; Hashemi, M.K. Farmers’ perceptions of safe use of pesticides: Determinants and training needs. Int. Arch. Occup. Environ. Health. 2012, 85, 57–66. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.H.; Ho, B.; Gao, S.R. Cognition and main influential factors of pesticide residues in dispersed farmers based on structural equation model. Chin. Rural Econ. 2011, 27, 35–48. [Google Scholar]
- Wang, J.H.; Ma, Y.T.; Li, Q. Agricultural products security and the choice of agricultural producers’ pesticide application behavior. J. Public Manag. 2015, 12, 117–126, 158. [Google Scholar]
- Zhang, Y.H.; Ma, J.J.; Kong, X.Z. Analysis on the factors influencing non-pollution and green pesticide behavior of farmers—An empirical analysis of 15 Counties in Shanxi, Shaanxi and Shandong Provinces. Chin. Rural Econ. 2004, 20, 41–49. [Google Scholar]
- Zhou, F.; Xu, X. Analyzing moral hazard behaviors of non-environmental pollution agri-product producers under the government regulation—Based on a survey of rural households in Jiangsu. J. Nanjing Agric. Univ. (Soc. Sci. Ed.) 2007, 7, 25–31. [Google Scholar]
- Zhu, D.; Zhang, X.L.; Niu, L.Y. Vegetable farmers’ willingness to adopt biopesticides. China Popul. Resour. Environ. 2014, 24, 64–70. [Google Scholar]
- Wang, J.H.; Ma, Y.T.; Liu, Z.; Shan, L.J. Behavior choice logic and influencing factors of agricultural producers’ pesticide application. China Popul. Resour. Environ. 2015, 25, 153–161. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.Q.; Zhu, Y.C. Influencing factors of farmers’ pesticides overuse. Res. Econ. Manag. 2013, 34, 86–91. [Google Scholar]
- Tan, H.M. Scientific understanding and effective response to rice quality and safety issues. Grain Sci. Technol. Econ. 2014, 39, 14–17. [Google Scholar]
- Zhao, Q.Q. Research on Present Status and Problems of Pesticide Application of Main Crops in China; Beijing Institute of Technology: Beijing, China, 2015. [Google Scholar]
- Beattie, B.R.; Taylor, C.R.; Watts, M.J. The Economics of Production; No. 338.5 B369; Wiley: New York, NY, USA, 1985. [Google Scholar]
- Norwood, F.B.; Marra, M.C. Pesticide productivity: Of bugs and biases. J. Agric. Resour. Econ. 2003, 28, 596–610. [Google Scholar]
- Shankar, B.; Thirtle, C. Pesticide productivity and transgenic cotton technology: The South African smallholder case. J. Agric. Econ. 2005, 56, 97–116. [Google Scholar] [CrossRef]
- Praneetvatakul, S.; Kuwattanasiri, D.; Waibel, H. The productivity of pesticide use in rice production of Thailand: A damage control approach. In Proceedings of the International Symposium on Sustaining Food Security and Managing Natural Resources in Southeast Asia: Challenges for the 21st Century, Chiang Mai, Thailand, 8–11 January 2002; p. 14. [Google Scholar]
- Schroder, D.; Headley, J.C.; Finley, R.M. The contribution of herbicides and other technologies to corn production in the Corn Belt region, 1964 to 1979. North Cent. J. Agric. Econ. 1984, 6, 95–104. [Google Scholar] [CrossRef]
- Stifel, D.; Minten, B. Isolation and agricultural productivity. Agric. Econ. 2008, 39, 1–15. [Google Scholar] [CrossRef]
- Talpaz, H.; Borosh, I. Strategy for pesticide use: Frequency and applications. Am. J. Agric. Econ. 1974, 56, 769–775. [Google Scholar] [CrossRef]
- Johnston, J.; DiNardo, J. Econometric Methods; McGraw-Hill: New York, NY, USA, 1972; Volume 2. [Google Scholar]
- Edwards, W. The theory of decision making. Psychol. Bull. 1954, 51, 380–417. [Google Scholar] [CrossRef] [PubMed]
- Doss, C.R.; Morris, M.L. How does gender affect the adoption of agricultural innovations? Agric. Econ. 2001, 25, 27–39. [Google Scholar] [CrossRef]
- Li, H.M.; Fu, X.H.; Wu, X.M. Farmers’ willingness to use pesticides safely and its influencing factors: A survey and analysis of 214 households in Guanghan City, Sichuan Province. J. Agrotech. Econ. 2007, 26, 99–104. [Google Scholar]
- Jallow, M.F.; Awadh, D.G.; Albaho, M.S.; Devi, V.Y.; Thomas, B.M. Pesticide risk behaviors and factors influencing pesticide use among farmers in Kuwait. Sci. Total Environ. 2017, 574, 490–498. [Google Scholar] [CrossRef] [PubMed]
- Zhu, D.; Kong, X.; Gu, J.P. Irrational equilibrium of excessive application of pesticides of farmers: Evidence from farmers in Southern China. Chin. Rural Econ. 2014, 30, 17–29. [Google Scholar]
- Hruska, A.J.; Corriols, M. The impact of training in integrated pest management among Nicaraguan maize farmers: Increased net returns and reduced health risk. Int. J. Occup. Environ. Health 2002, 8, 191–200. [Google Scholar] [CrossRef] [PubMed]
- Mekonnen, Y.; Agonafir, T. Pesticide sprayers’ knowledge, attitude and practice of pesticide use on agricultural farms of Ethiopia. Occup. Med. 2002, 52, 311–315. [Google Scholar] [CrossRef]
- Plianbangchang, P.; Jetiyanon, K.; Wittaya-Areekul, S. Pesticide use patterns among small-scale farmers: A case study from Phitsanulok, Thailand. Southeast Asian J. Trop. Med. Public Health 2009, 40, 401–410. [Google Scholar] [PubMed]
- Damalas, C.A.; Khan, M. Pesticide use in vegetable crops in Pakistan: Insights through an ordered probit model. Crop Prot. 2017, 99, 59–64. [Google Scholar] [CrossRef]
| Categories | N | % | |
|---|---|---|---|
| Gender | Male | 441 | 51.22 |
| Female | 420 | 48.78 | |
| Age | Below 18 | 3 | 0.35 |
| 18–25 | 33 | 3.83 | |
| 26–45 | 210 | 24.39 | |
| 46–60 | 408 | 47.39 | |
| 60 or above | 204 | 24.04 | |
| Education level | Primary school or below | 282 | 32.75 |
| Secondary school (junior) | 315 | 36.59 | |
| Secondary school (senior) | 189 | 21.95 | |
| College | 54 | 6.27 | |
| Bachelor degree or above | 21 | 2.44 | |
| Part-time jobs | Without other part-time jobs | 234 | 27.18 |
| With other part-time jobs | 627 | 72.82 | |
| Household size | 1–2 | 51 | 5.92 |
| 3 | 201 | 23.35 | |
| 4 | 243 | 28.22 | |
| 5 or above | 366 | 42.51 | |
| Household annual income | RMB 30,000 or below | 192 | 22.30 |
| RMB 30,000–50,000 | 261 | 30.31 | |
| RMB 50,000–100,000 | 216 | 25.09 | |
| RMB 10,000 or above | 192 | 22.30 | |
| Production mode | Individual family farms | 819 | 95.12 |
| Large and specialized family businesses | 15 | 1.74 | |
| Family farms | 9 | 1.05 | |
| Farmer cooperatives | 12 | 1.39 | |
| Others | 6 | 0.70 |
| Categories | N | % | |
|---|---|---|---|
| The use of protective measures when handling pesticides | No | 372 | 43.21 |
| Yes | 489 | 56.79 | |
| Knowledge about “Guideline for safety application of pesticides” | No | 726 | 84.32 |
| Yes | 135 | 15.68 | |
| To read the instructions on the label prior to the application | Absolutely not | 12 | 1.39 |
| Usually not | 132 | 15.33 | |
| Commonly | 303 | 35.19 | |
| Usually | 279 | 32.40 | |
| Surely | 135 | 15.68 | |
| Following the instructions and recommended dose on the label | Less than the recommended dose | 27 | 3.14 |
| Following the recommended dose | 333 | 38.68 | |
| More than the recommended dose | 234 | 27.18 | |
| Based on previous experience | 267 | 31.01 | |
| Understandings of the toxicity of pesticides | Without any understanding | 54 | 6.27 |
| With little understanding | 675 | 78.40 | |
| With comprehensive understanding | 132 | 15.33 | |
| Knowledge about types of prohibited pesticides | No | 459 | 53.31 |
| Yes | 402 | 46.69 | |
| Understanding of pesticide residue | No | 464 | 53.89 |
| Yes | 397 | 46.11 | |
| Understanding of “pre-harvest interval” (PHI) | No | 344 | 39.95 |
| Yes | 517 | 60.05 | |
| Judgement on whether massive use of pesticides imposes harms to the surrounding environment | No | 138 | 16.03 |
| Yes | 723 | 83.97 |
| Estimated Coefficient | ||
|---|---|---|
| C-D Production Function | Damage Control Model (Based on Weibull Distribution) | |
| d | 6.2391 *** (0.1262) | 6.6812 *** (0.1314) |
| Seed | −0.0188 * (0.0104) | −0.0189 * (0.0104) |
| Fertilizer | 0.0482 *** (0.0152) | 0.0487 *** (0.0152) |
| Machine | 0.0892 *** (0.0153) | 0.0893 *** (0.0153) |
| Labor | 0.0193 * (0.0117) | 0.0196 * (0.0117) |
| Transportation | −0.0368 *** (0.0076) | −0.0369 *** (0.0076) |
| Pesticide | 0.0354 *** (0.0114) | — |
| γ | — | 0.0733 ** (0.0337) |
| R2 | 0.2050 | 0.2048 |
| F Test | 16.7044 *** | 16.6566 *** |
| −2lnL | 1024.8126 | 1024.5536 |
| Variables | Variable Definition | Mean | S.D. | |
|---|---|---|---|---|
| Overuse of pesticide (Y) | Y1 derived by C-D Production Model | Dummy variable; without overuse = 0, overuse = 1 | 0.965 | 0.183 |
| Y2 derived by Damage Control Model | Dummy variable; without overuse = 0, overuse = 1 | 0.959 | 0.198 | |
| Gender | Dummy variable; male = 0, female = 1 | 0.488 | 0.500 | |
| Education level (Education) | Continuous variables; Primary level or below = 6, Secondary school (junior) = 9, Secondary (senior) = 12, College = 14, University or above = 16 | 9.160 | 2.769 | |
| Farming years (Farming) | Dummy variable; 20 years or less = 0, over 20 years = 1 | 0.648 | 0.478 | |
| Planting size (Size) | Continuous variables; 3 mu or below = 1, 3–6 mu = 2, 6–10 mu = 3, 10 mu or above = 4 | 1.864 | 0.959 | |
| Portion of farm income in household annual income (Income) | Interval variable; 30% or below = 1, 31–50% = 2, 51–80% = 3, 80% or above = 4 | 1.443 | 0.897 | |
| Knowledge about “Guideline for safety application of pesticides” (Standard) | Dummy variable; no = 0, yes = 1 | 0.157 | 0.364 | |
| Knowledge about types of prohibited pesticides (Poison) | Dummy variable; no = 0, yes = 1 | 0.467 | 0.499 | |
| Views towards frequent and massive use of pesticide on generating pesticide residue (Residue) | Dummy variable; no = 0, yes = 1 | 0.923 | 0.266 | |
| View towards massive use of pesticides against the surrounding environment (Environment) | Dummy variable; no = 0, yes = 1 | 0.840 | 0.367 | |
| Participation in pesticide training organized by the government (Train) | Dummy variable; no = 0, yes = 1 | 0.230 | 0.421 | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 Overuse of pesticide | 1.00 | ||||||||||
| 2 Gender | 0.07 ** | 1.00 | |||||||||
| 3 Education | 0.05 | −0.10 *** | 1.00 | ||||||||
| 4 Farming | −0.07 ** | −0.04 | −0.42 *** | 1.00 | |||||||
| 5 Size | 0.03 | −0.09 *** | 0.16 *** | −0.10 *** | 1.00 | ||||||
| 6 Income | 0.01 | −0.09 ** | −0.26 *** | 0.19 *** | 0.08 ** | 1.00 | |||||
| 7 Standard | −0.02 | −0.04 | 0.17 *** | −0.12 *** | 0.28 *** | −0.02 | 1.00 | ||||
| 8 Poison | 0.08 ** | −0.04 | −0.03 | 0.10 *** | 0.03 | 0.19 *** | 0.15 *** | 1.00 | |||
| 9 Residue | 0.09 *** | 0.02 | 0.05 | 0.01 | 0.05 | −0.06 * | 0.09 *** | 0.09 ** | 1.00 | ||
| 10 Environment | 0.12 *** | 0.01 | 0.06 * | −0.03 | 0.12 *** | 0.01 | 0.03 | 0.07 * | 0.05 | 1.00 | |
| 11 Train | 0.06 * | −0.02 | 0.20 *** | 0.06 * | 0.22 *** | −0.05 | 0.24 *** | 0.04 | 0.10 *** | 0.01 | 1.00 |
| Variables | Estimated Coefficients | |
|---|---|---|
| Y Determined by C-D Production Function | Y Determined by Damage Control Model (Weibull Distribution) | |
| Constant | 0.103 (0.862) | 0.355 (0.804) |
| Gender | 0.380 ** (0.192) | 0.321 * (0.181) |
| Education | 0.023 (0.042) | 0.017 (0.039) |
| Farming | −0.301 * (0.171) | −0.331 ** (0.166) |
| Size | 0.024 (0.116) | −0.064 (0.103) |
| Income | 0.115 (0.116) | 0.014 (0.099) |
| Standard | −0.465 * (0.255) | −0.378 (0.251) |
| Poison | 0.518 ** (0.213) | 0.477 ** (0.200) |
| Residue | 0.492 * (0.257) | 0.802 *** (0.223) |
| Environment | 0.628 *** (0.195) | 0.535 *** (0.191) |
| Train | 0.529 * (0.276) | 0.553 ** (0.267) |
| Restr. log likelihood | −130.178 | −146.375 |
| Akaike info criterion | 0.286 | 0.316 |
| LR statistic | 36.371 *** | 42.865 *** |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Chu, M.; Ma, Y. Measuring Rice Farmer’s Pesticide Overuse Practice and the Determinants: A Statistical Analysis Based on Data Collected in Jiangsu and Anhui Provinces of China. Sustainability 2018, 10, 677. https://doi.org/10.3390/su10030677
Wang J, Chu M, Ma Y. Measuring Rice Farmer’s Pesticide Overuse Practice and the Determinants: A Statistical Analysis Based on Data Collected in Jiangsu and Anhui Provinces of China. Sustainability. 2018; 10(3):677. https://doi.org/10.3390/su10030677
Chicago/Turabian StyleWang, Jianhua, May Chu, and Yuting Ma. 2018. "Measuring Rice Farmer’s Pesticide Overuse Practice and the Determinants: A Statistical Analysis Based on Data Collected in Jiangsu and Anhui Provinces of China" Sustainability 10, no. 3: 677. https://doi.org/10.3390/su10030677
APA StyleWang, J., Chu, M., & Ma, Y. (2018). Measuring Rice Farmer’s Pesticide Overuse Practice and the Determinants: A Statistical Analysis Based on Data Collected in Jiangsu and Anhui Provinces of China. Sustainability, 10(3), 677. https://doi.org/10.3390/su10030677





