Abstract
The objective of this study is to estimate the biomass and carbon of global-level mangroves as a special type of wetland. Mangrove ecosystems play an important role in regulating carbon cycling, thus having a significant impact on global environmental change. Extensive studies have been conducted for the estimation of mangrove biomass and carbon stock. However, this estimation at a global level has been insufficiently investigated because the spatial scale of interest is large and most existing studies are based on physically challenging fieldwork surveys that are limited to local scales. Over the past few decades, high-resolution geospatial data related to mangroves have been increasingly collected and processed using remote sensing and Geographic Information Systems (GIS) technologies. While these geospatial data create potential for the estimation of mangrove biomass and carbon, the processing and analysis of these data represent a big data-driven challenge. In this study, we present a spatially explicit approach that integrates GIS-based geospatial analysis and high-performance parallel computing for the estimation of mangrove biomass and carbon at the global level. This integrated approach provides support for enabling and accelerating the global-level estimation of mangrove biomass and carbon from existing high-resolution geospatial data. With this integrated approach, the total area, biomass (including above- and below-ground), and associated carbon stock of global mangroves are estimated as 130,420 km2, 1.908 Pg, and 0.725 Pg C for the year of 2000. The averaged aboveground biomass density of global mangroves is estimated as 146.3 Mg ha−1. Our analysis results demonstrate that this integrated geospatial analysis approach is efficacious for the computationally challenging estimation of global mangrove metrics based on high-resolution data. This global-level estimation and associated results are of great assistance for promoting our understanding of complex geospatial dynamics in mangrove forests.
1. Introduction
Large-scale assessments of natural resources provide important information for planning, management and conservation, and context for local or site-specific assessments. However, large-scale assessments are inherently difficult due to the large and complex data sets. The study in this article aims to estimate biomass and carbon in global-level mangrove forests to demonstrate an approach that integrates GIS-based geospatial analysis and high-performance parallel computing. Mangrove forests are important tropical wetland types growing within coastal marine environment [1,2]. They are recognized for having the highest carbon density among terrestrial ecosystems. Accordingly considerations about the distribution and extent of carbon associated with mangroves are highly relevant to terrestrial carbon cycling and the associated ecosystem services under global environmental or climate change [1,3]. However, as a result of land use and land cover change over the past several decades, large losses of mangroves at both the regional and global scales have been reported [2,4]. Biomass and carbon stocks related to mangroves can be a basis for averting degradation through payment for ecosystem service program (e.g., REDD+) and they are important to better understanding the global carbon cycle and the sustainability of mangrove ecosystems [3,5,6].
Along with increasing awareness in the importance of mangrove forests, many studies related to mangrove biomass and carbon stocks estimation have been conducted, typically through field survey [7,8,9]. However, the field survey approach is only suitable or feasible for site-specific or local-level studies. From the field survey results, the estimation of global mangrove biomass or carbon is typically based on a scaling approach (i.e., the multiplication of mean mangrove biomass density from fieldwork and the total area of mangrove forests). Further, Twilley et al. [10] developed a latitude-based model, extended from the scaling approach, for estimating mangrove biomass and carbon. Twilley et al.’s study gave 240,000 km2 of total mangrove area with 4.03 Pg C of carbon in mangrove biomass (2.34 Pg C from aboveground and 1.69 Pg C from belowground). Alongi [3] reported that the average carbon stock density at global level is 956 t C ha−1, which leads to 13 Pg C of ecosystem-level carbon stock for global mangrove forests given that the total area of global mangrove forests used in his study is 140,000 km2. Sanders et al. [11] estimated the total ecosystem-level carbon stock in global mangrove forests as 11.2 Pg C based on their fieldwork data in Australia, carbon stock data reported in the literature, and latitudinal information of mangroves from Giri et al. [12].
An alternative is to estimate mangrove biomass and carbon using geospatial data collected through geospatial technologies such as remote sensing and Geographic Information Systems (GIS) [5,13]. The advancement of geospatial technologies has made geographically referenced data increasingly available at fine spatial resolutions for large spatial extents. These geospatial datasets in combination with field survey data provide support for the estimation of mangrove biomass and carbon. Based on these data, models that establish the relationship between mangrove biomass and their drivers can be used to estimate mangrove biomass and carbon at global level. For example, Hutchison et al. [14] presented a climate model based on the temperature and precipitations of the regions where mangrove forests exist to estimate the global mangrove biomass. The climate model used by Hutchison et al. outperform the latitude-based model by Twilley et al. [10]. Hutchison et al.’s results show a total of 2.83 Pg of aboveground biomass (1.11 Pg for below-ground biomass) in global mangrove forests. The mangrove extent data from Spalding et al. [15], which gave a total mangrove area of 153,140.94 km2, was used in the study by Hutchison et al. Besides climate-based model, allometric models can be employed to estimate mangrove biomass and carbon from allometric variables represented by canopy heights (see [7,16]). This is attributed to the fact that the information of canopy heights can be derived from geospatial data that are remotely sensed, for example, from satellite-borne sensors. Fatoyinbo and Simard [5] applied an allometric model to estimate mangrove biomass from canopy heights in Africa. The information of mangrove canopy heights is extracted from the GIS-based overlay analysis between Shuttle Radar Topography Mission (SRTM) data and mangrove extent data classified from Landsat imagery.
The geospatial data and allometric models based on canopy height offer a means of estimating mangrove biomass and carbon in a convenient manner. However, it poses a grand challenge for the global-level mangrove biomass estimation because massive geospatial data are involved together with considerable computational demand. For example, the global SRTM data used for extracting canopy height information is now available at a spatial resolution of 30 m by 30 m (originally 90 m by 90 m before 2015). This corresponds to hundreds of gigabytes of storage needs just for the primary dataset. Even higher storage and computing capacities are required to process and analyze these datasets for the estimation of mangrove biomass and carbon at the global level. In other words, the use of these fine-resolution geospatial data for the global-level mangrove biomass and carbon estimation represents a big data-driven challenge (see [17,18,19]).
Therefore, to address this big data-driven challenge, the objective of this study is to conduct an estimation of global mangrove biomass and carbon by using a GIS-based spatial analysis approach integrated with parallel computing. The estimation is based on fine-resolution geospatial data available at global level. Please note that the fine resolution here is relative to the global scale. Geospatial data used in this study is based on a 30 m × 30 m spatial resolution, which is often referred to as medium spatial resolution (in a range of 10–100 m) in the literature of remote sensing [20]. We develop this spatially integrated approach to enable and accelerate the global-level estimation on high-performance computing. This spatially integrated approach is well-suited to geospatial data with even finer spatial resolutions.
2. Materials and Methods
2.1. Data
The global-level estimation of mangrove biomass and carbon is based on two datasets: global digital elevation model (DEM) data and global mangrove extent data (Figure 1, Table 1). The DEM includes two models: Digital Surface Model (DSM) and Digital Terrain Model (DTM). DSM includes the elevation information of all entities on the ground, such as buildings or forests, and DTM only represents the bare ground surface without any entities. SRTM data is a worldwide DSM with a 30 m by 30 m spatial resolution (previously available at 90- and 1000-m spatial resolutions) created for the year of 2000. The SRTM dataset (https://www2.jpl.nasa.gov/srtm/) was originally generated by the National Aeronautics and Space Administration (NASA) and the National Geospatial-Intelligence Agency (NGA), and released by US Geological Survey (USGS) in 2014. It includes 14,276 GeoTIFF tiles that contain the elevation information from 60° north latitude to 56° south latitude. The size of each SRTM tile is 3600 × 3600 pixels. The size of the entire SRTM dataset is about 315 GB.
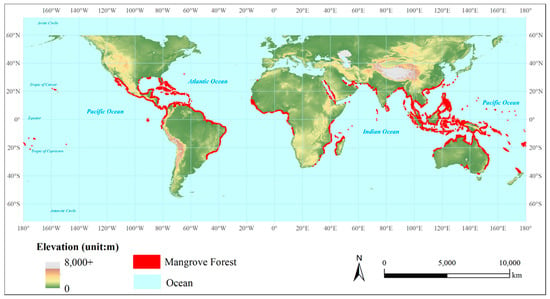
Figure 1.
Map of the global elevation and mangrove distribution [note that the map only shows Shuttle Radar Topography Mission (SRTM) digital elevation model (DEM) data, which are available from 60° north latitude to 56° south; mangrove distribution is based on the data from Giri et al. [12]; elevation is from SRTM DEM data].

Table 1.
Spatial datasets used in this study.
Global mangrove coverage dataset was created by USGS in 2000 (see [12] and http://data.unep-wcmc.org/datasets/4). It is a vector-based GIS dataset that has 1.4 million polygons representing the extent of mangroves. This mangrove extent dataset was generated from the classification of Global Land Survey (GLS) data and the Landsat Imagery. It was originally created as raster-based spatial dataset at a 30-m spatial resolution. From this dataset, there are approximately 137,760 km2 global mangrove extent in 117 countries and regions in the year of 2000 (see [12]).
2.2. Methods
The framework for the spatially explicit approach that integrates GIS-based geospatial analysis and high-performance parallel computing for the estimation of mangrove biomass and carbon consists of the following major steps: (1) selection of SRTM tiles, (2) extraction of mangrove canopy height, (3) calculation of mangrove area, (4) the estimation of biomass and carbon in mangrove forest, and (5) parallel computing that accelerates the spatially explicit estimation (Figure 2).
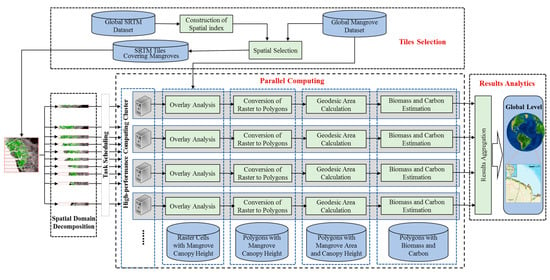
Figure 2.
Framework of a spatially explicit approach for the estimation of global mangrove biomass and carbon.
2.2.1. Selection of SRTM Tiles
The global SRTM dataset includes 14,276 tiles that cover the area from 60° north to 56° south latitude. As a first step, we exclude those SRTM tiles that do not contain mangroves to facilitate the entire analysis. Considering the amount of SRTM datasets, we used grid-based spatial indexing (see [21]) in which the bounding box of each SRTM tile was used as a spatial index grid. The necessity of using spatial indexing for addressing big spatial data challenges has been well acknowledged in the literature (see [22,23]). The grid-based spatial indexing relies on the use of a lattice of non-overlapping and fixed-size rectangles to index the spatial dimension of a study region (see [24]). Each entity (e.g., point, polylines, or polygons) of the original spatial data of interest is associated with an indexing rectangle (sometimes multiple). This indexing mechanism can efficiently support the spatial query or selection operations if the geospatial datasets of interest are complicated or large in size. The spatial index grid used in this study corresponds to the lattice of bounding boxes of SRTM tiles. Those spatial indexing rectangles that do not contain or intersect with mangrove extent polygons can be identified and excluded. Thus, by using this spatial indexing mechanism, we can efficiently select those SRTM tiles within or intersected with polygons of mangrove extent instead of using the original datasets. This grid-based spatial indexing also supports the subsequent analysis steps. As a result, a total of 1512 SRTM tiles that cover the extent of mangrove forests are identified.
2.2.2. Extraction of Mangrove Canopy Height
Given the SRTM tiles and mangrove extent data, we extract the canopy heights of mangroves by using GIS-based overlay analysis. Global SRTM data are raster-based and mangrove extent are vector-based. Thus, we extracted from SRTM tiles those raster cells that are located within the polygons of mangrove extent. It is assumed that the ground elevation that mangroves grow is zero (see [5]). In other words, if the value of a SRTM raster cell within mangrove polygons is positive, the value represents the canopy height of the mangroves in this raster cell. Therefore, we extract the canopy heights of mangroves from the overlay analysis between SRTM tiles and mangrove extent data (using clip function for raster data in ArcGIS (ESRI, Redlands, CA, USA)). Figure 3 shows the distribution of mangrove area in terms of canopy heights.
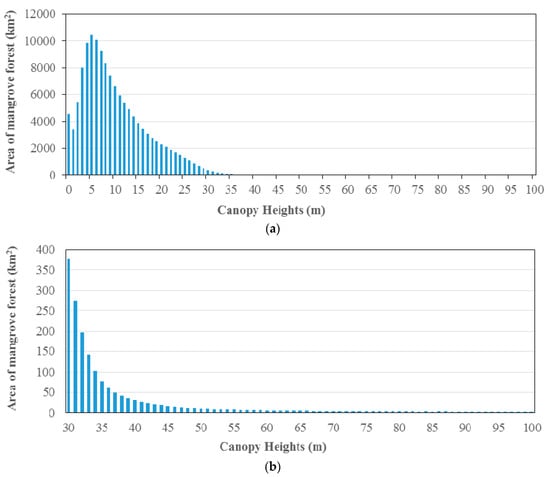
Figure 3.
Distribution of mangrove area with respect to canopy height in global mangrove forest. (a) distribution for canopy heights from 0 to 100 m; (b) distribution for canopy heights from 30 to 100 m.
It is suggested in the literature (see [5]) that high values of the canopy height cells may be associated with high uncertainties in SRTM data for the derivation of canopy heights. As a result, those mangrove cells with very high canopy heights (often in islands) need to be removed as Fatoyinbo and Simard [5] suggested (a threshold of 40 m was used in their study in Africa). For example, Figure 4 shows the spatial pattern of canopy heights of mangroves in a region in Bali Island, Indonesia. For the region classified as mangroves from Giri et al.’s dataset, canopy heights can be up to 1190 m. While this indicates the commission error (false alarm) in the remote sensing classification, those cells with very high canopy heights should not be considered in the estimation of mangrove biomass and carbon [5]. This suggests that a cut-off threshold needs to be applied. The tallest mangroves up to 64 m (individual height) were reported in Cayapas-Mataje reserve, Ecuador (see [15,25]). From the SRTM data, the maximum of mangrove canopy heights (averaged height instead of individual height) in this Reserve is 48 m. Thus, in this study, we used 48 m as the cut-off threshold to derive the canopy heights of mangroves for biomass estimation. Those mangrove cells with canopy heights higher than 48 m are filtered.
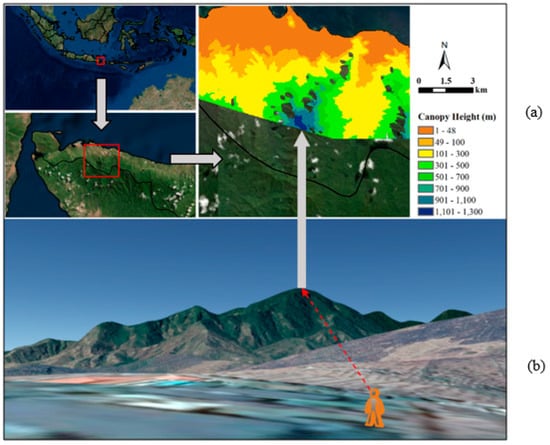
Figure 4.
Illustration on the need of cut-off threshold for the derivation of canopy heights of mangroves (The example region is in Bali Island, Indonesia). (a) 2D map of canopy heights of mangroves estimated from SRTM data and mangrove extent data from Giri et al. [12]; (b) 3D view of the example region (snapshots from Google Earth).
2.2.3. Calculation of Mangrove Area
Based on derived canopy heights of mangroves, we calculate the area of mangroves. A straightforward approach for area calculation is to count the number of raster cells and then multiply this number with the size of a raster cell (30 m by 30 m here). This approach is based on planar geometry and it may work for the case in which the number of raster cells is small. However, this study is targeted on the global level and the ellipsoid shape of the Earth will lead to the introduction of errors if we use the approach based on the planar geometry. Thus, we opted to use an alternative approach based on geodesic geometry (see [26]) to calculate the area of mangroves from raster cells. In other words, we calculate the geodesic area of raster cells of mangroves instead of planar area considering the scale of interest is large and the number of raster cells involved is extremely large. The way that we calculated geodesic area is to first convert raster cells of mangrove canopy height into polygons with geodesic coordinates, and then calculate the geodesic area of the polygons of mangrove canopy height. The use of this geodesic area approach is very important since it allows for the accurate calculation of area when the study extent of interest is large (this study here). As a result of this analysis step, we obtain a set of mangrove polygons that are vectorized from raster-based mangrove canopy height data. Each mangrove polygon is associated with a specific canopy height value and geodesic area.
2.2.4. The Estimation of Biomass and Carbon in Mangrove Forest
Given the set of mangrove polygons with the information of canopy heights and area, next step is to derive the mangrove biomass and carbon. We used the global allometric model (see [5,7] and Equation (1)) to conduct the estimation of aboveground biomass. Equations (2) and (3) show the derivation of belowground biomass (mangrove root biomass) and carbon stock in this study.
where b1i is the aboveground biomass (unit: Mg) associated with a mangrove polygon i. and hi is the mangrove canopy height of the mangrove polygon. ai is the area (unit: ha) of the mangrove polygon i. b2i and ci are the belowground biomass (unit: Mg) and the total carbon (unit: Mg C) of the corresponding mangrove polygon. The coefficients used in Equations (1)–(3) are based on the literature (see [5,9,27]). The first part (i.e., 10.8 × hi + 34.9) in Equation (1) is the global allometric model of canopy heights (unit: Mg ha−1). Once we obtain the above- and below-ground biomass and carbon of each mangrove polygon, we derive the total biomass and carbon at the global level or by regions via summation operations.
b1i = (10.8 × hi + 34.9) × ai
b2i = 0.38 × b1i
ci = 0.5 × (b1i + b2i)
2.2.5. Parallel Computing for Accelerated Geospatial Analysis of Mangrove Data
The estimation of biomass and carbon stock in mangrove forest at global level poses a big data challenge because the size of the datasets is massive and the computing demand for this estimation is huge. Desktop computing environments cannot cope with massive dataset and associated computing demand because of the physical limits on computing hardware configuration (e.g., memory, and computing power from CPUs). To overcome this big data challenge, we chose to use a parallel computing approach that allows for leveraging high-performance computing resources for acceleration. As advancement in cyberinfrastructure [28,29], high-performance computing resources such as computing clusters (with hundreds or thousands of CPUs or higher) are increasingly available. Parallel computing approaches allow for the partitioning of a large spatial analysis task that is challenging or infeasible for single CPUs into a set of smaller sub-tasks [18,30,31]. These smaller tasks, which are computationally efficient or feasible, can be deployed to the high-performance computing clusters and executed concurrently by the collection of multiple computing elements (CPUs) on these clusters. As a result, the entire spatial analysis task can be computationally affordable and accelerated via the divide-and-conquer mechanism built in parallel computing algorithms [30].
The parallel computing approach that we used in this study is based on spatial domain decomposition strategy (see [32]). The SRTM dataset that we selected from the original one has 1512 tiles. Each SRTM tile is further split into a set of sub-tiles, for example, using 1D (row-wise or column-wise) or 2D decomposition (see Figure 5 for illustration). The entire analysis steps for the estimation of mangrove biomass and carbon (from the extraction of mangrove canopy heights and area to the derivation of biomass and carbon) are applied to these sub-tiles each corresponding to a task. For example, if each tile is partitioned into 10 sub-tiles along row-wise direction (1D decomposition), the number of sub-tiles that we are dealing with is 15,120. That is, the number of computing tasks that we have for this example is 15,120. These analysis tasks are then scheduled by the head node of a computing cluster and assigned to computing nodes for parallel acceleration. Once these analysis tasks are completed, associated results (e.g., mangrove area, biomass, and carbon) are then aggregated to the levels of interest (e.g., global or country-level).

Figure 5.
Illustration of 1D and 2D spatial domain decomposition on a SRTM tile. (A) Row-wise decomposition; (B) column-wise decomposition; (C) the 2D domain decomposition. The location of the tile used: 5–6° N in latitude and 5–6° E in longitude (in Nigeria).
The computing cluster that we used is a Windows-based cluster with 30 computing nodes each having four CPUs (i.e., in total 120 CPUs are available for parallel acceleration; CPU clock rate: 3.4 GHz). These computing nodes are connected through a gigabit network switch. The operating system on each computing node is Windows Server 2012 R2. The job scheduling software for parallel computing is Microsoft HPC Pack 2012 R2 (version 4.2). We used geodatabase technologies to organize the geospatial data used in this study (SRTM data, mangrove extent, and country boundaries). ESRI ArcGIS (version 10.4) was used to support the spatial analyses in this study. Further, we used Python scripts to automate the processing and analysis of geospatial data.
3. Results
In this section, we report the results of parallel computing performance and global-level mangrove metrics, including area, biomass, and carbon.
3.1. Parallel Computing Performance
In this study, we used 1D row-wise spatial domain decomposition to split each SRTM tile into 10 smaller sub-tiles. That is, the total number of sub-tiles after spatial domain decomposition is 15,120. After excluding those sub-tiles without mangroves, we obtained 7604 sub-tiles that need to be analyzed for biomass and carbon estimation. These 7604 sub-tiles are then wrapped as tasks that are submitted to the Windows-based computing cluster for parallel acceleration. Sequential run based on a single CPU for analyzing all of these sub-tiles would require 57.6 h (307,386 s). However, only 1.46 h (5247 s) are needed to complete all the analysis when 120 CPUs are used for parallel computing. A metric of speedup, which is the ratio of sequential computing time over parallel computing time (see [30]), can be used to evaluate the acceleration performance of parallel algorithms. The 1.46 h of parallel computing time corresponds to a speed up of 39.52, which means the parallel computing approach using 120 CPUs can accelerate 39.52 times compared to the sequential computing approach.
3.2. Estimation Results of Global Mangrove Area, Biomass and Carbon
The total area of global-level mangroves is estimated as 130,420 km2 (see Table 2). The aboveground and belowground biomass in global mangrove forests are 1.908 Pg and 0.725 Pg. The total carbon stock in above- and below-ground biomass is 1.32 Pg C. The average aboveground biomass density is 146.3 Mg ha−1. Table 3 reports the mangrove area, biomass, and carbon for some representative countries.

Table 2.
Global-level mangrove metrics of biomass and biomass carbon estimated from this study in comparison with those reported in the literature.

Table 3.
Mangrove area, biomass, and carbon of representative countries (sorted by mangrove area derived from this study).
Figure 6 is a map of the estimated mangrove aboveground biomass density at country level. Figure 7 illustrates the spatially explicit pattern of mangrove aboveground biomass density for four example regions. Figure 8 depicts the relationship of aboveground biomass density of mangroves estimated from this study with latitude. The aboveground biomass density is summarized from our estimation results for each latitude (within 1 degree of band—i.e., 0–1°, 1–2°, …, and 39–40°). Equations (4)–(6) report the fitted models between estimated mangrove biomass density and latitude for the entire globe, northern hemisphere, and southern hemisphere (corresponding goodness-of-fits: 0.6584, 0.5484 and 0.6255).
where ABg, ABn and ABs are aboveground mangrove biomass density (unit: Mg ha−1) for the entire globe, northern hemisphere, and southern hemisphere. x is the absolute value of the latitude in decimal degree.
ABg = −2.5514 × x + 172.31
ABn = −2.8147 × x + 167.12
ABs = −3.0979 × x + 188.95
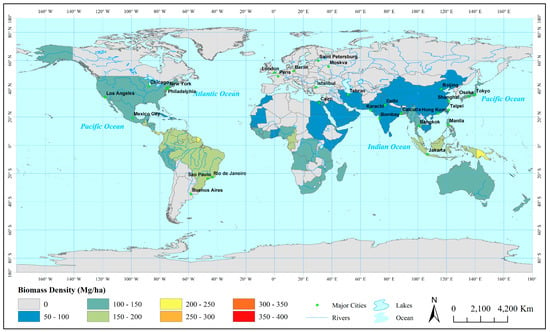
Figure 6.
Map of averaged aboveground biomass density of mangroves at country level.
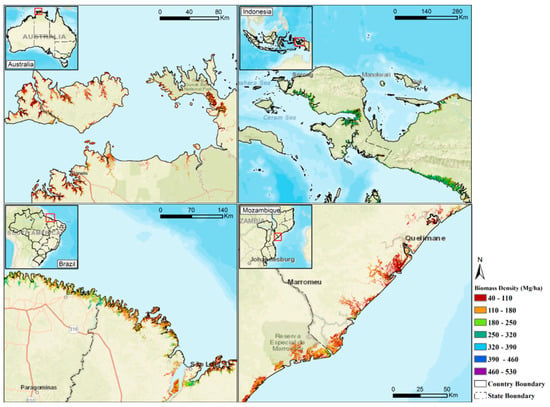
Figure 7.
Maps of aboveground biomass density of example regions. Four regions were selected from Australia, Indonesia, Brazil, and Mozambique (base maps of these maps are from ESRI World Street Map).
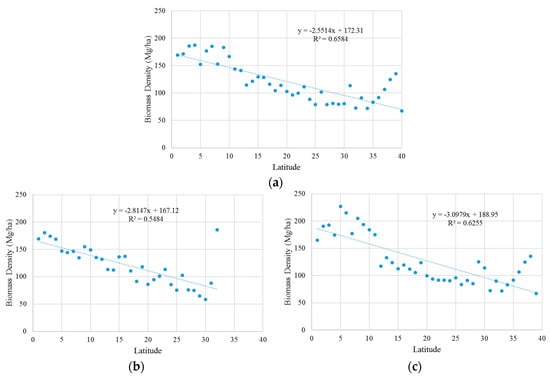
Figure 8.
Distribution of aboveground biomass density of mangroves along with latitude. (a) Global level; (b) northern hemisphere; (c) southern hemisphere.
4. Discussion
The estimation of mangrove metrics from the global-level geospatial datasets (including elevation and mangrove extent) is both data- and computation-intensive. The volume of original geospatial datasets in this study are hundreds of gigabytes. However, the spatial analyses algorithms (e.g., overlay analysis, vectorization) generate more intermediate data and require even more computing support. The parallel computing approach allows for dividing the entire spatial analysis task (including data and computation) that requires over 2 days of serial computing into a collection of smaller tasks that can be computed in parallel. The parallel computing time was reduced to 1.46 h when 120 CPUs are recruited to work together to conduct the spatially explicit estimation of mangrove metrics. The hourly-level parallel computing time instead of days for the sequential counterpart brings more flexibility and convenience for verifying, testing, and (re)using the GIS-based spatial analysis for the estimation of global-level mangrove biomass and carbon.
The estimated total area of global mangroves (130,420 km2) is lower than those reported in the literature (see Table 2). While the mangrove extent data used in this study is from Giri et al. [12], raster cells within a mangrove polygon are excluded in this study if the elevation of these cells is zero or higher than the cut-off threshold (48 m here). Mangrove area (140,000 km2) reported by Alongi [3] is approximated from Giri et al.’s work. The estimated mangrove area at the global level is different with that (153,141 km2) reported by Hutchison et al. [14], who used the mangrove extent data (covering from the year of 1999 to 2003) by Spalding et al. [15] (compiled from the classification of remote sensing imagery and partially from Spalding et al.’s previous work).
The estimated total mangrove aboveground biomass is 1.908 Pg at the global level, which is consistent with those reported in the literature (2.34 Pg from Twilley et al. [10] and 2.83 Pg from Hutchison et al. [14]). While these biomass values are consistent, the ways that these values were estimated are different. Twilley et al.’s estimation is based on the summation of aboveground biomass calculated from the multiplication of mean biomass density with mangrove area along 10° latitude. Hutchison et al. [14] derived the aboveground biomass by combining mean biomass estimated from their climate model (based on temperature and precipitation) and mangrove area from Spalding et al. [15]. We estimated global aboveground biomass by using an allometric model of mangrove canopy height and mangrove extent from Giri et al. [12].
The averaged aboveground biomass density in mangrove forests that we estimated is 146.3 Mg ha−1 at the global level. Compared with the literature, Hutchison et al. [14] reported 184.8 Mg ha−1 with a 95% confidence range from 142.1–222.0 Mg ha−1. The average aboveground biomass in global mangroves reported by Twilley et al. [10] is 178.2 Mg ha−1 with a standard deviation of 112.2 Mg ha−1. Our estimated result, while lower than those reported in the literature, falls well within the range of previously reported results. Further, our analysis gave an estimation of 1.32 Pg C for carbon stock in the above- and below-ground biomass of global mangrove forests. This carbon stock estimation is lower than those reported in the literature (1.82 Pg C reported by Alongi [3], and 1.568 Pg C from Sanders et al. [11]). The mangrove extent information used in these three studies (including our study) is from the same work by Giri et al. [12]. Assuming 86% of soil carbon in the ecosystem-level carbon (see Sanders et al. [11]), we obtain 9.4 Pg C of ecosystem-level carbon in global mangrove forest, lower than 13 Pg C by Alongi and 11.2 Pg C by Sanders et al.; see [3,11]).
The global allometric model of canopy height used in this study allows for the derivation of aboveground biomass density for each 30 m × 30 m raster cell of mangroves. The aboveground biomass density of mangroves for different regions or countries can be further summarized from these raster cells. From our analysis, the country with the highest aboveground biomass density of mangrove in top 20 countries worldwide in terms of mangrove area is Papua New Guinea (217.29 Mg ha−1), seconded by Venezuela (199.91 Mg ha−1). Indonesia ranks the third with 193.39 Mg ha−1. High aboveground biomass densities tend to concentrate in countries in Latin America and Southeast Asia (from a range of 98–217 Mg ha−1) (see Figure 5). Appendix A reports a comparison of our results for countries in Africa with those by Fatoyinbo and Simard [5]. The total mangrove area in Africa estimated using our approach (based on mangrove extent data from Giri et al. [12]) is 25,640.71 km2, which is slightly lower than that from Fatoyinbo and Simard’s study (25,960 km2). However, the total aboveground biomass estimated from this study is a little higher than that from Fatoyinbo and Simard. Correspondingly, the mean biomass density of mangrove in Africa that we estimated is 122.37 Mg/ha, a bit higher than that by Fatoyinbo and Simard. The difference between our results and those by Fatoyinbo and Simard [5] (including continental and country scales) lies in the use of different mangrove extent and SRTM data with alternative spatial resolutions (30 m for our study and 90 m for their study). Our mangrove extent data were classified (combination of both supervised and unsupervised classification) from Landsat remote sensing imagery by Giri et al. [12]; Fatoyinbo and Simard [5] applied a different classification algorithm (unsupervised classification) to extract mangrove extent in their study.
As a comparison with field measurements, we used in Zambezi River Delta, where a field inventory was conducted in 2013 (see [8,33]). Our estimated mean biomass density (for canopy height from 2–29 m) in this study region is 126.84 Mg/ha, which is slightly lower than that (140.81 Mg/C) derived from the results in the 2013 field inventory (fiver height classes covering 2–29 m [8]; see [34] for the detailed field data and relevant reports). This difference can be attributed to the use of alternative allometric models (an allometric model of diameter at breast height was used in Stringer et al. [8]), in addition to resolution of the source data. Despite the inherent difference between the remote sensing and field inventory assessments, our result of mean biomass density is in good agreement with that from the 2013 field inventory.
Our accelerated spatial analysis results also provide insights into the relationship between biomass density and latitude (i.e., the latitude model). Equations (7)–(9) are latitude models reported by Twilley et al. [10], Saenger and Snedaker [7], and Hutchison et al. [14]. The corresponding goodness of fit (R2) of these models are 0.5625, 0.48 and 0.139. Notations are the same as in Equations (4)–(6).
ABg = −7.291 × x + 298.5
ABg = −5.570 × x + 244.994
ABg = −4.617 × x + 239.9
Figure 9 depicts the plots of the latitude models generated from this study and existing studies in the literature. It can be seen from Figure 9a that aboveground biomass density in southern hemisphere are higher than that in northern hemisphere. But this difference becomes lower as increase in latitude. As we could see from Figure 9b, the aboveground biomass density from the global-level latitude model in this study (see Equation (4)) is lower in low latitudes (0–10°) than the other three models reported in the literature. This difference tends to be smaller as latitudes become higher (10–20°). For the latitude between 20–30°, this difference reaches the minimum. Once latitude higher than 30°, aboveground biomass density tends to be higher than other models (by Twilley et al. and Saenger and Snedaker; see [7,10]) or exhibit marginal difference (by Hutchison et al. [14]). Our estimation of aboveground biomass relies on mangrove canopy height data by applying the empirical model from Saenger and Snedaker [7], which is based on a regression approach of fieldwork results reported in the literature in terms of the relationship between biomass and canopy height. However, the range of canopy heights in the geospatial data derived from SRTM data and mangrove extent is different with that reported in the literature. For example, for low latitude regions (0–2°), the range of canopy heights varies from 1 to 48 m (the cut-off threshold) in the geospatial data used in this study. Yet, the corresponding canopy heights reported in the literature and used by the allometric model is from 15–26.4 m (see [7]). This leads to the fact that the mean canopy height from the geospatial data within 0–2° (12.62 m) is lower than that from the empirical allometric model. As a result, the mean biomass density for low latitude region estimated from this study tends to be lower than those reported in the literature.
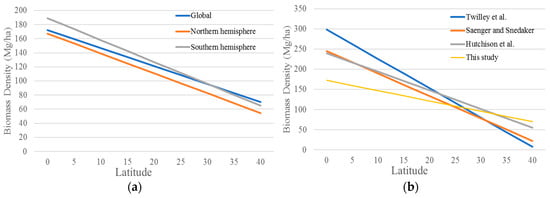
Figure 9.
Plots of latitude models from this study and existing studies in the literature. (a) Latitude models from this study for the entire globe, northern hemisphere, and southern hemisphere (b) latitude models at the global level from this study and existing studies.
Canopy height-based allometric model combined with remotely sensed data is well-suited to estimating biomass in mangrove forest. Of course, this approach for biomass estimation particularly at a large spatial scale is not limited to mangrove forests; it can be generalized for other types of forest if the allometric relationship between biomass and canopy heights is established. For example, Lefsky et al. [35] investigated the functional relationship between biomass and canopy heights in three forests (coniferous and deciduous) in tropical and temperate regions (one in Brazil and two in USA). Lefsky et al. stressed that canopy height is a reasonable indicator for biomass estimation from remote sensing data. Further, Zhang et al. [36] presented a remote sensing approach that combines metrics such as leaf area index and canopy heights to study forest biomass in California, USA. Zhang et al. [36] reported that forest biomass is strongly related to canopy heights for forests in the entire state of California. Thus, once the height-to-biomass relationship is available (e.g., estimated through fieldwork), it is feasible to apply the geospatial analysis approach in our study to other types of forests.
5. Conclusions
In this study, the GIS-based spatial analysis combined with high-performance and parallel computing provides unique support that enables the estimation of biomass and carbon in mangrove ecosystems at the global level. This global-level estimation is based on the processing and analysis of high-resolution geospatial data including global DEM and mangrove extent, which represents a big data challenge. The parallel computing approach developed in this study allows for the decomposition of large datasets and associated computation into smaller ones that are accelerated using high-performance computing resources. In other words, this global-level estimation is a data-intensive computing problem (see [37]) for which high-performance and parallel computing is an idealistic solution.
Our estimation of mangrove-related metrics (including area, biomass, and carbon) at the global level is different, but in general consistent, with those reported in the literature. The following aspects account for this difference: (1) datasets used in the estimation are different in terms of sources, spatial resolutions, or data acquisition time, and (2) processing or analysis methods (e.g., remote sensing imagery classification, or models of biomass) are different in terms of algorithms, parameters, or variables. Our estimation is based on the mangrove canopy height information and allometric model of canopy heights, and this estimation provide an alternative approach for the quantitative study of global-level mangrove ecosystems from a data-intensive perspective.
The big data-driven geospatial analytics of mangrove biomass and associated carbon in this study provide efficacious support for better understanding spatial heterogeneity in the mangrove forests at the global level. As the high-performance and parallel computing approach tackles the data- and compute-intensive challenges associated with this global-level estimation, the mangrove-related metrics derived from this study can be used to further the investigation of complex spatial dynamics in global mangrove ecosystems. This can be of great help in terms of informing policies for achieving long-term preservation and sustainability of these both ecologically and economically important wetland ecosystems. Our future work includes (1) application of allometric models of canopy height specific to countries or regions; (2) accuracy assessment of the analysis results including mangrove area and biophysical properties such as height, biomass, and carbon; (3) further evaluation of parallel acceleration performance; and (4) introduction of spatial statistics approaches (e.g., spatial autocorrelation) to investigate the spatially explicit characteristics of mangrove metrics.
Acknowledgments
The authors thank support from USDA Forest Service Grant “Development and Operation of a Web GIS-enabled Data Management Systems for the Santee Experiment Forest” and US NSF XSEDE Supercomputing Resource Allocation (SES170007).
Author Contributions
Wenwu Tang and Carl Trettin conceived and designed the experiments; Jiyang Shi and Xiang Zhao performed the experiments; Minrui Zheng and Jianxin Yang analyzed the data; Wenwu Tang wrote the paper with contribution from all other authors.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Mangrove area and aboveground biomass in Africa from this study in comparison with those reported by Fatoyinbo and Simard in 2013 [5] (AGB: aboveground biomass; DRC: Democratic Republic of the Congo).
Table A1.
Mangrove area and aboveground biomass in Africa from this study in comparison with those reported by Fatoyinbo and Simard in 2013 [5] (AGB: aboveground biomass; DRC: Democratic Republic of the Congo).
| Country | Fatoyinbo and Simard (2013) | This Study | ||||
|---|---|---|---|---|---|---|
| Area | Total AGB | Mean Biomass | Area | Total AGB | Mean Biomass | |
| (km2) | (Mg) | (Mg ha−1) | (km2) | (Mg) | (Mg ha−1) | |
| Angola | 154 | 1,441,200 | 93 | 295.57 | 3,626,791.37 | 122.70 |
| Benin | 18 | 137,719 | 76 | 30.76 | 214,831.39 | 69.84 |
| Cameroon | 1483 | 25,334,900 | 171 | 2122.16 | 38,866,367.62 | 183.15 |
| Congo | 15 | 267,603 | 178 | - | - | - |
| Côte d’Ivoire | 32 | 406,516 | 124 | 39.67 | 553,696.47 | 139.59 |
| Djibouti | 17 | 1,653,170 | 90 | 5.41 | 61,204.65 | 113.19 |
| DRC | 183 | 51,570 | 140 | 212.83 | 2,250,885.94 | 105.76 |
| Egypt | 1 | 8344 | 117 | 0.33 | 1923.45 | 58.14 |
| Equatorial Guinea | 181 | 2,922,420 | 161 | 220.06 | 3,960,141.62 | 179.96 |
| Eritrea | 49 | 640,038 | 129 | 46.90 | 443,969.75 | 94.67 |
| Gabon | 1457 | 23,840,000 | 162 | 1526.49 | 26,882,131.01 | 176.10 |
| Gambia | 519.11 | 5,509,300 | 106 | 666.14 | 5,694,597.99 | 85.49 |
| Ghana | 76 | 742,925 | 97 | 71.91 | 547,573.70 | 76.15 |
| Guinea | 1889 | 18,153,800 | 108 | 2286.30 | 22,873,857.63 | 100.05 |
| Guinea Bissau | 2806 | 31,712,300 | 113 | 2715.50 | 30,303,032.21 | 111.59 |
| Kenya | 192 | 2,294,820 | 119 | 381.96 | 3,580,841.84 | 93.75 |
| Liberia | 189 | 2,141,860 | 113 | 94.47 | 961,997.24 | 101.83 |
| Madagascar | 2059 | 24,856,900 | 121 | 2314.22 | 29,867,914.35 | 129.06 |
| Mauritania | 0.4 | 4156 | 95 | 0.51 | 4141.48 | 81.99 |
| Mozambique | 3054 | 30,974,100 | 101 | 2901.51 | 30,887,485.61 | 106.45 |
| Nigeria | 8573 | 94,788,000 | 111 | 6136.63 | 75,061,148.06 | 122.32 |
| Senegal | 1200 | 11,462,100 | 95 | 1197.74 | 9,149,049.33 | 76.39 |
| Sierra Leone | 955 | 10,655,600 | 112 | 1365.66 | 14,065,427.62 | 102.99 |
| Somalia | 30 | 436,907 | 143 | 17.36 | 136,751.57 | 78.79 |
| Sudan | 4 | 135,626 | 113 | 2.49 | 16,510.70 | 66.32 |
| South Africa | 12 | 40,018 | 100 | 16.96 | 225,023.10 | 132.71 |
| Togo | 2 | 15,861 | 78 | 4.74 | 36,790.55 | 77.68 |
| Tanzania | 809 | 11,037,800 | 136 | 966.45 | 13,493,199.77 | 139.62 |
| Africa | 25,960 | 301,665,553 | 116 | 25,640.71 | 313,767,286.04 | 122.37 |
References
- Alongi, D.M. Mangrove forests: Resilience, protection from tsunamis, and responses to global climate change. Estuar. Coast. Shelf Sci. 2008, 76, 1–13. [Google Scholar] [CrossRef]
- Donato, D.C.; Kauffman, J.B.; Murdiyarso, D.; Kurnianto, S.; Stidham, M.; Kanninen, M. Mangroves among the most carbon-rich forests in the tropics. Nat. Geosci. 2011, 4, 293–297. [Google Scholar] [CrossRef]
- Alongi, D.M. Carbon cycling and storage in mangrove forests. Annu. Rev. Mar. Sci. 2014, 6, 195–219. [Google Scholar] [CrossRef] [PubMed]
- Pendleton, L.; Donato, D.C.; Murray, B.C.; Crooks, S.; Jenkins, W.A.; Sifleet, S.; Craft, C.; Fourqurean, J.W.; Kauffman, J.B.; Marbà, N. Estimating global “blue carbon” emissions from conversion and degradation of vegetated coastal ecosystems. PLoS ONE 2012, 7, e43542. [Google Scholar] [CrossRef] [PubMed]
- Fatoyinbo, T.E.; Simard, A.M. Height and biomass of mangroves in Africa from ICESat/GLAS and SRTM. Int. J. Remote Sens. 2013, 34, 668–681. [Google Scholar] [CrossRef]
- Saenger, P.; Hegerl, E.; Davie, J.D. Global Status of Mangrove Ecosystems; International Union for Conservation of Nature and Natural Resources: Gland, Switzerland, 1983. [Google Scholar]
- Saenger, P.; Snedaker, S.C. Pantropical trends in mangrove above-ground biomass and annual litterfall. Oecologia 1993, 96, 293–299. [Google Scholar] [CrossRef] [PubMed]
- Stringer, C.E.; Trettin, C.C.; Zarnoch, S.J.; Tang, W. Carbon stocks of mangroves within the Zambezi River Delta, Mozambique. For. Ecol. Manag. 2015, 354, 139–148. [Google Scholar] [CrossRef]
- Kauffman, J.B.; Donato, D. Protocols for the Measurement, Monitoring and Reporting of Structure, Biomass and Carbon Stocks in Mangrove Forests; Center for International Forestry Research (CIFOR): Bogor, Indonesia, 2012. [Google Scholar]
- Twilley, R.; Chen, R.; Hargis, T. Carbon sinks in mangroves and their implications to carbon budget of tropical coastal ecosystems. Water Air Soil Pollut. 1992, 64, 265–288. [Google Scholar] [CrossRef]
- Sanders, C.J.; Maher, D.T.; Tait, D.R.; Williams, D.; Holloway, C.; Sippo, J.Z.; Santos, I.R. Are global mangrove carbon stocks driven by rainfall? J. Geophys. Res. Biogeosci. 2016, 121, 2600–2609. [Google Scholar] [CrossRef]
- Giri, C.; Ochieng, E.; Tieszen, L.L.; Zhu, Z.; Singh, A.; Loveland, T.; Masek, J.; Duke, N. Status and distribution of mangrove forests of the world using earth observation satellite data. Glob. Ecol. Biogeogr. 2011, 20, 154–159. [Google Scholar] [CrossRef]
- Tang, W.; Feng, W.; Jia, M.; Shi, J.; Zuo, H.; Trettin, C.C. The assessment of mangrove biomass and carbon in West Africa: A spatially explicit analytical framework. Wetl. Ecol. Manag. 2016, 24, 153–171. [Google Scholar] [CrossRef]
- Hutchison, J.; Manica, A.; Swetnam, R.; Balmford, A.; Spalding, M. Predicting global patterns in mangrove forest biomass. Conserv. Lett. 2014, 7, 233–240. [Google Scholar] [CrossRef]
- Spalding, M. World Atlas of Mangroves; Earthscan: London, UK, 2010. [Google Scholar]
- Fatoyinbo, T.E.; Simard, M.; Washington-Allen, R.A.; Shugart, H.H. Landscape-scale extent, height, biomass, and carbon estimation of Mozambique’s mangrove forests with Landsat ETM+ and Shuttle Radar Topography Mission elevation data. J. Geophys. Res. Biogeosci. 2008, 113. [Google Scholar] [CrossRef]
- Manyika, J.; Institute, M.G.; Chui, M.; Brown, B.; Bughin, J.; Dobbs, R.; Roxburgh, C.; Byers, A.H. Big Data: The Next Frontier for Innovation, Competition, and Productivity; McKinsey Global Institute: Washington, DC, USA, 2011. [Google Scholar]
- Tang, W.; Feng, W. Parallel map projection of vector-based big spatial data: Coupling cloud computing with graphics processing units. Comput. Environ. Urban Syst. 2017, 61, 187–197. [Google Scholar] [CrossRef]
- Yang, C.; Huang, Q.; Li, Z.; Liu, K.; Hu, F. Big Data and cloud computing: Innovation opportunities and challenges. Int. J. Digit. Earth 2017, 10, 13–53. [Google Scholar] [CrossRef]
- Lu, D. The potential and challenge of remote sensing-based biomass estimation. Int. J. Remote Sens. 2006, 27, 1297–1328. [Google Scholar] [CrossRef]
- Samet, H. Foundations of Multidimensional and Metric Data Structures; MOrgan Kaufmann: San Francisco, CA, USA, 2006. [Google Scholar]
- Eldawy, A.; Mokbel, M.F. A demonstration of spatialhadoop: An efficient mapreduce framework for spatial data. Proc. VLDB Endow. 2013, 6, 1230–1233. [Google Scholar] [CrossRef]
- Li, Z.; Hu, F.; Schnase, J.L.; Duffy, D.Q.; Lee, T.; Bowen, M.K.; Yang, C. A spatiotemporal indexing approach for efficient processing of big array-based climate data with MapReduce. Int. J. Geogr. Inf. Sci. 2017, 31, 17–35. [Google Scholar] [CrossRef]
- Tang, W. Parallel construction of large circular cartograms using graphics processing units. Int. J. Geogr. Inf. Sci. 2013, 27, 2182–2206. [Google Scholar] [CrossRef]
- Hamilton, S.E.; Collins, S. Livelihood responses to mangrove deforestation in the northern provinces of Ecuador. Bosque 2013, 34. [Google Scholar] [CrossRef]
- Torge, W.; Müller, J. Geodesy; Walter de Gruyter: Berlin, Germany, 2012. [Google Scholar]
- Komiyama, A.; Ong, J.E.; Poungparn, S. Allometry, biomass, and productivity of mangrove forests: A review. Aquat. Bot. 2008, 89, 128–137. [Google Scholar] [CrossRef]
- Atkins, D. Revolutionizing Science and Engineering through Cyberinfrastructure: Report of the National Science Foundation Blue-Ribbon Advisory Panel on Cyberinfrastructure; The University of Arizona Libraries: Tucson, AZ, USA, 2003. [Google Scholar]
- National Science Foundation (NSF). Cyberinfrastructure Vision for 21st Century Discovery; Report of NSF Council; Cyberinfrastructure Council, NSF: North Arlington, VA, USA, 2007.
- Wilkinson, B.; Allen, M. Parallel Programming: Techniques and Applications Using Networked Workstations and Parallel Computers, 2nd ed.; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2004. [Google Scholar]
- Tang, W.; Jia, M. Global sensitivity analysis of a large agent-based model of spatial opinion exchange: A heterogeneous multi-GPU acceleration approach. Ann. Assoc. Am. Geogr. 2014, 104, 485–509. [Google Scholar] [CrossRef]
- Ding, Y.; Densham, P.J. Spatial strategies for parallel spatial modelling. Int. J. Geogr. Inf. Syst. 1996, 10, 669–698. [Google Scholar] [CrossRef]
- Trettin, C.C.; Stringer, C.E.; Zarnoch, S.J. Composition, biomass and structure of mangroves within the Zambezi River Delta. Wetl. Ecol. Manag. 2016, 24, 173–186. [Google Scholar] [CrossRef]
- Trettin, C.C.; Stringer, C.E.; Zarnoch, S.J.; Tang, W.; Dai, Z. Mangrove Carbon Stocks in Zambezi River Delta, Mozambique; Forest Service Research Data Archive: Fort Collins, CO, USA, 2017.
- Lefsky, M.A.; Harding, D.J.; Keller, M.; Cohen, W.B.; Carabajal, C.C.; Del Bom Espirito, F.; Hunter, M.O.; de Oliveira, R. Estimates of forest canopy height and aboveground biomass using ICESat. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Zhang, G.; Ganguly, S.; Nemani, R.R.; White, M.A.; Milesi, C.; Hashimoto, H.; Wang, W.; Saatchi, S.; Yu, Y.; Myneni, R.B. Estimation of forest aboveground biomass in California using canopy height and leaf area index estimated from satellite data. Remote Sens. Environ. 2014, 151, 44–56. [Google Scholar] [CrossRef]
- Hey, T.; Tansley, S.; Tolle, K. (Eds.) The Fourth Paradigm: Data Intensive Scientific Discovery; Microsoft Research: Redmond, WA, USA, 2009. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).