Abstract
This paper aims to evaluate the sustainability of high-speed railway (HSR) construction projects in a comprehensive manner. To this end, the author established an index system, involving 4 primary indices, 9 secondary indices, and 32 tertiary indices. The analytic hierarchy process (AHP) and the unascertained measure were introduced to calculate the weights of these indices. Then, the index system was applied to evaluate the sustainability of the China’s Harbin-Dalian Passenger Dedicated Line (PDL). The results show that the Harbin-Dalian PDL project achieved good results in terms of process, economic benefit, impact, and sustainability, and will bring long-term benefits in the fields of tourism, economy, and transport capacity, as well as many other fields. In spite of its good overall sustainability, the project needs to further increase its economic benefits and reduce its negative environmental impact. For this purpose, it is necessary to adopt the management mode of “separation between network and transportation” and apply noise prevention measures like noise barriers, tunnels, and overhead viaducts. This research lays a solid basis for the sustainability evaluation of HSR construction projects, and simplifies the modelling process for designers of HSR.
1. History of HSR
High-speed railway (HSR) is considered to be one of the most important breakthroughs in passenger transport technology made in the 20th century. Being a safe, rapid, reliable, comfortable, and convenient mode of transport, HSR has injected new vitality into the existing railway transport system and became a symbol of modern society [1,2,3,4,5,6].
Opened in 1964, the Tōkaidō Shinkansen marked the dawn of the high-speed era, kicking off half a century of high-speed construction and research. At the sight of Japan’s success, developed countries quickly followed suit.
The most famous project is the Train à Grande Vitesse (TGV) in France. TGV Sud-Est, the first line of the project, was funded by the French government in 1976, and opened to the public between Paris and Lyon on 27 September 1981. The trains operate on the line at a maximum speed of 270 km·h−1 [7]. The commercial success of the first TGV led to an expansion of the network to different parts of France. The statistics of the International Union of Railways (UIC) show that the TGV had 2142 km of HSR in operation, 634 km under construction, and 1786 km being planned by the end of April 2017 [8].
The success of the TGV motivated other European countries to construct HSR within and across their borders, forming a high-speed network across the continent. These countries include Germany (1988), Italy (1988), Spain (1992), Belgium (1997), the United Kingdom (2003), and the Netherlands (2009). After the turn of the century, the high-speed boom spread eastwards to Asia. Different forms of HSR were built in Korea (2004) and China (2008).
Over the past 50 years, the global HSR network has transported about 15 billion passengers, about twice the world population. According to UIC statistics, 34,000 km of HSR had entered service by the end of 2016 [9], an increase of 14.86% compared to 2015 (Figure 1); the mileage rocketed up to 37,300 km by the end of April 2017, with another 15,900 km under construction [10]. Asia and Europe accounted for 98.07% of all HSR in service and under construction around the world (Figure 2).
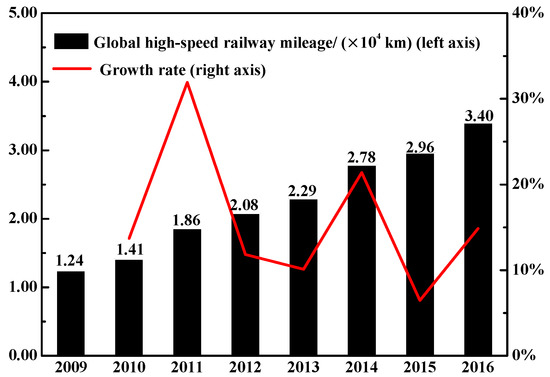
Figure 1.
Global total mileage of HSR till 2016.

Figure 2.
The global percentage of in-service under construction mileage of HSR in Asia, Europe, North America, and Africa in April 2017.
HSR construction is in full swing across China. In 2008, the Beijing–Tianjin Intercity Railway became the first line in the country to accommodate trains travelling at maximum speeds above 300 km. A boom of HSR construction ensued. By the end of April 2017, China had built the world’s longest high-speed network, consisting of 84 high-speed lines (segments). In total, there were 23,900 km of route in service, and 10,700 km under construction. The two mileages take up 57.87% and 97.72% of the global total, respectively [8].
With only a couple of years, China has caught up with the first movers in HSR and become the focal point of HSR development. The HSR has been recognized as a first product of Chinese manufacturing [11,12,13,14,15]. Guided by the “going global” strategy, China is actively building HSR linking up the countries along the overland and the maritime silk roads. Once completed, these railways will boost the development of infrastructure and regional economy in all the countries radiated by the “the Belt and Road” [16].
2. Requirements on HSR
HSR is a major booster of socioeconomic development and the cornerstone of many industries. However, the environmental impact of HSR should never be overlooked. Despite being more environmental friendly than traditional transport modes (e.g., highway), HSR has led to some environmental and resource problems due to the largescale construction and leapfrogging development. To solve the problems, the planners, constructors, and operators of HSR must strike a balance between railway, population, economy, environment, and resources, so that the HSR develops in a sustainable manner.
Sustainable development is the ultimate goal of transportation. The key to sustainable development of transportation industry lies in its coordination with society, economy, environment, and resources [17,18,19,20,21,22]. In this research, the sustainable development of HSR is investigated from both internal and external perspectives that are required to satisfy the operating framework in Figure 3 [23,24].
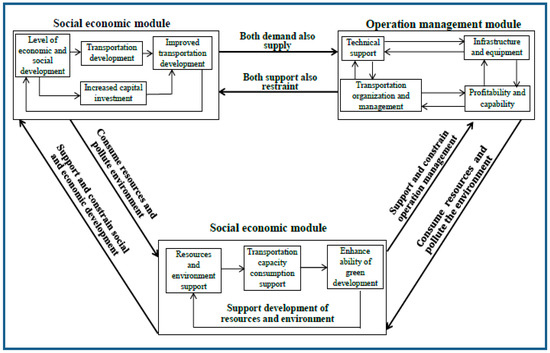
Figure 3.
Operating framework for the sustainable development of HSR [23,24].
The sustainable development of HSR should meet three conditions. First, HSR must adapt to the socioeconomic situation. The development of HSR both depends on social and economic factors and promotes socioeconomic development. Second, HSR development must be coordinated internally. The internal elements include infrastructure, transport equipment, scheduling, service provision, and software-hardware integration. Third, HSR should pursue green development and ecological harmony. For this purpose, the land and non-renewable resources ought to be utilized rationally, and environmental pollution and traffic accidents must be avoided.
Facing the above requirements, it is urgent to rationalize the planning and construction of HSR projects and realize the sustainable development of the HSR network. One of the viable options is to evaluate every aspect of HSR development and weigh the pros and cons of existing and impending projects. The comprehensive evaluation is critical to the healthy development of HSR [25].
3. Literature Review
The sustainability evaluation of HSR construction projects started late at home and abroad. The existing research emphasizes theoretical analysis over empirical evidence and lacks sufficient evaluation contents, systematic indices and feasible methods. The rationality, normality, and feasibility of the evaluation are yet to be improved.
The current evaluation methods include analytical hierarchy process (AHP) [26,27,28], neural network [29], fuzzy mathematics [27,30,31], multi-criteria decision analysis [32,33], fault tree analysis [34], visco-elastic model [35], transfer function [36], finite element [37], etc. Most of these approaches tackle a single aspect of sustainable development. Only a few support comprehensive evaluation, namely, neural network and fuzzy mathematics. The problem is these few methods perform poorly in index selection and weight determination.
The sustainability evaluation of HSR construction projects involves much uncertainty and covertness. In particular, many attributes are uncertain in the decision-making process. Hence, the evaluation should cover both quantitative and qualitative indices. The unascertained measure theory is an ideal way to deal with uncertain information and achieve a comprehensive evaluation. Nevertheless, it is difficult to determine the weight of a complex index system that relies solely on the unascertained measure theory.
To overcome the defect, it is necessary to introduce the AHP to the evaluation process. Taking the object as a system, the AHP makes decisions through decomposition, comparative judgment, and totalization. By this method, the factors of a complex system are divided into interconnected, orderly layers; the importance of each layer relative to the other layer is quantified, and the weight of each layer is determined mathematically. In this way, the decision is made according to objective reality.
In view of the above facts and the features of HSR construction projects, this paper establishes a complete index system for sustainability evaluation. The system has such four primary indices as process, economic benefits, effect, and sustainability. Then, the unascertained measure was adopted to create the sustainability evaluation model for HSR construction projects. Then, the model was applied to the sustainability evaluation of the Harbin-Dalian Passenger Dedicated Line (PDL). This research lays a solid basis for sustainability evaluation of HSR construction projects and simplifies the modelling process for designers of HSR.
4. Establishment of Evaluation Index System
The index system is essential to the accuracy and reliability of the sustainability evaluation. Based on the literature review, the author decided to carry out a questionnaire survey before setting up the index system. The questionnaire was prepared after interviewing 30 HSR experts working in national and local governments, construction companies, design institutions, railway management departments, advisory bodies, and research institutes. Prior to the survey, the preliminary questionnaire was validated with selected samples and optimized into a formal questionnaire. After the survey, a field investigation was carried out to extract common factors through the factor analysis.
Considering the correlation between the factors, the author constructed the index system for the sustainability evaluation of HSR construction projects. Four layers of indices were introduced, namely the target layer (main index), criteria layer (primary indices), sub-criteria layer (secondary indices), and solution layer (tertiary indices). The solution layer consists of 32 indices that explain the factors on the sub-criteria layer (Table 1). The goal is to describe the elements in the tertiary indices and obtain the values of the evaluation indices in light of the actual situation of the object. As mentioned above, the index system has such four primary indices as process, economic benefits, effect, and sustainability.

Table 1.
The evaluation index system for the sustainable development of HSR construction project [23,27].
The process evaluation index covers pre-bid decision-making, construction, and operation. These indices evaluate the actual project situation in the early stage, including work performance, construction quality, and operation efficiency. Based on the evaluation results, one can learn from the successes and failures, enhance the project quality, and elevate the management level.
The economic benefits include financial benefit and national economy. As its name suggests, the former index measures the financial benefit of the project. To evaluate the index, the income and expenses were acquired from the project’s financial statements, and the implementation of the national tax system was taken as a reference. According to Railway construction project economic evaluation methods and parameters (3nd edition) (Ministry of Housing and Urban-Rural Development of the PRC, National Development and Reform Commission of the PRC, Ministry of Railways of the PRC, 2012) [38] and literature [39], the financial benefit of the project was further split into profitability and debt paying ability. The latter index, national economy, is fundamental to the sustainable development of HSR construction projects. The index reflects the net contribution of project to the national economy, and discloses the economic effect of project cost and investment.
The social effect evaluation exists in the forms of social effect and environmental effect. From the sociological angle, this paper explores the social effect from four dimensions (Table 2). The environmental effect refers to the chemicals, wastes, noises, and electromagnetic radiations released during project construction and operations in the natural environment (e.g., water, air and soil). The evaluation results make it possible to minimize the adverse effects on the life of local residents and ecological system.

Table 2.
The index system of social effect evaluation.
The sustainability evaluation is prospective in nature. For sustainable development, the relevant internal and external factors are evaluated in scientific means, along with the realization and influence of the project. In light of the evaluation results, one can give advice on how to promote sustainable development from the perspectives of technology, economy, society, and environment.
5. Unascertained Measure Theory
Uncertainty exists extensively in objective and subjective worlds; the uncertain information includes two basic meanings: randomness and ambiguity [40,41]. In 1836, Mill [42] proposed firstly the concept of “uncertainty”. Stochastic problem was first proposed by the Soviet mathematician Kolmogorov in 1933, and he established probability theory and the axiomatic method [43]. In 1965, the concept of fuzzy information and fuzzy set theory was created by American scholar Zaden, who developed the study field of uncertainty [44]. Chinese scholar Deng founded the grey system theory in 1982 [45]. In 1991, Wang built a universal grey set on the basis of grey system theory; it involved a lot uncertain information [46]. Academician Wang, a famous Chinese scientist, put forward various types of information concepts, namely, unascertained information in 1990, which are different from random information and fuzzy information [47]. At present, there is a unified understanding of fuzzy information, random information, and gray information in uncertain information, but there is no uniform definition for unascertained information. However, theorists basically agree that unascertained information is the subjective uncertainty of decision makers because they lack information to determine the real state and quantity of the object. This creates subjective and cognitive uncertainty for decision makers due to the lack of objective information. It is fundamentally different from concepts like randomness (which only deals with what happens in the future), fuzziness (which reflects the nature of a certain object that does not have a clear definition or an evaluation target), and grayness.
Thanks to the concerted efforts of scholars like Álvaro [48] and Wu [49], so far, a systematic theory and method have been developed for unascertained information, which was first proposed by Academician Wang [47].
6. Establishment of Unascertained Measure Model
Set as evaluation objects of news sensitivity, set universe . The evaluation has first indices and . For has k secondary evaluation indices , and . Therefore, can be expressed as dimensional vector , means the value of the secondary indices of , which is ’s first index. Each has evaluate grades , the evaluation space is [40,41].
6.1. Single-Index Measure
6.1.1. Single-Index Measure Matrix
Set to express the degree that belongs to , which is the th evaluation class (rating). must meet the conditions as follows:
Define Equation (2) as the normalization and Equation (3) as the additivity. That which meets the three equations above is unascertained measurement. The matrix that follows is a single index measure matrix [50].
6.1.2. Distinction Weight of Single-Index
Using the concept of information entropy to define the peak of index .
in Equation (5) represents the number of the evaluate ratings, is the measure of single index, and the value of expresses the degree that different to each evaluation class. The distinction weight is as follows:
, , is the classification weights of . is the classification weight vector of secondary grade index [51].
6.2. First Grade Index Measure
Set expresses the degree that sample belongs to , which is the th evaluation class (rating).
Due to , and , is the unascertained measure. Define as measure evaluation vector of ’s composite indicator. The matrix is measure matrix of comprehensive index [52].
6.3. Determination of First Grade Index Weight by AHP
AHP was proposed by Saaty, an American operational research expert, in the 1970s [53]. It is a method of combining qualitative and quantitative, systematized and hierarchical qualities. It is a process of modeling and quantifying decision makers’ decision thinking processes for complex systems. By using AHP, decision makers decompose the complex problems into several levels and factors, and make simple comparisons and calculations among the factors, so that they can get the weight of different plans and provide the basis for the best plan selection. In AHP, in order to make the judgment quantified, the key is to quantitatively describe the relative superiority of any two schemes to a certain criterion. For a single criterion, the comparison between the two plans can always demonstrate the advantages and disadvantages. AHP adopts the 1–9 scale method to give the quantitative scale for the evaluation of different situations. This scale is adopted in matrices to look for relative criteria’s weights and to compare the alternatives linked to every criterion. Table 3 summarizes the basic ratio scale. All final weighted coefficients are shown in matrices. Alternatives and criteria can be ranked based on the overall aggregated weights in matrices. The alternative with the highest overall weight would be the most preferable [28,54].

Table 3.
Saaty’s scale for AHP pairwise comparisons [28,54].
Based on this first index’s judgment matrix, the weights of every first grade index can be calculated by the geometric calculation method of mean.
Then, by employing normalized processing, using the following equation:
The weight vector of first index is obtained: .
The largest characteristic roots can be calculated.
When solving practical problems, due to the complexity of objective phenomena and the mind’s cognitive limitations, our understanding of the problem is subjective and involves one-sidedness and fuzzy judgment; the structure of the judgment matrix is, therefore, may not fully meet the requirements of consistency, and often includes some deviation. The constructed judgement matrix does not always meet consistency condition. If the judgement matrix passes the consistency test, the calculated index weight can be adopted; if the consistency test is not passed, the judgement matrix needs to be adjusted. The consistency index is divided into complete consistency () and satisfactory consistency (), .
When , the judgment matrix is considered to be completely consistent. , it is considered that the judgment matrix is not completely consistent. , is the average random consistency index, and the value of are shown in Table 4 for the judgment matrix of = 1–14.

Table 4.
The mean random consistency index.
6.4. Identification
When the evaluation level is divided in order, the maximum membership degree is no longer applicable, so the credible degree criterion is usually adopted. For positive sequence partitioning, the confidence level is usually assumed to be ( > 0.5), and the value of is 0.6 or 0.7. Set:
7. Case Study
7.1. Overview
This section applies the established index system to evaluate the sustainable development of the Harbin-Dalian PDL, a typical HSR project in China. Harbin-Dalian PDL is put into operation by the end of 2012, marking the basic formation of “Four Vertical” in the “Four Vertical and Four Horizontal” of Chinese railway mainline. Harbin-Dalian PDL had finished the connection with existing HSR line of the Beijing-Shanghai and Beijing-Guangzhou. Since the operation of Harbin-Dalian PDL, it has not only shortened the distance of Heilongjiang, Jilin, and Liaoning provinces, but it has also strengthened regional economic integration.
Harbin-Dalian PDL runs through three provinces in Northeast China, 4 sub-provincial cities, and 6 prefecture-level cities. The total length stands at 921 km, including 553 km in Liaoning Province, 270 km in Jilin Province, and 81 km in Heilongjiang Province. Harbin-Dalian PDL starts from Dalian, through Yingkou, Anshan, Liaoyang, Shenyang, Tieling, Siping, Changchun, and Songyuan, and finally to Harbin (see Figure 4). According to the statistics of 2015, the 10 cities account for 40.90% of tourism resources, 46.53% of the population, and 59.87% of the total GDP in Northeast China [55]. Since its opening, the railway has effectively stimulated tourism in the cities along its route and across Northeast China.
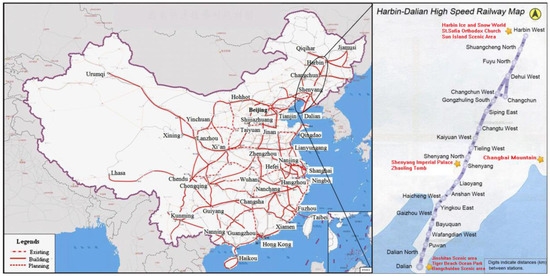
Figure 4.
Images of Harbin-Dalian PDL in China.
Harbin-Dalian PDL is the most advanced technology integration of China’s HSR, and its operation has become the most powerful explanation for China’s export of “China Railway High-speed” to countries along “the Belt and Road”.
Through the investigation and analysis of the HSR construction project, the comprehensive evaluation index can be divided into 5 grades: , correspond to . The direct choice of experts is given according to the multi-layered set of factors, and the number of experts supported as judgement of the index. In light of Saaty’s 1–9 ratio scale estimation, .
The secondary indices are quantified based on the basic data and expert scoring (by an expert panel consisting of 10 experts in the industry). The single measure vectors of the third indices (See Table 5) are obtained in light of the scores and the membership degree equation.

Table 5.
The weights of hierarchy and expert scoring results.
Thus, according to the vector measures, the measurement matrix of the secondary index is established as follows:
7.2. Weight Calculation of Second Grade Index
The weights of the secondary indices are calculated using information entropy. Below is the calculation of weight of process evaluation ():
Using Equation (5): , , , , , , , , and .
Using Equation (6): , , , , , , , , and .
Thus, level indices can be obtained under category weights:
The same way can be obtained under , , category weights:
7.3. Measure Calculation of First Grade Index
Using Equation (7), the measurement vector of the first index under process evaluation () is:
The measurement vector of the first index under evaluation of economic benefits () is:
The measurement vector of the first index under effect evaluation () is:
The measurement vector of the first index under sustainability evaluation () is:
Thus the measurement matrix of the first index is:
7.4. Determining the Classification Weight of First Grade Index
The first index judgment matrix is established using Saaty’s 1–9 scale, and AHP is applied to calculate the weights as the final results (see Table 5).
7.5. Calculation of Comprehensive Measure Vector
Point multiplication of the first index weight and the first measurement matrix results in judgment matrix as follows:
Thus the score is calculated as:
The calculation results show that the overall score of The Harbin-Dalian PDL is 7.2508, and the sustainable evaluation result is good.
7.6. Confidence Level Recognition
Confidence level recognition is performed using Equation (11) and the calculated comprehensive measurement vector. Here, is set as 0.7:
When = 0.7, , ; it shows that the confidence level recognition is good.
7.7. Result Discussion
According to the evaluation of the primary evaluation indices, the measurement vectors of process evaluation (), economic benefits (), effect evaluation () and sustainability evaluation () were all good. Thus, the results were discussed in the four aspects below.
7.7.1. Process Evaluation
In terms of process, the project performs well in decision-making, construction and operation. Good decision-making is revealed in route selection, as the railway links up four important sub-provincial cities and six prefecture-level cities. Moreover, the project lives up to all the technical requirements, especially the solution to frost heaving and snow accumulation. Since the railway was put into service, almost all performance parameters (e.g., ridership, operating cost, and equipment utilization) have reached the desired level.
Nonetheless, the project lags behind in investment control, mainly because of the construction difficulty and the management structure. (1) Construction difficulty: The Harbin-Dalian PDL, as the world’s first HSR in severe cold region, was constructed with the strictest standards. Due to the lack of precedent, the project budget was poorly estimated. For example, the cost of frost heaving control was not even included in the budget. (2) Management structure: The government is the sole financier of the project, and any attempt to reform the financing mode requires government approval. The investment is managed in a backward way with unclear responsibilities. What is worse, the investment and financing risk is poorly controlled. Specifically, the ticket pricing mechanism is unreasonable, the funds utilization is not well supervised, the relevant polices and regulations are incomplete, and the local governments fail to provide a good risk control platform.
7.7.2. Economic Benefits
In terms of economic benefits, the project boasts good financial and economic benefits. The PDL has contributed to the regional GDP, optimized resource allocation and utilization, accelerated industrial restructuring, and motivated tourism and other tertiary industries along its route.
However, due to high investment and heavy loans, the early phase of operation is overshadowed by huge pressure of repayment, resulting in poor financial performance. The financial dilemma is partially attributable to the outdated management mode. In Harbin-Dalian PDL, the railway network infrastructure (network) and the passenger/freight transportation (transportation) are still managed by the same entity. This goes against the more efficient and rational management mode of “separation between network and transportation” [56]. The new mode encourages competition and yields more profits.
7.7.3. Effect Evaluation
In terms of effect, the project has exerted fairly good social and environmental effects. The social effect is manifested by the optimized transport capacity and structure in the region, as well as the shorter travel time and rising income of local residents. As for the environmental effect, the pollution, noise, and electromagnetic radiation should be better despite the overall good environmental performance of the railway. In particular, the noise and radiation generated during the operation of the railway has disturbed the daily life of the residents.
To eliminate the noise effect, noise barriers should be installed along the route. The barriers must be able to suppress the noise on both sides of the railway from 65~75 dB to about 30~40 dB, such that the residents living along the route can sleep well at night. When the railway passes through the urban areas, it should be covered like a tunnel. The top cover can be made of cement of suitable thickness, and the supports can be made of steel mesh. Another solution is to build an underground tunnel for the railway in the urban areas. This approach can basically eliminate the negative effect on the environment along the route, but it is too costly to realize. Therefore, the basic principle of HSR construction is to maximize the use of overhead viaducts and avoidance of densely populated areas.
7.7.4. Sustainability Evaluation
In terms of sustainability, the project enjoys a good prospect of sustainable development. The sustainability is showcased by its advanced technology, immense popularity, high ridership, and sound mechanism. Besides, a virtuous circle is formed as the railway promotes the regional economy in Northeast China, which, in return, increases the demand for the railway. Most importantly, the PDL has revitalized the tourism in the region with its obvious time-space compression effect. The railway pulls the tourist spots close to tourist sources and cuts down the cost of tourists. Since the opening of the PDL, the journey time to tourist scenic spots in Northeast China has plunged across the board.
The average journey time to these tourist scenic spots has decreased from 7.4 h before the start-up of the PDL to 4.9 h at present, a drop of 2.5 h, while that between different cities has shrunk from 7.7 h to 5.4 h, a decrease of 2.3 h (See Table 6) [57]. The closer a tourist scenic spot/city is to the railway, the shorter the journey time. The greatest decrease occurred between Dalian and Harbin, located on each end of the railway, with a decline of over 80%. In general, Dalian, Changchun and Harbin experienced the most obvious changes in journey time (−3.6 h), followed by Anshan, Liaoyang, Shenyang, Tieling, and other cities along the route (−2 h). For the cities far away from the railway, the journey time was cut short by less than 1.5 h.

Table 6.
A comparison of accessibility indices before and after the operating of HSR [55].
7.7.5. Overall Result
The overall score of Harbin-Dalian PDL construction project is 7.2508, indicating that the world’s first HSR in severe cold region has a good sustainability. The project strengthens the link between central and southern Liaoning with the hinterland of Northeast China and draws together the high-quality resources in the three north-eastern provinces. The opening and operation of the PDL will bring long-term benefits to tourism, economy, transport capacity and many other fields.
For example, it only takes 1.5 h for passengers to travel on the PDL between Harbin, Changchun, and Shenyang, the three central cities in the region. Hence, these cities can efficiently share their education, medical, entertainment and other resources, achieve coordinated development of infrastructure, and accelerate regional economic integration. The same will happen to all the other cities along the route. The PDL itself is a moving economic corridor in Northeast China, with rapid flow of passengers, logistics, and information. The successful operation of the railway is critical to the revitalization of the old industrial base in the region.
To sum up, the author established an index system for the sustainability evaluation of HSR construction projects, calculated the index values by the unascertained measure, and applied the established model to evaluate the sustainability of Harbin-Dalian PDL. The evaluation results are consistent with the actual construction and operation status of the PDL, an evidence for the rationality and feasibility of the index system. The index system can improve the design, construction, and operation of HSR, and strengthen its ability to resist risks. The development of HSR plays an important role in increasing economic vitality, it is in line with the needs of the sustainable development of China’s economy. HSR will become the backbone transportation mode in the modern and integrated transportation system. We will further the planning and construction of HSR network, enrich the railway transportation infrastructure of “the Belt and Road”, accelerate China’s HSR going out pace.
8. Conclusions
Considering the various influencing factors on HSR sustainability, this paper created an evaluation index system from four primary aspects: process, economic benefits, effect, and sustainability. Then, the unascertained measure was introduced for comprehensive evaluation. The main conclusions and innovation points of this research are listed as follows.
- (1)
- The AHP was adopted to realize simultaneous qualitative and quantitative evaluations of influencing factors. Then, the weights were assigned in a rational and consistent manner, such that the importance of each index was measured correctly. This reflects the significance different among evaluation factors in the sustainability evaluation system.
- (2)
- The sustainability evaluation shows that the Harbin-Dalian PDL project achieved good results in process, economic benefits, effects, and sustainability, thanks to the excellent performance of decision-making, construction and operation. The opening and operation of the PDL will bring long-term benefits to tourism, the economy, transport capacity, and many other fields.
- (3)
- In spite of its good overall sustainability, the Harbin-Dalian PDL project needs to further increase its economic benefits and reduce its negative environmental effect. For this purpose, it is necessary to adopt the management mode of “separation between network and transportation” and apply noise prevention measures like noise barriers, tunnels, and overhead viaducts.
- (4)
- Facing the increasingly rapid development and construction of HSR, the sustainability evaluation of HSR construction projects needs to learn from the relatively mature research methods at home and abroad, in order to make up for the shortcomings of the existing research methods in terms of breadth and accuracy. The scientific evaluation system should be constructed to make the citation and index selection more scientific in the empirical research, and to strengthen the prediction of the impact capacity of the future construction of HSR, not just to analyze the impact of the existing HSR.
All in all, this research lays a solid basis for the sustainability evaluation of HSR construction projects and simplifies the modelling process for designers of HSR.
Acknowledgments
The authors gratefully acknowledge financial support from National Science and Technology Basic Work of Special Key Projects (2017FY10130), supported by National Natural Science Foundation of China (41511130033), supported by Research project of the Chinese Academy of Sciences (Y66Q034).
Author Contributions
This paper presents a team work research result written by the co-authors, Yongzhi Chang, Yang Yang, and Suocheng Dong. Suocheng Dong conceived and designed the study; Yongzhi Chang and Yang Yang analyzed the HSR construction project the data. With cross discussions of the research results, the co-authors have contributed substantially to the work reported.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yao, E.J.; Yang, Q.R.; Zhang, Y.S.; Sun, X.A. Study on high-speed rail pricing strategy in the context of modes competition. Discret. Dyn. Nat. Soc. 2013, 2013, 4–9. [Google Scholar] [CrossRef]
- Wang, Y.H.; Deng, X.M.; Marcucci, D.J.; Le, Y.E. Sustainable development planning of protected areas near cities: Case study in China. J. Urban Plan. Dev. 2013, 139, 133–143. [Google Scholar] [CrossRef]
- Ericson, J.A. A participatory approach to conservation in the Calakmul Biosphere Reserve, Campeche, Mexico. Landsc. Urban Plan. 2006, 74, 242–266. [Google Scholar] [CrossRef]
- Jansson, Å. Reaching for a sustainable, resilient urban future using the lens of ecosystem services. Ecol. Econ. 2013, 86, 285–291. [Google Scholar] [CrossRef]
- The State Council of the People’s Republic of China. About Print and Distribute “the Notice of National Resources City Sustainable Development Planning (2013–2020)” [EB/OL]. The Central Government Portal Website. Available online: http://www.gov.cn/zwgk/2013-12/03/content_2540070.htm (accessed on 3 December 2013).
- Moretti, L.; Moretti, M.; Ricci, S. Upgrading of Florence public transport to incorporate new tramlines. Ing. Ferrov. 2017, 72, 569–584. [Google Scholar]
- Arduin, J.P.; Ni, J.C. French TGV network development. Jpn. Railw. Trans. Rev. 2005, 40, 22–28. [Google Scholar]
- Huang, Y.; Ge, Y.J.; Ma, T.; Liu, X.F. Geopolitical space of China’s high-speed railway diplomacy. Prog. Geogr. 2017, 36, 1489–1499. [Google Scholar]
- Wu, H.; Liu, W.; Choul, K.S. The strategic marketing of China high-speed railway: Government behavior or market behavior. J. Mark. Stud. 2017, 25, 185–194. [Google Scholar]
- Lin, Y.T. Travel costs and urban specialization patterns: Evidence from China’s high speed railway system. J. Urban Econ. 2017, 98, 98–123. [Google Scholar] [CrossRef]
- Li, H.; Zhang, P.Y.; Cheng, Y.Q. Economic vulnerability of mining city—A case study of Fuxin City, Liaoning Province, China. Chin. Geogr. Sci. 2009, 19, 211–218. [Google Scholar] [CrossRef]
- Hayter, R.; Barnes, T.J. Labor market segmentation, flexibility and recession: A British Colombian case study. Environ. Plan. 1992, 10, 333–353. [Google Scholar] [CrossRef]
- Randall, J.E.; Ironside, R.G. Communities on the edge: An economic geography of resource-dependent communities in Canada. Can. Geogr. 1996, 40, 17–35. [Google Scholar] [CrossRef]
- Hilson, G. Sustainable development policies in Canada mining sector: An overview of government and industry efforts. Environ. Sci. Policy 2003, 3, 110. [Google Scholar]
- Jin, X.F.; Dong, S.C.; Liu, W.; Li, X. Study on relationship between industrial chain extension and evolution of resource-based city—A case study on Tongling city. Econ. Geogr. 2010, 30, 403–408. [Google Scholar]
- Swaine, M.D. Chinese Views and Commentary on the “One Belt, One Road” Initiative. China Leadersh. Monit. 2015, 1, 1–24. [Google Scholar]
- Greene, D.L.; Wegener, M. Sustainable transport. J. Transp. Geogr. 1997, 5, 177–190. [Google Scholar] [CrossRef]
- Hoogma, R.; Kemp, R.; Schot, J.; Truffer, B. Experimenting for sustainable transport: The Approach of Strategic Niche Management. Technol. Anal. Strateg. 2002, 23, 517–518. [Google Scholar]
- Litman, T. Developing Indicators for comprehensive and sustainable transport planning. Transp. Res. Rec. J. Transp. Res. Board 2007, 43, 10–15. [Google Scholar] [CrossRef]
- Elvik, R. The non-linearity of risk and the promotion of environmentally sustainable transport. Accid. Anal. Prev. 2009, 41, 849–855. [Google Scholar] [CrossRef] [PubMed]
- Hickman, R. Automobility in transition: A socio-technical analysis of sustainable transport. Transp. Rev. 2012, 33, 128–129. [Google Scholar] [CrossRef]
- O’Brien, O.; Cheshire, J.; Batty, M. Mining bicycle sharing data for generating insights into sustainable transport systems. J. Transp. Geogr. 2014, 34, 262–273. [Google Scholar] [CrossRef]
- Chang, Y.Z.; Dong, S.C. Study on green ecological assessment of high-speed railway construction project based on unascertained measure and AHP. Teh. Vjesn. 2017, 24, 1579–1589. [Google Scholar]
- Liu, Y.H. Study on Sustainable Development of China’s High-Speed Railways; Press of University of Chinese Academy of Sciences: Beijing, China, 2014. [Google Scholar]
- Litman, T.; Burwell, D. Issues in sustainable transportation. Int. J. Glob. Environ. 2006, 6, 331–347. [Google Scholar] [CrossRef]
- Chen, X.Y.; Chang, Y.L. The Study of evacuation passenger service level of Shanghai-Nanjing high-speed railway stations. Procedia Soc. Behav. Sci. 2013, 96, 265–269. [Google Scholar] [CrossRef]
- Chang, Y.Z.; Dong, S.C. Study on Post Evaluation of High-Speed Railway Based on FAHP and Matlab Simulation Calculation. Teh. Vjesn. 2017, 24, 1749–1758. [Google Scholar]
- Moretti, L.; Di Mascio, P.; Bellagamba, S. Environmental, human health and socio-economic effects of cement powders. Int. J. Environ. Res. Public Health 2017, 14, 645. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.H.; Yang, L.R.; Su, M.C.; Lin, J.Z. A rule extraction based approach in predicting derivative use for financial risk hedging by construction companies. Expert Syst. Appl. 2010, 37, 6510–6514. [Google Scholar] [CrossRef]
- Wang, Y.M.; Elhag, T.M.S. Fuzzy TOPSIS method based on alpha level sets with an application to bridge risk assessment. Expert Syst. Appl. 2006, 31, 309–319. [Google Scholar] [CrossRef]
- Cucala, A.P.; Fernández, A.; Sicre, C.; Domínguez, M. Fuzzy optimal schedule of high-speed train operation to minimize energy consumption with uncertain delays and driver’s behavioral response. Eng. Appl. Intell. 2012, 25, 1548–1557. [Google Scholar] [CrossRef]
- Chen, S.K.; Leng, Y.; Mao, B.H.; Liu, S. Integrated weight-based multi-criteria evaluation on transfer in large transport terminals: A case study of the Beijing South Railway Station. Transp. Res. Part A Policy Pract. 2014, 66, 13–26. [Google Scholar] [CrossRef]
- Luca, D.M.; Dell’Acqua, G.; Lamberti, R. High-speed rail track design using GIS and multi-criteria analysis. Procedia Soc. Behav. Sci. 2012, 54, 608–617. [Google Scholar] [CrossRef]
- Liu, P.; Yang, L.X.; Gao, Z.Y.; Li, S.K.; Gao, Y. Fault tree analysis combined with quantitative analysis for high-speed railway accidents. Saf. Sci. 2015, 79, 344–357. [Google Scholar] [CrossRef]
- Di Mascio, P.; Loprencipe, G.; Maggioni, F. Visco-elastic modeling for railway track structure layers. Ing. Ferrov. 2014, 69, 207–222. [Google Scholar]
- D’Andrea, A.; Loprencipe, G.; Xhixha, E. Vibration induced by rail traffic: Evaluation of attenuation properties in a bituminous sub-ballast layer. Procedia Soc. Behav. Sci. 2012, 53, 245–255. [Google Scholar] [CrossRef]
- Zoccali, P.; Cantisani, G.; Loprencipe, G. Ground-vibrations induced by trains: Filled trenches mitigation capacity and length influence. Constr. Build. Mater. 2015, 74, 1–8. [Google Scholar] [CrossRef]
- Ministry of Housing and Urban-Rural Development of the PRC; National Development and Reform Commission of the PRC; Ministry of Railways of the PRC. Railway Construction Project Economic Evaluation Methods and Parameters, 3nd ed.; China Planning Press: Beijing, China, 2012.
- Shuai, B.; Huang, W.C.; Li, M.L.; Wang, S.; Li, K.N. Railway benefit assessment summary of the World Bank and the Asian Development Bank. J. Transp. Syst. Eng. Inf. Technol. 2017, 3, 222–228. [Google Scholar]
- Chang, Y.Z.; Dong, S.C. Evaluation of sustainable development of resources-based cities in Shanxi Province based on unascertained measure. Sustainability 2016, 8, 585. [Google Scholar] [CrossRef]
- Chang, Y.Z.; Dong, S.C. Study on evaluation model of international trade in agricultural products based on unascertained measure. Chem. Eng. Trans. 2016, 51, 673–678. [Google Scholar]
- Mill, J. Whether political economy is useful? Lond. Rev. 1836, 2, 535–572. [Google Scholar]
- Kolmogorov, A.H. Foundations of the Theory Probability, 2nd ed.; Chelsea Publishing Company: New York, NY, USA, 1956. [Google Scholar]
- Zaden, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar]
- Deng, J.L. The Grey System (Society Economic); National Defence Industry Press: Beijing, China, 1985. [Google Scholar]
- Wang, Q.Y. Grey Mathematical Basis; HUST Press: Wuhan, China, 1996. [Google Scholar]
- Wang, G.Y. Unascertained information and its mathematical treatment. J. Harbin. Univ. Civ. Eng. Archit. 1990, 4, 1–3. [Google Scholar]
- Álvaro, F.; Sánchez, J.A.; Benedí, J.M. An integrated grammar-based approach for mathematical expression recognition. Pattern Recognit. 2016, 51, 135–147. [Google Scholar] [CrossRef]
- Wu, H.B.; Xu, J.H.; Ji, Y.; Wu, M. Uncertain flow calculations of a distribution network containing DG based on blind number theory. IET Gener. Transm. Distrib. 2017, 11, 1591–1597. [Google Scholar] [CrossRef]
- Chen, X.; Liu, Y.; Zhao, X.; Liang, Y.X. Coal industry international competitiveness research. Adv. Sci. Technol. Lett. 2016, 121, 222–226. [Google Scholar]
- Guo, C.Y.; Liu, Z.Q.; Zhang, C.Y. Evaluation on the express enterprise’s service quality of customers perception based on SPSS and unascertained measure model. Int. J. U E Ser. Sci. Technol. 2016, 9, 17–26. [Google Scholar]
- Li, S.C.; Wu, J.N.; Xu, Z.H.; Li, L.P. Unascertained measure model of water and mud inrush risk evaluation in karst tunnels and its engineering application. KSCE J. Civ. Eng. 2017, 21, 1170–1182. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytic Hierarchy Process; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Javid, P.J.; Nejat, A.; Hayhoe, K. Selection of CO2 mitigation strategies for road transportation in the United States using a multi-criteria approach. Renew. Sustain. Energy Rev. 2014, 38, 960–972. [Google Scholar] [CrossRef]
- National Bureau of Statistics. International City Statistical Yearbook 2016; China Statistics Press: Beijing, China, 2016.
- Di Mascio, P.; Loprencipe, G.; Moretti, L. Competition in rail transport: Methodology to evaluate economic impact of new trains on track. Sustainability, Eco-Efficiency and Conservation in Transportation Infrastructure Asset Management. In Proceedings of the 3rd International Conference on Transportation Infrastructure (ICIT), Pisa, Italy, 27 April 2014; pp. 669–675. [Google Scholar]
- Guo, J.K.; Wang, S.B.; Wang, H.; Liu, T.B. Impact of Harbin-Dalian high-speed railway on the spatial distribution of tourism supply and demand markets in Northeast China cities: Based on the accessibility of the scenic spots. Prog. Geogr. 2016, 35, 504–514. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).