Interannual Carbon and Nutrient Fluxes in Southeastern Taiwan Strait
Abstract
:1. Introduction
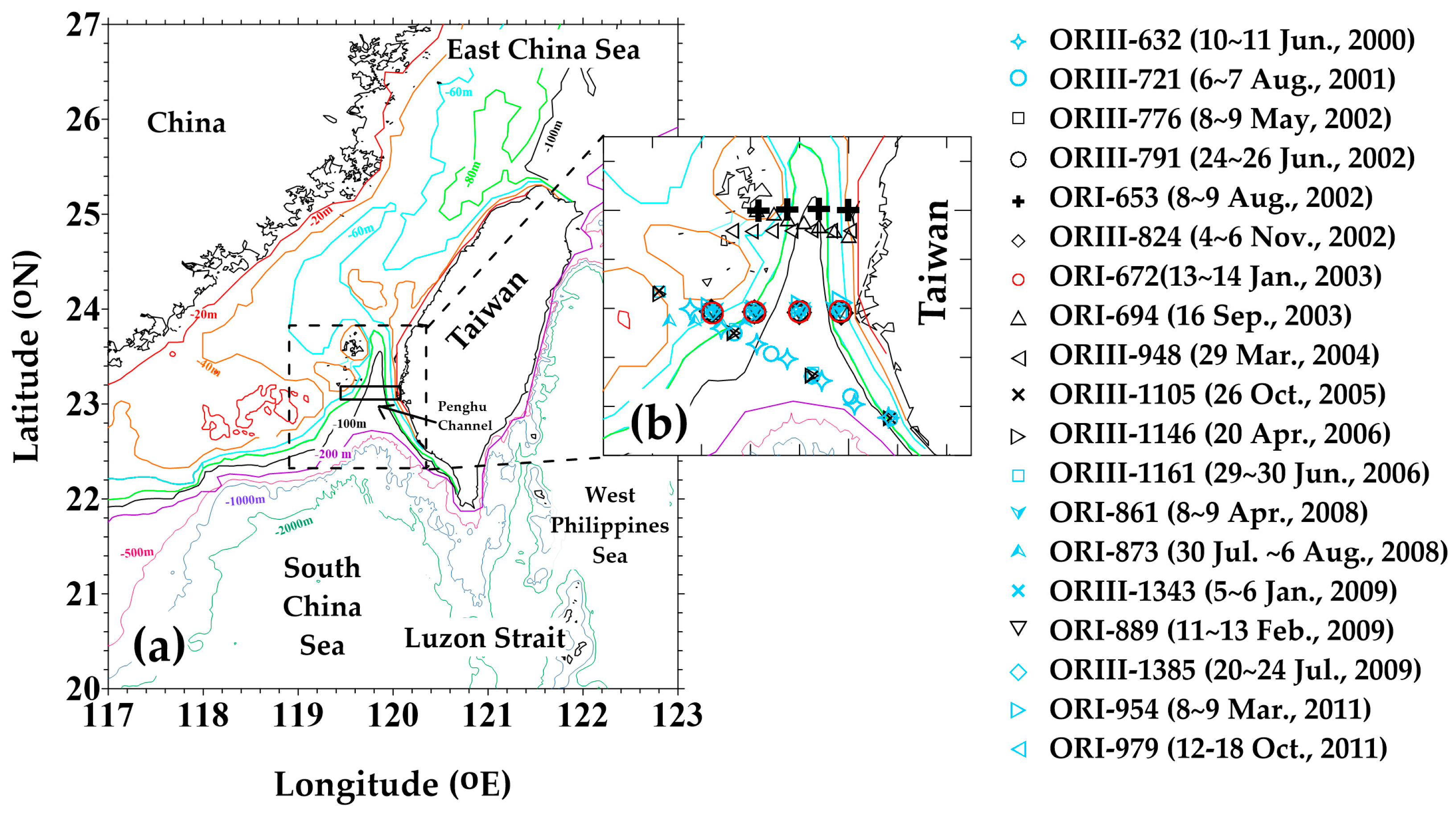
2. Materials and Methods
3. Results
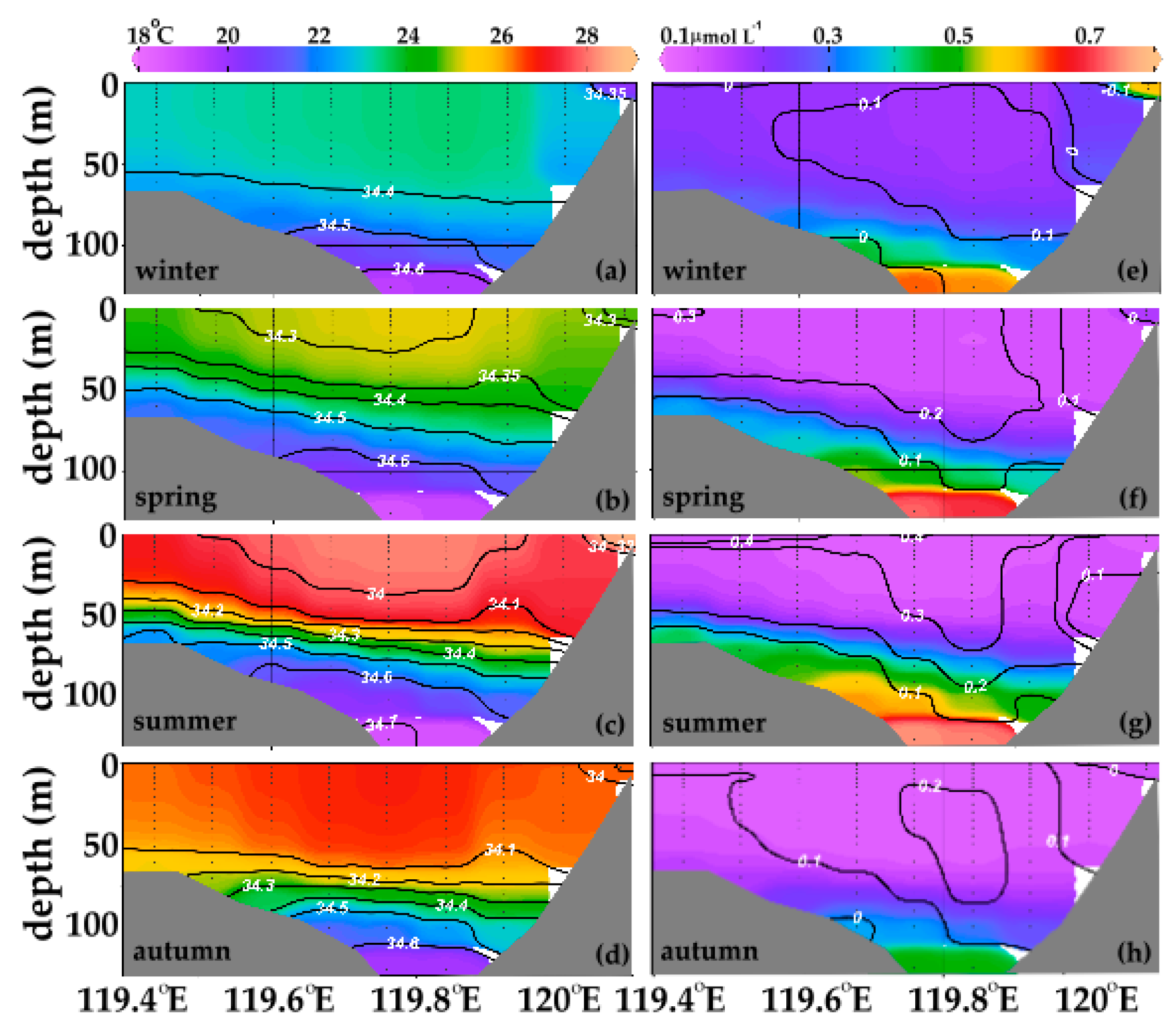
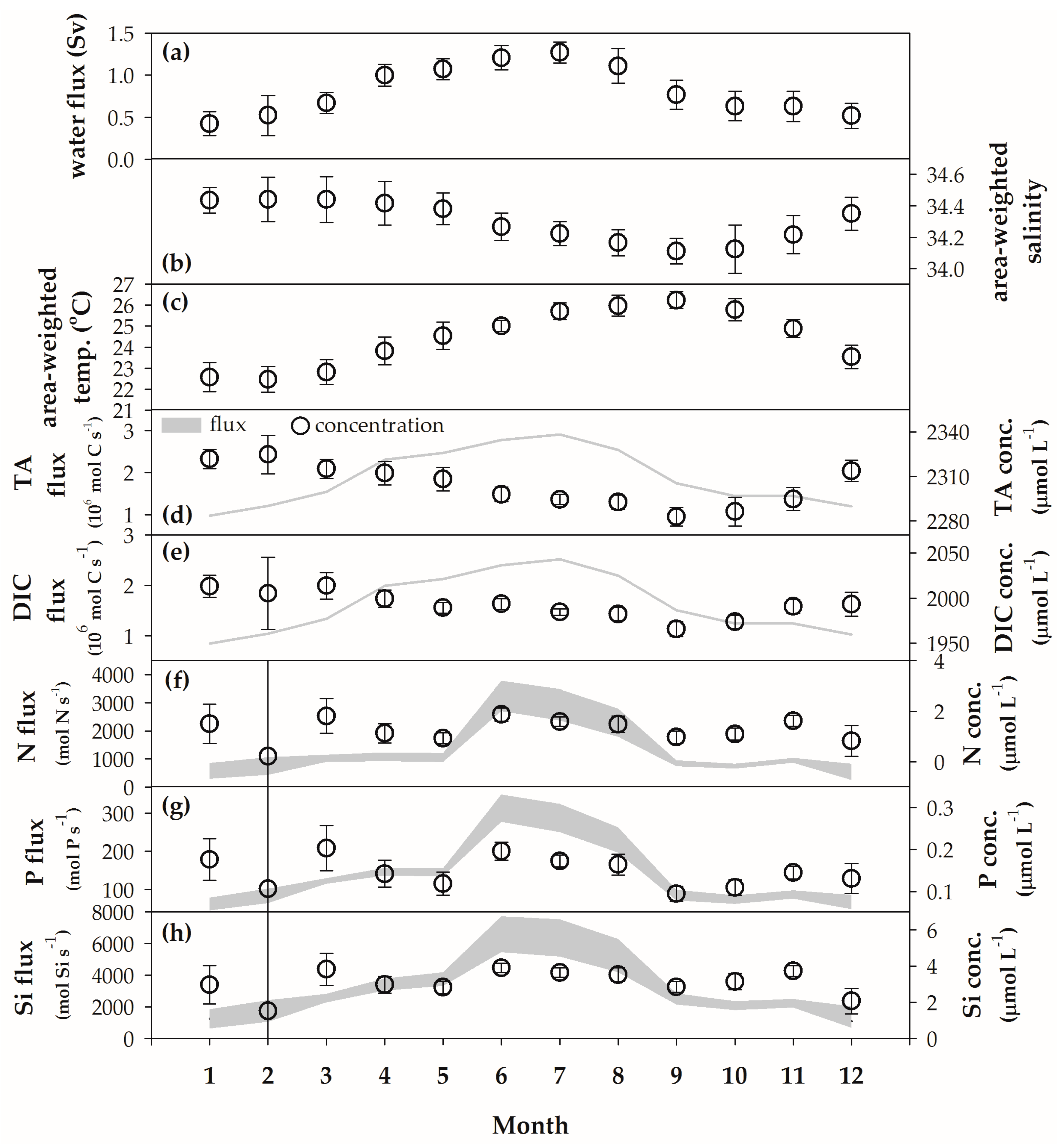
3.1. Seasonal Profiles
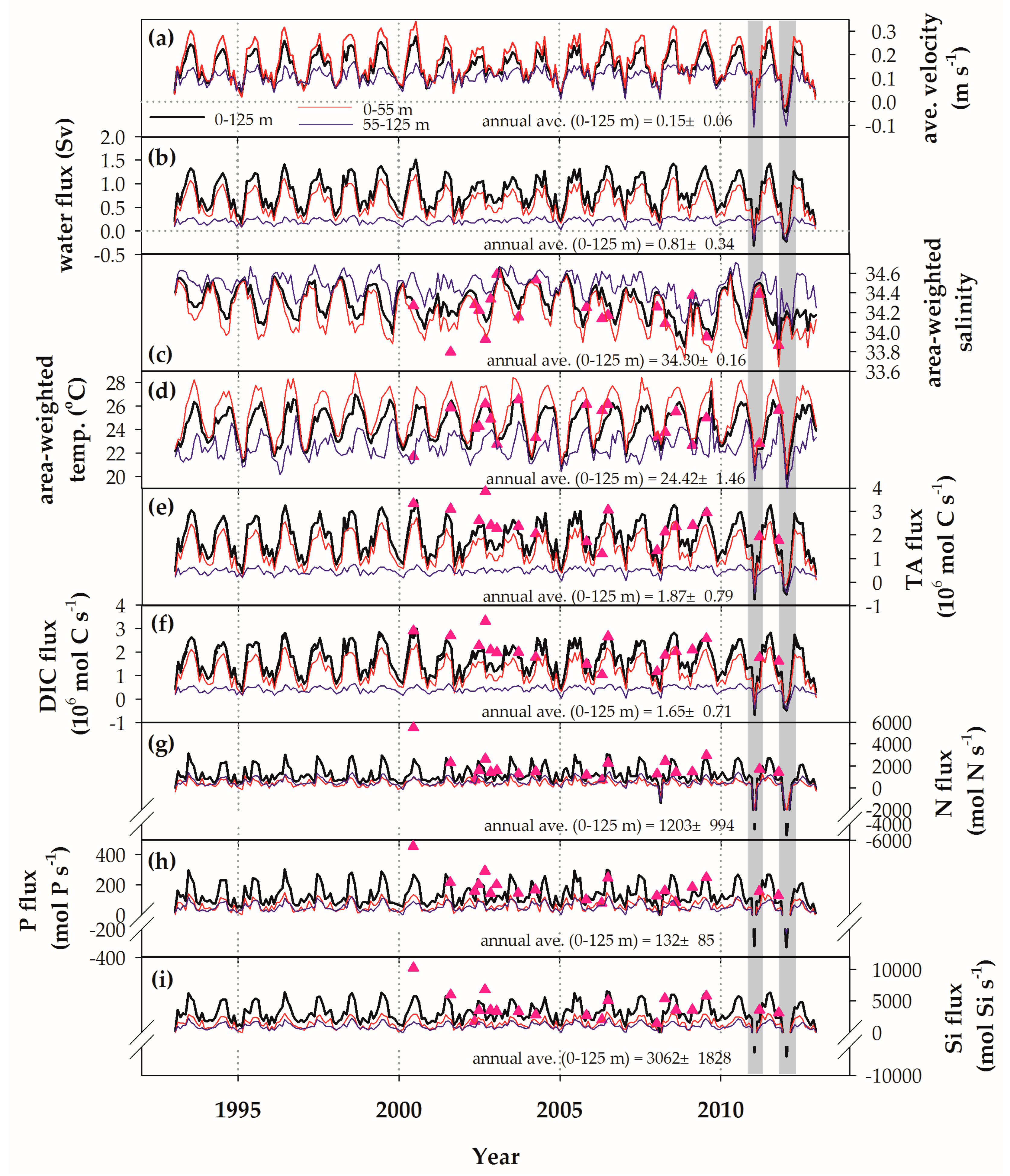
3.2. Time Series of Estimated Fluxes and Physical Data
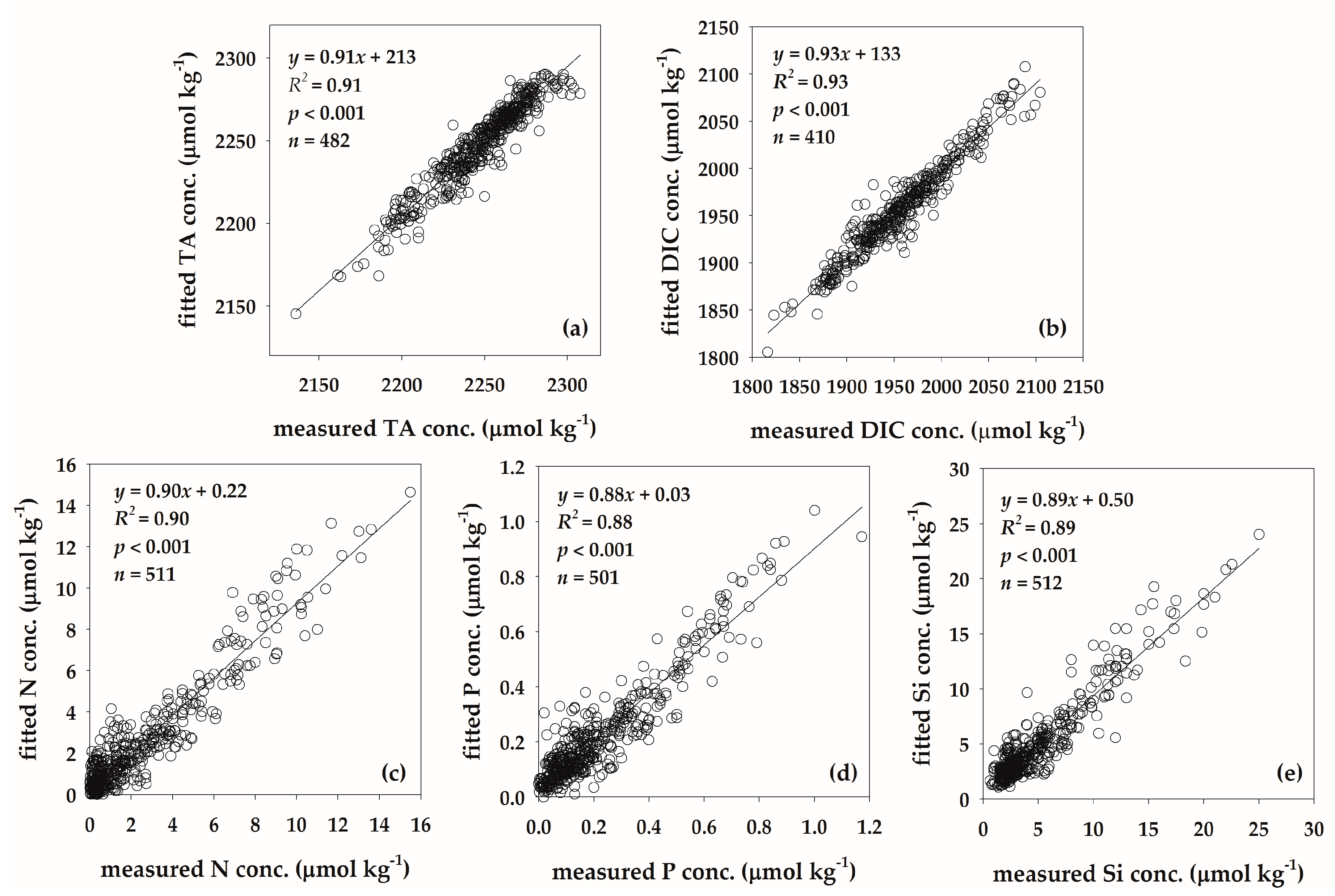
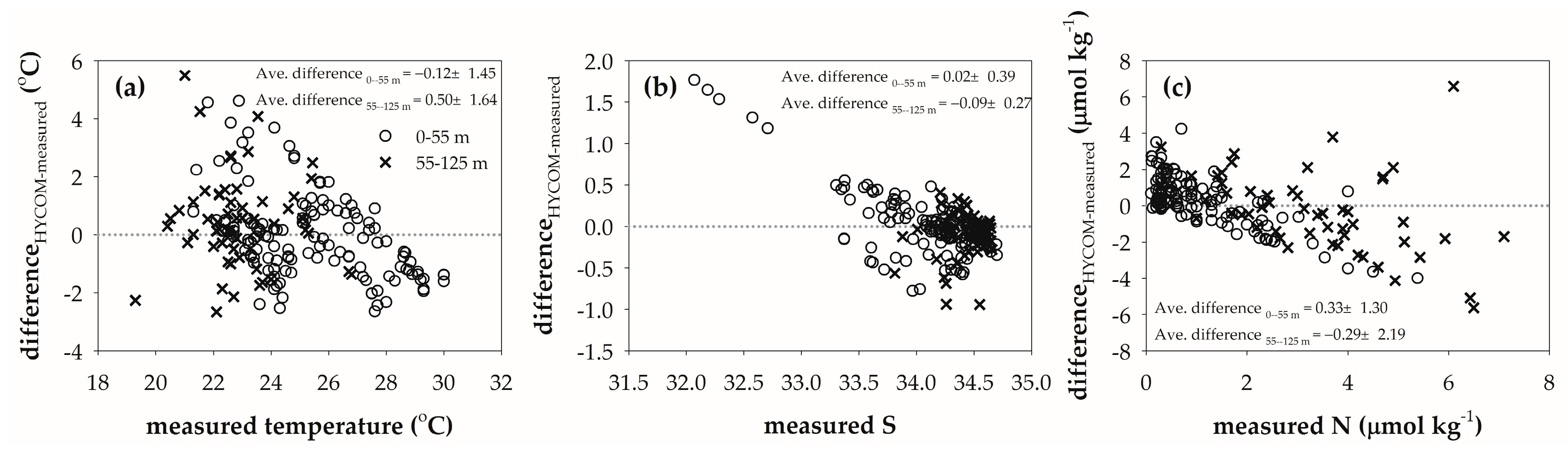
3.3. Comparison between Measured and Simulated Data
4. Discussion
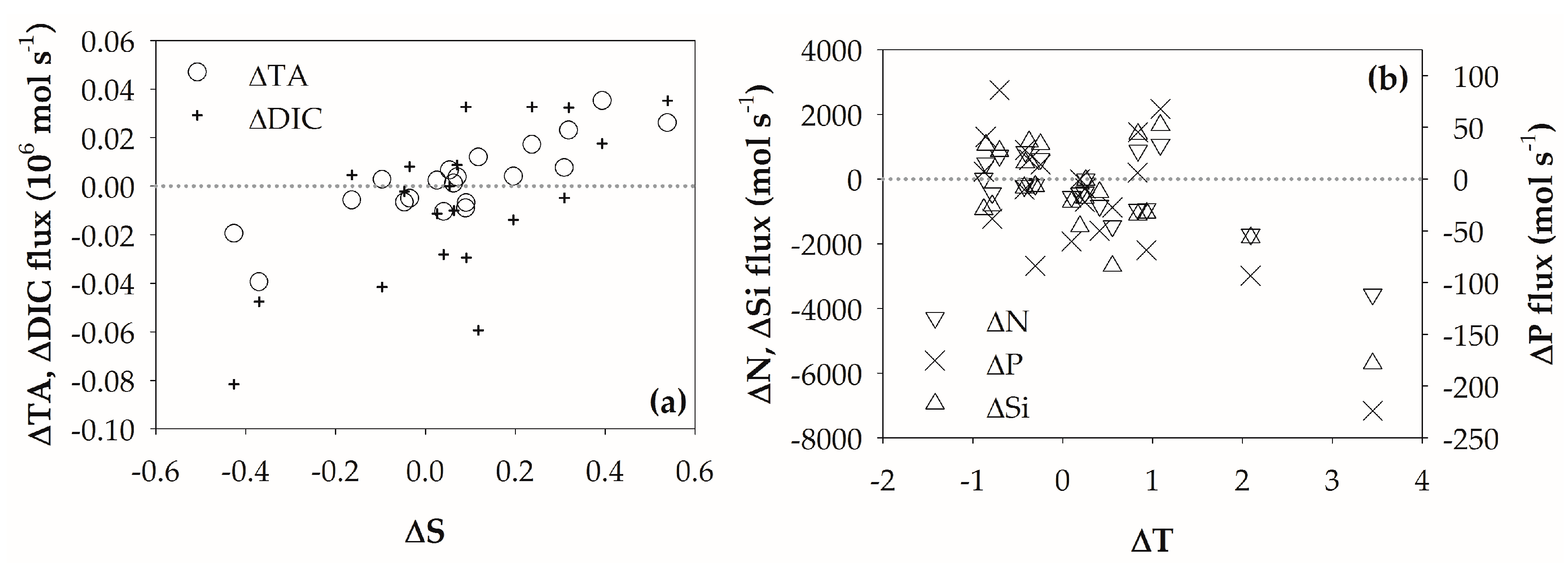
4.1. Annual Variation
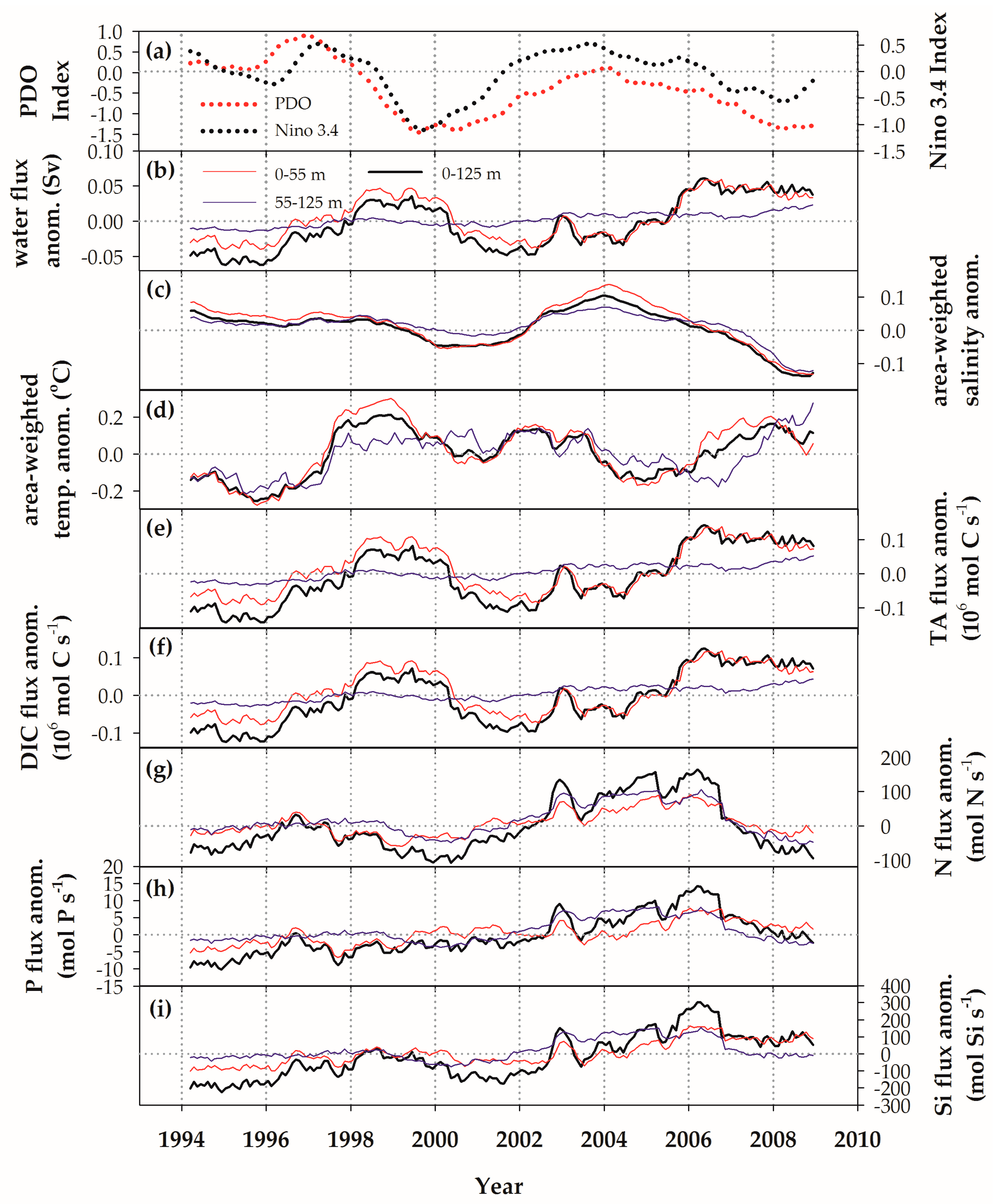
4.2. Interannual Variations
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
Appendix A.1. Model Selection
Appendix A.2. Prediction Interval of Daily Average of Chemical Parameters
References
- Chen, C.T.A.; Jan, S.; Huang, T.H.; Tseng, Y.H. Spring of no Kuroshio intrusion in the southern Taiwan Strait. J. Geophys. Res. Oceans 2010, 115, C08011. [Google Scholar] [CrossRef]
- Han, A.; Dai, M.; Gan, J.; Kao, S.-J.; Zhao, X.; Jan, S.; Li, Q.; Lin, H.; Chen, C.-T.; Wang, L. Inter-shelf nutrient transport from the East China Sea as a major nutrient source supporting winter primary production on the northeast South China Sea shelf. Biogeosciences 2013, 10, 8159–8170. [Google Scholar] [CrossRef]
- Chen, C.T.A.; Wang, S.L. Carbon, alkalinity and nutrient budgets on the East China Sea continental shelf. J. Geophys. Res. Oceans 1999, 104, 20675–20686. [Google Scholar] [CrossRef]
- Chen, C. The Kuroshio Intermediate Water is the major source of nutrients on the East China Sea continental shelf. Oceanol. Acta 1996, 19, 523–527. [Google Scholar]
- Li, M.; Xu, K.; Watanabe, M.; Chen, Z. Long-term variations in dissolved silicate, nitrogen, and phosphorus flux from the Yangtze River into the East China Sea and impacts on estuarine ecosystem. Estuar. Coast. Shelf Sci. 2007, 71, 3–12. [Google Scholar] [CrossRef]
- Zhou, M.-J.; Shen, Z.-L.; Yu, R.-C. Responses of a coastal phytoplankton community to increased nutrient input from the Changjiang (Yangtze) River. Cont. Shelf Res. 2008, 28, 1483–1489. [Google Scholar] [CrossRef]
- Gong, G.C.; Chang, J.; Chiang, K.P.; Hsiung, T.M.; Hung, C.C.; Duan, S.W.; Codispoti, L. Reduction of primary production and changing of nutrient ratio in the East China Sea: Effect of the three gorges dam? Geophys. Res. Lett. 2006, 33, L07610. [Google Scholar] [CrossRef]
- Lee, K.; Matsuno, T.; Endoh, T.; Ishizaka, J.; Zhu, Y.; Takeda, S.; Sukigara, C. A role of vertical mixing on nutrient supply into the subsurface chlorophyll maximum in the shelf region of the East China Sea. Cont. Shelf Res. 2017, 143, 139–150. [Google Scholar] [CrossRef]
- Liu, K.-K.; Tang, T.Y.; Gong, G.-C.; Chen, L.-Y.; Shiah, F.-K. Cross-shelf and along-shelf nutrient fluxes derived from flow fields and chemical hydrography observed in the southern East China Sea off northern Taiwan. Cont. Shelf Res. 2000, 20, 493–523. [Google Scholar] [CrossRef]
- Chen, C.-T.A. Rare northward flow in the Taiwan Strait in winter: A note. Cont. Shelf Res. 2003, 23, 387–391. [Google Scholar] [CrossRef]
- Chung, S.-W.; Jan, S.; Liu, K.-K. Nutrient fluxes through the Taiwan Strait in spring and summer 1999. J. Oceanogr. 2001, 57, 47–53. [Google Scholar] [CrossRef]
- Jan, S.; Sheu, D.D.; Kuo, H.M. Water mass and throughflow transport variability in the Taiwan Strait. J. Geophys. Res. Oceans 2006, 111, C12012. [Google Scholar] [CrossRef]
- Lin, S.; Tang, T.; Jan, S.; Chen, C.-J. Taiwan Strait current in winter. Cont. Shelf Res. 2005, 25, 1023–1042. [Google Scholar] [CrossRef]
- Naik, H.; Chen, C.-T.A. Biogeochemical cycling in the Taiwan Strait. Estuar. Coast. Shelf Sci. 2008, 78, 603–612. [Google Scholar] [CrossRef]
- Wu, C.-R.; Chao, S.-Y.; Hsu, C. Transient, seasonal and interannual variability of the Taiwan Strait current. J. Oceanogr. 2007, 63, 821–833. [Google Scholar] [CrossRef]
- Zhang, W.-Z.; Chai, F.; Hong, H.-S.; Xue, H. Volume transport through the Taiwan Strait and the effect of synoptic events. Cont. Shelf Res. 2014, 88, 117–125. [Google Scholar] [CrossRef]
- Huang, T.-H.; Chen, C.-T.A.; Zhang, W.-Z.; Zhuang, X.-F. Varying intensity of Kuroshio intrusion into southeast Taiwan Strait during ENSO events. Cont. Shelf Res. 2015, 103, 79–87. [Google Scholar] [CrossRef]
- Qu, T.; Mitsudera, H.; Yamagata, T. Intrusion of the north Pacific waters into the South China Sea. J. Geophys. Res. Oceans 2000, 105, 6415–6424. [Google Scholar] [CrossRef]
- Qu, T.; Kim, Y.Y.; Yaremchuk, M.; Tozuka, T.; Ishida, A.; Yamagata, T. Can Luzon Strait transport play a role in conveying the impact of ENSO to the South China Sea? J. Clim. 2004, 17, 3644–3657. [Google Scholar] [CrossRef]
- Wu, C.-R.; Wang, Y.-L.; Lin, Y.-F.; Chao, S.-Y. Intrusion of the Kuroshio into the South and East China Seas. Sci. Rep. 2017, 7, 7895. [Google Scholar] [CrossRef] [PubMed]
- Gong, G.-C.; Liu, K.K.; Liu, C.-T.; Pai, S.-C. The chemical hydrography of the South China Sea west of Luzon and a comparison with the West Philippine Sea. Terr. Atmos. Ocean Sci. 1992, 3, 587–602. [Google Scholar] [CrossRef]
- Pai, S.-C.; Yang, C.-C.; Riley, J.P. Formation kinetics of the pink azo dye in the determination of nitrite in natural waters. Anal. Chim. Acta 1990, 232, 345–349. [Google Scholar] [CrossRef]
- Pai, S.-C.; Yang, C.-C.; Riley, J. Effects of acidity and molybdate concentration on the kinetics of the formation of the phosphoantimonylmolybdenum blue complex. Anal. Chim. Acta 1990, 229, 115–120. [Google Scholar] [CrossRef]
- Cai, W.J.; Hu, X.; Huang, W.J.; Jiang, L.Q.; Wang, Y.; Peng, T.H.; Zhang, X. Alkalinity distribution in the western North Atlantic Ocean margins. J. Geophys. Res. Oceans 2010, 115, C08014. [Google Scholar] [CrossRef]
- Chen, C.; Wang, S. International intercalibration of carbonate parameters. Acta Oceanol. Sin. 1993, 15, 60–67. [Google Scholar]
- Gran, G. Determination of the equivalence point in potentiometric titrations. Part II. Analyst 1952, 77, 661–671. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning: With Applications in R; Springer: New York, NY, USA, 2013; ISBN 978-1-4614-7138-7. [Google Scholar]
- Casella, G.; Berger, R.L. Statistical Inference; Brooks-Cole: Pacific Grove, CA, USA, 2002; ISBN 978-0-5342-4312-8. [Google Scholar]
- Buck, R.C. Advanced Calculus; Waveland Press: Long Grove, IL, USA, 1978; ISBN 978-0-0700-8728-6. [Google Scholar]
- Isobe, A. Recent advances in ocean-circulation research on the Yellow Sea and East China Sea shelves. J. Oceanogr. 2008, 64, 569–584. [Google Scholar] [CrossRef]
- Fang, G.; Zhao, B.; Zhu, Y. Water volume transport through the Taiwan Strait and the continental shelf of the East China Sea measured with current meters. Elsevier Oceanogr. Ser. 1991, 54, 345–358. [Google Scholar] [CrossRef]
- Wang, Y.; Jan, S.; Wang, D. Transports and tidal current estimates in the Taiwan Strait from shipboard ADCP observations (1999–2001). Estuar. Coast. Shelf Sci. 2003, 57, 193–199. [Google Scholar] [CrossRef]
- Schlitzer, R. Ocean Data View. 2016. Available online: https://odv.awi.de/ (accessed on 31 December 2017).
- Jan, S.; Chao, S.-Y. Seasonal variation of volume transport in the major inflow region of the Taiwan Strait: The Penghu Channel. Deep Sea Res. Part II 2003, 50, 1117–1126. [Google Scholar] [CrossRef]
- Wu, C.R.; Chang, C.W. Interannual variability of the South China Sea in a data assimilation model. Geophys. Res. Lett. 2005, 32, L17611. [Google Scholar] [CrossRef]
- Nan, F.; Yu, F.; Xue, H.; Zeng, L.; Wang, D.; Yang, S.; Nguyen, K.-C. Freshening of the upper ocean in the South China Sea since the early 1990s. Deep Sea Res. Part I 2016, 118, 20–29. [Google Scholar] [CrossRef]
| Equation | Z = z0 + a × Salinity + b × Temperature + c × Salinity2 + d × Temperature2 + e × Salinity × Temperature | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Season | Parameter | z0 | a | b | c | d | e | Adj. R2 | RSE |
| winter | TA | −29,747.4 | 1432.897 | 520.565 | −15.022 | −0.890 | −13.908 | 0.83 | 8.0 |
| DIC | −139,348.9 | 7967.724 | 332.260 | −111.891 | 0.000 | −10.115 | 0.88 | 11.0 | |
| N | −3986.3 | 277.336 | −64.615 | −4.549 | 0.264 | 1.487 | 0.87 | 0.9 | |
| P | −221.0 | 14.045 | −1.649 | −0.213 | 0.015 | 0.026 | 0.82 | 0.1 | |
| Si | 5700.9 | −290.119 | −61.750 | 3.811 | 0.364 | 1.264 | 0.82 | 1.4 | |
| spring | TA | 87661.8 | −4651.633 | −529.212 | 63.373 | 0.663 | 14.462 | 0.72 | 6.9 |
| DIC | −98,869.3 | 5492.619 | 528.735 | −73.844 | 0.706 | −16.754 | 0.89 | 9.3 | |
| N | −7366.1 | 406.321 | 33.510 | −5.524 | 0.095 | −1.129 | 0.75 | 0.9 | |
| P | −322.4 | 16.496 | 3.403 | −0.203 | 0.005 | −0.108 | 0.70 | 0.1 | |
| Si | −3730.6 | 200.360 | 26.152 | −2.561 | 0.183 | −1.044 | 0.75 | 1.3 | |
| summer | TA | 10,896.0 | −465.743 | −106.446 | 6.380 | 0.226 | 2.735 | 0.87 | 11.2 |
| DIC | −3359.4 | 287.013 | 0.236 | −3.389 | 0.419 | −0.938 | 0.91 | 19.8 | |
| N | −261.8 | 9.595 | 6.794 | −0.006 | 0.066 | −0.314 | 0.93 | 1.0 | |
| P | -8.9 | 0.126 | 0.423 | 0.007 | 0.004 | −0.019 | 0.94 | 0.1 | |
| Si | 93.8 | 1.514 | −8.143 | −0.026 | 0.141 | 0.004 | 0.92 | 1.5 | |
| autumn | TA | 24,586.7 | −1270.450 | −119.310 | 18.098 | 0.013 | 3.409 | 0.93 | 6.3 |
| DIC | 8352.6 | −433.966 | 48.191 | 7.426 | −0.140 | −1.592 | 0.97 | 8.9 | |
| N | 78.9 | −12.115 | 10.617 | 0.317 | 0.028 | −0.370 | 0.92 | 0.7 | |
| P | 77.6 | −4.783 | 0.368 | 0.075 | 0.001 | −0.014 | 0.79 | 0.1 | |
| Si | 1843.8 | −94.930 | −14.806 | 1.260 | 0.071 | 0.303 | 0.86 | 1.1 | |
| Season | Parameter | Temp. Only | Temp. + Sal. (No Interaction) | Temp. + Sal. (with Interaction) |
|---|---|---|---|---|
| winter | TA | 0.02 | 0.80 | 0.83 |
| DIC | 0.77 | 0.87 | 0.88 | |
| N | 0.82 | 0.84 | 0.87 | |
| P | 0.82 | 0.82 | 0.82 | |
| Si | 0.81 | 0.81 | 0.82 | |
| spring | TA | 0.47 | 0.70 | 0.72 |
| DIC | 0.87 | 0.89 | 0.89 | |
| N | 0.75 | 0.74 | 0.75 | |
| P | 0.68 | 0.69 | 0.70 | |
| Si | 0.75 | 0.74 | 0.75 | |
| summer | TA | 0.70 | 0.87 | 0.87 |
| DIC | 0.87 | 0.91 | 0.91 | |
| N | 0.92 | 0.92 | 0.93 | |
| P | 0.94 | 0.94 | 0.94 | |
| Si | 0.93 | 0.93 | 0.92 | |
| autumn | TA | 0.74 | 0.93 | 0.93 |
| DIC | 0.96 | 0.97 | 0.97 | |
| N | 0.91 | 0.92 | 0.92 | |
| P | 0.77 | 0.79 | 0.79 | |
| Si | 0.85 | 0.86 | 0.86 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, T.-H.; Lun, Z.; Wu, C.-R.; Chen, C.-T.A. Interannual Carbon and Nutrient Fluxes in Southeastern Taiwan Strait. Sustainability 2018, 10, 372. https://doi.org/10.3390/su10020372
Huang T-H, Lun Z, Wu C-R, Chen C-TA. Interannual Carbon and Nutrient Fluxes in Southeastern Taiwan Strait. Sustainability. 2018; 10(2):372. https://doi.org/10.3390/su10020372
Chicago/Turabian StyleHuang, Ting-Hsuan, Zhixin Lun, Chau-Ron Wu, and Chen-Tung Arthur Chen. 2018. "Interannual Carbon and Nutrient Fluxes in Southeastern Taiwan Strait" Sustainability 10, no. 2: 372. https://doi.org/10.3390/su10020372
APA StyleHuang, T.-H., Lun, Z., Wu, C.-R., & Chen, C.-T. A. (2018). Interannual Carbon and Nutrient Fluxes in Southeastern Taiwan Strait. Sustainability, 10(2), 372. https://doi.org/10.3390/su10020372







