Spatial Spillover and the Influencing Factors Relating to Provincial Carbon Emissions in China Based on the Spatial Panel Data Model
Abstract
1. Introduction
2. Materials and Methodology
2.1. Model
2.2. Data
3. Methodology
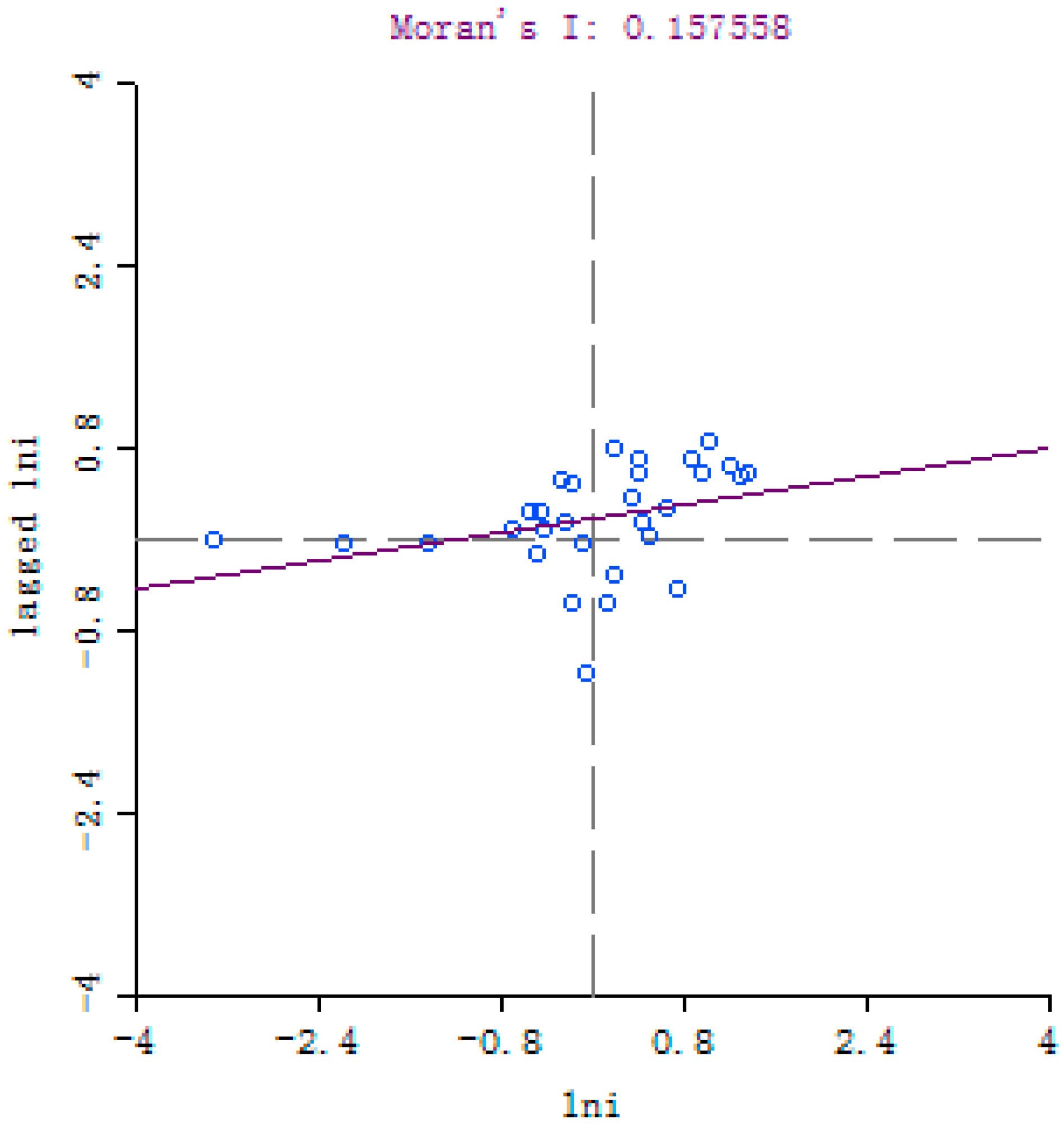
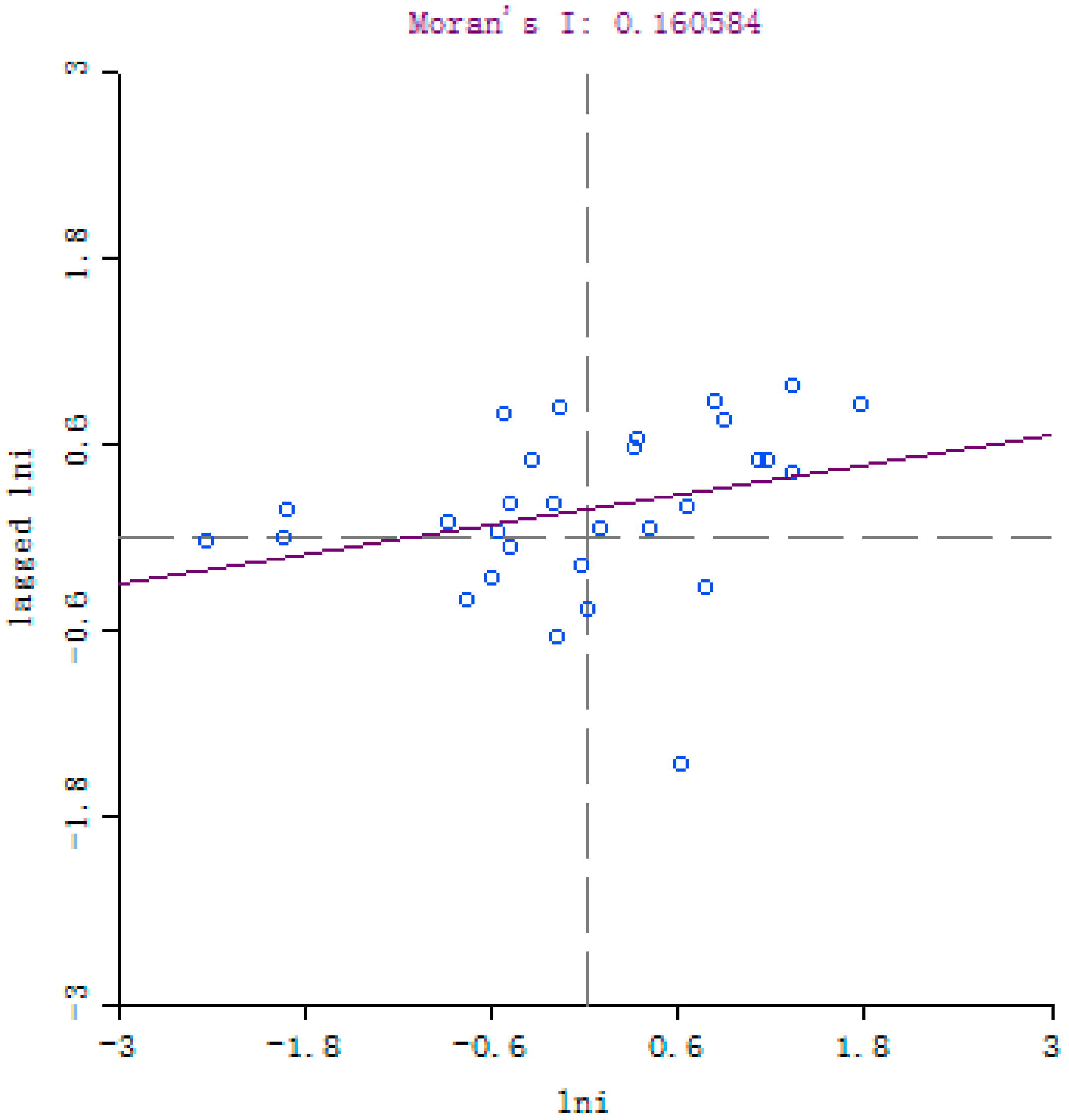
3.1. Global Spatial Autocorrelation Test
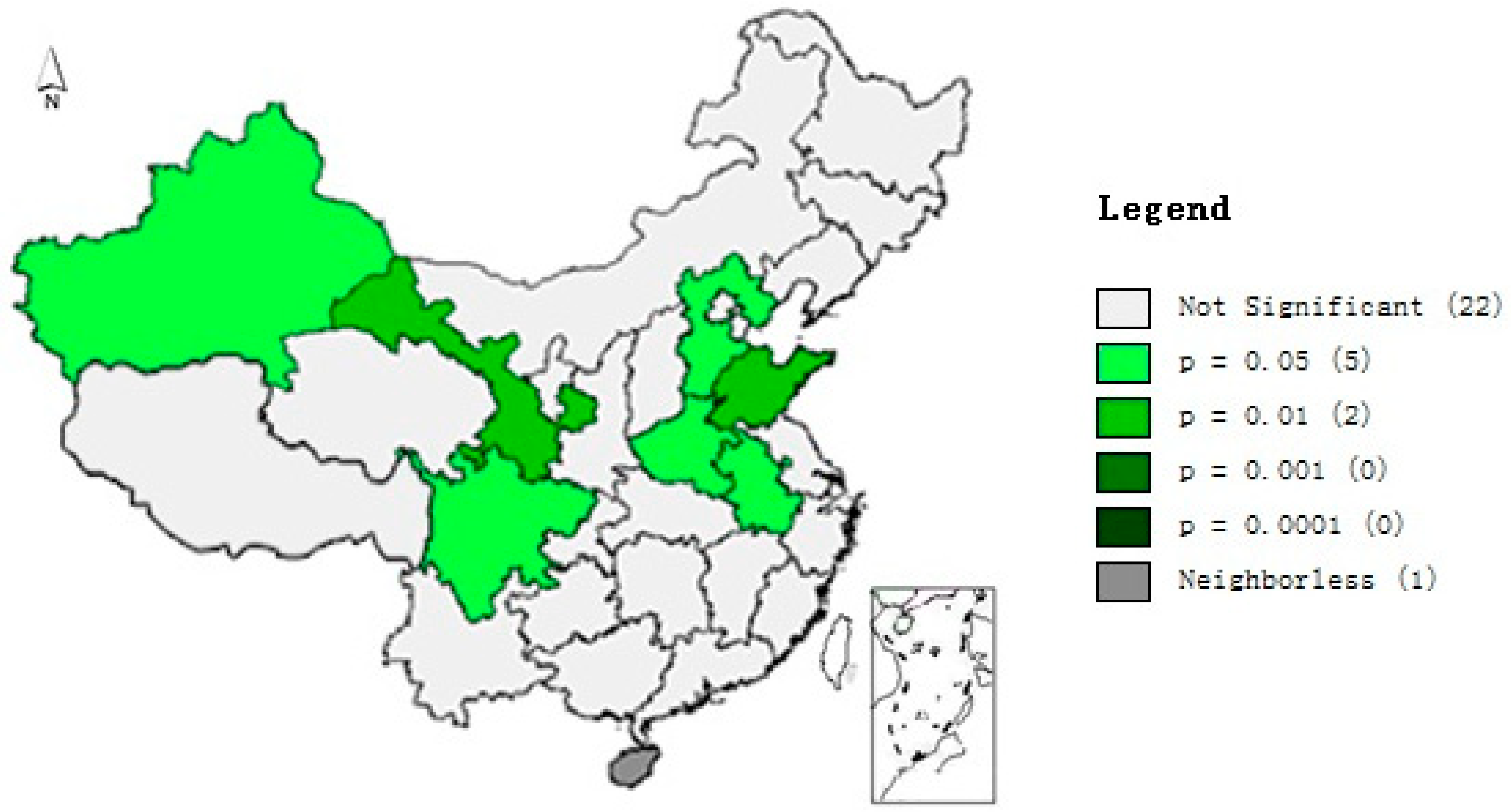
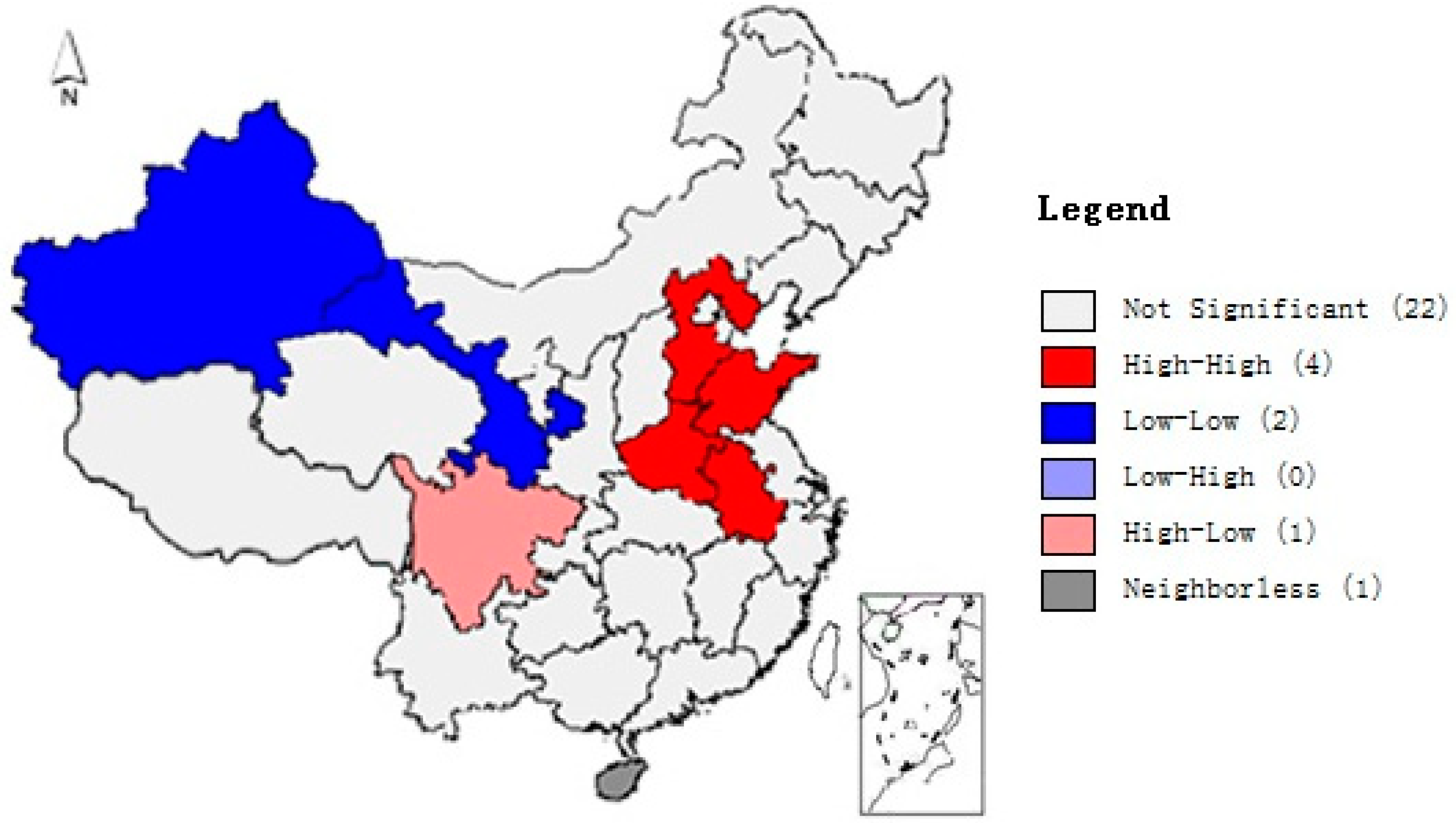
3.2. Local Spatial Autocorrelation Test
3.3. The Type of Econometric Model of the Spatial panel
4. Results and Discussion
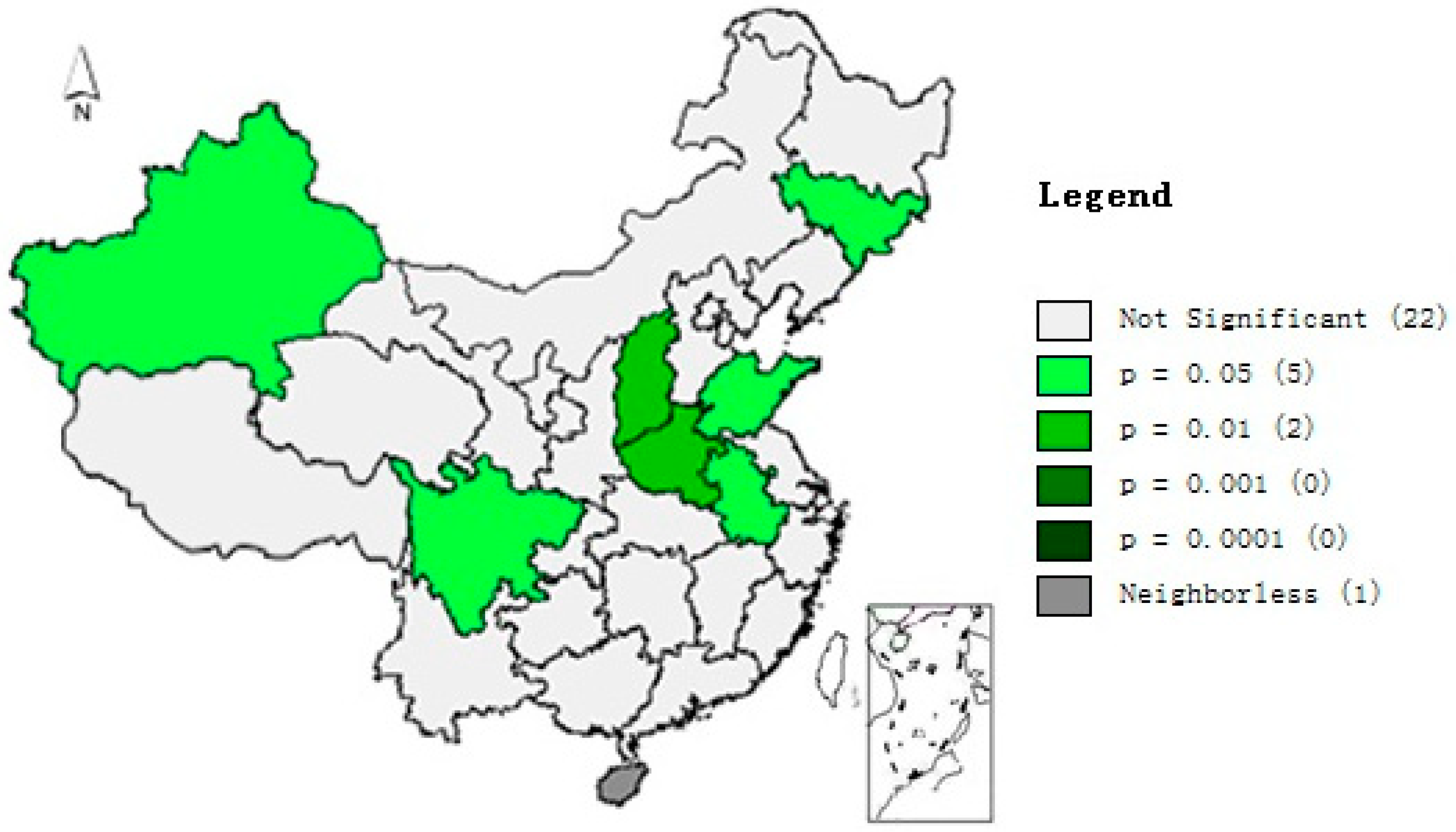
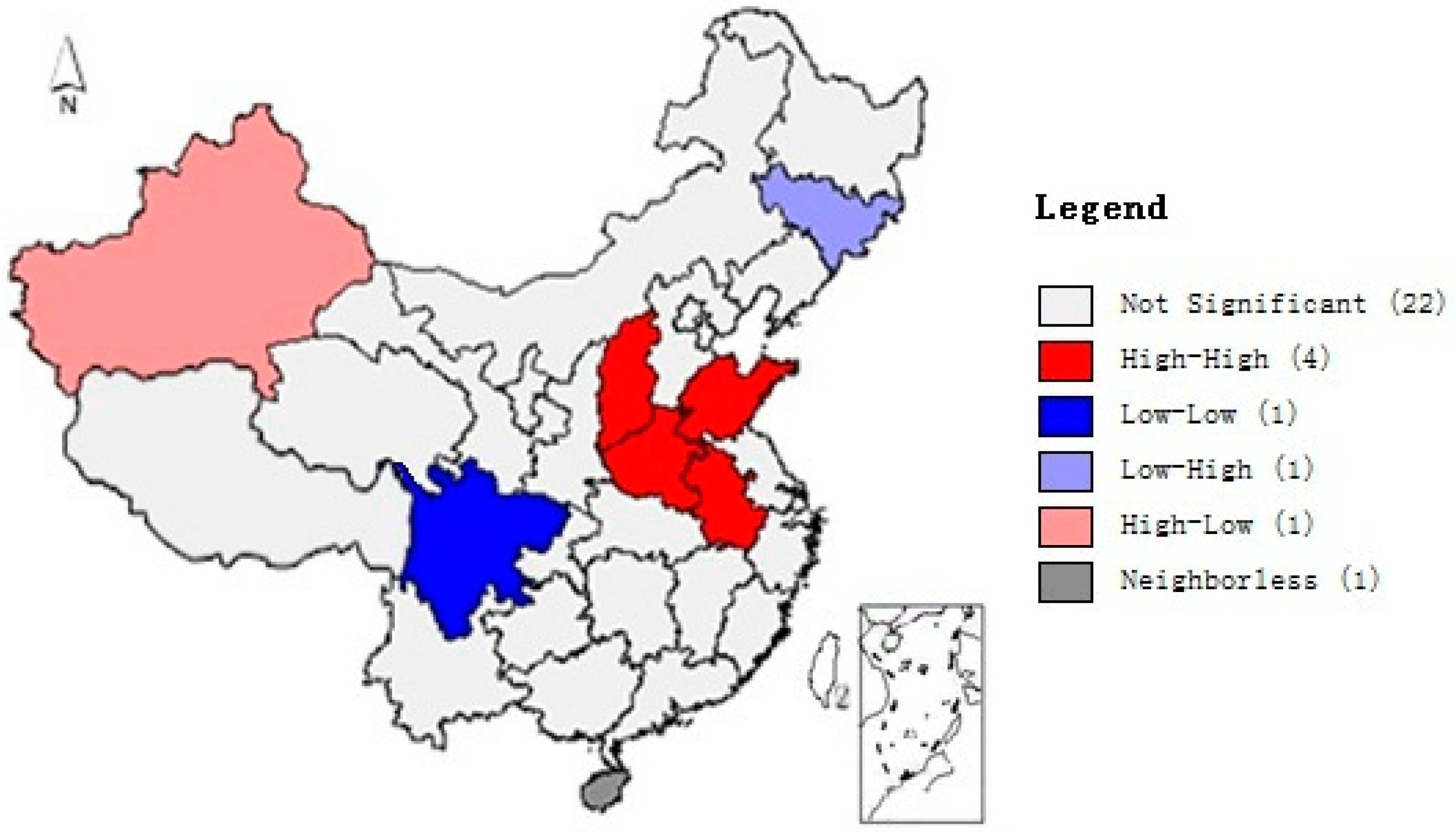
4.1. Whole Domain Moran’s I Test
4.2. Empirical Analysis on the Econometric Model of the Spatial panel
5. Conclusions and Policy Recommendation
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Christidou, M.; Panagiotidis, T.; Sharma, A. On the stationarity of per capita carbon dioxide emissions over a century. Econ. Model. 2013, 33, 918–925. [Google Scholar] [CrossRef]
- Dergiades, T.; Kaufmann, R.; Panagiotidis, T. Long-run changes in radiative forcing and surface temperature: The effect of human activity over the last five centuries. J. Environ. Econ. Manag. 2016, 76, 67–85. [Google Scholar] [CrossRef]
- Wu, L.; Kaneko, S.; Matsuoka, S. Driving Forces behind the Stagnancy of China’s Energy-related CO2 Emissions From 1996 to 1999: The Relative Importance of Structural Change, Intensity Change and Scale Change. Energy Policy 2005, 33, 319–335. [Google Scholar] [CrossRef]
- Zhao, Q.; Yan, Q.; Zhao, H. Research on Spatial Characteristics and Influencing Factors of Provincial Carbon Emissions in China. J. Beijing Inst. Technol. (Soc. Sci. Ed.) 2018, 20, 9–16. [Google Scholar]
- Li, J.; Chen, Y.; Li, Z.; Liu, Z. Quantitative Analysis of the Impact Factors of Conventional Energy Carbon Emissions in Kazakhstan Based on LMDI Decomposition and STIRPAT Model. Univ. Chin. Acad. Sci. J. Geogr. Sci. 2018, 28, 1001–1019. [Google Scholar] [CrossRef]
- Li, N.; Shi, M.; Yuan, Y. Impacts of Carbon Tax Policy on Regional Development in China: A Dynamic Simulation Based on a Multi-regional CGE Model. Acta Geogr. Sin. 2010, 65, 1569–1580. [Google Scholar]
- Weber, C.L.; Peters, G.P.; Guan, D. The contribution of Chinese exports to climate change. Energy Policy 2008, 36, 3572–3577. [Google Scholar] [CrossRef]
- Wang, C.; Chen, J.; Zou, J. Decomposition of energy-related CO2 emission in China: 1957–2000. Energy 2005, 30, 73–83. [Google Scholar] [CrossRef]
- Wang, H.; He, C. Energy Consumption, Economic Growth and CO2 Emissions in China: Analysis Based on Logarithm Mean Divisa Decomposure Method. Resour. Environ. Yangtze Basin 2010, 19, 18–23. [Google Scholar]
- Dhakal, S.; Shinji, K.; Hidefumi, I. CO2 Emissions from energy use in East Asian mega-cities: Driving factors and their contributions. Environ. Syst. Res. 2003, 31, 209–216. [Google Scholar] [CrossRef]
- Li, L.; Liu, J. Using LMDI to Analyze the Driving Forces in Industrial CO2 Intensity: Evidence for Xinjiang. Ecol. Econ. 2011, 4, 34–38. [Google Scholar]
- Zhao, A.; Li, D. EKC Test for China’s Carbon Dioxide Emissions and Analysis of Affecting Factors. Sci. Sci. Manag. S & T 2012, 33, 107–115. [Google Scholar]
- Fan, T.; Luo, R.; Fan, Y.; Zhang, L.; Chang, X. Study on Influence Factors for carbon Dioxide Emissions in China’s Chemical Industry with LMDI Method. China Soft Sci. 2013, 3, 166–174. [Google Scholar]
- Zhang, L.; Lei, J.; Zhang, X. Variation and Influent Factor of Carbon Emission of Primary Energy Consumption in Xinjiang during the Period 1952–2008. Resour. Sci. 2012, 34, 42–49. [Google Scholar]
- Song, D.; Lu, Z. The Factor Decomposition and Periodic Fluctuations of Carbon Emission in China. China Popul. Resour. Environ. 2009, 19, 18–24. [Google Scholar]
- He, W.; Zhang, K. The Decomposition on the Influencing Factors of China’s Steel Industry Carbon Emission. J. Ind. Technol. Econ. 2013, 1, 3–10. [Google Scholar]
- Zhu, Q.; Peng, X.Z.; Lu, Z.M.; Wu, K.Y. Factors Decomposition and Empirical Analysis of Variations in Energy Carbon Emission in China. Resour. Sci. 2009, 31, 2072–2079. [Google Scholar]
- Li, G.; Li, Z. Regional Difference and Influence Factors of China’s Carbon Dioxide Emissions. China Popul. Resour. Environ. 2010, 20, 22–27. [Google Scholar]
- He, X.; Zhang, Y. Influence Factors and Environmental Kuznets Curve Relink Effect of Chinese Industry’s Carbon Dioxide Emission—Empirical Research Based on STIRPAT Model with Industrial Dynamic Panel Data. China Ind. Econ. 2012, 1, 26–35. [Google Scholar]
- Zhu, Q.; Peng, X.Z.; Lu, Z.M.; Yu, J. Analysis Model and Empirical Study of Impacts from Population and Consumption on Carbon Emissions. China Popul. Resour. Environ. 2010, 20, 98–102. [Google Scholar]
- Qiang, H.E.; Guangming, L.V. Analysis of Ecological Environmental Impact Based on IPAT Model: A Case Study of Beijng. J. Central Univ. Finance Econ. 2008, 12, 83–88. [Google Scholar]
- Zhu, Y.; Zhang, S. Analysis of driving factors of Beijing’s economic carbon emissions based on STIRPAT model. Spec. Zone Econ. 2012, 1, 77–79. [Google Scholar]
- Tong, X.; Chen, K.; Li, G. Influencing Factors Analysis and Trend Forecasting of China’s Carbon Emissions: Empirical Study Based on STIRPAT and GM(1, 1) Models. J. Northeast Univ. (Nat. Sci.) 2015, 36, 297–300. [Google Scholar]
- York, R.; Rosa, E.A.; Dietz, T. STIRPAT, IPAT and impacts: Analytic tools for unpacking the driving forces of environmental impacts. Ecol. Econ. 2003, 46, 351–365. [Google Scholar] [CrossRef]
- Xu, G.; Liu, Z.; Jiang, Z. Decomposition Model and Empirical Study of Carbon Emissions for China, 1995–2004. China Popul. Resour. Environ. 2006, 16, 158–161. [Google Scholar]
- Hu, C.; Huang, X.; Zhong, T. Character of Carbon Emission in China and Its Dynamic Development Analysis. China Popul. Resour. Environ. 2008, 18, 46–50. [Google Scholar]
- Wu, Y. Spatial Panel Econometric of Tourism Economic Growth and Spillover Effects. Tour. Trib. 2014, 29, 16–24. [Google Scholar]
- IPCC. 2006 IPCC Guidelines for National Greenhouse Gas Inventories; IGES: Hayama, Japan, 2016. [Google Scholar]
- Wang, K.; Wang, C.; Chen, J. Analysis of the economic impact of different Chinese climate policy options based on a CGE model incorporating endogenous technological change. Energy Policy 2009, 37, 2930–2940. [Google Scholar] [CrossRef]
- Birdsall, N. Another Look at Population and Global Warming: Population, Health and Nutrition Policy Research; Working Paper; World Bank: Washington, DC, USA, 1992. [Google Scholar]
- Knapp, T.; Mookerjee, R. Population Growth and Global CO2 Emissions. Energy Policy 1996, 24, 31–37. [Google Scholar] [CrossRef]
- Tan, D.; Huang, X.; Hu, C. Analysis of the Relationship between Industrial Upgrading and Carbon Emission in China. Sichuang Environ. 2008, 2, 74–84. [Google Scholar]
| Data Resource | Coal | Oil | Natural Gas |
|---|---|---|---|
| US Department of Energy/Energy Information Administration | 0.702 | 0.478 | 0.389 |
| Japan Institute of Energy Economics | 0.756 | 0.586 | 0.449 |
| Chinese Academy of Engineering | 0.68 | 0.54 | 0.41 |
| National Greenhouse Gas Control Project | 0.748 | 0.583 | 0.444 |
| National Science and Technology Commission Climate Change Project | 0.726 | 0.583 | 0.409 |
| Beijing Project of the State Science and Technology Commission | 0.656 | 0.591 | 0.452 |
| Energy Research Institute of National Development and Reform Commission | 0.7476 | 0.5825 | 0.4435 |
| Test Summary | Chi-Sq. Statistic | Chi-Sq. d.f. * | Prob. |
|---|---|---|---|
| Random cross-section | 38.0591 | 9 | 0.0000 |
| Spatial Correlation Test | Test Method | Statistical Value | p-Value |
| LM test, no spatial lag * | 11.0838 | 0.001 | |
| Robust LM test, no spatial lag | 6.5504 | 0.010 | |
| LM test, no spatial error | 10.8496 | 0.001 | |
| Robust LM, test no spatial error | 6.3162 | 0.012 |
| Variable | No Fixed Effects | Fixed Effects | Random Effects | Spatial Fixed Effects | Time Period Fixed Effects |
|---|---|---|---|---|---|
| C | −0.8526 | −1.5471 | −0.8526 | −1.1804 | −0.9880 |
| LnP | 0.0187 | 0.2885 | 0.0187 | 0.2545 | 0.0257 |
| LnA | 0.9382 | 0.6198 | 0.9382 | 0.6707 | 0.9305 |
| LnT | −0.2736 | −0.2570 | −0.2736 | −0.2607 | −0.2723 |
| LnS | 1.6351 | 1.5627 | 1.6351 | 1.5329 | 1.6497 |
| LnF | 0.1556 | 0.6222 | 0.1556 | 0.0812 | 0.1538 |
| LnE | −0.5451 | −0.4269 | −0.5451 | −0.4669 | −0.5390 |
| LnEX | −0.1003 | −0.0301 | −0.1003 | −0.0320 | −0.1028 |
| LnU | −0.1108 | 0.0615 | −0.1108 | 0.0120 | −0.0958 |
| LnFD | 0.1762 | 0.2472 | 0.1763 | 0.2325 | 0.1755 |
| R2 | 0.7850 | 0.8095 | 0.7851 | 0.8081 | 0.7858 |
| Variable | SLPDM 1 | SDPDM 2 | ||||||
|---|---|---|---|---|---|---|---|---|
| No Fixed Effects I | Spatial Fixed Effects II | Time Period Fixed Effects III | Spatial and Time Period Fixed Effects IV | No Fixed Effects V | Spatial Fixed Effects VI | Time Period Fixed Effects VII | Spatial and Time Period Fixed Effects VIII | |
| C | 0.1689 | −3.3062 | ||||||
| LnP | −0.0045 | −0.4103 | 0.1810 | −0.6911 | 0.1852 | −0.0988 | 0.2372 | −0.5147 |
| LnA | 0.9907 | 0.8217 | 0.7231 | 0.2838 | 0.7891 | 1.3106 | 0.6811 | 0.7550 |
| LnT | −0.2965 | −0.1532 | −0.3315 | −0.1152 | −0.2388 | −0.0515 | −0.2497 | −0.0200 |
| LnS | 1.3399 | 0.6255 | 1.2624 | 0.6896 | 1.1290 | 0.3215 | 1.1173 | 0.4339 |
| LnF | 0.1322 | 0.1279 | 0.0517 | 0.1255 | 0.1355 | 0.1216 | 0.1068 | 0.0967 |
| LnE | −0.5648 | 0.1918 | −1.4017 | −0.2816 | 0.2471 | 0.0332 | −0.8388 | −0.1871 |
| LnEX | −0.0664 | −0.0193 | 0.0195 | −0.0746 | 0.1011 | 0.0350 | 0.1431 | −0.0409 |
| LnU | −0.2113 | 0.2865 | −0.0626 | 0.2030 | −0.2435 | 0.1658 | −0.2177 | 0.0249 |
| LnFD | 0.1123 | 0.0469 | 0.2620 | 0.0698 | 0.0723 | −0.0170 | 0.1289 | 0.0088 |
| WlnP | −0.0827 | −0.8726 | 0.2136 | −0.8286 | ||||
| WlnA | −0.1761 | −0.7375 | −0.2833 | −1.0520 | ||||
| WlnT | −0.0245 | −0.0527 | −0.1846 | 0.1048 | ||||
| WLnS | 0.9531 | 0.3775 | 1.1361 | 0.6726 | ||||
| WLnF | −0.0296 | 0.0359 | 0.0100 | 0.0772 | ||||
| WLnE | −1.068 | 0.1016 | −1.5495 | −0.3011 | ||||
| WLnEX | −0.2853 | −0.1138 | −0.1843 | −0.2753 | ||||
| WLnU | 0.5109 | −0.1759 | 0.8132 | −0.1093 | ||||
| WLnFD | 0.0219 | 0.1205 | 0.0775 | 0.0566 | ||||
| ρ | 0.0600 | −0.0300 | 0.0640 | 0.2625 | 0.3390 | 0.3110 | 0.3400 | 0.0330 |
| logL | −254.3434 | 200.0667 | −255.7443 | 207.1831 | −167.7281 | 264.3265 | −712.9441 | 328.9011 |
| R2 | 0.7904 | 0.9685 | 0.7976 | 0.9730 | 0.8577 | 0.9764 | 0.8651 | 0.9815 |
| Adj. R2 | 0.7874 | 0.8585 | 0.7416 | 0.2971 | 0.8379 | 0.8841 | 0.4247 | 0.5618 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tong, X.; Li, X.; Tong, L.; Jiang, X. Spatial Spillover and the Influencing Factors Relating to Provincial Carbon Emissions in China Based on the Spatial Panel Data Model. Sustainability 2018, 10, 4739. https://doi.org/10.3390/su10124739
Tong X, Li X, Tong L, Jiang X. Spatial Spillover and the Influencing Factors Relating to Provincial Carbon Emissions in China Based on the Spatial Panel Data Model. Sustainability. 2018; 10(12):4739. https://doi.org/10.3390/su10124739
Chicago/Turabian StyleTong, Xin, Xuesen Li, Lin Tong, and Xuan Jiang. 2018. "Spatial Spillover and the Influencing Factors Relating to Provincial Carbon Emissions in China Based on the Spatial Panel Data Model" Sustainability 10, no. 12: 4739. https://doi.org/10.3390/su10124739
APA StyleTong, X., Li, X., Tong, L., & Jiang, X. (2018). Spatial Spillover and the Influencing Factors Relating to Provincial Carbon Emissions in China Based on the Spatial Panel Data Model. Sustainability, 10(12), 4739. https://doi.org/10.3390/su10124739




