Evaluating Impacts of Overloaded Heavy Vehicles on Freeway Traffic Condition by a Novel Multi-Class Traffic Flow Model
Abstract
1. Introduction
2. Literature Review
- (1)
- A new dynamic PCE was designed for overloaded HVs, and it can represent the different influences present when traffic conditions change.
- (2)
- A new multi-class kinematic wave traffic flow model based on dynamic PCE is proposed with consideration for the driving performances of overloaded HVs.
- (3)
- The impacts of overloaded HVs on freeway traffic conditions are analyzed based on scenario tests.
3. Data and Vehicle Type Description
3.1. Freeway Toll Data
3.2. Characteristics of Different Vehicle Types
3.3. Overloading Ratio and Maximum Speed
4. Multi-Class Traffic Flow Model with Overloaded HVs
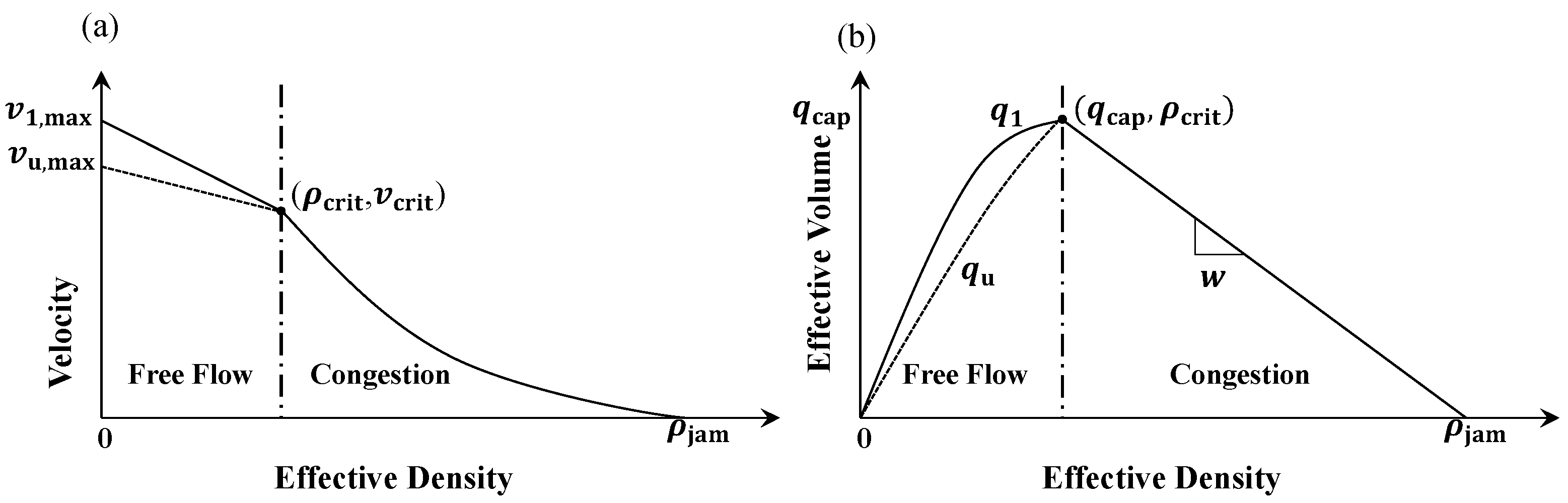
4.1. Multi-Class Fundamental Diagram
4.2. Definition of Dynamic PCE
4.3. Relationship between Vehicle Weight and Minimum Safe Headway
4.3.1. Free-Flow
4.3.2. Congestion
4.4. Effective Density and Effective Volume
4.4.1. Effective Density
4.4.2. Effective Volume of Multi-Class Traffic Flow
5. Validation of Model Results
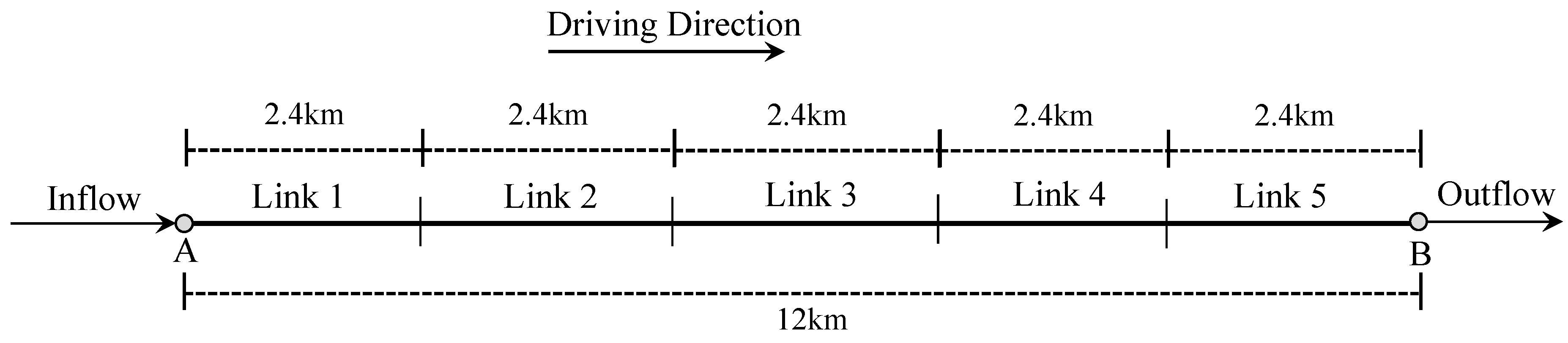
5.1. Model Preparation
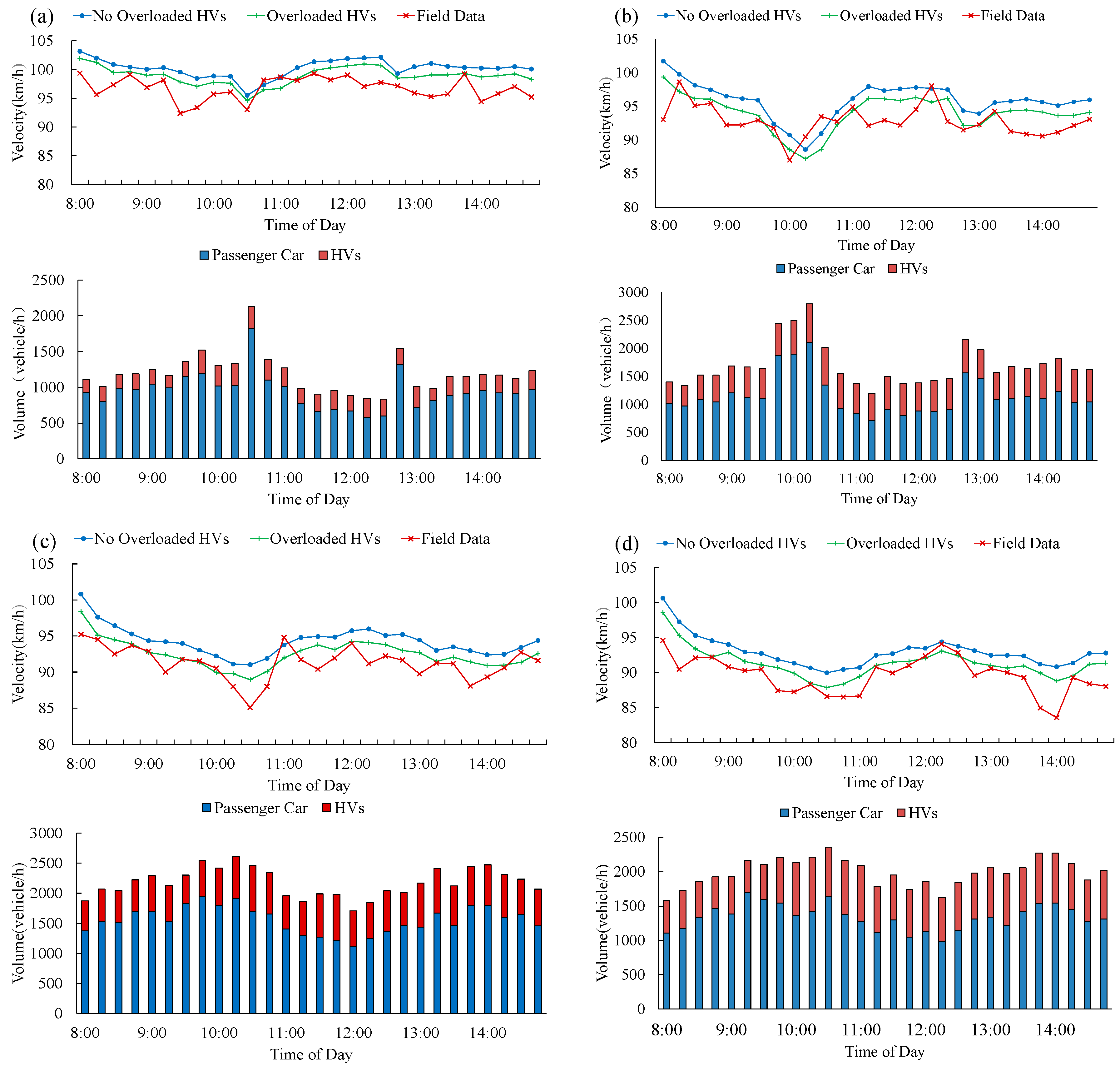
5.2. Model Results versus Real Traffic Data
6. Model Scenario Test
6.1. Preparation of the Scenario Test
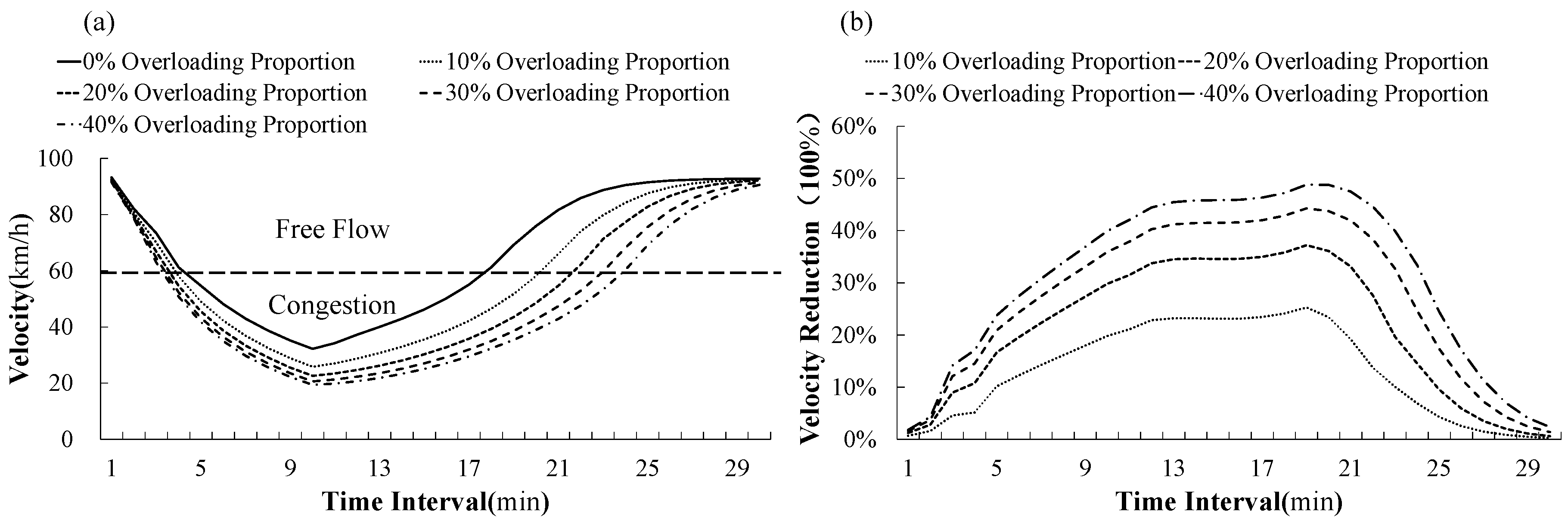
6.2. Scenario 1: Impact of the Overloading Proportion
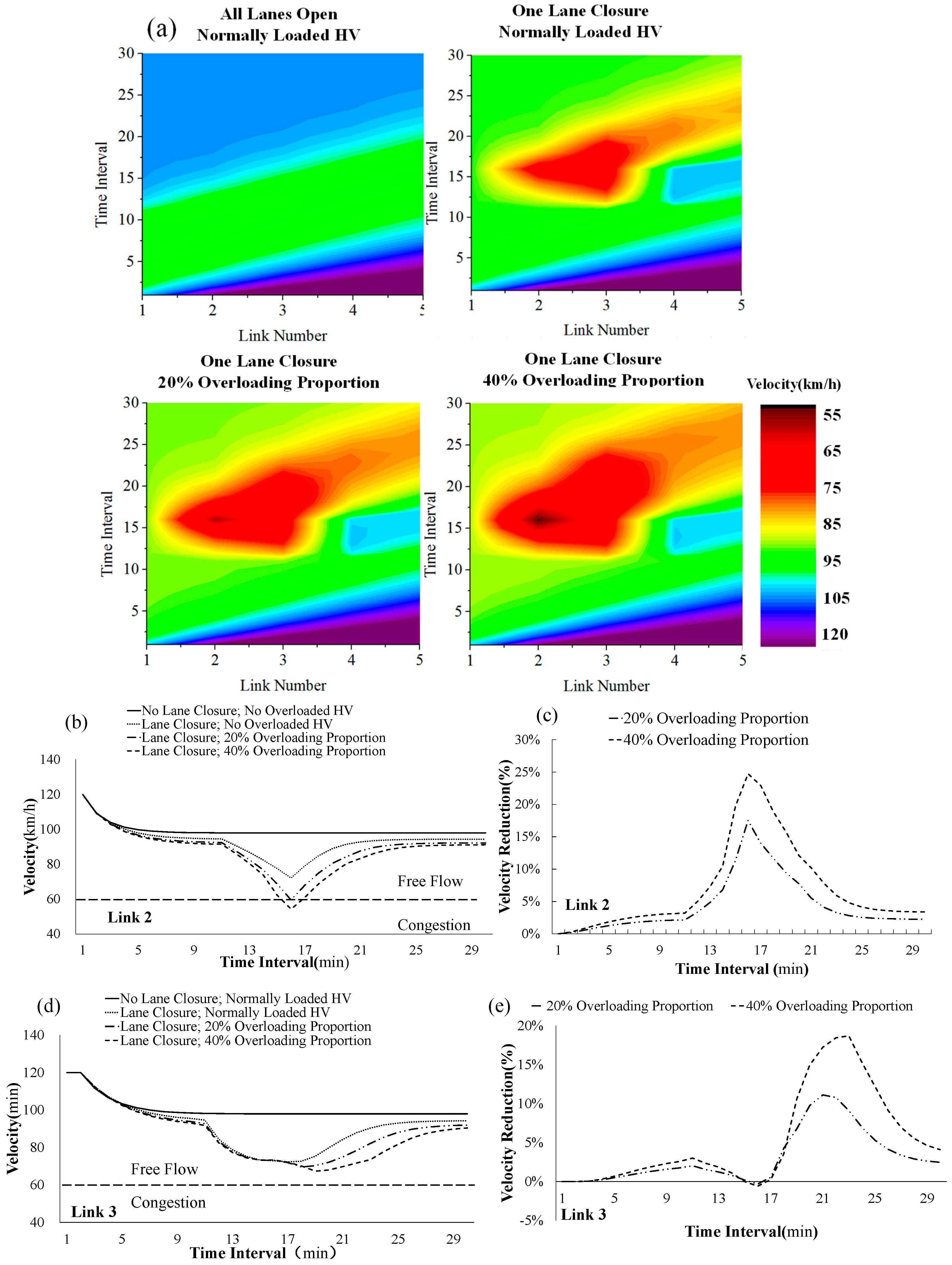
6.3. Scenario 2: Impact of the Overloaded HVs at Work Zones
6.4. Policy Suggestions
7. Conclusions and Recommendations
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| the maximum braking force of vehicle type u | |
| the length of vehicle type u | |
| the number of vehicle type u on link i | |
| the number of passenger cars on link i | |
| the data size from toll station i to j after data quality control in time period p | |
| the number of vehicles of class u arriving on link i during time interval k | |
| the number of vehicles of class u leaving from link i during time interval k | |
| the stopping distance of normal HVs | |
| the stopping distance of overloaded HVs | |
| the headway of vehicle type u on link i | |
| the travel time from entry station i to exit station j in time period p | |
| the model result of travel speed during time interval i | |
| the actual travel speed during time interval i | |
| the total weight of normal HVs | |
| the total weight of overloaded HVs | |
| the number of time intervals | |
| the proportion of vehicle type u against the total number of passenger cars and vehicle type u | |
| the overloading ratio | |
| the entry time of vehicle k entering during time period p | |
| the exit time of vehicle k | |
| the travel time along the on-ramp of entry station i | |
| the travel time along the off-ramp of exit station j | |
| the speed of vehicle type u | |
| the maximum speed of vehicle type u | |
| the maximum speed of vehicle type u when the overloading ratio is r | |
| the travel speed of overloaded HVs | |
| the critical speed | |
| the shockwave speed | |
| the length of link i | |
| the adjustment ratio of the HV proportion | |
| the dynamic PCE of vehicle type u on link i | |
| the density of vehicle type u on link i during time interval k | |
| the effective density | |
| the critical density | |
| the jam density |
Appendix A. The Solution of Effective Density
Appendix A1. Transformation of Effective Density
Appendix A2. Requirements on Parameters
Appendix A3. Solution of Effective Density
Appendix B. The Solution of the Density for Each Vehicle Type
References
- Ren, Y.; Wu, S. Analysis of heavy trucks’ effect on freeway traffic safety. In Proceedings of the 2011 International Conference on Electronic and Mechanical Engineering and Information Technology (EMEIT), Harbin, China, 12–14 August 2011. [Google Scholar]
- Xiao, R.; Li, B.; Chen, Y. Trend analysis of expressway transportation based on big data. J. Traffic Transp. Eng. 2015, 117, 85–90. [Google Scholar]
- Han, W.; Wu, J.; Cai, C.S.; Chen, S. Characteristics and dynamic impact of overloaded extra heavy trucks on typical highway bridges. J. Bridge Eng. 2014, 20, 05014011. [Google Scholar] [CrossRef]
- Zhou, H.W.; Li, G.X.; Shi, K.T. Jiangsu Freeway Traffic Condition Analyzing Report; Jiangsu Freeway Network Operation & Management Center: Nanjing, China, 2012. [Google Scholar]
- Manual, H.C. HCM2010. In Transportation Research Board; National Research Council: Washington, DC, USA, 2010. [Google Scholar]
- Aghabayk, K.; Sarvi, M.; Young, W. A macroscopic study of heavy vehicle traffic flow characteristics. In Proceedings of the ARRB Conference, Perth, Australia, 23–26 September 2012. [Google Scholar]
- Aghabayk, K.; Sarvi, M.; Young, W. Understanding the dynamics of heavy vehicle interactions in car-following. J. Transp. Eng. 2012, 138, 1468–1475. [Google Scholar] [CrossRef]
- Abdullah, A.S. Development of Integrated Weigh-in-Motion System and Analysis of Traffic Flow Characteristics considering Vehicle Weight; The University of Tokushima Japan: Tokushima, Japan, 2011. [Google Scholar]
- Saifizul, A.A.; Yamanaka, H.; Karim, M.R. Empirical analysis of gross vehicle weight and free flow speed and consideration on its relation with differential speed limit. Acc. Anal. Prev. 2011, 43, 1068–1073. [Google Scholar] [CrossRef] [PubMed]
- Dhamaniya, A.; Chandra, S. Concept of Stream Equivalency Factor for Heterogeneous Traffic on Urban Arterial Roads. J. Transp. Eng. 2013, 139, 1117–1123. [Google Scholar] [CrossRef]
- Cao, N.Y.; Sano, K. Estimating capacity and motorcycle equivalent units on urban roads in Hanoi, Vietnam. J. Transp. Eng. 2012, 138, 776–785. [Google Scholar] [CrossRef]
- Geistefeldt, J. Estimation of passenger car equivalents based on capacity variability. Transp. Res. Rec. 2009, 2130, 1–6. [Google Scholar] [CrossRef]
- De Luca, M.; Dell’Acqua, G. Calibrating the passenger car equivalent on Italian two line highways: A case study. Transport 2013, 29, 1–8. [Google Scholar]
- Ahmed, U.; Drakopoulos, A.; Ng, M. Impact of Heavy Vehicles on Freeway Operating Characteristics under Congested Conditions. Transp. Res. Rec. 2013, 2396, 28–37. [Google Scholar] [CrossRef]
- Mehar, A.; Chandra, S.; Velmurugan, S. Passenger Car Units at Different Levels of Service for Capacity Analysis of Multilane Interurban Highways in India. J. Transp. Eng. 2013, 140, 81–88. [Google Scholar] [CrossRef]
- van Lint, J.W.C.; Hoogendoorn, S.P.; Schreuder, M. Fastlane: New Multiclass First-Order Traffic Flow Model. Transp. Res. Rec. 2008, 2088, 177–187. [Google Scholar] [CrossRef]
- Ngoduy, D. Multiclass first-order traffic model using stochastic fundamental diagrams. Transportmetrica 2011, 7, 111–125. [Google Scholar] [CrossRef]
- Bellomo, N.; Dogbe, C. On the modeling of traffic and crowds: A survey of models, speculations, and perspectives. SIAM Rev. 2011, 53, 409–463. [Google Scholar] [CrossRef]
- Logghe, S.; Immers, L.H. Multi-class kinematic wave theory of traffic flow. Transp. Res. Part B Methodol. 2008, 42, 523–541. [Google Scholar] [CrossRef]
- Del Castillo, J.M. Three new models for the flow–density relationship: Derivation and testing for freeway and urban data. Transportmetrica 2012, 8, 443–465. [Google Scholar] [CrossRef]
- Daganzo, C.F. A behavioral theory of multi-lane traffic flow. Part I: Long homogeneous freeway sections. Transp. Res. Part B Methodol. 2002, 36, 131–158. [Google Scholar] [CrossRef]
- Chanut, S.; Buisson, C. Macroscopic model and its numerical solution for two-flow mixed traffic with different speeds and lengths. Transp. Res. Rec. 2003, 1852, 209–219. [Google Scholar] [CrossRef]
- Ngoduy, D.; Liu, R. Multiclass first-order simulation model to explain non-linear traffic phenomena. Phys. A Stat. Mech. Appl. 2007, 385, 667–682. [Google Scholar] [CrossRef]
- Van Wageningen-Kessels, F.; Van Lint, H.; Hoogendoorn, S.; Vuik, K. A New Generic Multi-class Kinematic Wave Traffic Flow Model: Model Development and Analysis of Its Properties. Transportation 2014, 29, 449–456. [Google Scholar]
- Van Wageningen-Kessels, F. Multi-Class Continuum Traffic Flow Models: Analysis and Simulation methods. Ph.D. Thesis, Delft University of Technology/TRAIL Research School, Delft, The Netherlands, 2013. [Google Scholar]
- Wang, X.; Chen, X. Travel time estimation of a single segment based on freeway toll data. In Proceedings of the 14th COTA International Conference of Transportation Professionals: Safe, Smart, and Sustainable Multimodal Transportation Systems, CICTP 2014, Changsha, China, 4–7 July 2014; pp. 2161–2174. [Google Scholar]
- Smulders, S. Control of freeway traffic flow by variable speed signs. Transp. Res. Part B Methodol. 1990, 24, 111–132. [Google Scholar] [CrossRef]
- Qu, X.; Zhang, J.; Wang, S. On the stochastic fundamental diagram for freeway traffic: model development, analytical properties, validation, and extensive applications. Transp. Res. Part B Methodol. 2017, 104, 256–271. [Google Scholar] [CrossRef]
- Daganzo, C.F. The cell transmission model: A dynamic representation of highway traffic consistent with the hydrodynamic theory. Transp. Res. Part B Methodol. 1994, 28, 269–287. [Google Scholar] [CrossRef]
- Qu, X.; Wang, S.; Zhang, J. On the fundamental diagram for freeway traffic: A novel calibration approach for single-regime models. Transp. Res. Part B Methodol. 2015, 73, 91–102. [Google Scholar] [CrossRef]
- Yang, D.; Jin, P.; Pu, Y.; Ran, B. Safe distance car-following model including backward-looking and its stability analysis. Eur. Phys. J. B 2013, 86, 92. [Google Scholar] [CrossRef]
- Marlina, S. Understanding the Dynamics of Truck Traffic on Freeways by Evaluating Truck Passenger Car Equivalent (PCE) in the Highway Capacity Manual (HCM) 2010; University of Colorado at Denver: Denver, CO, USA, 2012. [Google Scholar]
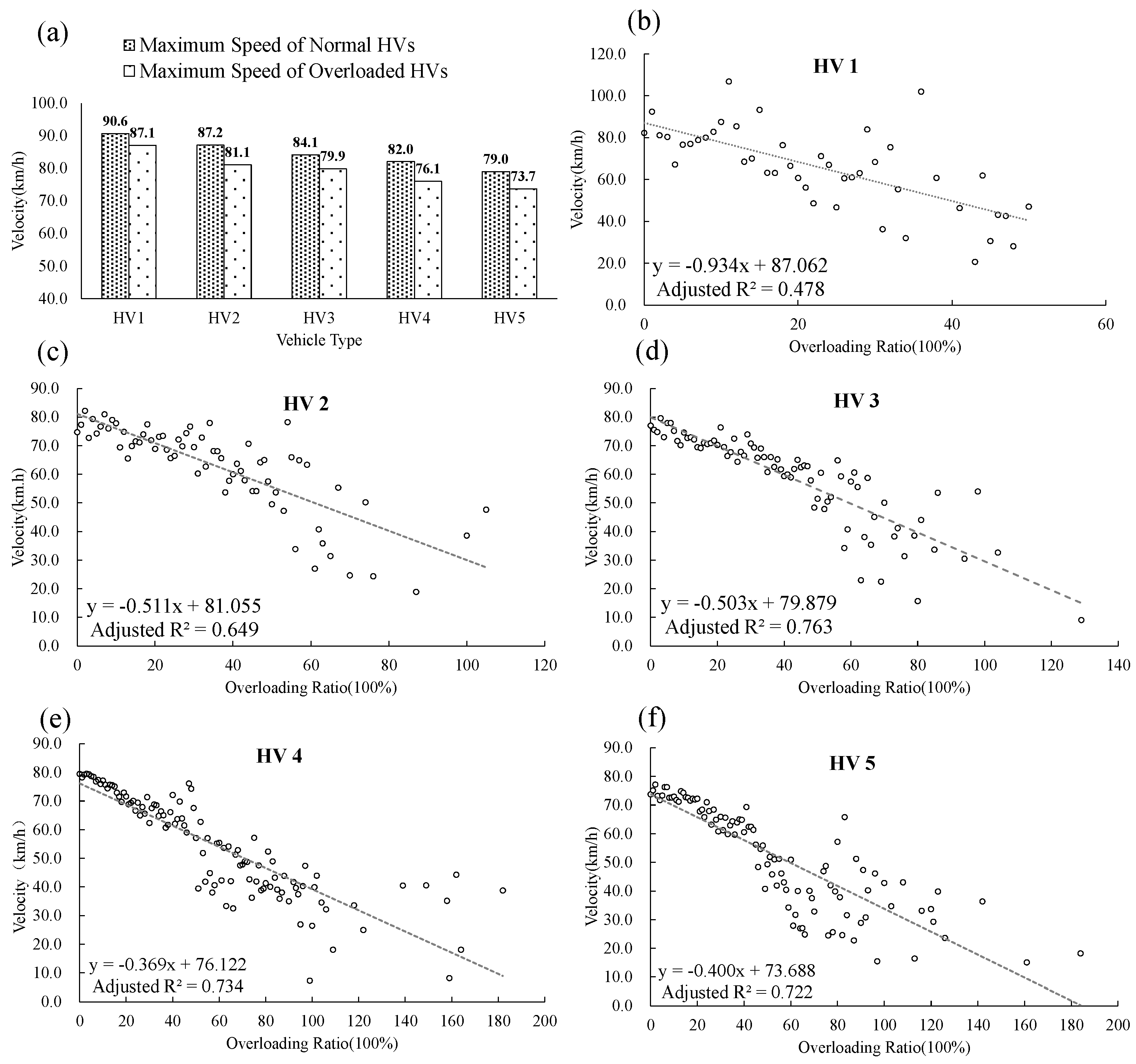
| Type ID | Classification Criteria PC: Vehicle Capacity HV: Total Weight Limit | Vehicle Length (m) | Traffic Volume Proportion in Jiangsu Province (%) | 90% Percentile Highest Travel Speed (km/h) |
|---|---|---|---|---|
| PC1 | ≤7 seats | 3.5–6 | 68.6 | 117.5 |
| PC2 | 8–9 seats | 6–9 | 2.0 | 100.9 |
| PC3 | 20–29 seats | 9–12 | 0.9 | 95.4 |
| PC4 | ≥40 seats | 12–13.7 | 1.3 | 93.8 |
| HV1 | ≤2 t | 3.5–4.5 | 6.2 | 90.6 |
| HV2 | 2–5 t (inclusive of 5 t) | 4.5–6 | 9.1 | 87.2 |
| HV3 | 5–10 t (inclusive of 10 t) | 6–8 | 4.1 | 84.1 |
| HV4 | 10–15 t (inclusive of 15 t) | 8–12 | 4.5 | 82.0 |
| HV5 | >15 t | 12–16.5 | 3.3 | 79.0 |
| Vehicle Type | Coefficients | t Stat | P-Value | Lower 95% | Upper 95% | Adjusted R2 | F-Statistic | Significance F | Observations | |
|---|---|---|---|---|---|---|---|---|---|---|
| HV1 | Constant | 87.062 | 21.592 | 1.053 × 10−24 | 78.930 | 95.194 | 0.478 | 39.440 | 1.430 × 10−07 | 45 |
| −0.934 | −6.280 | 1.430 × 1−07 | −1.235 | −0.634 | ||||||
| HV2 | Constant | 81.055 | 40.852 | 4.419 × 10−49 | 77.095 | 85.016 | 0.649 | 123.983 | 6.885 × 10−17 | 69 |
| −0.511 | −11.135 | 6.885 × 10−17 | −0.602 | −0.419 | ||||||
| HV3 | Constant | 79.879 | 50.288 | 9.353 × 10−62 | 76.717 | 83.040 | 0.763 | 254.289 | 2.059 × 10−26 | 81 |
| −0.503 | −15.946 | 2.059 × 10−26 | −0.566 | −0.440 | ||||||
| HV4 | Constant | 76.122 | 50.173 | 1.239 × 10−77 | 73.115 | 79.129 | 0.734 | 303.644 | 2.033 × 10−33 | 112 |
| −0.369 | −17.425 | 2.033 × 10−33 | −0.411 | −0.327 | ||||||
| HV5 | Constant | 73.688 | 44.483 | 2.998 × 10−67 | 70.401 | 76.975 | 0.722 | 257.511 | 2.681 × 10−29 | 101 |
| −0.400 | −16.047 | 2.681 × 10−29 | −0.449 | −0.350 | ||||||
| Principles | Requirements |
|---|---|
| P1. Multi-class traffic flow is a continuous flow. | R1. Given the density of each vehicle type, the class-specific speeds and flows are defined uniquely. |
| P2. Vehicles are conserved between adjacent segments, and they can only enter or exit through the freeway toll station. | R2. The model has a unique solution on the maximum flow (i.e., capacity). |
| P3. Traffic flow is a single-pipe flow, and the lane number only affects the segment capacity. | R3. In free flow, the speeds of each vehicle type can be different and are allowed to be constant or decrease with increasing density. |
| P4. Traffic flow is always in two regimes: free flow or congestion. | R4. In congestion, the speeds of each vehicle type have to decrease monotonously with density, and the speeds should be equal due to car-following driving behavior. |
| P5. Traffic is always in the equilibrium state. | R5. If the density reaches a certain threshold, the speeds of each vehicle type are all zero. |
| P6. Traffic consists of homogeneous groups of vehicles and drivers. | R6. If the density is zero, the speeds of each vehicle type are the class-specific free flow speed. |
| Parameters | Unit | Definition | PC1 | HV1 | HV2 | HV3 | HV4 | HV5 |
|---|---|---|---|---|---|---|---|---|
| m | the vehicle length of type u | 5 | 4 | 5 | 7 | 12 | 13 | |
| km/h | the maximum speed of type u | 117.5 | 90.6 | 87.2 | 84.1 | 82.0 | 79.0 | |
| km/h | the maximum speed of overloaded type u | 87.1 | 81.1 | 79.9 | 76.1 | 73.7 | ||
| s | the minimum safe headway of type u | 1 | 1 | 1.5 | 2 | 2.5 | 2.5 | |
| pce/h/ln | the capacity of single lane | 2200 | ||||||
| km/h | the critical speed | 60 | ||||||
| pce/m/ln | the critical density | 0.037 | ||||||
| pce/m/ln | the jam density | 0.2 | ||||||
| α | unit | adjustment ratio of proportion | 0.93 | |||||
| Test Date | Mean Square Error | F | P-Value | Fcrit |
|---|---|---|---|---|
| 1 July | 26.841 | 10.370 | 0.002 | 4.020 |
| 2 July | 45.108 | 6.096 | 0.017 | 4.020 |
| 4 July | 43.507 | 11.180 | 0.002 | 4.020 |
| 27 July | 37.815 | 7.874 | 0.007 | 4.020 |
| Date | Average Volume (Vehicle/h) | Overloading Proportion of HVs (%) | MAPE | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| PC1 | HV1 | HV2 | HV3 | HV4 | HV5 | No Overloaded HVs | Overloaded HVs | MAPE Reduction | ||
| 1 July | 883 | 47 | 70 | 48 | 28 | 48 | 16.2% | 3.78% | 2.08% | 45.0% |
| 2 July | 1083 | 114 | 199 | 81 | 47 | 101 | 13.9% | 3.66% | 2.50% | 31.7% |
| 4 July | 1195 | 118 | 186 | 113 | 71 | 114 | 17.3% | 3.34% | 1.72% | 48.5% |
| 27 July | 1251 | 119 | 205 | 118 | 55 | 160 | 15.8% | 3.58% | 2.38% | 33.5% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Zhao, P.; Tao, Y. Evaluating Impacts of Overloaded Heavy Vehicles on Freeway Traffic Condition by a Novel Multi-Class Traffic Flow Model. Sustainability 2018, 10, 4694. https://doi.org/10.3390/su10124694
Wang X, Zhao P, Tao Y. Evaluating Impacts of Overloaded Heavy Vehicles on Freeway Traffic Condition by a Novel Multi-Class Traffic Flow Model. Sustainability. 2018; 10(12):4694. https://doi.org/10.3390/su10124694
Chicago/Turabian StyleWang, Xiang, Po Zhao, and Yanyun Tao. 2018. "Evaluating Impacts of Overloaded Heavy Vehicles on Freeway Traffic Condition by a Novel Multi-Class Traffic Flow Model" Sustainability 10, no. 12: 4694. https://doi.org/10.3390/su10124694
APA StyleWang, X., Zhao, P., & Tao, Y. (2018). Evaluating Impacts of Overloaded Heavy Vehicles on Freeway Traffic Condition by a Novel Multi-Class Traffic Flow Model. Sustainability, 10(12), 4694. https://doi.org/10.3390/su10124694





