Application of Strongly Constrained Space Particle Swarm Optimization to Optimal Operation of a Reservoir System
Abstract
1. Introduction
2. Materials and Methods
2.1. Reservoir Optimization Problem
2.1.1. Function
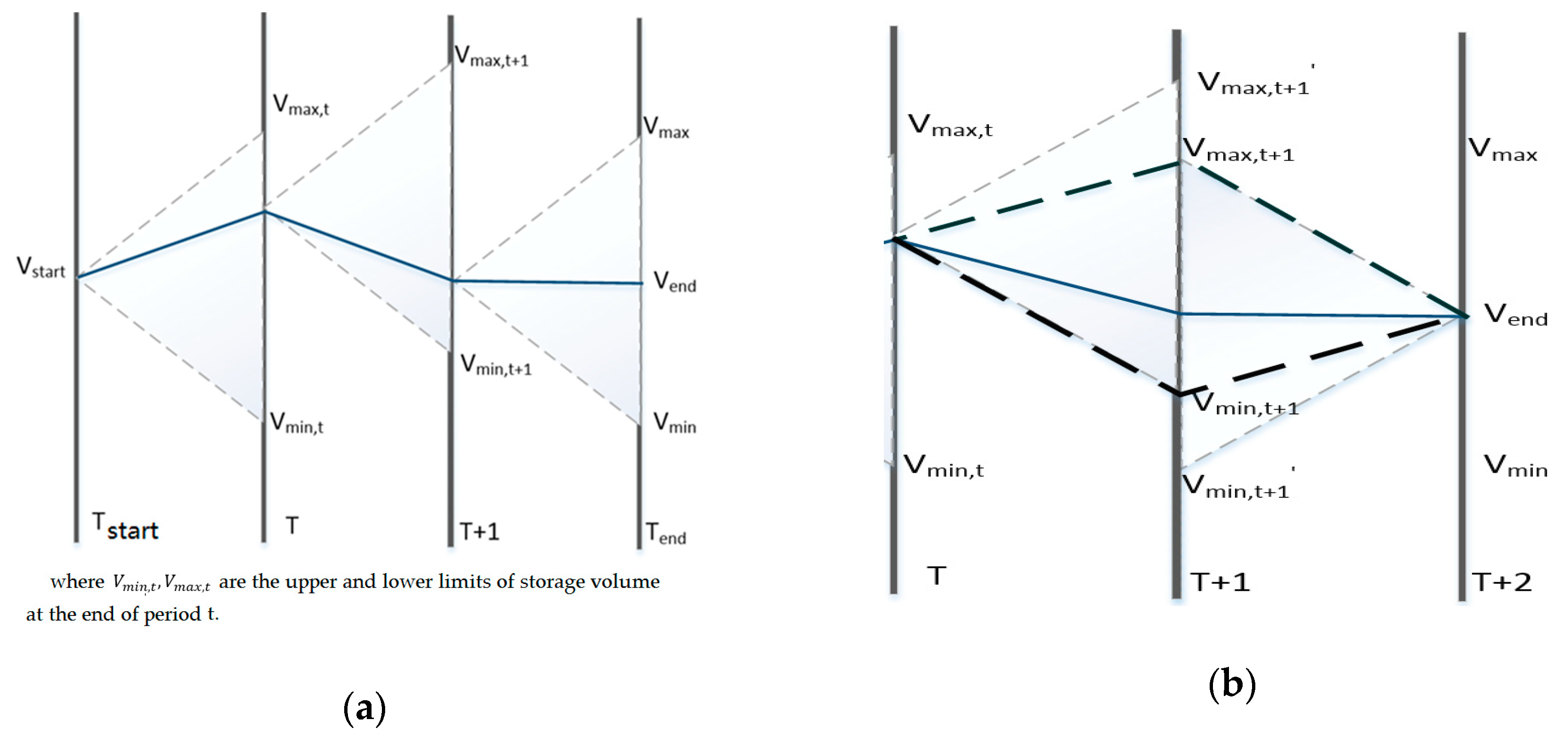
2.1.2. Constraints
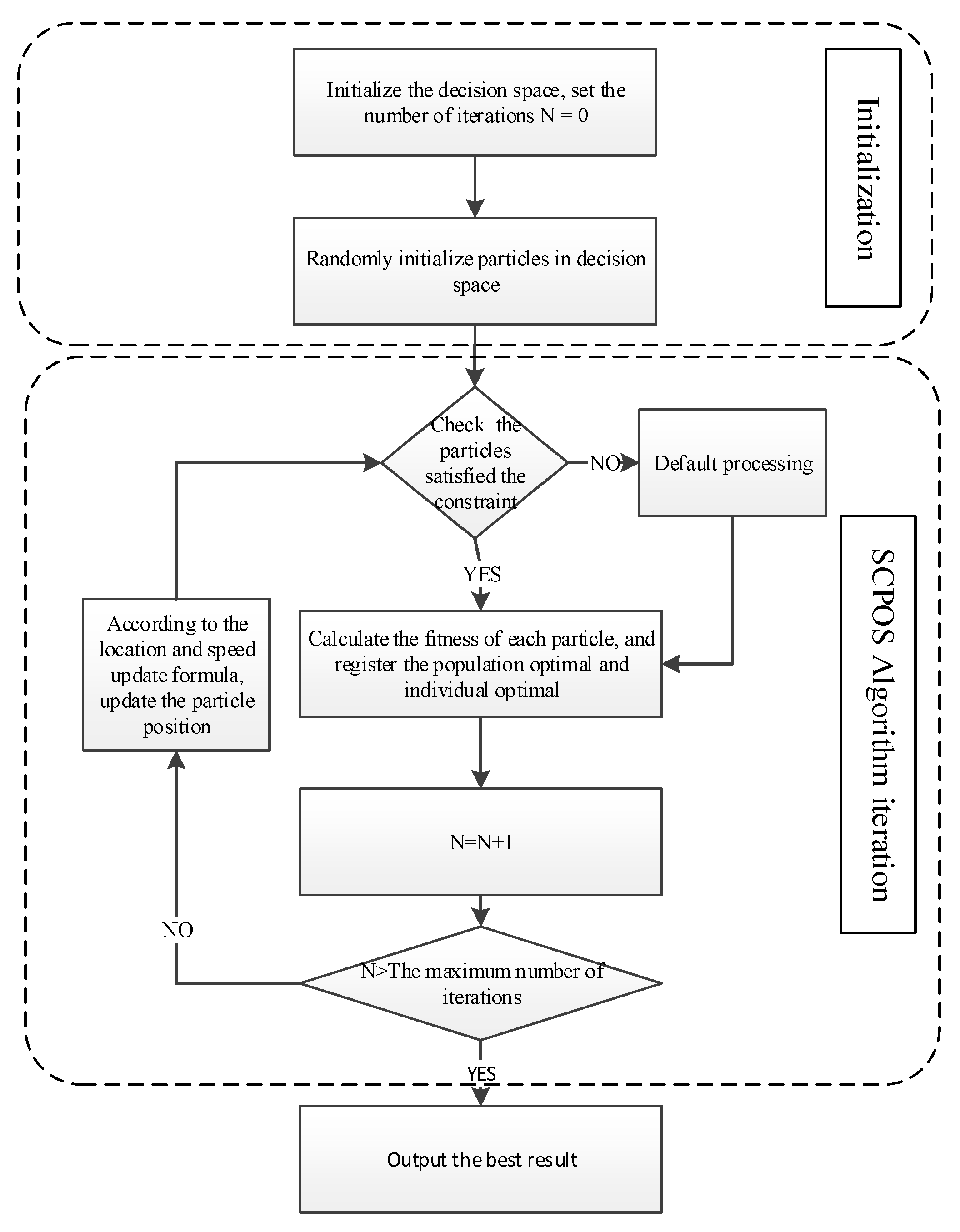
2.2. SCPSO Algorithm
2.2.1. Constraint Processing
2.2.2. Available Options
2.3. Case Study
3. Results
3.1. Benefit Value
3.2. Efficiency of SCPSO
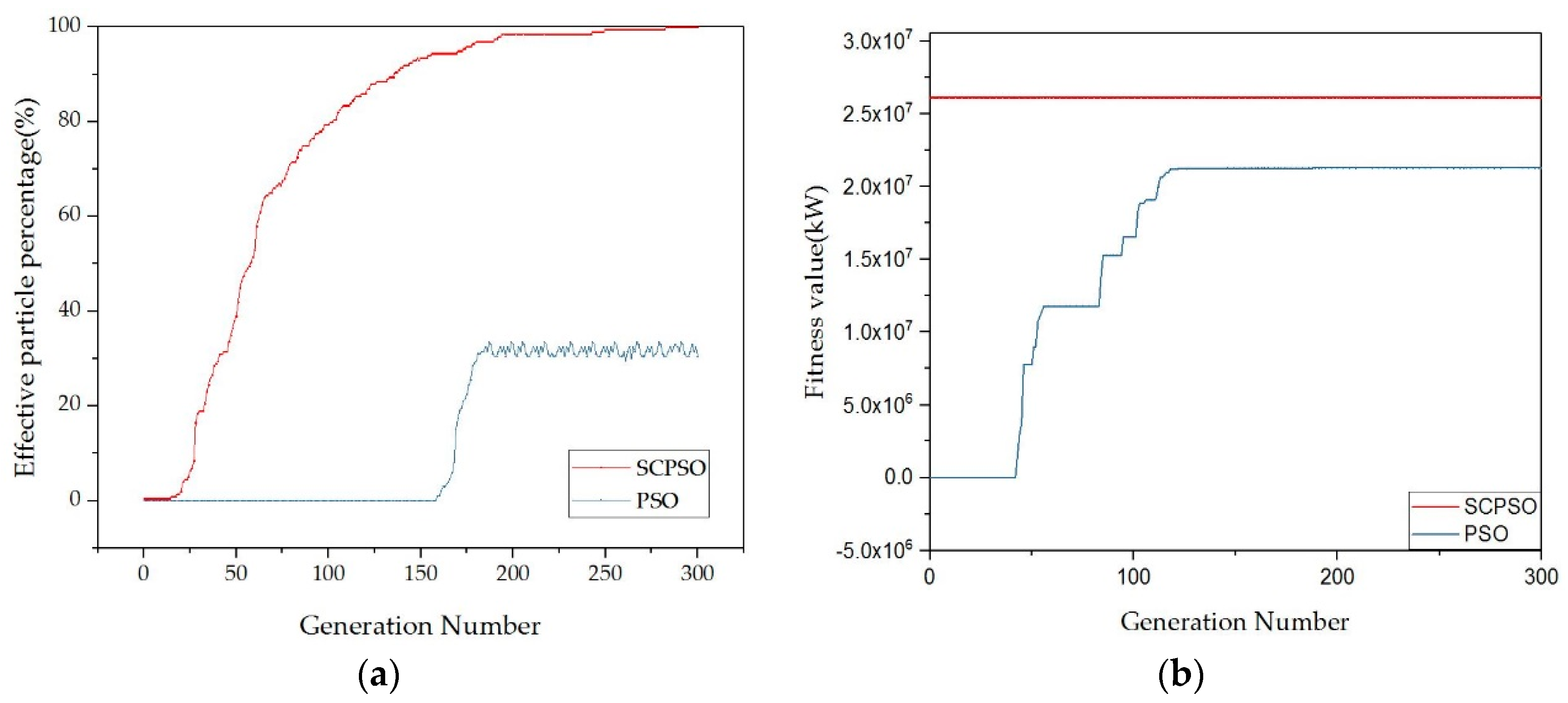
3.2.1. Effective Particles
3.2.2. Effective Particle Number
3.3. Stability of SCPSO
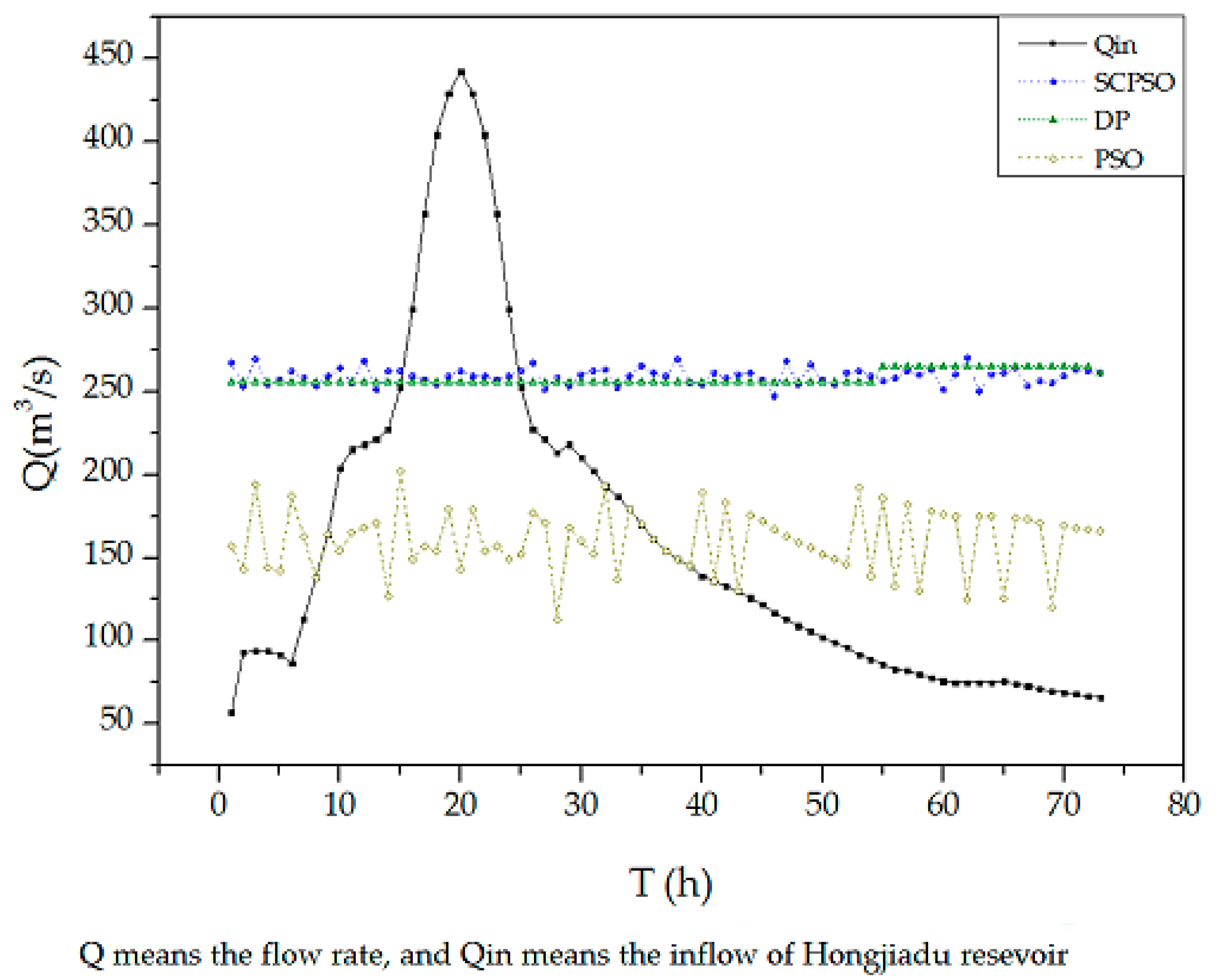
Process of Benefit Value
4. Discussion
4.1. Rationality of the Results
4.2. Effectiveness of the SCPSO Algorithm
4.2.1. Effective Particles
4.2.2. Convergence Speed
4.3. Study Limitations
5. Conclusions
- The SCPSO algorithm has good computational performance, and the results are obviously better than the standard PSO algorithm, which is basically consistent with the result of the DP algorithm.
- The SCPSO algorithm is also highly efficient, and its calculation time is basically the same as that of the standard PSO.
- The SCPSO algorithm has good computational stability; the results of multiple calculations are almost the same.
Funding
References
- AyhanDemirbaş. Global Renewable Energy Resources. Energy Sources 2006, 28, 14. [Google Scholar] [CrossRef]
- Castelletti, A.; Pianosi, F.; Soncini-Sessa, R. Water reservoir control under economic, social and environmental constraints ☆. Automatica 2008, 44, 1595–1607. [Google Scholar] [CrossRef]
- Rajeev, T.; Ashok, S. Dynamic load-shifting program based on a cloud computing framework to support the integration of renewable energy sources. Appl. Energy 2015, 146, 141–149. [Google Scholar] [CrossRef]
- Cheng, C.T.; Wang, W.C.; Xu, D.M.; Chau, K.W. Optimizing Hydropower Reservoir Operation Using Hybrid Genetic Algorithm and Chaos. Water Resour. Manag. 2008, 22, 895–909. [Google Scholar] [CrossRef]
- Asce, J.W.L.M. Optimal operation of multi reservoir systems: State-of the-art review. J. Water Resour. Plan. Manag. 2004, 130, 93–111. [Google Scholar] [CrossRef]
- Zhang, R.; Zhou, J.; Ouyang, S.; Zhang, H. Optimal operation of multi-reservoir system by multi-elite guide particle swarm optimization. Int. J. Electr. Power Energy Syst. 2013, 48, 58–68. [Google Scholar] [CrossRef]
- Cheng, C.T.; Liao, S.L.; Tang, Z.T.; Zhao, M.Y. Comparison of particle swarm optimization and dynamic programming for large scale hydro unit load dispatch. Energy Convers. Manag. 2009, 50, 3007–3014. [Google Scholar] [CrossRef]
- Papageorgiou, M. Optimal Multireservoir Network Control by the Discrete Maximum Principle. Water Resour. Res. 1985, 21, 1824–1830. [Google Scholar] [CrossRef]
- Sheble, G.B. Unit commitment literature synopsis. IEEE Trans. Power Syst. 2002, 9, 128–135. [Google Scholar] [CrossRef]
- Li, B.; He, Y.; Ren, L. Multisource hydrologic modeling uncertainty analysis using the IBUNE framework in a humid catchment. Stoch. Environ. Res. Risk Assess. 2017, 4, 1–14. [Google Scholar] [CrossRef]
- Yeh, W.-G.W. Reservoir Management and Operations Models: A State-of-the-Art Review. Water Resour. Res. 1985, 21, 1797–1818. [Google Scholar] [CrossRef]
- Ma, L.; Zhang, X.; Wang, H.; Qi, C. Characteristics and Practices of Ecological Flow in Rivers with Flow Reductions Due to Water Storage and Hydropower Projects in China. Water 2018, 10, 1091. [Google Scholar] [CrossRef]
- Zargar, M.; Samani, H.M.V.; Haghighi, A. Optimization of gated spillways operation for flood risk management in multi-reservoir systems. Nat. Hazards 2016, 82, 299–320. [Google Scholar] [CrossRef]
- Huang, H.; Yan, Z. Present situation and future prospect of hydropower in China. Renew. Sustain. Energy Rev. 2009, 13, 1652–1656. [Google Scholar] [CrossRef]
- Howson, H.R.; Sancho, N.G.F. A new algorithm for the solution of multi-state dynamic programming problems. Math. Program. 1975, 8, 104–116. [Google Scholar] [CrossRef]
- Dariane, A.B.; Farahmandfar, Z. A comparative study of marriage in honey bees optimisation (MBO) algorithm in multi-reservoir system optimization. Water SA 2013, 39, 327–334. [Google Scholar]
- Ming, B.; Liu, P.; Bai, T.; Feng, M. Improving optimization efficiency for reservoir operation using a search space reduction method. Water Resour. Manag. 2017, 31, 1173–1190. [Google Scholar] [CrossRef]
- Cheng, C.P.; Liu, C.W.; Liu, C.C. Unit commitment by Lagrangian relaxation and genetic algorithms. IEEE Trans. Power Syst. 2000, 15, 707–714. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Afshar, M.H. Large scale reservoir operation by constrained particle swarm optimization algorithms. J. Hydro-Environ. Res. 2012, 6, 75–87. [Google Scholar] [CrossRef]
- Reddy, M.J.; Kumar, D.N. Optimal reservoir operation using multi-objective evolutionary algorithm. Water Resour. Manag. 2006, 20, 861–878. [Google Scholar] [CrossRef]
- Zeng, X.; Hu, T.S.; Guo, X.N.; Li, X. Triggering mechanism for inter-basin water transfer-supply in multi-reservoir system. J. Hydraul. Eng. 2013, 44, 253–261. [Google Scholar]
- Wang, X.; Miao, Y. GAEM: A hybrid algorithm incorporating GA with EM for planted edited motif finding problem. Curr. Bioinform. 2014, 9, 463–469. [Google Scholar] [CrossRef]
- Pérez-Díaz, J.I.; Wilhelmi, J.R.; Arévalo, L.A. Optimal short-term operation schedule of a hydropower plant in a competitive electricity market. Energy Convers. Manag. 2010, 51, 2955–2966. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. IEEE Int. Conf. Neural Netw. 2002, 2, 1942–1948. [Google Scholar] [CrossRef]
- Azaiez, M.N.; Hariga, M.; Al-Harkan, I. A chance-constrained multi-period model for a special multi-reservoir system. Comput. Oper. Res. 2005, 32, 1337–1351. [Google Scholar] [CrossRef]
- Zhang, X.; Yu, X.; Qin, H. Optimal operation of multi-reservoir hydropower systems using enhanced comprehensive learning particle swarm optimization. J. Hydro-Environ. Res. 2016, 10, 50–63. [Google Scholar] [CrossRef]
- Chang, F.J.; Chen, L.; Chang, L.C. Optimizing the reservoir operating rule curves by genetic algorithms. Hydrol. Process. Int. J. 2005, 19, 2277–2289. [Google Scholar] [CrossRef]
- Kennedy, J.; Mendes, R. Population structure and particle swarm performance. In Proceedings of the 2002 Congress on Evolutionary Computation, Honolulu, HI, USA, 12–17 May 2002; Volume 2, pp. 1671–1676. [Google Scholar] [CrossRef]
- Snyder, W.L.; Powell, H.D.; Rayburn, J.C. Dynamic programming approach to unit commitment. IEEE Trans. Power Syst. 1987, 2, 339–348. [Google Scholar] [CrossRef]
- MezuraMontes Efrén Floresmendoza, J.I. Improved Particle Swarm Optimization in Constrained Numerical Search Spaces. In Nature-Inspired Algorithms for Optimisation; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Lakshminarasimman, L.; Subramanian, S. A modified hybrid differential evolution for short-term scheduling of hydrothermal power systems with cascaded reservoirs. Energy Convers. Manag. 2008, 49, 2513–2521. [Google Scholar] [CrossRef]
- Liu, P.; Nguyen, T.D.; Cai, X.; Jiang, X. Finding multiple optimal solutions to optimal load distribution problem in hydropower plant. Energies 2012, 5, 1413–1432. [Google Scholar] [CrossRef]
- Zhao, T.; Zhao, J.; Yang, D. Improved dynamic programming for hydropower reservoir operation. J. Water Resour. Plan. Manag. 2012, 140, 365–374. [Google Scholar] [CrossRef]
- Bai, T.; Wu, L.; Chang, J.; Huang, Q. Multi-objective optimal operation model of cascade reservoirs and its application on water and sediment regulation. Water Resour. Manag. 2015, 29, 2751–2770. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R.C. Fuzzy adaptive particle swarm optimization. In Proceedings of the 2001 Congress on Evolutionary Computation, Seoul, Korea, 27–30 May 2001; Volume 1, pp. 101–106. [Google Scholar] [CrossRef]
- Nabinejad, S.; Mousavi, S.J.; Kim, J.H. Sustainable basin-scale water allocation with hydrologic state-dependent multi-reservoir operation rules. Water Resour. Manag. 2017, 31, 3507–3526. [Google Scholar] [CrossRef]
- Hu, J.; Zeng, X. A hybrid PSO-BP algorithm and its application. In Proceedings of the 2010 Sixth International Conference on Natural Computation, Yantai, China, 10–12 August 2010; Volume 5, pp. 2520–2523. [Google Scholar]
- Afshar, M.H. Extension of the constrained particle swarm optimization algorithm to optimal operation of multi-reservoirs system. Int. J. Electr. Power Energy Syst. 2013, 51, 71–81. [Google Scholar] [CrossRef]
- Liu, P.; Li, L.; Guo, S.; Xiong, L.; Zhang, W.; Zhang, J.; Xu, C. Optimal design of seasonal flood limited water levels and its application for the Three Gorges Reservoir. J. Hydrol. 2015, 527, 1045–1053. [Google Scholar] [CrossRef]
- Guo, S.; Chen, J.; Li, Y.; Liu, P.; Li, T. Joint operation of the multi-reservoir system of the Three Gorges and the Qingjiang cascade reservoirs. Energies 2011, 4, 1036–1050. [Google Scholar] [CrossRef]
- Li, X.; Wei, J.; Li, T.; Li, R. Parallel dynamic programming algorithm for multi-reservoir system optimization. Adv. Water Resour. 2014, 67, 1–15. [Google Scholar] [CrossRef]
- Nie, S.K.; Wang, Y.J.; Xiao, S.; Liu, F. An adaptive chaos particle swarm optimization for tuning parameters of PID controller. Optim. Control. Appl. Methods 2017, 3, 1091–1102. [Google Scholar] [CrossRef]
- Al-Awami, A.T.; Zerguine, A.; Cheded, L.; Zidouri, A.; Saif, W. A new modified particle swarm optimization algorithm for adaptive equalization. Digit. Signal Process. 2011, 21, 195–207. [Google Scholar] [CrossRef]
- Yen, G.G.; Kadkol, A.A. A Culture-Based Particle Swarm Optimization Framework for Dynamic, Constrained Multi-Objective Optimization. Int. J. Swarm Intell. Res. 2012, 3, 1–29. [Google Scholar] [CrossRef]
- Jukna, S. Incremental versus non-incremental dynamic programming. Oper. Res. Lett. 2018, 46, 278–281. [Google Scholar] [CrossRef]
- Jia, C.; Yonggang, W.U.; Binqi, H.U.; Cheng, T. Improved Mathematical Model of Minimum Energy Consumption for Load Distribution of Cascade Hydropower Plants. Autom. Electr. Power Syst. 2017, 41, 155–160. [Google Scholar] [CrossRef]
- Zhong, P. Research and Application of Key Technologies for Real-Time Flood Control in River Basin. Ph.D. Thesis, Hohai University, Nanjing, China, 2006. [Google Scholar]
- Wu, Z.; Zhang, S.; Wang, T. A cooperative particle swarm optimization with constriction factor based on simulated annealing. Computing 2018, 100, 861–880. [Google Scholar] [CrossRef]
- Xu, B.; Zhong, P.A.; Wan, X.; Zhang, W.; Chen, X. Dynamic Feasible Region Genetic Algorithm for Optimal Operation of a Multi-Reservoir System. Energies 2012, 5, 2894–2910. [Google Scholar] [CrossRef]
- Kumar, T.V.V.; Arun, B. Materialized view selection using HBMO. Int. J. Syst. Assur. Eng. Manag. 2017, 8, 1–14. [Google Scholar] [CrossRef]

| Types | Hongjiadu | Unit |
|---|---|---|
| Normal water level | 1140 | m |
| Limit of water level | 1140 | m |
| Lowest water level | 1076 | m |
| Highest water level | 1142.34 | m |
| Output coefficient | 8.5 | |
| Generator assembly capacity | 600 | MW |
| Generator minimum output | 171.5 | MW |
| Minimum discharge | 50 | m3/s |
| Initial water level | 1139 | m |
| Terminal water level | 1139 | m |
| Downstream initial water level | 975 | m |
| Safety relief | 500 | m3/s |
| Storage capacity | 44.97 | 108m3 |
| Minimum storage capacity | 11.36 | 108m3 |
| Adjust ability | Yearly |
| Types | PSO | SCPSO | DP |
|---|---|---|---|
| Acceleration constant (C1) | 2.05 | 2.05 | - |
| Acceleration constant (C2) | 2.05 | 2.05 | - |
| Inertia weight (Wmax) | 0.9 | 0.9 | - |
| Inertia weight (Wmin) | 0.1 | 0.1 | - |
| Constriction factor X | 0.72 | 0.72 | - |
| Maximum particle velocity (Vmax) | 3 | 3 | - |
| Minimum particle velocity (Vmin) | −3 | −3 | - |
| Grid precision | 3000 | 3000 | 500 |
| Particle number | 500 | 500 | - |
| Number of iterations | 300 | 300 | - |
| DP | PSO | SCPSO | |
|---|---|---|---|
| Benefit Value | 26,095,710 | 21,264,810 | 26,106,335 |
| Times | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Average |
|---|---|---|---|---|---|---|---|---|---|---|---|
| DP | 76 | 75 | 75 | 74 | 76 | 75 | 75 | 76 | 76 | 75 | 75.3 |
| PSO | 18 | 17 | 17 | 18 | 17 | 17 | 18 | 17 | 18 | 18 | 17.5 |
| SCPSO | 26 | 23 | 28 | 25 | 32 | 24 | 25 | 26 | 24 | 25 | 25.8 |
| Particle Number | SCPSO | PSO | ||
|---|---|---|---|---|
| Output (kW) | Time (s) | Output (kW) | Time (s) | |
| 50 | 26,106,192 | 5 | 0 | 3 |
| 100 | 26,106,255 | 12 | 500,000 | 13 |
| 150 | 26,106,294 | 18 | 2,000,000 | 16 |
| 200 | 26,106,324 | 22 | 3,400,000 | 18 |
| 250 | 26,106,344 | 26 | 15,264,810 | 24 |
| 300 | 26,106,363 | 29 | 20,264,810 | 28 |
| 350 | 26,106,380 | 32 | 21,264,810 | 34 |
| 400 | 26,106,343 | 38 | 21,264,810 | 36 |
| 450 | 26,106,423 | 49 | 21,264,810 | 43 |
| 500 | 26,106,632 | 76 | 21,264,810 | 73 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Average | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| SCPSO | 26,106,760 | 26,106,755 | 26,106,794 | 26,106,724 | 26,106,784 | 26,106,713 | 26,106,730 | 26,106,743 | 26,106,723 | 26,106,762 | 26,106,749 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, L.; Wang, H.; Lu, B.; Qi, C. Application of Strongly Constrained Space Particle Swarm Optimization to Optimal Operation of a Reservoir System. Sustainability 2018, 10, 4445. https://doi.org/10.3390/su10124445
Ma L, Wang H, Lu B, Qi C. Application of Strongly Constrained Space Particle Swarm Optimization to Optimal Operation of a Reservoir System. Sustainability. 2018; 10(12):4445. https://doi.org/10.3390/su10124445
Chicago/Turabian StyleMa, Lejun, Huan Wang, Baohong Lu, and Changjun Qi. 2018. "Application of Strongly Constrained Space Particle Swarm Optimization to Optimal Operation of a Reservoir System" Sustainability 10, no. 12: 4445. https://doi.org/10.3390/su10124445
APA StyleMa, L., Wang, H., Lu, B., & Qi, C. (2018). Application of Strongly Constrained Space Particle Swarm Optimization to Optimal Operation of a Reservoir System. Sustainability, 10(12), 4445. https://doi.org/10.3390/su10124445





