Characterizing Livestock Production in Portuguese Sown Rainfed Grasslands: Applying the Inverse Approach to a Process-Based Model
Abstract
1. Introduction
2. Materials and Methods
2.1. Estimation of Plant and Livestock Parameters for the Pasture Systems
2.1.1. Data Characterization
2.1.2. Model Inputs Calculation
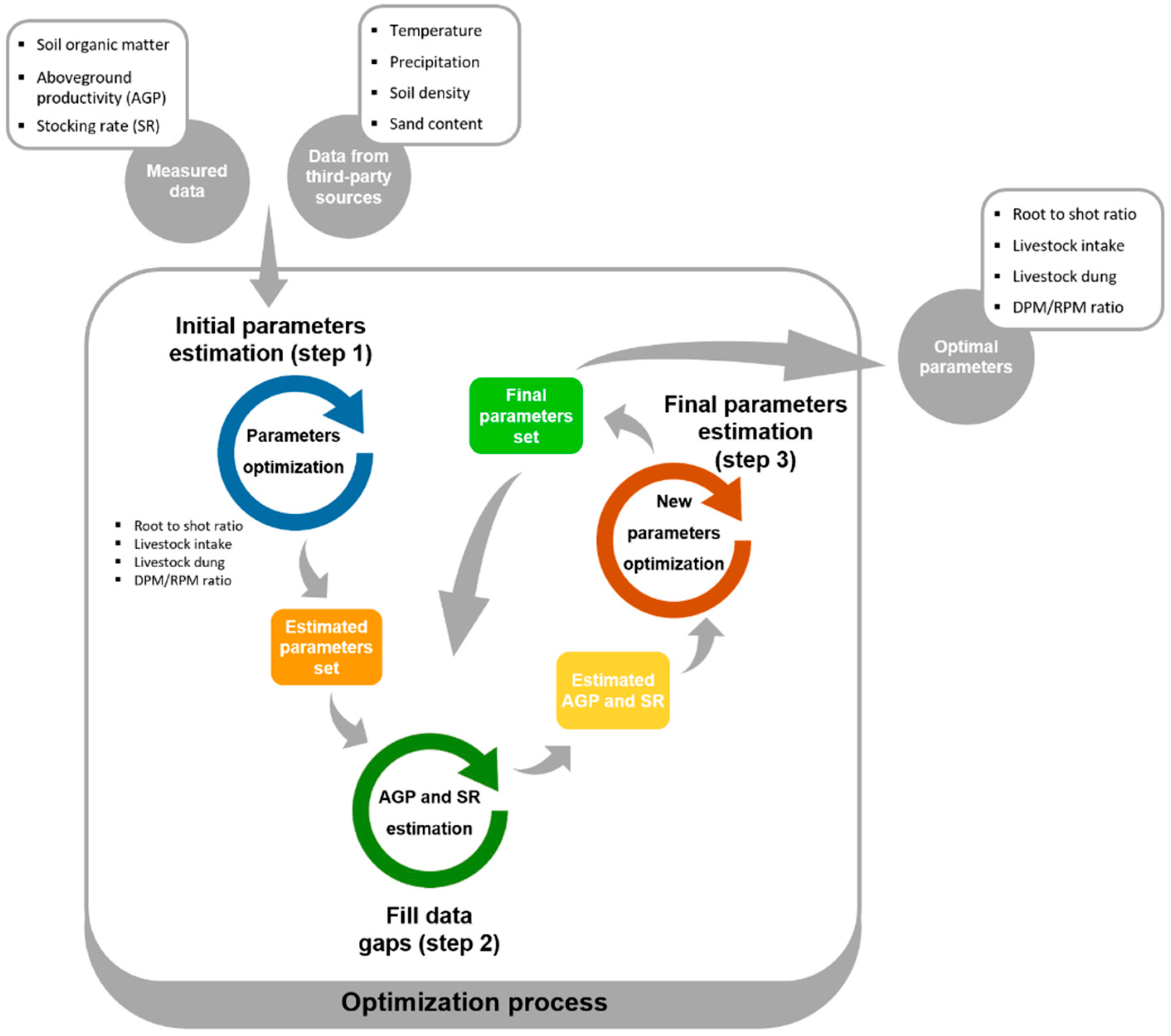
2.1.3. Optimization Procedure
- (1)
- Estimate parameters using only data points without missing data, i.e., estimate RS, LI, LD and DPM/RPM for the AGRO 87 and 71 farms and years without data gaps, i.e., where AGP, SR and SOM were all measured.
- (2)
- Use the SOM data and parameters obtained to estimate the required AGP and SR for the SOM increments in the remaining farms and years where AGP and SR from AGRO 87 and 71 data were missing.
- (3)
- Estimate RS, LI, LD and DPM/RPM ratio using the complete data set (i.e., using field-measured AGP and SR used in the first step and AGP and SR estimated in the second step). With the new set of parameters, we estimated AGP and SR again.
2.2. Estimation of Aboveground Productivity and Stocking Rate for an Additional SOM Data Set
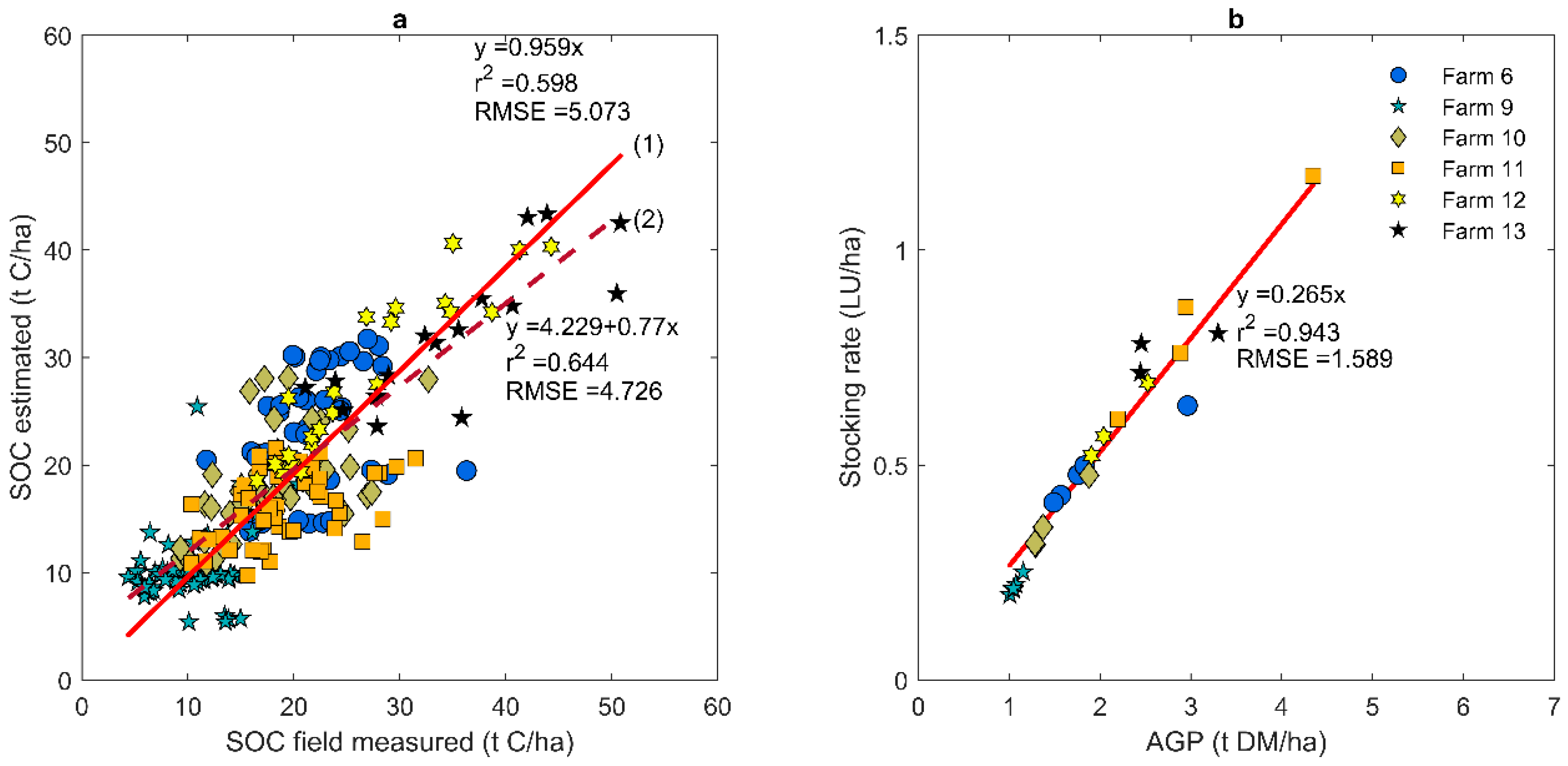
3. Results and Discussion
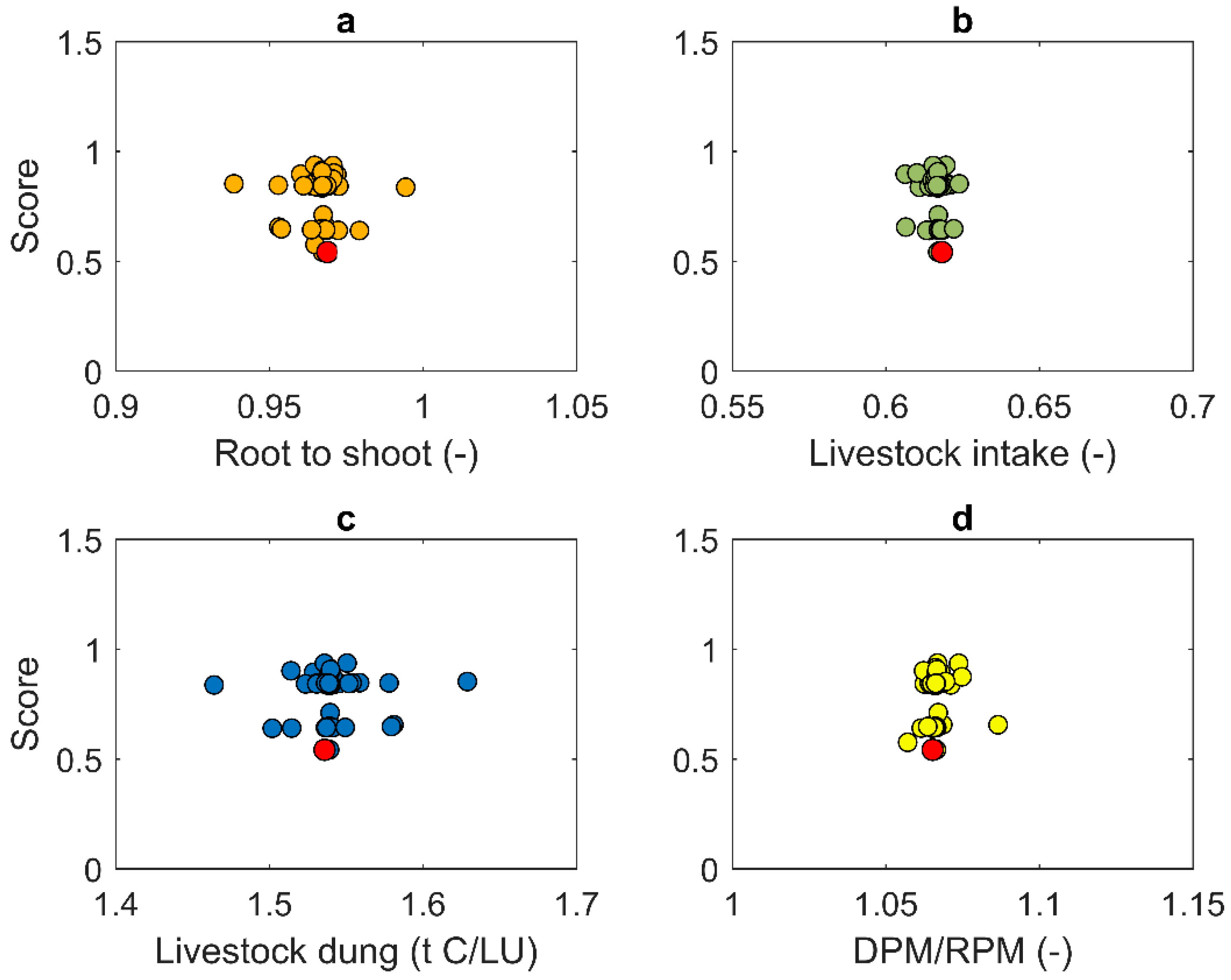
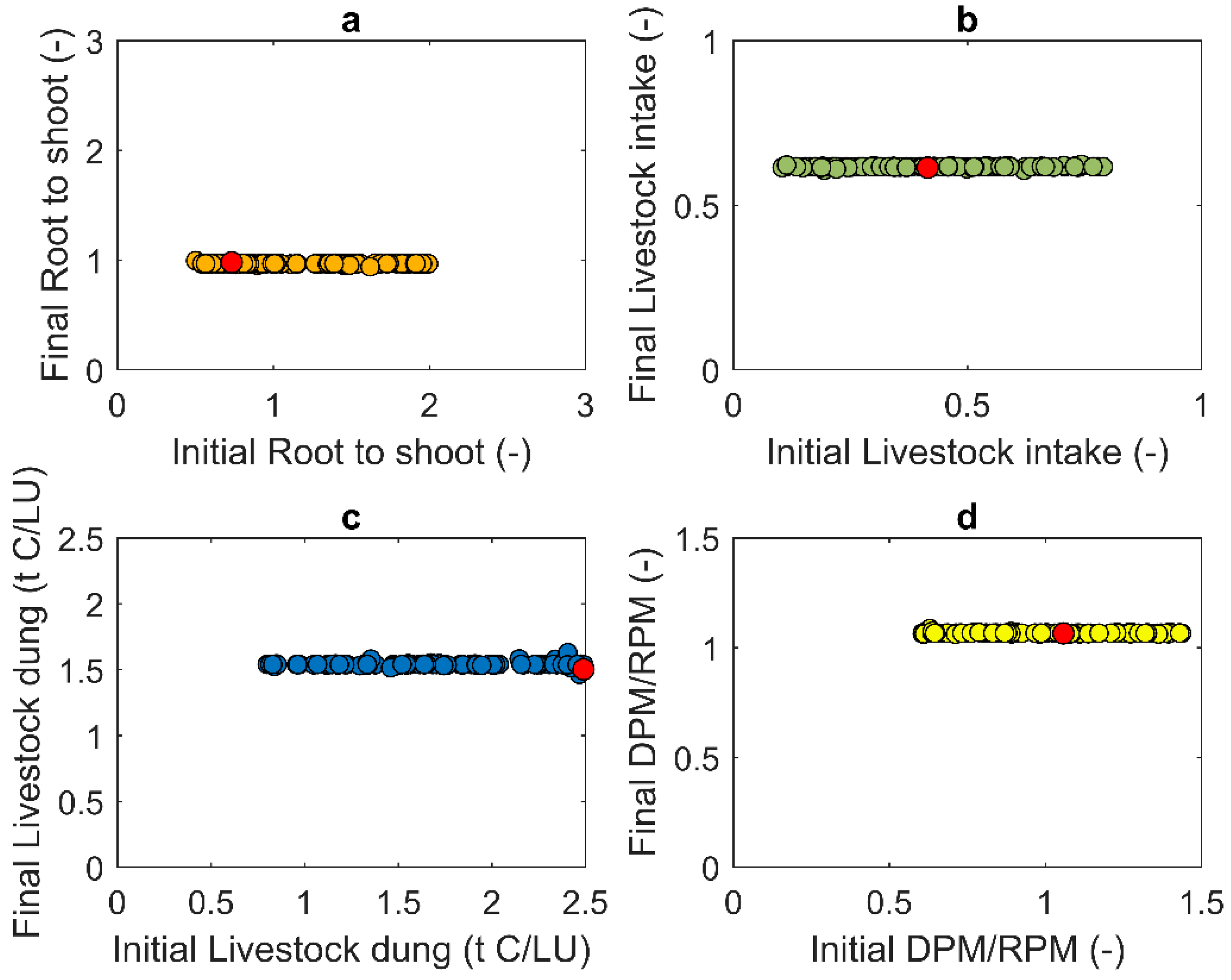
3.1. Estimation of Production Parameters for the Pasture Systems
3.2. Estimating AGP and SR for an Unrelated SOC Database
3.3. Main Limitations and Future Perspectives
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AGP | Aboveground productivity |
| BGP | Belowground productivity |
| C | Carbon |
| CF | Carbon fraction of the legumes and grasses |
| DM | Dry matter |
| DPM | Easily decomposable plant material |
| EDP | Energias de Portugal |
| GPCP | Global Precipitation Climatology Project |
| Ianimal | Carbon inputs from animal dung |
| Iplant | Carbon inputs from plant residue |
| IPCC | Intergovernmental Panel on Climate Change |
| LD | Livestock dung |
| LI | Livestock intake |
| LP DAAC | Land Processes Distributed Active Archive Center |
| LU | Livestock unit |
| N | Nitrogen |
| NLP | Nonlinear programming |
| PCF | Portuguese Carbon Fund |
| RothC | Rothamsted Carbon Model |
| RPM | Resistant plant material |
| RS | Root to shoot |
| SBP | Sown biodiverse permanent pastures rich in legumes |
| SOC | Soil organic carbon |
| SOM | Soil organic matter |
| SR | Stocking rate |
References
- Sloat, L.L.; Gerber, J.S.; Samberg, L.H.; Smith, W.K.; Herrero, M.; Ferreira, L.G.; Godde, C.M.; West, P.C. Increasing importance of precipitation variability on global livestock grazing lands. Nat. Clim. Chang. 2018, 8, 214–218. [Google Scholar] [CrossRef]
- Soliveres, S.; van der Plas, F.; Manning, P.; Prati, D.; Gossner, M.M.; Renner, S.C.; Alt, F.; Arndt, H.; Baumgartner, V.; Binkenstein, J.; et al. Biodiversity at multiple trophic levels is needed for ecosystem multifunctionality. Nature 2016, 536, 456–459. [Google Scholar] [CrossRef] [PubMed]
- Hector, A.; Bagchi, R. Biodiversity and ecosystem multifunctionality. Nature 2007, 448, 188–190. [Google Scholar] [CrossRef] [PubMed]
- Pereira, H.M.; Domingos, T.; Marta-Pedroso, C.; Proença, V.; Rodrigues, P.; Ferreira, M.; Teixeira, R.; Mota, R.; Nogal, A. Uma avaliação dos serviços dos ecossistemas em Portugal. In Ecossistemas e Bem-Estar Humano Avaliação para Portugal do Millennium Ecosystem Assessment; Escolar Editora: Lisboa, Portugal, 2009; pp. 687–716. [Google Scholar]
- Lal, R. Soil carbon sequestration impacts on global climate change and food security. Science 2004, 304. [Google Scholar] [CrossRef] [PubMed]
- Soussana, J.F.; Tallec, T.; Blanfort, V. Mitigating the greenhouse gas balance of ruminant production systems through carbon sequestration in grasslands. Animal 2010, 4, 334–350. [Google Scholar] [CrossRef] [PubMed]
- Teixeira, R.F.M. The cost-effectiveness of optimizing concentrated feed blends to decrease greenhouse gas emissions. Environ. Eng. Manag. J. 2018, 17, 999–1007. [Google Scholar] [CrossRef]
- Van Oijen, M.; Bellocchi, G.; Höglind, M. Effects of Climate Change on Grassland Biodiversity and Productivity: The Need for a Diversity of Models. Agronomy 2018, 8, 14. [Google Scholar] [CrossRef]
- Lal, R.; Negassa, W.; Lorenz, K. Carbon sequestration in soil. Curr. Opin. Environ. Sustain. 2015, 15, 79–86. [Google Scholar] [CrossRef]
- Peri, P.; Rosas, Y.; Ladd, B.; Toledo, S.; Lasagno, R.; Martínez Pastur, G. Modelling Soil Carbon Content in South Patagonia and Evaluating Changes According to Climate, Vegetation, Desertification and Grazing. Sustainability 2018, 10, 438. [Google Scholar] [CrossRef]
- Álvaro-Fuentes, J.; López, M.V.; Arrúe, J.L.; Moret, D.; Paustian, K. Tillage and cropping effects on soil organic carbon in Mediterranean semiarid agroecosystems: Testing the Century model. Agric. Ecosyst. Environ. 2009, 134, 211–217. [Google Scholar] [CrossRef]
- Kong, A.Y.Y.; Six, J.; Bryant, D.C.; Denison, R.F.; van Kessel, C. The Relationship between Carbon Input, Aggregation, and Soil Organic Carbon Stabilization in Sustainable Cropping Systems. Soil Sci. Soc. Am. J. 2005, 69, 1078. [Google Scholar] [CrossRef]
- Mokany, K.; Raison, R.J.; Prokushkin, A.S. Critical analysis of root: Shoot ratios in terrestrial biomes. Glob. Chang. Biol. 2006, 12, 84–96. [Google Scholar] [CrossRef]
- IPCC. 2006 IPCC Guidelines for National Greenhouse Gas Inventories. Institute for Global Environmental Strategies (IGES) for the Intergovernmental Panel on Climate Change; The Intergovernmental Panel on Climate Change (IPCC): Kanagawa, Japan, 2006. [Google Scholar]
- Chapman, D.F.; Parsons, A.J.; Cosgrove, G.P.; Barker, D.J.; Marotti, D.M.; Venning, K.J.; Rutter, S.M.; Hill, J.; Thompson, A.N. Impacts of Spatial Patterns in Pasture on Animal Grazing Behavior, Intake, and Performance. Crop Sci. 2007, 47, 399. [Google Scholar] [CrossRef]
- Lüscher, A.; Mueller-Harvey, I.; Soussana, J.F.; Rees, R.M.; Peyraud, J.L. Potential of legume-based grassland-livestock systems in Europe: A review. Grass Forage Sci. 2014, 69, 206–228. [Google Scholar] [CrossRef] [PubMed]
- Roughley, R.J.; Dart, P.J. Growth of Trifolium subterraneum L. Selected for Sparse and Abundant Nodulation as Affected by Root Temperature and Rhizobium Strain. J. Exp. Bot. 1970, 21, 776–786. [Google Scholar] [CrossRef]
- Smit, H.J.; Metzger, M.J.; Ewert, F. Spatial distribution of grassland productivity and land use in Europe. Agric. Syst. 2008, 98, 208–219. [Google Scholar] [CrossRef]
- Teixeira, R.F.M.; Domingos, T.; Canaveira, P.; Avelar, T.; Basch, G.; Belo, C.C.; Calouro, F.; Crespo, D.; Ferreira, V.G.; Martins, C. Carbon sequestration in biodiverse sown grasslands. Options Méditerranéennes Sustainable Mediterranean Grasslands and Their Multi-Functions 2008, A, 123–126. [Google Scholar]
- Valada, T.; Teixeira, R.; Martins, H.; Ribeiro, M.; Domingos, T. Grassland management options under Kyoto Protocol Article 3.4. Options Méditerranéennes Sustainable Mediterranean Grasslands and Their Multi-Functions 2012, A, 53–56. [Google Scholar]
- Teixeira, R.F.M. Sustainable Land Uses and Carbon Sequestration: The Case of Sown Biodiverse Permanent Pastures Rich in Legumes. Ph.D. Thesis, Instituto Superior Técnico, Lisbon, Portugal, 2010. [Google Scholar]
- Teixeira, R.F.M.; Domingos, T.; Costa, A.P.S.V.; Oliveira, R.; Farropas, L.; Calouro, F.; Barradas, A.M.; Carneiro, J.P.B.G. Soil organic matter dynamics in Portuguese natural and sown rainfed grasslands. Ecol. Model. 2011, 222, 993–1001. [Google Scholar] [CrossRef]
- Teixeira, R.F.M.; Proença, V.; Crespo, D.; Valada, T.; Domingos, T. A conceptual framework for the analysis of engineered biodiverse pastures. Ecol. Eng. 2015, 77, 85–97. [Google Scholar] [CrossRef]
- Morais, T.G.; Teixeira, R.F.M.; Domingos, T. The Effects on Greenhouse Gas Emissions of Ecological Intensification of Meat Production with Rainfed Sown Biodiverse Pastures. Sustainability 2018, 10, 4184. [Google Scholar] [CrossRef]
- Martins, H.; Canaveira, P.; Valada, T.; Alves, M.; Rodrigues, N.; Domingos, T. Relatório Final de Implementação do Contrato de Sequestro de Carbono Celebrado entre EDP e Terraprima 2015; Terraprima—Serviços Ambientais, Sociedade Unipessoal: Lda, Lisbon, Portugal, 2015. [Google Scholar]
- Poeplau, C. Estimating root: Shoot ratio and soil carbon inputs in temperate grasslands with the RothC model. Plant Soil 2016, 407, 293–305. [Google Scholar] [CrossRef]
- Cuddington, K.; Fortin, M.-J.; Gerber, L.R.; Hastings, A.; Liebhold, A.; O’Connor, M.; Ray, C. Process-based models are required to manage ecological systems in a changing world. Ecosphere 2013, 4, art20. [Google Scholar] [CrossRef]
- Monforti, F.; Lugato, E.; Motola, V.; Bodis, K.; Scarlat, N.; Dallemand, J.-F. Optimal energy use of agricultural crop residues preserving soil organic carbon stocks in Europe. Renew. Sustain. Energy Rev. 2015, 44, 519–529. [Google Scholar] [CrossRef]
- Coleman, K.; Jenkinson, D. RothC, A Model for the Turnover of Carbon in Soil—Model Description and Users Guide; Rothamsted Research: Harpenden Herts, UK, 2014. [Google Scholar]
- Byrne, K.; Kiely, G. Evaluation of Models (PaSim, RothC, CENTURY and DNDC) for Simulation of Grassland Carbon Cycling at Plot, Field and Regional Scale; 2005-FS-32-M1 STRIVE Report; Environmental Protection Agency: Washington, DC, USA, 2005. [Google Scholar]
- Diels, J.; Vanlauwe, B.; Van der Meersch, M.K.; Sanginga, N.; Merckx, R. Long-term soil organic carbon dynamics in a subhumid tropical climate: 13C data in mixed C3/C4 cropping and modeling with ROTHC. Soil Biol. Biochem. 2004, 36, 1739–1750. [Google Scholar] [CrossRef]
- Liu, D.L.; Chan, K.Y.; Conyers, M.K.; Li, G.; Poile, G.J. Simulation of soil organic carbon dynamics under different pasture managements using the RothC carbon model. Geoderma 2011, 165, 69–77. [Google Scholar] [CrossRef]
- Takahashi, S.; Nakagami, K.; Sakanoue, S.; Itano, S.; Kirita, H. Soil organic carbon storage in grazing pasture converted from forest on Andosol soil. Grassl. Sci. 2007, 53, 210–216. [Google Scholar] [CrossRef]
- Hashimoto, S.; Wattenbach, M.; Smith, P. Litter carbon inputs to the mineral soil of Japanese Brown forest soils: Comparing estimates from the RothC model with estimates from MODIS. J. For. Res. 2011, 16, 16–25. [Google Scholar] [CrossRef]
- Coleman, K.; Jenkinson, D.S.; Crocker, G.J.; Grace, P.R.; Klír, J.; Körschens, M.; Poulton, P.R.; Richter, D.D. Simulating trends in soil organic carbon in long-term experiments using RothC-26.3. Geoderma 1997, 81, 29–44. [Google Scholar] [CrossRef]
- Kutsch, W.L.; Bahn, M.; Heinemeyer, A. Soil Carbon Dynamics: An Integrated Methodology; Cambridge University Press: Cambridge, UK, 2009; ISBN 978-0521865616. [Google Scholar]
- Weihermüller, L.; Graf, A.; Herbst, M.; Vereecken, H. Simple pedotransfer functions to initialize reactive carbon pools of the RothC model. Eur. J. Soil Sci. 2013, 64, 567–575. [Google Scholar] [CrossRef]
- Carneiro, J.P.; Freixial, R.C.; Pereira, J.S.; Campos, A.C.; Crespo, J.P.; Carneiro, R. Relatório Final do Projecto AGRO 87 (Final Report of the Agro 87 Project, in Portuguese); Lisbon, Portugal, 2005. [Google Scholar]
- Rubel, F.; Kottek, M. Observed and projected climate shifts 1901–2100 depicted by world maps of the Köppen-Geiger climate classification. Meteorol. Z. 2010, 19, 135–141. [Google Scholar] [CrossRef]
- IPMA Climate Normals. Available online: http://www.ipma.pt/en/index.html (accessed on 18 January 2018).
- Barradas, A.M. Efecto de la Mejora de Pastos Naturales en Cuatro Tipos de Suelos Mediterráneos (Spanish); Universidad de Extremadura: Badajoz, Spain, 2009. [Google Scholar]
- Pribyl, D.W. A critical review of the conventional SOC to SOM conversion factor. Geoderma 2010, 156, 75–83. [Google Scholar] [CrossRef]
- Tóth, G.; Jones, A.; Montanarella, L. The LUCAS topsoil database and derived information on the regional variability of cropland topsoil properties in the European Union. Environ. Monit. Assess. 2013, 185, 7409–7425. [Google Scholar] [CrossRef] [PubMed]
- NASA Global Precipitation Analysis. Available online: http://precip.gsfc.nasa.gov/ (accessed on 20 Mar 2018).
- LP DAAC. MODIS/Terra Land Surface Temperature and Emissivity Monthly L3 Global 0.05Deg CMG. Available online: https://lpdaac.usgs.gov/dataset_discovery/modis/modis_products_table/mod11c3 (accessed on 20 Mar 2018).
- Jebari, A. Estimación de los Cambios en los Stocks de Carbono del Suelo Agrícola a Escala Regional: Impacto de los Usos del Suelo y del Manejo en la Comunidad Autónoma de Aragón. Master Thesis, Bilbao, Spain, 2016. [Google Scholar]
- Morais, T.G.; Silva, C.; Jebari, A.; Álvaro-Fuentes, J.; Domingos, T.; Teixeira, R.F.M. A proposal for using process-based soil models for land use Life cycle impact assessment: Application to Alentejo, Portugal. J. Clean. Prod. 2018, 192, 864–876. [Google Scholar] [CrossRef]
- Thornthwaite, C.W. An Approach toward a Rational Classification of Climate. Geogr. Rev. 1948, 38, 55. [Google Scholar] [CrossRef]
- Spearman, C. The Proof and Measurement of Association between Two Things. Am. J. Psychol. 1904, 72–101. [Google Scholar] [CrossRef]
- APA. Portuguese National Inventory Report on Greenhouse Gases, 1990–2018; Portuguese Environmental Agency: Amadora, Portugal, 2018. [Google Scholar]
- Román, P.; Martínez, M.M.; Pantoja, A. Farmer’s Compost Handbook—Experiences in Latin America; Food and Agriculture Organization: Rome, Italy, 2015. [Google Scholar]
- Gillet, F.; Murisier, B.; Buttler, A.; Gallandat, J.-D.; Gobat, J.-M. Influence of tree cover on the diversity of herbaceous communities in subalpine wooded pastures. Appl. Veg. Sci. 1999, 2, 47–54. [Google Scholar] [CrossRef]
- Belsky, A.J. Influences of Trees on Savanna Productivity: Tests of Shade, Nutrients, and Tree-Grass Competition. Ecology 1994, 75, 922–932. [Google Scholar] [CrossRef]
- Bell, D.T.; Johnson, F.L.; Gilmore, A.R. Dynamics of Litter Fall, Decomposition, and Incorporation in the Streamside Forest Ecosystem. Oikos 1978, 30, 76. [Google Scholar] [CrossRef]
- Parton, W.J.; Schimel, D.S.; Cole, C.V.; Ojima, D.S. Analysis of Factors Controlling Soil Organic Matter Levels in Great Plains Grasslands. Soil Sci. Soc. Am. J. 1987, 51, 1173–1179. [Google Scholar] [CrossRef]
- Garay, A.H.; Sollenberger, L.E.; McDonald, D.C.; Ruegsegger, G.J.; Kalmbacher, R.S.; Mislevy, P. Nitrogen Fertilization and Stocking Rate Affect Stargrass Pasture and Cattle Performance. Crop Sci. 2004, 44, 1348. [Google Scholar] [CrossRef]
- Derner, J.D.; Hart, R.H. Grazing-Induced Modifications to Peak Standing Crop in Northern Mixed-grass Prairie. Rangel. Ecol. Manag. 2007, 60, 270–276. [Google Scholar] [CrossRef]
- Schönbach, P.; Wan, H.; Schiborra, A.; Gierus, M.; Bai, Y.; Müller, K.; Glindemann, T.; Wang, C.; Susenbeth, A.; Taube, F. Short-term management and stocking rate effects of grazing sheep on herbage quality and productivity of Inner Mongolia steppe. Crop Pasture Sci. 2009, 60, 963. [Google Scholar] [CrossRef]
- National Research Council (NRC). Nutrient Requirements of Beef Cattle, 7th ed.; Press, N.A., Ed.; National Research Council: Washington, DC, USA, 2000. [Google Scholar]
- Gadberry, S. Beef Cattle Nutrition Series Part 3: Nutrient Requirement Tables; University of Arkansas Division of Agriculture: Little Rock, AR, USA, 1996. [Google Scholar]
- Matt Hersom Basic Nutrient Requirements of Beef Cows. Available online: http://edis.ifas.ufl.edu/an190 (accessed on 15 November 2018).
- Kirkpatrick, D.E.; Steen, R.W.J.; Unsworth, E.F. The effect of differing forage:concentrate ratio and restricting feed intake on the energy and nitrogen utilization by beef cattle. Livest. Prod. Sci. 1997, 51, 151–164. [Google Scholar] [CrossRef]
- Yan, T.; Agnew, R.; Gordon, F.; Porter, M. Prediction of methane energy output in dairy and beef cattle offered grass silage-based diets. Livest. Prod. Sci. 2000, 64, 253–263. [Google Scholar] [CrossRef]
- Simionesei, L.; Ramos, T.; Oliveira, A.; Jongen, M.; Darouich, H.; Weber, K.; Proença, V.; Domingos, T.; Neves, R. Modeling Soil Water Dynamics and Pasture Growth in the Montado Ecosystem Using MOHID Land. Water 2018, 10, 489. [Google Scholar] [CrossRef]
- Trancoso, A.R.; Braunschweig, F.; Chambel Leitão, P.; Obermann, M.; Neves, R. An advanced modelling tool for simulating complex river systems. Sci. Total Environ. 2009, 407, 3004–3016. [Google Scholar] [CrossRef] [PubMed]
- Catchpole, W.R.; Wheeler, C.J. Estimating plant biomass: A review of techniques. Aust. J. Ecol. 1992, 17, 121–131. [Google Scholar] [CrossRef]
- Sinha, S.; Jeganathan, C.; Sharma, L.K.; Nathawat, M.S. A review of radar remote sensing for biomass estimation. Int. J. Environ. Sci. Technol. 2015, 12, 1779–1792. [Google Scholar] [CrossRef]
- UNFCCC. Measurements for Estimation of Carbon Stocks in Afforestation and Reforestation Project Activities under the Clean Development Mechanism: A Field Manual; United Nations Climate Change Secretariat (UNFCCC): Bonn, Germany, 2015. [Google Scholar]
- Flombaum, P.; Sala, O.E. A non-destructive and rapid method to estimate biomass and aboveground net primary production in arid environments. J. Arid Environ. 2007, 69, 352–358. [Google Scholar] [CrossRef]
- Shoko, C.; Mutanga, O.; Dube, T. Determining Optimal New Generation Satellite Derived Metrics for Accurate C3 and C4 Grass Species Aboveground Biomass Estimation in South Africa. Remote Sens. 2018, 10, 564. [Google Scholar] [CrossRef]
- Purevdorj, T.; Tateishi, R.; Ishiyama, T.; Honda, Y. Relationships between percent vegetation cover and vegetation indices. Int. J. Remote Sens. 1998, 19, 3519–3535. [Google Scholar] [CrossRef]
- Rochon, J.J.; Doyle, C.J.; Greef, J.M.; Hopkins, A.; Molle, G.; Sitzia, M.; Scholefield, D.; Smith, C.J. Grazing legumes in Europe: A review of their status, management, benefits, research needs and future prospects. Grass Forage Sci. 2004, 59, 197–214. [Google Scholar] [CrossRef]
- Davidson, R.L. Effects of Soil Nutrients and Moisture on Root/Shoot Ratios in Lolium perenne L. and Trifolium repens L. Ann. Bot. 1969, 33, 571–577. [Google Scholar] [CrossRef]
- Kiaer, L.P.; Weisbach, A.N.; Weiner, J. Root and shoot competition: A meta-analysis. J. Ecol. 2013, 101, 1298–1312. [Google Scholar] [CrossRef]
- Ledgard, S.F. Nitrogen cycling in low input legume-based agriculture, with emphasis on legume/grass pastures. Plant Soil 2001, 228, 43–59. [Google Scholar] [CrossRef]
- Selbie, D.R.; Buckthought, L.E.; Shepherd, M.A. The Challenge of the Urine Patch for Managing Nitrogen in Grazed Pasture Systems. Adv. Agron. 2015, 129, 229–292. [Google Scholar] [CrossRef]
- Cameron, K.C.; Di, H.J.; Moir, J.L. Nitrogen losses from the soil/plant system: A review. Ann. Appl. Biol. 2013, 162, 145–173. [Google Scholar] [CrossRef]
- Guo, R.; Li, G.; Jiang, T.; Schuchardt, F.; Chen, T.; Zhao, Y.; Shen, Y. Effect of aeration rate, C/N ratio and moisture content on the stability and maturity of compost. Bioresour. Technol. 2012, 112, 171–178. [Google Scholar] [CrossRef] [PubMed]
- Leip, A.; Weiss, F.; Wassenaar, T.; Perez, I.; Fellmann, T.; Loudjani, P.; Tubiello, F.; Grandgirard, D.; Monni, S.; Biala, K. Evaluation of the Livestock Sector’s Contribution to the EU Greenhouse Gas Emissions (GGELS)—Final Report; European Commission, Joint Research Centre: Ispra, Italy, 2010. [Google Scholar]
- Garnett, T. Livestock-related greenhouse gas emissions: Impacts and options for policy makers. Environ. Sci. Policy 2009, 12, 491–503. [Google Scholar] [CrossRef]
- Steinfeld, H.; Gerber, P.; Wassenaar, T.; Castel, V.; Rosales, M.; de Haan, C. Livestock’s Long Shadow: Environmental Issues and Options; Food and Agriculture Organization of the United Nations (FAO): Rome, Italy, 2006. [Google Scholar]
- Shah, G.A.; Groot, J.C.J.; Shah, G.M.; Lantinga, E.A. Simulation of Long-Term Carbon and Nitrogen Dynamics in Grassland-Based Dairy Farming Systems to Evaluate Mitigation Strategies for Nutrient Losses. PLoS ONE 2013, 8, e67279. [Google Scholar] [CrossRef] [PubMed]
- Marschner, P.; Rengel, Z. Nutrient Cycling in Terrestrial Ecosystems; Springer: Berlin, Germany, 2007; ISBN 9783540680277. [Google Scholar]
- Teixeira, R.F.M.; Barão, L.; Morais, T.G.; Domingos, T. “BalSim”: A carbon, nitrogen and greenhouse gas mass balance model for pastures. Sustainability 2018, in press. [Google Scholar]
- Schlapfer, F.; Schmid, B. Ecosystem Effects of Biodiversity: A Classification of Hypotheses and Exploration of Empirical Results. Ecol. Appl. 1999, 9, 1–25. [Google Scholar] [CrossRef]
- Cederberg, C.; Stadig, M. System expansion and allocation in life cycle assessment of milk and beef production. Int. J. Life Cycle Assess. 2003, 8, 350–356. [Google Scholar] [CrossRef]
- Casey, J.W.W.; Holden, N.M.M. Quantification of GHG emissions from sucker-beef production in Ireland. Agric. Syst. 2006, 90, 79–98. [Google Scholar] [CrossRef]
- Ogino, A.; Kaku, K.; Osada, T.; Shimada, K.; Ogino, A.; Kaku, K.; Osada, T.; Shimada, K. Environmental impacts of the Japanese beef-fattening system with different feeding lengths as evaluated by a life-cycle assessment method. J. Anim. Sci. 2004, 82, 2115–2122. [Google Scholar] [CrossRef] [PubMed]
- Morais, T.G.; Teixeira, R.F.M.; Rodrigues, N.R.; Domingos, T. Carbon footprint of milk from pasture-based dairy farms in Azores, Portugal. Sustainability 2018, 10, 3658. [Google Scholar] [CrossRef]
- Van Kernebeek, H.R.J.; Oosting, S.J.; Feskens, E.J.M.; Gerber, P.J.; De Boer, I.J.M. The effect of nutritional quality on comparing environmental impacts of human diets. J. Clean. Prod. 2014, 73, 88–99. [Google Scholar] [CrossRef]
- Tilman, D.; Clark, M. Global diets link environmental sustainability and human health. Nature 2014, 515, 518–522. [Google Scholar] [CrossRef] [PubMed]
- Teixeira, R.F.M.; Domingos, T.; Costa, A.P.S.V.; Oliveira, R.; Farropas, L.; Calouro, F.; Barradas, A.M.; Carneiro, J.P.B.G. The dynamics of soil organic matter accumulation in Portuguese grasslands soils. Options Méditerranéennes Sustainable Mediterranean Grasslands and Their Multi-Functions 2008, A, 41–44. [Google Scholar]
- Teixeira, R.F.M.; Morais, T.G.; Domingos, T. A Practical Comparison of Regionalized Land Use and Biodiversity Life Cycle Impact Assessment Models Using Livestock Production as a Case Study. Sustainability 2018, 10, 4089. [Google Scholar] [CrossRef]
- Witt, G.B.; Noël, M.V.; Bird, M.I.; Beeton, R.J.S.; Menzies, N.W. Carbon sequestration and biodiversity restoration potential of semi-arid mulga lands of Australia interpreted from long-term grazing exclosures. Agric. Ecosyst. Environ. 2011, 141, 108–118. [Google Scholar] [CrossRef]
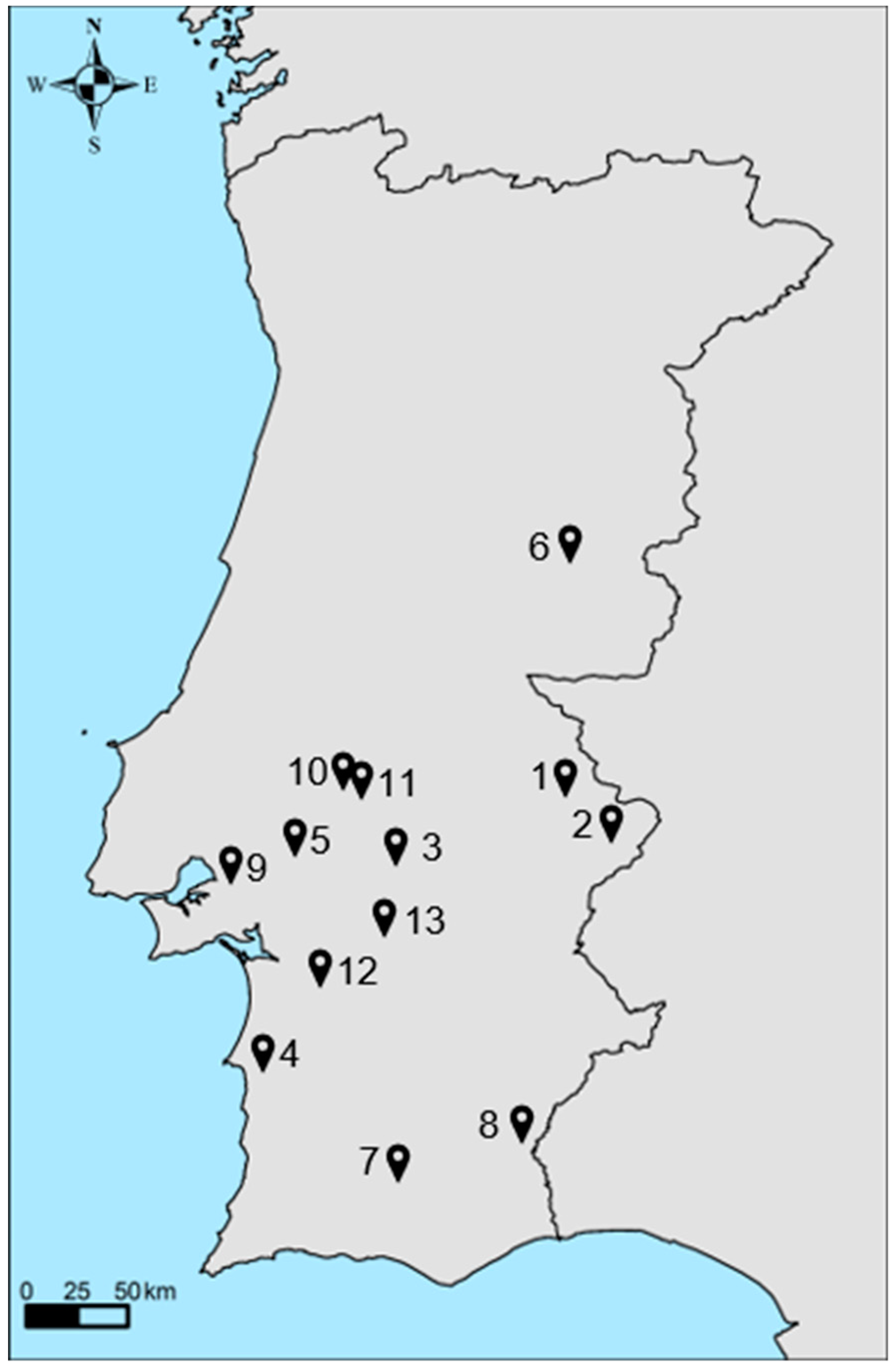

| Farm | Project | Production Years | Measured Data | Mean Annual Temperature (°C) | Mean Annual Precipitation (mm) |
|---|---|---|---|---|---|
| Farm 1 | AGRO 87 | 4 years (2001–2005) |
| 18 | 523 |
| Farm 2 | 20 | 471 | |||
| Farm 3 | 18 | 538 | |||
| Farm 4 | 18 | 494 | |||
| Farm 5 | 19 | 473 | |||
| Farm 6 | AGRO 87 and EDP | 9 years (2001–2005; 2006–2011) |
| 17 | 841 |
| Farm 7 | AGRO 71 | 3 years (2001–2004) |
| 19 | 583 |
| Farm 8 | 21 | 495 | |||
| Farm 9 | EDP | 5 years (2007–2012) | 18 | 899 | |
| Farm 10 | 4 years (2007–2011) | 18 | 593 | ||
| Farm 11 | 19 | 593 | |||
| Farm 12 | 3 years (2008–2011) | 20 | 602 | ||
| Farm 13 | 3 years (2008–2011) | 18 | 596 |
| Farm | Year | Aboveground Productivity (t DM/ha.yr) | Stocking Rate (LU/ha) |
|---|---|---|---|
| Farm 6 | 2006–2007 | 1.6 | 0.43 |
| 2007–2008 | 1.8 | 0.48 | |
| 2008–2009 | 1.5 | 0.41 | |
| 2009–2010 | 1.8 | 0.50 | |
| 2010–2011 | 3.0 | 0.64 | |
| Farm 9 | 2007–2008 | 1.0 | 0.20 |
| 2008–2009 | 1.0 | 0.21 | |
| 2009–2010 | 1.1 | 0.22 | |
| 2010–2011 | 1.0 | 0.21 | |
| 2011–2012 | 1.2 | 0.25 | |
| Farm 10 | 2007–2008 | 1.4 | 0.36 |
| 2008–2009 | 1.3 | 0.31 | |
| 2009–2010 | 1.3 | 0.32 | |
| 2010–2011 | 1.9 | 0.48 | |
| Farm 11 | 2007–2008 | 4.3 | 1.17 |
| 2008–2009 | 2.9 | 0.87 | |
| 2009–2010 | 2.9 | 0.76 | |
| 2010–2011 | 2.2 | 0.61 | |
| Farm 12 | 2008–2009 | 1.9 | 0.52 |
| 2009–2010 | 2.0 | 0.57 | |
| 2010–2011 | 2.5 | 0.69 | |
| Farm 13 | 2008–2009 | 3.3 | 0.81 |
| 2009–2010 | 2.4 | 0.71 | |
| 2010–2011 | 2.5 | 0.78 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morais, T.G.; Teixeira, R.F.M.; Rodrigues, N.R.; Domingos, T. Characterizing Livestock Production in Portuguese Sown Rainfed Grasslands: Applying the Inverse Approach to a Process-Based Model. Sustainability 2018, 10, 4437. https://doi.org/10.3390/su10124437
Morais TG, Teixeira RFM, Rodrigues NR, Domingos T. Characterizing Livestock Production in Portuguese Sown Rainfed Grasslands: Applying the Inverse Approach to a Process-Based Model. Sustainability. 2018; 10(12):4437. https://doi.org/10.3390/su10124437
Chicago/Turabian StyleMorais, Tiago G., Ricardo F. M. Teixeira, Nuno R. Rodrigues, and Tiago Domingos. 2018. "Characterizing Livestock Production in Portuguese Sown Rainfed Grasslands: Applying the Inverse Approach to a Process-Based Model" Sustainability 10, no. 12: 4437. https://doi.org/10.3390/su10124437
APA StyleMorais, T. G., Teixeira, R. F. M., Rodrigues, N. R., & Domingos, T. (2018). Characterizing Livestock Production in Portuguese Sown Rainfed Grasslands: Applying the Inverse Approach to a Process-Based Model. Sustainability, 10(12), 4437. https://doi.org/10.3390/su10124437







