Model of Predicting Cost Overrun in Construction Projects
Abstract
1. Introduction
2. The Concept of a Cost Prediction Model
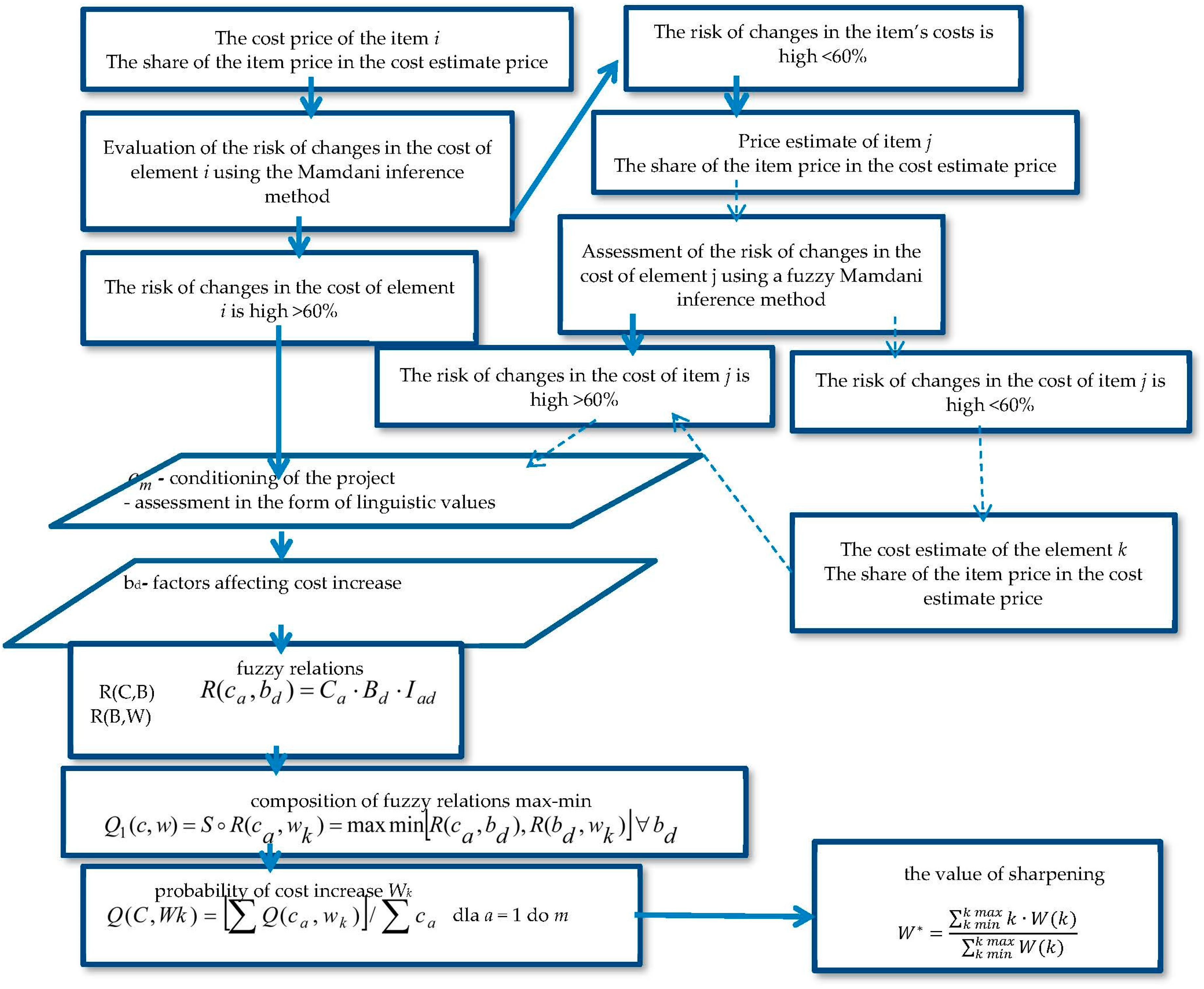
2.1. Scheme of the Cost Increase Prediction Model
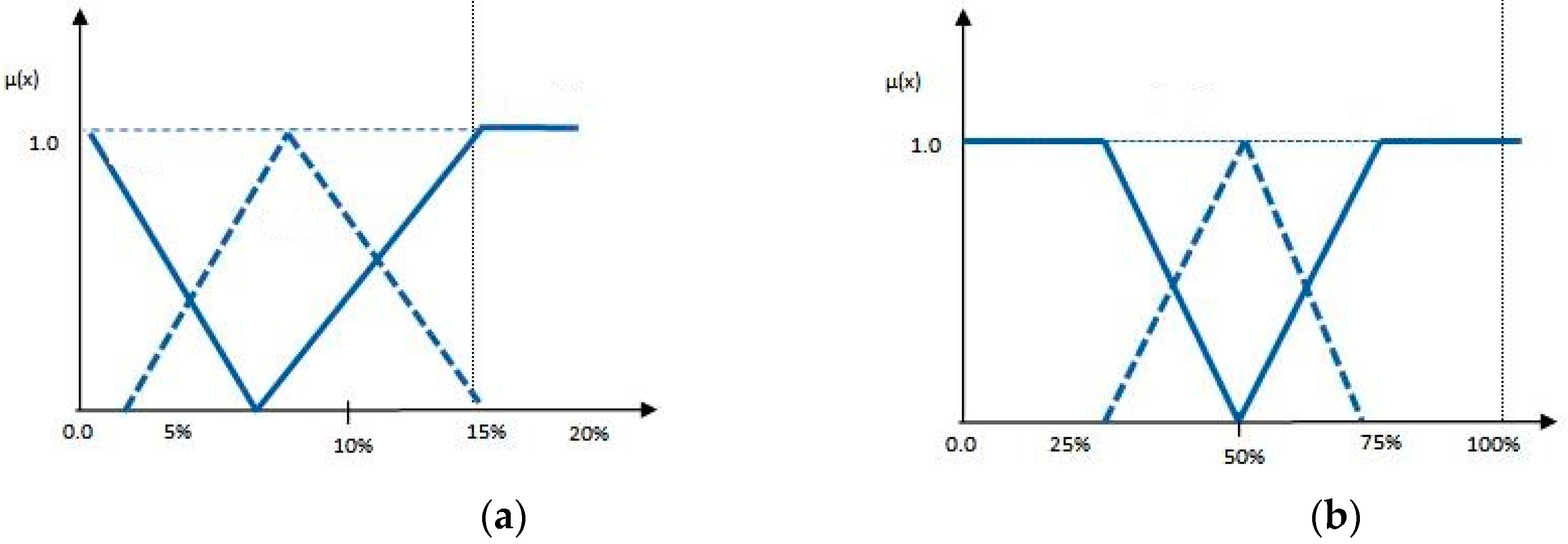
2.2. Development of the Cost Increase Prediction Model—I Stage
And “predicted changes in the number of works are high”
Or “the expected changes in the unit price are high”
Then “the risk of changing the cost of the item is high”
And “predicted changes in the number of works are low”
Or “the expected changes in the unit price are low”
Then “the risk of changing the cost of the item is average”
And “predicted changes in the number of works are high”
Or “the expected changes in the unit price are high”
Then “the risk of changing the cost of the item is high”
2.3. Development of the Cost Increase Prediction Model—II Stage
- ▪
- The decision maker determines the conditions of the project cm which may have an impact on cost increase (examples in Table 1).
- ▪
- Factors affecting cost increase are determined. These factors, unlike the conditions of the project, are characteristic of a given building element. Example factors are as follows: price range, change in unit price over time, time limit, the risk of replacement works, the risk of changing the amount of works.
- ▪
- The ranges of cost increases Wk are determined.
- ▪
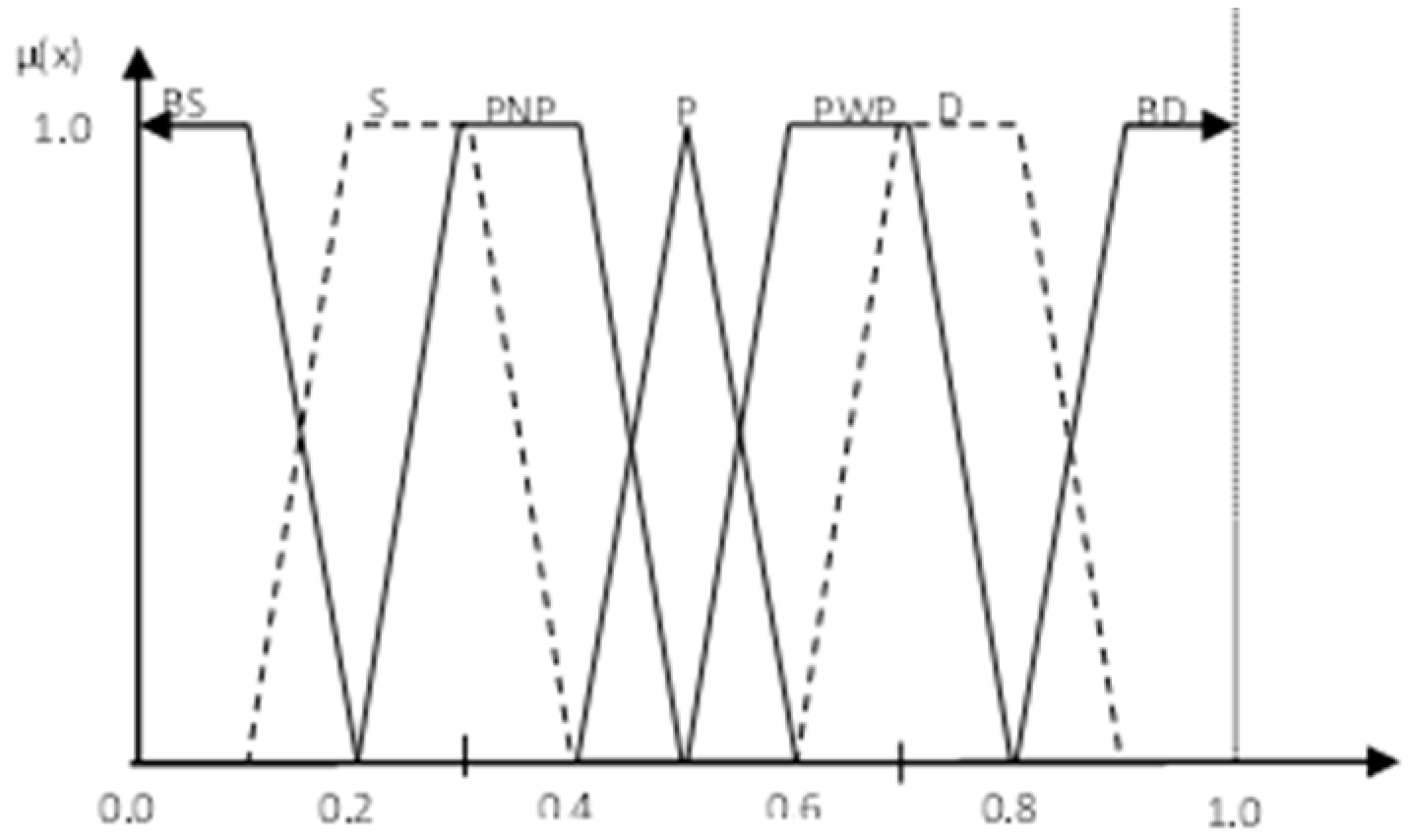
- The project conditions and factors using linguistic values are assessed: {Very Good (Very High), Good (High), Above Average, Average Good (Average High), Below Average, Weak (Low), Very Weak (Very Low)}.
- ▪
2.4. Calculation Example
- (1)
- Using (1), (2), (3) the risk of changing costs is assessed.
- (2)
- The following cost increase intervals are adopted:W1 = 10%; W2 = 25%; W3 = 40%; W4 = 55%; W5 = 70%; W6 = 85%; W7 = 100%.
- (3)
- The conditions of a given project are determined. The analysed example assumes: quality, completeness of project documentation, cost estimator experience, competitiveness in the tender.
- (4)
- Factors influencing the element cost increase are determined. Factors adopted: price range, change in the unit price of walls superseded in time, the risk of changing the number of works.
- (5)
- Basing on expert knowledge, values are established—the relationship between conditioning a and factor d. The results are presented in Table 6.
- (6)
- Relationships R(C,B) are calculated employing the formula in (5). The results are presented in Table 7.
- (7)
- Relationships R(B,W) are determined based on the most appropriate value of the cost increase for a given pair: determinant—factor, as specified in Table 8.
- (8)
- The max-min relationship is determined using the formula (6).
- (9)
- According to (8) the value of sharpening is determined:
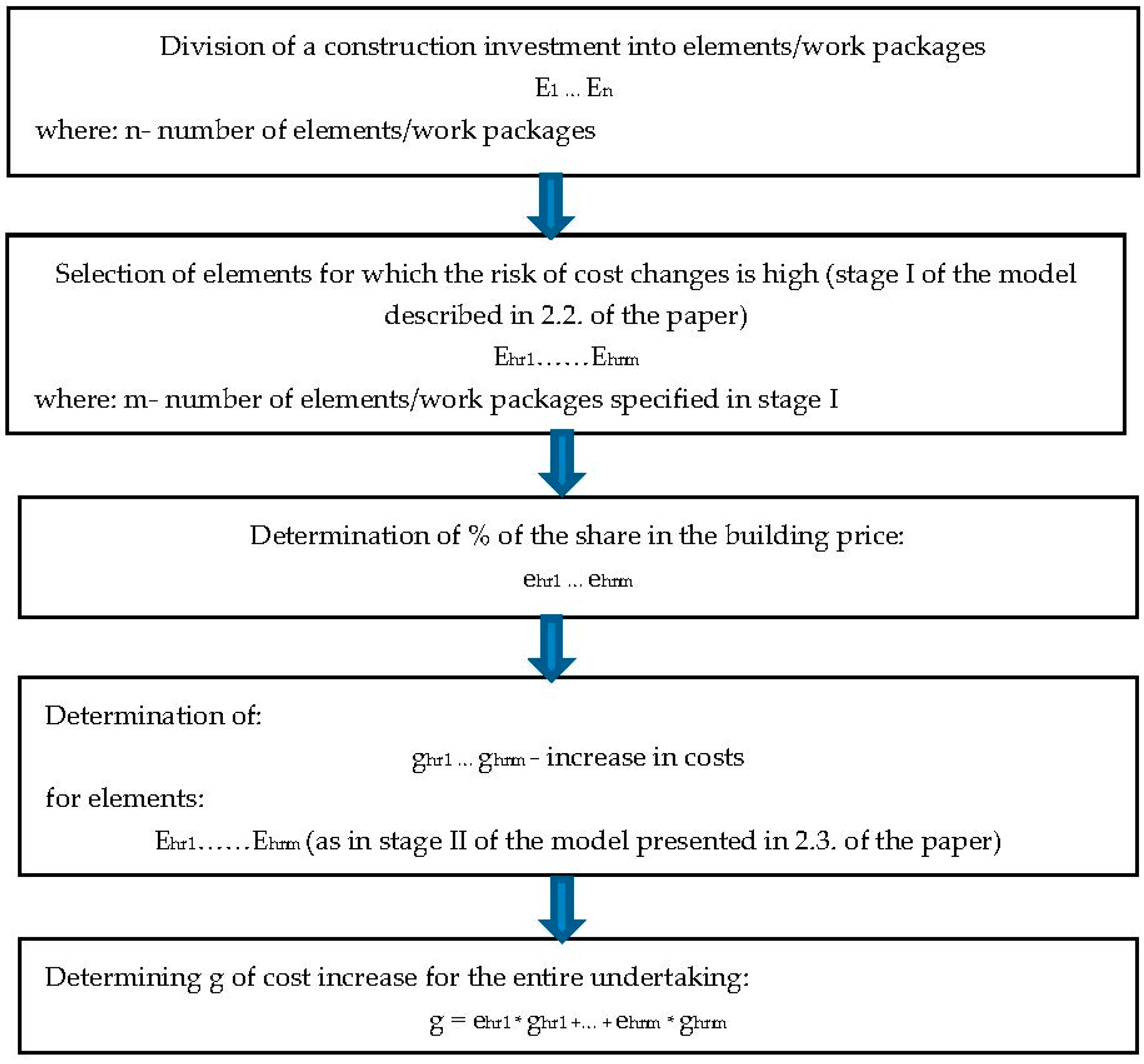
3. The Cost Increase Prediction Model for Whole Project
3.1. Case Study
- -
- cubic capacity: 2933.0 m3.
- -
- usable area: 263.49 m2.
3.2. Comparison of Model Results and Actual Cost Increase
4. Discussion
Funding
Conflicts of Interest
References
- Leśniak, A.; Plebankiewicz, E.; Zima, K. Cost calculation of building structures and building works in Polish conditions. Eng. Manag. Res. 2012, 1, 72–81. [Google Scholar] [CrossRef]
- Hinze, J.; Selstead, G.; Mahoney, J.P. Cost overruns on State of Washington construction contracts. Transp. Res. Rec. 13 1992, 51, 87–93. [Google Scholar]
- Flyvbjerg, B.; Holm, M.S.; Buhl, S. Underestimating Costs in Public Works Projects: Error or Lie? J. Am. Plan. Assoc. 2002, 68, 279–295. [Google Scholar] [CrossRef]
- Odeck, J. Cost overruns in road construction: What are their sizes and determinants? Transp. Policy 2004, 11, 43–53. [Google Scholar] [CrossRef]
- Skamris, M.K.; Flyvbjerg, B. Inaccuracy of traffic forecasts and cost estimates on large transportation projects. Transp. Policy 1997, 4, 141–146. [Google Scholar] [CrossRef]
- Love, P.E.D.; Wang, X.; Sing, C.; Tiong, R.L.K. Determining the Probability of Cost Overruns. J. Constr. Eng. Manag. 2013, 139, 321–330. [Google Scholar] [CrossRef]
- Cantarelli, C.C.; Flyvbjerg, B.; Molin, J.E.E.; van Wee, B. Cost Overruns in Large-Scale Transportation Infrastructure Projects: Explanations and their Theoretical Embeddedness. Eur. J. Transp. Infrastruct. Res. 2010, 10, 21. [Google Scholar]
- Sinesilassie, E.G.; Tabish, S.Z.S.; Jha, K.N. Critical factors affecting cost performance: A case of Ethiopian public construction projects. Int. J. Constr. Manag. 2018, 18, 108–119. [Google Scholar] [CrossRef]
- Asiedu, R.O.; Frempong, N.K.; Alfen, H.W. Predicting likelihood of cost overrun in educational projects. Eng. Constr. Arch. Manag. 2017, 24, 21–39. [Google Scholar] [CrossRef]
- El-Kholy, A.M. Predicting Cost Overrun in Construction Projects. Int. J. Constr. Eng. Manag. 2015, 4, 95–105. [Google Scholar] [CrossRef]
- Cantarelli, C.C.; Molin, E.J.E.; Van Wee, B.; Flyvbjerg, B. Characteristics of cost overruns for Dutch transport infrastructure projects and the importance of the decision to build and project phases. Transp. Policy 2012, 22, 49–56. [Google Scholar] [CrossRef]
- Derakhshanalavijeh, R.; Teixeira, J.M.C. Cost overrun in construction projects in developing countries, Gas-Oil industry of Iran as a case study. J. Civ. Eng. Manag. 2017, 23, 125–136. [Google Scholar] [CrossRef]
- Lind, H.; Brunes, F.; Lind, H.; Brunes, F. Explaining cost overruns in infrastructure projects : A new framework with applications to Sweden. Constr. Manag. Econ. 2015, 33, 554–568. [Google Scholar] [CrossRef]
- Koushki, P.A.; Al-Rashid, K.; Kartam, N. Delays and cost increases in the construction of private residential projects in Kuwait. J. Constr. Manag. Econ. 2005, 23, 285–294. [Google Scholar] [CrossRef]
- Abu Hammad, A.A.; Ali, S.M.A.; Sweis, G.J.; Basher, A. Prediction Model for Construction Cost and Duration in Jordan. Jordan J. Civ. Eng. 2008, 2, 250–266. [Google Scholar]
- Lowe, D.J.; Emsley, M.W.; Harding, A. Predicting Construction Cost Using Multiple Regression Techniques. J. Constr. Eng. Manag. 2006, 132, 750–758. [Google Scholar] [CrossRef]
- Attala, M.; Hegazy, T. Predicting Cost Deviation in Reconstruction Projects: Artificial Neural Networks Versus Regression. J. Constr. Eng. Manag. 2003, 129, 405–411. [Google Scholar] [CrossRef]
- Hegazy, T. Ayed Neural Network Model for Parametric Cost Estimation of Highway Projects. J. Constr. Eng. Manag. 1998, 124, 210–218. [Google Scholar] [CrossRef]
- Kim, K.J.; Kim, K. Preliminary Cost Estimation Model Using Case-Based Reasoning and Genetic Algorithms. J. Comput. Civ. Eng. 2010, 24, 499–505. [Google Scholar] [CrossRef]
- Dogan, S.Z.; Arditi, D.; Gunaydin, H.M. Determining Attribute Weights in A CBR Model for Early Cost Prediction of Structural System. J. Constr. Eng. Manag. 2006, 132, 1092–1098. [Google Scholar] [CrossRef]
- Ji, S.H.; Park, M.; Lee, H.S. Cost Estimation Model for Building Projects Using Case-Based Reasoning. Can. J. Civ. Eng. 2011, 38, 570–581. [Google Scholar] [CrossRef]
- Ahiaga-Dagbui, D.D.; Smith, S.D. Dealing with construction cost overruns using data mining. Constr. Manag. Econ. 2014, 32, 682–694. [Google Scholar] [CrossRef]
- Marzouk, M.; Amin, A. Predicting Construction materials prices using fuzzy logic and neural networks. J. Constr. Eng. Manag. 2013, 139, 1190–1198. [Google Scholar] [CrossRef]
- Knight, K.; Robinson Fayek, A. Use of fuzzy logic of predicting design cost overruns on building projects. J. Constr. Eng. Manag. 2002, 128, 503–512. [Google Scholar] [CrossRef]
- Newsletter Prices Buildings (BCO), Part I—Cubature Buildings; Sekocenbud OWEOB Promocja: Warszawa, Poland, 2018. (In Polish)
| Cost Overrun Categories | Causes | Study |
|---|---|---|
| Technical | Price rises Poor project design Incompleteness of estimations Scope changes Inappropriate organisational structure Inadequate decision-making process Inadequate planning process Additional works Replacement works | Cantarelli et al. (2010); Lind and Brunes (2015); Derakhshanalavijeh (2017) Hinze et al. (1992); Koushki et al. (2005); Cantarelli et al. (2010); Lind and Brunes (2015); Derakhshanalavijeh (2017) Cantarelli et al. (2010); Derakhshanalavijeh (2017) Koushki et al. (2005); Cantarelli et al. (2010); Lind, H and Brunes (2015) Cantarelli et al. (2010) Cantarelli et al. (2010) Cantarelli et al. (2010); Derakhshanalavijeh (2017) |
| Economical | Lack of incentives Lack of resources Inefficient use of resources (poor financing) | Cantarelli et al. (2010) Koushki et al. (2005); Cantarelli et al. (2010) Koushki et al. (2005); Cantarelli et al. (2010) |
| Contractual | Tendering strategy (open; selective) Procurement option (Design-bid-build; Design and build) | Hinze et al. (1992); Ahiaga-Dagbui and Smith (2014); El-Kholy (2015); Asiedu et al. (2017) Ahiaga-Dagbui and Smith (2014) |
| Psychological | Optimism bias among local officials Cognitive bias of people Cautious attitudes towards risk | Flyvbjerg et al. (2002); Cantarelli et al. (2010) Cantarelli et al. (2010) Flyvbjerg et al. (2002); Cantarelli et al. (2010) |
| Political | Deliberate cost underestimation Manipulation of forecasts | Flyvbjerg et al. (2002); Cantarelli et al. (2010) Flyvbjerg et al. (2002); Cantarelli et al. (2010) |
| Building Elements | A | B | C | D |
|---|---|---|---|---|
| % of the Share in the Building Price | ||||
| Raw state | 7.9 | 6.8 | 11.5 | 13.0 |
| Earthworks | 2.5 | 2.2 | 4.2 | 0.8 |
| Foundations | 2.0 | 1.7 | 1.9 | 3.8 |
| Underground walls | 1.9 | 1.6 | 2.6 | 3.8 |
| Insulation | 1.4 | 1.3 | 0.5 | 0.7 |
| Other | 0.1 | 0.0 | 2.3 | 3.9 |
| Building shell | 45.6 | 39.8 | 35.1 | 45.9 |
| Superstructure walls | 17.2 | 15.0 | 9.0 | 16.0 |
| Ceilings, vaults, stairs, landings | 10.5 | 9.1 | 12.3 | 12.8 |
| Partitions | 3.1 | 2.7 | 2.1 | 5.5 |
| Roor − structure + covering | 4.4 | 3.8 | 2.4 | 3.6 |
| Superstructure insulation | 5.1 | 4.5 | 3.7 | 5.2 |
| Other | 5.3 | 4.7 | 5.6 | 2.8 |
| Interior finishing state | 13.6 | 22.6 | 21.9 | 13.3 |
| Plaster and facing | 3.6 | 4.5 | 7.9 | 4.5 |
| Windows and doors | 7.9 | 6.8 | 6.2 | 5.0 |
| Other | 2.1 | 11.3 | 7.8 | 3.8 |
| Exterior finishing state | 17.6 | 15.4 | 10.1 | 10.2 |
| Other | 15.3 | 15.0 | 21.4 | 17.6 |
| Linguistic Values | Fuzzy Assessment (Interpretation) |
|---|---|
| VG/VH Very Good (Very High) | (0.8; 0.9; 1.0; 1.0) |
| G/H Good (High) | (0.6; 0.7; 0.8; 0.9) |
| AA Above Average | (0.5; 0.6; 0.7; 0.8) |
| A Average Good (Average High) | (0.4; 0.5; 0.5; 0.6) |
| BA Below Average | (0.2; 0.3; 0.4; 0.5) |
| W/L Weak (Low) | (0.1; 0.2; 0.3; 0.4) |
| VW/VL Very Weak (Very Low) | (0.0; 0.0; 0.1; 0.2) |
| Project Conditions | Evaluation | |
|---|---|---|
| Quality of project documentation | High | 0.6; 0.7; 0.8; 0.9 |
| Cost estimator’s experience | Very good | 0.8; 0.9; 1.0; 1.0 |
| Competitiveness in the tender | Average high | 0.4; 0.5; 0.5; 0.6 |
| Factors | Evaluation | |
|---|---|---|
| Price range | Very high | 0.8; 0.9; 1.0; 1.0 |
| Changing the unit price of walls of superstructure in time | Low | 0.1; 0.2; 0.3; 0.4 |
| The risk of changing the number of works | Low | 0.1; 0.2; 0.3; 0.4 |
| Project Conditioning (Ca) | Factors (Bd) | The Relationship between Conditioning and the Factor () |
|---|---|---|
| C1 | B1 | I11 = 0.10 |
| C1 | B2 | I12 = 0.10 |
| C1 | B3 | I13 = 1.00 |
| C2 | B1 | I21 = 0.50 |
| C2 | B2 | I22 = 0.50 |
| C2 | B3 | I23 = 0.50 |
| C3 | B1 | I31 = 0.20 |
| C3 | B2 | I32 = 0.20 |
| C3 | B3 | I33 = 0.50 |
| Relation R(C,B) | B1 | B2 | B3 |
|---|---|---|---|
| C1 | 0.75·0.925·0.10 = 0.069 | 0.75·0.25·0.10 = 0.019 | 0.75·0.25·1.00 = 0.188 |
| C2 | 0.93·0.925·0.50 = 0.430 | 0.93·0.25·0.50 = 0.116 | 0.93·0.25·0.50 = 0.116 |
| C3 | 0.50·0.925·0.20 = 0.093 | 0.50·0.25·0.20 = 0.025 | 0.50·0.25·0.50 = 0.063 |
| Relation R(B,B) | Increase W1 = 10% | Increase W2 = 25% | Increase W3 = 40% | Increase W4 = 55% | Increase W5 = 70% | Increase W6 = 85% | Increase W7 =100% | |
|---|---|---|---|---|---|---|---|---|
| C | B | |||||||
| C1 | B1 | 0.4 | 0.6 | 0.8 | 1 | 0.8 | 0.6 | 0.4 |
| C1 | B2 | 1 | 0.8 | 0.6 | 0.4 | 0.2 | 0 | 0 |
| C1 | B3 | 1 | 0.8 | 0.6 | 0.4 | 0.2 | 0 | 0 |
| C2 | B1 | 0.4 | 0.6 | 0.8 | 1 | 0.8 | 0.6 | 0.4 |
| C2 | B2 | 1 | 0.8 | 0.6 | 0.4 | 0.2 | 0 | 0 |
| C2 | B3 | 1 | 0.8 | 0.6 | 0.4 | 0.2 | 0 | 0 |
| C3 | B1 | 0.2 | 0.4 | 0.6 | 0.8 | 1 | 0.8 | 0.6 |
| C3 | B2 | 0.6 | 0.8 | 1 | 0.8 | 0.6 | 0.4 | 0.2 |
| C3 | B3 | 0.8 | 1 | 0.8 | 0.6 | 0.4 | 0.2 | 0 |
| Relation Composition Q(C,W) | Increase W1 = 10% | Increase W2 = 25% | Increase W3 = 40% | Increase W4 = 55% | Increase W5 = 70% | Increase W6 = 85% | Increase W7 = 100% |
|---|---|---|---|---|---|---|---|
| C1 | 0.188 | 0.188 | 0.188 | 1.188 | 0.188 | 0.069 | 0.069 |
| C2 | 0.400 | 0.430 | 0.430 | 0.430 | 0.430 | 0.430 | 0.400 |
| C3 | 0.093 | 0.093 | 0.093 | 0.093 | 0.093 | 0.093 | 0.093 |
| Q(C,W) | 0.310 | 0.330 | 0.330 | 0.330 | 0.330 | 0.270 | 0.260 |
| No. | Type and Scope of Works | Net Cost Price [EURO] |
|---|---|---|
| 1 | Wall and plaster work - demolition of unnecessary walls and pillars, forging door and window openings, supplementing or walling openings in walls, building partition walls of bricks, laying prefabricated lintels, making exhaust and ventilation ducts, mending cracks in brick walls, making internal plasters, fitting small elements in walls | 7644 |
| 2 | Renovation of ceilings - mould elimination in wooden elements, replacement of sound boarding and headliners, reinforcement of ceiling joists, mould elimination in 25% of the brick ceiling areas, execution of suspended ceilings with mineral wool insulation, cladding of fire protection boards in rooms with a wooden ceiling | 10,446 |
| 3 | Painting and cladding work - removal of internal wall plasters, along with making new plasters, veneering walls with glued tiles, filling and painting walls and ceilings with oil paints | 7189 |
| 4 | Carpentry works - removing old frames, windows and protective steel gratings with sills, fitting windows and window sills, door and window frames, internal and external doors, putting plaster on the jambs | 12,429 |
| 5 | Flooring works - removal of plastic floors, dismantling of wooden floors, horizontal water insulations in non-basement rooms, thermal insulation of Styrofoam boards in all rooms, new cement floors on reinforcing mesh, tile floors with baseboards, in bathrooms, kitchens and corridors, floors with plastic carpeting with baseboards in the rooms | 13,924 |
| 6 | Roof works - dismantling of chimneys, tar paper covering, flashing, gutters and downpipes, supplementing formwork, dehumidifying wooden elements of the roof, replacement of faceplates, repair of damaged places in brick walls, assembly of new flashings, breaking the cement floor of the roof together with making a new one, erection of new chimneys, fireproofing of wooden roof elements, roofing with tar paper, installation of new gutters and downpipes, removal of debris | 16,394 |
| 7 | Facade works - installation of external scaffolding, demolition of concrete elements, supplementation of external plasters, abrasive cleaning of brick walls, wall joints, foundation walls excavation, cleaning and plastering of foundation walls, damp insulation, foundation of ramps for the disabled and stairs, reinforced concrete stairs, reinforced concrete structure of the ramp for the disabled, balustrades, stair cladding and incline from stoneware tiles, backfilling excavations | 12,735 |
| 8 | Disassembly of the installation - disassembly of steel pipelines, washbasin and shower taps and boilers, disassembly of washbasins, fittings, as well as water and sewage equipment | 454 |
| 9 | Central heating installation - making new installation pipelines, steel radiator installations | 9438 |
| 10 | Sewage installation - execution of excavations and penetration of openings through walls and foundations, installation of new sewage pipelines together with instrumentation | 4498 |
| 11 | Water installation - execution of plastic pipelines with equipment installation | 3329 |
| 12 | Water connection - linear excavations with backfilling and compaction, making a water supply connection | 481 |
| 13 | Connection of rainwater and sanitary sewage system - execution of linear excavations and their strengthening, along with subsequent backfilling and hardening, installation of sewage and sewage wells, PVC pipe ducts | 4656 |
| 14 | Electrical and teletechnical installations - disassembly works, installation of multicore cables and cable wires in insulation, sockets, lighting fixtures, installation of switchboards with enclosures, | 8896 |
| 15 | Connection for central heating - execution of necessary excavations, disassembly of steel pipeline and concrete channel elements, breaking necessary openings, heat piping installations, debris removal | 2805 |
| Works Listed in Stage I | % of Share in the Cost Estimate Price | % of Cost Increase | Cost Increase for the Investment [%] |
|---|---|---|---|
| Renovation of ceilings | 9.01 | 43 | 3.87 |
| Roof works | 14.22 | 51 | 7.25 |
| Painting and cladding works | 6.23 | 64 | 3.99 |
| Flooring works | 12.07 | 21 | 2.53 |
| Facade works | 11.04 | 46 | 5.08 |
| No. | Type of Works | Net Cost Price [EURO] | Real Cost [EURO] | % of Difference | % of Share | Cost Increase [%] |
|---|---|---|---|---|---|---|
| 1 | Wall and plaster works | 7644 | 7650 | 0.08 | 6.63 | 0.01 |
| 2 | Renovation of ceilings | 10,446 | 15,434 | 47.75 | 9.01 | 4.33 |
| 3 | Painting and cladding works | 7189 | 12,358 | 71.90 | 6.23 | 4.48 |
| 4 | Carpentry works | 12,429 | 12,500 | 0.57 | 10.78 | 0.06 |
| 5 | Flooring works | 13,924 | 13,800 | −0.89 | 12.07 | −0.11 |
| 6 | Roof works | 16,394 | 21,057 | 28.44 | 14.22 | 4.04 |
| 7 | Facade works | 12,735 | 18,860 | 48.10 | 11.04 | 5.31 |
| 8 | Disassembly of the installation | 454 | 450 | −0.88 | 0.39 | −0.00 |
| 9 | Central heating installation | 9438 | 9442 | 0.04 | 8.18 | 0.00 |
| 10 | Sewage installation | 4498 | 4502 | 0.09 | 3.90 | 0.00 |
| 11 | Water installation | 3329 | 3343 | 0.42 | 2.89 | 0.01 |
| 12 | Water connection | 481 | 470 | −2.29 | 0.42 | −0.01 |
| 13 | Connection of rainwater and sanitary sewage system | 4656 | 5080 | 9.11 | 4.04 | 0.37 |
| 14 | Electrical and teletechnical installations | 8896 | 8600 | −3.33 | 7.71 | −0.26 |
| 15 | Connection of central heating | 2805 | 2830 | 0.89 | 2.43 | 0.02 |
| ∑ | 115,318 | 136,376 | 18.26 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Plebankiewicz, E. Model of Predicting Cost Overrun in Construction Projects. Sustainability 2018, 10, 4387. https://doi.org/10.3390/su10124387
Plebankiewicz E. Model of Predicting Cost Overrun in Construction Projects. Sustainability. 2018; 10(12):4387. https://doi.org/10.3390/su10124387
Chicago/Turabian StylePlebankiewicz, Edyta. 2018. "Model of Predicting Cost Overrun in Construction Projects" Sustainability 10, no. 12: 4387. https://doi.org/10.3390/su10124387
APA StylePlebankiewicz, E. (2018). Model of Predicting Cost Overrun in Construction Projects. Sustainability, 10(12), 4387. https://doi.org/10.3390/su10124387





