Sustainability in Agricultural Mechanization: Assessment of a Combined Photovoltaic and Electric Multipurpose System for Farmers
Abstract
:1. Introduction
2. Materials and Methods
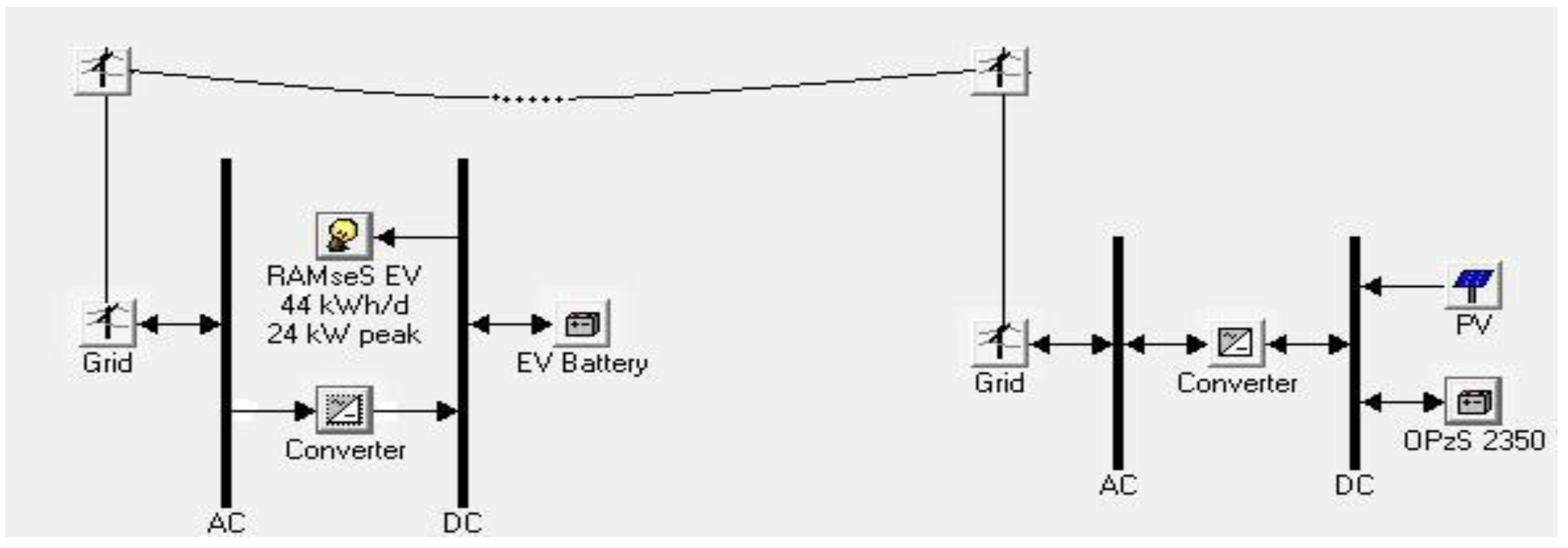
| Batteries | On-board EV battery | Stationary battery |
| Lead-gel dryfit | Lead-acid | |
| 48 | 45 | |
| 180@ C(5) | 1,910 @ C(24) | |
| 56 (8 × 7) | 23 | |
| 700 @ 75 % DOD | - | |
| 14 | 1 | |
| Panels | Cell efficiency (at STC) | 17% |
| Total panels area (A) | 72 m2 | |
| PR (fulfillment, Mismatch, inverter ...) | 0.75 | |
| Life-time (N) | 30 yr | |
| Panels installation region | Lebanon | |
| Yearly average irradiation (I) | 1,752 kWh/m2/yr |
| Power (hp) | Fuel Cons. (L/h) at 100% load | Fuel Tank (L) | Approximate Weight (kg) | Drive wheel | Fuel type | Battery (one) | 3 Point-hitch | PTO (rpm) | Crankcase oil (L) |
|---|---|---|---|---|---|---|---|---|---|
| 29.5 | 7.18 | 51.03 | 1316 | 4 | Diesel | 12 V, 40 Ah | I-category | 540 | 4.8 |
2.1. Environmental Life-Cycle Assessment (LCA)
| Solar cell technology | Emission (g/kWhel) | Test conditions | Ref. | ||
|---|---|---|---|---|---|
| CO2equ | SO2 | NOx | |||
| m-Si (1997) | 75 | 0.3 (sum of NOx and SO2) | - | [16] | |
| m-Si (2010) (estimation) | 30 | 0.1(sum of NOx and SO2) | - | [16] | |
| Rooftop grid-connected m-Si (2004) | 41 | - | - | I = 1700, PR = 0.75, E = 13.7% | [17] |
| Roof top m-Si grid connected(2000) | 60 | - | - | I = 1700, L = 30yr | [11] |
| m-Si (2006) | 35 | - | - | I = 1700k, R = 0.75, L = 30yr, E = 14% | [11] |
| Ground-mounted m-Si (case 1) (2004–2006) | 35 | 0.061 | 0.092 | I = 1700, PR = 0.8, L = 30 yr, E = 14% | [14] |
| Ground-mounted m-Si (case 2) (2004–2006) | 43 | 0.081 | 0.147 | I = 1700, PR = 0.8, L = 30 yr, E = 14% | [14] |
| Ground-mounted m-Si (case 3) (2004–2006) | 54 | 0.186 | 0.38 | I = 1700, PR = 0.8, E = 14%, L = 30 yr | [14] |
| In-roof m-Si at present(2006) | 35 | - | - | I = 1700, PR = 0.75, E = 14% | [18] |
| In-roof m-Si at future | 15.5 | - | - | I = 1700 PR = 0.75, E = 19% | [18] |
| Rooftop m-Si | 43 | - | - | I = 1700 | [19] |
| Emission (g/GWh) | As | Cd | Cr | Pb | Hg | Ni |
|---|---|---|---|---|---|---|
| 2.3 | 1 | 6 | 9.8 | 1 | 26 |
| CO2equ (sum of items below) | SO2 | NOx | CO | Ref. | |||
| CO2 | CH4 | N2O | |||||
| Stationary | 570 | 0.677 | 0.013 | 3.77 | 4.3 | 1.03 | [20] |
| EV battery | 970 | - | - | 6.8 | 6.3 | - | [21] |
| Emission parameters | BSFC | NOx | CO | PM | HC |
| Zero-Hour, Emission | - | 4.7279 | 1.532 | 0.20 | 0.278 |
| TAF | 1 | 1 | 1 | 1 | 1 |
| Deterioration Factor's coefficient (A) up to Tiers 3 | - | 0.008 | 0.151 | 0.473 | 0.027 |
| In g/GJ | CO2 | NOx | CO | PM | HC |
| Feedstock production | 1.692–3.4 (2.54) | 7.98–9.5 (8.74) | 1.395–5.1 (3.2475) | 0 | 24.064–27.8 (25.93) |
| Feedstock transportation | 0.6 | 15.04–20 (17.52) | 0.376–1.7 (1.038) | 0 | 0.93–26.1 (13.515) |
| Fuel production | 3–6.96 (4.98) | 4.9–8.04 (6.47) | 0–0.798 (0.399) | 0 | 10.03–57.036 (33.533) |
| Fuel distribution | 0.2–0.7 (0.45) | 1.504–10.6 (6.052) | 0.4–0.7 (0.55) | 0.1 | 0.303–1.079 (0.691) |
| Total | 8.57 | 38.782 | 5.2345 | 0.1 | 73.669 |
| kg/kg of curb weight | CO2equ | NOx | CO | PM | HC |
|---|---|---|---|---|---|
| Extraction & Mat. Process | 3.644 | 0.00506 | 0.012 | 0.00416 | 0.0011 |
| Manufacturing | 2.2453 | 0.0024 | 1.893 × 10–4 | 5.966 × 10–4 | - |
| End-of-Life | 0.0135 | 3.58 × 10–5 | 1.77 × 10–6 | 4.09 × 10–6 | - |
| Total | 5.9 | 0.00749 | 0.012191 | 0.00476 | 0.0011 |
2.2. Environmental LCA Using SimaPro
2.3. Economics LCA
2.4. Comparison Indicators
3. Results and Discussion
3.1. Monetary Effects of Environmental Emissions
| Emissions (kg) | CO2equ | SO2 | NOx | CO | PM | HC | As | Cd | Cr | Pb | Hg | Ni |
| RAMseS | ||||||||||||
| PV panels | 20,748 | 39 | 71 | - | - | - | 1.1 | 0.5 | 2.9 | 4.7 | 0.5 | 12.5 |
| Battery | 25,926 | 178 | 178 | 34 | - | - | - | - | - | - | - | - |
| EV Cons. | 10,478 | - | 13 | 22 | 8 | 2 | - | - | - | - | - | - |
| Total | 57,152 | 217 | 262 | 56 | 8 | 2 | 1.1 | 0.5 | 2.9 | 4.7 | 0.5 | 12.5 |
| ICEV | ||||||||||||
| Fuel Prod. | 75 | - | 339 | 46 | 1 | 644 | - | - | - | - | - | - |
| Fuel use | 726,093 | 222 | 5824 | 1963 | 178 | 369 | - | - | - | - | - | - |
| Vehicle Cons. | 30,735 | - | 39 | 64 | 25 | 6 | - | - | - | - | - | - |
| Total | 756,900 | 222 | 6202 | 2073 | 204 | 1019 | - | - | - | - | - | - |
| CO2equ | SO2 | NOx | CO | PM | HC | As | Cd | Cr | Pb | Hg | Ni | Ref. | |
| ICEV | |||||||||||||
| Euro/ton | - | 2895 | 2020 | 0.7 | 87671 | - | - | - | - | - | - | - | [34] |
| 29 | 2200 | 1500 | - | 22000 | - | - | - | - | - | - | - | [7] | |
| 18–48 | 9500 | 2000 | - | - | - | - | - | - | - | - | - | [2] | |
| 3–14 | 5000 | 4400 | - | 12000 | - | - | - | - | - | - | - | [35] | |
| Ave. (Euro/ton) | 32.5 | 5000 | 2480 | 0.7 | 40557 | - | - | - | - | - | - | - | |
| Cost (Euro) | 24596 | 1110 | 15381 | 1.45 | 8273 | - | - | - | - | - | - | ||
| RAMseS | |||||||||||||
| Euro/ton | 19 | 2939 | 2908 | - | 19539 | - | 8 × 104 | 39 × 103 | 31500 | 16 × 105 | - | 3800 | [20] |
| Cost (Euro) | 1086 | 638 | 756 | - | 164 | - | 88 | 19 | 88 | 7520 | - | 48 |
3.2. Economical Life-Cycle Comparison between Two Systems
| Parameters | Values in This study | Similar references | ||||||
| [3] | [36] | [30] | [37] | [38] | [39] | [27] | ||
| Unit cost of PV panels (€/Wp), UPV | 3 | - | - | 3.2 | 2.2 | 2.3 | 4.8 | 2.6 |
| Stationary battery unit cost (€/kWh), USB | 182 | - | - | 80 | 54 | - | 81 | 96 |
| Cost of BOS (% of CPV), CBOS | 11 | 5-10 | - | 4 | - | 17–47 | 8 | 3.2 |
| Unit cost of PCU (€/kWp), UPCU | 700 | - | - | 590 | - | 515–955 | 920 | 964 |
| PV life (year), N | 30 | - | 20 | 20 | 30 | 20 | 25 | 25 |
| PV O&M cost ratio (% of CPV), m | 1.2 | 2 | 1.3 | 2 | 3 | 3 | 1 | 1 |
| Discount rate (%), d | 5-12 | 10 | 10 | 7–15 | 8 | 10 | 5 | 4 |
| Inflation rate (%), i | 1-6 | - | - | 3–8 | 4 | - | - | 1.4 |
| Stationary battery life (year), LSB | 15 | - | - | - | 5 | 7 | 7 | 5 |
| Life of PCU (year), LPCU | 10 | - | 7 | - | - | 10 | 13 | 10 |
| Inflation rate of fuel (%), if | 5.6 | 0 | 5 | 5–10 | - | - | - | 1.4 |
| Unit cost of EV battery (€/kWh), UEVB | 262 | - | - | - | - | - | - | - |
| EV cost without battery (€), CEV | 15000 | - | - | - | - | - | - | - |
| EV salvage cost (% of CEV), SEV | 27 | - | - | - | - | - | - | - |
| Tax-Shelter-Insurance (% of CV), TSI | 2.45 | - | - | - | - | - | - | - |
| EV life (year), LEV | 15 | - | - | - | - | - | - | - |
| EV battery life (year), LEVB | 2 | - | - | - | - | - | - | - |
| Inflation rate of energy (%), ie | 5.6 | - | - | - | - | - | - | - |
| ICEV life (year), LICEV | 7.5 | - | - | - | - | - | - | - |
| Custom cost of ICEV (€), CICEV | 11250 | - | - | - | - | - | - | - |
| ICEV O&M cost (% of CICEV), CO&MICEV | 0.5/100 hr | - | - | - | - | - | - | - |
| ICEV salvage cost (% of CICEV), SICEV | 39 | - | - | - | - | - | - | - |
| RAMseS | Cini (€) | CR (€) | CO&M (€) | CENV (€) | LCC (€) | LCE (€/kWh) | NPV (€) | PBP (year) |
| Value | 97518 | SA | SA | 10000 | SA | SA | SA | SA |
| ICEV | Cini (€) | CREC (€) | CN-REC (€) | CENV (€) | LCC (€) | LCE (€/kWh] | NPV (€) | |
| Value | 15682 | SA | SA | 49000 | SA | SA | SA |
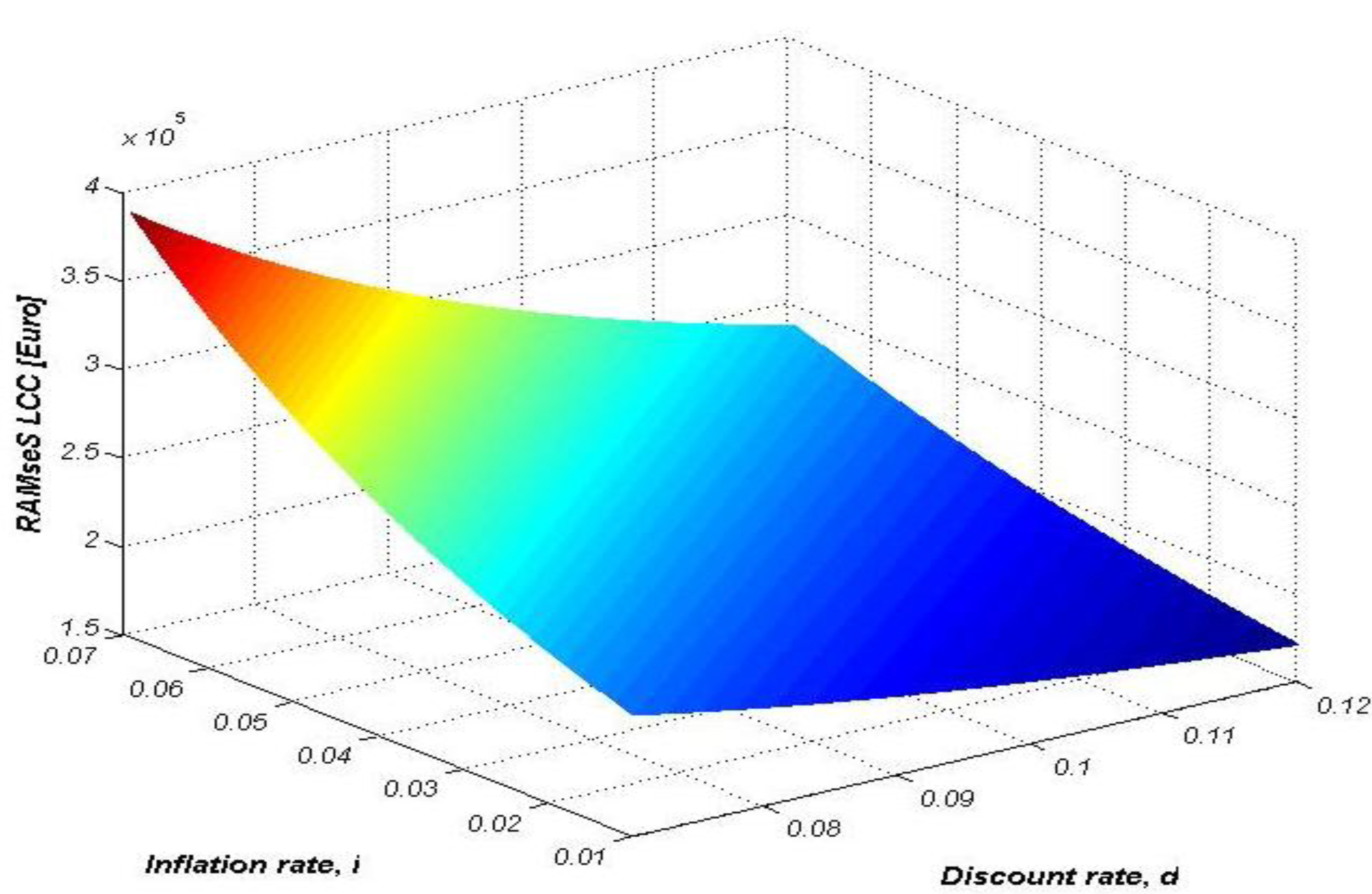
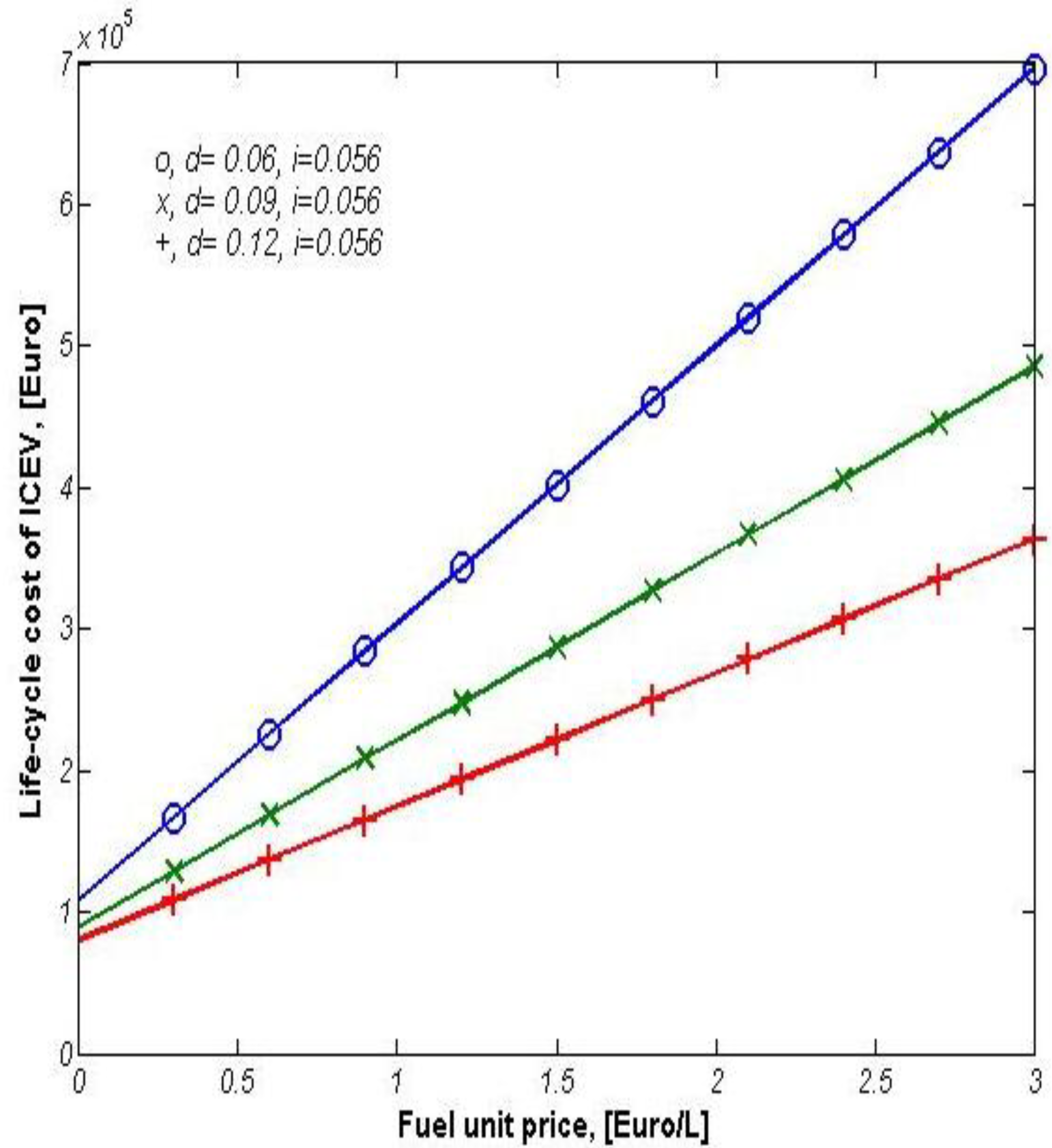
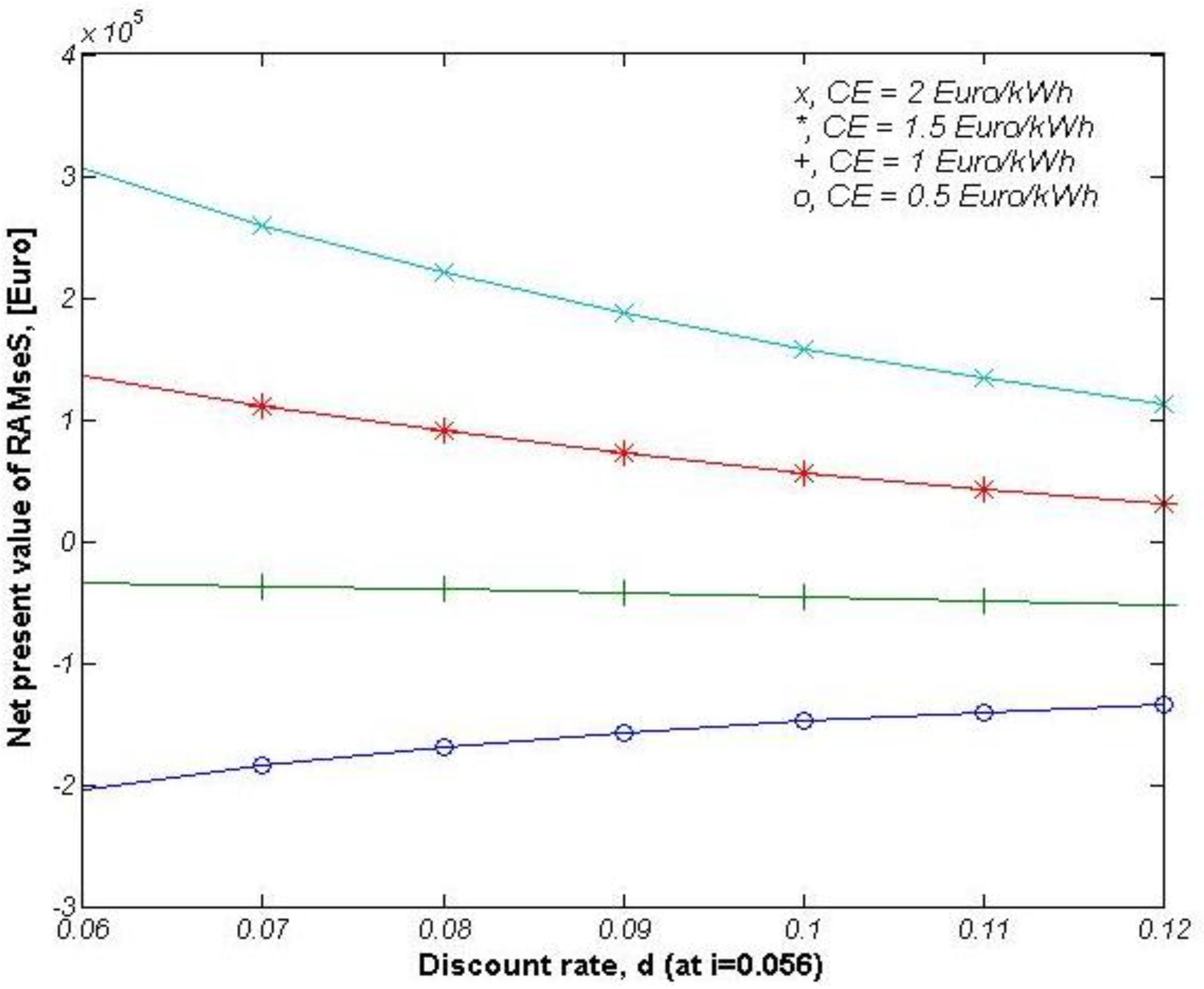
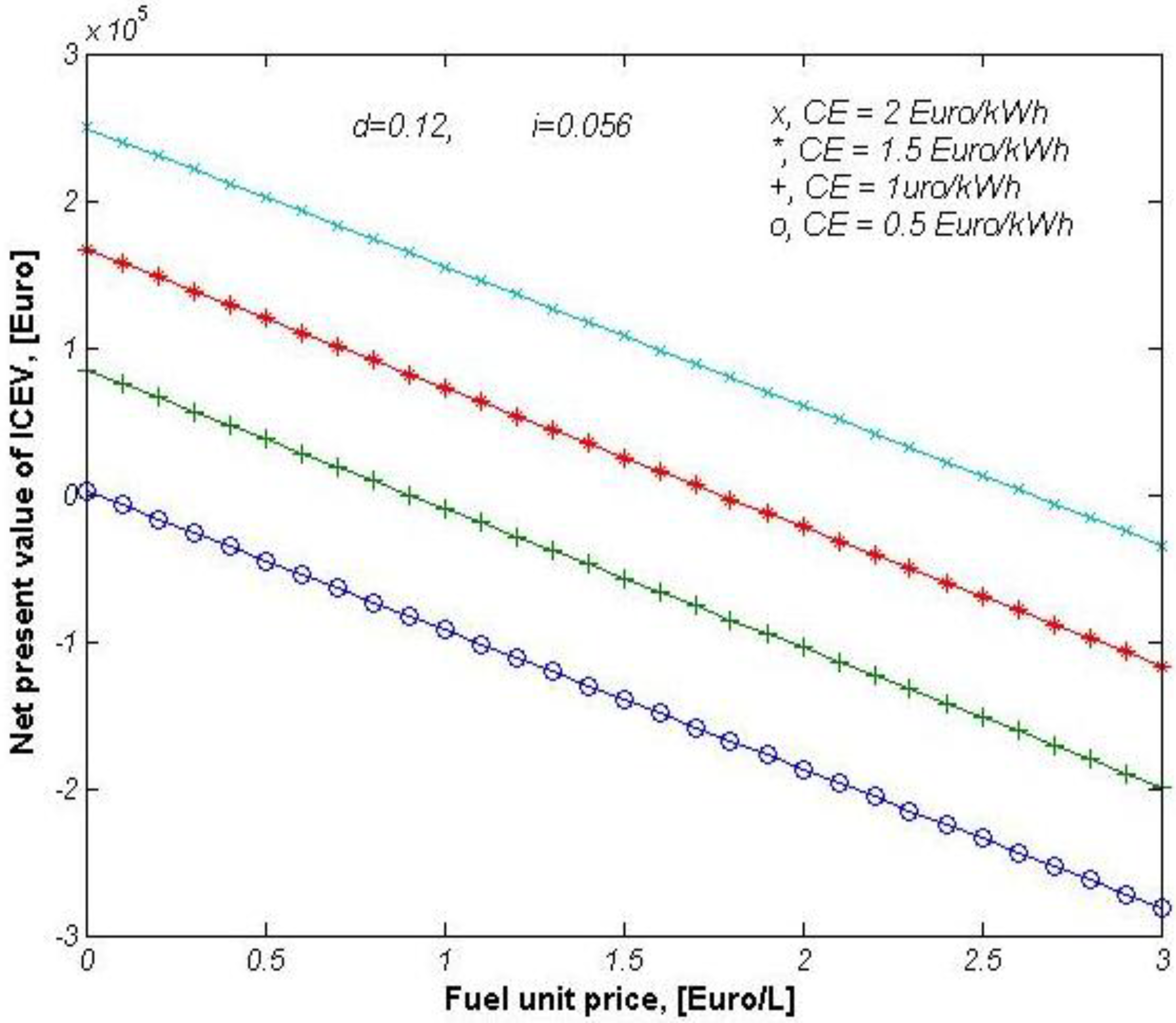
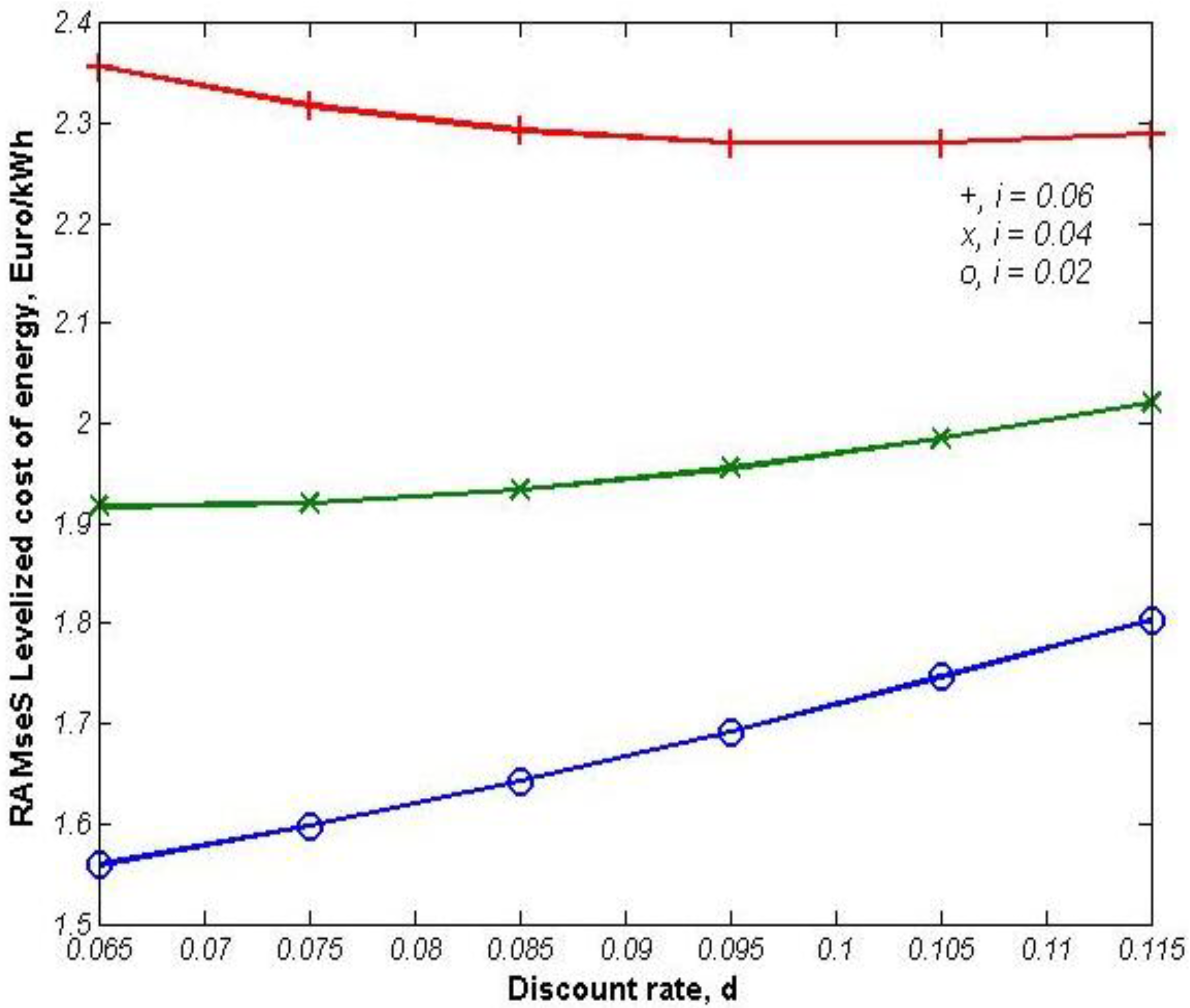
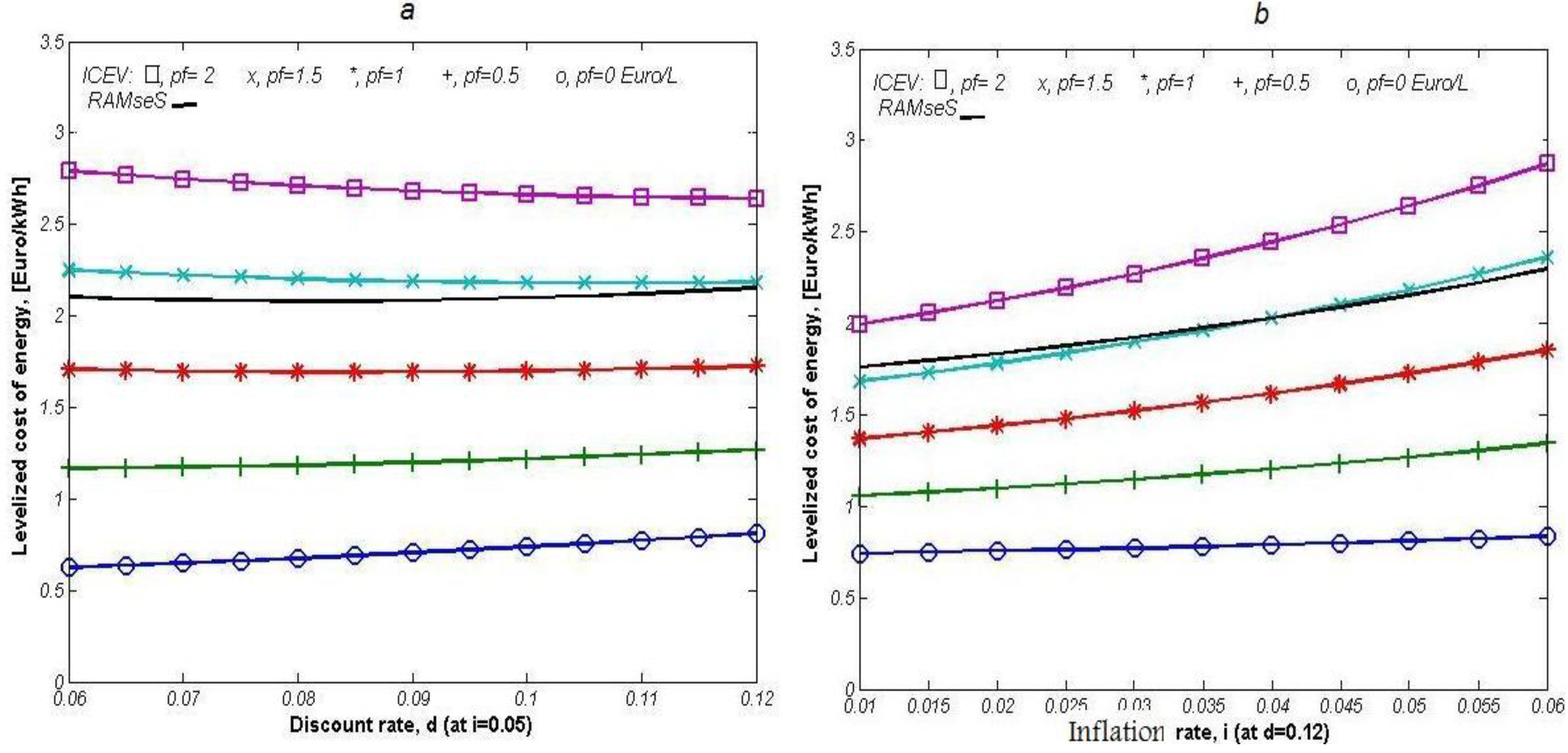


4. Conclusions
Nomenclature
| 4WD | 4 Wheel-Drive |
| ASABE | American Society of Agricultural and Biological Engineers |
| BOS | Balance Of System |
| AF | Annuities Factor |
| CBOS | Cost of BOS (% of CPV) |
| CEV | EV cost without battery (€) |
| CEVB | Cost of EV battery (€/kWh) |
| Cfuel | Cost of fuel (€) |
| CICEV | Custom cost of ICEV (€) |
| CL | Land cost (€) |
| CN-REC | Non-recurring costs of ICEV (€) |
| CO&M0 | Operation and maintenance cost for first year (€) |
| CO&M | Operation and maintenance cost (€) |
| CPCU | Cost of PCU (€/kWp) |
| CPV | Custom cost of PV (€/Wp) |
| CR | Replacement costs of RAMseS (€) |
| CREC | Recurring costs of ICEV (€) |
| CSB | Stationary battery cost (€/kWh) |
| CTSI | Cost of Tax-Shelter-Insurance (€) |
| Cyfuel | Yearly cost of fuel (€) |
| DF | Deterioration factor |
| d | Discount rate (%) |
| E | Conversion efficiency of PV |
| EFadj | Final emission after account for transient and deterioration (g/hp-hr) |
| EFss | Zero-hour, steady-state emission factor (g/hp-hr) |
| EV | Electric Vehicle |
| EVB | Electric Vehicle Battery |
| Eyear | Yearly collected energy by PV project (kWh) |
| G | Generation of electricity in life-cycle (kWh) |
| GHG | Green house gas |
| I | Solar irradiation (W/m2) |
| i | Inflation rate (%) |
| ICE | Internal combustion engine |
| ICEV | Internal Combustion Engine Vehicle |
| ie | Inflation rate of energy (%) |
| if | Inflation rate of fuel (%) |
| LCA | Life-Cycle Assessment |
| LCC | Life-Cycle Cost (€) |
| LCE | Levelized Cost of Energy (€/kWh) |
| LEV | EV life (year) |
| LEVB | EV battery life (year) |
| LICEV | ICEV life (year) |
| LPCU | Life of PCU (year) |
| LSB | Stationary battery life (year) |
| m | PV O&M cost ratio (% of CPV) |
| m-Si | Mono crystalline silicon |
| N | PV life (year) |
| NEVBR | Number of replacements of EV batteries |
| NEVR | Number of replacements of EV |
| NPCUR | Number of replacements of PCU |
| NPV | Net Present Value (€) |
| NRICEV | Replacing number of the ICEV |
| NSBR | Number of replacements of stationary batteries |
| PBP | Pay Back Period (year) |
| PCU | Power Conditioning Unit |
| PE | Energy sale price (€/kWh) |
| Pf | Fuel unit price (€/L) |
| PM | Particulate matter |
| PR | Performance Ratio |
| PV | Photovoltaic |
| RAMseS | Renewable energy Agriculture Multipurpose System for farmers |
| SB | Stationary Battery |
| SEV | EV salvage cost (% of CPV) |
| SICEV | ICEV salvage cost (% of CICEV) |
| soxcnv | Grams PM sulfur per grams sulfur in fuel consumed |
| soxbas | Default certification fuel sulfur weight percent |
| soxdsl | Episodic fuel sulfur weight percent |
| SPM adj | PM emission factor adjustment to account fuel sulfur content (g/hp-hr) |
| STC | Standard Test Condition (1000W/m2 irradiation, 25oC cell temperature, air mass 1.5) |
| TAF | Transient Adjustment Factor |
| TSI | Tax-Shelter-Insurance (% of CV) |
| UEVB | Unit cost of electric vehicle battery (€/kWh) |
| UPCU | Unit cost of PCU (€/kWp) |
| UPV | Unit cost of PV panels (€/Wp) |
| USB | Unit cost of stationary battery (€/kWh) |
| WTW | Well to Wheel |
Acknowledgments
References
- Basic Research Needs for Solar Energy Utilization. Report of the Basic Energy Sciences Workshop on Solar Energy Utilization, 18-21 April, 2005; California Institute of Technology: Pasadena, CA, USA, 2005.
- Mayeres, I.; Proost, S.; Vandercruyssen, D.; Nocker, L.D.; Panis, L.I.; Wouters, G.; Borger, B.D. The External Costs of Transportation. 2001. Final Report; Sustainable Mobility Program, Federal Office for Scientific, Technical and Cultural Affairs, Prime Minister’s Services State of Belgium: Brussels, Belgium, 2001. [Google Scholar]
- Granovskii, M.; Dincer, I.; Rosen, M.A. Economic and environmental comparison of conventional, hybrid, electric and hydrogen fuel cell vehicles. J. Power Sources 2006, 159, 1186–1193. [Google Scholar] [CrossRef]
- Bernal-Agustın, J.L.; Dufo-Lopez, R. Economical and environmental analysis of grid connected photovoltaic systems in Spain. Renew. Energ. 2006, 31, 1107–1128. [Google Scholar] [CrossRef]
- El-Kordy, M.N.; Badr, M.A.; Abed, K.A.; Ibrahim, S.M.A. Economical evaluation of electricity generation considering externalities. Renew. Energ. 2002, 25, 317–328. [Google Scholar] [CrossRef]
- Wies, R.W.; Johnson, R.A.; Agrawal, A.N.; Chubb, T.J. Simulink model for economic analysis and environmental impacts of a PV with diesel-battery system for remote villages. IEEE Trans. Power Syst. 2005, 20, 692–700. [Google Scholar] [CrossRef]
- Funk, K.; Rabl, A. Electric versus conventional vehicles: social costs and benefits in France. Trans. Res. Pt. D–Transp. Envrio. 1999, 4, 397–411. [Google Scholar] [CrossRef]
- National Aeronautics and Space Administration. Available online: http://www.nasa.gov/ (accessed 13 November, 2008).
- Exid Technology Industrial Energy. OPzS Solar battery catalogue. Available online: http://www.exide-nordic.com/pdf/manualer/Classic%20Solar%20(english).pdf (accessed 13 November, 2008).
- United States Department of Energy. Available online: http://www.fueleconomy.gov/feg/atv.shtml (accessed 13 November, 2008).
- Pacca, S.; Sivaraman, D.; Keoleian, G.A. Life Cycle Assessment of the 33 kW Photovoltaic System on the Dana Building at the University of Michigan: Thin Film Laminates, Multi-Crystalline Modules, and Balance of System Components. Report No. CSS05-09; Center for Sustainable Systems, University of Michigan: Ann Arbor, MI, USA, 2006. Available online: http://css.snre.umich.edu/css_doc/CSS05-09.pdf (accessed 13 November, 2008).
- John Deere Company. Available online: http://www.deere.com/en_US/ag/index.html (accessed 13 November, 2008).
- United States Environmental Protection Agency (EPA). Exhaust and crankcase emission factors for non-road engine modeling—compression-ignition; EPA420-P-04-009; 2004. Available online: http://www.epa.gov (accessed 13 November, 2008).
- Fthenakis, V.M.; Kim, H.C.; Alsema, E. Emissions from photovoltaic life cycles. Environ. Sci. Technol. 2008, 42, 2168–2174. [Google Scholar] [CrossRef] [PubMed]
- Meier, P.J. Life Cycle Assessment of Electricity Generation Systems and Application for Climate Change Policy Analysis. Ph.D Dissertation, University of Wisconsin-Madison, Madison, WI, USA, 2002. Available online: http://fti.neep.wisc.edu/pdf/fdm1181.pdf (accessed 13 November, 2008). [Google Scholar]
- Krauter, S.; Ruther, R. Considerations for the calculation of greenhouse gas reduction by photovoltaic solar energy. Renew. Energ. 2004, 29, 345–355. [Google Scholar] [CrossRef]
- Alsema, E.A.; Wild-Scholten, M.J. The real environmental impacts of crystalline silicon PV modules: an analysis based on up-to-date manufactures data. 2006. Available online: http://www.solarworld.de (accessed 13 November 2008).
- Alsema, E.A.; Wild-Scholten, M.J.; Fthenakis, V.M. Environmental impact of PV electricity generation a critical combustion of energy supply options. In Proceedings of the 21st European Photovoltaic Solar Energy Conference, Dresden, Germany, 2006; Available online: http://www.sense-eu.net (accessed 18 November 2008).
- Alsema, E.A.; Fthenakis, V.M. PV energy payback and greenhouse gas emissions: 2004 status, fact sheet. 2005. Available online: http://www.nrel.gov/pv/thin_film/docs (accessed 18 November 2008). [Google Scholar]
- Rydh, C.J. Environmental assessment of vanadium redox and lead-acid batteries for stationary energy storage. J. Power Sources 1999, 80, 21–29. [Google Scholar] [CrossRef]
- Rantik, M. Life cycle assessment of five batteries for electric vehicles under different charging regimes. The Swedish transport and communications research board (KFB), 1999. Available online: http://www.kfb.se (accessed 22 November 2008).
- United States Environmental Protection Agency (EPA). Available online: http://www.epa.gov (accessed 13 November 2008).
- American Society of Agricultural and Biological Engineers (ASABE). Agricultural Machinery Management Data; ASABE: St Joseph, MI, USA, 2006, 53th ed. Available online: http://asabe.org/ (accessed 27 November 2008).
- Automotive fuels for the future—the research for the alternatives. Available online: http://www.iea.org (accessed 13 November 2008).
- Dhingra, R.; Overly, J.G.; Davis, G.A. Life-Cycle Environmental Evaluation of Aluminum and Composite Intensive Vehicles; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 1999. Available online: http://eerc.ra.utk.edu (accessed 22 November 2008).
- Diaf, S.; Belhamel, M.; Haddadi, M.; Louche, A. Technical and economic assessment of hybrid photovoltaic/wind system with battery storage in Corsica island. Energ. Policy. 2008, 36, 743–754. [Google Scholar] [CrossRef]
- Lazou, A.A.; Papatsoris, A.D. The economics of photovoltaic stand-alone residential households: A case study for various European and Mediterranean locations. Sol. Energy Mater. Sol. Cells. 2000, 62, 411–427. [Google Scholar] [CrossRef]
- Shaahid, S.M.; Elhadidy, M.A. Technical and economic assessment of grid-independent hybrid photovoltaic-diesel-battery power systems for commercial loads in desert environments. Renew. Sust. Energ. Rev. 2007, 11, 1794–1810. [Google Scholar] [CrossRef]
- Kolhe, M.; Kolhe, S.; Joshi, J.C. Economic viability of stand-alone solar photovoltaic system in comparison with diesel-powered system for India. Energ. Economics 2002, 24, 155–165. [Google Scholar] [CrossRef]
- Nouni, M.R.; Mullick, S.C.; Kandpal, T.C. Photovoltaic projects for decentralized power supply in India: A financial evaluation. Energ. Policy 2006, 34, 3727–3738. [Google Scholar] [CrossRef]
- Hunt, D. Farm Power and Machinery Management, 10th ed.; Waveland Press: Long Grove, IL, USA, 2001; pp. 75–97. [Google Scholar]
- Khouzam, K.Y. Technical and economic assessment of utility interactive systems for domestic applications in south east Queensland. IEEE Trans. Energy Convers. 1999, 14, 1544–1550. [Google Scholar] [CrossRef]
- Bickel, P.; Friedrich, R. Environmental External Costs of Transport; Springer: Berlin, Germany, 2001; p. 231. [Google Scholar]
- Victoria Transport Policy Institute. Transportation cost and benefit analysis–air pollution costs. 2007. Available online: http://www.vtpi.org (accessed 15 November 2008).
- Monzon, A.; Guerrero, M.J. Valuation of social and health effects of transport-related air pollution in Madrid (Spain). Sci. Total Environ. 2004, 334-335, 427–434. [Google Scholar]
- Bouzidi, B.; Haddadi, M.; Belmokhtar, O. Assessment of a photovoltaic pumping system in the areas of the Algerian Sahara. Renew. Sustain. Energ. Rev. 2009, 13, 879–886. [Google Scholar] [CrossRef]
- Ajan, C.W.; Ahmed, S.S.; Ahmad, H.B.; Taha, F.; Mohd-Zin, A.A.B. On the policy of photovoltaic and diesel generation mix for an off-grid site: East Malaysian perspectives. Solar Energ. 2003, 74, 453–467. [Google Scholar] [CrossRef]
- Oparaku, O.U. Rural area power supply in Nigeria: A cost comparison of the photovoltaic, diesel/gasoline generator and grid utility options. Renew. Energ. 2003, 28, 2089–2098. [Google Scholar] [CrossRef]
- Celik, A.N. Present status of photovoltaic energy in Turkey and life cycle techno-economic analysis of a grid-connected photovoltaic-house. Renew. Sust. Energ. Rev. 2006, 10, 370–387. [Google Scholar] [CrossRef]
- The Business and Economy Database of Lebanon. Available online: http://www.databank.com.lb/ (accessed 6 November 2008).
- The 2008 World Factbook. Available online: http://www.photius.com/rankings/economy (accessed 6 November 2008).
© 2009 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Mousazadeh, H.; Keyhani, A.; Mobli, H.; Bardi, U.; El Asmar, T. Sustainability in Agricultural Mechanization: Assessment of a Combined Photovoltaic and Electric Multipurpose System for Farmers. Sustainability 2009, 1, 1042-1068. https://doi.org/10.3390/su1041042
Mousazadeh H, Keyhani A, Mobli H, Bardi U, El Asmar T. Sustainability in Agricultural Mechanization: Assessment of a Combined Photovoltaic and Electric Multipurpose System for Farmers. Sustainability. 2009; 1(4):1042-1068. https://doi.org/10.3390/su1041042
Chicago/Turabian StyleMousazadeh, Hossein, Alireza Keyhani, Hossein Mobli, Ugo Bardi, and Toufic El Asmar. 2009. "Sustainability in Agricultural Mechanization: Assessment of a Combined Photovoltaic and Electric Multipurpose System for Farmers" Sustainability 1, no. 4: 1042-1068. https://doi.org/10.3390/su1041042
APA StyleMousazadeh, H., Keyhani, A., Mobli, H., Bardi, U., & El Asmar, T. (2009). Sustainability in Agricultural Mechanization: Assessment of a Combined Photovoltaic and Electric Multipurpose System for Farmers. Sustainability, 1(4), 1042-1068. https://doi.org/10.3390/su1041042




