Going Back to Fundamentals: Three Marriageable Actions for Thalassemia and Carrier Population Management

Abstract

We investigated the impact of three marriageable actions: normal-to-carrier, carrier-to-normal, and carrier-to-carrier marriages on thalassemia and carrier populations. The well-known strategy is limiting the carrier-to-carrier marriage to reduce the thalassemia population. Thus, the other two marriageable actions were often ignored. Other than a simple explanation of their genetic consequences, their important aspect in the thalassemia inheritance mechanism has never been studied at the population level. Moreover, there is no mathematical model investigating problem of interest for blood disorders at the population level. Hence, we developed a mathematical model to examine the possibility of eradication/reduction of thalassemia and carrier populations through each of the three marriageable actions in the long-term. We conducted computer simulations with the demographic data of the United Arab Emirates in which high thalassemia carrier prevalence is identified. We found that promoting more carrier-to-normal marriage will eventually have the same effects on marriage reconsideration for carrier-carrier couples, contributing to the reduction of the carrier population in the long-term. Interestingly, the normal-to-carrier marriage does not necessarily have a similar effect on thalassemia and carrier populations as that of the carrier-to-normal marriage. Thus, the two marriageable actions should be distinguished and also seriously considered in education and public awareness campaigns for thalassemia.

1. Introduction

Thalassemia is a genetic blood disorder that causes abnormal form of hemoglobin, consequently damaging red blood cells. Thus, this disorder often results in anemia. There are two types of thalassemia: $\alpha$ and $\beta$ thalassemia depending on which genes and how many genes in the hemoglobin have been affected. If all $\alpha$ genes or $\beta$ genes in the hemoglobin are affected, thalassemia (major) is diagnosed. On the other hand, if only a partial number of genes are damaged or missing, $\alpha$ or $\beta$ thalassemia carrier (minor) is diagnosed [1,2,3,4,5,6]. Thalassemia major usually causes a chronic and life-long anemia that should be treated with frequent blood transfusions and removal of excessive iron deposition due to the frequent blood transfusions unless a 100% matched bone marrow transplant is available, which is a rare possibility. Although these days the number of thalassemia majors in many countries might not be considered high due to thalassemia management efforts in such countries, the life-long blood transfusion treatment can outrank the consumption of any other treatments requiring blood use. This can become a burden on the public healthcare system. Worldwide, 9 million thalassemia carrier women become pregnant annually and 1.33 million pregnancies are at risk of a thalassemia major condition [7,8].

A consanguineous marriage known as an intera-family marriage, i.e., a marriage among close cousins has been a popular norm of marriage in the Middle East and North Africa (MENA) region. As a result, it became one of the major causes of widespread thalassemia in this region [9,10,11,12,13,14,15]. Despite the outcome, the consanguineous marriage tradition still continues. The scope of consanguineous marriage practice in some MENA countries is around 25% to 54% out of all marriage practices [13,16,17,18]. Consequently, not only the thalassemia population but also the high prevalence of thalassemia carriers has become a public health concern. To lower the thalassemia prevalence, there have been great efforts in the MENA region. For example, the United Arab Emirates (UAE) government has launched a nationwide campaign for premarital screening and newborn baby screening to raise public awareness and identify the thalassemia carrier population since 2008. Since 2012, the premarital screening has become mandatory to all about-to-marry couples in order to screen for any possible genetic diseases such as thalassemia [19]. Although premarital screening offers carrier–carrier couples a non-directive genetic counseling including that of the risk of having a thalassemia baby [20], the final decision to marry is upon them, and many carrier–carrier couples proceed to marry. Additionally, it is worth mentioning that pregnancy termination due to thalassemia is not allowed as a prevention of thalassemia in the UAE. Today, the number of affected births has been almost halved compared to that at the time before the introduction of prevention measures in the UAE [9,21].

However, the prevalence of thalassemia carriers is still high and a public health concern in many MENA countries [13,16,17,18]. A high carrier population can imply a high possibility of carrier-to-carrier marriage that can give birth to a thalassemia baby with a 25% chance and a carrier baby with a 50% chance. The production of carrier babies is a potential cause of the increase in the thalassemia population. Interventions such as newborn baby screening, premarital screening, and genetic counseling is expected to affect behavioral and psychological changes in lifestyle and marriage decision when people are aware of their genetic characteristics. Even though the newborn baby screening serves as one of the important medical records, people tend to forget about it and their memory only gets refreshed with premarital screening that can influence their marriage decision. Although there are public awareness campaigns on thalassemia from time to time, there is a wide time gap between the times of newborn baby screening and premarital screening. Then, the question is whether there has been an adequate effort or input in education and public health regarding thalassemia carriers so that the consequence of carrier-to-carrier marriage was well informed to the general public during this time gap. The answer seems to be no as there is a high prevalence of thalassemia carriers at present. For example, the prevalence of thalassemia carriers in the UAE was around 8.5% between 2007 and 2010 [20]. With the rapid population growth in the UAE, the prevalence of thalassemia carriers was expected to grow as well.

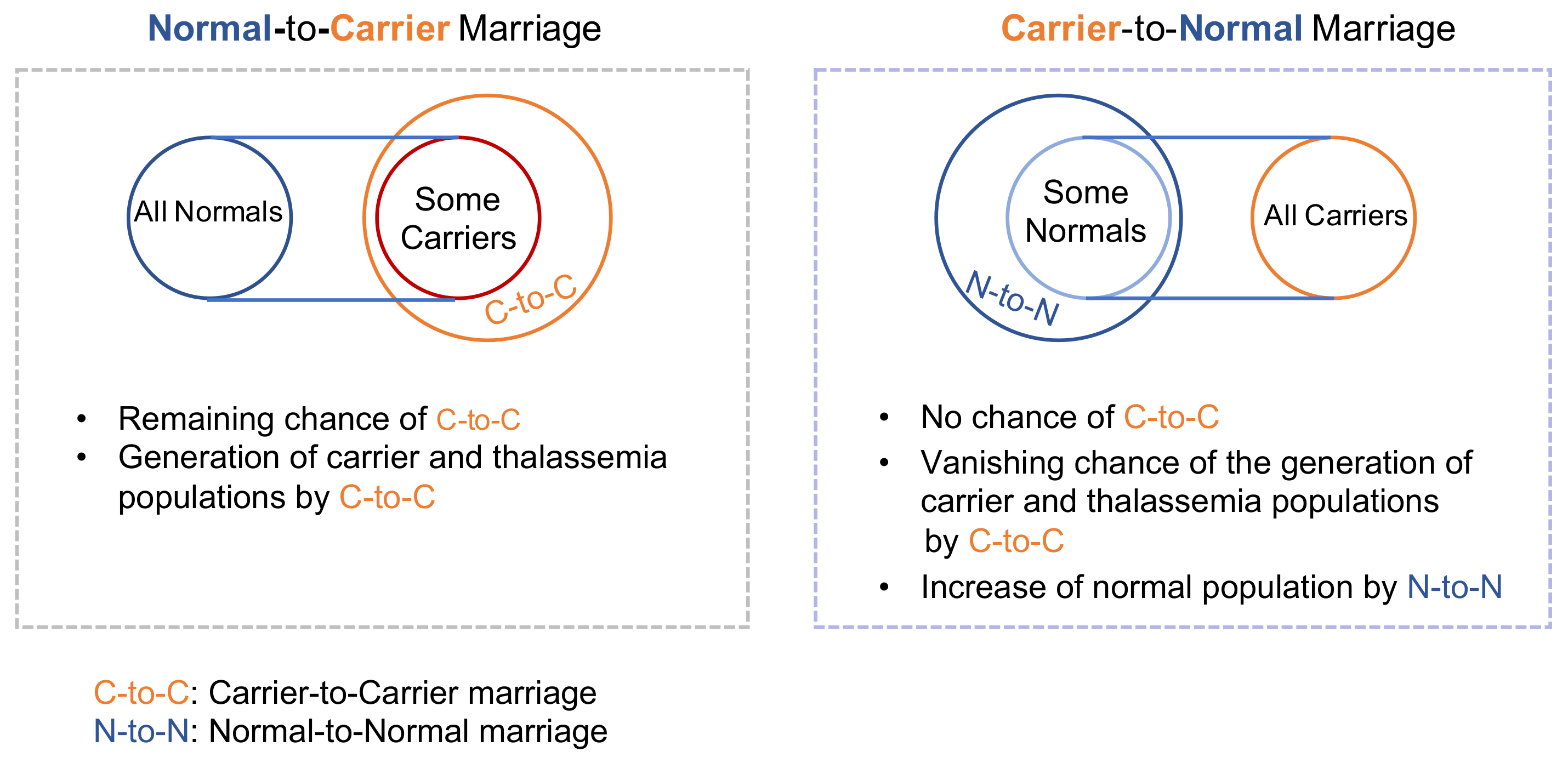
Since thalassemia and carrier status can pass down to the next generation via marriage, newborn baby screening, premarital screening, and public campaigns for thalassemia heavily focus on identifying the carrier population and carrier-to-carrier marriage. This is why other types of marriageable actions such as normal-to-carrier and carrier-to-normal marriages were completely ignored. As mentioned earlier, the reconsideration of carrier-to-carrier marriage may not always result from premarital screening and genetic counseling performed right before the wedding. Here, normal-to-carrier marriage means that a normal individual chooses to marry a carrier individual. Carrier-to-normal marriage implies that a carrier individual decides to marry a normal individual. The two marriageable actions are different although the final number of couples is the same as normal–carrier couples. However, as the pool of the normal population is usually larger than that of the carrier population, the chance of normal-to-carrier marriage is different from that of carrier-to-normal marriage. Therefore, the two marriageable actions should be distinguished. Since marriage reconsideration of carrier-to-carrier marriage is not always guaranteed, the normal-to-carrier/carrier-to-normal marriages should be promoted beforehand as an alternative form of marriage reconsideration of carrier-to-carrier marriage. In other words, during the time gap between newborn screening and premarital screening, the benefits and effects of the two marriageable actions should be continuously campaigned and disseminated to the general public. If such an environment is accomplished, even the non-carrier populations can seriously embrace the public health concern of thalassemia, and the carrier population can have adequate time to consider their marriage course after a careful search for the available options without being stigmatized by their genetic characteristics and rushing to a decision after the premarital screening.

So far, other than a simple explanation of the genetic consequences of normal-to-carrier and carrier-to-carrier marriages, no formal assessment has ever been made on the type of impact of normal-to-carrier, carrier-to-normal, and carrier-to-carrier on thalassemia and carrier populations. Moreover, there is no mathematical model to investigate this question before. In this paper, to provide policy-makers, health care workers, educators, and the general public with a concrete base for a sustainable campaign and education about the benefits and effects of these three marriageable actions, we develop a mathematical model to assess the three marriageable actions. Then, we experiment with different cases by varying the chances of normal-to-carrier, carrier-to-normal, and carrier-to-carrier marriages at a time and observe how each case can affect thalassemia, carrier, and married population groups. This experiment is conducted using computer simulations with the UAE demographic data. We also provide mathematical proofs to ensure that our model is biologically plausible and applicable to real-life problems. The organization of the paper is as follows. In Section 2, we describe our mathematical model, and explain variables and parameters. In Section 3 we present the assessment results of the three marriageable actions via the computer simulations of our model using the UAE demographic data. Finally, the discussion and future work are presented in Section 4.

2. Methods

We propose a modeling study via a dynamic model and computer simulations to investigate three marriageable actions that can impact on thalassemia and carrier populations. Here, the dynamic model refers to a mathematical model that describes the population dynamics such as the increase or decrease in a specific population group via differential equations. A dynamic model and computer simulations can experiment with hypothetical situations that may not be immediately identifiable by clinical or observational studies due to the difficulties inherent in human subject studies. For example, for our study purpose, we cannot force people to marry. In this situation, we can create a dynamic model based on the literature and data, and test different possible scenarios via computer simulations using demographic data available.

Since a genetic disease is passed to the next generation through marriage, we divide the whole UAE population into male and female subpopulation groups in our dynamic model. Then, our dynamic model considers a complete human life cycle such as being born, growing into children, reaching a marriageable age, getting married, giving birth, and death. This is why we included a few more subpopulation groups than only males and females. Then, we classify the whole population further into the following:

(i)

Children population under the age of 20: normal children $G_M$/$G_F$ and (thalassemia) carrier children $G_C^M$/$G_C^F;$

(ii)

Single adult population over the age of 20: normal adult singles $S_M$/$S_F$ and carrier adult singles $C_M$/$C_F$;

(iii)

Thalassemia major population: $T_M$/$T_F$;

(iv)

Married population groups: normal-to-normal married group $U_1,$ normal-to-carrier/ carrier-to-normal married group $U_2,$ and carrier-to-carrier married group $U_3,$

where M and F stand for male and female, respectively. The normal population indicates individuals who did not inherit thalassemia genes from either of their parents. The carrier (thalassemia) population is a group of people who have a thalassemia gene inherited from one (both) of their parents. Thalassemia major can be either $\alpha$ or $\beta$ thalassemia, depending on a specific country or community of interest. For example, thalassemia major would mean $\beta$ thalassemia in the UAE. In order to describe the different marriageable actions, we need to distinguish between single males and females. That is why we set up male and female single population groups. However, once people get married, they are no longer singles. Thus, these married male and female individuals should be considered in a separate group, i.e., a married group. Thus, the three married population groups can be interpreted as the mixed groups of males and females who get married. Therefore, the half of a married population group should be males and the other half females. The new-born babies will depend on the number of married couples, i.e., half the size of a married population group. That is why we do not need to create married male or married female population groups like singles population groups. In our model, there are several types of population transitions as follows. Once a baby is born, the boy or girl will be screened as either normal, carrier, or thalassemia. Thus, any baby will be moved to one of the three types of children groups. When they reach the age of 20, they will be transferred to the young adult groups based on their thalassemia status. After their getting married, these married individuals will be moved to one of the three married groups such as normal-to-normal, normal-to-carrier/carrier-to-normal, and carrier-to-carrier marriage groups.

With the above population groups (compartments), we develop a compartment model and describe the dynamics between the compartments by differential equations. For the proposed model, we assume the following:

A1.

Thalassemia control measures are newborn baby screening and premarital screening.

A2.

The newborn baby screening is given to almost all newborn babies, and the premarital screening is provided to all about-to-marry couples.

A3.

People who receive a thalassemia control measure can reconsider their marriage decision.

A4.

Thalassemia major population group has a very low chance of marriage due to prolonged treatments. Hence, the marriage rate of the thalassemia major population groups is negligible.

A5.

Marriageable actions are actions of searching for spouses by marriageable adults who are above twenty years of age.

A6.

Since three marriageable actions such as normal-to-carrier, carrier-to-normal and carrier-to-carrier marriages can affect thalassemia and carrier populations, they will be in focus. A normal-to-carrier (carrier-to-normal) marriage means that a normal (carrier) individual chooses to marry a carrier (normal) individual. A carrier-to-carrier marriage implies that a carrier individual decides to marry a carrier individual.

A7.

Except for the thalassemia major population group, all other groups can marry with certain marriage rates.

A8.

The combinations of possible marriages among single males and females are

•

normal male × normal female

•

normal male × carrier female or carrier male × normal female

•

carrier male × carrier female

Then, the dynamic model consists of a set of thirteen differential equations. The details of the model and analysis can be found in Appendix A.1. We conducted computer simulations of our model to estimate the future trend of thalassemia and carrier populations in UAE and investigate the different cases of the three marriageable actions with the UAE demographic data as in

Table 1. Literature based and estimated parameter values.

Parameter	Male	Female	Ref.
Birth rates	$b_M=8716$	$b_F=7954$	[22]
Child mortality rates ${}^{†}$	$d_M^G=0.014$	$d_F^G=0.008$	[23]
Adult death rates ${}^{†}$	$d_M=0.003$	$d_F={\mu }^{††}=0.0019$	[22]
Thalassemia induced death rate ${}^{†}$	$d_T=0.016$	$d_T=0.016$	[1]
Proportion of young adults ${}^{†}$	${\gamma }_M=0.0433$	${\gamma }_F=0.0447$	[19]
Newborn baby screening rate	${\beta }_S^M={\beta }_S^F=1$		[6]
Thalassemia detection adjusting rates	${\eta }_T^M=0.0083$	${\eta }_T^F=0.0075$	[6]
Thalassemia carrier
detection adjusting rates	${\eta }_{CG}^M=0.0416$	${\eta }_{CG}^F=0.05416$	[17]
Premarital screening rates ${}^{†}$	${\alpha }_S^M=0.0227$	${\alpha }_S^F=0.0223$	[22]
Chance of normal population
getting married with carrier population	${\epsilon }_1=0.5$ *		−
Chance of carrier population
getting married with normal population	${\epsilon }_2=0.5$ *		−
Marriage reconsideration rate
of carrier-carrier couples	$\nu =0.3$ *		−

^† The unit of the parameter values is per person. ^†† $\mu$ represents the proportion of married population who died during their marriage. * These parameter values are initially assigned to our computer simulations and will be varied for further investigations of their impacts.

. The parameter values related to the three marriageable actions in Table 1 are initially given to our computer simulations and will be varied later to see their impacts on the three marriageable actions. The sensitivities of the model parameters on variables is considered in order to measure the burden of the problem of interest. For each variable, the sensitivity regarding parameters is estimated as they change over time, then the variance of the variable with respect to each parameter considered is plotted in a box plot.

All our simulations were generated with the R software [24], and the sensitivity analysis with the Flexible Modeling Environment (FME) package [25] (See R code in Supplementary Materials).

3. Results

In our model, we implemented two types of interventions such as newborn baby screening and premarital screening. These two interventions are widely available in the UAE. With these thalassemia interventions in our model, we focused on the steady state, an eventual state in the long-term of the model. We mathematically proved that each population group will stay positive at all times. This implies that a thalassemia-free state will not exist, which means that the eradication of thalassemia in the long-term will not be possible even with the above-mentioned interventions. The detailed analytical result can be found in Appendix A. This does not mean that these interventions are not effective at all but that they are not effective enough to eradicate thalassemia. Thus, we still need to promote these interventions to reduce thalassemia population or keep the thalassemia population to a desired level.

3.1. Impact of the Three Marriageable Actions

The reason why thalassemia population can stay above zero at all times is because of the existence of the carrier population. The carrier population can be generated through a marriage among normal and carrier individuals. We investigated the effect of the three key rates such as the marriage reconsideration rate $\left(\nu \right)$ among carrier–carrier couples, the chance (${\epsilon }_1$) of normal population getting married with carrier population, and the chance $\left({\epsilon }_2\right)$ of carrier population getting married with normal population on the thalassemia and carrier populations in the long-term via computer simulations with the UAE demographic data as shown in 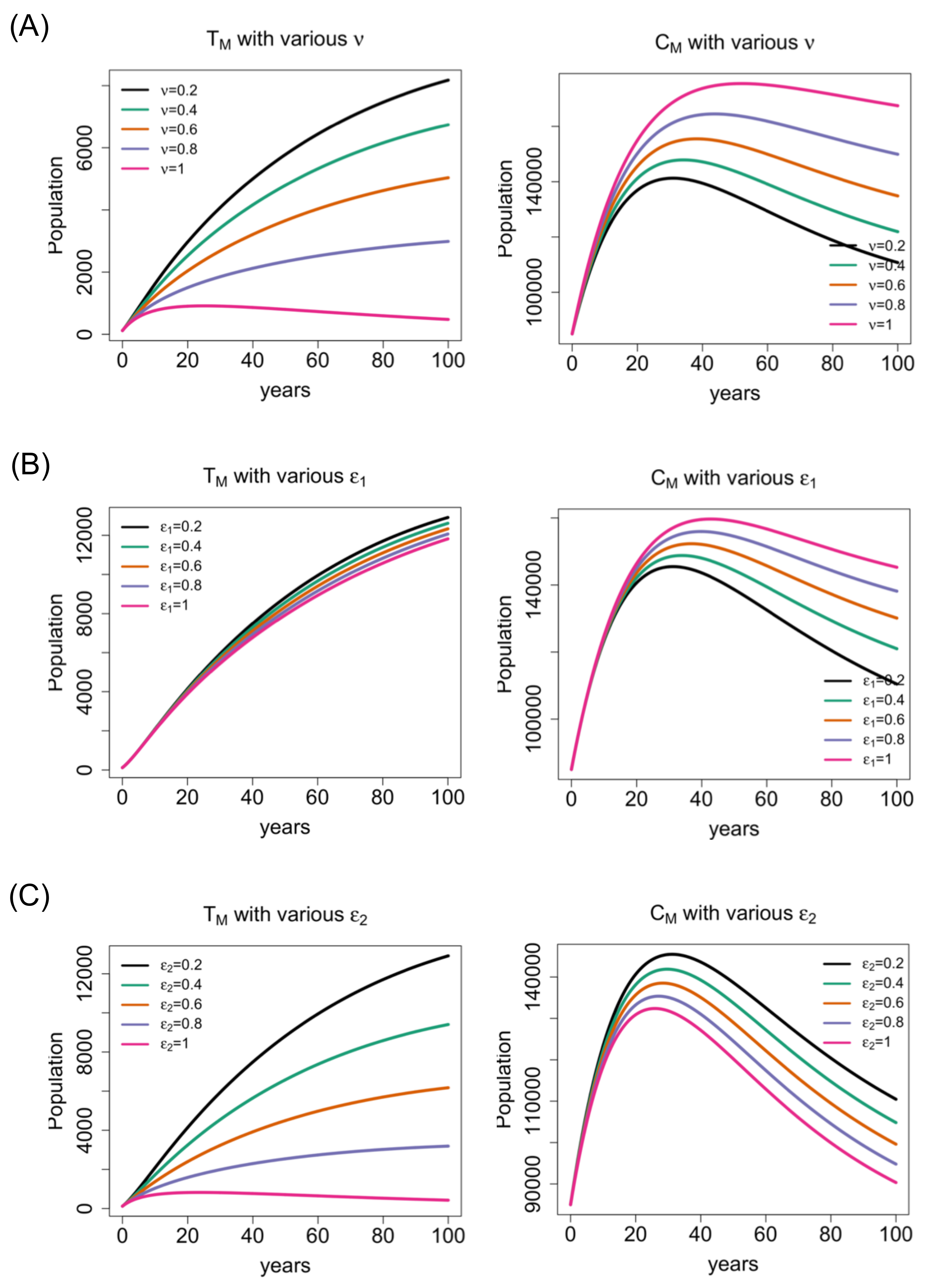Table 1. For such computer simulations, we fixed all parameter values, but varied the marriage reconsideration rate and the chances of normal (carrier) population getting married with carrier (normal) population in the period of 100 years. Although Figures 1 and 3 show increasing only or decreasing trends, these graphs eventually reach steady states (some positive numbers) in the long-term. Since the male and female groups in each subpopulation showed similar patterns on their long-term trends, for simplicity, we will present the results of only the single male and married population.

Figure 1A–C show the impact of the three key rates ($\nu ,$${\epsilon }_1,$ and ${\epsilon }_2$) on thalassemia and carrier population groups. As the marriage reconsideration rate increases, more carrier-to-carrier marriages are dropped. Thus, such carrier couples come back to their single status, which will eventually lead to the reduction in thalassemia population and the increasing magnitude in the trend of the carrier population at any single time point as shown in Figure 1A The reduction in thalassemia population is also observed when the chance of carrier-to-normal marriage increases shown in Figure 1C. This outcome is expected as the more the number of carrier individuals get married with normal individuals, the less carrier-to-carrier marriage occurs consequently, and more is the reduction in the thalassemia population. On the contrary, the change in the chance of normal-to-carrier marriage does not significantly reduce the magnitude in the trend of thalassemia population at any single time point in Figure 1B. Thus, the promotion of normal-to-carrier marriage may not be effective in reducing the thalassemia population to a desired level.

For the carrier population, as the chance of normal population getting married with carrier population increases, the magnitude in the trend of carrier population at any single time point will increase in Figure 1B. This outcome is expected since normal-to-carrier marriage can have a carrier baby with a 50% chance. On the other hand, as the chance of carrier-to-normal marriage increases, the magnitude in the trend of carrier population at any single time point will decrease shown in Figure 1C. This is counter intuitive. However, it can be interpreted as follows. It is true that carrier-to-normal marriage can give birth to a carrier baby with the same 50% chance as that of a normal-to-carrier marriage. In the most extreme situation, let us assume that all carrier individuals choose to marry normal people (see Figure 2). Then, in the next generation, only the 50% of the precedent carrier population will be produced, which results in a 50% reduction in the carrier population in the next generation. On the other hand, if all normal people get married to carrier individuals, the carrier population at the level of 50% of the precedent normal population will be generated in the next generation, i.e., the 50% increase in the carrier population in the next generation. Thus, even if the extreme situation is not considered, this phenomenon will occur through normal-to-carrier and carrier-to-normal marriages, respectively. Moreover, pursuing carrier-to-normal marriage can imply dropping carrier-to-carrier marriage in the aspect of the decision of the carrier population and, consequently, the 50% chance of giving birth to a carrier baby by the carrier-to-carrier marriage is eliminated (see Figure 2).

That is why the choice of carrier population to marry normal population has an indirect impact on the reduction in the carrier population as well as that on the thalassemia population. Overall, the magnitude in the trend of carrier population at any single time point seems to be far more reduced by an increase in the chance of carrier-to-normal marriage than marriage reconsideration or normal-to-carrier marriage. This result is the most distinguished feature of our study, i.e., the impact of normal-to-carrier marriage and that of carrier-to-normal marriage on carrier and thalassemia populations are indeed different.

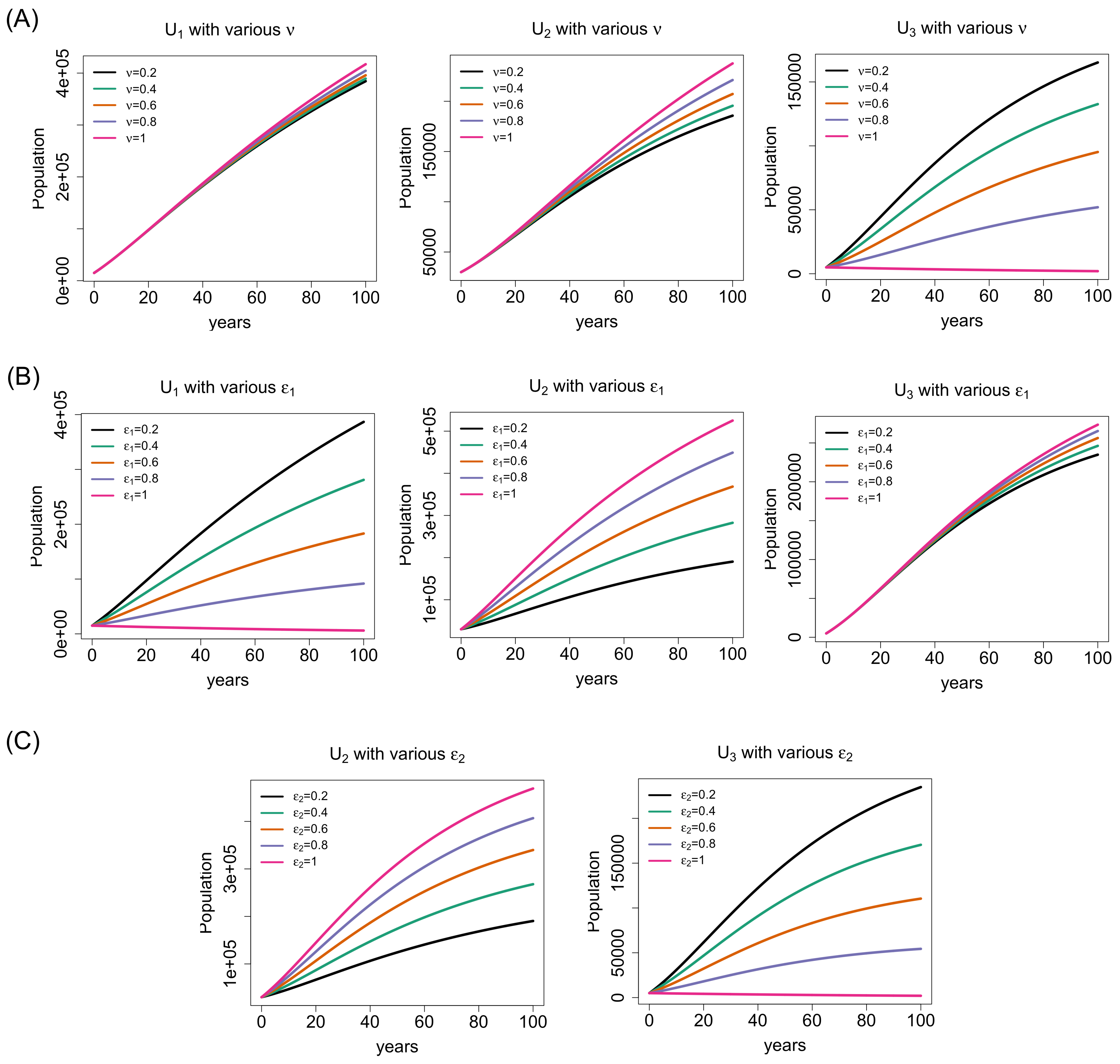
Figure 3 demonstrates the effect of the three key rates (marriage reconsideration rate ($\nu$), chance of normal-to-carrier marriage (${\epsilon }_1$), and chance of carrier-to-normal marriage (${\epsilon }_2$)) on married population. Figure 3A presents how the three groups of marriage such as normal-to-normal ($U_1$), normal-to-carrier/carrier-to-normal ($U_2$), and carrier-to-carrier ($U_3$) can change as the marriage reconsideration rate ($\nu$) increases. Since the marriage reconsideration is exercised by carrier–carrier couples, the changes in the marriage reconsideration rate does not noticeably affect the magnitude in the trend of normal-to-normal and normal-to-carrier/carrier-to-normal marriage groups at any single time point. However, as the marriage reconsideration rate increases, of course, a more number of carrier-to-carrier marriages will be dropped, i.e., the magnitude in the trend of carrier-to-carrier marriage will decrease or tend to zero if 100% carrier-to-carrier marriages are reconsidered. In reality, not all carrier-to-carrier marriages will be reconsidered and, hence, there will be always a positive number of carrier-to-carrier marriages. This is why the level of thalassemia and carrier populations will continuously stay positive since the carrier-to-carrier marriage has the 50% chance of giving birth to a carrier baby and 25% chance to a thalassemia baby.

Figure 3B,C explain the impact of the changes in the chances of normal-to-carrier and carrier-to-normal marriages on the three marriage groups. We observe that the normal-to-normal marriage is not affected by the chance of carrier-to-normal marriage at all and hence omit the plot in Figure 3C. The carrier-to-carrier marriage does not show much difference in magnitude in its trend at any single time point by the the change in the chance of normal-to-carrier marriage in Figure 3B. As the chance of normal-to-carrier marriage increases, more normal-to-carrier marriages and less normal-to-normal marriages are seen in Figure 3B as well. The carrier-to-normal/normal-to-carrier marriage group evolved in the same trend in magnitude at any single time point as the chances of normal-to-carrier marriage and carrier-to-normal marriage increase. However, the carrier-to-carrier marriage group evolved in the opposite direction to that of the carrier-to-normal/normal-to-carrier marriage group under the chance of carrier-to-normal marriage found in Figure 3C. Such a trend in the carrier-to-carrier marriage group under the increasing chance of carrier-to-normal marriage was observed in the trend of the carrier population as well (see the second figure in Figure 1C.

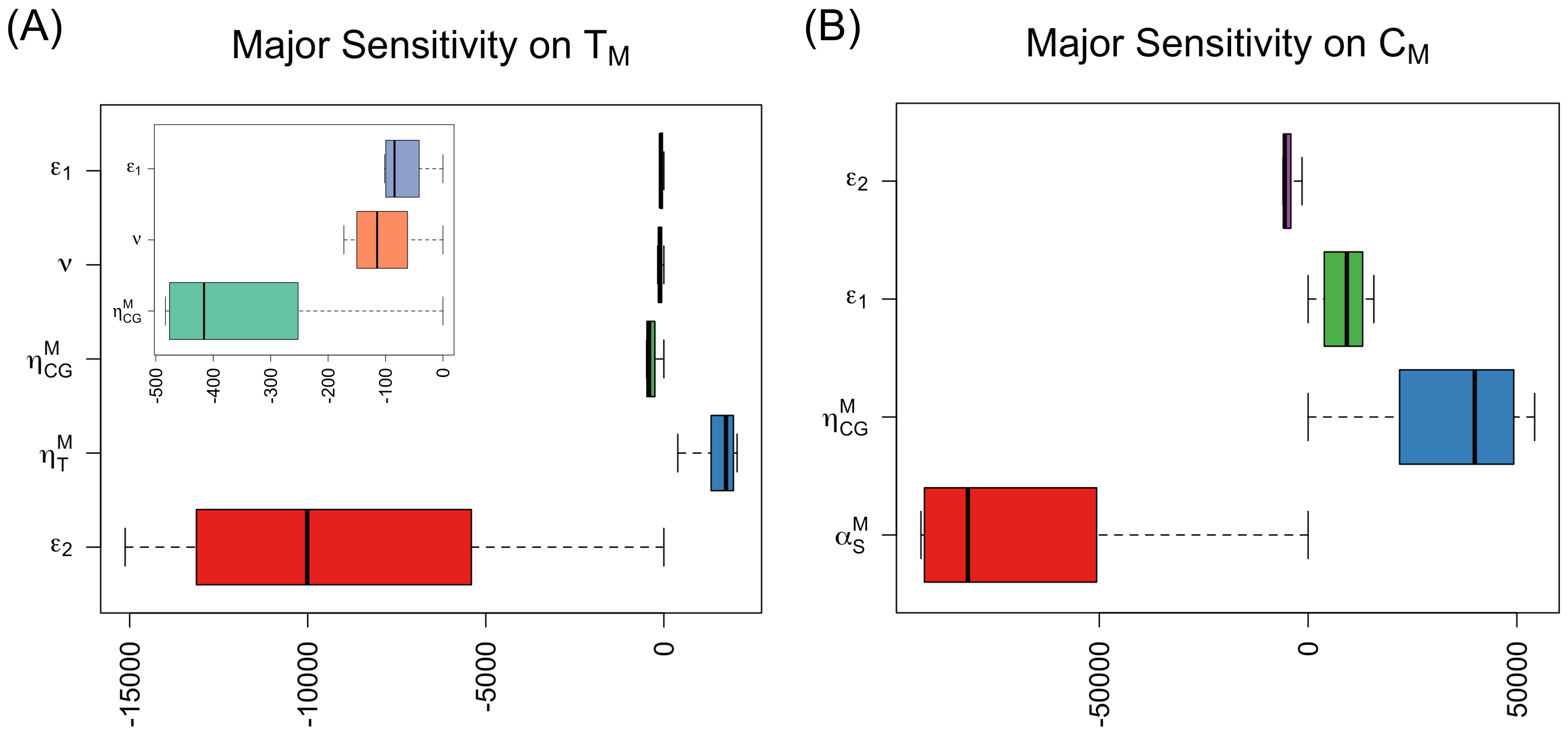
3.2. Sensitivity Analysis of the Selected Model Parameters

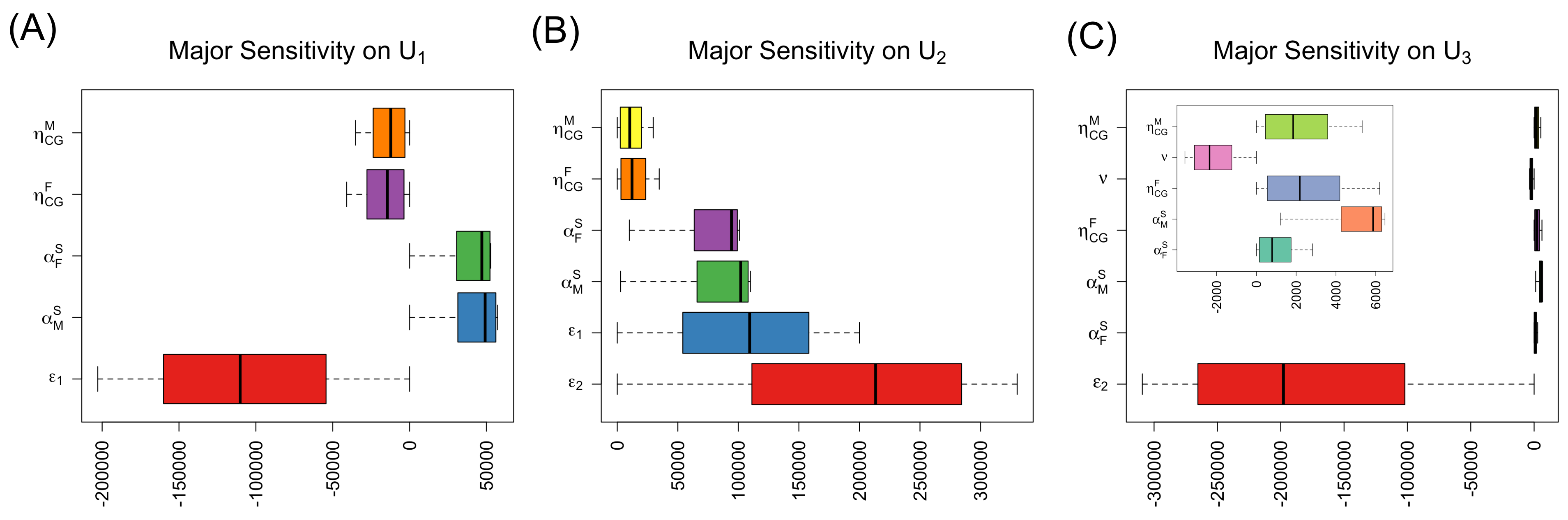
The results of the future trend change by varying the three key parameter values were confirmed by the sensitivity analysis of parameters as well. We included the sensitivity analyses of significant parameters whose absolute means are greater than 5000. In fact, 5000 represents approximately 1% of the total UAE male or female nationals assuming that half of the total population (approximately 1 million) is males or females.

Figure 4A,B show the sensitivity results on thalassemia ($T_M$) and carrier populations ($C_M$). In Figure 4A, we can easily see the largest reduction in the thalassemia population with the chance (${\epsilon }_2$) of carrier-to-normal marriage, whereas the impact of marriage reconsideration rate ($\nu$) or the chance (${\epsilon }_1$) of normal-to-carrier marriage on the thalassemia population is minimal. Furthermore, thalassemia or carrier babies identified through the newborn baby screening implies higher thalassemia or carrier population shown with thalassemia major and carrier screening rates (${\eta }_T^M$ and ${\eta }_{CG}^M$) in Figure 4A,B, respectively. The large impact of the chance (${\epsilon }_2$) of carrier-to-normal marriage induces a decrease in thalassemia in Figure 4A and carrier populations in Figure 4B. The sensitivity results of the chances of carrier-to-normal marriage and normal-to-carrier marriage on carrier population are reflected in Figure 1B,C, respectively. The result in Figure 4B is counter intuitive but a similar explanation can be found from that of Figure 1C.

Figure 5A–C display the sensitivity analysis of parameters on three married groups.

The more the carrier babies are screened via the newborn baby screening (i.e., the higher ${\eta }_{CG}^M$ and ${\eta }_{CG}^F$), the less the normal-to-normal marriages and the more the normal-to-carrier/carrier-to-normal and carrier-to-carrier marriages occur. As the chance (${\epsilon }_1$) of normal-to-carrier marriage increases, the normal-to-normal marriage decreases shown in Figure 5A. Figure 5C shows the sensitivity results of the two key parameters as follows: the more carrier-to-carrier marriages are dropped (i.e., $\nu$ increases), the smaller carrier-to-carrier marriage group will be. Additionally, the more carrier-to-normal marriage is encouraged (i.e., ${\epsilon }_2$ increases), the less carrier-to-carrier marriage will occur. This phenomenon can be an explanation to the counter intuitive reverse magnitude in the trend of the carrier (single) population shown in Figure 1C. Additionally, there is a huge impact difference between the marriage reconsideration rate ($\nu$) and the chance (${\epsilon }_2$) of carrier-to-normal marriage on the carrier-to-carrier marriage group ($U_3$), which will consequently affect the magnitude in the trend of carrier population at any single time point as found in Figure 1A,C. As observed in Figure 3B,C, the chances (${\epsilon }_1$ and ${\epsilon }_2$) of normal-to-carrier and carrier-to-normal marriages positively affect the normal-to-carrier/carrier-to-normal marriage group ($U_2$) in Figure 5B. In fact, the chance (${\epsilon }_2$) of carrier-to-normal marriage seems to have the impact twice as large as that of the chance (${\epsilon }_1$) of normal-to-carrier marriage on the normal-to-carrier/carrier-to-normal marriage group ($U_2$). The sensitivity results described in Figure 5B,C may lead to an insightful marriage intervention strategy for carrier population.

4. Discussion

In this paper, we investigated the long-term impact of the three key marriageable actions on thalassemia and carrier populations in the UAE in terms of the chance of normal-to-carrier marriage, the chance of carrier-to-normal marriage and marriage reconsideration of carrier-to-carrier marriage via a mathematical model. To the best of our knowledge, there is no mathematical model applied to a genetic disease or any blood disorders in order to assess how much effective possible marriageable actions can be in the eradication of thalassemia or reduction in carrier population before. Our model considered two sexes, age and social status (children, single adults, and married adults), and three genetic groups of normal, (thalassemia) carrier, and thalasemia (major). Two thalassemia control measures were implemented, namely newborn baby screening and premarital screening that has been mandatory in the UAE in recent years. Hence, in total, we developed a population dynamics model of thirteen subpopulation groups and described their interactions via differential equations. Our model showed that the eradication of thalassemia in the UAE is not possible even with the two control measures and the key marriageable actions. However, that does not mean that the two control measures and three marriageable actions are ineffective to sustain the current thalassemia situation in the UAE. At least the two control measures, newborn baby screening and premarital screening, can raise an awareness or disseminate educational message about their genetic situation and thereby can play a role to help people to carefully search for their spouses in the future.

Regarding the three key marriageable actions, this study concludes:

1.

The eradication of thalassemia can be achieved by the 100% marriage reconsideration of carrier–carrier couples;

2.

Promoting normal-to-carrier marriage will not achieve the eradication of thalassemia at all, but can help reduce the thalassemia population by a small point;

3.

Encouraging carrier-to-normal marriage will make the eradication of thalassemia possible because of its indirect effect of reconsideration of carrier-to-carrier marriage (i.e., the more carrier-to-normal marriage the less carrier-to-carrier marriage);

4.

Carrier-to-normal marriage may be more effective in reducing the carrier population than normal-to-carrier marriage.

At a glimpse, a normal-to-carrier marriage, i.e., a normal individual chooses to marry a carrier person, and a carrier-to-normal marriage, i.e., a carrier individual seeks to marry a normal individual, would be the same. However, the two types of marriages have a huge difference as mentioned before. First of all, the proportion of carrier-to-normal marriage in carrier population may be bigger than that of the normal-to-carrier marriage in normal population since normal population size is often bigger than the carrier population size. Moreover, normal-to-carrier marriage does not necessarily mean the reduction in carrier-to-carrier marriage in the carrier population. Of course, a seemingly quick solution for the eradication of thalassemia would be the 100% reconsideration of carrier-to-carrier marriages. However, realistically, it will not be always possible since marriage reconsideration of a carrier–carrier couple because of the premarital screening result may not be an easy decision. As our simulation and sensitivity results showed, encouraging a carrier-to-normal marriage may take a longer time, but be less drastic to exercise to maintain a desired level of thalassemia and carrier populations that will lead to a gradual eradication of both population groups in the long-term plan.

From the time of newborn baby screening, children and their parents should be imparted learning on thalassemia and its treatment procedure, information on how to avoid such a genetic consequence in their next generation, and/or marriage choices if the children are thalassemia carriers. As a harmonized society, information not only on thalassemia but also on thalassemia carriers should be given to the general public from an early age so that thalassemia or carrier children will not be stigmatized by their genetic status; hence, carrier children can be ready for their marriage choice as naturally as possible. A regular public awareness campaign for thalassemia usually focused on promoting a screening for thalassemia at the time of birth and then before marriage in many affected countries including the UAE. However, it should include the awareness of thalassemia carrier and possible marriage choices as well. Furthermore, the benefits and effects of the three marriageable actions should be continuously educated to the general public from early ages so that the general public can seriously consider the public health concern of thalassemia and carrier population, and thalassemia/carrier population groups are not stigmatized by their genetic status. The continuous efforts of rising attention to these three marriageable actions can provide a stable environment for the carrier population to search for available marriage options with enough time so that they can naturally avoid of passing thalassemia and carrier status to the next generation.

Moreover, hypothetically, if all carrier individuals marry normal individuals in all successive generations, thalassemia will be eventually eradicated in any country carrying thalassemia and carrier populations. This hypothesis is based on the assumption that the pool of the normal population is much larger than that of the carrier population. Thus, an investigation of the optimal pool size of normal population for the potential eradication of thalassemia and the reduction in carrier population can be an interesting avenue to the future work.