Genomic Prediction of Root Traits via Aerial Traits in Soybean Using Canonical Variables

Abstract

The phenotypic evaluation of root traits in soybeans presents challenges in breeding due to its high cost and the requirement for experimental plot destruction. Establishing relationships between aerial and root traits is crucial, given the relative ease of phenotypic evaluations for aerial traits. Therefore, this study aims to utilize the canonical correlation technique to estimate latent variables, subsequently employing GBLUP for the genomic prediction of the root traits (length, volume, surface area, and dry mass) using phenotypic information from aerial part traits (hypocotyl diameter and dry mass). Our results demonstrate the effectiveness of the technique in predicting the root part, even when not directly evaluated. The agreement observed between the top 10% of individuals selected based on the canonical variable and each root trait individually was considered moderate or substantial. This enables the simultaneous selection of genotypes based on both trait groups, providing a valuable approach for soybean breeding programs.

1. Introduction

Soybean (Glycine max (L.) Merril) is an herbaceous oleaginous plant with a C3 metabolism and great genetic variability [1,2]. The grain is highly versatile, finding applications in the production of various products and by-products across the agroindustry, chemical, and food sectors [3]. Consequently, soybeans are being increasingly cultivated worldwide [3,4].

Drought stress stands out as a significant limitation to soybean yield globally [5,6,7]. One strategy employed to mitigate issues related to drought stress involves identifying materials with superior phenotypes in root development, facilitating better plant performance through more efficient water absorption [8]. Specifically, deeper root systems with higher densities enable more efficient soil water extraction. To define the phenotype of the material regarding root superiority, it is essential to measure root traits such as root angle, diameter, length, surface area, and depth [8].

Despite obtaining interesting results [9,10], phenotyping root traits is a time-consuming and challenging technique, complicating the improvement process based on these traits [11,12]. Given the delay in measuring root traits, understanding relationships between these and easily measurable traits, such as aerial traits, becomes crucial. These relationships may allow the selection of better genotypes for root traits based on aerial traits without significant losses in the selection of these genotypes. In practical terms, this possibility would reduce the time and cost of evaluating the roots of genotypes in a breeding program. A statistical method that can be used to study the relationships between groups of traits, for example, aerial and root, is canonical correlation. Canonical correlation (CC) analysis is a multivariate technique that seeks to determine linear combinations, denoted by canonical variables, that maximize the correlation between the two sets of characteristics of interest [13].

Another approach that can be employed to accelerate the development of new cultivars, can increase genetic gain, and is particularly useful when measuring phenotypes proves difficult or expensive is genome-wide selection (GWS) [14]. GWS uses information from molecular markers, based on the principles of linkage disequilibrium between genes and markers, to predict the genetic merit of genotypes, making it possible later to select genotypes based on their respective genotypic information [15].

Genomic best linear unbiased prediction (GBLUP) is the most applied genomic prediction method in soybeans [16]. However, genomic prediction in soybeans is usually used for individual traits, disregarding any relationship between traits or groups of traits [17,18]. Nevertheless, since the traits could be correlated, multi-trait approaches could improve predictive ability by borrowing information between traits controlled by pleiotropy or linkage genes [19,20,21]. But generally, these methods require defining a balance in breeding objectives during selection by the breeders [22]. Thus, an approach that simultaneously incorporates information from multiple traits through latent variables that maximize the correlation between those groups of traits in the selection process may be of interest.

In this context, the present study aims: (1) to investigate the relationship between root and aerial traits in soybean through canonical correlation analysis; (2) to use canonical latent variables as pseudo-phenotypes in genomic prediction; (3) to compare selected individuals using canonical latent variables and individual traits with univariate GBLUP.

2. Materials and Methods

2.1. Plant Material

The experiment was conducted in the year 2021 during the period from September to November in the greenhouse of the Federal University of Viçosa, located in Viçosa-MG at latitude S 20°45′14″, longitude W 45°52′54″, and an altitude of 649 m [23]. One hundred commercial soybean cultivars from different seed companies, distinct transgenic events, growth types, and relative maturity groups were sown. The experiment was conducted according to the methodology proposed and described by Nascimento et al. [24] in a randomized block design with three replications, each corresponding to a plot.

Due to destructive nature of root phenotypic evaluations, to avoid root intertwining, each experimental plot comprised a plant that was grown in a three-liter pot containing a substrate composed of soil and sand in a 2:1 ratio. The substrate was moistened to near field capacity, considering a clayey loam soil with tension values of −10 kPa until the V2 stage [25,26]. After the V2 stage, the tension was maintained at −1200 kPa for a period of 20 days. The pots were regularly weighed, and the volume of evapotranspiration water was replenished [24].

Cultural practices followed technical recommendations for soybean cultivation [27]. Phenotypic traits related to aerial and root traits were destructively evaluated for each plot. Hypocotyl diameter in millimeters (HD) was measured with a digital pachymeter for aerial traits. Plant height in centimeters (PH) was determined as the length of plants from the ground to the peak of the main stem.

For root traits, the roots were washed to remove substrate materials and then stored in a 70% alcohol solution at 4 °C. The WinRHIZOPro^® software (version 2009) [28] was used to measure total root length in centimeters (TRL), root volume (RV), and projected surface area (PSA). After evaluation in WinRHIZOPro^®, the roots were dried in an oven at 65 °C for 48 h and then weighed using a precision balance to obtain the root dry mass (RDM) in grams.

2.2. Genotypic Data Analysis

Individuals were genotyped using the iScan Illumina platform (Illumina, Inc., San Diego, CA, USA) with the “BARC-SoySNP6k” chip at Deoxi Biotecnologia Ltd.a^®, in Araçatuba, SP. The 5403 SNP markers obtained were subjected to quality control through filtering based on the minor allele frequency (MAF) criterion, removing markers with MAF < 0.05. After filtering, 3957 SNP markers were retained for subsequent analyses.

2.3. Phenotypic Data Analysis

The collected data were initially adjusted for effects of the experimental blocks. Correction for experimental effects was performed using mixed linear models (REML/BLUP) [29]. The model considered a randomized block design with three replications and the evaluation of 100 genotypes, expressed as:

$$\mathbf{y}=\mathsf{\mu }+\mathbf{X}\mathbf{b}+\mathbf{Z}\mathbf{g}+\mathsf{\epsilon },$$

(1)

where the vector $\mathbf{y}$ represents the phenotypes, $\mathsf{\mu }$ is the general mean, and the vectors $\mathbf{b}$ and $\mathbf{g}$ correspond to the random effects of blocks and genotypes, respectively. Here, $\mathbf{b}~\mathrm{N}(\mathbf{0},\mathbf{I}{\mathsf{\sigma }}_{\mathrm{b}}^{²})$ and $\mathbf{g}~\mathrm{N}(\mathbf{0},\mathbf{I}{\mathsf{\sigma }}_{\mathrm{g}}^{²})$, where $\mathbf{I}$ represents an identity matrix, ${\mathsf{\sigma }}_{\mathrm{b}}^{²}$ and ${\mathsf{\sigma }}_{\mathrm{g}}^{²}$ represents the variance components of blocks and genotypes, respectively, and $\mathsf{\epsilon }$ represents the vector of residual effects, with $\mathsf{\epsilon }~\mathrm{N}(\mathbf{0},\mathbf{I}{\mathsf{\sigma }}_{\mathsf{\epsilon }}^{²})$, where ${\mathsf{\sigma }}_{\mathsf{\epsilon }}^{²}$ is the residual variance components. $\mathbf{X}$ and $\mathbf{Z}$ are the incidence matrices of random effects, associated with block and genotype effects, respectively. Genetic random effects values were predicted and utilized in subsequent analyses.

The adjusted phenotypic data was used as input (pseudo-phenotypes) in the canonical correlation analysis. The two trait vectors of aerial (A—group I) and root (R—group II) parts are defined as follows:

$${\mathbf{A}}^{\mathrm{t}}=\left[{\mathrm{u}}_{\mathrm{H}\mathrm{D}}{\mathrm{u}}_{\mathrm{P}\mathrm{H}}\right],$$

(2)

$${\mathbf{R}}^{\mathrm{t}}=\left[{\mathrm{v}}_{\mathrm{R}\mathrm{D}\mathrm{M}}{\mathrm{v}}_{\mathrm{R}\mathrm{V}}{\mathrm{v}}_{\mathrm{P}\mathrm{S}\mathrm{A}}{\mathrm{v}}_{\mathrm{T}\mathrm{R}\mathrm{L}}\right],$$

(3)

where ${\mathrm{u}}_{\mathrm{H}\mathrm{D}}$, ${\mathrm{u}}_{\mathrm{P}\mathrm{H}}$, ${\mathrm{v}}_{\mathrm{R}\mathrm{D}\mathrm{M}}$, ${\mathrm{v}}_{\mathrm{R}\mathrm{V}}$, ${\mathrm{v}}_{\mathrm{P}\mathrm{S}\mathrm{A}}$, and ${\mathrm{v}}_{\mathrm{T}\mathrm{R}\mathrm{L}}$ represent the corrected traits of hypocotyl diameter, plant height, root dry mass, root volume, projected surface area, and total root length, respectively. ${\mathbf{A}}^{\mathrm{t}}$ and ${\mathbf{R}}^{\mathrm{t}}$ represent the concatenate vectors for ${\mathrm{u}}_{\mathrm{H}\mathrm{D}}$ and ${\mathrm{u}}_{\mathrm{P}\mathrm{H}}$, ${\mathrm{v}}_{\mathrm{R}\mathrm{D}\mathrm{M}}$, ${\mathrm{v}}_{\mathrm{R}\mathrm{V}}$, ${\mathrm{v}}_{\mathrm{P}\mathrm{S}\mathrm{A}}$, and ${\mathrm{v}}_{\mathrm{T}\mathrm{R}\mathrm{L}}$, respectively.

Given ${\mathbf{A}}^{\mathrm{t}}$ and ${\mathbf{R}}^{\mathrm{t}}$ as vectors of observations for the traits constituting groups I and II, respectively. ${\mathbf{A}}_1$ and ${\mathbf{R}}_1$ represents the first linear combination (first canonical pair) of the traits in groups I and II, it follows that:

$${\mathrm{A}}_1={\mathrm{a}}_{\mathrm{H}\mathrm{D}}{\mathrm{u}}_{\mathrm{H}\mathrm{D}}+{\mathrm{a}}_{\mathrm{P}\mathrm{H}}{\mathrm{u}}_{\mathrm{P}\mathrm{H}},$$

(4)

$${\mathrm{R}}_1={\mathrm{b}}_{\mathrm{R}\mathrm{D}\mathrm{M}}{\mathrm{v}}_{\mathrm{R}\mathrm{D}\mathrm{M}}+{\mathrm{b}}_{\mathrm{R}\mathrm{V}}{\mathrm{v}}_{\mathrm{R}\mathrm{V}}+{\mathrm{b}}_{\mathrm{P}\mathrm{S}\mathrm{A}}{\mathrm{v}}_{\mathrm{P}\mathrm{S}\mathrm{A}}+{\mathrm{b}}_{\mathrm{T}\mathrm{R}\mathrm{L}}{\mathrm{v}}_{\mathrm{T}\mathrm{R}\mathrm{L}},$$

(5)

where ${\mathbf{a}}^{\mathrm{t}}=\left[{\mathrm{a}}_{\mathrm{H}\mathrm{D}}{\mathrm{a}}_{\mathrm{P}\mathrm{H}}\right]$ and ${\mathbf{b}}^{\mathrm{t}}=\left[{\mathrm{b}}_{\mathrm{R}\mathrm{D}\mathrm{M}}{\mathrm{b}}_{\mathrm{R}\mathrm{V}}{\mathrm{b}}_{\mathrm{P}\mathrm{S}\mathrm{A}}{\mathrm{b}}_{\mathrm{T}\mathrm{R}\mathrm{L}}\right]$ represent two-column row vectors of group I trait weights and a four-column row vector of group II trait weights, respectively.

In this manner, the first canonical correlation was defined as the one that maximized the relationship between ${\mathrm{A}}_1$ and ${\mathrm{R}}_1$. Thus, the functions ${\mathrm{A}}_1$ and ${\mathrm{R}}_1$ constitute the first associated pair of the canonical correlation, according to the expression below:

$$\mathrm{r}=\frac{\widehat{\mathrm{C}\mathrm{o}\mathrm{v}}({\mathrm{A}}_1,{\mathrm{R}}_1)}{\widehat{\mathrm{V}}\left({\mathrm{A}}_1\right)\widehat{\mathrm{V}}\left({\mathrm{R}}_1\right)},$$

(6)

$$\widehat{\mathrm{C}\mathrm{o}\mathrm{v}}\left({\mathrm{A}}_1,{\mathrm{R}}_1\right)={\mathbf{a}}^{\mathbf{t}}{\mathbf{S}}_{\mathbf{12}}\mathbf{b},$$

(7)

$$\widehat{\mathrm{V}}\left({\mathrm{A}}_1\right)={\mathbf{a}}^{\mathbf{t}}{\mathbf{S}}_{\mathbf{11}}\mathbf{a},$$

(8)

$$\widehat{\mathrm{V}}\left({\mathrm{R}}_2\right)={\mathbf{b}}^{\mathbf{t}}{\mathbf{S}}_{\mathbf{22}}\mathbf{b},$$

(9)

where ${\mathbf{S}}_{\mathbf{11}}$ is the $2\times 2$ covariance matrix between the traits of group I, ${\mathbf{S}}_{\mathbf{22}}$ is the 4$\times$4 covariance matrix between the traits of group II, and ${\mathbf{S}}_{\mathbf{12}}$ is the 2$\times$4 covariance matrix between the traits of groups I and II. Therefore, the first canonical correlation (${\mathrm{r}}^1$) between the linear combinations of the traits of groups I and II is given by ${\mathrm{r}}^1={\left({\mathsf{\lambda }}_1\right)}^{1/2}$, where $\mathsf{\lambda }$1 is the largest eigenvalue corresponding to the matrix ${\mathbf{R}}_{\mathbf{11}}^{-1}{\mathbf{R}}_{\mathbf{12}}{\mathbf{R}}_{\mathbf{22}}^{-1}{\mathbf{R}}_{\mathbf{21}}$, which is square and has asymmetric order 2. The first canonical pair is given by ${\mathrm{A}}_1={\mathbf{a}}^{\mathbf{t}}\mathbf{A}$ and ${\mathrm{R}}_1={\mathbf{R}}^{\mathbf{t}}\mathbf{Y}$, where $\mathbf{a}$ is the associated eigenvector to the first eigenvalue of ${\mathbf{R}}_{\mathbf{11}}^{-1}{\mathbf{R}}_{\mathbf{12}}{\mathbf{R}}_{\mathbf{22}}^{-1}{\mathbf{R}}_{\mathbf{21}}^{-1}$ and $\mathbf{b}$ is the eigenvector associated with the first eigenvalue of ${\mathbf{R}}_{\mathbf{22}}^{-1}{\mathbf{R}}_{\mathbf{21}}{\mathbf{R}}_{\mathbf{11}}^{-1}{\mathbf{R}}_{\mathbf{12}}$.

The other correlations and canonical pairs are estimated using the eigenvalues and eigenvectors corresponding to the order-specific correlation estimate. The canonical correlations were carried out between group I, formed by the aerial part traits (HD and PH), and group II, composed by the root part traits (RDM, RV, PSA and TRL), according to the method proposed by Hotelling [30,31], through the statistical package “mVar.pt” [32] implemented in the R software (R Version 4.3.1) [33].

2.4. Genomic Prediction Model

The adjusted phenotypes and scores from the latent canonical variables related to aerial traits (A₁) were utilized as pseudo-phenotypes to predict the genetic merit of the individuals. The GBLUP [34] was used to estimate the additive genetic values, as expressed below:

$$\mathbf{y}=\mathbf{X}\mathbf{b}+\mathbf{Z}\mathbf{u}+\mathsf{\epsilon },$$

(10)

where $\mathbf{y}$ is the vector of latent canonical variables or adjusted phenotypes, $\mathbf{b}$ is the vector of fixed effects, $\mathrm{u}$ is the vector of genomic estimated breeding values of the genotypes, with $\mathbf{u}~\mathrm{N}(\mathbf{0},\mathbf{G}{\mathsf{\sigma }}_{\mathrm{u}}^{²})$, where ${\mathsf{\sigma }}_{\mathrm{u}}^{²}$ is the additive genetic variance and $\mathrm{G}$ is the genomic relationship matrix given by $\mathbf{G}=\frac{\mathbf{W}{\mathbf{W}}^{\mathbf{t}}}{{\sum }_{\mathrm{i}=1}^{\mathrm{n}}2{\mathrm{p}}_{\mathrm{i}}{\mathrm{q}}_{\mathrm{i}}}$ [35], where ${\mathrm{p}}_{\mathrm{i}}$ and ${\mathrm{q}}_{\mathbf{i}}$ are the allele frequencies of the $\mathrm{i}\mathrm{t}\mathrm{h}$ marker and $\mathrm{W}$ is the incidence matrix for SNPs; $\mathsf{\epsilon }$ is the residual effects vector, with $\mathsf{\epsilon }~\mathrm{N}(\mathbf{0},\mathbf{I}{\mathsf{\sigma }}_{\mathsf{\epsilon }}^{²})$, where ${\mathsf{\sigma }}_{\mathsf{\epsilon }}^{²}$ is the residual variance and $\mathbf{I}$ represents an identity matrix. $\mathbf{X}$ and $\mathbf{Z}$ are the incidence matrices of fixed and random effects, respectively.

Genomic prediction analyzes were conducted using the “sommer” package [36] in the R software [33].

2.5. Evaluation of the Methodology

In order to assess the predictive ability (PA) of all of the fitted models, the Pearson’s correlation between the estimated genetic merit and the adjusted phenotypic values on each trait individually and by latent canonical variable related to aerial traits (A₁) were calculated. A five-fold cross-validation (CV) random process was carried out. This process was repeated randomly 50 times. The data set is divided into five populations. At the k-th fold (k = 1, …, 5), the k-th population is used as a validation population. The remaining populations were used as a training population. For each of the five folds, the PA was estimated by Pearson’s correlation coefficient between the estimated genetic merit from each evaluated model, the adjusted phenotypic values on each trait individually, and by latent canonical variable related to aerial traits (A1). Additionally, based on genetic merit, the top 10% individuals were selected for each approach used. In possession of these individuals, the agreement between the selected individuals was calculated, based on each trait individually and by the A₁, using Cohen’s Kappa coefficient (K) [37]:

$$\mathrm{K}=\frac{{\mathrm{P}}_{\mathrm{o}}-{\mathrm{P}}_{\mathrm{e}}}{1-{\mathrm{P}}_{\mathrm{e}}},$$

(11)

where ${\mathrm{P}}_{\mathrm{o}}$ is the proportion of cases correctly classified calculated as ${\mathrm{P}}_{\mathrm{o}}=\frac{\mathrm{t}\mathrm{p}+\mathrm{t}\mathrm{n}}{{\mathrm{n}}_{\mathrm{T}}}$, ${\mathrm{P}}_{\mathrm{e}}$ is the probability of agreement calculated as ${\mathrm{P}}_{\mathrm{e}}=\frac{\mathrm{t}\mathrm{p}+\mathrm{f}\mathrm{n}}{{\mathrm{n}}_{\mathrm{T}}}\times \frac{\mathrm{t}\mathrm{p}+\mathrm{f}\mathrm{p}}{{\mathrm{n}}_{\mathrm{T}}}\times \frac{\mathrm{f}\mathrm{p}+\mathrm{t}\mathrm{n}}{{\mathrm{n}}_{\mathrm{T}}}\times \frac{\mathrm{f}\mathrm{n}+\mathrm{t}\mathrm{n}}{{\mathrm{n}}_{\mathrm{T}}}$, where ${\mathrm{n}}_{\mathrm{T}}$ is the total of individuals in the testing sets, $\mathrm{t}\mathrm{p}$ denotes the true positives, $\mathrm{t}\mathrm{n}$ denotes the true negatives, $\mathrm{f}\mathrm{p}$ denotes the false positives, and $\mathrm{f}\mathrm{n}$ denotes the false negatives. The cross-validation approach was repeated 50 times.

3. Results

3.1. Canonical Correlation Analysis

The estimated values of the Pearson correlation coefficient between the evaluated traits were significant according to a t-test considering 1 and 5% of significance and ranged from 0.15 to 0.96 (Figure 1).

The estimated canonical correlation values were equal to 0.59 (p < 0.01) and 0.26 (p < 0.01) for, respectively, the first and second canonical pairs (

Table 1. Canonical correlations (r) and estimated canonical pairs (A_1, R₁ as first pairs and A_2, R₂ as second pairs) between aerial (A—Group I) and root (R—Group II) traits in commercial soybean cultivars.

Groups	Traits	Canonical Pairs
		1°	2°
Aerial (A1 and A2)	HD	−13.79	1.89
	PH	0.39	−0.10
Root (R1 and R2)	RDM	−49.58	12.20
	RV	−10.28	77.64
	PSA	1.05	−8.04
	TRL	−0.03	0.29
	r	0.59 *	0.26 *
	p-value	4.80 × 10−10	1.07 × 10−2

* Statistically significant at 5% of significance by the Wilks test. HD: hypocotyl diameter; PH: plant height; RDM: root dry mass; RV: root volume; PSA: projected surface area; TRL: total root length.

). A one-unit increase in HD lead to a 13.79 decrease in the first canonical variable (Table 1). The canonical coefficients from the first canonical pair showed that, for the root dry mass (RDM), a one-unit increase resulted in a 49.58 decrease in the first canonical variable when all of other variables are held constant. In a similar way, a one-unit increase in root volume led to a 77.64 increase in the second canonical variable, with the other predictors held constant (Table 1).

3.2. Heritability and Prediction Accuracy

The estimates of heritability obtained with the GBLUP model, as the proportion of genetic variance divided by the total phenotypic variance, for the six evaluated traits (HD, PH, RDM, RV, PSA, and TRL) ranged from low (0.09) to high (0.66) (

Table 2. Heritability (${\mathrm{h}}^2$) obtained using the univariate GBLUP model for each trait and based on the latent variable obtained from canonical variable analysis.

Groups	Traits	${\mathbf{h}}^2$
Aerial	HD	0.14
	PH	0.37
Root	RDM	0.66
	RV	0.09
	PSA	0.19
	TRL	0.21
Latent Variable	A1	0.32

HD: hypocotyl diameter; PH: plant height; RDM: root dry mass; RV: root volume; PSA: projected surface area; TRL: total root length; ${\mathrm{A}}_1$: Latent Variable obtained for the aerial traits group.

). The estimate of heritability for the latent variable (A₁) (0.32) was higher than for the univariate traits analysis, except for RDM (0.66) and PH (0.37) (Table 2).

The estimated predictive ability (PA) ranged from 0.47 to 0.73 (

Table 3. Predictive ability ($\mathrm{P}\mathrm{A}$), standard error of predictive ability $\mathrm{S}\mathrm{E}\left(\mathrm{P}\mathrm{A}\right)$, mean Cohen’s Kappa coefficient ($\mathrm{K}$), and standard error of Kappa coefficient of Cohen $\mathrm{S}\mathrm{E}\left(\mathrm{K}\right)$ of genomic prediction using univariate GBLUP in each trait and based on the latent variable obtained by canonical correlation.

Groups	Traits	$\mathbf{P}\mathbf{A}$	$\mathbf{S}\mathbf{E}\left(\mathbf{P}\mathbf{A}\right)$	$\mathbf{K}$	$\mathbf{S}\mathbf{E}\left(\mathbf{K}\right)$
Aerial	HD	0.61	0.0219	0.29	0.0401
	PH	0.73	0.0153	0.52	0.0291
Root	RDM	0.59	0.0208	0.44	0.0297
	RV	0.55	0.0271	0.18	0.0431
	PSA	0.47	0.0272	0.25	0.0415
	TRL	0.51	0.0231	0.24	0.0397
Latent variable	A1	0.57	0.0246	0.35	0.0305

HD: hypocotyl diameter; PH: plant height; RDM: root dry mass; RV: root volume; PSA: projected surface area; TRL: total root length. ${\mathrm{A}}_1$: Latent Variable obtained for the aerial traits group.

). For these traits, the highest accuracy values were 0.73 and 0.61, observed for PH and HD, respectively (Table 3). The PA obtained for A1 (0.57) was higher than those estimated for the traits related to Root (RV, PSA and TRL), except for RDM (0.59). In relation to aerial traits, the PA of A₁ was lower in comparison with PH and close to the HD trait (0.61) (Table 3). The low standard deviation associated with PA revealed the good precision of the estimates of PA.

The Cohen’s Kappa coefficient ($\mathrm{K}$) represents the agreement between the top 10% of individuals selected based on each trait individually, compared with the those selected based on ${\mathrm{A}}_1$. The estimated Cohen’s Kappa coefficient ranged from 0.32 to 0.88 (

Table 4. Estimates of the Cohen’s Kappa coefficients (lower triangular) for the evaluated traits and the latent variable obtained for the aerial traits group (upper triangular) The value in parentheses is the standard error of the mean considering 50 repetitions.

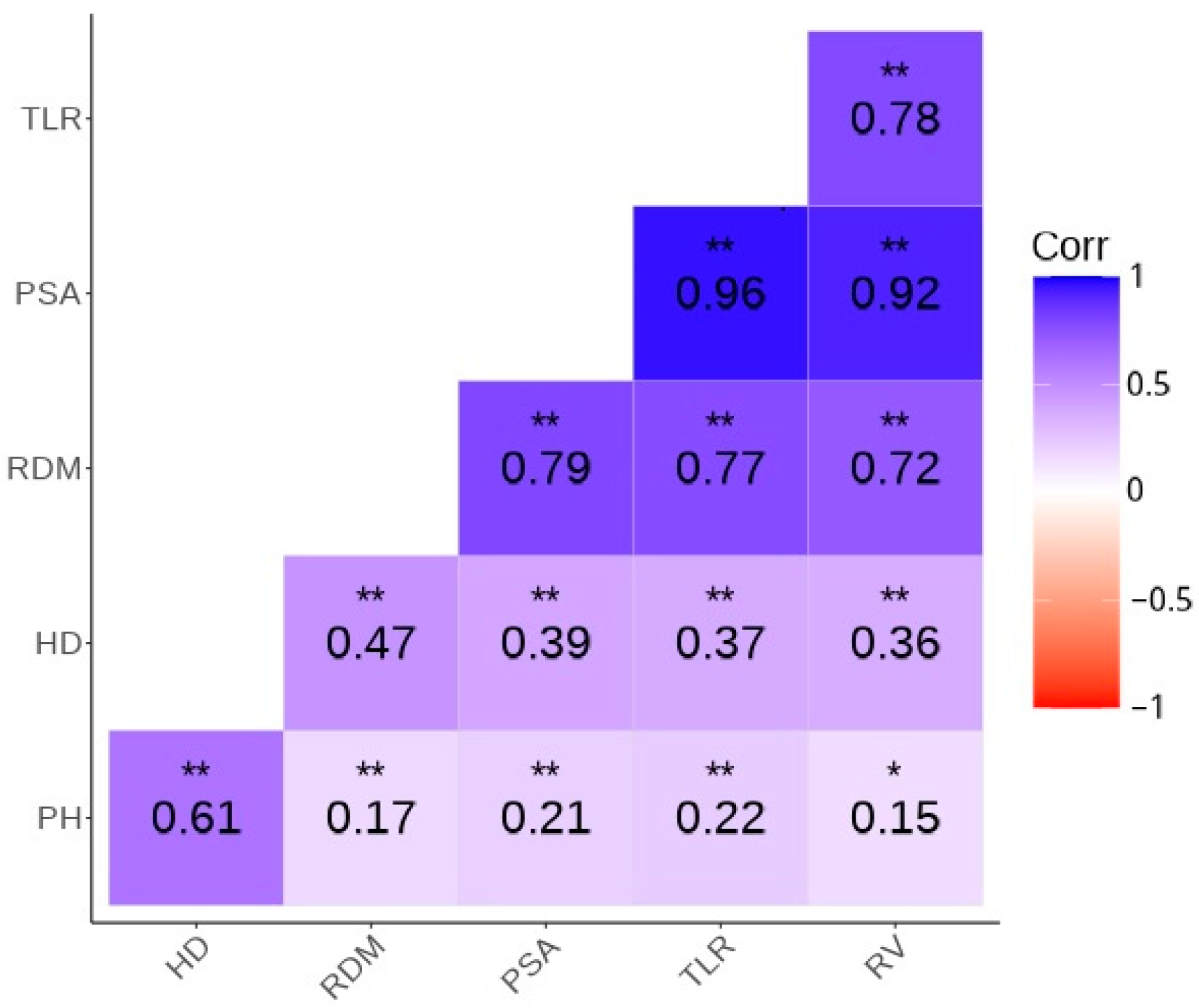
Trait	PSA	HD	TLR	PH	RDM	RV	A1
PSA	1	-	-	-	-	-	-
HD	0.54 (0.03)	1	-	-	-	-	-
TLR	0.88 (0.03)	0.54 (0.03)	1	-	-	-	-
PH	0.40 (0.02)	0.51 (0.02)	0.52 (0.02)	1	-	-	-
RDM	0.63 (0.03)	0.60 (0.02)	0.60 (0.03)	0.41 (0.02)	1	-	-
RV	0.79 (0.03)	0.51 (0.02)	0.72 (0.04)	0.46 (0.02)	0.56 (0.024)	1	-
A1	0.50 (0.02)	0.70 (0.03)	0.49 (0.02)	0.32 (0.02)	0.69 (0.01)	0.46 (0.02)	1

HD: hypocotyl diameter; PH: plant height; RDM: root dry mass; RV: root volume; PSA: projected surface area; TRL: total root length. ${\mathrm{A}}_1$: Latent Variable obtained for the aerial traits group.

). Specifically, the Cohen’s Kappa values between A₁ and the root traits were equal to 0.50 (A₁ versus PSA), 0.49 (A₁ versus TLR), 0.69 (A₁ versus RDM), and 0.46 (A₁ versus RV) (Table 4). The associated low standard error of the mean leads to good precision of the calculated values.

4. Discussion

This study introduces a novel approach that combines canonical correlation analysis and genomic prediction. The idea is to use a latent variable given by a linear combination of aerial traits to predict the genetic merit of genotypes for root traits, which requires destructive, laborious, and expensive evaluation. The joint phenotyping of aerial and root traits was used to evaluate predictive ability of our proposal through a cross-validation approach.

Some studies employ selection indexes considering several methods to identify promising genotypes for interested traits in soybeans [38,39], including associating these with genomic prediction approaches [40]. However, selection indexes do not allow us to explore the correlations between traits to predict genotypic values for unobserved phenotypes. To circumvent this bottleneck, multi-trait models could be used to improve predictive ability accounting for covariance between traits [21]. Nevertheless, these models do not eliminate the need to gather the trait information into an index for select genotypes [41]. The proposal in this study could be a manner to explore the advantages of both methods in a simpler way.

The high correlations observed between the root traits were similar to those observed by Dayoub et al. [42], except for TLR and PSA, which the study did not observe a significant correlation. Overall, the Pearson correlation between aerial and root traits was low but statistically significant (Figure 1). These results suggest the possibility of using an indirect selection approach, despite the low magnitude of Pearson correlation showing that effective results might not be achieved.

On the hand, the magnitudes of the canonical correlation coefficients were high (0.59) and moderate (0.26) for the first and second pair of canonical variables, respectively. The canonical variables are constructed with the aim to maximize the correlation between the two sets of traits [43]. Thus, our first pair of canonical variables (latent variables) maximizes the association between the aerial and root trait sets. In a practical context, it suggests that the canonical variable referent to aerial traits (A₁) may be used as a pseudo-phenotype to perform an indirect selection to root traits.

The use of latent variables has been used with success in plant breeding. For example, Paixão et al. [44] used factor analysis (FA) to elucidate the structure of relations of the evaluated traits, form new variables, and use them, as pseudo-phenotypes, to predict the genetic merit of canephora coffee individuals. On the other hand, principal component analysis (PCA) can be employed to extract latent variables, effectively reducing dimensionality while enabling the assessment of genetic diversity [45,46]. The crucial distinction between these approaches lies in their interpretation (construction) of latent variables. While canonical correlation analysis seeks to maximize the shared information between two sets of traits, both factor analysis (FA) and principal component analysis (PCA) focus on explaining internal structure. FA aims to capture the underlying “factors” influencing covariance (trait associations), while PCA prioritizes explaining the bulk of variability (individual trait variances).

The estimated heritability of the latent variable (${\mathrm{A}}_1)$ was higher than those for RV, PSA and TRL indicating that selection based on ${\mathrm{A}}_1$ may be a promising strategy. Specifically, the lowest estimated heritability, that is, RV = 0.09, was similar to that observed by Getnet [47]. The estimated heritabilities for RDM (0.66), HD (0.14), PH (0.37), PSA (0.19), TRL (0.21), and PSA (0.19) were similar to those presented in Xavier et al. [48], Yan et al. [49], and Conte et al. [50].

Overall, the PA for A₁ (0.57$\pm 0.02$) was equal or higher than those obtained for all root traits (RDM = 0.59$\pm 0.02$; RV = 0.55$\pm 0.03$; PSA = 0.47$\pm 0.03$; TRL = 0.51$\pm 0.02$). Regarding the aerial traits, the PA for A₁ was similar to (HD = 0.61$\pm 0.02)$ or lower (0.73$\pm 0.02$) than those obtained by individual analysis. These results demonstrate that it is possible to use the latent variable A₁ to predict the genetic merit of soybean genotypes. The PA for some soybean traits was reported by Bandillo et al. [51], corroborating with the results obtained in our study.

To assess the agreement between A₁ and individual root traits, we estimated Cohen’s Kappa coefficients using the top 10% of GEBVs. According to Landis and Koch [52], A₁ exhibited moderate agreement with PSA (0.50) and TRL (0.49) and substantial agreement with RDM (0.69). While agreement with RV was slightly lower (0.46), these findings collectively suggest A₁’s potential as a promising pseudo-phenotype for root trait evaluation in practical applications.

Overall, this study demonstrates the effectiveness of combining the latent variable A₁ with genomic selection to predict individual genetic merit for root traits in soybean breeding. This is particularly interesting because root trait evaluation is challenging and expensive, often hindering selection for improved genotypes. As Crossa et al. [53] emphasize, genomic prediction shines in such scenarios, enabling the efficient culling of inferior genotypes and reducing phenotyping costs. Our findings pave the way for utilizing A₁ as a powerful tool to accelerate development of superior soybean varieties with enhanced root systems.

5. Conclusions

The approach provides a way to predict and select promising genotypes considering multiple traits simultaneously, differing from the use of selection indexes by exploiting a latent variable that maximizes correlation between groups of traits. Also, it differs from multi-trait approaches by gathering all traits’ information into a single variable, making the selection process simpler.

The combination of canonical correlation analysis with genomic selection was efficient to predict individual genetic merit for root traits (length, volume, surface area, and dry mass) in soybean breeding. The agreement observed between the top 10% individuals selected based on the canonical variable and each root traits individually was considered moderate or substantial.