Abstract
Biological adhesive systems in both geckoes and climbing plants share similar hierarchical structures, such as the toe-seta-spatula structure in geckoes and the root-rootlet-hair structure in English ivy (Hedera helix). The former operates at a spectrum of length scales that are much smaller than the latter. Consequently, the spatula adhesion in geckoes exhibits a flaw-insensitive behavior, or in other words, the large-scale-bridging characteristics shield the stress singularities at the adhesive contact front. In contrast, adventitious root hairs from commonly seen household climbing plants are of several tens to hundreds of micrometers long, so that the adhesive contact appears to resemble a linear elastic crack and thus would have a very low pulling force for de-adhesion. This apparent contradiction between modeling and observations is resolved in this work by a coupled transport–adhesion mechanism, in which an adhesive layer that carries gluing nanoparticles flows towards the adhesive contact front. This provides an effective way to shield the stress singularity, resulting in a scenario that completely differs from gecko adhesion. Finite element simulations have been conducted to illustrate this proposed mechanism and then compared to available experimental observations in the literature.
1. Introduction
A vast number of recent studies have shown the critical role played by hierarchical structures in animals (such as reptiles and insects) that achieve superior adhesive performance with the surrounding materials, such as the toe-seta-spatula structure in geckoes that leads to a high degree of conformity with the rough substrate and a large de-adhesion force at the spatula scale [1,2,3]. The adhesive contact of any two bodies could resemble a crack problem that possesses stress singularities at the crack tips, if the range of action of the adhesive forces is much smaller than the crack size or other geometric features. The adhesive contact analysis falls into the so-called Johnson–Kendall–Roberts (JKR) limit [4], as will be explained later in this work. However, if the long-range surface interaction has a spatial range that is comparable to, or larger than, the geometric feature size, the resulting adhesive contact will not have the stress singularities. This reaches the Derjaguin–Muller–Toporov (DMT) limit [4], or the large-scale-bridging limit in fracture mechanics. In gecko adhesion, the smallest spatula level which has a feature size of micrometers will correspond to the large-scale-bridging DMT limit, thus displaying a flaw-insensitive behavior and resulting in a high de-adhesion force. The toe-seta-spatula hierarchy provides the needed contact compliance, due to the slender geometric features, so that the true contact area with respect to the nominal contact area will be sufficiently high to ensure an overall large de-adhesion force. More recent studies reveal other interesting factors, such as the formation of an ordered nanometer-thin lipid film on the gecko setae that might contribute the strong adhesion [5]. However, the hierarchical structure by itself can indeed be proven to be a leading mechanism of biomimetic devices (e.g., [6]).
On the other hand, climbing plants, such as vines and ivies in typical household environments, at a first glance, appear to have the same strategy to reach a strong attachment (i.e., a strong adhesion to the surrounding surface). Figure 1 shows several hierarchy levels, including stem, roots, rootlets, root hairs, and attachment pads (also see Figure 2a,b). While this resembles the hierarchical structure in gecko toes, a major difference lies on the sub-millimeter root hair as opposed to nanometer spatula. This makes a huge difference in whether the contact behavior is JKR-like or DMT-like. As will be addressed later in this paper, from a mere consideration of material and geometric parameters, the adhesive contact between the root hair and the substrate is JKR-like, and the contact edge has singular stress fields similar to in a crack problem. Consequently, a high attachment strength would not be realized for root hairs from this mechanistic point of view, which contradicts to the observations. Noting the permanent attachment of climbing plants during growth, it is therefore proposed by many studies [7,8] that the attachment mechanism is governed by a sequence of scenarios, including the initial physical contact between the root hairs and the substrate, the closure of the gaps and cavities between the mating surfaces, chemical adhesion, and finally the shape change of the root hairs. However, this commonly accepted view merely shows the correlation between adhesion and growth but does not offer a theoretical explanation of the coupling mechanism between mechanics and chemistry, nor does it demonstrate a direct relationship to the establishment of the strong attachment, especially because the JKR limit (i.e., crack-like adhesive contact) would lead to a low de-adhesion force.

Figure 1.
A hierarchical structure of roots and root hairs can be observed in a household climbing plant (photos taken at Knoxville, TN in Summer 2022).
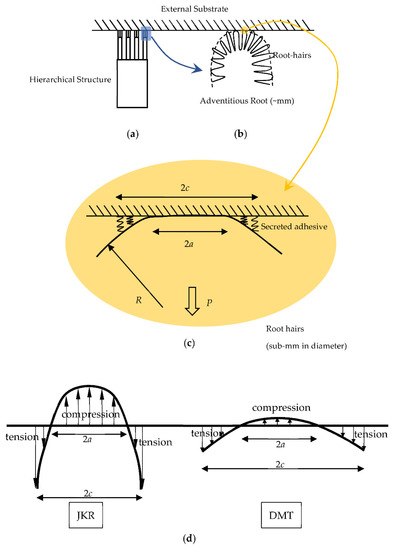
Figure 2.
(a) Schematic illustration of a hierarchical structure that adheres to a substrate (shown as shaded). (b) The lowest scale shows the hair–substrate adhesion at the tip of an adventitious root. (c) The contact problem between a root hair (with a spherical tip radius of R) and a rigid platen. Due to the secreted adhesive, tensile stress is developed at the contact edge. Within the contact size a, a compressive stress is established. The long-range adhesion operates in the annular zone between a and c. The external force P is acted at faraway. (d) The contrasting JKR and DMT responses of adhesive contacts.
A series of recent experiments have provided critical insights into a more plausible interpretation of the root hair adhesion. Zhang and co-authors [9,10,11] found that a nanocomposite thin layer, containing nanoparticles of several tens of nanometers in size, is secreted on the free surface of the root hair that is adjacent to the adhesive contact front, followed by the advancing of this contact front in accord with further secretion. Specifically, Lenaghan and Zhang [11] developed a novel video microscopy apparatus and collected real-time observation of the secretion of the nanocomposite adhesive from the hair tip of English ivy (Hedera helix). The secretion process lasted about 4~6 h, during which the growth of both the individual hair contact size (sub-millimeter size) and the nominal root–substrate contact was observed to approximately double. Follow-up works by Burris, Lenaghan, Stewart, and their co-authors [12,13,14,15] conducted bioproduction and molecular analysis of such nanoparticles, which provided more insights into the biochemical mechanisms involved in the generation of such an adhesive layer for enhanced attachment.
Despite these extensive anatomic and biochemical investigations in climbing plants [7,8,9,10,11,12,13,14,15], important questions remain to be addressed in terms of the attachment mechanism. This present work focuses a contact mechanics model, while our knowledge on the molecular biology and biochemistry aspects of climbing plants is still lacking. As schematically shown in Figure 2, it is proposed here that millimeter-sized roots adhere to the surrounding substrate via the sub-millimeter-sized root hairs, which secrete a glue-like nanocomposite adhesive as motivated from the above experimental works by Zhang, Lenaghan, Burris, Stewart, and others [9,10,11,12,13,14,15]. What is the driving force for the secretion process? Is it really critical to have a transport–adhesion coupling in order to achieve a strong attachment that defies the JKR limit with a poor de-adhesion force? The hair–substrate contact does not involve external pressing force, so the adhesive contact growth must be self-driven. An appropriate model must include a constitutive relationship for the secretion process, and also allows the calculation of interfacial stress distribution on the contact. This will be discussed in Section 2, where we propose a cohesive interface model to study the above coupled transport–adhesion process. Finite element simulations will be presented in Section 3, with focus placed on the growth rate of the contact size. A contrast between JKR and DMT contact responses is schematically drawn in Figure 2d, which will form the basis for our discussions and summary to be presented in Section 4.
2. Model
As shown in Figure 2c, the key process involved in climbing plants is the hair–substrate adhesive contact. Without adhesion, the contact stress is compressive in a contact radius of with an applied pushing force. The introduction of adhesive interaction between the hair surface and the substrate leads to tensile stress (schematically shown by springs here) in an annular zone between and , and the balanced force at far-away referent point can be either pulling or pushing. The extent of the ratio relies on the contact stress analysis and the interface interaction model as described below.
The adhesive contact problem can be studied by a cohesive interface model, which prescribes a constitutive relationship between the interface traction, , and the interface separation, . The density of secreted nanoparticles is given by , and the saturated value is . Thus, we can define a state variable, that belongs in the [0, 1] interval. The interface traction–separation relationship can be specified as a smooth function with an initial rising part, followed by an exponential decay, as given by the following mathematical representation [4]:
where is the maximum interface tensile strength at , and is a characteristic length. For a tensile traction, the state variable will increase due to the secretion process.
The detailed transport mechanism involved in the secretion is still under investigation [16,17]. The simplest form should involve a stress function and a multiplicative factor of as in the first-order chemical reaction system. The latter is due to the consideration of the secretion process from the surface not covered by the nanoparticles. Borrowing the knowledge from microtubule-based fluid flow in water transport in trees [17], we adopt the Poiseuille law in which the flow flux is proportional to the applied pressure. The above two lines of considerations lead to
where is a rate constant that depends on the fluid viscosity and the size of the microtubules inside the plant that provide the fluid transport conduits [16,17]. Clearly, 1/ sets a characteristic time scale, which would be determined to be around half an hour by comparing to experiments of Lenaghan and Zhang [11], as will be explained later.
The boundary value problem specified in Figure 2c can be solved by a commercial finite element software, ABAQUS (Simula Co., Providence, RI, USA), with the cohesive constitutive law in Equations (1) and (2) implemented as a user-element subroutine (UEL). As shown in Figure 3, the root hair with a spherical tip radius of R is meshed into axisymmetric triangular elements, while the four-node cohesive elements connect the rigid platen and the surface of the root hair. In our calculations, the platen (i.e., the surrounding surface) is first brought from far-away to the onset of contact, and then the gradual evolution of will lead to the determination of contact stress and and in Figure 2c. The resulting force on the rigid platen is recorded as a function of the normalized time, . The representative result in Figure 3 shows the compressive stress inside a and the tensile stress in the annular zone of ~.
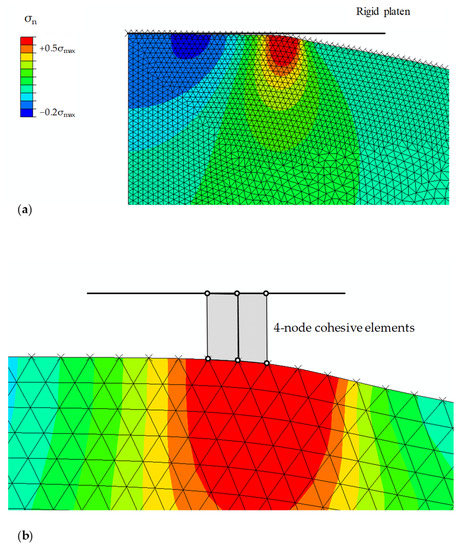
Figure 3.
Finite element simulation setup. (a) The axisymmetric contact with the development of stress concentration that corresponds to Figure 2c. (b) The four-node cohesive element based on Equations (1) and (2).
3. Results
Early works on the adhesion of deformable spheres include the JKR theory and the DMT theory, and later a unified Maugis–Tabor model [4]. They predict different pull-off forces, being (JKR) and (DMT), where w is the work of adhesion. According to our model in Equation (1), we have . As shown schematically in Figure 2d, for the JKR limit, the adhesion induces a singular tensile stress field at the contact edge (i.e., ). However, in the DMT theory, the surface force remains outside the contact radius with >>. The transitional behavior is characterized by the Maugis parameter
where E is the Young’s modulus of the material. This parameter is interpreted as the ratio of the elastic deformation to the range of action of the adhesive forces. Large values of corresponds to large radius and/or compliant solids (JKR limit), and small values to small radius and/or stiff solids (DMT limit).
Our finite element framework presented in Section 2 and Figure 3 can successfully reproduce these two limits as explained below. Moreover, the coupled transport equation in Equation (2) provides additional capabilities for the study of plant adhesion. Three representative cases are presented in Figure 4 and Figure 5.
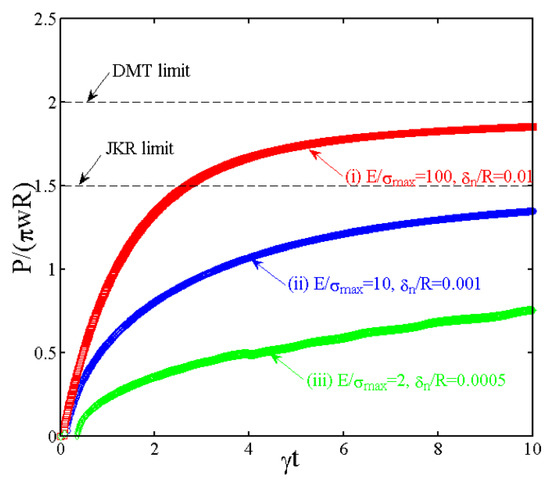
Figure 4.
The transient response of the normal force for three representative cases. The ivy root hair contact falls into Case (iii), which corresponds to the JKR behavior.
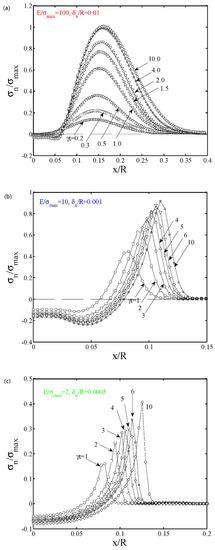
Figure 5.
(a–c) The evolution of the normal contact stress versus the radial coordinate x (normalized by the spherical tip radius R) for three representative cases. The contact growth (e.g., experimental work in [11]) can be reproduced in the JKR limit in Case (iii).
- Case #1: = 100, = 0.01, and = 0.174. This case approaches the DMT limit because of a small . A realistic example is the gecko spatula adhesion, which has a tip radius of ~100 nm, a van der Waals interaction with of a few nanometers, ~4 GPa, and ~40 MPa.
- Case #2: = 10, = 0.001, and = 1.74. This example lies on the DMT–JKR transition behavior.
- Case #3: = 2, = 0.0005, and = 6.41. This case approaches the JKR limit because of a large . For the rootlet hairs in our climbing plant, we use ~100 μm, ~of a few nanometers, of about 10~100 MPa, and ~20 MPa. Again, this leads to a van der Waals energy density of about 100 mJ/m2.
With these estimates, we can now demonstrate the contrasting behavior between the JKR and DMT responses under a transport mechanism. Using the parameters for gecko spatulae, Case #1 approaches the DMT limit, and the pulling force will be flaw insensitive. As also shown in Figure 5a, in this DMT limit, the contact size a and the cohesive zone size c barely change with respect to , while the increase in the tensile stress at the contact edge drives the increase in according to Equation (2). For the other two cases (#2 and #3), JKR limit is successfully calculated. Normal stress distributions in Figure 5b,c demonstrate a continuous increase in both a and c, but the ratio remains as nearly a constant with respect to . Case #3 corresponds to the representative material and geometric parameters in the climbing plant. In this case, a larger leads to a smaller ratio; the JKR limit solution corresponds to . A larger will also lead to a slower growth of contact size, as shown by the comparison between Cases #2 and #3.
When comparing to the English ivy experiments in [11], it is noted that the weak adhesive interaction between plant materials, the low modulus, and the large hair diameter led to a large , as shown by the estimates in the above. Therefore, the root hair adhesion tends to be JKR-like in the beginning. That is, ivy root hair behaves crack-like (JKR limit), while the gecko spatula approaches the DMT limit and thus behaves as flaw-insensitive. This explains why it is very difficult to break the gecko adhesion to the surrounding, but the corresponding force to separate the plant adhesion is low at the initial contact. However, the coupled transport–adhesion mechanism provides an alternative way to establish a strong attachment. That is, the initial JKR behavior indeed leads to a very weak attachment, but the edge of the adhesive contact gives a singular tensile stress that drives a high flux of fluid secretion according to the Poiseuille law in Equation (2). As a consequence, not only both a and c increase, but also a strong de-adhesion force is eventually established when .
Our predicted behavior in Figure 5c compares favorably with experimental observations. As discussed in the Introduction, Lenaghan and Zhang [11] developed a novel video setup to record the contact growth and the secretion of gluing material at the contact edge. Indeed, our material and geometric parameters are based on estimates from their experiment. The only missing parameter is the rate constant . Admittedly, our transport equation takes a simple Poiseuille law, as borrowed from water transport in plants (evaporation pressure, capillary force, and others can all be lumped into a stress-driven term for this microtubule transport phenomenon [16,17]). As for the contact size increase versus the elapsed time in [11], the contact size doubles within about 3.3 h. Comparing to our predictions in Figure 5c, this leads to an estimate of a rate constant of about 3.03 h−1.
4. Summary
A hierarchical structure is often found in geckoes and climbing plants that both display a strong adhesion with the surrounding surface. The slender geometric features on the intermediate and large scales provide the needed contact compliance in order to increase the degree of contact conformity. The smallest length scale in gecko adhesion is sufficiently low and the material (e.g., keratin) is sufficiently stiff, so that the contact behavior is of the DMT limit, resulting in a large adhesion and also the flaw-insensitivity. In contrast, the smallest length scale in climbing plants is often too large and the material is too compliant, so the contact behavior is of the JKR limit and the de-adhesion process is flaw-sensitive. However, in reality, there is a coupled biological process that defies this scenario in climbing plant attachment. Motivated by in situ measurements of contact growth and adhesive secretion, we have proposed a coupled transport–adhesion model and conducted finite element simulations to illustrate how the strong attachment can be achieved even under the JKR limit, since the singular tensile stress field now triggers a high flux of secretion of the adhesive layer. This new perspective makes a case for revisiting a lot of experimental studies in plants and other similar biological materials.
Author Contributions
Conceptualization, M.G.; methodology, Y.L.; writing, Y.L. and M.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data included in this work can be obtained from the authors.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Autumn, K.; Liang, Y.A.; Hsieh, S.T.; Zesch, W.; Chan, W.P.; Kenny, T.W.; Fearing, R.; Full, R.J. Adhesive force of a single gecko foot-hair. Nature 2000, 405, 681–685. [Google Scholar] [CrossRef] [PubMed]
- Arzt, E.; Gorb, S.; Spolenak, R. From micro to nano contacts in biological attachment devices. Proc. Natl. Acad. Sci. USA 2003, 100, 10603–10606. [Google Scholar] [CrossRef] [PubMed]
- Gao, H.; Ji, B.; Jäger, I.L.; Arzt, E.; Fratzl, P. Materials become insensitive to flaws at nanoscale: Lessons from nature. Proc. Natl. Acad. Sci. USA 2003, 100, 5597–5600. [Google Scholar] [CrossRef] [PubMed]
- Maugis, D. Adhesion of spheres: The JKR-DMT transition using a Dugdale model. J. Coll. Interface Sci. 1992, 150, 243–269. [Google Scholar] [CrossRef]
- Rasmussen, M.H.; Holler, K.R.; Baio, J.E.; Jaye, C.; Fischer, D.A.; Gorb, S.N.; Weidner, T. Evidence that gecko setae are coated with an ordered nanometer-thin lipid film. Biol. Lett. 2022, 18, 20220093. [Google Scholar] [CrossRef] [PubMed]
- Ou, L.; Dai, L.; Stone, M.; Xia, Z.; Wang, Z.L. Carbon nanotube arrays with strong shear binding-on and easy normal lifting-off. Science 2008, 322, 238–242. [Google Scholar]
- Steinbrecher, T.; Danninger, E.; Harder, D.; Speck, T.; Kraft, O.; Schwaiger, R. Quantifying the attachment strength of climbing plants: A new approach. Acta Biomater. 2010, 6, 1497–1504. [Google Scholar] [CrossRef] [PubMed]
- Melzer, B.; Steinbrecher, T.; Seidel, R.; Kraft, O.; Schwaiger, R.; Speck, T. The attachment strategy of English ivy: A complex mechanism acting on several hierarchical levels. J. R. Soc. Interface 2010, 7, 1383–1389. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Liu, M.; Prest, H.; Fischer, S. Nanoparticle secreted from ivy rootlets for surface climbing. Nano Lett. 2008, 8, 1277–1280. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Zhao, X.; Zhang, M. Adhesion mechanics of ivy nanoparticles. J. Coll. Interface Sci. 2010, 344, 533–540. [Google Scholar] [CrossRef] [PubMed]
- Lenaghan, S.C.; Zhang, M. Real-time observation of the secretion of a nanocomposite adhesive from English ivy (Hedera helix). Plant Sci. 2012, 183, 206–211. [Google Scholar] [CrossRef] [PubMed]
- Burris, J.N. Nanocomposite Adhesive of English Ivy (Hedera helix): Bioproduction, Nanoparticle Isolation, and Molecular Analysis. Ph.D. Thesis, University of Tennessee, Knoxville, TN, USA, 2016. [Google Scholar]
- Burris, J.N.; Lenaghan, S.C.; Zhang, M.; Stewart, C.N. Nanoparticle biofabrication using English ivy (Hedera helix). J. Nnaobiotech. 2012, 10, 41. [Google Scholar] [CrossRef]
- Lenaghan, S.C.; Burris, J.N.; Chourey, K.; Huang, Y.; Xia, L.; Lady, B.; Sharma, R.; Pan, C.; LeJeune, Z.; Foister, S.; et al. Isolation and chemical analysis of nanoparticles from English ivy (Hedera helix L.). J. R. Soc. Interface 2013, 10, 20130392. [Google Scholar] [CrossRef]
- Burris, J.N.; Lenaghan, S.C.; Stewart, C.N., Jr. Climbing plants: Attachment adaptations and bioinspired innovations. Plant Cell Rep. 2018, 37, 565–574. [Google Scholar] [CrossRef] [PubMed]
- Steudle, E. The cohesion-tension mechanism and the acquisition of water by plant roots. Annu. Rev. Plant Physiol. Plant Mol. Biol. 2001, 52, 847–875. [Google Scholar] [CrossRef] [PubMed]
- Gross, S.P. Hither and yon: A review of bi-directional microtubule-based transport. Phys. Biol. 2004, 1, R1–R11. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).