Enhancing Understanding of the Impact of Climate Change on Malaria in West Africa Using the Vector-Borne Disease Community Model of the International Center for Theoretical Physics (VECTRI) and the Bias-Corrected Phase 6 Coupled Model Intercomparison Project Data (CMIP6)
Abstract
1. Introduction
2. Materials and Methods
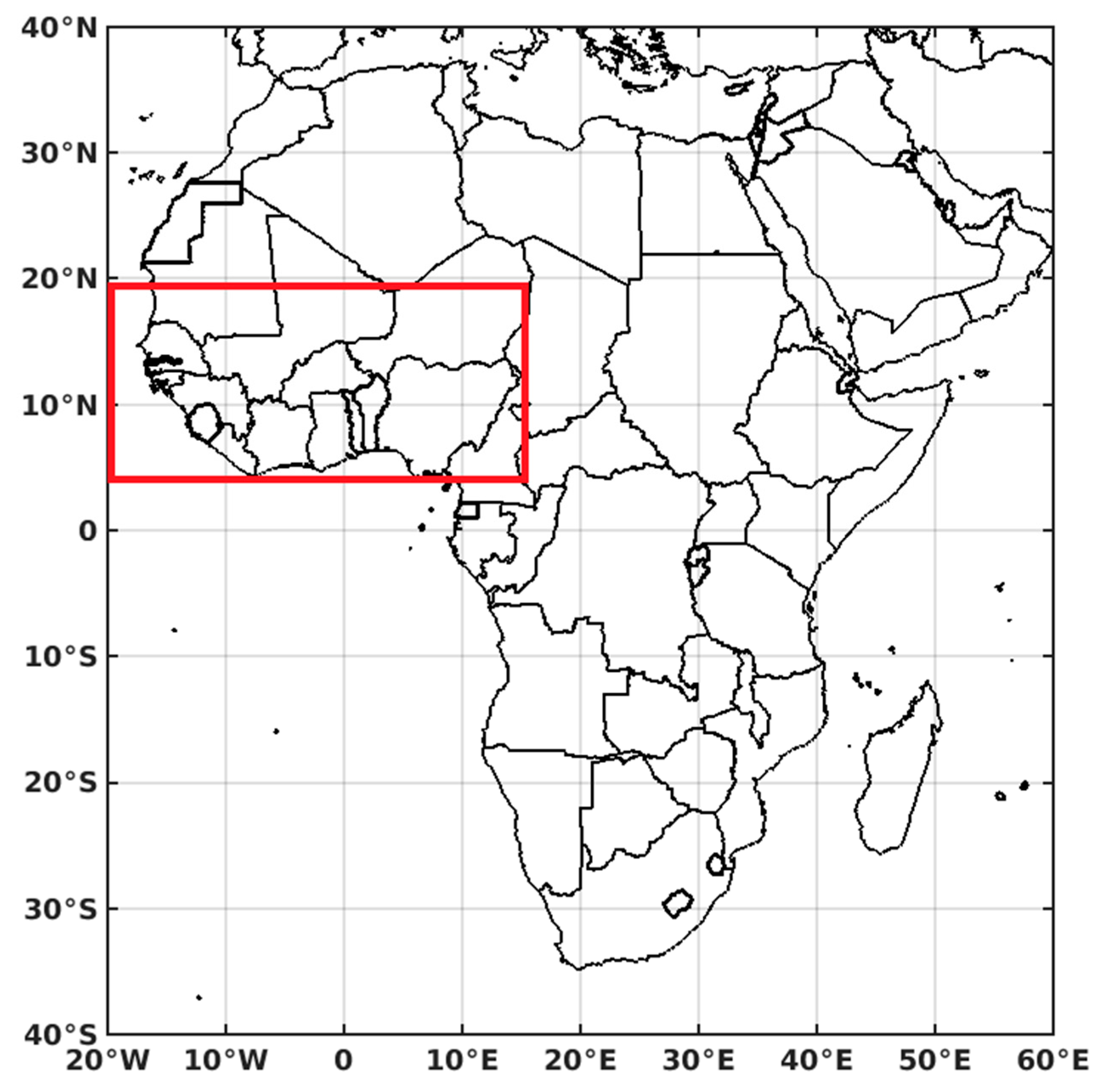
2.1. Study Area
2.2. Malaria Surveillance Data
2.3. Bias-Corrected CMIP6 GCM Models Used in This Study
2.4. VECTRI Malaria Model
2.5. Method
3. Results and Discussion
3.1. Models’ Evaluation
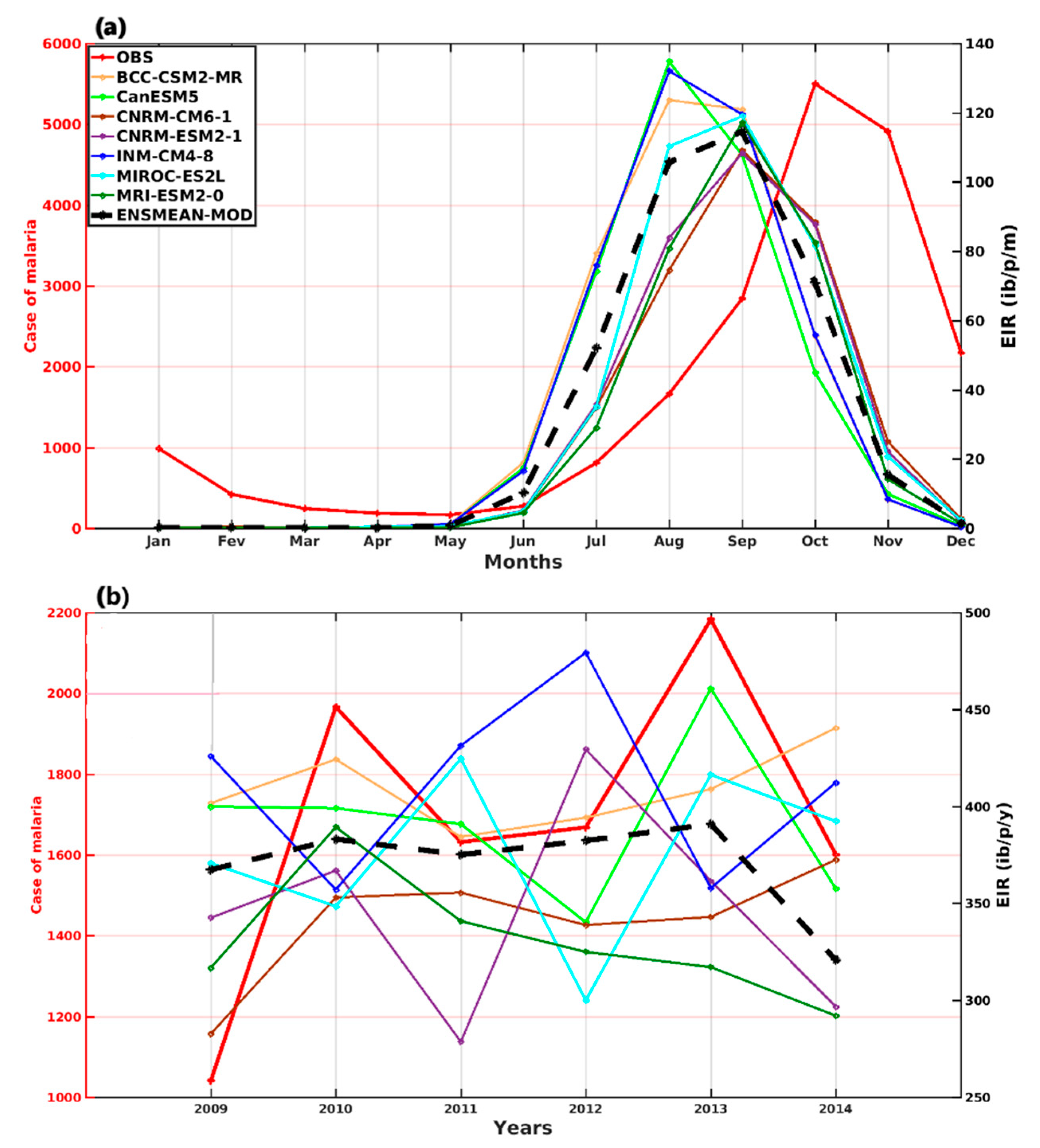
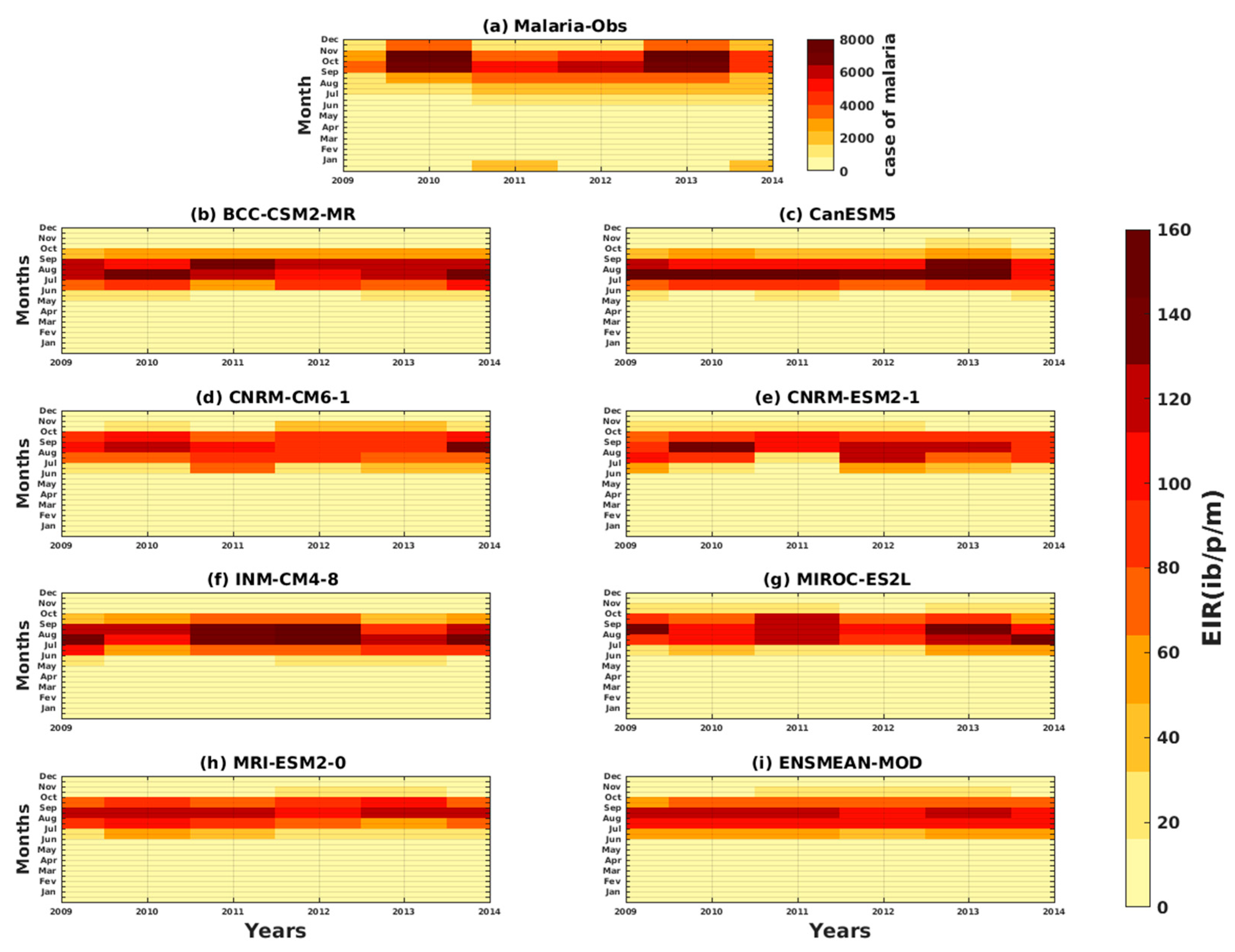
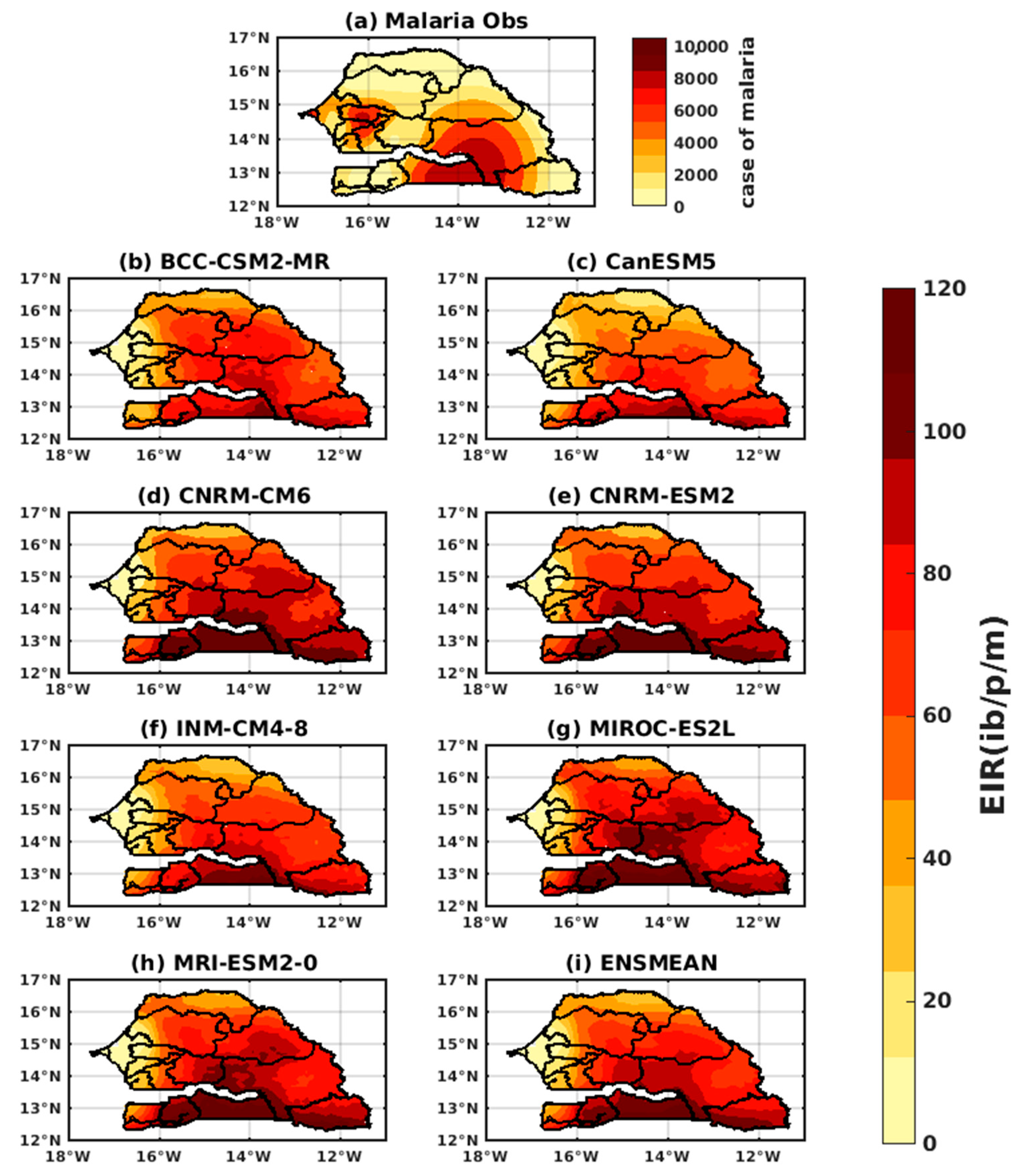
3.1.1. VECTRI Model’s Performance with Observed Malaria Cases in Senegal
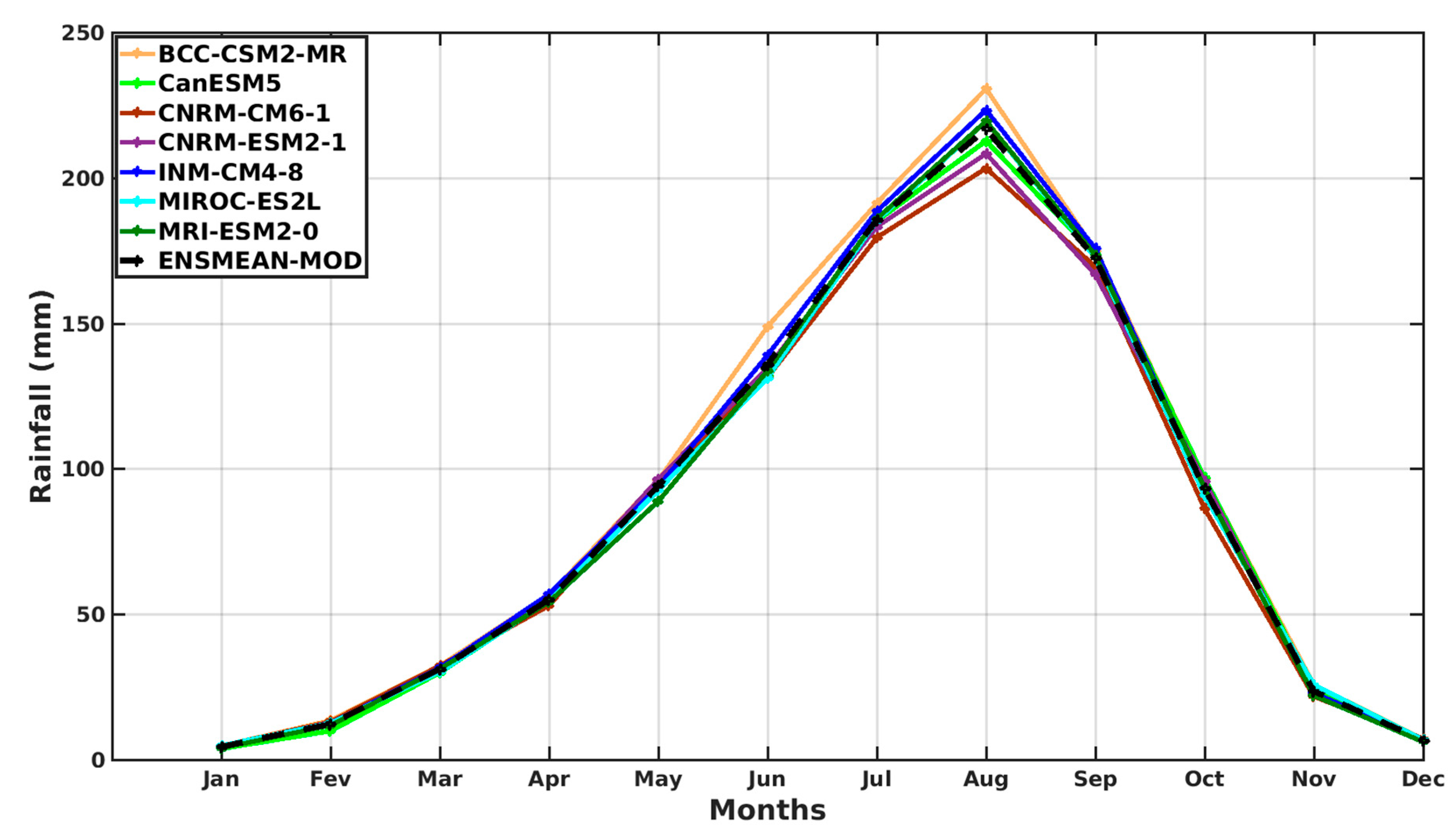
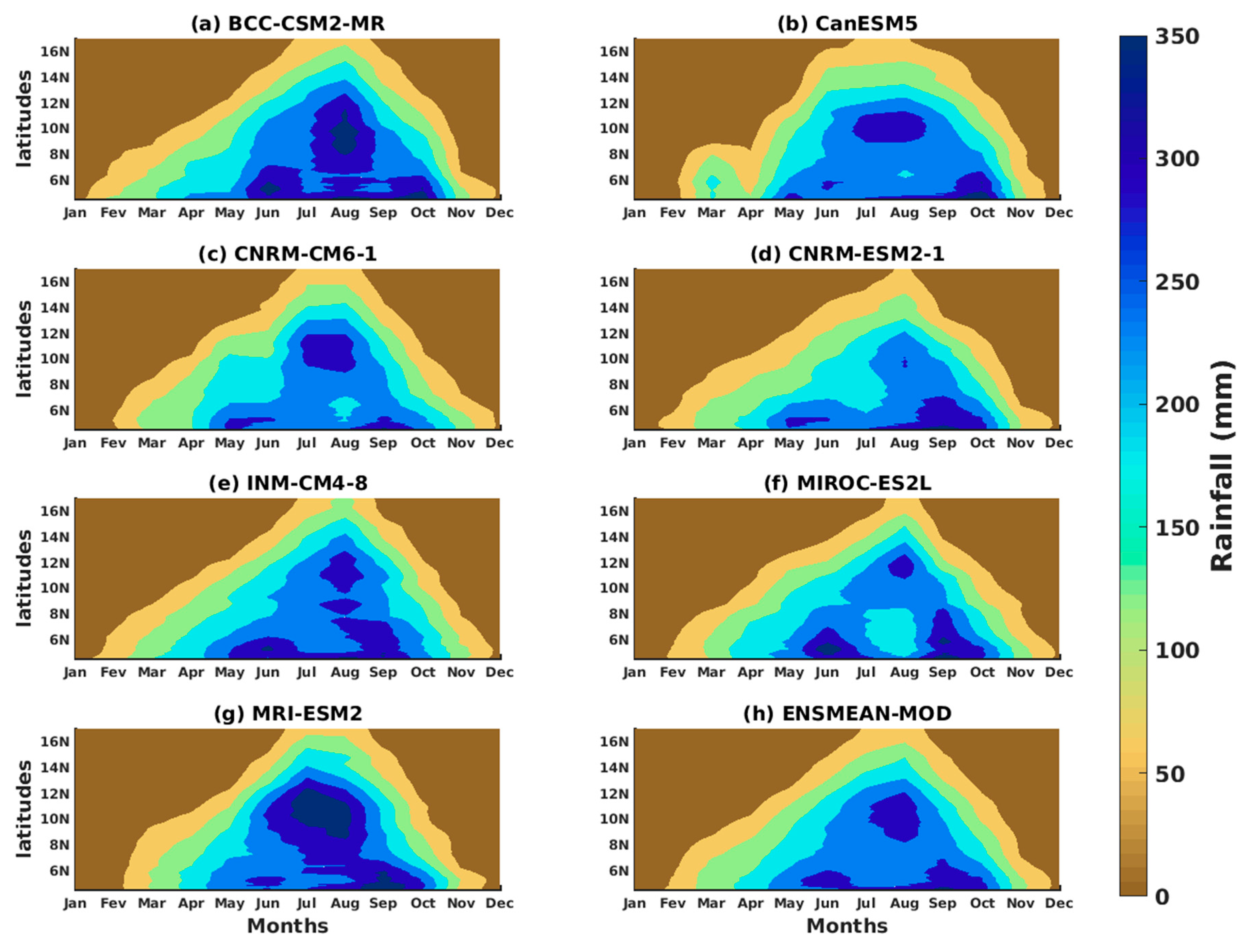
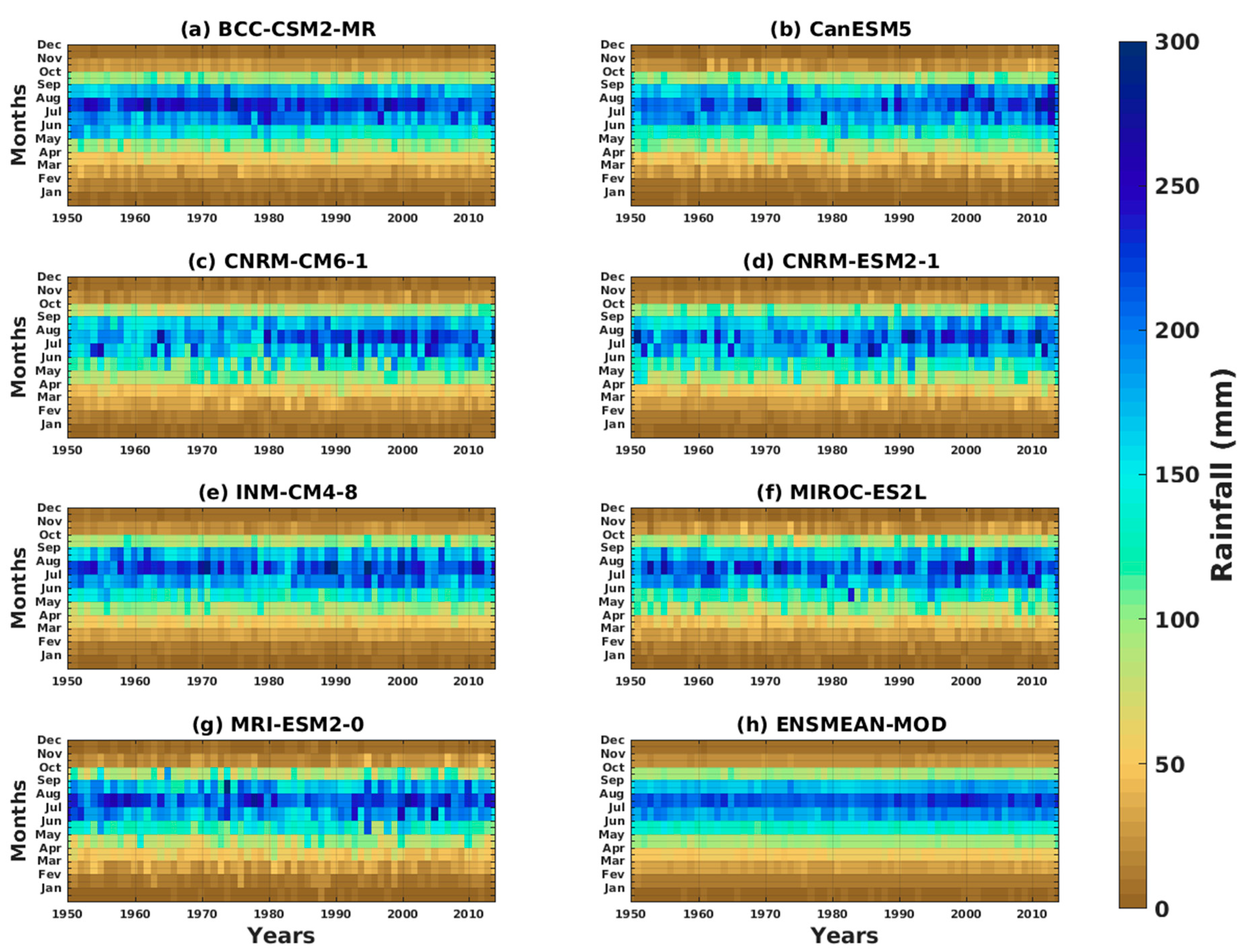
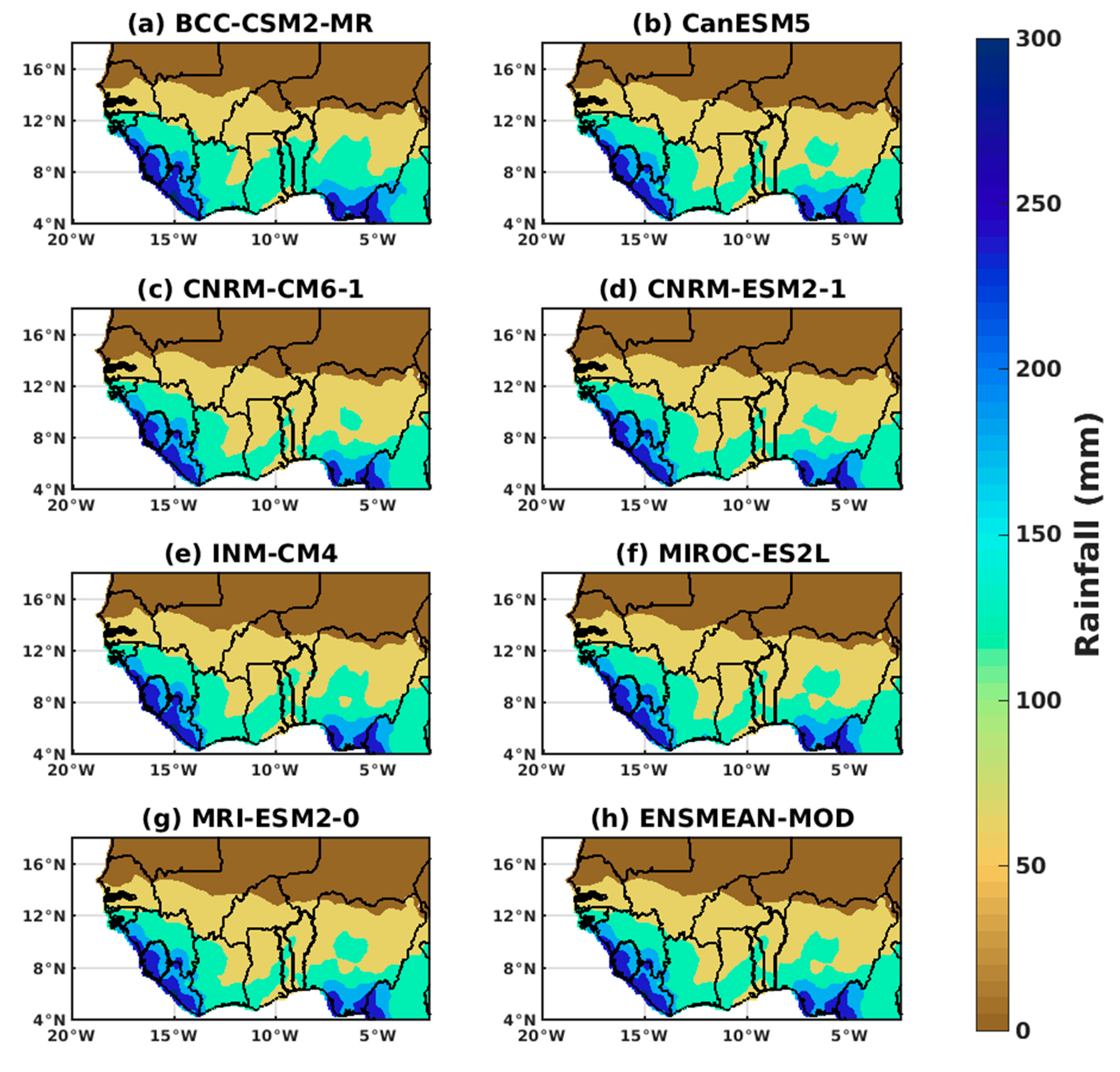
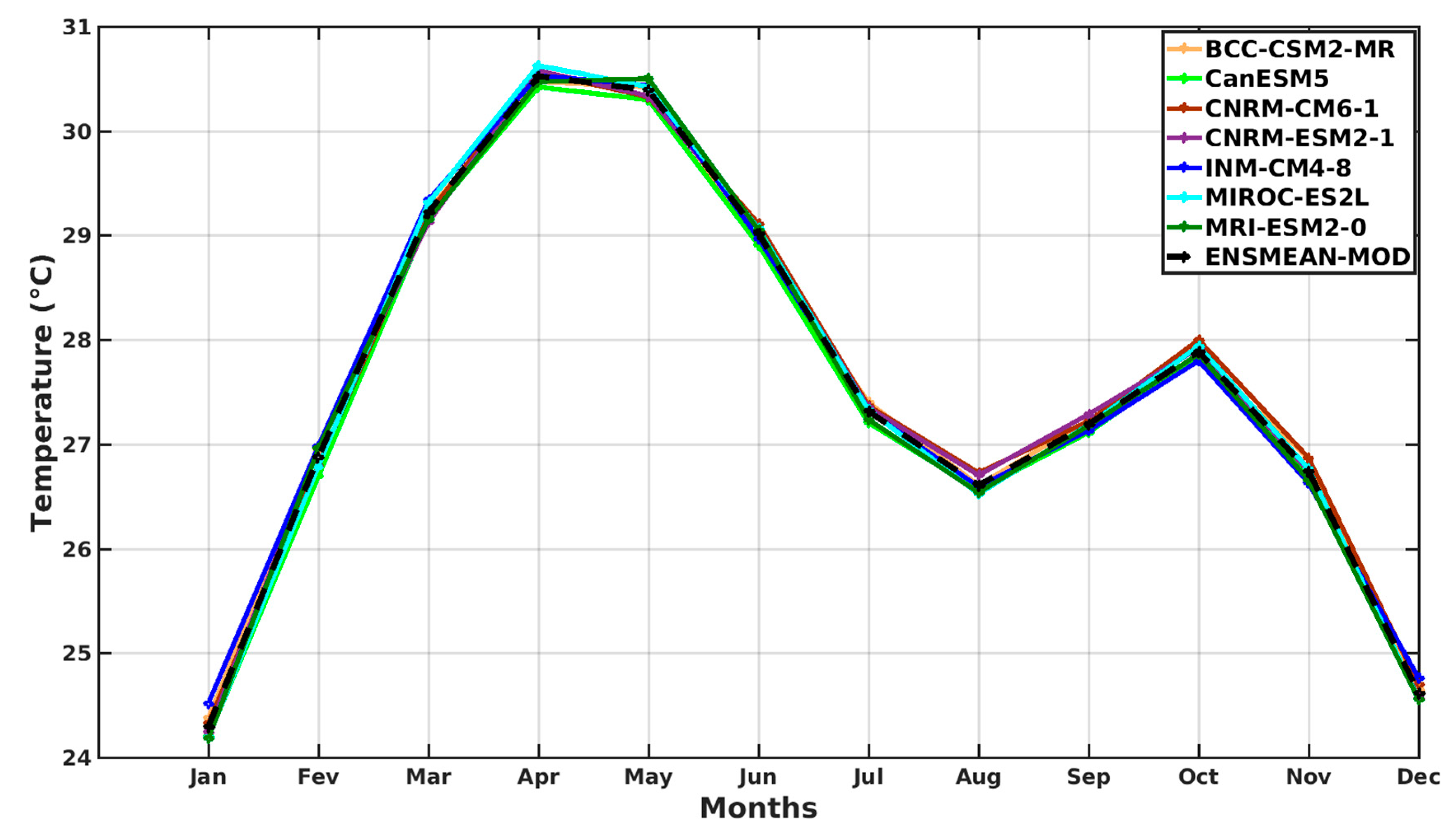
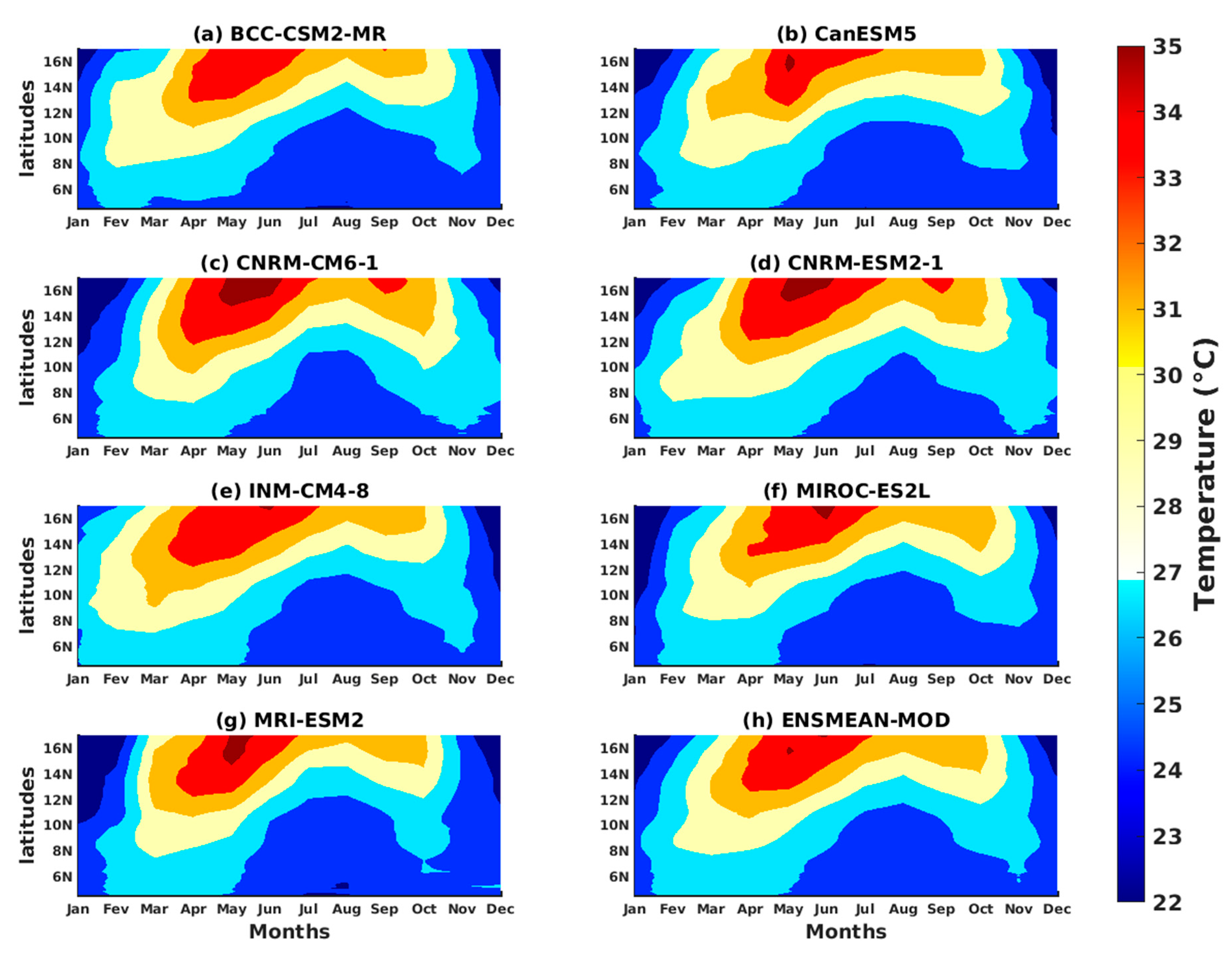
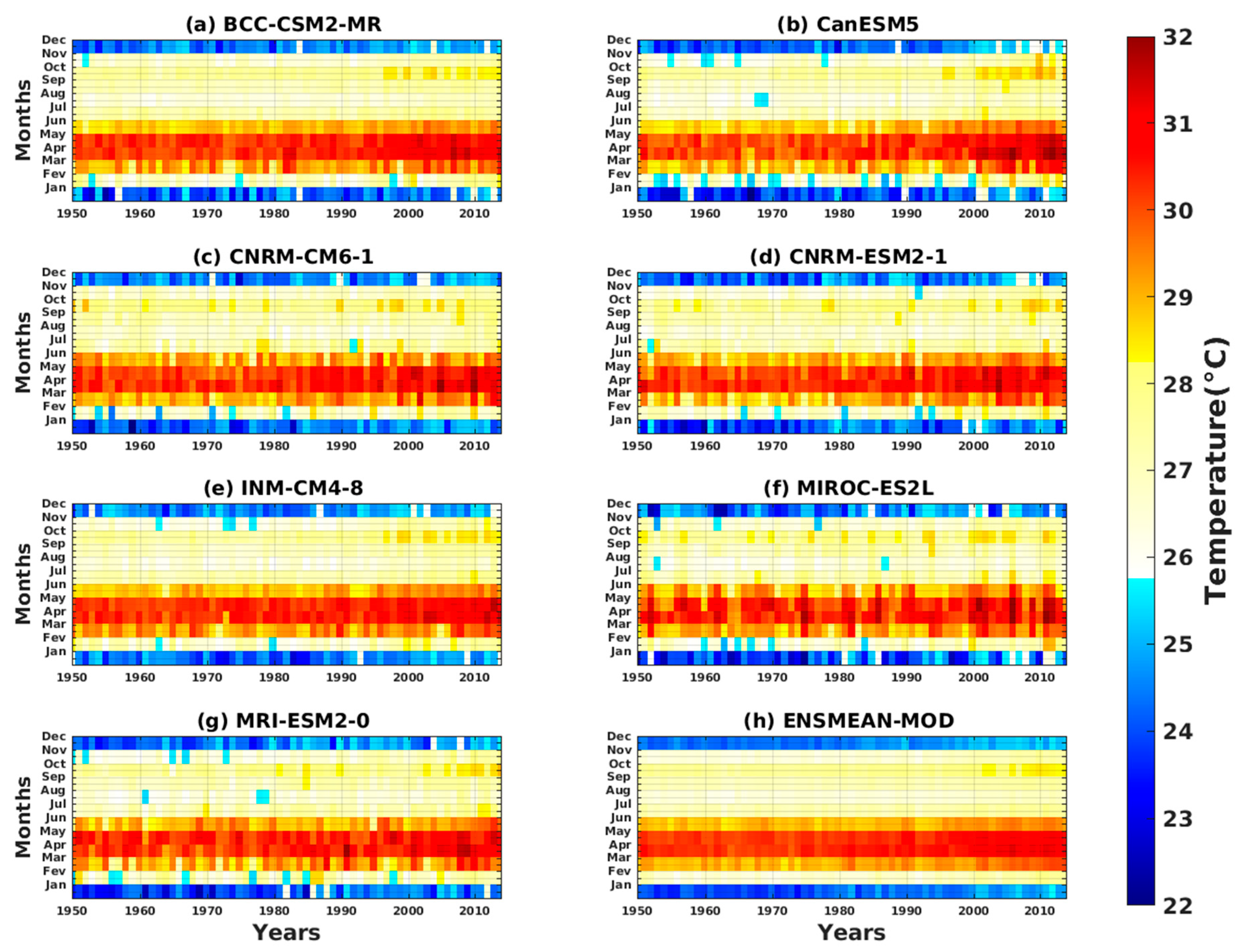
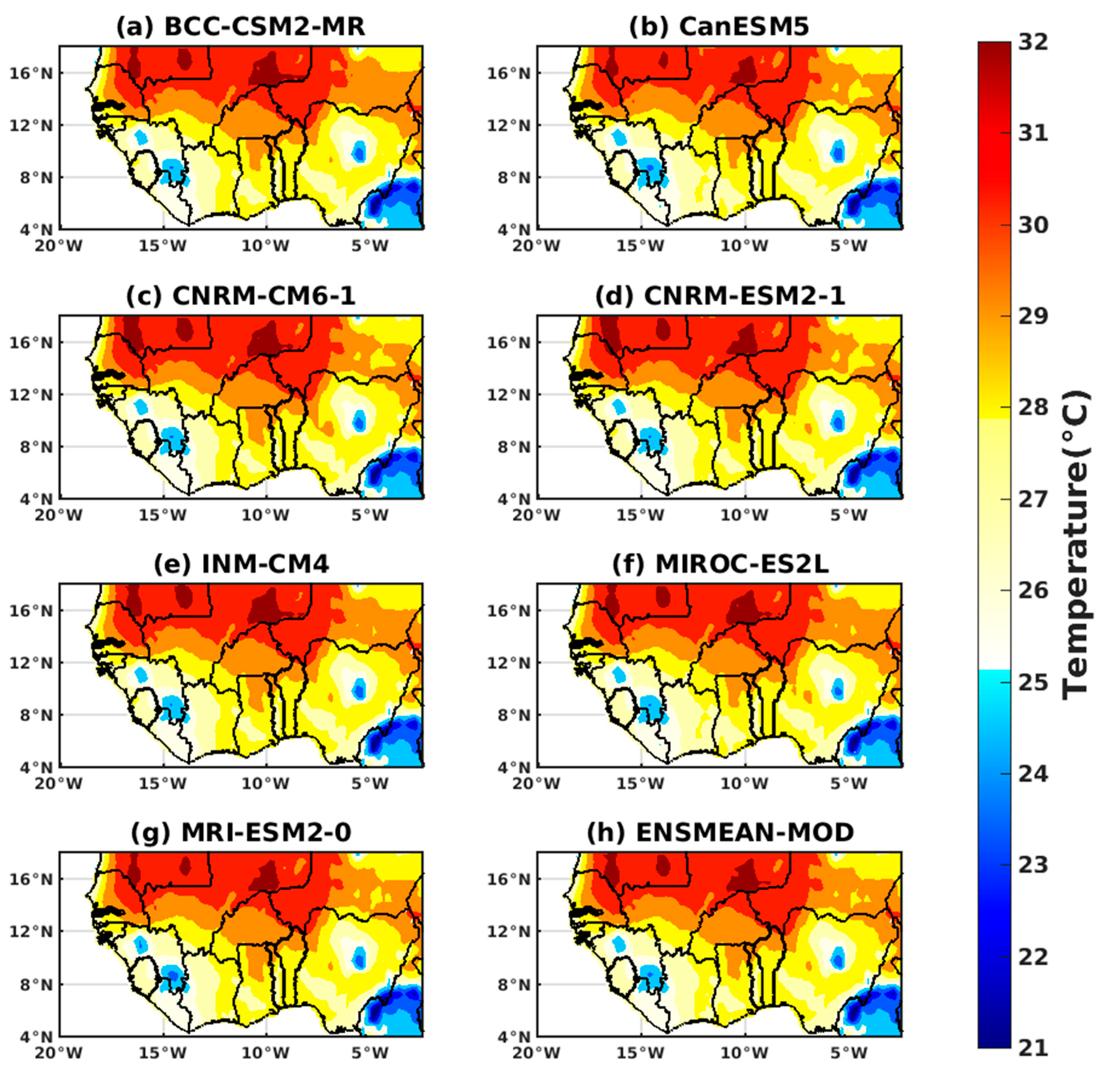
3.1.2. Spatio-Temporal Variability of Rainfall and Temperature over West Africa Using CMIP6 Data
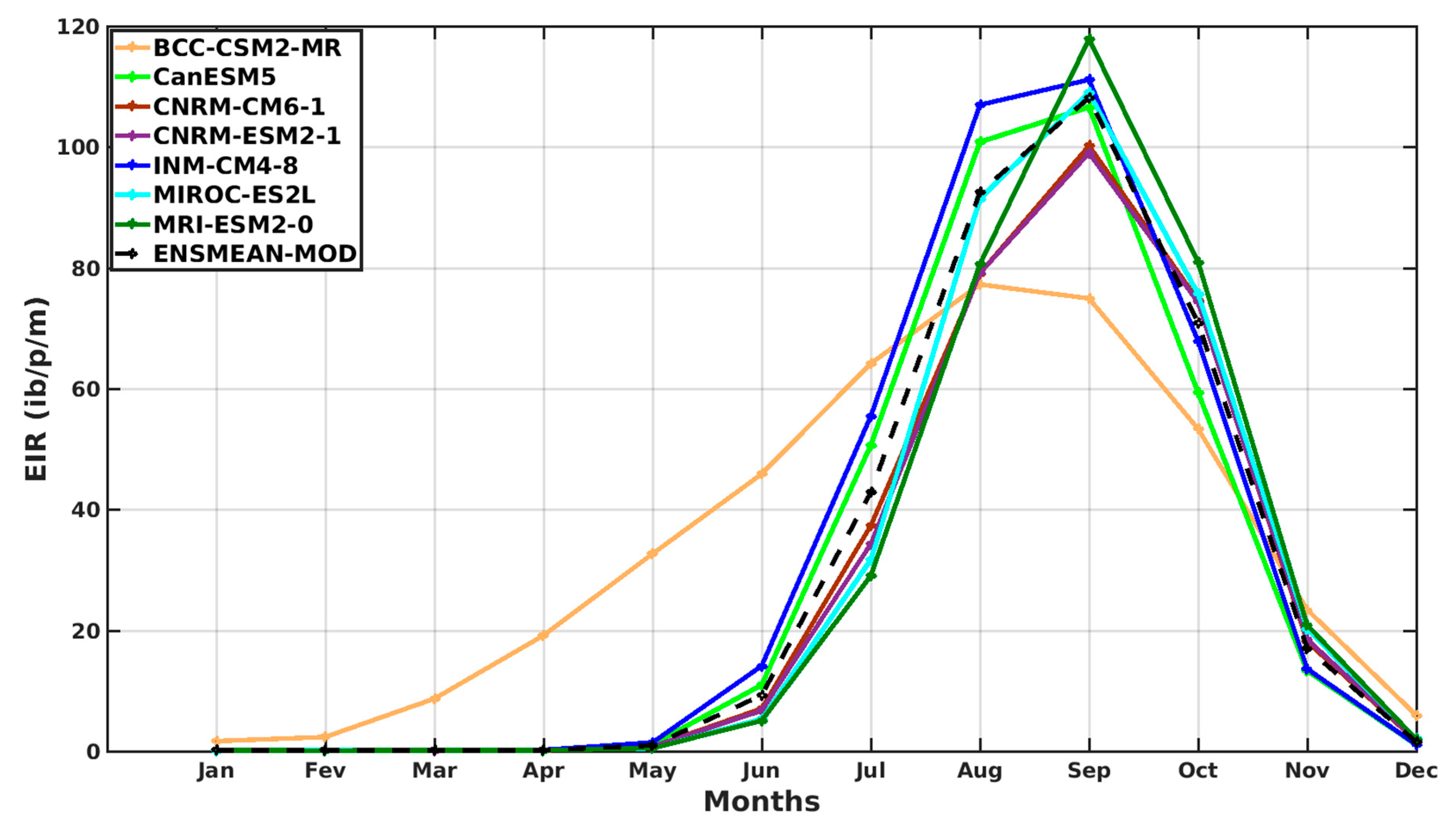
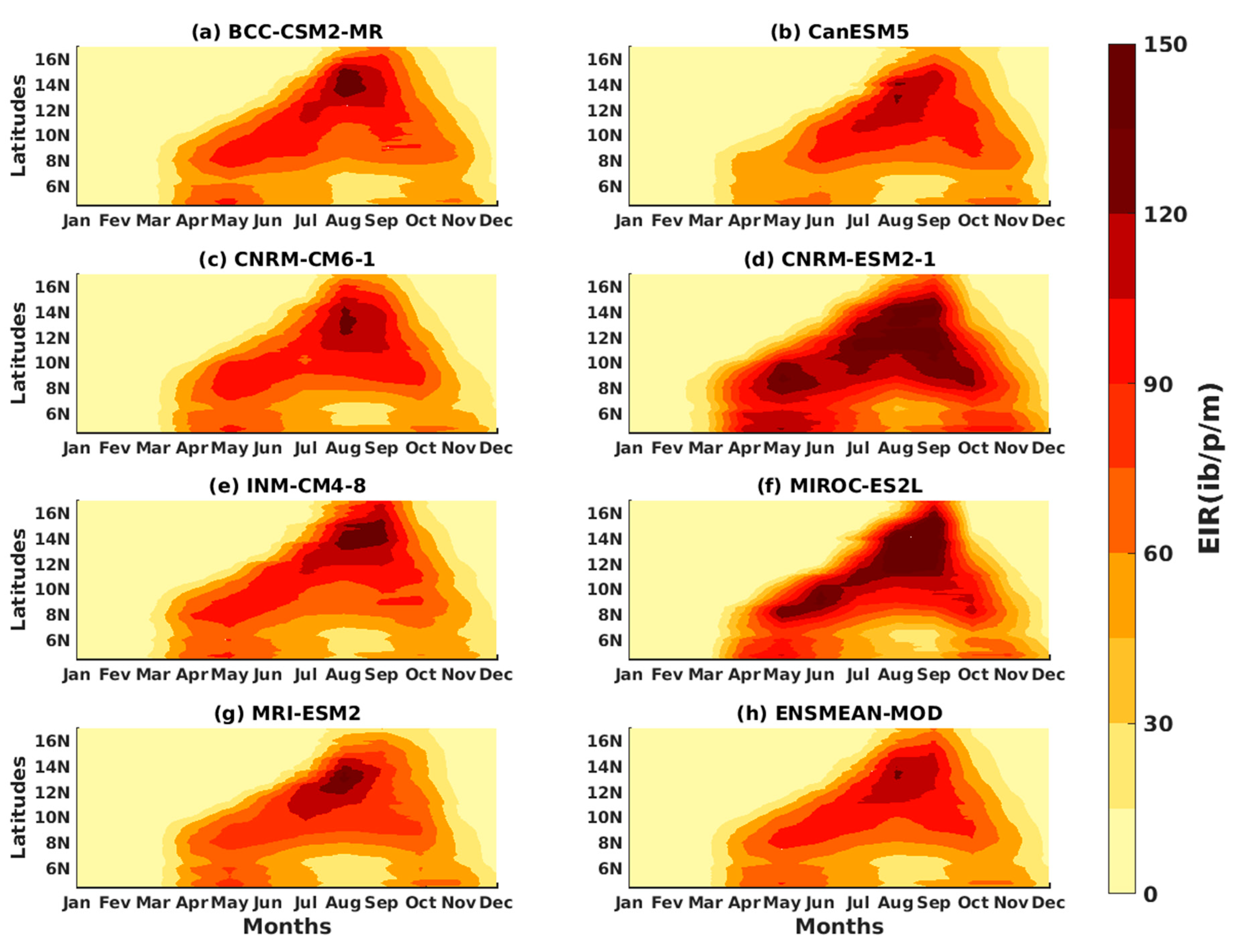
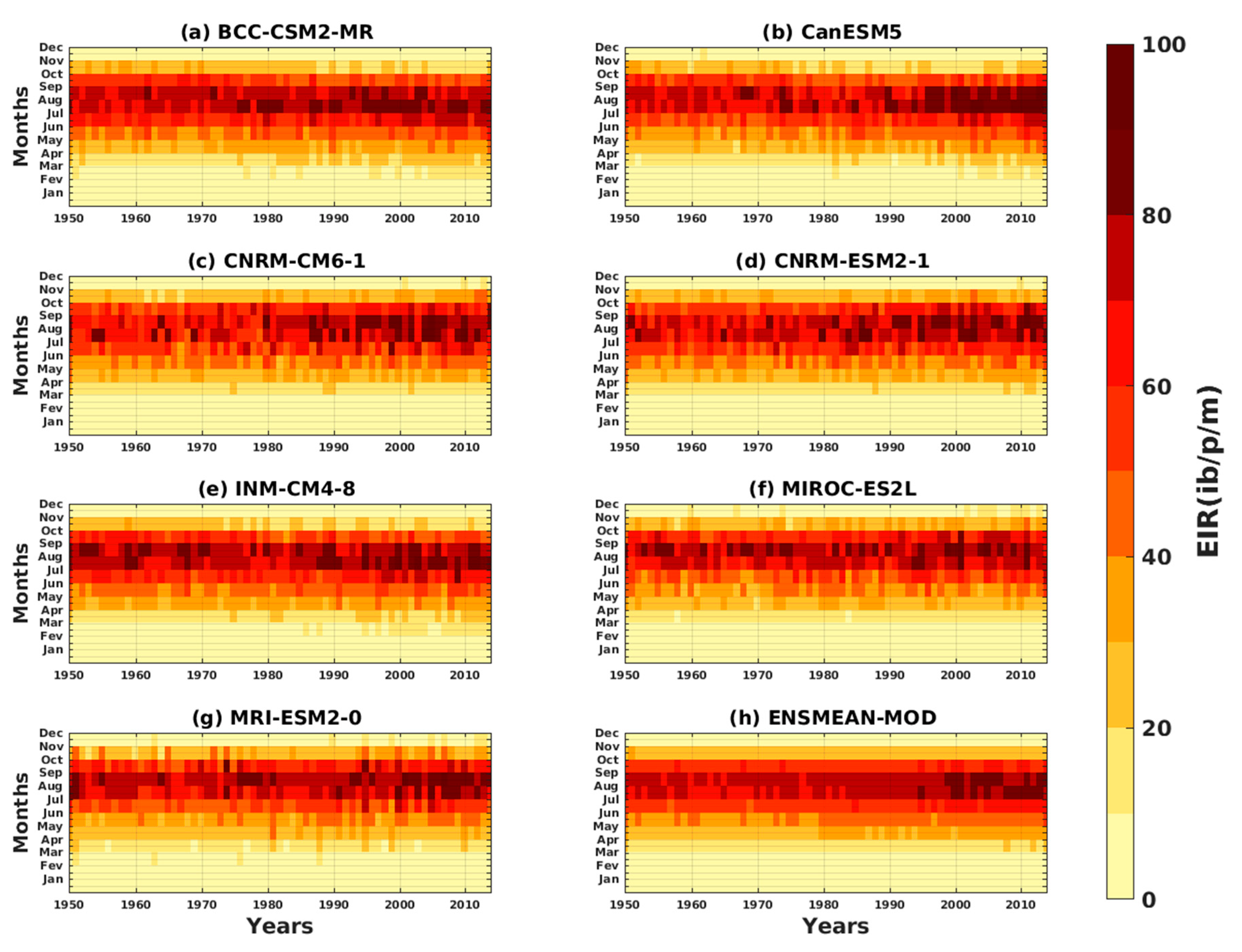
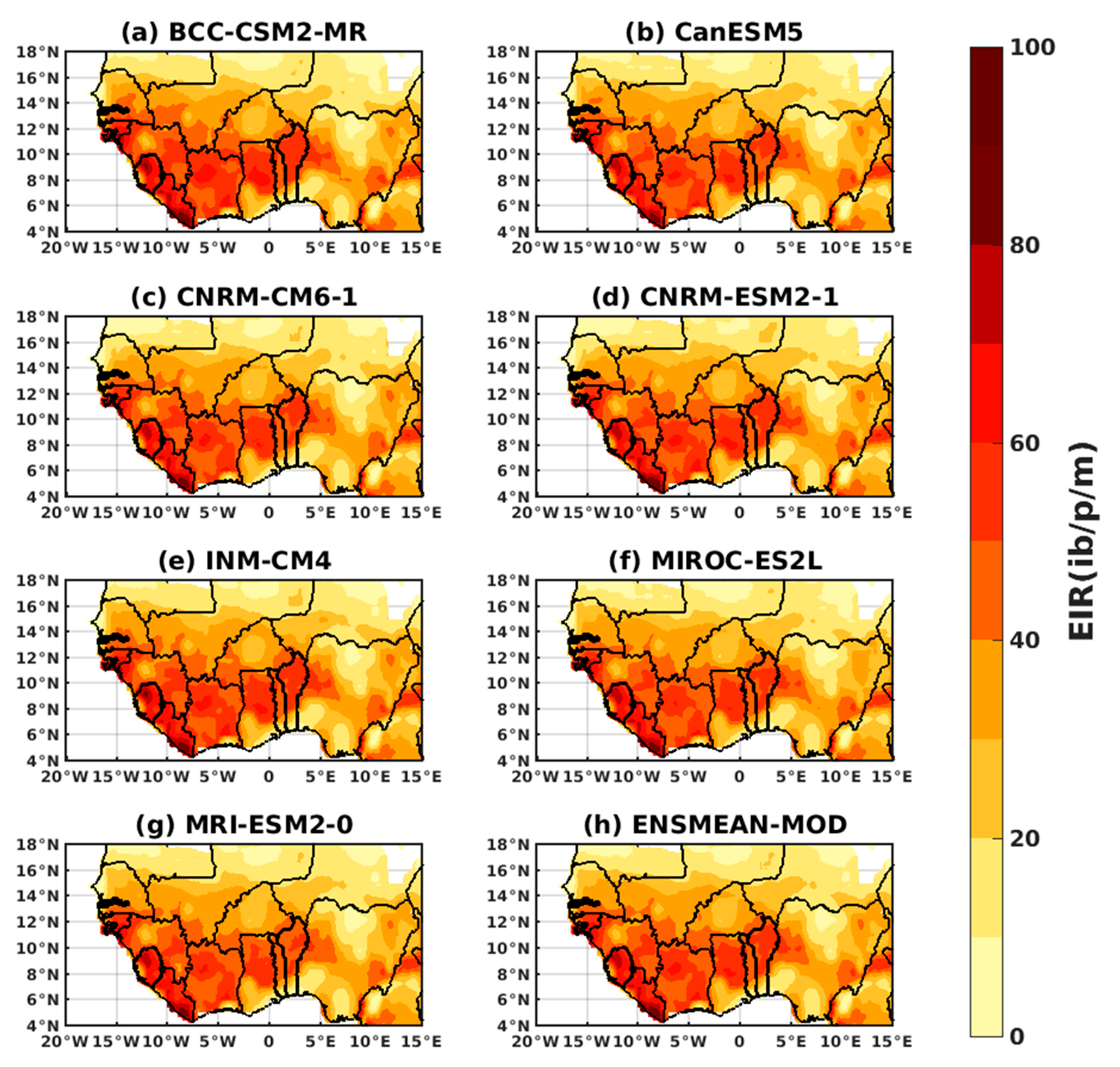
3.1.3. Evaluation of the VECTRI Model in West Africa
3.2. Future Climate Impacts on Malaria
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Noguer, A. Les facteurs influençant la distribution géographique du paludisme dans le monde. Globe Rev. Genev. Géogr. 1979, 119, 15–25. [Google Scholar] [CrossRef]
- Mouchet, J.; Faye, O.; Julvez, J.; Manguin, S. Drought and Malaria Retreat in the Sahel, West Africa. Lancet 1996, 348, 1735–1736. [Google Scholar] [CrossRef] [PubMed]
- Bayoh, M.N.; Lindsay, S.W. Effect of Temperature on the Development of the Aquatic Stages of Anopheles gambiae Sensu Stricto (Diptera: Culicidae). Bull. Entomol. Res. 2003, 93, 375–381. [Google Scholar] [CrossRef] [PubMed]
- Mason, S.J.; Thomson, M.C.; Connor, S.J.; Phindela, T. Use of rainfall and sea surface temperature monitoring for malaria early warning in Botswana. Am. J. Trop. Med. Hyg. 2005, 73, 214–221. [Google Scholar] [CrossRef]
- De Silva, P.M.; Marshall, J.M. Factors Contributing to Urban Malaria Transmission in Sub-Saharan Africa: A Systematic Review. J. Trop. Med. 2012, 2012, 819563. [Google Scholar] [CrossRef] [PubMed]
- Dasgupta, S. Burden of Climate Change on Malaria Mortality. Int. J. Hyg. Environ. Health 2018, 221, 782–791. [Google Scholar] [CrossRef]
- World Malaria Report 2022. Available online: https://www.who.int/teams/global-malaria-programme/reports/world-malaria-report-2022 (accessed on 2 August 2023).
- Diouf, I.; Adeola, A.M.; Abiodun, G.J.; Lennard, C.; Shirinde, J.M.; Yaka, P.; Ndione, J.-A.; Gbobaniyi, E.O. Impact of Future Climate Change on Malaria in West Africa. Theor. Appl. Clim. 2022, 147, 853–865. [Google Scholar] [CrossRef]
- Kleinschmidt, I.; Omumbo, J.; Briët, O.; Van De Giesen, N.; Sogoba, N.; Mensah, N.K.; Windmeijer, P.; Moussa, M.; Teuscher, T. An Empirical Malaria Distribution Map for West Africa. Trop. Med. Int. Health 2001, 6, 779–786. [Google Scholar] [CrossRef]
- Caminade, C.; Kovats, S.; Rocklov, J.; Tompkins, A.M.; Morse, A.P.; Colón-González, F.J.; Stenlund, H.; Martens, P.; Lloyd, S.J. Impact of Climate Change on Global Malaria Distribution. Proc. Natl. Acad. Sci. USA 2014, 111, 3286–3291. [Google Scholar] [CrossRef]
- Tompkins, A.M.; Ermert, V. A Regional-Scale, High Resolution Dynamical Malaria Model That Accounts for Population Density, Climate and Surface Hydrology. Malar. J. 2013, 12, 65. [Google Scholar] [CrossRef]
- Tompkins, A.M.; Colón-González, F.J.; Di Giuseppe, F.; Namanya, D.B. Dynamical Malaria Forecasts Are Skillful at Regional and Local Scales in Uganda up to 4 Months Ahead. GeoHealth 2019, 3, 58–66. [Google Scholar] [CrossRef] [PubMed]
- Fall, P.; Diouf, I.; Deme, A.; Sene, D. Assessment of Climate-Driven Variations in Malaria Transmission in Senegal Using the VECTRI Model. Atmosphere 2022, 13, 418. [Google Scholar] [CrossRef]
- Fall, P.; Diouf, I.; Deme, A.; Diouf, S.; Sene, D.; Sultan, B.; Famien, A.M.; Janicot, S. Bias-Corrected CMIP5 Projections for Climate Change and Assessments of Impact on Malaria in Senegal under the VECTRI Model. Trop. Med. Infect. Dis. 2023, 8, 310. [Google Scholar] [CrossRef] [PubMed]
- Chemison, A.; Ramstein, G.; Tompkins, A.M.; Defrance, D.; Camus, G.; Charra, M.; Caminade, C. Impact of an Accelerated Melting of Greenland on Malaria Distribution over Africa. Nat. Commun. 2021, 12, 3971. [Google Scholar] [CrossRef] [PubMed]
- Tompkins, A.M.; Thomson, M.C. Uncertainty in Malaria Simulations in the Highlands of Kenya: Relative Contributions of Model Parameter Setting, Driving Climate and Initial Condition Errors. PLoS ONE 2018, 13, e0200638. [Google Scholar] [CrossRef] [PubMed]
- Asare, E.; Amekudzi, L. Assessing Climate Driven Malaria Variability in Ghana Using a Regional Scale Dynamical Model. Climate 2017, 5, 20. [Google Scholar] [CrossRef]
- Fosah, S.; Mbouna, A.D.; Efon, E.; Achu, D.F.; Andre, L.; Dikande, A.M. Influences of Rainfall and Temperature on Malaria Endemicity in Cameroon: Emphasis on Bonaberi District. GEP 2022, 10, 46–66. [Google Scholar] [CrossRef]
- Sultan, B.; Janicot, S.; Diedhiou, A. The West African Monsoon Dynamics. Part I: Documentation of Intraseasonal Variability. J. Clim. 2003, 16, 3389–3406. [Google Scholar] [CrossRef]
- Sultan, B.; Janicot, S. The West African Monsoon Dynamics. Part II: The “Preonset” and “Onset” of the Summer Monsoon. J. Clim. 2003, 16, 3407–3427. [Google Scholar] [CrossRef]
- Navarro-Racines, C.; Tarapues, J.; Thornton, P.; Jarvis, A.; Ramirez-Villegas, J. High-Resolution and Bias-Corrected CMIP5 Projections for Climate Change Impact Assessments. Sci. Data 2020, 7, 7. [Google Scholar] [CrossRef]
- Xu, Z.; Han, Y.; Tam, C.-Y.; Yang, Z.-L.; Fu, C. Bias-Corrected CMIP6 Global Dataset for Dynamical Downscaling of the Historical and Future Climate (1979–2100). Sci. Data 2021, 8, 293. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Yang, Z.-L. An Improved Dynamical Downscaling Method with GCM Bias Corrections and Its Validation with 30 Years of Climate Simulations. J. Clim. 2012, 25, 6271–6286. [Google Scholar] [CrossRef]
- Marchi, M.; Castellanos-Acuña, D.; Hamann, A.; Wang, T.; Ray, D.; Menzel, A. ClimateEU, Scale-Free Climate Normals, Historical Time Series, and Future Projections for Europe. Sci. Data 2020, 7, 428. [Google Scholar] [CrossRef] [PubMed]
- Giorgi, F.; Mearns, L.O. Introduction to Special Section: Regional Climate Modeling Revisited. J. Geophys. Res. Atmos. 1999, 104, 6335–6352. [Google Scholar] [CrossRef]
- Sarr, A. Multi-Scale Characteristics of Precipitation and Temperature over West Africa Using SMHI-RCA Driven by GCMs under RCP8.5. Am. J. Clim. Change 2017, 6, 455–486. [Google Scholar] [CrossRef]
- Gutowski, W.J.; Ullrich, P.A.; Hall, A.; Leung, L.R.; O’Brien, T.A.; Patricola, C.M.; Arritt, R.W.; Bukovsky, M.S.; Calvin, K.V.; Feng, Z.; et al. The Ongoing Need for High-Resolution Regional Climate Models: Process Understanding and Stakeholder Information. Bull. Am. Meteorol. Soc. 2020, 101, E664–E683. [Google Scholar] [CrossRef]
- Michelangeli, P.-A.; Vrac, M.; Loukos, H. Probabilistic Downscaling Approaches: Application to Wind Cumulative Distribution Functions. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Vrac, M.; Drobinski, P.; Merlo, A.; Herrmann, M.; Lavaysse, C.; Li, L.; Somot, S. Dynamical and Statistical Downscaling of the French Mediterranean Climate: Uncertainty Assessment. Nat. Hazards Earth Syst. Sci. 2012, 12, 2769–2784. [Google Scholar] [CrossRef]
- Vrac, M.; Friederichs, P. Multivariate—Intervariable, Spatial, and Temporal—Bias Correction. J. Clim. 2015, 28, 218–237. [Google Scholar] [CrossRef]
- Vautard, R.; Noël, T.; Li, L.; Vrac, M.; Martin, E.; Dandin, P.; Cattiaux, J.; Joussaume, S. Climate Variability and Trends in Downscaled High-Resolution Simulations and Projections over Metropolitan France. Clim. Dyn. 2013, 41, 1419. [Google Scholar] [CrossRef]
- Lavaysse, C.; Vrac, M.; Drobinski, P.; Lengaigne, M.; Vischel, T. Statistical Downscaling of the French Mediterranean Climate: Assessment for Present and Projection in an Anthropogenic Scenario. Nat. Hazards Earth Syst. Sci. 2012, 12, 651–670. [Google Scholar] [CrossRef]
- Famien, A.M.; Janicot, S.; Ochou, A.D.; Vrac, M.; Defrance, D.; Sultan, B.; Noël, T. A Bias-Corrected CMIP5 Dataset for Africa Using the CDF-t Method—A Contribution to Agricultural Impact Studies. Earth Syst. Dynam. 2018, 9, 313–338. [Google Scholar] [CrossRef]
- Bruyère, C.L.; Done, J.M.; Holland, G.J.; Fredrick, S. Bias Corrections of Global Models for Regional Climate Simulations of High-Impact Weather. Clim. Dyn. 2014, 43, 1847–1856. [Google Scholar] [CrossRef]
- Dai, A.; Rasmussen, R.M.; Ikeda, K.; Liu, C. A New Approach to Construct Representative Future Forcing Data for Dynamic Downscaling. Clim. Dyn. 2020, 55, 315–323. [Google Scholar] [CrossRef]
- Pachauri, R.K.; Reisinger, A. Bilan 2007 des Changements Climatiques: Rapport de Synthèse. Groupe D’experts Intergouvernemental sur L’evolution du Climat: Geneva, Switzerland, 2007; ISBN 978-92-9169-222-4. [Google Scholar]
- O’Neill, B.C.; Tebaldi, C.; van Vuuren, D.P.; Eyring, V.; Friedlingstein, P.; Hurtt, G.; Knutti, R.; Kriegler, E.; Lamarque, J.-F.; Lowe, J.; et al. The Scenario Model Intercomparison Project (ScenarioMIP) for CMIP6. Geosci. Model. Dev. 2016, 9, 3461–3482. [Google Scholar] [CrossRef]
- O’Neill, B.C.; Kriegler, E.; Ebi, K.L.; Kemp-Benedict, E.; Riahi, K.; Rothman, D.S.; van Ruijven, B.J.; van Vuuren, D.P.; Birkmann, J.; Kok, K.; et al. The Roads Ahead: Narratives for Shared Socioeconomic Pathways Describing World Futures in the 21st Century. Glob. Environ. Change 2017, 42, 169–180. [Google Scholar] [CrossRef]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An Overview of CMIP5 and the Experiment Design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
- Wu, T.; Lu, Y.; Fang, Y.; Xin, X.; Li, L.; Li, W.; Jie, W.; Zhang, J.; Liu, Y.; Zhang, L.; et al. The Beijing Climate Center Climate System Model (BCC-CSM): The Main Progress from CMIP5 to CMIP6. Geosci. Model. Dev. 2019, 12, 1573–1600. [Google Scholar] [CrossRef]
- Swart, N.C.; Cole, J.N.S.; Kharin, V.V.; Lazare, M.; Scinocca, J.F.; Gillett, N.P.; Anstey, J.; Arora, V.; Christian, J.R.; Hanna, S.; et al. The Canadian Earth System Model Version 5 (CanESM5.0.3). Geosci. Model. Dev. 2019, 12, 4823–4873. [Google Scholar] [CrossRef]
- Voldoire, A.; Saint-Martin, D.; Sénési, S.; Decharme, B.; Alias, A.; Chevallier, M.; Colin, J.; Guérémy, J.-F.; Michou, M.; Moine, M.-P.; et al. Evaluation of CMIP6 DECK Experiments with CNRM-CM6-1. J. Adv. Model. Earth Syst. 2019, 11, 2177–2213. [Google Scholar] [CrossRef]
- Séférian, R.; Delire, C.; Decharme, B.; Voldoire, A.; Salas y Melia, D.; Chevallier, M.; Saint-Martin, D.; Aumont, O.; Calvet, J.-C.; Carrer, D.; et al. Development and Evaluation of CNRM Earth System Model—CNRM-ESM1. Geosci. Model. Dev. 2016, 9, 1423–1453. [Google Scholar] [CrossRef]
- Volodin, E.M.; Mortikov, E.V.; Kostrykin, S.V.; Galin, V.Y.; Lykossov, V.N.; Gritsun, A.S.; Diansky, N.A.; Gusev, A.V.; Iakovlev, N.G.; Shestakova, A.A.; et al. Simulation of the Modern Climate Using the INM-CM48 Climate Model. Russ. J. Numer. Anal. Math. Model. 2018, 33, 367–374. [Google Scholar] [CrossRef]
- Hajima, T.; Watanabe, M.; Yamamoto, A.; Tatebe, H.; Noguchi, M.A.; Abe, M.; Ohgaito, R.; Ito, A.; Yamazaki, D.; Okajima, H.; et al. Development of the MIROC-ES2L Earth System Model and the Evaluation of Biogeochemical Processes and Feedbacks. Geosci. Model. Dev. 2020, 13, 2197–2244. [Google Scholar] [CrossRef]
- Yukimoto, S.; Kawai, H.; Koshiro, T.; Oshima, N.; Yoshida, K.; Urakawa, S.; Tsujino, H.; Deushi, M.; Tanaka, T.; Hosaka, M.; et al. The Meteorological Research Institute Earth System Model Version 2.0, MRI-ESM2.0: Description and Basic Evaluation of the Physical Component. J. Meteorol. Soc. Jpn. Ser. II 2019, 97, 2019–2051. [Google Scholar] [CrossRef]
- Detinova, T.S. Age-Grouping Methods in Diptera of Medical Importance with Special Reference to Some Vectors of Malaria. Monogr. Ser. World Health Organ. 1962, 47, 13–191. [Google Scholar] [CrossRef] [PubMed]
- Armstrong, J.A.; Bransby-Williams, W.R. The Maintenance of a Colony of Anopheles Gambiae, with Observations on the Effects of Changes in Temperature. Bull. World Health Organ. 1961, 24, 427–435. [Google Scholar] [PubMed]
- Kirby, M.J.; Lindsay, S.W. Effect of Temperature and Inter-Specific Competition on the Development and Survival of Anopheles Gambiae Sensu Stricto and An. arabiensis Larvae. Acta Trop. 2009, 109, 118–123. [Google Scholar] [CrossRef]
- Martens, W.J.M.; Niessen, L.W.; Rotmans, J.; McMichael, A.J. Potential Impact of Global Climate Change on Malaria Risk. Environ. Health Perspect. 1995, 103, 458–464. [Google Scholar] [CrossRef]
- Martens, W.; Jetten, T.; Rotmans, J.; Niessen, L. Climate Change and Vector-Borne Diseases: A Global Modelling Perspective. Glob. Environ. Change 1995, 5, 195–209. [Google Scholar] [CrossRef]
- Martin-Rosales, W.; Leduc, C. Dynamiques de Vidange d’une Mare Temporaire Au Sahel: L’exemple de Banizoumbou (Sud-Ouest Du Niger). C. R. Geosci. 2003, 335, 461–468. [Google Scholar] [CrossRef]
- Jepson, W.F.; Moutia, A.; Courtois, C. The Malaria Problem in Mauritius: The Bionomics of Mauritian Anophelines. Bull. Entomol. Res. 1947, 38, 177–208. [Google Scholar] [CrossRef] [PubMed]
- Bomblies, A.; Duchemin, J.-B.; Eltahir, E.A. A Mechanistic Approach for Accurate Simulation of Village Scale Malaria Transmission. Malar. J. 2009, 8, 223. [Google Scholar] [CrossRef] [PubMed]
- Ermert, V.; Fink, A.H.; Jones, A.E.; Morse, A.P. Development of a New Version of the Liverpool Malaria Model. I. Refining the Parameter Settings and Mathematical Formulation of Basic Processes Based on a Literature Review. Malar. J. 2011, 10, 35. [Google Scholar] [CrossRef] [PubMed]
- Paaijmans, K.P.; Heusinkveld, B.G.; Jacobs, A.F.G. A Simplified Model to Predict Diurnal Water Temperature Dynamics in a Shallow Tropical Water Pool. Int. J. Biometeorol. 2008, 52, 797–803. [Google Scholar] [CrossRef] [PubMed]
- Meinshausen, M.; Nicholls, Z.R.J.; Lewis, J.; Gidden, M.J.; Vogel, E.; Freund, M.; Beyerle, U.; Gessner, C.; Nauels, A.; Bauer, N.; et al. The Shared Socio-Economic Pathway (SSP) Greenhouse Gas Concentrations and Their Extensions to 2500. Geosci. Model Dev. 2020, 13, 3571–3605. [Google Scholar] [CrossRef]
- Appawu, M.; Owusu-Agyei, S.; Dadzie, S.; Asoala, V.; Anto, F.; Koram, K.; Rogers, W.; Nkrumah, F.; Hoffman, S.L.; Fryauff, D.J. Malaria Transmission Dynamics at a Site in Northern Ghana Proposed for Testing Malaria Vaccines. Trop. Med. Int. Health 2004, 9, 164–170. [Google Scholar] [CrossRef] [PubMed]
- Shililu, J.; Ghebremeskel, T.; Mengistu, S.; Fekadu, H.; Zerom, M.; Mbogo, C.; Githure, J.; Novak, R.; Brantly, E.; Beier, J.C. High Seasonal Variation in Entomologic Inoculation Rates in Eritrea, a Semi-Arid Region of Unstable Malaria in Africa. Am. J. Trop. Med. Hyg. 2003, 69, 607–613. [Google Scholar] [CrossRef] [PubMed]
- Fontenille, D.; Lochouarn, L.; Diatta, M.; Sokhna, C.; Dia, I.; Diagne, N.; Lemasson, J.-J.; Ba, K.; Tall, A.; Rogier, C.; et al. Four Years’ Entomological Study of the Transmission of Seasonal Malaria in Senegal and the Bionomics of Anopheles gambiae and A. arabiensis. Trans. R. Soc. Trop. Med. Hyg. 1997, 91, 647–652. [Google Scholar] [CrossRef]
- Sokhina, C.S.; Trape, J.-F.; Robert, V. Gametocytaemia in Senegalese Children with Uncomplicated Falciparum Malaria Treated with Chloroquine, Amodiaquine or Sulfadoxine + Pyrimethamine. Parasite 2001, 8, 243–250. [Google Scholar] [CrossRef][Green Version]
- Nouaceur, Z. La reprise des pluies et la recrudescence des inondations en Afrique de l’Ouest sahélienne. Physio-Géo Géogr. Phys. Environ. 2020, 15, 89–109. [Google Scholar] [CrossRef]
- La Mousson Afrique Ouest. Available online: https://www.cnrs.fr/cw/dossiers/dosclim1/rechfran/4theme/cycledeleau/moussonAfOuest.html (accessed on 13 August 2023).
- Salack, S.; Giannini, A.; Diakhaté, M.; Gaye Amadou, T.; Muller, B. Oceanic Influence on the Sub-Seasonal to Interannual Timing and Frequency of Extreme Dry Spells over the West African Sahel. Clim. Dyn. 2014, 42, 189–201. [Google Scholar] [CrossRef]
- Balme, M.; Lebel, T.; Amani, A. Années Sèches et Années Humides Au Sahel: Quo Vadimus? Hydrol. Sci. J. 2006, 51, 254–271. [Google Scholar] [CrossRef]
- Ali, A.; Lebel, T. The Sahelian Standardized Rainfall Index Revisited. Int. J. Climatol. 2009, 29, 1705–1714. [Google Scholar] [CrossRef]
- Guichard, F.; Kergoat, L.; Hourdin, F.; Léauthaud, C.; Barbier, J.; Mougin, É.; Diarra, B. Chapter 1. Climate Warming Observed in the Sahel since 1950. In Rural Societies in the Face of Climatic and Environmental Changes in West Africa; Lalou, R., Oumarou, A., Sanni, M.A., Sultan, B., Arame Soumaré, M., Eds.; Synthèses; IRD Éditions: Marseille, France, 2020; pp. 23–41. ISBN 978-2-7099-2425-2. [Google Scholar]
- Isnard, H. Le mécanisme du climat de l’ouest africain. L’Inf. Géogr. 1952, 16, 98–100. [Google Scholar] [CrossRef]
- Deme, A.; Gaye, A.T.; Hourdin, F. Chapter 3. Climate Projections in West Africa: The Obvious and the Uncertain. In Rural Societies in the Face of Climatic and Environmental Changes in West Africa; Sultan, B., Lalou, R., Sanni, M.A., Oumarou, A., Arame Soumaré, M., Eds.; IRD Éditions: Marseille, France, 2017; pp. 61–86. ISBN 978-2-7099-2424-5. [Google Scholar]
- Lavaysse, C.; Flamant, C.; Janicot, S.; Parker, D.J.; Lafore, J.-P.; Sultan, B.; Pelon, J. Seasonal Evolution of the West African Heat Low: A Climatological Perspective. Clim. Dyn. 2009, 33, 313–330. [Google Scholar] [CrossRef]
- Gbobaniyi, E.; Sarr, A.; Sylla, M.B.; Diallo, I.; Lennard, C.; Dosio, A.; Dhiédiou, A.; Kamga, A.; Klutse, N.A.B.; Hewitson, B.; et al. Climatology, Annual Cycle and Interannual Variability of Precipitation and Temperature in CORDEX Simulations over West Africa. Int. J. Climatol. 2014, 34, 2241–2257. [Google Scholar] [CrossRef]
- Guichard, F.; Kergoat, L.; Hourdin, F.; Léauthaud, C.; Barbier, J.; Mougin, É.; Diarra, B. Chapitre 1. Le Réchauffement Climatique Observé Depuis 1950 au Sahel; IRD Éditions: Marseille, France, 2015; ISBN 978-2-7099-2147-3. [Google Scholar]
- Janicot, S.; Thorncroft, C.D.; Ali, A.; Asencio, N.; Berry, G.; Bock, O.; Bourles, B.; Caniaux, G.; Chauvin, F.; Deme, A.; et al. Large-Scale Overview of the Summer Monsoon over West Africa during the AMMA Field Experiment in 2006. Ann. Geophys. 2008, 26, 2569–2595. [Google Scholar] [CrossRef]
- Lavaysse, C.; Flamant, C.; Evan, A.; Janicot, S.; Gaetani, M. Recent Climatological Trend of the Saharan Heat Low and Its Impact on the West African Climate. Clim. Dyn. 2016, 47, 3479–3498. [Google Scholar] [CrossRef]
- Mouchet, J.; Manguin, S.; Sircoulon, J.; Laventure, S.; Faye, O.; Onapa, A.W.; Carnevale, P.; Julvez, J.; Fontenille, D. Evolution of Malaria in Africa for the Past 40 Years: Impact of Climatic and Human Factors. J. Am. Mosq. Control Assoc. 1998, 14, 121–130. [Google Scholar]
- Mafwele, B.J.; Lee, J.W. Relationships between Transmission of Malaria in Africa and Climate Factors. Sci. Rep. 2022, 12, 14392. [Google Scholar] [CrossRef]
- Diouf, I.; Rodriguez Fonseca, B.; Caminade, C.; Thiaw, W.M.; Deme, A.; Morse, A.P.; Ndione, J.-A.; Gaye, A.T.; Diaw, A.; Ndiaye, M.K.N. Climate Variability and Malaria over West Africa. Am. J. Trop. Med. Hyg. 2020, 102, 1037–1047. [Google Scholar] [CrossRef] [PubMed]
- Bousema, J.T.; Gouagna, L.C.; Drakeley, C.J.; Meutstege, A.M.; Okech, B.A.; Akim, I.N.J.; Beier, J.C.; Githure, J.I.; Sauerwein, R.W. Plasmodium falciparum Gametocyte Carriage in Asymptomatic Children in Western Kenya. Malar. J. 2004, 3, 18. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Afrane, Y.A.; Little, T.J.; Lawson, B.W.; Githeko, A.K.; Lo, E. Deforestation and Vectorial Capacity of Anopheles gambiae Giles Mosquitoes in Malaria Transmission, Kenya. Emerg. Infect. Dis. J. 2008, 14, 1533. [Google Scholar] [CrossRef] [PubMed]
- Craig, M.H.; Snow, R.W.; le Sueur, D. A Climate-Based Distribution Model of Malaria Transmission in Sub-Saharan Africa. Parasitol. Today 1999, 15, 105–111. [Google Scholar] [CrossRef] [PubMed]
- Carnevale, P.; Robert, V. Les Anophèles: Biologie, Transmission du Plasmodium et Lutte Antivectorielle; Carnevale, P., Robert, V., Eds.; IRD Éditions: Marseille, France, 2009; ISBN 978-2-7099-1662-2. [Google Scholar]
- Chaturvedi, S.; Dwivedi, S. Understanding the Effect of Climate Change in the Distribution and Intensity of Malaria Transmission over India Using a Dynamical Malaria Model. Int. J. Biometeorol. 2021, 65, 1161–1175. [Google Scholar] [CrossRef] [PubMed]
- Mbouna, A.D.; Tamoffo, A.T.; Asare, E.O.; Lenouo, A.; Tchawoua, C. Malaria Metrics Distribution under Global Warming: Assessment of the VECTRI Malaria Model over Cameroon. Int. J. Biometeorol. 2023, 67, 93–105. [Google Scholar] [CrossRef] [PubMed]
- Diouf, I.; Suárez-Moreno, R.; Rodríguez-Fonseca, B.; Caminade, C.; Wade, M.; Thiaw, W.M.; Deme, A.; Morse, A.P.; Ndione, J.-A.; Gaye, A.T.; et al. Oceanic Influence on Seasonal Malaria Incidence in West Africa. Weather Clim. Soc. 2022, 14, 287–302. [Google Scholar] [CrossRef]
- Bomblies, A.; Eltahir, E.A.B. Assessment of the Impact of Climate Shifts on Malaria Transmission in the Sahel. EcoHealth 2009, 6, 426–437. [Google Scholar] [CrossRef]
- Yamana, T.K.; Bomblies, A.; Eltahir, E.A.B. Climate Change Unlikely to Increase Malaria Burden in West Africa. Nat. Clim. Change 2016, 6, 1009–1013. [Google Scholar] [CrossRef]
- Caminade, C.; Jones, A.E. Malaria in a Warmer West Africa. Nat. Clim. Change 2016, 6, 984–985. [Google Scholar] [CrossRef]
- Hulme, M.; Mitchell, J.; Ingram, W.; Lowe, J.; Johns, T.; New, M.; Viner, D. Climate Change Scenarios for Global Impacts Studies. Glob. Environ. Change 1999, 9, S3–S19. [Google Scholar] [CrossRef]
- Hulme, M.; Doherty, R.; Ngara, T.; New, M.; Lister, D. African Climate Change: 1900–2100. Clim. Res. 2001, 17, 145–168. [Google Scholar] [CrossRef]
- Arab, A.; Jackson, M.C.; Kongoli, C. Modelling the Effects of Weather and Climate on Malaria Distributions in West Africa. Malar. J. 2014, 13, 126. [Google Scholar] [CrossRef]
- Shapiro, L.L.M.; Whitehead, S.A.; Thomas, M.B. Quantifying the Effects of Temperature on Mosquito and Parasite Traits That Determine the Transmission Potential of Human Malaria. PLoS Biol. 2017, 15, e2003489. [Google Scholar] [CrossRef]
- Abeku, T.A. Response to Malaria Epidemics in Africa. Emerg. Infect. Dis. 2007, 13, 681–686. [Google Scholar] [CrossRef]
- Rodríguez-Fonseca, B.; Mohino, E.; Mechoso, C.R.; Caminade, C.; Biasutti, M.; Gaetani, M.; Garcia-Serrano, J.; Vizy, E.K.; Cook, K.; Xue, Y.; et al. Variability and Predictability of West African Droughts: A Review on the Role of Sea Surface Temperature Anomalies. J. Clim. 2015, 28, 4034–4060. [Google Scholar] [CrossRef]
- Tanser, F.C.; Sharp, B.; le Sueur, D. Potential Effect of Climate Change on Malaria Transmission in Africa. Lancet 2003, 362, 1792–1798. [Google Scholar] [CrossRef]
- Martens, P.; Kovats, R.S.; Nijhof, S.; de Vries, P.; Livermore, M.T.J.; Bradley, D.J.; Cox, J.; McMichael, A.J. Climate Change and Future Populations at Risk of Malaria. Glob. Environ. Change 1999, 9, S89–S107. [Google Scholar] [CrossRef]
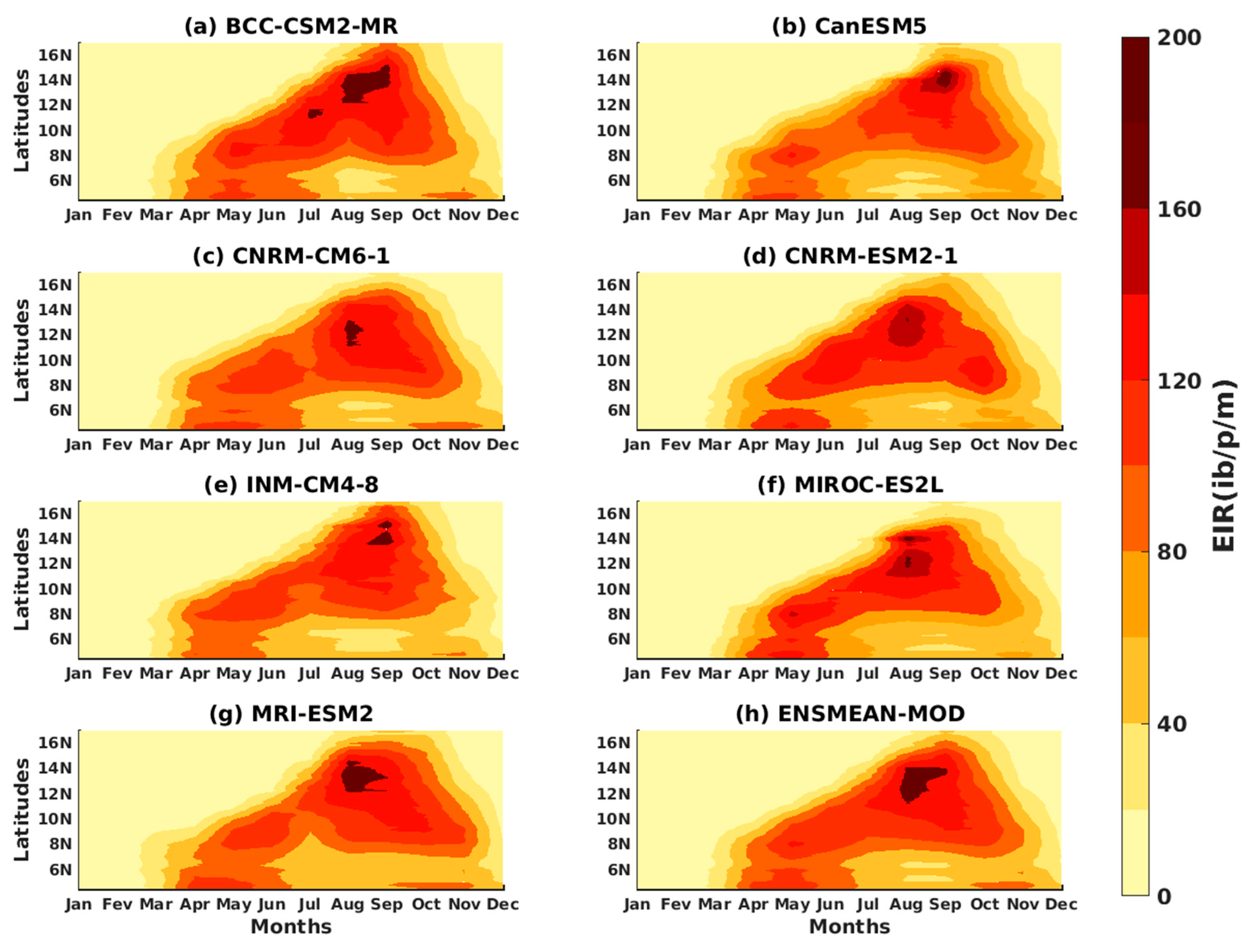
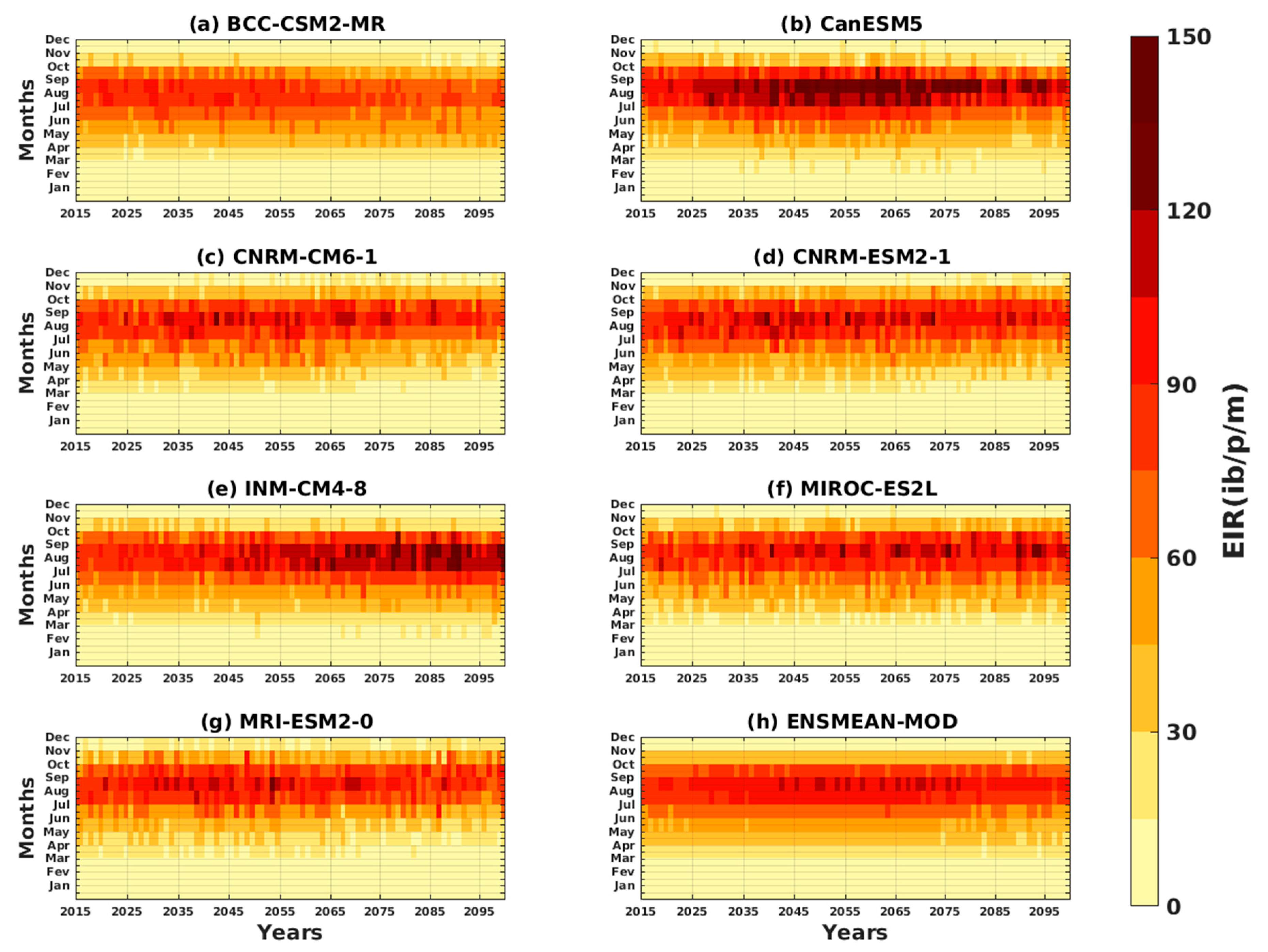
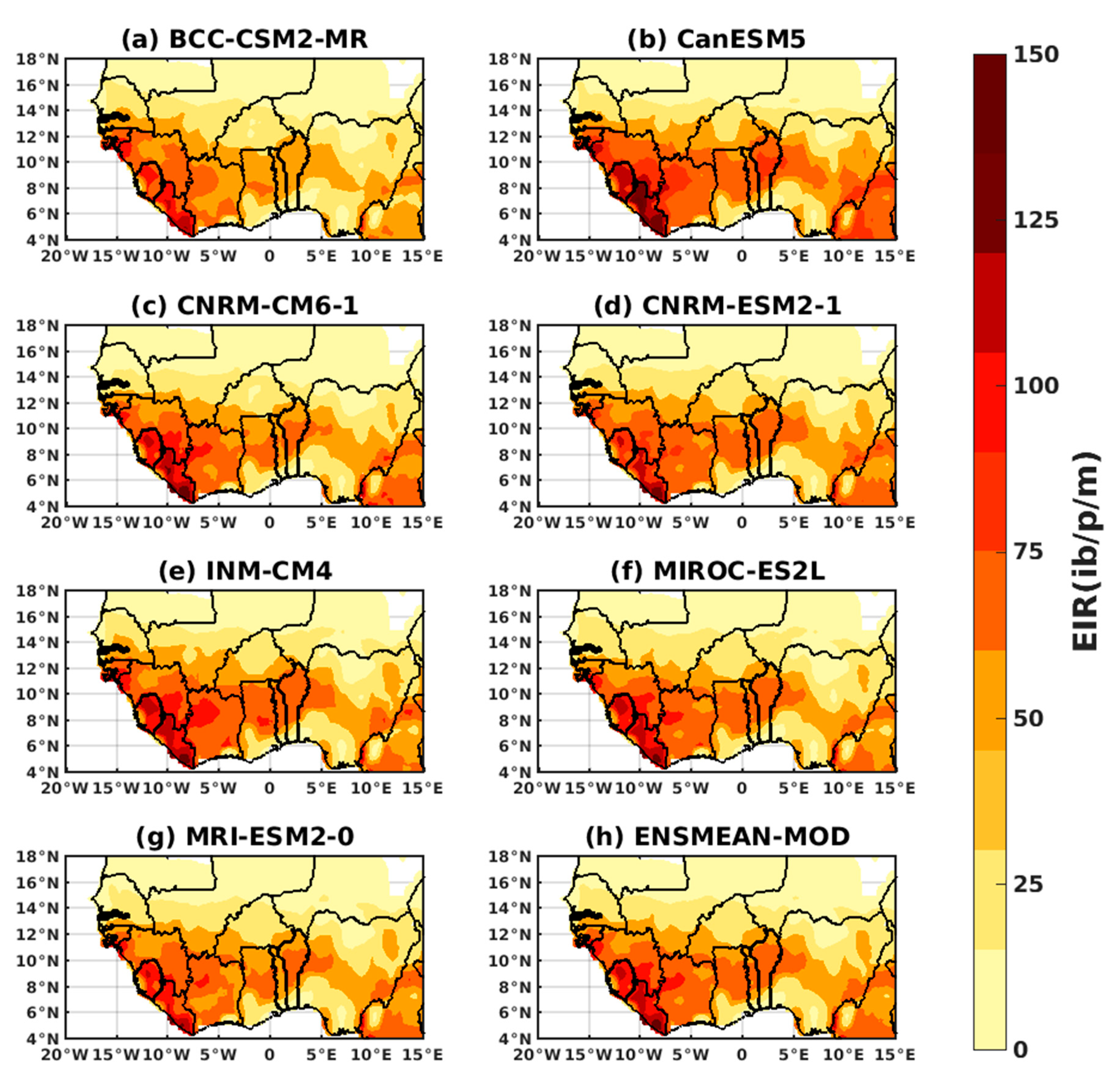
| Country | Latitudes | Longitude |
|---|---|---|
| Benin | 9.30° N | 2.31° E |
| Burkina Faso | 12.23° N | 1.56° W |
| Ivory Coast | 7.54° N | 5.54° W |
| Cape Verde | 15.12° N | 23.60° W |
| Gambia | 13.44° N | 15.31° W |
| Ghana | 7.94° N | 1.02° W |
| Guinea | 9.94° N | 13.67° W |
| Guinea-Bissau | 11.80° N | 15.18° W |
| Liberia | 6.42° N | 9.42° W |
| Mali | 17.57° N | 3.99° W |
| Mauritania | 20.93° N | 17.06° W |
| Niger | 17.60° N | 8.08° E |
| Nigeria | 9.08° N | 8.67° E |
| Senegal | 14.49° N | 14.45° W |
| Sierra Leon | 8.46° N | 11.77° W |
| Togo | 8.61° N | 0.82° E |
| Region | Latitude | Longitude |
|---|---|---|
| Dakar | 14.73° N | 17.50° W |
| Diourbel | 14.65° N | 16.23° W |
| Fatick | 14.21° N | 16.35° W |
| Kaffrine | 14.10° N | 15.55° W |
| Kaolack | 14.13° N | 16.07° W |
| Kedougou | 12.57° N | 12.22° W |
| Kolda | 12.88° N | 14.97° W |
| Louga | 15.62° N | 16.22° W |
| Matam | 15.63° N | 13.25° W |
| Sedhiou | 12.70° N | 15.55° W |
| Saint-Louis | 16.05° N | 16.45° W |
| Tambacounda | 13.77° N | 13.68° W |
| Thies | 14.80° N | 16.95° W |
| Ziguinchor | 12.55° N | 16.27° W |
| Seven CMIP6 Global Climate Models | |||
|---|---|---|---|
| Model Name | Modeling Center | Approximate Grid Spacing | Key Reference |
| BCC-CSM2-MR | Beijing Climate Center (China) | 1.125° × 1.125° | [40] |
| CanESM5 | Canadian Centre for Climate Modelling and Analysis (Canada) | 2.81° × 2.81° | [41] |
| CNRM-CM6-1 | Centre National de Recherches Météorologiques-Centre Européen de Recherches et de Formation Avancée en Calcul Scientifique (France) | 0.5° × 0.5° | [42] |
| CNRM-ESM2-1 | Centre National de Recherches Météorologiques Earth system model (France) | 1° × 1° | [43] |
| INM-CM4-8 | Institute of Numerical Mathematics, Russian Academy of Science, Moscow 119991 (Russia) | 2° × 1.5° | [44] |
| MIROC-ES2L | Japan Agency for Marine-Earth Science and Technology, Kanagawa 236-0001 (Japan) | 2.8° × 2.8° | [45] |
| MRI-ESM2 | Meteorological Research Institute, Japan Meteorological Agency (Japan) | 1.125° × 1.125° | [46] |
| Symbol | Value | Units | Description | Reference |
|---|---|---|---|---|
| 250 | Total evaporation and infiltration losses | based on [52] | ||
| 90.9 | K day | Larvae growth in degree days | [53] | |
| 37.1 | K day | Gonotrophic cycle in degree days | [47] | |
| 111 | day | Sporogonic cycle in degree days | [47] | |
| 1 | Pond growth rate factor | |||
| 0.45 | [51] | |||
| 0.054 | [51] | |||
| 300 | Carrying capacity of water bodies | [54] | ||
| 0.825 | Larvae base daily survival rate | [55] | ||
| 0.3 | [55] | |||
| 2 | Pond water offset from air temperature | [56] | ||
| 16 | for larvae development | based on [3] | ||
| 38 | for larvae development | based on [3] | ||
| 7.7 | for egg development | [47] | ||
| 16 | for sporogonic cycle | [55] | ||
| 50 | Population density zoophilic factor | set by tuning | ||
| 0.04 |
| Parameters | Definition | Unity |
|---|---|---|
| population | population density | N.m−2 |
| rain | rainfall | mm day−1 |
| temp | temperature | °C |
| water frac | fraction of grid box covered by pond breeding sites | % |
| vector | mosquito density | N.m−2 |
| larvae | larvae density | N.m−2 |
| larvae biomass | larvae biomass | Mg.m−2 |
| PRd | % of population with detectable malaria (day 10+) | |
| hbr | human biting rate | number of bites person−1 day−1 |
| cspr | Circum sporozoite protein ratio (eir/hbr) fraction | fraction |
| Eir | entomological inoculation rate (number of infectious bites) | number person−1 day−1 |
| cases | number of new cases | fraction |
| immunity | proportion of immune population | fraction |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fall, P.; Diouf, I.; Deme, A.; Diouf, S.; Sene, D.; Sultan, B.; Janicot, S. Enhancing Understanding of the Impact of Climate Change on Malaria in West Africa Using the Vector-Borne Disease Community Model of the International Center for Theoretical Physics (VECTRI) and the Bias-Corrected Phase 6 Coupled Model Intercomparison Project Data (CMIP6). Microbiol. Res. 2023, 14, 2148-2180. https://doi.org/10.3390/microbiolres14040145
Fall P, Diouf I, Deme A, Diouf S, Sene D, Sultan B, Janicot S. Enhancing Understanding of the Impact of Climate Change on Malaria in West Africa Using the Vector-Borne Disease Community Model of the International Center for Theoretical Physics (VECTRI) and the Bias-Corrected Phase 6 Coupled Model Intercomparison Project Data (CMIP6). Microbiology Research. 2023; 14(4):2148-2180. https://doi.org/10.3390/microbiolres14040145
Chicago/Turabian StyleFall, Papa, Ibrahima Diouf, Abdoulaye Deme, Semou Diouf, Doudou Sene, Benjamin Sultan, and Serge Janicot. 2023. "Enhancing Understanding of the Impact of Climate Change on Malaria in West Africa Using the Vector-Borne Disease Community Model of the International Center for Theoretical Physics (VECTRI) and the Bias-Corrected Phase 6 Coupled Model Intercomparison Project Data (CMIP6)" Microbiology Research 14, no. 4: 2148-2180. https://doi.org/10.3390/microbiolres14040145
APA StyleFall, P., Diouf, I., Deme, A., Diouf, S., Sene, D., Sultan, B., & Janicot, S. (2023). Enhancing Understanding of the Impact of Climate Change on Malaria in West Africa Using the Vector-Borne Disease Community Model of the International Center for Theoretical Physics (VECTRI) and the Bias-Corrected Phase 6 Coupled Model Intercomparison Project Data (CMIP6). Microbiology Research, 14(4), 2148-2180. https://doi.org/10.3390/microbiolres14040145








