Enhanced A*–Fuzzy DWA Hybrid Algorithm for AGV Path Planning in Confined Spaces
Abstract
1. Introduction
- The improved A* algorithm incorporates dynamic weight factors, integrating actual costs with estimated costs to significantly enhance the flexibility of the evaluation function;
- Cubic quasi-uniform B-spline curves are applied to effectively ensure local path smoothness and substantially reduce unnecessary turns;
- The path generated by the improved A* algorithm serves as the global reference for the Dynamic Window Approach (DWA);
- Sub-target points are selected globally through a rolling window mechanism, guiding the DWA to avoid local minima and maintain real-time navigation performance;
- A fuzzy controller is introduced to dynamically adjust the weight parameters of heading angle, obstacle avoidance strategy, and speed control in real time, thereby reducing the number of path inflection points in narrow environments.
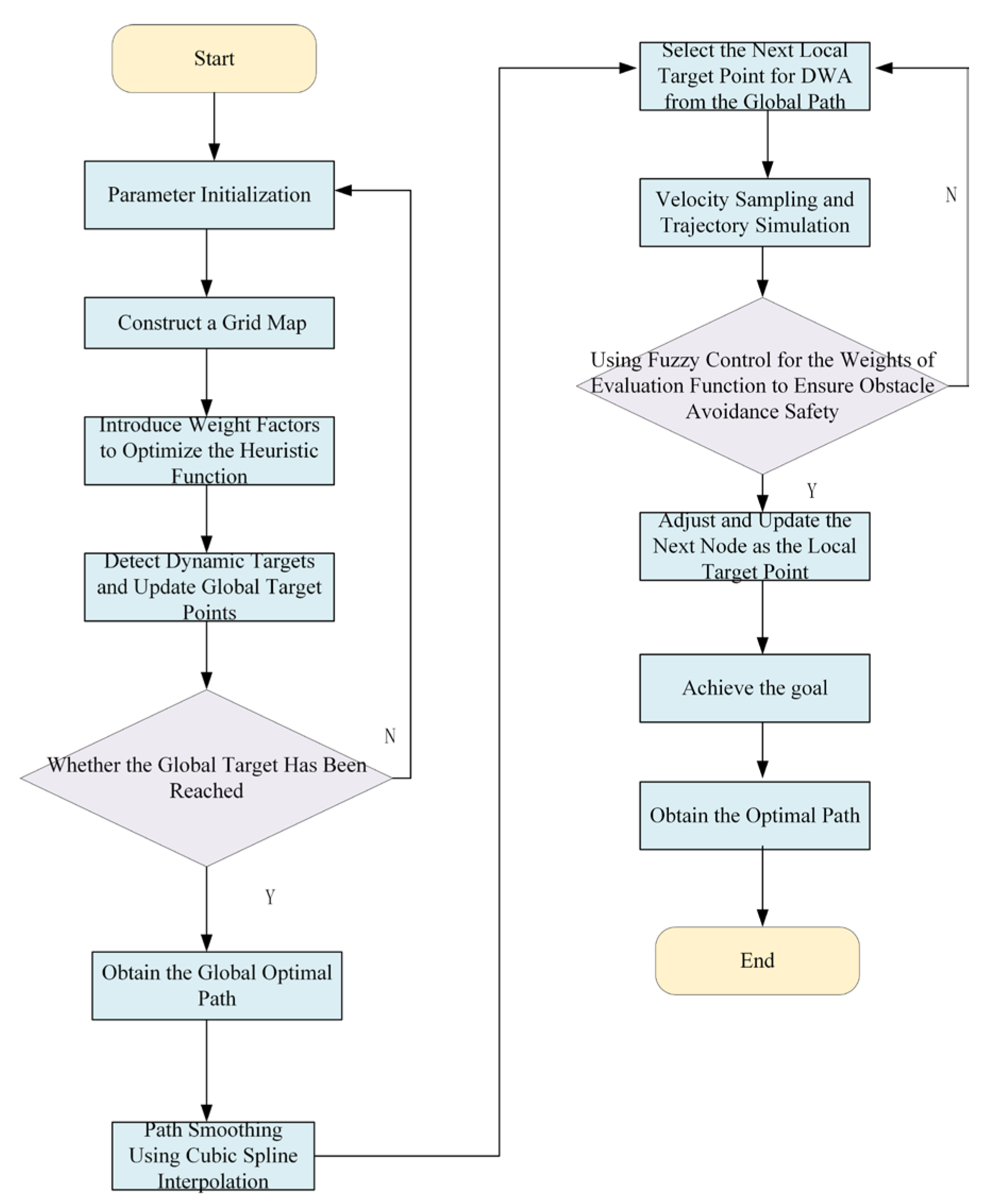
2. Improved A* Algorithm
2.1. Traditional A* Algorithm
2.2. Improved A* Algorithm
2.3. Path Smoothing Optimization Based on Cubic Quasi-Uniform β-Spline
3. Hybrid Improved A* and Fuzzy-Controlled Dynamic Window Approach
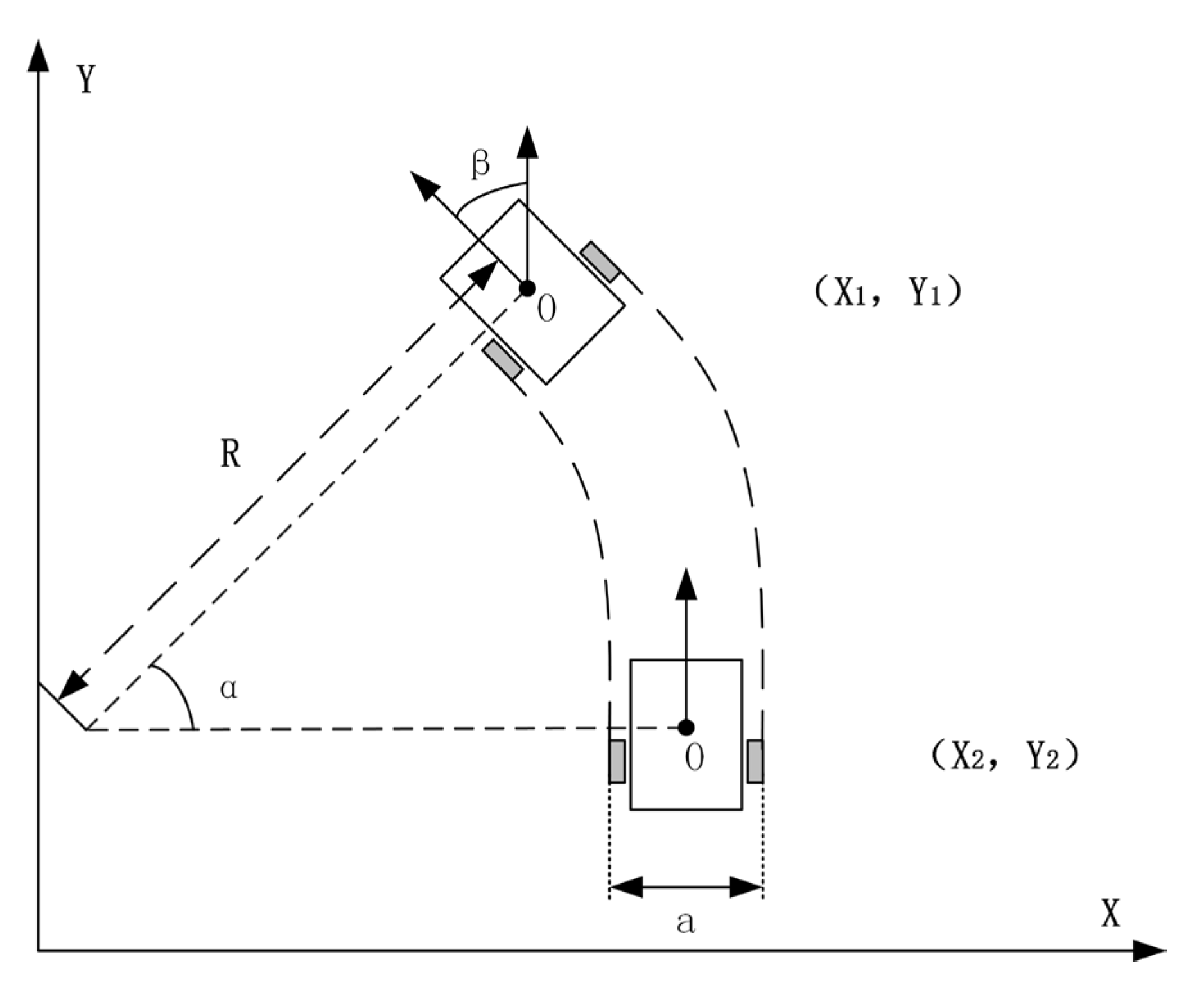
3.1. AGV Kinematic Model
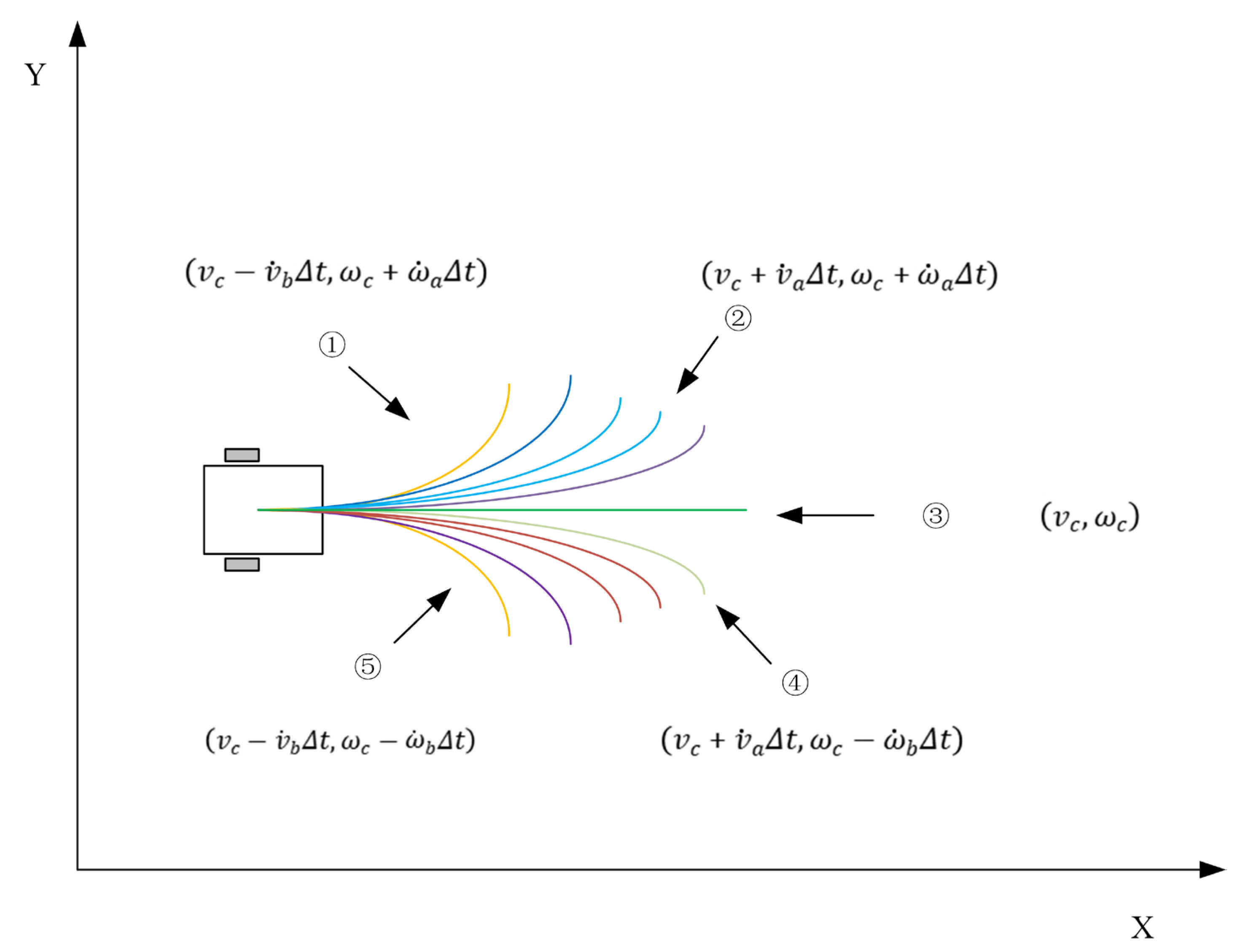
3.2. Speed Sampling and Trajectory Prediction
- (1)
- Heading Angle Evaluation Function
- (2)
- Obstacle Avoidance Safety Evaluation Function
- (3)
- Velocity Evaluation Function
3.3. Fuzzy Control
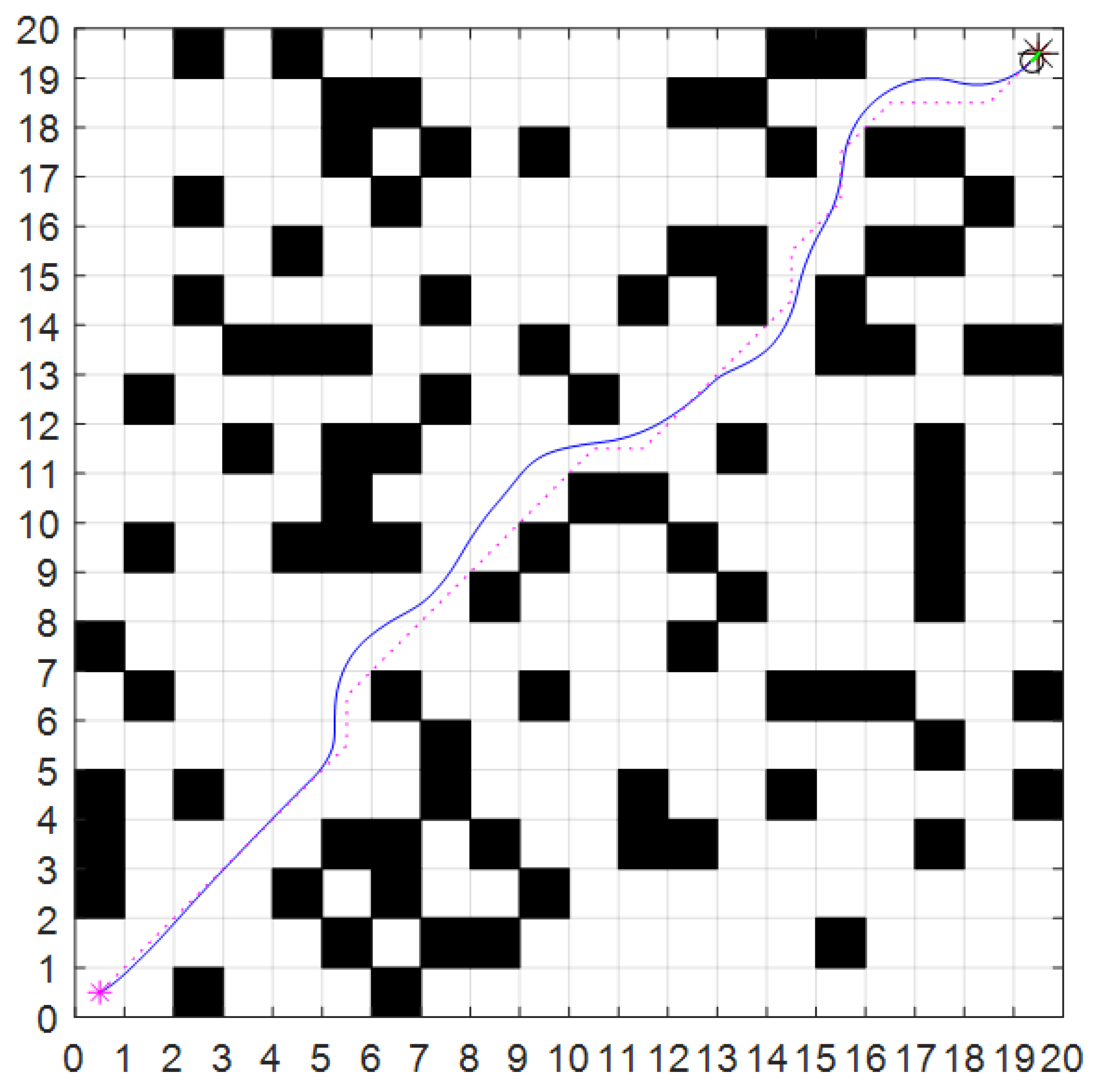
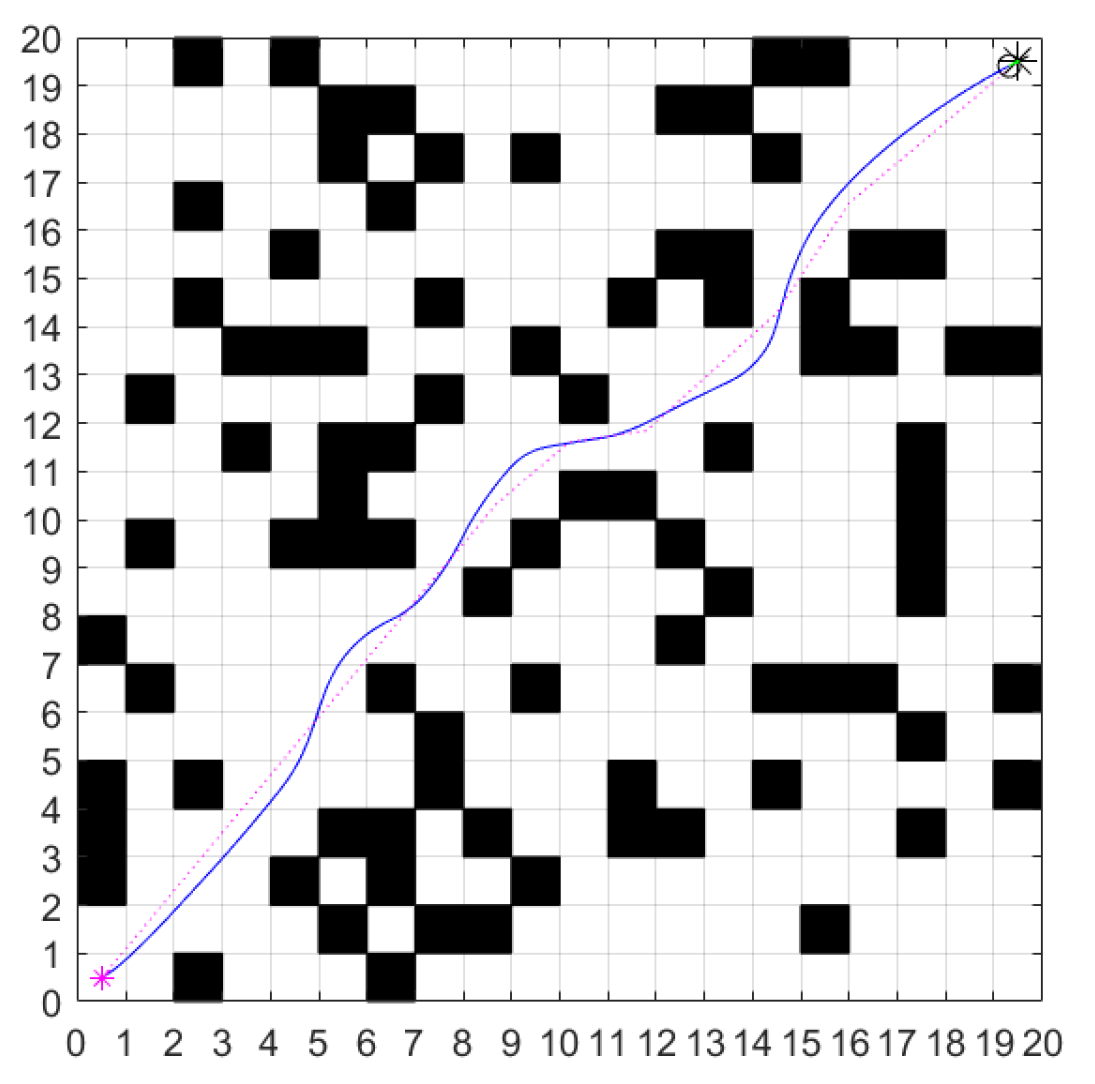
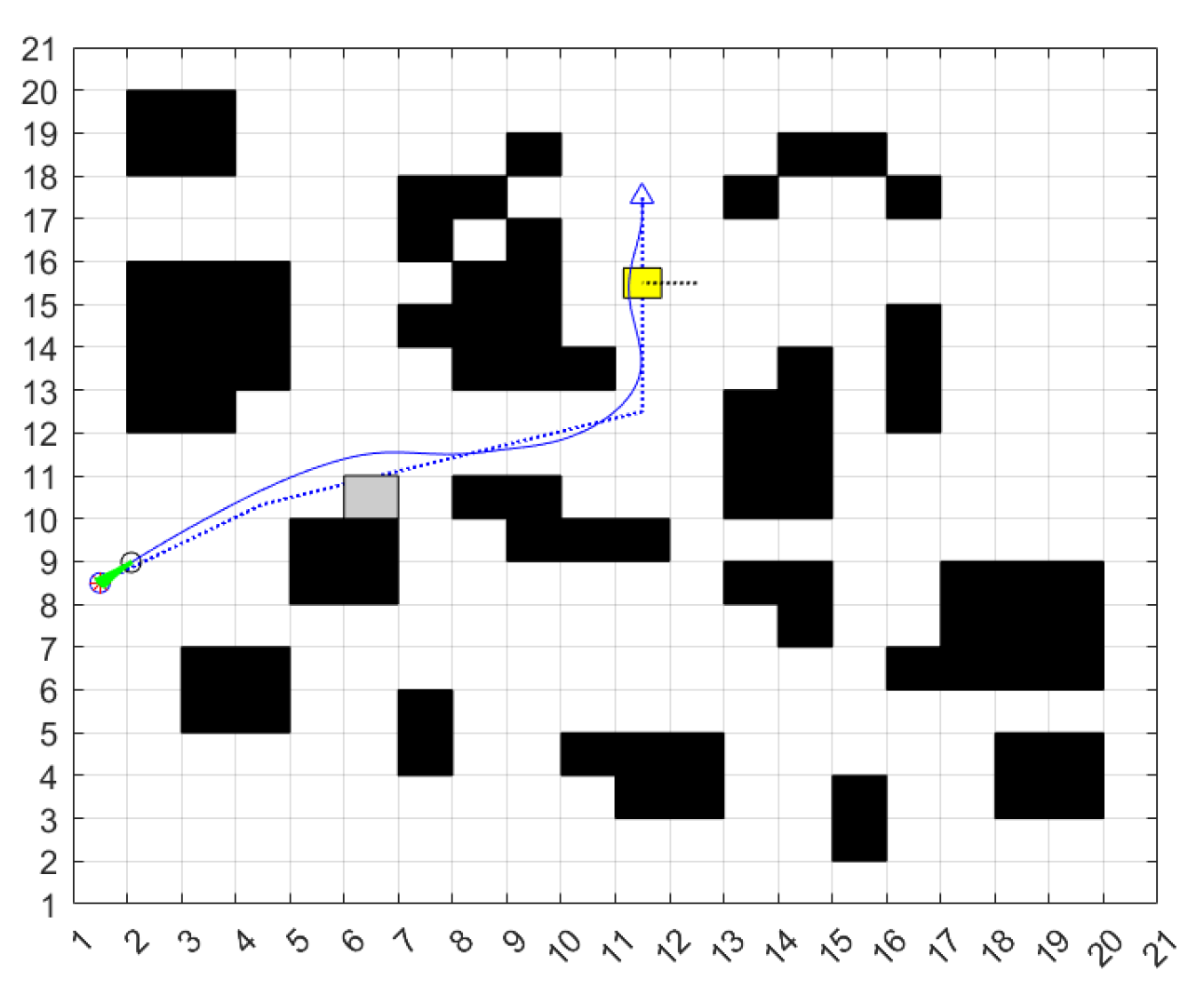
4. Simulation Experiment and Analysis
4.1. Simulation
| Algorithm | Path Length | Running Time/s | Inflection Points/No. | Turning Angle/Deg |
|---|---|---|---|---|
| Fusion-Enhanced A* and Fuzzy DWA | 26.313 | 101.0338 | 75 | 95 |
| Hybrid RRT-DWA Algorithm | 27.782 | 104.826 | 81 | 80.2 |
| Hybrid PSO-DWA Algorithm | 27.714 | 114.3049 | 78 | 77.2 |
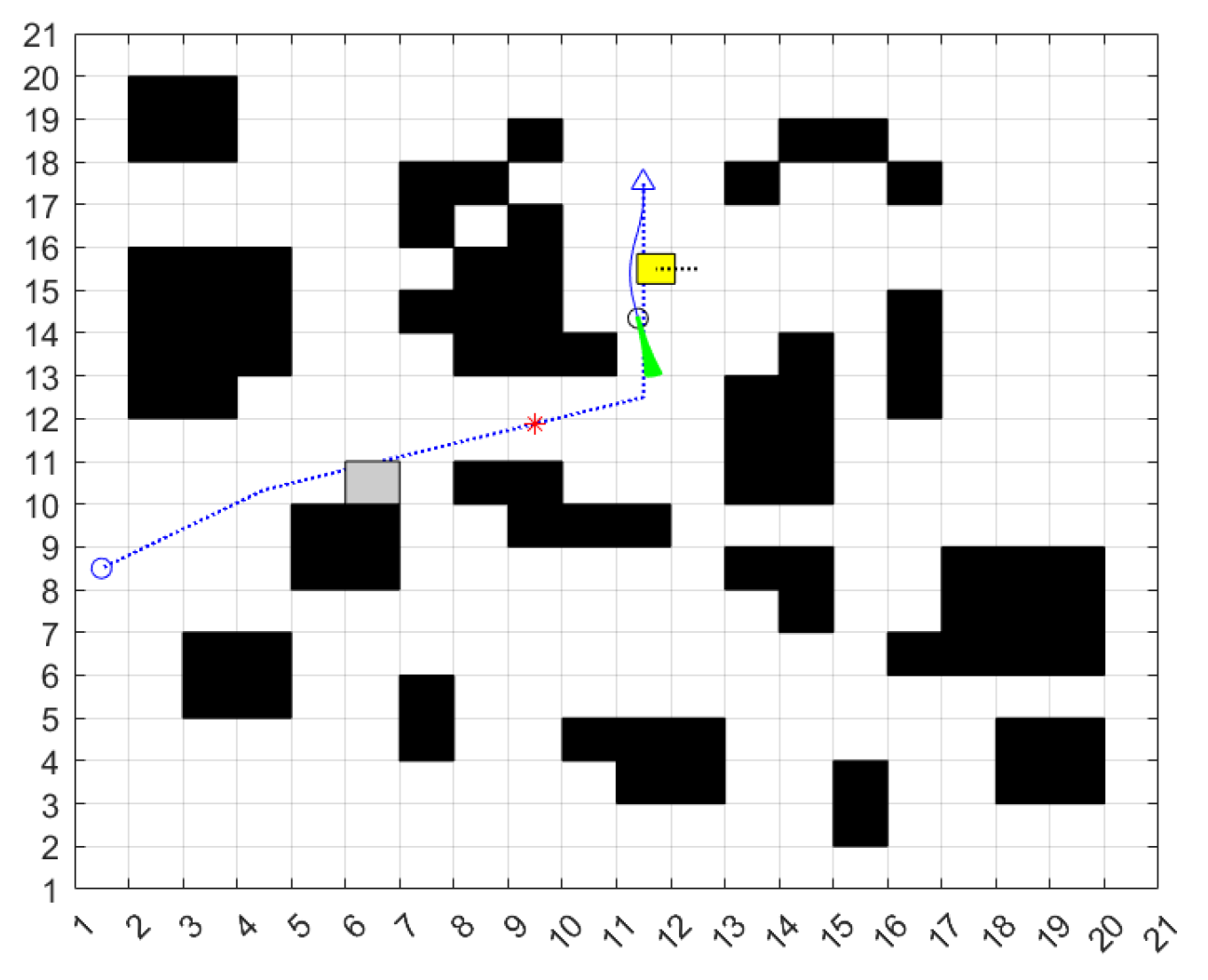
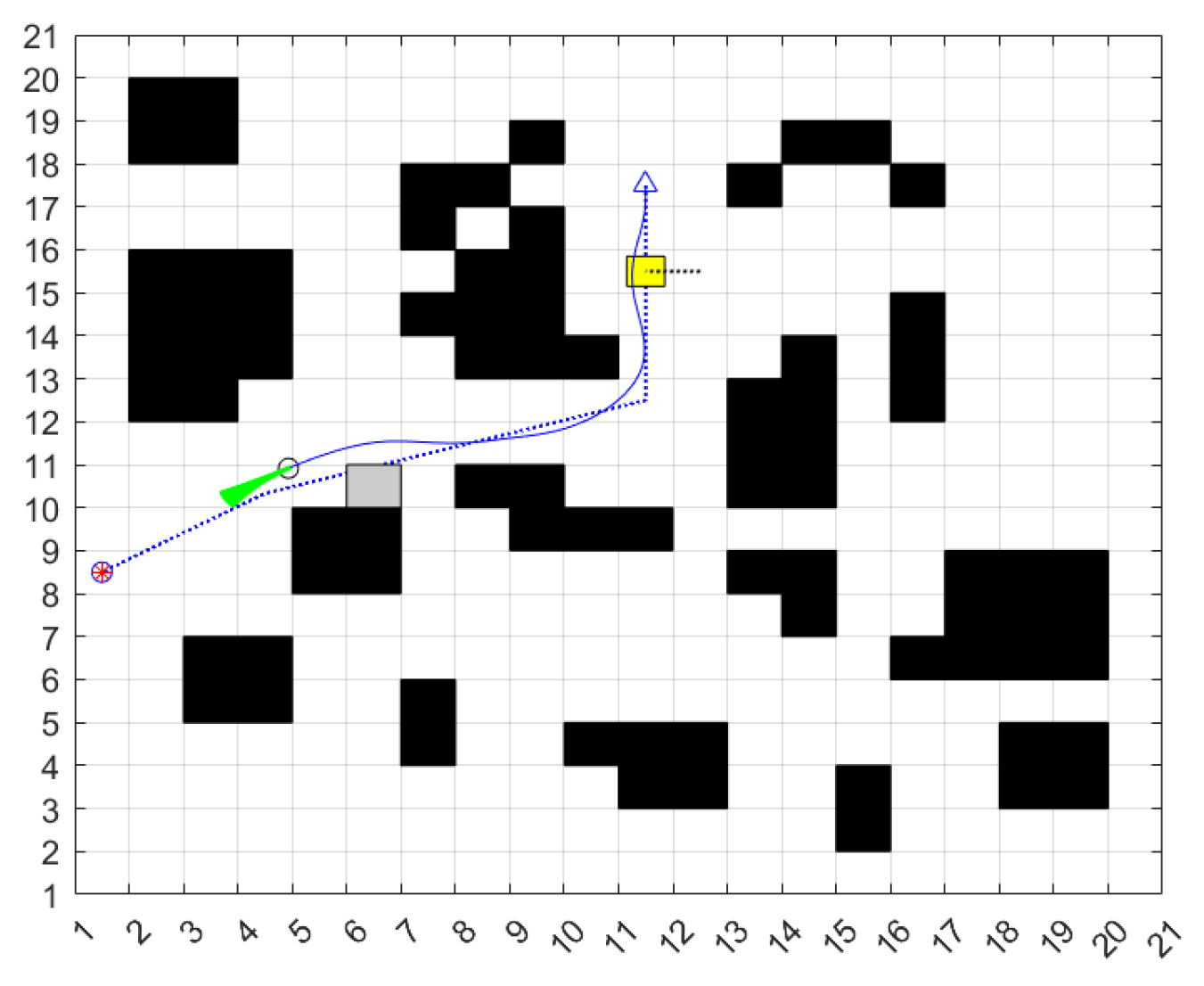
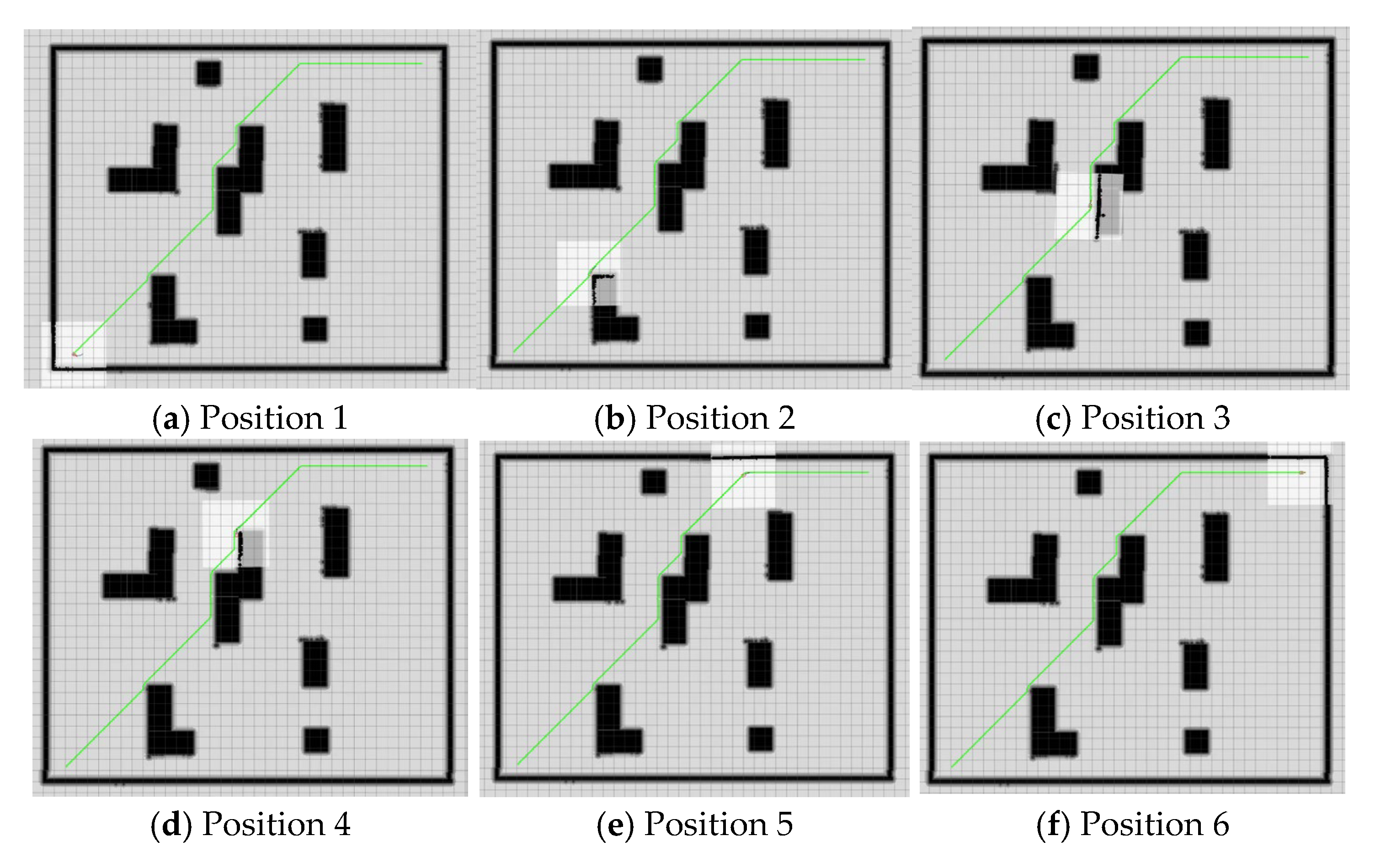
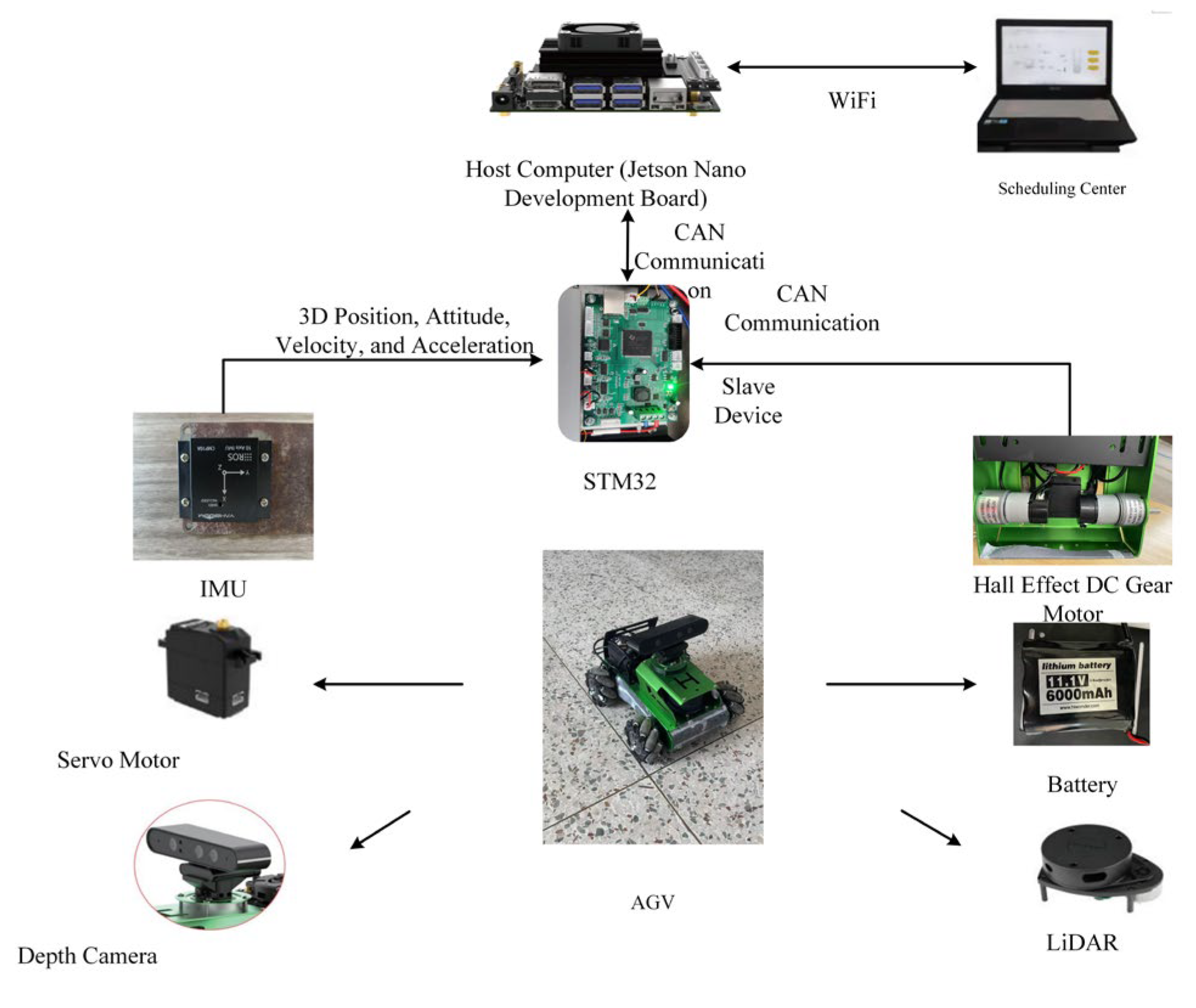
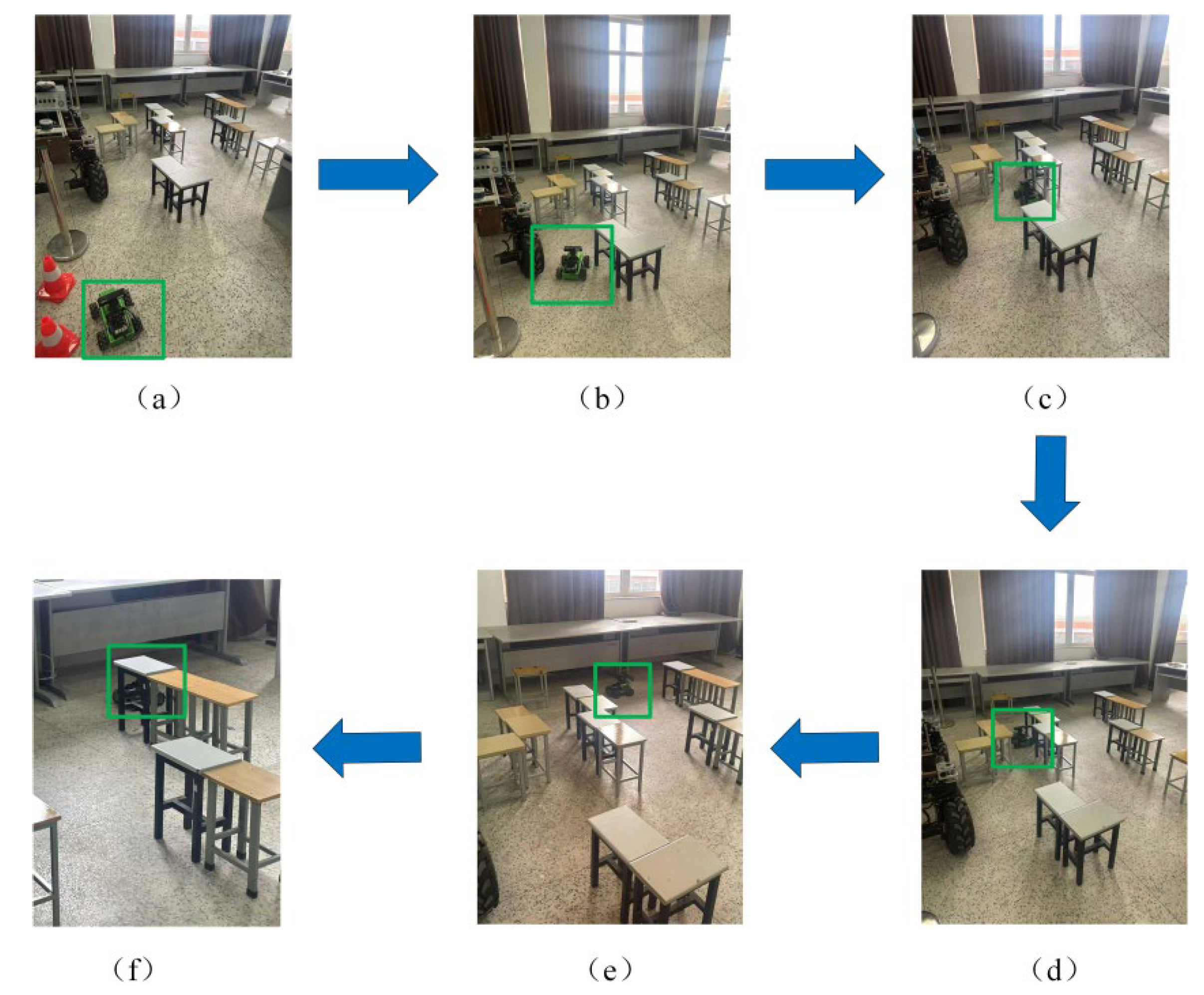
4.2. Experiment
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, J.; Ling, H.; Tang, Z.; Song, W.; Lu, A. Path planning of USV in confined waters based on improved A∗ and DWA fusion algorithm. Ocean Eng. 2025, 322, 120475. [Google Scholar] [CrossRef]
- Gu, C.; Liu, S.; Li, H.; Yuan, K.; Bao, W. Research on hybrid path planning of underground degraded environment inspection robot based on improved A* algorithm and DWA algorithm. Robotica 2025, 43, 887–908. [Google Scholar] [CrossRef]
- Zhang, W.; Li, W.; Zheng, X.; Sun, B. Improved A* and DWA fusion algorithm based path planning for intelligent substation inspection robot. Meas. Control 2025. [Google Scholar] [CrossRef]
- Chen, X.; Hu, R.; Luo, K.; Wu, H.; Biancardo, S.A.; Zheng, Y.; Xian, J. Intelligent ship route planning via an A∗ search model enhanced double-deep Q-network. Ocean. Eng. 2025, 327, 120956. [Google Scholar] [CrossRef]
- Nhouchi, A.; Said, S.B.; Abdallah, M.A.B.; Aifaoui, N. A real-time A* algorithm for trajectories generation and collision avoidance in uncertain environments for assembly applications. Comput. Ind. Eng. 2025, 202, 110959. [Google Scholar] [CrossRef]
- Zhou, Z.; Song, Y.; Li, S. Optimal Path Planning Algorithm of Indoor AGV Enhanced with HHO and Sector-Wide Field DWA. Unmanned Syst. 2025. [Google Scholar] [CrossRef]
- Xu, X.; Zeng, J.; Zhao, Y.; Lü, X. Research on global path planning algorithm for mobile robots based on improved A. Expert Syst. Appl. 2023, 243, 122922. [Google Scholar] [CrossRef]
- Xu, D.; Yang, J.; Zhou, X.; Xu, H. Hybrid path planning method for USV using bidirectional A* and improved DWA considering the manoeuvrability and COLREGs. Ocean Eng. 2024, 298, 117210. [Google Scholar] [CrossRef]
- Zhang, D.; Chen, C.; Zhang, G. AGV path planning based on improved A-star algorithm. In Proceedings of the 2024 IEEE 7th Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 15–17 March 2024; IEEE: New York, NY, USA, 2024; Volume 7, pp. 1590–1595. [Google Scholar]
- Han, C.; Li, B. Mobile robot path planning based on improved A* algorithm. In Proceedings of the 2023 IEEE 11th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), Chongqing, China, 8–10 December 2023; IEEE: New York, NY, USA, 2023; Volume 11, pp. 672–676. [Google Scholar]
- Zammit, C.; Van Kampen, E.J. Comparison between A* and RRT algorithms for 3D UAV path planning. Unmanned Syst. 2022, 10, 129–146. [Google Scholar] [CrossRef]
- Sang, H.; You, Y.; Sun, X.; Zhou, Y.; Liu, F. The hybrid path planning algorithm based on improved A* and artificial potential field for unmanned surface vehicle formations. Ocean Eng. 2021, 223, 108709. [Google Scholar] [CrossRef]
- Xiao, J.; Yu, X.; Sun, K.; Zhou, Z.; Zhou, G. Multiobjective path optimization of an indoor AGV based on an improved ACO-DWA. Math. Biosci. Eng. 2022, 19, 12532–12557. [Google Scholar] [CrossRef]
- Xu, L.; Xi, M.; Gao, R.; Ye, Z.; He, Z. Dynamic path planning of UAV with least inflection point based on adaptive neighborhood A* algorithm and multi-strategy fusion. Sci. Rep. 2025, 15, 8563. [Google Scholar] [CrossRef] [PubMed]
- Tang, G.; Tang, C.; Claramunt, C.; Hu, X.; Zhou, P. Geometric A-star algorithm: An improved A-star algorithm for AGV path planning in a port environment. IEEE Access 2021, 9, 59196–59210. [Google Scholar] [CrossRef]
- Fu, B.; Chen, L.; Zhou, Y.; Zheng, D.; Wei, Z.; Dai, J.; Pan, H. An improved A* algorithm for the industrial robot path planning with high success rate and short length. Robot. Auton. Syst. 2018, 106, 26–37. [Google Scholar] [CrossRef]
- Chang, L.; Shan, L.; Jiang, C.; Dai, Y. Reinforcement based mobile robot path planning with improved dynamic window approach in unknown environment. Auton. Robot. 2021, 45, 51–76. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, Z.; Xue, Y.; Deng, Z.; Qin, H. Local path planning of under-actuated AUV based on VADWA considering dynamic model. Ocean Eng. 2024, 310, 118705. [Google Scholar] [CrossRef]
- Zhang, B.; Cao, J.; Li, X.; Chen, W.; Zheng, X.; Zhang, Y.; Song, Y. Minimum dose walking path planning in a nuclear radiation environment based on a modified A* algorithm. Ann. Nucl. Energy 2024, 206, 110629. [Google Scholar] [CrossRef]
- Wu, B.; Chi, X.; Zhao, C.; Zhang, W.; Lu, Y.; Jiang, D. Dynamic path planning for forklift AGV based on smoothing A* and improved DWA hybrid algorithm. Sensors 2022, 22, 7079. [Google Scholar] [CrossRef]
- Liu, W.; Chen, L.; Wang, R.; Wan, Y. Trajectory planning for AGV based on the improved artificial potential field-A* algorithm. Meas. Sci. Technol. 2024, 35, 096312. [Google Scholar] [CrossRef]
- Stavrinidis, S.; Zacharia, P.; Xidias, E. A Fuzzy Control Strategy for Multi-Goal Autonomous Robot Navigation. Sensors 2025, 25, 446. [Google Scholar] [CrossRef]
- Yin, Y.; Chen, Z.; Liu, G.; Yin, J.; Guo, J. Autonomous navigation of mobile robots in unknown environments using off-policy reinforcement learning with curriculum learning. Expert Syst. Appl. 2024, 247, 123202. [Google Scholar] [CrossRef]
- Jin, Z.; Qin, Z.; Zhang, X.; Guan, C. A leader-following consensus problem via a distributed observer and fuzzy input-to-output small-gain theorem. IEEE Trans. Control. Netw. Syst. 2022, 9, 62–74. [Google Scholar] [CrossRef]
- Jin, Z.; Sun, X.; Qin, Z.; Ahn, C.K. Fuzzy small-gain approach for the distributed optimization of T–S fuzzy cyber–physical systems. IEEE Trans. Cybern. 2022, 53, 6491–6502. [Google Scholar] [CrossRef]
- Jin, Z.; Li, H.; Qin, Z.; Wang, Z. Gradient-free cooperative source-seeking of quadrotor under disturbances and communication constraints. IEEE Trans. Ind. Electron. 2024, 72, 1969–1979. [Google Scholar] [CrossRef]

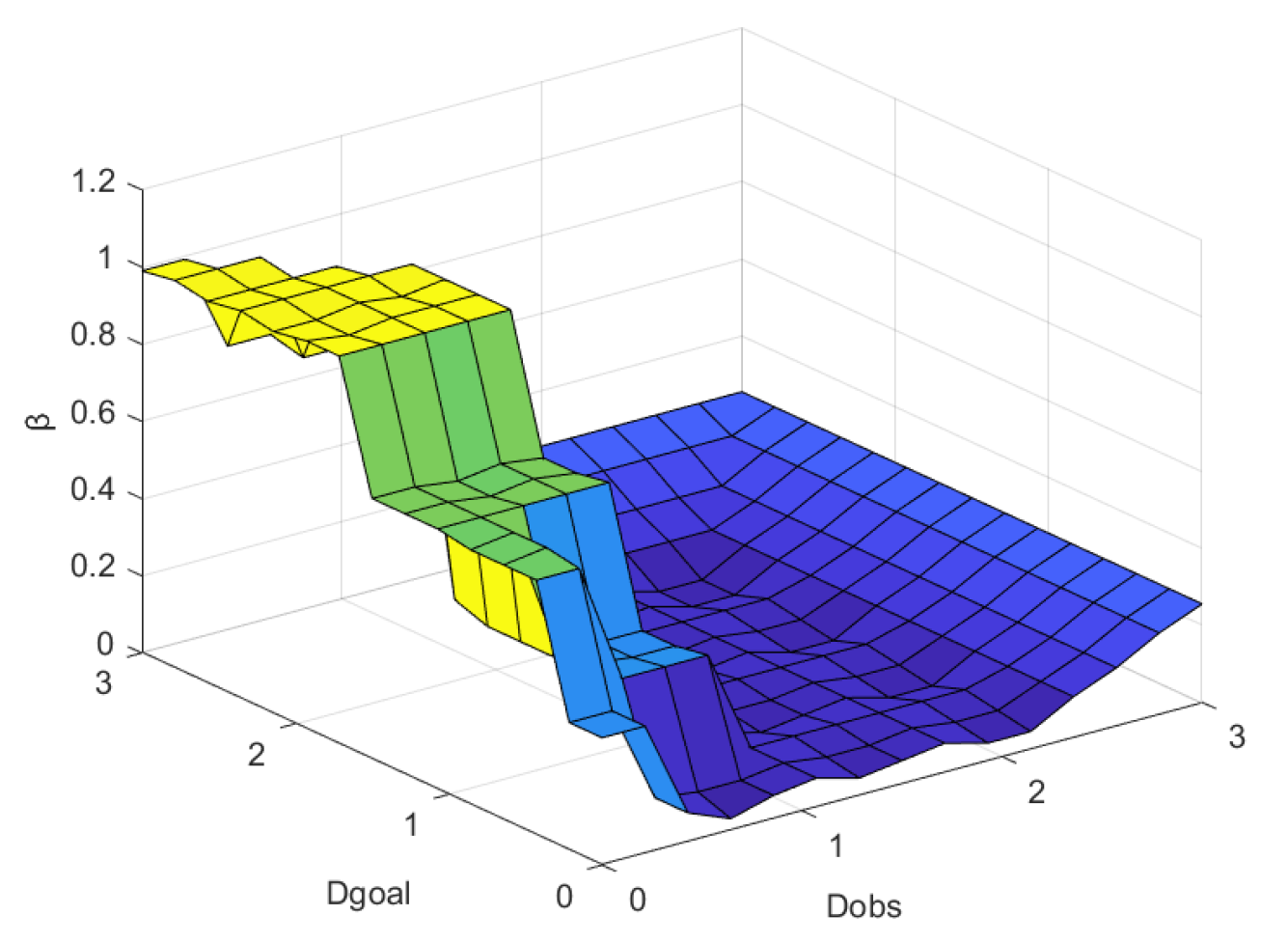
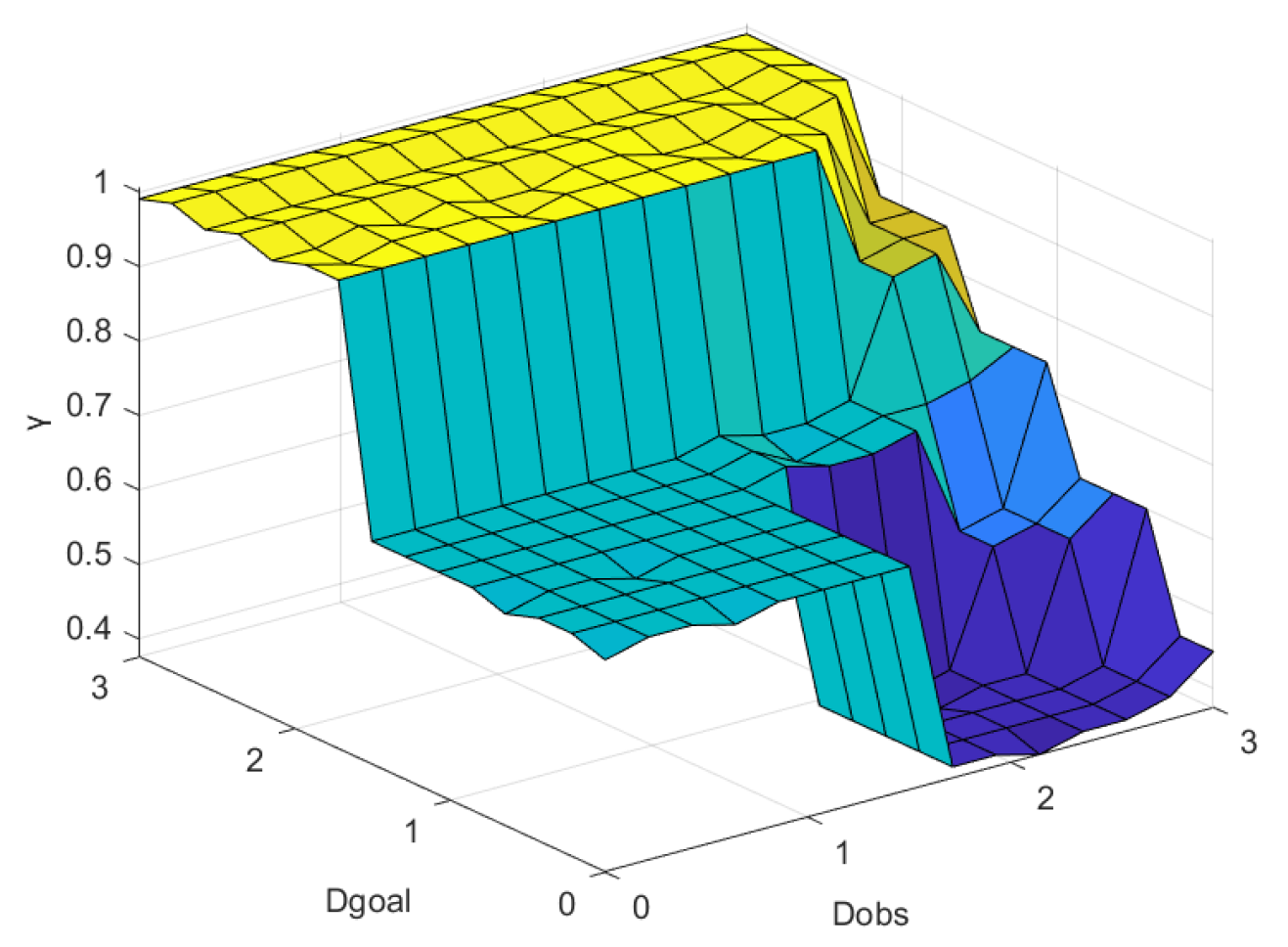
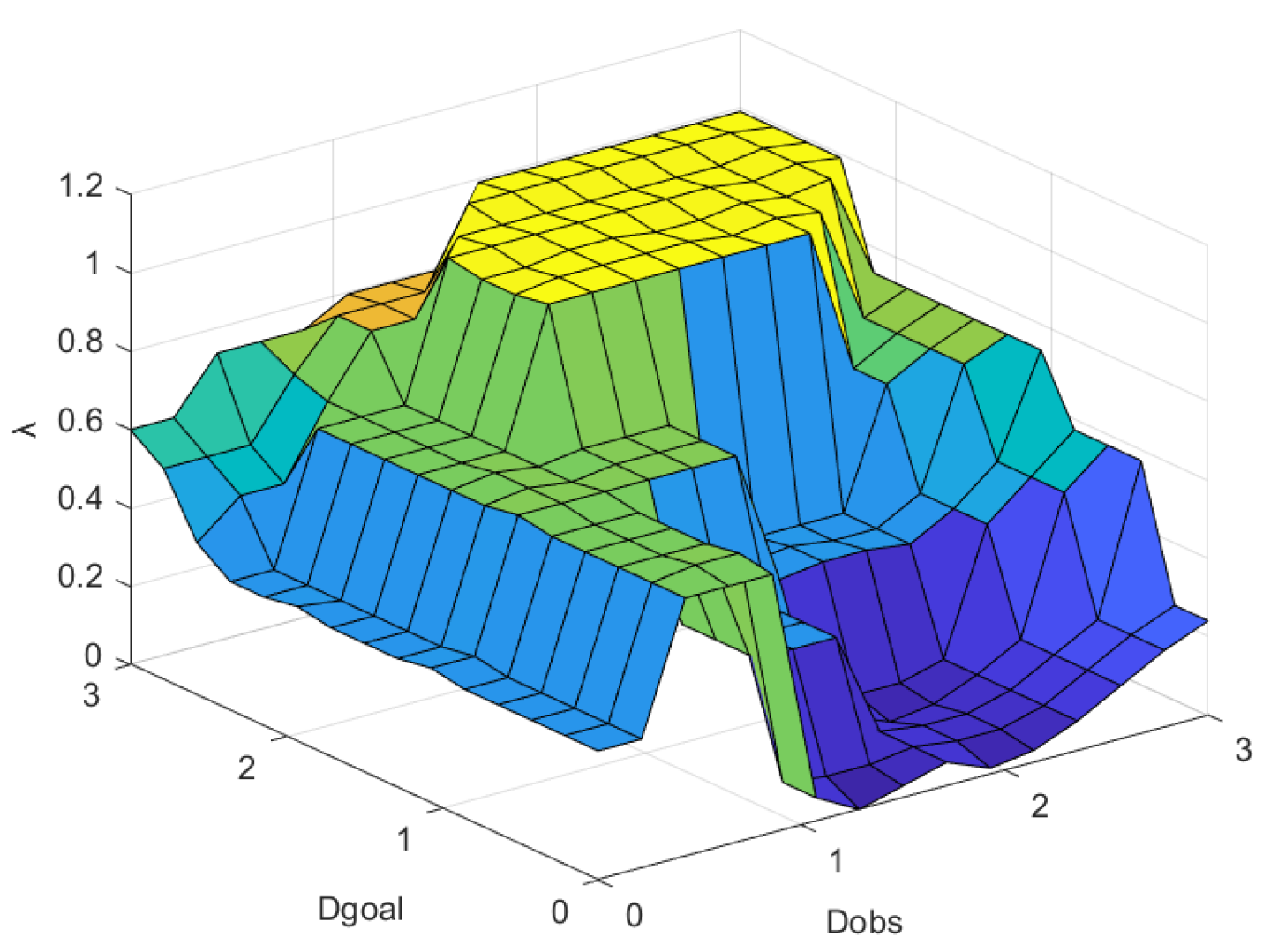
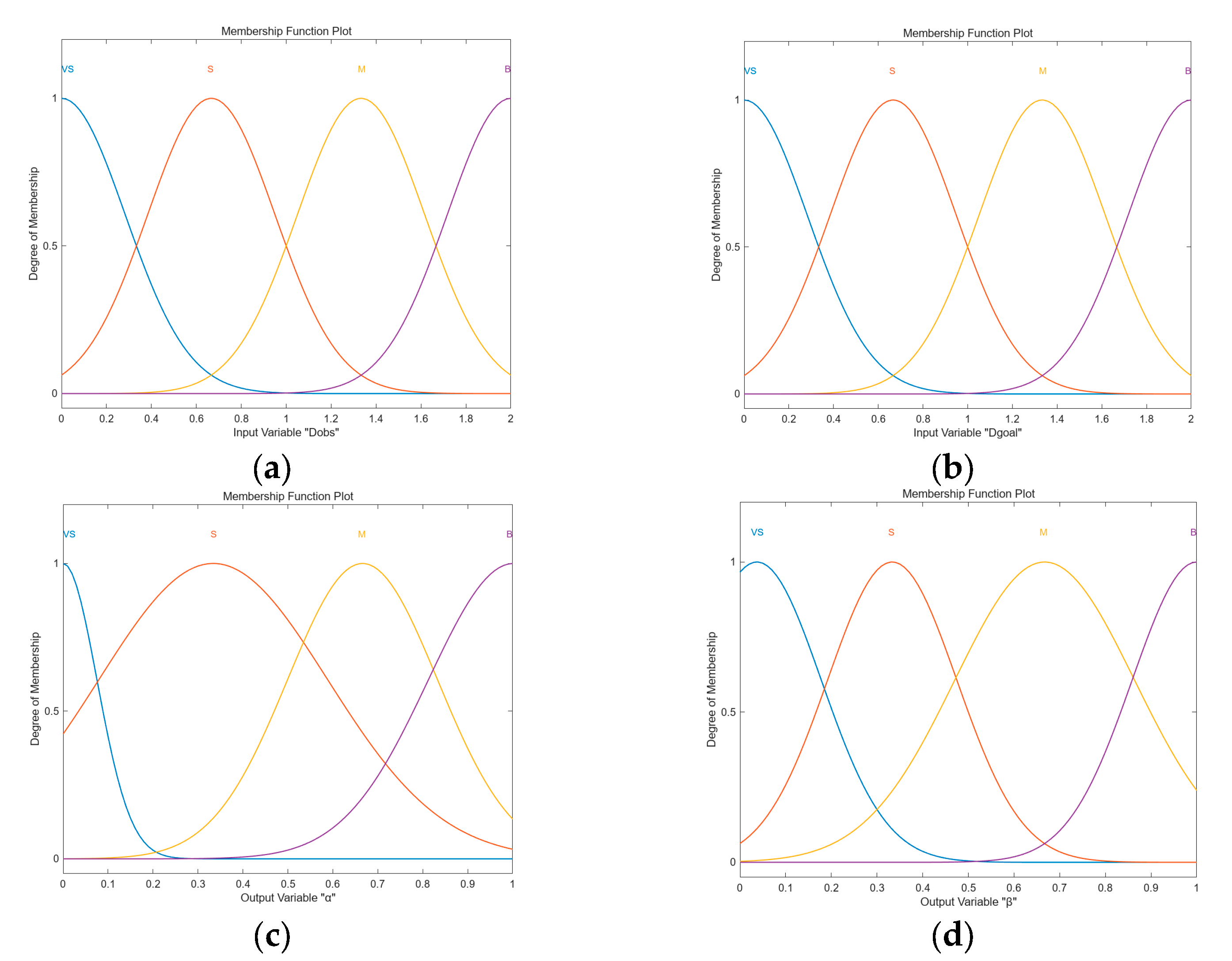
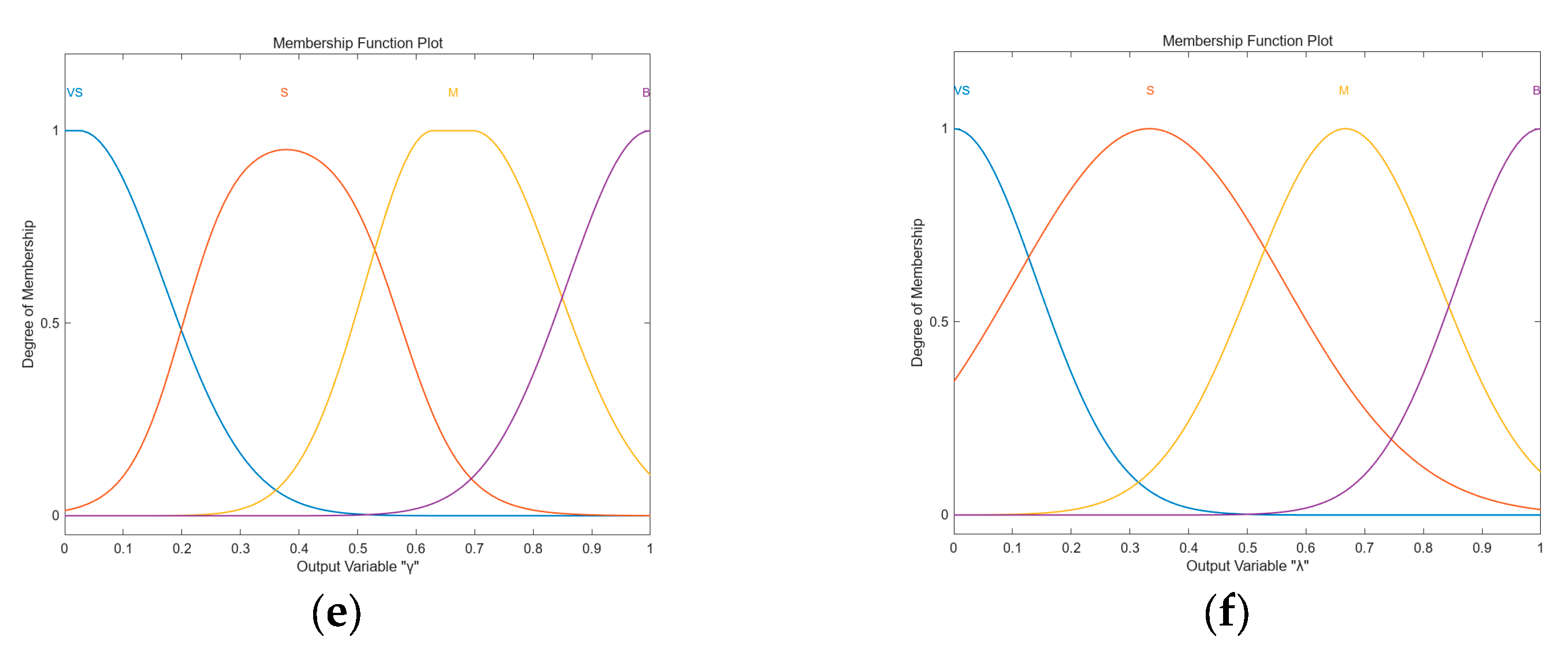
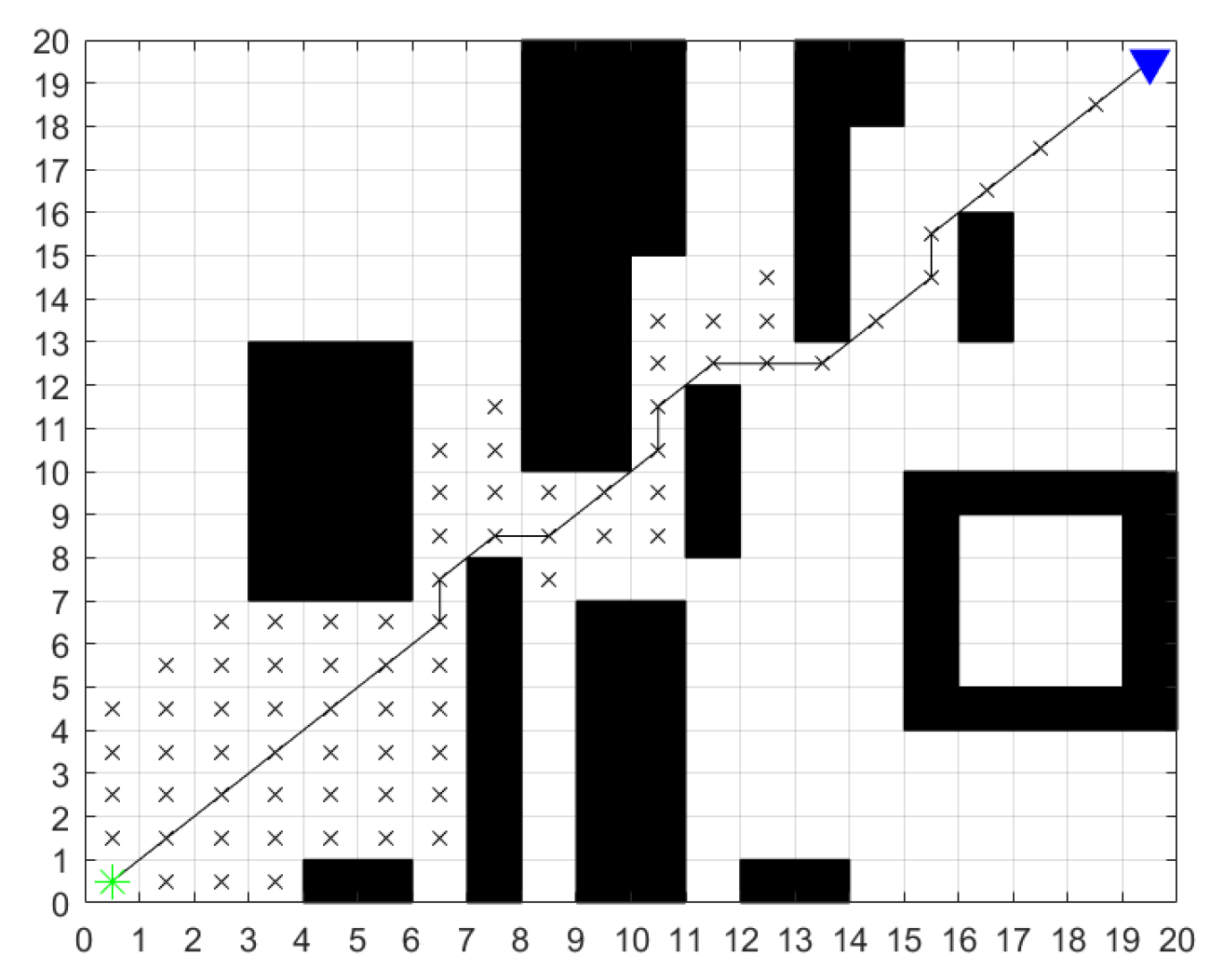
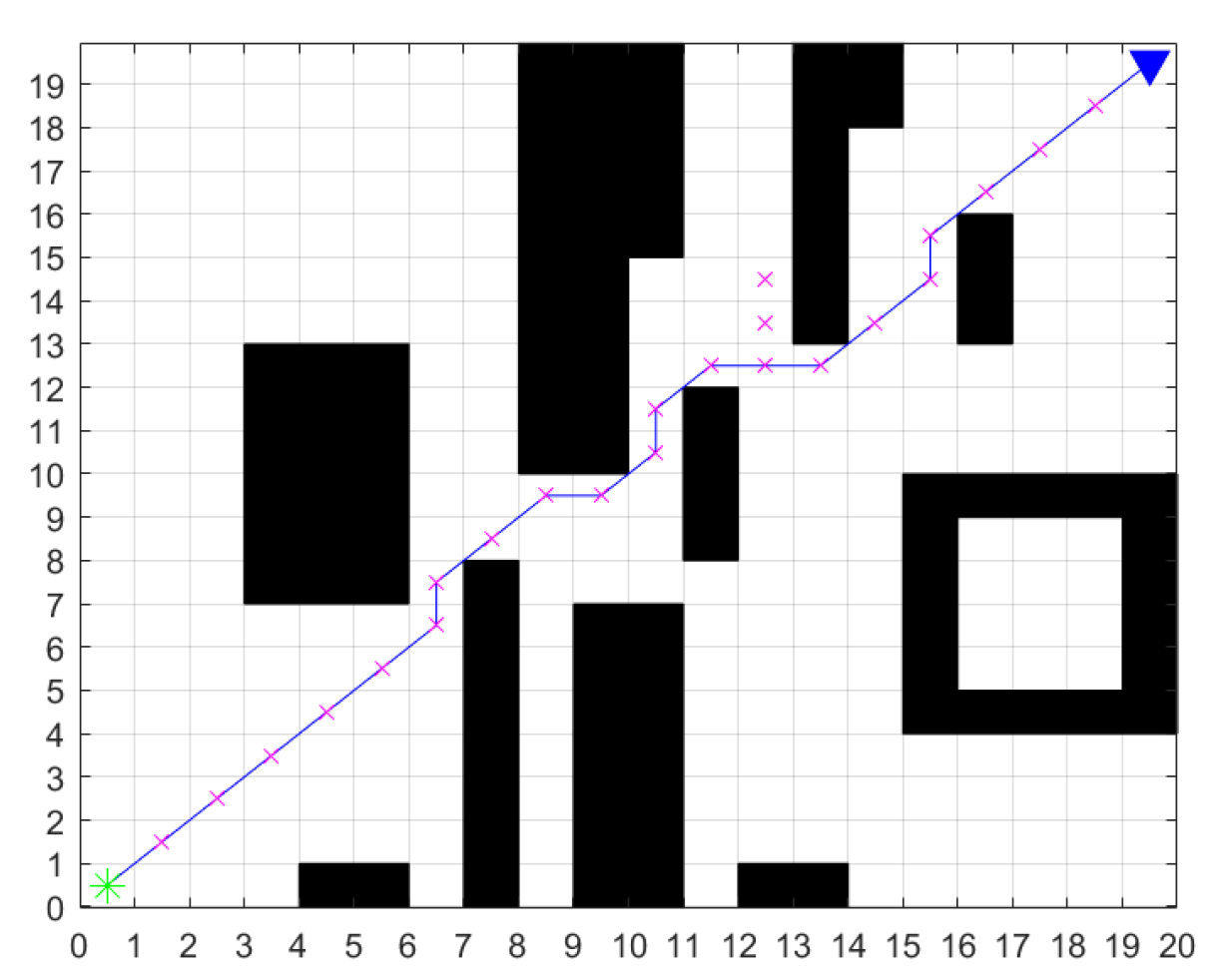
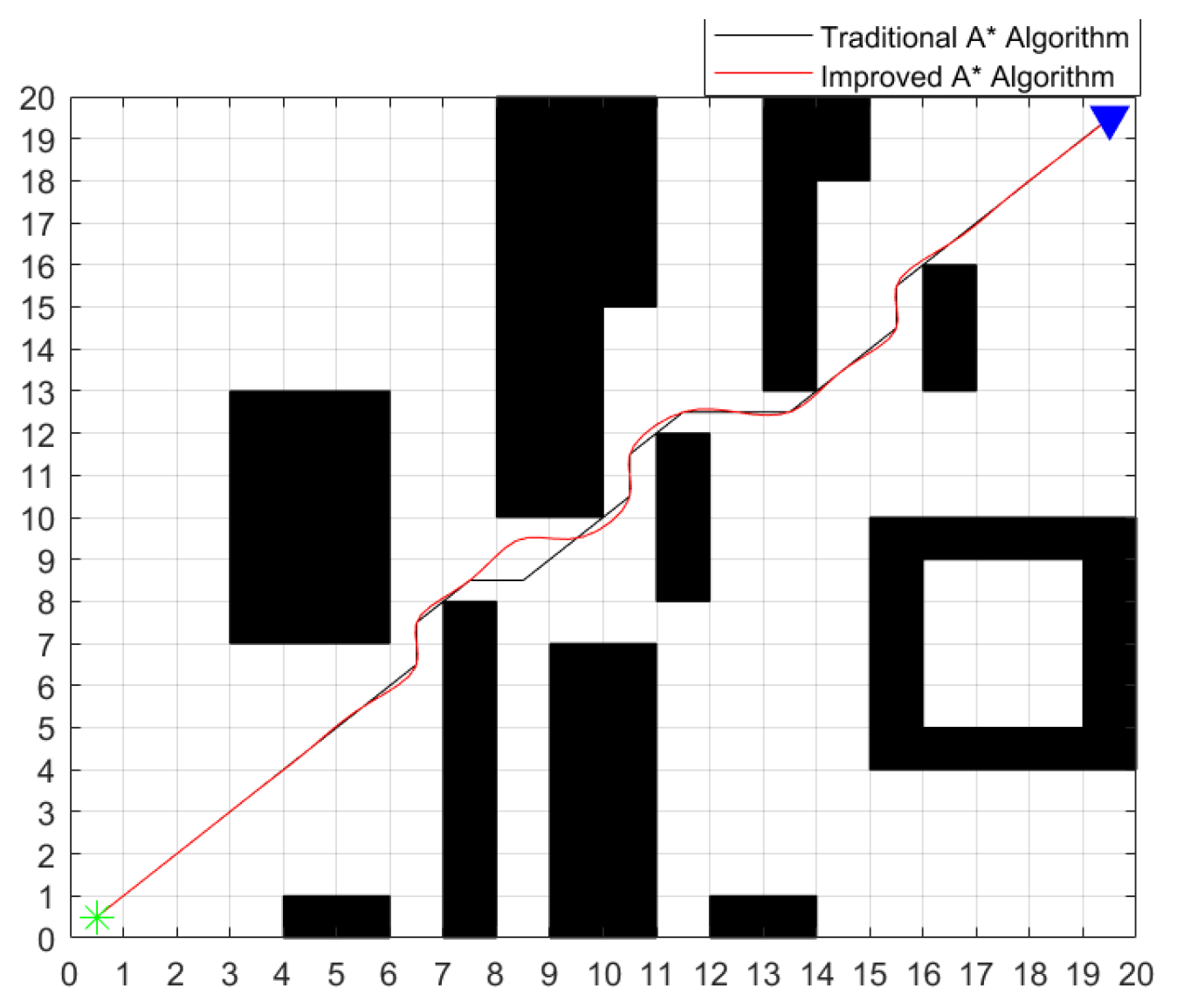


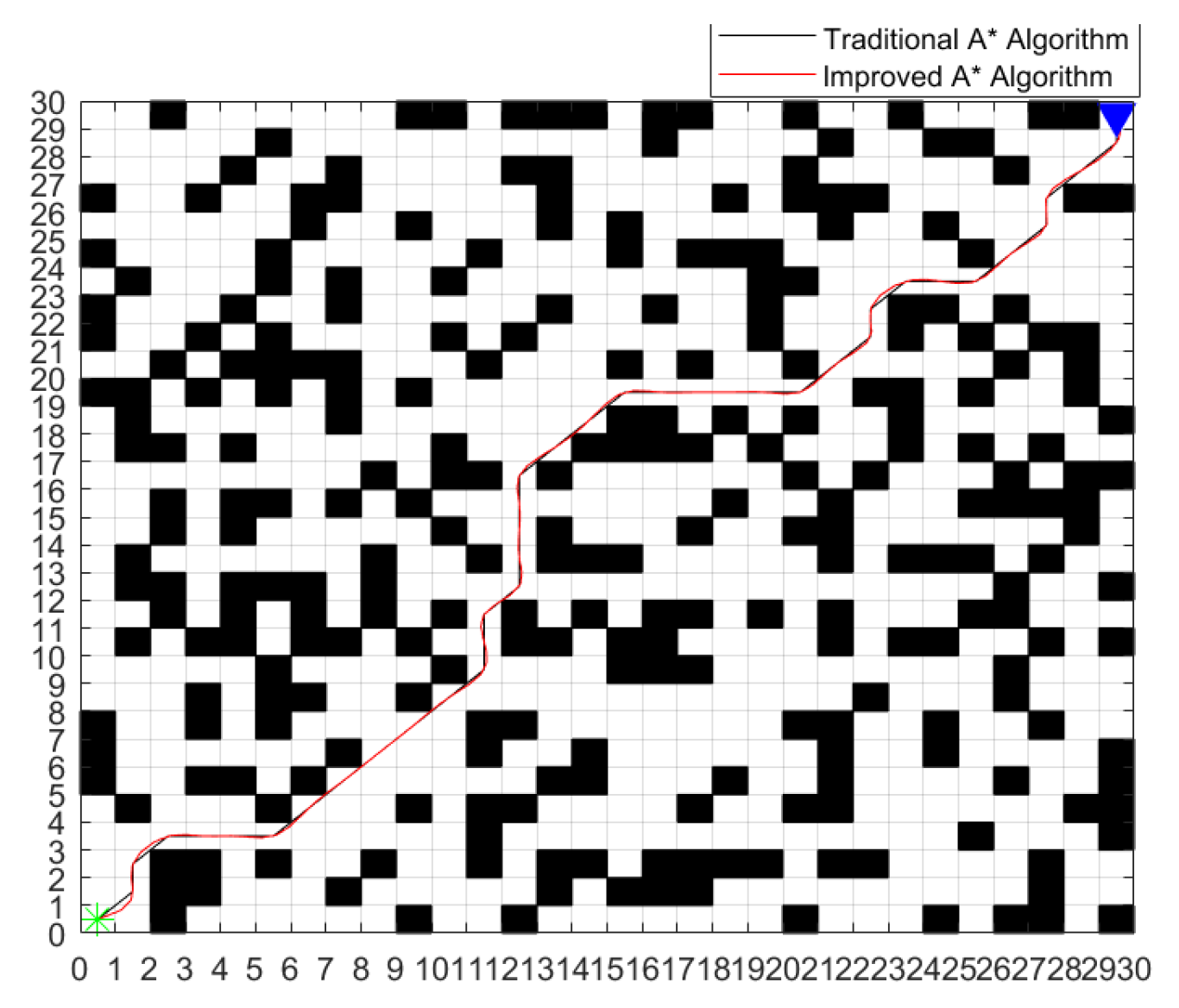




| Number | Input | Output | ||||
|---|---|---|---|---|---|---|
| D_obs | D_goal | α | β | γ | λ | |
| 1 | VS | VS | S | S | M | S |
| 2 | VS | S | S | M | M | S |
| 3 | VS | M | S | M | M | S |
| 4 | VS | B | S | B | B | S |
| 5 | S | VS | M | VS | M | M |
| 6 | S | S | M | S | M | M |
| 7 | S | M | S | M | M | M |
| 8 | S | B | S | B | B | M |
| 9 | M | VS | M | VS | M | VS |
| 10 | M | S | M | VS | M | S |
| 11 | M | M | M | VS | M | M |
| 12 | M | B | M | VS | B | B |
| 13 | B | VS | B | VS | S | VS |
| 14 | B | S | B | VS | S | VS |
| 15 | B | M | B | VS | M | S |
| 16 | B | B | B | VS | B | B |
| Map Specification | Algorithm | Path Length | Running Time/s |
|---|---|---|---|
| 20 × 20 | Traditional A* Algorithm | 27.87 | 0.043 |
| Improved A* Smoothing Algorithm | 28.31 | 0.028 | |
| 30 × 30 | Traditional A* Algorithm | 54.62 | 0.18 |
| Improved A* Smoothing Algorithm | 54.92 | 0.08 |
| Situation | Path Length | Running Time/s | Inflection Points/No. |
|---|---|---|---|
| Gazebo Robotics Simulator | 2.6 | 0.6 | 6 |
| experiment | 2.8 | 0.75 | 7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Liu, W. Enhanced A*–Fuzzy DWA Hybrid Algorithm for AGV Path Planning in Confined Spaces. World Electr. Veh. J. 2025, 16, 538. https://doi.org/10.3390/wevj16090538
Xu Y, Liu W. Enhanced A*–Fuzzy DWA Hybrid Algorithm for AGV Path Planning in Confined Spaces. World Electric Vehicle Journal. 2025; 16(9):538. https://doi.org/10.3390/wevj16090538
Chicago/Turabian StyleXu, Yang, and Wei Liu. 2025. "Enhanced A*–Fuzzy DWA Hybrid Algorithm for AGV Path Planning in Confined Spaces" World Electric Vehicle Journal 16, no. 9: 538. https://doi.org/10.3390/wevj16090538
APA StyleXu, Y., & Liu, W. (2025). Enhanced A*–Fuzzy DWA Hybrid Algorithm for AGV Path Planning in Confined Spaces. World Electric Vehicle Journal, 16(9), 538. https://doi.org/10.3390/wevj16090538





