Active and Reactive Power Scheduling of Distribution System Based on Two-Stage Stochastic Optimization
Abstract
1. Introduction
- For the active and reactive power scheduling problem of the distribution network, a two-stage stochastic rolling optimization framework is proposed to reduce the model solution difficulty. By decoupling active and reactive power scheduling, the first stage performs active power dispatch by considering the energy exchange between different nodes with multi-energy, while the second stage performs reactive power compensation based on the first-stage scheduling plan.
- For the active power dispatch at the first stage, the elastic scheduling capacity of EVs at each node is obtained through the aggregation of EV charging demand considering the random and nonlinear mobility of EV charging demand. Then, a simulation-based Rollout method is proposed to improve the active power dispatch policy of the distribution network in an online fashion which can achieve operational cost optimization.
- For the reactive power compensation at the second stage, a scenario-based second-order cone programming method is proposed to achieve the stochastic rolling optimization for the voltage performance improvement of the distribution network based on the optimized aggregated total power of EVs. Numerical experiments demonstrate that the proposed method can achieve economic and secure optimization of the distribution network.
2. Problem Formulation
2.1. Stochastic Rolling Optimization Model for Power Scheduling
2.2. Active Power Dispatch Model for the First Stage
2.3. Reactive Power Compensation Model for the Second Stage
3. Solution Methodology
3.1. Simulation-Based Rollout for First-Stage Model
3.2. Scenario-Based Second-Order Cone Programming for Second-Stage Model
3.3. Algorithm Summary
| Algorithm 1: Simulation-based Rollout for first-stage model. |
|
| Algorithm 2: Scenario-based second-order cone programming for second-stage model. |
|
4. Numerical Results
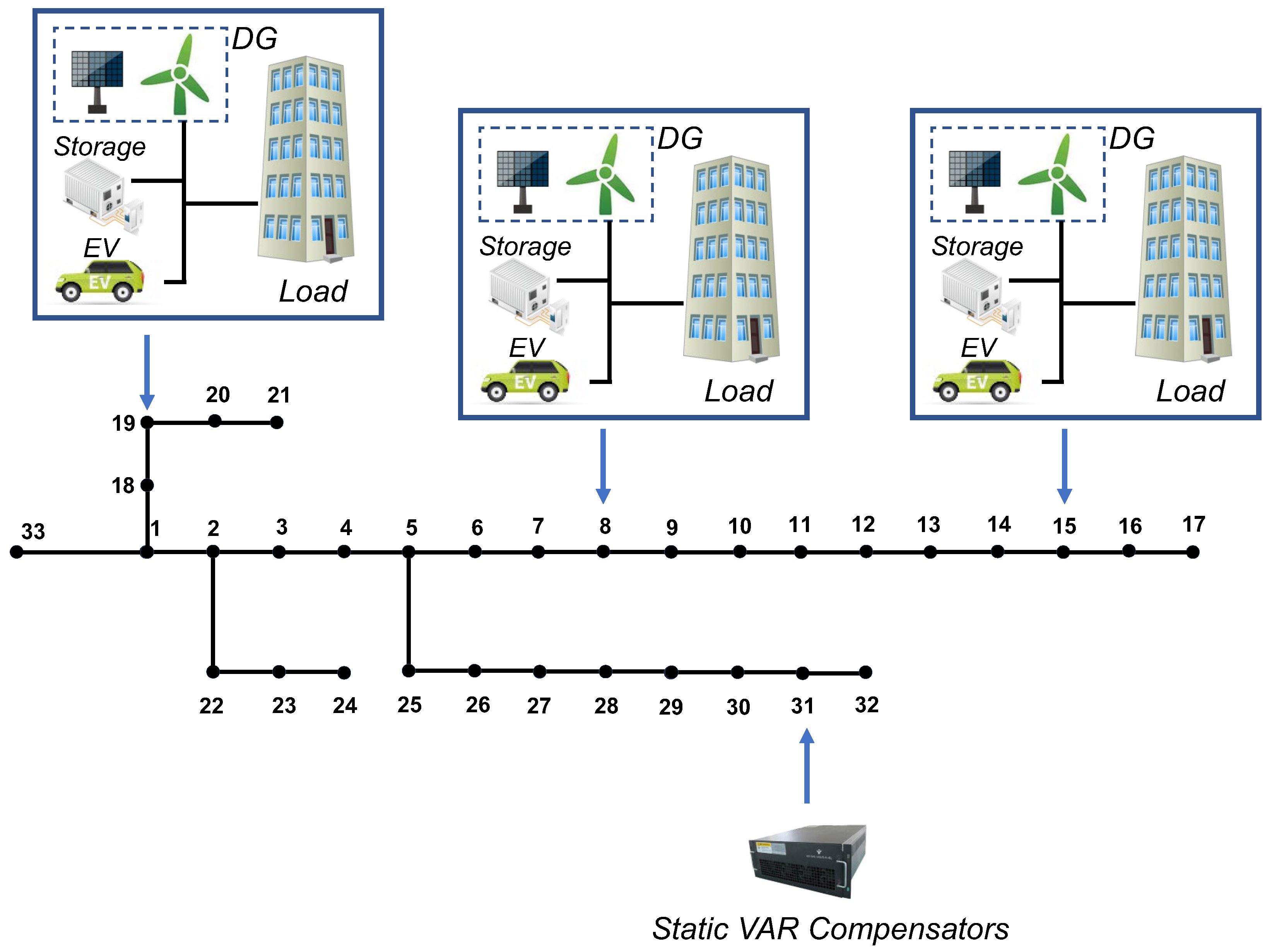
4.1. Experiment Settings
4.2. Overall Performance of the Two-Stage Stochastic Optimization
- Improved dispatch policy under multiple simulations. In this case, the proposed simulation-based Rollout method is applied with . The base policy is set as follows. EVs will be charged as soon as possible. Each node will firstly meet its own demand and then provide surplus power to the energy storage and other nodes in turn. When the demand of the node is still unsatisfied by power exchange among the nodes, a node will finally purchase power from the grid.
- Improved dispatch policy under a single simulation. In this case, the proposed simulation-based Rollout method is applied with . This case is used to demonstrate the importance of the consideration of the uncertainties in the distributed wind/solar generation and EV charging demand.
- Improved dispatch policy with no power exchange among nodes. In this case, the proposed simulation-based Rollout method is applied with and no consideration of power exchange among nodes.
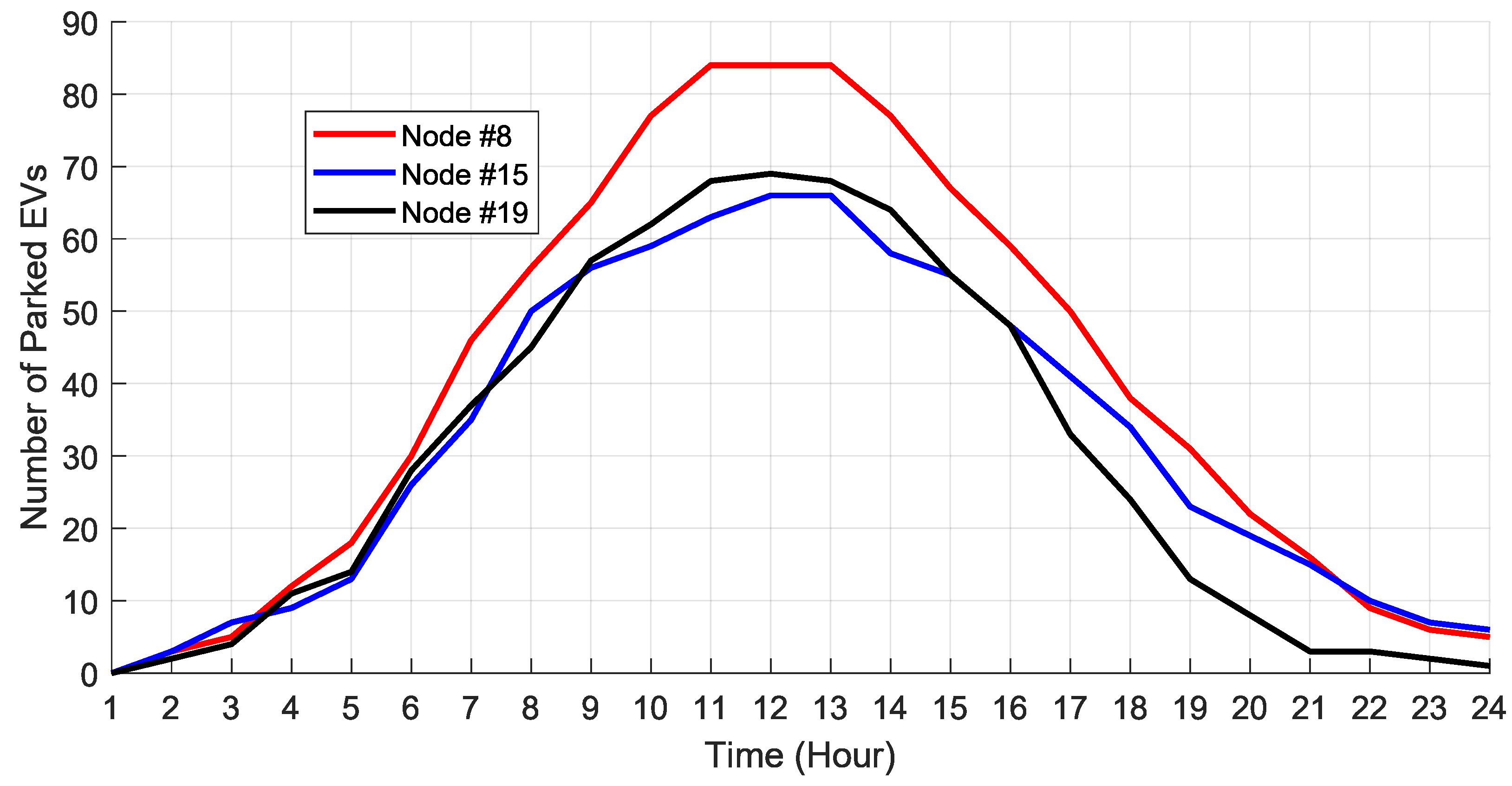
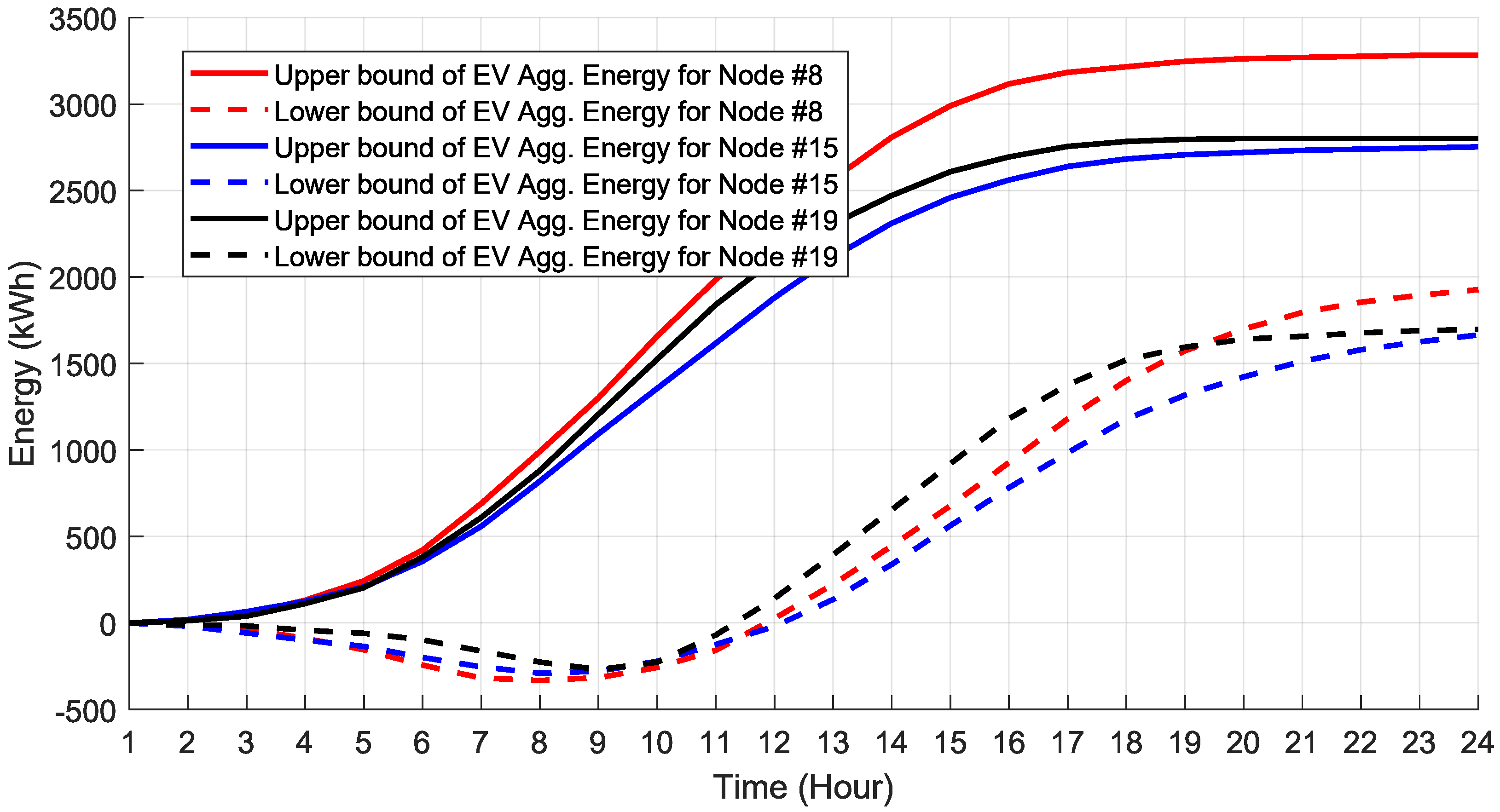
4.3. EV Control Analysis
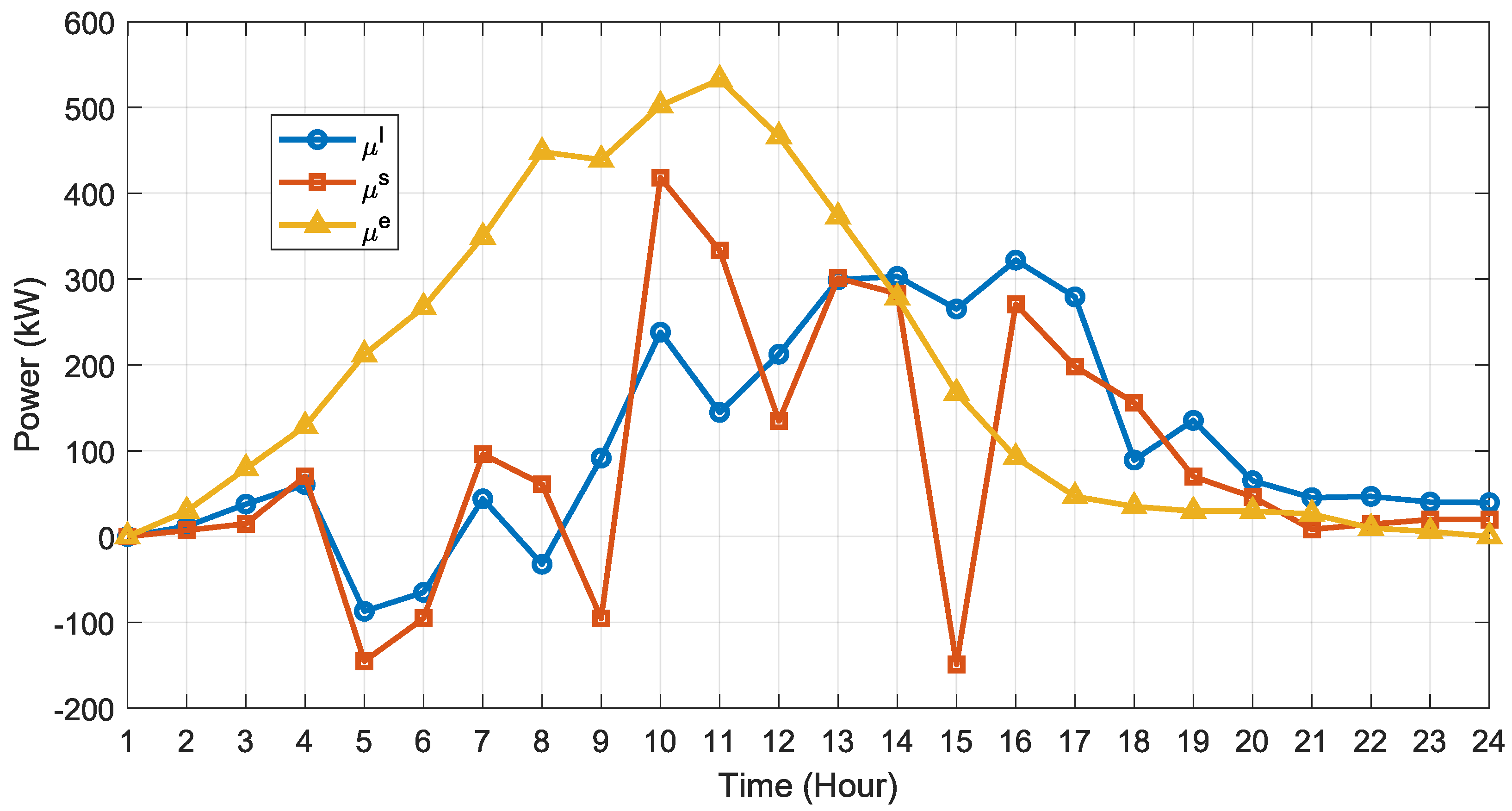
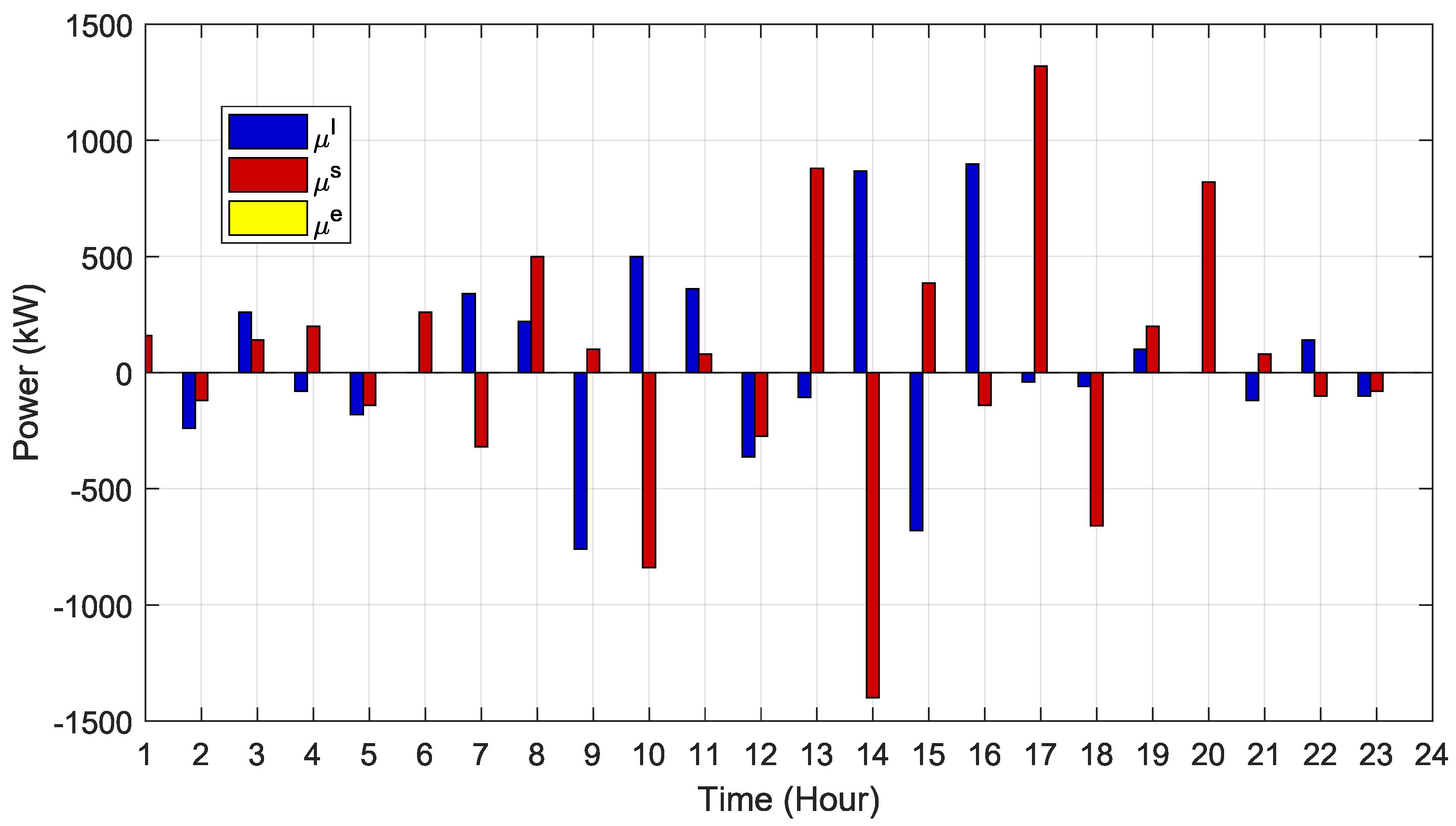
4.4. Power Exchange and Procurement Analysis
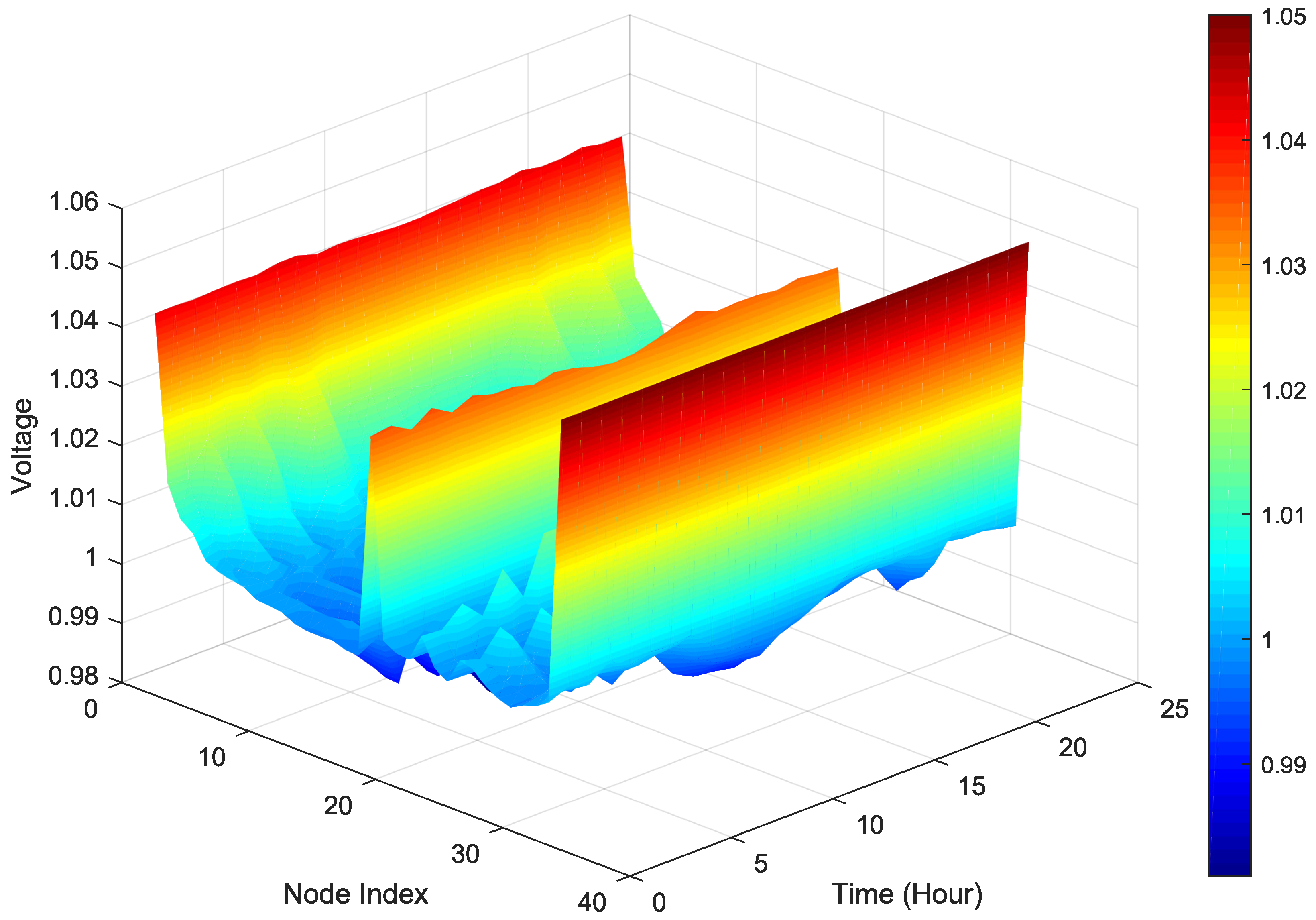
4.5. Voltage Performance Analysis
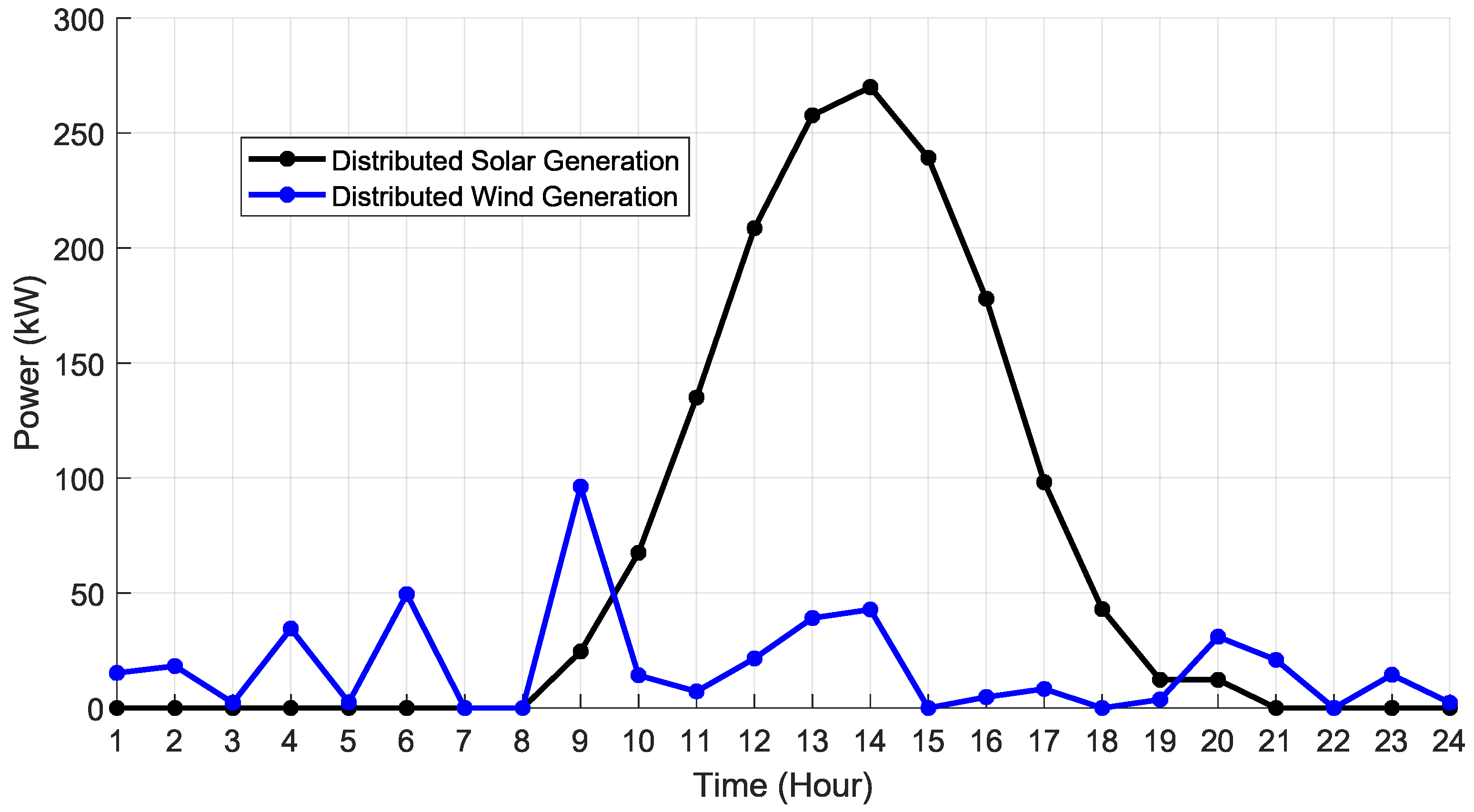
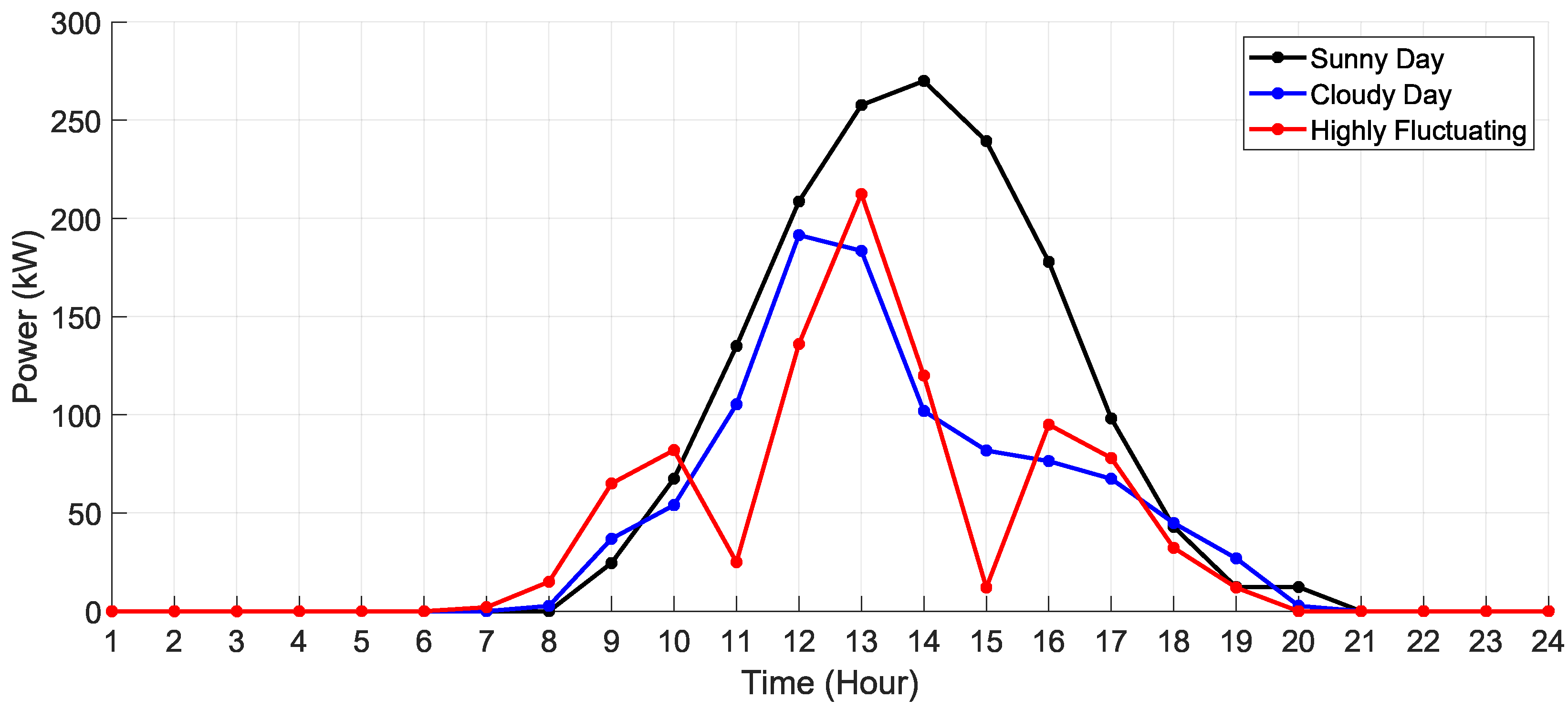
4.6. Distributed Solar Power Fluctuation Analysis
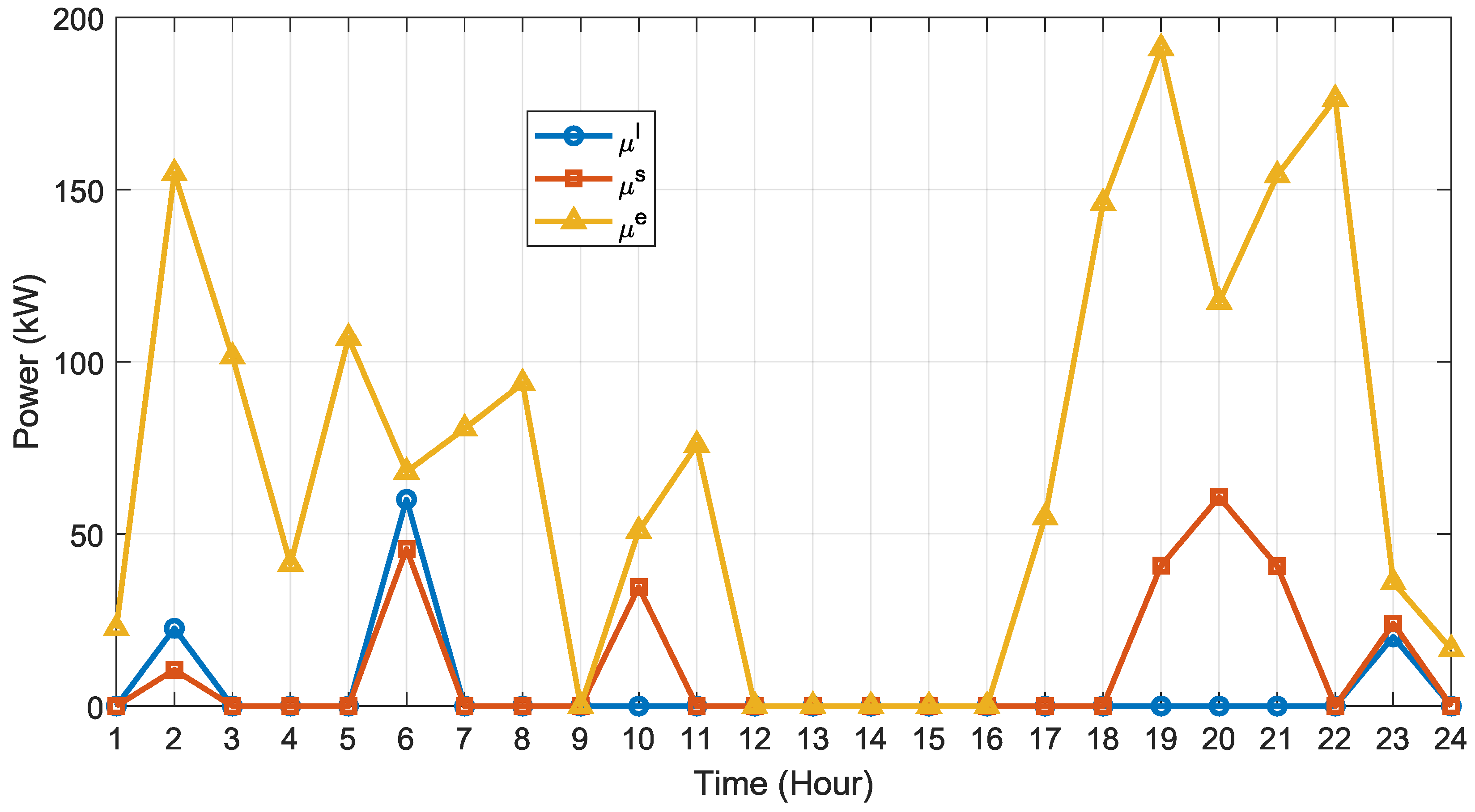
4.7. Energy Storage Control Analysis
4.8. Operation Analysis for Different IEEE Test Grid
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ntombela, M.; Musasa, K.; Moloi, K. A comprehensive review of the incorporation of electric vehicles and renewable energy distributed generation regarding smart grids. World Electr. Veh. J. 2023, 14, 176. [Google Scholar] [CrossRef]
- Hemavathi, S.; Shinisha, A. A study on trends and developments in electric vehicle charging technologies. J. Energy Storage 2022, 52, 105013. [Google Scholar] [CrossRef]
- Cui, D.; He, J.; Cheng, X.; Liu, Z. Electric vehicle charging transaction model based on alliance blockchain. World Electr. Veh. J. 2023, 14, 192. [Google Scholar] [CrossRef]
- Li, C.X.; Shah, N.; Li, Z.; Liu, P. Modelling of wind and solar power output uncertainty in power systems based on historical data: A characterisation through deterministic parameters. J. Clean. Prod. 2024, 484, 144233. [Google Scholar] [CrossRef]
- Fambri, G.; Diaz-Londono, C.; Mazza, A.; Badami, M.; Sihvonen, T.; Weiss, R. Techno-economic analysis of power-to-gas plants in a gas and electricity distribution network system with high renewable energy penetration. Appl. Energy 2022, 312, 118743. [Google Scholar] [CrossRef]
- Lan, Y.; Zhai, Q.Z.; Liu, X.M.; Guan, X.H. Fast stochastic dual dynamic programming for economic dispatch in distribution systems. IEEE Trans. Power Syst. 2022, 38, 3828–3840. [Google Scholar] [CrossRef]
- Hu, J.D.; Ye, C.J.; Ding, Y.; Tang, J.J.; Liu, S. A distributed MPC to exploit reactive power V2G for real-time voltage regulation in distribution networks. IEEE Trans. Smart Grid 2021, 13, 5768–588. [Google Scholar] [CrossRef]
- Fu, J.; Han, Y.; Li, W.; Feng, Y.; Zalhaf, A.S.; Zhou, S.; Yang, P.; Wang, C. A novel optimization strategy for line loss reduction in distribution networks with large penetration of distributed generation. Int. J. Electr. Power Energy Syst. 2022, 150, 109112. [Google Scholar] [CrossRef]
- Lin, J.; Qiu, J.; Liu, G.; Yao, Z.; Yuan, Z.; Lu, X. A fuzzy logic approach to power system security with non-ideal electric vehicle battery models in vehicle-to-grid systems. IEEE Internet Things J. 2025, 12, 21876–21891. [Google Scholar] [CrossRef]
- Liang, H.J.; Pirouzi, S. Energy management system based on economic flexi-reliable operation for the smart distribution network including integrated energy system of hydrogen storage and renewable sources. Energy 2024, 293, 130745. [Google Scholar] [CrossRef]
- Li, Y.; Feng, B.; Wang, B.; Sun, S.C. Photovoltaic consumption strategy of distribution network considering carbon emission and user experience. Energy 2022, 245, 123226. [Google Scholar] [CrossRef]
- Shi, X.; Xu, Y.; Chen, G.; Guo, Y. An augmented Lagrangian-based safe reinforcement learning algorithm for carbon-oriented optimal scheduling of EV aggregators. IEEE Trans. Smart Grid 2023, 15, 795–809. [Google Scholar] [CrossRef]
- Jian, J.; Zhang, M.; Xu, Y.; Tang, W.; He, S. An analytical polytope approximation aggregation of electric vehicles considering uncertainty for the day-ahead distribution network dispatching. IEEE Trans. Sustain. Energy 2023, 15, 160–172. [Google Scholar] [CrossRef]
- Xu, X.; Qiu, Z.; Zhang, T.; Gao, H. Distributed source-load-storage cooperative low-carbon scheduling strategy considering vehicle-to-grid aggregators. J. Mod. Power Syst. Clean Energy 2024, 12, 440–453. [Google Scholar] [CrossRef]
- Moghari, P.; Chabanloo, R.M.; Torkaman, H. Distribution system reconfiguration based on MILP considering voltage stability. Electr. Power Syst. Res. 2023, 222, 109523. [Google Scholar] [CrossRef]
- Chowdhury, M.M.; Biswas, B.D.; Kamalasadan, S. Second-order cone programming (SOCP) model for three phase optimal power flow (OPF) in active distribution networks. IEEE Trans. Smart Grid 2023, 14, 3732–3743. [Google Scholar] [CrossRef]
- Guo, C.Y.; Wang, X.; Zheng, Y.H.; Zhang, F. Optimal energy management of multi-microgrids connected to distribution system based on deep reinforcement learning. Int. J. Electr. Power Energy Syst. 2021, 131, 107048. [Google Scholar] [CrossRef]
- Li, H.P.; He, H.B. Learning to operate distribution networks with safe deep reinforcement learning. IEEE Trans. Smart Grid 2022, 13, 1860–1872. [Google Scholar] [CrossRef]
- Lu, Y.; Xiang, Y.; Huang, Y.; Yu, B.; Weng, L.G.; Liu, J.Y. Deep reinforcement learning based optimal scheduling of active distribution system considering distributed generation, energy storage and flexible load. Energy 2023, 271, 127087. [Google Scholar] [CrossRef]
- Dolatabadi, S.H.; Ghorbanian, M.; Siano, P.; Hatziargyriou, N.D. An enhanced IEEE 33 bus benchmark test system for distribution system studies. IEEE Trans. Power Syst. 2021, 36, 2565–2572. [Google Scholar] [CrossRef]
- Zhang, H.C.; Hu, Z.C.; Xu, Z.W.; Song, Y.H. Evaluation of achievable vehicle-to-grid capacity using aggregate PEV model. IEEE Trans. Power Syst. 2016, 32, 784–794. [Google Scholar] [CrossRef]
- Powell, W.B. Reinforcement Learning and Stochastic Optimization: A Unified Framework for Sequential Decisions; Wiley: Hoboken, NJ, USA, 2022. [Google Scholar]
- Bertsekas, D. Multiagent reinforcement learning: Rollout and policy iteration. IEEE CAA J. Autom. Sin. 2021, 8, 249–272. [Google Scholar] [CrossRef]
- Long, T.; Jia, Q.S.; Wang, G.M.; Yang, Y. Efficient real-time EV charging scheduling via ordinal optimization. IEEE Trans. Smart Grid 2021, 12, 4029–4038. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Kailas, S.; Badyal, S.; Gil, S.; Bertsekas, D. Multiagent reinforcement learning: Rollout and policy iteration for pomdp with application to multirobot problems. IEEE Trans. Robot. 2023, 40, 2003–2023. [Google Scholar] [CrossRef]
- Lin, Z.C.; Huang, X.R.; Xiao, X. A novel model predictive control formulation for wave energy converters based on the reactive rollout method. IEEE Trans. Sustain. Energy 2022, 13, 491–500. [Google Scholar] [CrossRef]
- Puterman, M.L. Markov Decision Processes; John Wiley & Sons: Hoboken, NJ, USA, 1994. [Google Scholar]
- Zeng, F.; Yuan, X.; Pan, Y.; Wang, M.; Miao, H.; Han, H.; Lyu, S. GWO-based charging price determination for charging station with competitor awareness. Electr. Eng. 2024, 106, 7587–7601. [Google Scholar] [CrossRef]
- Wu, L.; Shahidehpour, M.; Li, Z. Comparison of scenario-based and interval optimization approaches to stochastic SCUC. IEEE Trans. Power Syst. 2011, 27, 913–921. [Google Scholar] [CrossRef]
- Rujeerapaiboon, N.; Schindler, K.; Kuhn, D.; Wiesemann, W. Scenario reduction revisited: Fundamental limits and guarantees. Math. Program. 2022, 191, 207–242. [Google Scholar] [CrossRef]
- Alizadeh, F.; Goldfarb, D. Second-order cone programming. Math. Program. 2003, 95, 3–51. [Google Scholar] [CrossRef]
- Baran, M.; Wu, F. Network reconfiguration in distribution systems for loss reduction and load balancing. IEEE Trans. Power Del. 1989, 4, 1401–1407. [Google Scholar] [CrossRef]
- Li, J.; Xiao, Y.; Lu, S. Optimal configuration of multi microgrid electric hydrogen hybrid energy storage capacity based on distributed robustness. J. Energy Storage 2024, 76, 109762. [Google Scholar] [CrossRef]
- Bach, K. A novel method for global voltage sag compensation in IEEE 69 bus distribution system by dynamic voltage restorers. J. Eng. Sci. Technol. 2019, 14, 1893–1911. [Google Scholar]


| References | Economic Dispatch | Operation Security | Uncertain DG | Uncertain Charging Demand | EV Aggregation |
|---|---|---|---|---|---|
| [3,17] | ✓ | ✓ | |||
| [4] | ✓ | ||||
| [5] | ✓ | ||||
| [6] | ✓ | ✓ | ✓ | ||
| [7,11] | ✓ | ✓ | |||
| [8] | ✓ | ||||
| [9,19] | ✓ | ✓ | |||
| [10] | ✓ | ✓ | ✓ | ✓ | |
| [12,13,14] | ✓ | ✓ | ✓ | ||
| [15,16] | ✓ | ✓ | |||
| [18] | ✓ | ✓ | ✓ | ||
| Proposed Work | ✓ | ✓ | ✓ | ✓ | ✓ |
| Node | Active Power | Reactive Power | Node | Active Power | Reactive Power |
|---|---|---|---|---|---|
| 1 | 93.33 kw | 48 kvar | 18 | 84 kw | 32 kvar |
| 2 | 84 kw | 32 kvar | 19 | 84 kw | 32 kvar |
| 3 | 112 kw | 64 kvar | 20 | 84 kw | 32 kvar |
| 4 | 56 kw | 24 kvar | 21 | 84 kw | 32 kvar |
| 5 | 56 kw | 16 kvar | 22 | 84 kw | 40 kvar |
| 6 | 186.67 kw | 80 kvar | 23 | 392 kw | 160 kvar |
| 7 | 186.67 kw | 80 kvar | 24 | 392 kw | 160 kvar |
| 8 | 56 kw | 16 kvar | 25 | 56 kw | 20 kvar |
| 9 | 56 kw | 16 kvar | 26 | 56 kw | 20 kvar |
| 10 | 42 kw | 24 kvar | 27 | 56 kw | 16 kvar |
| 11 | 56 kw | 28 kvar | 28 | 112 kw | 56 kvar |
| 12 | 56 kw | 28 kvar | 29 | 186.67 kw | 480 kvar |
| 13 | 112 kw | 64 kvar | 30 | 140 kw | 56 kvar |
| 14 | 56 kw | 8 kvar | 31 | 196 kw | 80 kvar |
| 15 | 56 kw | 16 kvar | 32 | 56 kw | 32 kvar |
| 16 | 56 kw | 16 kvar | 33 | 0 kw | 0 kvar |
| 17 | 84 kw | 32 kvar |
| Parameter | Setting | Parameter | Setting |
|---|---|---|---|
| 66 kWh | P | 6.6 kW | |
| 0.9 | 0.1 | ||
| 1200 kWh | 0.5 CNY/kWh | ||
| 0.35 CNY/kWh | 0.35 CNY/kWh | ||
| T | 24 h | 300 kW | |
| −0.2 MVar | 1 MVar |
| Policy | Oper. Cost | Purchasing Cost | EV Oper. Profit | EV Sub. Cost | Solar Gen. Cost | Wind Gen. Cost |
|---|---|---|---|---|---|---|
| CNY 88.06 | CNY 83.51 | CNY −3547.58 | CNY 1478.50 | CNY 1623.60 | CNY 450.03 | |
| CNY 524.81 | CNY 266.49 | CNY −3293.81 | CNY 1478.50 | CNY 1623.60 | CNY 450.03 | |
| CNY 1330.83 | CNY 2020.28 | CNY −4241.58 | CNY 1478.50 | CNY 1623.60 | CNY 450.03 |
| Scenario | Sunny | Cloudy | Highly Fluctuating |
|---|---|---|---|
| Total Operation Cost | CNY 88.06 | CNY 234.76 | CNY 350.81 |
| Electricity Purchasing Cost | CNY 83.51 | CNY 286.95 | CNY 343.43 |
| Test Grid | Oper. Cost | Purchasing Cost | EV Oper. Profit |
|---|---|---|---|
| 69-bus with | CNY 266.36 | CNY 126.57 | CNY |
| 69-bus with | CNY 1894.40 | CNY 2197.70 | CNY |
| 33-bus with | CNY 88.06 | CNY 83.51 | CNY |
| References | Model Requirement | Stochastic Optimization | Computation Enhancement | Policy Optimality |
|---|---|---|---|---|
| [8,11] | Weak | Not Supported | No | Near Optimal |
| [15,16] | Strong | Not Supported | Yes | Optimal |
| [17,18,19] | Weak | Supported | No | Near Optimal |
| Proposed Solution | Weak | Supported | Yes | Near Optimal |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Ren, J.; He, Q.; Dong, D.; Zou, H. Active and Reactive Power Scheduling of Distribution System Based on Two-Stage Stochastic Optimization. World Electr. Veh. J. 2025, 16, 515. https://doi.org/10.3390/wevj16090515
Xu Y, Ren J, He Q, Dong D, Zou H. Active and Reactive Power Scheduling of Distribution System Based on Two-Stage Stochastic Optimization. World Electric Vehicle Journal. 2025; 16(9):515. https://doi.org/10.3390/wevj16090515
Chicago/Turabian StyleXu, Yangchao, Jia Ren, Qiang He, Dongyang Dong, and Haoxiang Zou. 2025. "Active and Reactive Power Scheduling of Distribution System Based on Two-Stage Stochastic Optimization" World Electric Vehicle Journal 16, no. 9: 515. https://doi.org/10.3390/wevj16090515
APA StyleXu, Y., Ren, J., He, Q., Dong, D., & Zou, H. (2025). Active and Reactive Power Scheduling of Distribution System Based on Two-Stage Stochastic Optimization. World Electric Vehicle Journal, 16(9), 515. https://doi.org/10.3390/wevj16090515





