Research on Combined Thermal Management System of Power Battery and Air Conditioning Based on MPC

Abstract

Efficient thermal management of power batteries is critical for the safety of new energy vehicles. In this study, we present a novel combined thermal management system that integrates the battery-cooling system with the air-conditioning system. The system employs model predictive control (MPC) to regulate the battery water pump. To evaluate its performance, the MPC strategy is compared with ON-OFF, PID, and fuzzy control strategies. The system model was established and simulated in a high-temperature environment (40 °C) based on a plug-in hybrid electric vehicle (PHEV). The results demonstrate that the MPC-controlled pump exhibits the fastest response speed, maintaining battery temperature fluctuations within 1 °C, comparable to fuzzy control but with significantly lower power consumption. Specifically, the MPC strategy reduces pump power consumption by 46.3% compared to ON-OFF control, 31.3% compared to PID control, and 36% compared to fuzzy control. Based on a comprehensive evaluation of pump response speed, battery temperature fluctuation, and pump power consumption, MPC exhibits the best overall performance.

1. Introduction

In the process of transition from traditional fuel vehicles to new energy vehicles, the power battery is the most core component and the importance of maintaining battery performance is self-evident. Excessive battery temperature will not only reduce battery capacity and safety, but may also cause thermal runaway after serious heat accumulation, resulting in serious accidents. The thermal behavior and thermal runaway propagation in lithium-ion battery systems has been investigated, analyzing triggering factors, propagation pathways, and mitigation strategies to enhance battery safety design [1]. Warning methods have been proposed for lithium-ion battery thermal runaway, covering sensor-based monitoring, model prediction, and signal recognition techniques, with an emphasis on multi-parameter fusion for reliable detection [2]. Advances in thermal management systems for next-generation power batteries have been discussed, including phase-change materials, optimized liquid/air cooling, and novel heat dissipation structures, focusing on improving thermal uniformity and energy efficiency [3]. Thermal management systems for EV batteries have been discussed, comparing air/liquid/phase-change cooling technologies and discussing challenges for high-energy-density battery thermal control [4]. In order to ensure the safety of batteries, an efficient BTMS (battery thermal management system) is needed [5]. Power batteries are limited in size and weight due to their wide range of use and variable operating load [6]. Therefore, innovating the best architecture, algorithm, and operation mode of the battery thermal management system, improving the timeliness and energy efficiency of battery thermal management [7,8], and greatly improving the cycle stability and safety reliability of the power battery [9,10] play a crucial role in the safe operation and wide application of new energy vehicles.

Temperature is an important factor affecting the performance, cycle life, and safety of batteries for pure electric vehicles. Especially, excessive temperature may cause the decomposition, combustion, or even explosion of chemical materials inside the lithium-ion battery [11,12,13,14]. Therefore, it is necessary to carry out reasonable and efficient battery thermal management to ensure the stability, cycle life, and safety of power batteries. At present, a large number of scholars have carried out research on the thermal management of power batteries. Cen et al. [15] designed a tubular heat exchanger for direct cooling of batteries. By improving the inlet and outlet positions of the tubular heat exchanger, the uneven temperature of each unit in the battery pack was effectively reduced. Wang et al. [16] introduce and adopt a new type of refrigerant CO₂ into an electric vehicle heat pump system and experimentally verify that the CO₂ heat pump system has a better heating performance in cold climates. Lv et al. [17] filled a kind of graphene-oxide-modified silica gel between the cylindrical cell and the water-cooling tube. The cooling performance of the system is significantly improved. The above three articles focus on improving pipeline structure or using better heat transfer coefficient materials to improve cooling performance.

Amini et al. [18] designed a collaborative thermal management system for the air cooling of batteries and the crew cabin. The system exchanges heat between the cooled crew cabin air and the battery. But the cooling of the battery is limited by the cooling condition of the crew cabin, so it is difficult for this system to conduct independent thermal management of the crew cabin and battery. Cen et al. [19] built an electric vehicle air-conditioning system to control battery temperature. The PID control method is used to adjust the compressor. The temperature of the battery pack can maintain 24–27 °C. Zhang et al. [20] proposed a cooperative control strategy (Com-VOVs mode) integrating compressor and variable-opening valve coordination for battery-refrigerant cooling and AC systems, experimentally demonstrating its efficacy in enhancing system COP by 52.24%, reducing the cold plate pressure drop by 52.24%. Zhang et al. [21] established a bench experiment of a battery liquid cooling and air-conditioning collaborative system. The influence of different thermal expansion valves on refrigerant distribution regulation under different operating conditions was compared and analyzed. The results show that the electronic expansion valve can keep the air outlet temperature stable and save energy consumption up to 20%. These four articles are all about coupling the air-conditioning system to the battery-cooling loop to improve the cooling effect of the battery.

An intelligent codesign strategy should be developed to balance the thermal management and cost control for an integrated system. Wang et al. [22] proposed an optimization design method for the TSV array, which can achieve the thermal management of a 3-D integrated system. These proposed methods are all focused on the thermal management of an integrated system. Generally, the thermal dissipation performance is increased with an increasing number of TTSVs, but the cost is also increased. Jordan et al. [23] evaluate the cost scaling analysis holistically to consider the entire system cost. The framework reveals that the optimal PCM thickness (which minimizes the USD per kW h cost of the thermal battery) is often on the order of cm and depends exactly on the PCM properties and operational parameters.

Current research on battery thermal management systems primarily focuses on architectural design and materials, with limited attention given to control strategies. As an essential component of thermal management system design, the control strategy significantly influences system performance. In this study, we aim to bridge this gap by adopting a model predictive control strategy to regulate the pump speed in the battery-cooling circuit under high-temperature conditions. This approach aims to further stabilize battery temperatures and enhance the reliability of the thermal management system. By integrating the battery-cooling circuit with the air-conditioning circuit and leveraging MPC, we aim to contribute to the advancement of thermal management technologies for new energy vehicles. First, a high-fidelity thermal model of the battery-cooling circuit is developed, validated against experimental data. Second, an MPC strategy to optimize pump speed is designed while balancing cooling efficiency and energy consumption. Third, the MPC approach is compared with conventional PID, ON-OFF, and fuzzy control in terms of energy savings and temperature stability.

2. Experimental Processes

Based on a PHEV, an integrated coupling system of air conditioning and battery cooling is built in this paper. The circulating system uses the refrigerant R134a and consists of a compressor, condenser, expansion valve, evaporator, heat exchanger, and battery module.

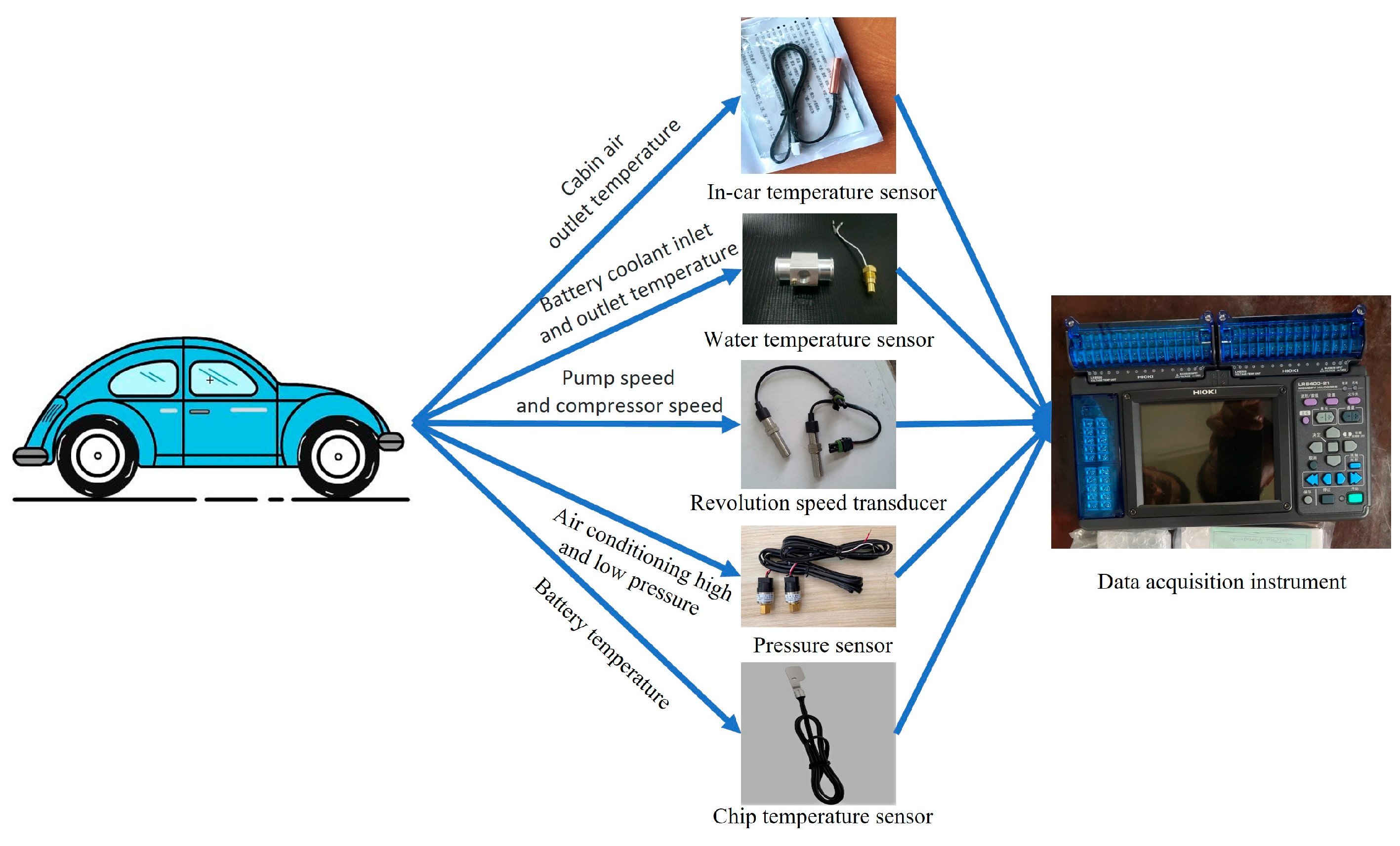
Ten groups of data need to be collected according to the requirement of establishing the state-space equation of the thermal management system coupled with battery and air conditioning. It is necessary to measure the pump speed of the battery loop, compressor speed, compressor inlet and outlet pressure, operating conditions, ambient temperature, battery inlet and outlet coolant temperature, battery temperature, and crew cabin temperature. The basic parameters of the batteries are shown in

Table 1. Basic parameters of battery.

Parameters	Unit	Value
Nominal voltage	V	350
Nominal capacity	Ah	37
Resistance	mΩ	1.6

. In order to accurately measure the power battery temperature, 12 temperature monitoring points are set inside the battery, and the average value is taken. These sensor data signals are read by a data acquisition instrument through CAN protocol communication. The flow chart of this test is shown in Figure 1. The experimental data was collected in the constant temperature environmental chamber, and the environmental chamber and its schematic diagram are shown in Figure 2 and Figure 3, respectively.

Vehicle selection is representative of WLTC (World Light Vehicle Test Cycle) working conditions, as shown in Figure 4. The operating condition can cover the range of an actual vehicle operating at high temperature and facilitate accurate description and evaluation of thermal management performance. In this study, the ambient temperature is defined as 40 °C. Humidity is 50% and air density is 1.185 kg/m³. Before the high-temperature test, the vehicle is immersed in a high-temperature environment for at least 0.5 h, and the light intensity of 850 ± 45 W/m² is maintained during the immersion and test. The four-wheel drive hub platform is equipped with a large fan to simulate the air flow when the vehicle is running. The maximum wind speed is no less than 160 km/h, and the maximum air output is more than 10,000 m³/h.

Table 2. Sensor introduction.

Sensor	Data Acquisition Instrument	Chip Temperature Sensor	Water Temperature Sensor	Revolution Speed Transducer	In-Car Temperature Sensor	Pressure Sensor
Brand	HIOKI	SONGDAO	ShengWang	TYHC	TELESKY	Sanhua
Type	LR8500	PT100	ST28-40	CYT-9100	TC5K	YCQB05L01
Range	/	−200–850 °C	−40–150 °C	0–12,000 rev/min	−40–125 °C	0–20 bar
Precision	/	±0.15	1.5%	±0.1%	±0.2 °C	0.8%

below shows the manufacturers and product models of each sensor used in this experiment.

3. Modeling and Validation of Thermal Management Systems

3.1. Thermal Management System Structure Design Scheme

The structure of the battery and air conditioning coupling thermal management system studied in this paper is shown in Figure 5, which consists of two modules, namely, the battery-cooling system and the air-conditioning system. The battery thermal management subsystem consists of a battery water cooling plate, water pump, radiator, heat exchanger, and so on. The air-conditioning circuit consists of a compressor, evaporator, radiator, expansion valve, blower, and so on. The battery circuit dissipates heat at high temperature through the heat exchanger and the refrigerant in the air-conditioning circuit.

3.2. Modeling of Thermal Management System

3.2.1. Heat Generation Model of Battery

The process of charging and discharging a power battery is accompanied by complex chemical reactions. There is also a loss of energy in the process of achieving energy storage and release. This lost energy is converted into heat which raises the temperature of the battery. There are four main energy losses during the operation of lithium-ion batteries: reaction heat Q_r, polarization heat Q_p, joule heat Q_j, and side reaction heat Q_s. The total heat generated by the battery can be expressed as

$$Q=Q_r+Q_p+Q_j+Q_s$$

(1)

where $Q_r$ is the heat generated by reversible electrochemical reaction inside the battery. $Q_p$ is the heat generated by the polarization reaction of the battery. $Q_j$ is the heat generated by the internal resistance of the battery. $Q_s$ is the heat generated by side reactions, self-discharge and other phenomena inside the battery.

(1)

Heat of reaction $Q_r$

The heat of reaction refers to the heat change caused by the movement of lithium ions between the positive and negative electrodes of the battery during the process of charging and discharging. This electrochemical reaction is reversible. When the battery is charged, it is negative; when the battery is discharged, the value is positive. The heat of reaction can be calculated by the following formula:

$$Q_r={\displaystyle \frac{nMQI}{mF}}$$

(2)

where F is the Faraday constant. I is the current during charging and discharging. n indicates the number of batteries. m is the electrode mass. M is the molar mass.

When the temperature of lithium-ion battery is lower than 70 °C, Joule heat and polarization heat are the main sources of heat of the battery, and the reaction heat is very small, accounting for only about 1% of the total heat of the battery. Under normal circumstances, the working temperature of the battery pack of pure electric vehicles is within 0~45 °C, and working conditions above 70 °C rarely occur. Therefore, when calculating the total calorific value of the battery, the reaction heat can be ignored.

(2)

Polarized heat $Q_p$

With the increase in the number of cycles of lithium-ion batteries, the active material of the electrode degrades and produces internal resistance of polarization, which mainly includes ohmic resistance, concentration resistance, and electrochemical resistance. The heat of polarization is the heat generated by the internal resistance of polarization in the process of battery charging and discharging. The polarization heat is positive both during charging and discharging. The heat of polarization can be calculated by the following formula:

$$Q_p=I^2{R}_p=I^2\left(R_0+R_n+R_d\right)$$

(3)

where $R_p$ is the internal resistance of battery polarization. $R_0$ is the internal resistance of ohmic polarization. $R_n$ is the internal resistance of concentration range. $R_d$ is the internal resistance of electrochemical polarization.

(3)

Joule heat

Joule heat refers to the heat generated by the internal resistance of the battery in the process of charging and discharging. It is the main source of the heat of the battery, and it is positive whether in the process of charging or discharging. Joule heat can be calculated by the following formula:

$$Q_j=I^2{R}_{\mathsf{\Omega }}$$

(4)

where R_Ω is the ohmic internal resistance of a single battery.

(4)

Heat of secondary reaction Q_s

When the lithium-ion battery overcharge and overdischarge phenomenon occurs, the battery will have a side reaction phenomenon; that is, the electrode material of the battery will decompose because of self-discharge, electrolyte will decompose at high temperature, and the heat generated by this is called the side reaction heat. However, because battery overcharge and overdischarge conditions rarely occur, and the calorific value of the auxiliary reaction heat is very small, the auxiliary reaction heat can be ignored in the calculation of the total calorific value of the battery.

Based on the above analysis, the total heat generated by the battery can be considered as

$$Q=Q_r+Q_p=I^{2}r=I^2\left(r_{\mathsf{\Omega }}+r_p\right)$$

(5)

where r is the total resistance of the battery, which can be considered as the sum of the ohmic internal resistance r_Ω and the polarization internal resistance r_p.

3.2.2. Heat Exchanger Model

In order to simplify the thermodynamic model of the heat exchanger, the heat transfer coefficient and pressure drop are determined by the following assumptions: (1) Chiller’s heat dissipation to the surrounding environment can be ignored. (2) The change in kinetic energy and potential energy of the fluid can be ignored. (3) There is no heat source or water tank in Chiller’s wall or cooling medium. (4) Fluid temperature is uniform across the cross-section of the flow. (5) Chiller’s surface efficiency is balanced and stable.

The heat transfer process of the heat exchanger can be calculated according to the heat transfer model of two fluids flowing through the inter-wall heat exchanger. The calculation method is as follows:

$$Q=m_A{C}_{P_A}\left(T_{Ao}-T_{Ai}\right)=m_B{C}_{P_B}\left(T_{Bo}-T_{Bi}\right)={\displaystyle \frac{∆T_m}{R}}$$

(6)

where $m_A$ is the mass flow rate of the fluid in channel A. $C_{P_A}$ is the specific heat capacity of the fluid in channel A. $T_{Ao}$ is the cold liquid temperature at the outlet of runner A. $T_{Ai}$ is the cold liquid temperature at the entrance of runner A. $m_B$ is the mass flow rate of the fluid in channel B. $C_{P_B}$ is the specific heat capacity of the fluid in channel B. $T_{Bo}$ is the cold liquid temperature at the exit of runner B. $T_{Bi}$ is the cold liquid temperature at the entrance of runner B.

The logarithmic mean temperature difference in the heat transfer process is calculated by the following formula:

$$∆T_m={\displaystyle \frac{∆T_{max}-∆T_{min}}{In\frac{∆T_{max}}{∆T_{min}}}}={\displaystyle \frac{{(T}_{Ai}-T_{Bo})-\left(T_{Ao}-T_{Bi}\right)}{In\frac{T_{Ai}-T_{Bo}}{T_{Ao}-T_{Bi}}}}$$

(7)

The total thermal resistance of the heat transfer process can still be written as the heat resistance of the fluid on both sides of the wall and the thermal resistance of the wall itself in series. The calculation is as follows:

$$R={\displaystyle \frac{1}{n{A}_p}}\left({\displaystyle \frac{1}{h_A}}+{\displaystyle \frac{\delta }{\lambda }}+{\displaystyle \frac{1}{h_B}}\right)$$

(8)

where $A_p$ is the single-layer heat transfer area of the plate heat exchanger. n is the number of heat exchanger layers. $h_A$ is the convective heat transfer coefficient of the fluid in channel A. $h_B$ is the convective heat transfer coefficient of the fluid in channel B. δ is the thickness of the heat exchanger wall. λ is the thermal conductivity of the heat exchanger material.

3.2.3. Compressor Model

The compressor selected in this paper is a scroll compressor. A mathematical model according to the following isoentropy-efficiency formula is established:

$${\eta }_s=0.85-0.046667\theta$$

(9)

where $\theta$ is the compressor rotation angle.

In addition, the relationship between suction and exhaust temperatures by using the polytropic equation of ideal adiabatic isentropic compression and assuming the ideal state of compressor suction is as follows:

$${\displaystyle \frac{T_{discharge}}{T_{suction}}}=1+{\displaystyle \frac{1}{{\eta }_s}}({\theta }^{1-\left(1-\gamma \right)}-1)$$

(10)

where $\gamma$ is the compressor pressure ratio.

3.2.4. Thermal Expansion Valve Model

In the system, the thermal expansion valve is described as a throttling hole. Since the sum of kinetic and potential energy between the inlet and outlet and the heat transfer between the two changes very little, the expansion of the liquid from condensing pressure to evaporation pressure is generally considered to be isoenthalpy, and the corresponding flow rate can be expressed as

$$m_{ref}=C_{txv}{A}_{txv}\sqrt{(P_{txv,i}-P_{txv,o})/V_{txv,i}}$$

(11)

$P_{txv,i}$ and $P_{txv,o}$ are, respectively, the inlet and outlet pressure of the valve, and $A_{txv}$ is the flow cross-sectional area, which can be calculated by the following formula:

$$A_{txv}={\displaystyle \frac{k_A}{\sqrt{2}{C}_{txv}}}$$

(12)

$k_A$ is the characteristic parameter of thermal expansion valve related to evaporation temperature, $C_{txv}$ is the valve flow coefficient modified by the experiment, and their expressions are, respectively,

$$k_A=5.367\times {10}^{-5}+1.358\times {10}^{-7}{T}_{evaporating}$$

(13)

$$C_{txv}=0.187+4.84\times {10}^{-7}{P}_{txv,i}-0.579{\chi }_{txv,o}$$

(14)

where ${\chi }_{txv,o}$ is the refrigerant flow rate at the valve outlet.

3.3. Thermal Management System Model Validation

After setting the system model parameters, the constructed model system is verified. In the experiment, the pressure and temperature of the system are the easiest to measure, so the two parameters are mainly verified by the simulation model.

The temperature variation curves of the coolant at the inlet and outlet of the battery during the test and simulation are shown in Figure 6 and Figure 7, respectively. It can be seen that after the car starts, the initial temperature of the coolant is 40 °C. Because the battery uses a heat exchanger and air-conditioning circuit refrigerant for heat exchange, the battery inlet coolant quickly drops from 40 °C to near 25 °C. After cooling the battery, the temperature of the outlet coolant of the battery decreases from 40 °C to near 29 °C. After 1500 s WLTC enters the high-speed condition, the heat production of the battery increases, the speed of the pump increases, and the heat exchange between the battery coolant and the refrigerant increases, so that the temperature of the coolant at the inlet and outlet of the battery decreases. By comparing the test and simulation curves, the difference between the temperature curve of the inlet and outlet coolant of the battery in the simulation model and that of the real car is small. The simulation model basically reflects the cooling process of the battery in the real car.

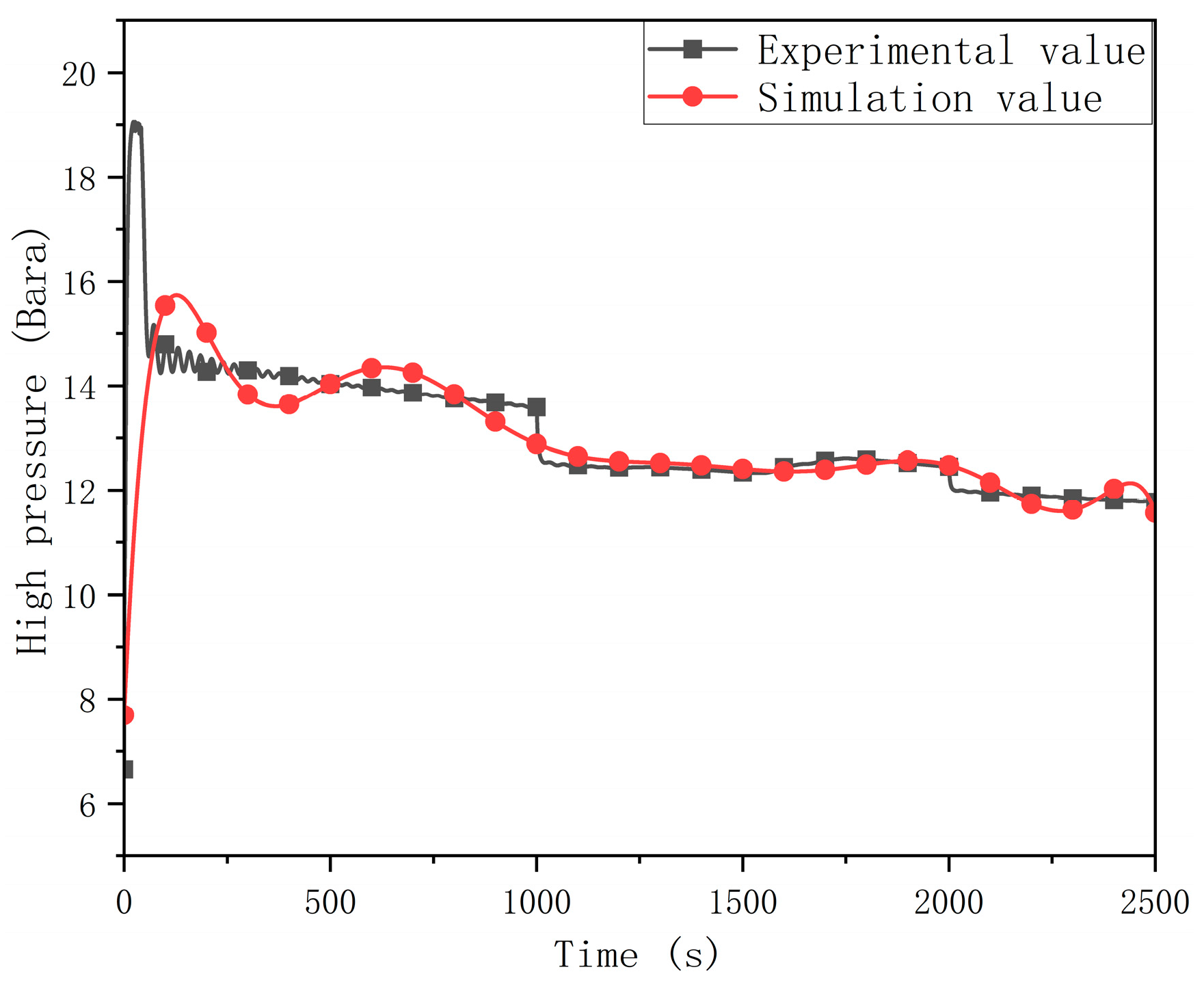
In the process of test and simulation, the pressure curves of the compressor inlet and outlet are shown in Figure 8 and Figure 9, respectively. In the initial stage, in order to cool the crew cabin and battery, the compressor speed rises rapidly, making the outlet pressure rise rapidly. In the 1500–2000 s period, the heat exchange between the battery and the refrigerant increases, and the compressor outlet pressure increases. By comparing the two curves, it can be seen that the variation trend and value of the compressor speed curve of the simulation model are similar to those of the real vehicle. It shows that the simulation model basically reflects the actual operation of the compressor.

4. Model Predictive Controller Modeling

There are three key parts in the realization of MPC, which are the prediction model, rolling optimization and feedback correction. Based on the above three elements, the basic principle of MPC is shown in Figure 10.

The model predictive control block diagram is shown in Figure 11, including an MPC controller, controlled object and state estimator. The controlled object in this paper is the battery-cooling system. The system is modeled in state space as the model of MPC. Then, through model prediction, objective function, and constraint optimization solution, the optimal pump speed of the battery circuit at the current time is obtained. The optimal results are input into the actual AMEsim physical model. Then the simulation value of the battery temperature is input to the MPC controller, and the optimization solution is carried out again to obtain the control sequence for a period of time in the future and the continuous online cycle.

In this paper, the MPC controller is constructed in the form of a state-space equation. The model needs to be discretized. Considering the interference factors of other external environments, the discrete state-space model of the system is shown as follows:

$${x\left(k+1\right)=Ax\left(k\right)+B}_{u}u\left(k\right)+B_{d}v\left(k\right)$$

(15)

$$y\left(k\right)=Cx\left(k\right)$$

(16)

where x(k+1), x(k), u(k), v(k), and y(k), respectively, represent the state quantity at the moment k+1 and the state variable, input variable, measurable disturbance variable, and output variable at the moment k. A, B_u, B_d, and C are, respectively, the state matrix, input matrix, measurable interference matrix, and output matrix.

In this paper, the battery-cooling system is modeled based on the state-space equation as the controlled object. The state-space equation of the battery-cooling system is regarded as a black box model. The system matrix A and the control matrix B are regarded as unknown parameters, and the output matrix C is the unit matrix. After selecting the input, output, and state quantity of the state-space equation, the parameters of the corresponding matrix can be obtained through the parameter identification toolbox of MATLAB/Simulink 2022 driven by the test data.

$$\left[\dot{\begin{array}{c}{x}_1\\ \dot{\begin{array}{c}{x}_2\\ \dot{\begin{array}{c}{x}_3\\ \dot{\begin{array}{c}{x}_4\\ \dot{x_5}\end{array}}\end{array}}\end{array}}\end{array}}\right]=\left(\begin{array}{ccccc}{a}_1& a_2& a_3& a_4& a_5\\ a_6& a_7& a_8& a_9& a_{10}\\ a_{11}& a_{12}& a_{13}& a_{14}& a_{15}\\ a_{16}& a_{17}& a_{18}& a_{19}& a_{20}\\ a_{21}& a_{22}& a_{23}& a_{24}& a_{25}\end{array}\right)\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\\ x_4\\ x_5\end{array}\right]+\left(\begin{array}{ccccc}{b}_1& b_2& a_3& a_4& a_5\\ b_6& b_7& a_8& a_9& a_{10}\\ b_{11}& b_{12}& a_{13}& a_{14}& a_{15}\\ b_{16}& b_{17}& a_{18}& a_{19}& a_{20}\\ b_{21}& b_{22}& a_{23}& a_{24}& a_{25}\end{array}\right)\left[\begin{array}{c}{u}_1\\ u_2\\ u_3\\ u_4\\ u_5\end{array}\right]$$

(17)

$$\left[\begin{array}{c}{y}_1\\ y_2\\ y_3\\ y_4\\ y_5\end{array}\right]=\left(\begin{array}{ccccc}1& 0& 0& 0& 0\\ 0& 1& 0& 0& 0\\ 0& 0& 1& 0& 0\\ 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 1\end{array}\right)\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\\ x_4\\ x_5\end{array}\right]$$

(18)

Combined with measurable data collection, external controls or influences on the battery-cooling system, such as pump speed, compressor speed, vehicle speed, and ambient temperature, are selected as input variables. After several parameter selections and comparison of the subsequent identification results, in this paper, the state-space equation of five states and five inputs is selected as the system model for high-temperature heat pump air conditioning. Among them, battery temperature, crew cabin temperature, air-conditioning compressor high and low pressure, and battery outlet temperature represent the state quantities. Pump speed, compressor speed, vehicle speed, battery inlet water temperature, and ambient temperature are used as input. The output matrix is the unit matrix, which directly outputs the state quantity of the system. The state-space model expression of the battery-cooling system is shown in Formulas (17) and (18).

The Simulink model to be identified is shown in Figure 12. Plant is the equation of state space to be identified, and its parameters are set as variables of the workspace. Matrices A and B are square matrices of order 5, with 50 unknown parameters to be identified.

The state-space equation of the heat pump system after parameter identification is shown in Equations (19) and (20).

$$A=\left(\begin{array}{ccccc}-2.897e-09& -8.411e-04& -4.352e-03& 6.664e-05& 9.580e-04\\ -4.293e-05& 0& 1.629e-03& 6.075e-04& 3.631e-03\\ -2.221e-03& -8.195e-06& 2.291e-09& 0& 0\\ 5.683e-14& 1.037e-13& 2.411e-14& 1.774e-10& 5.039e-14\\ 0& 0& 0& 0& 0\end{array}\right)$$

(19)

$$B=\left(\begin{array}{ccccc}4.577e-06& 1.964e-05& 2.253e-04& -7.614e-03& 4.991e-03\\ 9.176e-05& -1.047e-04& 4.508e-06& -7.706e-03& 4.986e-03\\ 4.539e-05& -1.677e-05& 1.258e-04& -1.849e-03& 3.114e-03\\ 4.918e-13& 2.695e-12& 2.104e-14& 4.383e-14& 6.944e-14\\ 0& 0& 0& 0& 0\end{array}\right)$$

(20)

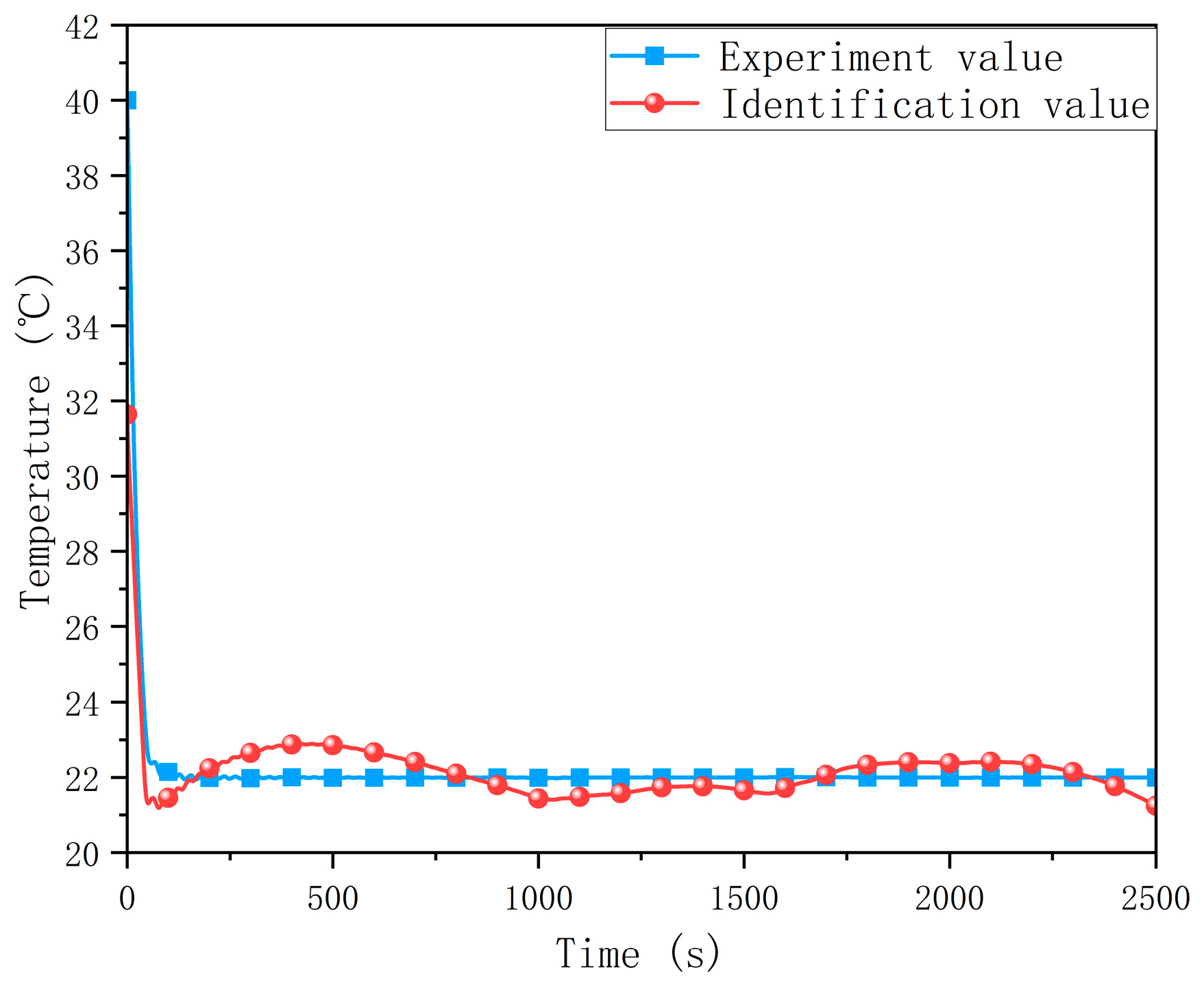
The comparison between the output results of parameter identification and the test data is shown in Figure 13, Figure 14, Figure 15 and Figure 16. The MRE (mean relative error) between the battery temperature parameter identification and the test data is 1.08%. The MRE of the cockpit temperature parameter identification and the test data is 2.00%. The MRE of the system high pressure parameter identification and the test data is 1.77%. The MRE of the low-pressure parameter identification and the test data is 1.02%. Although the data of the parameter identification curve has a large mutation in some moments, the overall trend of change is the same as that of the test data. It has a good identification accuracy. State-space equation modeling can well reflect the actual performance of the actual battery-cooling system under high-temperature refrigeration conditions. Therefore, in the rest of the paper, the identified state-space equation is used as the control model to design the MPC controller.

Based on the identified state-space equation, it is used as the controlled object plant of the battery-cooling system. The controller parameters are adjusted through the MPC method. Then the state-space equation is replaced by the built model as the controlled object.

5. Results and Analysis

Real-time calculation is carried out based on the compressor speed, vehicle speed, outlet temperature of the battery-cooling loop, and ambient temperature. The co-simulation model is shown in Figure 17. Figure 17 contains the MPC model, co-simulation model, and thermal management model. The time step was carefully selected as 0.1 s through sensitivity analysis to balance computational efficiency and control accuracy. This setting ensures stable convergence while capturing the battery’s dynamic characteristics.

To verify the MPC scheme, the simulation results are compared with those of ON-OFF, PID, and fuzzy control strategies. The simulation conditions are all the same, the initial temperature is 40 °C, and the operating condition is WLTC.

Figure 18 below shows the pump speed curves of the battery loop using various control strategies. The temperature limit set by various control strategies is 28 °C. In the initial stage of simulation, for ON-OFF, PID, and fuzzy, the control pump speed is 800 rev/min; only the pump speed controlled by MPC is around 780 rev/min. Because the battery temperature reached the set offline temperature of 28 °C after 400 s under ON-OFF control, and the battery temperature did not reach the set upper temperature of 38 °C in the later time, the rotational speed was always 0 after 400 s. The PID control brings the pump speed down from 800 rev/min to near 200 rev/min. Because of the increase in battery heat, the PID controller controls the pump speed up to 420 rev/min, and the pump speed also decreases in the high-speed condition. The fuzzy control pump speed in the vicinity of 400 s from 800 rev/min drops quickly down to 0. Then with the working conditions moving into high-speed conditions, the pump speed rises. After running in a WLTC condition, the speed drops and the speed of the pump drops rapidly. Among the four strategies controlled by MPC, the speed of the battery water pump decreases first, and the speed remains at the lowest value between 500 and 1000 s. The speed begins to enter the high-speed condition after 1000–1500 s, and the speed of the battery water pump starts to rise rapidly with the fastest rising rate. At 1500–150 s, the speed enters the overspeed condition. The rising pump speed is second only to fuzzy control.

Figure 19 below shows the pump energy consumption of the battery loop using various control strategies. The power of each control strategy varies with the trend of pump speed, and the ON-OFF control has the highest power consumption. The second is fuzzy control, which is 7.6% lower than ON-OFF power consumption. Third is PID control; its power consumption is 3.6% lower than fuzzy control. The MPC-controlled water pump has the lowest power consumption, 31.3% lower than PID.

Figure 20 below shows the battery temperature changes using various control strategies. ON-OFF controls the battery temperature to drop to 28 °C around 400 s. Because the pump stops running, the battery temperature fluctuates the most. The temperature of the PID-controlled battery overshot by about 0.5 °C from 500 s to 1500 s. The vehicle speed entered the overdrive condition between 1500 s and 1800 s, the heat production of the battery increased rapidly, and the temperature of the battery rose by 2 °C. Then, the vehicle speed decreased and the temperature of the battery gradually dropped as the second cycle came. Fuzzy control and MPC have the same trend of temperature change before 400 s. Before 1100 s, the temperature change of the fuzzy control and MPC battery are basically the same. Between 1100 s and 1250 s, the temperature is lower than that of MPC because the speed of the fuzzy control pump is higher. The fuzzy and MPC pump speeds are more sensitive, so they are more stable than the other two control effects.

The control effect of the four control strategies is analyzed comprehensively. The ON-OFF control effect is the worst and the energy consumption is the highest. Although the pump energy consumption of PID control is 3.6% lower than fuzzy control, the temperature fluctuation is 1 °C higher than fuzzy control. The pump controlled by MPC has the lowest power consumption, its response speed is similar to fuzzy control, and its energy consumption is 36% lower than fuzzy control. For energy consumption, battery temperature change, and pump response speed, three aspects of comprehensive analysis, the MPC controller’s effect is the best.

Figure 21 shows the thermal management system consumption with different control strategies. The ON-OFF control exhibited the highest energy consumption of 1.07 kWh. The MPC demonstrated superior energy consumption of 0.98 kWh, attributable to its predictive optimization and dynamic adjustment capabilities. The 8.4% reduction in energy use from ON-OFF to MPC underscores the importance of advanced control algorithms in sustainable thermal management.

6. Conclusions

The research focuses on a thermal management system for PHEV batteries. The whole process from thermal management scheme design to performance testing is elaborated. The control strategy of water pump in the battery circuit thermal management system is discussed in depth. In the research of this paper, the contents of innovation or practical significance include the following aspects:

(1) This paper combined vehicle thermal management and simulation modeling: the power battery, air-conditioning system, and other core components of the heat production principle are analyzed and derived. An integrated thermal management simulation model is established according to the above principles. The accuracy of the battery air-conditioning coupling model is verified by a real vehicle experiment, which provides convenience for the performance simulation analysis of thermal management systems by using the model.

(2) When establishing the model to predict the controller model, this paper used a parameter identification method to establish the state-space equation of battery-circuit and air-conditioning coupling, so as to test the control effect of the MPC controller. The process of MPC controller establishment is simplified. In comparison with the experimental data, the average relative errors of the identified state-space equation output battery temperature, cockpit temperature, and high and low pressure at the compressor inlet and outlet are 1.08%, 2.00%, 1.77%, and 1.02%, respectively.

(3) In this paper, MPC and ON-OFF, PID, and fuzzy control strategies are compared. The MPC and fuzzy control pump response speed is the fastest, while the battery temperature fluctuation is the least. The power consumption of the MPC pump is 36% lower than that of fuzzy control and 31.3% lower than PID control. Comprehensive analysis from three aspects—battery water pump response speed, power consumption, and battery temperature stability—shows that the MPC controller has the best control performance.