Collaborative Optimization Method of Structural Lightweight Design Integrating RSM-GA for an Electric Vehicle BIW
Abstract
1. Introduction
2. Methodology
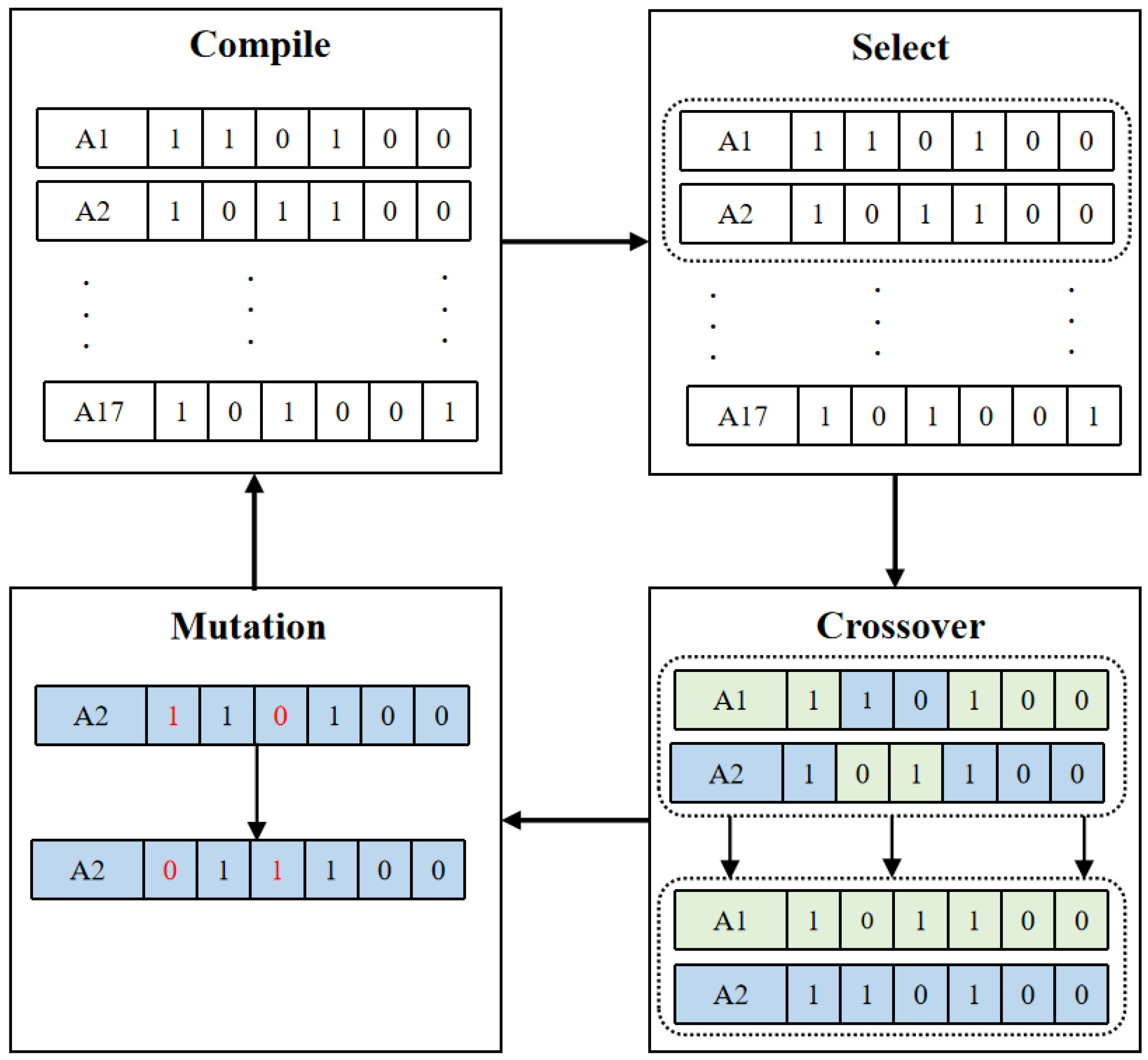
2.1. Genetic Algorithm
- (1)
- Selection operator: The selection operator is based on the fitness evaluation method. By inheriting the individuals with high fitness in the population, the selection operator can avoid gene loss and improve global convergence and computing efficiency. Commonly used methods include fitness proportional selection or Monte Carlo selection (shown in Formula (1)), best individual preservation, and the expected value method.In Formula (1): Pi—the probability of individual i being selected; Fi—fitness of individual i.
- (2)
- Crossover operator: The crossover operator is used in the genetic algorithm to generate new individuals, and two new chromosomes are generated through the exchange of several gene values on two chromosomes. The last three gene values of the two chromosomes are exchanged to produce two new chromosomes.
- (3)
- Mutation operator: Mutation operation simulates the mutation of natural genes, and the mutation in binary coding is to reverse the gene on some loci, replacing 0 with 1 or replacing 1 with 0.where represents the mutated gene value. is the lower limit value for the point of variation. denotes the upper limit value for the point of variation. r is a random number within the range of [0, 1] that conforms to a uniform probability distribution.
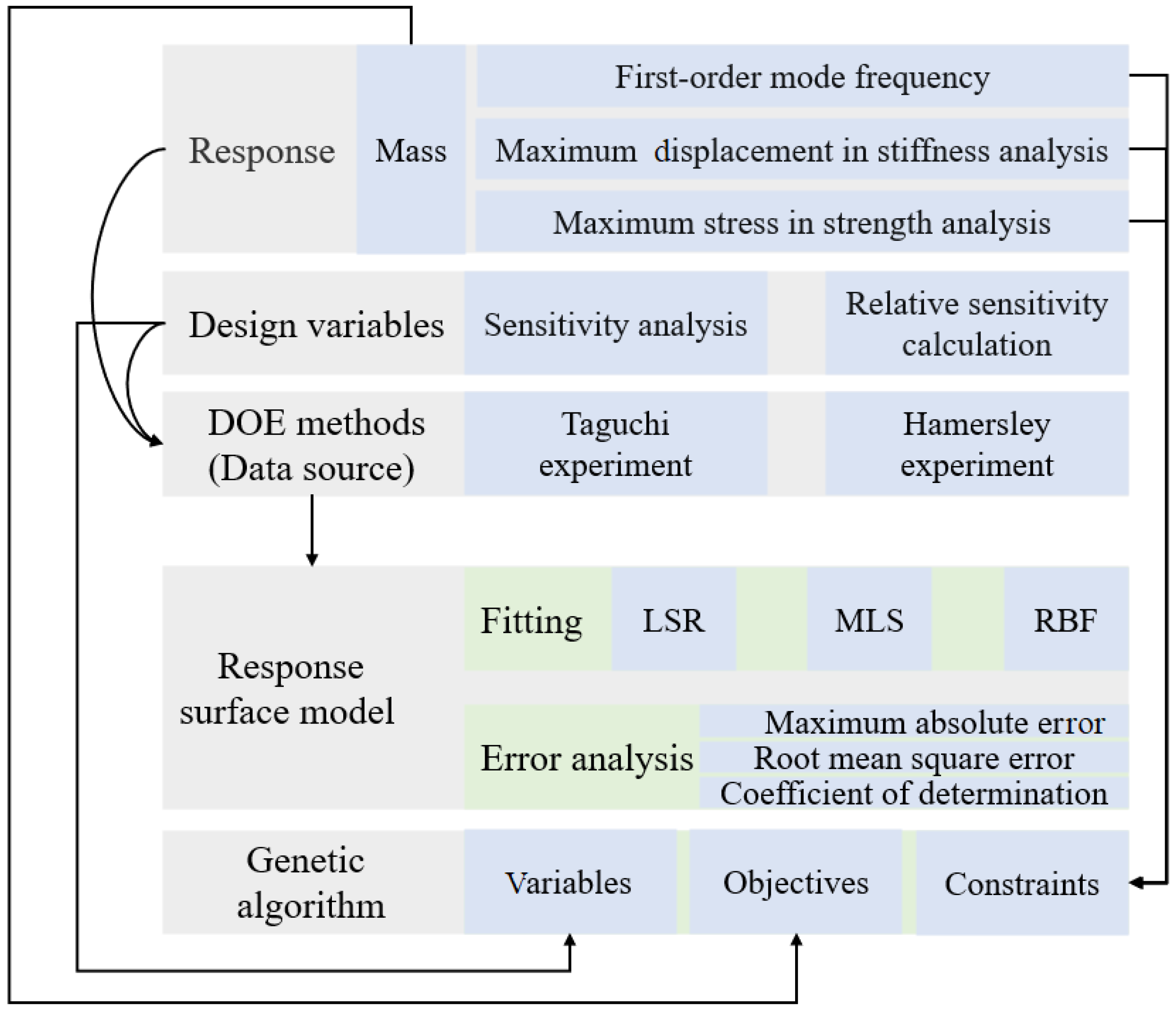
2.2. Genetic Algorithm Based on the Response Surface
3. Model Building and Analysis
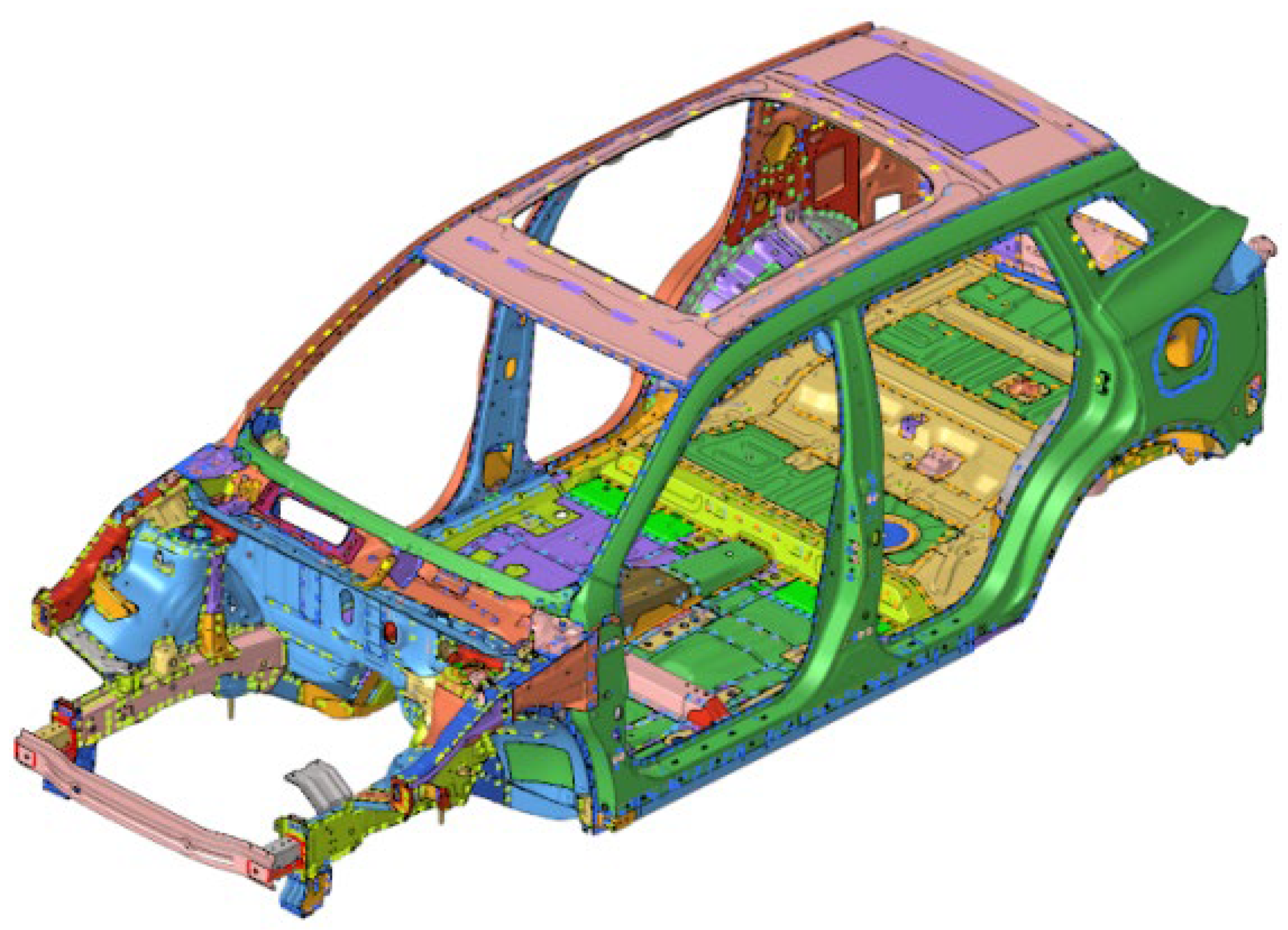
3.1. Model Building
3.2. Modal Analysis
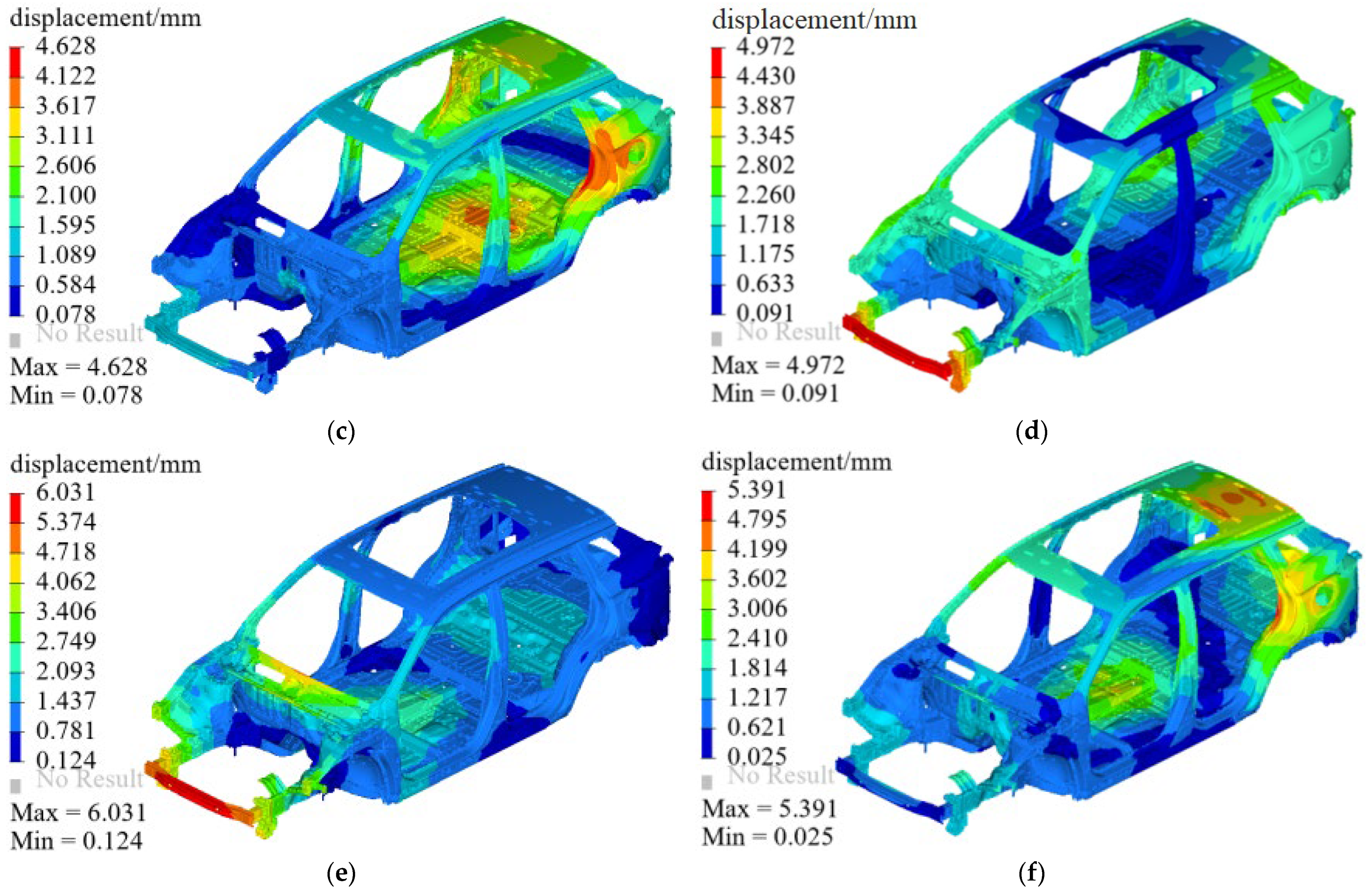
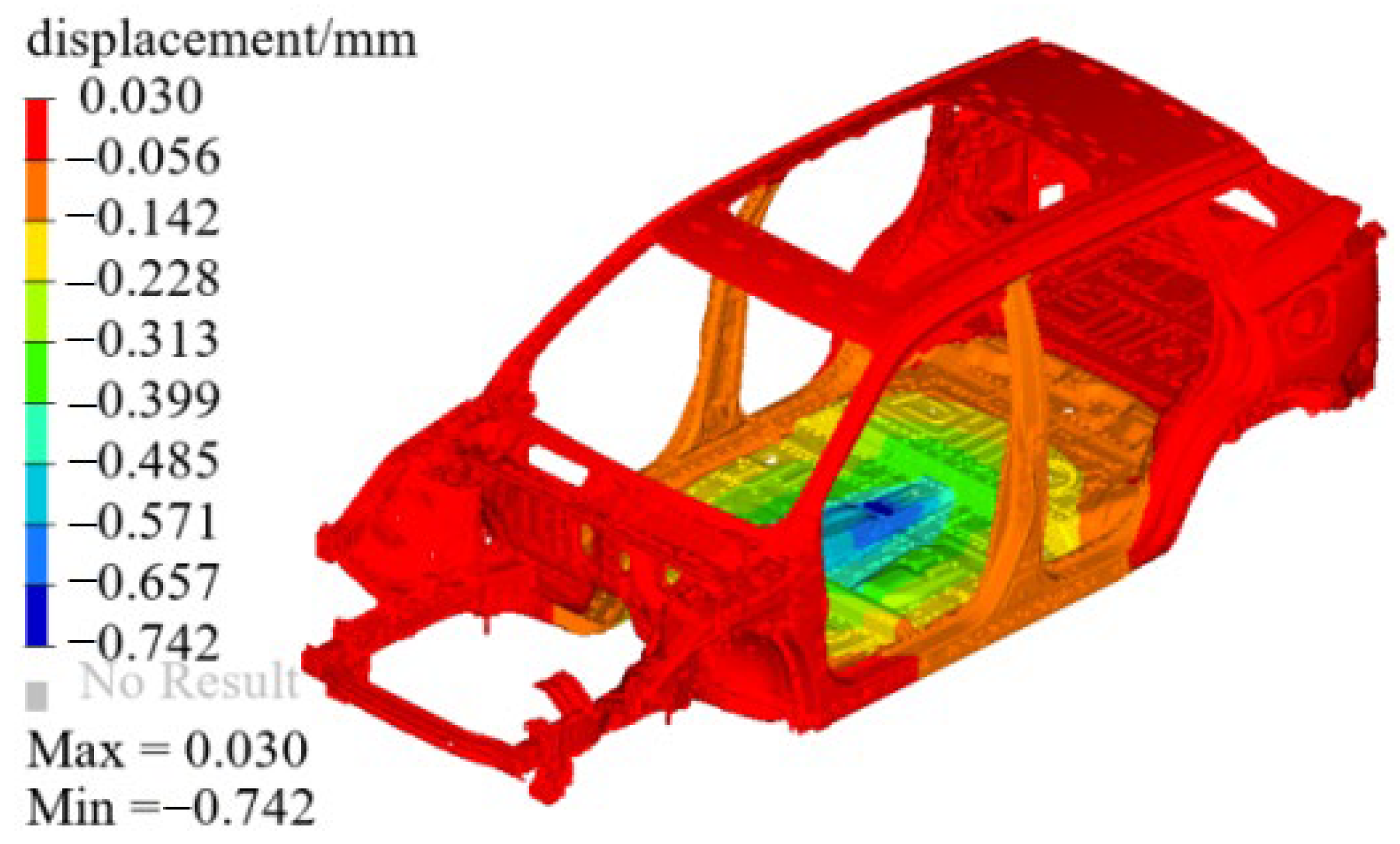
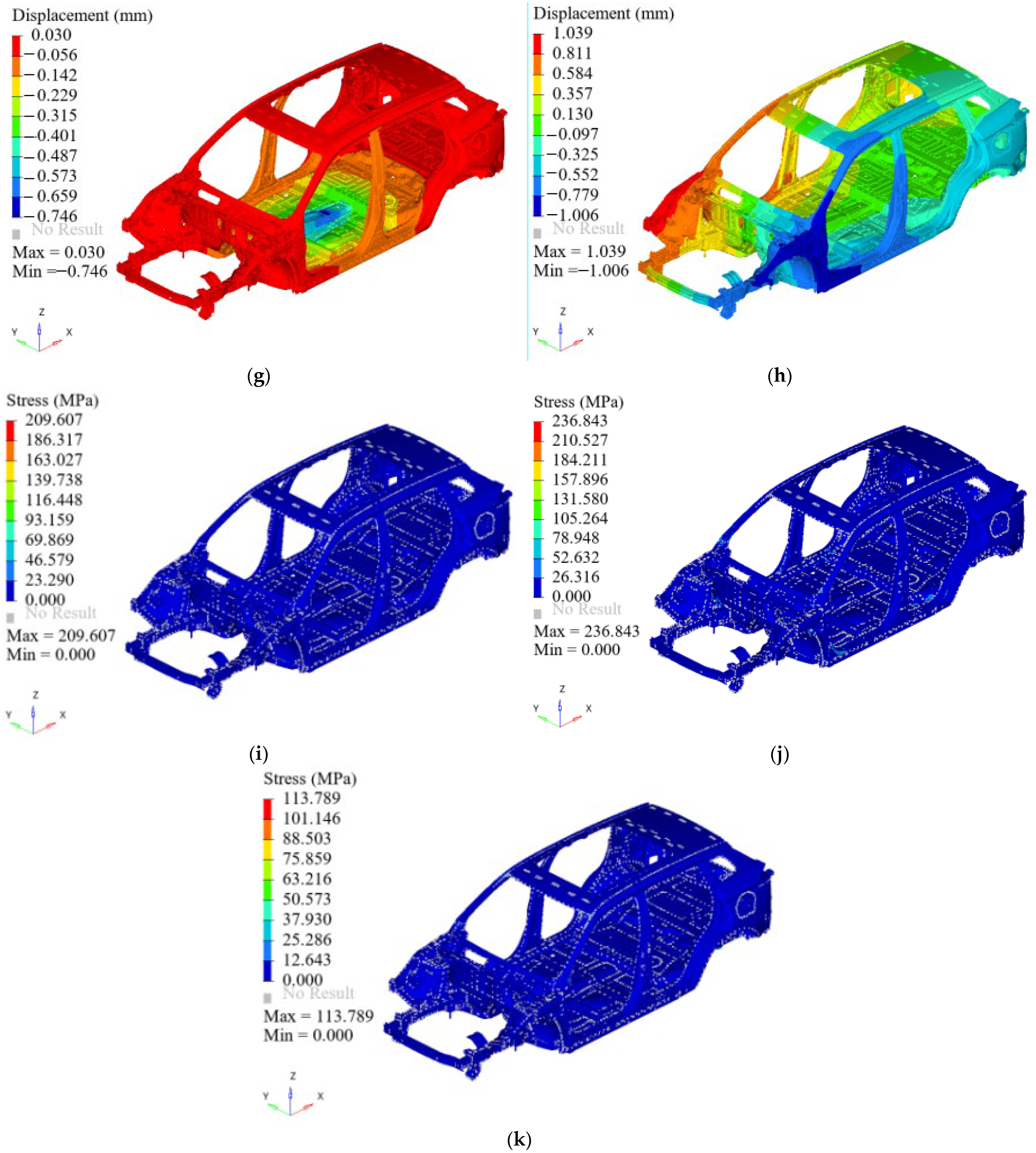
3.3. Stiffness Analysis
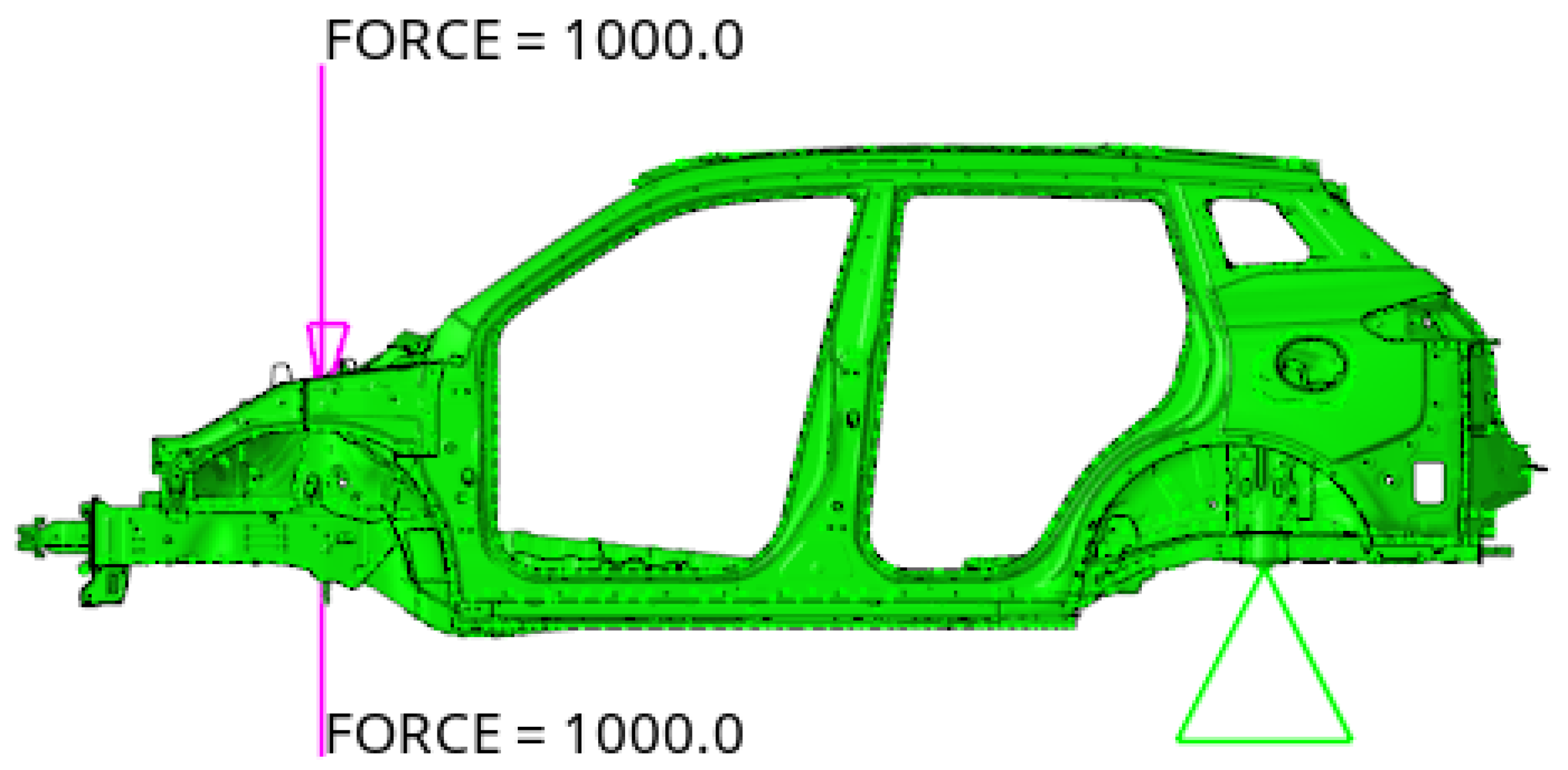
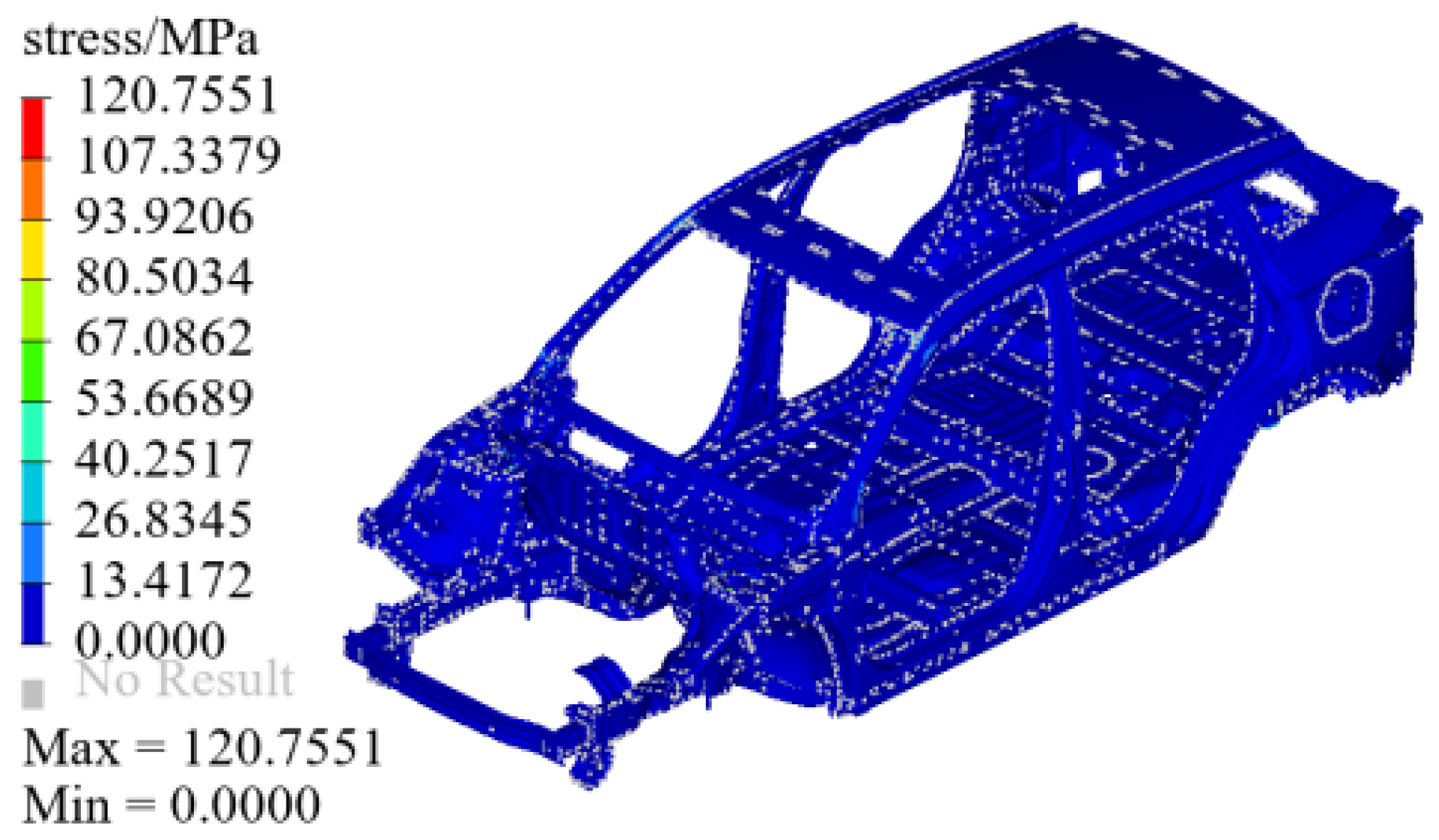
3.4. Analysis of Strength
4. Sensitivity Analysis and Relative Sensitivity Calculation
4.1. Sensitivity Analysis
4.2. Calculation of Relative Sensitivity
5. DOE Methods and Response Surface Creation
5.1. DOE Methods
- 1.
- Full factor experiment analyzes different factors at all levels to obtain all design schemes, which can most accurately analyze the influence of different factors on the response. The number of analyses of the full factor and the factor is level-dependent (as shown in Equation (3)). However, if the 17 factors in this subject are divided into three levels, too many experiments are not appropriate.In the formula: N—the number of experiments; n—the number of factor levels; m—the number of factors.
- 2.
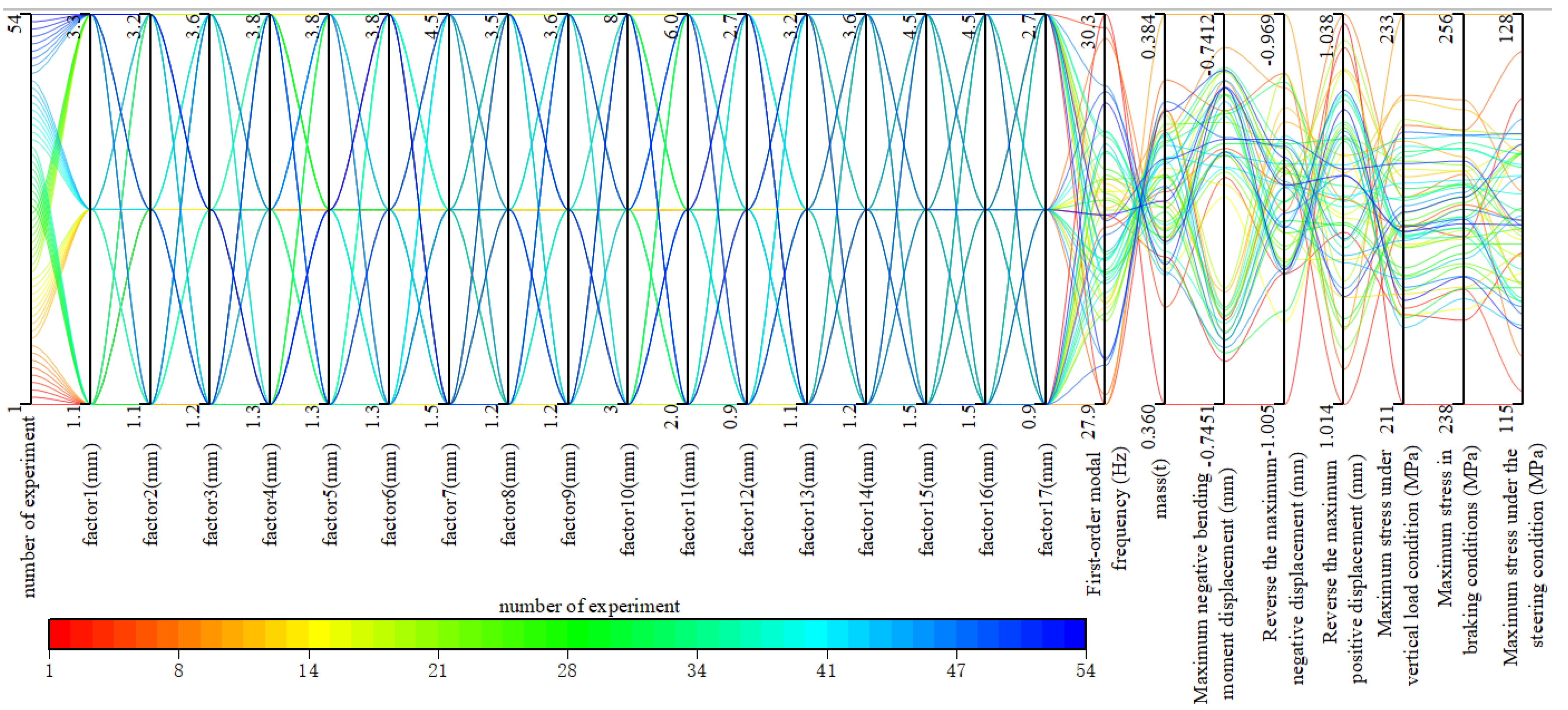
- The Taguchi experiment uses the orthogonal array to study the interaction effect of different factors at various levels [31]. In Japan, 80% of the quality improvement methods are through the Taguchi experiment method. Through this method, the sample points are evenly distributed, and the number of experiments is greatly reduced compared with the full factor. The Taguchi experiment was conducted for 54 experiments with 17 factors and three levels (as shown in Table 4). To analyze and understand the data from the Taguchi experiments, this paper uses parallel coordinate plots to describe the 54 experimental situations (as shown in Figure 17). The figure includes the complex cross-influences of 17 variables corresponding to eight responses. The 54 experiments are equivalent to 54 lines passing through these vertical coordinate axes, linking the changes in responses caused by the variables.
- 3.
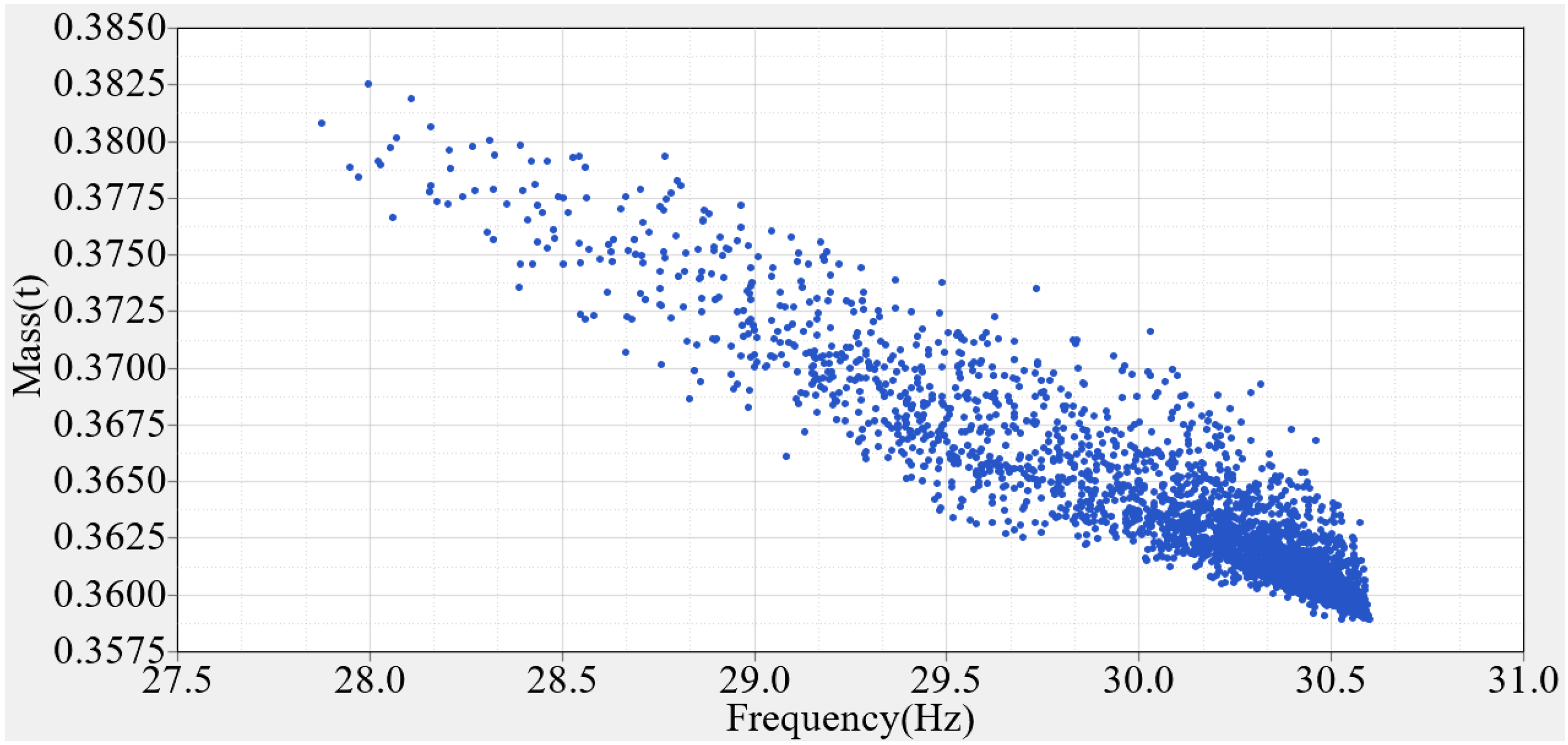
- Hammersley sampling is a super-uniformly distributed sampling method [32], which is represented by converting the original data into decimal numbers in the interval [0, 1]. Compared with the Latin hypercube experiment, the uniformity of the Hammersley experiment is better in processing the 189 experimental data collection (as shown in Figure 18).
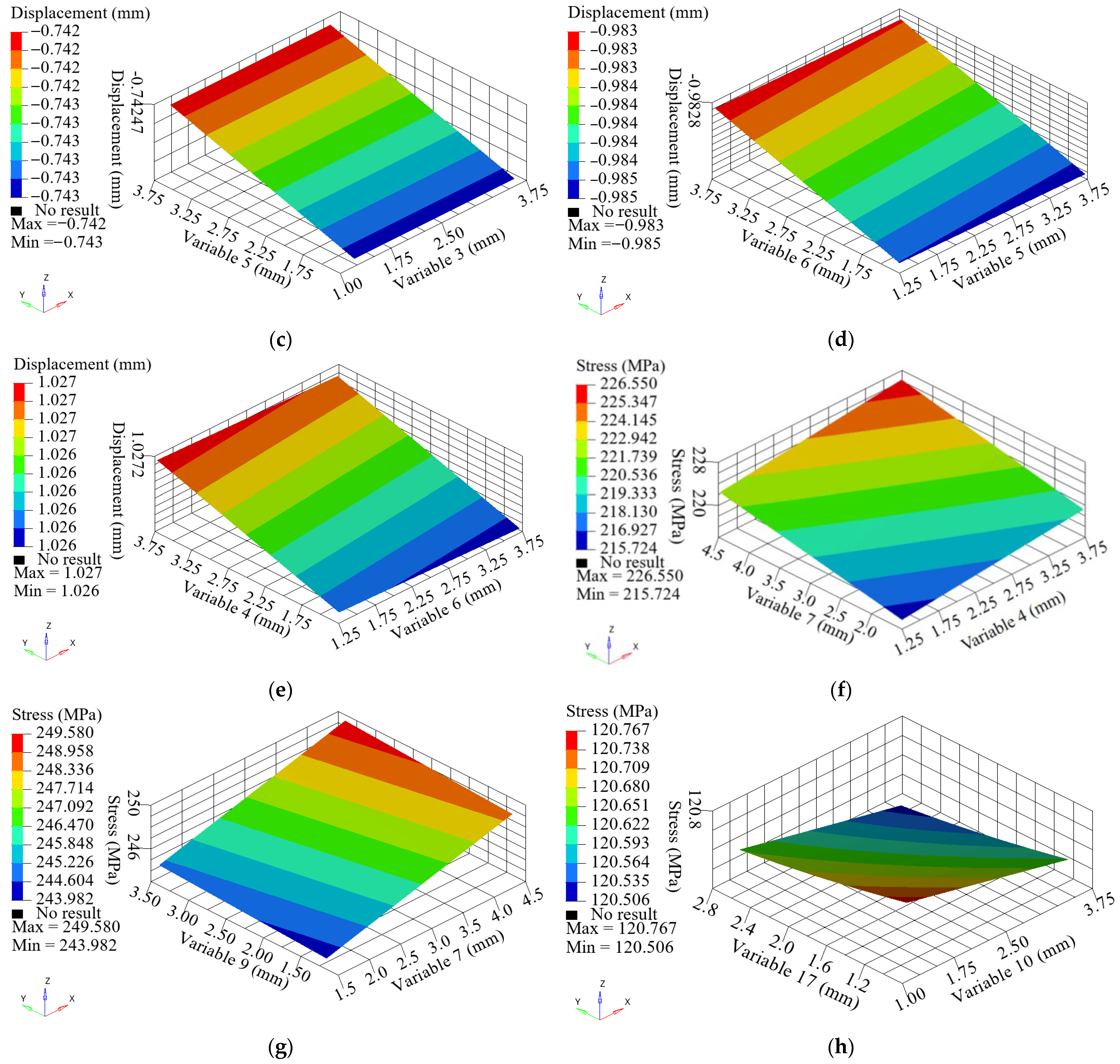
5.2. Create the Response Surface Model
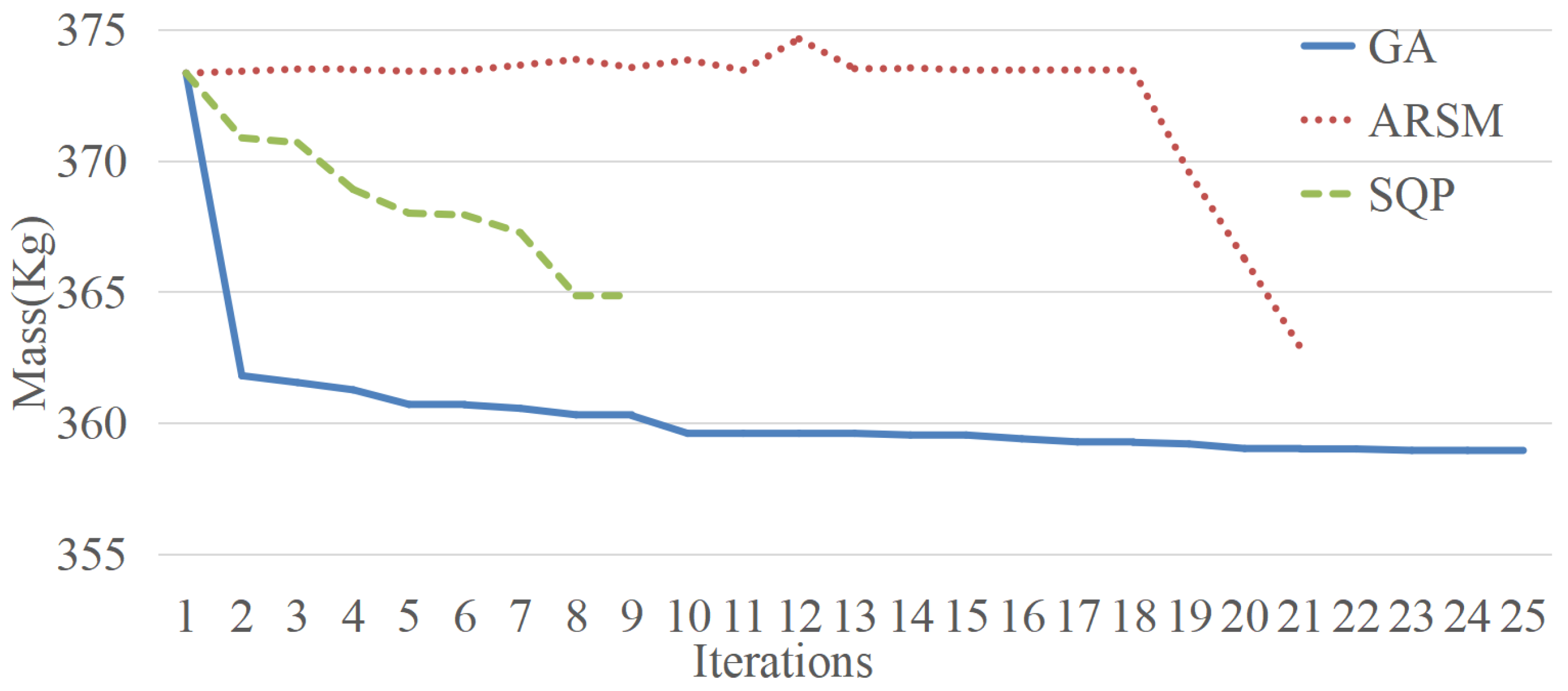
6. Results of Model Optimization
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wenlong, S.; Xiaokai, C.; Lu, W. Analysis of energy saving and emission reduction of vehicles using light weight materials. Energy Procedia 2016, 88, 889–893. [Google Scholar] [CrossRef]
- Haugen, M.J.; Paoli, L.; Cullen, J.; Cebon, D.; Boies, A.M. A fork in the road: Which energy pathway offers the greatest energy efficiency and CO2 reduction potential for low-carbon vehicles? Appl. Energy 2021, 283, 116295. [Google Scholar] [CrossRef]
- Shi, T.; Si, S.; Chan, J.; Zhou, L. The carbon emission reduction effect of technological innovation on the transportation industry and its spatial heterogeneity: Evidence from China. Atmosphere 2021, 12, 1169. [Google Scholar] [CrossRef]
- Xie, G.; Fu, B.; Li, H.; Du, W.; Zhong, Y.; Wang, L.; Geng, H.; Zhang, J.; Si, L. A gradient-enhanced physics-informed neural networks method for the wave equation. Eng. Anal. Bound. Elem. 2024, 166, 105802. [Google Scholar] [CrossRef]
- Martin, N.P.; Bishop, J.D.; Boies, A.M. How well do we know the future of Co2 emissions? Projecting fleet emissions from light duty vehicle technology drivers. Environ. Sci. Technol. 2017, 51, 3093–3101. [Google Scholar] [CrossRef]
- Zhong, Y.; Xie, G.; Geng, H.; Hou, J.; Zhao, D.; He, W. Thermal analysis for plate structures using a transformation BEM based on complex poles. Comput. Math. Appl. 2024, 161, 32–42. [Google Scholar] [CrossRef]
- Ito, K.; Sallee, J.M. The economics of attribute-based regulation: Theory and evidence from fuel economy standards. Rev. Econ. Stat. 2018, 100, 319–336. [Google Scholar] [CrossRef]
- Park, J.H.; Kim, S.K.; Choi, B.I.; Lee, H.J.; Lee, Y.H.; Kim, J.S.; Kim, K.J. Optimal design of rear chassis components for lightweight automobile using design of experiment. Mater. Werkst. 2010, 41, 391–397. [Google Scholar] [CrossRef]
- Bastien, C.; Christensen, J.; Blundell, M.V.; Kurakins, J. Lightweight Body in White Design Using Topology-, Shape-and Size Optimisation. World Electr. Veh. J. 2012, 5, 137–148. [Google Scholar] [CrossRef]
- Kiani, M.; Shiozaki, H.; Motoyama, K. Simulation-based design optimisation to develop a lightweight body-in-white structure focusing on dynamic and static stiffness. Int. J. Veh. Des. 2015, 67, 219–236. [Google Scholar] [CrossRef]
- Duan, L.; Liu, X.; Xu, W.; Xu, D.; Shi, L.; Jiang, H. Thickness-based subdomian hybrid cellular automata algorithm for lightweight design of BIW under side collision. Appl. Math. Model. 2022, 102, 170–193. [Google Scholar] [CrossRef]
- Topac, M.M.; Karaca, M.; Aksoy, B.; Deryal, U.; Bilal, L. Lightweight design of a rear axle connection bracket for a heavy commercial vehicle by using topology optimisation: A case study. Mechanics 2020, 26, 64–72. [Google Scholar] [CrossRef]
- Hong, N.P.; Youngdoo, K.; Young, C. Lightweight design with metallic additively manufactured cellular structures. J. Comput. Des. Eng. 2022, 9, 155–167. [Google Scholar] [CrossRef]
- Xiong, F.; Wang, D.; Ma, Z.; Chen, S.; Lv, T.; Lu, F. Structure-material integrated multi-objective lightweight design of the front end structure of automobile body. Struct. Multidiscip. Optim. 2018, 57, 829–847. [Google Scholar] [CrossRef]
- Güler, T.; Demirci, E.; Yıldız, A.R.; Yavuz, U. Lightweight design of an automobile hinge component using glass fiber polyamide composites. Mater. Test. 2018, 60, 306–310. [Google Scholar] [CrossRef]
- Lu, S.; Ma, H.; Xin, L.; Zuo, W. Lightweight design of bus frames from multi-material topology optimization to cross-sectional size optimization. Eng. Optim. 2019, 51, 961–977. [Google Scholar] [CrossRef]
- Zhou, B.; Chen, J.; Zhang, Y.; Yang, S.; Lu, H. Optimization of laser spiral welding using Response surface methodology and genetic algorithms. J. Intell. Fuzzy Syst. 2023, 45, 2381–2392. [Google Scholar] [CrossRef]
- Liu, Z.; Li, H.; Zhu, P. Diversity enhanced particle swarm optimization algorithm and its application in vehicle lightweight design. J. Mech. Sci. Technol. 2019, 33, 695–709. [Google Scholar] [CrossRef]
- Liao, S.; Zhong, L.; Yi, L. Enhancing Vehicle Lightweight Design Process with Genetic Algorithm-Optimized BP Neural Network and Topology Optimization: A Comprehensive Study. Preprint 2024. [Google Scholar] [CrossRef]
- Chen, Z.; Jia, P.; Fan, Y.; Liu, Z. Parameter analysis and optimization of friction pendulum bearings in underground stations based on genetic algorithm. J. Earthq. Eng. 2022, 26, 7814–7831. [Google Scholar] [CrossRef]
- Alateyah, A.I.; El-Taybany, Y.; El-Sanabary, S.; El-Garaihy, W.H.; Kouta, H. Experimental investigation and optimization of turning polymers using RSM, GA, hybrid FFD-GA, and MOGA methods. Polymers 2022, 14, 3585. [Google Scholar] [CrossRef]
- Li, Q.; Tu, G.; Zhang, X.; Cheng, S.; Yang, T. Application of a back propagation neural network model based on genetic algorithm to in situ analysis of marine sediment cores by X-ray fluorescence core scanner. Appl. Radiat. Isot. 2022, 184, 110191. [Google Scholar] [CrossRef]
- Vukadinović, A.; Radosavljević, J.; Đorđević, A.; Protić, M.; Petrović, N. Multi-objective optimization of energy performance for a detached residential building with a sunspace using the NSGA-II genetic algorithm. Sol. Energy 2021, 224, 1426–1444. [Google Scholar] [CrossRef]
- Appadurai, M.; Raj, E.F. Finite element analysis of composite wind turbine blades. In Proceedings of the 2021 7th International Conference on Electrical Energy Systems (ICEES), Chennai, India, 11–13 February 2021; pp. 585–589. [Google Scholar] [CrossRef]
- Viano, D.C.; White, S.D. Seat strength in rear body block tests. Traffic Inj. Prev. 2016, 17, 502–507. [Google Scholar] [CrossRef]
- Yoon, D.S.; Kim, G.W.; Choi, S.B. Response time of magnetorheological dampers to current inputs in a semi-active suspension system: Modeling, control and sensitivity analysis. Mech. Syst. Signal Process. 2021, 146, 106999. [Google Scholar] [CrossRef]
- Panaro, D.B.; Frunzo, L.; Mattei, M.R.; Luongo, V.; Esposito, G. Calibration, validation and sensitivity analysis of a surface-based ADM1 model. Ecol. Model. 2021, 460, 109726. [Google Scholar] [CrossRef]
- Owais, M.; Moussa, G.S. Global sensitivity analysis for studying hot-mix asphalt dynamic modulus parameters. Constr. Build. Mater. 2024, 413, 134775. [Google Scholar] [CrossRef]
- Idriss, L.K.; Owais, M. Global sensitivity analysis for seismic performance of shear wall with high-strength steel bars and recycled aggregate concrete. Constr. Build. Mater. 2024, 411, 134498. [Google Scholar] [CrossRef]
- Politis, S.N.; Colombo, P.; Colombo, G.; Rekkas, D.M. Design of experiments (DoE) in pharmaceutical development. Drug Dev. Ind. Pharm. 2017, 43, 889–901. [Google Scholar] [CrossRef]
- Patel, N.S.; Parihar, P.L.; Makwana, J.S. Parametric optimization to improve the machining process by using Taguchi method: A review. Mater. Today Proc. 2021, 47, 2709–2714. [Google Scholar] [CrossRef]
- Li, Q.; Zhao, N. Probabilistic power flow calculation based on importance-Hammersley sampling with Eigen-decomposition. Int. J. Electr. Power Energy Syst. 2021, 130, 106947. [Google Scholar] [CrossRef]
- Chelladurai, S.J.; Murugan, K.; Ray, A.P.; Upadhyaya, M.; Narasimharaj, V.; Gnanasekaran, S. Optimization of process parameters using response surface methodology: A review. Mater. Today Proc. 2021, 37, 1301–1304. [Google Scholar] [CrossRef]
- Long, T.; Wu, D.; Guo, X.; Wang, G.G.; Liu, L. Efficient adaptive response surface method using intelligent space exploration strategy. Struct. Multidiscip. Optim. 2015, 51, 1335–1362. [Google Scholar] [CrossRef]
- Lin, X.; Wang, Z.; Zeng, S.; Huang, W.; Li, X. Real-time optimization strategy by using sequence quadratic programming with multivariate nonlinear regression for a fuel cell electric vehicle. Int. J. Hydrogen Energy 2021, 46, 13240–13251. [Google Scholar] [CrossRef]















| Material Type | Application Unit | Elastic Modulus (MPa) | Poisson Ratio | Density (t/mm3) | Yield Strength (MPa) |
|---|---|---|---|---|---|
| B280VK steel | Supporting part | 207,000 | 0.3 | 7.83 × 10−9 | 280~420 |
| B340DP steel | Pillar A, pillar B and pillar C | 210,000 | 0.3 | 7.8 × 10−9 | 340~500 |
| DC01 steel | Flooring | 210,000 | 0.3 | 7.83 × 10−9 | ≥280 |
| DCO4 steel | Car cowl panel | 210,000 | 0.3 | 7.82 × 10−9 | ≥250 |
| B240ZK steel | Other sheet metal parts | 207,000 | 0.3 | 7.8 × 10−9 | 240~380 |
| Check Type | Display | Standard |
|---|---|---|
| Mesh edge length | Length | 7.5–20 mm |
| Jacobi | Jcaobin | >0.7 |
| Quadrilateral internal angle | Interior Angle Quad | 40°~135° |
| Triangular internal angle | Interior Angle Tria | 20°~120° |
| Skewness | Skewness | <60° |
| Aspect ratio | aspect ratio | 3 |
| Working Condition | Constrain | Load | ||||||
|---|---|---|---|---|---|---|---|---|
| Constraint Position | X | Y | Z | X | Y | Z | g | |
| Vertical impact | Left front suspension | ✓ | ✓ | ✓ | 0 | 0 | −3g | 9800 |
| Right front suspension | ✓ | ✓ | ||||||
| Left rear suspension | ✓ | ✓ | ||||||
| Right rear suspension | ✓ | |||||||
| Braking | Left front suspension | ✓ | ✓ | ✓ | −1g | −1g | 9800 | |
| Right front suspension | ✓ | ✓ | ✓ | |||||
| Left rear suspension | ✓ | ✓ | ||||||
| Right rear suspension | ✓ | ✓ | ||||||
| Steering direction | Left front suspension | ✓ | ✓ | ✓ | 1g | −1g | 9800 | |
| Right front suspension | ✓ | ✓ | ✓ | |||||
| Left rear suspension | ✓ | ✓ | ✓ | |||||
| Right rear suspension | ✓ | ✓ | ✓ | |||||
| Factor | 3 Levels (mm) | Initial Value (mm) | Factor | 3 Levels (mm) | Initial Value (mm) | ||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.1 | 2.2 | 3.3 | 2.2 | 10 | 1.2 | 2.4 | 3.6 | 2.4 |
| 2 | 1.05 | 2.1 | 3.15 | 2.1 | 11 | 2.5 | 5 | 7.5 | 5 |
| 3 | 1.2 | 2.4 | 3.6 | 2.4 | 12 | 2 | 4 | 6 | 4 |
| 4 | 1.25 | 2.5 | 3.75 | 2.5 | 13 | 0.9 | 1.8 | 2.7 | 1.8 |
| 5 | 1.25 | 2.5 | 3.75 | 2.5 | 14 | 1.05 | 2.1 | 3.15 | 2.1 |
| 6 | 1.25 | 2.5 | 3.75 | 2.5 | 15 | 1.5 | 3 | 4.5 | 3 |
| 7 | 1.5 | 3 | 4.5 | 3 | 16 | 1.5 | 3 | 4.5 | 3 |
| 8 | 1.2 | 2.4 | 3.6 | 2.4 | 17 | 0.9 | 1.8 | 2.7 | 1.8 |
| 9 | 1.15 | 2.3 | 3.45 | 2.3 | |||||
| Fitting Method | Formula Expression | Nonlinear Problem | Noise Effect | Fitting Accuracy | Fitting Efficiency |
|---|---|---|---|---|---|
| LSM | √ | × | √ | Medium | Fastest |
| MLS | × | √ | √ | Good | Faster |
| Kriging | × | √ | × | Best | Faster |
| RBF | × | √ | × | Best | Faster |
| Respond | Maximum Absolute Error | Root Mean Square Error | Coefficient of Determination (R2) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| A | B | C | A | B | C | A | B | C | |
| a | 3.01 × 10−7 | 8.23 × 10−7 | 7.57 × 10−7 | 1.21 × 10−7 | 3.53 × 10−7 | 2.88 × 10−7 | 1 | 1 | 1 |
| b | 0.0064 | 0.1269 | 0.0107 | 0.0020 | 0.0376 | 0.0028 | 0.999 | 0.995 | 0.999 |
| c | 6.20 × 10−5 | 2.43 × 10−4 | 7.50 × 10−5 | 2.52 × 10−5 | 9.11 × 10−5 | 2.79 × 10−5 | 0.998 | 0.992 | 0.998 |
| d | 3.78 × 10−4 | 0.0016 | 5.63 × 10−4 | 1.37 × 10−4 | 8.21 × 10−4 | 1.58 × 10−4 | 0.999 | 0.983 | 0.998 |
| e | 2.85 × 10−4 | 8.85 × 10−4 | 3.12 × 10−4 | 1.02 × 10−4 | 4.57 × 10−4 | 1.21 × 10−4 | 0.999 | 0.993 | 0.999 |
| f | 0.7984 | 1.6467 | 0.9647 | 0.0871 | 0.4176 | 0.1037 | 0.999 | 0.989 | 0.998 |
| g | 9.09 × 10−13 | 0.0499 | 0.0226 | 3.17 × 10−13 | 0.0211 | 0.0057 | 1 | 0.999 | 0.999 |
| h | 1.85 × 10−13 | 0.1102 | 0.0313 | 5.24 × 10−14 | 0.0396 | 0.0097 | 1 | 0.999 | 0.999 |
| The Initial Value (mm) | ARSM | GA | SQP | ||
|---|---|---|---|---|---|
| Design variable ID | 1 | 2.2 mm | 1.3 mm | 1.1 mm | 2.07 mm |
| 2 | 2.1 mm | 1.25 mm | 0.86 mm | 1.95 mm | |
| 3 | 2.4 mm | 1.42 mm | 0.96 mm | 2.26 mm | |
| 5 | 2.5 mm | 1.51 mm | 1 mm | 2.43 mm | |
| 6 | 2.5 mm | 1.48 mm | 1.27 mm | 2.41 mm | |
| 4 | 2.5 mm | 1.48 mm | 1.04 mm | 2.23 mm | |
| 7 | 3 mm | 1.78 mm | 1.35 mm | 2.63 mm | |
| 9 | 2.3 mm | 1.36 mm | 1.06 mm | 1.9 mm | |
| 8 | 2.4 mm | 1.42 mm | 0.97 mm | 0.96 mm | |
| 11 | 5 mm | 3.75 mm | 2.52 mm | 4.84 mm | |
| 12 | 4 mm | 2.37 mm | 1.6 mm | 1.6 mm | |
| 13 | 1.8 mm | 1.07 mm | 0.78 mm | 1.14 mm | |
| 14 | 2.1 mm | 1.25 mm | 0.95 mm | 1.42 mm | |
| 10 | 2.4 mm | 1.42 mm | 1.03 mm | 2.21 mm | |
| 15 | 3 mm | 1.78 mm | 1.43 mm | 2.84 mm | |
| 16 | 3 mm | 1.78 mm | 1.69 mm | 2.81 mm | |
| 17 | 1.8 mm | 1.44 mm | 2.64 mm | 1.85 mm | |
| Target | Mass (kg) | 373.34 | 362.9 | 359 | 364.9 |
| Constraint | First-order modal frequency (Hz) | 29.067 | 30.097 | 30.563 | 30.332 |
| Maximum negative-displacement in the Z-direction of bending stiffness (mm) | −0.742 | −0.744 | −0.7457 | −0.743 | |
| Maximum negative-displacement in the Z-direction of torsional stiffness (mm) | −0.983 | −0.998 | −1.006 | −0.995 | |
| Maximum positive-displacement of torsional stiffness in the Z direction (mm) | 1.025 | 1.034 | 1.039 | 1.037 | |
| Maximum stress under vertical load condition (MPa) | 221.201 | 211.9 | 209.6 | 214.9 | |
| Maximum stress under braking conditions (MPa) | 246.92 | 239.9 | 236.8 | 242.4 | |
| Maximum stress under steering conditions (MPa) | 120.755 | 116 | 113.8 | 115.4 | |
| The average accuracy rate of the simulation results compared to the optimized results | 99.98% | 99.84% | 99.97% | ||
| Quality variation (kg) | −10.44 kg | −14.34 kg | −8.44 kg | ||
| Initial Value | Results of Optimization | Effect of Optimization | Percentage of Optimized Results | |
|---|---|---|---|---|
| Total mass (kg) | 373.34 | 359 | −14.34 | −3.84% |
| First-order mode frequency (Hz) | 29.0677 | 30.56368 | 1.49598 | 5.14% |
| Bending stiffness (N/mm) | 25,014.07 | 24,830.84 | −183.23 | −0.73% |
| Torsional stiffness (N·m/°) | 22,410.39 | 22,041.63 | −368.76 | −1.64% |
| Maximum stress under vertical impact condition (MPa) | 221.201 | 209.6 | −11.601 | −5.24% |
| Maximum stress under braking conditions (MPa) | 246.92 | 236.8 | −10.12 | −4.09% |
| Maximum stress in steering condition (MPa) | 120.755 | 113.8 | −6.955 | −5.75% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Sun, S.; Fang, H.; Hu, X.; Hou, J.; Zhong, Y. Collaborative Optimization Method of Structural Lightweight Design Integrating RSM-GA for an Electric Vehicle BIW. World Electr. Veh. J. 2025, 16, 415. https://doi.org/10.3390/wevj16080415
Li H, Sun S, Fang H, Hu X, Hou J, Zhong Y. Collaborative Optimization Method of Structural Lightweight Design Integrating RSM-GA for an Electric Vehicle BIW. World Electric Vehicle Journal. 2025; 16(8):415. https://doi.org/10.3390/wevj16080415
Chicago/Turabian StyleLi, Hongjiang, Shijie Sun, Hong Fang, Xiaojuan Hu, Junjian Hou, and Yudong Zhong. 2025. "Collaborative Optimization Method of Structural Lightweight Design Integrating RSM-GA for an Electric Vehicle BIW" World Electric Vehicle Journal 16, no. 8: 415. https://doi.org/10.3390/wevj16080415
APA StyleLi, H., Sun, S., Fang, H., Hu, X., Hou, J., & Zhong, Y. (2025). Collaborative Optimization Method of Structural Lightweight Design Integrating RSM-GA for an Electric Vehicle BIW. World Electric Vehicle Journal, 16(8), 415. https://doi.org/10.3390/wevj16080415






