Adaptive and Collaborative Hierarchical Optimization Strategies for a Multi-Microgrid System Considering EV and Storage

Abstract

The disordered nature of electric vehicle (EV) charging and user electricity consumption behaviors has intensified the strain on the grid. Meanwhile, energy storage technologies and microgrid interconnections still lack effective supply–consumption regulations and cost–benefit optimization mechanisms. Therefore, the system’s operational efficiency holds significant potential for improvement. This paper proposes hierarchical optimization strategies for the multi-microgrid system to address these issues. In the lower layer, for the charging states of EVs in a single microgrid, an improved simulation method to enhance accuracy and a recursion mechanism of an energy storage margin band to facilitate intelligent EV-to-grid interaction are proposed. Additionally, in conjunction with demand management, an adaptive optimization method and a Pareto decision method are proposed to achieve optimal peak shaving and valley filling for both the EVs and load, yielding a 38.5% reduction in the total electricity procurement costs. The upper layer is built upon the EV–load management strategies of microgrids in the lower layers and evolves into a distributed interconnection structure. Furthermore, a dynamic optimization mechanism based on state mapping and a collaborative optimization method are proposed to improve storage benefits and energy synergies, achieving a 22.1% reduction in the total operating cost. The results provided demonstrate that the proposed strategy optimizes the operation of the multi-microgrid system, effectively enhancing the overall operational efficiency and economic performance.

1. Introduction

With the global energy transition accelerating toward a low-carbon and distributed structure, the rapid development of smart grid technologies has driven the evolution of power system load characteristics toward increased dynamism and complexity [1]. As a prominent example of novel loads, the large-scale integration of EV fleets and controllable loads not only reshapes the traditional, centralized demand side profile but also facilitates multi-layer buffering and regulation capabilities alongside energy storage systems. Meanwhile, cross-microgrid energy shares furnish new avenues for system-level resource optimization. Consequently, the requirements for EV scheduling, controllable load dispatch, storage management, and energy interconnection are intricately interwoven across both the temporal and spatial dimensions, and only their organic integration and coordinated optimization can better adapt to and integrate with the evolving demands of future energy systems, strengthening dynamic responsiveness and self-organizing capabilities, thereby improving the economic efficiency and environmental compatibility while maintaining safe and stable operations [2].

1.1. Literature Review

EV charging behavior is influenced by user habits and weather conditions, exhibiting randomness and intermittency in time and space. With the increasing penetration of EVs, their disordered charging behavior is disrupting the grid’s supply–consumption balance, load stability, power quality, and energy absorption, threatening the safe operation of the power system [3]. Existing prediction methods struggle to capture EVs’ complex and extreme charging patterns effectively. Although simulation methods, such as Monte Carlo simulations, have shown some progress, they still have limitations. For instance, reference [4] utilizes Monte Carlo simulations to estimate the driving and charging behaviors of EVs and simulate the charging power demand. However, the volatility introduced by random seeds and variables necessitates multiple simulations to obtain stable results, resulting in limited efficiency and accuracy. Reference [5] proposes a conditional Latin Hypercube simulation method, which improves sample representation and model training efficiency by incorporating conditions and constraints. However, this approach does not fully address the impact of multi-dimensional data on the simulation accuracy. Therefore, further advancements in simulation and prediction accuracy are necessary to address the complexities of EVs’ charging behavior.

The widespread adoption of EVs in power applications has introduced new energy storage characteristics to the power system while simultaneously increasing the complexity of microgrid systems’ load structure and functionality [6]. As a result, traditional demand-side management methods are facing unprecedented challenges [7]. Reference [8] proposes a two-tier optimization scheme to enhance resource and load flexibility, but it overlooks the impact of EVs as a new type of load. Reference [9] introduces photovoltaic and energy storage, considering the mobility of EVs for home energy management. However, it fails to fully account for the impact of complex load characteristics on the system. Therefore, further research is needed to explore how to leverage the energy storage potential of EVs and the flexibility of controllable loads in optimizing power dispatch, which will be crucial for ensuring the stable operation of the power system, improving resource utilization, and enhancing the economic efficiency of users.

The diversity, intermittency, and volatility of load demand and supply in microgrid systems pose significant challenges to maintaining the supply–consumption balance [10], leading to power curtailment, reverse overload, and frequent fluctuations [11]. To address these challenges, energy storage systems are introduced to enable the centralized management of source–grid–load–storage integration [12]. This approach effectively handles demand fluctuations and peak–valley loads, ensuring the power supply’s flexibility, continuity, and stability [13]. Reference [14] proposes an energy storage configuration method that utilizes wind and solar energy volatility to mitigate fluctuations in renewable energy output and enhance grid stability. However, it does not thoroughly explore the dynamic response characteristics or the cost-effectiveness of energy storage systems within the grid. Reference [15] analyzes the return on investment, medium- to long-term demand response strategy, and capacity allocation, but neglects to consider the real-time operational status of energy storage in integrated management systems. Furthermore, with the rapid advancement of energy internet technologies, traditional centralized management models increasingly reveal limitations regarding adaptability, flexibility, and timeliness. The concept of multi-grid interconnection for information cooperation and resource sharing is becoming more critical [16]. Despite this, energy storage equipment’s investment efficiency and resource utilization remain low. Therefore, new management approaches for the operation and configuration of energy storage, particularly within multi-grid interconnection environments, are crucial for enhancing resource utilization and economic efficiency [17].

This paper mainly addresses the research areas of integration and coordination at the multi-microgrid system level, where supply- and consumption-side optimization are tightly coupled across both temporal and spatial dimensions. Independent optimization often leads to resource inefficiency and grid instability; therefore, it is imperative to devise coordinated optimization strategies that integrate these elements organically to enhance operational efficiency and economic performance at the system level. The critical research questions are as follows.

(1)

Concentrated on the highly disordered nature of EVs, which hinders effective EV-to-grid interaction and pronounced spatiotemporal coupling with controllable loads, it is imperative to develop a coordinated consumption-side optimization strategy to enhance the economic efficiency and operational stability at the microgrid level.

(2)

Concentrated on the lack of storage benefits and energy synergies within the source–grid–load–storage integrated management framework, it is imperative to devise a collaborative supply-side optimization strategy to enhance the resource utilization and economic efficiency of storage management and energy interconnection.

1.2. Contribution

Building on the background outlined above, this paper thoroughly examines the unique characteristics of a multi-microgrid, distributed, interconnected system and proposes hierarchical optimization strategies to address the challenges of EV-to-grid interaction, demand response, storage management, and energy interconnection. Essentially, within a single microgrid system, the lower layer coordinates the energy storage features of EVs and the adjustable characteristics of controllable loads to achieve optimal scheduling for peak shaving and valley filling. Based on the EV–load optimization results from the lower layer, the upper layer, within a multi-microgrid interconnection framework, further investigates strategies for energy storage configuration, operation, and cross-microgrid energy sharing to improve the storage benefits and energy synergies. The principal contributions are as follows.

(1)

Focusing on the microgrid integrated with EVs, a Voronoi-based adaptive genetic algorithm optimization for the Latin Hypercube is proposed to enhance the simulated realism of EV driving conditions. Additionally, the concept and recursion mechanism of the energy storage margin band are proposed to serve as the foundation for the efficient optimization of EV-to-grid interaction.

(2)

Building on the simulated EV storage margin band, a cooperative operation mechanism between EV-to-grid interaction and controllable load dispatch is further explored. Furthermore, an adaptive optimization method for EV storage operation and demand response is proposed to leverage the storage capabilities of EVs and tap into the potential of demand-side management.

(3)

A Nash-Topsis method is proposed to determine the optimal strategy from the dual objective Pareto front of the optimization results. This approach effectively improves synergy and efficiency in the multi-objective optimization process.

(4)

Building on the integrated management of source–grid–load–storage, a synchronous optimization mechanism for energy storage configuration and operation is further explored. Meanwhile, a dynamic optimization mechanism based on state mapping is proposed to significantly enhance the SOC and resource utilization of energy storage.

(5)

A collaborative optimization method for storage management and energy interconnection is proposed based on a comprehensive exploration of their synergistic operation mechanism, to effectively enhance the system’s economic efficiency and environmental sustainability.

The paper’s structure is defined as follows. The bottom-up hierarchical optimization framework for the multi-microgrid system is described in Section 2. Section 3.1 and Section 3.2, respectively, present the improved simulation method and the recursion mechanism of the energy storage margin band to facilitate intelligent EV-to-grid interaction. The adaptive optimization method and the Pareto decision method for EV storage operation and demand response to enhance peak shaving and valley filling are presented in Section 4.1 and Section 4.3. The dynamic optimization mechanism based on state mapping and the collaborative optimization method for storage management and energy interconnection to improve storage benefits and energy synergies are, respectively, presented in Section 5.1 and Section 5.2. Finally, Section 6 presents the conclusions.

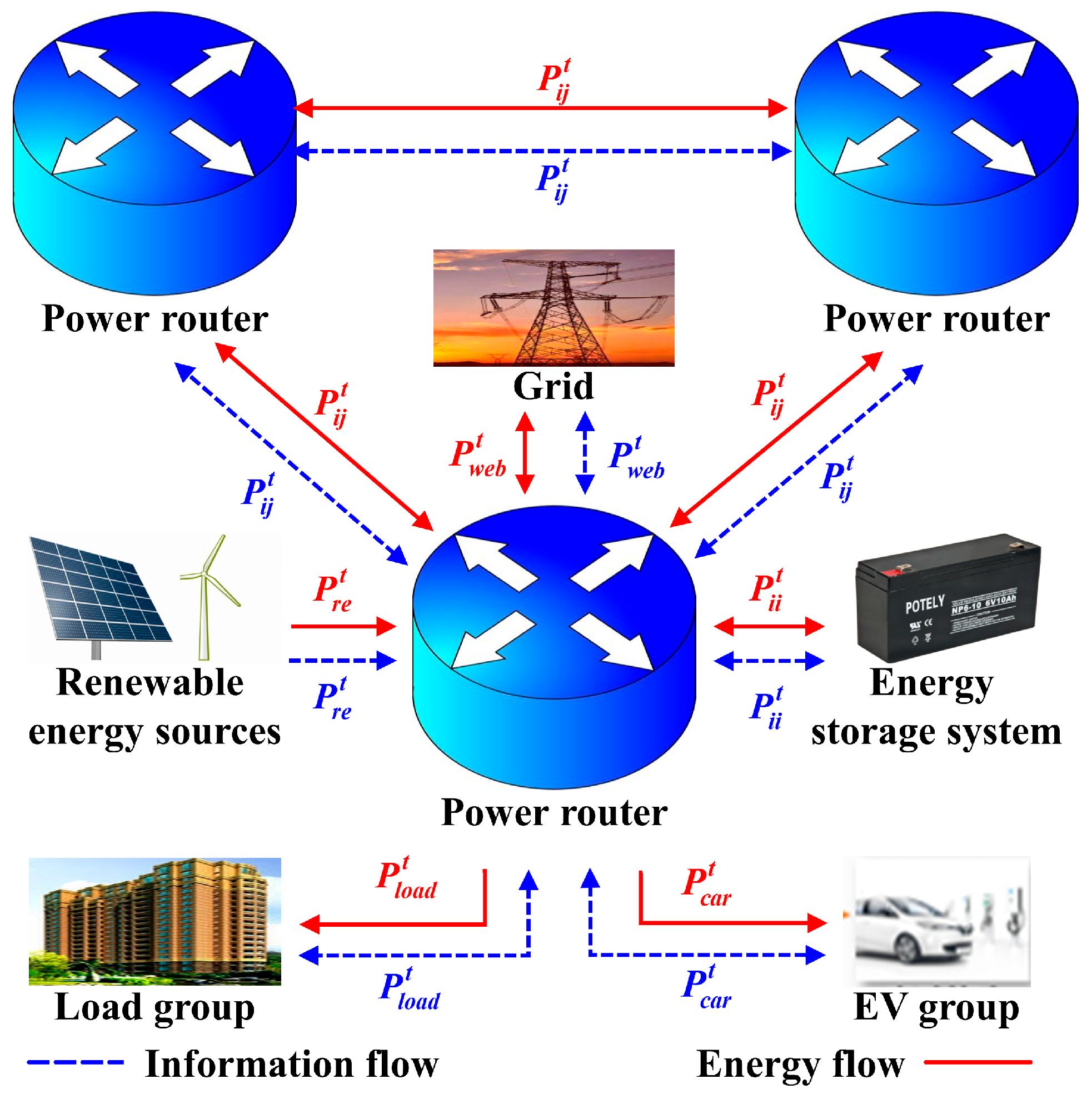
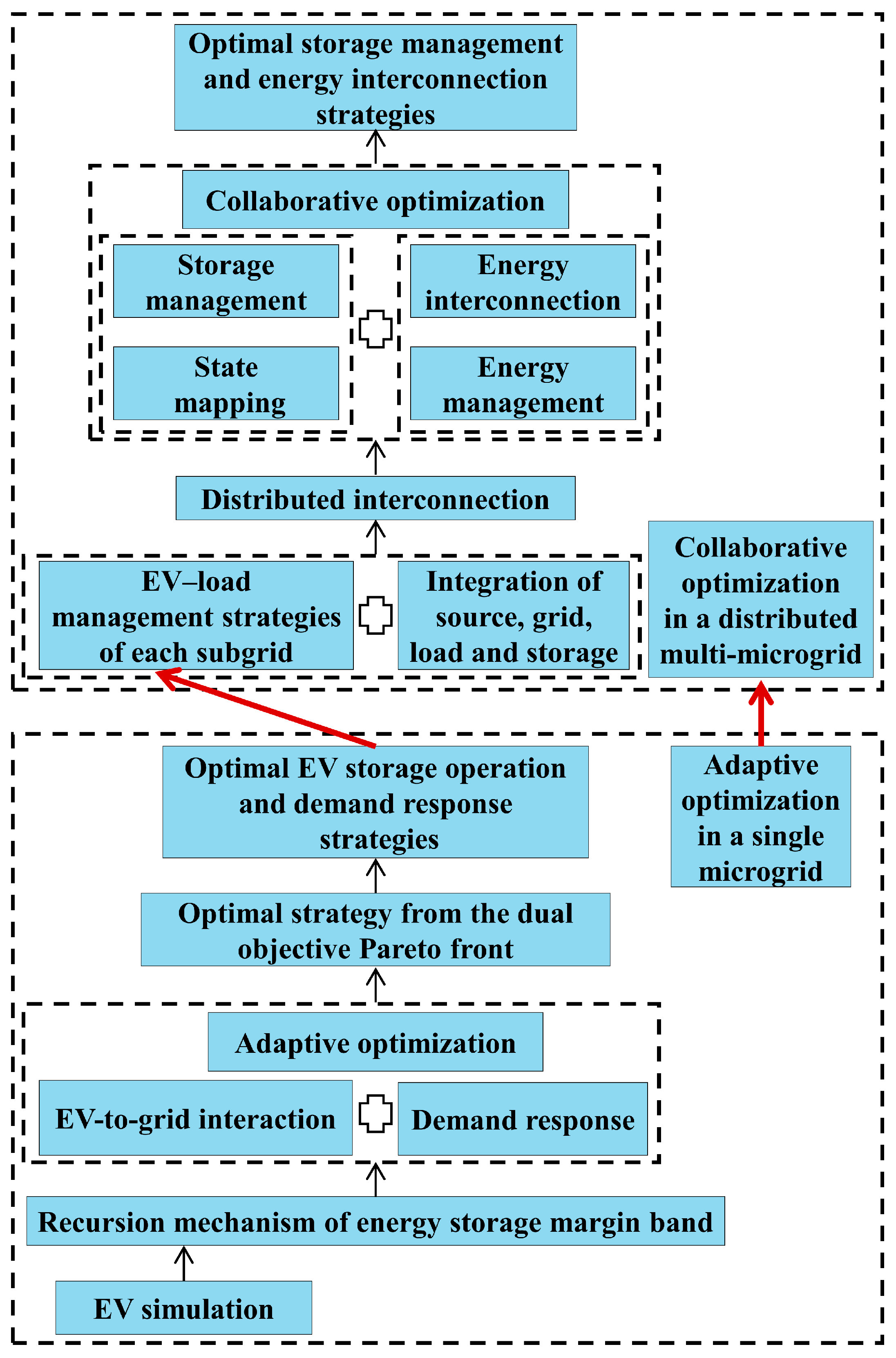
2. Hierarchical Optimization Framework for Multi-Microgrid System

With the continuous development of energy internet technology, the traditional centralized management model of a single microgrid, which integrates source, grid, load, and storage, increasingly reveals limitations in adaptability, flexibility, and timeliness. Meanwhile, the concept of multi-grid interconnection, focused on information cooperation and resource sharing, has emerged and is demonstrating an increasingly important role. Therefore, based on cooperative game theory and interconnection support potential, a three-microgrid interconnected system is proposed, facilitated by the distributed interconnection of power routers [18]. This system aims to enhance the collaboration between microgrids, enabling more refined and autonomous energy optimization and scheduling. It also increases the utilization of renewable energy and improves the economic efficiency of system operations. In subgrid failures or energy supply–consumption imbalances, neighboring microgrids can communicate to provide mutual support, ensuring the system’s safe and reliable operation (as shown in Figure 1).

This paper addresses the multifaceted requirements of EV scheduling, controllable load dispatch, storage management, and energy interconnection in a multi-microgrid distributed interconnected system by proposing a bottom-up hierarchical optimization framework (as shown in Figure 2).

In this framework, the lower layer concentrates on the power consumption side within each subgrid. To begin with, the EV-to-grid interaction of EVs entering a single microgrid is first addressed by simulating and recursing the energy storage margin band. An adaptive optimization for EV charging and controllable load scheduling is then developed, integrating consumption-side management with the dual objectives of economic efficiency and user comfort. Finally, the optimal strategy is derived from the dual-objective Pareto frontier, aiming to achieve peak shaving and economic improvement. The optimized results are then transmitted to the upper layer, where supply-side scheduling is coordinated across the entire system.

In the upper layer, building on the optimized EV–load scheduling results from the lower layer, integrated source–grid–load–storage management is achieved by incorporating a multi-source grid-connected mode of renewable energy [19]. A multi-microgrid distributed interconnection system is then established. Collaborative optimization is employed to explore and optimize the storage management strategy and energy interconnection solutions, thereby further enhancing the system’s economic efficiency and environmental sustainability.

3. Improved Simulation Method and Recursion Mechanism of Energy Storage Margin Band for EV

3.1. Voronoi-Based Adaptive Genetic Algorithm Optimization for Latin Hypercube Simulation of EVs

Compared to traditional electricity loads, EV loads have greater energy storage capabilities. Optimizing their charging and discharging behaviors by effectively utilizing these storage characteristics can significantly enhance microgrids’ economic and environmental benefits [20].

Due to the stochastic and intermittent nature of EVs’ temporal and spatial distribution, prediction methods struggle to capture their complex and extreme charging patterns. Simulation methods, such as Monte Carlo, are commonly used to model EV states; however, they are inefficient and require numerous samples. Additionally, the inherent variability hampers the detection of low-probability events, resulting in the uneven sampling of extreme cases and triggering truncation effects.

In contrast, the Latin Hypercube simulation method [21] can thoroughly explore the entire parameter space by uniformly dividing each variable’s distribution interval with equal probability and randomly selecting sample points. This approach achieves a uniform coverage of each dimension, resulting in a high simulation accuracy with a smaller sample size, thereby reducing the dependency of accuracy on the sample size and enhancing the efficiency and stability of the sampling process. However, when handling multi-dimensional samples, aggregation may occur, compromising the simulation’s realism.

An improved Latin Hypercube simulation method is proposed to address these issues, incorporating the spatial division function from the Voronoi graph theory to measure the simulation homogeneity. This function serves as an objective in conjunction with adaptive genetic algorithms to minimize the aggregation of multi-dimensional simulation parameters and achieve balanced, independent simulations of EVs in both time and space.

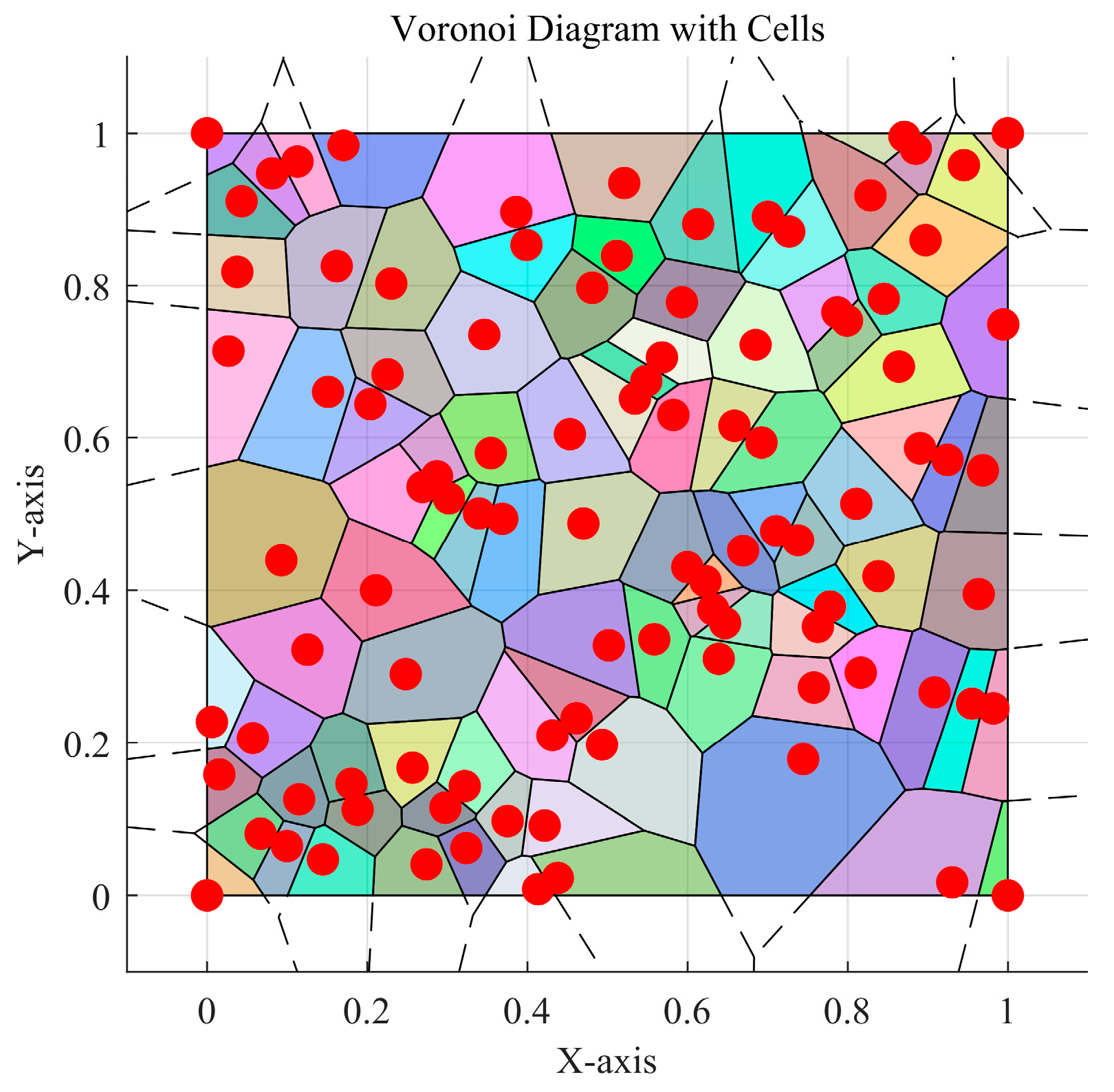
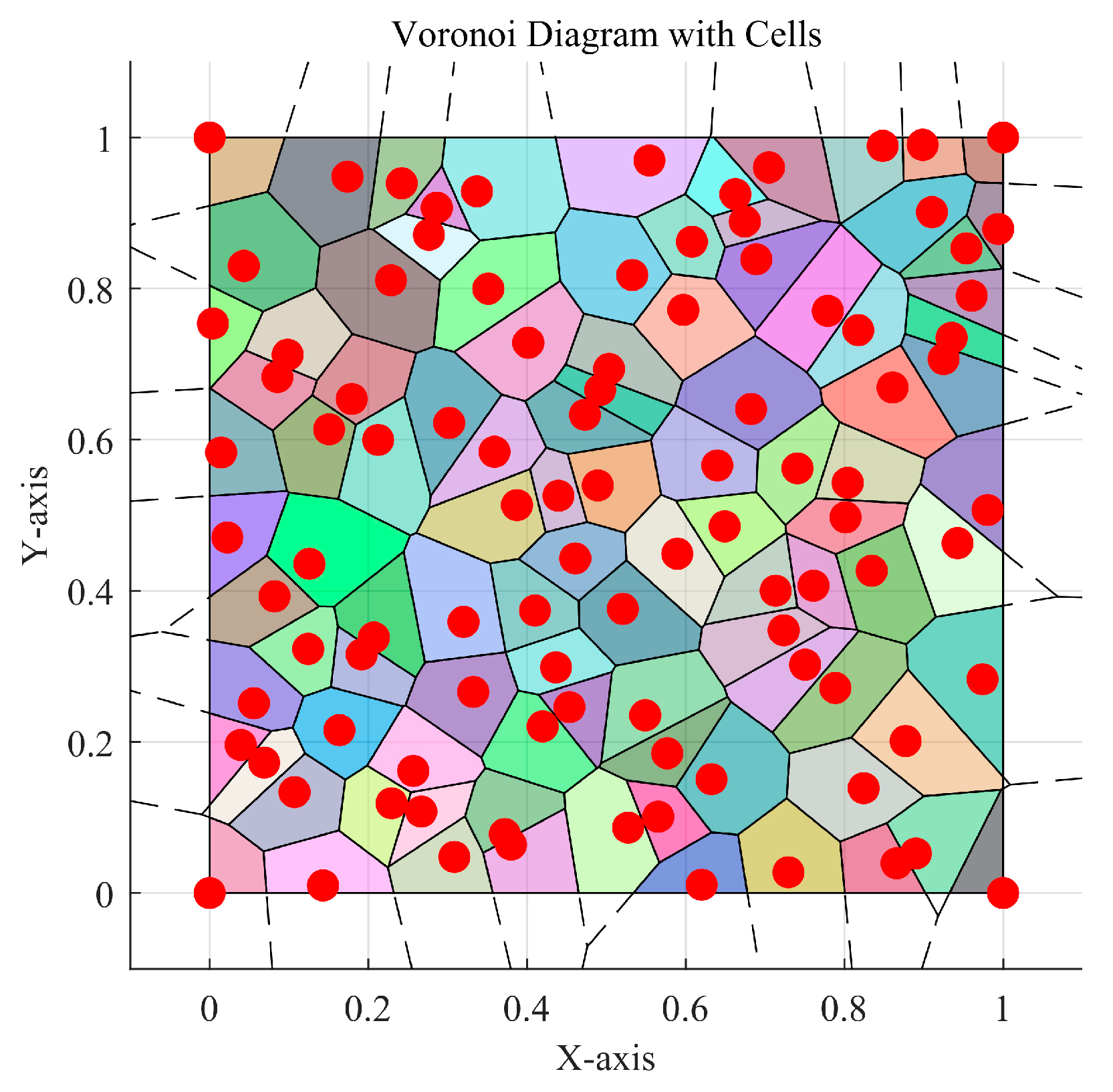
3.1.1. Theory of Voronoi Diagrams

Voronoi, a geometric segmentation tool, is widely used in GIS, data analysis, and optimization problems [22]. Its core principle involves a set of discrete points $\left\{P_1,P_2,\dots ,P_{\mathrm{n}}\right\}$ that divide the space into regions using bisectors, such that any point within a region is closest to a specified point, forming a Voronoi region.

$$V(P_i)=\left\{x\in R^2|d(x,P_i)<d(x,P_j),\forall j\ne i\right\}$$

(1)

where $V(P_i)$ denotes the Voronoi region of point $P_i$, which consists of all points $x$ that satisfy the condition; $d(x,P_i)$ denotes the Euclidean distance between the point $x$ and the generating point $P_i$.

3.1.2. Adaptive Genetic Algorithms

Genetic algorithms, inspired by Darwin’s principle of natural selection, simulate the processes of inheritance, mutation, and selection in evolution [23]. They are particularly effective in solving complex non-linear and non-convex optimization problems. To enhance the convergence speed and search capability, an adaptive strategy is employed that dynamically adjusts the crossover and mutation probabilities.

In the early stage of optimization, a higher crossover probability and lower mutation probability increase the search space diversity while minimizing random perturbations, preserving high-quality solutions. As the algorithm approaches the optimal solution, a lower crossover probability and higher mutation probability enhance the local search capability and reduce the risk of converging to a local optimum, thus maintaining solution diversity [24].

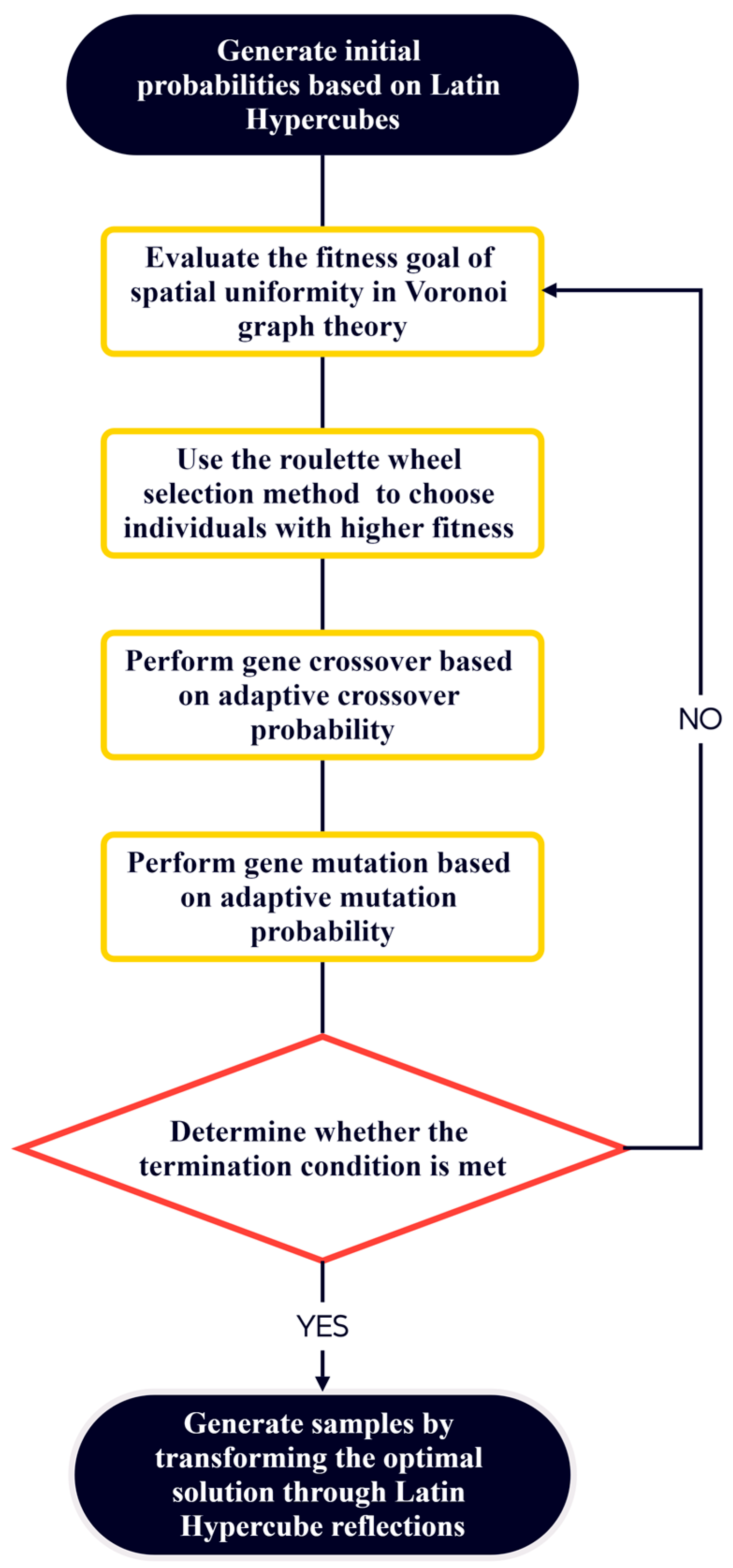
3.1.3. Voronoi-Based Adaptive Genetic Algorithm Optimization for Latin Hypercube

Improvements to the Latin Hypercube method are made in the following steps (as shown in Figure 3):

• Compute the definite integral of the probability density function of each dimension to obtain the cumulative distribution function $F_1$ and $F_2$.
• Use the probability values of the cumulative distribution function as the sample space, dividing it into $N$ non-overlapping sub-intervals of equal size, each spaced by $1/N$.
• Perform random sampling within each sample space of each dimension. For each interval, generate a random number uniformly distributed within the interval and calculate the corresponding probability value using the following formula:

  $$q_i^1,q_i^2=\left({\displaystyle \frac{1}{N}}\right)\times r+{\displaystyle \frac{i-1}{N}}$$

  (2)

  where $N$ is the number of samples or intervals; $i$ is the index of each interval; $r$ is a random number between 0 and 1; $q_i^1$ and $q_i^2$ denote the probability value.
• Population initialization: Construct the decision variables to define a permutation sequence, which is then applied to the sampled probability values to generate two-dimensional sample points:

  $$\left\{\begin{array}{l}{x}^1=\left(x_1^1,x_2^1,\dots ,x_N^1\right),\hspace{1em}{x}_k^1\in \{1,2,\dots ,N\}\\ x^2=\left(x_1^2,x_2^2,\dots ,x_N^2\right),\hspace{1em}{x}_k^2\in \{1,2,\dots ,N\}\end{array}\right.$$

  (3)

  $$\{(q_{x_k^1}^1,q_{x_k^2}^2)\},k=1,2,\dots N$$

  (4)

  where $x^1$ and $x^2$ are the decision variables to be optimized; $(q_{x_k^1}^1,q_{x_k^2}^2)$ denotes the corresponding two-dimensional sample point set formed from them.
• Fitness evaluation: To assess population quality, the Voronoi diagram theory is applied to evaluate the uniformity of the spatial distribution of the probability values $q_1^i$, $q_2^i$ obtained through random sampling, which serves as the objective for the fitness function.

  $$f(x^1,x^2)=max(P_{Voronoi}\{(q_{x_k^1}^1,q_{x_k^2}^2)\})-min(P_{Voronoi}\{(q_{x_k^1}^1,q_{x_k^2}^2)\}),k=1,2,\dots ,N$$

  (5)

  where $P_{Voronoi}\{(q_{x_k^1}^1,q_{x_k^2}^2)\}$ denotes the area of the Voronoi polygon formed by the set of points with probability values.
• Selection: Based on the fitness function values, a roulette wheel selection method is used to choose individuals with higher fitness for the next round of evolution.
• Crossover: New individuals are generated by performing partial gene crossover on selected individuals based on the adaptive crossover probability to simulate natural gene recombination.

  $$p_c(g)=p_c^{initial}-{\displaystyle \frac{g}{G}}\times (p_c^{initial}-p_c^{final})$$

  (6)

  where $p_c(g)$ denotes the corresponding crossover probability; $g$ and $G$ are the current and total iteration number; $p_c^{initial}$ and $p_c^{final}$ denote the initial and final crossover probability.
• Mutation: To prevent the algorithm from converging to local optima, random mutation operations are applied based on the adaptive mutation probability, enhancing the diversity of the new population.

  $$p_m(g)=p_m^{initial}+{\displaystyle \frac{g}{G}}\times (p_m^{final}-p_m^{initial})$$

  (7)

  where $p_m(g)$ denotes the corresponding mutation probability; $p_m^{initial}$ and $p_m^{final}$ denote the initial and final mutation probability.
• Iteration and termination: The selection, crossover, and mutation processes are repeated to generate new populations until the termination conditions are met, either by reaching a predetermined number of iterations or when there is no significant improvement in fitness.
• Through reverse mapping, each final probability value is substituted into the inverse of the cumulative distribution function to obtain the corresponding data samples.

  $$\{(P^1,P^2)\}=\{(F_1^{-1}(q_{{\tilde{x}}_k^1}^1),F_2^{-1}(q_{{\tilde{x}}_k^2}^2))\}$$

  (8)

  where $P^1$ and $P^2$ are the final data samples; $F_1^{-1}$ and $F_2^{-1}$ are the inverse functions of the cumulative distribution functions; ${\tilde{x}}_k^1$ and ${\tilde{x}}_k^2$ denote the final sequences.

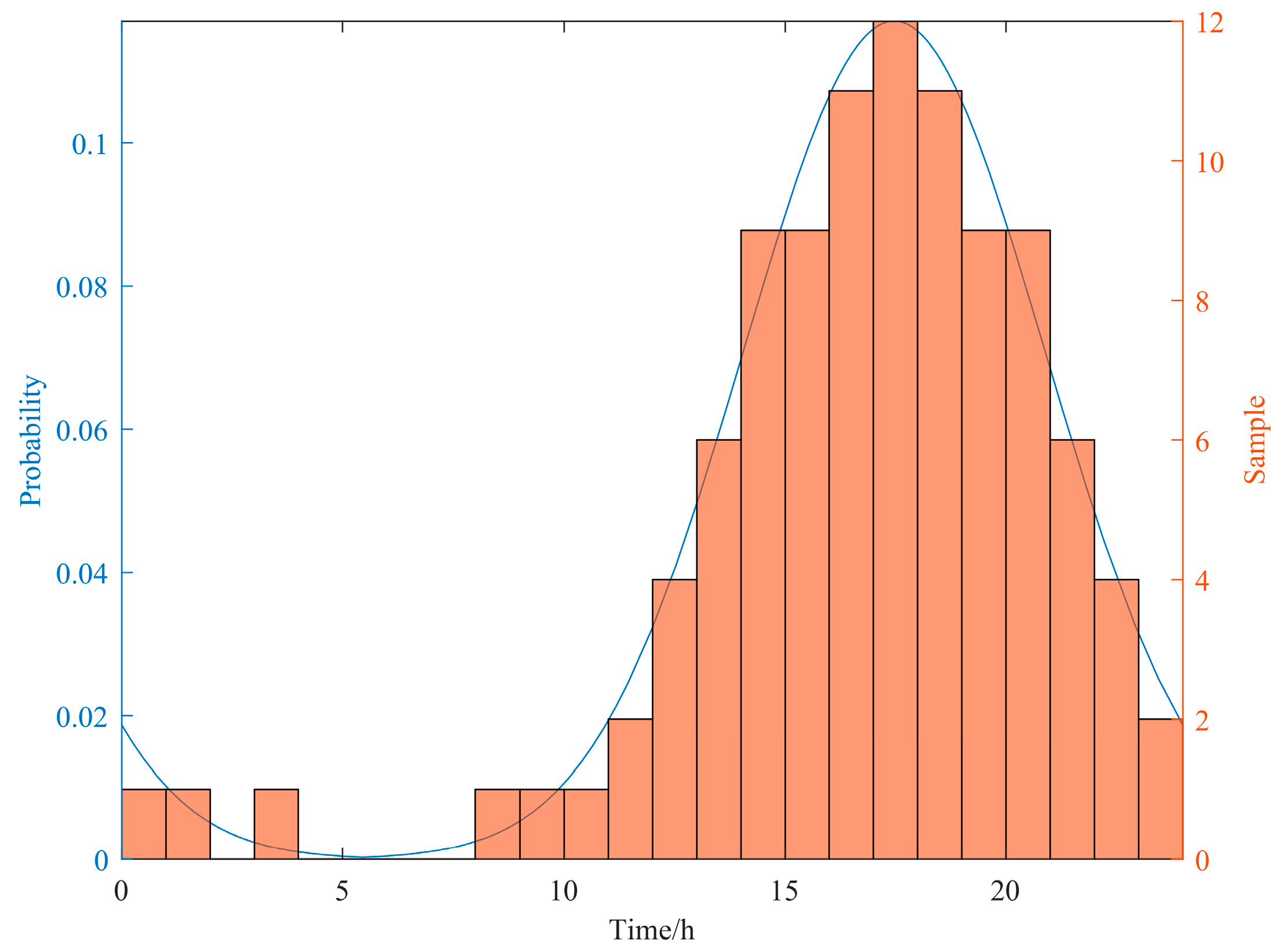
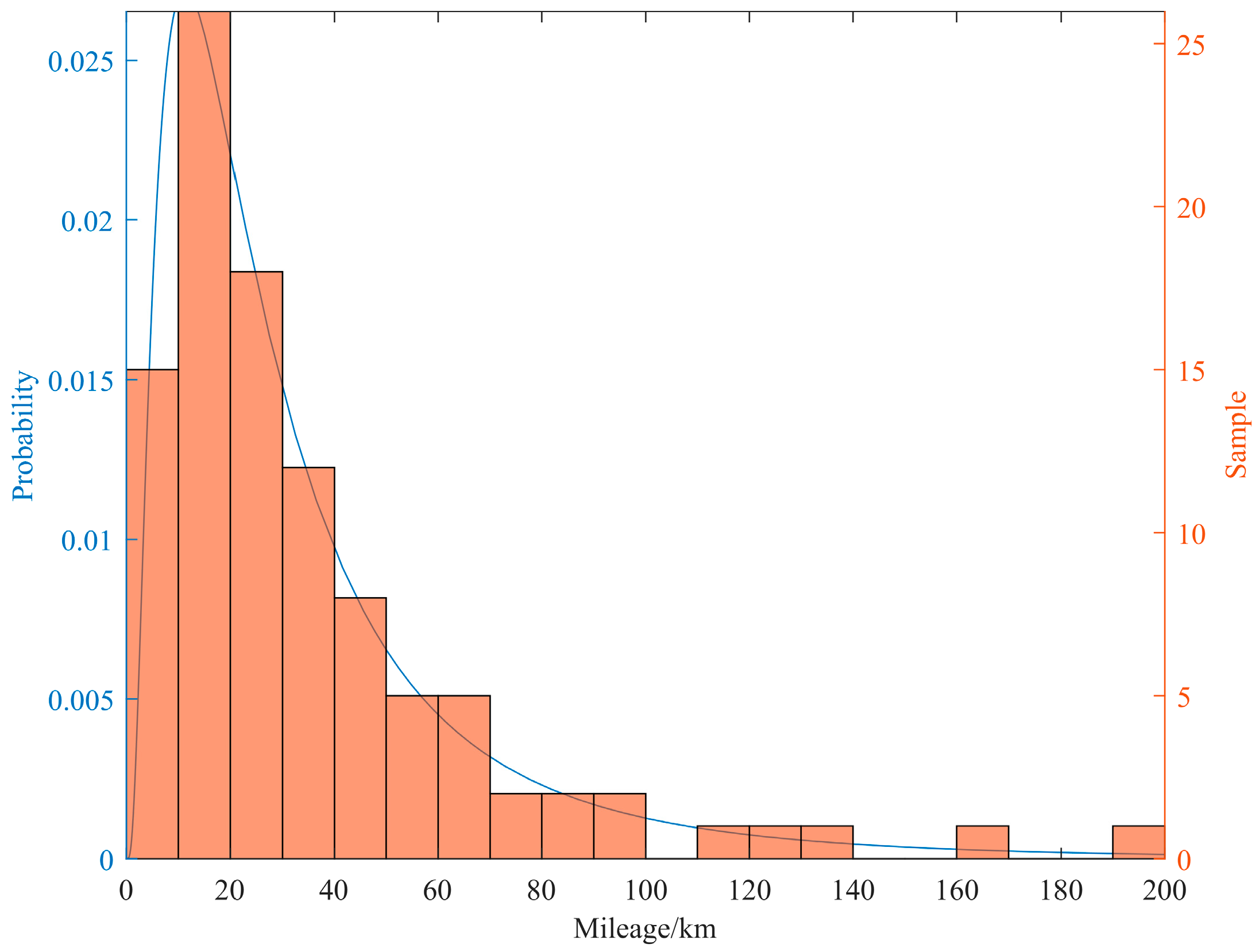
3.1.4. Analysis of Simulation Results

The charging moment of an EV is defined as the end-of-day driving time. According to statistics from the National Highway Traffic Safety Administration [25], the probability density functions of the end-of-day driving time and mileage are as follows:

$$f_t(x)=\left\{\begin{array}{c}{\displaystyle \frac{1}{x{\sigma }_t\sqrt{2\pi }}}exp[-{\displaystyle \frac{{(x-{\mu }_t)}^2}{2{\sigma }_t^2}}],{\mu }_t-12\le x\le 24\\ {\displaystyle \frac{1}{x{\sigma }_t\sqrt{2\pi }}}exp[-{\displaystyle \frac{{(x+24-{\mu }_t)}^2}{2{\sigma }_t^2}}],0\le x\le {\mu }_t-12\end{array}\right.$$

(9)

$$f_L(x)={\displaystyle \frac{1}{x{\sigma }_L\sqrt{2\pi }}}exp[-{\displaystyle \frac{{(lnx-{\mu }_L)}^2}{2{\sigma }_L^2}}]$$

(10)

As illustrated in Figure 4 and Figure 5, a comparative analysis was conducted between the proposed improved and the conventional Latin Hypercube simulation method, where the red circles denote the sampled two-dimensional points and the colored polygons delineate the Voronoi regions corresponding to each point relative to the rest of the sample set. The results demonstrate that the proposed method effectively mitigates the multi-dimensional aggregation phenomenon, significantly enhancing the realism of the simulation. The obtained data of the EVs’ charging moment and driving mileage are presented in Figure 6 and Figure 7.

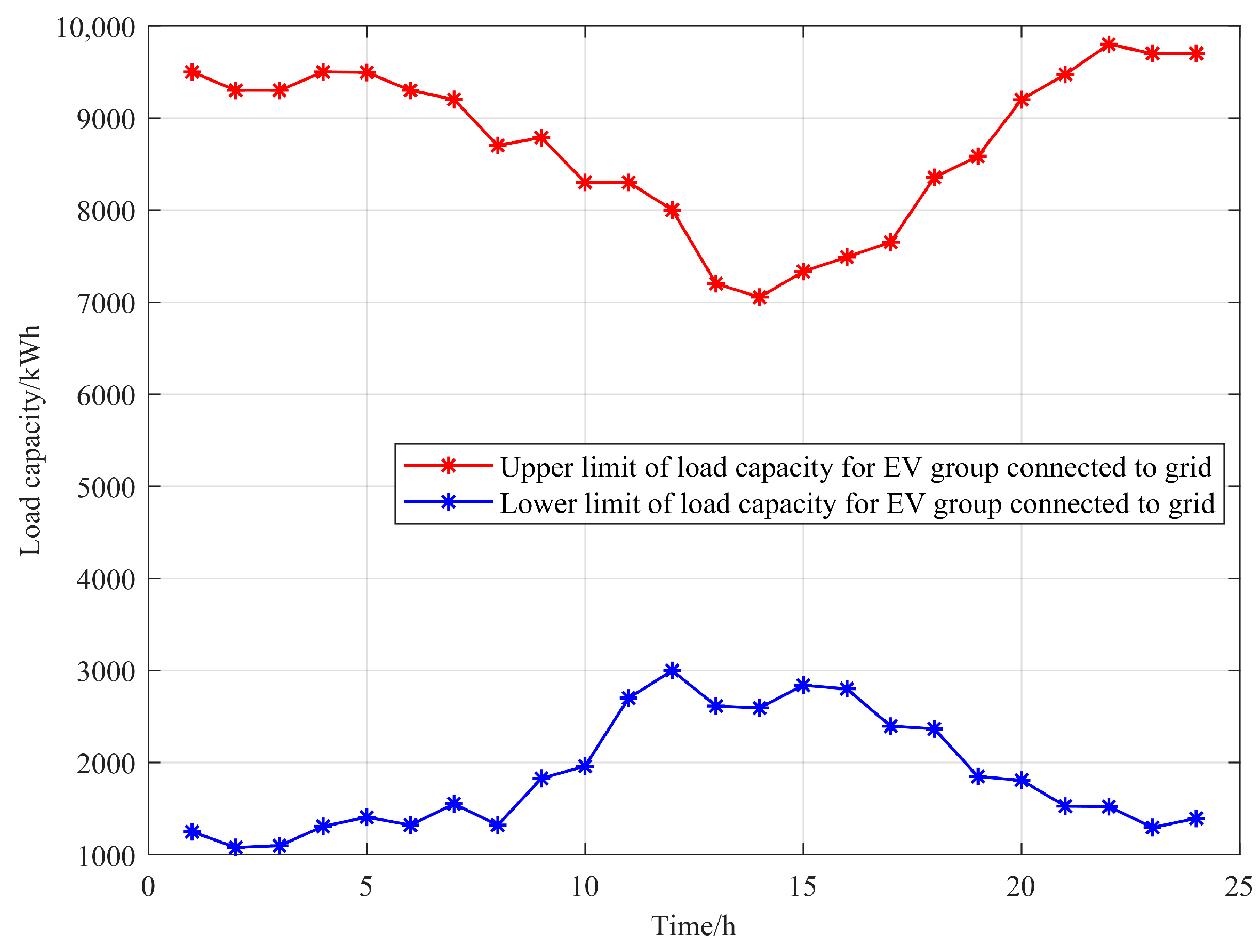
3.2. Recursion Mechanism of Energy Storage Margin Band for EV Fleet Access to the Grid

The two-dimensional data of the daily charging moment and driving mileage for each EV obtained via the simulation method are insufficient to directly support EV-to-grid interaction control. Therefore, by incorporating the average speed and consumption, these data need to be further transformed into the charging start/end moment and corresponding energy surplus information for each EV, serving as the critical input for EV-to-grid interaction. The EV parameters are shown in

Table 1. EV parameters.

Parameter	Value
$E_{EV}^{consume}$	0.5 kWh/km
$W_{EV}^{capacity}$	100 kWh
$\nu$	10 km/h
$W_{EV}^{tolerance}$	10 kWh
$P_{EV}^{charge}$$/P_{EV}^{discharge}$	30 kW

.

$$\{\begin{array}{c}{T}_{start}=⌊T_{charge}⌋\\ W_{EV}^{consume}=L\times E_{EV}^{consume}\\ W_{EV}^{in}=W_{EV}^{out}-W_{EV}^{consume}\\ T_L=⌈L/\nu ⌉\\ T_{end}=24+T_{start}-T_L\\ T_C=T_{end}-T_{start}\end{array}$$

(11)

where $T_{start}$ is the beginning moment of the charging of EV, obtained by rounding down the charging moment $T_{charge}$; $W_{EV}^{consume}$ denotes the power consumption of EV after driving distance $L$; $E_{EV}^{consume}$ denotes the power consumption of EV driving per kilometer; $W_{EV}^{in}$ denotes the power consumption at the moment of entering the grid; $W_{EV}^{out}$ denotes the power consumption at the moment of leaving the grid, which is also the off-grid full capacity $W_{EV}^{capacity}$; $T_L$ is the driving time of EV; $\nu$ is the average hourly speed of EV; $T_{end}$ is the end moment of the charging of EV; and $T_C$ is the charging time of EV.

Based on the maximum charging and discharging power of EV, the controllable operating state of the battery is recursed within the maximum and minimum charging limits, defining this range as the energy storage margin band. This allows each vehicle to freely regulate charging and discharging within the prescribed power limits, introducing substantial new distributed and flexible energy storage units.

$$\left\{\begin{array}{c}{t}_1=\left(W_{EV}^{in}-W_{EV}^{tolerance}\right)/P_{EV}^{discharge}\\ t_2=T_C-t_1-\left(W_{EV}^{out}-W_{EV}^{tolerance}\right)/P_{EV}^{charge}\\ t_3=\left(W_{EV}^{capacity}-W_{EV}^{in}\right)/P_{EV}^{charge}\end{array}\right.$$

(12)

$$W_{EV}^{max}(t)=\left\{\begin{array}{c}{W}_{EV}^{in}+P_{EV}^{charge}\times t,0\le t<t_3\\ W_{EV}^{capacity},t_3\le t<T_C\end{array}\right.$$

(13)

$$W_{EV}^{min}\left(t\right)=\left\{\begin{array}{c}{W}_{EV}^{in}-P_{EV}^{discharge}\times t,0\le t<t_1\\ W_{EV}^{tolerance},t_1\le t<t_2\\ W_{EV}^{tolerance}+P_{EV}^{charge}\times \left(t-t_2\right),t_2\le t<T_C\end{array}\right.$$

(14)

where $W_{EV}^{tolerance}$ denotes the min capacity of the EV battery; $P_{EV}^{charge}$ and $P_{EV}^{discharge}$ denote the max charging and discharging power; and $W_{EV}^{max}$ and $W_{EV}^{min}$ denote the upper and lower limit of EV energy storage margin.

Finally, by aggregating the energy storage margin bands of individual EVs, a macro-level controllable energy storage capability scope is constructed, as shown in Figure 8, representing the collective charging and discharging capacity available from the EV fleet at different time points, which enable the dispatch system to dynamically program a compliant curve for optimized scheduling, thereby enhancing grid flexibility and stability.

$$\left\{\begin{array}{c}{W}_{EVs}^{max}(t)={\displaystyle \sum _{i=1}^N}{W}_{EV.i}^{max}(t)\\ W_{EVs}^{min}(t)={\displaystyle \sum _{i=1}^N}{W}_{EV.i}^{min}(t)\end{array}\right.$$

(15)

where $W_{EVs}^{max}$ and $W_{EVs}^{min}$ denote the max and min energy margin limits of the EV fleet, respectively; $W_{EV.i}^{max}$ and $W_{EV.i}^{min}$ denote the upper and lower limit of $i$th EV energy storage margin.

This recursion mechanism of energy storage margin band for EV fleet transforms distributed, constrained, and variable EV battery resources into a scalable virtual storage asset that the grid can perceive, quantify, and schedule in real time. By serving as a bridge and quantification tool to assess the fleet’s maximum potential service capability, it facilitates intelligent EV-to-grid interaction.

4. Adaptive Optimization for EV Storage Operation and Demand Response in a Single Microgrid

4.1. Adaptive Optimization Method for EV Storage Operation and Demand Response

With the widespread interaction of EVs, microgrid systems’ load structure and functionality have become increasingly complex, posing significant challenges to traditional consumption-side management methods. EVs add to the load and introduce bidirectional interaction with the grid, resulting in more substantial and unpredictable load fluctuations. In situations such as power shortages, external failures, or load fluctuations, EVs can serve as a flexibly regulated emergency power reserve, quickly responding and providing short-term support to critical loads, thereby ensuring the continuity of power supply, which enhances the speed and effectiveness of demand response and strengthens the grid’s ability to manage uncertain events.

For this purpose, targeted dispatch strategies must be developed to enhance the overall performance of the power system, ensuring efficient energy distribution and economic operation. Based on the energy storage margin band of the EV fleet, its storage characteristics of EV-to-grid interaction are leveraged to drive a dynamic energy storage system with varying maximum charging and discharging power and capacity. Simultaneously, by integrating the dispatch flexibility of demand-side controllable loads, the charging and discharging strategies for EVs, along with controllable load allocation, are synchronously optimized based on time-of-day tariffs to achieve peak shaving and valley filling, enhancing the grid’s economic performance and resilience to fluctuations.

Considering the constraints of controllable loads, EVs, and power balance, dual objective functions are established to optimize both the economy of power purchase and the comfort of power consumption.

4.1.1. Restrictive Condition

• Upper and lower bounds on controllable loads and total daily balance constraints:

  $$\left\{\begin{array}{c}{\displaystyle \sum _{t=1}^{24}}{P}_{flex}(t)={\displaystyle \sum _{t=1}^{24}}{P}_{flex0}(t)\\ P_{flex0}^{min}(t)\le P_{flex}(t)\le P_{flex0}^{max}(t)\end{array}\right.$$

  (16)

  where $P_{flex0}$ and $P_{flex}$ denote the controllable load before and after optimization; $P_{flex0}^{max}$ and $P_{flex0}^{min}$ denote the upper and lower limits of 0.5 and 2 times the controllable loads before optimization.
• Energy storage margin bands and daily start/end balance constraints of EV fleet:

  $$\left\{\begin{array}{c}{W}_{EVs}(24)=W_{EVs}(0)\\ W_{EVs}^{min}(t)\le W_{EVs}(t)\le W_{EVs}^{max}(t)\end{array}\right.$$

  (17)

  where $W_{EVs}(t)$ denotes the storage surplus of the EV fleet after optimization.
• Charging and discharging power balance and upper and lower bound constraints of EV fleet:

  $$\left\{\begin{array}{c}{W}_{EVs}^{real}=W_{EVs}(t)-W_{EVs}^{in}(t)+W_{EVs}^{out}(t)\\ P_{EVs}(t)={\displaystyle \frac{\mathsf{\Delta }{W}_{EVs}^{real}}{\mathsf{\Delta }t}}/{\phi }_{ch},\mathsf{\Delta }{W}_{EVs}^{real}(t)>0\\ P_{EVs}(t)={\displaystyle \frac{\mathsf{\Delta }{W}_{EVs}^{real}}{\mathsf{\Delta }t}}\times {\phi }_{dch},\mathsf{\Delta }{W}_{EVs}^{real}(t)<0\\ -N(t)\times P_{EV}^{discharge}\le P_{EVs}(t)\le N(t)\times P_{EV}^{charege}\end{array}\right.$$

  (18)

  where ${\phi }_{ch}$ and ${\phi }_{dch}$ are the EV’s charging and discharging efficiency value of 0.9; $P_{EVs}$ denotes the charging or discharging power of the EV fleet; $W_{EVs}^{in}$ and $W_{EVs}^{out}$ denote the power of the EV fleet entering and leaving the grid; $N(t)$ denotes the number of EVs connected to the grid at each time.
• Power balance constraints:

  $$P_{web}(t)=P_{EVs}(t)+P_{flex}(t)$$

  (19)

  where $P_{web}$ denotes the power supply from the grid to EVs and controllable loads.

4.1.2. Objective Function

• Economy objective function: This function focuses solely on the total cost of purchased electricity for the EV and controllable load segments, ignoring the non-dispatchable fixed load factor.

  $$\min \left(F_1\right)=\sum _{t=1}^{24}{P}_{web}(t)\times C(t)$$

  (20)

  where $C(t)$ is time-of-day tariffs.
• Comfort objective function: This function aims to reduce the fluctuation of controllable loads before and after dispatch while considering the user electricity demand.

  $$\min \left(F_2\right)=\sqrt{{{\displaystyle \sum }}_{t=1}^{24}{\mid P_{flex}(t)-P_{flex0}(t) \mid }^2}$$

  (21)

4.2. CMOEA-MS Multi-Objective Optimization Algorithm

For the constructed multi-constraint, objective, stage game model, with EV-to-grid interaction and controllable load designated as the decision variables, the PlatEMO simulation platform [26] is utilized, employing the CMOEA-MS algorithm [27] for optimization. This algorithm has been implemented with internal joint processing mechanisms for objective functions and constraint violations. This approach addresses the challenge of balancing objective optimization and constraint satisfaction in complex feasible domains, achieving high efficiency in convergence. The basic principles and key methods are as follows:

• Basic principles

CMOEA-MS handles objectives and constraints in two adaptive phases to efficiently explore both feasible and infeasible regions:

(1)

Phase A: When most solutions are infeasible, equal priority is given to objectives and constraints, encouraging exploration across infeasible regions.

(2)

Phase B: Once most solutions are feasible, higher priority is given to constraints over objectives, guiding the search along feasible boundaries and refining solutions within the feasible region.

2.

Key methods

(1)

Dynamic Fitness Assessment: The fitness evaluation is adjusted based on the phase, balancing exploration in Phase A and prioritizing feasibility in Phase B.

(2)

Shift-Based Density Estimation: Applied in Phase A to measure the minimum shift distance between solutions, maintaining diversity while ensuring convergence toward the feasible domain without excessively focusing on constraint satisfaction.

(3)

Constraint Violation Metrics: Quantifies constraint violations in both phases, guiding the selection process in Phase B to prioritize feasibility.

CMOEA-MS efficiently balances feasibility, convergence, and diversity through a two-phase dynamic optimization framework and a flexible objective–constraint balancing mechanism. This approach enhances both global exploration and local optimization capabilities. The algorithm implementation procedure is as follows (Algorithm 1):

Algorithm 1: Procedure of CMOEA-MS

1. Initialize Population: Randomly generate an initial population and evaluate each individual’s fitness. 2. Parent Selection and Offspring Generation: Apply binary tournament selection to choose parents from the current population. Generate offspring through crossover and mutation operations; then, merge the offspring with the current population to create a new generation. 3. Feasibility Check: Calculate the proportion of feasible solutions in the population. If the proportion of feasible solutions is less than λ, proceed to Stage A; otherwise, proceed to Stage B. 4. Stage A: In this stage, density estimation and constraint violation are fitness evaluation metrics, treating goal optimization and constraint satisfaction equally. 5. Stage B: In this stage, apply the constraint dominance principle to prioritize feasible solutions, ensuring that constraints are satisfied first. 6. Following Generation Selection: If the conditions are met, select the best-adapted individuals from the current population to form the next generation. 7. Termination: If the maximum number of iterations or other termination criteria are met, end the algorithm and output the final population. Otherwise, return to step 2 to continue the process.

4.3. Nash-Topsis Method for Solving Pareto Frontier Solutions

In multi-objective optimization problems, the simultaneous attainment of optimality across all objectives is infeasible; consequently, the solution set constitutes a Pareto front of non-dominated trade-offs, from which a single satisfactory final decision needs to be selected. The Topsis method is commonly used to solve such strategy selection problems [28], with the core idea of ranking solutions based on their distance from the ideal solution. The optimal solution should be as close as possible to the positive ideal solution, but as far as possible from the negative ideal. However, the Topsis method relies on subjective weight allocation judgment, which restricts its adaptability. Additionally, the distance metric employed by Topsis fails to capture fairness considerations in practical scenarios. Finally, when confronted with large, complex Pareto-optimal solution sets, standard data normalization procedures often prove inadequate.

To address these limitations, the Nash-Topsis method is proposed. This method enhances the decision-making process’s accuracy, flexibility, and applicability by overcoming the shortcomings of the traditional Topsis approach.

4.3.1. The Nash Negotiation Game

Nash negotiation [29] is a key model in game theory that seeks to provide fair and mutually beneficial solutions for multiple participants. While each point on the Pareto frontier represents a Pareto-optimal solution, these solutions do not always satisfy fairness requirements. The Nash negotiation solution addresses this by balancing the interests of all parties involved. By introducing a reservation utility principle of maximizing the product of all parties’ utilities to select a specific, fair solution from the Pareto frontier, the negotiation outcome becomes both reasonable and sustainable, yielding a fair and equitable agreement.

$$x_{Nash}=argmax\left((f_1(x)-d_1)(f_2(x)-d_2)\right)$$

(22)

where $x_{Nash}$ denotes the Nash negotiation solution; $x$ is the negotiation proposal; $f_1(x)$ and $f_2(x)$ are the utility functions of negotiators; $d_1$ and $d_2$ are the reservation utilities of negotiators.

4.3.2. Nash-Topsis Method

The Topsis method is improved by incorporating the max-min normalization approach and refining the core distance measurement into an indicator derived from the solution of the Nash negotiation game. The improved method follows these basic steps:

(1)

The max-min normalization method is used to scale data of different magnitudes to the same range, thereby eliminating the impact of magnitude on the analysis results.

$${\tilde{f}}_i(x)={\displaystyle \frac{f_i(x)-min(f_i(x))}{max(f_i(x))-min(f_i(x))}},i=1,2$$

(23)

where ${\tilde{f}}_i(x)$ denotes the standard utility function after max-min normalization.

(2)

Based on the properties of the indicators, positive and negative ideal solutions are identified:

$$\left\{\begin{array}{c}{A_i}^{+}=\{max({\tilde{f}}_i(x))\mid i\in J_1,min({\tilde{f}}_i(x))\mid i\in J_2\}\\ {A_i}^{-}=\{min({\tilde{f}}_i(x))\mid i\in J_1,max({\tilde{f}}_i(x))\mid i\in J_2\}\end{array}\right.$$

(24)

where ${A_i}^{+}$ and ${A_i}^{-}$ denote the positive and negative ideal solutions; $J_1$ and $J_2$ are the set of benefit and cost indicators.

(3)

The Nash metrics of the scenarios versus the ideal solution are calculated:

$$\left\{\begin{array}{c}D{(x)}^{+}=1/{\displaystyle \prod _{i=1}^2}({\tilde{f}}_i(x)-A_i^{+})\\ D{(x)}^{-}=1/{\displaystyle \prod _{i=1}^2}({\tilde{f}}_i(x)-A_i^{-})\end{array}\right.$$

(25)

where $D{(x)}^{+}$ and $D{(x)}^{-}$ denote Nash metrics of the scenarios versus the ideal and non-ideal solution.

(4)

The relative closeness is calculated and ranked, and the optimal solution is selected:

$$C(x)={\displaystyle \frac{D{(x)}^{-}}{D{(x)}^{+}+D{(x)}^{-}}}$$

(26)

$$x_{best}=argmaxC(x)$$

(27)

where $C(x)$ denotes the relative closeness; $x_{best}$ denotes the optimal solution.

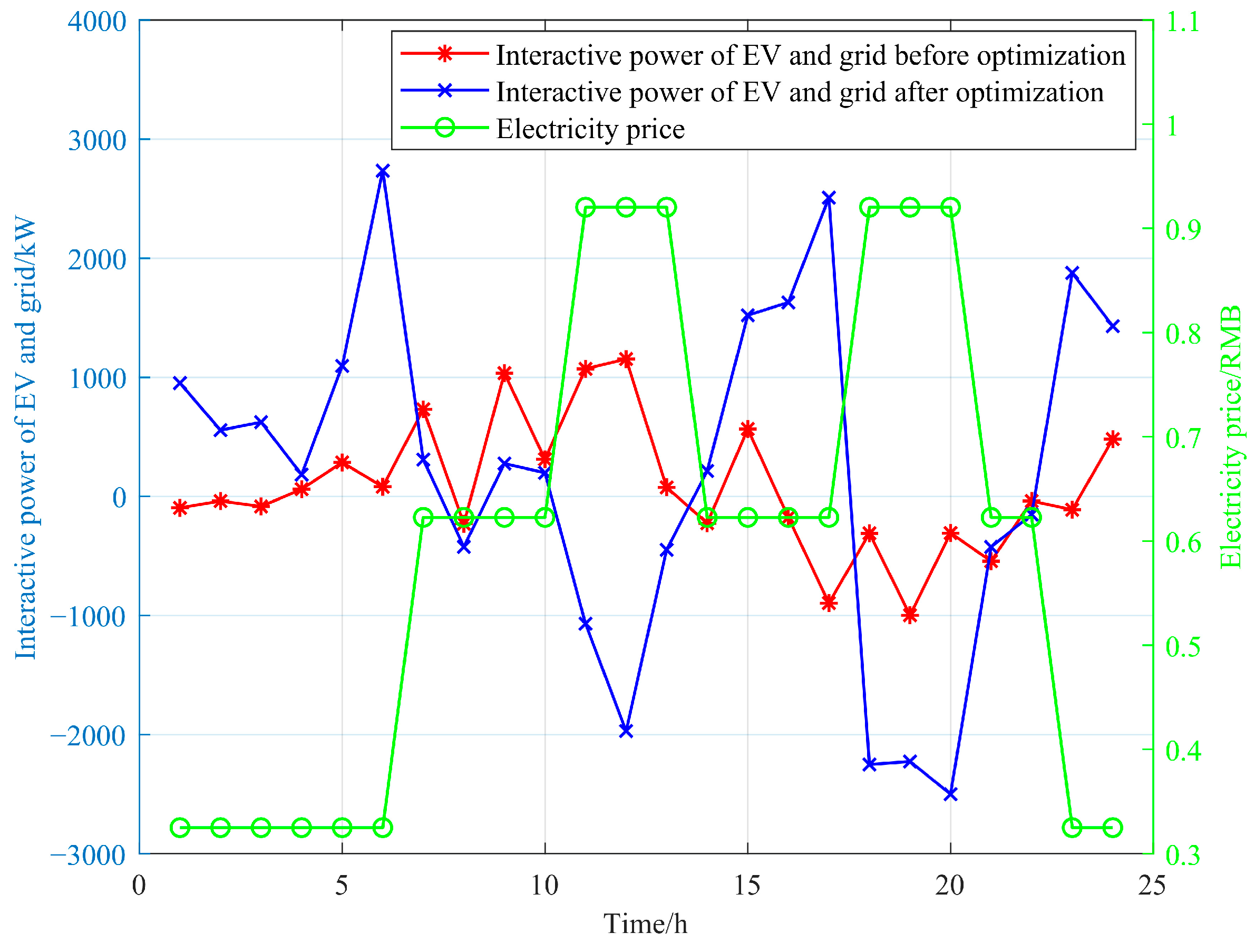
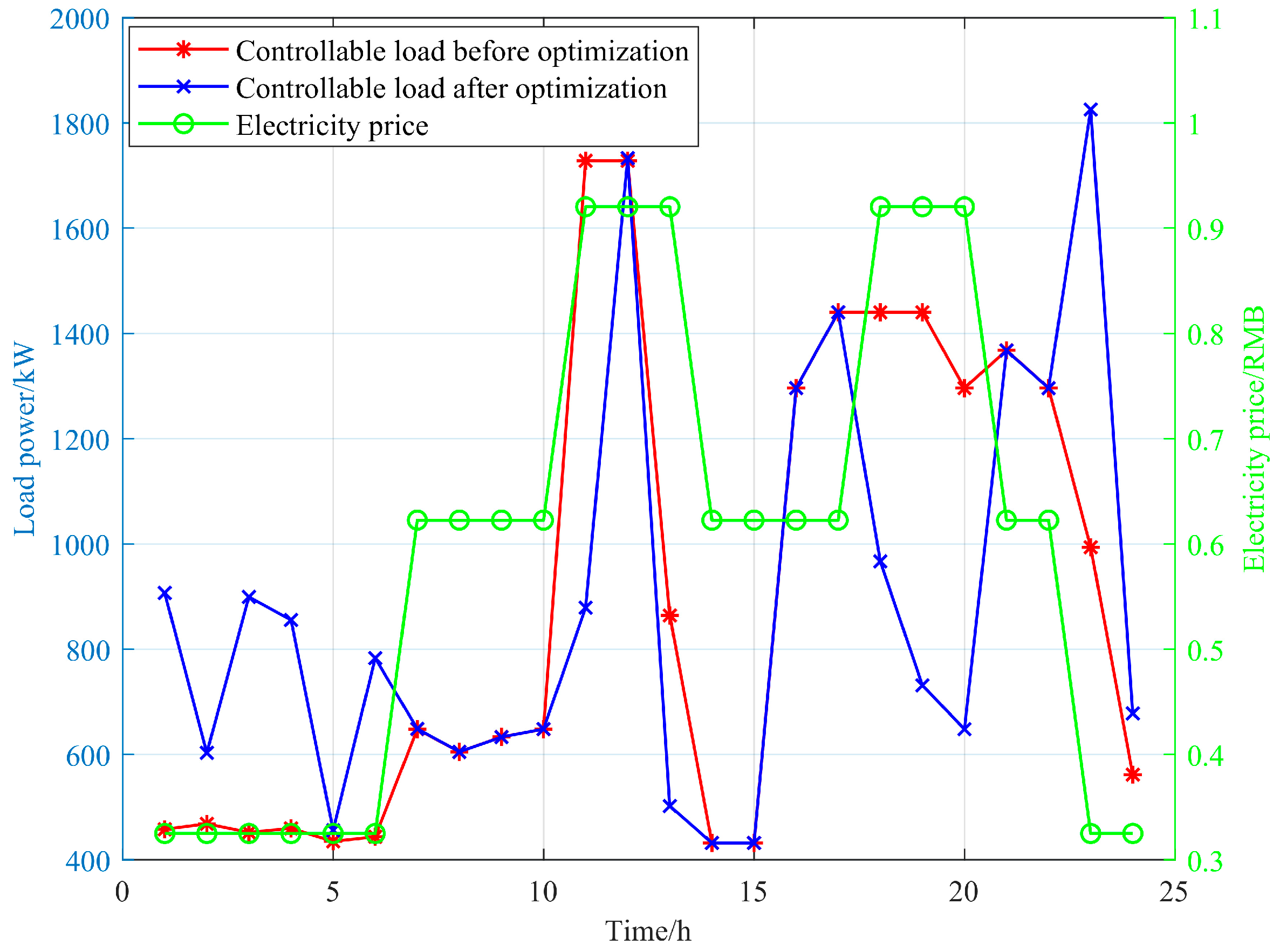
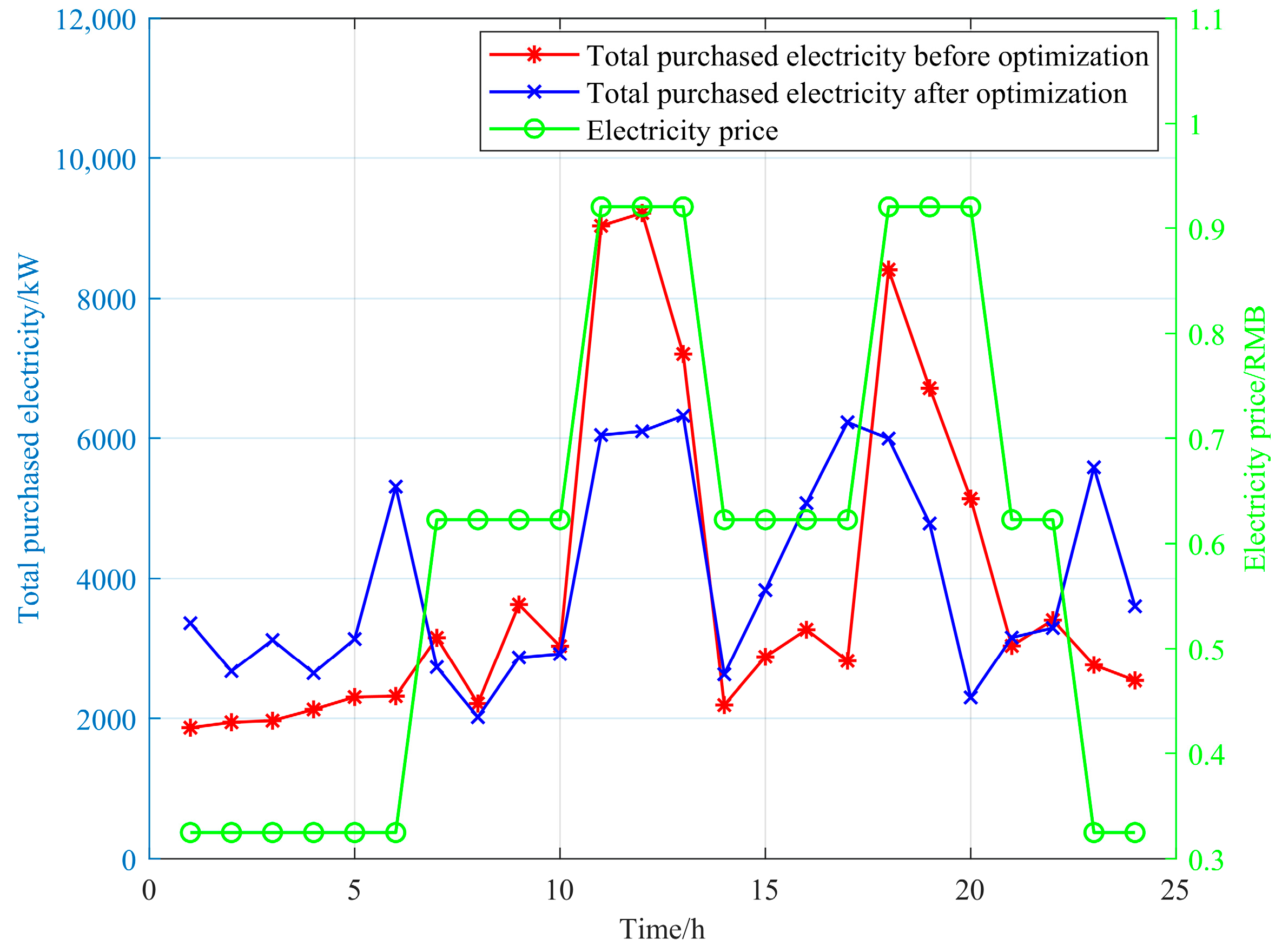
4.4. Analysis of Optimization Results from Single-Microgrid Simulation

Finally, the EV charging and discharging, as well as controllable load optimization results, are derived for each subgrid in the multi-microgrid system, with subgrid 3 serving as an example (as shown in Figure 9).

In a comparison of optimization algorithms, the Pareto front yielded by CMOEA-MS consistently lies nearer to both objective axes than those of NSGA-II and NSGA-III, thereby demonstrating a superior trade-off performance across both objectives.

In a comparison of Pareto decision methods, the classical Topsis optimum appears at the extreme end of the Pareto front, above the curve, indicating that the improvement of some objectives excessively sacrifices others, resulting in a comparatively inferior overall outcome. In contrast, the Nash-Topsis method selects its optimum below the midsection of the front curve, delivering superior aggregate objective function values across all criteria.

An analysis of the optimal solution results selected by the Nash-Topsis method is shown in Figure 10, Figure 11 and Figure 12.

Figure 10 presents the results of the EV storage operation optimization, emphasizing the role of EVs as distributed energy storage assets in EV-to-grid interactions. The EV charges during low-load and off-peak tariff periods, between 0–4 and 14–17 h, and discharges power back to the microgrid during peak periods, from 11–13 to 18–20 h. This strategy effectively achieves peak shaving and valley filling. Moreover, the implemented dynamic regulation mechanism harmonizes supply and consumption within the microgrid, mitigating load fluctuations, reducing peak power demand, and decreasing reliance on the grid.

Figure 11 illustrates the results of demand response optimization. Before optimization, the controllable load exhibits significant fluctuations, with a clear peak–valley difference. After participating in the scheduling optimization, the peak value and the peak–valley difference are significantly reduced. The peak demand is effectively shifted to the low-demand valley periods, and the controllable load curve becomes smoother, achieving the desired effect of peak shaving and valley filling. As a result, the grid’s overall economic performance and ability to resist volatility are notably improved.

The optimization strategy for EV storage operation and demand response significantly enhances the microgrid’s economic efficiency by dispatching 13.4% of the controllable loads, albeit with a slight sacrifice in electricity comfort (as shown in Figure 12). Before optimization, the total cost of electricity purchased for the user’s EVs and controllable loads is CNY 15,819.4. After optimization, this cost is reduced to CNY 9724, representing a 38.5% reduction.

Ultimately, all of the optimization results from each subgrid are transmitted to the upper layer as the corresponding consumption-side states within the system.

5. Collaborative Optimization for Storage Management and Energy Interconnection in a Distributed Multi-Microgrid

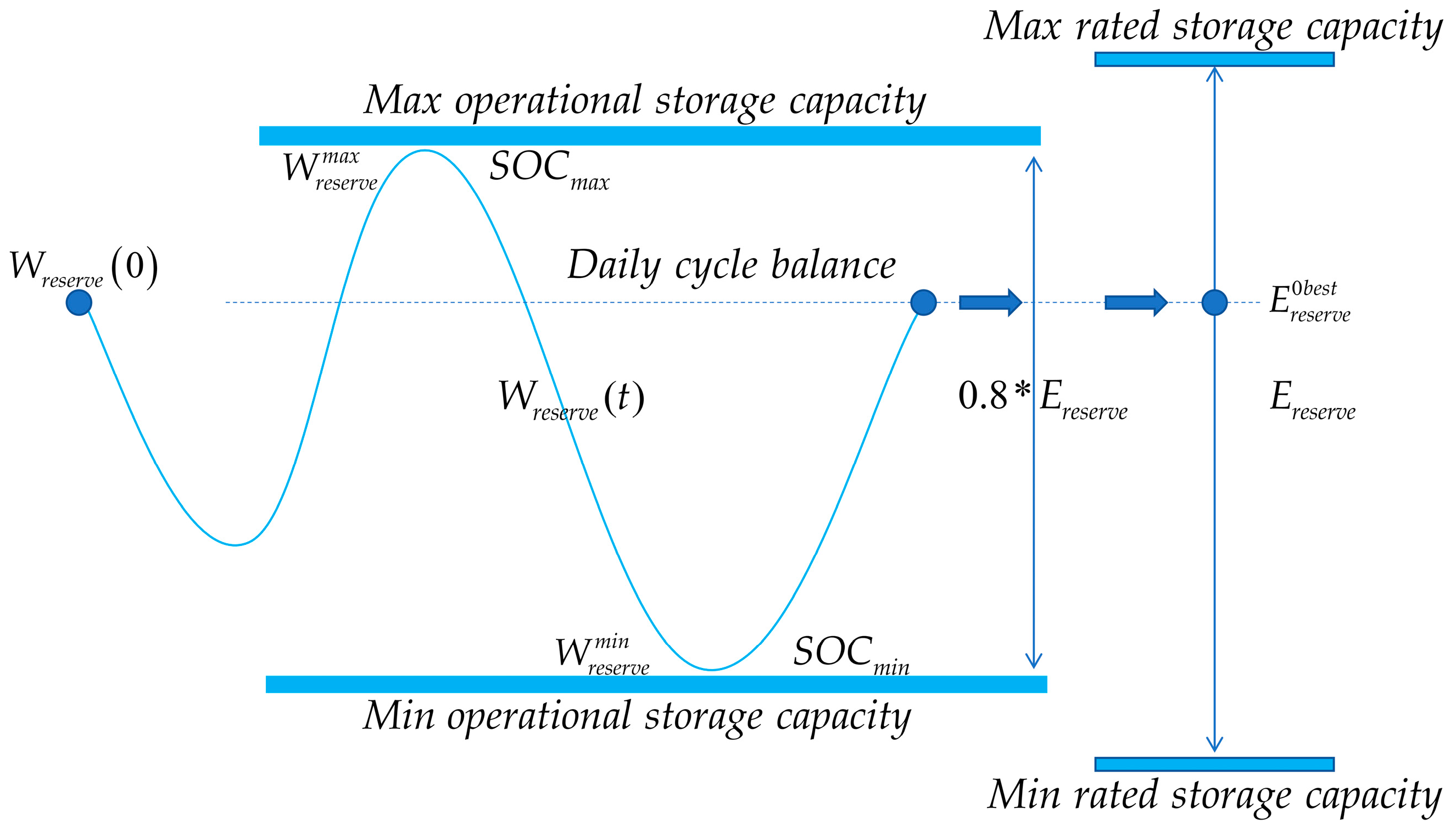
5.1. Dynamic Optimization Mechanism for Energy Storage Based on State Mapping

As the core component of the energy internet, the power router enables the integrated management of source–grid–load–storage within the power system, playing a crucial role in optimizing the use of renewable energy sources, as well as enhancing the power supply reliability, flexibility, and consumption capacity. The renewable energy sources considered in this paper include photovoltaic and wind power, with data sourced from the literature [30].

$$P_{re}=P_{pv}+P_{wt}$$

(28)

where $P_{re}$ denotes the power generated by renewable energy; $P_{pv}$ denotes the power generated by photovoltaic; $P_{wt}$ denotes the power generated by wind.

Grid-connected power generation from multiple sources, such as wind and photovoltaic energy, can significantly enhance energy utilization and supply stability. However, the intermittent and fluctuating nature of renewable energy sources, combined with the variability of demand, makes it challenging to balance supply and consumption. This results in power curtailment, reverse overload, and frequent fluctuations. To address these challenges, energy storage systems have been integrated into microgrids to provide flexible responses to supply–consumption fluctuations and peak–valley variations, ensuring the supply’s continuity, stability, and flexibility.

As a critical component of the energy management system, the energy storage system operates based on the principles of electrochemical reactions. The energy surplus and state-of-charge level of the battery are reflected by the change in charging and discharging processes, which can be mathematically expressed as

$$W_{reserve}(t+1)=\left\{\begin{array}{c}{W}_{reserve}(t)+P_{reserve}^{ch}(t)\mathsf{\Delta }t\times {\eta }^{ch}\\ W_{reserve}(t)-P_{reserve}^{dch}(t)\mathsf{\Delta }t/{\eta }^{dch}\end{array}\right.$$

(29)

$$SOC(t)=W_{reserve}(t)/E_{reserve}$$

(30)

where $W_{reserve}(t)$ denotes the real-time storage surplus; ${\eta }^{ch}$ and ${\eta }^{dch}$ are the storage’s charging and discharging efficiency value of 0.9; $P_{reserve}^{ch}$ and $P_{reserve}^{dch}$ denote the current charging and discharging power; $SOC(t)$ denotes the real-time charging state; $E_{reserve}$ denotes the storage capacity.

The SOC of the energy storage during operation must remain within its allowable operating range, and at the end of the day, it must return to its initial value to ensure sustainable cycling. Accordingly, the following constraints must be satisfied:

$$SOC(0)=SOC(24)$$

(31)

$$0.1\le SOC(t)\le 0.9$$

(32)

The total cost of the energy storage system is predominantly determined by the rated capacity and power. Traditional methods treat these as independent parameters and employ a progressive or iterative optimization approach of “configuring to optimizing”. This results in decisions made during the configuring stage locking the feasible domain of the scheduling stage, ultimately yielding only “step-by-step optimization” rather than “global optimization”, making it difficult to synergistically balance between investment cost and operational revenue and ultimately increasing the overall system cost.

Moreover, the charging and discharging processes are subject to multiple requirements, with decision variables and constraint equations mutually coupled, resulting in a significant decrease in solution efficiency. Additionally, conventional methods often subjectively initialize the dispatch process with a fixed SOC level (50% or the historical average), lacking a dynamic response to the real-time state of the microgrid. Consequently, the system lacks sufficient ability to intelligently respond to peak and valley pricing signals, substantially undermining both its arbitrage potential and regulation capability.

To address this, a dynamic optimization mechanism for energy storage based on state mapping is proposed, in which the configuration objectives—storage capacity, power, and daily cycle SOC—are directly coupled with the storage’s operational state into a single decision variable set. This unified mechanism enables the simultaneous global optimization of both configuration and optimization, thereby overcoming the shortcomings of local optima in conventional approaches and enhancing both the energy utilization efficiency and the economic performance of the storage system, as shown in Figure 13.

During the variation in the energy storage operating state, the maximum and minimum storage surpluses are coupled with the corresponding upper and lower bounds of the SOC. By employing the state-mapping mechanism, the storage configuration is systematically linked to these boundary conditions, ensuring the physical feasibility and consistency between operational states and configuration parameters.

$$E_{reserve}={\displaystyle \frac{\left(W_{reserve}^{max}-W_{reserve}^{min}\right)}{\left(SO{C}_{max}-SO{C}_{min}\right)}}$$

(33)

where $W_{reserve}^{max}$ and $W_{reserve}^{min}$ denote the max and min surpluses of storage operation state; $SO{C}_{max}$ and $SO{C}_{min}$ denote the upper and lower bounds of SOC, with values of 0.9 and 0.1.

Furthermore, based on the energy storage capacity and operating state, the optimal initial surplus of storage and the corresponding initial SOC value are configured:

$$E_{reserve}^{0best}=E_{reserve}\times SO{C}_{min}+W_{reserve}\left(0\right)-W_{reserve}^{min}$$

(34)

$$SO{C}_{reserve}^{0best}=W_{reserve}^{0best}/E_{reserve}$$

(35)

where $E_{reserve}^{0best}$ and $SO{C}_{reserve}^{0best}$ denote the optimized configured initial energy surplus and SOC level of the energy storage system.

5.2. Collaborative Optimization Method for Storage Management and Energy Interconnection

The dynamic optimization of energy storage based on state mapping effectively leverages the management capabilities of the energy storage system, enhancing flexibility and efficiency in addressing the fluctuations and intermittency of source and load. Additionally, the distributed interconnected structure of multi-microgrid maximizes the dispatchability potential of energy storage [31], enhancing the coordination and dispatch of energy. By combining and exploiting both strengths, a collaborative optimization method for storage management and energy interconnection is proposed. This integrated approach promotes the dual maximization of the system’s resource utilization and economic performance. The energy storage allocation price and power supply interaction efficiency are shown in

Table 2. Energy storage allocation price and power supply interaction efficiency.

Parameter	Value
$C^{reserve}$	0.411 CNY/kWh
$C^{power}$	0.027 CNY/kW
${\gamma }_{ii}$	1
${\gamma }_{ij}$	0.9

.

5.2.1. Restrictive Condition

In the distributed optimization architecture, subgrids formulate energy management strategies through information exchange and energy transfer. Since the energy management strategies of these subgrids are interdependent, ensuring their coordinated operation is crucial for maintaining system stability and enhancing the overall performance.

(1)

Self-power and interacting power constraints:

$$\left\{\begin{array}{c}{P}_{ii}^{min}(t)\le P_{ii}(t)\le P_{ii}^{max}(t)\hspace{1em}\\ P_{ij}^{min}(t)\le P_{ij}(t)\le P_{ij}^{max}(t)\hspace{1em}i\ne j\end{array}\right.$$

(36)

where $P_{ij}$ denotes the interaction power supply from the storage.

(2)

Power supply interaction switching constraints:

$$\left[\begin{array}{c}{P}_1^{supply}(t)\\ ⋮\\ P_3^{supply}(t)\end{array}\right]=diag(\left[\begin{array}{ccc}{\gamma }_{11}& \dots & {\gamma }_{13}\\ ⋮& \ddots & ⋮\\ {\gamma }_{31}& \dots & {\gamma }_{33}\end{array}\right]\times \left[\begin{array}{ccc}{P}_{11}(t)& \dots & P_{13}(t)\\ ⋮& \ddots & ⋮\\ P_{31}(t)& \dots & P_{33}(t)\end{array}\right])$$

(37)

(3)

Power balance constraints:

$$P_i^{web}(t)=P_i^{load}(t)+P_i^{supply}(t)-P_i^{re}(t)$$

(38)

where $P_i^{web}$ denotes the power purchased from the grid.

(4)

SOC cyclic balance constraints:

$$SOC(24)=SOC(0)$$

(39)

5.2.2. Objective Function

The total operating cost of the system is the power purchased from the grid and the configuration of energy storage for the power and capacity:

$$\left\{\begin{array}{c}min\left(F\right)=F_1+F_2\\ F_1={\displaystyle \sum _{i=1}^3}{\displaystyle \sum _{t=1}^{24}}{P}_i^{web}(t)\times C(t)\\ F_2={\displaystyle \sum _{i=1}^3}{P}_i^{reserve}\times C^{reserve}+{\displaystyle \sum _{i=1}^3}max\left|{\displaystyle \sum _{j=1}^3}{P}_{ij}\left(t\right)\right|\times C^{power}\end{array}\right.$$

(40)

where $P_i^{reserve}$ denotes the energy storage capacity; $C^{reserve}$ is the average daily storage capacity cost [32]; $C^{power}$ is the average daily storage power cost.

5.3. IMODE Single-Objective Optimization Algorithm

The PlatEMO platform is utilized to apply the IMODE algorithm [33] to address this large, single-objective, multi-constraint problem. The IMODE algorithm is an enhanced version of the differential evolution (DE) algorithm, which integrates multiple DE operators and adjusts their application based on the solution’s quality and diversity. This adaptive approach significantly improves the algorithm’s performance in the following basic steps:

• Basic principles

IMODE improves the algorithmic performance on optimization problems by dynamically allocating resources among multiple DE operators in conjunction with a dynamic search strategy.

(1)

Multi-Operator Cooperative Evolution: The initial population is partitioned into sub-populations, each evolving under a distinct DE mutation strategy, and individuals are reallocated adaptively based on the performance of their operators.

(2)

Dynamic Resource Strategy: The population size decreases linearly to balance exploration and exploitation, with SQP local search applied in the final 15% of evaluations to finely adjust the current best solution.

2.

Key methods

(1)

Dynamic Multi-Operator Resource Allocation: The operators are ranked by solution quality and diversity to allocate more individuals to high-performers, while parameter self-adapting mechanisms are incorporated to minimize manual tuning.

(2)

Diversity Preservation and Balance: An archive strategy is employed to retain historically inferior solutions, and random binomial or exponential crossover operators prevent premature convergence, maintaining an exploration–exploitation balance.

The algorithm implementation procedure is as follows (Algorithm 2):

Algorithm 2: Procedure of IMODE

1. Initial Population Generation: Generate an initial population randomly and divide it into sub-populations. 2. Sub-population Mutation: Assign each sub-population a different differential evolution (DE) mutation strategy to generate new candidate solutions. 3. Solution Evaluation: Calculate new solutions’ objective function values, compare with current individuals, and select the better solution to proceed to the next generation. 4. Adaptive Operator Adjustment: Dynamically adjust the operator allocation based on the quality and diversity ratio of the population. 5. Population Size Reduction: Gradually reduce the population size to accelerate convergence during the evolutionary process. 6. Local Optimization: Apply the SQP method to refine the optimal solution during the final 15% of the evolution process. 7. Termination: If the maximum number of function evaluations is reached or other termination criteria are met, output the optimal solution. Otherwise, continue the iteration.

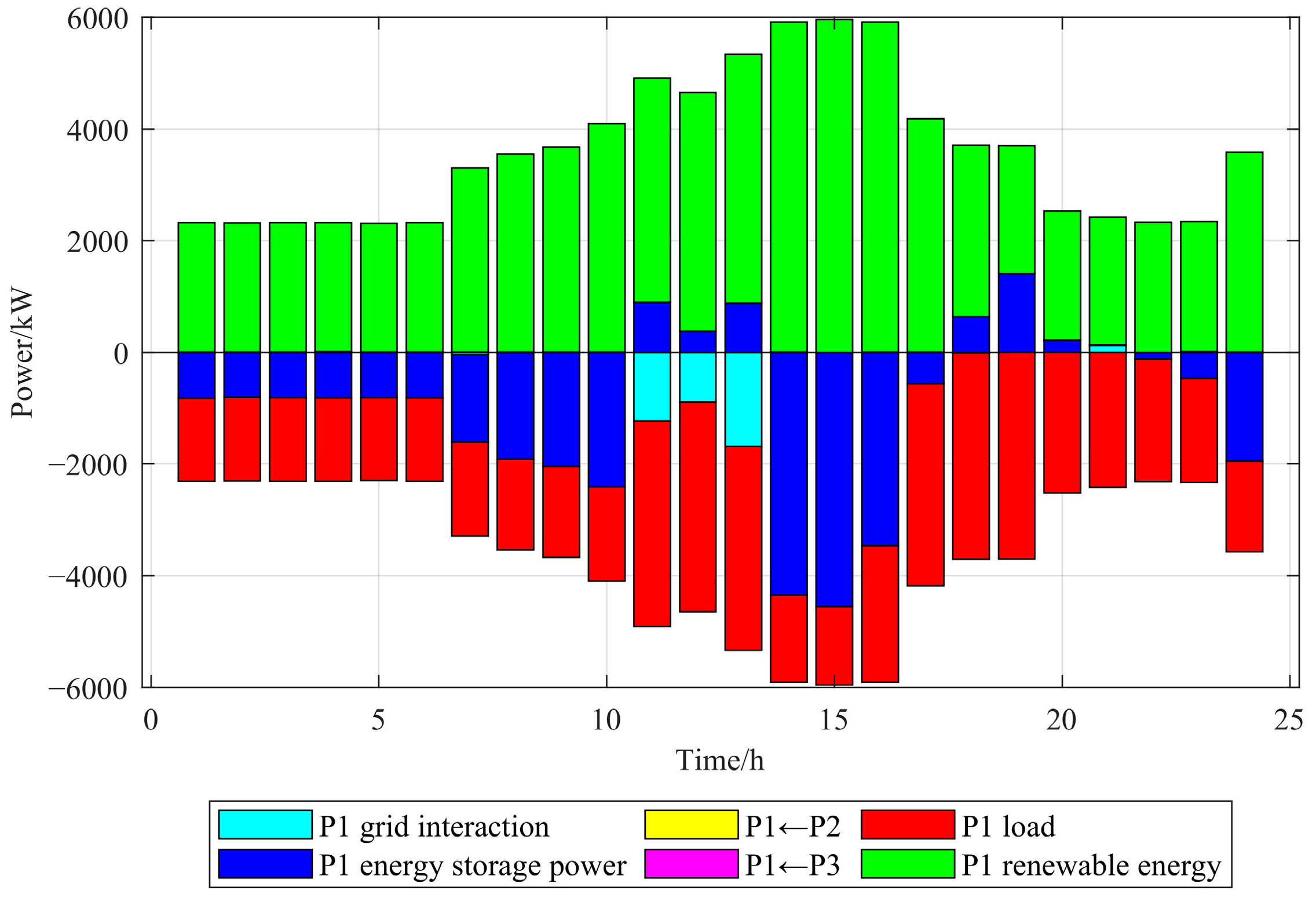
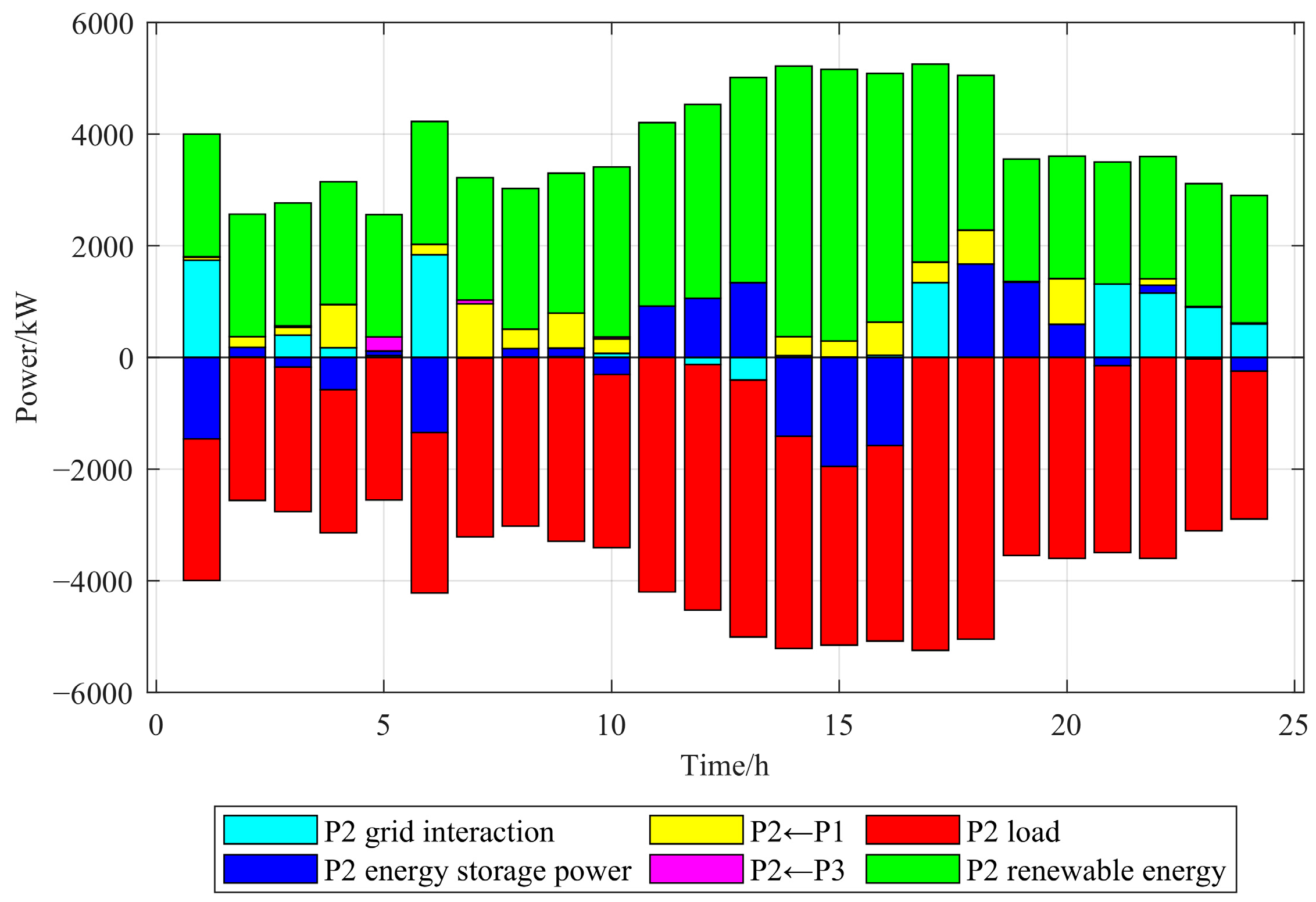
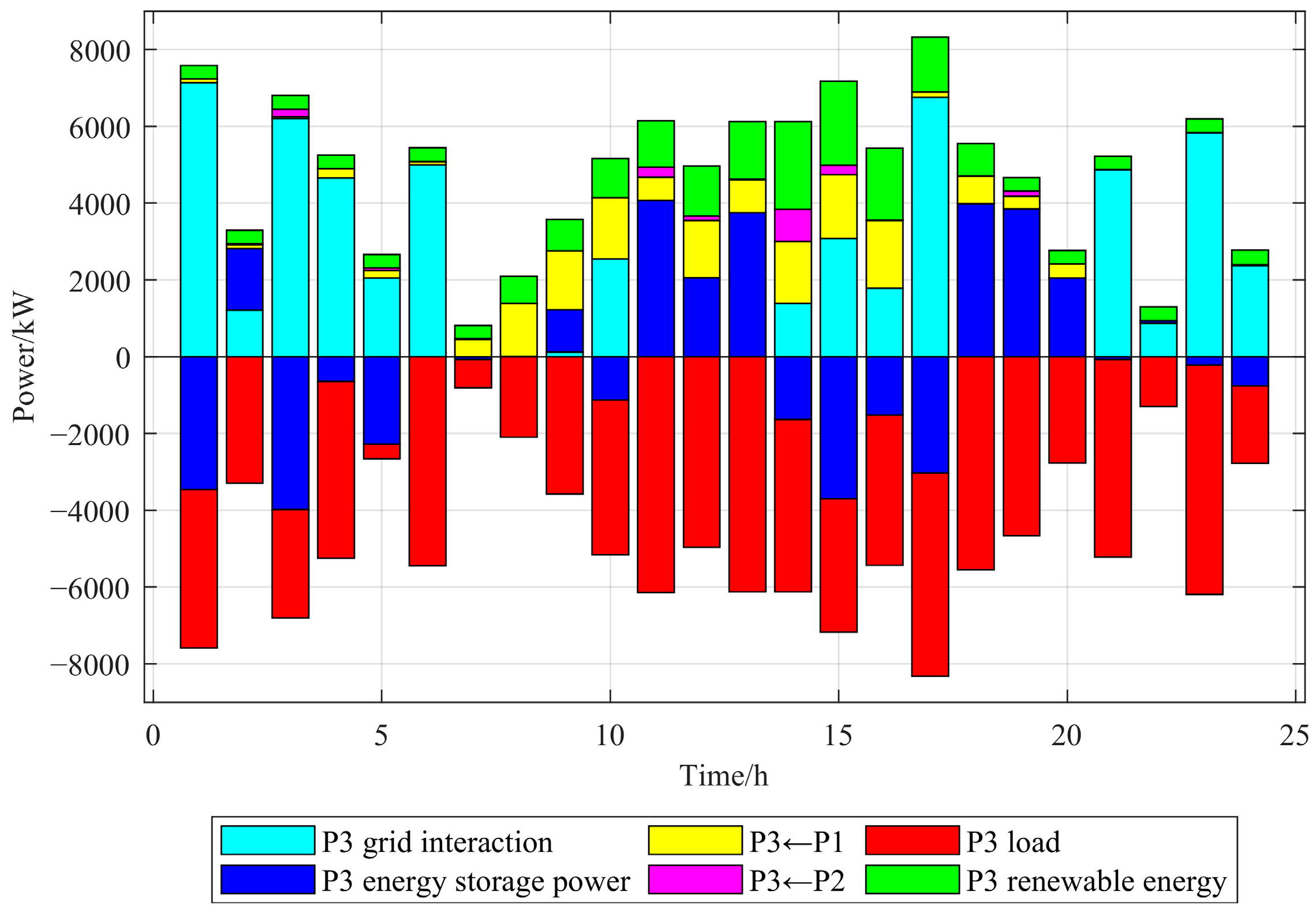
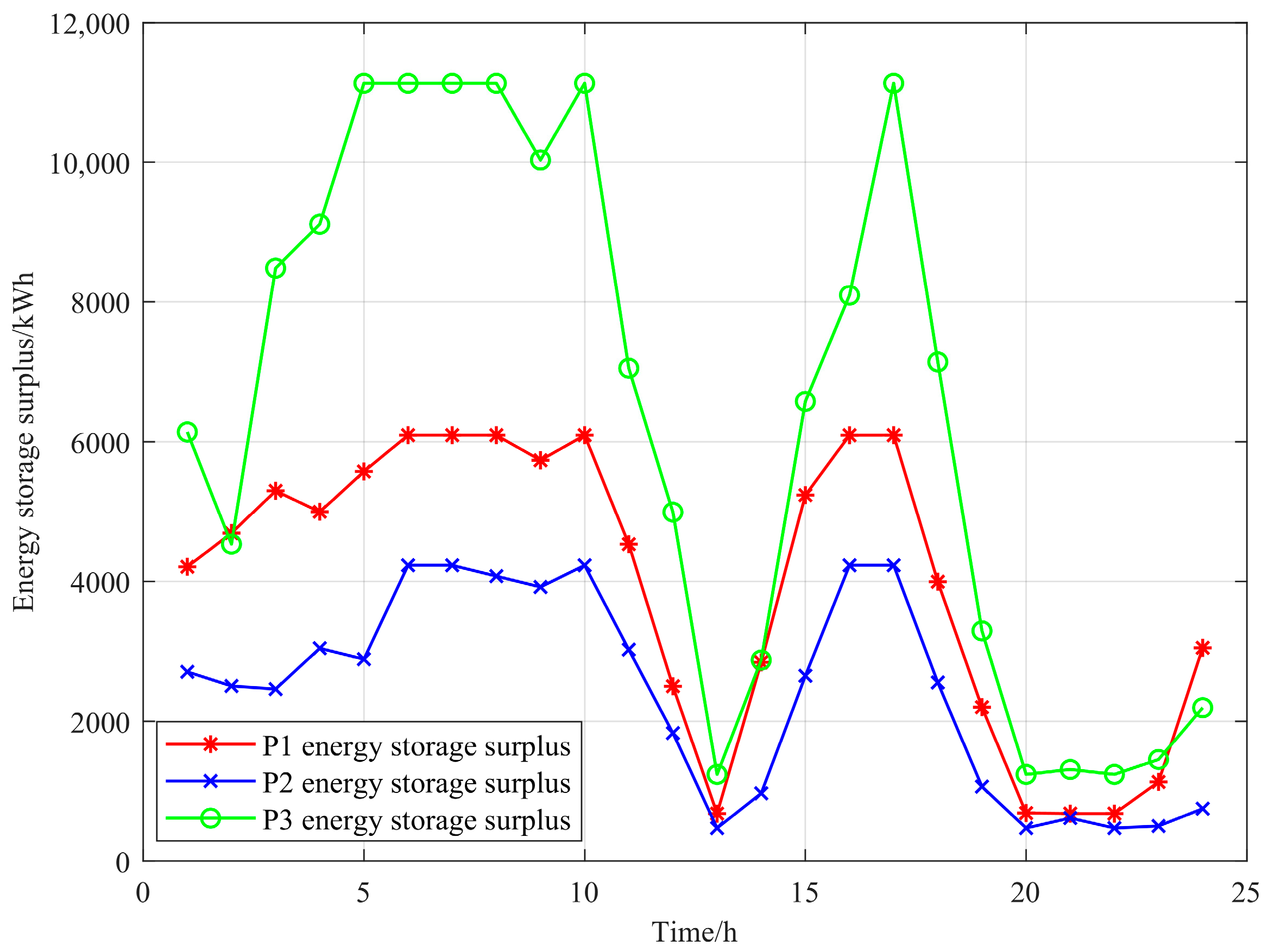
5.4. Analysis of Optimization Results from Multi-Microgrid Simulation

As shown in Figure 14, P1 has a sufficient energy supply and low load demand, allowing it to achieve self-sufficiency with minimum reliance on other microgrids for energy. Additionally, it has the flexibility to store excess energy or transfer it to other microgrids during periods of peak demand.

As shown in Figure 15, P2’s energy supply and load demand are generally well synchronized, with a staggered pattern during peak tariff periods (11–13 and 18–20), which allows P2 to receive a small amount of external supply while maximizing the benefits of energy storage. By storing energy during off-peak periods and releasing it during peak periods, P2 can achieve higher economic efficiency.

As shown in Figure 16, P3 experiences an insufficient energy supply and high load demand, requiring it to rely on excess energy from other microgrids most of the time. During low-demand periods, it interacts with the grid to manage load supply and storage while relying on its storage system to discharge power during peak times. To support the high load and fluctuation demand, P3 is configured with a significantly larger storage capacity and power to achieve stability and flexibility in the power supply (as shown in Figure 17 and Figure 18). The energy storage configurations and settings are shown in

Table 3. Energy storage configuration and settings.

	P1 Energy Storage	P2 Energy Storage	P3 Energy Storage
Initial SOC	52.5%	26.5%	21.8%
Max Energy Capacity/kWh	6771.9	4698.8	12,361.6
Max Charging Power/kW	2393.3	1685.1	3953.1
Max Discharging Power/kW	2100.4	1673.3	4075.0

.

The collaborative optimization for storage management and energy interconnection within a distributed multi-microgrid interconnection system effectively minimizes excess energy waste and enhances power resource management, thereby improving the overall economic efficiency of the system. Before optimization, the total operating cost of the system is CNY 46,354.2. After optimization, the system’s grid power purchase cost is reduced to CNY 26,070.7, and the energy storage allocation cost is CNY 10,017.5, resulting in a total operating cost of CNY 36,088.2, which reflects a cost reduction of 22.1%.

6. Conclusions

In this paper, to address the two core challenges, the disordered nature of EV charging and user electricity consumption behavior intensifying grid strain, and the lack of effective supply–consumption regulations and cost–benefit optimization mechanisms in energy storage technology and microgrid interconnections, adaptive and collaborative hierarchical optimization strategies are proposed for scheduling EVs and controllable loads, along with optimizing storage management and energy interconnection in a multi-microgrid distributed system, which successfully overcome the identified issues and effectively enhance the overall operational efficiency and economic performance. The following conclusions can be drawn from this paper:

(1)

Building on the EV storage margin band within a single microgrid to facilitate EV-to-grid interaction, the lower layer explores a cooperative operation mechanism that integrates EV-to-grid interaction with controllable load dispatch. An adaptive optimization method for EV storage operation and demand response is proposed to leverage the energy storage capabilities of EVs while harnessing the potential of demand-side management. Through the dispatch of 13.4% of the controllable loads, this method accomplishes effective peak shaving and valley filling with a negligible impact on user comfort. Consequently, it achieves a 38.5% reduction in the total electricity cost associated with the user’s EVs and controllable loads, significantly improving the microgrid system’s economic efficiency and operational stability.

(2)

Building on the EV–load management strategy at the lower microgrid layer, the upper layer further develops a synchronous optimization mechanism for energy storage operation and configuration. A dynamic optimization mechanism based on state mapping is proposed, where the operational state of the energy storage system is mapped to the configuration objectives, enabling a simultaneous optimization solution. This method significantly enhances the SOC utilization rate of energy storage and improves the economic efficiency of the configuration, ultimately achieving optimal storage management.

(3)

Additionally, as the distributed interconnected structure of the multi-microgrid can maximize the dispatch potential of energy storage, a collaborative optimization method for storage management and energy interconnection is proposed based on a comprehensive exploration of their synergistic operation mechanism. By simultaneously maximizing resource utilization and economic performance, this method effectively reduces excess energy waste and enhances power resource management. Consequently, the total system operating cost is reduced by 22.1%, significantly enhancing the overall system’s resource utilization and economic performance.

For the proposed optimization algorithm, taking the adaptive genetic algorithm as an example, it leverages the linear tuning of crossover and mutation rates to boost convergence and diversity, but its fixed linear schedules depend on manual parameter setting and ignore population dynamics, risking premature convergence or excessive randomness, and the other algorithms also have similar problems.

Future research should prioritize the advancement of next-generation smart grid architectures to achieve deep multi-energy coupling and dynamic market integration, while increasingly improving optimization algorithms and leveraging AI-driven decision-making to enhance the operational efficiency. Emphasis should be placed on multi-timescale and multi-scenario collaborative optimization to enhance system adaptability, resilience, and operational efficiency in response to real-world uncertainties and dynamic conditions.