Abstract
Multimodal transport refers to the integrated transportation in a logistics system in the form of multiple transportation modes, such as highway, railway, waterway, etc. In recent years, the deep integration of electric trucks and route optimization has significantly improved the cost-effectiveness and operational efficiency of multimodal transportation. It has provided strong support for the sustainable development of the logistics system. Based on whether to consider low-carbon requirements, uncertainty, and special cargo transportation, the literature is divided into five areas: traditional multimodal transport path optimization, multimodal transport path optimization considering low-carbon requirements, multimodal transport path optimization considering uncertainty, multimodal transport path optimization considering low-carbon requirements and uncertainty, and multimodal transport path optimization considering special transport needs. In this paper, we searched the literature on multimodal path optimization after 2016 in WOS (Web of Science) and CNKI (China National Knowledge Infrastructure), and found that the number of publications in 2024 is three times that in 2016. We collected 130 relevant studies to summarize the current state of research. Finally, with the development of multimodal transport to collaborative transport and the improvement of the application of in-depth learning in different fields, the research mainly focuses on two future research directions: collaborative transport and the use of in-depth learning to solve uncertain problems, and combining it with the problem of multimodal transport route optimization to explore more efficient and perfect transport solutions.
1. Introduction
1.1. Background
Multimodal transport achieves the goal of reducing costs and increasing efficiency by connecting various modes of transport services and unifying standards. In recent years, the transportation network has been gradually improved, the mileage of roads and railways has continued to increase, and the container throughput of railways and waterways has also shown an upward trend [1]. During this development process, the integration of various new technologies has reshaped the entire transportation ecosystem, not only reducing energy consumption but also reducing traffic congestion and improving transportation efficiency, bringing significant benefits to improving the multimodal transport system [2]. The multimodal transport route optimization problem is a comprehensive decision-making problem involving multiple factors such as economy, environment, and service. Under the national dual carbon policy, multimodal transport has received much attention due to its key role in reducing environmental impact and improving efficiency. However, there will be various uncertainties during the transportation process, and there will be multiple optimization goals such as economy, environment, and service. How to solve these complex problems is the core challenge of multimodal transport route optimization. At the same time, electric trucks are developing rapidly, which is one of the core trends, offering transformative potential for the sustainable design of multimodal transport systems [3]. Therefore, it is particularly important to deal with uncertainties in the transportation process and effectively integrate these emerging technologies. The container throughput and infrastructure construction are shown in Figure 1 and Figure 2.
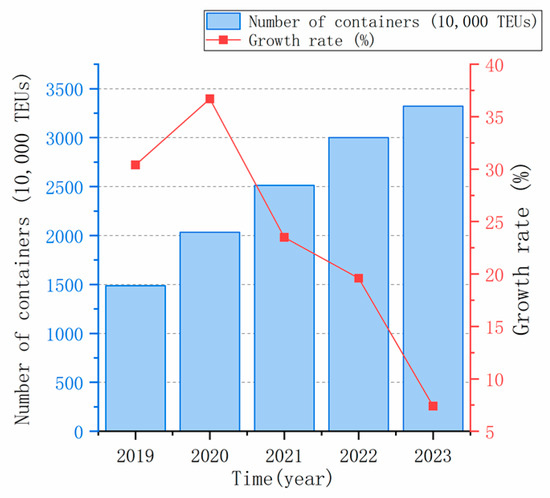
Figure 1.
Container throughput.
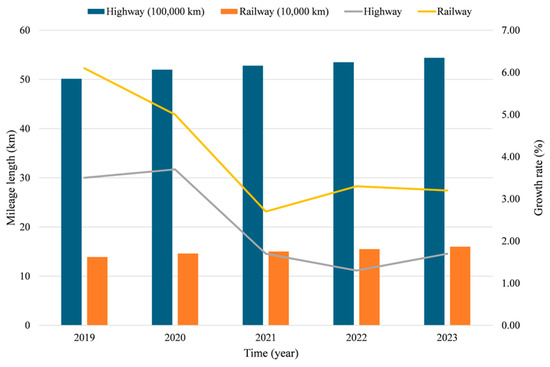
Figure 2.
Infrastructure construction.
China’s multimodal transportation is in a rapid development stage. Although there is a large increase in the number of public rail lines every year, it is relatively small compared to the whole intermodal network, resulting in an imperfect basic intermodal network. Ye et al. [4] explore the development of multimodal transportation, indicating an increasing demand for building new infrastructure. Moreover, as intermodal transportation moves towards intelligence and efficiency, intelligent integration and energy efficiency management of electric trucks are one of the key strategies to improve system sustainability and efficiency [5]. At the same time, integrating advanced digital technologies and ensuring environmental sustainability in logistics is becoming a necessity for the new intermodal transportation concept of the current times [6,7].
1.2. Multimodal Transport Path Optimization Review
To ensure the continuous development of multimodal transport path optimization, it is necessary to focus on the problem of cooperative scheduling in the transport process. Zhang et al. [8] proposed that the key to the high-quality development of multimodal transport is the efficient connection of various modes of transportation, to achieve collaborative scheduling. Shen et al. [9] conducted a review based on domestic and international literature, analyzed and explored the operation mechanism, development mode, and evolution trend of multimodal transport, and mentioned that the suitable multimodal transport development mode in China is to focus on coordinating modes of transport to create an integrated scheduling-type multimodal transport system.
The complexity of multimodal transport route optimization mainly stems from its multi-objective nature and multiple uncertainties, which pose significant challenges in the design of solutions [10,11]. Claudia et al. [12] reviewed the literature on multimodal transportation up to 2020. It was found that the phenomenon of single transportation is still prominent. A current topic of high research interest is the research considering carbon emission and trans-shipment cost, and many scholars are indeed performing related work at present. In the multimodal transport path optimization literature from 2016 to the present, more scholars have begun to consider more complex situations, and they use low carbon as the background to consider the multi-objective problem and multiple uncertainty problems in transport, which undoubtedly makes the problem increasingly complicated.
Although there is an increasing amount of research on multimodal transport route optimization, it is often scattered across different sub-problems and modeling and solution methods. The core goal of this article is not just to list the problems, models, and methods, but to deeply analyze the internal connections between these problems through a systematic and comprehensive framework. By comparing the applicability and limitations of different models, we can sort out the context of the evolution of methods, and finally propose the organic integration direction of future research based on this. Through analysis and summarization, the following problems in the existing research have been identified: (1) The multimodal path optimization problem encompasses a variety of types of problems, and the current research lacks a persuasive and clear classification framework. (2) The path optimization problem has been proved to be a typical NP-hard problem, which has been studied by a large number of scholars. However, for this kind of problem, most scholars analyze the specific problem and model the solution and lack of statistics and perform comparisons of existing models and algorithms. The multimodal transportation path optimization network is shown in Figure 3. (3) Despite the numerous academic research results on path optimization problems, their practical applications still lag behind. Existing studies rarely summarize and analyze the potential future research directions and possible challenges in development. To comprehensively solve the multimodal transportation path optimization problem, the following work is carried out:
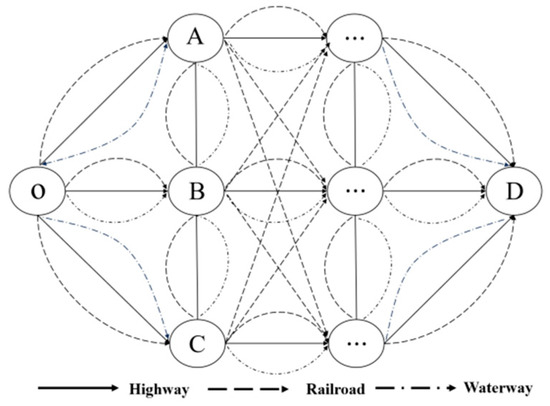
Figure 3.
Multimodal route optimization network diagram. Among them, O represents the origin, and D represents the destination. A, B, and C represent transit hubs.
- (1)
- Existing research articles on multimodal path optimization are collected and classified according to the research object. Based on this classification, a structured classification framework that distinguishes it from other studies is proposed to analyze the focus areas and applicable scenarios of various types of models.
- (2)
- The mathematical modeling approaches adopted for different path optimization problems are also considered. Moreover, the problem is essentially an NP-hard problem, and it is more complicated to obtain the optimal solution directly; the common solution algorithms for solving this problem are summarized.
- (3)
- The current research status of the multimodal transportation path optimization problem is summarized and the potential future research directions discussed.
The structure of the subsequent part of this paper is as follows: Section 2 analyzes in detail the current research status of domestic and foreign scholars on multimodal transportation path optimization problems according to different research objectives and other factors. Section 3 summarizes the mathematical modeling methods according to the characteristics of various types of models and summarizes and analyzes the solution algorithms. Section 4 summarizes and puts forward two potential future directions according to the current research status. Section 5 gives the main conclusions of the research. The structural framework of this paper is illustrated in Figure 4.
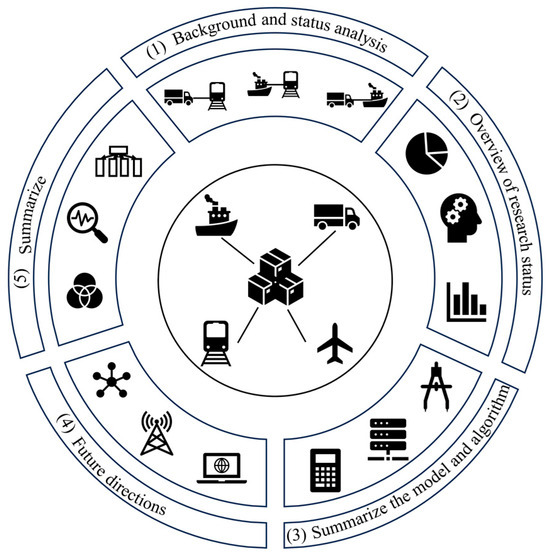
Figure 4.
The structural framework diagram. (1) Background introduction and overall summary of multimodal transport. (2) Analysis of the current research status both domestically and internationally. (3) Summary and analysis of the models and algorithms used in the research institute. (4) Future prospects and key research directions. (5) Summary.
2. Overview of Research Status
The multimodal transportation path optimization problem has been a research topic of high interest; in recent years, there have been increasing numbers of papers related to this field. Searching with “multimodal transportation” as the keyword, we can see the number of articles published by CNKI (China National Knowledge Infrastructure) and WOS (Web of Science) in recent years and the growth rate, as shown in more detail in Figure 5 and Figure 6.
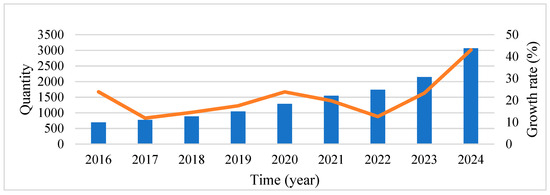
Figure 5.
Number of published articles in WOS on multimodal transportation.
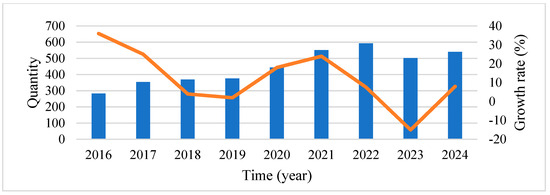
Figure 6.
Number of published articles in CNKI on multimodal transportation.
A comprehensive review of the literature on multimodal path optimization from 2016 to 2025 was conducted by searching for the relevant keywords, “multimodal transportation”, “path optimization”, and “vehicle scheduling”, on CNKI and WOS, respectively. The literature relevant to the study was selected. Then, the references as well as the keywords of these studies were searched and studied again to broaden the search scope. Finally, after a rigorous screening process to exclude some lower-relevance studies as well as lower-value studies, 130 studies were selected to be analyzed and categorized with respect to the date of the studies, as shown in Figure 7. According to the research hotspots and directions in recent years, the multimodal transport path optimization problems are classified into five categories here: traditional multimodal transport path optimization, multimodal transport path optimization considering carbon emission, multimodal transport path optimization considering uncertainties, multimodal transport path optimization considering uncertainties under low carbon emission, and multimodal transport path optimization considering special needs (shown in Figure 8).
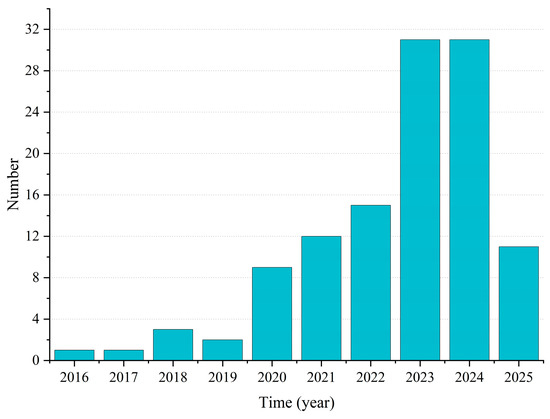
Figure 7.
Statistics of literature publication years.
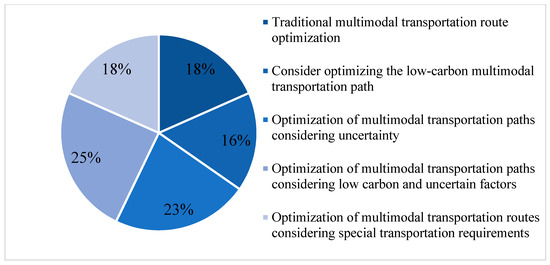
Figure 8.
Research directions.
The multimodal transportation path optimization problem involves a variety of transportation modes as well as transit scheduling. Meanwhile, different transportation objectives, different transportation modes, and different model algorithms lead to a path optimization process full of complexity, dynamics, and other characteristics. Here, under the five general directions, the literature is further subdivided according to the different research objectives. The overall literature category framework is shown in Figure 9.
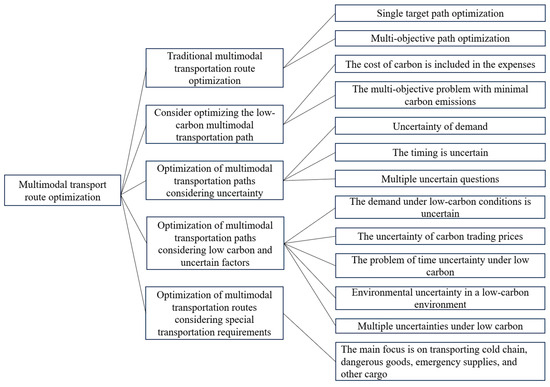
Figure 9.
Overall framework of research status.
The rest of this chapter will review the literature by breaking it down into five major directions as well as a number of minor directions, following the framework shown above.
2.1. Traditional Multimodal Transportation Path Optimization
Before the promulgation of the national low-carbon policy, few scholars have considered low-carbon issues and various uncertainty factors when studying multimodal transportation path planning. Therefore, the research that has not yet considered the low-carbon environment and uncertainty factors is categorized as the traditional multimodal transportation path planning problem. Domestic and international research on the optimization of traditional multimodal transport routes mainly focuses on single-objective optimization or multi-objective optimization with cost optimization and time optimization.
2.1.1. Single-Objective Multimodal Transportation Path Optimization
Cost optimization is one of the most fundamental aims in the multimodal route optimization problem. The goal is to minimize overall transport costs by quantifying the various transport costs, time penalty costs, damage compensation costs, etc., and to achieve cost reductions and efficiencies by taking into account more real influencing factors [13].
Some scholars focus on cost calculation and pricing problems [14]. Kovalenko et al. [15] extended a theoretical framework for evaluating the generalized transportation cost of multimodal transport solutions in the maritime sector. Pian et al. [16] addressed the problem of equilibrium pricing of direct container road transport versus intermodal transport via dry ports taking into account scale discounts for rail transportation.
Cargo transportation is required to be completed within a certain timeframe, which requires comprehensive consideration of constraints such as the node operation time window, mode of transportation, fixed departure moments, and collection time window at the endpoint in the freight transportation process [17,18]. Peng et al. [19] established a 0–1 integer planning model with cost minimization for the dual constraint problem of intermodal path optimization with time windows and schedules. In order to manage deviations in transit time and the risk of loss or damage to goods in transit. Zhang [20] introducing time penalty costs and damage costs into the optimization framework, with the lowest combined cost as the model objective. But it is often not enough for cost calculations to consider only these few external factors. In practice, Guo [21] proposed a co-optimization strategy for multi-period sourcing and multimodal transport, which takes into account cost factors such as sourcing, transport, trans-shipment, and storage costs incurred by early arrivals. A mixed-integer planning model is developed to minimize the overall operating costs of cross-border e-commerce enterprises by arranging procurement, transportation, and storage strategies. Liang [22] quantified multimodal transportation satisfaction by using the affiliation function of trapezoidal fuzzy numbers and obtained a soft time window for the cargo arrival time frame. Farahani et al. [23] used an advanced multimodal transportation service network model (AI-SNM). A mixed-integer planning model is constructed with the objective of cost minimization by considering multiple modes of transportation, resource constraints, and time window constraints in the intermodal transportation process. Wang [24] considered both objective problems of time and cost in modeling; their conversion of the objective function of cost minimization into constraints achieved the conversion from multi-objective to single-objective problems, reducing the complexity of the model and the difficulty of solving it.
Most of the studies have only considered the transportation of single-commodity flow, and some studies have also addressed the problem of multi-commodity flow. Qi et al. [25] constructed a container multimodal transport path optimization model with the minimum total cost including transportation, trans-shipment, waiting, and penalty for multi-tasks with different receiving and dispatching places and different time windows, while considering the shift restrictions and the influence of the capacity of water and railway transportation. Multi-commodity transportation is more complex than single-commodity flows because it involves multiple origins and multiple points of shipment.
2.1.2. Multi-Objective Intermodal Transportation Path Optimization
Compared with single-objective optimization, the multi-objective model for intermodal path optimization has a higher complexity in both modeling architecture and solutions than the single-objective model. The reason for this is the unavoidable conflict between multiple optimization objectives, which requires the researcher to design a finer-grained co-optimization mechanism [26]. In this regard, there are more studies aiming at minimizing the total cost and time of transport [27]. For example, Wu et al. [28] studied the container intermodal transportation problem under the condition of considering the time value of goods, container box type, and other factors, established a dual-objective optimization model, and then discussed how to balance these two conflicting objectives so that they can apply the linear weighting method to transform the dual-objective problem into a single-objective problem. And Wang et al. [29] established a bi-objective optimization model with the objectives of minimizing cost and maximizing customer satisfaction considering inventory and road disruption. Seo et al. [30] explored various alternative routes for exporting laptop computers from Chongqing, China, to Rotterdam, the Netherlands, considering multiple objectives such as transportation cost, transit time, and other objectives for the path selection.
In summary, in multi-objective optimization, compared to single-objective problems, the model will be more complex, because often there is a phenomenon of benefit backwardness between various factors for some relatively simple single-objective models, which can use the exact algorithm to solve. But for multi-objective problems, how to deal with the weight relationship between each objective, how to choose the appropriate algorithm for solving the problem is a problem that requires extra attention. Table 1 is the summary table of traditional multimodal transportation path optimization research.

Table 1.
Summary of research on traditional multimodal transport route optimization.
2.2. Optimization of Intermodal Transport Routes with Low-Carbon Considerations
In the context of China’s dual carbon policy, transportation, as the second largest carbon-emitting sector, has become an important field in which to reduce carbon emissions through multimodal transport. By optimizing the route mix, it can significantly reduce the overall carbon emissions, helping to achieve global and Chinese carbon neutrality targets [31]. On the other hand, this not only reduces transport costs by taking advantage of the cost advantages of rail and water transport, but also enhances competitiveness in the long term by avoiding the risk of future carbon taxes and obtaining government subsidies. Therefore, the optimization of multimodal transport routes considering low carbon is an inevitable choice driven by multiple factors such as environmental pressures, policies and regulations, and economic benefits [32].
Compared with the traditional multimodal transport path optimization problem, considering low carbon emissions undoubtedly makes the model more complicated. Scholars have made various attempts on how to address the carbon emission problem, which are mainly divided into two kinds: one is to count the carbon emission cost into the total cost and establish a multi-objective model with the lowest total cost or including the total cost, and the other is to directly establish the model with the minimum carbon emission as an optimization objective.
2.2.1. Problems of Including Carbon Price in Costs
The main solution to this problem is mainly the introduction of carbon cost variables into traditional transportation cost models. A single-objective optimization function that incorporates a variety of transportation economic costs, time costs, carbon emission costs, and a combination of other costs must be constructed and solved for minimizing the total cost [33]. This approach can drive transportation choices toward low-carbon modes such as rail and water.
Aiming at the different impacts of different policies on the carbon price, Zhang et al. [34] constructed a minimum cost multimodal transport path optimization model including carbon emission cost according to carbon emission, carbon tax, carbon trading, and carbon compensation policies, and analyzed and compared the path optimization problems under different carbon emission policies through different examples. Guo [1] constructed a minimum-cost multimodal transport path optimization model with the total cost including carbon emission cost by taking into account the factor of railroad skylight. Wu et al. [35] and Chen et al. [36] internalized carbon emission into carbon tax cost to solve the problem.
The above findings suggest that the increase in the price of carbon has facilitated a modal shift in transportation from road to waterways and railroads. At the same time, the structure of the intermodal transportation network has become thinner, and total carbon emissions have decreased. On the other hand, an appropriate carbon price can promote a balanced freight structure and reduce carbon emissions.
2.2.2. Multi-Objective Problem with Carbon Emission Minimization
However, a single cost target has certain limitations, which can be summarized in two points. The first is that the goal of cost minimization will inevitably sacrifice other goals, for example, choosing low-cost, high-emission paths and low-reliability routes [37]. Secondly, the quantification of carbon emission costs can lead to optimization results that are detached from complex real-world environments [38]. Therefore, minimizing carbon emissions as one of the goals is a good solution.
The essence of the multi-objective intermodal route optimization problem including carbon minimization is to construct a system that can maintain a balance between cost and environment. The problem requires a bi-objective or multi-objective optimization model [39]. The main objectives considered are minimizing cost, time and carbon emissions. This is more complex than the single-objective problem. In practice, Liu et al. [40], Wan et al. [41], Yin et al. [42] and Hou et al. [43] all considered the factor of carbon emission in the optimization of multimodal transport paths and established a multi-objective optimization model with minimum carbon emission, cost and time [44]. Wu et al. [45,46] have repeatedly studied the multimodal transport path optimization problem in a low-carbon environment and constructed a multi-objective green multimodal transport optimization model by considering the cost and carbon emission minimization at the same time.
In summary, the introduction of the carbon cost problem in the calculation of cost, in the establishment of a single-objective problem with the goal of cost minimization, is less difficult both in the establishment of the model and the difficulty of the solution if it is a multi-objective problem established directly with the minimization of carbon emissions; many scholars are also attempting to convert multi-objective processing into single-objective processing. Table 2 presents a summary of research on multimodal transportation path optimization in a low-carbon environment.

Table 2.
Summary of research on multimodal transport route optimization considering low-carbon.
2.3. Multimodal Transportation Path Optimization Considering Uncertainties
In practice, multimodal transportation is subject to multiple uncertainties, such as fluctuations in demand, time delays, capacity rationing, extreme weather and policy changes [47]. Incorporating these uncertainties into the optimization model not only enhances the system robustness, but also improves the on-time performance of the overall intermodal transportation system [48]. Depending on the focus of the research, the consideration of uncertainty problems can be broadly categorized into five groups: demand uncertainty, time uncertainty, environmental uncertainty, uncertainty in the carbon price, and the more complex problem of multiple uncertainties. We summarize this part of the problem, and find that current research focuses primarily on demand uncertainty.
2.3.1. Consideration of Demand Uncertainties
The demand uncertainty factor refers to the fact that in the process of multimodal transportation, the demand for cargo transportation has a large change or is difficult to accurately predict and grasp due to a variety of reasons, such as market environment, seasonal changes, and unexpected events. This uncertainty may lead to changes in cargo transport volume, transport time, transport mode, etc., thus affecting the optimization decision of multimodal transport path [49].
Uncertainty in demand increases transportation costs and time. Therefore, many scholars try to use various methods to solve this problem. For example, Li [50] designed a two-stage stochastic planning-based transit point location and sequential decision-making path planning for uncertain demand, thus realizing the design of cost-effective multimodal transportation network. Qiu et al. [51] introduced the theory of time value of goods to measure the loss of time value of goods in the transportation process and used the scenario method in robust optimization to establish a robust optimization model of multimodal transportation paths with the lowest cost synthesis. Sun et al. [52] and Yu et al. [53] constructed a fuzzy multi-objective model by using the triangular fuzzy number and the fuzzy ranking method of Žimmerne for the clear treatment of the uncertain demand, in response to the multimodal transport path optimization problem in the procurement chain due to fluctuations in commodity types and demand. Chen et al. [54] built an uncertainty model and used an improved genetic algorithm to solve the uncertainty of the type of goods and demand. Another study constructed stochastic planning models and incorporated uncertainty factors such as commodity type and demand in the procurement process, providing more forward-looking and flexible decision support for multimodal transportation route and mode optimization [55]. This not only significantly reduces transportation costs and operational risk, but also improves on-time performance and system emergency response.
2.3.2. Considering Problems with Time Uncertainty
Regarding the multimodal transportation path optimization problem under time uncertainty, in the multimodal transportation process, multiple shipments need to be transported from the starting point to the endpoint within a specified time through a combined transportation network that includes three modes of transportation: road, rail, and waterway. Due to the limited capacity of transshipment nodes and transportation routes, transportation delays or congestion may occur, which leads to the loss of time value of goods and an increase in transportation cost [56,57]. Tong [58] used triangular fuzzy numbers and opportunity-constrained planning theory to solve the multimodal transportation path optimization problem under the condition of transportation time uncertainty. Zhang et al. [59] proposed a multiorganization-weighting and Q-weighting method based on a positively skewed distribution to depict the uncertainty of time, using an optimization framework based on multi-objective weighting and Q-learning to deal with time uncertainty.
During the implementation of multimodal transportation, the intervention of natural and human factors can lead to uncertainty in the values of cargo transportation speed, on-time delivery probability thresholds, and transit time values [60,61]. Guo et al. [62] considered this problem and incorporated practical constraints in the parameter uncertainty to develop and solve a robust shortest-circuit mixed-integer programming model based on multimodal transportation networks under transportation time uncertainty.
2.3.3. The Problem of Considering Multiple Uncertainties
Considering multiple uncertainties simultaneously in multimodal path optimization is a complex but crucial task [63]. In the multimodal transportation path optimization problem considering multiple uncertainties, Tang et al. [64] considers the dynamic correlation between transit time and transportation demand, constructs a multi-objective model with the lowest total transportation cost and total transportation time, and uses opportunity constrained planning theory to clarify the model. Li et al. [65] studied the uncertainty problem of different cargo transportation as well as time in Yangtze River container intermodal path optimization and designed a dynamic planning algorithm based on depth-first traversal for intermodal path optimization to achieve the solution. Lu et al. [66] studied the fuzzy intercontinental intermodal path problem with the uncertainty of time and train capacity and established an uncertainty model to solve it. Peng [67] introduced Monte Carlo (MC) simulation to deal with the uncertainty of transportation time and cost. A multi-objective path optimization model for intermodal transportation with the objective of minimizing the total transportation time and cost was developed.
Unforeseen events during transportation may lead to disruptions or delays. He et al. [68] proposed a network modeling and robustness assessment method for intermodal freight networks with respect to unforeseen events. Xu et al. [69] considered the use of collaborative multimodal transportation with its flexible and sustainable features to solve the problem of uncertainty considering the unforeseen situations and uncertainty in demand during transportation. Guo et al. [70] used a storage service strategy to investigate the multicycle intermodal transportation path problem with time and train capacity uncertainty. They investigated the multi-period intermodal routing and transportation planning problem using a stored service strategy to build a robust mixed-integer planning model with the objective of time minimization, and solved it using an improved Dijkstra algorithm.
Based on the above several studies considering uncertainties, it can be seen that most of the uncertainties such as demand and time are handled using triangular fuzzy numbers and opportunity constrained planning theory. A summary of multimodal route optimization studies considering uncertainties is shown in Table 3.

Table 3.
Summary of multimodal transport route optimization research considering uncertain factors.
2.4. Optimization of Multimodal Transportation Paths Considering Low Carbon and Uncertain Factors
With the increasing heat of intermodal transport, scholars’ research on intermodal transport path optimization has increased in depth, starting from the very beginning of modeling and solving the problem purely for containerized freight transport, and later beginning to consider the carbon price and various uncertainties in the cost calculation. Zhang studies various uncertainty problems under low carbon emission based on the uncertainty of demand under low carbon emission [71], the uncertainty of demand and carbon trading price [72] and the uncertainty of demand and time under low carbon emission [73]. Currently, multimodal transportation path optimization under low-carbon conditions considering multiple uncertainties such as demand, time, and environment is the most popular problem.
2.4.1. Demand Uncertainty Problem Under Low Carbon
Research on multimodal transportation uncertainty mainly focuses on demand, and fluctuations in freight demand can lead to a chain effect of transportation cost and time consumption, which in turn affects the selection of transportation options [74]. There are various ways to deal with demand uncertainty in the problem of low-carbon intermodal transport path optimization under consideration of demand uncertainty.
When dealing with the problem of demand uncertainty, a model of demand certainty can be established, and then uncertainty factors are added, to construct the formation of a low-carbon multimodal transportation path optimization model under uncertain demand [75,76,77]. Liu [78] constructed a robust optimization framework based on a deterministic demand-based multimodal transport infrastructure model for the risks arising from demand fluctuations and changeover waiting during transportation. Waiting costs due to mismatch between train and aircraft schedules are taken into account in the cost calculations, in addition to traditional transportation and transit costs. And carbon emission constraints or carbon costs are introduced into the model according to various forms of low-carbon policies such as emission allowances, carbon taxes, and subsidies, in order to ensure the feasibility and low-carbon benefits of the worst-case scenario.
There are many other ways of dealing with demand uncertainty. For example, the introduction of fuzzy functions or the use of Monte Carlo simulations and the law of large numbers have been used to good effect [79]. In practice, Hu [80] combined carbon emissions and operating costs under one target framework. The objective function is reshaped through the carbon tax mechanism, and fuzzy demand is introduced to portray procurement uncertainty to quantitatively assess the impacts of different combinations of subsidies and energy mixes on pathway choices. Wang [81] established a single-objective model to minimize the total cost and then followed the transformation steps of Bertsima robust optimization method to solve the problem by using dyadic theory.
The fuzzy opportunity constraint theory is also an effective method to deal with uncertainty, which can use either triangular fuzzy numbers or trapezoidal fuzzy numbers according to the specific demand, and use opportunity constraint planning to deal with the uncertain demand expressed by trapezoidal fuzzy numbers according to the specific problem [82,83,84,85]. Deng et al. [86] dealt with the uncertainty problem by first transforming the multi-objective problem into a single-objective problem using the linear weighting method, and then making the model clear through the trapezoidal fuzzy number as well as the opportunity-constrained planning theory. Others have proposed a two-objective 0-1 stochastic path optimization model based on this model for two policy scenarios. Combined with the expectation processing of stochastic demand such as seasonal fluctuation and sudden replenishment, an overall trade-off between total cost minimization and carbon emission reduction is made. This treatment realizes the balance between green and economic benefits under different carbon tax scenarios [87].
2.4.2. Uncertainty Problem of Carbon Trading Price
Under the low-carbon environment, carbon emission becomes an important index to measure the environmental friendliness of transportation modes. Path optimization requires the selection of transportation modes and paths with low carbon emissions. The change in carbon trading price has a large impact on the total cost [88].
In considering the low-carbon multimodal transport path optimization problem under the uncertainty of carbon trading price, Li [89] considered the uncertainty of demand and the stochasticity of carbon trading price. A robust stochastic optimization model for container intermodal transport was constructed with the objective function of minimizing the total transport cost. Yang et al. [90], in order to solve the cold chain multimodal transportation path optimization problem under the uncertainty of carbon trading price, used the triangular fuzzy number to describe the carbon trading price based on the existing characteristics of carbon trading price changes in the market.
2.4.3. Problem Considering Time Uncertainty
In the low-carbon multimodal transport path optimization problem under the consideration of time uncertainty, the research on multimodal transport timeliness mainly focuses on the receiving time window [19]. Ai et al. [91] comprehensively considered the effects of transportation cost, time, and carbon emission, paid attention to the uncertainty of node operation time, generated random numbers to enrich the data through Box-Muller transformation, and used Monte Carlo simulation to generate the statistical characteristics of the total transportation time under the uncertainty of transportation time. Chen et al. [92] considered the low-carbon problem of the receiving time window in multimodal transportation path optimization, designed a soft time window for receiving goods based on shipper’s satisfaction, and used the Z fuzzy affiliation function to describe the functional relationship between transportation time and consignee’s satisfaction. Zhou et al. [93], on the other hand, used trapezoidal fuzzy numbers to portray the uncertainty characteristics of transportation time and transit time in multimodal transportation.
2.4.4. Consideration of Environmental Uncertainty
Environmental uncertainty refers to random disruptions caused by external natural disasters and fluctuations in infrastructure conditions. These events create the risk of transportation disruptions such as road closures and port shutdowns. In the low-carbon multimodal transport path optimization problem under consideration of environmental uncertainty, Li et al. [94], for the multimodal transport path planning problem under uncertain environment, built a model with cost, time, and carbon emission as the optimization objectives, and used a combination of game theory and weighted summation to obtain the optimal multimodal transport path. Yang et al. [95] established a low-carbon and low-cost multimodal transport path optimization model under fuzzy demand and fuzzy transport time, considering that enterprises must ensure robustness and risk-resistance when making plans.
2.4.5. Considering Multiple Uncertainties Under Low Carbon
Combining the uncertainty factors mentioned above, the main ones are demand uncertainty, time uncertainty, carbon price uncertainty, and environmental uncertainty. In the low-carbon multimodal transport path optimization problem, multiple uncertainties are considered [96,97]. Zhang et al. [98] considered the uncertainties of demand and time as well as mandatory carbon emission, carbon tax, carbon trading, and carbon offset policies in the multimodal transport process. A fuzzy demand opportunity constraint planning model and a fuzzy time interval planning model were developed. Dai [99] considered the multimodal transportation path optimization problem under various uncertainties including carbon price in the multimodal transportation process, and built a path optimization model considering different carbon policies. Sun et al. [100] took into account the various uncertainties of cost and time in multimodal transportation, introduced the road congestion index and the hybrid embedded time window, and constructed a model including the cost of transportation, carbon emission, and time penalties. Li et al. [101] analyzed the transportation cost, carbon emission cost and time penalty cost when the stochastic distribution is obeyed for the problem of time, demand and capacity uncertainty, so as to obtain the more ideal scheme under different weights. A summary of multimodal transport route optimization studies considering low carbon and uncertainty factors is shown in Table 4.

Table 4.
Summary of multimodal transport route optimization studies considering low carbon and uncertainty factors.
2.5. Multimodal Transport Route Optimization Considering Special Transport Needs
Research on the optimization of multimodal transport routes for special transport needs mainly focuses on the transport of cold chains, dangerous goods, emergency supplies and other goods. Multimodal transportation for special transportation needs should take more factors into consideration, and, at present, the transportation of special cargoes often takes into account the low carbon and uncertainty factors.
2.5.1. Cold Chain Multimodal Transportation Path Planning
A cold chain is often used in the transportation of fresh products or some medicines, the common point of these items being that they need to be kept in a specific temperature range to ensure freshness and quality, and the excessive use of refrigeration will lead to an increase in carbon emissions. Timeliness is very important in cold chain transportation, which requires the vehicle to be very fast. Li [102] considered adding high-speed rail transportation to multimodal transportation for the small-volume and time-sensitive transportation needs of fresh products. Cui [103] established a refrigerated container multimodal transport path optimization model with the minimum total transport time, minimum total transport cost, and maximum satisfaction of the cargo owner as the multi-objectives based on constructing a time-varying network during the actual operation of refrigerated container multimodal transport. Meng et al. [104] simultaneously considered the characteristics of cold chain transportation and intermodal transportation, combined customer satisfaction with the quality and time of fresh products, introduced customer satisfaction parameters, and considered low-carbon strategies.
Most of the cold chain multimodal transportation studies consider the transportation demand as a fixed value, and the carbon emission of refrigerated container refrigeration is considered to be related to the transportation distance. However, in the actual transportation process, the goods transported in the cold chain are affected by natural conditions and market factors, and there is uncertainty in the transportation demand; refrigerated containers still need refrigeration and generate carbon emissions when they are transiting at the nodes or stopping and waiting on the way, and the correlation between carbon emissions from refrigeration of reefer containers and the transportation time is stronger [105,106]. Liu et al. [107] considered the carbon emission limitation and solved the problem of rail/water transportation in the process of multimodal transportation, which has a time limit as well as the refrigeration cost and cargo difference in the transportation of reefer containers.
2.5.2. Multimodal Transportation Path Planning for Emergency Supplies
The transportation of emergency supplies has time urgency and importance, and needs to be delivered to the disaster area in the shortest time. A combination of multiple modes of transportation, such as highway, railroad, and aviation, is chosen to cope with different traffic conditions. Zhang et al. [108] used the joint transportation method for the urgency of emergency material transportation after a disaster and the realistic mode of level-by-level deployment.
The objectives are different at different times after an emergency. Yuan et al. [109] proposed a multi-stage emergency material multimodal transportation scheduling framework based on the characteristics of different phases of emergency relief, considering uncertainty factors and material dispatching needs. The three phases, respectively, aim at minimizing material dispatch time, material satisfaction, and dispatch cost. Maghfiroh et al. [110] proposed a multimodal distribution model for multimodal transportation with a three-level chain, with supply chain nodes at the first level, logistic operation areas at the second level, and disaster-stricken areas at the third level.
The transportation process of emergency supplies is full of uncertainties; for example, it may face challenges such as traffic congestion and road disruption, etc. Meng et al. [111] proposed a hierarchical assignment-based multimodal transportation strategy link to deal with disruption risk and network uncertainty in response to the dynamic uncertainty of natural disasters. Liu et al. [112] established a reliable path optimization model for multimodal transportation of emergency supplies under double uncertainty by considering shift limitations, time-variation, uncertainty of transportation demand, cost constraints, the risk of nodes infected with epidemics, and node trans-shipment capacity constraints.
When an emergency event occurs, rescue needs to be mobilized from the surrounding areas first. Li et al. [113] took this into account and used multimodal transportation to deal with the emergency transportation problem, and in this way established an emergency rescue and multimodal transportation optimization model that considered multiple types. Guo et al. [114] also brought the multimodal transportation idea into the emergency transportation problem and established a multi-objective mixed-integer planning model to address the problem. Wang [115] realized the decision-making of emergency logistics transportation vehicle paths by determining the feasibility of intermodal solutions using the results of calculating the space-cum-capacity with the help of a perfect intermodal transportation network.
2.5.3. Multimodal Transportation Path Planning for Dangerous Goods and Bulk Cargoes
Dangerous goods transportation is high-risk and requires special transportation and security measures. Moreover, dangerous goods may leak, explode, and lead to other dangerous situations during transportation, posing a threat to people and the environment.
In the study of multimodal transportation path optimization problems for dangerous goods, Zhang et al. [116] considered the increasing use of intermodal transport of dangerous goods in recent years and the clustering of trans-shipment volume at network transfer points, which led to higher safety risks, and therefore proposed a site selection based on the risk classification of transfer points as well as a charging strategy. Zhang [117], Zhou et al. [118] and others found that the demand for liquefied natural gas (LNG), a clean energy source, is increasing, and the former aimed to minimize the total intermodal transport cost minus the establishment provided by the port as the goal to optimize LGN carrier allocation, storage planning, and transportation planning. The latter constructed a two-stage integer planning optimization model with minimum cost to optimize the routes.
Other related scholars have considered the research problem of carbon emission in hazardous materials transportation. Zahra et al. [119] considered the factors of accident probability, emission factor, and storage cost uncertainty, and built a mixed-integer model with multi-objective uncertainty in terms of carbon emission, risk, and cost minimization, using robust pairwise approach to deal with uncertainty, and a bounded-objective approach to deal with three conflicting objectives.
Large cargoes are characterized by a long form factor, large height, irregular shape, and large mass, and are non-disintegrable. When considering intermodal path planning for large cargo transportation, it is necessary to comprehensively consider several aspects, including cargo attributes, transportation mode selection, and transportation route optimization. Wang et al. [120] considered the use of multimodal transportation methods to transport large cargoes, introduced the energy consumption factor, designed the formula for calculating the carbon emissions of the multimodal transportation of large cargoes during in-transit transportation, transformation and reloading, and considered constraints such as post-loading contour dimensions of large cargoes, limit boundaries, the load-bearing capacity of bridges, and node reloading capacity in an integrated manner, taking into account the transformation of transportation road sections. A summary of research on multimodal transport route optimization considering special transport needs is shown in Table 5.

Table 5.
Summary of research on multimodal transport route optimization considering special transport needs.
3. Model and Algorithm Analysis
Through the above grasp of the current status and trend of research on multimodal transport path optimization problems, it can be found that more and more scholars focus on multimodal transport with the combination of low carbon and uncertainty conditions. Most authors consider the uncertainty of demand and carbon trading price, and less consideration is given to the uncertainty of node operation time and unexpected situations in the multimodal transportation process.
3.1. Summary and Analysis of Optimization Models
In terms of model building, according to the analysis of the current state of research, it is found that the optimization that only considers a single objective is beginning to become less, and more scholars are beginning to consider multi-objective optimization problems. In the single-objective optimization problems, most of them take cost and time minimization as the objective, and there are many scholars who also use carbon price to calculate carbon emission, and then calculate it into the cost, so that the model construction and algorithm are simpler compared to the multi-objective optimization problems that consider cost and carbon emission minimization at the same time.
In multi-objective optimization problems, the main objective is to minimize the cost and time, or to minimize the cost, time and carbon emissions as the optimization objective. The treatment for multi-objective optimization can also be mainly divided into the following two kinds.
The first one is the scalarization method; the main idea of this method is to merge multiple targets into a single target in some way, turning it into a single objective optimization problem to solve. The main ones that are used more often are weighted sum, ε-constraint, hierarchical planning and goal programming, as shown in Table 6 below.

Table 6.
Scalarization method summary.
The second kind is Pareto-front generation. Instead of merging objectives, this method directly searches for a set of non-dominated solution sets. This method relies heavily on evolutionary algorithms, heuristic algorithms or meta-heuristics for the solution. The model objectives are summarized in Table 7 and Figure 10.

Table 7.
Summary of model target types.
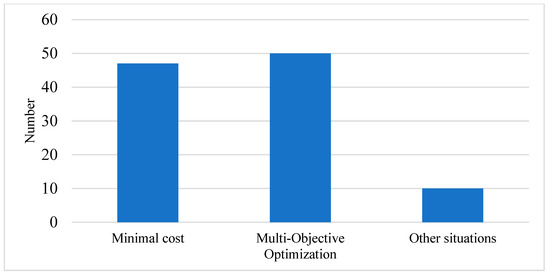
Figure 10.
Optimization objectives.
3.2. Summary of Methods for Dealing with Uncertainty Problems
The second part of the chapter provides a detailed summary of the uncertainties, as well as describing the model construction and its treatment in various problems and situations. These uncertainties affect both the accurate prediction of a single objective and cause dynamic changes in the trade-offs between multiple objectives. Therefore, if a deterministic model is directly applied to such practical problems, it is easy to obtain routes that are infeasible or suboptimal in reality. Thus, many scholars have put a lot of effort into it, aiming to make the model more robust to various possible fluctuations and for better performance. We summarize and analyze these methods for dealing with uncertainty and classify them into five types, namely stochastic programming, robust optimization, fuzzy programming, scenario-based analysis, and chance-constrained programming.
3.2.1. Stochastic Programming
The basic idea of this approach is to consider objectives such as transportation time and cost as random variables. A stochastic planning model is constructed by modeling the different scenarios in which they may occur [67]. The main common forms are two-stage as-you-go planning [87] and multi-stage stochastic planning [91]. They both involve dividing the decision-making process into two or more stages, each of which may face different uncertainty events. This is more in line with the dynamic scheduling of multimodal transportation in real situations [96], but it also has more obvious drawbacks. This is because of the high computational cost of solving high latitude in complex problems. And the multi-objective Pareto frontier presents a very chaotic state in the stochastic environment. For the selection of the optimal solution, it is necessary to design an additional index system [97].
3.2.2. Robust Optimization
This approach is different from the idea of stochastic planning. Robust optimization is to obtain the worst-case optimal solution by considering all possible uncertainties [88]. The advantage of this method is that it does not require an exact probability distribution, but only the upper and lower bounds or covariance information of the parameters. Also, because the goal of this method of solving is the worst-case solution, it ensures that it is still feasible in the worst case [89]. However, its drawbacks are just as obvious. In recent studies, because the researchers are usually more conservative in the setting of various uncertainties, the results obtained are often not optimal solutions. This method also faces the problem of large computational complexity in multi-objective robust solving [98].
3.2.3. Fuzzy Programming
The basic idea of fuzzy planning is to model uncertain parameters as fuzzy numbers or fuzzy sets, and then carve out the uncertainty range by means of a subordination function. Unlike the previous two methods, this method evaluates the likelihood of uncertainty in a certain interval by means of an affiliation function, thus achieving the purpose of quantifying uncertainty [58]. Two common types of affiliation functions are triangular fuzzy numbers as well as trapezoidal fuzzy numbers [59]. Fuzzy planning has a better performance in problems that lack clear information about the probability distribution and can give the best or the worst results at the same time. It is more suitable for scenarios where more subjective uncertainties are considered. However, this also leads to a high degree of subjectivity in the selection of the affiliation function and parameter setting. Therefore, the model and the results are less interpretable [90]. Moreover, in multi-objective optimization problems, if different affiliation functions are set for each objective, it will lead to complex model construction and larger computation [92].
3.2.4. Scenario-Based Analysis
This approach simulates various scenarios in real situations by constructing typical scenarios and then performs deterministic multi-objective optimization under different scenarios. The solution sets obtained under the multiple scenarios obtained are then further analyzed and filtered [17]. This approach is similar to the stochastic planning approach, but it does not require the exact probabilities that the stochastic planning approach requires to be assigned to each scenario. And its multi-scenario design also dictates that it can obtain Pareto solution sets for multiple scenarios. The main approaches to scenario generation are historical data-driven analysis, extreme and sensitivity analysis, and Monte Carlo simulation coupled with importance sampling [23]. The results of this method are more intuitive and easy to adapt to the real situation. In addition, the discreteness of scenario settings makes it easy to independently analyze them. However, it also has the more obvious disadvantage that the choice and design of scenarios have a large impact on the results. Also, neglecting extreme situations can lead to failure when unexpected events are encountered in reality [76].
3.2.5. Chance-Constrained Programming
There is another way of dealing with uncertainty, in addition to the methods described above. Probabilistic constraint planning is the process of taking certain key constraints and allowing them to be guaranteed to hold for the model with a certain level of tolerance [75]. This approach makes it easier to represent acceptable levels of risk under different problems by expressing uncertainty constraints using probabilities. On the other hand, in the multimodal transportation problem, the timeliness of cargo arrival is more important, and this method makes it possible to impose a direct constraint on time [111]. However, this method is used in fewer scenarios and the solution complexity grows exponentially in multi-objective optimization scenarios.
By summarizing these five methods and summarizing the literature in Section 2, a summary Table 8 is obtained as shown below.

Table 8.
Literature summary and classification of uncertainty problems.
3.3. Summary and Analysis of Solution Methods
For algorithms, the main ones are exact algorithms and heuristic algorithms. The most used heuristic algorithm is genetic algorithm, and there are many other bionic intelligence algorithms, such as whale optimization algorithm [35], Harris Hawk algorithm [83] and hybrid sand cat swarm optimization algorithm [100]. Although heuristic algorithms are flexible and efficient and can deal with large-scale data, nonlinear constraints, and multi-objective functions, the solution results change with the change in parameters, with a high degree of dependence on the parameters set by the researchers’ autonomy, and there is a certain probability that they will fall into the local optimal solution. Therefore, most researchers enhance the genetic algorithm based on specific problem analyses, thereby developing the elite strategy-based improved genetic algorithm [25], the fuzzy adaptive non-dominated sorting genetic algorithm [90], the Monte Carlo genetic algorithm [112], and so on.
Some other scholars have tried to combine multiple heuristic algorithms based on different advantages, both hybrid optimization algorithms, such as genetic algorithm based on simulated annealing [64], and particle swarm algorithm based on simulated annealing [86]. Accurate algorithms, on the other hand, are solved using mathematical optimization software, such as CPLEX 12.8, etc., and the algorithms used are mainly K-short-circuit algorithm and Dijkstra’s algorithm. A summary table of algorithms is shown in Table 9 and Figure 11.

Table 9.
Summary of algorithm types.
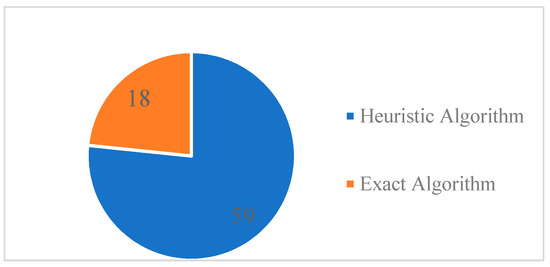
Figure 11.
Using algorithmic statistics.
The various optimization algorithms mentioned above as well as those not mentioned are summarized and shown in Table 10.

Table 10.
Summary of solution algorithms.
By summarizing and organizing the above algorithms, the following conclusions are obtained.
- The choice of exact solution algorithms or heuristic and meta-heuristic algorithms mainly depends on the size of the problem as well as the size of the dimension. When the problem size is small and the model constructed is linear, the use of the exact solution methods should be considered. But when the objective dimension is high and the network size increases, it is recommended to use various meta-heuristic algorithms to solve the approximate solution.
- NSGA 2 is by far the most used method for multi-objective optimization problems. However, when the number of objectives is larger or the problem is more complex, NSGA 3 or a modified GA or other model should be used.
- Because of the increasing complexity of the problems being studied, there is currently no single algorithm that can satisfy all needs in most studies. As a result, the use of various optimization algorithms superimposed on each other has emerged. For example, a global search is performed first and, then, a local search is performed to obtain the optimal approximate solution.
4. Future Directions
Based on the above grasp of the research status and trend of the container intermodal transportation path optimization problem, the following two potential research directions are proposed.
4.1. Collaborative Scheduling Problem of Intermodal Transportation Path Planning
The core of collaborative scheduling for multimodal transportation path planning lies in designing a seamless and optimal path for cargo across multiple modes of transportation such as road, rail, water, and air. Collaboration is where its difficulty lies, as this problem goes far beyond simple path splicing. It requires that the schedules of different modes of transportation must be precisely matched and physical space resources must be coordinated. The ultimate goal is to optimize the system as a whole while meeting strict time window requirements, cost budgets, and other complex constraints.
To address this issue, some scholars consider automated, unmanned scenarios. Zhao [121] takes the three directions of automated terminal public–water intermodal transportation, automated terminal public–rail–water intermodal transportation, and port–public hybrid collector truck fleet scheduling as backgrounds, respectively, and establishes an unmanned collector truck scheduling model to reduce transportation costs. Li [122], for the NVOCC (Non-Vessel Operating Common Carrier) multimodal transportation scheduling and organization optimization problem, divided the transportation organization optimization problem with multiple transportation origins and multiple transportation destinations into three phases of initial consolidation, trunk transportation, and end distribution, and decomposed it into two major types of transportation scheduling problems.
The key to promoting the high-quality development of China’s multimodal transportation is to clarify the key technologies applicable to China’s multimodal transportation linkage, build a multimodal transportation linkage key technology system, and synergistically develop and apply them in the production practice [8,9]. Compared with the previous multimodal transport path optimization problem, the high flexibility and real-time information of collaborative transport can further improve transport efficiency [123], and the flexible and sustainable characteristics of collaborative multimodal transport can solve the problem of uncertainty [65,114]. Therefore, future research will focus on the issues of how to realize the flexible selection of three modes of transfer, namely, public, railway, and water, how to make transfer decisions based on real-time information of vehicle operation, and how to make full use of the flexibility provided by coordinated transport through real-time mode changes in path optimization problems to reduce the total cost of transfer. The collaborative transportation architecture is shown in Figure 12.
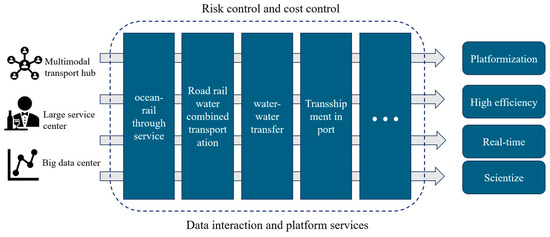
Figure 12.
Intermodal collaborative transport architecture.
4.2. Demand Forecasting Problem in Multimodal Transportation Path Planning
Currently, most scholars use methods such as fuzzy number and opportunity constrained planning theory to solve the uncertainty of demand and time in the multimodal transportation process. However, with the rapid development of computer hardware capability, deep learning models rely on their strong learning ability and will have good prediction effect in the face of various uncertainties in the process of multimodal transportation path optimization.
Deep learning, as a powerful machine learning technology, has significant advantages in dealing with complex and nonlinear problems. By constructing time series prediction models or regression models, deep learning can capture seasonal, cyclical, and trend changes in transportation demand, thus improving the accuracy of prediction. Using historical transportation data, deep learning models can learn and predict future transportation demand. This helps companies plan transportation resources and routes to cope with demand uncertainty.
Scholars have already started to use deep learning to address demand uncertainty in multimodal transportation. Applying the dynamic prediction of intermodal freight transportation volume, Wang [124] and Peng [125] used the Pearson correlation coefficient method for feature extraction of influencing factors, and then built a combined prediction model based on the seasonal autoregressive moving average model as well as long and short-term memory neural networks based on the characteristics of sea-rail intermodal transport volume data. Wang et al. [126] developed a framework for OD traffic prediction in intelligent and multimodal urban transportation systems using FusionTransNet.
The emergence of deep learning techniques has profoundly changed various application domains, including path prediction in transportation networks [127]. Deineko et al. [128] found that path optimization problems can be solved using deep learning methods, and neural combinatorial optimization can achieve real-time decision-making under uncertainty by considering the current overall state after learning. Ferjani et al. [129] proposed a decision support system coupled with simulation and optimization models. The system helps in evaluating various routes and generating optimal solutions based on user preferences and considering environmental considerations.
Other scholars have considered the privacy issues in performing demand forecasting, resulting in the fact that existing multimodal demand forecasting methods are often unable to use shared raw data to improve demand forecasting performance. Attentional federated learning programs have been designed. The research gap in enhancing multimodal demand forecasting without relying on direct data sharing has been addressed [130].
With the development of multimodal transportation, scholars are beginning to use more innovative and effective model architectures and solution algorithms to solve more practical multimodal transportation path optimization problems. For uncertainties such as demand, deep learning methods can be used for regression prediction to help enterprises more flexibly choose the three modes of transportation—public, railway and water—in order to help enterprises realize cost reduction and efficiency. For the uncertainty of demand, as well as time, environment, and other uncertainties, the deep learning model will also have a very good performance. For example, in the prediction problem of freight volume demand, in addition to using traditional sequence models, neural networks such as CNN (Convolutional Neural Network) and GNN (Graph Neural Network) can also be considered for regression prediction problems with multiple input indicators, single or multiple output indicators. The input can be multiple sets of time series indicator data or more complex multimodal data. However, obtaining and processing such data is often difficult, and more complex data processing methods need to be considered. Meanwhile, network training is also a relatively complex problem, because of issues such as network construction and hyperparameter selection. So, how to construct a suitable network and how to choose the hyperparameter combination that best matches the input data and model will also be a topic of high research interest in the future. The framework for regression prediction using CNN is shown in Figure 13.
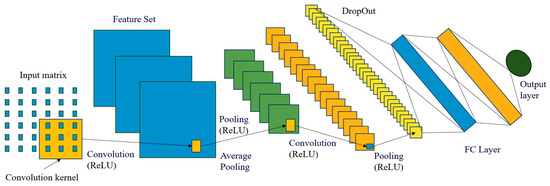
Figure 13.
CNN regression prediction framework.
Finally, we summarized the various possible applications of deep learning models in multimodal transportation path optimization and analyzed their advantages, disadvantages, and applicable scenarios, as shown in Table 11.

Table 11.
Application of deep learning in multimodal transportation.
5. Conclusions
In recent years, many scholars have conducted research on the path planning problem for various modes of transportation such as sea–rail intermodal transportation, public–rail intermodal transportation, public–rail–water intermodal transportation, etc., and have considered low-carbon policies and various uncertainties, as well as researched the solution to the transportation of special items through intermodal transportation. According to the research directions and objectives of the existing literature, this paper is divided into the following: traditional intermodal transport path optimization, intermodal transport path optimization considering carbon emission, intermodal transport path optimization considering uncertainties, intermodal transport path optimization considering uncertainties under low carbon conditions, intermodal transport path optimization considering special needs; the paper is subdivided again for a review.
Meanwhile, model building and model solving for different research directions and objectives are summarized and analyzed, and the methods commonly used by scholars to solve various problems are summarized.
Finally, the current rapid development of cooperative transportation and the wide application of deep learning in various fields are considered. Based on this review, two future research directions are proposed: the cooperative scheduling problem in multimodal transportation path planning and the demand forecasting problem in multimodal transportation path planning.
This article systematically reviews the evolution trend of multimodal transport path optimization from a single objective to multiple objectives, and from static modeling to dynamic collaboration. The model construction methods and solution methods for different problems are also systematically analyzed. We also summarize the methods for handling uncertain problems, which is currently one of the research hotspots. The emphasis on using deep learning methods for regression prediction of uncertain demand in a low-carbon context is a potential research focus in the future. Predicting future transportation demand through deep learning regression helps enterprises plan transportation resources and paths in advance to reduce costs and unnecessary losses. Therefore, when developing the path planning scheme, it is necessary to comprehensively consider multiple objectives, such as carbon emission situation, transportation time, cost, etc., and find the balance point between multiple objectives to achieve the overall scheme optimization. It is worth noting that as electric truck technology gradually matures, its application in the multimodal transportation system is also increasingly attracting attention. Compared with traditional fuel trucks, electric trucks can significantly reduce carbon emissions during transportation. At the same time, deep learning models are used to make reasonable predictions of demand and other dynamic information, and real-time adjustments are made to the operation path to ensure that transportation efficiency is maximized.
Author Contributions
W.L.: Formal analysis, Writing—original draft, Conceptualization, Funding acquisition. Y.W.: Software, Methodology, Data curation, Writing—original draft preparation. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Hubei Provincial Natural Science Foundation Project-Xiangyang innovation and development joint fund (2025AFD064), The Key Consulting Project for Institute Local Cooperation of Chinese Academy of Engineering (HB2024B07) and the Philosophy and Social Science Research Project of Hubei Provincial Department of Education (23Q171).
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
The authors acknowledge the Open Fund of Hubei Key Laboratory of Power System Design and Test for Electrical Vehicle.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Guo, F.C. Route Optimization of Railway Container Multimodal Transport Considering Railway Skylights. Master’s Thesis, Dalian Jiaotong University, Dalian, China, 2023; p. 000092. [Google Scholar]
- Li, W.; Wang, B.; Sun, R.; Ai, L.; Lin, Z. Energy-efficient multimodal mobility networks in transportation digital twins: Strategies and optimization. Energy 2025, 318, 134587. [Google Scholar] [CrossRef]
- Yang, S.; Chen, C.; Li, A.; Wang, Q.; Zhang, L.; Chen, F.; Zhou, S.; Yan, X. Electric flying vehicles: A promising approach towards multidimensional transportation. eTransportation 2025, 24, 100412. [Google Scholar] [CrossRef]
- Ye, J.; Jiang, Y.; Chen, J.; Liu, Z.Y.; Guo, R.Z. Joint optimisation of transfer location and capacity for a capacitated multimodal transport network with elastic demand: A bi-level programming model and paradoxes. Transp. Res. Part E Logist. Transp. Rev. 2021, 156, 102540. [Google Scholar] [CrossRef]
- Hoffelner, M.; Kopeinig, J.; Schieler, P. The future of freight: Evaluating the environmental and economic benefits of diesel, LNG, and electric trucks in multimodal transport. Res. Transp. Bus. Manag. 2025, 59, 101319. [Google Scholar] [CrossRef]
- Fareed, A.G.; De Felice, F.; Forcina, A.; Petrillo, A. Role and applications of advanced digital technologies in achieving sustainability in multimodal logistics operations: A systematic literature review. Sustain. Futur. 2024, 8, 100278. [Google Scholar] [CrossRef]
- Komashinskiy, V.; Malygin, I.; Korolev, O. Introduction into cognitive multimodal transportation systems. Transp. Res. Procedia 2020, 50, 273–279. [Google Scholar] [CrossRef]
- Zhang, Y.Z.; Li, H.J.; Zhang, W.H.; Yang, J.L. Research on the Construction of Common Key Technology System for Multimodal Transport Connection. China Eng. Sci. 2023, 25, 212–224. [Google Scholar] [CrossRef]
- Shen, D.Y.; Li, X.Z. Multimodal Transport Operation Mechanism, Development Mode and Evolution Trend: An Analysis Based on SCI, Peking University Core and CSSCI Journals (2013–2023). Railw. Transp. Econ. 2024, 46, 96–105. [Google Scholar]
- Tanwar, R.; Agarwal, P.K. Multimodal integration in India: Opportunities, challenges, and strategies for sustainable urban mobility. Multimodal Transp. 2025, 4, 100210. [Google Scholar] [CrossRef]
- Cherednichenko, K.; Ivannikova, V.; Sokolova, O.; Yanchuk, M. Model of transport safety assessment in multimodal transportation systems. Transport 2023, 38, 204–213. [Google Scholar] [CrossRef]
- Archetti, C.; Peirano, L.; Speranza, M.G. Optimization in multimodal freight transportation problems: A survey. Eur. J. Oper. Res. 2022, 299, 1–20. [Google Scholar] [CrossRef]
- Yin, C.; Lu, Y.; Xu, X.; Tao, X. Railway freight subsidy mechanism based on multimodal transportation. Transp. Lett. 2020, 13, 716–727. [Google Scholar] [CrossRef]
- Ru, S. Vehicle logistics intermodal route optimization based on Tabu search algorithm. Sci. Rep. 2024, 14, 11859. [Google Scholar] [CrossRef] [PubMed]
- Kovalenko, A.; Mathisen, T.A.; Pruyn, J. Generalized transport costs in intermodal shipping: The context of the Northeast Passage. J. Shipp. Trade 2024, 9, 25. [Google Scholar] [CrossRef]
- Pian, F.; Chen, Y.; Pang, S.H.; Su, M. Game pricing of container road and multimodal transport considering railway discounts. J. Transp. Syst. Eng. Inf. Technol. 2022, 22, 1–10. [Google Scholar] [CrossRef]
- Hu, Z.A.; Cai, J.; Luo, H. Multimodal transport path optimization under mixed uncertainty conditions. J. Beijing Jiaotong Univ. 2023, 47, 32–40. [Google Scholar]
- Chen, D.; Peng, S.; Lian, F.; Yang, Z. Optimization of a Japan–Europe multimodal transportation corridor. Transp. Res. Part A Policy Pract. 2023, 175, 103782. [Google Scholar] [CrossRef]
- Peng, Y.; Xiao, Y.P.; Zhou, X.; Liu, S. Optimization of multimodal transportation routes with time window and schedule constraints. Sci. China Technol. Pap. 2021, 16, 211–216. [Google Scholar]
- Zhang, H.; Li, Y.; Zhang, Q.; Chen, D. Route Selection of Multimodal Transport Based on China Railway Transportation. J. Adv. Transp. 2021, 2021, 9984659. [Google Scholar] [CrossRef]
- Guo, F.; Liang, J.; Niu, R.; Huang, Z.; Liu, Q. Robust optimization of a procurement and routing strategy for multiperiod multimodal transport in an uncertain environment. Eur. J. Oper. Res. 2025. [Google Scholar] [CrossRef]
- Liang, X.K. Research on Optimization of Railway Container Multimodal Transport Scheme with Time Windows. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2016. [Google Scholar]
- Farahani, N.Z.; Noble, J.S.; McGarvey, R.G.; Enayati, M. An advanced intermodal service network model for a practical transition to synchromodal transport in the US Freight System: A case study. Multimodal Transp. 2022, 2, 100051. [Google Scholar] [CrossRef]
- Wang, Y.; Song, R.; Zhao, Z.; Zhao, R.; Zhang, Z. A multimodal material route planning problem considering key processes at work zones. PLoS ONE 2024, 19, e0300036. [Google Scholar] [CrossRef]
- Qi, P.A.; Ji, M.J.; Feng, Z.; Qi, J. Research on optimization scheme of multimodal transportation routes for multi-task containers. Ind. Eng. Manag. 2022, 27, 54–63. [Google Scholar]
- Chen, D.; Zhang, Y.; Gao, L.; Thompson, R.G. Optimizing multimodal transportation routes considering container use. Sustainability 2019, 11, 5320. [Google Scholar] [CrossRef]
- Huang, C.; Sun, H.; Liu, C.; Zhang, X.; Gao, T.; Tian, J. Research on Container Multimodal Transportation Multi-Objective Path Optimization From Hinterlands to Shanghai Port. IEEE Access 2025, 13, 32794–32807. [Google Scholar] [CrossRef]
- Wu, X.L.; Kou, Q.; Wang, Y.B. Optimization of international container multimodal transportation routes considering cargo time value. Highw. Transp. Res. Dev. 2023, 40, 239–247. [Google Scholar]
- Wang, N.M.; Wang, X.N.; Shi, W.X. Research on dual-objective optimization of multimodal transportation considering inventory and disruptions. Front. Eng. Manag. Sci. Tech. 2023, 42, 26–34. [Google Scholar] [CrossRef]
- Seo, Y.J.; Chen, F.; Roh, S.Y. Multimodal transportation: The case of laptop from Chongqing in China to Rotterdam in Europe. Asian J. Shipp. Logist. 2017, 33, 155–165. [Google Scholar] [CrossRef]
- Okyere, S.; Yang, J.; Adams, C.A. Optimizing the Sustainable Multimodal Freight Transport and Logistics System Based on the Genetic Algorithm. Sustainability 2022, 14, 11577. [Google Scholar] [CrossRef]
- Zhang, D.Z.; Wan, Z.Q.; Li, Y.S.; Zhou, S.Q.; Bin, S. Research on optimization of multimodal transportation network design from a low-carbon perspective. Railw. Sci. Eng. 2024, 21, 1793–1804. [Google Scholar]
- Cui, T.; Shi, Y.; Wang, J.; Ding, R.; Li, J.; Li, K. Practice of an improved many-objective route optimization algorithm in a multimodal transportation case under uncertain demand. Complex Intell. Syst. 2025, 11, 136. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, J.Y.; Yuan, X.M.; Jiang, Y.D. Research on multimodal transportation route selection considering economies of scale under different carbon reduction policies. Ind. Eng. Manag. 2022, 27, 22–31. [Google Scholar]
- Wu, Z.Y.; Dai, Y.; Ju, C.X.; Hu, B.J.; Hu, X. Multi-objective multimodal transportation route selection based on whale optimization algorithm. J. Chongqing Jiaotong Univ. (Nat. Sci. Ed.) 2022, 41, 6–13. [Google Scholar]
- Chen, W.Y.; Gong, H.; Fang, X.P. Optimization of multimodal transportation routes considering transport carbon tax and quality commitment. J. Railw. Sci. Eng. 2022, 19, 34–41. [Google Scholar]
- Binsfeld, T.; Hamdan, S.; Jouini, O.; Gast, J. On the optimization of green multimodal transportation: A case study of the West German canal system. Ann. Oper. Res. 2024, 1–60. [Google Scholar] [CrossRef]
- Deng, H.X.; Song, Y.J. Multi-objective path planning for multimodal transportation considering carbon emissions. J. Chongqing Univ. Tech. (Nat. Sci.) 2022, 36, 219–225. [Google Scholar]
- Wang, N. Research on Multi-Objective Optimization of Loading Scheduling for Transfer Vehicles in Road-Water Multimodal Transportation. Master’s Thesis, Lanzhou University of Technology, Lanzhou, China, 2023; p. 001588. [Google Scholar]
- Liu, Q.W.; Zhao, Z.R. Comparison and analysis of algorithms for optimizing multimodal transportation routes considering carbon emissions. Ind. Eng. Manag. 2022, 27, 53–59. [Google Scholar]
- Wan, J.; Long, Y.F.; Chen, X.H. Optimization of multimodal transportation routes for Sino-Russian commodities based on an improved fireworks algorithm. J. Tianjin Univ. (Sci. Tech.) 2022, 55, 291–298. [Google Scholar]
- Yin, C.Z.; Peng, H.H.; Tao, X.Z.; Zhang, Z.A. Collaborative optimization of multimodal transportation based on improved NSGA-II. Shanghai Marit. Univ. J. 2023, 44, 39–44. [Google Scholar]
- Hou, Y.J.; Liang, C.J. Optimization of container multimodal transportation network based on underground logistics system. Comput. Eng. Appl. 2024, 60, 314–325. [Google Scholar]
- Zhen, Y.D.; Yang, B. Multi-target planning of container multimodal transport under uncertainty. Comput. Appl. Softw. 2018, 35, 21–26. [Google Scholar]
- Wu, P.; Ji, H.T.; Lin, F.; Cheng, J. Multi-objective optimization of green multimodal transportation routes and speeds with service time windows. Oper. Res. Manag. Sci. 2024, 33, 35–41. [Google Scholar]
- Wu, P.; Li, Z.; Ji, H.T. Green multimodal transportation route and speed optimization considering emission control areas. Transp. Syst. Eng. Inf. Technol. 2023, 23, 20–29. [Google Scholar]
- Ma, F.; Liu, B.Y.; Ren, W.; Wang, Q.Q.; Liu, Q. Study on the influence mechanism of fragile factors in multimodal transportation systems based on stochastic Petri nets. Railw. Transp. Econ. 2023, 45, 113–120. [Google Scholar]
- Koohathongsumrit, N.; Meethom, W. A fuzzy decision-making framework for route selection in multimodal transportation networks. Eng. Manag. J. 2022, 34, 689–704. [Google Scholar] [CrossRef]
- Pfoser, S. Developing user-centered measures to increase the share of multimodal freight transport. Res. Transp. Bus. Manag. 2022, 43, 100729. [Google Scholar] [CrossRef]
- Li, S.X.; Chen, Z.; Liu, L.P. Intermodal Logistic Network Design under Uncertain Demand. J. Donghua Univ. (Nat. Sci.) 2018, 44, 550–554. [Google Scholar]
- Qiu, Y.; Hu, J.H.; Guo, J.Y.; Liu, K.Y. A route selection method for multimodal transportation considering the time value of goods under uncertain demand. Railw. Sci. Eng. 2024, 21, 994–1003. [Google Scholar]
- Sun, Y. A Fuzzy Multi-Objective Routing Model for Managing Hazardous Materials Door-to-Door Transportation in the Road-Rail Multimodal Network With Uncertain Demand and Improved Service Level. IEEE Access 2020, 8, 172808–172828. [Google Scholar] [CrossRef]
- Yu, X.Q.; Lang, M.; Wang, W.; Yu, X. Multimodal transportation routing optimization considering fuzzy demands. J. Beijing Jiaotong Univ. 2018, 42, 23–29. [Google Scholar]
- Chen, X.H.; Hu, X.H.; Liu, H.B. Low-Carbon Route Optimization Model for Multimodal Freight Transport Considering Value and Time Attributes. Socio-Economic Plan. Sci. 2024, 96, 102108. [Google Scholar] [CrossRef]
- Guo, F.; Niu, R.L.; Huang, Z.H. Robust optimization of procurement and routing strategy of multi-period multimodal transport in uncertain environment. Chin. J. Manag. Sci. 2024, 1–12. [Google Scholar] [CrossRef]
- Zhao, X.; Zhu, X.F.; Zhang, Y. Robust optimization of green multimodal transport routes considering service priority. Shanghai Marit. Univ. J. 2022, 43, 21–27. [Google Scholar]
- Wang, X.; Zhang, P.; Du, Z.; Tian, A.-Q.; Lv, H. Research on optimization of international multimodal transportation routes based on uncertainty theory. Transp. Res. Rec. 2024, 2678, 798–821. [Google Scholar] [CrossRef]
- Tong, H. Rail consignment path planning based on multimodal transport: Considering the time uncertainty condition. J. Eng. Proj. Prod. Manag. 2023, 13, 104–112. [Google Scholar] [CrossRef]
- Zhang, H.; Huang, Q.; Ma, L.; Zhang, Z.Y. Sparrow search algorithm with adaptive t distribution for multi-objective low-carbon multimodal transportation planning problem with fuzzy demand and fuzzy time. Expert Syst. Appl. 2024, 238, 122042. [Google Scholar] [CrossRef]
- Chen, M.L.; Zhao, X.J.; Deng, X.G.; Zheng, C.J.; Du, M.Q. Multimodal transport route optimization under uncertainty. J. Highw. Transp. Res. Dev. 2021, 38, 143–150. [Google Scholar]
- Yang, J.; Liang, D.; Zhang, Z.; Wang, H.; Bin, H. Path optimization of container multimodal transportation considering differences in cargo time sensitivity. Transp. Res. Rec. 2024, 2678, 1279–1292. [Google Scholar] [CrossRef]
- Guo, J.; Liu, T.; Song, G.; Guo, B. Solving the robust shortest path problem with multimodal transportation. Mathematics 2024, 12, 2978. [Google Scholar] [CrossRef]
- Zhang, M.; Han, X.L. Multi-objective fuzzy chance-constrained programming for low-carbon multimodal transport route optimization. Comput. Appl. 2023, 43, 636–644. [Google Scholar]
- Tang, R.; Hu, J.H.; Wen, C.W.; Zhang, W.J. Multimodal transport route choice considering dynamic transfer times under uncertain demand. J. Nanjing Tech Univ. (Nat. Sci. Ed.) 2023, 45, 554–562. [Google Scholar]
- Li, J.; Liang, X.L.; Zhao, S.; Zhang, Y. Dynamic programming algorithm for container multimodal transport route optimization in the Yangtze River. Comput. Eng. Des. 2021, 42, 3067–3075. [Google Scholar]
- Lu, Y.; Lang, M.; Sun, Y.; Li, S.Q. A fuzzy intercontinental road-rail multimodal routing model with time and train capacity uncertainty and fuzzy programming approaches. IEEE Access 2020, 8, 27532–27548. [Google Scholar] [CrossRef]
- Peng, Y.; Luo, Y.J.; Jiang, P.; Yong, P.C. The route problem of multimodal transportation with timetable: Stochastic multi-objective optimization model and data-driven simheuristic approach. Eng. Comput. 2022, 39, 587–608. [Google Scholar] [CrossRef]
- He, Z.; Navneet, K.; van Dam, W.; Mieghem, P. Robustness assessment of multimodal freight transport networks. Reliab. Eng. Syst. Saf. 2021, 207, 107315. [Google Scholar] [CrossRef]
- Xu, X.; Wang, H.; Deng, P. Exploring the optimization of synchromodal transportation path under uncertainties. J. Mar. Sci. Eng. 2023, 11, 577. [Google Scholar] [CrossRef]
- Guo, F.; Xu, Y.; Huang, Z.H.; Wu, Y.X. Collaborative optimization of routing and storage strategy of multi-period multimodal transport in an uncertain environment. Comput. Oper. Res. 2024, 167, 106676. [Google Scholar] [CrossRef]
- Zhang, X.; Jiang, Y.D.; Yuan, X.M. Low-carbon multimodal transport path optimization under demand uncertainty. Fuzzy Syst. Math. 2020, 34, 163–174. [Google Scholar]
- Zhang, X.; Yuan, X.M.; Jiang, Y.D. Multimodal transport path optimization under demand and carbon trading price uncertainty. Syst. Eng.—Theory Pract. 2021, 41, 2609–2620. [Google Scholar]
- Zhang, X.; Zhang, H.Y.; Yuan, X.M.; Hao, Y.C. Low-carbon multimodal transport path optimization under dual uncertainty. J. Beijing Jiaotong Univ. (Soc. Sci. Ed.) 2022, 21, 113–121. [Google Scholar]
- Deng, M.J.; Dai, Y.Z.; Li, X. Robust optimization of low-carbon multimodal transport path under demand uncertainty. Ind. Eng. 2023, 26, 104–113. [Google Scholar]
- Lu, J.H. Research on Low-Carbon Multimodal Transport Path Optimization Considering Uncertain Demand. Master’s Thesis, Chang’an University, Xi’an, China, 2023; p. 002561. [Google Scholar]
- Jiang, Y.D. Research on Low-Carbon Multimodal Transport Path Optimization of Containers Under Demand Uncertainty. Master’s Thesis, Yanshan University, Qinhuangdao, China, 2020; p. 001339. [Google Scholar]
- Zhang, S.S. Research on Container Multimodal Transport Path Optimization Under Demand Uncertainty in the Context of Low Carbon. Master’s Thesis, Southeast University, Nanjing, China, 2023; p. 001540. [Google Scholar]
- Liu, Z.; Zhou, S.; Liu, S. Optimization of multimodal transport paths considering a low-carbon economy under uncertain demand. Algorithms 2025, 18, 92. [Google Scholar] [CrossRef]
- Yuan, X.M.; Jiang, Y.D.; Zhang, X. Robust optimization of fuzzy multimodal transport path based on interval under low-carbon policy. Ind. Eng. Manag. 2021, 26, 134–141. [Google Scholar]
- Hu, X.; Cheng, R.; Chen, X.; Zhao, J.; Liu, F.; Zhou, X. Optimization and implementation strategy for low-carbon multimodal transport routes: A collaborative approach between government and transport enterprises. J. Clean. Prod. 2025, 502, 145341. [Google Scholar] [CrossRef]
- Wang, J.H. Optimization of Container Low-Carbon Multimodal Transport Path Under Demand Uncertainty. Master’s Thesis, Lanzhou Jiaotong University, Lanzhou, China, 2023; p. 000312. [Google Scholar]
- Sun, W.J. Research on Road-Rail-Water Multimodal Transport Path Optimization Considering Uncertain Demand in a Low-Carbon Environment. Master’s Thesis, East China Jiaotong University, Nanchang, China, 2023; p. 000679. [Google Scholar]
- Huang, Q.; Zhang, H.Z.; Ma, L.; Yang, J.H. Hybrid Harris’ hawk optimization algorithm for solving low-carbon multimodal transport path planning problem with fuzzy demand. Comput. Appl. Res. 2023, 40, 2978–2983. [Google Scholar]
- Wang, Q. Research on Low-Carbon Multimodal Transport Path Optimization Under Uncertainty. Master’s Thesis, Lanzhou Jiaotong University, Lanzhou, China, 2023; p. 000647. [Google Scholar]
- Zhang, X.R. Multimodal Transport Path Optimization Based on Low-Carbon Transportation Under Uncertain Demand. Master’s Thesis, Lanzhou Jiaotong University, Lanzhou, China, 2021; p. 001389. [Google Scholar]
- Deng, X.P.; Chen, L.; Tian, S.H. Multimodal transport path optimization considering mixed time windows under uncertain demand. J. Chongqing Univ. Posts Telecommun. (Nat. Sci. Ed.) 2021, 33, 689–698. [Google Scholar]
- Zhang, X.; Chen, H.; Zhang, H.; Yuan, X. Dual objective multimodal transportation path optimization based on different carbon tax mechanisms under uncertain demand. J. Highw. Transp. Res. Dev. (Engl. Ed.) 2025, 19, 52–60. [Google Scholar] [CrossRef]
- Cheng, X.Q.; Jin, C.; Yao, Q.G.; Wang, C. Robust optimization of multimodal transport route choice problem under carbon trading policy. Chin. J. Manag. Sci. 2021, 29, 82–90. [Google Scholar]
- Li, M.; Sun, X. Path optimization of low-carbon container multimodal transport under uncertain conditions. Sustainability 2022, 14, 14098. [Google Scholar] [CrossRef]
- Yang, H.L.; Yu, G. Low-carbon multimodal transport path optimization for cold chain under carbon trading price uncertainty. Transp. Syst. Eng. Inf. 2024, 24, 5–14. [Google Scholar]
- Ai, Z.Y.; Zhang, X.; Wu, X. Design of China-Europe container multimodal transport service network. J. Railw. Sci. Eng. 2024, 21, 2217–2228. [Google Scholar]
- Chen, D.J.; Li, Y.; Ni, S.Q.; Yang, Y. Green multimodal transport path optimization under soft constraints of receiving time windows. Comput. Simul. 2020, 37, 209–214. [Google Scholar]
- Zhou, J.L.; Zhang, Y.G.; Xiao, Y.; Wang, J. Multi-objective path optimization model and algorithm for multimodal transport under uncertain time. Transp. Syst. Eng. Inf. 2024, 24, 1–17. [Google Scholar]
- Li, L.; Zhang, Q.; Zhang, T.; Zou, Y.; Zhao, X. Optimum Route and Transport Mode Selection of Multimodal Transport with Time Window under Uncertain Conditions. Mathematics 2023, 11, 3244. [Google Scholar] [CrossRef]
- Yang, Z.; Deng, L.B.; Di, Y.Z.; Li, C.L. Multimodal transport path optimization based on fuzzy demand and fuzzy transport time. Control Theory Appl. 2024, 41, 967–976. [Google Scholar]
- Zhu, C.; Zhu, X. Multi-objective path-decision model of multimodal transport considering uncertain conditions and carbon emission policies. Symmetry 2022, 14, 221. [Google Scholar] [CrossRef]
- Zhang, X.; Jin, F.-Y.; Yuan, X.-M.; Zhang, H.-Y. Low-carbon multimodal transportation path optimization under dual uncertainty of demand and time. Sustainability 2021, 13, 8180. [Google Scholar] [CrossRef]
- Zhang, T.; Cheng, J.; Zou, Y. Multimodal transportation routing optimization based on multi-objective Q-learning under time uncertainty. Complex Intell. Syst. 2024, 10, 3133–3152. [Google Scholar] [CrossRef]
- Dai, Y.Z. Robust Optimization of Multimodal Transport Routes Under Multiple Uncertainties in a Low-Carbon Policy Context. Master’s Thesis, East China Jiaotong University, Nanchang, China, 2023; p. 000631. [Google Scholar]
- Sun, Z.; Yang, Q.; Liu, J.; Zhang, X.; Sun, Z.X. A path planning method based on hybrid sand cat swarm optimization algorithm of green multimodal transportation. Appl. Sci. 2024, 14, 8024. [Google Scholar] [CrossRef]
- Li, J.; Yang, B.; Zhu, X.L. Path Optimization of Green Multimodal Transportation under Mixed Uncertainties. J. Transp. Syst. Eng. Inf. Technol. 2019, 19, 13–19. [Google Scholar]
- Li, Y.M.; Qiu, M.; Yan, K.L.; Liu, X.X. Route choice for fresh products considering time windows with high-speed rail participation in multimodal transportation. J. Chongqing Jiaotong Univ. (Nat. Sci. Ed.) 2021, 40, 54–61. [Google Scholar]
- Cui, M.H. Optimization of Multimodal Transport Routes for Refrigerated Containers Considering Uncertain Transfer Times at Nodes. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2023; p. 000586. [Google Scholar]
- Meng, J.J.; Shi, K.; Liu, Y.; Li, D.; Jiang, T.; Jiang, X.; Liu, X. Optimization of low-carbon cold chain multimodal transport routes based on customer satisfaction. Packag. Eng. 2024, 45, 268–275. [Google Scholar]
- Su, H.; Li, H.J. Optimization of low-carbon multimodal transport routes for refrigerated containers under uncertain demand. Railw. Transp. Econ. 2024, 47, 1–9. [Google Scholar]
- Sun, J.Q.; Wang, S.N.; Yan, S.X. Route choice for multimodal transport of refrigerated containers considering carbon emissions. Dalian Marit. Univ. J. 2022, 48, 57–65. [Google Scholar]
- Liu, S.; Shu, W.; Peng, Y.; Shao, Y.M.; Le, M.L. Reliable route optimization for multimodal transport of emergency supplies under dual uncertainties. Transp. Syst. Eng. Inf. 2023, 23, 58–66. [Google Scholar]
- Zhang, Y.P.; Cui, N.; Zhang, B. Multi-objective optimization of emergency supply based on multimodal transport. China Saf. Sci. J. 2023, 33, 230–238. [Google Scholar]
- Yuan, R.P.; Wang, W.; Li, J.T.; Zhao, Q. Multi-stage scheduling of emergency supplies via multimodal transport under uncertainty. Oper. Res. Manag. 2023, 32, 33–39. [Google Scholar]
- Maghfiroh, M.F.N.; Hanaoka, S. Multi-modal relief distribution model for disaster response operations. Prog. Disaster Sci. 2020, 6, 100095. [Google Scholar] [CrossRef]
- Meng, L.; Wang, X.; He, J.; Han, C.F.; Hu, S.L. A two-stage chance constrained stochastic programming model for emergency supply distribution considering dynamic uncertainty. Transp. Res. Part E Logist. Transp. Rev. 2023, 179, 103296. [Google Scholar] [CrossRef]
- Liu, S.; Shao, Y.M.; Peng, Y. Optimization of multimodal transport routes for refrigerated containers under carbon emission constraints. Appl. Math. Mech. 2020, 41, 204–215. [Google Scholar]
- Li, C.; Han, P.; Zhou, M.; Gu, M. Design of multimodal hub-and-spoke transportation network for emergency relief under COVID-19 pandemic: A meta-heuristic approach. Appl. Soft Comput. 2023, 133, 109925. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.; Liu, H.; Liu, T.; Song, G.P.; Guo, B. The multi-objective shortest path problem with multimodal transportation for emergency logistics. Mathematics 2024, 12, 2615. [Google Scholar] [CrossRef]
- Wang, Z. Optimization method for vehicle scheduling in emergency logistics based on multimodal transport. Electron. Des. Eng. 2022, 30, 6–9. [Google Scholar]
- Zhang, G.X.; Su, G.P.; Xu, B.T.; Zhong, H.L. Network design for multimodal transport of dangerous goods with risk-based grading and pricing at transfer points. Oper. Res. Manag. 2024, 33, 118–125. [Google Scholar]
- Zhang, H.; Wu, Y.; Zhen, L.; Jin, Y.; Wang, S. Optimization problems in liquefied natural gas transport and storage for multimodal transport companies. Electron. Res. Arch. 2024, 32, 4828–4844. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, T.; Liang, G.; Fu, W.; Zhang, D.; Peng, S. Route optimization for LNG tank container multimodal transport based on cross-docking terminals. Sci. Technol. Eng. 2024, 24, 8269–8279. [Google Scholar]
- Zahra, Z.; Jabbarzadeh, A. A multi-objective robust optimization approach for green location-routing planning of multimodal transportation systems under uncertainty. J. Clean. Prod. 2021, 291, 125293. [Google Scholar]
- Wang, J.; Cheng, Y.L.; Yang, Y.H.; Zhang, G.Y. Route optimization for multimodal transport of oversized cargo considering carbon emissions. Transp. Syst. Eng. Inf. 2024, 24, 1–11. [Google Scholar]
- Zhao, Y. Research on Unmanned Truck Scheduling in the Context of Multimodal Transport. Master’s Thesis, Southeast University, Nanjing, China, 2020; p. 001532. [Google Scholar]
- Li, L. Research on Multimodal Transport Scheduling Schemes for a Non-Truck Operating Common Carrier. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2019. [Google Scholar]
- Duan, L.W.; Wu, X.L. A review of research on empty container repositioning in container multimodal transport. Railw. Transp. Econ. 2024, 46, 82–97. [Google Scholar]
- Wang, Y.; Li, W.; Qi, X.; Yu, Y. A Weight Assignment-Enhanced Convolutional Neural Network (WACNN) for Freight Volume Prediction of Sea–Rail Intermodal Container Systems. Algorithms 2025, 18, 319. [Google Scholar] [CrossRef]
- Peng, W.L. Research on Combined Forecasting Model of Sea-Rail Intermodal Transport Volume Based on Deep Learning. Master’s Thesis, Dalian Maritime University, Dalian, China, 2023; p. 000918. [Google Scholar]
- Wang, B.; Leng, Y.; Wang, G.; Wang, Y. FusionTransNet for Smart Urban Mobility: Spatiotemporal Traffic Forecasting Through Multimodal Network Integration. arXiv 2024, arXiv:2405.05786. [Google Scholar]
- Prakash, S.; Sharma, B. A Novel Approach for Route Prediction in Multimodal Transport Networks: A Monte Carlo Simulation and Long Short-Term Memory-based Model. Eng. Sci. 2024, 29, 1145. [Google Scholar] [CrossRef]
- Deineko, E.; Jungnickel, P.; Kehrt, C. Learning-Based Optimisation for Integrated Problems in Intermodal Freight Transport: Preliminaries, Strategies, and State of the Art. Appl. Sci. 2024, 14, 8642–8662. [Google Scholar] [CrossRef]
- Ferjani, A.; El Yaagoubi, A.; Boukachour, J.; Duvallet, C. An Optimization-Simulation Approach for Synchromodal Freight Transportation. Multimodal Transp. 2024, 3, 100151. [Google Scholar] [CrossRef]
- Li, C.; Liu, W. Multimodal Transport Demand Forecasting via Federated Learning. IEEE Trans. Intell. Transp. Syst. 2024, 25, 4009–4020. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).