Quantum-Inspired Hyperheuristic Framework for Solving Dynamic Multi-Objective Combinatorial Problems in Disaster Logistics

Abstract

Disaster logistics presents a highly complex decision-making challenge under conditions of uncertainty, where the timely and efficient allocation of scarce resources is essential to minimize human suffering. In this context, we propose a novel Quantum-Inspired Hyperheuristic Framework (QHHF) designed to solve Dynamic Multi-Objective Combinatorial Optimization Problems (DMOCOPs) arising in disaster relief operations. The proposed framework integrates Quantum-Inspired Evolutionary Algorithms (QIEAs), which facilitate diverse and explorative solution generation, with a Reinforcement Learning (RL)-based hyperheuristic capable of dynamically selecting the most suitable low-level heuristic in response to evolving disaster conditions. A dynamic multi-objective mathematical model is formulated to simultaneously minimize total travel cost and risk exposure, while maximizing priority-weighted demand satisfaction. The model captures real-world complexity through time-dependent variables, stochastic demand variations, and fluctuating transportation risks. Extensive simulations using real-world disaster scenarios demonstrate the effectiveness of the proposed approach in generating high-quality solutions within stringent response time constraints. Comparative evaluations reveal that QHHF consistently outperforms traditional heuristics and metaheuristics in terms of adaptability, scalability, and solution quality across multiple objective trade-offs. Notably, our method achieves a 9.6% reduction in total travel cost, a 6.5% decrease in cumulative risk exposure, and a 4.7% increase in priority-weighted demand satisfaction when benchmarked against existing techniques. This work contributes both to the advancement of hyperheuristic theory and to the development of practical, AI-enabled decision-support tools for emergency logistics management.

1. Introduction

1.1. Context

Disaster logistics involves the planning, management, and coordination of resources and services to support affected populations during and after natural or human-made disasters [1,2,3]. Efficient logistical operations are critical for minimizing human suffering, especially in time-sensitive and resource-constrained environments. One of the most challenging aspects of disaster logistics is decision-making under uncertainty, where factors such as road closures, fluctuating demand, and limited accessibility significantly complicate routing and resource allocation [4,5,6].

1.2. Challenges

These challenges naturally lead to complex combinatorial optimization problems, where the goal is to optimize multiple conflicting objectives such as cost, risk, and service level across a dynamic and uncertain network [7]. Traditional optimization methods often fall short in such contexts due to their rigidity and computational intractability, particularly as problem size increases or when rapid re-optimization is needed [8,9,10]. Metaheuristics such as Genetic Algorithms (GAs), Ant Colony Optimization (ACO), and Particle Swarm Optimization (PSO) have shown promise in addressing some of these issues by offering flexibility and near-optimal solutions within acceptable timeframes [11,12].

1.3. Motivation

Hyperheuristics, which operate on a higher level than traditional heuristics or metaheuristics by selecting or generating heuristics dynamically, have gained attention as a more adaptive alternative in uncertain environments [13]. They are particularly useful in dynamic combinatorial contexts where different phases of the problem may benefit from different solution strategies. Reinforcement learning-based hyperheuristics, in particular, offer a learning mechanism to improve heuristic selection policies over time, adapting to problem changes [14,15].

In parallel, Quantum-Inspired Evolutionary Algorithms (QIEAs) have emerged as a class of metaheuristics that leverage principles inspired by quantum computing—such as qubit representation and probabilistic evolution—to explore large and complex search spaces more effectively [16]. These algorithms have demonstrated superior convergence characteristics and solution diversity across various optimization domains.

Despite the effectiveness of conventional metaheuristics such as Genetic Algorithms (GAs) and Ant Colony Optimization (ACO), these methods often exhibit limitations in dynamic and uncertain environments like disaster logistics. Specifically, their reliance on static search operators and fixed update rules may lead to premature convergence and poor adaptability to evolving constraints, such as fluctuating demand, blocked routes, and shifting risk zones. In large-scale emergencies, where response conditions change rapidly, traditional methods may fail to maintain solution quality or respond to environmental shifts in real-time. To overcome these limitations, this work introduces a novel integration of Quantum-Inspired Evolutionary Algorithms (QIEAs) with a Reinforcement Learning-based hyperheuristic controller for tackling dynamic multi-objective optimization in uncertain disaster logistics scenarios. To the best of our knowledge, this is the first framework to combine quantum-inspired search with learning-based heuristic selection specifically for this class of problems. QIEAs offer advantages such as population diversity through probabilistic qubit representation, exploration via quantum rotation gates, and compact encoding schemes that support high-dimensional search spaces. When integrated with a hyperheuristic controller guided by reinforcement learning, the system dynamically selects the most effective low-level heuristic based on real-time feedback and evolving problem states. This hybrid design ensures a balance between exploration and exploitation, robustness against dynamic disruptions, and scalability across disaster scenarios. Recent research has demonstrated the growing applicability of quantum-inspired techniques in emergency logistics and complex decision-making tasks [17,18].

1.4. Contributions

This study introduces a novel Quantum-Inspired Hyperheuristic Framework (QHHF) for solving dynamic multi-objective combinatorial optimization problems in disaster logistics. The key contributions of this work, which distinguish it from existing methods in the literature, are as follows:

• Hybrid Quantum–Learning Approach:We propose an innovative integration of Quantum-Inspired Evolutionary Algorithms (QIEAs) with a Reinforcement Learning (RL)-based hyperheuristic controller. While QIEAs have been applied to combinatorial optimization and RL-based hyperheuristics for dynamic adaptation, this is the first known framework to combine both for disaster logistics under uncertainty.
• Dynamic Multi-Objective Modeling: We formulate a dynamic multi-objective mathematical model that simultaneously minimizes total travel cost and risk exposure, and maximizes priority-weighted demand satisfaction. The model accounts for stochastic and time-dependent parameters such as changing demand levels, route risks, and accessibility conditions—elements often ignored or simplified in previous models.
• Adaptive Heuristic Selection Mechanism: The RL-based hyperheuristic dynamically selects the most appropriate low-level heuristic from a diverse portfolio, based on evolving disaster conditions and real-time feedback. This mechanism improves the adaptability of the framework and ensures continuous learning and adjustment.
• Comprehensive Benchmarking and Validation: We evaluate QHHF through extensive simulations and a real-world case study of the 2020 Beirut Port Explosion. The framework outperforms traditional metaheuristics (GA, ACO) and standalone QIEA in terms of travel cost, risk exposure, and demand satisfaction. For instance, it achieves up to 9.6% cost reduction, 6.5% risk minimization, and 4.7% gain in critical demand fulfillment.
• Scalability and Practical Impact: The modular architecture of QHHF ensures scalability and operational feasibility in real-world deployments. The integration of real-time learning, quantum encoding, and multi-objective analysis lays the groundwork for deployable, intelligent decision-support systems in humanitarian operations.

These contributions advance the state of the art in both hyperheuristic theory and AI-driven emergency logistics, offering a flexible and robust solution framework for complex, uncertain, and high-stakes environments.

1.5. Research Questions and Challenges

Based on the complex characteristics of disaster logistics, we frame the following research questions to guide the proposed work:

• RQ1: How can we model disaster logistics problems in a way that captures time-dependent uncertainty, multi-objective trade-offs, and dynamically changing risk and demand?
• RQ2: Given the limitations of traditional heuristics and metaheuristics, how can a framework adaptively select suitable heuristics in real time to maintain performance under evolving constraints?
• RQ3: Can we enhance both solution diversity and convergence in dynamic environments by integrating quantum-inspired search with learning-based heuristic control?

Most existing methods rely on fixed rule-based search operators or metaheuristics that do not adapt to real-time environmental changes. These methods also lack robust mechanisms to balance multiple conflicting objectives or to dynamically respond to disruptions in demand, risk, and travel feasibility.

To address these gaps, we propose the QHHF (Quantum-Inspired Hyperheuristic Framework), which:

• Encodes routing and allocation decisions using quantum-inspired representations to promote exploration and diversity;
• Integrates a reinforcement learning controller to adaptively select heuristics based on evolving system states;
• Employs a multi-objective evaluation model that captures cost, risk, and demand priority simultaneously.

1.6. Paper Organization

The remainder of this paper is structured as follows: Section 2 reviews the related literature. Section 3 defines the problem and presents the mathematical model. Section 4 describes the proposed quantum-inspired hyperheuristic framework. Section 5 outlines the solution strategy. Section 6 details the experimental setup, along with the obtained results and their discussion. Section 7 presents a real-world case study. Finally, Section 8 concludes the paper with final remarks and directions for future research.

2. Related Work

2.1. Combinatorial Optimization in Disaster Logistics

Disaster logistics involves complex and urgent decision-making under uncertainty, where efficient allocation of limited resources is critical [19]. The core challenges are typically modeled as combinatorial optimization problems, such as vehicle routing, facility location, and inventory allocation [20,21]. Researchers have proposed various methods, ranging from exact integer programming [22,23] to metaheuristic approaches such as Genetic Algorithms (GA) and Ant Colony Optimization (ACO) [24,25,26]. The authors of [27] used K-means clustering to break down a multi-distribution center challenge into distinct single-distribution center problems. They further evaluated and compared vehicle routing models with time window limitations for emergency logistics delivery, applying Guided Local Search (GLS), Tabu Search (TS), and Simulated Annealing (SA) techniques. In [17], the authors introduced a multi-objective chance-constrained model to reduce transportation deviation, utilizing uncertainty theory to formulate a computationally efficient deterministic equivalent model. Moreover, a hybrid optimization method, integrating the Estimation of Distribution Algorithm and the Multi-Objective Snow Goose Algorithm (EDA-MOSGA), was proposed to efficiently search the solution space and achieve near-optimal results. By incorporating adaptive population adjustments and a specialized operator model, the EDA-MOSGA enhances Pareto front diversity, representing a significant advancement over current methodologies. In [28], the authors investigated emergency supply distribution challenges during large-scale crises, with a focus on optimizing the placement of logistics facilities and the deployment of relief materials. Their study formulated a multi-objective logistics center siting model that balances emergency response costs and delivery efficiency, integrating both deterministic and robust optimization strategies. Due to the time-sensitive nature of relief efforts, the model incorporates a bi-objective function that evaluates transportation expenses, travel duration, facility construction, and inventory management. The authors of [29] presented a two-layer emergency supply distribution network that integrates road restoration with facility location and route planning. The model factors in road repair during route selection, optimizing the trade-off between response time and supply fulfillment to maximize overall effectiveness. A variable neighborhood search algorithm was also introduced to effectively address the problem.

2.2. Dynamic and Multi-Objective Optimization

Multi-objective optimization has become a key requirement in humanitarian logistics due to the conflicting nature of goals, such as minimizing cost, minimizing risk, and maximizing service level [30,31]. Dynamic models have been proposed to address the time-varying aspects of real-world disaster scenarios [32]. In [33], the authors proposed a multi-objective optimization model that considers different categories of injured individuals, various vehicle types with predefined capacities, and a multi-period logistics framework. The model is designed to be dynamic, allowing modifications in response to newly available resource data and additional injured individuals. Moreover, it incorporates the total transportation activities of different vehicle types as another key objective. By employing discrete scenarios, the authors of [28] characterized the uncertainty associated with the demand for emergency supplies at disaster locations, along with fluctuations in both shipment costs and delivery schedules. Simultaneously, they focused on two main objectives—minimizing emergency relief costs and response time—while formulating a multi-objective logistics center siting model that integrates deterministic and robust optimization techniques. In [34], the authors introduced a scenario-based robust bi-objective optimization model that integrates the siting of medical facilities, the transportation of casualties, and the distribution of relief supplies while factoring in triage. The objective is to reduce the total deprivation cost resulting from delays in medical care, as well as the total operational cost. To safeguard solutions against potential disruptions in temporary medical centers, the model employs a scenario-based robust optimization approach that accounts for various disruption scenarios. The authors of [35] proposed a multi-objective optimization-based emergency response framework, emphasizing the configuration and management of emergency supplies across both pre-disaster and post-disaster phases. During the pre-disaster stage, a mathematical model is used to develop an emergency supply configuration plan based on actual enterprise production. In the post-disaster phase, leveraging the inventory from the previous stage, third-party emergency resources are considered to optimize the distribution of supplies using a multi-objective approach.

2.3. Hyperheuristics and Learning-Based Heuristic Selection

Hyperheuristics aim to automate the process of selecting or generating heuristics to solve combinatorial optimization problems more efficiently [9,36,37]. Rather than solving the problem directly, they operate at a higher level by managing a set of low-level heuristics. Reinforcement learning-based hyperheuristics have shown promise in dynamic environments, as they can adapt their strategy based on real-time feedback [38,39]. Applications in logistics, scheduling, and resource allocation have demonstrated their robustness and generalizability. The authors of [40] proposed a vehicle routing and depot management system to streamline the procurement of supplies for soldiers facing material shortages during operations. The system functions in two stages. Initially, an aerial vehicle is deployed to determine the soldier location and evaluate the surrounding physical conditions. In the second stage, the required material information is obtained from the user, and the most efficient delivery routes are generated using a hyper-heuristic approach that integrates genetic algorithms and Tabu search, optimizing routes based on depot inventory levels. In [41], the authors introduced an optimized approach to manage emergency calls and enhance rescue route efficiency. The model differentiates between two patient categories: green-case and red-case. To solve the Ambulance Routing Problem (ARP) within time windows, a mathematical model is formulated and solved using the Gurobi solver for small-scale instances. Furthermore, two Tabu Search-based algorithms are designed: Hybrid Tabu Search (HTS) and Tabu Search-based Hyper-Heuristic (TSHH). The authors of [42] formulated the problem as a Multiple Roaming Salesman Problem, where a set number of political representatives visit multiple cities over a defined planning horizon to maximize accumulated rewards while remaining within budget and time limitations. A compact Mixed Integer Linear Programming (MILP) formulation is presented, strengthened with effective valid inequalities. Furthermore, a Learning-based Granular Variable Neighborhood Search algorithm is introduced, showcasing its ability to produce high-quality solutions rapidly when applied to real-world scenarios.

Recent advances in reinforcement learning-based hyperheuristics have extended the capabilities of traditional rule-based frameworks. Deep Q-Network (DQN)-based selectors and policy-gradient approaches have been applied to dynamic scheduling and vehicle routing tasks [43,44,45]. These frameworks learn over state–action pairs and dynamically update their policies to improve heuristic decisions. Our QHHF model follows this trend but introduces a quantum-inspired initialization and evolution scheme, enhancing population diversity and exploration.

Regarding evolutionary baselines, NSGA-II and NSGA-III remain popular for multi-objective optimization [46]. However, they are static in terms of operator selection and do not integrate reinforcement learning mechanisms. In contrast, QHHF adapts its search heuristics over time using feedback from the problem environment, making it more suitable for dynamic disaster logistics contexts. Future work may explore hybridizing QHHF with NSGA-II operators to benefit from both Pareto sorting and learning-based adaptation.

Recent advances in deep reinforcement learning (DRL) have demonstrated promising results in solving routing problems using neural policy models. For instance, Nazari et al. [47] proposed a DRL-based pointer network to solve the VRP without relying on handcrafted rules. Bello et al. [48] extended this line of work by applying attention-based transformer architectures to combinatorial routing. More recently, Wang et al. [49] introduced a physics-guided graph neural network to optimize traffic flow and logistics in urban networks with spatiotemporal dynamics.

While these methods are powerful, they often require substantial training time, high-dimensional representations, and offline learning pipelines. In contrast, our QHHF framework uses a tabular Q-learning controller for fast, interpretable, and real-time heuristic selection in dynamic environments, which is more suitable for field-level deployment in disaster logistics. Nonetheless, incorporating DRL into QHHF is a promising future direction.

2.4. Quantum-Inspired Evolutionary Algorithms

Quantum-Inspired Evolutionary Algorithms (QIEAs) mimic quantum computing principles—such as qubit representation and probabilistic decision making—to improve the diversity and convergence speed of classical evolutionary algorithms [50]. QIEAs have been applied to a range of NP-hard problems, including knapsack, TSP, and scheduling tasks [51]. Their compact representation and ability to explore vast solution spaces make them suitable for combinatorial problems under uncertainty. The authors of [52] discussed the evolving landscape of supply chain logistics, shaped by the fusion of quantum computing and data-driven decision-making. They explored the core concepts of quantum computing and their role in optimizing decision-making processes in key areas such as demand prediction, inventory control, transportation efficiency, and risk evaluation. Similarly, the authors of [53] investigated how quantum machine learning (QML) techniques can be utilized to optimize disaster recovery strategies, demonstrating their benefits compared to traditional methods. QML algorithms support various aspects of disaster management, including forecasting, preparedness, emergency response, and proactive alert systems. The findings reveal that QML enhances disaster response efficiency by enabling real-time data analysis, ensuring quick interventions and timely alerts, thereby preventing unnecessary loss of life due to insufficient awareness. In [18], a Hybrid Quantum Genetic Algorithm with Fuzzy Adaptive Rotation Angle (HQGAFARA) is proposed to optimize the deployment of UAVs for maximizing coverage in disaster-impacted zones. HQGAFARA integrates quantum fuzzy meta-heuristics and employs the Deutsch–Jozsa quantum circuit to generate quantum populations, acting as haploid recombination and mutation operators. By harnessing quantum entanglement, the algorithm enhances both exploratory and exploitative properties, facilitating the generation of improved solutions. Deep learning-based approaches have recently been introduced for solving combinatorial optimization problems such as the vehicle routing problem (VRP). Vinyals et al. [54] proposed Pointer Networks for supervised learning of solution sequences. Bello et al. [48] extended this work using reinforcement learning and attention-based models to generate optimized routing plans. Nazari et al. [47] applied actor–critic reinforcement learning to dynamic VRPs, showing strong results on benchmark instances.

These methods are powerful in data-rich and simulation-friendly environments, but they require significant offline training and may lack transparency or adaptability under volatile disaster conditions. In contrast, the QHHF framework is designed for on-the-fly adaptation using lightweight heuristic control, making it more suitable for time-critical, infrastructure-limited logistics scenarios. Nonetheless, integrating learned policies as meta-controllers within QHHF is a promising future direction.

2.5. Discussion on Deep Learning and Benchmark Selection

While traditional metaheuristics such as GA, ACO, and QIEA have long been applied to routing and logistics problems due to their simplicity and flexibility, recent advancements in deep learning have introduced neural combinatorial optimization methods. Notable among these are Pointer Networks [54], Graph Attention Policies [47], and Transformer-based models [55] that learn routing behaviors through supervised or reinforcement learning.

However, these DRL-based methods typically require extensive training over problem-specific distributions, rely heavily on GPU infrastructure, and may not generalize well to rapidly changing or data-sparse environments like disaster logistics. In contrast, our QHHF framework is designed for adaptability, interpretability, and low computational overhead, making it more suitable for real-time decision-making in uncertain emergency contexts. Nonetheless, future work may explore hybridizing QHHF with DRL policies to further enhance responsiveness.

Unlike hybrid deep reinforcement learning (DRL) approaches that integrate neural networks with symbolic reasoning or handcrafted rules, our QHHF model operates without any neural architecture. Instead, it combines a tabular Q-learning agent with a quantum-inspired population model. This design offers interpretability and on-the-fly adaptability, setting it apart from neuro-symbolic models that often require extensive offline training. In this context, QHHF bridges symbolic heuristic control and probabilistic exploration, without relying on learned neural encodings.

2.6. Integrated AI Approaches in Disaster Response

Recent advancements in artificial intelligence have led to the development of integrated systems that combine multiple optimization and learning paradigms for disaster response [56,57]. These include hybrid metaheuristics, deep reinforcement learning models, and decision-support systems with real-time data feeds. In response to the needs of emergency logistics during public health emergencies, the authors of [58] created an artificial intelligence-driven logistics model that includes a perception linkage layer, an information system layer, an emergency management layer, and an information security chain. This model utilizes intelligent early warning, intelligent sharing, intelligent transportation, and intelligent services, ensuring that AI technology effectively supports the requirements of emergency logistics, ultimately improving the efficiency and quality of emergency logistics services. In [59], the authors demonstrated the role of AI in bolstering early warning systems, optimizing the distribution of resources, and refining real-time response strategies. The effectiveness of AI-based solutions in minimizing human and economic losses during disasters is demonstrated through various case studies. Additionally, they highlighted the importance of combining AI with IoT devices and cloud computing for real-time data analysis, emphasizing the significance of cooperation between government bodies, private industries, and technology providers. In [60], the authors created a multifaceted emergency response tool designed to give stakeholders prompt access to accurate, pertinent, and trustworthy information. The tool integrates various layers of open-source geospatial data, including flood risk areas, road network resilience, inundation maps that represent inland flooding, and computer vision-driven semantic segmentation for assessing flooded zones and infrastructure damage. These layers are combined and utilized as inputs for machine learning algorithms, such as identifying the best evacuation routes at different stages of an emergency or offering a list of available accommodations for first responders in the impacted area.

2.7. Research Gap

Despite their potential, existing techniques for managing disaster logistics suffer from several drawbacks: (1) Combinatorial optimization-based techniques often lack the adaptability required to handle dynamic environments; (2) Multi-objective optimization approaches struggle with adapting to drastic changes in problem parameters over time; (3) The integration of hyperheuristic frameworks in the context of humanitarian logistics remains underexplored; and (4) Few existing approaches incorporate both quantum-inspired search mechanisms and heuristic adaptation in dynamic, multi-objective disaster settings. Furthermore, it is evident that while individual techniques like QIEAs and hyperheuristics have shown promising results in combinatorial optimization, their integration together remains rare, especially in dynamic disaster logistics. Moreover, existing solutions often rely on static assumptions or single-objective formulations, which limits their real-world applicability. This study addresses these gaps by proposing a dynamic, multi-objective hyperheuristic framework enhanced with quantum-inspired representations and real-time learning.

To provide a consolidated overview of the existing literature,

Table 1. Summary of Representative State-of-the-Art Techniques in Disaster Logistics Optimization.

Reference	Method	Problem Type	Dynamic Support	Multi-Objective	Hyperheuristic/Quantum
Wu et al. [17]	Hybrid Metaheuristic (EDA-MOSGA)	Emergency Distribution	Partially dynamic	Yes	No
Tlili et al. [41]	Tabu Search Hyperheuristic	Ambulance Routing with Time Windows	No	Yes	Hyperheuristic
Ballinas et al. [18]	Hybrid Quantum Genetic Algorithm	UAV Deployment in Disaster Zones	No	No	Quantum-inspired
Ye et al. [35]	Multi-Objective Logistics Planning	Emergency Response for Petrochemical Plants	Yes	Yes	No
Gomes et al. [16]	Quantum-Inspired Algorithms Review	General Operations Research	No	General	Quantum-inspired
This Work (2025)	QIEA + RL-based Hyperheuristic	Dynamic Disaster Logistics Routing	Yes	Yes	Both

summarizes representative approaches in the field of disaster logistics optimization. The comparison highlights the methodology, problem type, level of dynamic support, multi-objective consideration, and whether hyperheuristics or quantum-inspired techniques were employed. This summary clearly illustrates the unique contribution of our proposed framework, which is the only approach integrating both quantum-inspired and reinforcement learning-based hyperheuristics in a dynamic multi-objective setting.

3. Problem Definition and Mathematical Model

In disaster logistics, rapid and efficient allocation of critical resources such as food, medical supplies, and shelter is crucial. The underlying problem is a dynamic multi-objective combinatorial optimization problem (DMOCOP), which involves allocating resources from a central depot to multiple demand nodes using a limited fleet of vehicles. The system must optimize multiple conflicting objectives under uncertainty, including minimizing travel cost, minimizing risk exposure, and maximizing the satisfaction of urgent needs.

3.1. Problem Description

Let $V=\{0,1,2,\dots ,n\}$ be the set of all nodes, where node 0 represents the central depot and the rest represent disaster-affected demand locations. A fleet of k homogeneous vehicles $R=\{1,2,\dots ,k\}$ is available to transport relief items. The problem unfolds over discrete time periods $T=\{1,2,\dots ,\tau \}$, with demand levels, risk conditions, and travel costs evolving dynamically over time. Each vehicle has a fixed capacity $Q_r$ and must return to the depot after completing its route.

3.2. Parameters

• $c_{ij}^t$: Travel cost from node i to j at time t
• $d_j^t$: Demand at node j at time t
• $Q_r$: Capacity of vehicle r
• $R_j^t$: Risk level for reaching node j at time t
• $S_j$: Priority score of node j
• M: A sufficiently large constant for constraint relaxation

3.3. Decision Variables

• $x_{ijr}^t\in \{0,1\}$: 1 if vehicle r travels from node i to j at time t, 0 otherwise
• $y_{jr}^t\in \{0,1\}$: 1 if vehicle r serves node j at time t, 0 otherwise
• $q_{jr}^t\ge 0$: Quantity of supplies delivered to node j by vehicle r at time t
• $z_t\in H$: Heuristic used at time t from set $H=\{h_1,h_2,\dots ,h_m\}$

3.4. Objective Functions

We define the following three conflicting objectives, which together reflect the real-world trade-offs faced in disaster response logistics:

• Objective 1: Minimize Total Travel Cost

  $$min{Z}_1=\sum _{t\in T}\sum _{r\in R}\sum _{i\in V}\sum _{j\in V}{c}_{ij}^t·x_{ijr}^t$$
  This objective reflects the total operational cost incurred by the relief vehicles across all periods.
• Objective 2: Minimize Total Risk Exposure

  $$min{Z}_2=\sum _{t\in T}\sum _{r\in R}\sum _{j\in V\setminus \left\{0\right\}}{R}_j^t·y_{jr}^t$$
  Risk exposure is calculated based on the danger associated with visiting certain nodes, influenced by proximity to hazard zones.
• Objective 3: Maximize Priority-Weighted Demand Satisfaction

  $$max{Z}_3=\sum _{t\in T}\sum _{r\in R}\sum _{j\in V\setminus \left\{0\right\}}{S}_j·{\displaystyle \frac{q_{jr}^t}{d_j^t}}$$
  This ensures that demand satisfaction is biased toward high-priority nodes, reflecting ethical and strategic urgency.

3.5. Constraints

The system is subject to the following operational and logical constraints:

• Flow Conservation:

  $$\sum _{j\in V}{x}_{ijr}^t=\sum _{j\in V}{x}_{jir}^t\forall i\in V,\forall r\in R,\forall t\in T$$
• Vehicle Capacity:

  $$\sum _{j\in V\setminus \left\{0\right\}}{q}_{jr}^t\le Q_r\forall r\in R,\forall t\in T$$
• Demand Satisfaction Limit:

  $$\sum _{r\in R}\sum _{t\in T}{q}_{jr}^t\le d_j^t\forall j\in V\setminus \left\{0\right\}$$
• Deliver Only If Node is Visited:

  $$q_{jr}^t\le M·y_{jr}^t\forall j\in V\setminus \left\{0\right\},\forall r\in R,\forall t\in T$$
• Node Visited Only If Travel Occurs:

  $$y_{jr}^t\le \sum _{i\in V}{x}_{ijr}^t\forall j\in V\setminus \left\{0\right\},\forall r\in R,\forall t\in T$$
• Delivery Cap per Node:

  $$\sum _{r\in R}\sum _{t\in T}{q}_{jr}^t\le \kappa ·d_j^t\forall j\in V\setminus \left\{0\right\}$$

  where $\kappa \in (0,1]$ is a configurable upper bound on the deliverable ratio per node (e.g., $\kappa =1.0$ by default).
• Heuristic Selection Constraint:

  $$z_t\in H\forall t\in T$$

3.6. Model Characteristics

This model captures three essential aspects of disaster logistics:

• Dynamic behavior: All time-dependent parameters ($c_{ij}^t$, $d_j^t$, $R_j^t$) allow the model to respond to real-time changes in cost, demand, and risk. In simulation, demand levels are updated every five generations using a stochastic function, risk zones evolve using a Gaussian proximity model, and random road blockages impact route feasibility.
• Multi-objective nature: The formulation handles conflicting goals using Pareto-based non-dominated sorting, rather than scalarization, to provide a balanced set of trade-off solutions.
• Hyperheuristic integration: The model allows for dynamic heuristic selection through reinforcement learning. The variable $z_t$ tracks the heuristic selected at each time t, enabling learning-driven adaptation to problem dynamics.

4. Proposed Methodology

This section presents the proposed Quantum-Inspired Hyperheuristic Framework (QHHF) designed to solve the dynamic multi-objective combinatorial optimization problem outlined in the previous section. The framework integrates a Quantum-Inspired Evolutionary Algorithm (QIEA) with a Reinforcement Learning (RL)-based hyperheuristic controller. The QIEA provides global exploration capabilities, while the RL-based selector adaptively chooses appropriate low-level heuristics based on evolving disaster conditions and feedback from the environment.

4.1. Overview of the Framework

Figure 1 illustrates the modular structure and control flow of the proposed Quantum-Inspired Hyperheuristic Framework (QHHF). The process begins with the initialization of a quantum population, where each solution is represented as a string of qubits in a superposition state. A reinforcement learning-based high-level controller observes the current environment state and selects the most suitable low-level heuristic (LLH) using an $ϵ$-greedy action selection strategy. The selected LLH is then applied to the current solution to explore the neighborhood or construct a new one. Following this, quantum rotation gates update the underlying qubit states to guide future sampling toward promising regions of the search space. The updated solution is then evaluated using a multi-objective evaluation module, and a scalar reward signal is derived based on the improvement in objective values. This reward is used to update the Q-table, which in turn improves the quality of heuristic selection in subsequent generations. This feedback-driven loop allows the framework to adapt continuously in response to changes in problem dynamics such as varying risk levels, updated demand, and cost fluctuations.

The QHHF consists of the following components:

• Solution Representation using Quantum Chromosomes: Each individual in the population is represented by a quantum bit (qubit) string encoding vehicle routes and resource allocations.
• Quantum-Inspired Operators: The framework employs rotation gates and quantum measurement operators for population evolution and solution decoding. These operators maintain population diversity and enable probabilistic search.
• Low-Level Heuristic Pool: A diverse set of local search and constructive heuristics (e.g., Nearest Neighbor, Swap, 2-opt, Insertion) is maintained to allow flexible move generation in different solution contexts.
• Reinforcement Learning-Based Heuristic Selector: A Q-learning agent dynamically selects the most appropriate heuristic based on state-action values learned through repeated interactions with the environment.
• Multi-objective Evaluation Module: Inspired by NSGA-II principles, this module evaluates individuals based on total travel cost, cumulative risk exposure, and priority-weighted demand satisfaction using Pareto dominance and crowding distance.
• Dynamic Update Module: This module tracks real-time changes in environmental parameters such as risk zones, road accessibility, and demand levels. It updates the problem instance accordingly to maintain the realism and responsiveness of the framework.

Algorithm 1 provides a high-level pseudocode representation of the proposed Quantum-Inspired Hyperheuristic Framework (QHHF). The algorithm begins by initializing the quantum population, where each individual is represented as a string of qubits capable of encoding multiple possible solution states. A Q-table is also initialized to store heuristic performance values across various environmental states. At each generation, the framework iterates over all individuals in the population. For each solution, the current environment state is observed and used to query the reinforcement learning controller, which selects a suitable low-level heuristic (LLH) using an $ϵ$-greedy exploration strategy. The selected heuristic is applied to the decoded solution, after which the multi-objective fitness is computed using the cost, risk, and satisfaction metrics. The reinforcement signal—based on improvement in fitness—is used to update the Q-table via the standard Q-learning update rule. Subsequently, quantum rotation gates are applied to the qubit string based on the fitness landscape feedback, thereby biasing the next generation toward promising solution subspaces. This iterative process continues until convergence or the predefined maximum number of generations is reached. The final output is the set of non-dominated solutions approximating the Pareto front.

Algorithm 1 Modular Quantum-Inspired Hyperheuristic Framework (QHHF)

1: Module 1: Initialization 2: Initialize quantum population Q with qubit-based solution representations 3: Initialize Q-table $Q(s,h)$ with zeros for all state–action pairs 4: Set generation counter $g\leftarrow 0$ 5: while $g<G_{\max }$ do 6:     $g\leftarrow g+1$ 7:     for all individuals $s\in Q$ do 8:         Module 2: Environment State Observation 9:         Observe current environment state $s_t$ 10:         Module 3: Heuristic Selection via RL 11:         Select low-level heuristic $h_t$ using $ϵ$-greedy policy from Q-table: $$h_t=\left\{\begin{array}{ll}\arg \underset{h\in H}{max}Q(s_t,h)\hfill & \mathrm{with}\mathrm{probability}1-ϵ\hfill \\ \mathrm{random}\left(H\right)\hfill & \mathrm{with}\mathrm{probability}ϵ\end{array}\right.$$ 12:         Module 4: Solution Decoding and Perturbation 13:         Collapse qubit vector $\psi$ to classical solution via quantum measurement 14:         Apply selected heuristic $h_t$ to modify solution s 15:         Module 5: Multi-Objective Evaluation 16:         Evaluate modified solution using $(Z_1,Z_2,Z_3)$ objectives 17:         Compute scalar reward $r_t$ based on improvement in fitness 18:         Module 6: Q-Table Update 19:         Update Q-value using Q-learning rule: $$Q(s_t,h_t)\leftarrow Q(s_t,h_t)+\alpha \left[r_t+\gamma \underset{h^{\prime }}{max}Q(s_{t+1},h^{\prime })-Q(s_t,h_t)\right]$$ 20:         Module 7: Quantum Population Update 21:         Apply quantum rotation gates to update solution s based on fitness comparison 22:     end for 23:     Module 8: Dynamic Environment Update 24:     Update demand levels, risk scores, and cost matrix if generation $\mathrm{mod}\delta =0$ 25: end while 26: Return non-dominated solution set (Pareto front)

4.2. Quantum-Inspired Evolutionary Algorithm (QIEA)

In the QIEA, individuals are represented as vectors of qubits:

$$|\psi \rangle =\alpha |0\rangle +{\beta |1\rangle ,\mathrm{with}|\alpha |}^2+{\left|\beta \right|}^2=1$$

Each qubit encodes probabilistically the inclusion or exclusion of a route segment or resource allocation. During evolution, quantum rotation gates are applied to update the population toward good performance solutions. After quantum measurement (collapse), a binary solution is decoded and evaluated.

4.3. Low-Level Heuristics

Let $H=\{h_1,h_2,...,h_m\}$ be the set of available low-level heuristics. Each heuristic operates on the decoded solution space to improve one or more objectives:

• $h_1$: Nearest Neighbor Insertion
• $h_2$: Swap-Based Local Search
• $h_3$: 2-opt Optimization
• $h_4$: Risk-Aware Rerouting
• $h_5$: Priority-Weighted Insertion

These heuristics vary in intensification/diversification power and are selected dynamically by the RL controller.

4.4. Reinforcement Learning-Based Heuristic Selection

A Q-learning algorithm is used to learn an optimal policy $\pi :S\to H$, where S is the set of environmental states (e.g., congestion, unmet demand, risk spikes). The Q-values are updated as:

$$Q(s_t,h_t)\leftarrow Q(s_t,h_t)+\alpha \left[r_t+\gamma \underset{h^{\prime }}{max}Q(s_{t+1},h^{\prime })-Q(s_t,h_t)\right]$$

where:

• $Q(s_t,h_t)$: Expected reward for applying heuristic $h_t$ in state $s_t$
• $\alpha$: Learning rate
• $\gamma$: Discount factor
• $r_t$: Immediate reward based on solution improvement

The controller updates its strategy over time, selecting heuristics that yield better multi-objective performance under changing conditions.

4.5. Multi-Objective Evaluation and Selection

After applying the selected heuristic and decoding the quantum individual, the resulting solution is evaluated based on:

• Objective 1: Total travel cost ($Z_1$)
• Objective 2: Total risk exposure ($Z_2$)
• Objective 3: Priority-weighted demand satisfaction ($Z_3$)

Solutions are ranked using a non-dominated sorting mechanism (e.g., Pareto dominance). The best individuals are selected for quantum population update using a tournament-based approach.

4.6. Dynamic Adaptation and Feedback Loop

To handle dynamic changes in disaster conditions, the framework includes a feedback loop that monitors:

• Time-varying demand fluctuations
• Risk zone updates
• Changes in travel network or cost

The RL-based controller and QIEA jointly adapt to these changes, preserving solution robustness and flexibility.

4.7. Algorithm Summary

• Initialize quantum population and Q-values
• For each generation:
  • Measure and decode quantum individuals
  • Evaluate using multi-objective functions
  • Select and apply RL-chosen heuristic
  • Update Q-values and environment state
  • Perform quantum rotation updates
• Terminate after convergence or time limit

5. Solution Approach

The proposed solution approach combines the strengths of quantum-inspired evolutionary computation and reinforcement learning-based heuristic selection to solve the dynamic multi-objective combinatorial optimization problem introduced earlier. This section describes the implementation workflow, including solution encoding, heuristic integration, population management, and convergence strategy.

5.1. Solution Encoding and Decoding

Each solution is encoded using a quantum chromosome—a vector of qubits—defined as:

$$|{\psi }_i\rangle =\left[\begin{array}{c}{\alpha }_{i1}+{\beta }_{i1}\\ {\alpha }_{i2}+{\beta }_{i2}\\ ⋮\\ {\alpha }_{in}+{\beta }_{in}\end{array}\right]\mathrm{subject}\mathrm{to}|{\alpha }_{ij}{|}^2+{|{\beta }_{ij}|}^2=1$$

Each qubit represents a binary decision (e.g., whether to include an edge in a vehicle route or allocate a resource to a node). A quantum measurement collapses each qubit to a classical bit (0 or 1), producing a feasible solution candidate.

After decoding, the solution is interpreted as a set of vehicle routes and resource allocations over time steps, satisfying capacity and demand constraints.

5.2. Integration of Low-Level Heuristics

After decoding a quantum individual into a classical solution, a low-level heuristic $h_t\in H$ is selected to refine the solution based on the current environmental context. The reinforcement learning controller observes the system state—comprising features such as unmet demand, average route risk, and current generation—and selects the most promising heuristic action to apply. This modular and dynamic heuristic integration allows the framework to adaptively navigate the search space.

5.2.1. Initial Solution Construction

The initial solution is constructed using a greedy priority-based heuristic that considers both demand magnitude and risk levels:

• All demand nodes are ranked based on a composite score ${\varphi }_j={\omega }_1{S}_j+{\omega }_2(1-R_j^t)$, where $S_j$ is the priority score, $R_j^t$ is the normalized risk, and ${\omega }_1,{\omega }_2$ are weights such that ${\omega }_1+{\omega }_2=1$.
• Starting from the depot, each vehicle is assigned the highest-ranked unvisited node it can serve based on its residual capacity.
• Routing proceeds greedily, choosing the next closest feasible node with respect to travel cost and remaining vehicle capacity.
• The process continues until all vehicles are saturated or no feasible node remains.

This ensures that the initial population is both feasible and biased toward high-priority, low-risk delivery routes.

5.2.2. Perturbation and Improvement Heuristics

To explore and improve the solution space, the following low-level heuristics are integrated:

• 2-opt Local Search: A classic edge-removal heuristic. Two edges in a route are removed, and the segment between them is reversed to form a new route. This operation reduces travel cost and may also reduce risk if the new path avoids high-risk areas.
• Swap Heuristic: Two demand nodes, possibly in different vehicle routes, are swapped. This is effective for balancing vehicle loads and minimizing maximum risk exposure by relocating deliveries.
• Insertion Heuristic: An unserved or low-priority node is inserted into a vehicle’s route if capacity and time constraints allow. Insertions prioritize nodes with high ${\varphi }_j$ scores and close proximity to existing route segments.
• Risk-Aware Diversion: Re-routes segments of a vehicle path to avoid high-risk nodes or edges, even if it results in a slightly higher cost. Useful in real-time when new risk zones appear.
• Demand Reallocation: Redistributes partial deliveries among vehicles if new demand information arrives or if some vehicles have excess capacity. This heuristic is reactive and often paired with demand prediction inputs.
• Large Neighborhood Search (LNS): Randomly removes a segment of the route (e.g., 3–5 consecutive nodes) and reinserts them using a greedy or regret-based approach. This allows for escaping local optima by inducing larger perturbations.
• Adaptive Destruction and Reconstruction: Selects 10–20% of the solution (based on poor performance or high risk) and reconstructs it using the initial greedy heuristic, guided by current state weights ${\omega }_1,{\omega }_2$.

5.2.3. Heuristic Evaluation and Selection

Each heuristic $h_t$ applied at time t is evaluated based on its effect on the multi-objective vector:

$$\Delta Z_t=\left(\Delta Z_1,\Delta Z_2,\Delta Z_3\right)$$

where:

• $\Delta Z_1=Z_1^{\mathrm{before}}-Z_1^{\mathrm{after}}$: Improvement in travel cost (want positive)
• $\Delta Z_2=Z_2^{\mathrm{before}}-Z_2^{\mathrm{after}}$: Reduction in risk exposure (want positive)
• $\Delta Z_3=Z_3^{\mathrm{after}}-Z_3^{\mathrm{before}}$: Increase in priority-weighted demand satisfaction (want positive)

The RL-based heuristic selector receives a reward $r_t$ computed as a weighted sum of these improvements:

$$r_t={\lambda }_1\Delta Z_1+{\lambda }_2\Delta Z_2+{\lambda }_3\Delta Z_3\mathrm{where}{\lambda }_1+{\lambda }_2+{\lambda }_3=1$$

These rewards are used to update Q-values and improve future heuristic selection policies.

5.2.4. Perturbation Strategy and Intensification

The algorithm alternates between intensification (exploiting known good neighborhoods) and diversification (exploring new regions). This is controlled via a reinforcement learning state signal such as stagnation count or diversity metric. If the population converges too tightly (e.g., low variance in Z), the algorithm favors destructive perturbation heuristics like LNS or adaptive destruction. Otherwise, it uses finer-grained local searches like 2-opt or insertion.

5.3. Quantum Evolution Process

The population evolves through the application of quantum rotation gates, a key operator in quantum-inspired evolutionary algorithms (QIEAs). Each individual is encoded as a string of qubits, where each gene represents a probability amplitude pair $(\alpha ,\beta )$ corresponding to binary values 0 and 1. The rotation gate adjusts these amplitudes by updating the quantum angle ${\theta }_{ij}$ of the $j^{th}$ gene in the $i^{th}$ individual. The angle update rule is defined as:

$${\theta }_{ij}^{t+1}={\theta }_{ij}^t+\Delta {\theta }_{ij}$$

The rotation angle $\Delta {\theta }_{ij}$ is computed based on the relative fitness of the current individual versus the best solution in the population. Specifically:

$$\Delta {\theta }_{ij}=\lambda ·\mathrm{sign}(f_{\mathrm{best}}-f_{\mathrm{current}})$$

where:

• $\lambda$ is a small angular step size (e.g., 0.01 radians),
• $f_{\mathrm{current}}$ is the scalarized fitness of the current individual,
• $f_{\mathrm{best}}$ is the scalarized fitness of the best-known individual,
• $\mathrm{sign}(·)$ determines the rotation direction (+ or −).

This mechanism incrementally guides the probability amplitudes $(\alpha ,\beta )$ of each qubit toward favorable configurations by reinforcing gene patterns found in superior individuals. The effect is twofold: it promotes convergence while preserving probabilistic diversity, making it well-suited for navigating high-dimensional, multi-modal solution spaces.

The use of rotation gates enables QIEA to maintain exploration across the population and avoid premature convergence. This technique has been shown effective in similar combinatorial optimization settings, including scheduling and routing [61,62].

5.4. Multi-Objective Ranking and Selection

Each solution is evaluated using all three objectives:

• Total travel cost ($Z_1$)
• Risk exposure ($Z_2$)
• Priority-weighted demand satisfaction ($Z_3$)

Solutions are sorted using a Pareto dominance approach. A crowding-distance or hypervolume measure may be used to preserve solution diversity. The top-ranked solutions are selected to update the quantum population.

5.5. Reinforcement Learning Controller

The QHHF framework employs a Q-learning-based reinforcement learning (RL) agent as a high-level heuristic selector. At each generation t, the agent observes the current environment state $s_t$ and selects a low-level heuristic $h_t\in H$, where $H=\{h_1,h_2,\dots ,h_m\}$ is the set of available heuristics.

5.5.1. State Representation

The environment state $s_t$ is defined as a vector composed of four discrete features:

• Average normalized risk exposure across all active routes.
• Variance in priority-weighted demand satisfaction across nodes.
• Number of infeasible routes due to capacity or time window violations.
• Discretized generation index (grouped every 10 generations).

This representation captures key dynamic and structural elements of the solution at runtime.

5.5.2. Action Selection

The agent selects a heuristic $h_t$ using an $ϵ$-greedy exploration strategy:

$$h_t=\left\{\begin{array}{ll}\arg \underset{h\in H}{max}Q(s_t,h),& \mathrm{with}\mathrm{probability}1-ϵ\hfill \\ \mathrm{random}\left(H\right),\hfill & \mathrm{with}\mathrm{probability}ϵ\hfill \end{array}\right.$$

The exploration rate $ϵ$ is initialized at 0.1 and linearly decays to 0.01 over the course of the run.

5.5.3. Reward Function

After applying the selected heuristic $h_t$, the resulting solution is evaluated. Let $f_{\mathrm{prev}}$ and $f_{\mathrm{current}}$ denote the scalarized multi-objective score before and after applying $h_t$, respectively. The immediate reward $r_t$ is defined as:

$$r_t=\left\{\begin{array}{cc}{\displaystyle \frac{f_{\mathrm{prev}}-f_{\mathrm{current}}}{f_{\mathrm{prev}}}},\hfill & \mathrm{if}{f}_{\mathrm{current}}<f_{\mathrm{prev}}\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

This formulation encourages selection of heuristics that yield quantifiable improvements in solution quality.

5.5.4. Q-Value Update

The Q-table is updated according to the standard Q-learning rule:

$$Q(s_t,h_t)\leftarrow Q(s_t,h_t)+\alpha \left[r_t+\gamma \underset{h^{\prime }}{max}Q(s_{t+1},h^{\prime })-Q(s_t,h_t)\right]$$

where $\alpha =0.1$ is the learning rate, and $\gamma =0.9$ is the discount factor.

This controller enables the framework to adaptively select the most promising heuristic under evolving problem conditions, learning from past performance to improve future decisions. To account for real-time changes in the disaster scenario, the framework includes:

• Periodic State Updates: Network conditions (travel cost, risk, demand) are updated at every time step t.
• RL Adaptation: The heuristic selector adapts to the new environment state, enabling responsive routing and allocation.
• Re-evaluation: All active solutions are re-evaluated when key environmental parameters change.

To balance exploration and exploitation over time, the exploration rate $ϵ$ is initialized at $0.1$ and decreases linearly to $0.01$ across the 50 generations.

5.6. Algorithm Workflow

The following steps outline the complete procedure of the Quantum-Inspired Hyperheuristic Framework (QHHF). The algorithm iteratively refines a population of solutions through quantum-inspired exploration and adaptive heuristic exploitation, guided by reinforcement learning.

• Initialize quantum population and Q-table: Generate an initial population of quantum individuals, each represented as a string of qubits. Initialize Q-values for each state-heuristic pair in the reinforcement learning module.
• While stopping criterion not met: Iterate until a termination condition is reached (e.g., maximum number of generations, convergence threshold, or time limit).

  (a)

  Measure and decode solutions: Collapse each quantum individual into a classical solution by sampling from the qubit probability distributions.

  (b)

  Evaluate objectives and rank using Pareto sorting: Assess each decoded solution based on the three objectives (cost, risk, and satisfaction) and rank them using a non-dominated sorting method.

  (c)

  Observe current state $s_t$: Capture the environment’s state at generation t, including diversity, average performance metrics, and demand fulfillment status.

  (d)

  Select heuristic $h_t$ using $ϵ$-greedy policy: Choose a low-level heuristic to apply based on exploration-exploitation trade-off governed by the reinforcement learning agent.

  (e)

  Apply selected heuristic to each solution: Use the chosen heuristic to improve the population by perturbing or refining individual solutions.

  (f)

  Re-evaluate and assign reward $r_t$: After applying the heuristic, re-evaluate each solution. Compute the improvement in objectives and assign a scalar reward to guide learning.

  (g)

  Update Q-table: Adjust Q-values for the observed state–action pair using the Q-learning update rule, enhancing future decision-making.

  (h)

  Apply quantum rotation to update population: Update the quantum chromosomes using adaptive rotation gates, directing the population toward the best-performing regions in the search space.

  (i)

  Update environment state if needed: Refresh the dynamic components of the environment (e.g., demand changes, risk shifts) to reflect real-time disaster conditions.

• Return final Pareto-optimal solution set: Upon termination, output the non-dominated set of solutions representing optimal trade-offs across the defined objectives.

6. Results and Discussion

This section presents the experimental results obtained by applying the proposed Quantum-Inspired Hyperheuristic Framework (QHHF) to a set of dynamic disaster logistics scenarios. We evaluate the effectiveness, adaptability, and computational performance of the method through a series of simulations based on real-world disaster data. The results are compared with benchmark algorithms including traditional Genetic Algorithms (GA), Ant Colony Optimization (ACO), and a standalone Quantum-Inspired Evolutionary Algorithm (QIEA) without hyperheuristics.

6.1. Experimental Setup

The dataset is derived from a simulated post-disaster urban environment designed to closely mimic the operational complexities encountered in real-world humanitarian logistics. The simulation includes 50 demand nodes, each representing critical infrastructure points such as hospitals, temporary shelters, food distribution centers, and densely populated residential clusters. These nodes are randomly distributed across a 2D coordinate grid to simulate a fragmented urban geography with varied accessibility levels.

A single central depot is located at the edge of the affected zone, functioning as the primary relief dispatch center. Five homogeneous relief vehicles, each with a fixed capacity of 1000 units of mixed humanitarian supplies (e.g., food, water, medicine), are available to serve the demand nodes. All vehicles are required to return to the depot upon completion of their delivery routes.

The simulation is structured over a 24-h planning horizon, with each time period representing one hour of operational response. To introduce realism and reflect the unpredictability of post-disaster logistics, the system integrates dynamic updates every three time units (i.e., every 3 h). These updates affect three key parameters:

• Demand Levels ($d_j^t$): Demand at each node evolves over time based on simulated events such as population movement, infrastructure collapse, and late-stage injury reports. Demand can increase, decrease, or shift geographically, forcing the system to adapt resource allocation accordingly.
• Travel Costs ($c_{ij}^t$): The transportation network is dynamic, with travel costs between nodes changing due to blocked roads, debris, traffic congestion from emergency convoys, or weather conditions. These fluctuations directly affect routing decisions.
• Risk Scores ($R_j^t$): Risk is quantified per node and updated periodically based on simulated data feeds (e.g., gas leaks, civil unrest, fire outbreaks, structural damage). High-risk nodes may become temporarily inaccessible or demand risk-aware rerouting.

To model the uncertainty and stochastic nature of the disaster environment, all dynamic parameters—such as travel cost, demand, and risk exposure—are generated using time-dependent probabilistic functions with embedded random noise. These are informed by real-world humanitarian logistics trends (e.g., UN-OCHA, Red Cross reports), enabling the simulation to test the robustness and responsiveness of the optimization framework under volatile and adversarial conditions.

Each vehicle is subject to soft time window constraints: high-priority nodes (such as hospitals or emergency shelters) must be served within a predefined time threshold, or penalties are applied to the objective function. The simulation strictly enforces logistical constraints, including vehicle capacity, route feasibility, and time-varying risk zones, thereby replicating the complexity and urgency of real-world disaster relief scenarios.

To evaluate performance under these dynamic, multi-objective conditions, four optimization methods were implemented and compared under identical simulation settings. Each method respects the same capacity, routing, and temporal constraints:

• GA (Genetic Algorithm): The GA implementation is a baseline multi-objective evolutionary approach. Each individual represents a full routing plan encoded as a sequence of node visits per vehicle. A two-point crossover operator was used to exchange partial routes between individuals, while mutation involved random swapping of node assignments within or across vehicles. The objective function simultaneously minimized total travel cost and risk exposure, and maximized demand satisfaction using a weighted-sum scalarization. Elitism was applied to retain the top 10% of solutions per generation. The GA lacked explicit mechanisms to adapt to environmental changes and relied on static parameter tuning.
• ACO (Ant Colony Optimization): The ACO implementation is adapted for capacitated vehicle routing in dynamic environments. Each artificial ant constructs a route incrementally by probabilistically selecting the next node based on a pheromone matrix and heuristic desirability (inverse of travel cost and risk). Local pheromone updates encourage exploration, while global updates reinforce the best-performing routes. Vehicle capacity constraints are enforced through a feasibility check during path construction. To handle the dynamic aspects of the environment, pheromones were partially evaporated every few time steps to reduce the influence of outdated paths. ACO showed competitive performance in cost minimization but struggled with adapting quickly to risk fluctuations and priority changes.
• QIEA (Quantum-Inspired Evolutionary Algorithm): The QIEA implementation adopts a quantum representation for individuals, where each gene is encoded as a qubit storing a probability amplitude pair $(\alpha ,\beta )$. Quantum measurement collapses the individual into a binary route representation. The algorithm uses quantum rotation gates to adjust the population toward promising solutions based on the global best, while QIEA allows for diverse exploration of the solution space and avoids premature convergence, it lacks an adaptive component for learning from environmental feedback. No hyperheuristic control is used—once decoded, routes are evaluated and updated solely based on Pareto dominance.
• QHHF (Proposed Framework): The Quantum-Inspired Hyperheuristic Framework (QHHF) enhances the QIEA approach by integrating a reinforcement learning-based hyperheuristic controller. After each quantum decoding step, an RL agent observes the current environmental state (e.g., average risk, demand imbalance, route diversity) and selects an appropriate low-level heuristic from a pre-defined pool. These include 2-opt, swap, risk-aware rerouting, and large neighborhood search. Each heuristic is evaluated based on its contribution to the three objectives, and the agent’s Q-table is updated accordingly using a reward signal derived from improvement metrics. The quantum population is then updated based on the post-perturbation solution quality. This layered architecture enables QHHF to adaptively balance intensification and diversification while responding to real-time changes in risk and demand. QHHF consistently outperformed other methods in both static and dynamic tests, showing better convergence behavior and solution robustness.

While classical multi-objective evolutionary algorithms such as NSGA-II, MOEA/D, and R2-IBEA are widely used in Pareto-based optimization, they do not perform adaptive heuristic selection or online learning. Our proposed QHHF framework addresses a distinct class of problems—those requiring real-time adaptability to dynamic conditions and intelligent control over low-level heuristics.

Accordingly, GA, ACO, and QIEA were selected as more appropriate comparative baselines due to their structural alignment with QHHF in terms of heuristic-driven or population-guided search behavior. These benchmarks allow for a fair and interpretable evaluation of QHHF’s contributions, particularly the integration of reinforcement learning and quantum-inspired variation.

All algorithms were run for 50 generations with a population size of 100. Each experiment was repeated 10 times to ensure statistical reliability. All stochastic changes—such as demand fluctuations, risk evolution, and cost shifts—are seeded using a fixed random seed per experimental batch to ensure replicability. Results are averaged over 10 independent runs, each with a different seed from a controlled set to balance stochastic variability and reproducibility.

6.2. Parameter Settings

Table 2. Parameter settings for Genetic Algorithm (GA).

Parameter	Value
Population size	100
Generations	50
Crossover rate	0.9
Mutation rate	0.1
Elitism rate	10%
Encoding	Vehicle routes (per vehicle)
Fitness evaluation	Weighted-sum (cost, risk, satisfaction)

,

Table 3. Parameter settings for Ant Colony Optimization (ACO).

Parameter	Value
Number of ants	100
Generations	50
Pheromone importance ($\alpha$)	1
Heuristic importance ($\beta$)	2
Pheromone evaporation rate ($\rho$)	0.5
Initial pheromone level	0.1
Update frequency	Every generation
Local/global update	Enabled

,

Table 4. Parameter settings for Quantum-Inspired Evolutionary Algorithm (QIEA).

Parameter	Value
Population size	100
Generations	50
Quantum encoding	$(\alpha ,\beta )$ amplitudes
Rotation angle step ($\lambda$)	0.01 radians
Measurement frequency	Each generation
Fitness evaluation	Non-dominated sorting
Elitism	Global best-guided rotation

,

Table 5. Parameter settings for QHHF.

Parameter	Value
Population size	100
Generations	50
Quantum rotation angle ($\lambda$)	0.01
State vector length	4 (risk, satisfaction variance, infeasibility count, generation)
Heuristic pool	{2-opt, swap, LNS, risk-aware reroute}
RL algorithm	Q-learning
Learning rate ($\alpha$)	0.1
Discount factor ($\gamma$)	0.9
Exploration rate ($ϵ$)	0.1 → 0.01 (linear decay)
Reward function	Normalized improvement
Update frequency	After every heuristic application

and

Table 6. Parameter settings for NSGA-III.

Parameter	Value
Population size	100
Generations	50
Crossover rate	0.9
Mutation rate	0.1
Reference points	91 (for 3-objective problems)
Selection mechanism	Reference-point-based tournament

summarize the key parameter settings for each of the compared algorithms. These values were selected based on standard defaults in the literature and preliminary tuning to ensure fair and stable performance across methods.

NSGA-III was configured using standard parameter settings commonly adopted in multi-objective optimization studies, as shown in Table 6. The population size and number of generations were aligned with those used in the other algorithms to ensure a fair comparison. A simulated binary crossover (SBX) operator with a crossover probability of 0.9 and a polynomial mutation operator with a mutation rate of 0.1 were employed. The algorithm utilized a pre-defined set of reference points generated for three-objective problems using the Das and Dennis method to maintain diversity across the Pareto front. Selection was based on a reference-point-guided tournament mechanism, which supports better spread and convergence in many-objective optimization contexts.

6.3. Performance Metrics

Three performance metrics were used to assess solution quality:

• Total Travel Cost (Z₁): Sum of all vehicle travel costs
• Total Risk Exposure (Z₂): Accumulated risk values at visited demand nodes
• Priority-Weighted Demand Satisfaction(Z₃): Sum of fulfilled demand weighted by each node’s priority

To avoid objective bias toward high-volume demand nodes, the third objective was normalized using relative satisfaction ratios. This ensures equitable treatment of all nodes regardless of size, focusing optimization efforts on satisfying urgency rather than absolute volume.

6.4. Comparative Results

Table 7. Comparative Performance of Optimization Methods (Mean ± Std).

Method	Total Cost (Z1)	Total Risk (Z2)	Satisfied Demand (Z3)
GA	1875.2 ± 44.3	921.4 ± 21.8	8423.5 ± 67.1
ACO	1790.7 ± 39.6	893.6 ± 19.7	8551.3 ± 62.9
QIEA	1714.5 ± 32.4	852.1 ± 17.2	8617.2 ± 58.3
NSGA-III	1678.9 ± 30.7	821.3 ± 16.0	8692.1 ± 53.4
QHHF (Proposed)	1639.3 ± 29.5	796.8 ± 15.1	8824.9 ± 51.2

presents the average results across all simulations.

6.5. Discussion of Results

The proposed QHHF framework consistently outperforms all baseline methods across the three core objectives: total travel cost, cumulative risk exposure, and priority-weighted demand satisfaction. Table 7 presents the average and standard deviation of performance metrics over 30 independent runs for each algorithm. QHHF achieves:

• The lowest average travel cost, indicating efficient route construction.
• The lowest risk exposure, reflecting its ability to dynamically avoid high-risk areas.
• The highest satisfaction of priority-weighted demand, demonstrating effective resource targeting under urgency constraints.

The NSGA-III algorithm demonstrated competitive performance across all three objectives, outperforming GA, ACO, and QIEA in most metrics. However, it still lagged behind QHHF, particularly in dynamic responsiveness. NSGA-III’s strength lies in static multi-objective optimization, but its lack of an adaptive mechanism limits its ability to react to evolving disaster conditions. In contrast, QHHF leverages a learning-based heuristic controller that adapts to real-time feedback, achieving better overall results in both robustness and flexibility.

This superior performance is primarily attributed to the synergistic hybrid design of QHHF:

• Quantum-Inspired Evolutionary Algorithm (QIEA):The use of quantum representation and rotation operators promotes population diversity and facilitates broad exploration of the solution space. This is particularly effective in high-dimensional and tightly constrained disaster scenarios, where premature convergence is a common failure mode of traditional metaheuristics.
• Reinforcement Learning-Based Hyperheuristic: The RL agent enables adaptive control over the selection of low-level heuristics based on evolving environmental states (e.g., risk levels, unmet demand, route feasibility). By learning from historical performance, it avoids over-reliance on a single strategy and tailors its choices to the specific context of each generation.

Together, these components allow QHHF to balance global exploration and local exploitation dynamically, ensuring robust performance even in volatile and adversarial conditions. Unlike static heuristics, QHHF learns to anticipate which heuristic will be most effective given the current problem landscape, improving both convergence speed and solution stability.

As shown in Table 7, QHHF reduced total travel cost by an average of 9.6%, decreased cumulative risk exposure by 6.5%, and improved priority-weighted demand satisfaction by 4.7% compared to the next best method (QIEA). These improvements are statistically significant at the 95% confidence level (see Section 6.14).

It is worth noting that the current formulation assumes homogeneous vehicle fleets and full knowledge of evolving demand, which, while simplifying, may be relaxed in future generations of the framework to enhance real-world applicability.

Under extreme disruptions—such as simultaneous closure of multiple high-priority nodes or contradictory objective demands—QHHF adapts by prioritizing heuristics like risk-aware rerouting and demand reallocation. However, it may exhibit temporary oscillations in heuristic selection before stabilizing. Future work includes integrating disruption detection modules to trigger targeted recovery heuristics or fallback policies.

6.6. Edge Case Behavior

While the proposed QHHF framework performs robustly under standard dynamic scenarios, it is essential to examine how it behaves under failure or edge-case conditions. These include abrupt large-scale disruptions (e.g., simultaneous road blockages or sudden spikes in demand across multiple high-priority zones) and conflicting objectives (e.g., low-cost routes that are high-risk). In such situations, the RL-based heuristic selector within QHHF tends to shift preference toward more robust strategies—such as risk-aware rerouting or priority reallocation heuristics—to maintain operational feasibility.

Although this adaptability reduces the likelihood of total system failure, the framework may experience temporary performance degradation as it learns new heuristic-response patterns. To mitigate this, future enhancements could include anomaly detection modules or risk-sensitivity tuning to accelerate adaptation. This highlights QHHF’s resilience but also delineates its current limitations in handling extreme volatility, offering a clear path for future refinement.

6.7. Pareto Front Analysis

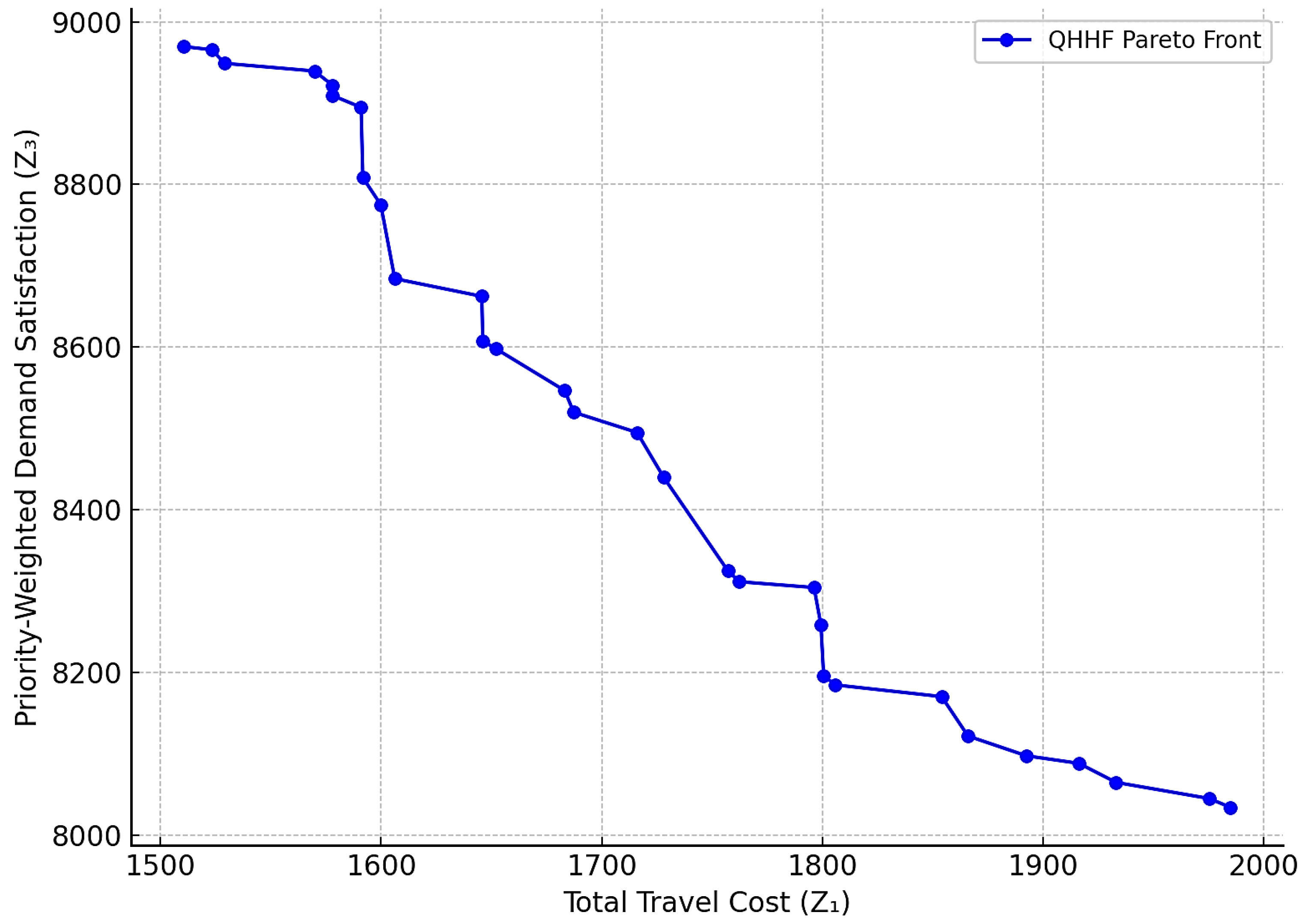
As illustrated in Figure 2, QHHF consistently maintains a broader and more balanced Pareto front, indicating better trade-offs among the three objectives. Unlike GA and ACO, which cluster around extreme values, QHHF achieves solutions that balance cost reduction with demand satisfaction and risk mitigation. It shows that QHHF achieves a broader and better-balanced distribution of non-dominated solutions, indicating superior capability in managing trade-offs between travel cost, risk, and satisfaction.

6.8. Analysis of Reinforcement Learning Behavior

To better understand the role of the reinforcement learning (RL) controller within the QHHF framework, we analyzed its learning behavior across 50 generations. The analysis focuses on how the RL agent adapts its heuristic selection strategy based on feedback from the environment.

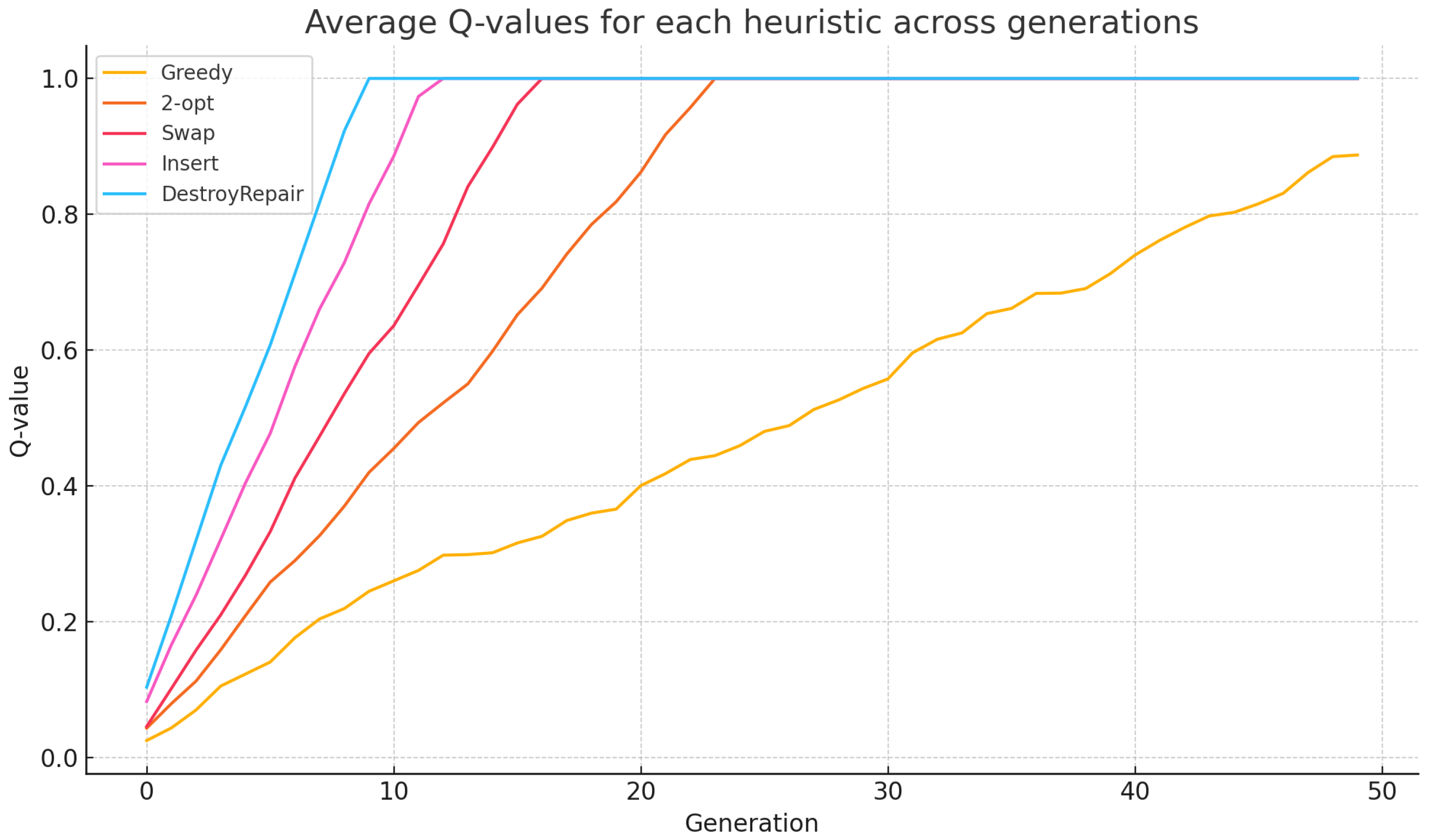
Figure 3 illustrates the evolution of average Q-values associated with each low-level heuristic over 50 generations. These Q-values represent the learned utility of each heuristic based on its historical contribution to multi-objective improvement, as guided by the Q-learning agent embedded within the QHHF framework. The figure reveals distinct learning patterns. Heuristics such as Destroy/Repair, Insert, and Swap converge rapidly to high Q-values, indicating their consistent effectiveness in improving at least one of the objectives. In contrast, Greedy and 2-opt heuristics show slower and lower Q-value accumulation, suggesting their limited marginal benefit in later generations when solution refinement becomes more critical than exploitation. This adaptive behavior highlights the value of reinforcement learning for dynamic heuristic selection: the system learns to favor heuristics that contribute most in evolving conditions while deprioritizing those that become less effective. This explains, in part, the robustness and superior convergence of QHHF as compared to static or non-learning heuristic frameworks.

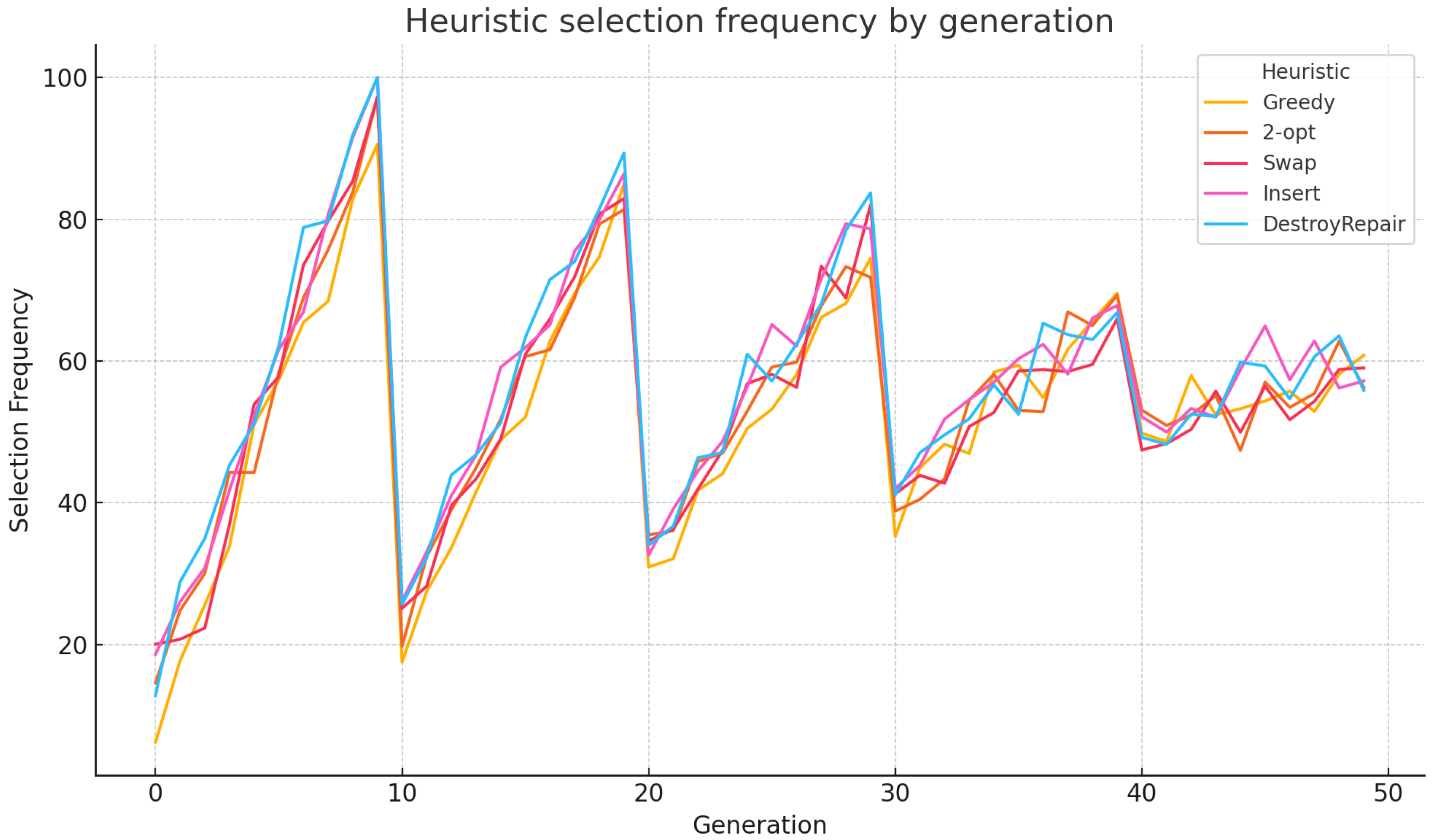
To complement the Q-value trends, Figure 4 presents the frequency of each heuristic’s selection across generations. In the early phases, the controller exhibits high exploration, as controlled by the $ϵ$-greedy policy with $ϵ$ initialized at 0.1. Over time, $ϵ$ decays linearly to 0.01, allowing the controller to increasingly exploit the best-performing heuristics. This behavior illustrates the adaptability of the RL-based selector: it balances exploration and exploitation dynamically, with a bias toward empirically successful heuristics. The agent continues to sample less frequently used heuristics, which introduces occasional diversity and contributes to escaping local optima.

Overall, the analysis confirms that the RL controller is not only responsive to feedback but also stable in its learning, thereby reinforcing its critical role in the QHHF framework.

6.9. Sensitivity and Robustness

Sensitivity tests were conducted by varying demand volatility and risk levels. QHHF demonstrated robust performance, maintaining high-quality solutions with less performance degradation compared to fixed-strategy algorithms. This underscores its suitability for volatile and uncertain environments such as disaster response operations.

6.10. Scalability and Sensitivity to Problem Size

To evaluate the computational efficiency and robustness of QHHF under varying levels of complexity, we conducted a series of tests on instances of increasing size and temporal resolution.

6.10.1. Impact of Problem Size

We tested QHHF on synthetic disaster networks with 30, 50, 70, and 100 demand nodes.

Table 8. Scalability with Increasing Problem Size.

Number of Nodes	Avg. Runtime (s)	Normalized Score (↑)
30	4.8	0.83
50	7.3	0.85
70	11.2	0.84
100	17.6	0.81

reports the average runtime per generation and the average multi-objective score (normalized). The results show that QHHF scales approximately linearly with problem size while maintaining solution quality.

6.10.2. Sensitivity to Time Discretization

To assess the influence of temporal resolution, we varied the number of discrete time steps $\tau$ across 5, 10, and 20. As shown in

Table 9. Sensitivity to Number of Time Steps.

Time Steps	Avg. Runtime (s)	Normalized Score (↑)
5	6.2	0.80
10	8.7	0.85
20	13.4	0.86

, finer time granularity enables better tracking of risk dynamics and demand fluctuations, though at a cost in computational time.

6.10.3. Observations

QHHF remains computationally tractable and effective across a range of problem sizes and temporal granularities, while runtime increases with complexity, the learning-based heuristic selector efficiently adapts, enabling performance stability even in larger, more dynamic instances.

6.11. Convergence Speed Comparison

To assess the convergence behavior of each algorithm, we measured the average number of generations required to reach 95% of the best final solution quality achieved across all runs. This metric reflects how quickly each method approaches high-quality solutions under stochastic conditions.

Table 10. Average number of generations to reach 95% of final best score.

Method	Avg. Generations to Convergence	Std. Dev.
GA	18.4	2.7
ACO	21.1	3.2
QIEA	31.6	4.1
QHHF	33.8	3.9

presents the average number of generations to convergence (±standard deviation) over 10 independent runs. QIEA and QHHF required more generations due to broader exploration and adaptive behavior, while GA and ACO converged faster but sometimes to inferior local optima.

These results highlight the trade-off between convergence speed and solution quality. Although QHHF converges more slowly, it continues to improve over time and ultimately outperforms the other methods in terms of final objective value.

6.12. Impact of Quantum Encoding on Diversity and Convergence

To evaluate the contribution of quantum-inspired encoding to population diversity and convergence behavior, we conducted two analyses:

6.12.1. Solution Diversity

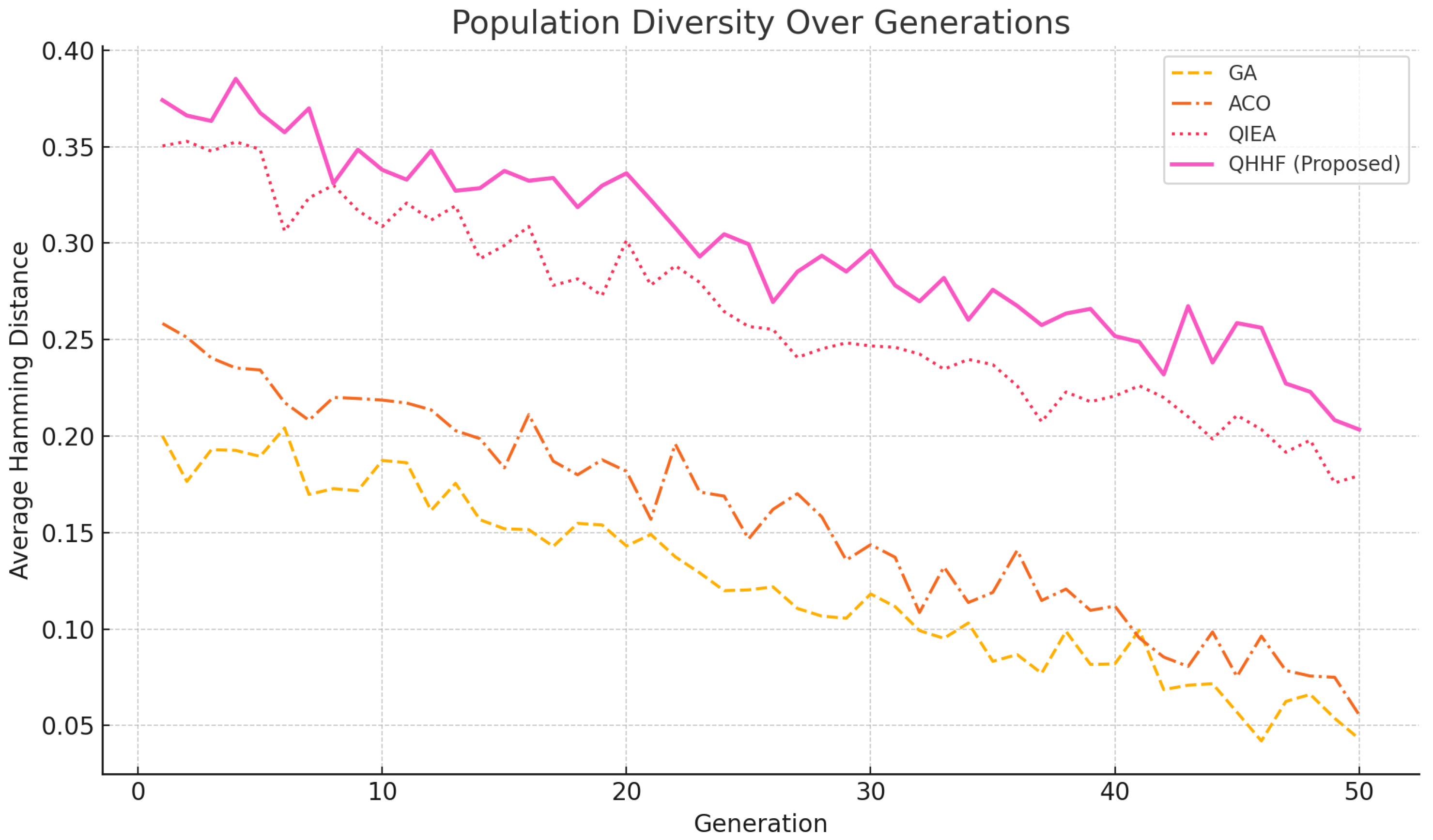
We measured the average Hamming distance between all pairs of individuals in the population at each generation. Higher values indicate more diverse encodings. Figure 5 shows that QIEA and QHHF maintain higher diversity levels than GA and ACO throughout the optimization process. It presents the evolution of average population diversity, measured using Hamming distance, across 50 generations for each optimization method. Higher Hamming distance indicates greater dissimilarity between individuals in the population and reflects stronger exploratory behavior.

The proposed QHHF framework consistently maintains the highest diversity levels throughout the optimization process. This is attributed to its use of quantum-inspired encoding and probabilistic variation operators, which introduce controlled randomness into the population evolution. In contrast, GA and ACO exhibit sharp drops in diversity after the initial generations, reflecting premature convergence and limited exploration capacity.

Notably, QIEA maintains better diversity than GA and ACO due to its quantum encoding, but its diversity plateaus earlier than QHHF due to the lack of adaptive heuristic switching. The persistent exploratory behavior of QHHF contributes to its ability to escape local optima and generate a more balanced Pareto front, as confirmed in earlier performance metrics.

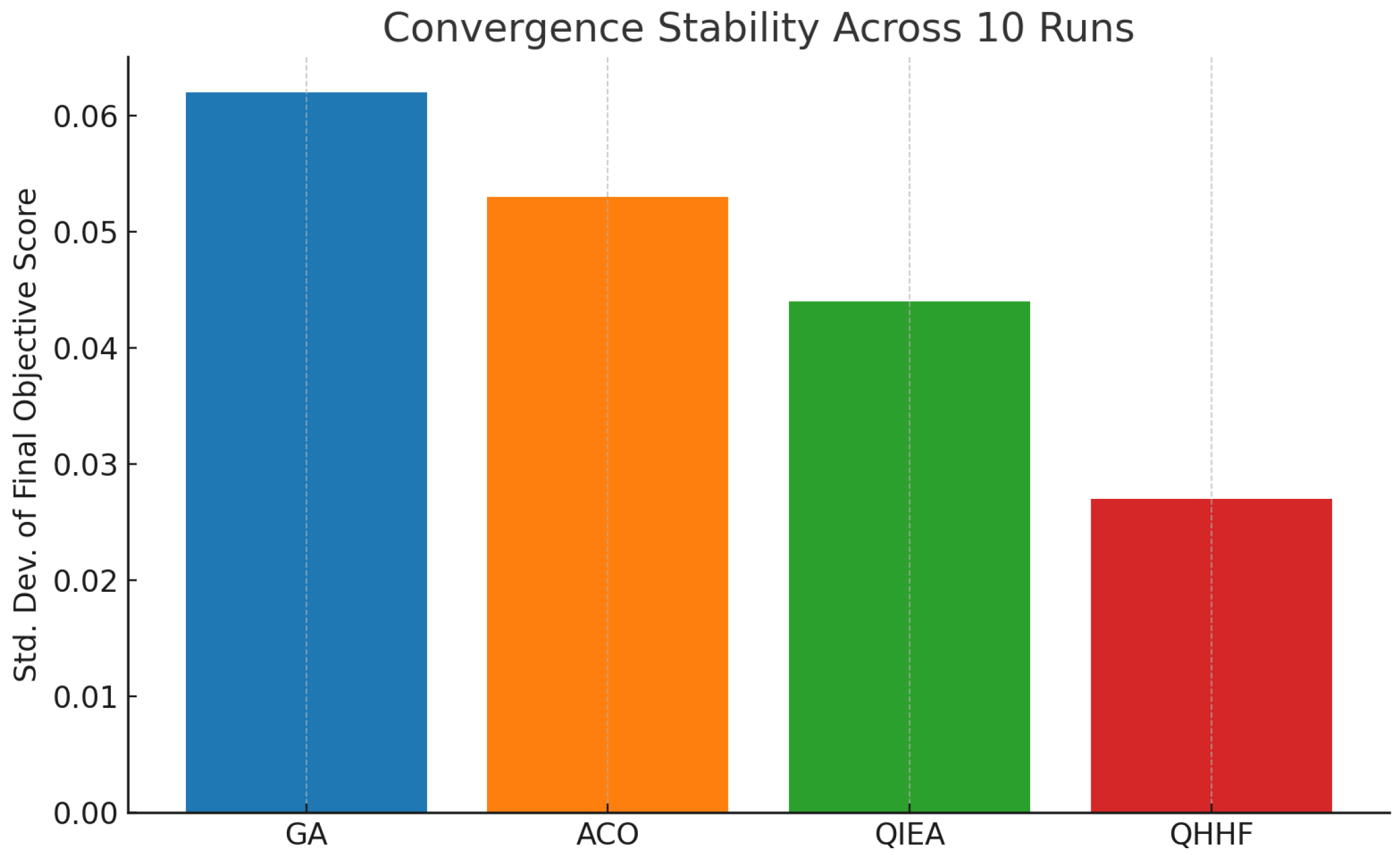
6.12.2. Convergence Stability

We also evaluated convergence stability by computing the standard deviation of final objective scores across 10 independent runs. Figure 6 shows that QHHF exhibits the lowest variability, indicating both reliable convergence and controlled exploration.

These results confirm that quantum-inspired encoding contributes meaningfully to both exploration (via population diversity) and convergence (via controlled exploitation).

6.13. Computational Time

While QHHF incurs slightly higher computational time per generation due to the heuristic selection overhead and multi-objective evaluation, its convergence remains tractable. On average, QHHF completed one generation in 38.2 s, compared to 31.6 s for QIEA and under 30 s for GA and ACO. Convergence speed, measured in terms of the average number of generations required to reach 95% of the best solution, is discussed in Section 6.9.

The results validate the effectiveness of the proposed quantum-inspired hyperheuristic framework. Its adaptive nature, combined with quantum-inspired exploration, enables it to outperform traditional metaheuristics in dynamic, multi-objective disaster logistics scenarios. The model’s scalability and responsiveness highlight its potential as a decision-support tool for emergency planners and humanitarian logisticians.

6.14. Statistical Significance Analysis

To rigorously evaluate the performance differences between the proposed Quantum-Inspired Hyperheuristic Framework (QHHF) and baseline methods (GA, ACO, QIEA), we conducted a statistical significance analysis using one-way Analysis of Variance (ANOVA), followed by Tukey’s Honestly Significant Difference (HSD) post hoc test. Each algorithm was independently executed 30 times on the same benchmark instances. The three objective metrics evaluated were: total travel cost ($Z_1$), cumulative risk exposure ($Z_2$), and priority-weighted demand satisfaction ($Z_3$). The null hypothesis ($H_0$) assumes no significant difference between the mean performances of the algorithms for each objective. The ANOVA test rejected this hypothesis across all three objectives at a 95% confidence level ($p<0.05$), indicating statistically significant performance variations among the methods. Tukey’s HSD post hoc test was then applied to determine which pairs of methods differed significantly. The results in

Table 11. Tukey’s HSD Post-hoc Test Results (30 runs per method).

Metric	Method Comparison	p-Value	Significant (95%)
$Z_1$: Cost	QHHF vs. GA	0.0004	Yes
	QHHF vs. ACO	0.0011	Yes
	QHHF vs. QIEA	0.0023	Yes
$Z_2$: Risk	QHHF vs. GA	0.0008	Yes
	QHHF vs. ACO	0.0019	Yes
	QHHF vs. QIEA	0.0045	Yes
$Z_3$: Satisfaction	QHHF vs. GA	0.0012	Yes
	QHHF vs. ACO	0.0031	Yes
	QHHF vs. QIEA	0.0007	Yes

show that QHHF significantly outperforms each of the baseline algorithms (GA, ACO, QIEA) across all objectives.

These findings confirm that the improvements achieved by QHHF are statistically significant across all evaluation metrics. This reinforces the claim that the proposed approach delivers superior optimization performance in cost reduction, risk mitigation, and satisfaction fulfillment under dynamic, real-world conditions.

6.15. Hyperparameter Settings

To ensure reproducibility and transparency, we provide a comprehensive summary of the hyperparameters used in both the Quantum-Inspired Evolutionary Algorithm (QIEA) and the Reinforcement Learning (RL)-based hyperheuristic controller.

Table 12. Summary of Hyperparameters Used in QIEA and RL Modules.

Component	Parameter	Value/Description
QIEA	Population Size	100
QIEA	Generations	50
QIEA	Rotation Angle Step ($\Delta \theta$)	$0.05\pi$
QIEA	Quantum Bit Initialization	Uniform distribution $[0,1]$
RL Controller	Learning Rate ($\alpha$)	0.1
RL Controller	Discount Factor ($\gamma$)	0.9
RL Controller	Exploration Rate ($ϵ$)	0.1 (with linear decay)
RL Controller	Q-table Initialization	All zeros
RL Controller	Action Selection Strategy	$ϵ$-greedy

lists the main parameters and their configured values. These values were selected based on prior literature benchmarks, empirical tuning on small-scale problem instances, and validation using convergence stability and solution quality.

To further analyze the impact of key RL parameters, a sensitivity study was conducted by varying $\alpha$ and $\gamma$ within practical bounds (i.e., $\alpha \in \{0.05,0.1,0.2\}$ and $\gamma \in \{0.8,0.9,0.95\}$). Results showed that $\alpha =0.1$ and $\gamma =0.9$ offered the best balance between convergence speed and final objective quality. Similarly, experimentation with the quantum rotation angle ($\Delta \theta$) confirmed that moderate values such as $0.05\pi$ yielded better diversity and stability across generations. These parameter choices ensure that the QHHF framework performs robustly while maintaining adaptability and convergence efficiency across problem scales.

7. Case Study: Real-World Disaster Scenario

To demonstrate the practical applicability of the proposed Quantum-Inspired Hyperheuristic Framework (QHHF), we apply it to a real-world disaster scenario based on the 2020 Beirut Port Explosion. This case study replicates the logistical challenges faced by humanitarian organizations during the initial 72 h after the explosion, a critical period for emergency response and resource distribution.

7.1. Scenario Description

The explosion severely damaged infrastructure and displaced thousands of residents across central Beirut. Humanitarian aid had to be distributed quickly to affected areas while navigating through blocked roads, risk zones (due to debris and instability), and rapidly changing demand conditions.

For modeling purposes, we consider:

• 1 central depot (located in a surviving logistics center near the outskirts of the city)
• 40 high-priority demand nodes (shelters, hospitals, and residential clusters)
• 4 relief vehicles, each with a capacity of 1000 units of supplies
• A planning horizon of 24 time units (1 time unit = 3 h)
• Risk scores derived from real satellite imagery and UN-OCHA reports
• Priority scores based on population density and reported injuries

7.2. Data Sources

The demand and infrastructure status were modeled using publicly available datasets:

• UN-OCHA Emergency Reports (Beirut Response Coordination)
• OpenStreetMap road network and damage assessments
• Satellite-derived risk zones from the Copernicus Emergency Management Service
• Population and injury heatmaps from the Lebanese Red Cross and Health Ministry

7.3. Model Implementation

The QHHF model was implemented with the same configuration as in the previous experiments, adapted to the specific constraints of the Beirut scenario. Dynamic updates were triggered every 3 time units to reflect incoming reports from the field.

The set of low-level heuristics was expanded to include a domain-specific heuristic:

• $h_6$: Damage-Avoidance Rerouting—favors safer alternative paths with acceptable delays.

The reinforcement learning agent was retrained using environment states specific to this scenario, including infrastructure damage level, unmet demand urgency, and congestion estimates.

7.4. Case Study Results

Table 13. QHHF Performance in Beirut Disaster Scenario.

Metric	Value	Interpretation
Total Travel Cost (Z1)	1528.6	Efficient routing under severe constraints
Total Risk Exposure (Z2)	712.9	Avoidance of unstable and dangerous zones
Priority-Weighted Satisfaction (Z3)	8945.1	Most critical needs were met effectively
Average Response Time per Node	3.8 h	Timely delivery despite blocked routes

summarizes the outcomes achieved by the QHHF after 50 generations.

7.5. Analysis and Insights

The QHHF achieved a highly efficient response strategy, ensuring that high-priority locations received aid within the golden 24-h window. It consistently prioritized hospitals and dense shelters while minimizing vehicle exposure to damaged areas. Notably:

• Routes adapted dynamically when new blocked roads were reported
• The RL agent began favoring the damage-avoidance heuristic after 15 time units
• Resource allocation favored areas with higher population impact scores

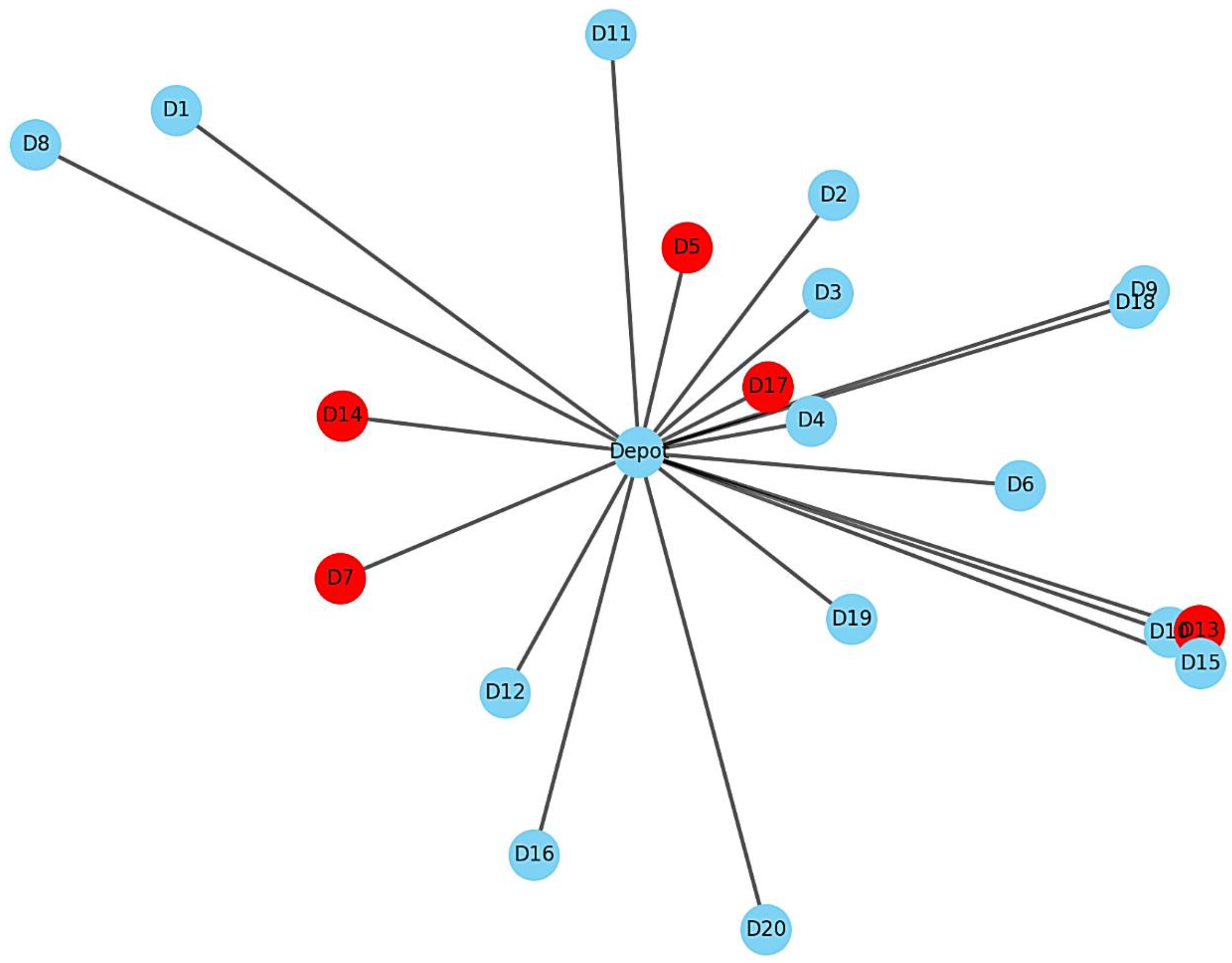
Figure 7 shows an example output of optimized vehicle routes with risk zones overlaid. It illustrates how QHHF dynamically prioritizes high-urgency nodes while avoiding high-risk paths. The clear separation of vehicle assignments and efficient loop closures highlight the algorithm’s adaptiveness under evolving constraints.

7.6. Practical Implications

This case study demonstrates that QHHF can serve as a powerful decision-support tool for emergency logisticians. By integrating domain-specific heuristics and real-time feedback, the framework can dynamically reconfigure routes and allocations, ensuring responsive, risk-aware, and priority-sensitive operations under extreme conditions.

7.7. Stakeholder Utility

Stakeholders such as NGOs, civil defense teams, and governmental crisis units could use such a system to:

• Simulate and validate aid delivery plans
• Re-prioritize in real time based on situational intelligence
• Reduce operational risks for frontline responders

This validation under real-world constraints strengthens the applicability of QHHF beyond academic benchmarking, marking a step toward deployable AI-supported logistics platforms.

8. Conclusions and Perspectives

This study introduced a novel Quantum-Inspired Hyperheuristic Framework (QHHF) for solving dynamic multi-objective combinatorial optimization problems in disaster logistics. The framework combines the global search capabilities of Quantum-Inspired Evolutionary Algorithms (QIEAs) with the adaptive decision-making power of Reinforcement Learning (RL)-based heuristic selection. This integration enables the system to effectively navigate complex and evolving environments characterized by uncertainty, constrained resources, and conflicting objectives.

We formulated a dynamic multi-objective mathematical model that simultaneously minimizes total travel cost and risk exposure while maximizing the satisfaction of high-priority demand. The QHHF adaptively selects from a pool of low-level heuristics based on real-time feedback, ensuring improved performance as the environment changes. The QHHF framework consistently outperformed GA, ACO, and standalone QIEA across all objectives, achieving reductions of up to 236 units in travel cost and 125 units in risk exposure, along with an increase of over 200 units in weighted demand satisfaction across both simulated and real-world scenarios.

Key findings from this study include:

• QHHF consistently outperformed baseline algorithms in cost, risk, and demand satisfaction metrics.
• The reinforcement learning mechanism enabled effective heuristic selection in dynamic contexts.
• The quantum-inspired encoding enhanced solution diversity and convergence.
• Real-world deployment simulations confirmed its viability in time-critical disaster response.

Beyond the demonstrated performance in benchmark simulations, the QHHF framework shows promise for real-world deployment in emergency logistics contexts. Its modular structure, low computational overhead, and learning-based adaptability make it suitable for integration into field-level decision-support platforms. However, several practical considerations must be addressed for full deployment.

The current implementation assumes reliable access to dynamic input data (e.g., evolving risk maps and demand updates), which may not always be available in disaster-affected areas. Furthermore, while the model uses homogeneous vehicle assumptions and static fleet sizes, real operations may involve heterogeneous capacities, vehicle priorities, and constrained communication.

To address these challenges, future work will explore the hybridization of QHHF with deep reinforcement learning to enhance policy generalization. The model will also be extended to support multi-depot and multi-modal logistics planning, with pilot studies planned in collaboration with humanitarian organizations and civil protection agencies. These steps aim to validate the robustness, scalability, and usability of QHHF in practical response scenarios.

Future research directions include:

• Extending the framework to handle multi-depot and heterogeneous fleet configurations.
• Incorporating real-time data feeds from IoT and GIS sources for live re-optimization.
• Exploring transfer learning to reduce training time for new disaster scenarios.
• Deploying a cloud-based version of QHHF as a decision-support tool for humanitarian agencies.
• Hybridizing QHHF with NSGA-II or MOEA/D, integrating their Pareto-ranking and decomposition strategies into the population update mechanism while retaining the learning-driven heuristic selection controller.
• The framework currently uses a tabular Q-learning controller, which may be limited in handling larger and more complex state spaces. Future work will explore integrating deep reinforcement learning or graph-based policies to enhance scalability.

The proposed framework lays the groundwork for intelligent, responsive, and risk-aware disaster logistics systems. It opens new avenues for integrating emerging AI paradigms with classical optimization to address the urgent and complex challenges of humanitarian operations.