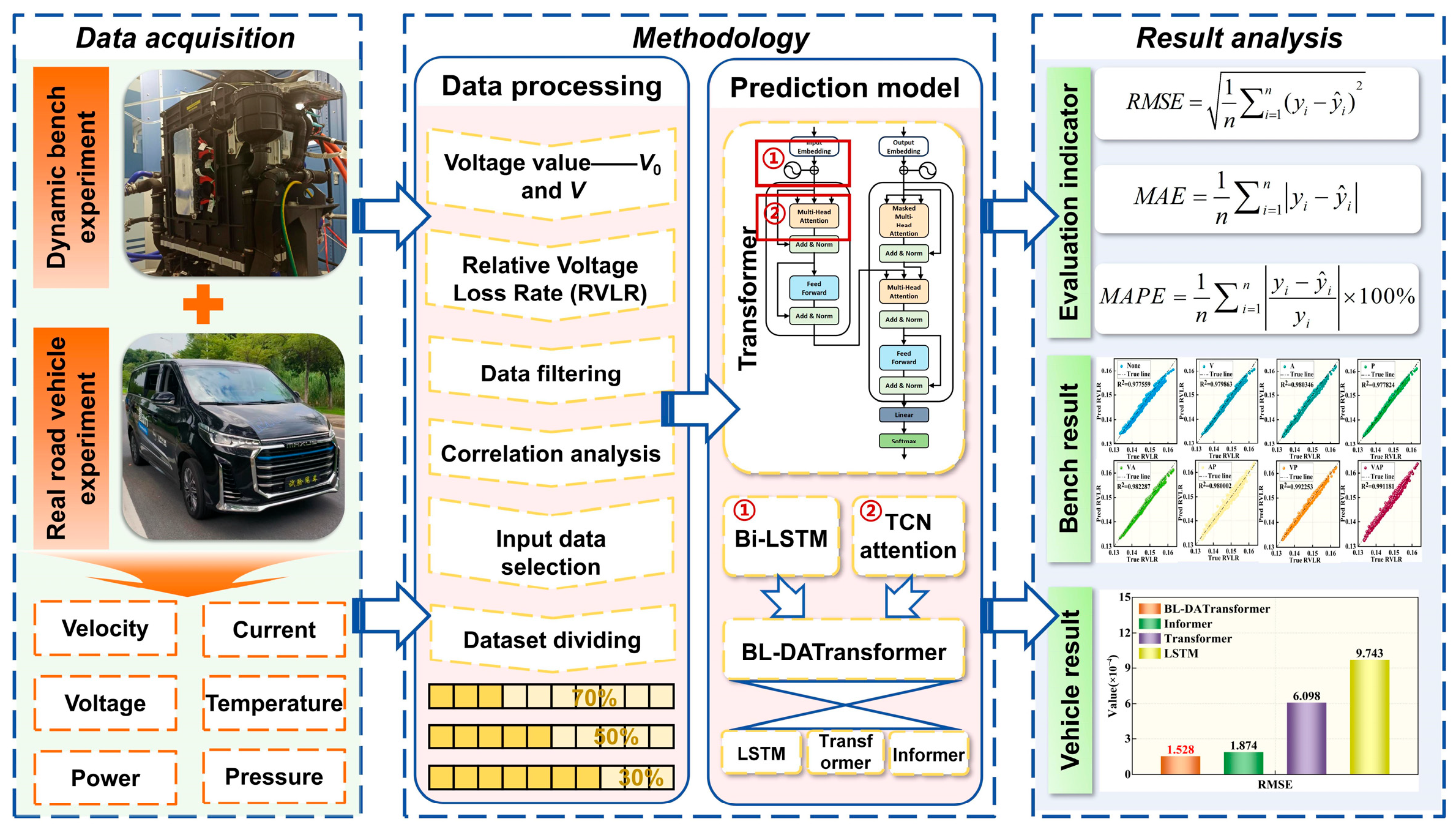
BL-DATransformer Lifespan Degradation Prediction Model of Fuel Cell Using Relative Voltage Loss Rate Health Indicator
Abstract
1. Introduction
- 1.
- A fuel cell lifespan degradation prediction method based on a Bidirectional Long Short-Term Memory Dual Attention Transformer (BL-DATransformer) model is proposed, integrating analysis of the impact of operating features, the introduction of Bidirectional Long Short-Term Memory (Bi-LSTM) dynamic encoding, and a temporal convolutional attention mechanism that enhances the prediction performance.
- 2.
- The dynamic bench experiment data and real-world road driving data are combined to validate the proposed prediction method, and the Relative Voltage Loss Rate (RVLR) is utilized to characterize the aging properties of the fuel cell in these two operational environments.
2. Data
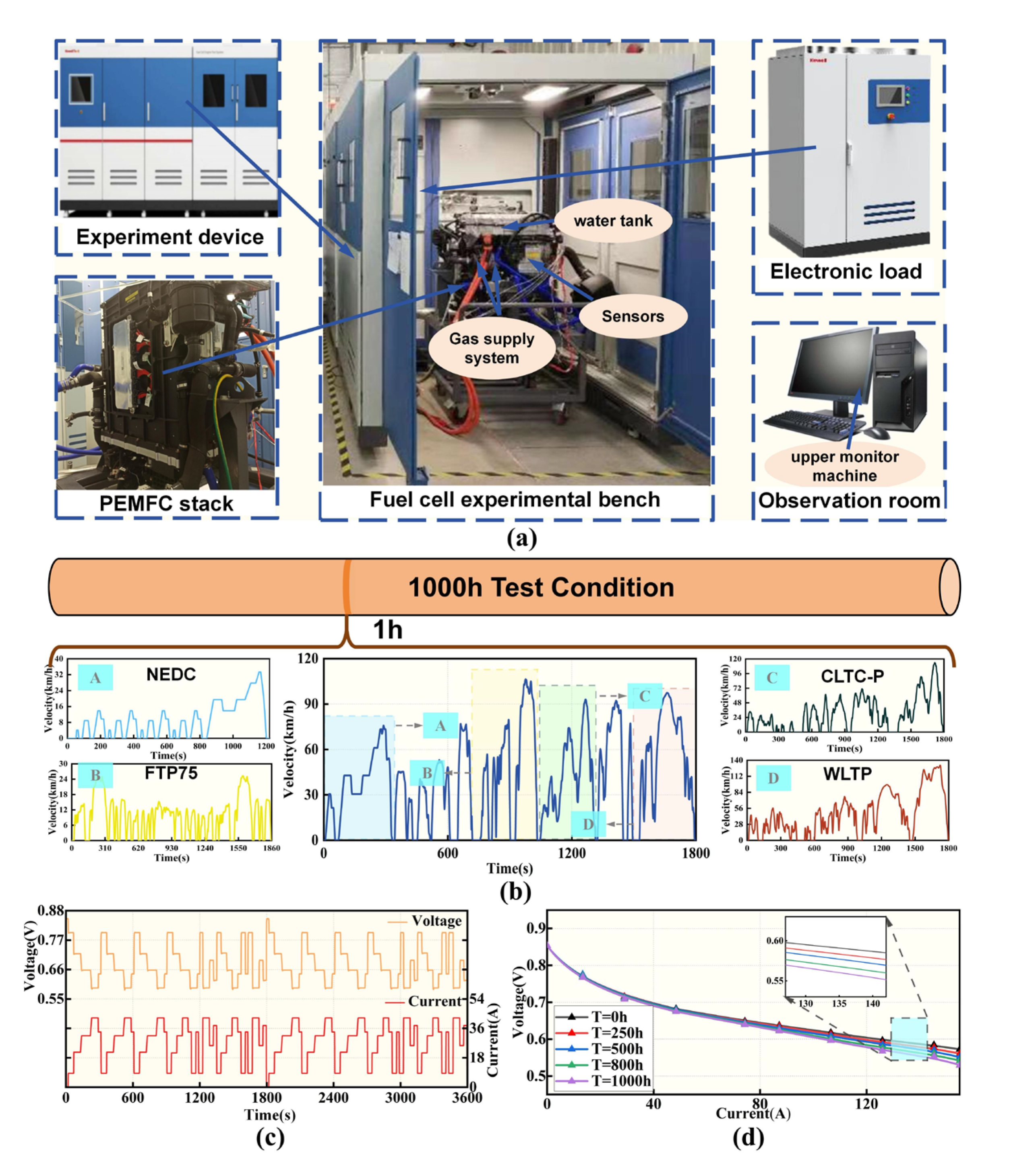
2.1. Dynamic Bench Experiment Data
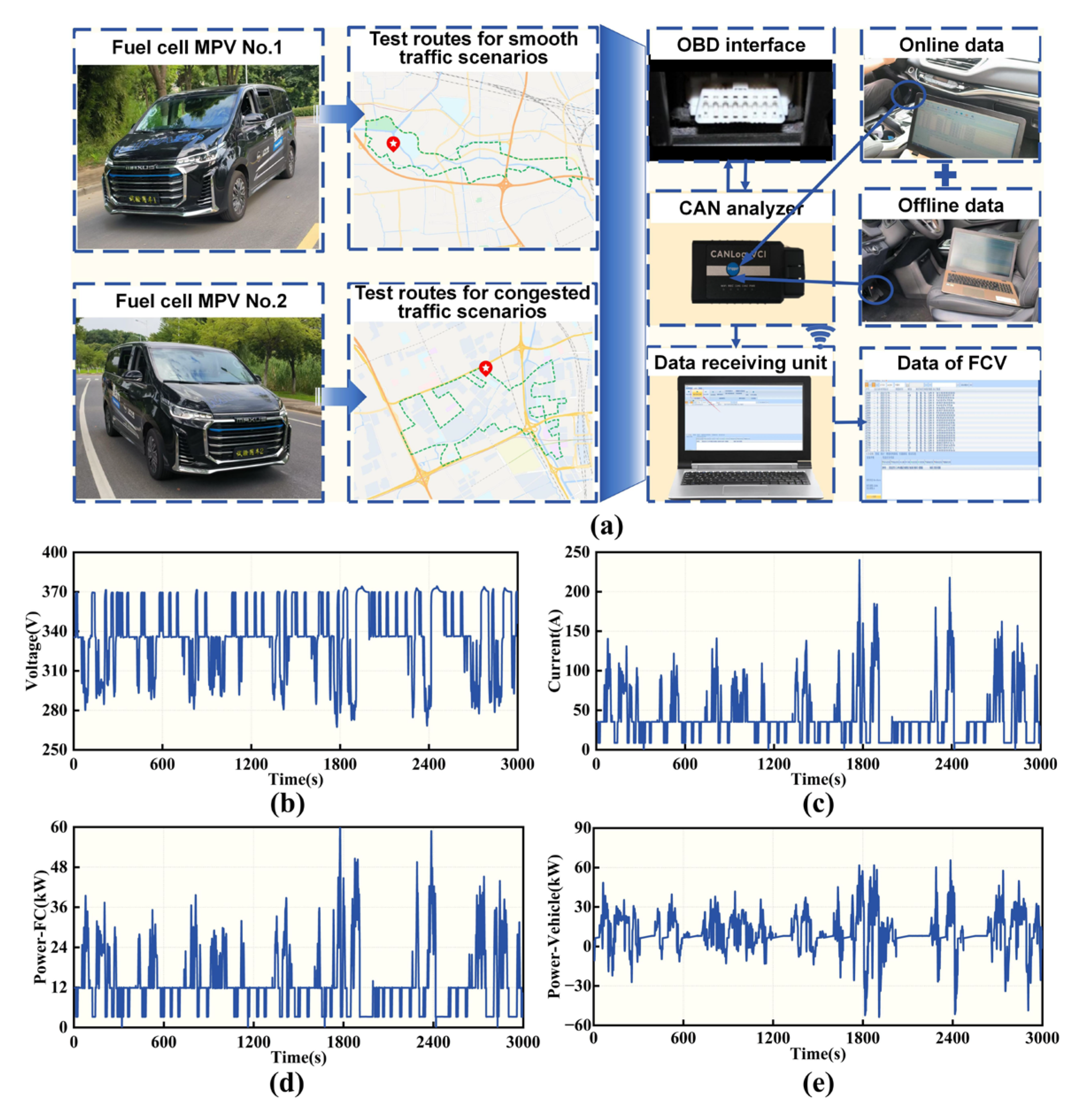
2.2. Road Driving Experiment Data
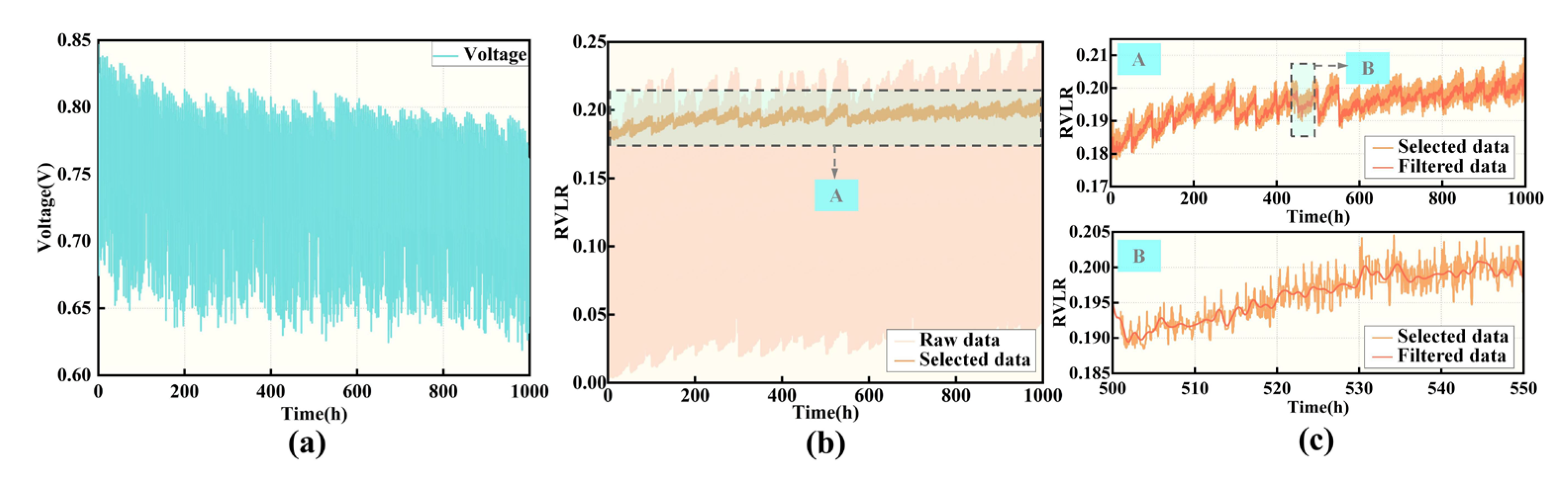
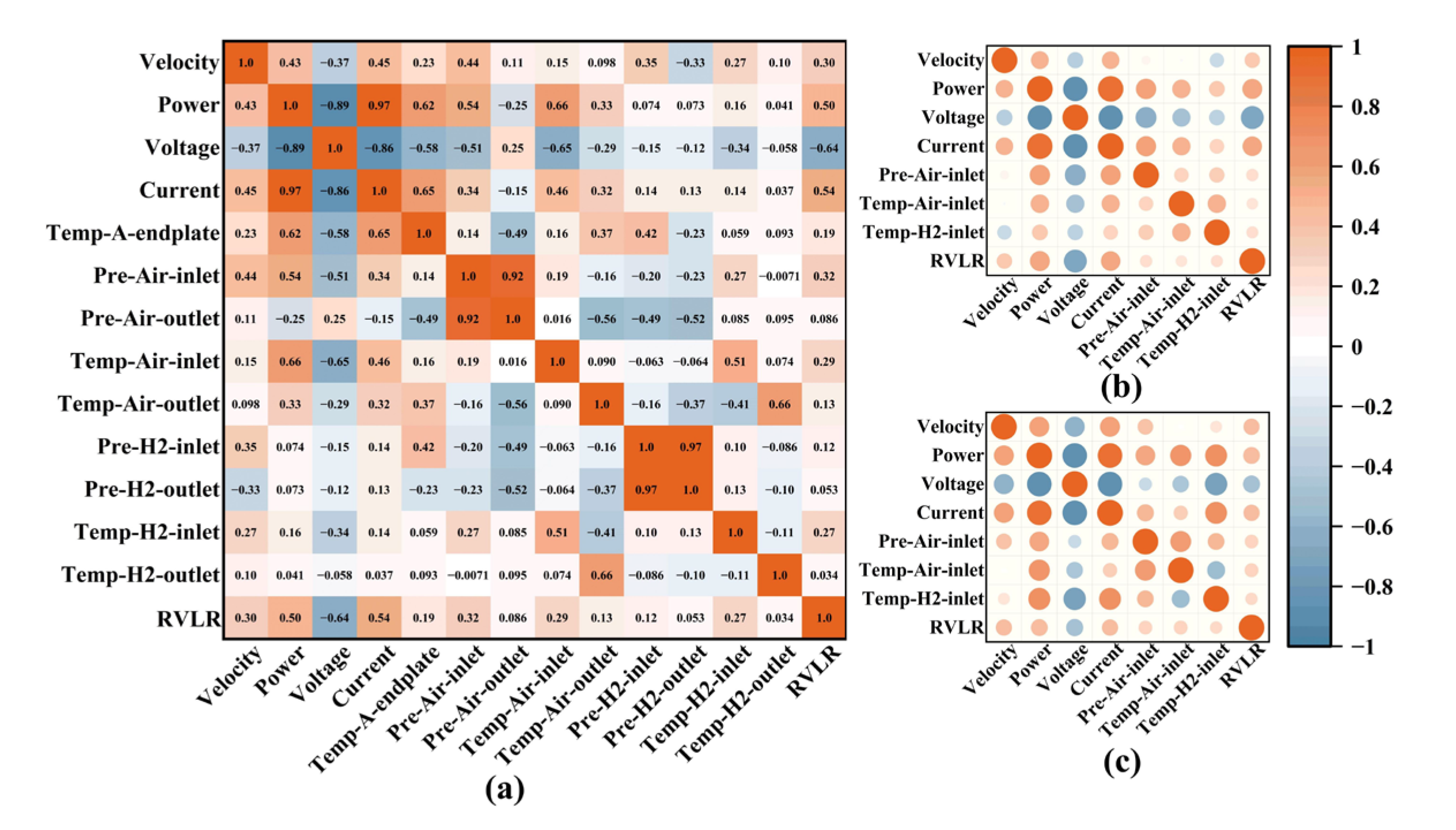
2.3. Health Indicator Calculation and Data Processing
2.4. Data Correlation Analysis
3. Method
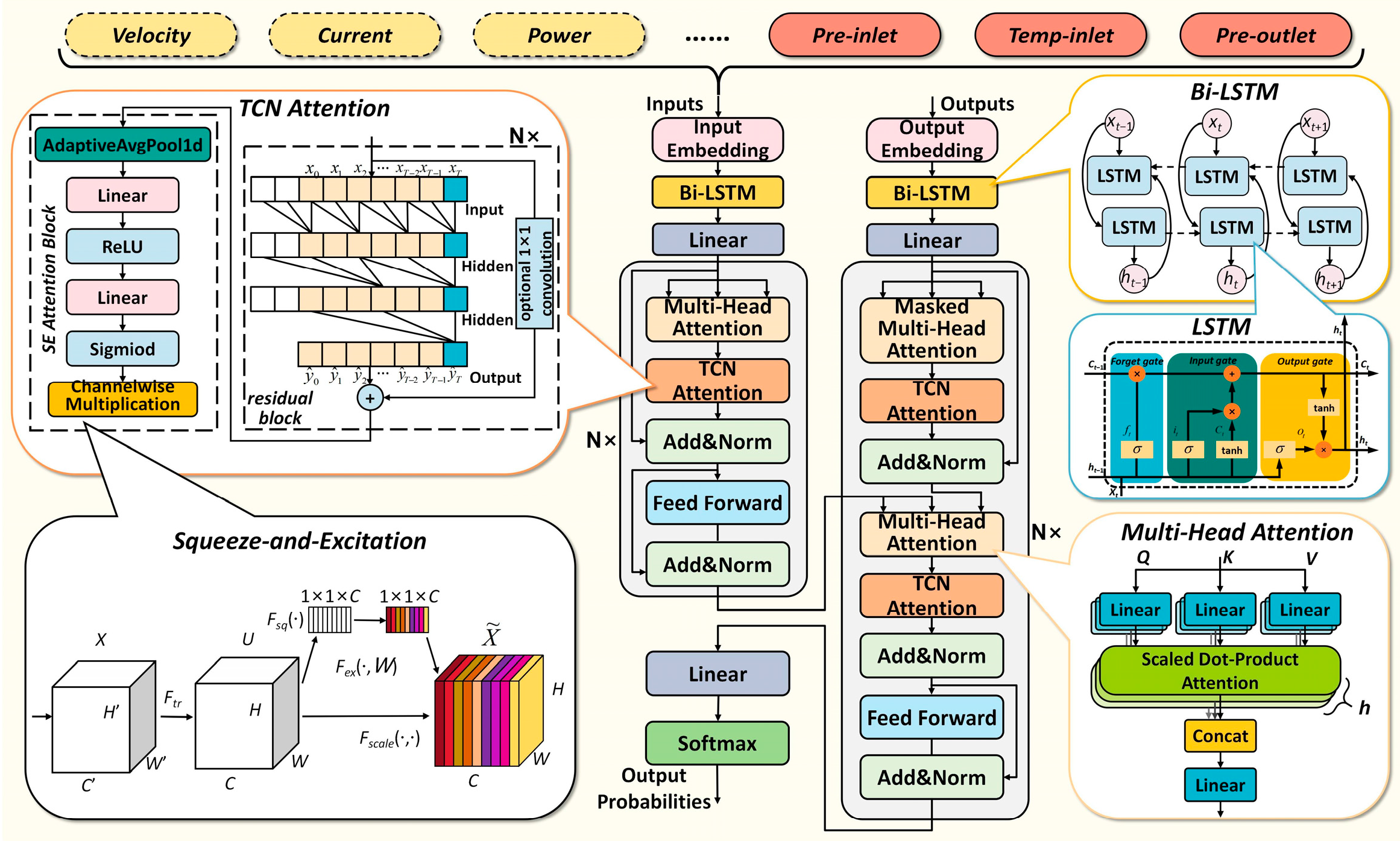
3.1. BL-DATransformer Lifespan Degradation Prediction Model
3.1.1. Input Layer
3.1.2. Encoder
3.1.3. Decoder
3.2. Evaluation Indicators
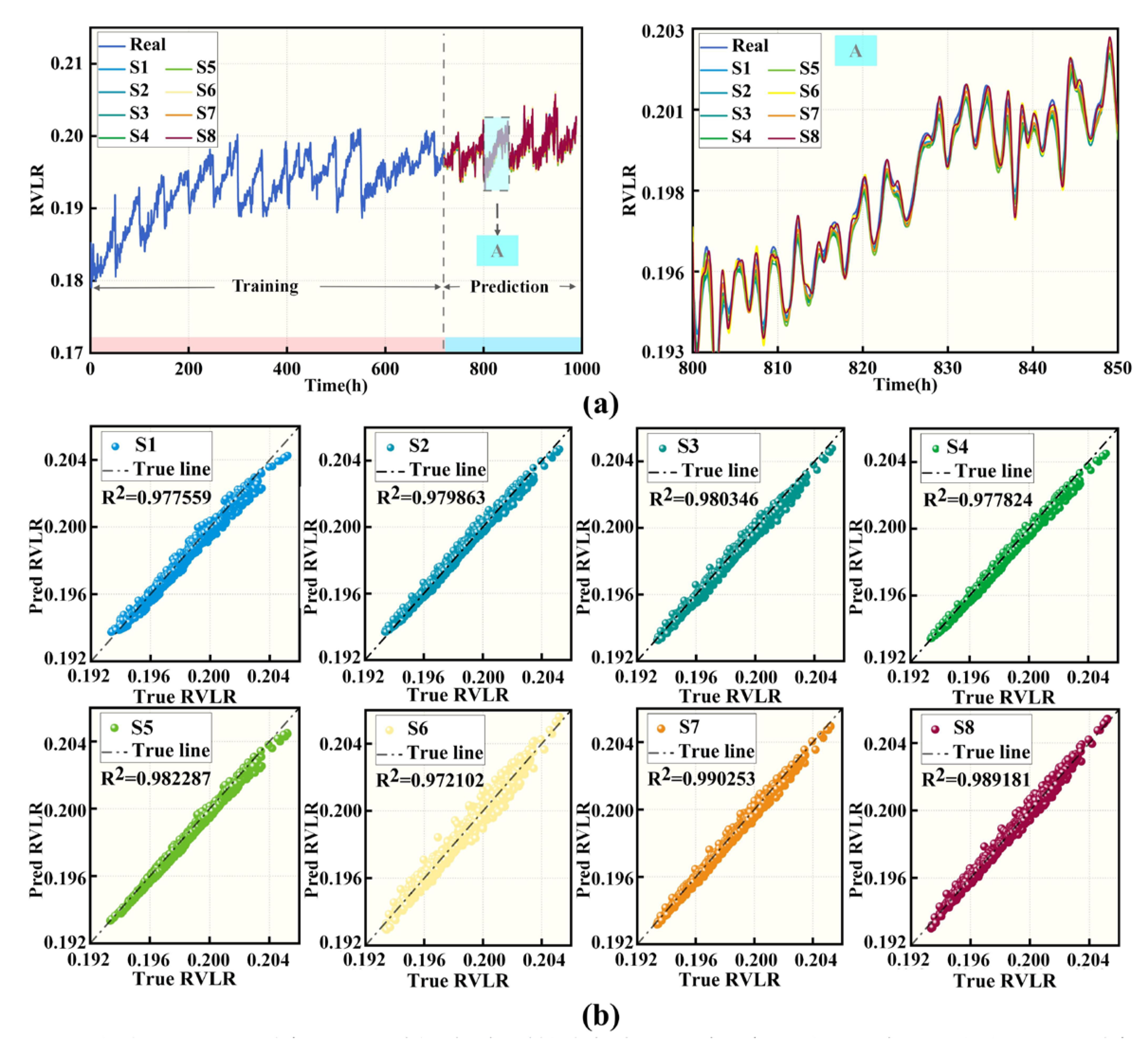
3.3. Impact of Input Features on Model Performance
3.4. Ablation Study
4. Results and Discussion
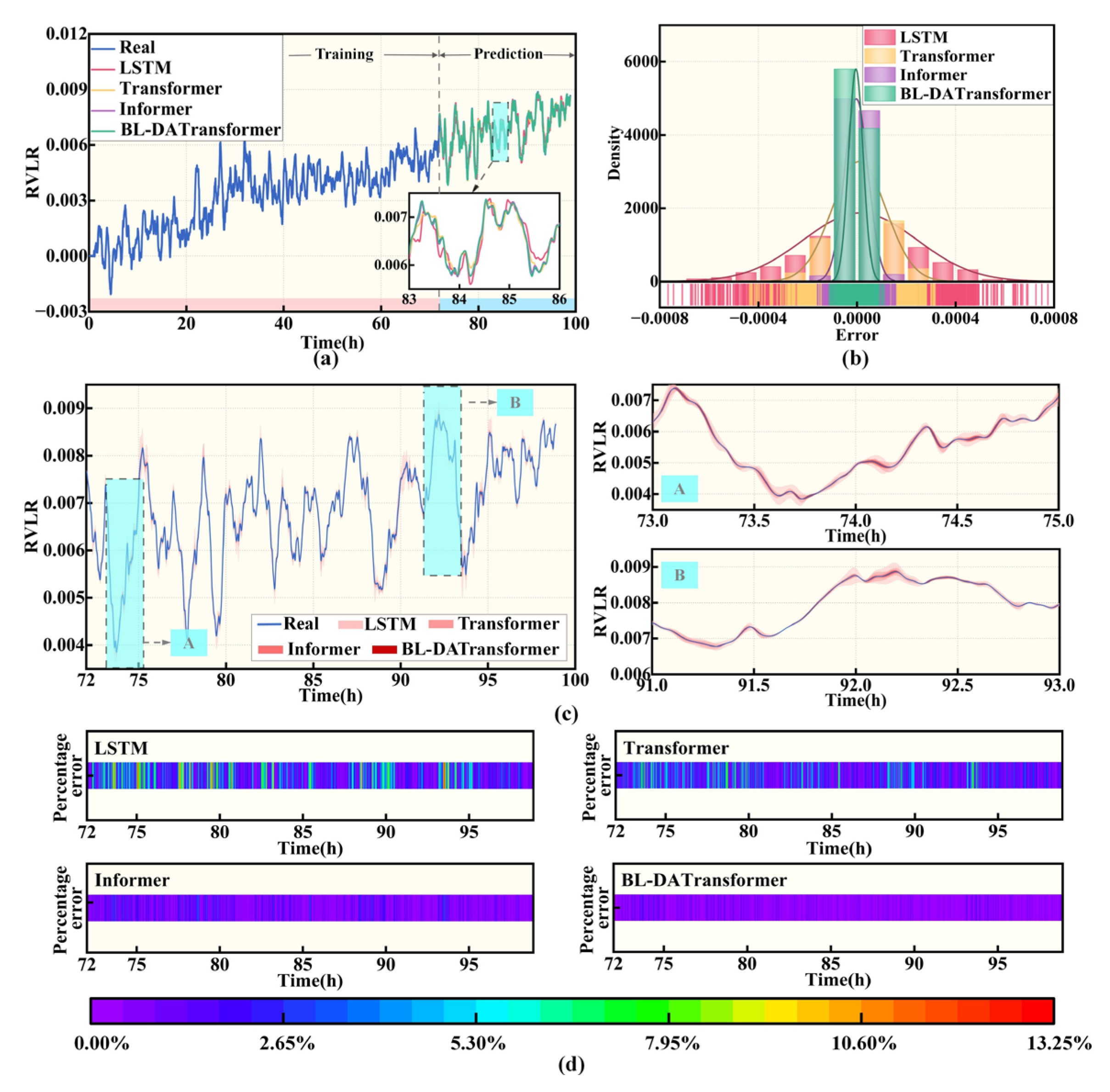
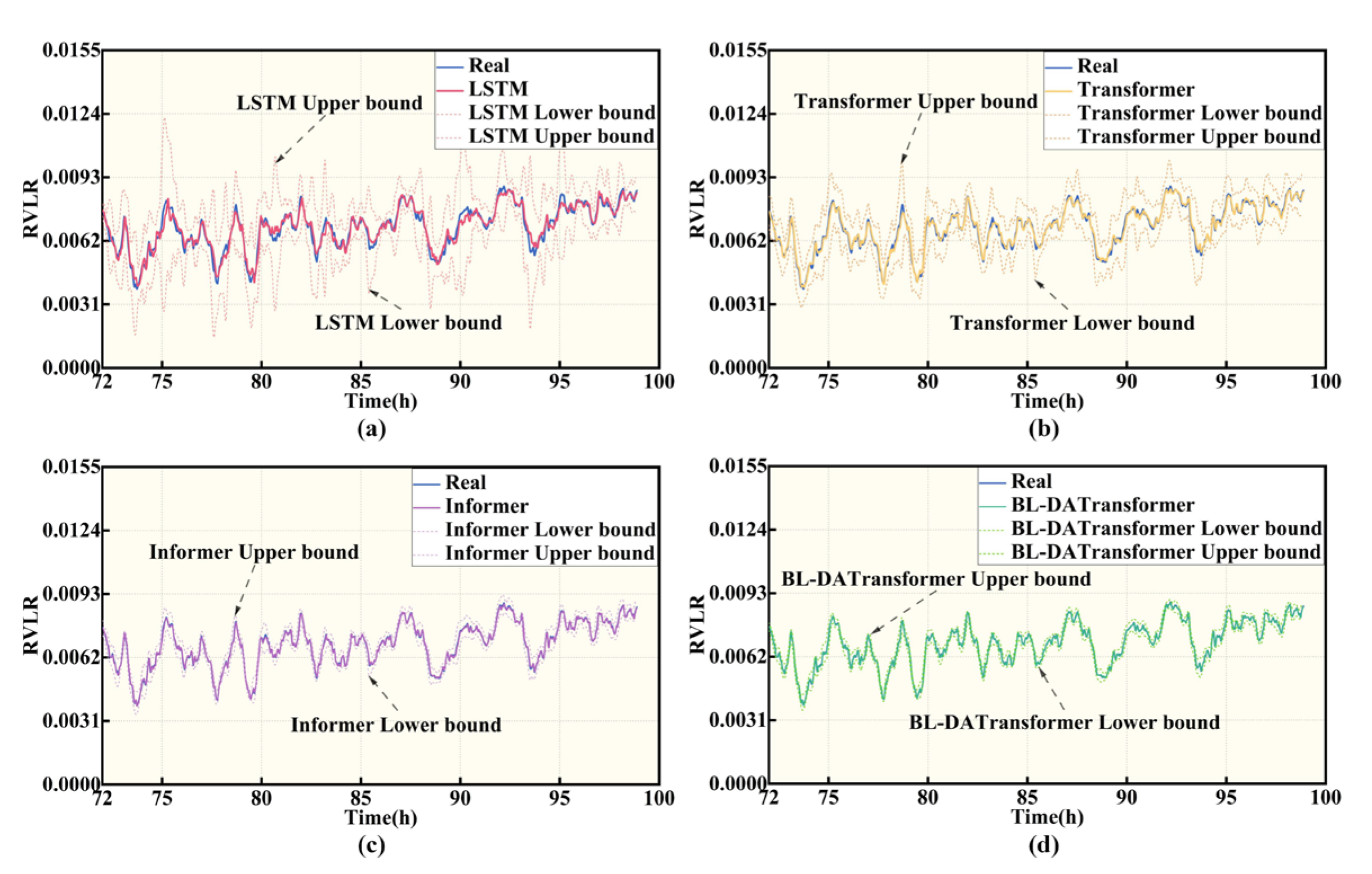
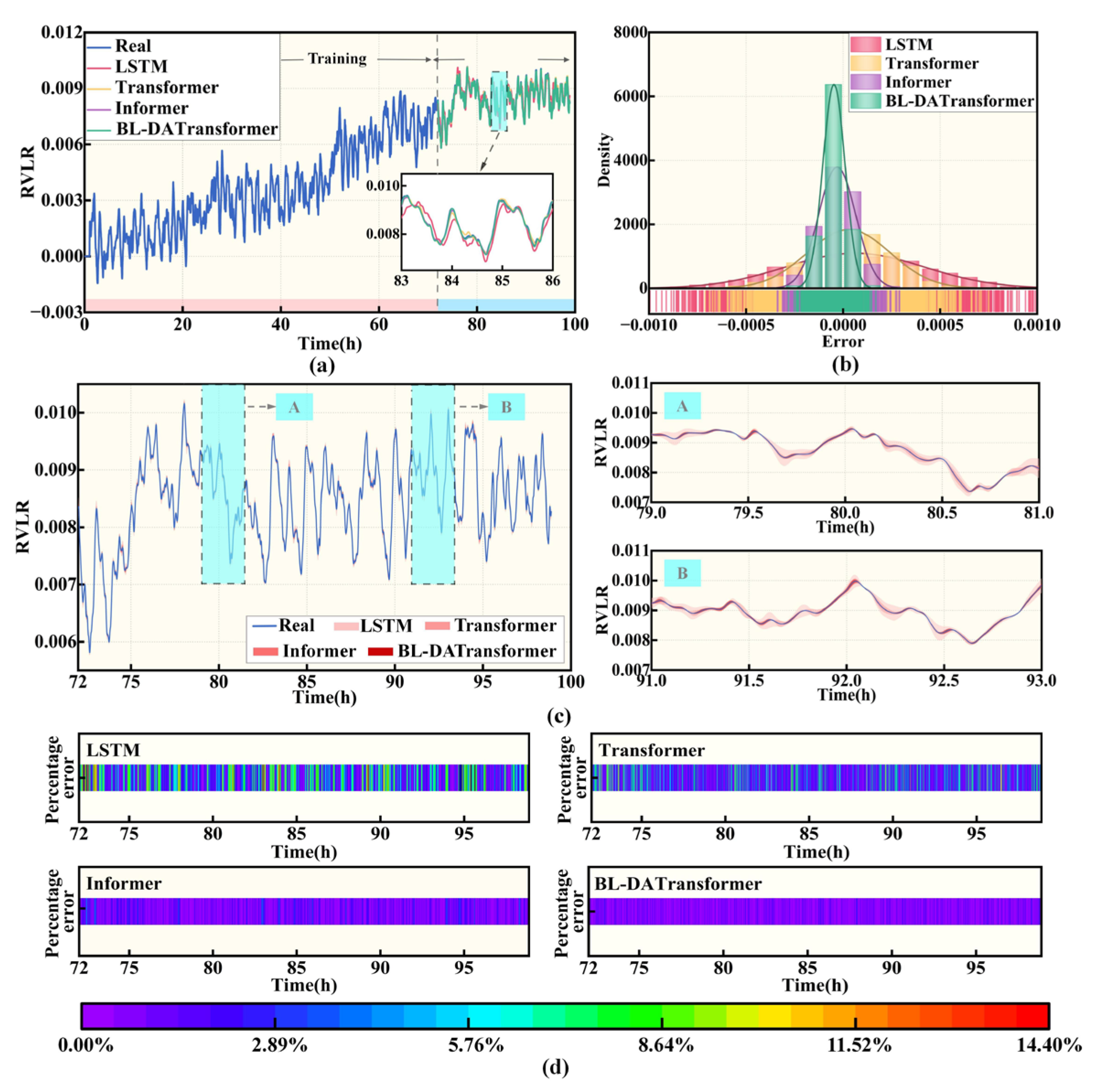
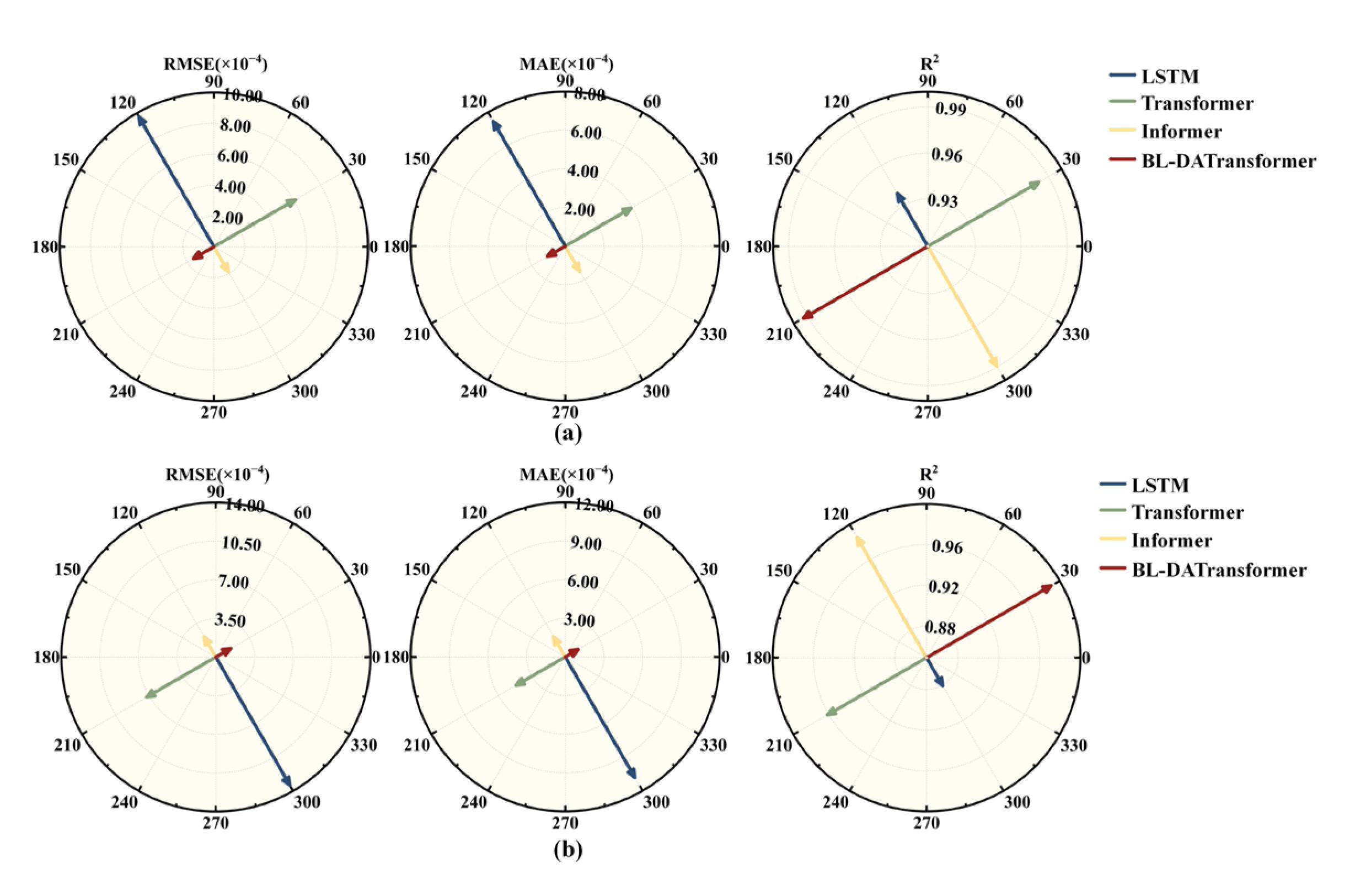
4.1. Results Between Different Models
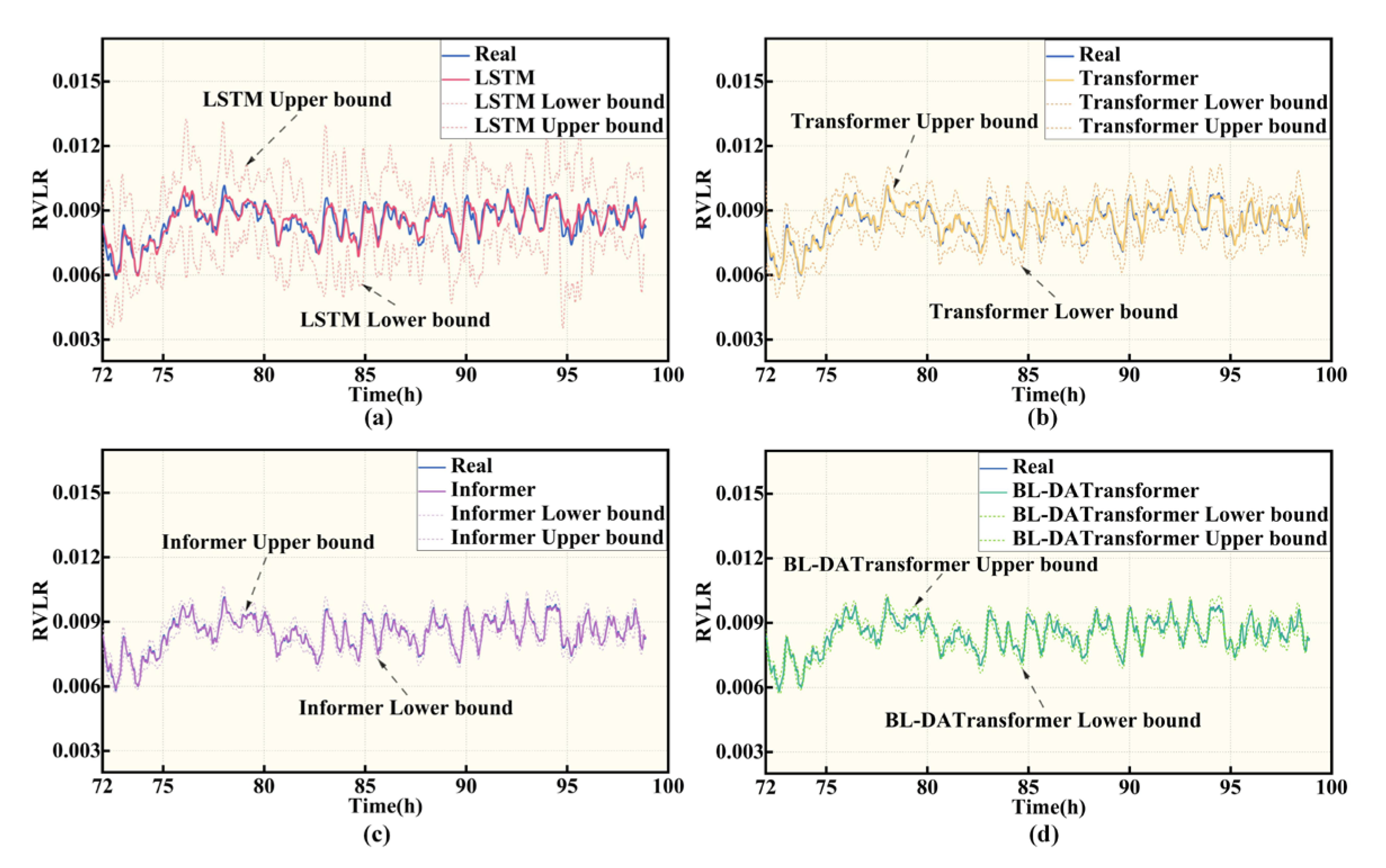
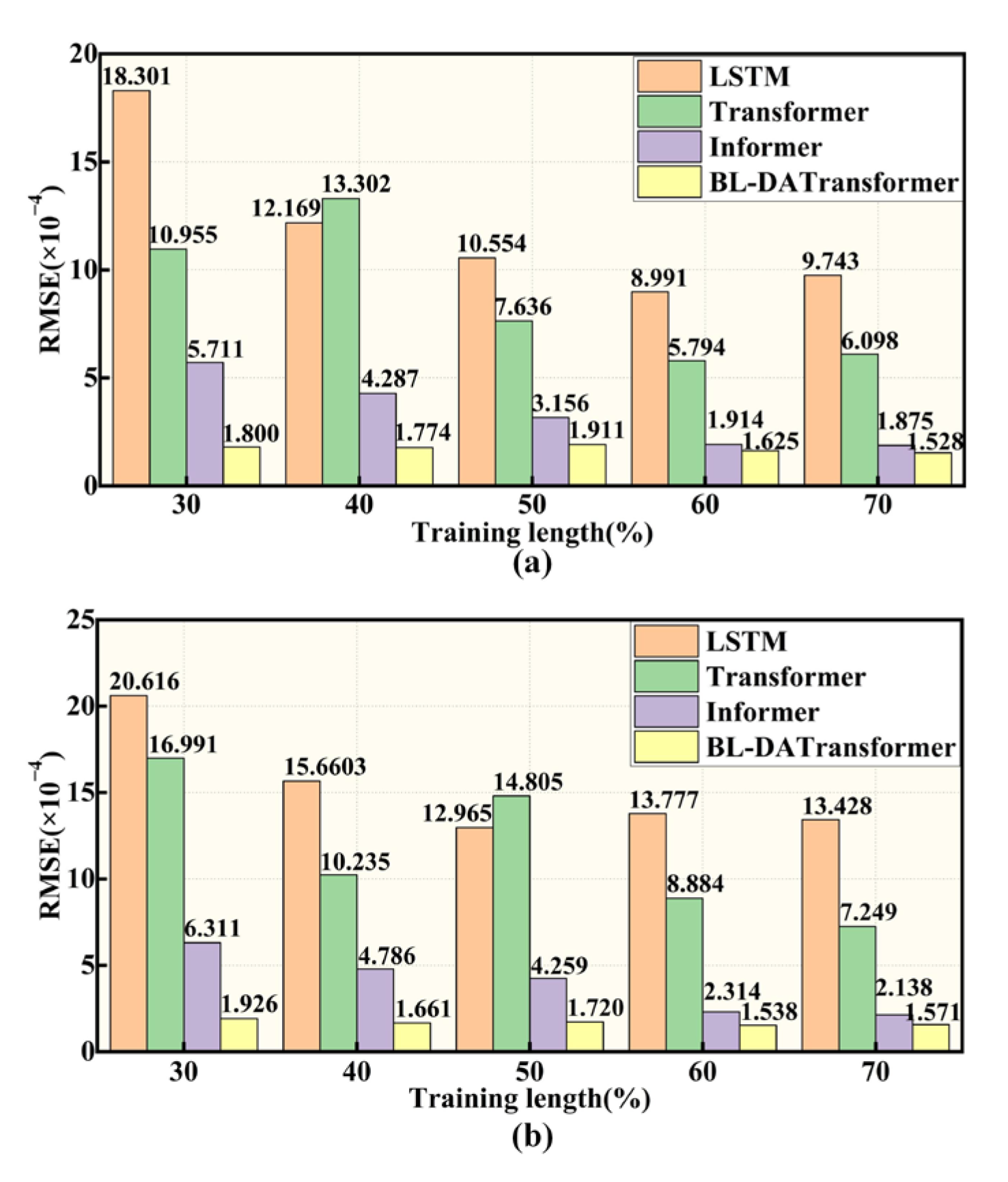
4.2. Results Under Different Training Lengths
5. Conclusions
- (1)
- Dynamic bench experiments and real road driving experiments are conducted, and fuel cell lifespan degradation data from different environments and durations are obtained through Savitzky-Golay filtering and data correlation analysis. A Bi-LSTM dynamic encoding method is proposed to replace the positional encoding in the Transformer, and a temporal convolutional network attention mechanism is incorporated. A prediction model based on BL-DATransformer is established and applied to fuel cells operating under urban conditions.
- (2)
- Based on the established BL-DATransformer prediction model and bench test data, the contribution of different input features to the model prediction results is analyzed. The model proposed is compared with three typical fuel cell lifespan degradation prediction models under different road traffic conditions and different training lengths. The results show that under different traffic conditions and different training lengths, the RMSE of BL-DATransformer is always lower than 0.0002, which is better than LSTM, Transformer, and Informer. It can be seen that the model proposed in this paper not only has the ability to predict the long-term and short-term fuel cell lifespan degradation at multiple time scales, but also has higher prediction accuracy and better generalization ability.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PEMFC | Proton Exchange Membrane Fuel Cell |
| FCV | Fuel Cell Vehicle |
| Pt | Platinum |
| RNN | Recurrent Neural Network |
| CNN | Convolutional Neural Network |
| LSTM | Long Short-Term Memory |
| TFT | Temporal Fusion Transformer |
| FC-DLC | Fuel Cell Dynamic Load Cycle |
| GRU | Gated Recurrent Unit |
| HI | Health Indicator |
| RPLR | Relative Power Loss Rate |
| BL-DATransformer | Bidirectional Long Short-Term Memory Dual Attention Transformer |
| Bi-LSTM | Bidirectional Long Short-Term Memory |
| RVLR | Relative Voltage Loss Rate |
| CLTC-P | China Light-Duty Vehicle Test Cycle-Passenger Car |
| FTP75 | Federal Test Procedure |
| NEDC | New European Driving Cycle |
| WLTP | Worldwide Harmonized Light Vehicles Test Procedure |
| MPV | Multi-Purpose Vehicle |
| API | Application Programming Interface |
| CAN | Controller Area Network |
| OBD | On-Board Diagnostic |
| LAN | Local Area Network |
| BoL | Beginning of Life |
| SG | Savitzky-Golay |
| TCN | Temporal Convolutional Network |
| SE | Squeeze-and-Excitation |
| ReLU | Rectified Linear Unit |
| RMSE | Root Mean Square Error |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percentage Error |
| R2 | R-Squared |
References
- Li, K.R.; Hong, J.C.; Zhang, C.; Liang, F.W.; Yang, H.X.; Ma, F.; Wang, F.C. Health state monitoring and predicting of proton exchange membrane fuel cells: A review. J. Power Sources 2024, 612, 234828. [Google Scholar] [CrossRef]
- Hu, D.H.; Hou, W.S.; Xiang, C.J.; Lu, D.G.; Yang, Q.Q.; Li, J.W.; Wang, J. Waste heat utilization performance verification of Heat Exchanger Only Thermal Management System for fuel cell vehicle. J. Clean. Prod. 2023, 428, 139479. [Google Scholar] [CrossRef]
- Hua, Z.G.; Zheng, Z.X.; Pahon, E.; Péra, M.C.; Gao, F. A review on lifetime prediction of proton exchange membrane fuel cells system. J. Power Sources 2022, 529, 231256. [Google Scholar] [CrossRef]
- Zhang, C.Z.; Zhang, Y.Q.; Wang, L.; Deng, X.Z.; Liu, Y.; Zhang, J.J. A health management review of proton exchange membrane fuel cell for electric vehicles: Failure mechanisms, diagnosis techniques and mitigation measures. Renew. Sustain. Energy Rev. 2023, 182, 113369. [Google Scholar] [CrossRef]
- Olabi, A.G.; Wilberforce, T.; Abdelkareem, M.A. Fuel cell application in the automotive industry and future perspective. Energy 2021, 214, 118955. [Google Scholar] [CrossRef]
- Zhou, J.M.; Zhang, J.M.; Yi, F.Y.; Feng, C.X.; Wu, G.P.; Li, Y.Z.; Zhang, C.Z.; Wang, C.L. A real-time prediction method for PEMFC life under actual operating conditions. Sustain. Energy Technol. Assess. 2024, 70, 103949. [Google Scholar] [CrossRef]
- Lu, D.; Hu, D.; Wang, J.; Wei, W.; Zhang, X. A Data-Driven Vehicle Speed Prediction Transfer Learning Method With Improved Adaptability Across Working Conditions for Intelligent Fuel Cell Vehicle. IEEE Trans. Intell. Transp. Syst. 2025, 1–11. [Google Scholar] [CrossRef]
- Tang, Y.; Yuan, W.; Pan, M.Q.; Wan, Z.P. Experimental investigation on the dynamic performance of a hybrid PEM fuel cell/battery system for lightweight electric vehicle application. Appl. Energy 2011, 88, 68–76. [Google Scholar] [CrossRef]
- Chen, H.; Zhao, X.; Zhang, T.; Pei, P. The reactant starvation of the proton exchange membrane fuel cells for vehicular applications: A review. Energy Convers. Manag. 2019, 182, 282–298. [Google Scholar] [CrossRef]
- Song, K.; Huang, X.; Huang, P.Y.; Sun, H.; Chen, Y.H.; Huang, D.Y. Data-driven health state estimation and remaining useful life prediction of fuel cells. Renew. Energy 2024, 227, 120491. [Google Scholar] [CrossRef]
- Macauley, N.; Watson, M.; Lauritzen, M.; Knights, S.; Wang, G.G.; Kjeang, E. Empirical membrane lifetime model for heavy duty fuel cell systems. J. Power Sources 2016, 336, 240–250. [Google Scholar] [CrossRef]
- Ou, M.Y.; Zhang, R.F.; Shao, Z.F.; Li, B.; Yang, D.J.; Ming, P.W.; Zhang, C.M. A novel approach based on semi-empirical model for degradation prediction of fuel cells. J. Power Sources 2021, 488, 229435. [Google Scholar] [CrossRef]
- Pei, P.C.; Meng, Y.N.; Chen, D.F.; Ren, P.; Wang, M.K.; Wang, X.Z. Lifetime prediction method of proton exchange membrane fuel cells based on current degradation law. Energy 2023, 265, 126341. [Google Scholar] [CrossRef]
- He, W.B.; Liu, T.; Ming, W.Y.; Li, Z.Z.; Du, J.G.; Li, X.K.; Guo, X.D.; Sun, P.Y. Progress in prediction of remaining useful life of hydrogen fuel cells based on deep learning. Renew. Sustain. Energy Rev. 2024, 192, 114193. [Google Scholar] [CrossRef]
- Nguyen, K.T.P.; Medjaher, K. A new dynamic predictive maintenance framework using deep learning for failure prognostics. Reliab. Eng. Syst. Saf. 2019, 188, 251–262. [Google Scholar] [CrossRef]
- Wu, Y.M.; Breaz, E.; Gao, F.; Miraoui, A. A Modified Relevance Vector Machine for PEM Fuel-Cell Stack Aging Prediction. IEEE Trans. Ind. Appl. 2016, 52, 2573–2581. [Google Scholar] [CrossRef]
- Wu, Y.M.; Breaz, E.; Gao, F.; Paire, D.; Miraoui, A. Nonlinear Performance Degradation Prediction of Proton Exchange Membrane Fuel Cells Using Relevance Vector Machine. IEEE Trans. Energy Convers. 2016, 31, 1570–1582. [Google Scholar] [CrossRef]
- Huo, W.W.; Li, W.E.; Zhang, Z.H.; Sun, C.; Zhou, F.K.; Gong, G.Q. Performance prediction of proton-exchange membrane fuel cell based on convolutional neural network and random forest feature selection. Energy Convers. Manag. 2021, 243, 114367. [Google Scholar] [CrossRef]
- Chen, K.; Laghrouche, S.; Djerdir, A. Proton Exchange Membrane Fuel Cell Prognostics Using Genetic Algorithm and Extreme Learning Machine. Fuel Cells 2020, 20, 263–271. [Google Scholar] [CrossRef]
- Wang, C.; Li, Z.L.; Outbib, R.; Dou, M.F.; Zhao, D.D. Symbolic deep learning based prognostics for dynamic operating proton exchange membrane fuel cells. Appl. Energy 2022, 305, 117918. [Google Scholar] [CrossRef]
- Ma, R.; Yang, T.; Breaz, E.; Li, Z.L.; Briois, P.; Gao, F. Data-driven proton exchange membrane fuel cell degradation predication through deep learning method. Appl. Energy 2018, 231, 102–115. [Google Scholar] [CrossRef]
- Wilberforce, T.; Alaswad, A.; Perez, A.G.; Xu, Y.C.; Ma, X.H.; Panchev, C. Remaining useful life prediction for proton exchange membrane fuel cells using combined convolutional neural network and recurrent neural network. Int. J. Hydrogen Energy 2023, 48, 291–303. [Google Scholar] [CrossRef]
- Sun, B.; Liu, X.D.; Wang, J.Y.; Wei, X.Z.; Yuan, H.; Dai, H.F. Short-term performance degradation prediction of a commercial vehicle fuel cell system based on CNN and LSTM hybrid neural network. Int. J. Hydrogen Energy 2023, 48, 8613–8628. [Google Scholar] [CrossRef]
- Zheng, L.; Hou, Y.P.; Zhang, T.; Pan, X.M. Performance prediction of fuel cells using long short-term memory recurrent neural network. Int. J. Energy Res. 2021, 45, 9141–9161. [Google Scholar] [CrossRef]
- Li, H.W.; Qiao, B.X.; Hou, Z.C.; Liu, J.N.; Yang, Y.; Lu, G.L. An interpretable data-driven method for degradation prediction of proton exchange membrane fuel cells based on temporal fusion transformer and covariates. Int. J. Hydrogen Energy 2023, 48, 25958–25971. [Google Scholar] [CrossRef]
- Zuo, B.; Cheng, J.S.; Zhang, Z.H. Degradation prediction model for proton exchange membrane fuel cells based on long short-term memory neural network and Savitzky-Golay filter. Int. J. Hydrogen Energy 2021, 46, 15928–15937. [Google Scholar] [CrossRef]
- Jouin, M.; Gouriveau, R.; Hissel, D.; Péra, M.C.; Zerhouni, N. Prognostics of PEM fuel cell in a particle filtering framework. Int. J. Hydrogen Energy 2014, 39, 481–494. [Google Scholar] [CrossRef]
- Zuo, J.; Lv, H.; Zhou, D.M.; Xue, Q.; Jin, L.M.; Zhou, W.; Yang, D.J.; Zhang, C.M. Deep learning based prognostic framework towards proton exchange membrane fuel cell for automotive application. Appl. Energy 2021, 281, 115937. [Google Scholar] [CrossRef]
- Tian, L.; Gao, Y.; Yang, H.Y.; Wang, R.K. Multi-scenario long-term degradation prediction of PEMFC based on generative inference informer model. Appl. Energy 2025, 377, 124398. [Google Scholar] [CrossRef]
- Liu, M.; Wu, D.; Yin, C.; Gao, Y.; Li, K.; Tang, H. Prediction of voltage degradation trend for a proton exchange membrane fuel cell city bus on roads. J. Power Sources 2021, 512, 230435. [Google Scholar] [CrossRef]
- Chen, K.; Laghrouche, S.; Djerdir, A. Fuel cell health prognosis using Unscented Kalman Filter: Postal fuel cell electric vehicles case study. Int. J. Hydrogen Energy 2019, 44, 1930–1939. [Google Scholar] [CrossRef]
- Pan, R.; Yang, D.; Wang, Y.J.; Chen, Z.H. Health degradation assessment of proton exchange membrane fuel cell based on an analytical equivalent circuit model. Energy 2020, 207, 118185. [Google Scholar] [CrossRef]
- Zhang, D.C.; Cadet, C.; Yousfi-Steiner, N.; Bérenguer, C. Proton exchange membrane fuel cell remaining useful life prognostics considering degradation recovery phenomena. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2018, 232, 415–424. [Google Scholar] [CrossRef]
- Chen, J.Y.; Zhou, D.; Lyu, C.; Lu, C. A novel health indicator for PEMFC state of health estimation and remaining useful life prediction. Int. J. Hydrogen Energy 2017, 42, 20230–20238. [Google Scholar] [CrossRef]
- Hua, Z.G.; Zheng, Z.X.; Pahon, E.; Péra, M.C.; Gao, F. Remaining useful life prediction of PEMFC systems under dynamic operating conditions. Energy Convers. Manag. 2021, 231, 113825. [Google Scholar] [CrossRef]
- Yang, J.B.; Wang, L.; Zhang, B.; Zhang, H.; Wu, X.H.; Xu, X.H.; Deng, P.Y.; Peng, Y.Q. Remaining useful life prediction of vehicle-oriented PEMFC systems based on IGWO-BP neural network under real-world traffic conditions. Energy 2024, 291, 130334. [Google Scholar] [CrossRef]
- Wang, Y.P.; Wang, K.; Wang, B.W.; Yin, Y.; Zhao, H.H.; Han, L.H.; Jiao, K. A Data-Driven Approach to Lifespan Prediction for Vehicle Fuel Cell Systems. IEEE Trans. Transp. Electrif. 2023, 9, 5049–5060. [Google Scholar] [CrossRef]
- Lv, J.F.; Yu, Z.L.; Zhang, H.C.; Sun, G.H.; Muhl, P.; Liu, J.X. Transformer Based Long-Term Prognostics for Dynamic Operating PEM Fuel Cells. IEEE Trans. Transp. Electrif. 2024, 10, 1747–1757. [Google Scholar] [CrossRef]
- Zhou, Y.P.; Huang, M.H.; Chen, Y.P.; Tao, Y. A novel health indicator for on-line lithium-ion batteries remaining useful life prediction. J. Power Sources 2016, 321, 1–10. [Google Scholar] [CrossRef]
- Hu, D.H.; Hu, Z.F.; Wang, J.; Li, J.W.; Lu, M.; Ding, H.; Wei, W.X.; Zhang, X.Y.; Wang, C. CL-Kansformer model for SOC prediction of hydrogen refueling process in fuel cell vehicles. J. Power Sources 2025, 626, 235772. [Google Scholar] [CrossRef]
- Mughees, N.; Mohsin, S.A.; Mughees, A.; Mughees, A. Deep sequence to sequence Bi-LSTM neural networks for day-ahead peak load forecasting. Expert Syst. Appl. 2021, 175, 114844. [Google Scholar] [CrossRef]

| Ref. | Model | Baseline Model | Data Sources | Health Indicator | Evaluation Indicators |
|---|---|---|---|---|---|
| [22] | CNN-BiRNN | LSTM, RNN | Static condition test bench | Voltage | RMSE = 0.0031, MAPE = 0.0468 |
| [26] | Dropout-LSTM | LSTM | Static condition test bench | Voltage | RMSE = 0.0041, MAPE = 0.0557 |
| [35] | DI-ESN | SI-ESN | Dynamic condition test bench | RPLR | RMSE = 0.0098, MAPE = 0.0976 |
| [25] | TFT | LSTM, GRU | Dynamic condition test bench | Voltage | RMSE = 0.0067, MAE = 0.0035 |
| [23] | CEEMD-CNN-LSTM | LSTM, CNN | Real vehicle road operation | Voltage | RMSE = 1.6606, MAPE = 0.0035 |
| [36] | IGWO-BP | BP, GWO-BP | Real vehicle road operation | RPLR | RMSE = 0.0013, MAPE = 0.0100 |
| Parameter | Value |
|---|---|
| Pt loading (mg/cm2) | 0.35 |
| Hydrogen inlet temperature (°C) | 75 |
| Air inlet temperature (°C) | 75 |
| Hydrogen inlet pressure (kPa) | 110 |
| Air inlet pressure (kPa) | 110 |
| Fuel cell operating temperature (°C) | 80 |
| Component | Parameter | Value |
|---|---|---|
| Vehicle | Equipment mass (kg) | 2550 |
| Overall dimension (mm) | 5225 × 1980 × 1938 | |
| Driving range (km) | >600 | |
| Fuel cell | Dimension (mm) | 790 × 598 × 820 |
| Rated power (kW) | 83.5 | |
| Peak power (kW) | 92 | |
| Service life (h) | ≥10,000 | |
| Motor | Rated power (kW) | 70 |
| Peak power (kW) | 150 | |
| Battery | rated capacity (Ah) | 37 |
| Hydrogen storage system | Volume (L) | 158 |
| Nominal pressure (MPa) | 70 |
| Scheme Number | Model | Gas Status Features | Abbreviation |
|---|---|---|---|
| Scheme 1 | BL-DATransformer | - | S1 |
| Scheme 2 | Pre-Air-inlet | S2 | |
| Scheme 3 | Temp-Air-inlet | S3 | |
| Scheme 4 | Temp-H2-inlet | S4 | |
| Scheme 5 | Pre-Air-inlet + Temp-Air-inlet | S5 | |
| Scheme 6 | Temp-Air-inlet + Temp-H2-inlet | S6 | |
| Scheme 7 | Pre-Air-inlet + Temp-H2-inlet | S7 | |
| Scheme 8 | Pre-Air-inlet + Temp-Air-inlet + Temp-H2-inlet | S8 |
| Scheme | RMSE (×10−3) | MAE (×10−3) | MAPE (%) | R2 | Prediction Time (s) |
|---|---|---|---|---|---|
| S1 | 0.949 | 0.869 | 0.050 | 0.977 | 574.4170 |
| S2 | 0.917 (↓3.38%) | 0.866 (↓0.35%) | 0.048 (↓9.30%) | 0.979 (↑0.23%) | 591.2543 |
| S3 | 1.016 (↑7.07%) | 0.897 (↑3.27%) | 0.048 (↓9.69%) | 0.980 (↑0.27%) | 585.2365 |
| S4 | 0.927 (↓2.28%) | 0.871 (↑0.16%) | 0.049 (↓6.11%) | 0.978 (↑0.03%) | 589.2548 |
| S5 | 0.905 (↓4.65%) | 0.863 (↓0.71%) | 0.050 (↓1.63%) | 0.982 (↑0.48%) | 607.3032 |
| S6 | 0.926 (↓2.33%) | 0.831 (↓4.37%) | 0.045 (↓11.76%) | 0.972 (↓0.46%) | 614.8530 |
| S7 | 0.840 (↓11.50%) | 0.797 (↓8.31%) | 0.042 (↓16.33%) | 0.990 (↑1.29%) | 602.7953 |
| S8 | 0.852 (↓10.16%) | 0.777 (↓10.59%) | 0.041 (↓18.51%) | 0.989 (↑1.17%) | 643.2589 |
| Model | Component | RMSE (×10−4) | MAE (×10−4) | MAPE (%) | R2 |
|---|---|---|---|---|---|
| Transformer | Transformer | 6.099 | 3.946 | 0.151 | 0.983 |
| L-Transformer | LSTM, Transformer | 5.268 | 3.682 | 0.122 | 0.983 |
| BL-Transformer | Bi-LSTM, Transformer | 4.041 | 3.369 | 0.077 | 0.985 |
| DATransformer | TCN attention, Transformer | 2.995 | 2.117 | 0.051 | 0.990 |
| BL-DATransformer | Bi-LSTM, TCN attention, Transformer | 1.528 | 1.066 | 0.046 | 0.992 |
| Model | Parameters |
|---|---|
| LSTM | Hidden size: 128, Batch size: 32, Learning rate: 0.001, Dropout rate: 0.2, Epoch: 50, Optimizer: Adam |
| Transformer | Attention head: 8, Num Layer: 3, Batch size: 64, Learning rate: 0.0005, Dropout rate: 0.1, Epoch: 50, Optimizer: Adam |
| Informer | Attention head: 4, Distilling layer: 2, Num Layer: 2, Batch size: 64, Learning rate: 0.0003, Dropout rate: 0.1, Epoch: 50, Optimizer: Adam |
| Traffic Conditions | Model | RMSE (×10−4) | MAE (×10−4) | MAPE (%) | R2 | Prediction Time (s) |
|---|---|---|---|---|---|---|
| Smooth | LSTM | 9.743 | 7.466 | 0.298 | 0.938 | 324 |
| Transformer | 6.099 | 3.947 | 0.151 | 0.983 | 478 | |
| Informer | 1.874 | 1.521 | 0.051 | 0.989 | 282 | |
| BL-DATransformer | 1.528 | 1.067 | 0.046 | 0.993 | 603 | |
| Congested | LSTM | 13.427 | 10.806 | 0.265 | 0.881 | 341 |
| Transformer | 7.249 | 4.397 | 0.171 | 0.961 | 486 | |
| Informer | 2.137 | 1.822 | 0.054 | 0.985 | 289 | |
| BL-DATransformer | 1.571 | 1.162 | 0.046 | 0.990 | 614 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Wang, J.; Hu, D.; Lu, D.; Zhang, X.; Wei, W.; Ding, H.; Zhang, S. BL-DATransformer Lifespan Degradation Prediction Model of Fuel Cell Using Relative Voltage Loss Rate Health Indicator. World Electr. Veh. J. 2025, 16, 290. https://doi.org/10.3390/wevj16060290
Xu Y, Wang J, Hu D, Lu D, Zhang X, Wei W, Ding H, Zhang S. BL-DATransformer Lifespan Degradation Prediction Model of Fuel Cell Using Relative Voltage Loss Rate Health Indicator. World Electric Vehicle Journal. 2025; 16(6):290. https://doi.org/10.3390/wevj16060290
Chicago/Turabian StyleXu, Yinjie, Jing Wang, Donghai Hu, Dagang Lu, Xiaoyan Zhang, Wenxuan Wei, Hua Ding, and Shupei Zhang. 2025. "BL-DATransformer Lifespan Degradation Prediction Model of Fuel Cell Using Relative Voltage Loss Rate Health Indicator" World Electric Vehicle Journal 16, no. 6: 290. https://doi.org/10.3390/wevj16060290
APA StyleXu, Y., Wang, J., Hu, D., Lu, D., Zhang, X., Wei, W., Ding, H., & Zhang, S. (2025). BL-DATransformer Lifespan Degradation Prediction Model of Fuel Cell Using Relative Voltage Loss Rate Health Indicator. World Electric Vehicle Journal, 16(6), 290. https://doi.org/10.3390/wevj16060290







