Abstract
Evaluating the dynamic impact properties of automotive steels is critical for structural design and material selection, but physical testing methods result in high costs and long lead times. In this study, a dataset was constructed by collecting data from high-speed tensile experiments on 65 automotive steels. Five machine learning models, including ridge regression, support vector machine regression, gradient boosted regression tree, random forest, and adaptive boosting regression, were developed to predict the yield strength (YS), ultimate tensile strength (UTS), and fracture elongation (FE) of automotive steels at 100/s using the composition, sample size, and quasi-static mechanical properties of automotive steels as input variables. To further improve the prediction accuracy, stacked ensemble ideas were used to integrate these single models. The results show that the ensemble model has higher prediction accuracy and generalization performance for mechanical properties at 100/s compared to a single model. When predicting the YS, UTS, and FE at 100/s, their 10-fold cross-validated average R2 are 0.913, 0.92, and 0.8, respectively. Most importantly, the Shapley additive explanation (SHAP)-based method reveals major features that significantly affect tensile properties at intermediate strain rates. The proposed methodology facilitates reductions in physical test requirements and costs.
1. Introduction
High-strength body materials mean good crashworthiness. However, unlike static loading, the deformation of the material during a collision that occurs in a vehicle is a dynamic response process that covers a range of strain rates from 1 to 103/s [1]. It has long been shown that strain rate has a large effect on the mechanical properties of materials. For example, X. Yang et al. [2] studied the dynamic tensile behavior of S690 high-strength structural steel at intermediate strain rates, and the results show that S690 steel shows rate dependence at intermediate strain rates and that the yield stress and tensile strength increase with the increase in strain rate. The mechanical properties of three steels—Q355, Q460, and Q620—were studied at high strain rates. The results demonstrate that strain rate hardening significantly affects the strength of the steels [3]. The tensile properties of high-strength low-alloy (HC420LA) steel at 0.001–500/s were investigated by J. Cui et al. [4]. By performing tensile tests on a 1.5 mm HC420LA steel plate, it can be concluded based on the results that the yield strength, tensile strength, and elongation of the HC420LA steel plate under quasi-static conditions were 429 MPa, 556 MPa, and 49.1%, respectively. Further, the elongation of this steel plate increased from 49.1% to 88.1% with the increase in strain rate, indicating that the strain rate has a significant effect on the forming properties of HC420LA. Therefore, it is crucial to study the dynamic mechanical behavior of automotive materials when selecting and designing the distribution of materials in vehicle development. Currently, the primary method of obtaining data on the dynamic response of materials is through physical experiments such as high-speed tensile tests. Even though the method is able to accurately predict the mechanical properties of materials at different strain rates, there are many limitations. On the one hand, physical experiments have high costs and long lead times. Typically, the cost of a single high-speed tensile test is several thousand RMB or more, and the price increases as the strain rate of the test increases. Secondly, the preparation of the specimen and the related processing will take a lot of time. On the other hand, physical experimental methods are unable to reveal the relationship between chemical composition, process parameters, and dynamic mechanical properties.
In recent years, computer technology has been widely used in the field of materials science [5,6]. Machine learning (ML) is a data-driven approach to making predictions by learning large amounts of sample data and extracting patterns and regularities from the data. In the field of metallic materials, ML has been used to facilitate the synthesis of materials, predict the mechanical properties of materials, and optimize the composition of materials to improve the properties of alloys. In the prediction of mechanical properties, many scholars have established the relationship between composition, process parameters, properties through machine learning. For example, N. Bhat and A.S. Barnard et al. [7] proposed a class regression model to achieve accurate prediction of tensile properties of aluminum alloys. H. Gong and Q. Fan et al. effectively predicted the dynamic compressive strength, critical rupture strain, and impact absorbed energy with an accuracy of more than 86.11% using a trained random forest regression model [8]. S.-G. Li et al. [9] achieved high-accuracy prediction of the fatigue life of metallic materials using a conditional generative adversarial network (cGAN) and machine learning algorithms. S. Wang et al. [10] proposed an optimized machine learning model for the prediction of mechanical properties of quenched and tempered steels, and the accurate prediction of mechanical properties of quenched and tempered steels was achieved by comparing and analyzing multiple algorithms with the best model.
However, these previous studies have been devoted to the prediction of properties under quasi-static conditions and there is a gap in the prediction of material properties under high strain rates. In this study, a dataset of high-speed tensile mechanical properties of automotive steels was constructed. Through five machine learning models, the mapping relationship between the basic information of automotive steel and its YS, UTS, and fracture elongation (FE) at intermediate strain rates was established. Further, a super learner was built to further improve the prediction performance. Most importantly, the SHAP algorithm explored the quantitative correlation of input and output variables and identified the major determinants of the three tensile properties. The proposed method provides guidance and reference for reducing physical experiments and designing new materials for vehicles. A research architecture diagram of this work is shown in Figure 1.
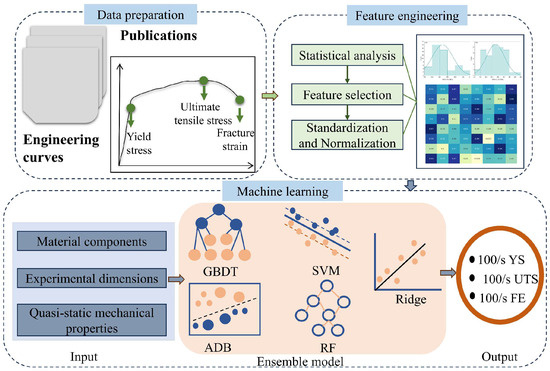
Figure 1.
Research architecture diagram for this work.
2. Methods
2.1. Data Collection and Preprocessing
In this work, high-speed tensile experimental data of 65 automotive steels were collected to constitute a dataset from national and international published papers [4,11,12,13,14,15,16]. A total of 106 samples in the dataset each contained 23 input features and 3 outcomes covering chemical composition, sample size, quasi-static mechanical properties, and mechanical properties at 100/s. The distribution of major steel grades in the dataset and the statistical description of their features are shown in Figure 2 and Table 1, respectively.
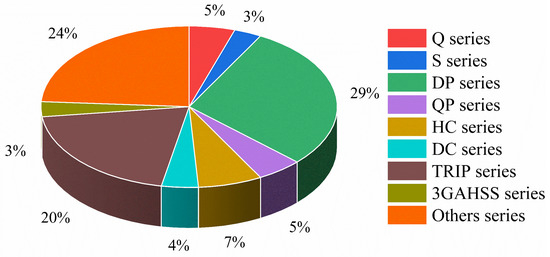
Figure 2.
Distribution of main steel grades.

Table 1.
Statistical description of all features.
Data preprocessing is crucial for the initial dataset since data quality is a decisive factor for model accuracy. In general, data preprocessing includes missing value filling, removing redundant features, and normalization. Removing redundant features is a key step in data preprocessing because redundant features can lead to a decrease in the accuracy of the model. In this work, the Person correlation coefficient [17] shown in Equation (1) is used to calculate the degree of correlation between features and labels, x and y represent different mechanical property parameters, and represent point i of x and y, and are the average value of x and y, and n is the number of points.
Considering that the sample size has an influence on the tensile properties, especially the thickness, when performing tensile experiments and that the quasi-static tensile properties are closely related to the dynamic tensile properties, these features are retained by default. Among the material compositions, most of the elements have less influence on the tensile properties, and the optimization of the material compositions is the main purpose of this feature selection.
Next, since different features may have different magnitudes or orders of magnitude, this may result in certain features dominating the computation while others are relatively unimportant. To eliminate this effect, a min–max scale technique [18] is used to map the values of all features to [0, 1], avoiding inconsistencies in the magnitudes from affecting the analysis results. The processed values are calculated from Equation (2).
where and represent the minimum and maximum values of x, respectively.
2.2. Machine Learning Model Building and Performance Evaluation
The main objective of this study was to develop a data-driven predictive model to map the tensile mechanical properties of various grades of steel plates at 100/s. For the traditional physical experimental approach, material samples were prepared for conducting tensile tests at different strain rates, and the acquired data were further processed to obtain their key mechanical properties. The data-driven approach saves on those steps and relies on existing datasets to establish the relationship between the basic material information and the key mechanical properties of high-speed tensile, saving cost and cycle time to a large extent. In this work, five regression prediction models were developed, including ridge regression, support vector machine regression (SVR), random forest (RF), gradient boosted tree regression (GBDT), and adaptive boosting regression (Adaboost). In the present study, 80% of the dataset was randomly selected as the training set, and the remaining part was the testing set. Before modeling, the internal parameters were determined by a random search, different sets of hyperparameters were randomly tested for a given ML model, 10-fold cross-validation was performed on the training set, the parameter set with the lowest average loss was taken as the best mode. The “10-fold cross-validation” process divides the dataset into 10 subsets, with each of the subsets selected in turn for validation testing and the remaining 9 subsets were used for training the model. Finally, the final performance of the model is verified on a test set.
Typically, the best predictive model should be chosen; however, to improve the machine learning model’s generalization and robustness, a super learner is built based on the stacking idea [19]. The individual learners described above are treated as base learners, and the best ensemble model is found by infinite enumeration. The core idea behind a super learner is to average the predictions of multiple base learners with different weights in order to obtain more accurate prediction results.
The coefficient of determination () and mean absolute error (MAE) are used as evaluation criteria for the ML model, which are given by Equations (3) and (4). For R2, this value ranges from −1 to 1. The closer its value is to 1, the better the model predicts, and vice versa. For MAE, the lower its value, the better the model predicts.
where denotes the model-predicted value and denotes the actual value.
2.3. Shapley Additive Explanation (SHAP)
Machine learning models, although capable of establishing mapping relationships between features and labels, lack interpretability, and their prediction process is often referred to as a “black box”. To explain how the actual values of the features affect the three tensile properties at intermediate strain rates, we compute the Shapley values of the features using the SHAP method [20], which measures the contribution of the features to the predicted values. Each value of a feature corresponds to a Shapley value, and a positive or negative Shapley value indicates whether the value of the feature has a boosting or degrading effect on the model’s predicted value, respectively. SHAP is a method for interpreting the predictions of machine learning models based on game-theoretic Shapley values. The SHAP method seeks to assign a score to each feature that represents how much the feature contributes to the final prediction. The Shapley value is a method for fairly distributing the contributions of the players in a cooperative game. In SHAP, each feature is treated as a player, and the model’s prediction is treated as the outcome of the cooperative game. SHAP provides an additive explanatory model in which the model’s prediction can be decomposed into the sum of the baseline prediction and the contribution of each feature [21].
3. Results and Discussion
3.1. Feature Selection Results
A correlation thermogram between the chemical composition and the target parameters is shown in Figure 3. According to Figure 3, the distribution of values of the correlation coefficient ranges from −1 to 1, where being closer to 1 means the stronger the positive correlation between features and labels, and being closer to −1 means the stronger the negative correlation between features and labels. In terms of the distribution of colors, a color closer to brown indicates a stronger positive correlation, closer to cyan indicates a stronger negative correlation, and closer to white indicates no correlation. As can be seen from the significant labeling in the figure, C, Si, Mn, S, Al, Ti, Fe, and N have strong correlations with the target parameters. This is consistent with our a priori knowledge, specifically that C is the key element that determines the hardness and strength of steel. As C content increases, the hardness and strength of steel increases, but plasticity and toughness decrease. Si increases the strength and hardness of steel and helps to deoxidize and refine the grain; it also improves high-temperature resistance and oxidation resistance. Manganese improves the strength and hardness of steel while maintaining good plasticity and toughness; it helps to eliminate the undesirable effects of S, such as thermal embrittlement, thus improving weldability and cold working properties. Mn increases the material’s resistance to strain hardening during dynamic tensile processes; S is a detrimental element in steel because it causes thermal embrittlement and reduces the steel’s low-temperature toughness; Al deoxidizes and forms stable oxides that improve the steel’s corrosion resistance; and Ti combines with N and C to form stable titanium carbide and titanium nitride, which reduces the aggregation of these elements at grain boundaries and improves the steel’s corrosion resistance and weldability. Therefore, the above component features are retained, and the remaining irrelevant features are removed.
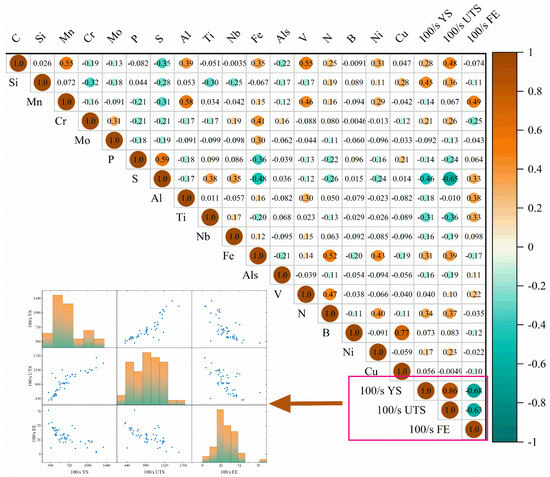
Figure 3.
The Pearson correlation coefficient map.
3.2. Model-Predicted Performance Results
3.2.1. Single Model
The average R2 and MAE values of the five machine learning algorithms used to predict the 10-fold cross-validation for 100/s YS, UTS, and FE are shown in Figure 4a,b, and detailed information is shown in Table S1. SVR had the lowest prediction accuracy, predicting an average R2 below 0.5 for all three target parameters, and it also had the highest MAE. Ridge improves the prediction performance of 100/s YS and UTS to a large extent and improves the prediction performance of 100/s FE, but to a lesser extent, compared to SVR. Unlike Ridge and SVR, which are single weak estimators, the remaining three models integrate multiple weak estimators and their predictive performance is better. Their prediction performance improves tremendously compared to Ridge and SVR, with average R2 higher than 0.8 for predicting both 100/s YS and 100/s UTS, and average performance higher than 0.6 for predicting 100/s FE, with significantly lower MAE. In particular, for 100/s YS, 100/s UTS, and 100/s FE, the models with the best predictive performance are GBDT, RF, and GBDT, respectively, with average R2 around 0.887, 0.87, and 0.708, respectively, and the corresponding MAEs are also the lowest among all models.
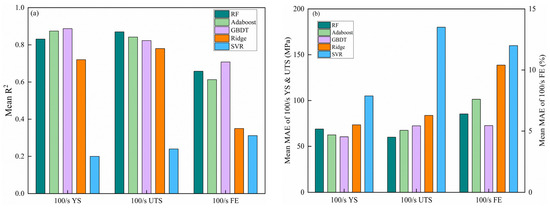
Figure 4.
Performance of five ML models on a test set: (a) mean , (b) mean MAE.
3.2.2. Ensemble Model
In addition, in order to obtain better prediction results, an ensemble learning model is constructed using the above model as the basic model. Considering the poor fitting effect of ridge regression, we use it as a meta-model and the remaining four models as basic models, and then cross-combine them to seek the best combination model. The predictive performance of all ensemble models is shown in Figure 5a. The results show that the predictive performance of the ensemble model is significantly improved compared to the single models. For example, the RF-Adaboost model is optimal when predicting 100/s YS with average R2 and MAE of 0.913 and 50.5 MPa, respectively. The GBDT-Adaboost model exhibits the lowest MAE and the highest R2 when predicting the 100/s UTS in the test set with values of 55.1 MPa and 0.92, respectively. And, the Adaboost-GBDT-SVR model is the best prediction model of 100/s FE in the testing set with MAE and R2 values of 5% and 0.8, respectively. Among some previous studies, they predicted strength better and elongation less well. Specifically, the R2 for predicting strength was above 0.9, but for predicting elongation, the R2 was only about 0.7 [7,22]. In this study, we have substantially improved the accuracy of the prediction of elongation. More detailed information can be found in Table 2. It is therefore concluded that the stack model provides a greater improvement in predicting dynamic mechanical performance than the single models, suggesting that the ensemble approach based on the underlying models is better suited to learning complex relationships and therefore reduces prediction bias.
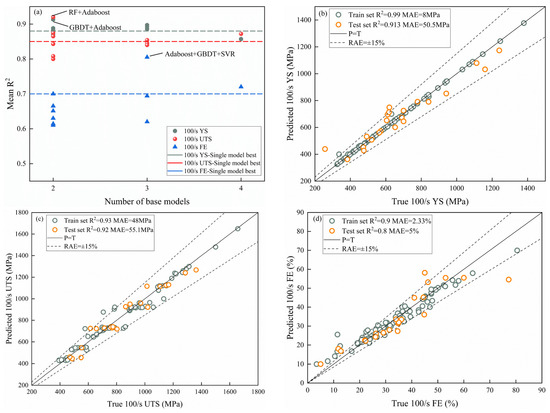
Figure 5.
(a) Performance of all ensemble models on the test set. (b,d) Predicted vs. actual values for the best ensemble model: (b) 100/s YS, (c) 100/s UTS, and (d) 100/s FE.

Table 2.
Performance of each ensemble model.
In order to better assess the learning and generalization capabilities of the integrated model visually, Figure 5b–d plots the predicted values against the true values, where the solid line represents 0 error and the dashed line represents a relative absolute error of 15%. As can be seen in Figure 5, the predicted values of 100/s YS and 100/s UTS are close to the diagonal line, demonstrating good fit. However, the data points for the 100/s FE values are far off the diagonal, indicating poor fitting performance. One possible reason is that FE is closely related to the micro-parameters and the current features are not sufficient to map their relationship; on the other hand, the current data samples are small, which leads to insufficient model training. Based on the above analysis, it can be concluded that the ensemble model performs well in predicting 100/s UTS and 100/s YS but poorly in predicting 100/s FE. Therefore, the ensemble model is chosen to predict 100/s UTS and 100/s YS. However, further research and exploration is needed to find more appropriate features and/or use more appropriate models for 100/s FE prediction. In addition, methods such as increasing the amount of training data as well as mesh tuning parameters are needed to achieve better predictions.
3.3. SHAP-Based Analysis of Feature Importance
3.3.1. For 100/s YS
Figure 6a illustrates the average contribution of each feature to the 100/s YS regression prediction model. From the figure, we can clearly see the ranking of the importance of each feature. Quasi-static YS has the greatest influence, followed by Quasi-static UTS, Quasi-static FE, Mn, FE, and S. Other additional elements have less importance, which may be related to their low content in the steel. Among the previous studies [23], the contribution of the element AI was greater than that of Mn when predicting the YS. However, the results of this paper are the opposite.
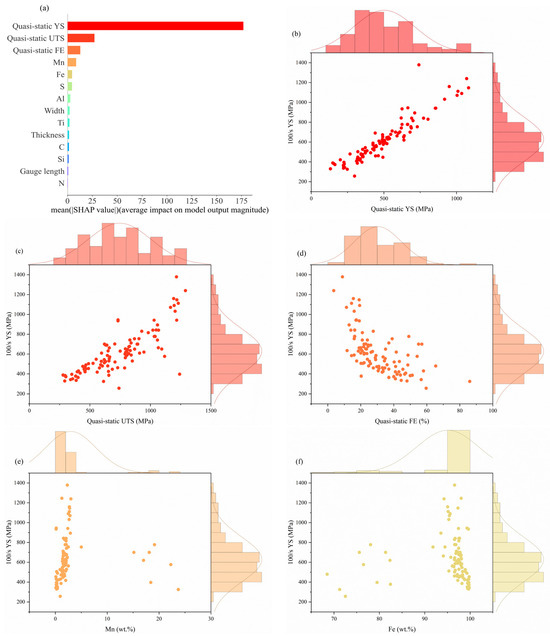
Figure 6.
(a) Feature importance of the best ensemble model; (b–f) joint scatterplot of different input features vs. 100/s YS: (b) quasi-static YS, (c) quasi-static UTS, (d) quasi-static FE, (e) Mn, and (f) Fe.
Figure 6b–f show joint scatter plots of higher importance features with 100/s YS. As the quasi-static YS and quasi-static UTS increase, the 100/s YS increases consequently, which is related to the strain-rate effect, and the strain-rate strengthening mechanism suggests that the strength increases with the strain rate [14,24]. As can be seen in Figure 6d, 100/s YS is smaller as the quasi-static FE increases, which is in line with our consistent knowledge of strength and elongation. In addition, too small or too large a Mn content can lead to a lower yield strength. When the Mn content is low, Mn cannot be sufficiently solidified in the aluminum matrix to form a solid solution, resulting in a weakening of the solid solution strengthening effect, which in turn leads to lower yield strength. Excessive Mn content may lead to oversaturation of the solid solution of Mn in the aluminum matrix, which may lead to the precipitation of Mn and the formation of second-phase particles, which, if oversized or unevenly distributed, may weaken the material properties, again leading to a reduction in yield strength.
3.3.2. For 100/s UTS
Figure 7a illustrates the average contribution of each feature to the 100/s UTS regression prediction model. From the figure, we can clearly see the ranking of the importance of each feature. Quasi-static UTS has the greatest influence, followed by quasi-static YS, Ti, quasi-static FE, width, Mn, thickness, and Si. An interesting thing is that the contribution of the Mn element is much larger than that of the AI element in predicting the UTS, contrary to previous studies [23].
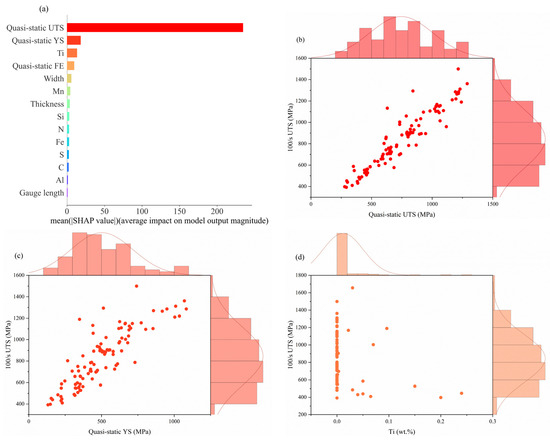
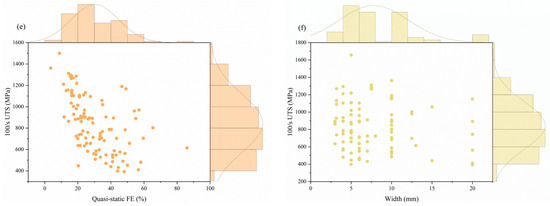
Figure 7.
(a) Feature importance of the best ensemble model; (b–f) joint scatterplot of different input features vs. 100/s UTS: (b) quasi-static UTS, (c) quasi-static YS, (d) Ti, (e) quasi-static FE, and (f) width.
Figure 7b–f shows joint scatter plots of higher importance features with 100/s UTS. The relationship between quasi-static mechanical properties and 100/s UTS is similar to their relationship with 100/s YS and is not discussed here. From Figure 7d, it can be concluded that too little or too much Ti content leads to a decrease in tensile strength, so the content of Ti element needs to be controlled during material design to improve the tensile strength. A reliable explanation is that Ti is an effective grain refiner. The right amount of Ti forms stable nitrides (e.g., TiN) and carbides (e.g., TiC) with nitrogen (N) and carbon (C) in the steel. These compounds are stable at high temperatures and prevent the grain from growing, thus refining the grain. The finer the grain, the stronger the material. If the Ti content is too low, the grain refinement effect is weakened and the grain size increases, resulting in lower tensile strength. Secondly, excessive Ti may lead to excessive precipitation of TiN or TiC, and these compounds, if oversized or unevenly distributed, will reduce the plasticity and toughness of the material, thereby reducing the tensile strength. For width, as the width increases, the cross-sectional area of the sample increases with it, i.e., resulting in lower tensile strength.
3.3.3. For 100/s FE
From Figure 8a, it is easy to see that the top three features contributing most to the prediction of 100/s FE are the properties under quasi-static conditions, followed by Fe, C, Mn, width, and Si. From Figure 8b–f, it can be seen that 100/s FE is negatively correlated with the quasi-static mechanical properties, which is consistent with the previous discussion. Secondly, too much C will lead to a decrease in FE due to the fact that too much C leads to the formation of more carbides (e.g., Fe3C), which are hard and brittle and tend to be distributed along the grain boundaries, resulting in a decrease in the plasticity and toughness of the steel and, hence, in the elongation after fracture.
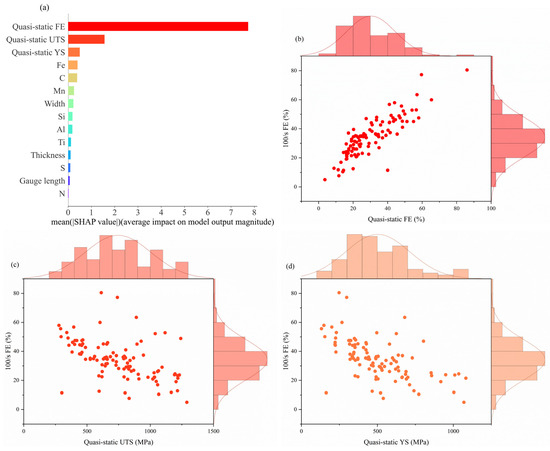
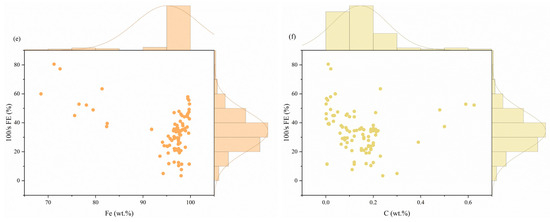
Figure 8.
(a) Feature importance of the best ensemble model; (b–f) joint scatterplot of different input features vs. 100/s FE: (b) quasi-static FE, (c) quasi-static UTS, (d) quasi-static FE, (e) Fe, and (f) C.
4. Conclusions
In this paper, interpretable integrated machine learning is used to predict the tensile properties of automotive steels at intermediate strain rates. This method can provide insights for predicting the dynamic mechanical properties of steel and designing automotive high-strength steel by using the interpretable ML method, which is conducive to reducing cost and cycle time. The main findings are as follows:
- A dataset was constructed by collecting the high-speed tensile experimental data of 65 kinds of automotive steels. Based on five ML algorithms, including Ridge regression, SVR, RF, GBDT, and Adaboost, the composition, sample size, quasi-static mechanical properties, and mechanical properties at 100/s were established. Compared with these models, GBDT is considered to be the best model for predicting 100/s YS and 100/FE, and RF is the best model for predicting 100/s UTS.
- Based on the idea of stacking integration, a super learner is built based on the ML model mentioned above to further improve the model prediction performance. The results show that the integrated model has better predictive performance and generalization performance, and the R2 scores are as high as 0.913, 0.92, and 0.8, with lower MAE on the test sets of 100/s YS, 100/s UTS, and 100/s FE.
- Based on a SHAP analysis, the main characteristics that significantly affect the tensile properties at intermediate strain rates are revealed, in which the quasi-static mechanical properties dominate. Secondly, Mn, Ti, and C have significant effects on the prediction of YS, UTS, and FE, respectively.
In future research, more strain-rate ranges and key parameters should be included. Meanwhile, combining them with the material constitutive equations and applying them to automobile collision material cards will provide data and technical support for reducing the development cycle of collision simulation.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/wevj16030123/s1, Table S1: Best performing hyperparameters for various ML models.
Author Contributions
Data curation, H.W.; Funding acquisition, Z.Z.; Methodology, H.W.; Resources, F.L., H.Z., J.L. and K.Y.; Software, H.W.; Supervision, Z.Z. and H.Z.; Validation, F.L. and J.L.; Writing—original draft, H.W.; Writing—review and editing, Z.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This paper is supported by the Open Fund of National Key Laboratory of Intelligent Vehicle Safety Technology (IVSTSKL-202305), the Jiangsu Materials Big Data Public Technical Service Platform (BM2021007), the Industrial Application Materials Big Data Platform project, and Chongqing Jiaotong University-Yangtze Delta Advanced Material Research Institute Provincial-level Joint Graduate Student Cultivation Base (JDLHPYJD2021008).
Data Availability Statement
The original contributions presented in the study are included in the article or Supplementary Materials, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Tang, Z.Y.; Huang, J.N.; Ding, H.; Cai, Z.; Misra, R. On the dynamic behavior and relationship to mechanical properties of cold-rolled Fe-0.2 C-15Mn-3Al steel at intermediate strain rate. Mater. Sci. Eng. A 2019, 742, 423–431. [Google Scholar] [CrossRef]
- Yang, X.; Yang, H.; Lai, Z.; Zhang, S. Dynamic tensile behavior of S690 high-strength structural steel at intermediate strain rates. J. Constr. Steel Res. 2020, 168, 105961. [Google Scholar] [CrossRef]
- Li, W.; Chen, H. Tensile performance of normal and high-strength structural steels at high strain rates. Thin-Walled Struct. 2023, 184, 110457. [Google Scholar] [CrossRef]
- Cui, J.; Wang, Q.; Dong, D.; Jiang, H.; Zhang, X.; Li, G. A study on the constitutive equation of HC420LA steel subjected to high strain rates. J. Mater. Res. 2019, 34, 1034–1042. [Google Scholar] [CrossRef]
- Rajendra, P.; Girisha, A.; Naidu, T.G. Advancement of machine learning in materials science. Mater. Today Proc. 2022, 62, 5503–5507. [Google Scholar] [CrossRef]
- Golmohammadi, M.; Aryanpour, M. Analysis and evaluation of machine learning applications in materials design and discovery. Mater. Today Commun. 2023, 35, 105494. [Google Scholar] [CrossRef]
- Bhat, N.; Barnard, A.S.; Birbilis, N. Improving the prediction of mechanical properties of aluminium alloy using data-driven class-based regression. Comput. Mater. Sci. 2023, 228, 112270. [Google Scholar] [CrossRef]
- Gong, H.; Fan, Q.; Xie, W.; Zhang, H.; Yang, L.; Xu, S.; Cheng, X. Mining the relationship between the dynamic compression performance and basic mechanical properties of Ti20C based on machine learning methods. Mater. Des. 2023, 226, 111633. [Google Scholar] [CrossRef]
- Li, S.-G.; Chen, Q.-R.; Huang, L.; Chen, M.; Wei, C.-D.; Yue, Z.-J.; Liu, R.-X.; Tong, C.; Liu, Q. Data-driven approach to predict the fatigue properties of ferrous metal materials using the cGAN and machine-learning algorithms. Adv. Manuf. 2024, 12, 447–464. [Google Scholar] [CrossRef]
- Wang, S.; Li, J.; Zuo, X.; Chen, N.; Rong, Y. An optimized machine-learning model for mechanical properties prediction and domain knowledge clarification in quenched and tempered steels. J. Mater. Res. Technol. 2023, 24, 3352–3362. [Google Scholar] [CrossRef]
- Zhu, Y.; Yang, H.; Zhang, S. Dynamic mechanical behavior and constitutive models of S890 high-strength steel at intermediate and high strain rates. J. Mater. Eng. Perform. 2020, 29, 6727–6739. [Google Scholar] [CrossRef]
- Wang, H.; Huo, J.; Liu, Y. Experimental study on dynamic tensile performance of Q345 structural steel considering thickness differences. In Structures; Elsevier: Amsterdam, The Netherlands, 2023; pp. 891–910. [Google Scholar]
- Chen, J.; Shu, W.; Li, J. Constitutive model of Q345 steel at different intermediate strain rates. Int. J. Steel Struct. 2017, 17, 127–137. [Google Scholar] [CrossRef]
- Yu, P.; Zhang, J.; Zhang, C.; Zhao, J. Strain-rate-dependent constitutive and damage models for a low-yielding-strength steel under dynamic loadings. J. Mech. Sci. Technol. 2021, 35, 4405–4417. [Google Scholar] [CrossRef]
- Alturk, R.; Hector, L.G.; Matthew Enloe, C.; Abu-Farha, F.; Brown, T.W. Strain rate effect on tensile flow behavior and anisotropy of a medium-manganese TRIP steel. JOM 2018, 70, 894–905. [Google Scholar] [CrossRef]
- Madivala, M.; Bleck, W. Strain rate dependent mechanical properties of TWIP steel. JOM 2019, 71, 1291–1302. [Google Scholar] [CrossRef]
- Benesty, J.; Chen, J.; Huang, Y. On the importance of the Pearson correlation coefficient in noise reduction. IEEE Trans. Audio Speech Lang. Process. 2008, 16, 757–765. [Google Scholar] [CrossRef]
- Ruppert, D. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Taylor & Francis: Abingdon, UK, 2004. [Google Scholar]
- Laan, M.J.v.d.; Polley, E.C.; Hubbard, A.E. Super Learner. Stat. Appl. Genet. Mol. Biol. 2007, 6, 23. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.-I. A unified approach to interpreting model predictions. Adv. Neural Inf. Process. Syst. 2017, 30, 4765–4774. [Google Scholar]
- Mangalathu, S.; Hwang, S.-H.; Jeon, J.-S. Failure mode and effects analysis of RC members based on machine-learning-based SHapley Additive exPlanations (SHAP) approach. Eng. Struct. 2020, 219, 110927. [Google Scholar] [CrossRef]
- Hou, H.; Wang, J.; Ye, L.; Zhu, S.; Wang, L.; Guan, S. Prediction of mechanical properties of biomedical magnesium alloys based on ensemble machine learning. Mater. Lett. 2023, 348, 134605. [Google Scholar] [CrossRef]
- Suh, J.S.; Kim, Y.M.; Yim, C.D.; Suh, B.-C.; Bae, J.H.; Lee, H.W. Interpretable machine learning-based analysis of mechanical properties of extruded Mg-Al-Zn-Mn-Ca-Y alloys. J. Alloys Compd. 2023, 968, 172007. [Google Scholar] [CrossRef]
- Mukhopadhyay, A.; Das, S.; Mukhopadhyay, G. Effect of Pre-Strain and Strain Rate on Deformation and Fracture Behavior of Automotive Grade Interstitial Free Steel Sheets. J. Mater. Eng. Perform. 2024, 1–17. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).