Optimal Incentive Mechanism: Balancing the Complex Risk Preferences of Shared Battery Swapping Station Enterprises Under Dual Asymmetric Information
Abstract
1. Introduction
2. Literature Review
3. Model
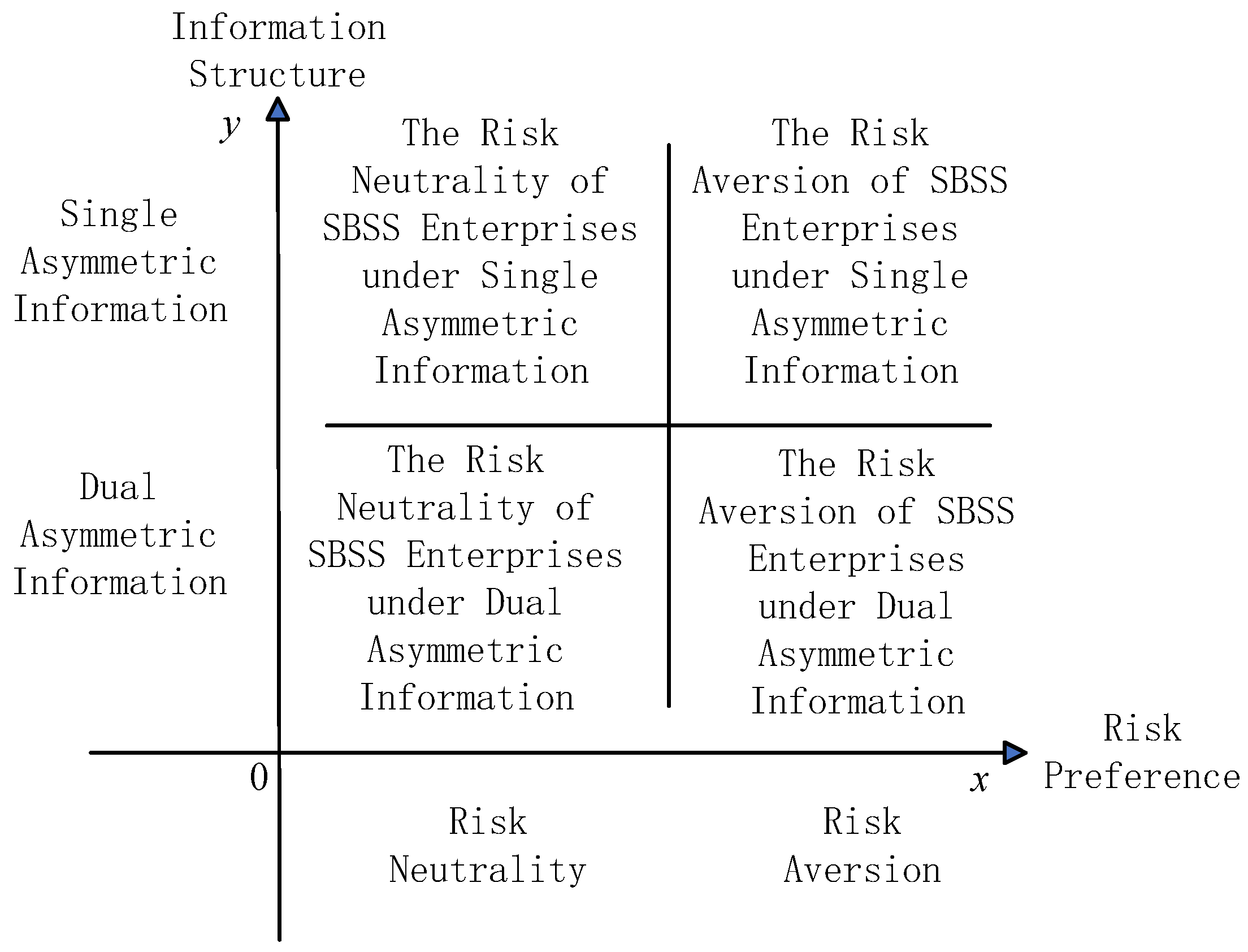
4. Single Incentive Mechanism
4.1. The Risk Neutrality of SBSS Construction Enterprises Under Single Asymmetric Information
4.2. The Risk Aversion of SBSS Construction Enterprises Under Single Asymmetric Information
4.3. Optimal Incentive Coefficient Under Single Asymmetric Information
4.4. Optimal Fixed Subsidy Under Single Asymmetric Information
5. Dual Incentive Mechanism
5.1. The Risk Neutrality of SBSS Construction Enterprises Under Dual Asymmetric Information
5.2. The Risk Aversion of SBSS Construction Enterprises Under Dual Asymmetric Information
5.3. Optimal Incentive Coefficient Under Dual Asymmetric Information
5.4. Optimal Fixed Subsidy Under Dual Asymmetric Information
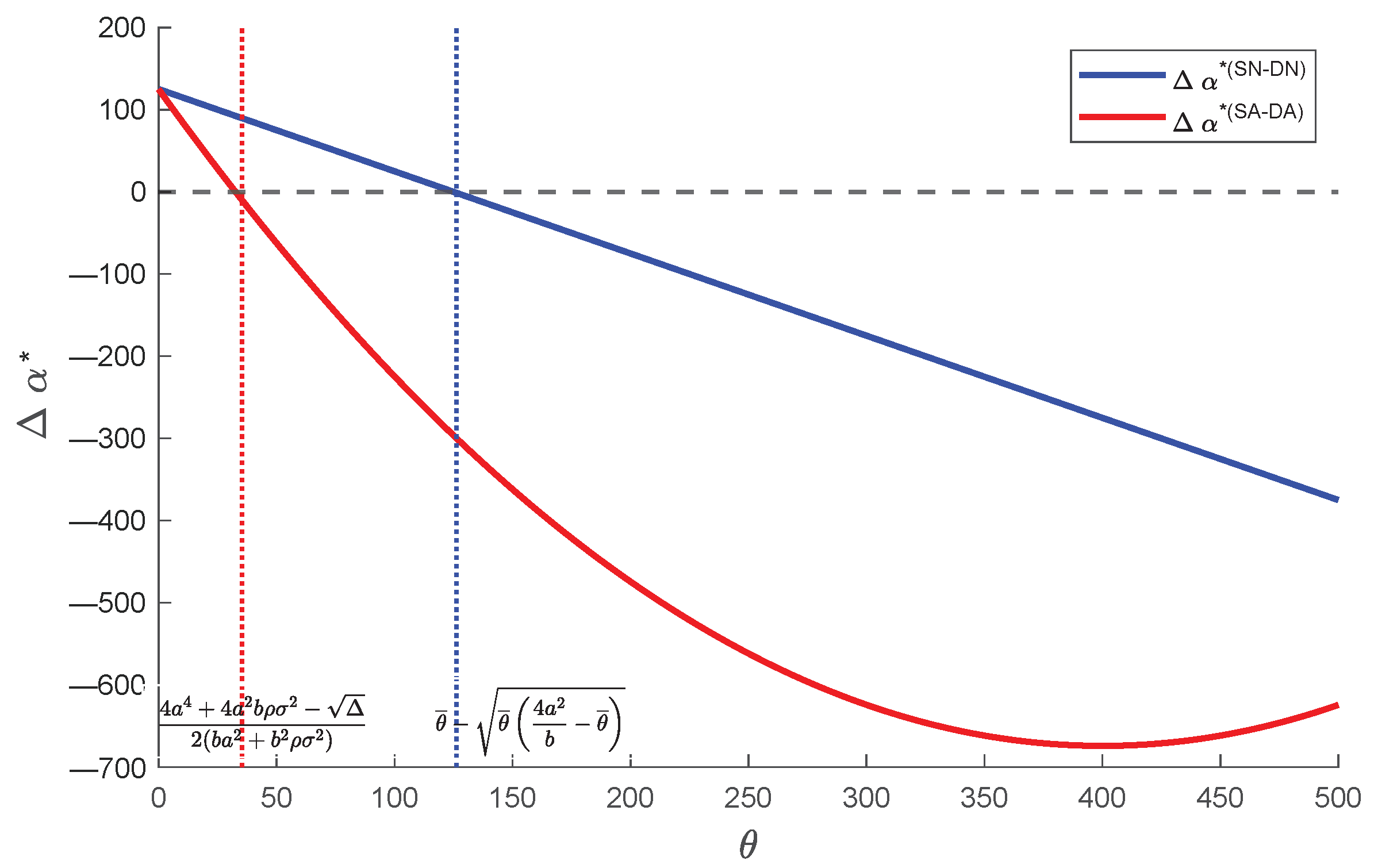
5.5. Balancing Risk Preference and Asymmetry Information Through Incentive Mechanisms
5.5.1. The Impact of Asymmetry Information on Incentive Coefficient
5.5.2. The Impact of Asymmetry Information on Fixed Subsidies
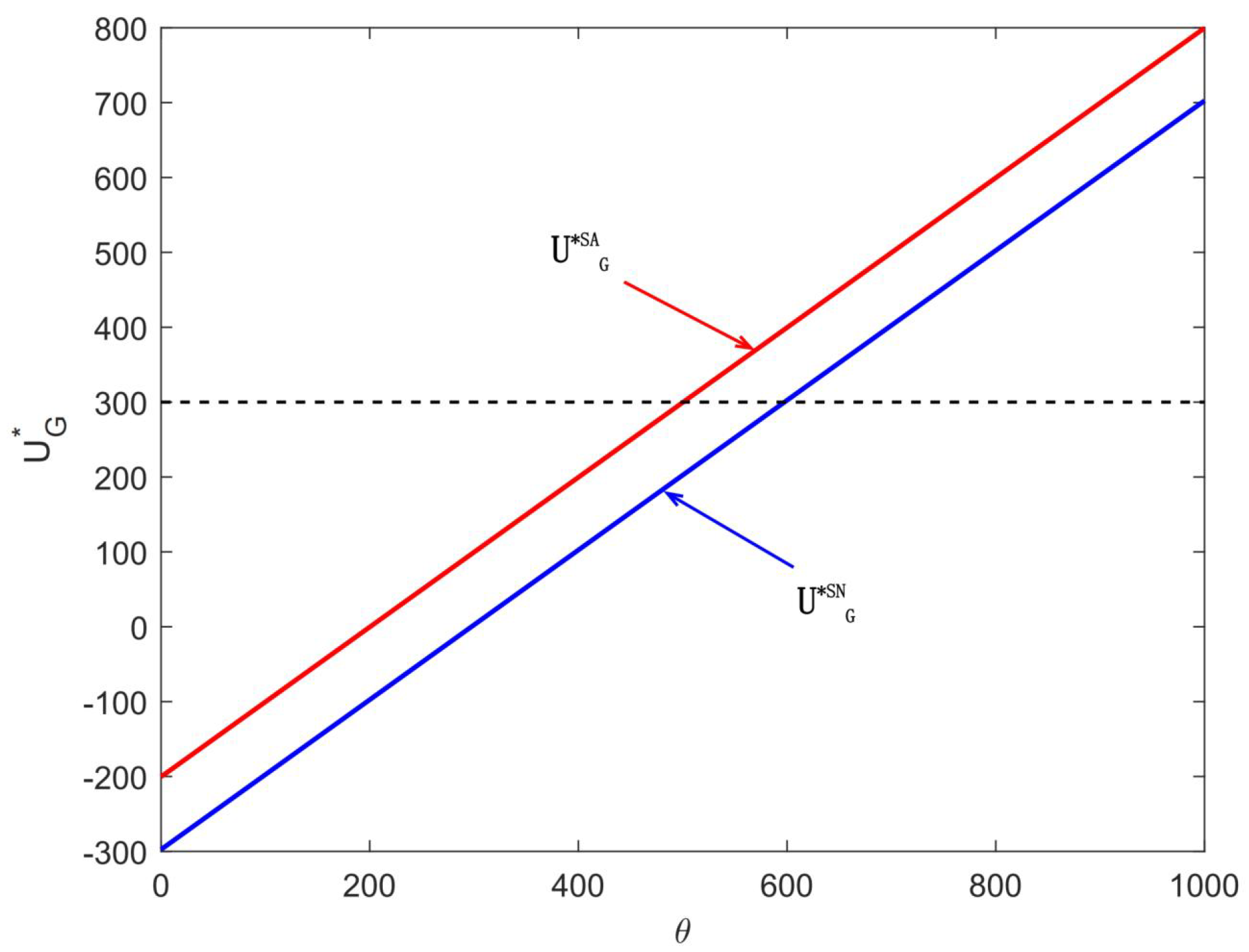
6. Balancing Utility and Complexity
6.1. Risk Preferences and Utility Trade-Offs
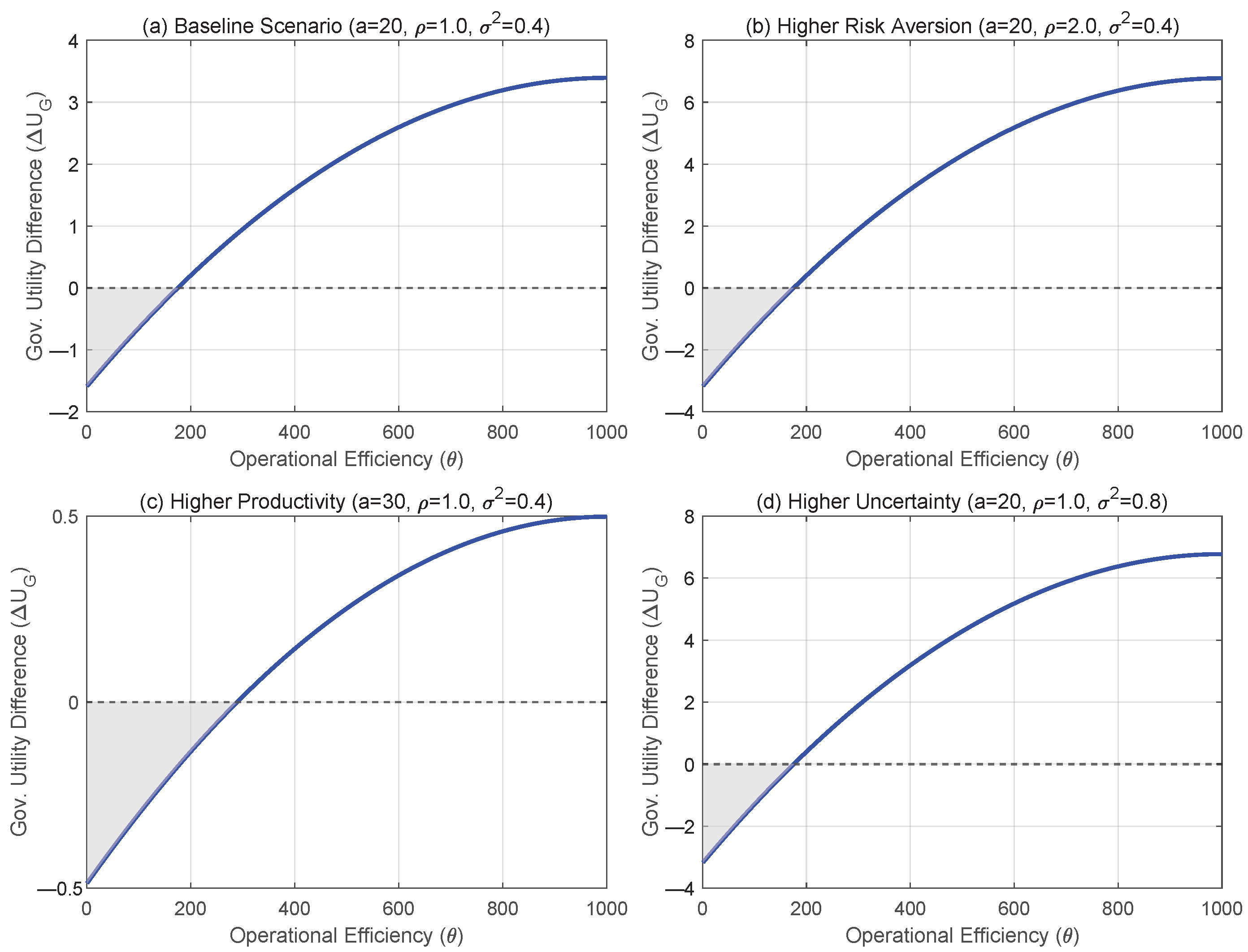
6.2. Operational Efficiency and Utility Trade-Off
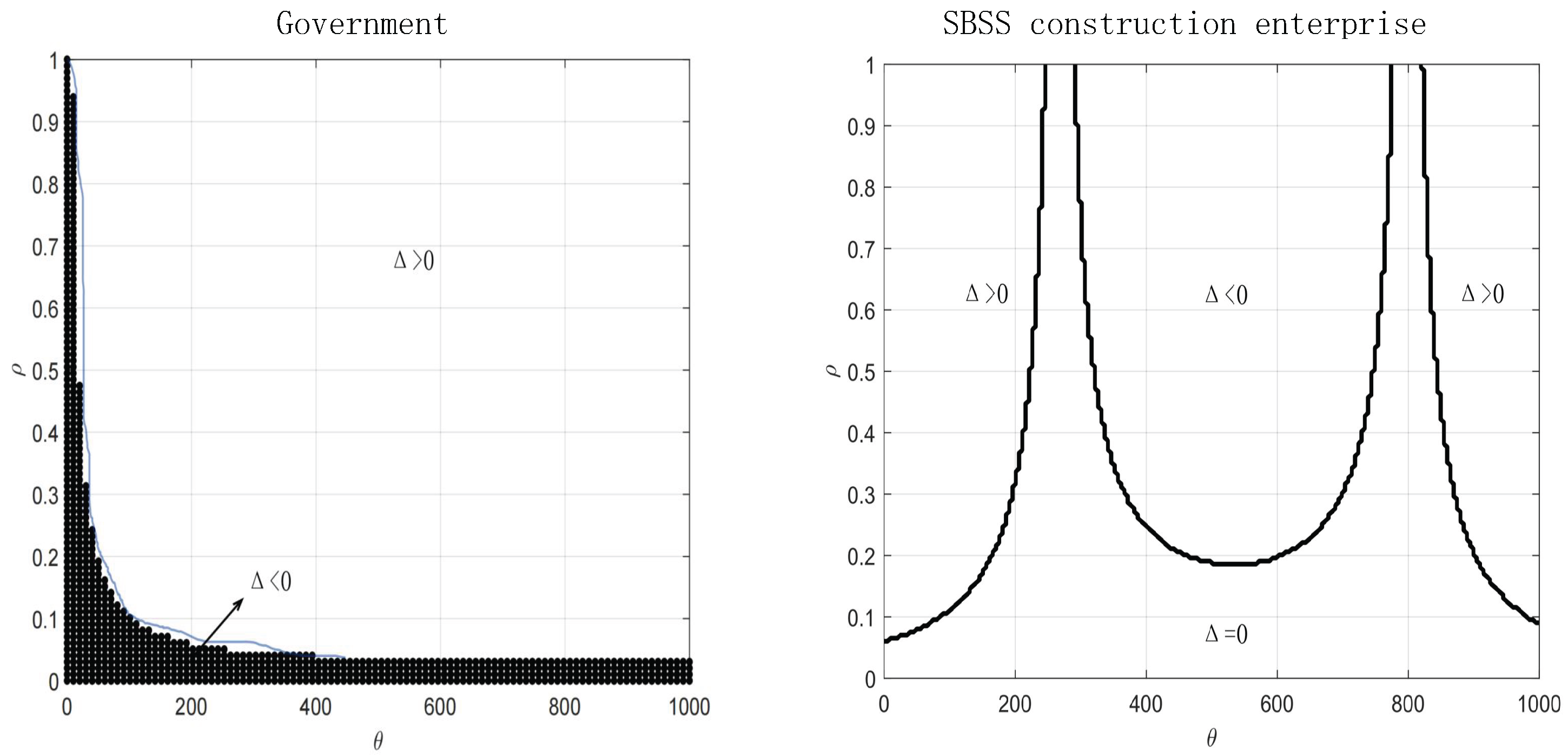
6.3. Sensitivity Analysis and Robustness
7. Conclusions
7.1. Summary of Findings
7.2. Management Policy Recommendations
7.3. Limitations and Future Research
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| EV | Electric Vehicle |
| BSS | Battery Swapping Station |
| SBSS | Shared Battery Swapping Station |
| LL | Limited Liability |
| IC | Incentive Compatibility |
| PC | Participation Constraints |
Appendix A
Appendix B
| Algorithm A1 Pseudo-code for Calculating Government’s Utility Difference () | |
| 1: | Input: Model parameters |
| 2: | Output: A plot of versus |
| 3: | Initialize a grid of values from 0 to |
| 4: | Initialize arrays and of the same size as |
| 5: | for each in do |
| 6: | // — Calculate utility under DN (risk-neutral) — |
| 7: | |
| 8: | |
| 9: | |
| 10: | {Calculated numerically} |
| 11: | |
| 12: | |
| 13: | // — Calculate utility under DA (risk-averse) — |
| 14: | |
| 15: | |
| 16: | |
| 17: | {Calculated numerically} |
| 18: | |
| 19: | end for |
| 20: | {Calculate the difference array} |
| 21: | Plot as a function of |
| 22: | Add title, axis labels, and a horizontal reference line at . |
References
- Freeman, M. The tax implications of HR 5376: Inflation Reduction Act of 2022. Tenn. CPA J. 2022, 67, 22–23. [Google Scholar]
- Wu, H. A survey of battery swapping stations for electric vehicles: Operation modes and decision scenarios. IEEE Trans. Intell. Transp. Syst. 2021, 23, 10163–10185. [Google Scholar] [CrossRef]
- Xie, R.; Wei, W.; Wu, Q.; Ding, T.; Mei, S. Optimal service pricing and charging scheduling of an electric vehicle sharing system. IEEE Trans. Veh. Technol. 2019, 69, 78–89. [Google Scholar] [CrossRef]
- Zhang, Y.; You, P.; Cai, L. Optimal charging scheduling by pricing for EV charging station with dual charging modes. IEEE Trans. Intell. Transp. Syst. 2018, 20, 3386–3396. [Google Scholar] [CrossRef]
- Cozzi, P. Smart Battery Management Through Pooling and Swapping: A Business Case Analysis for the Italian EV Market. Ph.D. Thesis, Politecnico di Torino, Torino, Italy, 2022. [Google Scholar]
- Jalees, S.; Hussain, A.; Iqbal, R.; Raza, W.; Ahmad, A.; Saleem, A.; Majeed, M.K.; Faheem, M.; Ahmad, N.; Rehman, L.N.U.; et al. Functional PBI membrane based on polyimide covalent organic framework for durable lithium metal battery. J. Energy Storage 2024, 101, 113985. [Google Scholar] [CrossRef]
- Ahmad, F.; Alam, M.S.; Alsaidan, I.S.; Shariff, S.M. Battery swapping station for electric vehicles: Opportunities and challenges. IET Smart Grid 2020, 3, 280–286. [Google Scholar] [CrossRef]
- Mirrlees, J.A. The theory of moral hazard and unobservable behaviour: Part I. Rev. Econ. Stud. 1999, 66, 3–21. [Google Scholar] [CrossRef]
- Akerlof, G.A. The market for “lemons”: Quality uncertainty and the market mechanism. In Uncertainty in Economics; Elsevier: Amsterdam, The Netherlands, 1978; pp. 235–251. [Google Scholar] [CrossRef]
- Holmstrom, B.; Milgrom, P. Aggregation and linearity in the provision of intertemporal incentives. Econometrica 1987, 55, 303–328. [Google Scholar] [CrossRef]
- Laffont, J.J.; Martimort, D. Collusion under asymmetric information. Econometrica 1997, 65, 875–911. [Google Scholar] [CrossRef]
- Laffont, J.J.; Martimort, D. The firm as a multicontract organization. J. Econ. Manag. Strategy 1997, 6, 201–234. [Google Scholar] [CrossRef]
- Tian, F.; Astashkina, E.; Duenyas, I. Dynamic contract design in the presence of double moral hazard. Manag. Sci. 2024, 71, 6319–7222. [Google Scholar] [CrossRef]
- Hosseini, M.; Milner, J.; Romero, G. Dynamic relocations in car-sharing networks. Oper. Res. 2024, 73, 1723–2295. [Google Scholar] [CrossRef]
- Zhang, F.; Zhang, R. Trade-in remanufacturing, customer purchasing behavior, and government policy. Manuf. Serv. Oper. Manag. 2018, 20, 601–616. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, Z. A dynamic principal–agent problem with one-sided commitment. Math. Oper. Res. 2024. [Google Scholar] [CrossRef]
- Morozov, I.; Seiler, S.; Dong, X.; Hou, L. Estimation of preference heterogeneity in markets with costly search. Mark. Sci. 2021, 40, 871–899. [Google Scholar] [CrossRef]
- Dillon, R.L.; Bier, V.M.; John, R.S.; Althenayyan, A. Closing the gap between decision analysis and policy analysts before the next pandemic. Decis. Anal. 2023, 20, 109–132. [Google Scholar] [CrossRef]
- Cheng, Y.; Fan, T.; Zhou, L. Optimal strategies of automakers with demand and credit price disruptions under the dual-credit policy. J. Manag. Sci. Eng. 2022, 7, 453–472. [Google Scholar] [CrossRef]
- Comelli, A. Battery Swapping Systems-From a Business Oriented Analysis to a Practical Case Study. Ph.D. Thesis, Politecnico di Torino, Torino, Italy, 2020. [Google Scholar]
- Jiang, Z.Z.; Li, K.; Tang, C.S.; Yang, S.A. Offering EV Battery Swapping as a Service: EV Manufacturers or Battery Producers? Working Paper 4779240, SSRN, 2024. Available online: https://ssrn.com/abstract=4779240 (accessed on 15 September 2024).
- Deck, C.; Huang, R.J.; Tzeng, L.Y.; Zhao, L. A simple approach for measuring higher-order Arrow-Pratt coefficients of risk aversion. Manag. Sci. 2024, 71, 6319–7222. [Google Scholar] [CrossRef]
- Pesenti, S.M.; Jaimungal, S.; Saporito, Y.F.; Targino, R.S. Risk budgeting allocation for dynamic risk measures. Oper. Res. 2024, 73, 1151–1722. [Google Scholar] [CrossRef]
- Hou, C.F.; Lu, M.S. Allocating inventory risk in retail supply chains: Risk aversion, information asymmetry, and outside opportunity. Manuf. Serv. Oper. Manag. 2024, 26, 1508–1525. [Google Scholar] [CrossRef]
- Liu, P. Risk sharing with Lambda value at risk. Math. Oper. Res. 2025, 50, 313–333. [Google Scholar] [CrossRef]
- Smith, J.E. Risk sharing, fiduciary duty, and corporate risk attitudes. Decis. Anal. 2004, 1, 114–127. [Google Scholar] [CrossRef]
- Maskin, E.; Qian, Y.; Xu, C. Incentives, information, and organizational form. Rev. Econ. Stud. 2000, 67, 359–378. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Y.; Li, Q.; Zhang, J. Research on Coordination Strategy of Electric Vehicle Supply Chain Under Battery Swapping Mode. Working Paper 4665250, SSRN. 2023. Available online: https://ssrn.com/abstract=4665250 (accessed on 7 September 2024).
- Zhang, P.; Jin, L.; Wang, Y. Optimizing mechanisms for promoting low-carbon manufacturing industries towards carbon neutrality. Renew. Sustain. Energy Rev. 2023, 183, 113516. [Google Scholar] [CrossRef]
- Zhu, J.; Dou, Z.; Yan, X.; Yu, L.; Lu, Y. Exploring the influencing factors of carbon neutralization in Chinese manufacturing enterprises. Environ. Sci. Pollut. Res. 2023, 30, 2918–2944. [Google Scholar] [CrossRef] [PubMed]
- Benkhodja, M.T.; Fromentin, V.; Ma, X. Macroeconomic effects of green subsidies. J. Clean. Prod. 2023, 410, 137166. [Google Scholar] [CrossRef]
- He, H.; Chen, W.; Zhou, Q. Subsidy allocation strategies for power industry’s clean transition under Bayesian Nash equilibrium. Energy Policy 2024, 185, 113920. [Google Scholar] [CrossRef]
- Rasmusen, E. Games and Information; Basil Blackwell: Oxford, UK, 1989; Volume 13. [Google Scholar]
- Fereidouni, M.; Nault, B.R. Using subsidies, fines, and restitution with budget balance to combat digital piracy. Manag. Sci. 2025, 71, 7223–8095. [Google Scholar] [CrossRef]
- Baldacci, B.; Manziuk, I.; Mastrolia, T.; Rosenbaum, M. Market making and incentives design in the presence of a dark pool: A Stackelberg actor–critic approach. Oper. Res. 2023, 71, 727–749. [Google Scholar] [CrossRef]
- Song, J.M.; Zhao, Y.; Xu, X. Incentives and gaming in collaborative projects under risk-sharing partnerships. Manuf. Serv. Oper. Manag. 2021, 23, 453–470. [Google Scholar] [CrossRef]
- Guan, X.; Cao, H.; Li, K.J.; Ding, Y. Product safety and liability with deceptive advertising and moral hazard. Mark. Sci. 2025, 44, 287–305. [Google Scholar] [CrossRef]
- Momeni, B.; Mohebbi, S. Differential game theoretic models for designing water conservation incentives. Decis. Anal. 2025, 22, 89–168. [Google Scholar] [CrossRef]
- He, L.; Chen, L. The incentive effects of different government subsidy policies on green buildings. Renew. Sustain. Energy Rev. 2021, 135, 110123. [Google Scholar] [CrossRef]
- Cai, D.; Zhang, G.; Lai, K.h.; Guo, C.; Su, B. Government incentive contract design for carbon reduction innovation considering market value under asymmetric information. Energy Policy 2024, 186, 114009. [Google Scholar] [CrossRef]
- Jin, L. Optimal design of licensing contracts innovators under asymmetric information. J. Syst. Eng. 2025, 40, 1–14. [Google Scholar] [CrossRef]
- Zhang, R.; Zhu, J.; Lei, M. A study on the design of incentive contracts for platform economy regulation based on dual principal–agents. Systems 2024, 12, 343. [Google Scholar] [CrossRef]
- Wang, L.; Pan, F. Incentive mechanism analysis of environmental governance using multitask principal–agent model. Sustainability 2023, 15, 4126. [Google Scholar] [CrossRef]
- Liang, Y.; Liang, X.; Wei, H. Sustainable quality-incentive contract design of public technology innovation procurement under asymmetry information. Sustainability 2023, 15, 8773. [Google Scholar] [CrossRef]
- Jin, L. Optimal patent licensing and SR investment strategy under asymmetric information. J. Syst. Eng. 2024, 39, 500–513. [Google Scholar] [CrossRef]
- Hu, W.; Ma, C.; Zhao, H.; Dong, T. The strategic choice of co-opetition automobile supply chain under “dual-credit” policy. J. Syst. Eng. 2024, 39, 109–127. [Google Scholar] [CrossRef]
- He, H. Incentive mechanism of utility tunnel PPP projects with user involvement. Sustainability 2023, 15, 10771. [Google Scholar] [CrossRef]
- Du, C.; Wang, C.; Yang, Y. Incentive contract design for governmental forest ecological benefit compensation under information asymmetry. Forests 2024, 15, 2145. [Google Scholar] [CrossRef]
- Ding, C.; Li, Y.; Cui, Z. Understanding how heterogeneous agents affect principal’s returns: Perspectives from short-termism and Bayesian learning. J. Manag. Sci. Eng. 2023, 8, 342–368. [Google Scholar] [CrossRef]
- Yang, Y.; Sun, Y. Dynamic robust contract and incentive strategy under model uncertainty. J. Manag. Sci. Eng. 2025, 10, 465–485. [Google Scholar] [CrossRef]
- Zhang, X.; Huang, J.; Shen, C. Retailers’ incentives for green investment in differentiated competition channels. J. Manag. Sci. Eng. 2023, 8, 465–489. [Google Scholar] [CrossRef]
- Laffont, J.J.; Martimort, D. The theory of incentives: The principal–agent model. In The Theory of Incentives; Princeton University Press: Princeton, NJ, USA, 2009. [Google Scholar] [CrossRef]
- Bolton, P.; Dewatripont, M. Contract Theory; MIT Press: Cambridge, MA, USA, 2004. [Google Scholar]
- Liao, C.S.; Lu, S.H.; Shen, Z.J.M. The electric vehicle touring problem. Transp. Res. Part B Methodol. 2016, 86, 163–180. [Google Scholar] [CrossRef]
- Yu, J.; Williams, E.; Ju, M. Analysis of material and energy consumption of mobile phones in China. Energy Policy 2010, 38, 4135–4141. [Google Scholar] [CrossRef]
- Sheng. Layout Evaluation and Incentive Mechanism Design of Electric Vehicle Charging Piles Based on Charging Sharing. Ph.D. Thesis, Beijing Jiaotong University, Beijing, China, 2020. [CrossRef]
- Arrow, K.J. Aspects of the Theory of Risk Bearing; The Yrjö Jahnsson Foundation: Helsinki, Finland, 1965. [Google Scholar]
- Pratt, J.W. Risk aversion in the small and in the large. In Uncertainty in Economics; Elsevier: Amsterdam, The Netherlands, 1978; pp. 59–79. [Google Scholar] [CrossRef]




| Symbol | Description | Type/Note |
|---|---|---|
| Choice Variables | ||
| Fixed subsidy and incentive coefficient. | in dual asymmetry. | |
| e | Effort level exerted by the SBSS enterprise. | Agent’s choice, . |
| Parameters | ||
| Operational efficiency level of the enterprise. | Agent’s type, . | |
| a | Marginal productivity of effort. | Exogenous, . |
| b | Marginal cost of effort. | Exogenous, . |
| Coefficient of absolute risk aversion. | Agent’s risk preference, . | |
| Variance of the random output shock. | Exogenous, . | |
| Reservation utility of the enterprise. | Exogenous. | |
| Functions | ||
| Delivered production output, . | Output function. | |
| Cost of effort, . | Cost function. | |
| Total remuneration, . | Contract function. | |
| Utility of the government and enterprise. | Objective functions. | |
| PDF and CDF of the type distribution. | Distribution functions. | |
| Hazard rate, . | Hazard rate function. | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, L.; Lan, Y.; Hu, M.; Gong, A. Optimal Incentive Mechanism: Balancing the Complex Risk Preferences of Shared Battery Swapping Station Enterprises Under Dual Asymmetric Information. World Electr. Veh. J. 2025, 16, 631. https://doi.org/10.3390/wevj16110631
He L, Lan Y, Hu M, Gong A. Optimal Incentive Mechanism: Balancing the Complex Risk Preferences of Shared Battery Swapping Station Enterprises Under Dual Asymmetric Information. World Electric Vehicle Journal. 2025; 16(11):631. https://doi.org/10.3390/wevj16110631
Chicago/Turabian StyleHe, Lei, Yanfei Lan, Mingmao Hu, and Aihong Gong. 2025. "Optimal Incentive Mechanism: Balancing the Complex Risk Preferences of Shared Battery Swapping Station Enterprises Under Dual Asymmetric Information" World Electric Vehicle Journal 16, no. 11: 631. https://doi.org/10.3390/wevj16110631
APA StyleHe, L., Lan, Y., Hu, M., & Gong, A. (2025). Optimal Incentive Mechanism: Balancing the Complex Risk Preferences of Shared Battery Swapping Station Enterprises Under Dual Asymmetric Information. World Electric Vehicle Journal, 16(11), 631. https://doi.org/10.3390/wevj16110631








