Fuzzy Control with Modified Fireworks Algorithm for Fuel Cell Commercial Vehicle Seat Suspension
Abstract
1. Introduction
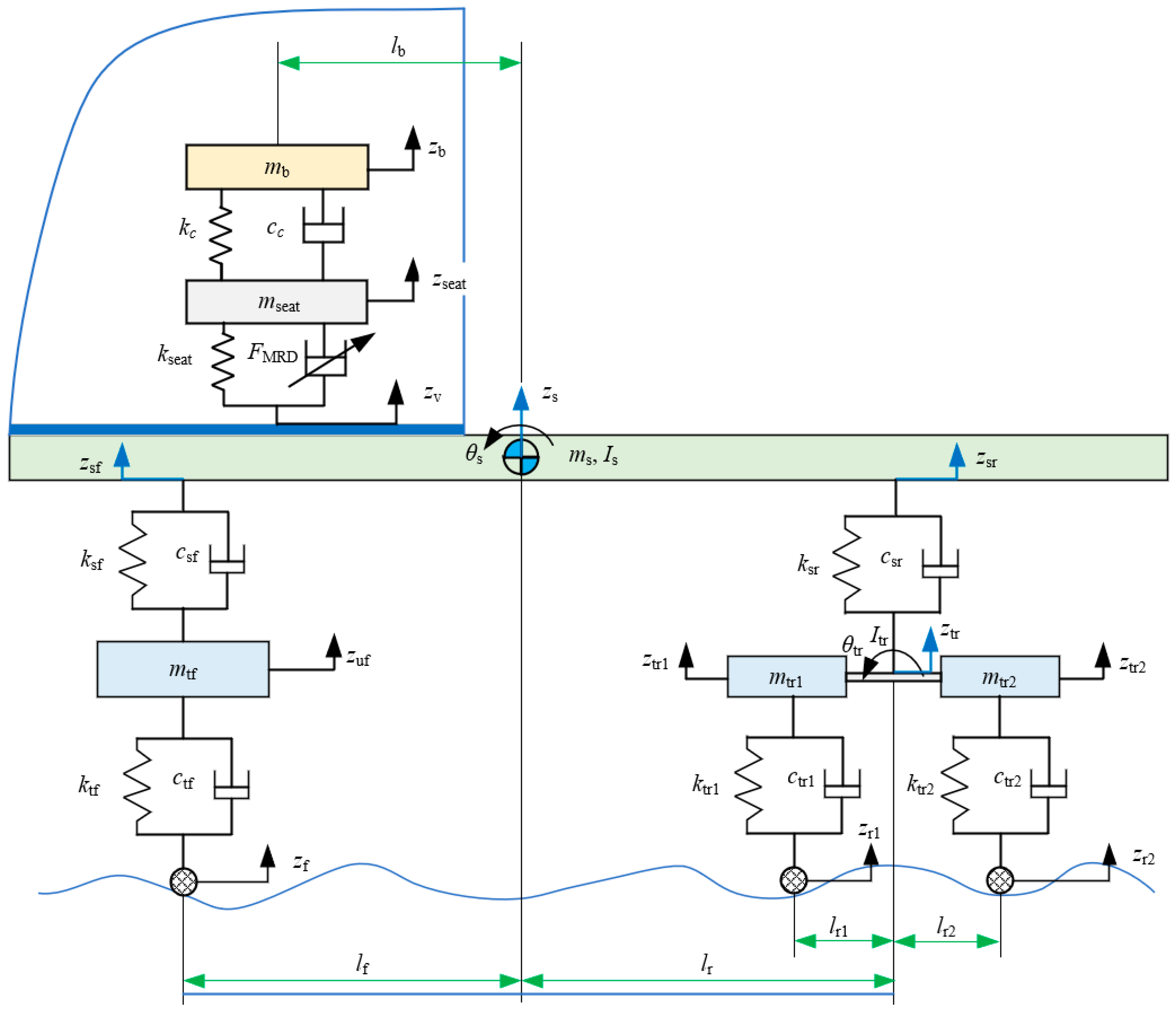
2. Vehicle Model and Semi-Active Suspension Modeling
2.1. Vehicle Model
2.2. MRD Modeling
3. Modified Fireworks Algorithm and Fuzzy Controller Design
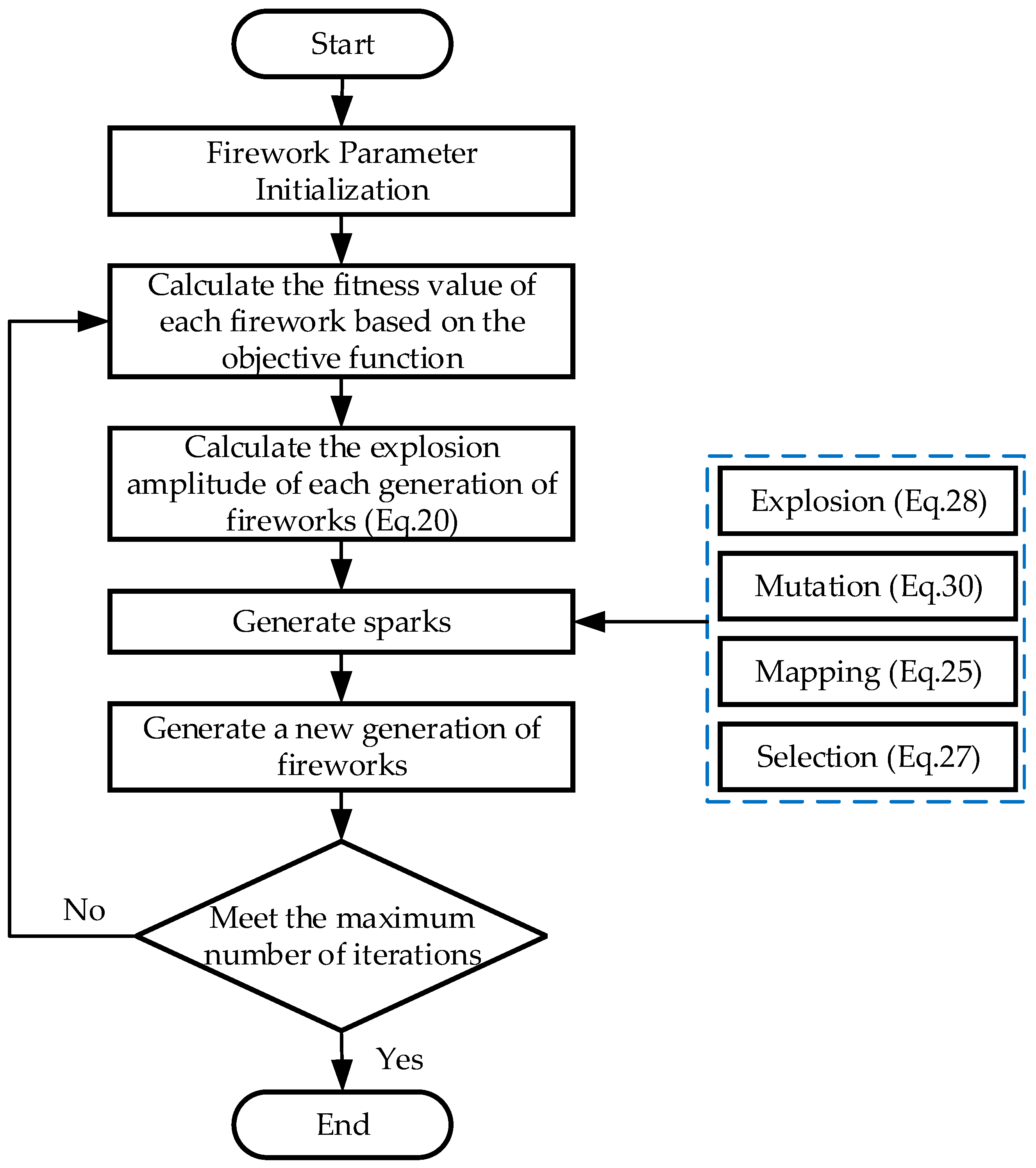
3.1. Modified Fireworks Algorithm
- (1)
- Fireworks Algorithm
- (2)
- Modified Fireworks Algorithm
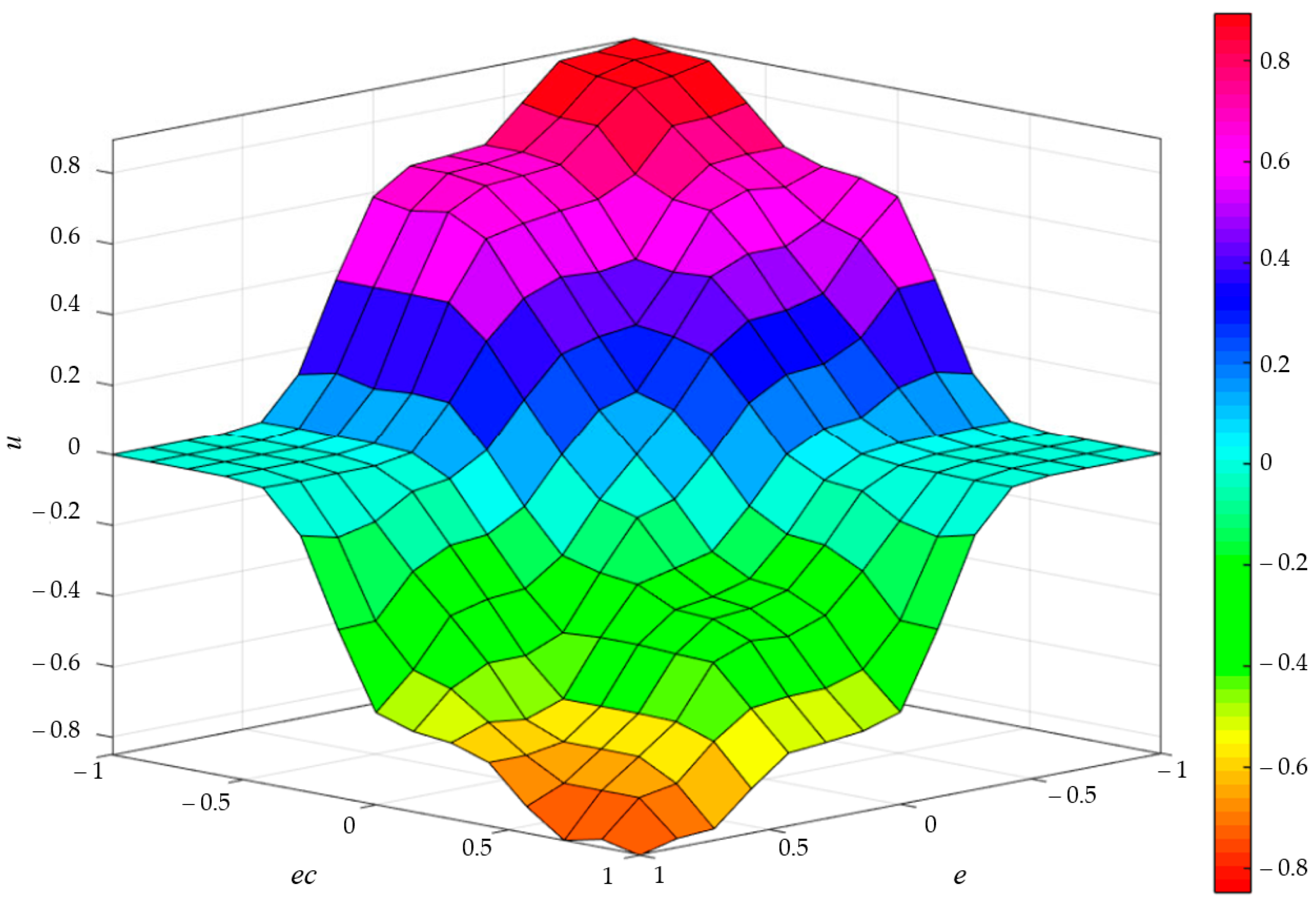
3.2. Fuzzy Logic Controller
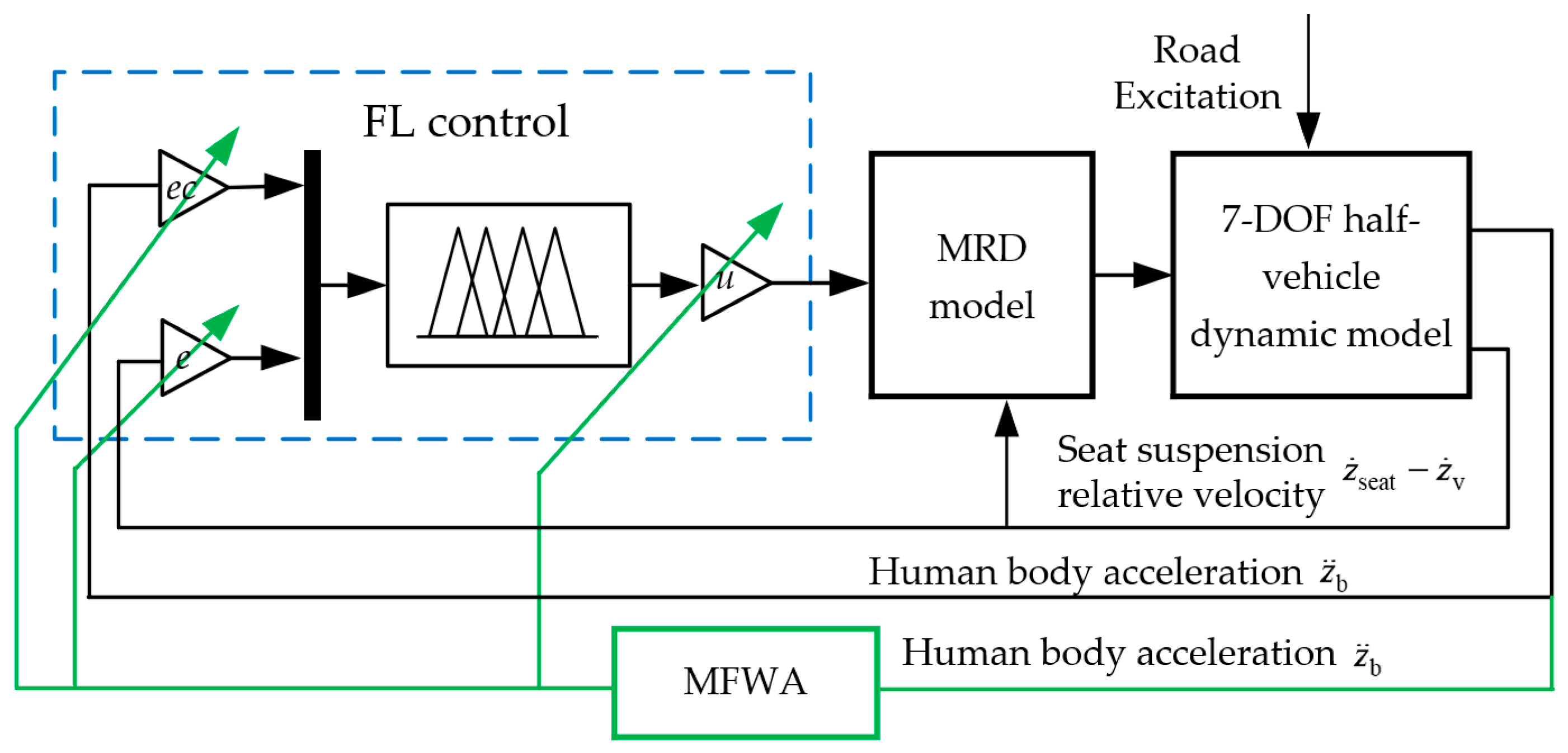
3.3. MFWA-FL CONTROL
4. Simulation Results and Analysis
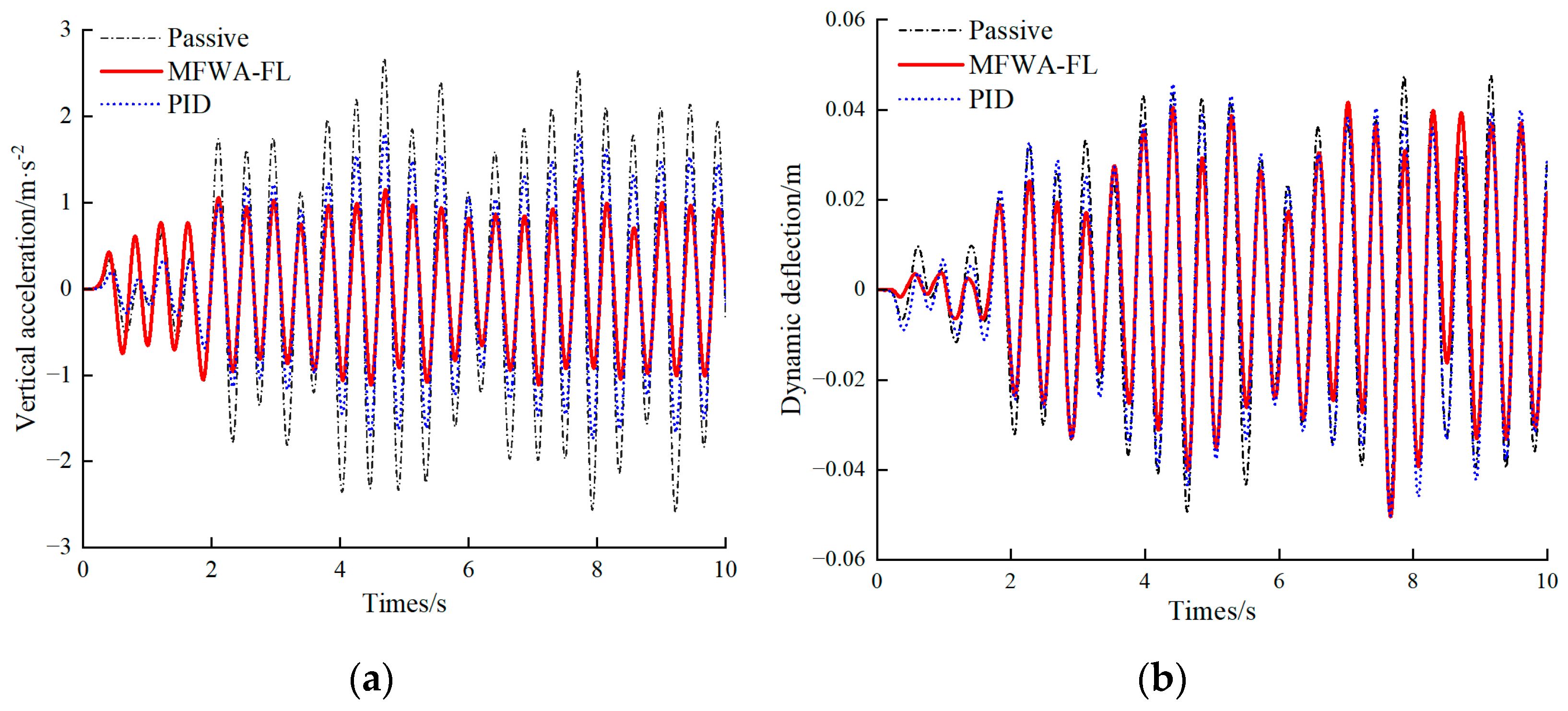
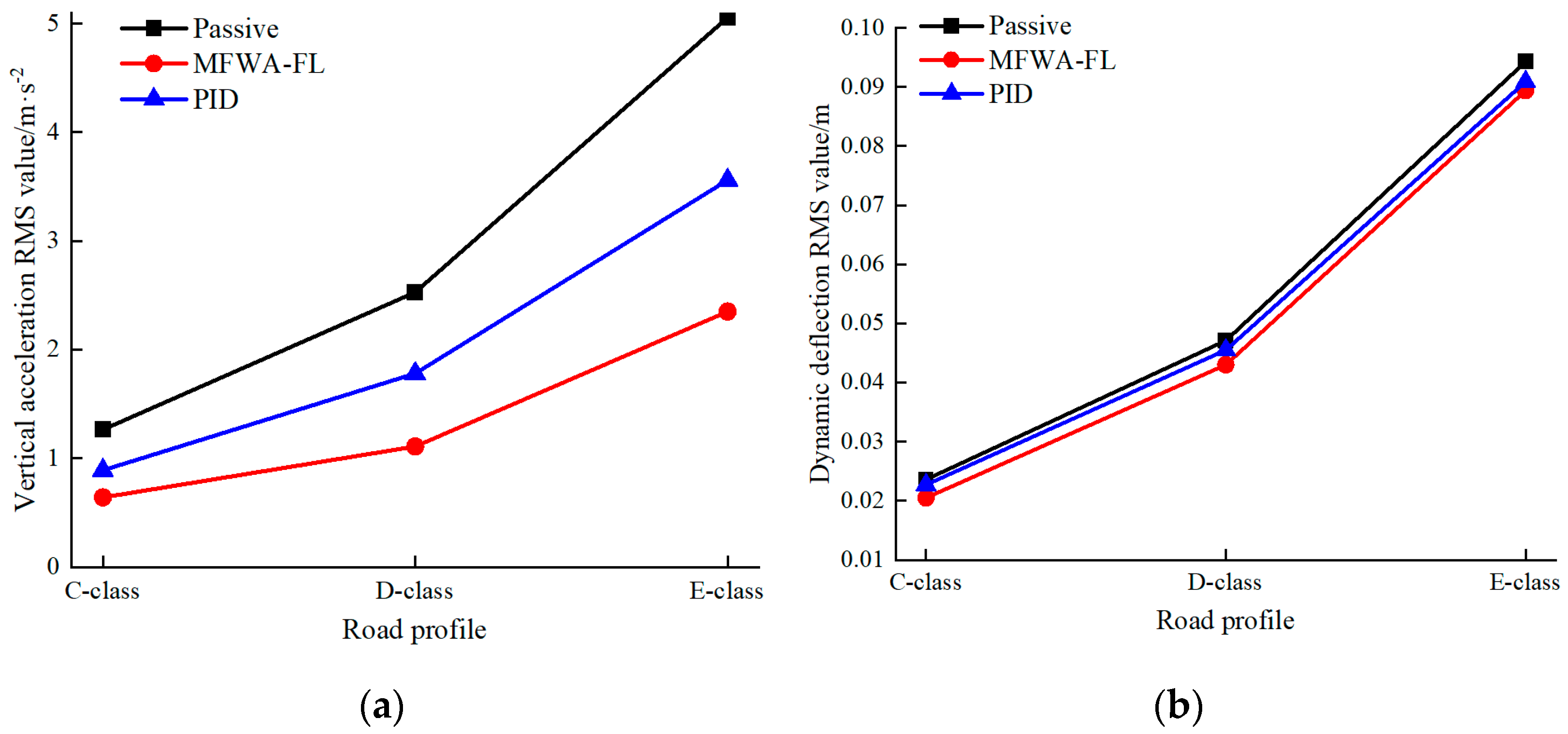
4.1. Random Road Excitation
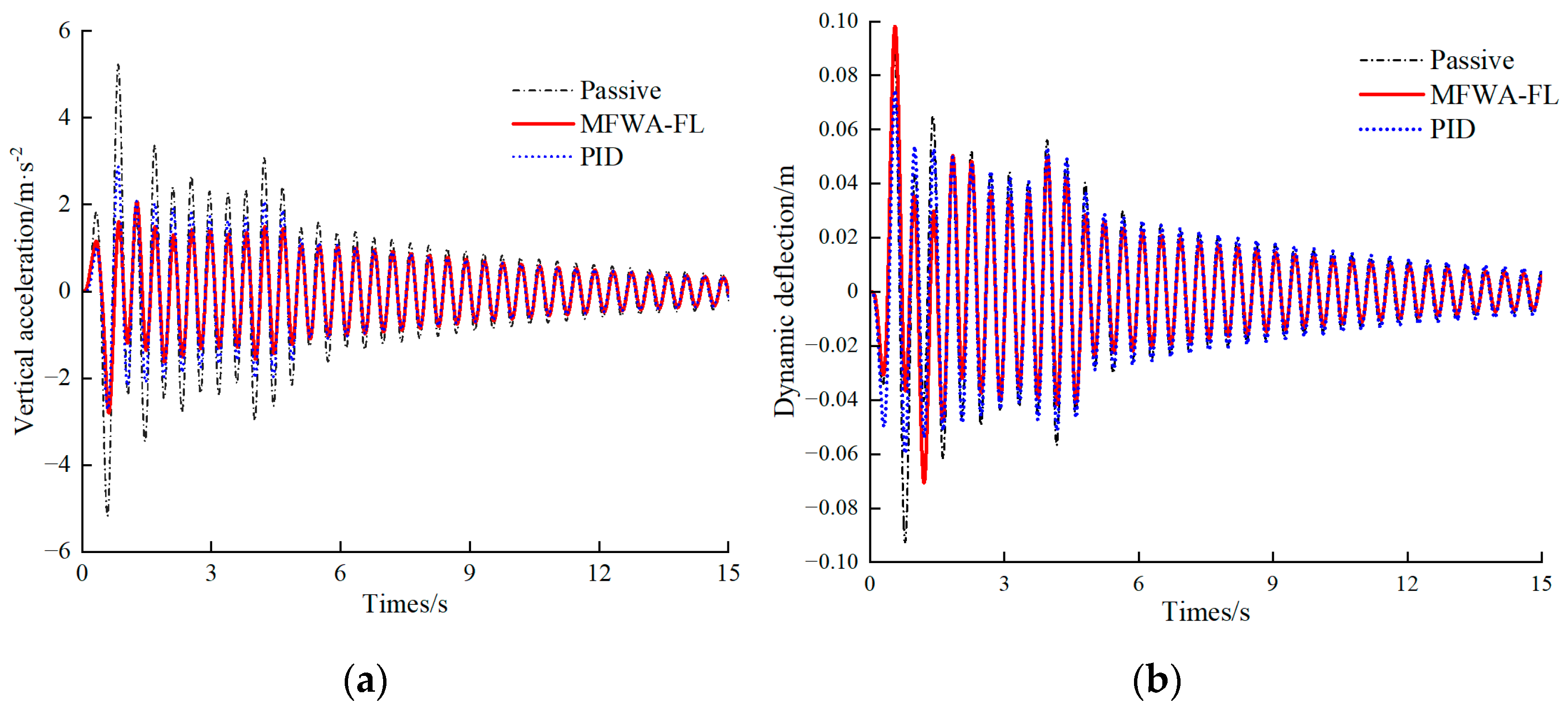
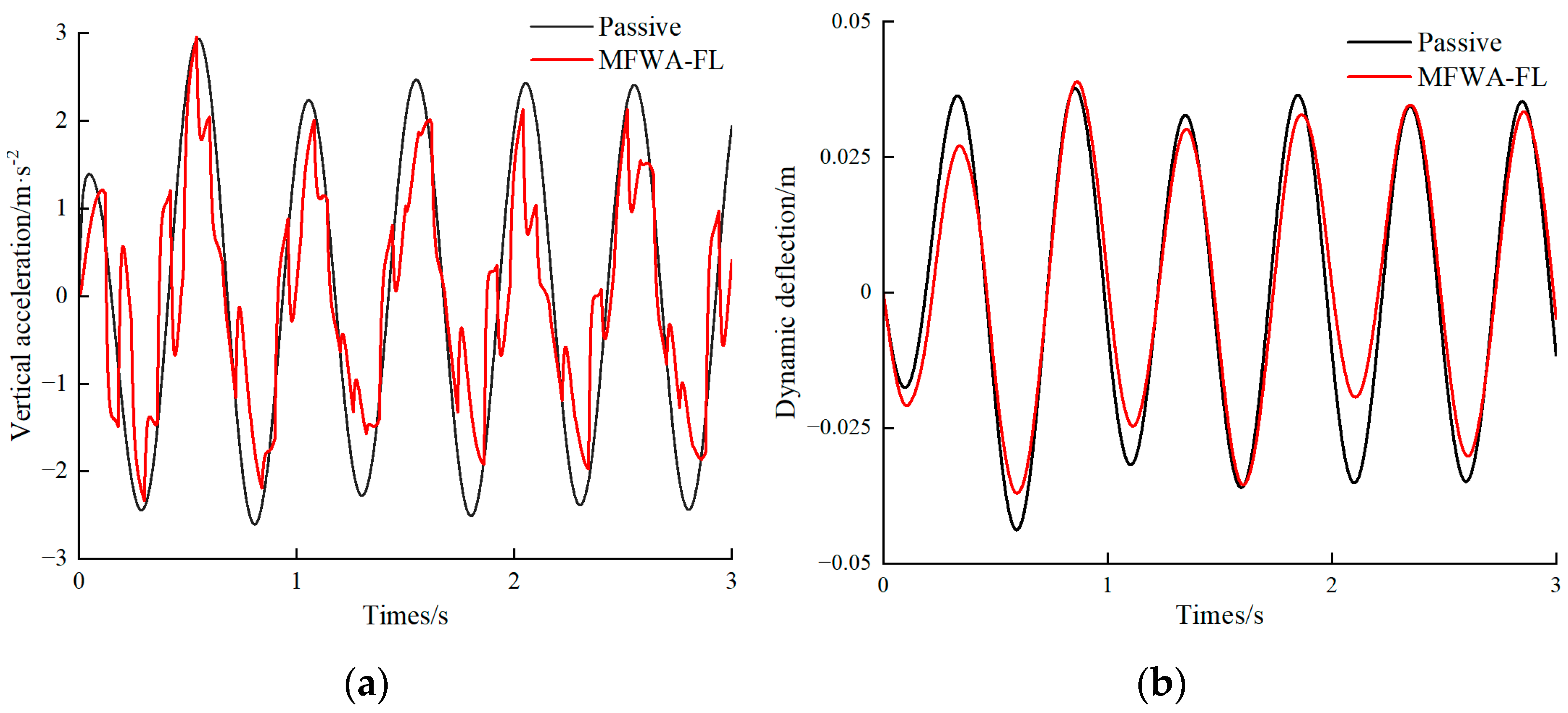
4.2. Bump Road Excitation
4.3. Experimental Validation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ABC | Artificial Bee Colony |
| ACO | Ant Colony Optimization |
| CSA | Cuckoo Search |
| ECU | Electronic Control Unit |
| FCCVs | Fuel cell commercial vehicles |
| FL | Fuzzy logic |
| FLC | Fuzzy logic controller |
| FWA | Fireworks Algorithm |
| GAs | Genetic Algorithms |
| HIL | Hardware in the loop |
| LQG | Linear Quadratic Gaussian |
| MFWA | Modified Fireworks Algorithm |
| MRD | Magnetorheological damper |
| MSE | Mean squared error |
| PID | Proportional–Integral–Derivative |
| PSO | Particle Swarm Optimization |
| 7-DOF | Seven-degree-of-freedom |
Appendix A
References
- Albatayneh, A.; Juaidi, A.; Jaradat, M.; Manzano-Agugliaro, F. Future of electric and hydrogen cars and trucks: An overview. Energies 2023, 16, 3230. [Google Scholar] [CrossRef]
- Jokela, T.; Kim, B.; Gao, B.; Wellers, M.; Peng, Z. A review of fuel cell technology for commercial vehicle applications. Int. J. Heavy Veh. Syst. 2021, 28, 650–678. [Google Scholar] [CrossRef]
- Kast, J.; Vijayagopal, R.; Gangloff, J.J.; Marcinkoski, J. Clean commercial transportation: Medium and heavy duty fuel cell electric trucks. Int. J. Hydrog. Energy 2017, 42, 4508–4517. [Google Scholar] [CrossRef]
- Togun, H.; Basem, A.; Abdulrazzaq, T.; Biswas, N.; Abed, A.M.; dhabab, J.M.; Chattopadhyay, A.; Slimi, K.; Paul, D.; Barmavatu, P.; et al. Development and comparative analysis between battery electric vehicles (BEV) and fuel cell electric vehicles (FCEV). Appl. Energy 2025, 388, 125726–125741. [Google Scholar] [CrossRef]
- Douadi, O.; Ravi, R.; Faqir, M.; Balasubramanian, D.; Kale, U.; Kilikevičius, A. A study on zero-emission vehicle technologies: Comparing hydrogen fuel cell and battery electric solutions for decarbonization of transportation. Therm. Sci. Eng. Prog. 2025, 66, 103990–104015. [Google Scholar] [CrossRef]
- Hebala, A.; Abdelkader, M.I.; Ibrahim, R.A. Comparative analysis of energy consumption and performance metrics in fuel cell, battery, and hybrid electric vehicles under varying wind and road conditions. Technologies 2025, 13, 150. [Google Scholar] [CrossRef]
- Li, Y.; Dai, L.; Guo, Z.; Chi, M. Carbody abnormal lateral vibration failure of high–speed train induced by the coupling factor of the wheel re–profiling method and excessive rail wear. Eng. Fail. Anal. 2024, 160, 108170–108186. [Google Scholar] [CrossRef]
- Metered, H.; Ibrahim, I.M. Vibration mitigation of commercial vehicle active tandem axle suspension system. SAE Int. J. Commer. Veh. 2022, 15, 275–288. [Google Scholar] [CrossRef]
- Sureshkumar, G.; Kumaraswamidhas, L.A.; Pham, D. Optimization of structural parameters through objective-evaluation of ride comfort in a heavy-duty commercial vehicle. Cogent Eng. 2020, 7, 1743408. [Google Scholar] [CrossRef]
- Lv, X.; Ji, Y.; Zhao, H.; Zhang, J.; Zhang, G.; Zhang, L. Research review of a vehicle energy-regenerative suspension system. Energies 2020, 13, 441. [Google Scholar] [CrossRef]
- Long, G.; Ding, F.; Zhang, N.; Zhang, J.; Qin, A. Regenerative active suspension system with residual energy for in-wheel motor driven electric vehicle. Appl. Energy 2020, 260, 114180–114197. [Google Scholar] [CrossRef]
- Atindana, V.A.; Xu, X.; Kwaku, N.J.; Akayeti, A.; Jiang, X. A novel semi-active control of an integrated chassis and seat quasi-zero stiffness suspension system for off-road vehicles. J. Vib. Control 2024, 30, 5536–5559. [Google Scholar] [CrossRef]
- Qiu, C.; Liu, X.; Shen, Y. Improvement of the vehicle seat suspension system incorporating the mechatronic inerter element. World Electr. Veh. J. 2023, 14, 29. [Google Scholar] [CrossRef]
- Zha, J.; Nguyen, V.; Su, B.; Jiao, R.; Ni, D. Performance of the seat suspension system using negative stiffness structure on improving the driver’s ride comfort. SAE Int. J. Veh. Dyn. Stab. NVH 2022, 6, 135–146. [Google Scholar] [CrossRef]
- Chen, X.; Wang, Z.; Shi, H.; Jiang, N.; Zhao, S.; Qiu, Y.; Liu, Q. Review of agricultural machinery seat semi-active suspension systems for ride comfort. Machines 2025, 13, 246. [Google Scholar] [CrossRef]
- Li, P.; Dong, X.; Ran, J.; Fei, Z.; Wu, L.; Xu, D. Performance evaluation of a novel semi-active absorption and isolation co-control strategy with magnetorheological seat suspension for commercial vehicle. Smart Mater. Struct. 2024, 33, 105016–105029. [Google Scholar] [CrossRef]
- Yan, S.; Sun, W.; Gao, H. Vibration suppression for motor-driven uncertain active suspensions with hard constraints and analysis of energy consumption. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 618–630. [Google Scholar] [CrossRef]
- Maciejewski, I.; Pecolt, S.; Blazejewski, A.; Jereczek, B.; Glowinski, S.; Krzyzynski, T. Energy harvesting effectiveness of an active horizontal seat suspension under random vibration of varying intensity. Mech. Syst. Signal Process. 2025, 237, 113000–113021. [Google Scholar] [CrossRef]
- Čerškus, A.; Šešok, N.; Bučinskas, V. Implementation of lookup tables for different optimization strategies of semi-active car suspension system. J. Vibroeng. 2025, 27, 497–524. [Google Scholar] [CrossRef]
- Feng, H.; Zhou, Y.; Li, S.; Cheng, G.; Ma, S.; Li, Y. Adaptive backstepping control with time-delay compensation for MR-damper-based vehicle seat suspension. Actuators 2025, 14, 178. [Google Scholar] [CrossRef]
- Shi, X.; Li, H.; Fu, K. Design of a direct current controller for magnetorheological semi-active suspensions with nonlinear constraints. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2024, 239, 3266–3277. [Google Scholar] [CrossRef]
- Ahn, D.V.; Kim, K.; Oh, J.; Seo, J.; Lee, J.W.; Park, Y.J. Optimal control of semi-active suspension for agricultural tractors using linear quadratic gaussian control. Sensors 2023, 23, 6474. [Google Scholar] [CrossRef]
- Ding, R.; Wang, P.; Li, A.; Wang, R.; Sun, D.; Xu, K. H∞ control and experimental study of MR semi-active suspension with actuator response delay. Metrol. Meas. Syst. 2024, 31, 797–812. [Google Scholar] [CrossRef]
- Samaroo, K.; Awan, A.W.; Islam, S. Semi-active suspension design for an in-wheel-motor-driven electric vehicle using a dynamic vibration-absorbing structure and PID-controlled magnetorheological damper. Machines 2025, 13, 47. [Google Scholar] [CrossRef]
- Zhang, K.; As’arry, A.; Zhu, L.; Hairuddin, A.A.; Hassan, M.K.; Md Zain, M.Z. Enhancing ride comfort of semi-active suspension through collaboration control using dung beetle optimizer optimized Fuzzy PID controller. Adv. Mech. Eng. 2025, 17, 1–14. [Google Scholar] [CrossRef]
- Sun, Y.; Qiang, H.; Wang, L.; Ji, W.; Mardani, A. A fuzzy-logic-system-based cooperative control for the multielectromagnets suspension system of maglev trains with experimental verification. IEEE Trans. Fuzzy Syst. 2023, 31, 3411–3422. [Google Scholar] [CrossRef]
- Fang, Y.; Bai, R. Adaptive fuzzy sensor failure compensation for active suspension systems with multiple sensor failures. Syst. Sci. Control Eng. 2021, 10, 229–240. [Google Scholar] [CrossRef]
- Hsiao, C.-Y.; Wang, Y.-H. Evaluation of ride comfort for active suspension system based on self-tuning fuzzy sliding mode control. Int. J. Control Autom. Syst. 2022, 20, 1131–1141. [Google Scholar] [CrossRef]
- Chen, L.; Wang, Q.; Hu, C. Adaptive fuzzy command filtered backstepping control for uncertain pure-feedback systems. ISA Trans. 2022, 129, 204–213. [Google Scholar] [CrossRef]
- Soudani, M.S.; Aouiche, A.; Ghanai, M.; Chafaa, K. Advanced active suspension control: A three-input fuzzy logic approach with jerk feedback for enhanced performance and robustness. Measurement 2024, 229, 114326–114347. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, D.; Mi, J. Fuzzy decision rule-based online classification algorithm in fuzzy formal decision contexts. IEEE Trans. Fuzzy Syst. 2023, 31, 3263–3277. [Google Scholar] [CrossRef]
- Tayyebi, S. An adaptive fuzzy sliding mode control under model uncertainties and disturbances: Second-order non-linear system. J. Braz. Soc. Mech. Sci. 2021, 43, 533–543. [Google Scholar] [CrossRef]
- Brás, G.; Silva, A.M.; Wanner, E.F. A genetic algorithm for rule extraction in fuzzy adaptive learning control networks. Genet. Program. Evolvable Mach. 2024, 25, 1–14. [Google Scholar] [CrossRef]
- Singh, N.; Sharma, A.K.; Tiwari, M.; Jasiński, M.; Leonowicz, Z.; Rusek, S.; Gono, R. Robust control of SEDCM by fuzzy-PSO. Electronics 2023, 12, 355. [Google Scholar] [CrossRef]
- Mao, J. Optimizing enterprise marketing project portfolios using fuzzy ant colony optimization. Int. J. Comput. Commun. Control 2024, 19, 1–14. [Google Scholar] [CrossRef]
- Nitish; Singh, A.K. Design of enhanced active suspension system with metaheuristic-based LQG control and ANFIS-based actuation. Mech. Based Des. Struct. Mach. 2025, 53, 6196–6227. [Google Scholar] [CrossRef]
- Florea, A.; Cofaru, I.; Patrausanu, A.; Cofaru, N.; Fiore, U. Superposition of populations in multi-objective evolutionary optimization of car suspensions. Eng. Appl. Artif. Intel. 2023, 126, 107026–107040. [Google Scholar] [CrossRef]
- Ma, K.; Zhang, Y.; Ren, C.; Chen, Y.; Zhou, P.; Chen, Y. Effect of time-delay feedback control on vehicle seat vibration reduction and suspension performance. J. Low Freq. Noise Vib. Act. Control 2022, 41, 1214–1233. [Google Scholar] [CrossRef]
- Abdul Zahra, A.K.; Abdalla, T.Y. Design of fuzzy super twisting sliding mode control scheme for unknown full vehicle active suspension systems using an artificial bee colony optimization algorithm. Asian J. Control 2020, 23, 1966–1981. [Google Scholar] [CrossRef]
- He, S.; Chen, K.; Xu, E.; Wang, W.; Jiang, Z.; Chiementin, X. Commercial vehicle ride comfort optimization based on intelligent algorithms and nonlinear damping. Shock Vib. 2019, 2019, 2973190. [Google Scholar] [CrossRef]
- Chen, Y.; Li, L.; Zhao, X.; Xiao, J.; Wu, Q.; Tan, Y. Simplified hybrid fireworks algorithm. Knowl.-Based Syst. 2019, 173, 128–139. [Google Scholar] [CrossRef]
- Wei, W.; Ouyang, H.; Zhang, C.; Li, S.; Fu, L.; Gao, L. Dynamic collaborative fireworks algorithm and its applications in robust pole assignment optimization. Appl Soft Comput 2021, 100, 106999–110717. [Google Scholar] [CrossRef]
- Lei, K.; Wu, Y. Dynamic multi-swarm competitive fireworks algorithm for global optimization and engineering constraint problems. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 2023, 31, 619–648. [Google Scholar] [CrossRef]
- Aleardi, M.; Pierini, S.; Sajeva, A. Assessing the performances of recent global search algorithms using analytic objective functions and seismic optimization problems. Geophysics 2019, 84, R767–R781. [Google Scholar] [CrossRef]
- Gholizadeh, S.; Milany, A. An improved fireworks algorithm for discrete sizing optimization of steel skeletal structures. Eng. Optim. 2018, 50, 1829–1849. [Google Scholar] [CrossRef]
- Wei, W.; Ouyang, H.; Li, S.; Zhao, X.; Zou, D. A modified fireworks algorithm with dynamic search interval based on closed-loop control. Math. Comput. Simul. 2022, 200, 329–360. [Google Scholar] [CrossRef]
- Yadav, A.M.; Tripathi, K.N.; Sharma, S.C. An enhanced multi-objective fireworks algorithm for task scheduling in fog computing environment. Clust. Comput. 2021, 25, 983–998. [Google Scholar] [CrossRef]
- Yang, C.; Liu, K.; Jiao, X.; Wang, W.; Chen, R.; You, S. An adaptive firework algorithm optimization-based intelligent energy management strategy for plug-in hybrid electric vehicles. Energy 2022, 239, 122120–122135. [Google Scholar] [CrossRef]
- Zhang, Y.; Luo, T.; Guo, J.; Li, X. Study on the dual-segment arctangent model of magnetorheological damper (MRD). Smart Mater. Struct. 2024, 34, 15024–015038. [Google Scholar] [CrossRef]
- Steven Diaz-Choque, C.; Felix-Herran, L.C.; Galluzzi, R.; Cespi, R.; Lozoya-Santos, J.D.J.; Ramirez-Mendoza, R.A. Adaptive control strategy for automotive magnetorheological dampers based on artificial neural networks. IEEE Access 2025, 13, 60455–60469. [Google Scholar] [CrossRef]
- Jin, Z.; Yang, F.; Rui, X.; Jiang, M.; Wang, J. Design, modeling, and vibration control of a damper based on magnetorheological fluid and elastomer. Actuators 2024, 13, 241. [Google Scholar] [CrossRef]
- El Majdoub, K.; Ghani, D.; Giri, F.; Chaoui, F.Z. Adaptive semi-active suspension of quarter-vehicle with magnetorheological damper. J. Dyn. Syst. Meas. Control 2015, 137, 021010. [Google Scholar] [CrossRef]
- Phu, D.X.; An, J.-H.; Choi, S.-B. A novel adaptive PID controller with application to vibration control of a semi-active vehicle seat suspension. Appl. Sci. 2017, 7, 1055. [Google Scholar] [CrossRef]
- Meng, X.; Tan, Y. Multi-guiding spark fireworks algorithm: Solving multimodal functions by multiple guiding sparks in fireworks algorithm. Swarm Evol. Comput. 2024, 85, 101458. [Google Scholar] [CrossRef]
- ISO 2631-1:1997; Mechanical vibration and shock — Evaluation of human exposure to whole-body vibration — Part 1: General requirements. International Organization for Standardization: Geneva, Switzerland, 1997.



| Parameters | Value | Description |
|---|---|---|
| mtf | 565 kg | Front axle mass |
| mtr1 | 495 kg | Middle axle mass |
| mtr2 | 495 kg | Rear axle mass |
| ms | 7800 kg | Vehicle body mass |
| mseat | 28 kg | Seat mass |
| mb | 55 kg | 5/7 human body mass |
| Is | 5885 kg·m2 | Vehicle body moment of inertia |
| Itr | 35 kg·m2 | Equalizer suspension moment of inertia |
| ktf | 1,000,000 N·m−1 | Front axle tire stiffness |
| ktr1 | 1,000,000 N·m−1 | Middle axle tire stiffness |
| ktr2 | 1,000,000 N·m−1 | Rear axle tire stiffness |
| ksf | 7,345,000 N·m−1 | Front suspension spring stiffness |
| ksr | 20,560,000 N·m−1 | Rear suspension spring stiffness |
| kseat | 4600 N·m−1 | Seat suspension spring stiffness |
| kc | 90,000 N·m−1 | Seat cushion stiffness |
| ctf | 1000 N·s·m−1 | Front axle tire damping |
| ctr1 | 1000 N·s·m−1 | Middle axle tire damping |
| ctr2 | 1000 N·s·m−1 | Rear axle tire damping |
| csf | 4564 N·s·m−1 | Front suspension damper damping |
| csr | 66,885 N·s·m−1 | Rear suspension damper damping |
| cc | 2500 N·s·m−1 | Seat cushion damping |
| lf | 2.318 m | Distance from front axle to vehicle body center of gravity |
| lr | 3.782 m | Distance from equalizer suspension center to vehicle body center of gravity |
| lr1 | 0.86 m | Distance from middle axle to equalizer suspension center |
| lr2 | 0.86 m | Distance from rear axle to equalizer suspension center |
| lb | 1.335 m | Distance from seat center to vehicle body center of gravity |
| Parameters | Value | Description |
|---|---|---|
| k0 | 0 N·m−1 | Linear spring stiffness |
| C0a | 990 N·s·m−1 | Viscous damping coefficient |
| C0b | 3095 N·s·m−1·V−1 | Viscous damping coefficient influenced by |
| αa | 545 N·m−1 | Stiffness of ω |
| αb | 620 N·m−1 | Stiffness of ω influenced by v |
| λ | 4 | Positive parameter of hysteresis loop |
| ρ | 48 | Positive parameter of hysteresis loop |
| β | 48 | Positive parameter of hysteresis loop |
| Parameter Name | Value | Parameter Name | Value |
|---|---|---|---|
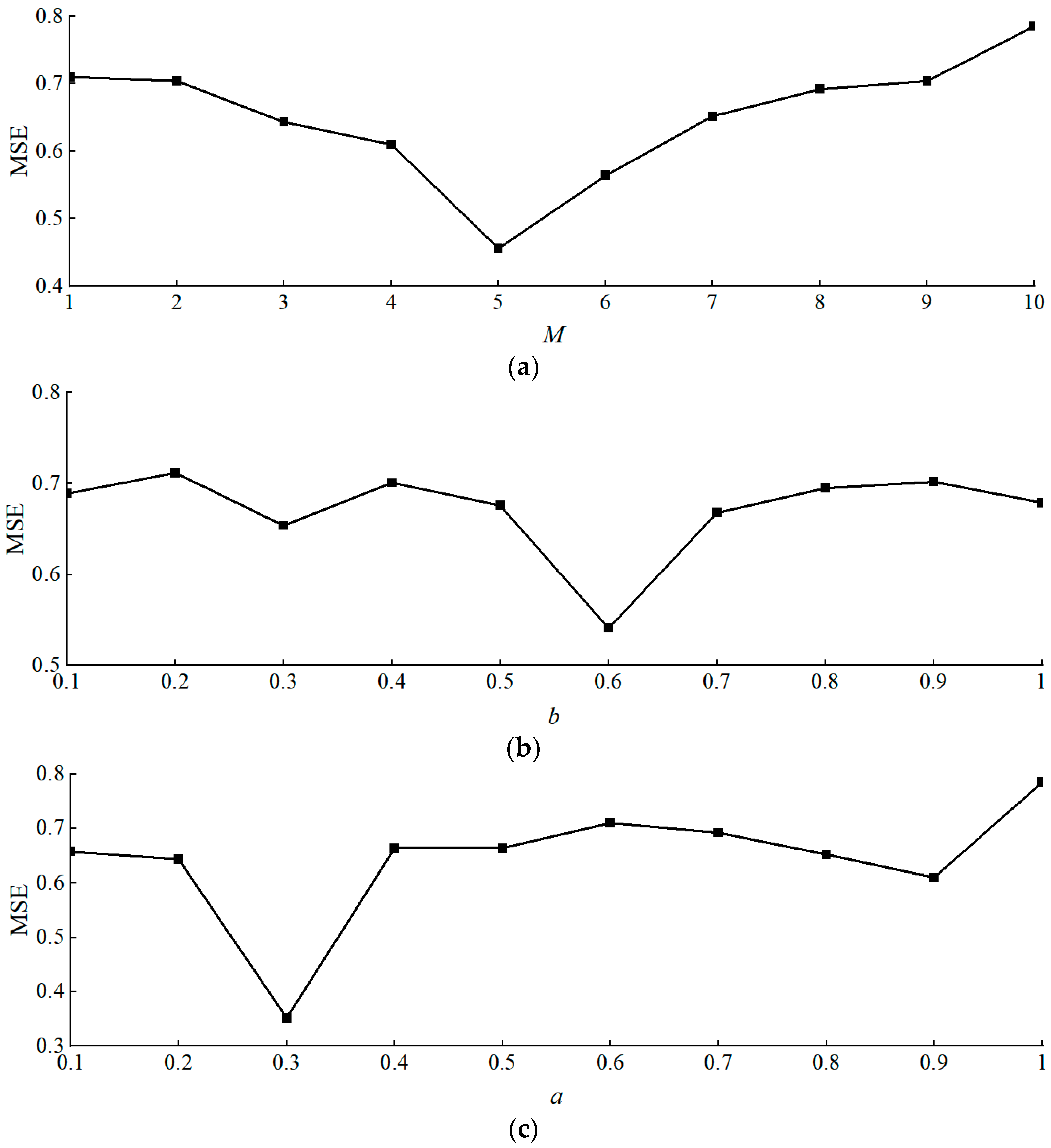
| Population, N | 50 | Spark number, M | 5 |
| Iteration, Tmax | 100 | Given constant, a | 0.3 |
| Dimension, k | 3 | Given constant, b | 0.6 |
| Variation spark number, B | 5 |
| u | ec | |||||||
|---|---|---|---|---|---|---|---|---|
| NB | NM | NS | ZE | PS | PM | PB | ||
| e | NB | PB | PB | PM | PM | ZE | ZE | ZE |
| NM | PB | PB | PM | PS | ZE | ZE | ZE | |
| NS | PM | PM | PS | PS | ZE | ZE | ZE | |
| ZE | PM | PM | PS | ZE | NS | NS | NM | |
| PS | ZE | ZE | ZE | NS | NS | NS | NM | |
| PM | ZE | ZE | ZE | NS | NM | NM | NB | |
| PB | ZE | ZE | ZE | NM | NM | NB | NB | |
| Index | Passive | MFWA-FL | PID |
|---|---|---|---|
| Vertical acceleration (m/s2) | 1.264 (benchmark) | 0.641 (49.29%) | 0.890 (29.59%) |
| Dynamic deflection (m) | 0.024 (benchmark) | 0.021 (12.50%) | 0.023 (4.17%) |
| Index | Passive | MFWA-FL | PID |
|---|---|---|---|
| Vertical acceleration (m/s2) | 0.925(benchmark) | 0.527(43.03%) | 0.631(31.78%) |
| Dynamic deflection (m) | 0.017(benchmark) | 0.015(11.76%) | 0.016(5.88%) |
| Index | Vertical acceleration (m/s2) | Dynamic Deflection (m) | ||
|---|---|---|---|---|
| Passive | MFWA-FL | Passive | MFWA-FL | |
| Experiment | 1.681 | 1.078 | 0.021 | 0.019 |
| simulation | 1.795 | 1.054 | 0.023 | 0.018 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, N.; Chen, X. Fuzzy Control with Modified Fireworks Algorithm for Fuel Cell Commercial Vehicle Seat Suspension. World Electr. Veh. J. 2025, 16, 585. https://doi.org/10.3390/wevj16100585
Jiang N, Chen X. Fuzzy Control with Modified Fireworks Algorithm for Fuel Cell Commercial Vehicle Seat Suspension. World Electric Vehicle Journal. 2025; 16(10):585. https://doi.org/10.3390/wevj16100585
Chicago/Turabian StyleJiang, Nannan, and Xiaoliang Chen. 2025. "Fuzzy Control with Modified Fireworks Algorithm for Fuel Cell Commercial Vehicle Seat Suspension" World Electric Vehicle Journal 16, no. 10: 585. https://doi.org/10.3390/wevj16100585
APA StyleJiang, N., & Chen, X. (2025). Fuzzy Control with Modified Fireworks Algorithm for Fuel Cell Commercial Vehicle Seat Suspension. World Electric Vehicle Journal, 16(10), 585. https://doi.org/10.3390/wevj16100585





