Study on Frequency-Response Optimization of Electric Vehicle Participation in Energy Storage Considering the Strong Uncertainty Model
Abstract
1. Introduction
2. Strong Uncertainty Model
2.1. Strong Uncertainty Factors
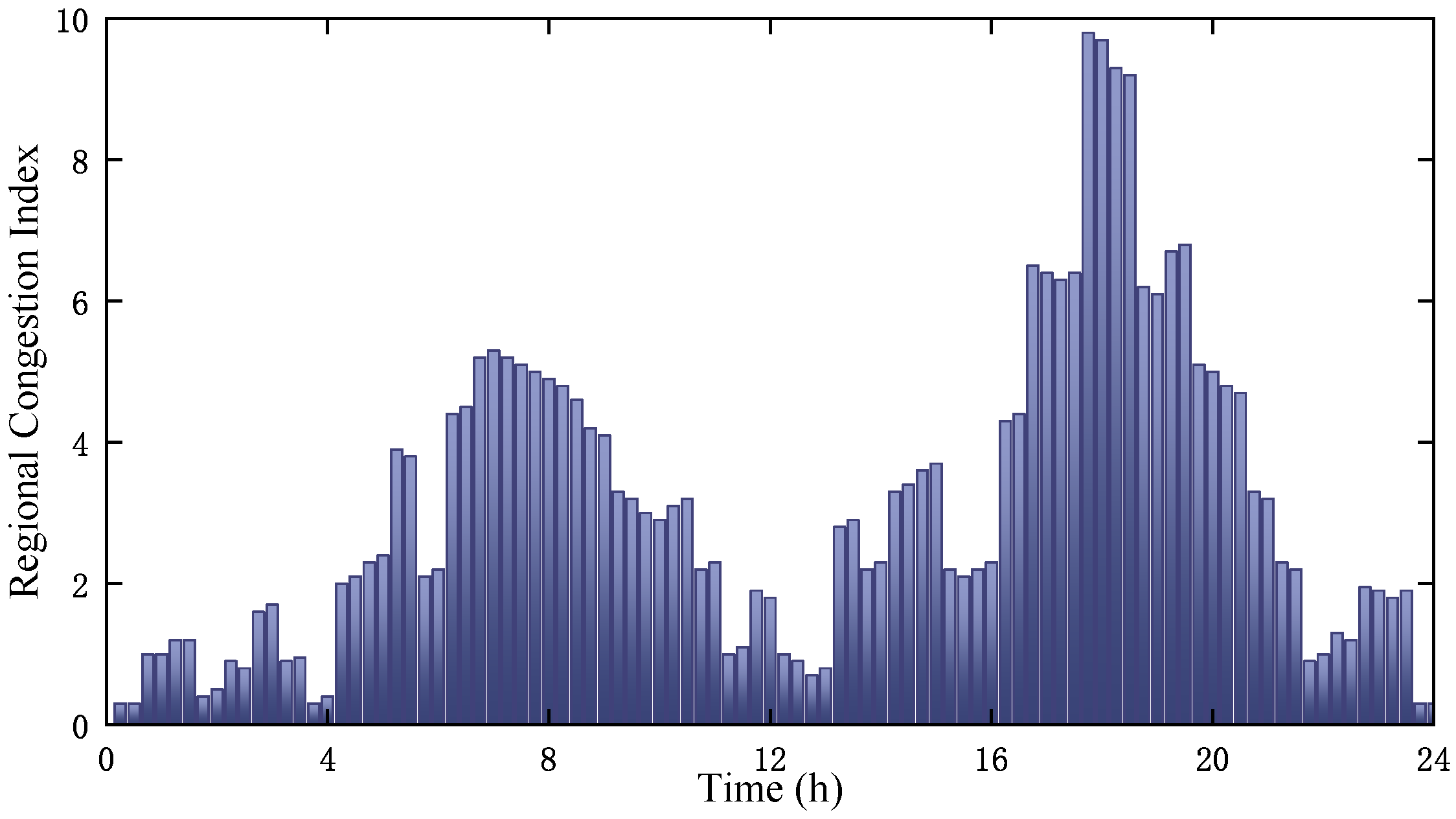
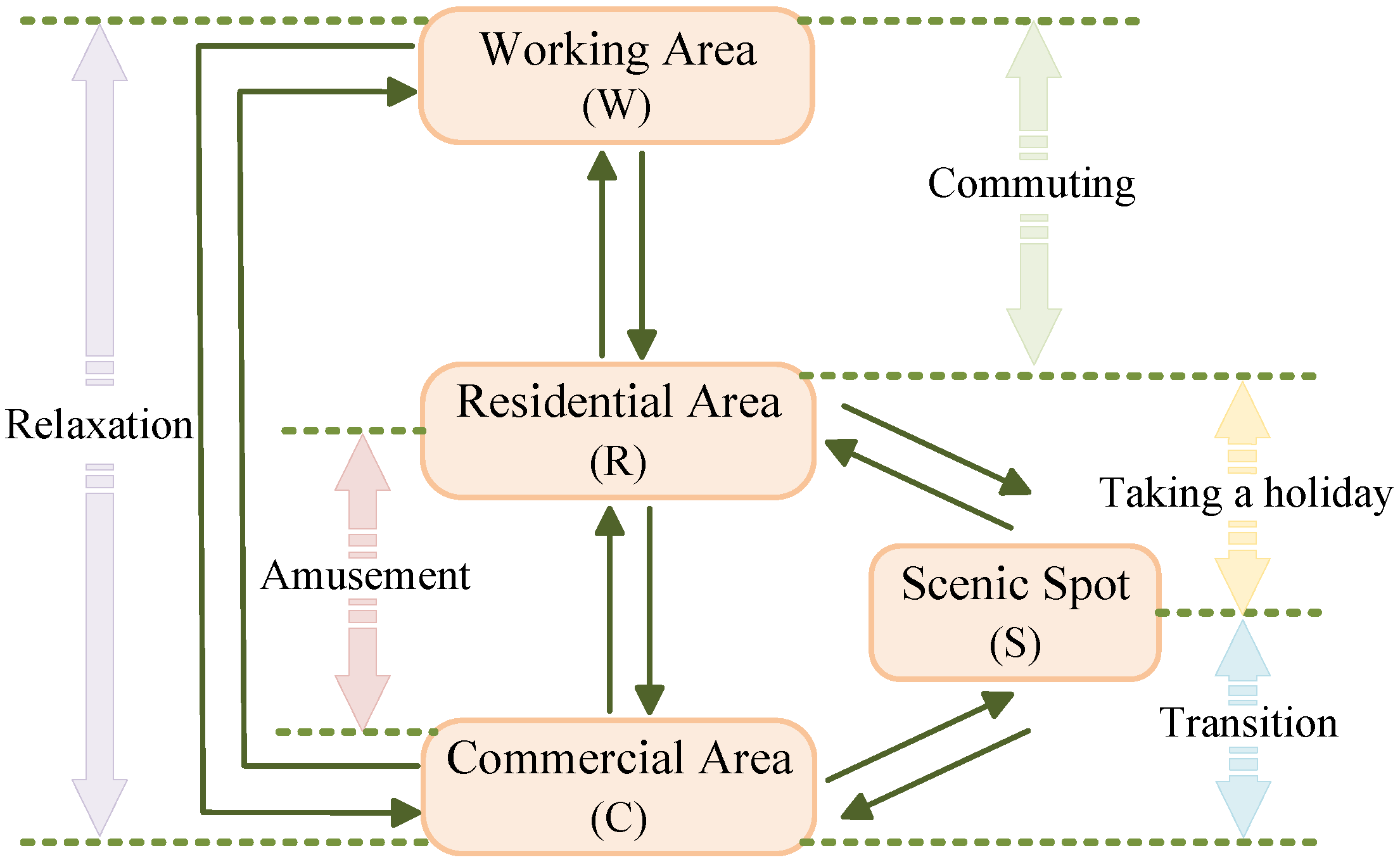
2.1.1. Temporal-Spatial Characteristics
2.1.2. Energy Storage Resources
2.1.3. Users’ Willingness to Respond
2.2. Access Probability
2.3. Trip Chain
3. Frequency Optimization Model
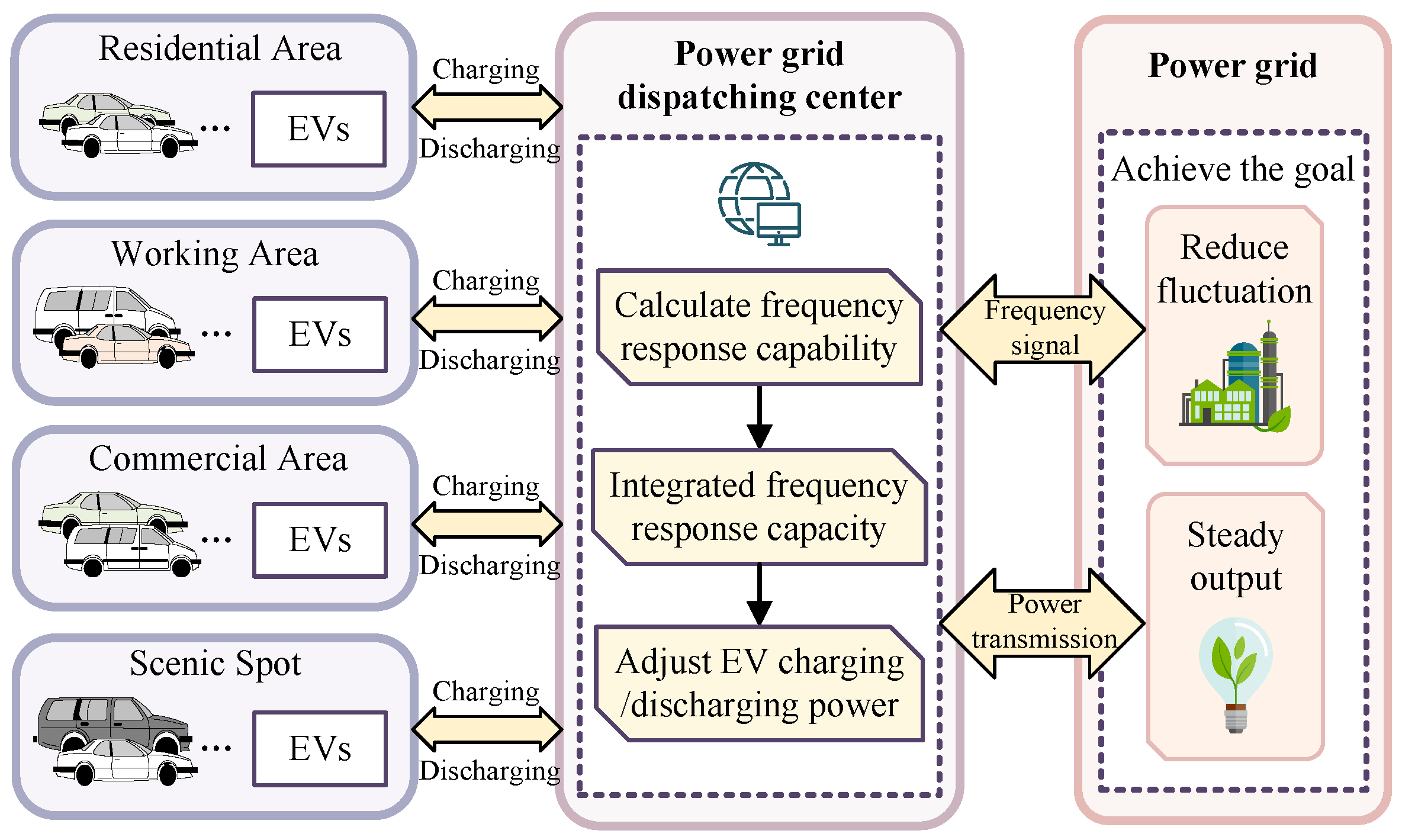
3.1. EV Participation in the Energy Storage Framework
3.2. EVs’ Frequency-Response Capability
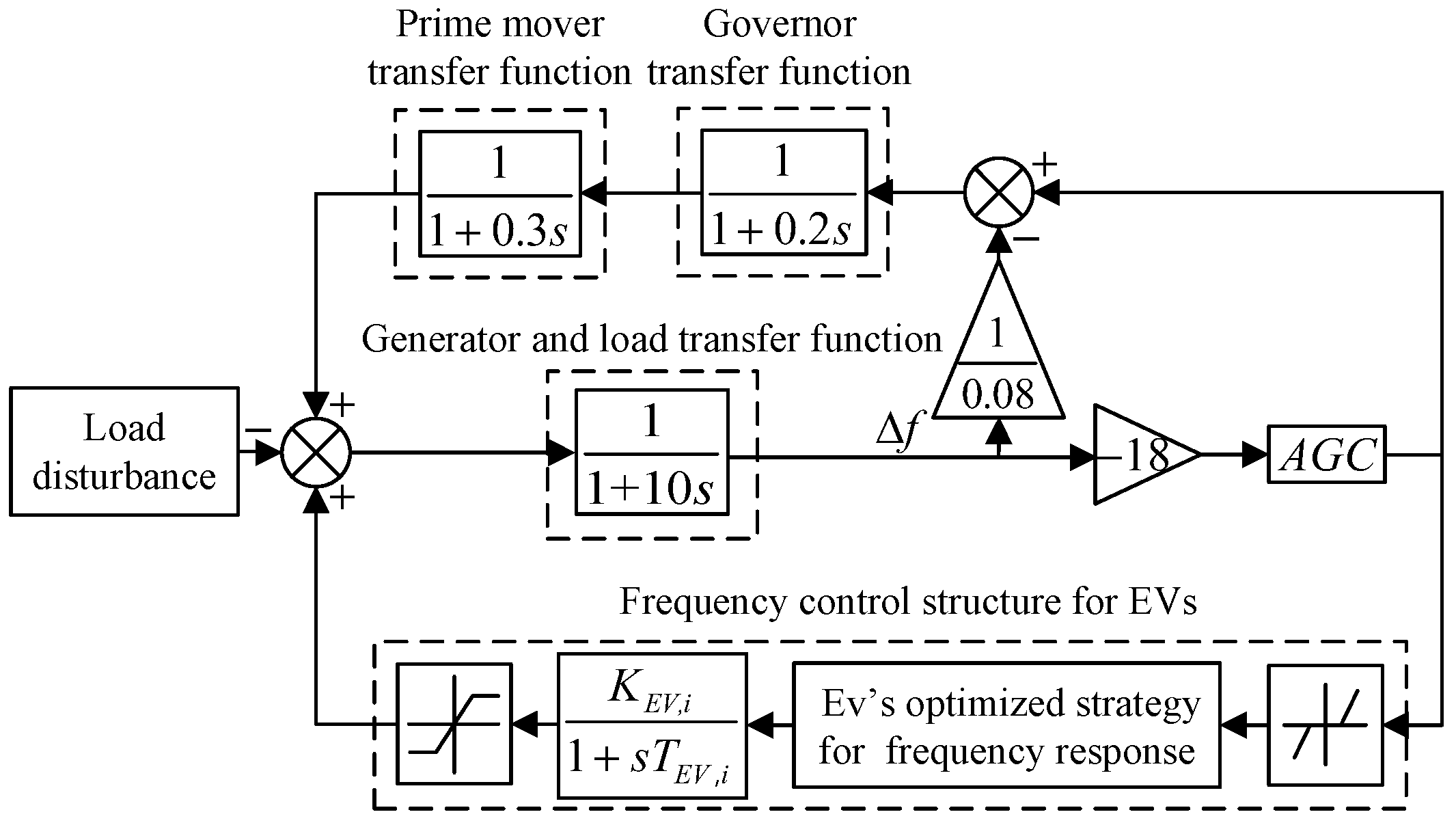
3.3. The Control Structure for Frequency Response
- The Monte Carlo method is used to extract the transfer state, trip time, driving time, and residence time of a single EV in one day. Calculate separately the SOC after arriving at each location.
- If , it indicates that the SOC of the EV has a surplus, allowing it to participate in energy storage. Then, continue to assess the user’s willingness to respond. Otherwise, it only meets the user’s original charging requirements and does not participate in frequency optimization after forced charging to satisfy the travel task’s needs.
- If , it means that users are willing to accept power grid regulation while participating in energy storage. The power grid dispatching center receives the signal of the frequency offset for EV output control. Otherwise, it only meets the user’s original charging requirements and they do not participate in frequency optimization.
- The grid dispatching center controls the time when the EV accesses the grid. If , the frequency is increased so the EV absorbs the excess active power of the grid by charging. If , the frequency is lowered so the EV provides active power for the grid by discharging. At the same time, the EV power is kept within the maximum charging power and the maximum discharging power . If the limit is exceeded, the power distribution is re-adjusted.
- According to the number of EV clusters accessing each site, the power for frequency response from all EVs is integrated to form the total adjustment power of the EV clusters.
4. Analysis and Application of Examples
4.1. Introduction of Examples
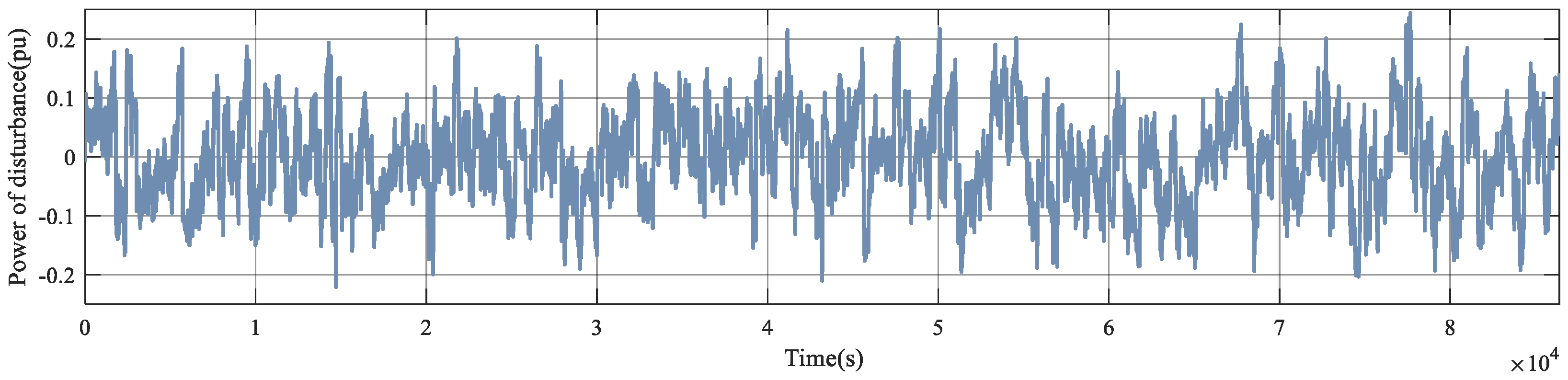
4.2. Analysis of Scenario Application
5. Conclusions
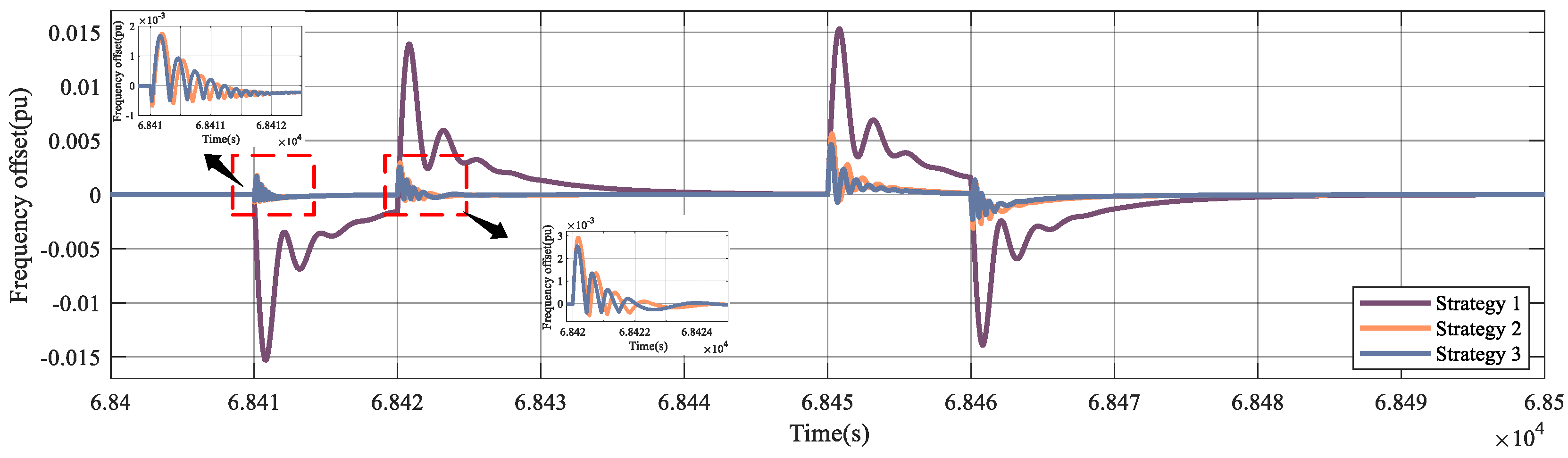
- Under various load disturbances, the model can dramatically lower the amplitude of the frequency fluctuations and shorten their correction times. In the scenario application, it is verified that the model substantially decreases the maximum frequency offset by 69.41% and the minimum frequency offset by 66.69%. This enhances the grid’s power supply quality, encourages the sale of electricity, and advances the creation of clean, low-carbon power systems.
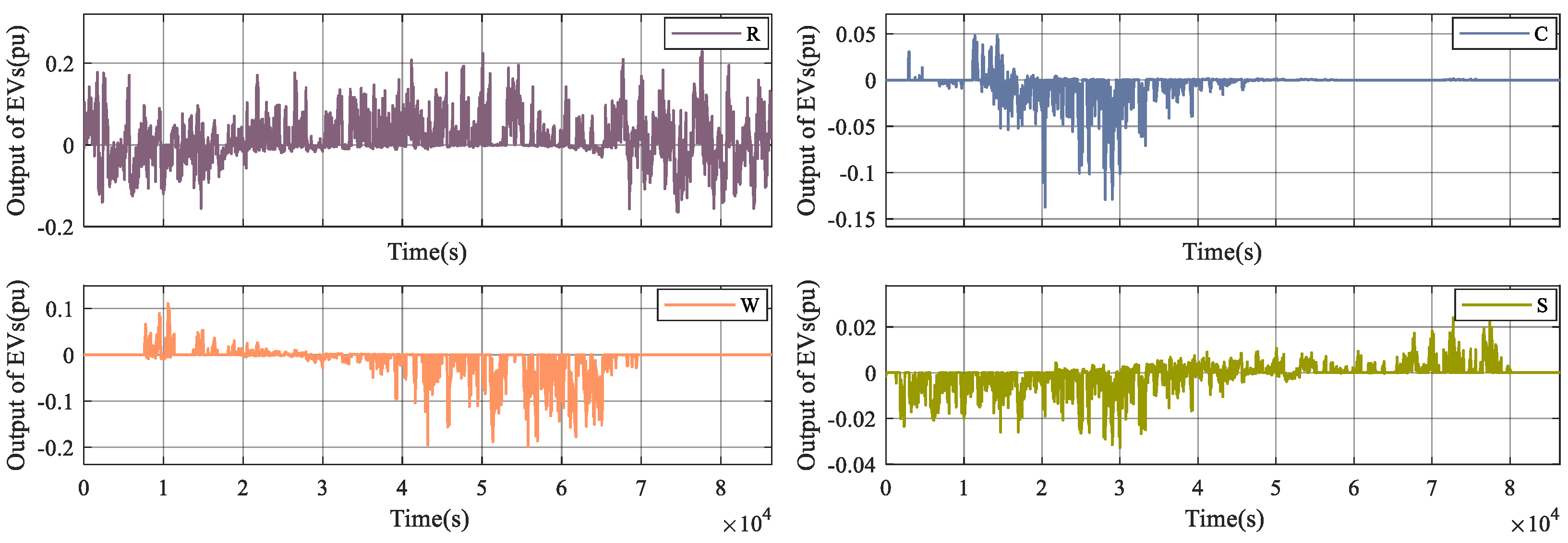
- EVs in various locations can optimize the frequency fluctuations of the power grid according to their own response capabilities in different time periods, and the output of EVs in residential areas is most evident under the travel rules.
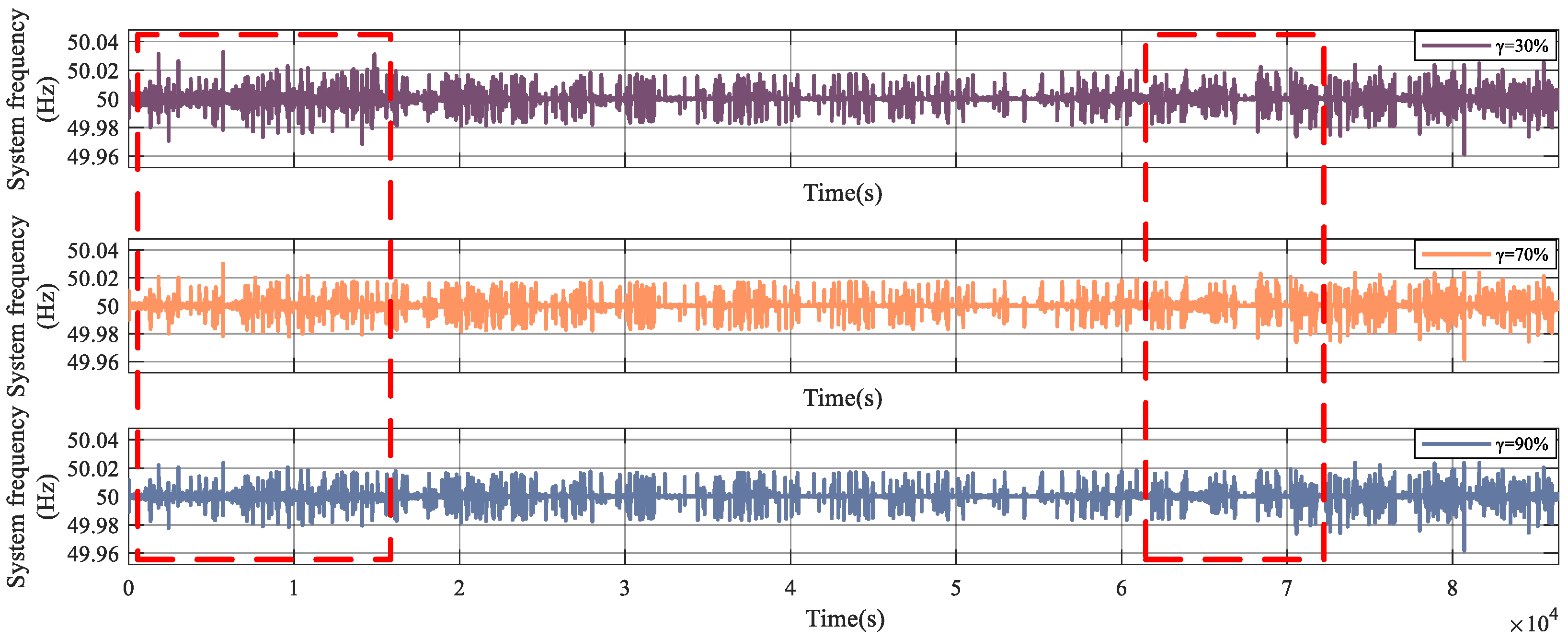
- When a larger proportion of users are willing to respond actively, the system frequency is more stable and the frequency adjustments are more effective.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dahmane, Y.; Chenouard, R.; Ghanes, M.; Ruiz, M. Optimal Electric Vehicle Fleet Charging Management with a Frequency Regulation Service. World Electr. Veh. J. 2023, 14, 152. [Google Scholar] [CrossRef]
- Yue, Y.; Xin, A.; Zhang, J.; Liu, Y. Orderly Charging and Discharging Group Scheduling Strategy for Electric Vehicles. Appl. Sci. 2023, 13, 13156. [Google Scholar] [CrossRef]
- Kushwaha, P.; Prakash, V.; Yamujala, S.; Bhakar, R. Fast frequency response constrained electric vehicle scheduling for low inertia power systems. J. Energy Storage 2023, 62, 106944. [Google Scholar] [CrossRef]
- Zhou, K.; Cheng, L.; Lu, X.; Wen, L. Scheduling model of electric vehicles charging considering inconvenience and dynamic electricity prices. Appl. Energy 2020, 276, 115455. [Google Scholar] [CrossRef]
- Thorat, R.; Bhatt, P. Electric vehicle participation for optimized load frequency control in a multi-area restructured power system. Int. J. Model. Simul. 2024, 1–14. [Google Scholar] [CrossRef]
- Jan, M.; Xin, A.; Abdelbaky, M.; Rehman, H.; Iqbal, S. Adaptive and fuzzy PI controllers design for frequency regulation of isolated microgrid integrated with electric vehicles. IEEE Access 2020, 8, 87621–87632. [Google Scholar] [CrossRef]
- Vishnoi, S.; Nikolovski, S.; Raju, M.; Kirar, M.; Rana, A.; Kumar, P. Frequency stabilization in an interconnected micro-grid using smell agent optimization algorithm-tuned classical controllers considering electric vehicles and wind turbines. Energies 2023, 16, 2913. [Google Scholar] [CrossRef]
- Yao, E.; Liu, T.; Lu, T.; Yang, Y. Optimization of electric vehicle scheduling with multiple vehicle types in public transport. Sustain. Cities Soc. 2020, 52, 101862. [Google Scholar] [CrossRef]
- Liu, T.; Wang, P.; Peng, Q.; Zhang, M.; Wang, T.; Meng, J. Operation-Area-Constrained Adaptive Primary Frequency Support Strategy for Electric Vehicle Clusters. J. Mod. Power Syst. Clean Energy 2023, 11, 1982–1994. [Google Scholar] [CrossRef]
- Qi, Y.; Huang, Q.; Yang, L.; Zhou, C.; Pan, C. Status update frequency optimization for In-vehicle LAN route based on deep Q-learning. Results Control Optim. 2022, 8, 100163. [Google Scholar] [CrossRef]
- Angelim, J.; Affonso, C. Effects of long-range electric vehicles on distribution system using probabilistic analysis. Int. J. Electr. Power Energy Syst. 2023, 147, 108868. [Google Scholar] [CrossRef]
- Niu, M.; Zhang, G.; Xiao, R.; Li, J. Frequency Security Assessment of Power System Under Random Excitation Based on the Time Beyond Security Range. In Proceedings of the 2023 5th Asia Energy and Electrical Engineering Symposium (AEEES), Chengdu, China, 23–26 March 2023; pp. 743–748. [Google Scholar]
- Ding, L.; Yang, J.; Ke, S.; Shi, X.; Fan, P.; Wang, H. A V2G power response model based on the prediction, evaluation, and correction of charging stations real-time frequency regulation capability. IET Gener. Transm. Distrib. 2024, 19, e13347. [Google Scholar] [CrossRef]
- Muhssin, M.; Obaid, Z.; Al-Anbarri, K.; Cipcigan, L.; Ajaweed, M. Local dynamic frequency response using domestic electric vehicles. Int. J. Electr. Power Energy Syst. 2021, 130, 106920. [Google Scholar] [CrossRef]
- Yang, Z.; Yang, F.; Hu, W.; Zhang, Z.; Zhou, X. Delay compensation control strategy for electric vehicle participating in frequency regulation based on MPC algorithm. Electronics 2022, 11, 2341. [Google Scholar] [CrossRef]
- Ahmad, P.; Choudhary, N.; Singh, N.; Singh, A. Primary frequency control by fuzzy-based participation controller for plug-in electric vehicles. Smart Sci. 2023, 11, 447–459. [Google Scholar] [CrossRef]
- Li, Z.; Ma, C. A temporal–spatial charging coordination scheme incorporating probability of EV charging availability. Appl. Energy 2022, 325, 119838. [Google Scholar] [CrossRef]
- Li, X.; Jenn, A. An integrated optimization platform for spatial-temporal modeling of electric vehicle charging infrastructure. Transp. Res. Part D Transp. Environ. 2022, 104, 103177. [Google Scholar] [CrossRef]
- Ge, X.; Shi, L.; Fu, Y.; Muyeen, S.; Zhang, Z.; He, H. Data-driven spatial-temporal prediction of electric vehicle load profile considering charging behavior. Electr. Power Syst. Res. 2020, 187, 106469. [Google Scholar] [CrossRef]
- Ma, C.; Zhou, J.; Xu, X.; Xu, J. Evolution regularity mining and gating control method of urban recurrent traffic congestion: A literature review. Swarm Evol. Comput. 2020, 2020, 5261580. [Google Scholar] [CrossRef]
- Shankar, R.; Marco, J. Method for estimating the energy consumption of electric vehicles and plug-in hybrid electric vehicles under real-world driving conditions. IET Intell. Transp. Syst. 2013, 7, 138–150. [Google Scholar] [CrossRef]
- Mangipinto, A.; Lombardi, F.; Sanvito, F.; Pavičević, M.; Quoilin, S.; Colombo, E. Impact of mass-scale deployment of electric vehicles and benefits of smart charging across all European countries. Appl. Energy 2022, 312, 118676. [Google Scholar] [CrossRef]
- Cai, L.; Zhang, Q.; Dai, N.; Xu, Q.; Gao, L.; Shang, B.; Xiang, L.; Chen, H. Optimization of Control Strategy for Orderly Charging of Electric Vehicles in Mountainous Cities. World Electr. Veh. J. 2022, 13, 195. [Google Scholar] [CrossRef]
- Molloy, J.; Schatzmann, T.; Schoeman, B.; Tchervenkov, C.; Hintermann, B.; Axhausen, K. Observed impacts of the Covid-19 first wave on travel behaviour in Switzerland based on a large GPS panel. Transp. Policy 2021, 104, 43–51. [Google Scholar] [CrossRef]
- Liu, X.; Qiao, S.; Liu, Z. A survey on load frequency control of multi-area power systems: Recent challenges and Strategies. Energies 2023, 16, 2323. [Google Scholar] [CrossRef]
- Correia, A.; Moura, P.; Almeida, A. Technical and Economic Assessment of Battery Storage and Vehicle-to-Grid Systems in Building Microgrids. Energies 2022, 15, 8905. [Google Scholar] [CrossRef]
- Shangguan, X.; Zhang, C.; He, Y.; Jin, L.; Jiang, L.; Spencer, J. Robust load frequency control for power system considering transmission delay and sampling period. IEEE Trans. Ind. Inform. 2020, 17, 5292–5303. [Google Scholar] [CrossRef]
- Guo, J. Application of a novel adaptive sliding mode control method to the load frequency control. Eur. J. Control 2021, 57, 172–178. [Google Scholar] [CrossRef]
- Li, B.; Chen, F.; Jiang, P.; Ren, J.; Liu, J.; Song, Z. Study on structure evolution features of different rank coals under shock load. Coal Sci. Technol. 2021, 49, 217–227. [Google Scholar]
- Kang, S.; Liu, T.; Liu, H.; Hu, Y.; Hou, X. Dynamic analysis and optimal control of stochastic information cross-dissemination and variation model with random parametric perturbations. PLoS ONE 2024, 19, e0303300. [Google Scholar] [CrossRef]
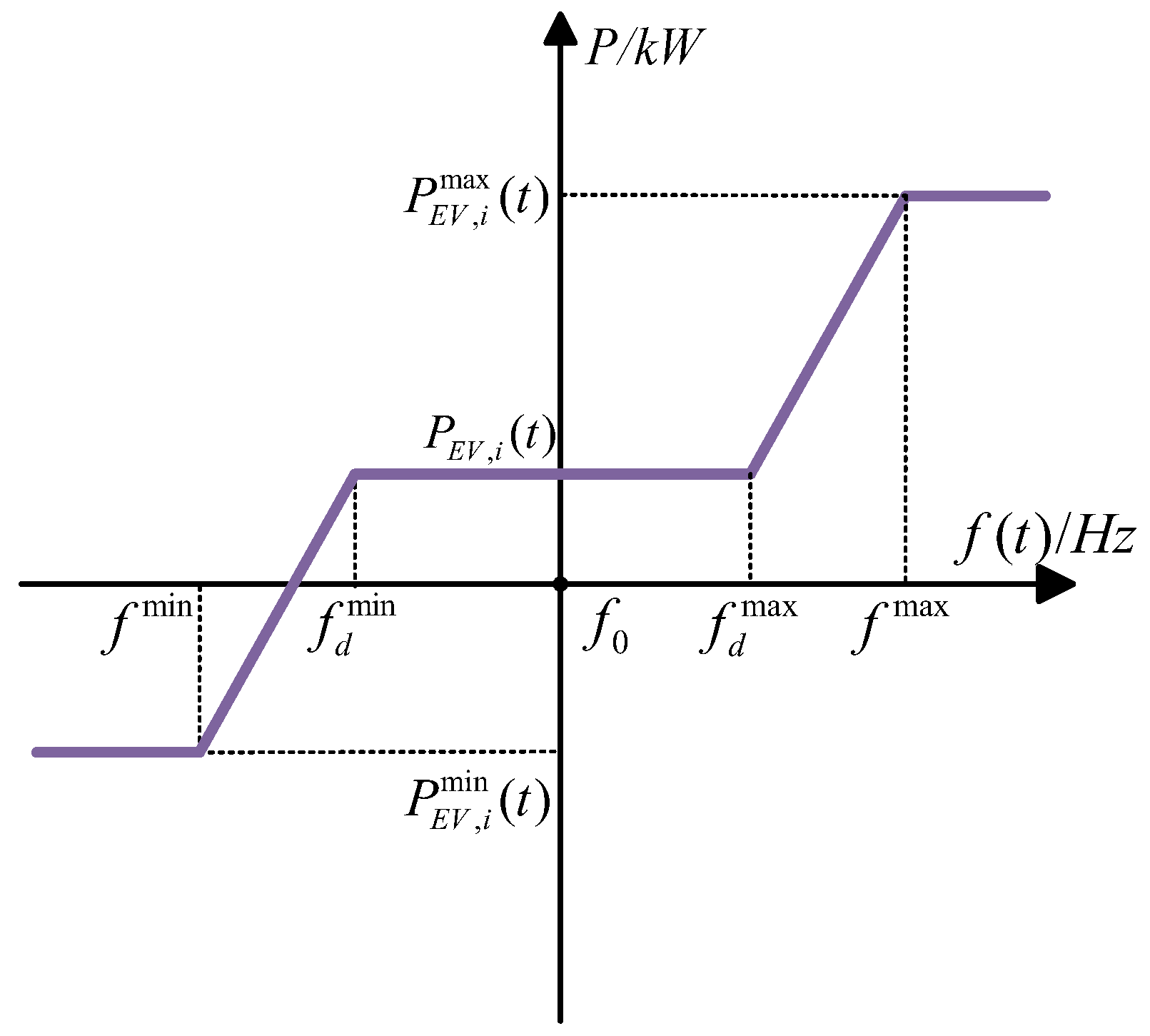



| Characteristic Quantity | Common Distribution Rule | Parameter Value |
|---|---|---|
| First trip time | Normal distribution | N(8.04,1.74) |
| Driving time | Logarithmic normal distribution | LN(1.04,0.74) |
| Residence time of R | Weibull distribution | W(195.789,1.153) |
| Residence time of W | Generalized extreme value distribution | GEV(438.45,164.51,−0.234) |
| Residence time of C/S | Generalized extreme value distribution | GEV(68.52,41.76,0.657) |
| Traffic Index | Congestion Condition | Coefficient of Velocity Influence |
|---|---|---|
| [0,2] | Unblocked | 1 |
| [2,4] | Basic unblocked | 0.67 |
| [4,6] | Light congestion | 0.56 |
| [6,8] | Moderate congestion | 0.5 |
| [8,10] | Heavy congestion | 0.28 |
| Transfer State | State 1 | State 2 | State 3 |
|---|---|---|---|
| Transition probability |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| U(30,85) | U(0.7,0.9) | ||
| U(0.11,0.21) | 0.9 | ||
| 10 | 0.2 | ||
| 7 | 0.7 | ||
| 0.35 | U(0.94,0.98) |
| Kind of Load Disturbance | Strategy | Rise Time/s | Overshoot/pu | Setting Time/s |
|---|---|---|---|---|
| Step load disturbance | 1 | 0.51 | 0.01531 | 26 |
| 2 | 0.083 | 0.00180 | 9 | |
| 3 | 0.073 | 0.00174 | 8 | |
| Shock load disturbance | 1 | 0.48 | 0.01391 | 22 |
| 2 | 0.12 | 0.00305 | 8 | |
| 3 | 0.098 | 0.00265 | 7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, L.; Yang, C.; Li, J.; Liu, Y.; Yan, J.; Zou, X. Study on Frequency-Response Optimization of Electric Vehicle Participation in Energy Storage Considering the Strong Uncertainty Model. World Electr. Veh. J. 2025, 16, 35. https://doi.org/10.3390/wevj16010035
Cai L, Yang C, Li J, Liu Y, Yan J, Zou X. Study on Frequency-Response Optimization of Electric Vehicle Participation in Energy Storage Considering the Strong Uncertainty Model. World Electric Vehicle Journal. 2025; 16(1):35. https://doi.org/10.3390/wevj16010035
Chicago/Turabian StyleCai, Li, Chenxi Yang, Junting Li, Yuhang Liu, Juan Yan, and Xiaojiang Zou. 2025. "Study on Frequency-Response Optimization of Electric Vehicle Participation in Energy Storage Considering the Strong Uncertainty Model" World Electric Vehicle Journal 16, no. 1: 35. https://doi.org/10.3390/wevj16010035
APA StyleCai, L., Yang, C., Li, J., Liu, Y., Yan, J., & Zou, X. (2025). Study on Frequency-Response Optimization of Electric Vehicle Participation in Energy Storage Considering the Strong Uncertainty Model. World Electric Vehicle Journal, 16(1), 35. https://doi.org/10.3390/wevj16010035






