Abstract
The increasing adoption of batteries in a variety of applications has highlighted the necessity of accurate parameter identification and effective modeling, especially for lithium-ion batteries, which are preferred due to their high power and energy densities. This paper proposes a comprehensive framework using the Levenberg–Marquardt algorithm (LMA) for validating and identifying lithium-ion battery model parameters to improve the accuracy of state of charge (SOC) estimations, using only discharging measurements in the N-order Thevenin equivalent circuit model, thereby increasing computational efficiency. The framework encompasses two key stages: model parameter identification and model verification. This framework is validated using experimental measurements on the INR 18650-20R battery, produced by Samsung SDI Co., Ltd. (Suwon, Republic of Korea), conducted by the Center for Advanced Life Cycle Engineering (CALCE) battery group at the University of Maryland. The proposed framework demonstrates robustness and accuracy. The results indicate that optimization using only the discharging data suffices for accurate parameter estimation. In addition, it demonstrates excellent agreement with the experimental measurements. The research underscores the effectiveness of the proposed framework in enhancing SOC estimation accuracy, thus contributing significantly to the reliable performance and longevity of lithium-ion batteries in practical applications.
1. Introduction
Lithium-ion batteries (LIBs) are considered the cornerstone of modern-world technology, as they are characterized by high energy and power density, efficiency, a long lifespan, low self-discharge, and a fast charging capability, and are relatively lightweight [1,2,3]. These attributes make LIBs essential for a variety of applications, including mobile devices, renewable energy storage, and electric vehicles [4,5]. As technology advances, the importance of accurately simulating and modeling these batteries becomes evident. However, the development of precise physical models that accurately capture the intricate internal static and dynamic processes of LIBs is a challenging task. In practical applications, the effectiveness of battery management systems (BMSs) heavily relies on the accuracy of battery models to monitor SOC and predict state of health (SOH), as these critical states are usually immeasurable and must be estimated from model-based algorithms [6].
To enhance the resilience and safety of electric vehicles (EVs), it is imperative to consider the properties of lithium-ion batteries. Accurately identifying the model parameters of these batteries can significantly improve the effectiveness of battery management systems by facilitating condition monitoring and fault diagnosis. Battery models are categorized into the following three types, each of which will be discussed in detail below: black-box models [7], equivalent circuit models [8], and electrochemical models [9,10]. Each category underpins both theoretical analysis and practical application, thereby facilitating the development of advanced battery management systems [11].
The electrochemical model provides an in-depth understanding of the internal reaction mechanisms of batteries from an electrochemical standpoint, highlighting the significance of its parameters. Despite its detailed accuracy, the model’s complexity and the large number of parameters make it challenging to apply in electric vehicle simulations or battery management systems, especially with varying battery materials [12].
Recent advances in machine learning (ML) and data-driven techniques have significantly impacted various electrical engineering applications, including model parameters calibration [13,14,15], anomaly detection [16,17], oscillation localization [18,19], spoofing detection [20], and SOC estimation across various operational states [21]. By utilizing neural networks (NNs), the black-box model effectively addresses the high nonlinearity of internal parameters in lithium-ion batteries during reactions, capitalizing on the networks’ robust self-learning abilities. However, the model’s accuracy is closely tied to the quality and availability of training data, which limits its adaptability [22,23].
The equivalent circuit model (ECM) effectively describes the voltage characteristics of lithium-ion batteries during charge and discharge cycles by modeling the battery as a circuit configuration, with components including resistors, voltage sources, and Resistor Capacitor (RC) networks, thereby capturing the battery’s dynamic and static properties. This method emphasizes characteristics, like open circuit voltage, and internal resistances sidestepping the intricate internal electrochemical examinations needed in alternative models [24,25]. The ECM distinguishes from electrochemical and data-driven models by offering distinct advantages: it is flexible in several battery types, can be represented mathematically, and its parameters are easier to identify than for other models [26]. The ECM is categorized into two main types: fractional order models and integer order models [27]. Integer order models encompass various configurations, including the Rint model [28], the Thevenin model [29], the Partnership for a New Generation of Vehicle (PNGV) model [30], and multi-order models [31].
Different studies have systematically explored parameter identification for lithium-ion batteries, with the different optimization methodologies broadly categorized into four categories [32]. The first category is meta-heuristic optimization methods, such as the genetic algorithm and particle swarm optimization, which have been widely used for the identification of parameters in battery modeling due to their flexibility and robustness. However, these methods require high levels of computational power and, in most cases, their convergence rate is comparatively slow [33,34]. In contrast, least squares methods are preferred due to their simplicity, efficiency, and fast convergence, which is suited for real-time applications [35]. The second category is least squares methods, which include both linear and nonlinear approaches. This category is widely used due to their highly computationally efficient nature and ease of implementation [35]. These techniques are very useful when the rapid approximation of parameters is required, for example in real-time systems monitoring and control [36,37]. First-order ECMs with hysteresis are developed in [38], utilizing the Levenberg–Marquardt algorithm for parameter identification. Similarly, a first-order ECM using recursive least squares (RLS) and recursive total least squares (RTLS) was developed in [39] to enhance the performance of battery ECM parameter identification. Meanwhile, the work in [36] investigated a second-order ECM model, introducing a novel variable recursive least squares (VRLS) algorithm, and compared it with RLS and adaptive forgetting factor recursive least squares (AFFRLS) methods. In their study, their findings highlighted that VRLS offered a high accuracy, compared to other methods, and further recommended to integrate VRLS with advanced algorithms to enhance the evaluation of battery state the of health/charge. In addition, the work in [40] utilized a very efficient RLS algorithm to obtain battery measurement outliers, which also demonstrated its applicability in the real world [40]. The third category is analytical equations, which present a direct and mathematically precise approach for parameter estimation, as they provide a set of equations based on the fundamentals of the physical and chemical properties of the battery. This method is particularly valuable in theoretical studies and detailed computer modeling, since it imposes a high demand on a understanding of the batteries’ operation. It assists the researchers with fine-tuning and managing the various variables in an accurate manner, thereby enabling the researchers to gain insights into batteries’ behaviors under various circumstances [41,42]. The fourth, and last, category is the Kalman filter-based algorithm; this category is effectively capable of tracking the battery system’s dynamic state under an uncertainty condition. They are suitable for real-time prediction due to their fast response when updating the new set of data, which allows them to be employed in electric vehicle batteries, specifically for estimating the state of charge [43,44]. The following studies utilized the Kalman filter for parameter identification: in [45], the authors described an approach to estimate the lithium-ion battery temperatures using an electro-thermal model and an extended Kalman filter instead of additional sensors. The method’s effectiveness and feasibility were validated through both simulations and experimental tests. The work in [46] presented a reduced-order model of an electrochemical battery for online control systems, as this method integrated frameworks of porous electrodes and concentrated-solution theory.
A sigma-point Kalman filter was used to manage inaccuracies, accurately predicting internal variables, voltage, and SOC across various temperatures and operational states. In [47], an adaptive unscented Kalman filter is developed using an extended single-particle model to estimate lithium-ion battery states beyond state of charge, including concentrations and potentials. This approach, validated both experimentally and numerically, is crucial for enhancing safety and managing degradation in real-time battery management systems.
In this work, we propose a new framework for battery modeling and parameter identification using hybrid optimization approach. This framework has been verified on INR 18650-20R Battery. The main contributions of this study are summarized as follows:
- We developed and implemented a new robust framework for model validation and parameter identification for lithium-ion batteries, leveraging a hybrid optimization approach that combines the Gauss–Newton algorithm and gradient descent technique, the so-called Levenberg–Marquardt algorithm.
- This framework effectively balances the precision of Gauss–Newton with the robustness of gradient descent, making it particularly valuable for parameter identification problems.
- This framework has been verified using experimental measurements on the INR 18650-20R battery, conducted by the Center for Advanced Life Cycle Engineering (CALCE) battery group at the University of Maryland.
- This work presented a comprehensive comparative study between various types of models, specifically first-, second-, and third-order models.
The remainder of this article is organized as follows: Section 2 provides a brief theoretical overview of battery modeling and parameterization. The proposed methodology is outlined in Section 3. Section 4 details the experimental methodology. A summary of the main numerical results is presented in Section 5. Finally, the conclusions are drawn in Section 6.
2. Battery Modeling
To ensure the stability and accuracy of lithium-ion battery models and enhance battery management systems performance, it is essential to accurately predict battery behavior under various operating conditions by establishing mathematical relationships among the characteristics of the batteries parameters, comprising capacitance, internal resistance, open-circuit voltage (OCV), and SOC [48]. To facilitate a better understanding of this model, it is essential to recognize that the ECM fundamentally characterizes a battery by employing a combination of electrical components that simulate its behavior. The battery can be conceptualized as a complex system, where elements such as resistors and capacitors interact to represent the charging and discharging processes. By accurately modeling these interactions, the ECM enables the prediction of battery performance under varying conditions, which is critical for the optimization of battery management systems in practical applications. In this study, we employ the N-order Thevenin RC equivalent circuit model depicted in Figure 1, which includes an OCV, a series resistance (), and a parallel to network to capture transient responses. The variable n represents the number of parallel RC branches, considering the order of the ECM [49,50].
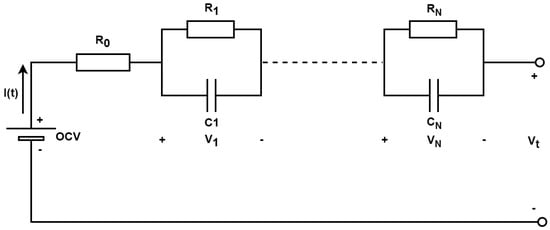
Figure 1.
ECM of the Li-ion battery model that consists of N pairs of resistors and capacitors connected in parallel, using Thevenin’s method.
The proposed approach in this work involves expressing the model parameters as functions of the SOC to capture the dynamic characteristics of the battery. Three battery models were established and tested in this work, namely the first-order model, the second-order model, and the third-order model. The first-order model is a simple representation, while the second- and third-order models have more RC branches to characterize the transient response. To find the dependencies of SOC and model parameters, experimental data are gathered, which are then used to parameterize the models [51]. In this case, when comparing these models, the goal is to identify a model that balances complexity and accuracy, providing valuable insights for the development and enhancement of battery management systems and then reflecting on the measurement of the SOC and SOH [52].
When analyzing the electrical behavior of the ECM of a battery, we apply Kirchhoff’s laws to derive the fundamental equations. The following are the basic equations for the voltage and currents and the internal parameters of the battery. Therefore, the total voltage across the battery is given by [53], as follows:
where OCV represents the open-circuit voltage of the battery, denotes the passing current in the circuit, represents the series resistance, and refers to the voltage across the parallel i-th RC branch. The voltage () across the capacitor () in each parallel i-th RC branch changes over time, as shown in the following equation:
where is the initial voltage across the capacitor at , and , where represents the time constant for the parallel i-th RC branch. To capture the transient response of the battery, first-order, second-order, and third-order models were developed. Each model has a different number of RC branches, which provide different levels of accuracy when representing the battery’s dynamics [48,51,53,54]. The following equations govern the three types of ECMs for N, ranging from one to three, as follows:
- First-Order Model ():
- Second-Order Model ():
- Third-Order Model ():where , , and , which represent time constants for different parallel RC branches. These time constants, along with the resistors , , , and , are unknown parameter values. By using the LMA and experimental data provided by the CALCE group, the values of these parameters are determined. The battery is then dynamically simulated under various operating conditions, revealing insights into its efficiency and performance. The obtained parameters are validated on a different set of data to ensure their accuracy. These details will be discussed in more depth in the following section. Incorporating the SOC dependency into the ECM, particularly within the Thevenin model, provides a more accurate representation of the battery’s behavior in real-world applications.
3. Methodology
The proposed framework validates the battery models and optimizes the inaccurate model parameter values. As illustrated in Figure 2, the proposed framework consists of several components, as follows:
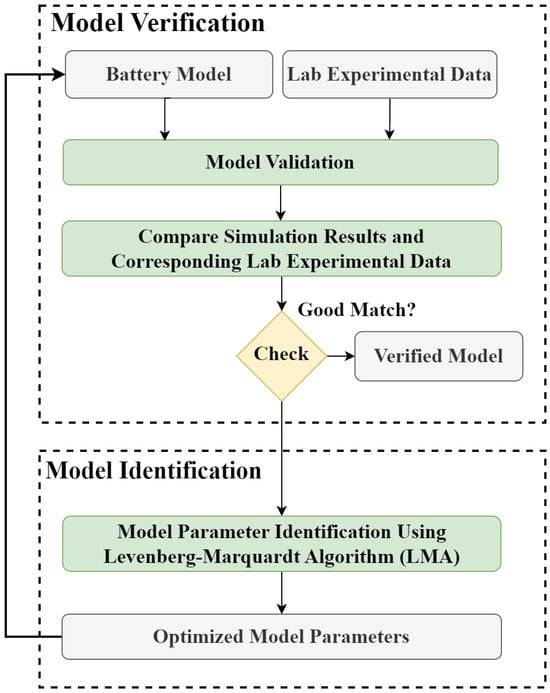
Figure 2.
The proposed framework for battery model verification and parameter identification.
- Model Verification: This step involves validating the battery model by comparing the simulation results to lab experimental measurements. The model will be verified if it matches accurately with simulation data, and ensures that the model parameters are accurately tuned.
- Model Parameter Identification: In this step, the LMA is utilized, to obtain and optimize the model parameters. If the simulation results match well with the experimental lab measurements, the model is verified, and there is no need for this step.
In the following subsections, we will thoroughly explore the Levenberg–Marquardt algorithm and the evaluation criteria, both of which are integral to the framework.
3.1. Levenberg–Marquardt Algorithm (LMA)
The LMA is a powerful and versatile optimization technique extensively used in various scientific and engineering domains, particularly for solving complex non-linear least squares problems [55,56]. In the context of battery modeling, where accurate parameter identification is critical for predicting the behavior of lithium-ion batteries under different operating conditions, the LMA serves as an essential tool.
Battery models, like the ECM employed in this study, rely on the accurate estimation of parameters such as internal resistance, capacitance, and open-circuit voltage (OCV) to simulate the dynamic behavior of a battery [57]. However, these parameters are often difficult to determine directly from experimental data, due to the non-linear nature of battery systems. This is where the LMA plays a crucial role.
The LMA is a hybrid optimization method that combines the advantages of the Gauss–Newton algorithm and gradient descent [58]. The Gauss–Newton algorithm is known for its rapid convergence when dealing with problems where the function can be well-approximated by a linear model near the optimal point. However, it can be sensitive to initial estimates and may fail to converge for more complex, non-linear problems. On the other hand, gradient descent is more robust and can navigate the complex error surface of non-linear problems, but often at the cost of slower convergence [59].
By integrating these two methods, the LMA achieves a balance between convergence speed and stability. It adjusts the step size during iterations by introducing a damping parameter that controls the influence of the gradient descent method versus the Gauss–Newton approach [60]. This dynamic adjustment is particularly useful for battery modeling, where the non-linear relationships between parameters and the SOC can lead to challenging optimization landscapes.
In practical terms, applying the LMA to battery modeling allows for the iterative refinement of model parameters, ensuring that the simulated battery behavior aligns closely with real-world experimental data. This alignment is vital for the development of accurate and reliable BMSs, which depend on precise models to monitor and control battery performance, extending the lifespan and safety of lithium-ion batteries in various applications [61].
The following section provides a detailed explanation of the LMA mathematical foundations and its specific application within our proposed framework for optimizing the ECM parameters in this study. This includes the derivation of the update equations, the role of the damping parameter, and the iterative process that leads to the convergence of the model parameters. We assume that is the objective function to be minimized, where x is the parameter vector. The goal is to find the parameter values that minimize this function. The update rule can be expressed as follows [58,62]:
where represents a Hessian matrix, while denotes the gradient matrix. Therefore, is assumed to be a sum of squares function, as expressed in the next equation, which follows:
where is the difference between the target and the network output. Then, the following can be shown:
and
The Jacobian matrix is as follows:
and
The Gauss–Newton method assumes that , leading to the following update equation:
The Levenberg–Marquardt modification to the Gauss–Newton method introduces a damping parameter to control the step size and ensure convergence. The modified update rule is as follows:
In this algorithm, the parameter usually starts at 0.01. If a step results in an increased , the significance of is increased by a factor of 10. Conversely, if decreases, is divided by 10. In this technique, the adjustment of allows the algorithm to switch between the rapid convergence of the Gauss–Newton method and the stability of gradient descent, ensuring robust performance across various optimization problems.
3.2. Evaluation Criteria
In this work, the root mean square error (RMSE) and mean absolute error (MAE) were utilized as metrics to measure the difference between the experimental measurement and simulation measurement. These formulas are defined as follows:
where K is the total number of samples and and are the experimental measurement and simulation measurement at time k, respectively. Together, RMSE and MAE provide a comprehensive evaluation of the proposed approach performance [63].
3.3. Parameter Extraction Process
The parameter extraction in this study was accomplished using the LMA, an iterative method that effectively combines the strengths of the Gauss–Newton method with gradient descent. By applying this algorithm to the ECM equations and utilizing the experimental data provided, we were able to accurately identify the unknown model parameters. In this context, the battery modeling section, along with the detailed subsections on the LMA and the evaluation criteria, elaborate on this process. The comparison of simulated models based on the ECM with experimental data, using RMSE and MAE, was critical in precisely determining the unknown parameters, ensuring that the model closely aligns with the real-world performance of the battery.
4. Experimental Methodology
In order to thoroughly identify model parameters and validate the SOC estimation’s performance for lithium-ion batteries, a comprehensive experimental setup was implemented. This section provides a comprehensive overview of the methodology used to test INR 18650-20R battery cells, covering the procedures, equipment, and data collection methods employed to ensure precise and reliable outcomes.
4.1. Experimental Setup
The CALCE battery group [64] conducted experiments using INR 18650-20R battery cells, which involved discharging the cells with a negative-pulse current, incorporating a relaxation period at each 10% decrement in SOC. Subsequently, the cells were charged following the same routine but with a positive-pulse current and a relaxation period of around two hours [64,65]. This experiment facilitated a detailed assessment of the battery’s performance across various operating conditions, primarily aiming to identify model parameters. The specific steps of the test procedure were as follows:
- An incremental OCV test using negative pulse discharge (PD) or positive pulse charge (PC) tests:
- C-rate: The pulse charge–discharge tests were conducted using a current corresponding to a C-rate of 0.5C [64]. The C-rate is the rate at which a battery is charged or discharged [66,67]. For example, in our experiments, the rated capacity was 2 Ah, and a C-rate of 0.5C meant the battery was charged or discharged at half the usual rate, taking two hours to complete. The corresponding charging or discharging current would be 1 A.
- Pulsing time: The pulsing time refers to the duration of each charge or discharge pulse [68]. In our experiments, each pulse lasted 12 min, for both the discharging and charging currents [64].
- Rest time: Rest time is the period between pulses during which the battery is allowed to stabilize [68]. In our experiments, the rest time was two hours for both the discharging and charging currents [64].
- Discharging and charging currents: The current profiles for discharging and charging are shown in Figure 3 and Figure 4, respectively.
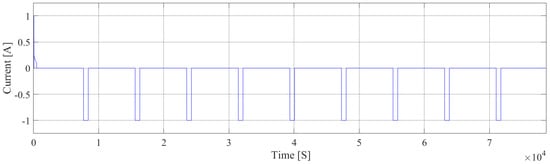 Figure 3. Experimental discharging current.
Figure 3. Experimental discharging current.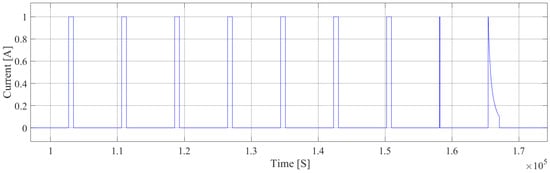 Figure 4. Experimental charging current.
Figure 4. Experimental charging current. - Temperature: PD and PC tests were performed at a controlled temperature of 25 °C to ensure consistent and reliable results.
- Estimation method development: Using PD test results, an estimation method for OCV–SOC was developed.
- Method validation: The developed method was validated using results from the PC test.
Figure 5 illustrates the test bench for battery test experiments [69]. Detailed descriptions of the test bench can be found in [64,65]. The experiments involved testing INR 1865-20R batteries, which are commonly used in EVs. These batteries have a maximum capacity of 2 Ah. During the tests, the batteries were placed in a temperature chamber where the cell temperature was precisely controlled and measured. An Arbin BT2000 system (Arbin Instruments, College Station, TX, USA) was employed to manage the charging and discharging processes was employed to manage the charging and discharging processes.

Figure 5.
Experimental setup for battery tests.
4.2. Assumptions and Limitations
This study operates under several key assumptions to ensure the validity and applicability of the proposed framework, as follows:
- Nonlinear model behavior: The proposed ECM is inherently nonlinear, with parameters that vary in a stepwise manner with the SOC. This assumption helps the model accurately capture the dynamic behavior of the battery across different SOC ranges.
- Temperature control: The model assumes that the battery operates under a controlled temperature environment (25 °C) during both the charging and discharging phases. This minimizes the impact of temperature fluctuations on the accuracy of the model’s parameters.
- Constant discharge rates: The model is based on the assumption of a constant discharge rate during parameter identification. Consistency in discharge rates is crucial for maintaining the validity of the identified parameters.
The primary limitation of this approach can be summarized as follows:
- Applicability to battery packs: While the model has been validated for a single cell, extending the proposed method to battery packs introduces challenges, such as managing inter-cell variations, thermal management, and balancing issues. Future work will focus on refining the model to address these complexities.
- Operating conditions: The model’s performance might be affected by operating conditions not covered in this study, such as extreme temperatures or varying discharge rates. These factors can introduce non-linearity that is not accounted for by the current model configuration.
- SOC step-wise variations: The assumption of step-wise changes in model parameters with SOC, while useful for single-cell analysis, may require refinement when applied to battery packs where SOC variations are more gradual and influenced by inter-cell differences.
- Limited experimental data: The parameter identification and model validation were based on a controlled set of experiments. Expanding the model’s applicability would require additional data collection under a broader range of conditions, including different battery chemistries, sizes, operating environments, and varying C-rates.
4.3. Experimental Data
In this study, the INR 18650-20R battery cell was chosen, which is shown in Figure 6. Data provided by the CALCE battery group [64] highlight its suitability for the experiment. The chemistry components of the INR 18650-20R are a lithium–nickel–manganese–cobalt oxide (LiNiMnCo) cathode and a synthetic graphite anode [70,71,72,73,74,75], and it is renowned for its robust stability and superior performance. Table 1 shows the characteristics of the battery as provided by the manufacturer, highlighting its key attributes.

Figure 6.
A cylindrical INR 18650-20R cell utilized in this study.

Table 1.
INR 18650-20R Battery Characteristics.
This choice of battery ensures that the experimental results are relevant and applicable to real-world EV applications. The collected data from the pulse charge–discharge and incremental OCV–SOC tests provide a robust foundation for developing and validating model parameter identification methods under varying conditions.
5. Results and Discussion
In this research, we conducted a quantitative evaluation of the proposed approach on real-world cases to demonstrate its capability to calibrate model parameters and validate the effectiveness of the proposed algorithm. Specifically, the performance of the LMA was assessed by applying it to first-order, second-order, and third-order battery models.
After verifying the battery model, it became evident that identifying and optimizing the model parameters was necessary. During the identification phase, only discharging measurements were used. The first-order model demonstrated slightly higher error metrics, with an RMSE of and an MAE of , yet still maintained a commendable level of accuracy, as shown in Figure 7. The second-order model achieved an RMSE of and an MAE of , as shown in Figure 8, reflecting a performance that, while better than that of the first-order model, was marginally inferior to the third-order model. The third-order model demonstrated superior performance with an RMSE of and an MAE of , as shown in Figure 9. This indicates a high accuracy in fitting the training data. In addition to the accuracy metrics, we also analyzed the computational efficiency of the models to provide a comprehensive evaluation of their performance. The time required to estimate the unknown parameters varied significantly with model complexity. Specifically, the first-order model required 182 min for parameter estimation, the second-order model required 245 min, and the third-order model required 593 min. This increase in computation time with model complexity underscores the trade-off between accuracy and computational efficiency; while the third-order model offered the highest accuracy, it also demanded the most computational resources. This trade-off is crucial for applications where computational resources are limited or when real-time performance is essential.
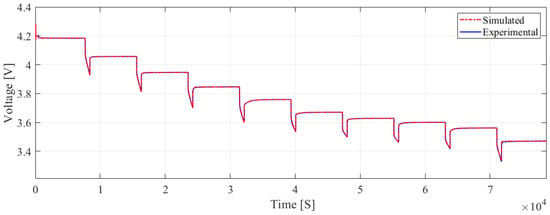
Figure 7.
The simulation and experimental comparison results of the described by the first-order RC equivalent circuit model during the discharge phase.
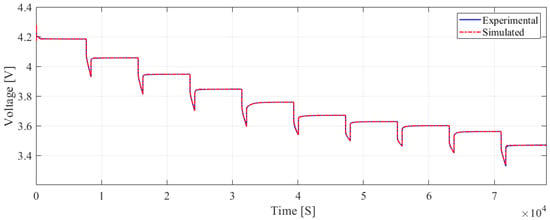
Figure 8.
The simulation and experimental comparison results of the described by the second-order RC equivalent circuit model during the discharge phase.
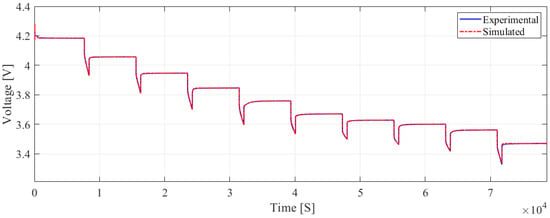
Figure 9.
The simulation and experimental comparison results of the described by the third-order RC equivalent circuit model during the discharge phase.
The specific parameter values for the first, second, and third-order models are presented in Table 2, Table 3, and Table 4, respectively, providing a comprehensive overview of their characteristics and performance metrics.

Table 2.
The identified parameters of the INR 18650-20R battery for the first-order RC equivalent circuit model.

Table 3.
The identified parameters of the INR 18650-20R battery for the second-order RC equivalent circuit model.

Table 4.
The identified parameters of the INR 18650-20R battery for the third-order RC equivalent circuit model.
To verify the performance of the optimized battery model, it was evaluated on unseen data (charging measurements) to assess their generalization capabilities. The first-order model (Figure 10) had an RMSE of and an MAE of , suggesting it had the highest error among the three models during verification. The second-order model (Figure 11) performed better than the first-order model, with an RMSE of and an MAE of , but it was still not as accurate as the third-order model. The third-order model (Figure 12) showed an RMSE of and an MAE of , indicating a slight degradation in performance compared to the identification phase. During the validation phase, we observed a slight increase in both the RMSE and MAE compared to the identification phase. This increase, although slight, can be attributed to the differences between the charging and discharging processes, which introduce varying dynamic behaviors in the battery. Specifically, while the discharging data were used to optimize the model parameters, the charging data were employed to validate the model, naturally resulting in a slight increase in errors due to the distinct operational characteristics of charging. Despite this, the model maintained a high level of accuracy, showcasing its robustness and ability to generalize across different phases of battery operation. The results of the validation phase, including the observed RMSE and MAE values, are summarized in Table 5. This comprehensive analysis highlights the algorithm’s adaptability and precision when handling complex modeling challenges.
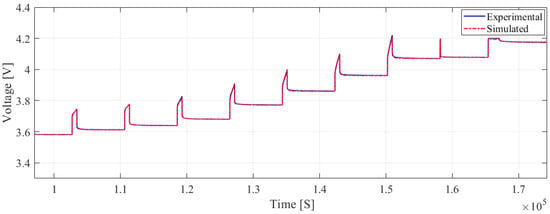
Figure 10.
Terminal voltage prediction for the first-order model during the pulse charging validation experiment.
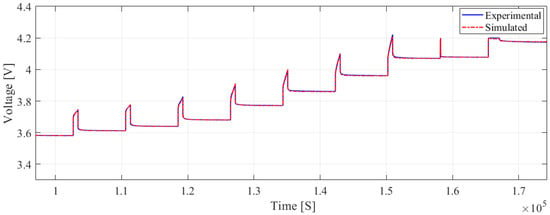
Figure 11.
Terminal voltage prediction for the second-order model during the pulse charging validation experiment.
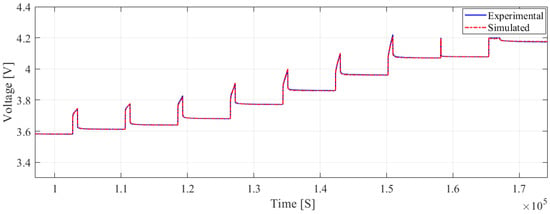
Figure 12.
Terminal voltage prediction for the third-order model during the pulse charging validation experiment.

Table 5.
A comparative analysis of the different model orders during the identification and verification phases.
6. Conclusions
In recent years, the adoption of batteries has expanded significantly across a broad range of applications. Their capacities vary widely, ranging from a few watts and watt-hours to several megawatts and megawatt-hours. Among the various types of batteries, lithium-ion batteries stand out as the most promising option, due to their high power and energy densities. Consequently, in the last few decades, many models have been proposed to represent their behavior.
This paper proposed a framework for validating and identifying lithium-ion batteries’ model parameters to enhance the accuracy of SOC estimation by reducing modeling errors in the N-order Thevenin equivalent circuit model. The proposed framework comprises two stages: (1) model verification, and (2) model parameter identification. The framework is validated using the lab measurements of the INR 18650-20R battery. The results indicate that optimizing the battery model using only the charging measurements is sufficient. The simulation results obtained with the optimized model, using the LMA in MATLAB/Simulink, show good agreement with previous experimental results. Although our study focused on single-cell models, the principles of our method are applicable to battery packs, which consist of multiple cells connected in series and/or parallel configurations. Future work will involve extending this method to battery packs, addressing variations in cell characteristics, and incorporating considerations for balancing and thermal management. These advancements will enhance the scalability and practical applicability of the proposed modeling framework.
Author Contributions
Conceptualization, A.A. and M.M.; methodology, A.A. and M.M.; software, A.A., M.M. and F.A.; validation, M.M. and F.A.; formal analysis, A.A., M.M. and F.A.; investigation, A.A. and M.M.; resources, M.M. and F.A.; writing—original draft preparation, A.A. and M.M.; writing—review and editing, A.A. and M.M.; visualization, A.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data used in this study is provided by the Center for Advanced Life Cycle Engineering (CALCE) battery group at the University of Maryland. They are available at the following link: [https://calce.umd.edu/battery-data] (accessed on 20 June 2024).
Acknowledgments
The authors would like to thank the Deanship of Scientific Research at Shaqra University for supporting this work.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AFFRLS | adaptive forgetting factor recursive least squares |
| BMS | battery management system |
| CALCE | Center for Advanced Life Cycle Engineering |
| ECM | equivalent circuit model |
| EV | electric vehicle |
| LIBs | lithium-ion batteries |
| LMA | Levenberg–Marquardt algorithm |
| MAE | mean absolute error |
| OCV | open-circuit voltage |
| PC | pulse charge |
| PD | pulse discharge |
| PNGV | partnership for a new generation of vehicle |
| RC | resistor capacitor |
| RMSE | root mean square error |
| RLS | recursive least squares |
| RTLS | recursive total least squares |
| SOC | state of charge |
| SOH | state of health |
| VRLS | variable recursive least squares |
| ML | machine learning |
References
- Lu, L.; Han, X.; Li, J.; Hua, J.; Ouyang, M. A review on the key issues for lithium-ion battery management in electric vehicles. J. Power Sources 2013, 226, 272–288. [Google Scholar] [CrossRef]
- Manthiram, A. An outlook on lithium ion battery technology. ACS Cent. Sci. 2017, 3, 1063–1069. [Google Scholar] [CrossRef] [PubMed]
- Singh, A.N.; Kim, M.H.; Meena, A.; Wi, T.U.; Lee, H.W.; Kim, K.S. Na/Al Codoped Layered Cathode with Defects as Bifunctional Electrocatalyst for High-Performance Li-Ion Battery and Oxygen Evolution Reaction. Small 2021, 17, 2005605. [Google Scholar] [CrossRef]
- Li, J.; Li, L.; Li, Z.; Jiang, Z.; Gu, J. Co-estimation of parameters and state of charge for lithium-ion battery. J. Electroanal. Chem. 2022, 907, 116011. [Google Scholar] [CrossRef]
- Whittingham, M.S. History, evolution, and future status of energy storage. Proc. IEEE 2012, 100, 1518–1534. [Google Scholar] [CrossRef]
- Gao, Y.; Liu, K.; Zhu, C.; Zhang, X.; Zhang, D. Co-estimation of state-of-charge and state-of-health for lithium-ion batteries using an enhanced electrochemical model. IEEE Trans. Ind. Electron. 2021, 69, 2684–2696. [Google Scholar] [CrossRef]
- Hong, J.; Zhang, H.; Xu, X. Thermal fault prognosis of lithium-ion batteries in real-world electric vehicles using self-attention mechanism networks. Appl. Therm. Eng. 2023, 226, 120304. [Google Scholar] [CrossRef]
- Chang, C.; Wang, S.; Tao, C.; Jiang, J.; Jiang, Y.; Wang, L. An improvement of equivalent circuit model for state of health estimation of lithium-ion batteries based on mid-frequency and low-frequency electrochemical impedance spectroscopy. Measurement 2022, 202, 111795. [Google Scholar] [CrossRef]
- Liu, K.; Gao, Y.; Zhu, C.; Li, K.; Fei, M.; Peng, C.; Zhang, X.; Han, Q.L. Electrochemical modeling and parameterization towards control-oriented management of lithium-ion batteries. Control Eng. Pract. 2022, 124, 105176. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, Q.; Huang, H.; Yang, B.; Dong, H.; Zhang, J. An electrochemical–thermal model of lithium-ion battery and state of health estimation. J. Energy Storage 2022, 47, 103528. [Google Scholar] [CrossRef]
- Adaikkappan, M.; Sathiyamoorthy, N. Modeling, state of charge estimation, and charging of lithium-ion battery in electric vehicle: A review. Int. J. Energy Res. 2022, 46, 2141–2165. [Google Scholar] [CrossRef]
- Xu, L.; Lin, X.; Xie, Y.; Hu, X. Enabling high-fidelity electrochemical P2D modeling of lithium-ion batteries via fast and non-destructive parameter identification. Energy Storage Mater. 2022, 45, 952–968. [Google Scholar] [CrossRef]
- Matar, M.; Xu, B.; Elmoudi, R.; Olatujoye, O.; Wshah, S. A deep learning-based framework for parameters calibration of power plant models using event playback approach. IEEE Access 2022, 10, 72132–72144. [Google Scholar] [CrossRef]
- Wshah, S.; Shadid, R.; Wu, Y.; Matar, M.; Xu, B.; Wu, W.; Lin, L.; Elmoudi, R. Deep learning for model parameter calibration in power systems. In Proceedings of the 2020 IEEE International Conference on Power Systems Technology (POWERCON), Bangalore, India, 14–16 September 2020; pp. 1–6. [Google Scholar]
- Alsarayreh, M.; Mohamed, O.; Matar, M. Modeling a practical dual-fuel gas turbine power generation system using dynamic neural network and deep learning. Sustainability 2022, 14, 870. [Google Scholar] [CrossRef]
- Matar, M.; Xia, T.; Huguenard, K.; Huston, D.; Wshah, S. Anomaly Detection in Coastal Wireless Sensors via Efficient Deep Sequential Learning. IEEE Access 2023, 11, 110260–110271. [Google Scholar] [CrossRef]
- Matar, M.; Xia, T.; Huguenard, K.; Huston, D.; Wshah, S. Multi-head attention based bi-lstm for anomaly detection in multivariate time-series of wsn. In Proceedings of the 2023 IEEE 5th International Conference on Artificial Intelligence Circuits and Systems (AICAS), Hangzhou, China, 11–13 June 2023; pp. 1–5. [Google Scholar]
- Matar, M.; Estevez, P.G.; Marchi, P.; Messina, F.; Elmoudi, R.; Wshah, S. Transformer-based deep learning model for forced oscillation localization. Int. J. Electr. Power Energy Syst. 2023, 146, 108805. [Google Scholar] [CrossRef]
- Matar, M. Intelligent Wide-Area Monitoring Systems Using Deep Learning; The University of Vermont and State Agricultural College: Burlington, VT, USA, 2023. [Google Scholar]
- Almutairy, F.; Scekic, L.; Matar, M.; Elmoudi, R.; Wshah, S. Detection and mitigation of gps spoofing attacks on phasor measurement units using deep learning. Int. J. Electr. Power Energy Syst. 2023, 151, 109160. [Google Scholar] [CrossRef]
- Matar, M.; Mavalizadeh, H.; Brahma, S.; Almassalkhi, M.R.; Wshah, S. Learning the state-of-charge of heterogeneous fleets of distributed energy resources with temporal residual networks. J. Energy Storage 2023, 70, 107979. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, T.; Hong, J.; Zhang, H.; Yang, J. Energy management strategy of a novel parallel electric-hydraulic hybrid electric vehicle based on deep reinforcement learning and entropy evaluation. J. Clean. Prod. 2023, 403, 136800. [Google Scholar] [CrossRef]
- Wang, Q.; Ye, M.; Wei, M.; Lian, G.; Wu, C. Co-estimation of state of charge and capacity for lithium-ion battery based on recurrent neural network and support vector machine. Energy Rep. 2021, 7, 7323–7332. [Google Scholar] [CrossRef]
- Chen, D.; Xiao, L.; Yan, W.; Guo, Y. A novel hybrid equivalent circuit model for lithium-ion battery considering nonlinear capacity effects. Energy Rep. 2021, 7, 320–329. [Google Scholar] [CrossRef]
- Guo, W.; Sun, Z.; Vilsen, S.B.; Meng, J.; Stroe, D.I. Review of “grey box” lifetime modeling for lithium-ion battery: Combining physics and data-driven methods. J. Energy Storage 2022, 56, 105992. [Google Scholar] [CrossRef]
- Xie, J.; Wei, X.; Bo, X.; Zhang, P.; Chen, P.; Hao, W.; Yuan, M. State of charge estimation of lithium-ion battery based on extended Kalman filter algorithm. Front. Energy Res. 2023, 11, 1180881. [Google Scholar] [CrossRef]
- Zhou, W.; Zheng, Y.; Pan, Z.; Lu, Q. Review on the battery model and SOC estimation method. Processes 2021, 9, 1685. [Google Scholar] [CrossRef]
- Hou, J.; Xu, J.; Lin, C.; Jiang, D.; Mei, X. State of charge estimation for lithium-ion batteries based on battery model and data-driven fusion method. Energy 2024, 290, 130056. [Google Scholar] [CrossRef]
- Sahhouk, M.A.; Aziz, J.; Ardani, M. State of Charge Estimation of Second Life Batteries Using First Order Thevenin Model. In Proceedings of the 2023 IEEE Conference on Energy Conversion (CENCON), Kuching, Malaysia, 23–24 October 2023; pp. 53–57. [Google Scholar]
- Wang, X.; Ye, P.; Liu, S.; Zhu, Y.; Deng, Y.; Yuan, Y.; Ni, H. Research Progress of Battery Life Prediction Methods Based on Physical Model. Energies 2023, 16, 3858. [Google Scholar] [CrossRef]
- Chen, K.; Zhou, S.; Liu, K.; Gao, G.; Wu, G. State of charge estimation for lithium-ion battery based on whale optimization algorithm and multi-kernel relevance vector machine. J. Chem. Phys. 2023, 158, 104110. [Google Scholar] [CrossRef]
- Kalogiannis, T.; Hosen, M.S.; Sokkeh, M.A.; Goutam, S.; Jaguemont, J.; Jin, L.; Qiao, G.; Berecibar, M.; Van Mierlo, J. Comparative study on parameter identification methods for dual-polarization lithium-ion equivalent circuit model. Energies 2019, 12, 4031. [Google Scholar] [CrossRef]
- Reddy, A.K.V.K.; Narayana, K.V.L. Meta-heuristics optimization in electric vehicles-an extensive review. Renew. Sustain. Energy Rev. 2022, 160, 112285. [Google Scholar] [CrossRef]
- Cheng, Y.S. Identification of parameters for equivalent circuit model of Li-ion battery cell with population based optimization algorithms. Ain Shams Eng. J. 2024, 15, 102481. [Google Scholar] [CrossRef]
- Du, X.; Meng, J.; Zhang, Y.; Huang, X.; Wang, S.; Liu, P.; Liu, T. An information appraisal procedure: Endows reliable online parameter identification to lithium-ion battery model. IEEE Trans. Ind. Electron. 2021, 69, 5889–5899. [Google Scholar] [CrossRef]
- El Marghichi, M.; Loulijat, A.; El Hantati, I. Variable recursive least square algorithm for lithium-ion battery equivalent circuit model parameters identification. Period. Polytech. Electr. Eng. Comput. Sci. 2023, 67, 239–248. [Google Scholar] [CrossRef]
- Meng, J.; Stroe, D.I.; Ricco, M.; Luo, G.; Teodorescu, R. A simplified model-based state-of-charge estimation approach for lithium-ion battery with dynamic linear model. IEEE Trans. Ind. Electron. 2018, 66, 7717–7727. [Google Scholar] [CrossRef]
- Tran, M.K.; Mevawala, A.; Panchal, S.; Raahemifar, K.; Fowler, M.; Fraser, R. Effect of integrating the hysteresis component to the equivalent circuit model of Lithium-ion battery for dynamic and non-dynamic applications. J. Energy Storage 2020, 32, 101785. [Google Scholar] [CrossRef]
- Du, X.; Meng, J.; Liu, K.; Zhang, Y.; Wang, S.; Peng, J.; Liu, T. Online identification of lithium-ion battery model parameters with initial value uncertainty and measurement noise. Chin. J. Mech. Eng. 2023, 36, 7. [Google Scholar] [CrossRef]
- Ouyang, Q.; Chen, J.; Zheng, J. State-of-charge observer design for batteries with online model parameter identification: A robust approach. IEEE Trans. Power Electron. 2019, 35, 5820–5831. [Google Scholar] [CrossRef]
- Madani, S.S.; Schaltz, E.; Knudsen Kær, S. An electrical equivalent circuit model of a lithium titanate oxide battery. Batteries 2019, 5, 31. [Google Scholar] [CrossRef]
- Garnier, H. Direct continuous-time approaches to system identification. Overview and benefits for practical applications. Eur. J. Control 2015, 24, 50–62. [Google Scholar] [CrossRef]
- Hou, J.; Liu, J.; Chen, F.; Li, P.; Zhang, T.; Jiang, J.; Chen, X. Robust lithium-ion state-of-charge and battery parameters joint estimation based on an enhanced adaptive unscented Kalman filter. Energy 2023, 271, 126998. [Google Scholar] [CrossRef]
- Feng, J.; Cai, F.; Yang, J.; Wang, S.; Huang, K. An adaptive state of charge estimation method of lithium-ion battery based on residual constraint fading factor unscented Kalman filter. IEEE Access 2022, 10, 44549–44563. [Google Scholar] [CrossRef]
- Pang, H.; Guo, L.; Wu, L.; Jin, J.; Zhang, F.; Liu, K. A novel extended Kalman filter-based battery internal and surface temperature estimation based on an improved electro-thermal model. J. Energy Storage 2021, 41, 102854. [Google Scholar] [CrossRef]
- Miguel, E.; Plett, G.L.; Trimboli, M.S.; Lopetegi, I.; Oca, L.; Iraola, U.; Bekaert, E. Electrochemical model and sigma point Kalman filter based online oriented battery model. IEEE Access 2021, 9, 98072–98090. [Google Scholar] [CrossRef]
- Li, W.; Fan, Y.; Ringbeck, F.; Jöst, D.; Han, X.; Ouyang, M.; Sauer, D.U. Electrochemical model-based state estimation for lithium-ion batteries with adaptive unscented Kalman filter. J. Power Sources 2020, 476, 228534. [Google Scholar] [CrossRef]
- Campagna, N.; Castiglia, V.; Miceli, R.; Mastromauro, R.A.; Spataro, C.; Trapanese, M.; Viola, F. Battery models for battery powered applications: A comparative study. Energies 2020, 13, 4085. [Google Scholar] [CrossRef]
- Asim, A.M.; Ahmed, O.A.; Ibrahim, A.M.; El-Khattam, W.A.; Talaat, H.E. A Novel Dynamic Li-Ion Battery Model for the Aggregated Charging of EVs. World Electr. Veh. J. 2023, 14, 336. [Google Scholar] [CrossRef]
- Alavi, S.M.M.; Mahdi, A.; Payne, S.J.; Howey, D.A. Identifiability of generalized randles circuit models. IEEE Trans. Control Syst. Technol. 2016, 25, 2112–2120. [Google Scholar] [CrossRef]
- Hu, T.; Zanchi, B.; Zhao, J. Simple analytical method for determining parameters of discharging batteries. IEEE Trans. Energy Convers. 2011, 26, 787–798. [Google Scholar] [CrossRef]
- Omariba, Z.B.; Zhang, L.; Kang, H.; Sun, D. Parameter identification and state estimation of lithium-ion batteries for electric vehicles with vibration and temperature dynamics. World Electr. Veh. J. 2020, 11, 50. [Google Scholar] [CrossRef]
- Meng, J.; Luo, G.; Ricco, M.; Swierczynski, M.; Stroe, D.I.; Teodorescu, R. Overview of lithium-ion battery modeling methods for state-of-charge estimation in electrical vehicles. Appl. Sci. 2018, 8, 659. [Google Scholar] [CrossRef]
- Knap, V.; Stroe, D.I.; Teodorescu, R.; Swierczynski, M.; Stanciu, T. Comparison of parametrization techniques for an electrical circuit model of Lithium-Sulfur batteries. In Proceedings of the 2015 IEEE 13th International Conference on Industrial Informatics (INDIN), Cambridge, UK, 22–24 July 2015; pp. 1278–1283. [Google Scholar]
- Gavin, H.P. The Levenberg–Marquardt Algorithm for Nonlinear Least Squares Curve-Fitting Problems. Available online: https://people.duke.edu/~hpgavin/lm.pdf (accessed on 20 June 2024).
- Yu, H.; Wilamowski, B.M. Levenberg–marquardt training. In Intelligent Systems; CRC Press: Boca Raton, FL, USA, 2018; pp. 1–12. [Google Scholar]
- Chen, P.; Lu, C.; Mao, Z.; Li, B.; Wang, C.; Tian, W.; Li, M.; Xu, Y. Evaluation of various offline and online ECM parameter identification methods of lithium-ion batteries in underwater vehicles. Acs Omega 2022, 7, 30504–30518. [Google Scholar] [CrossRef]
- Dridi, T.; Jouini, H.; Dafaoui, E.; El Mhamedi, A.; Mami, A. Comprative Study of two Classical Optimization Algorithms Solving Economic Dispatch Problem. In Proceedings of the 13ème Conference Internationale de Modelisation, Optimisation et Simulation (MOSIM2020), Agadir, Morocco, 12–14 November 2020. [Google Scholar]
- Moré, J.J. The Levenberg–Marquardt algorithm: Implementation and theory. In Proceedings of the Numerical Analysis: Proceedings of the Biennial Conference, Dundee, UK, 28 June–1 July 1977; Springer: Berlin/Heidelberg, Germany, 2006; pp. 105–116. [Google Scholar]
- Sapna, S.; Tamilarasi, A.; Kumar, M.P. Backpropagation learning algorithm based on Levenberg Marquardt Algorithm. Comp Sci Inf. Technol (CS IT) 2012, 2, 393–398. [Google Scholar]
- Gabbar, H.A.; Othman, A.M.; Abdussami, M.R. Review of battery management systems (BMS) development and industrial standards. Technologies 2021, 9, 28. [Google Scholar] [CrossRef]
- Dridi, T.; Jouini, H.; Mami, A.; El Mhamedi, A.; Dafaoui, E.M. Application of the Levenberg–Marquardt Algorithm in Solving the Economic Emission Dispatch Problem Integrating Renewable Energy. Eng. Technol. Appl. Sci. Res. 2022, 12, 8850–8855. [Google Scholar] [CrossRef]
- Yang, F.; Li, W.; Li, C.; Miao, Q. State-of-charge estimation of lithium-ion batteries based on gated recurrent neural network. Energy 2019, 175, 66–75. [Google Scholar] [CrossRef]
- Center for Advanced Life Cycle Engineering (CALCE). University of Maryland. Available online: https://calce.umd.edu/battery-data (accessed on 20 June 2024).
- Zheng, F.; Xing, Y.; Jiang, J.; Sun, B.; Kim, J.; Pecht, M. Influence of different open circuit voltage tests on state of charge online estimation for lithium-ion batteries. Appl. Energy 2016, 183, 513–525. [Google Scholar] [CrossRef]
- Rubenbauer, H.; Henninger, S. Definitions and reference values for battery systems in electrical power grids. J. Energy Storage 2017, 12, 87–107. [Google Scholar] [CrossRef]
- Saxena, S.; Xing, Y.; Kwon, D.; Pecht, M. Accelerated degradation model for C-rate loading of lithium-ion batteries. Int. J. Electr. Power Energy Syst. 2019, 107, 438–445. [Google Scholar] [CrossRef]
- Qin, Y.; Du, J.; Lu, L.; Gao, M.; Haase, F.; Li, J.; Ouyang, M. A rapid lithium-ion battery heating method based on bidirectional pulsed current: Heating effect and impact on battery life. Appl. Energy 2020, 280, 115957. [Google Scholar] [CrossRef]
- Xing, Y.; He, W.; Pecht, M.; Tsui, K.L. State of charge estimation of lithium-ion batteries using the open-circuit voltage at various ambient temperatures. Appl. Energy 2014, 113, 106–115. [Google Scholar] [CrossRef]
- Malik, M.; Chan, K.H.; Azimi, G. Review on the synthesis of LiNixMnyCo1-x-yO2 (NMC) cathodes for lithium-ion batteries. Mater. Today Energy 2022, 28, 101066. [Google Scholar] [CrossRef]
- Li, T.; Yuan, X.Z.; Zhang, L.; Song, D.; Shi, K.; Bock, C. Degradation mechanisms and mitigation strategies of nickel-rich NMC-based lithium-ion batteries. Electrochem. Energy Rev. 2020, 3, 43–80. [Google Scholar] [CrossRef]
- Guo, J.; Li, Y.; Meng, J.; Pedersen, K.; Gurevich, L.; Stroe, D.I. Understanding the mechanism of capacity increase during early cycling of commercial NMC/graphite lithium-ion batteries. J. Energy Chem. 2022, 74, 34–44. [Google Scholar] [CrossRef]
- Lee, S.J.; Han, J.G.; Lee, Y.; Jeong, M.H.; Shin, W.C.; Ue, M.; Choi, N.S. A bi-functional lithium difluoro (oxalato) borate additive for lithium cobalt oxide/lithium nickel manganese cobalt oxide cathodes and silicon/graphite anodes in lithium-ion batteries at elevated temperatures. Electrochim. Acta 2014, 137, 1–8. [Google Scholar] [CrossRef]
- Liu, S.; Xiong, L.; He, C. Long cycle life lithium ion battery with lithium nickel cobalt manganese oxide (NCM) cathode. J. Power Sources 2014, 261, 285–291. [Google Scholar] [CrossRef]
- Ko, G.; Jeong, S.; Park, S.; Lee, J.; Kim, S.; Shin, Y.; Kim, W.; Kwon, K. Doping strategies for enhancing the performance of lithium nickel manganese cobalt oxide cathode materials in lithium-ion batteries. Energy Storage Mater. 2023, 60, 102840. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).