Simple Method for Determining Loss Parameters of Electric Cars
Abstract
1. Introduction
1.1. Context
1.2. Literature Review
1.3. Statement of the Problem
1.4. Approach
2. Materials and Methods
2.1. Vehicle Energy Considerations
2.2. Energy Flow Modeling of Electric Vehicles
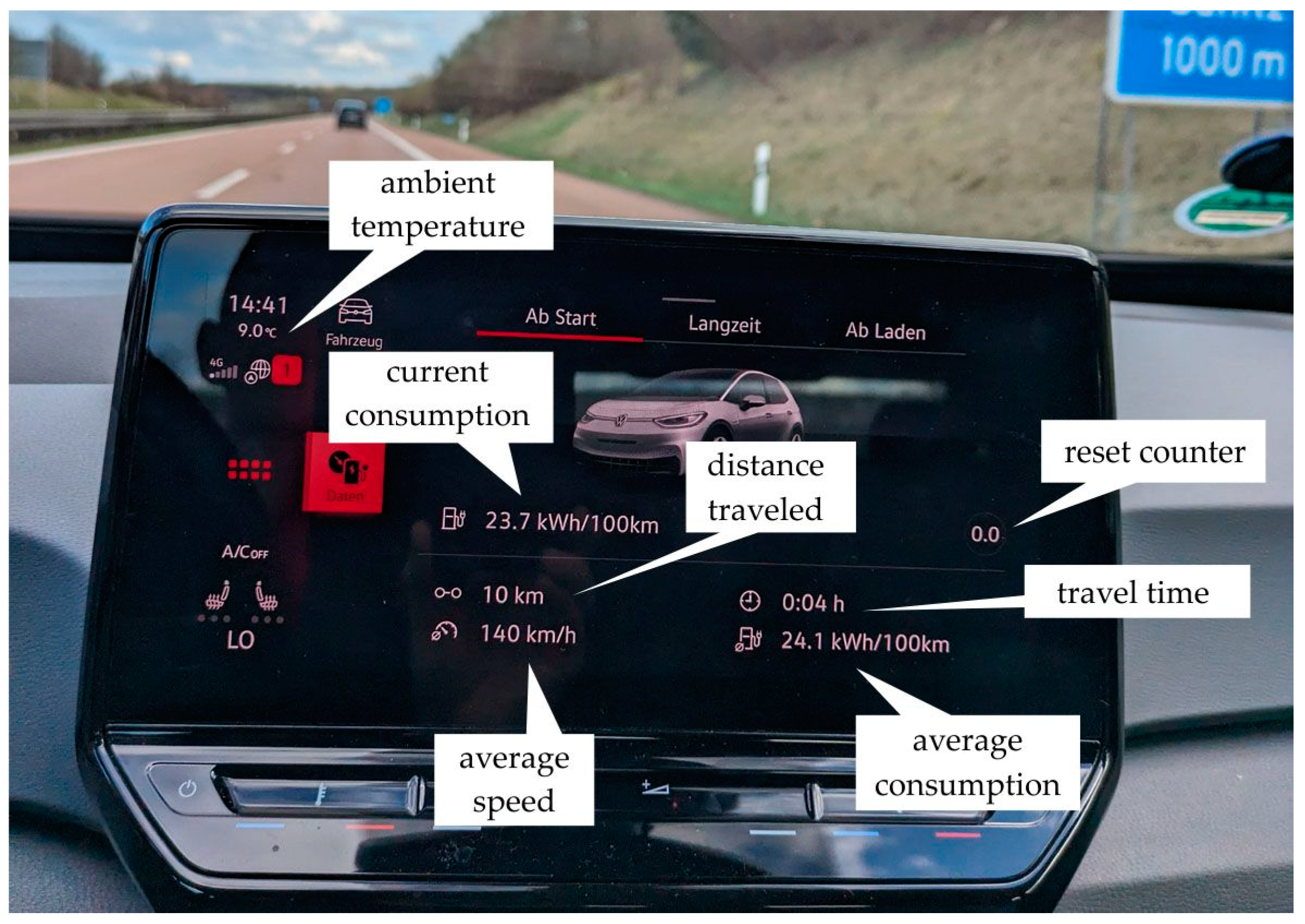
2.3. Procedure of Driving Data Collection
2.4. Mathematical Determination of the Parameters of the Power Function
3. Results
3.1. Driving Results
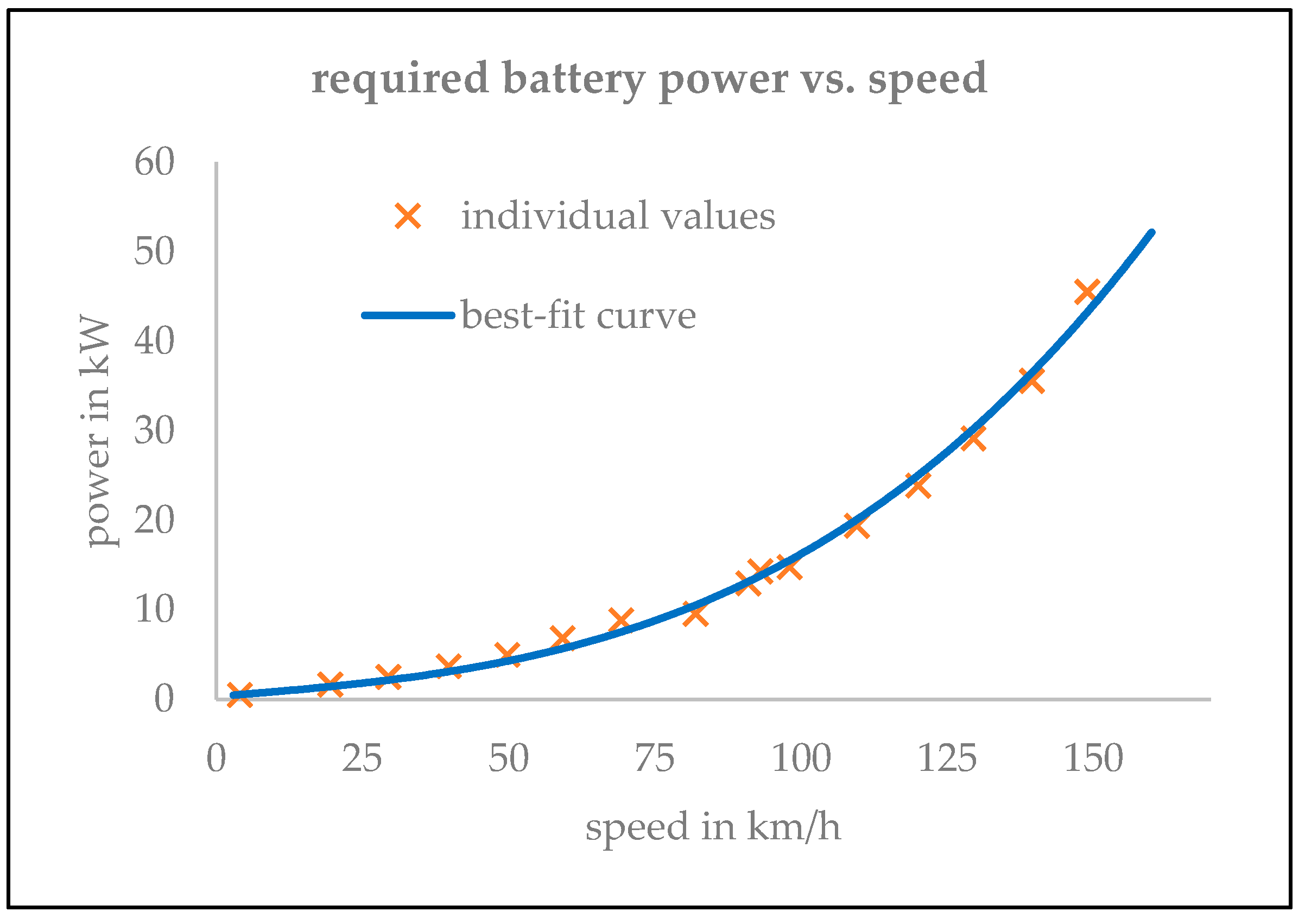
3.2. Determination of Vehicle Loss Parameters
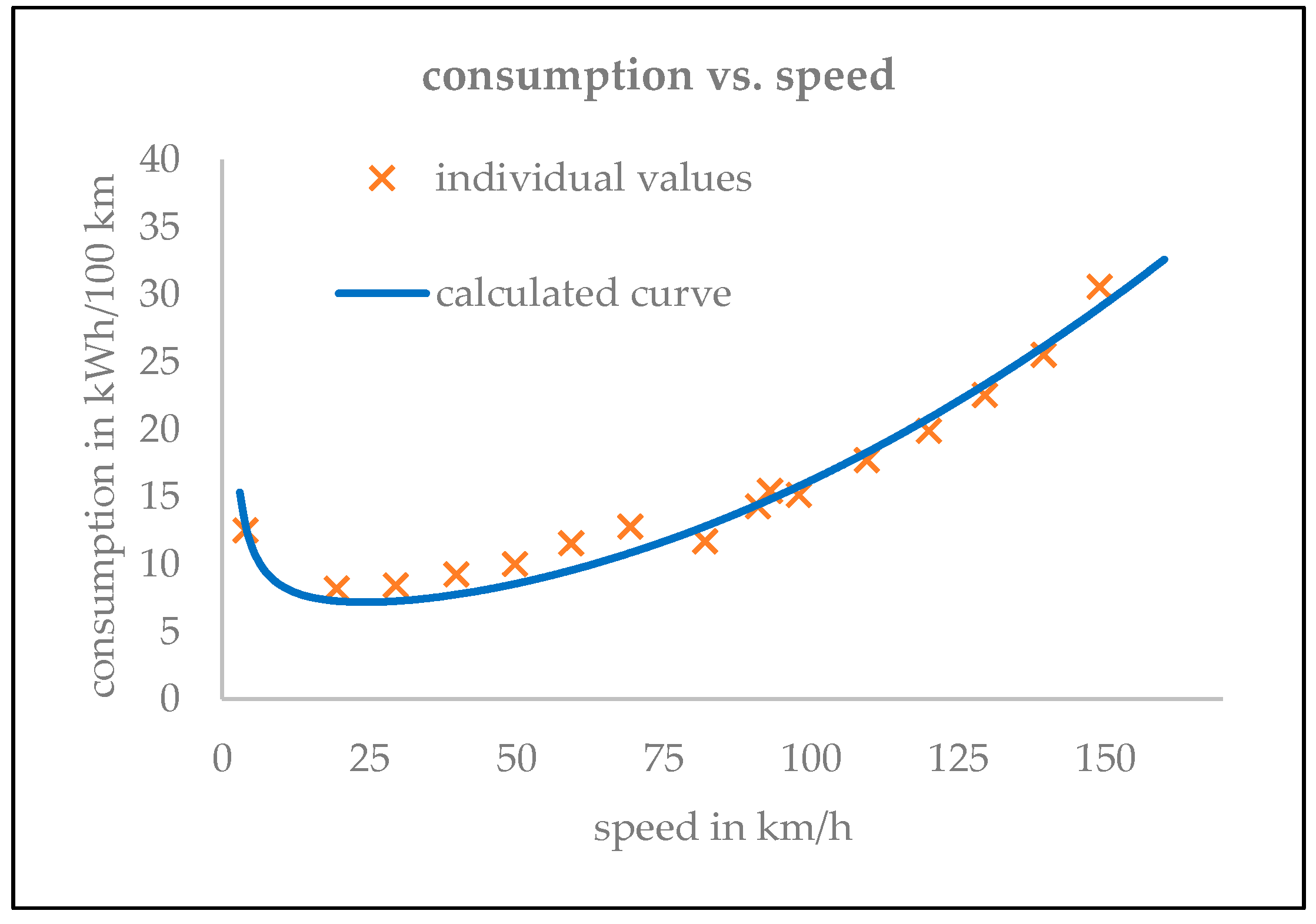
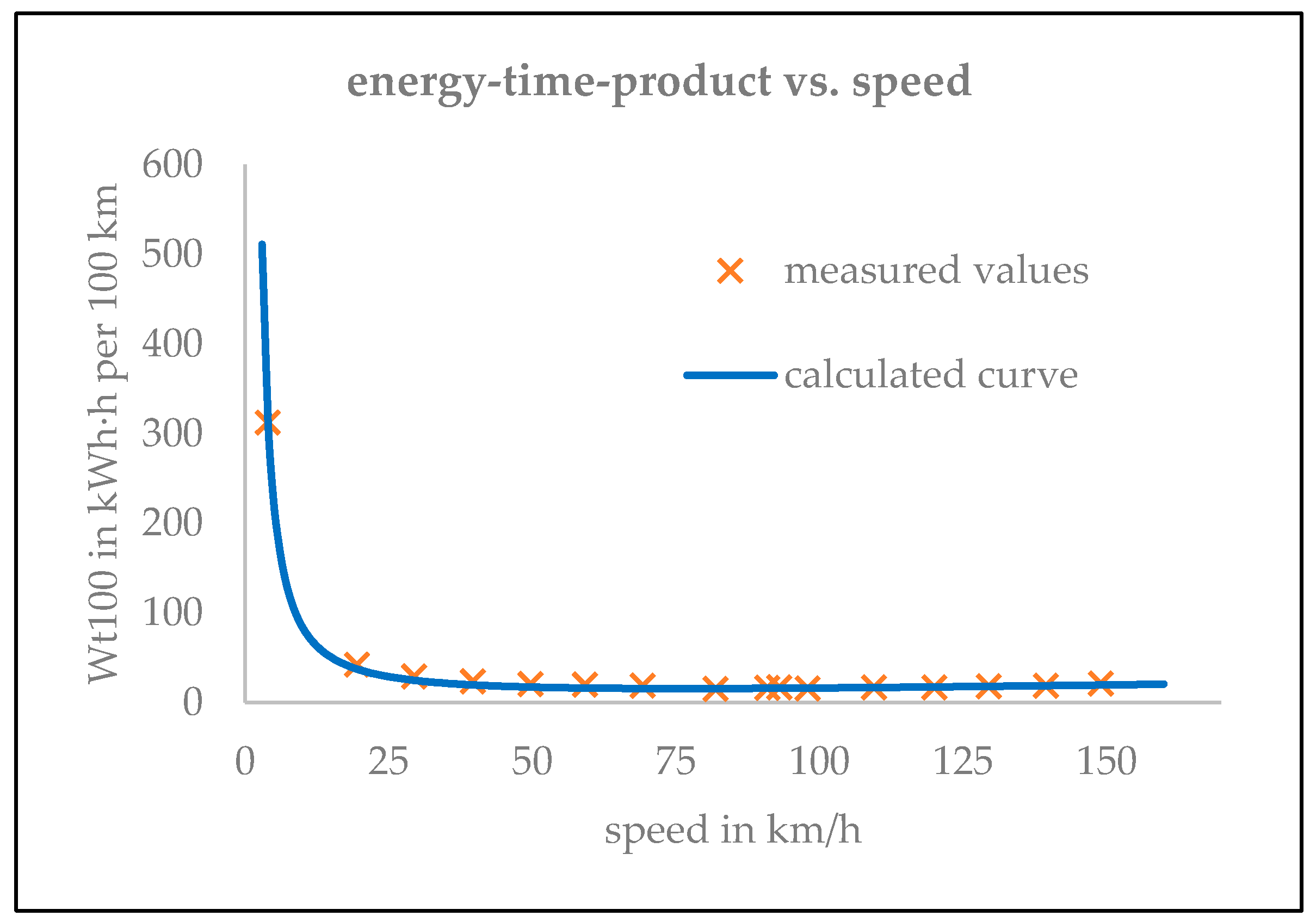
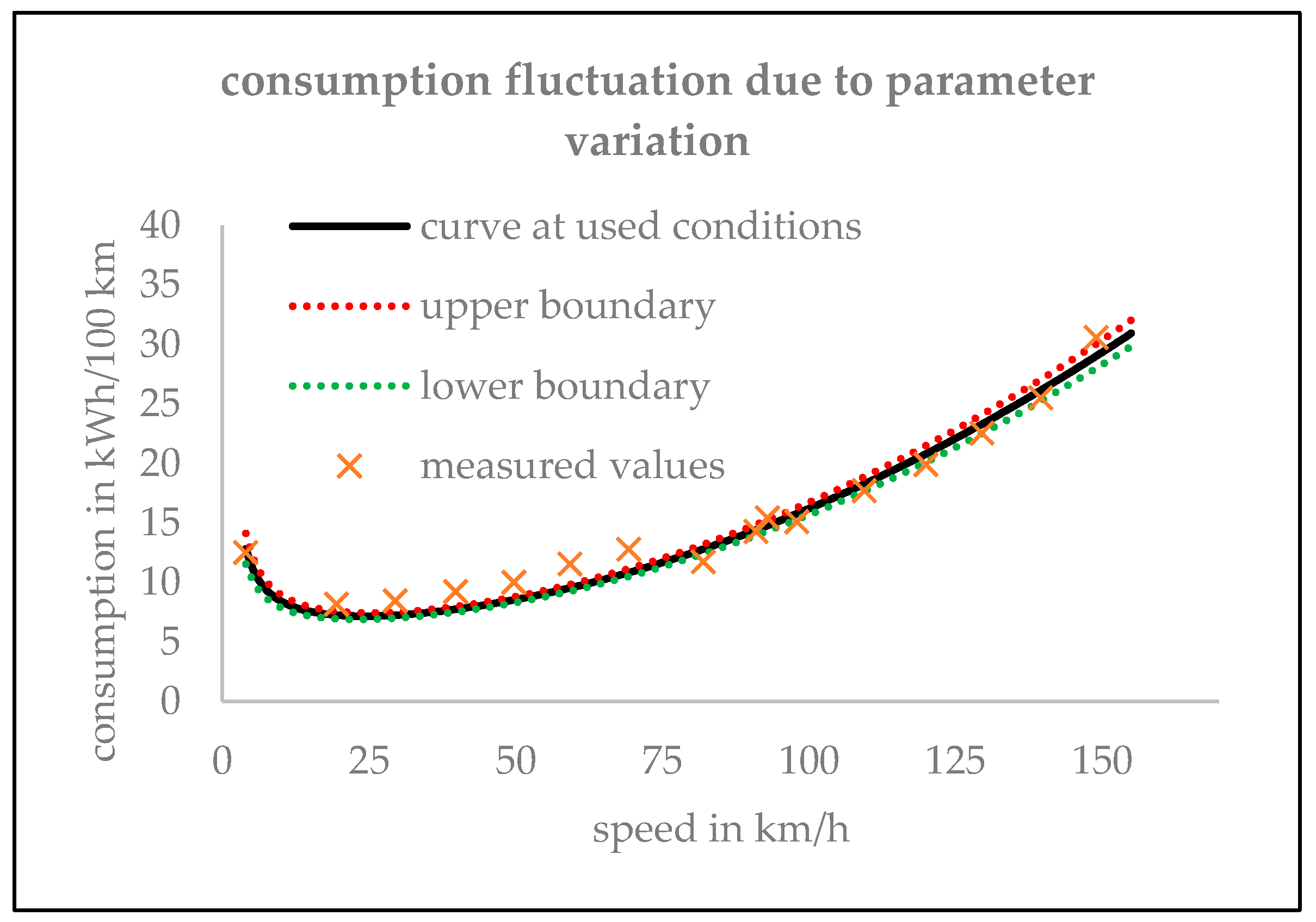
3.3. Consumption Considerations
4. Discussion
5. Conclusions
6. Disclaimer
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- European Parliament. EU Ban on the Sale of New Petrol and Diesel Cars from 2035 Explained. Available online: https://www.europarl.europa.eu/topics/en/article/20221019STO44572/eu-ban-on-sale-of-new-petrol-and-diesel-cars-from-2035-explained (accessed on 11 May 2024).
- Stevic, Z.; Radovanovic, I. Energy Efficiency of Electric Vehicles. In New Generation of Electric Vehicles; InTech Open: London, UK, 2012; pp. 93–134. [Google Scholar] [CrossRef][Green Version]
- Mavlonov, J.; Ruzimov, S.; Tonoli, A.; Amati, N.; Mukhitdinov, A. Sensitivity Analysis of Electric Energy Consumption in Battery Electric Vehicles with Different Electric Motors. World Electr. Veh. J. 2023, 14, 36. [Google Scholar] [CrossRef]
- Mruzek, M.; Gajdáč, I.; Kučera, L.; Barta, D. Analysis of Parameters Influencing Electric Vehicle Range. Proc. Eng. 2016, 134, 165–174. [Google Scholar] [CrossRef]
- Szumska, E.; Jurecki, R. Parameters Influencing on Electric Vehicle Range. Energies 2021, 14, 4821. [Google Scholar] [CrossRef]
- Jaswal, A.; Madhurakavi, R.; Chandrasekaran, P. Low Rolling Resistance Tires and Their Impact on Electric Vehicles. SAE Technol. Pap. 2017, 28, 1941. [Google Scholar] [CrossRef]
- Beckers, C.; Besselink, I.; Nijmeijer, H. Combined Rolling Resistance and Road Grade Estimation Based on EV Powertrain Data. IEEE Trans. Veh. Technol. 2023, 72, 3201–3213. [Google Scholar] [CrossRef]
- Andriaminahy, F.; Amamou, A.; Kelouwani, S.; Zioui, N.; Ghobadpour, A.; Agbossou, K. Comparative Study of Vehicle Aerodynamic and Rolling Resistance Coefficients Estimation Methods. In Proceedings of the 2019 IEEE Vehicle Power and Propulsion Conference (VPPC), Hanoi, Vietnam, 14–17 October 2019. [Google Scholar]
- Van Greunen, R.; Oosthuizen, C. Data Driven Methods for Finding Coefficients of Aerodynamic Drag and Rolling Resistance of Electric Vehicles. World Electr. Veh. J. 2023, 14, 134. [Google Scholar] [CrossRef]
- Kiyakli, A.; Solmaz, H. Modeling of an Electric Vehicle with MATLAB/Simulink. Int. J. Automot. Sci. Technol. 2018, 2, 9–15. [Google Scholar] [CrossRef]
- Banuri, S.; Qayyum, U.; Qureshi, K.; Ahmed, A. Investigation of Drag Coefficients for Various Car Models. In Proceedings of the 17th IBCAST—2020: 17th International Bhurban Conference on Applied Sciences and Technology (IBCAST), Islamabad, Pakistan, 14–18 January 2020. [Google Scholar]
- Anderson, L.; Larsen, J.; Fraser, E.S.; Schmidt, B.; Dyre, J.C. Rolling Resistance Measurement and Model Development. J. Transp. Eng. 2014, 141, 2. [Google Scholar] [CrossRef]







| Vehicle Type | ID.3 Pro Performance |
|---|---|
| Total energy content of battery | 62 kWh |
| Motor | permanent magnet synchronous motor |
| Continuous power | 70 kW |
| Peak power | 150 kW |
| Peak torque | 310 Nm |
| Vehicle mass including one driver | appr. 1900 kg |
| Projected frontal area | 2.36 m2 |
| Drag coefficient | 0.267 |
| Tires | Bridgestone Turanza Eco |
| Tire dimension | 215/45R20 |
| Set tire pressure 2 | front and back: 2.5 bar |
| Transmission gear | one gear |
| Speed (km/h) | Consumption (kWh/100 km) | Battery Power (kW) | Ambient Temperature (°C) | Air Density 1 (kg/m3) |
|---|---|---|---|---|
| 4.0 | 12.50 | 0.5 | 13 | 1.2335 |
| 19.5 | 8.18 | 1.6 | 8 | 1.2560 |
| 29.5 | 8.43 | 2.5 | 8 | 1.2560 |
| 39.8 | 9.20 | 3.7 | 8 | 1.2549 |
| 49.8 | 9.98 | 5.0 | 8 | 1.2566 |
| 59.3 | 11.53 | 6.8 | 8 | 1.2577 |
| 69.3 | 12.78 | 8.8 | 8 | 1.2538 |
| 82.0 | 11.70 | 9.6 | 15 | 1.2260 |
| 91.0 | 14.25 | 13.0 | 6 | 1.2628 |
| 93.0 | 15.40 | 14.3 | 12 | 1.2400 |
| 98.0 | 15.10 | 14.8 | 13 | 1.2357 |
| 109.5 | 17.70 | 19.4 | 12 | 1.2390 |
| 120.0 | 19.90 | 23.9 | 12 | 1.2400 |
| 129.5 | 22.50 | 29.1 | 11 | 1.2411 |
| 139.5 | 25.50 | 35.6 | 9 | 1.2510 |
| 149.0 | 30.55 | 45.5 | 9 | 1.2521 |
| Function Parameter | Obtained Numerical Value |
|---|---|
| parameter in kg/m | 0.4938 |
| parameter in h3/km3·kW 1 | 1.05842·10−5 |
| parameter in N | 191.9 |
| parameter in kWh/km 1 | 0.05331 |
| parameter (equals to static power ) | 0.3 |
| Projected vehicle frontal area | 2.36 m2 |
| Air drag coefficient | 0.267 |
| Average ambient temperature 1 | 10 °C |
| Air density 2 | 1.247 kg/m3 |
| Acceleration due to gravity | 9.81 m/s2 |
| Speed (km/h) | Consumption (kWh/100 km) | Driving Time t100 1 (h) | Energy–Time Product (kWh h) |
|---|---|---|---|
| 4.0 | 12.50 | 25.00 | 312.50 |
| 19.5 | 8.18 | 5.13 | 41.92 |
| 29.5 | 8.43 | 3.39 | 28.56 |
| 39.8 | 9.20 | 2.52 | 23.14 |
| 49.8 | 9.98 | 2.01 | 20.05 |
| 59.3 | 11.53 | 1.69 | 19.45 |
| 69.3 | 12.78 | 1.44 | 18.45 |
| 82.0 | 11.70 | 1.22 | 14.27 |
| 91.0 | 14.25 | 1.10 | 15.66 |
| 93.0 | 15.40 | 1.08 | 16.56 |
| 98.0 | 15.10 | 1.02 | 15.41 |
| 109.5 | 17.70 | 0.91 | 16.16 |
| 120.0 | 19.90 | 0.83 | 16.58 |
| 129.5 | 22.50 | 0.77 | 17.37 |
| 139.5 | 25.50 | 0.72 | 18.28 |
| 149.0 | 30.55 | 0.67 | 20.50 |
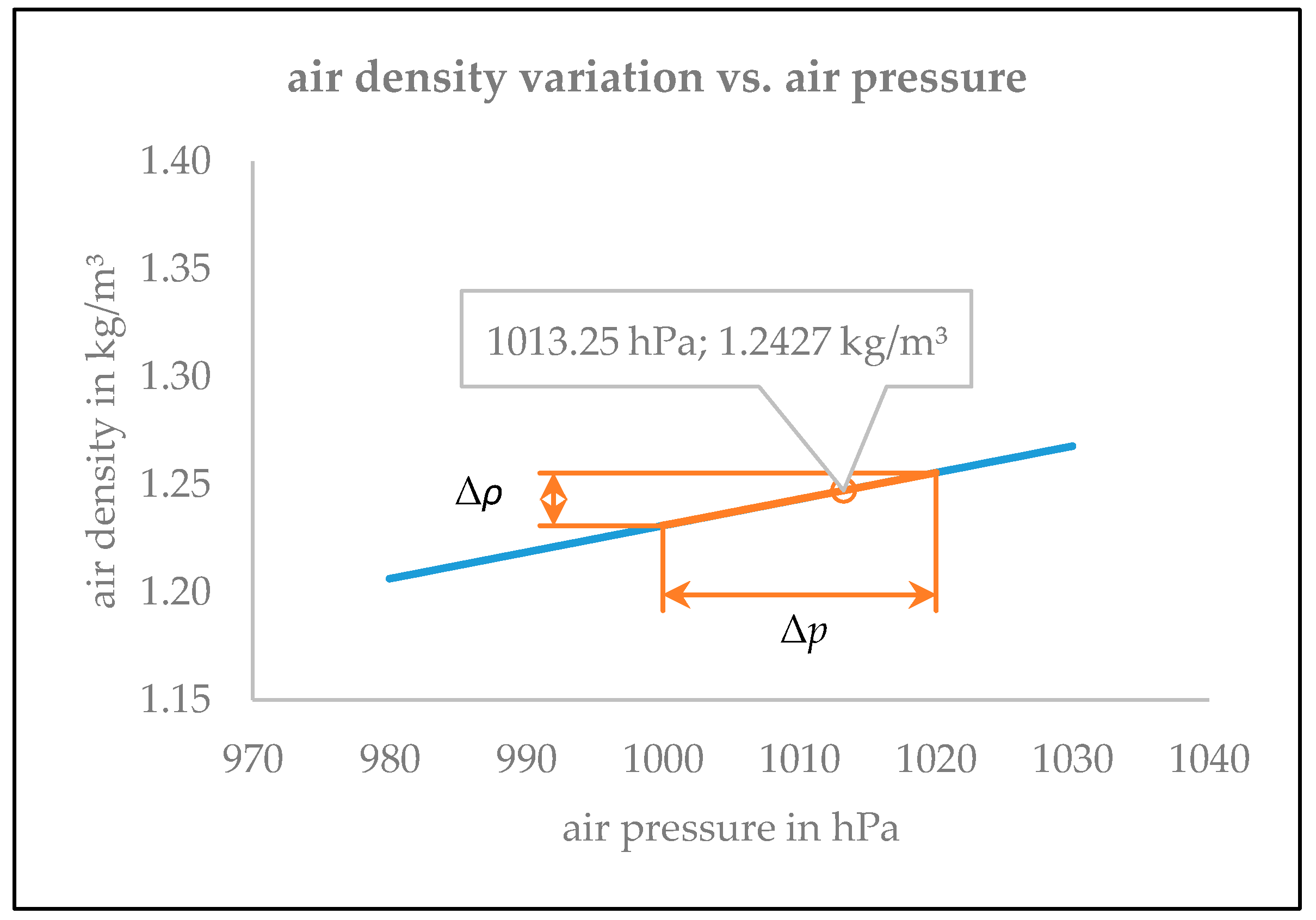
| Due to Temperature 1 | Due to Air Pressure 2 | Boundary Values | |
|---|---|---|---|
| max | |||
| min |
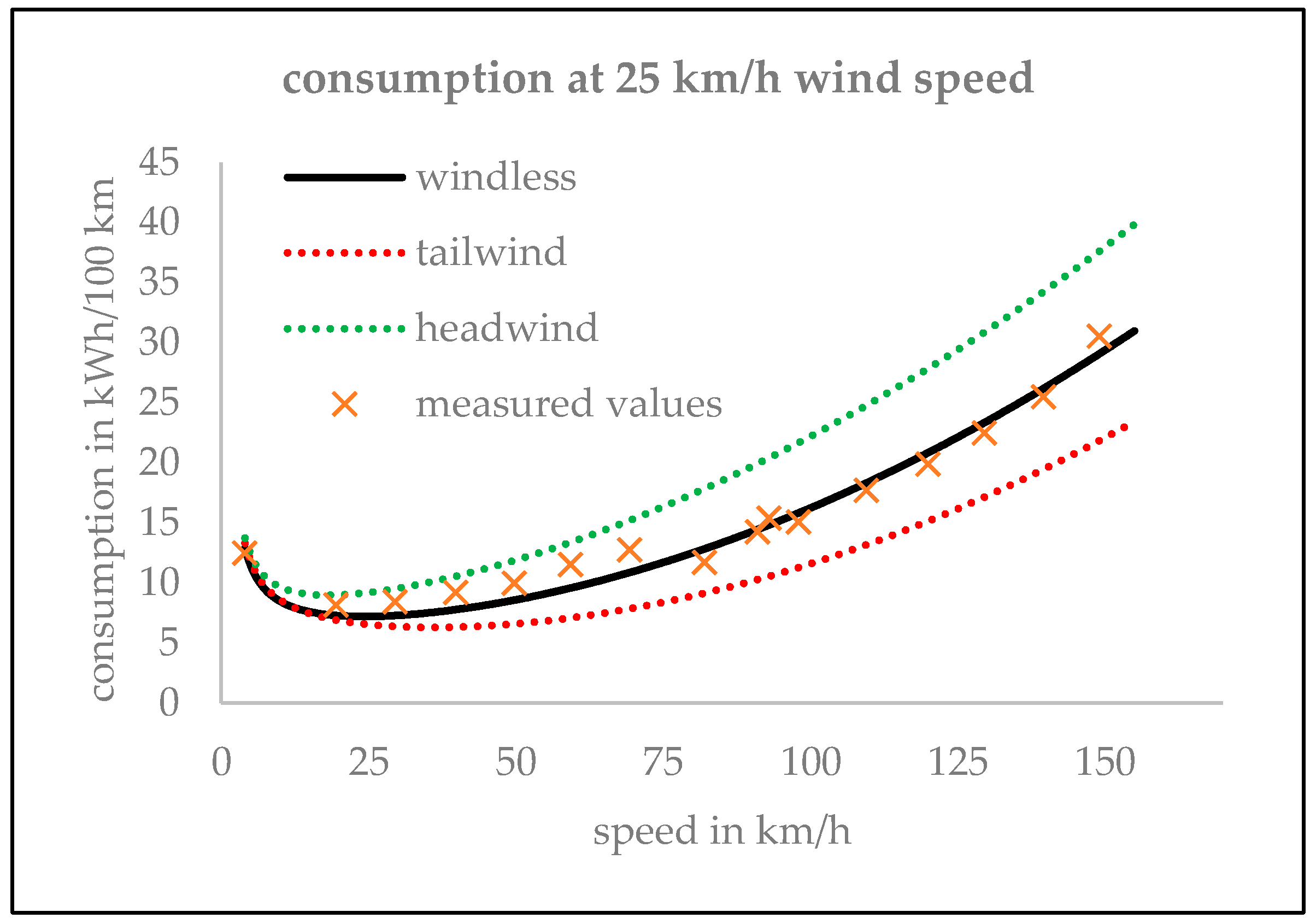
| Wind Direction | Battery Power | Consumption |
|---|---|---|
| outward drive with headwind | 4.22 kW | 10.55 kWh/100 km |
| return drive with tailwind | 2.53 kW | 6.32 kWh/100 km |
| average of cycle run | 3.37 kW | 8.44 kWh/100 km |
| windless drive | 3.11 kW | 7.77 kWh/100 km |
| difference 1 | 0.26 kW (8.5%) | 0.66 kWh/100 km (8.5%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wego, A.; Schubotz, S. Simple Method for Determining Loss Parameters of Electric Cars. World Electr. Veh. J. 2024, 15, 298. https://doi.org/10.3390/wevj15070298
Wego A, Schubotz S. Simple Method for Determining Loss Parameters of Electric Cars. World Electric Vehicle Journal. 2024; 15(7):298. https://doi.org/10.3390/wevj15070298
Chicago/Turabian StyleWego, Ansgar, and Stefan Schubotz. 2024. "Simple Method for Determining Loss Parameters of Electric Cars" World Electric Vehicle Journal 15, no. 7: 298. https://doi.org/10.3390/wevj15070298
APA StyleWego, A., & Schubotz, S. (2024). Simple Method for Determining Loss Parameters of Electric Cars. World Electric Vehicle Journal, 15(7), 298. https://doi.org/10.3390/wevj15070298





