Abstract
Future field work tasks will require mountain tractors to pass through rough terrain with limited human supervision. The wheel–soil interaction plays a critical role in rugged terrain mobility. In this paper, an algorithm for the estimation of soil characteristic parameters based on the Simpson numerical integration method and Gauss–Newton iteration method is presented. These parameters can be used for passability prediction or in a traction control algorithm to improve tractor mobility and to plan safe operation paths for autonomous navigation systems. To verify the effectiveness of the solving algorithm, different initial values and soils were selected for simulation calculations of soil characteristic parameters such as internal friction angle, settlement index, and the joint parameter of soil cohesion modulus and friction modulus. The results show that the error was kept within 2%, and the calculation time did not exceed 0.84 s, demonstrating high robustness and real-time performance. To test the applicability of the algorithm model, further research was conducted using different wheel parameters of electric mountain tractors under wet clay conditions. The results show that these parameters also have high accuracy and stability with only a few iterations. Thus, the estimation algorithm can meet the requirements of quickly and accurately identifying soil characteristic parameters during tractor operation. A criterion for the passability of wheeled tractors through unknown terrain is proposed, utilizing identified soil parameters.
1. Introduction
The future farmland work will require tractors to perform challenging unmanned operation tasks in hilly and mountainous terrains to ensure the safety of drivers [1,2,3]. The task objective includes crossing rugged terrain with high autonomy. Without the knowledge of terrain characteristics, it will be difficult to effectively control the tractor to complete the expected tasks on time. An example of mission failure is a wheeled tractor trapped on sandy terrain. To achieve these goals, future control and planning methods must consider the operating environment of tractors to fully utilize their capabilities and improve mobility.
From the dynamics of wheel terrain interaction, it can be seen that soil parameters play a crucial role in determining vehicle traction and wheel drive torque [4,5]. For example, wheeled tractors have very different mobility characteristics when driving on loose sand compared to hard clay. Estimating soil characteristic parameters will enable unmanned tractors to predict their ability to safely traverse different terrains [6,7]. It is also possible to improve traction or reduce energy consumption by adjusting its motion control and work route planning strategies [8]. Therefore, soil characteristic parameter estimation is an important task in achieving the unmanned operation of tractors in harsh weather environments.
Some researchers have studied terrain parameter estimation. Usually, these methods involve using specialized testing equipment for offline estimation [9,10]. The parameter estimation of a legged walking system was studied in [11], but this method relies on feedback from multi-axis force sensors embedded in the robot’s legs and is not suitable for wheeled systems. A terrain parameter estimation method for tracked vehicles was proposed in [12]. This method assumes a highly simplified force coefficient model for the interaction between tracks and terrain, which is not suitable for deformable rough terrain. Iagnemma et al. proposed a method for the online estimation of soil cohesion and internal friction angle using wheeled mobile robots applied to planetary probes [13]. This algorithm is based on a simplified form of classical ground mechanics equations and uses the linear least squares method to calculate terrain parameters in real time. But it is not specified whether it is applicable to all soils, and the estimation effect on other soil parameters needs to be verified. Kang et al. proposed an online soil parameter estimation method suitable for cohesive terrain [14]. The method applied the measurement of wheel torque, slip, sinkage, and weight on the wheel to compute cohesion and internal friction angles efficiently. However, to have stable and converging estimation values, the conditioning of data is needed. Liu et al. established a wheel–soil analysis model which is linearly related to terrain stiffness and shear strength [15]. In a steady state, the relative error between the estimated value and the experimental value is less than 7%. Hutangkabodee et al. presented a novel technique for identifying soil parameters for a wheeled vehicle traversing unknown terrain based on the Newton–Raphson method [16]. The key soil parameters to be identified are the internal friction angle, shear deformation modulus, and lumped pressure–sinkage coefficient. This method is suitable for off-road wheeled vehicles with sufficiently high wheel hub pressure. However, improper selection of the initial value of the algorithm can lead to an incorrect solution or no solution. Therefore, based on this method, Yang et al. combined machine vision to classify ground types and provided suggestions for initial value selection so that the recognition error of terrain parameters was less than 12.58% [17]. Ray used Bayesian multiple-model estimation and an available terrain model to estimate the physical soil properties and stress distribution parameters that relate to vehicle mobility in real time [18]. But these models need to use proprioceptive sensors such as an accelerometer, rate gyros, wheel speeds, motor currents, and ground speed. Thus, the calculation cost is relatively high. Xue et al. tested the applicability of dynamic Bayesian estimation techniques in parameter estimation for traction models. A real-time estimation method for wheel terrain parameters based on training a multiple-output least squares support vector machine (LS-SVM) was studied [19]. Li et al. used an adaptive robust extended Kalman filter to estimate the internal friction angle and sinking index [20]. But the other parameters were fixed to nominal values. A summary of the recent developments in soil parameter estimation methods is presented in Table 1.

Table 1.
Summary of soil parameter estimation methods.
Due to the low soil bearing capacity and adhesion capacity in hilly and mountainous areas, it is easy to for wheel sinking and slipping to occur, even causing an inability to drive normally, resulting in the tractor’s mobility being reduced, soil structure damage, intensified tire wear, and increased energy consumption, which brings great difficulties to agricultural production [21,22,23,24,25,26]. The fast and accurate identification of wheel soil parameters during tractor operation can realize the predictive control of traction and driving wheel torque, improve the tractor’s passability, and, thus, help implement effective path planning and provide a data base for unmanned or intelligent driving.
This study focuses on the problem of wheel sinking and slipping in the context of electric mountain tractors in hilly and mountainous environments. An estimation algorithm for three key soil characteristic parameters, internal friction angle, settlement index, and the joint parameter of soil cohesion modulus and friction modulus, is presented. The algorithm relies on simplified forms of classical wheel–soil interaction equations and uses a Gauss–Newton iteration method to compute soil parameters in real time. The method is computationally efficient and thus suitable for implementation on a tractor. Also, the method uses sensors that are likely to be part of tractor systems and thus does not add to system complexity. Simulation results show that the algorithm can accurately and efficiently identify soil characteristic parameters for various soil types.
2. Algorithm for Solving Soil Characteristic Parameters
The passability of a tractor when driving on soft ground is mainly reflected in the interaction between the wheels and the soil. The vehicle system and soil system each constitute a relatively complex nonlinear system, and their interactions are more complex. This is the fundamental reason why it is difficult to accurately establish a model for passability research which involves a large number of vehicle configuration parameters, soil parameters, and dynamic response parameters. To establish an estimation system for soil characteristic parameters, it is necessary to first clarify the key parameters.
The driving modes or postures of mountain tractors are diverse, including straight driving, turning, uphill and downhill driving, etc. The research that focuses on the passability problem under each driving mode is not the same. The work presented in this article is mainly aimed at the passability problem of tractors driving on continuous flat and soft ground in a straight line.
Among the theoretical models of vehicle ground passability, the semi-empirical model is the most classic, combining vehicle dynamics, soil mechanics, and other theories to analyze the wheel–soil interaction, and the key parameters of soil characteristics are basically reflected in this model. Therefore, a semi-empirical model is used here to solve the key parameters of soil characteristics.
Figure 1 shows the force distribution of tractor wheels on soft ground using a semi-empirical model, where all the forces applied are wheel forces [27,28]. When the driving torque T and the vertical load W act on a wheel with radius r and width b, the wheel rolls forward, and a normal force and shear force are generated on the wheel–soil contact surface, which are used to balance the vertical load and overcome the travelling resistance and to provide the driving force required for the vehicle to move forward, i.e., the hook traction force DP. Z is the amount of wheel sinking, and is the wheel–soil interaction angle. The contact angle range between the wheel and the ground is , where is the angle of the ground first contacted by the rigid wheel in the vertical direction, i.e., the wheel’s entry angle, and is the angle of the ground last leaving the rigid wheel in the vertical direction, i.e., the wheel’s departure angle.
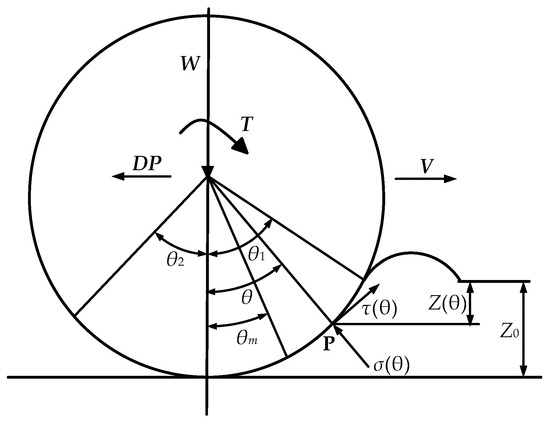
Figure 1.
Schematic diagram of force distribution interaction between rigid wheel and soft ground.
The passability of a tractor mainly depends on the resistance caused by soil deformation and the traction force provided by the hook, which can be calculated through the mechanical property model of the soil in principle. The semi-empirical model is constructed based on the theory of shear action, and the relevant parameters are solved as follows:
2.1. Wheel Sinkage
Under the action of vertical load and driving torque, when a rigid wheel is traveling on loose soil, the soil will deform and sink, and the wheel sinking amount Z0 is obtained from the geometrical relationship.
where is the angle between the vertical direction and the point where the wheel first contacts the ground.
If the total sinkage of the tractor during operation can be determined, the range of the interaction area between the rigid wheel and the soil can be confirmed. The amount of sinkage Z at the point in the area of action is:
2.2. Normal Stress of Interface
In order to calculate the normal stress generated at the interface of the wheel–soil interaction, researchers have proposed a number of bearing pressure models, including the model proposed by the Soviet scholar Birulia, the model proposed by the American scholar Bekker, and the improved model proposed by the British scholar Reece. Among them, the earliest and most widely used is the bearing pressure model proposed by Bekker, which assumes that the effect of the vertical deformation of soil under wheel load is equivalent to the deformation of soil under the pressure of a flat plate and determines the relationship equation of normal stress through pressure bearing tests [29]:
where b is the length of the short side of the contact surface between the wheel and the soil, which is generally taken as the tire width; is the cohesion modulus; kφ is the friction modulus; and n is the subsidence index.
At present, the distribution law of normal stress is not quite certain, and a unified theoretical method for determining the location of the maximum stress point has not yet been formed. Wong and Reece used an empirical formula to determine the location of the maximum stress point [30]:
where is the point of maximum normal stress in the region of action; are empirical coefficients; and δ represents the wheel slip rate.
In the action region from the maximum normal stress point to the beginning of the interface or the end of the interface , the normal stress decreases along the rim of the wheel. And we make the following assumption: the normal stresses are the same at the equivalent location points and , which have similar distances to and , respectively. The model specifies counterclockwise as positive and clockwise as negative; therefore,
Then,
According to Bekker’s pressure subsidence formula, in the region of action from to ,
Within the region of action to ,
Since is mainly related to the degree of rut recovery, it is generally considered that the rut recovery is slower; is smaller and can be considered as 0, and it can be expressed as:
Substitute Equation (4):
2.3. Shear Stress of Interface
In the interaction between wheels and soil, the shear stress generated depends on shear deformation or displacement. Currently, the most commonly used is the soil shear model proposed by Janosi et al. [16], whose shear stress is expressed as follows:
where j is the soil shear deformation; K is the shear elastic modulus of the soil; is the maximum shear stress of the soil; c is the soil cohesion; is the normal stress of the wheel–soil interface; and φ is the internal friction angle of the soil.
By analyzing the shear model described in the above equation, it is found that it has the following characteristics:
(1) When j = 0, = 0; when j tends towards ∞, = ;
(2) increases with j, and the rate of increase is first fast and then slow;
Therefore, a function that satisfies the above characteristics can be used to replace the more complex shear characteristic model formula. Based on this principle, the original shear model Equation (11) can be simplified to Equation (12). Figure 2 shows a comparison of the distribution curves between the improved shear model and the original shear model. From the graph, it can be seen that the trajectories of the two curves are basically the same, with almost no difference.
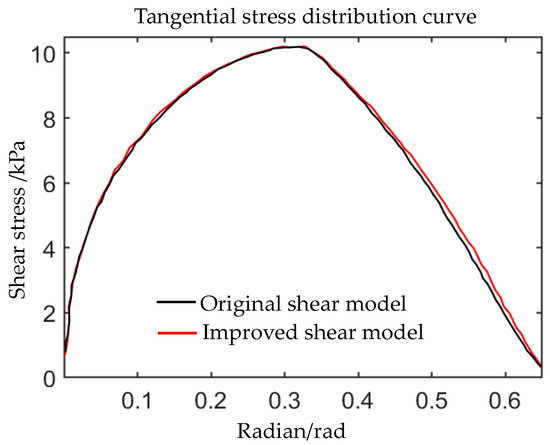
Figure 2.
Comparison of the distribution curves of the improved shear stress model and the original shear model.
From the Janosi shear stress model, it can be seen that the shear stress of the rigid wheel is closely related to the soil shear displacement, and the shear displacement can be determined by analyzing the sliding speed Vj of the wheel.
When the tractor accelerates forward, the actual distance traveled by the driving wheel is less than the distance that should be traveled during pure rolling, which is called wheel slip. Generally, the degree of wheel slip is represented by the slip rate. The slip rate is defined as the ratio of the difference between the theoretical rolling speed and the actual moving speed of the wheel to the theoretical rolling speed:
where V represents the overall forward linear speed of the wheel, i.e., the actual moving speed; is the rolling angular velocity of the wheel.
As shown in Figure 3, for any point P on the wheel soil interface, its velocity can be divided into horizontal moving velocity V and tangential velocity . Therefore, the slip velocity of the wheel Vj can be obtained from velocity vector analysis:
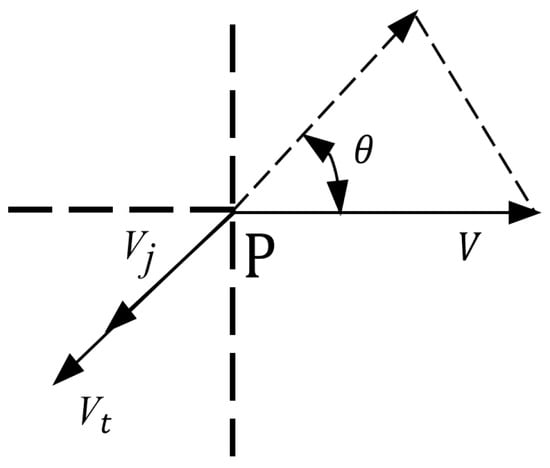
Figure 3.
Vector diagram of the velocity at point P on the outer edge of the wheel.
Substituting Equation (13):
P in the figure represents any point on the outer edge of the wheel, and the slip velocity of the wheel Vj is divided into horizontal movement velocity V and tangential velocity through vector analysis.
The shear displacement j(θ) of the contact point between the wheel and the soil can be obtained by the following equation:
Combining the above formula, the expression for shear stress distribution can be obtained [31]:
2.4. Mechanics Equation of Wheel–Soil Interaction
Since the value of K is generally small, is a number extremely close to 1. The shear stress is less affected by the slip rate. In order to reduce the computational difficulty and accelerate the solution speed, this paper fixed the slip rate as a constant.
In the study of rigid wheel–soil stress, it is found that generally appears near the middle position of the action region. Therefore, in this study, in order to facilitate the analysis of the empirical coefficients and , it is assumed that is in the middle position of the action region, that is:
Combining the wheel–soil relationship and soil stress analysis, the mechanics equation between the rigid wheel and soil can be obtained:
2.5. Algorithm for Solving Soil Characteristic Parameters
There are five common parameters for describing soil characteristics, the adhesion coefficient c, internal friction angle φ, cohesive modulus kc, friction modulus kφ, and subsidence index n. The effects of these parameter changes on vertical load W, hook traction force DP, and driving torque T were experimentally tested. The results show that W, DP, and T are insensitive to changes in the values of the adhesion coefficient c, i.e., the changes in c only slightly change the values of W, DP, and T. Therefore, the solution of c is not considered in this paper, and it is considered as a known value during the solution process. So, these four parameters φ, kc, kφ and n are selected here to represent soil characteristics.
Due to the fact that W, DP, and T can be directly measured by onboard sensors, these four soil characteristic parameters can be calculated through Equations (20)–(22), as shown in the algorithm framework in Figure 4.
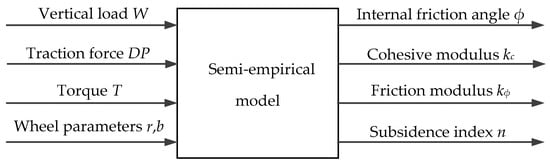
Figure 4.
Algorithm framework for estimation of soil characteristic parameters.
3. Algorithm Simplification
Due to the complex integration relationship between soil characteristic parameters and driving wheel dynamic parameters in Equations (20)–(22), it is difficult to directly apply them to solve soil characteristics. In order to balance the engineering practicality and computational accuracy of semi-empirical models, the Simpson numerical integration method is used to simplify the integration formula in the solving algorithm in order to reduce the calculation time and meet the real-time requirements of the algorithm [32,33].
The Simpson formula is represented as follows:
Suppose:
In the study of wheel–soil interaction relationship, it has been found that often occurs near the middle of the interaction region, and the rebound part of generally soft soil has a relatively small support effect on rigid wheels, i.e., is smaller, so for the sake of convenience in research, it is generally assumed that .
Using the Simpson formula to simplify the above formula, it can be concluded that:
As can be seen from the previous equation,
Then,
As can be seen from the previous equation,
Then,
As can be seen from the previous equation,
Then,
As can be seen from the previous equation,
Then,
Similarly, for ,
Thus, the expressions of W, DP, and T can be simplified by the above equation:
Integrating the above equations, it can be concluded that:
Due to the fact that the mathematical model in the above equation consists of three nonlinear equation systems but four soil characteristic parameters need to be solved, in order to facilitate the solution, the two parameters of the soil cohesion modulus and soil friction modulus kφ are merged to form joint parameter KL:
KL can be detected through two wheels of different widths during actual operation. Therefore, it can be concluded that:
Simplifying Equations (35) and (36) together:
4. Algorithm Solving and Simulation
4.1. Solving Based on Gauss–Newton Iteration Method
The Newton iteration method, also known as the Newton–Raphson method, is a method that was proposed by Newton in the 17th century to approximately solve equations in real and complex fields. It is a classic algorithm for solving nonlinear least squares estimation problems.
The standard format for the Newton iteration method [34] is:
The Gauss–Newton iteration method is an algorithm that improves upon the typical Newton iteration method. Its basic idea is to use the Taylor series expansion to approximate the nonlinear regression model and then, through multiple iterations, adjust the regression coefficients multiple times to continuously approximate the optimal regression coefficient of the nonlinear regression model. Finally, it minimizes the sum of squared residuals of the original model.
The iterative formula is:
The algorithm for solving soil characteristic parameters based on the Gauss–Newton iteration method is shown in Figure 5.
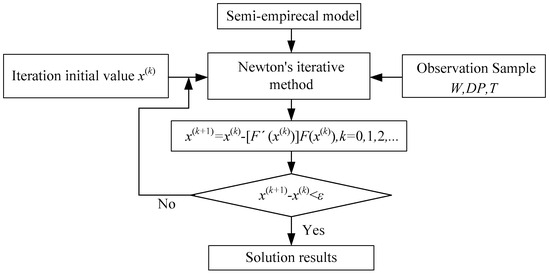
Figure 5.
Block diagram of Gauss–Newton iterative solution method.
The actual measurements, such as the vehicle dynamic corresponding parameters (W, DP, T) and wheel–soil characteristic parameters (c, K, r, b, etc.), constitute the random observation sample x(k) input for the solution model. The soil characteristic parameters (Kc, Kφ, φ, and n) constitute the model output x(k+1). The process starts from the set initial value and continuously updates until the error is less than the set error threshold ε. Among them, F’(x(k)) is the Jacobi matrix of the Gauss–Newton iteration method, also known as the sensitivity coefficient.
4.2. Algorithm Simulation and Discussion
We conducted simulation experiments on the established estimation model of soil characteristic parameters. The experimental data used parameters from wet clay and sandy loam ground tests, and the corresponding soil characteristic parameters measured in the experimental environment are shown in Table 2.

Table 2.
Soil characteristic parameters and vehicle parameters.
According to the established estimation model for the soil characteristic parameters, the slip rate is controlled to be 0.2; simulation experiments were carried out by selecting two representative soils commonly found in hilly mountainous conditions.
The principle of the Gauss–Newton iteration method states that its algorithm stability is closely related to the initial value of the iteration [35]. Therefore, it can be considered to detect the feasibility of the algorithm by selecting different initial iteration values. The iterative process is shown in Figure 6, Figure 7 and Figure 8. When the error between the initial value and the true value is set to 20%, after six iterations, the parameters tend to converge and are relatively close to the true value. The error is within 2%. And the durations under wet clay and sandy loam conditions were 0.37 and 0.73 s, respectively. The iteration results are shown in Table 3.
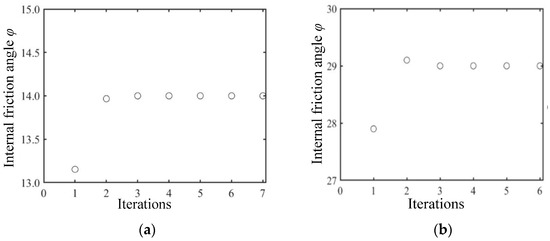
Figure 6.
Iteration of soil internal friction angle for different soils based on the condition of 20% initial value error from the true value. (a) Based on wet clay; (b) based on sandy loam.
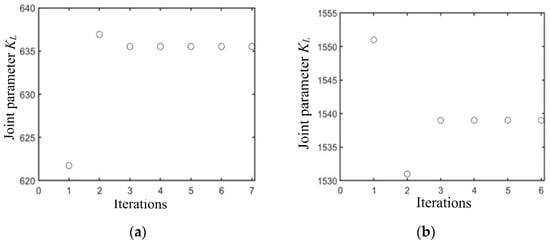
Figure 7.
Iteration of joint parameter for different soils based on the condition of 20% initial value error from the true value condition. (a) Based on wet clay; (b) based on sandy loam.
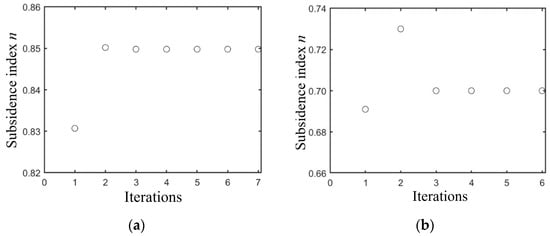
Figure 8.
Iteration of subsidence index for different soils based on the condition of 20% initial value error from the true value. (a) Based on wet clay; (b) based on sandy loam.

Table 3.
Iteration results for soil parameters based on 20% error from true value.
We changed the initial iteration value again and set the true value error to 50%. The iteration process is shown in Figure 9, Figure 10 and Figure 11. The iteration results are shown in Table 4. The error is also within 2%. And the durations under wet clay and sandy loam conditions were 0.44 and 0.84 s, respectively. From the solution results, it can be seen that when the initial value deviates from the true value within a certain range, the number of iterations will increase, but the resulting error is still small, and the time taken is relatively short.
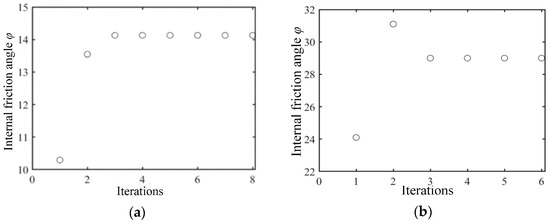
Figure 9.
Iteration of soil internal friction angle for different soils based on the condition of 50% initial value error from the true value. (a) Based on wet clay; (b) based on sandy loam.
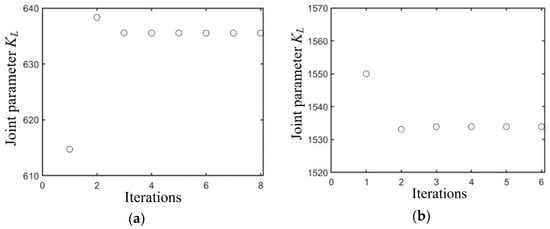
Figure 10.
Iteration of the joint parameter for different soils based on the condition of 50% initial value error from the true value. (a) Based on wet clay; (b) based on sandy loam.
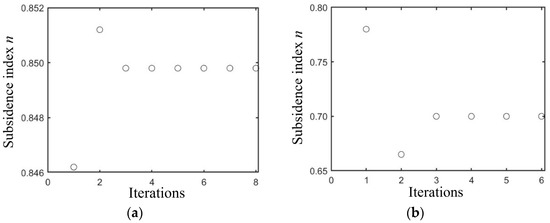
Figure 11.
Iteration of the subsidence index for different soils based on the condition of 50% initial value error from the true value. (a) Based on wet clay; (b) based on sandy loam.

Table 4.
Iteration results for soil parameters based on 50% error from true value.
In order to further verify the universality of the model, the simulation was performed again by changing the tractor parameters under wet clay conditions. The soil characteristic parameters and the tractor parameters are shown in Table 5. Similar to the above verification process, numerical values with an error of 20% and 50% from the true value were used as initial iteration values to substitute into the model. The iteration results are shown in Table 6 and Table 7. From the solution results, it can be seen that under changing the conditions of the experimental tractor, the mean error is also within 2%, and the computing time is within 0.6 s, which indicates that the algorithm has universality.

Table 5.
Soil characteristic parameters and tractor parameters.

Table 6.
Iteration results of different tractors based on 20% error from true value.

Table 7.
Iteration results of different tractors based on 50% error from true value.
5. The Use of Identified Soil Parameters
The soil characteristic parameter identification method presented in this study can enhance the driving performance of wheeled tractors on unfamiliar terrains, offering the most optimal approach for vehicle design and operation. This section examines whether a particular terrain can be traversed based on the identified soil parameters.
When the driving wheel torque is less than the torque required to cross the terrain, the driving wheels will slip, preventing the tractor from moving. To address this scenario, a traversability criterion for wheeled tractors on unknown terrains can be established, as depicted in Figure 12.
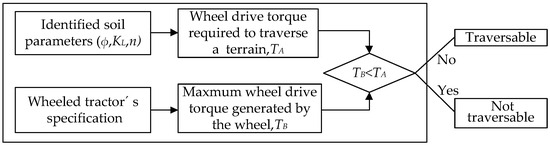
Figure 12.
Traversability criterion for wheeled tractors.
With the application of Equation (18), the identified soil parameters can be utilized to forecast the wheel drive torque required for wheeled tractors to traverse various terrains. Figure 13 depicts the wheel drive torques required for two distinct terrains. If the wheel drive torque is 500 N·m, the tractor will be capable of traversing sandy loam, which necessitates wheel drive torques of less than 200 N·m, but it will not be able to traverse wet clay, whose wheel drive torque required for passage through is approximately 1000 N·m.
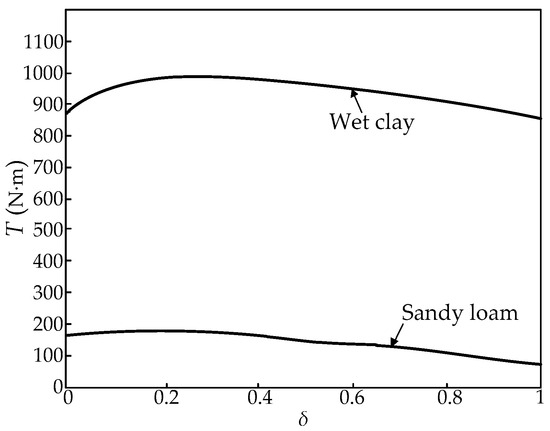
Figure 13.
Drive torques required for wheel tractor to traverse two distinct terrains.
6. Conclusions
In order to solve the problem of wheel subsidence and the sliding of electric mountain tractors in hilly and mountainous environments, an estimation algorithm for wheel soil characteristic parameters based on the Gauss–Newton iteration method has been proposed. The algorithm has the following characteristics:
- (1)
- Due to the complexity and exponential form of the shear stress model, it requires a large amount of computation and high accuracy in subsequent calculations. Therefore, this paper adopted feature extraction to simplify the model from an exponential function to a linear function, and the experimental results prove that the simplification is reasonable.
- (2)
- Owing to the nonlinear characteristics of the algorithm for solving soil characteristic parameters, calculations are difficult. The algorithm was simplified using the Simpson formula and solved using the Newton iteration method. Due to the simplified algorithm not requiring numerical integration for each calculation cycle, the solving speed is improved.
- (3)
- To verify the stability of the solving algorithm, different initial iteration values with an error of 20% or 50% from the true value were selected for simulation calculations of soil characteristic parameters such as internal friction angle, settlement index, and the join parameter of soil cohesion modulus and friction modulus. The results showed that the error was kept within 2%, and the calculation time did not exceed one second, which demonstrates that the algorithm has strong robustness to measurement noise and initial conditions.
- (4)
- In order to further verify the universality of the model, different soil and tractor parameters were used to test the algorithm, and the calculation time did not exceed one second, and the calculation accuracy was basically consistent, which means it can meet the requirements for quickly and accurately identifying soil characteristic parameters.
- (5)
- Through utilizing identified soil parameters to forecast the driving torque needed for a wheeled tractor to traverse terrain and contrasting it with the maximum driving torque that the wheels can generate, one can ascertain whether a tractor is capable of traversing unfamiliar terrain.
In the future, soil characteristic parameter estimation can be combined with traction control to improve the passability and efficiency of tractors operating in hilly and mountainous areas. It can also be applied to ground classification, constructing GIS maps with soil parameter information, and providing data sources for the analysis of the passability and path planning of unmanned tractors in operating areas.
Author Contributions
Conceptualization, Z.X. and T.F.; methodology, Z.X. and T.F.; software, T.F.; validation, L.X., H.X. and Z.L.; formal analysis, J.Z.; investigation, H.X. and Z.L.; resources, J.Z.; data curation, H.X. and J.Z.; writing—original draft preparation, Z.X. and T.F.; writing—review and editing, Z.X.; visualization, Z.X. and Z.L.; supervision, L.X.; project administration, L.X.; funding acquisition, L.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Scientific and Technological Research Project of Henan Province, grant number 222102110233, and the National Key Research and Development Program of China, grant number 2022YFD2001203.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ren, H.; Wu, J.; Lin, T.; Yao, Y.; Liu, C. Research on an Intelligent Agricultural Machinery Unmanned Driving System. Agriculture 2023, 13, 1907. [Google Scholar] [CrossRef]
- He, Z.; Bao, Y.; Yu, Q.; Lu, P.; He, Y.; Liu, Y. Dynamic path planning method for headland turning of unmanned agricultural vehicles. Comput. Electron. Agric. 2023, 206, 107699. [Google Scholar] [CrossRef]
- Mathankumar, M.; Thirumoorthi, P. Robo Farming-A platform for unmanned agriculture. Int. J. Innov. Technol. Explor. Eng. 2018, 8, 249–252. [Google Scholar]
- Karpman, E.; Kövecses, J.; Holz, D.; Skonieczny, K. Discrete element modelling for wheel-soil interaction and the analysis of the effect of gravity. J. Terramech. 2020, 91, 139–153. [Google Scholar] [CrossRef]
- Tsubaki, H.; Ishigami, G. Experimental study on wheel-soil interaction mechanics using in-wheel sensor and particle image velocimetry Part I: Analysis and modeling of normal stress of lightweight wheeled vehicles. J. Terramech. 2021, 93, 23–39. [Google Scholar] [CrossRef]
- Gao, H.B.; Li, W.H.; Ding, L.; Deng, Z.Q.; Liu, Z. A method for on-line soil parameters modification to planetary rover simulation. J. Terramech. 2012, 49, 325–339. [Google Scholar] [CrossRef]
- Liu, W.; Wang, R.C.; Ding, R.K.; Meng, X.P.; Yang, L. On-line estimation of road profile in semi-active suspension based on unsprung mass acceleration. Mech. Syst. Signal Process. 2020, 135, 106370. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, M.; Yin, Y.; Rong, X.; Li, Y.; Hua, Z. Static gait planning method for quadruped robot walking on unknown rough terrain. IEEE Access 2019, 7, 177651–177660. [Google Scholar] [CrossRef]
- Shibly, H.; Iagnemma, K.; Dubowsky, S. An equivalent soil mechanics formulation for rigid wheels in deformable terrain, with application to planetary exploration rovers. J. Terramech. 2005, 42, 1–13. [Google Scholar] [CrossRef]
- Yoshida, K.; Watanabe, T.; Mizuno, N.; Ishigami, G. Terramechanics-based analysis and traction control of a lunar/planetary rover. In Field and Service Robotics: Recent Advances in Reserch and Applications; Springer: Berlin/Heidelberg, Germany, 2006; pp. 225–234. [Google Scholar]
- Caurin, G.; Tschichold-Gurman, N. The development of a robot-terrain interaction system for walking machines. In Proceedings of the 1994 IEEE International Conference on Robotics and Automation, San Diego, CA, USA, 8–13 May 1994; Volume 2, pp. 1013–1018. [Google Scholar]
- Le, A.T.; Rye, D.C.; Durrant-Whyte, H.F. Estimation of track-soil interactions for autonomous tracked vehicles. In Proceedings of the International Conference on Robotics and Automation, Albuquerque, NM, USA, 25 April 1997; Volume 2, pp. 1388–1393. [Google Scholar]
- Iagnemma, K.; Kang, S.; Shibly, H.; Dubowsky, S. Online terrain parameter estimation for wheeled mobile robots with application to planetary rovers. IEEE Trans. Robot. 2004, 20, 921–927. [Google Scholar] [CrossRef]
- Kang, S. Terrain Parameter Estimation and Traversability Assessment for Mobile Robots. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2003. [Google Scholar]
- Liu, Z.L.; Guo, J.L.; Ding, L.; Gao, H.; Guo, T.; Deng, Z. Online estimation of terrain parameters and resistance force based on equivalent sinkage for planetary rovers in longitudinal skid. Mech. Syst. Signal Process. 2019, 119, 39–54. [Google Scholar] [CrossRef]
- Hutangkabodee, S.; Zweiri, Y.H.; Seneviratne, L.D.; Althoefer, K. Performance prediction of a wheeled vehicle on unknown terrain using identified soil parameters. In Proceedings of the IEEE International Conference on Robotics and Automation, Orlando, FL, USA, 15–19 May 2006; pp. 3356–3361. [Google Scholar]
- Yang, F.; Lin, G.; Zhang, W. Terrain classification for terrain parameter estimation based on a dynamic testing system. Sens. Rev. 2015, 35, 329–339. [Google Scholar] [CrossRef]
- Ray, L.E. Autonomous terrain parameter estimation for wheeled vehicles. Unmanned Syst. Technol. X 2008, 6962, 505–516. [Google Scholar]
- Xue, L.; Li, J.; Zou, M.; Zong, W.; Huang, H. In situ identification of shearing parameters for loose lunar soil using least squares support vector machine. Aerosp. Sci. Technol. 2016, 53, 154–161. [Google Scholar] [CrossRef]
- Li, Y.; Ding, L.; Zheng, Z.; Yang, Q.; Zhao, X.; Liu, G. A multi-mode real-time terrain parameter estimation method for wheeled motion control of mobile robots. Mech. Syst. Signal Process. 2018, 104, 758–775. [Google Scholar] [CrossRef]
- Chelf, F.; Gobbi, M.; Holjevac, N. Vehicle subsystems’ energy losses and model-based approach for fuel efficiency estimation towards an integrated optimization. Int. J. Veh. Des. 2018, 76, 46–81. [Google Scholar] [CrossRef]
- Son, J.; Kim, Y.; Kang, S.; Ha, Y. Enhancing Safety through Optimal Placement of Components in Hydrogen Tractor: Rollover Angle Analysis. Agriculture 2024, 14, 315. [Google Scholar] [CrossRef]
- Alonso, A.; Froidevax, M.; Javaux, M.; Laloy, E.; Mattern, S.; Roisin, C.; Vanclooster, M.; Bielders, C. Fine-resolution profile-scale data to depict the impact of tillage treatment and machine traffic on agricultural soil structure and hydrologic properties. Data Brief 2023, 51, 109759. [Google Scholar] [CrossRef]
- Wang, L.-J.; Ma, S.; Jiang, J.; Zhao, Y.-G.; Zhang, J.-C. Spatiotemporal variation in ecosystem services and their drivers among different landscape heterogeneity units and terrain gradients in the southern hill and mountain belt, China. Remote Sens. 2021, 13, 1375. [Google Scholar] [CrossRef]
- Allman, M.; Dudáková, Z.; Jankovský, M.; Vlčková, M.; Juško, V.; Tomčík, D. Soil compaction after increasing the number of wheeled tractors passes on forest soils in west Carpathians. Forests 2022, 13, 109. [Google Scholar] [CrossRef]
- Toivio, J.; Helmisaari, H.S.; Palviainen, M.; Lindeman, H.; Ala-Ilomäki, J.; Sirén, M.; Uusitalo, J. Impacts of timber forwarding on physical properties of forest soils in southern Finland. For. Ecol. Manag. 2017, 405, 22–30. [Google Scholar] [CrossRef]
- Zerbato, L.; Vella, A.D.; Galvagno, E.; Vigliani, A.; Data, S.; Sacchi, M.E. A Numerical Analysis of Terrain and Vehicle Characteristics in Off-Road Conditions through Semi-Empirical Tire Contact Modelling; SAE Technical Paper: 2024-01-2297; SAE: Atlanta, GA, USA, 2024. [Google Scholar]
- Zhang, K.; Zhang, Y.; Xu, P. An algorithm for parameter identification of semi-empirical tire model. SAE Int. J. Veh. Dyn. Stab. NVH 2021, 5, 379–396. [Google Scholar] [CrossRef]
- Shi, Y.; Liu, J.; Huang, D.; Xu, M.; Zhai, S.; Zhang, W.; Jiang, P. Prediction and Experimental Study of Tire Slip Rate Based on Chassis Sinkage Amount. Agriculture 2023, 13, 665. [Google Scholar] [CrossRef]
- Jasoliya, D.; Untaroiu, A.; Untaroiu, C. A review of soil modeling for numerical simulations of soil-tire/agricultural tools interaction. J. Terramech. 2024, 111, 41–64. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, S.; Feng, Q.; Qi, S.; Han, S.; Chen, L. Topological shape optimisation of a novel whole bead structure based on an interlaminar shear stress criterion. Int. J. Mech. Mater. Des. 2022, 18, 961–974. [Google Scholar] [CrossRef]
- Siricharuanun, P.; Erden, S.; Ali, M.A.; Budak, H.; Chasreechai, S.; Sitthiwirattham, T. Some new Simpson’s and Newton’s formulas type inequalities for convex functions in quantum calculus. Mathematics 2021, 9, 1992. [Google Scholar] [CrossRef]
- Ali, A.H.; Páles, Z. Estimates of linear expressions through factorization. J. Approx. Theory 2024, 299, 106019. [Google Scholar] [CrossRef]
- Li, C.Z.; Yuan, C.; Cui, A.G. Newton’s Iteration Method for Solving the Nonlinear Matrix Equation X+∑i=1m A i* X− 1 A i= Q. Mathematics 2023, 11, 1578. [Google Scholar] [CrossRef]
- Argyros, I.K.; Hilout, S. On the Gauss–Newton method. J. Appl. Math. Comput. 2011, 35, 537–550. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).