An Enhanced State-Space Modeling for Detecting Abnormal Aging in VRLA Batteries
Abstract
1. Introduction
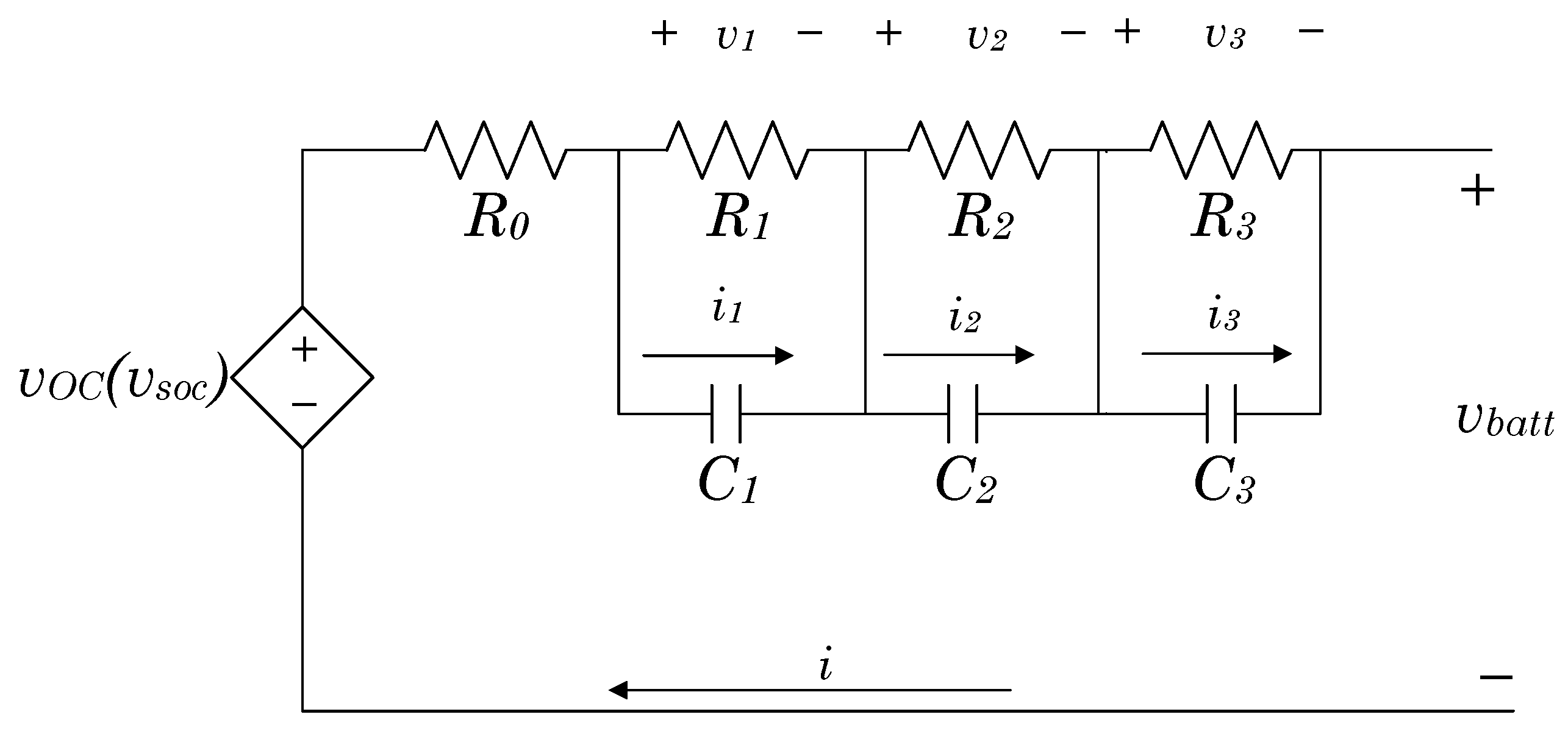
2. Battery Equivalent Circuit Model
- Measurable variables: the voltage () is the model output, and the current (i) is the model input [7]; the temperature is considered constant for this work.
- Dynamic response parameters: represents the instantaneous voltage/current change and the other elements splits the transient response into the time constants [30].
- Battery states: These represent the energy storage and the modification of the battery response [31].
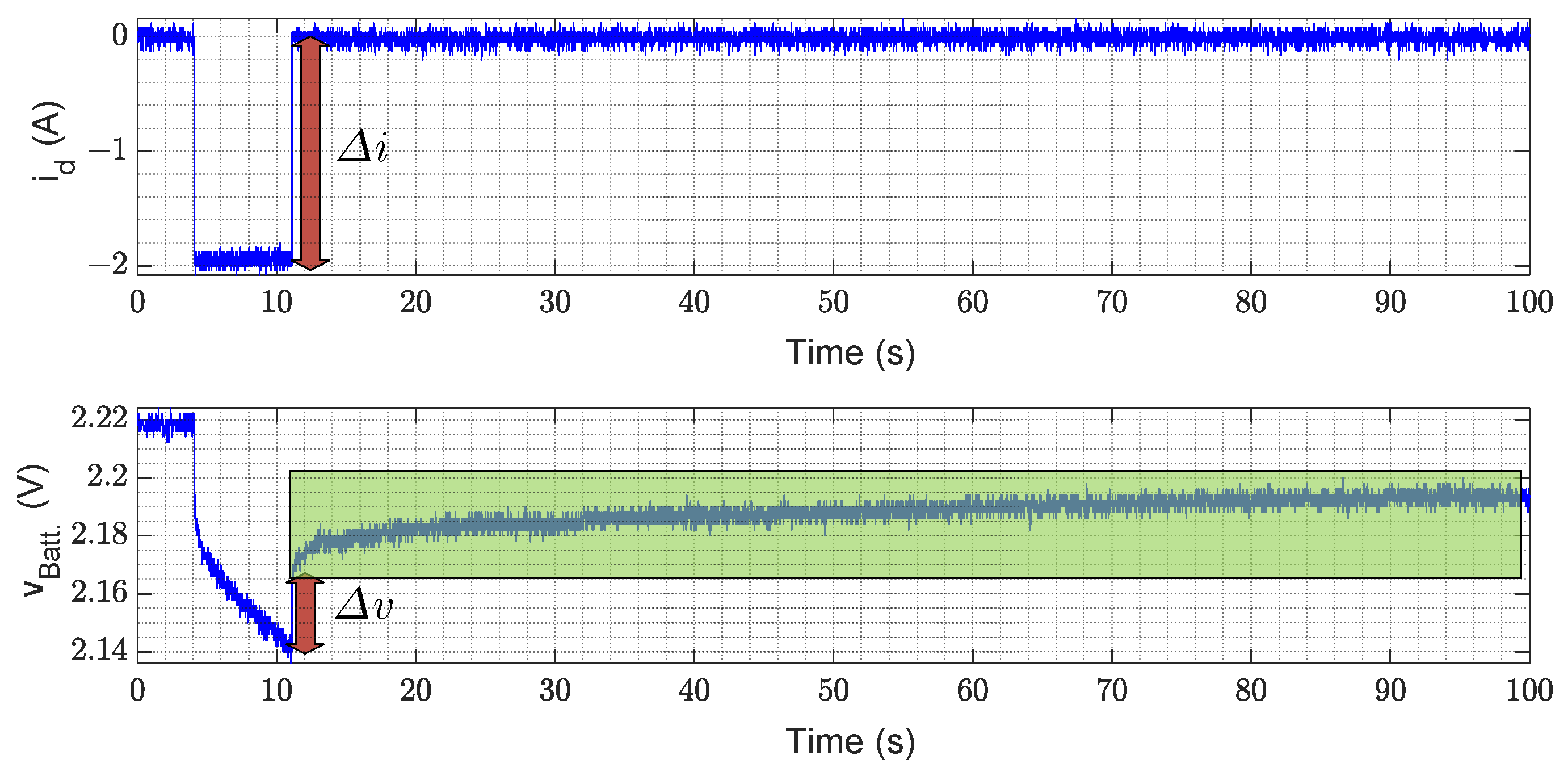
2.1. Model Parameter Identification
2.2. Equivalent Electric Circuit Model
- (a)
- It is dependent on the current sensor precision.
- (b)
- It is susceptible to deviations created by different initial conditions.
- (c)
- The integral action is prone to bias depending on cumulative errors developed for offsets, which forces the use of anti-windup techniques.
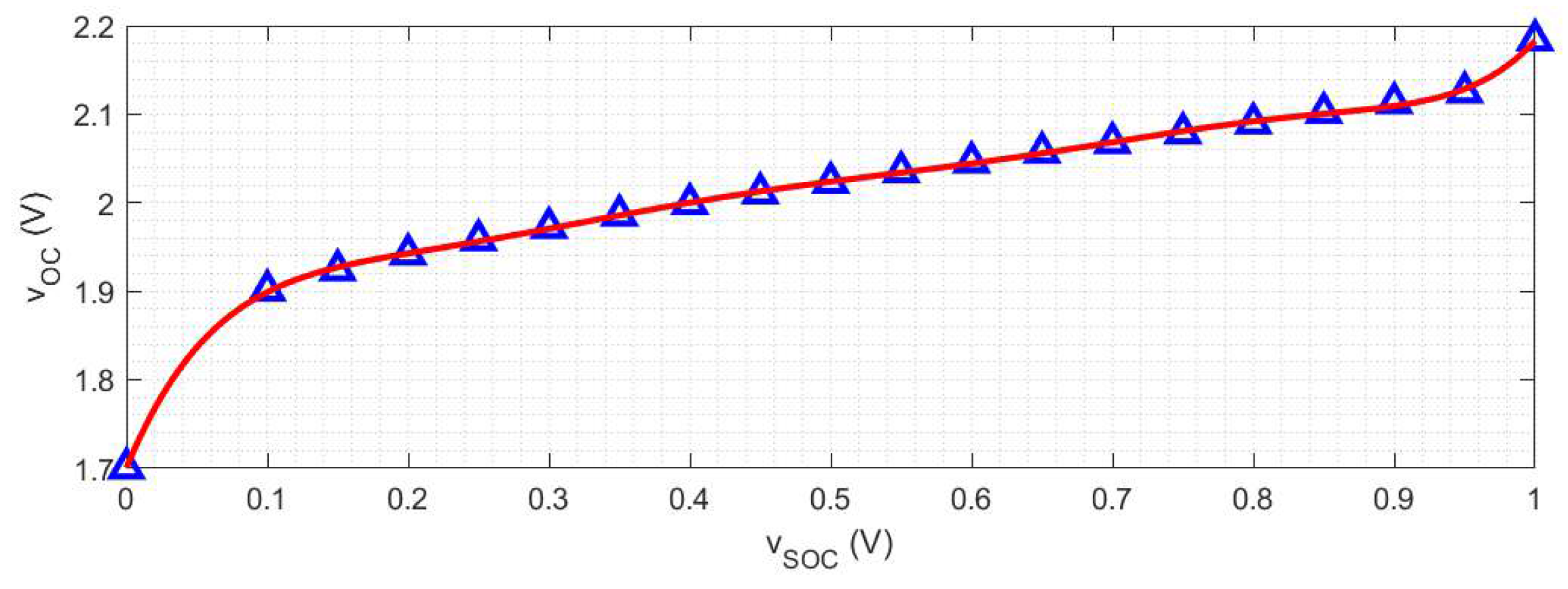
2.3. Nonlinear State-of-Charge Observer
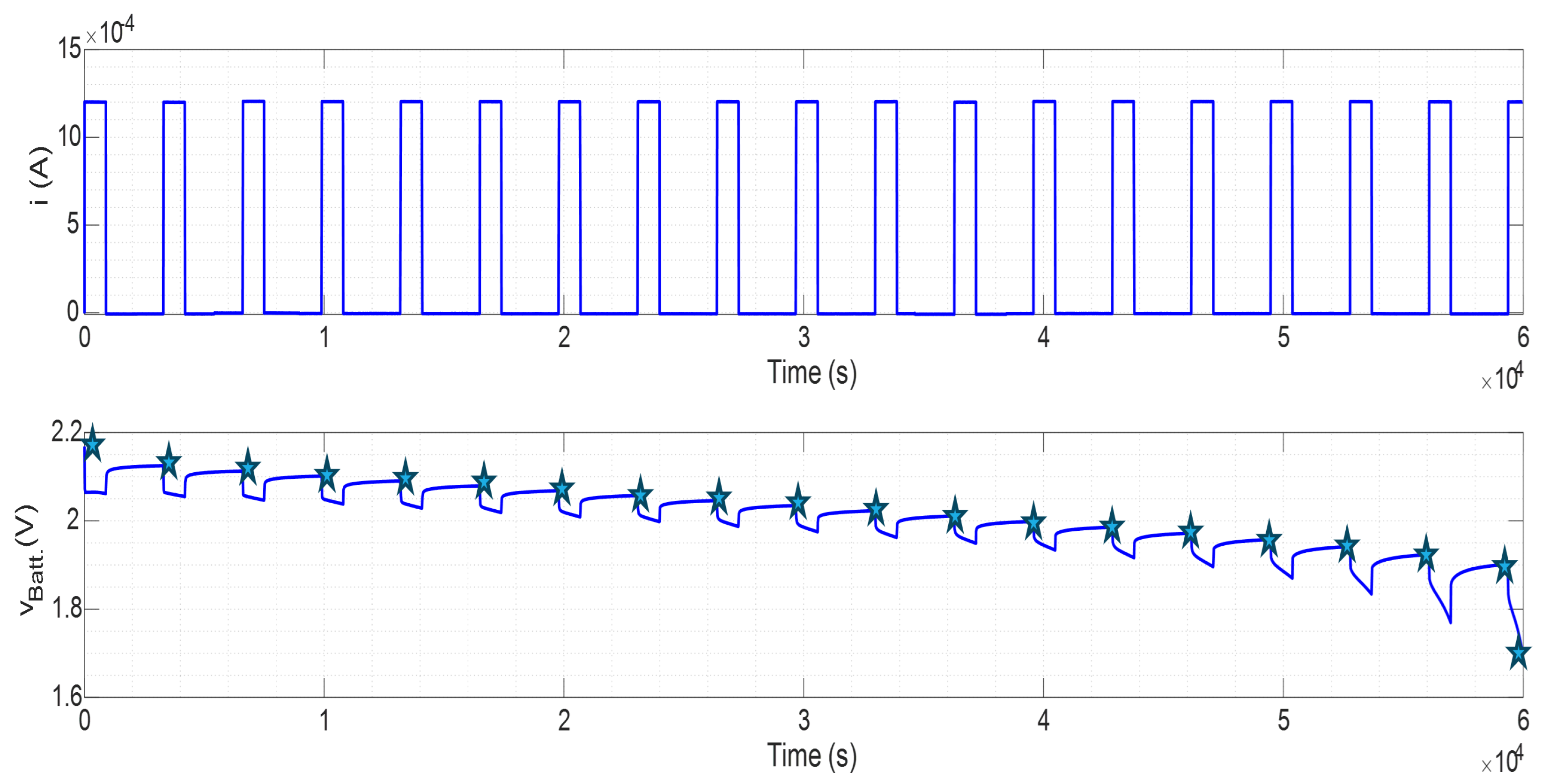
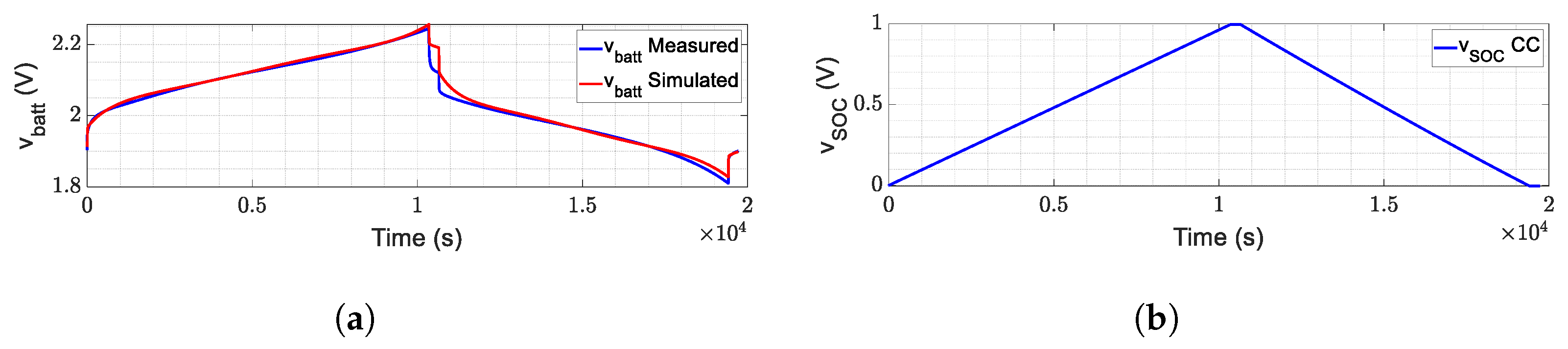
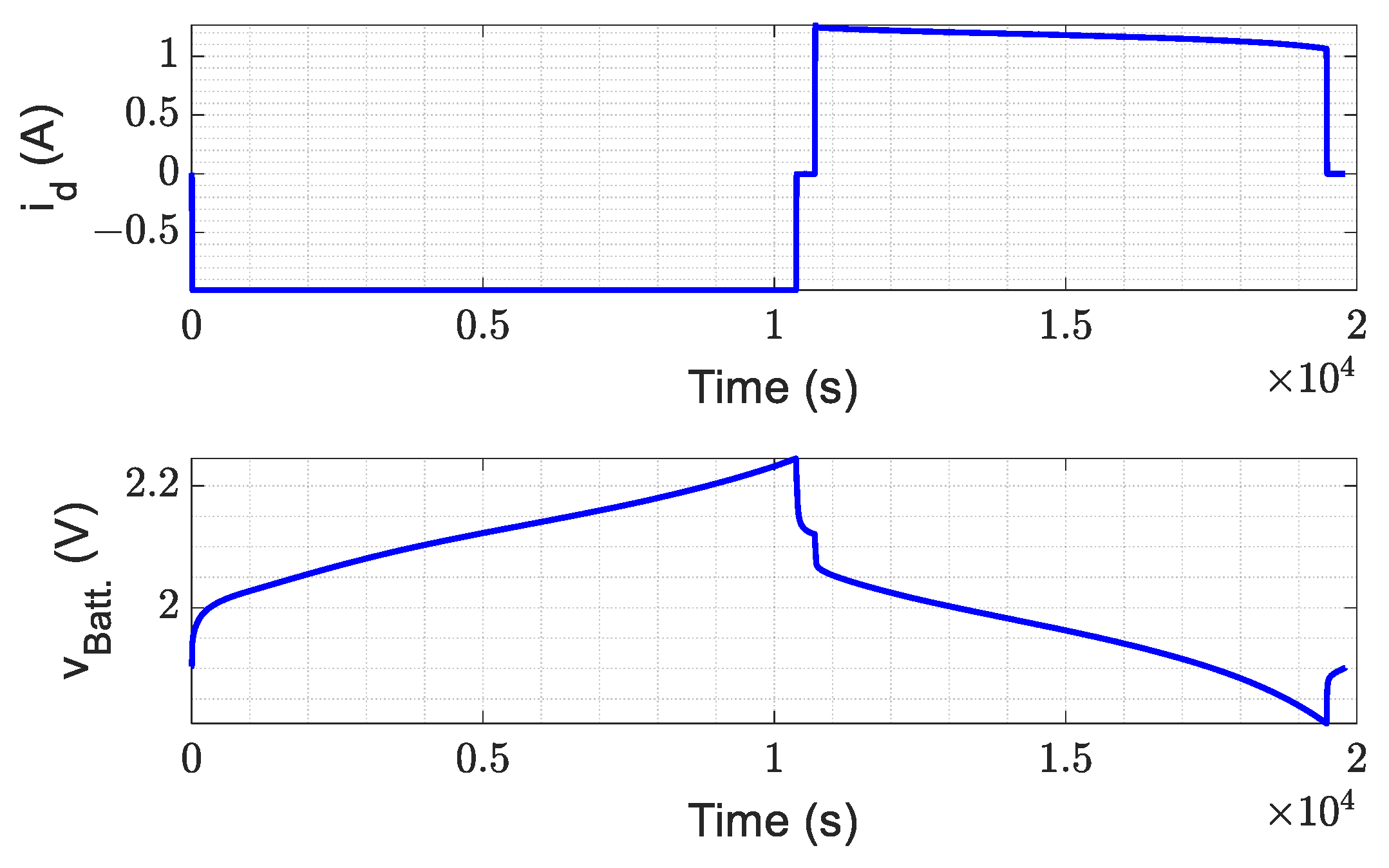
3. Experimental Validation
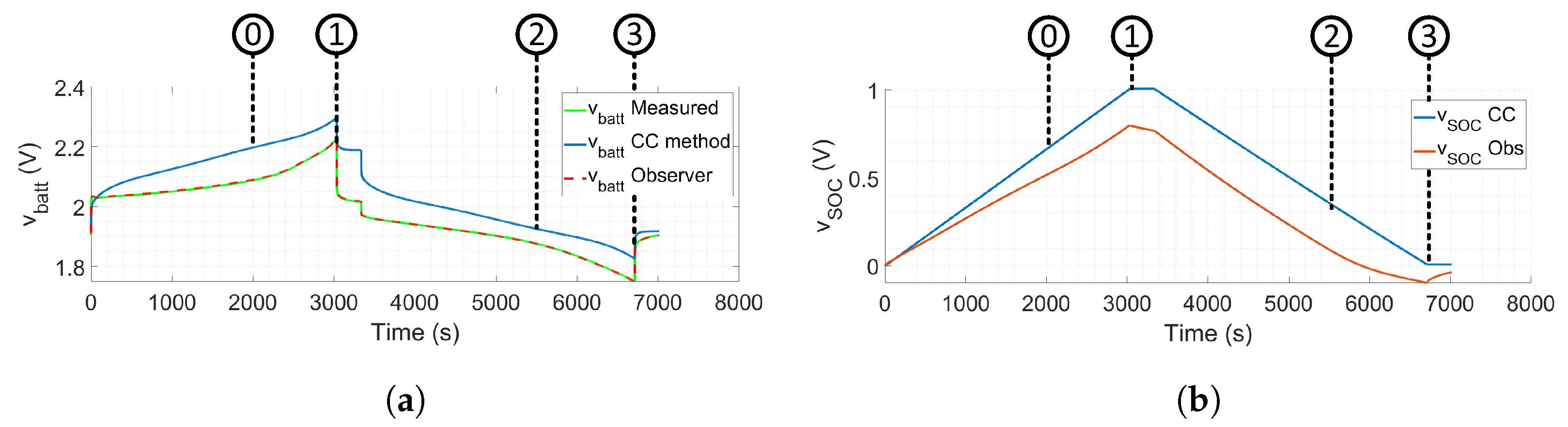
- Marker 0 shows that the observer has a better performance when tracking the voltage measurement.
- Marker 1 shows how the CC estimates more SOC than the observer.
- Marker 2 shows how the CC estimates 32% of the SOC when the observer estimates 0%.
- Marker 3 shows how the CC estimates the end of SOC when the battery has been over-discharged since Marker 2.
- The time it takes to complete the charge is increasingly shorter due to capacity lost.
- has more obvious differences because it represents the most significant time constant.
- The transient movements are abrupt as the battery ages due to parametric variation.
- The most relevant changes occurred at the beginning and end of SOC due to the non-linear response.
- Initial overshoot appears in the and graphs.
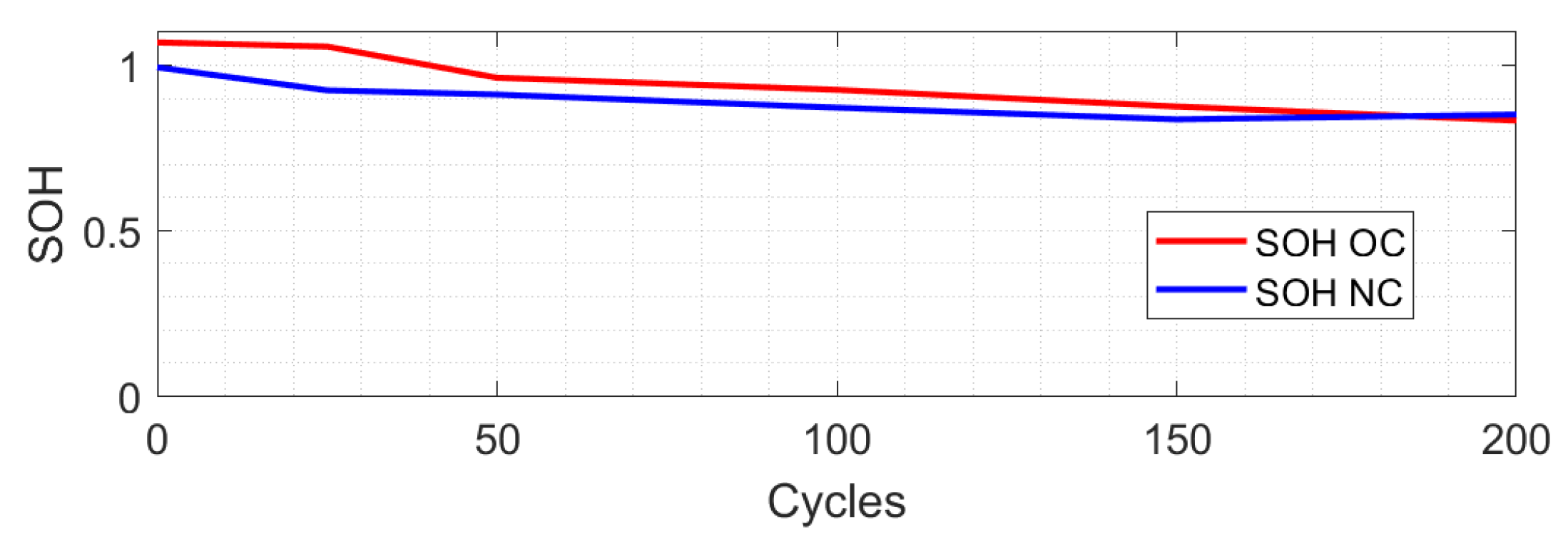
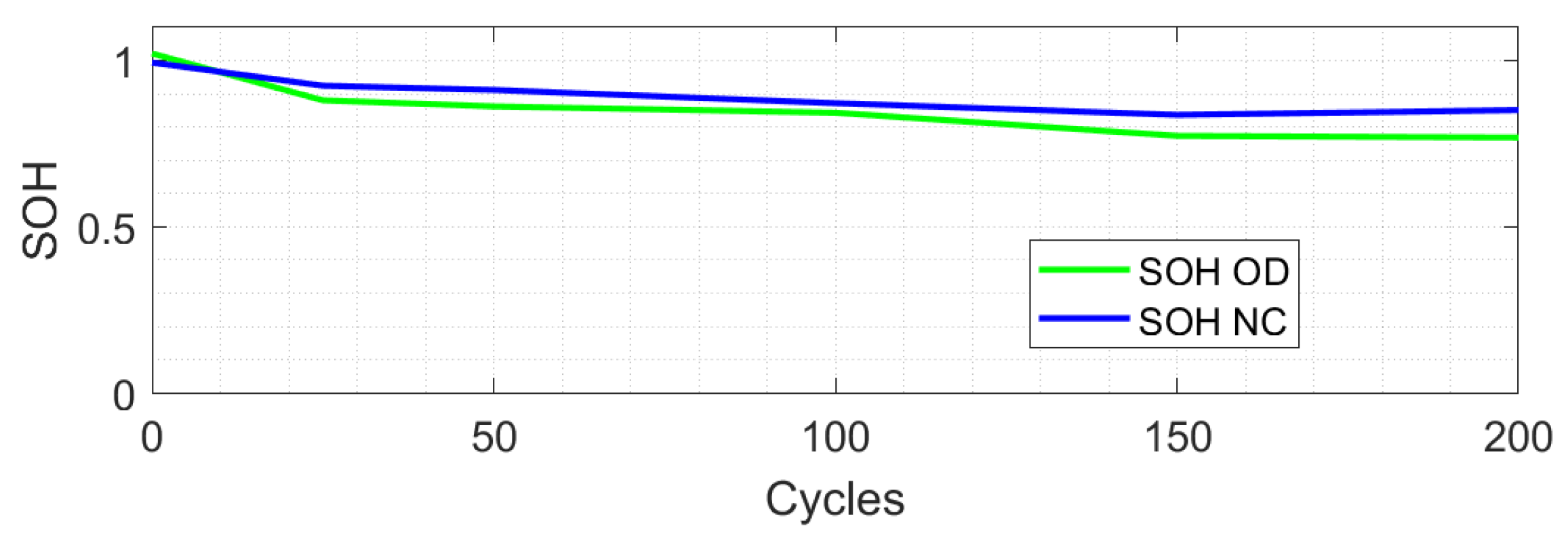
4. Over-Charge and Over-Discharge Test
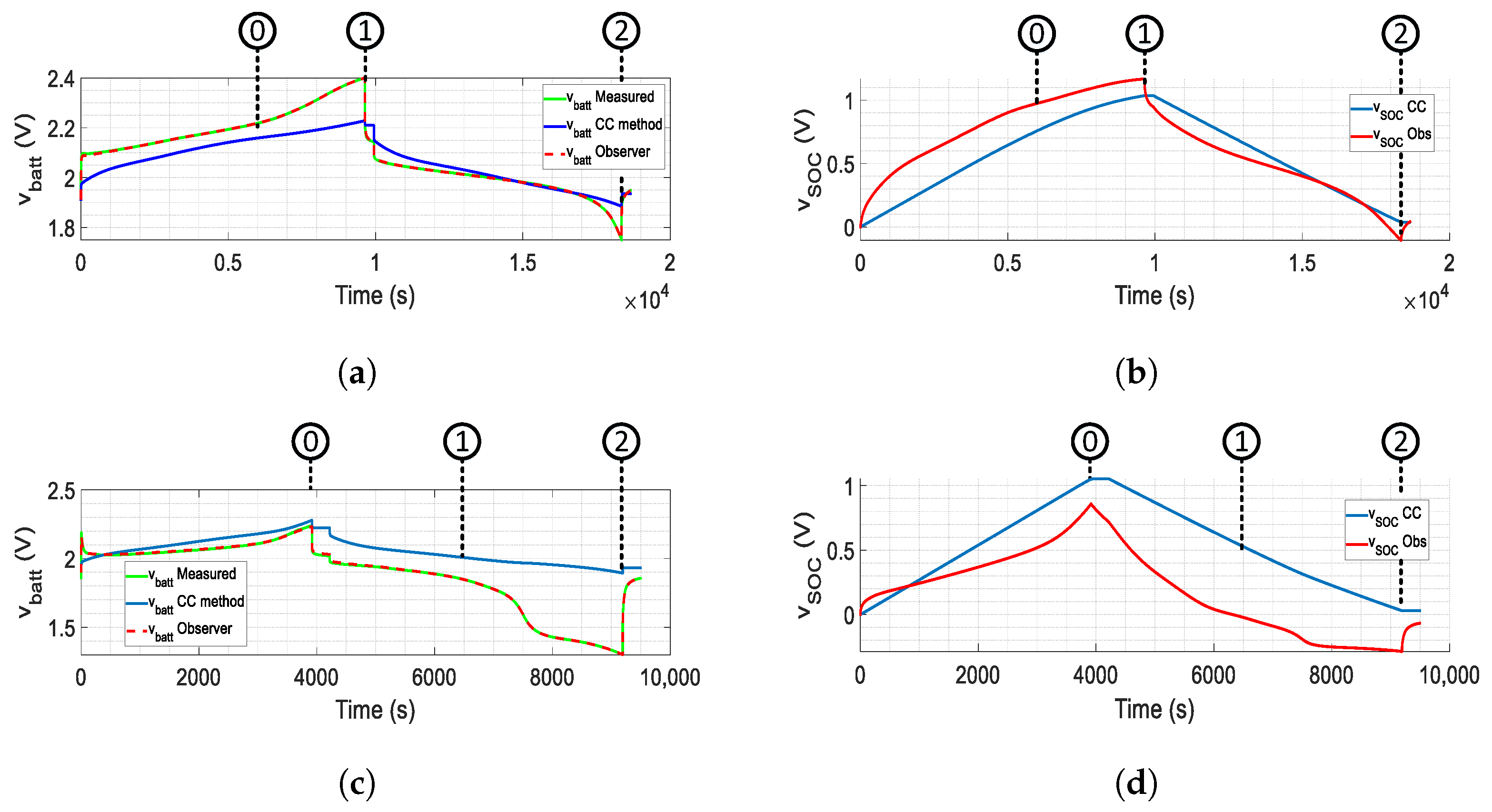
- The over-charge case in marker 0 shows how the observer identifies that the battery is over 100% of the SOC.
- The over-charge case marker 1 shows a significant difference from the CC model.
- The over-discharge case in marker 1 shows how the observer identifies that the battery falls to 0% of SOC.
- The over-discharge case Marker 2 shows a significant difference from the CC model.
- Over-charge marker 2 and over-discharge marker 0 show that the CC model has a close approach.
- Both the effects of over-charge and over-discharge modify the instantaneous response, which is directly related to the loss of active material. By rapidly wearing out the battery, the material is forced to lose effectiveness before the expected time.
- The over-charge conditions are strongly reflected in the reactions with a lower time constant, being associated with the effects of the electrical double layer and corrosion.
- Over-discharge conditions have a longer response time, making it possible to associate them with diffusion effects and hard sulfation.
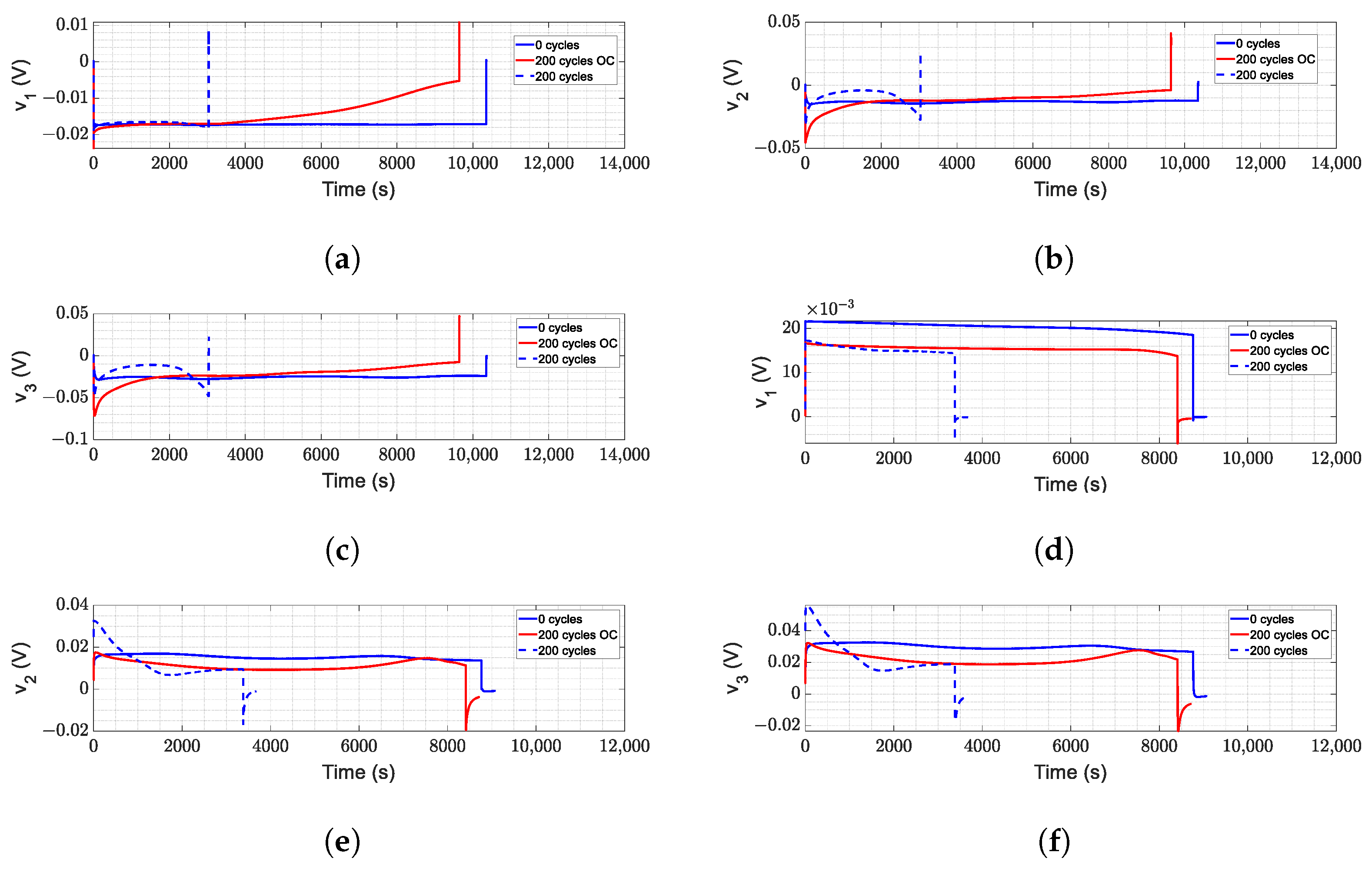
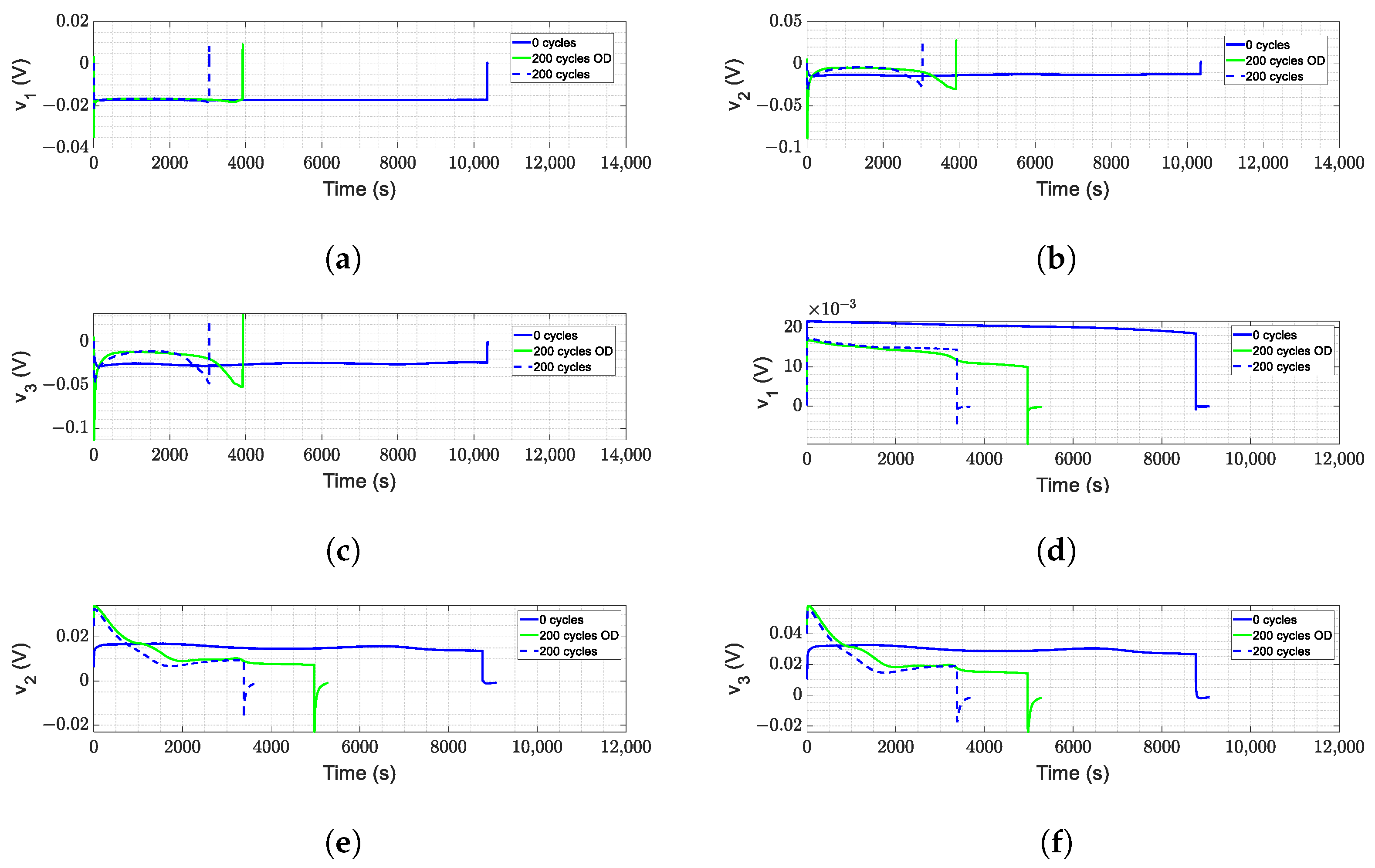
- corresponds to instantaneous changes graphically; this is reflected in the overshoots in Figure 9, both in charging and discharging, increasing progressively with aging; in the same way, it appears more aggressively with over-charge and over-discharge, particularly when charging the battery.
- and correspond to the changes present in the smallest time constants. The values are modified in all cases; however, it has a relevant change in the over-charge in Figure 12 since, during the charge, it is in these elements where the drop in the amplitude has a noticeable change in proportion to its expected nominal values. Likewise, during discharge, this time constant dampens the first moments in conjunction with the absence of the expected overshoot.
- and correspond to the reactions with the middle time constant; in this case, the variations in these elements are progressive with respect to aging, and although it showed changes between normal aging and aging due to misuse, it does not reveal such compelling information. However, together with the rest of the variations, it allows us to validate that they are changes due to misuse or errors in the estimation.
- and correspond to variations in the slower time constants, and it is these changes that mainly contribute to the voltage oscillations during charging and discharging. These effects are present during aging under normal conditions and are accentuated during aging due to over-discharge and, on the contrary, are attenuated during aging due to over-charge.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| EEC | Equivalent electric circuit |
| CC | Coulomb Counting |
| SOC | State of charge |
| SOH | State of health |
| VRLA | Valve regulated lead-acid |
| Nomenclature | |
| Instantaneous change in current [A] | |
| Instantaneous change in voltage [V] | |
| Correction factor | |
| Capacitance of the first arrangement [F] | |
| Capacitance of the second arrangement [F] | |
| Capacitance of the third arrangement [F] | |
| Remaining capacity [Ah] | |
| Battery nominal capacity [Ah] | |
| i | Demanded current [A] |
| Serial resistance [] | |
| Resistance of the first arrangement [] | |
| Resistance of the second arrangement [] | |
| Resistance of the third arrangement [] | |
| t | Desired time [s] |
| Initial time of evaluation [s] | |
| Final time of evaluation [s] | |
| Voltage in parallel arrangement [V] | |
| Voltage in parallel arrangement [V] | |
| Voltage in parallel arrangement [V] | |
| Terminal voltage [V] | |
| Open Circuit Voltage [V] | |
| State of Charge Voltage [V] |
References
- Sharma, S.; Panwar, A.K.; Tripathi, M. Storage technologies for electric vehicles. J. Traffic Transp. Eng. 2020, 7, 340–361. [Google Scholar] [CrossRef]
- Sanguesa, J.A.; Torres-Sanz, V.; Garrido, P.; Martinez, F.J.; Marquez-Barja, J.M. A review on electric vehicles: Technologies and challenges. Smart Cities 2021, 4, 372–404. [Google Scholar] [CrossRef]
- Pan, Z.; Quynh, N.V.; Ali, Z.M.; Dadfar, S.; Kashiwagi, T. Enhancement of maximum power point tracking technique based on PV-Battery system using hybrid BAT algorithm and fuzzy controller. J. Clean. Prod. 2020, 274, 123719. [Google Scholar] [CrossRef]
- Maddukuri, S.; Malka, D.; Chae, M.S.; Elias, Y.; Luski, S.; Aurbach, D. On the challenge of large energy storage by electrochemical devices. Electrochim. Acta 2020, 354, 136771. [Google Scholar] [CrossRef]
- Haider, S.N.; Zhao, Q.; Li, X. Data driven battery anomaly detection based on shape based clustering for the data centers class. J. Energy Storage 2020, 29, 101479. [Google Scholar] [CrossRef]
- IEEE-650-5318; IEEE Standard for Qualification of Class 1E Static Battery Chargers, Inverters, and Uninterruptible Power Supply Systems for Nuclear Power Generating Stations. IEEE: Piscataway, NJ, USA, 2018. Available online: https://standards.ieee.org/ieee/650/5318/ (accessed on 1 July 2021).
- Plett, G.L. Battery Management Systems, Volume I: Battery Modeling; Artech House: New York, NY, USA, 2015; Volume 1. [Google Scholar]
- Lai, C.S.; Locatelli, G.; Pimm, A.; Wu, X.; Lai, L.L. A review on long-term electrical power system modeling with energy storage. J. Clean. Prod. 2021, 280, 124298. [Google Scholar] [CrossRef]
- May, G.J.; Davidson, A.; Monahov, B. Lead batteries for utility energy storage: A review. J. Energy Storage 2018, 15, 145–157. [Google Scholar] [CrossRef]
- Yu, Y.; Mao, J.; Chen, X. Comparative analysis of internal and external characteristics of lead-acid battery and lithium-ion battery systems based on composite flow analysis. Sci. Total. Environ. 2020, 746, 140763. [Google Scholar] [CrossRef]
- Ahuja, R.; Blomqvist, A.; Larsson, P.; Pyykkö, P.; Zaleski-Ejgierd, P. Relativity and the lead-acid battery. Phys. Rev. Lett. 2011, 106, 018301. [Google Scholar] [CrossRef]
- Levy, S.C.; Bro, P. Battery Hazards and Accident Prevention; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1994. [Google Scholar]
- Rand, D.A.J.; Holden, L.; May, G.; Newnham, R.; Peters, K. Valve-regulated lead/acid batteries. J. Power Sources 1996, 59, 191–197. [Google Scholar] [CrossRef]
- Huang, S.C.; Tseng, K.H.; Liang, J.W.; Chang, C.L.; Pecht, M.G. An online SOC and SOH estimation model for lithium-ion batteries. Energies 2017, 10, 512. [Google Scholar] [CrossRef]
- Plett, G.L. Battery Management Systems, Volume II: Equivalent-Circuit Methods; Artech House: New York, NY, USA, 2015; Volume 2. [Google Scholar]
- Sun, S.; Sun, J.; Wang, Z.; Zhou, Z.; Cai, W. Prediction of battery soh by cnn-bilstm network fused with attention mechanism. Energies 2022, 15, 4428. [Google Scholar] [CrossRef]
- Liu, W.; Xu, Y.; Feng, X.; Wang, Y. Optimal fuzzy logic control of energy storage systems for V/f support in distribution networks considering battery degradation. Int. J. Electr. Power Energy Syst. 2022, 139, 107867. [Google Scholar] [CrossRef]
- Hughes, M.; Barton, R.; Karunathilaka, S.; Hampson, N. The estimation of the residual capacity of sealed lead-acid cells using the impedance technique. J. Appl. Electrochem. 1986, 16, 555–564. [Google Scholar] [CrossRef]
- Yu, R.; Liu, G.; Xu, L.; Ma, Y.; Wang, H.; Hu, C. Review of Degradation Mechanism and Health Estimation Method of VRLA Battery Used for Standby Power Supply in Power System. Coatings 2023, 13, 485. [Google Scholar] [CrossRef]
- Badeda, J.; Kwiecien, M.; Schulte, D.; Sauer, D.U. Battery state estimation for lead-acid batteries under float charge conditions by impedance: Benchmark of common detection methods. Appl. Sci. 2018, 8, 1308. [Google Scholar] [CrossRef]
- Majchrzycki, W.; Jankowska, E.; Baraniak, M.; Handzlik, P.; Samborski, R. Electrochemical impedance spectroscopy and determination of the internal resistance as a way to estimate Lead-acid batteries condition. Batteries 2018, 4, 70. [Google Scholar] [CrossRef]
- Kwiecien, M.; Badeda, J.; Huck, M.; Komut, K.; Duman, D.; Sauer, D.U. Determination of SoH of lead-acid batteries by electrochemical impedance spectroscopy. Appl. Sci. 2018, 8, 873. [Google Scholar] [CrossRef]
- Tao, L.; Ma, J.; Cheng, Y.; Noktehdan, A.; Chong, J.; Lu, C. A review of stochastic battery models and health management. Renew. Sustain. Energy Rev. 2017, 80, 716–732. [Google Scholar] [CrossRef]
- Olarte, J.; Martínez de Ilarduya, J.; Zulueta, E.; Ferret, R.; Kurt, E.; Lopez-Guede, J.M. High Temperature VLRA Lead Acid Battery SOH Characterization Based on the Evolution of Open Circuit Voltage at Different States of Charge. JOM 2021, 73, 1251–1260. [Google Scholar] [CrossRef]
- Tran, N.T.; Khan, A.B.; Choi, W. State of charge and state of health estimation of AGM VRLA batteries by employing a dual extended kalman filter and an ARX model for online parameter estimation. Energies 2017, 10, 137. [Google Scholar] [CrossRef]
- Pilatowicz, G.; Budde-Meiwes, H.; Schulte, D.; Kowal, J.; Zhang, Y.; Du, X.; Salman, M.; Gonzales, D.; Alden, J.; Sauer, D. Simulation of SLI lead-acid batteries for SoC, aging and cranking capability prediction in automotive applications. J. Electrochem. Soc. 2012, 159, A1410. [Google Scholar] [CrossRef]
- Sadabadi, K.K.; Ramesh, P.; Tulpule, P.; Rizzoni, G. Design and calibration of a semi-empirical model for capturing dominant aging mechanisms of a PbA battery. J. Energy Storage 2019, 24, 100789. [Google Scholar] [CrossRef]
- Sadabadi, K.K.; Jin, X.; Rizzoni, G. Prediction of remaining useful life for a composite electrode lithium ion battery cell using an electrochemical model to estimate the state of health. J. Power Sources 2021, 481, 228861. [Google Scholar] [CrossRef]
- Xiong, R. Battery Management Algorithm for Electric Vehicles; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Picciano, N. Battery Aging and Characterization of Nickel Metal Hydride and Lead-Acid Batteries. Ph.D. Thesis, The Ohio State University, Columbus, OH, USA, 2007. [Google Scholar]
- Hu, X.; Feng, F.; Liu, K.; Zhang, L.; Xie, J.; Liu, B. State estimation for advanced battery management: Key challenges and future trends. Renew. Sustain. Energy Rev. 2019, 114, 109334. [Google Scholar] [CrossRef]
- Sun, X.; Ji, J.; Ren, B.; Xie, C.; Yan, D. Adaptive forgetting factor recursive least square algorithm for online identification of equivalent circuit model parameters of a lithium-ion battery. Energies 2019, 12, 2242. [Google Scholar] [CrossRef]
- Baccouche, I.; Jemmali, S.; Manai, B.; Omar, N.; Essoukri Ben Amara, N. Improved OCV model of a Li-ion NMC battery for online SOC estimation using the extended Kalman filter. Energies 2017, 10, 764. [Google Scholar] [CrossRef]
- Johansson, A.; Medvedev, A. An observer for systems with nonlinear output map. Automatica 2003, 39, 909–918. [Google Scholar] [CrossRef]
- Xia, B.; Chen, C.; Tian, Y.; Sun, W.; Xu, Z.; Zheng, W. A novel method for state of charge estimation of lithium-ion batteries using a nonlinear observer. J. Power Sources 2014, 270, 359–366. [Google Scholar] [CrossRef]
- Chen, C.T. Linear System Theory and Design, Holt; Rinhart and Winston: Orlando, FL, USA, 1984. [Google Scholar]
- Khalil, H.K. Nonlinear Systems, 3rd ed.; Prentice Hall: East Lansing, MI, USA, 2002; Volume 115. [Google Scholar]
- IEC-60095-1; IEC Standard for Lead-Acid Starter Batteries—Part 1: General Requirements and Methods of Test. IEC: Geneva, Switzerland, 2018. Available online: https://webstore.iec.ch/en/publication/59834 (accessed on 1 March 2020).
- Power-Sonic. Rechargeable Sealed Lead-Acid Battery PS-260 2 Volts 6.0 Amps. Hrs. 2008. Available online: https://www.power-sonic.com/wp-content/uploads/2018/12/PS-260%20technical%20specifications_US.pdf (accessed on 1 September 2019).


| Methodology | Measurement | Contribution | Ref. |
|---|---|---|---|
| EIS | Low frequency. | Obtain extra information about batteries in operation. | [20] |
| Internal resistance. | Impedance is more sensitive to aging than internal resistance. | [21] | |
| High frequency. | Detects SOH under laboratory conditions. | [22] | |
| Stochastic | Dynamic response. | Estimates SOH and detects parametric changes. | [23] |
| Open circuit voltage | at 0% State of charge. | Confirmation method for conventional SOH estimation. | [24] |
| Kalman filter | Dynamic response. | Detect the State of Charge (SOC) and SOH at different aging conditions. | [25] |
| Semi-empirical model | Dynamic response. | The EEC model variations due to capacity loss have a proportional increase. | [26] |
| The model gives additional information that suggests aging detection in parametric changes. | [27,28] |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| F | |||
| F | |||
| F |
| Comparison | Marker 0 | Marker 1 | Marker 2 | Marker 3 |
|---|---|---|---|---|
| Measured— Simulated | v | v | v | v |
| Measured— Observer | v | v | v | v |
| CC— Obs | v | v | v | v |
| Comparison over-charge | Marker 0 | Marker 1 | Marker 2 |
| Measured— Simulated | v | v | v |
| Measured— Observer | v | v | v |
| CC— Obs | v | v | v |
| Comparison over-discharge | Marker 0 | Marker 1 | Marker 2 |
| Measured— Simulated | v | v | v |
| Measured— Observer | v | v | v |
| CC— Obs | v | v | v |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Velasco-Arellano, H.; Visairo-Cruz, N.; Núñez-Gutiérrez, C.A.; Segundo-Ramírez, J. An Enhanced State-Space Modeling for Detecting Abnormal Aging in VRLA Batteries. World Electr. Veh. J. 2024, 15, 507. https://doi.org/10.3390/wevj15110507
Velasco-Arellano H, Visairo-Cruz N, Núñez-Gutiérrez CA, Segundo-Ramírez J. An Enhanced State-Space Modeling for Detecting Abnormal Aging in VRLA Batteries. World Electric Vehicle Journal. 2024; 15(11):507. https://doi.org/10.3390/wevj15110507
Chicago/Turabian StyleVelasco-Arellano, Humberto, Nancy Visairo-Cruz, Ciro Alberto Núñez-Gutiérrez, and Juan Segundo-Ramírez. 2024. "An Enhanced State-Space Modeling for Detecting Abnormal Aging in VRLA Batteries" World Electric Vehicle Journal 15, no. 11: 507. https://doi.org/10.3390/wevj15110507
APA StyleVelasco-Arellano, H., Visairo-Cruz, N., Núñez-Gutiérrez, C. A., & Segundo-Ramírez, J. (2024). An Enhanced State-Space Modeling for Detecting Abnormal Aging in VRLA Batteries. World Electric Vehicle Journal, 15(11), 507. https://doi.org/10.3390/wevj15110507








