Vehicle State Estimation Based on Sage–Husa Adaptive Unscented Kalman Filtering

Abstract

To combat the impacts of uncertain noise on the estimation of vehicle state parameters and the high cost of sensors, a state-observer design with an adaptive unscented Kalman filter (AUKF) is developed. The design equation of the state observer is derived by establishing the vehicle’s three degrees-of-freedom (DOF) model. On this basis, the Sage–Husa algorithm and unscented Kalman filter (UKF) are combined to form the AUKF algorithm to adaptively update the statistical feature estimation of measurement noise. Finally, a co-simulation using Carsim and Matlab/Simulink confirms the algorithm is effective and reasonable. The simulation results demonstrate that the proposed algorithm, compared with the UKF algorithm, increases estimation accuracy by 19.13%, 32.8%, and 39.46% in yaw rate, side-slip angle, and longitudinal velocity, respectively. This is because the proposed algorithm adaptively adjusts the measurement noise covariance matrix, which can estimate the state parameters of the vehicle more accurately.

1. Introduction

Faced with the shortage of oil resources and increasing environmental pollution, electric vehicles (EVs) are considered the key to solving these problems. With the growing demand for vehicle handling characteristics and active safety in various application scenarios associated with the next-generation EVs control, more and more advanced vehicle stability control and driver assistance systems have been developed, such as active front-wheel steering (AFS), direct yaw moment control (DYC), and four-wheel steering (4WS), etc. [1]. At the core of these advanced control methods is the accurate vehicle dynamic state information, such as yaw rate, longitudinal vehicle speed, lateral and longitudinal acceleration, and side-slip angle, etc. The control effect is primarily influenced by the accuracy of the vehicle state information and the real-time availability of obtaining this information.

However, it is too expensive to equip mass-production vehicles with high-precision inertial navigation sensors (INS) and global navigation satellite systems (GNSS), and low-cost onboard sensors may fail to measure dynamic state information accurately [2]. Moreover, some of the critical state parameters are hard to measure directly, such as roll of the vehicle body. Consequently, the estimation of vehicle dynamic state is widely explored and adopted, which is the process of using sensor data and estimation schemes to estimate the dynamic state of vehicles [3].

Currently, state parameter estimation methods are broadly classified into three major categories, kinematics model-based estimation methods, data-driven-based estimation methods, and dynamics model-based estimation methods [4].

The kinematic methods, concerning the motion of vehicles, estimate the vehicle state information by directly integrating the lateral acceleration and yaw rate signals of vehicle sensors [5,6]. However, this method also integrates the noisy signals of the system, and the accumulated error increases with time, which can lead to significant deviations in the estimation results. The estimation results are also affected by unknown factors, such as sensor drift errors or calibration errors caused by temperature. Therefore, the method has some limitations.

With artificial intelligence’s rapid development and application, data-driven estimation methods based on data are gradually becoming familiar. For example, neural networks estimate state parameter based on deep learning and supervised learning methods. This method does not require an accurate model. It only involves using neural networks to train the data from real-vehicle tests and verify the training effect through real-vehicle tests [7,8,9]. Novi et al. [9] obtained data from the Vi-Grade model, trained the artificial neural network (ANN), and combined ANN with UKF to estimate the side-slip angle. However, this training mode is mainly offline and more dependent on the existing data. In addition, changes in vehicle parameters can lead to changes in the fitted relationship derived from and based on the original data, bringing some bias to the estimation results.

For dynamic model-based methods, vehicle state information is estimated by leveraging different vehicle and tire dynamic models. Therefore, the accuracy of the model can have a significant impact on the estimation results. The vehicle dynamic models currently used are mainly 2-DOF models, 3-DOF models, and 7-DOF models [10]. Sun Wen et al. [11] used a 2-DOF model, which does not consider the effect of longitudinal motion on the state parameters. Jeong et al. [12] used the same model and established a linear tire model. However, a linear model will affect the estimation performance of the algorithm when the vehicle is running in a nonlinear region. The 7-DOF model, on the other hand, has a complex structure, which undoubtedly increases the computational effort of the algorithm. Therefore, the 3-DOF model, which considers lateral, yaw, and longitudinal motions, becomes the preferred choice. Based on this, the estimation methods can be further divided into filter-based vehicle state estimation, such as the Kalman filter (KF), extended Kalman filter (EKF), unscented Kalman filter (UKF), particle filter (PF), unscented particle filter (UPF), etc., and observer-based vehicle state estimation, such as sliding mode observer [13], nonlinear observer, etc.

KF is a linear optimal filter that obtains a posterior optimal estimate based on the system’s state equation, measurement equation, and the statistical properties of noise between them, using observations and prior forecast. References [14,15] used KF to estimate vehicle parameters. However, systems are often nonlinear, and the linear model-based KF estimator cannot be applied in all cases. So, the KF needs to be improved. Currently, EKF and UKF are relatively popular. The EKF expands the nonlinear equations in a Taylor series around priori state estimates, and then uses the KF to handle the linear problem [16,17]. For the EKF algorithm, the accuracy of the vehicle model parameters significantly impacts the estimation accuracy. Compared to the EKF, UKF uses sigma points instead of the Taylor series expansion. In most cases, sigma points approximate nonlinear transformation better than linearization. It can eliminate the process of calculating complex Jacobi matrices, and its accuracy is higher in dealing with more complex nonlinear problems [18,19]. Huang Yuhao et al. [20] compared UKF with EKF, proving that UKF has a higher accuracy. In addition, many scholars have also studied state estimation based on PF [21,22]. Chu Wenbo et al. [23] proposed an information-fusion observer based on the UPF algorithm. Although the UPF algorithm can handle nonlinear and non-Gaussian distributions, it is computationally intensive, affecting its efficiency and real-time requirement.

Regarding the UKF algorithm, matrices $Q$ and $R$ are both noise covariance matrices, and their values usually require experience or trial and error to determine. However, the noise constantly changes when a vehicle is driving, and the original UKF cannot achieve sound filtering effects under different working conditions. Therefore, some scholars have proposed a filtering method for adaptive adjustment of the noise covariance matrix, which enables better adaptability and robustness for the filtering algorithm. Wang Zhenpo et al. [24] combined UKF with fuzzy control to realize the process’s adaptive adjustment of measuring the noise covariance matrix. Fan Tiane et al. [25] used shallow long short-term memory networks (LSTM) to optimize UKF. The estimation error of battery state of charge (SOC) and state of energy (SOE) is reduced to 0.43% and 0.46%, respectively. Li Gang et al. [26] introduced a Sage–Husa adaptive EKF algorithm and enhanced the adaptive rules built upon it, which increased the estimation accuracy of the center of mass’s side-slip angle. Zhou Bing et al. [27] suggested a double adaptive unscented Kalman filter algorithm based on the fuzzy control adaptive adjustment of slip rate to address the issue of starting value sensitivity in semi-trailer state estimation. Xu Daxing et al. [28] proposed an improved algorithm based on Sage–Husa for process noise and provided an accurate estimation method for process noise statistics. Luo Zeyuan et al. [29] researched the transient interference problem of the Sage–Husa algorithm and proposed the divergence calculation technique. The simulation results show that the improved algorithm has strong robustness.

When the process noise variance is known or small, Yang Rui et al. [30] used the Sage–Husa algorithm to estimate the noise variance. However, in the Sage–Husa algorithm, compensating for both $Q$ and $R$ at the same time can easily lead to a divergence in the filtering results, and the process noise covariance matrix $Q$ has a certain degree of robustness after compensation [31,32,33]. In comparison, the size of the measurement noise covariance matrix $R$ has a more significant impact on the filtering effect.

Through research on existing achievements, this paper proposes an adaptive unscented Kalman filter method based on the Sage–Husa algorithm to obtain vehicle state parameters under uncertain noise interference accurately. This algorithm takes the front wheel angle and vehicle lateral acceleration as input signals, ignoring the process noise covariance matrix $Q$ update, and adaptively adjusts the statistical feature estimation of the system measurement noise. Moreover, we improve the estimator to ensure that the covariance of the measurement noise is always positive to prevent the filtering results from diverging. Finally, we verified the rationality of the algorithm through joint simulation with Carsim and Matlab/Simulink, and typical operating condition experiments were conducted.

The main contributions of this paper are as follows:

(1)

The Sage–Husa algorithm is improved to avoid non-positive definiteness of the covariance matrix and to ensure its positivity.

(2)

The improved Sage–Husa algorithms are adopted to dynamically update the mean and covariance matrices of the measurement noise, which effectively improves the filtering accuracy and prevents its divergence.

(3)

Sage–Husa algorithm is integrated with the UKF algorithm to form the AUKF algorithm for dynamic vehicle state estimation. The simulation results demonstrate that AUKF increases estimation accuracy by 19.13%, 32.8%, and 39.46% in yaw rate, side-slip angle, and longitudinal velocity, respectively, proving the algorithm’s validity in providing accurate vehicle state information for active vehicle safety control.

The structure of this paper is as follows.

In Section 2, we establish the vehicle dynamics model and the tire model. Section 3 describes the principle and implementation of UKF and AUKF. Section 4 presents the comparative simulation results of UKF and AUKF. Section 5 provides a summary of this work.

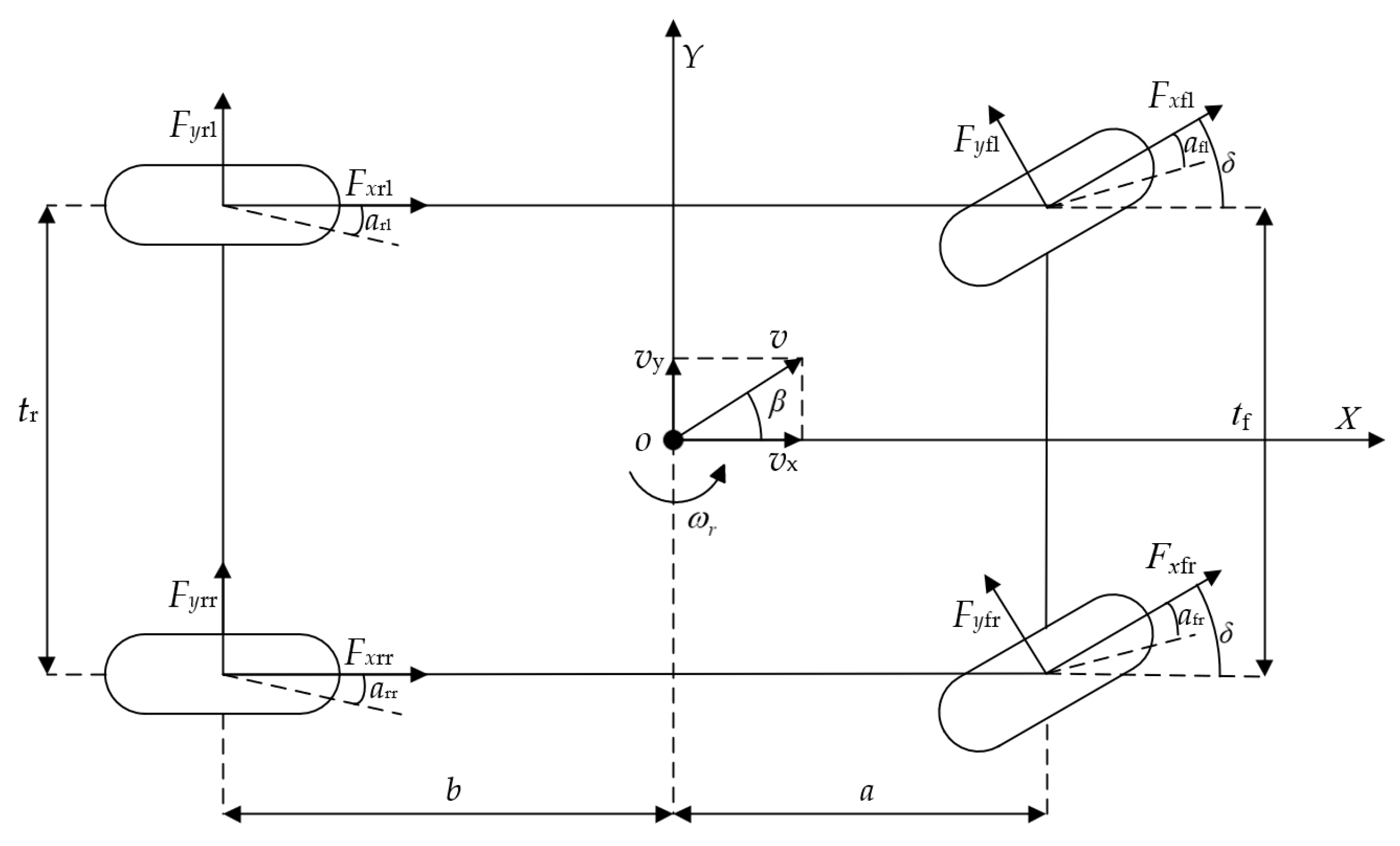
2. Vehicle State Parameter Estimation Model

2.1. 3-DOF Vehicle Dynamics Model

A non-linear 3-DOF vehicle dynamic model with lateral, longitudinal, and yaw is built, based on a linear 2-DOF model [34] as shown in Figure 1, to simulate the vehicle motion state more accurately and reliably under various road circumstances. This model treats the car as if it were a rigid body, ignoring the pitch, roll, and vertical motions, as well as air resistance and tire-rolling resistance. Meanwhile, this model assumes that the steering angles of the two front wheels are equal.

The 3-DOF’s vehicle dynamics model equations are as follows

The longitudinal dynamic equation is

$$m{a}_x=(F_{x\mathrm{fl}}+F_{x\mathrm{fr}})\cos \delta -(F_{y\mathrm{fl}}+F_{y\mathrm{fr}})\sin \delta +F_{x\mathrm{rl}}+F_{x\mathrm{rr}}$$

(1)

The lateral dynamic equation is

$$m{a}_y=(F_{x\mathrm{fl}}+F_{x\mathrm{fr}})\sin \delta -(F_{y\mathrm{fl}}+F_{y\mathrm{fr}})\cos \delta +F_{y\mathrm{rl}}+F_{y\mathrm{rr}}$$

(2)

The yaw dynamics equation is

$$I_z{\dot{\omega }}_r=\frac{t_{\mathrm{f}}}{2}[(F_{x\mathrm{fr}}-F_{x\mathrm{fl}})\cos \delta +(F_{y\mathrm{fl}}-F_{y\mathrm{fr}})\sin \delta ]+\frac{t_{\mathrm{r}}}{2}(F_{x\mathrm{rr}}-F_{x\mathrm{rl}})+a[(F_{x\mathrm{fl}}+F_{x\mathrm{fr}})\sin \delta +(F_{y\mathrm{fl}}+F_{y\mathrm{fr}})\cos \delta ]-b(F_{y\mathrm{fl}}+F_{y\mathrm{fr}})$$

(3)

where $m$ is the vehicle mass; $F_x$ and $F_y$ are the longitudinal and lateral forces of the wheels, respectively; $\mathrm{fl}$, $\mathrm{fr}$, $\mathrm{rl}$ and $\mathrm{rr}$ represent the left front wheel, right front wheel, left rear wheel and right rear wheel, respectively; $t_{\mathrm{f}}$ and $t_{\mathrm{r}}$ are wheelbases of the front and rear wheels of automobiles; ${\dot{\omega }}_r$ is the yaw acceleration of the vehicle; $I_z$ is the moment of inertia of the vehicle around the $Z$ axis; and $a$ and $b$ are the distance between the center of gravity of the vehicle and the front and rear axles, respectively.

From the vehicle’s dynamics model equations, the state equation and measurement equation of the 3-DOF vehicle can be derived as follows

$$\{\begin{array}{l}{\dot{\omega }}_r=\frac{(a^2{k}_1+b^2{k}_2)}{I_z{v}_x}{\omega }_r+\frac{a{k}_1-b{k}_2}{I_z}\beta -\frac{a{k}_1}{I_z}\delta \\ \dot{\beta }=(\frac{a{k}_1-b{k}_2}{m{v}_x^2}-1){\omega }_r+\frac{k_1+k_2}{m{v}_x}\beta -\frac{k_1}{m{v}_x}\delta \\ {\dot{v}}_x={\omega }_r\beta v_x+a_x\end{array}$$

(4)

$$a_y=\frac{a{k}_1-b{k}_2}{m{v}_x}{\omega }_r+\frac{k_1+k_2}{m}\beta -\frac{k_1}{m}\delta$$

(5)

where $k_1$ and $k_2$ are the cornering stiffness of the front and rear axle, respectively; $v_x$ is the vehicle longitudinal speed; $\delta$ is the front wheel steering angle; $\beta$ is side-slip angle; ${\omega }_r$ is yaw rate; and $a_x$ and $a_y$ are the longitudinal and lateral acceleration of the vehicle, respectively.

The mechanism for maintaining vehicle stability relies heavily on sensors. This paper estimates the side-slip angle, yaw rate, and longitudinal vehicle speed from the vehicle’s lower-cost longitudinal acceleration and steering-angle sensor outputs. For nonlinear systems, the standard state space formulae are

$$\{\begin{array}{l}X(k)=f(X(k-1),u(k))+W(k)\\ Z(k)=h(X(k),u(k))+V(k)\end{array}$$

(6)

where $f$ and $h$ are nonlinear state-equation functions and observation-equation functions, respectively; $X(k)$ is the state vector that cannot be observed directly; $u(k)$ is the control-input vector; $W(k)$ is the system Gauss white noise and its covariance matrix is $Q$; and $V(k)$ is the measurement of Gauss white noise and its covariance matrix is $R$.

The two-dimensional system-input vector is defined as

$$u={\left[\delta a_x\right]}^{\mathrm{T}}$$

(7)

The three-dimensional system-state vector is defined as

$$X={\left[{\omega }_r \beta v_x\right]}^{\mathrm{T}}$$

(8)

The system-observation vector is defined as

$$Z={\left[a_y\right]}^{\mathrm{T}}$$

(9)

2.2. Tire Model

Tires are one of the most essential components of automobiles. In the simulation analysis, the precision of the selected tire model should match the accuracy of the built 3-DOF vehicle model, and the tires have the structural complexity and nonlinearity of mechanical properties. Therefore, it is imperative to select the appropriate tire model.

The most often used formula in vehicle dynamics studies is H.B. Pacejka’s “magic tire”. It is a model of a tire constructed by a unique sine function. One set of straightforward formulas with excellent simulation accuracy thoroughly explain the mechanical properties of tires under various operating circumstances [35]. It can be provided as follows

$$y=D\sin \left\{C\arctan [Bx-E(Bx-\arctan (Bx))]\right\}$$

(10)

$$Y(X)=y(x)+\Delta S_{\mathrm{v}}$$

(11)

$$x=X+\Delta S_{\mathrm{h}}$$

(12)

where $Y$ denotes the lateral or longitudinal force; $x$ represents the side-slip angle $\beta$ or slip rate $s$; $y$ is the tire-roll angle; $D$ is the peak value, representing the maximum of the curve; $C$ is the shape factor of the curve, i.e., whether the curve symbolizes longitudinal force, lateral force or correction moment; $B$ is the stiffness factor; $E$ is the curvature factor and represents the shape near the maximum value of the curve. $S_{\mathrm{v}}$ represents the offset in the vertical direction of the curve, and $S_{\mathrm{h}}$ represents the offset in the horizontal direction of the curve.

Then, the longitudinal and lateral forces of the tire can be expressed as

$$F_{xij}=D_{ij}\sin \left\{C_{ij}{\tan }^{-1}[B_{ij}(1-E_{ij})s_{ij}+E_{ij}{\tan }^{-1}(B_{ij}{s}_{ij})]\right\}$$

(13)

$$F_{yij}=D_{ij}\sin \left\{C_{ij}{\tan }^{-1}[B_{ij}(1-E_{ij})a_{ij}+E_{ij}{\tan }^{-1}(B_{ij}{a}_{ij})]\right\}$$

(14)

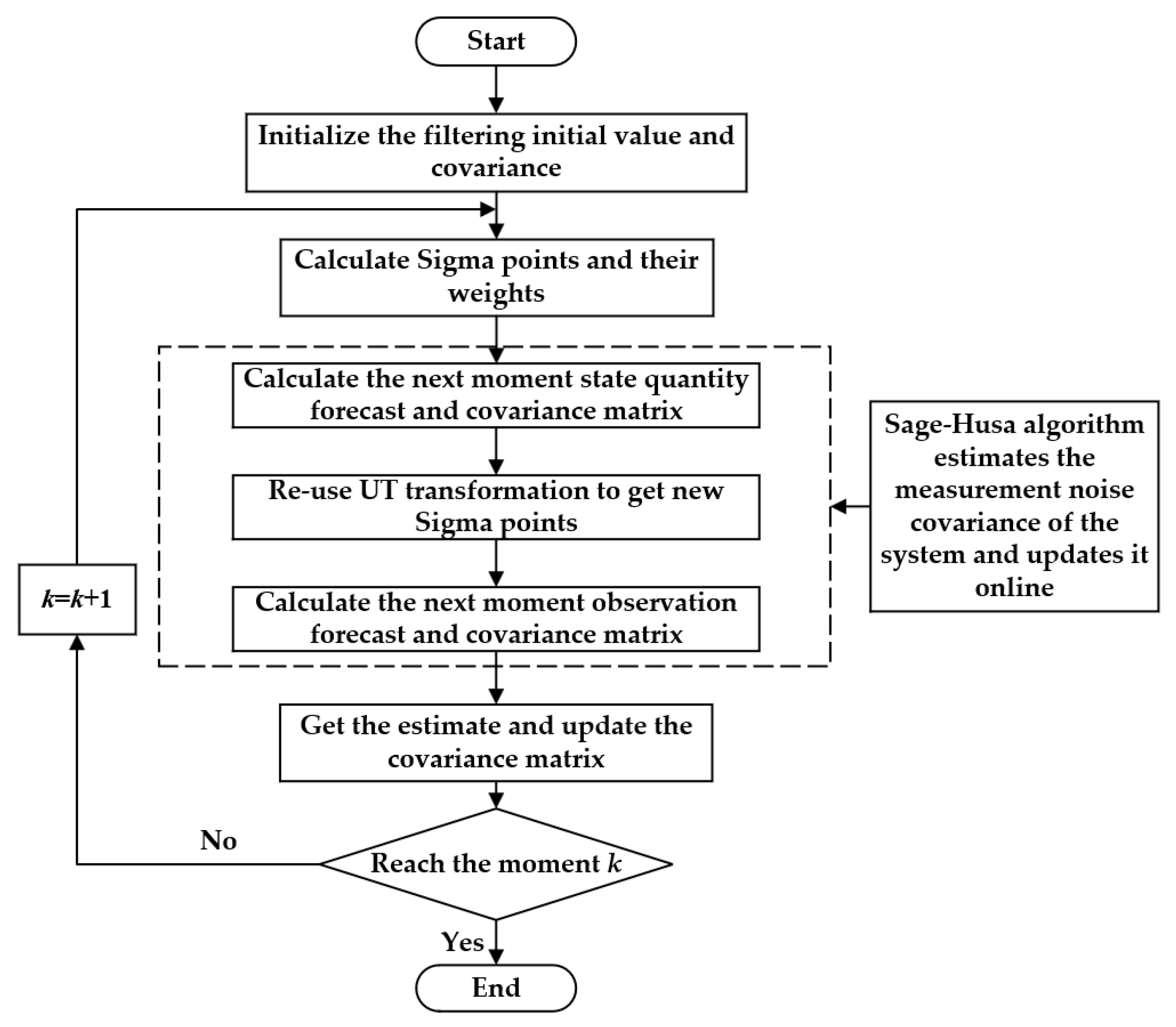
3. Vehicle State Parameter Estimation Based on AUKF

3.1. UKF Algorithm

The main idea of UKF is to transform a nonlinear system into a linear system for processing by unscented transformation (UT). The UKF algorithm is expressed as follows [36]:

(1)

Obtain a set of sampling points (sigma points) and calculate the corresponding weights of these sampling points

It is assumed that the $\overline{X}$ and variance $P$ of the n-dimensional random variable state vector $X$ are known. Then, by obtaining 2n + 1 sigma points $X$ and the appropriate weights via the subsequent unscented transformation, the statistical properties of $f(x)$ may be computed.

$$\{\begin{array}{l}{X}^{(0)}=\overline{X}, i=0\\ X_{k-1}{}^{(i)}=\overline{X}+{(\sqrt{(n+\lambda )P})}_i, i=1~n\\ X_{k-q}{}^{(i)}=\overline{X}-{(\sqrt{(n+\lambda )P})}_i, i=n+1~2n\end{array}$$

(15)

These sampling sites’ related weights are determined as

$$\{\begin{array}{l}{\omega }_m{}^{(0)}={\omega }_c{}^{(0)}=\frac{\lambda }{n+\lambda }, i=0\\ {\omega }_m{}^{(i)}={\omega }_c{}^{(i)}=\frac{1}{2(n+\lambda )}, i=1~2n\end{array}$$

(16)

where $\lambda$ is used to reduce the overall prediction error, which can be chosen based on experience but should ensure that the matrix $(n+\lambda ) P$ is a positive semi-definite. The subscripts $m$ and $c$ stand for the mean and covariance, respectively.

(2)

According to Equations (15) and (16), a set of sampling points and their corresponding weights are calculated

$$X^{(i)}(k|k)=[\widehat{X}(k|k), \widehat{X}(k|k)+\sqrt{(n+\lambda )P(k|k)}, \widehat{X}(k|k)-\sqrt{(n+\lambda )P(k|k)}]$$

(17)

(3)

One-step prediction of the set of 2n + 1 sigma points using the state equation

$$X^{(i)}(k+1|k)=f[X^{(i)}(k|k), k]$$

(18)

(4)

Calculation of one-step prediction and covariance matrix of the system state variables

$$\stackrel{⌢}{X}(k+1|k)={\displaystyle \sum _{i=0}^{2n}{\omega }^{(i)}}{X}^{(i)}(k+1|k)$$

(19)

$$P_{x_k}={\displaystyle \sum _{i=0}^{2n}{\omega }^{(i)}}[X^{(i)}(k+1|k)-\stackrel{⌢}{X}(k+1|k)]{[X^{(i)}(k+1|k)-\stackrel{⌢}{X}(k+1|k)]}^{\mathrm{T}}+Q$$

(20)

(5)

The predicted observations are calculated by bringing sigma points into the observation equation

$$Z^{(i)}(k+1|k)=h [X^{(i)}(k+1|k), k+1]$$

(21)

(6)

The mean, covariance and cross-covariance are calculated analogously to Equations (19) and (20)

$$\overline{Z}(k+1|k)={\displaystyle \sum _{i=0}^{2n}{\omega }^{(i)}}{Z}^{(i)}(k+1|k)$$

(22)

$$P_{z_k}={\displaystyle \sum _{i=0}^{2n}{\omega }^{(i)}}[Z^{(i)}(k+1|k)-\overline{Z}(k+1|k)]{[Z^{(i)}(k+1|k)-\overline{Z}(k+1|k)]}^{\mathrm{T}}+R$$

(23)

$$P_{x_k{z}_k}={\displaystyle \sum _{i=0}^{2n}{\omega }^{(i)}}[X^{(i)}(k+1|k)-\stackrel{⌢}{X}(k+1|k)]{[Z^{(i)}(k+1|k)-\overline{Z}(k+1|k)]}^{\mathrm{T}}$$

(24)

(7)

Kalman gain matrix is calculated

$$K(k+1)=P_{x_k{z}_k}{P}_{z_k}^{-1}$$

(25)

(8)

System status and covariance matrix are updated

$$\stackrel{⌢}{X}(k+1|k+1)=\stackrel{⌢}{X}(k+1|k)+K(k+1)[Z(k+1)-\overline{Z}(k+1|k)]$$

(26)

$$P(k+1|k+1)=P(k+1|k)-K(k+1)P_{z_k}{K}^{\mathrm{T}}(k+1)$$

(27)

3.2. AUKF Algorithm

The Sage–Husa algorithm is a maximum a posteriori (MAP) estimation algorithm [37]. When the noise means and covariance matrix are unknown, the magnitudes of $q$, $r$, $Q$, and $R$ are approximated online from the observations. In the estimate phase, the Sage–Husa method optimizes the filtering performance by raising the weighting coefficients of the fresh data by an asymptotic elimination factor, reducing the influence of time-old data on the present estimation results.

For the uncertainty of measurement noise in the actual process, this paper proposes an adaptive unscented Kalman filter algorithm based on the Sage–Husa theory and updates $R_k$ online to reduce the algorithm’s complexity without affecting the accuracy. Its flow chart is shown in Figure 2. The AUKF algorithm, in contrast to the conventional UKF algorithm, continuously corrects and estimates the model parameters, as well as the statistical characteristics of the noise based on its quantitative data, which can decrease the estimation error, suppress filtering divergence, and increase filtering accuracy.

The steps are as follows

$$d_k=\frac{1-\gamma }{1-{\gamma }^k}$$

(28)

$${\epsilon }_k=Z_k-h[\overline{X}(k|k-1)]-r_k$$

(29)

$${\widehat{r}}_k=(1-d_k){\widehat{r}}_{k-1}+d_k[Z_k-{\displaystyle \sum _{i=0}^{2n}{\omega }^{(i)}}{Z}^{(i)}(k|k-1)]$$

(30)

$${\widehat{R}}_k=(1-d_k){\widehat{R}}_{k-1}+d_k[{\epsilon }_k{\epsilon }_k^{\mathrm{T}}-{\displaystyle \sum _{i=0}^{2n}{\omega }^{(i)}}[Z^{(i)}(k+1|k)-\overline{Z}(k+1|k)]{[Z^{(i)}(k+1|k)-\overline{Z}(k+1|k)]}^{\mathrm{T}}]$$

(31)

where $r_k$ represents the observed noise’s mean, while $R_k$ represents its covariance; ${\epsilon }_k$ is a new information sequence, representing the discrepancy between the actual and expected observations; $\gamma$ is a gradual elimination factor, and the range of values is 0~1.

Sage–Husa adaptive filtering is suboptimal filtering, so the filtering results sometimes diverge. The primary cause is that filter divergence may result from subtraction in a solution of Equation (31) for $R_k$ because it has a non-positive definite condition. To guarantee that $R_k$ is positive, the following techniques are employed in this paper

$${\widehat{R}}_k=(1-d_k){\widehat{R}}_{k-1}+d_k({\epsilon }_k{\epsilon }_k^{\mathrm{T}}), {\widehat{R}}_k\le 0$$

(32)

4. Simulation Results and Analyses

In order to verify the accuracy and feasibility of the proposed vehicle state observer based on the Sage–Husa adaptive UKF algorithm, co-joint simulation performs in Carsim and MATLAB/Simulink. Finally, the estimation results of AUKF and UKF are compared. All simulations below are carried out in Matlab R2020a and Carsim2019 running on a laptop computer with AMD R7-5800H CPU @3.2 GHz and 16 GB RAM.

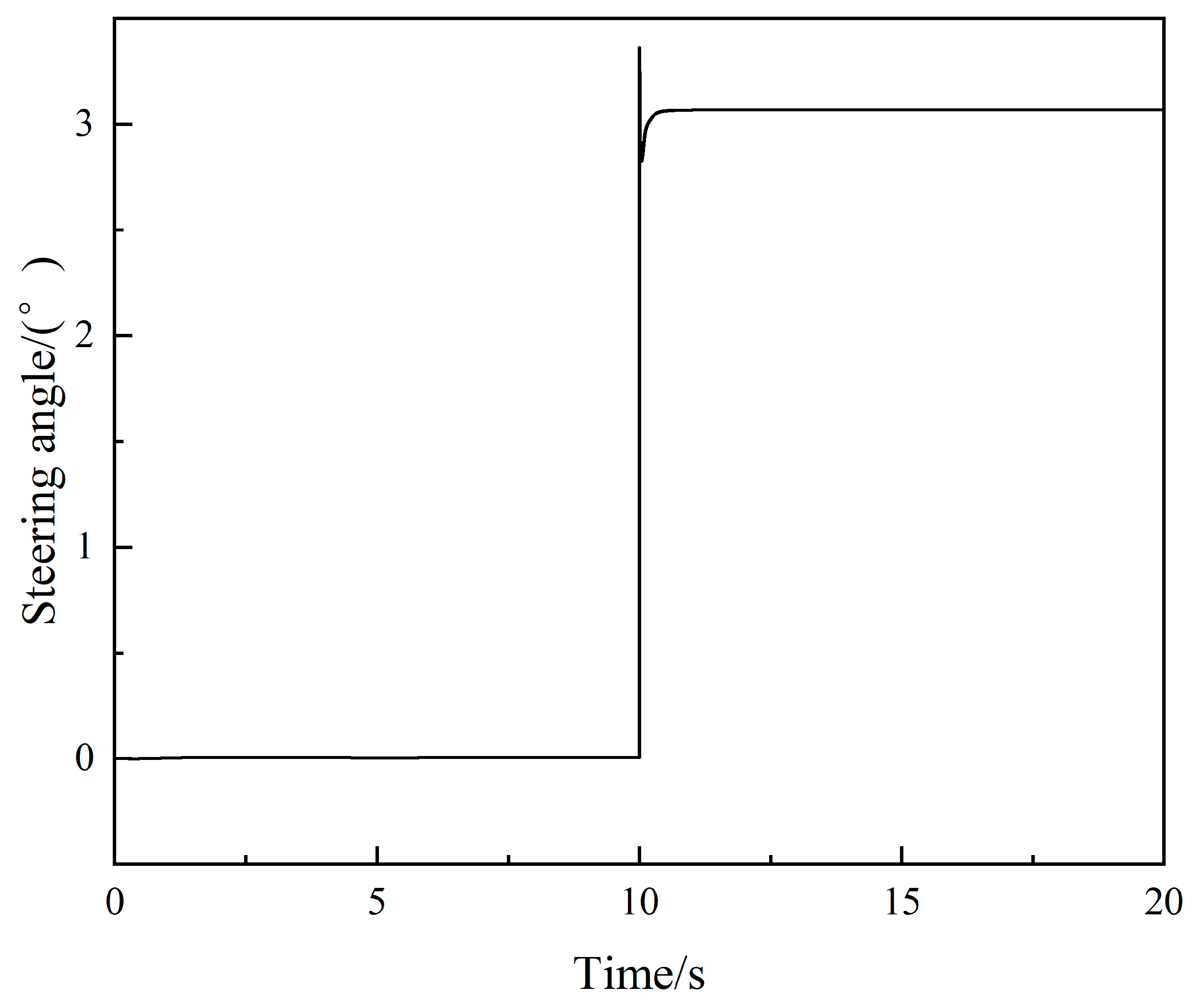
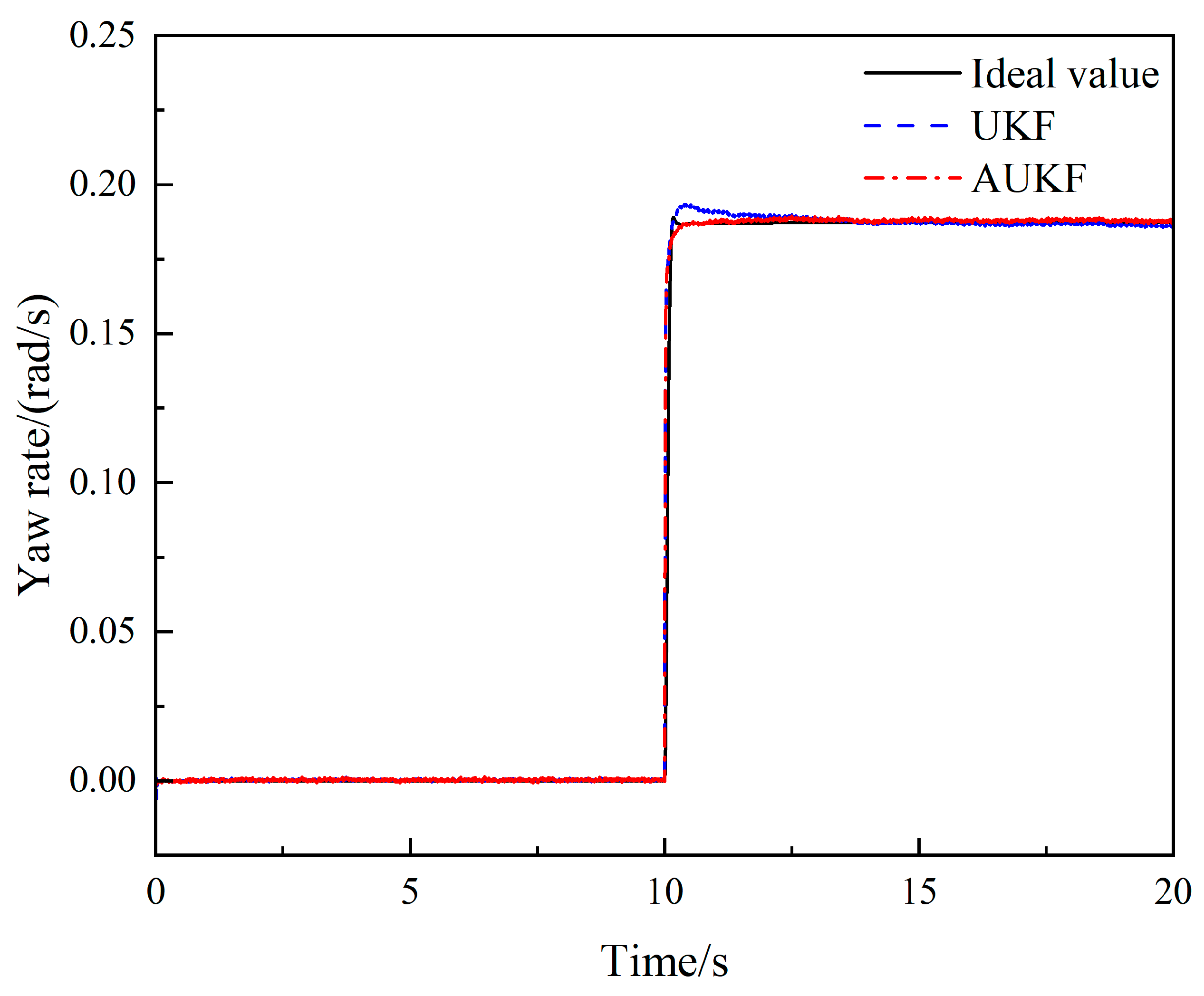
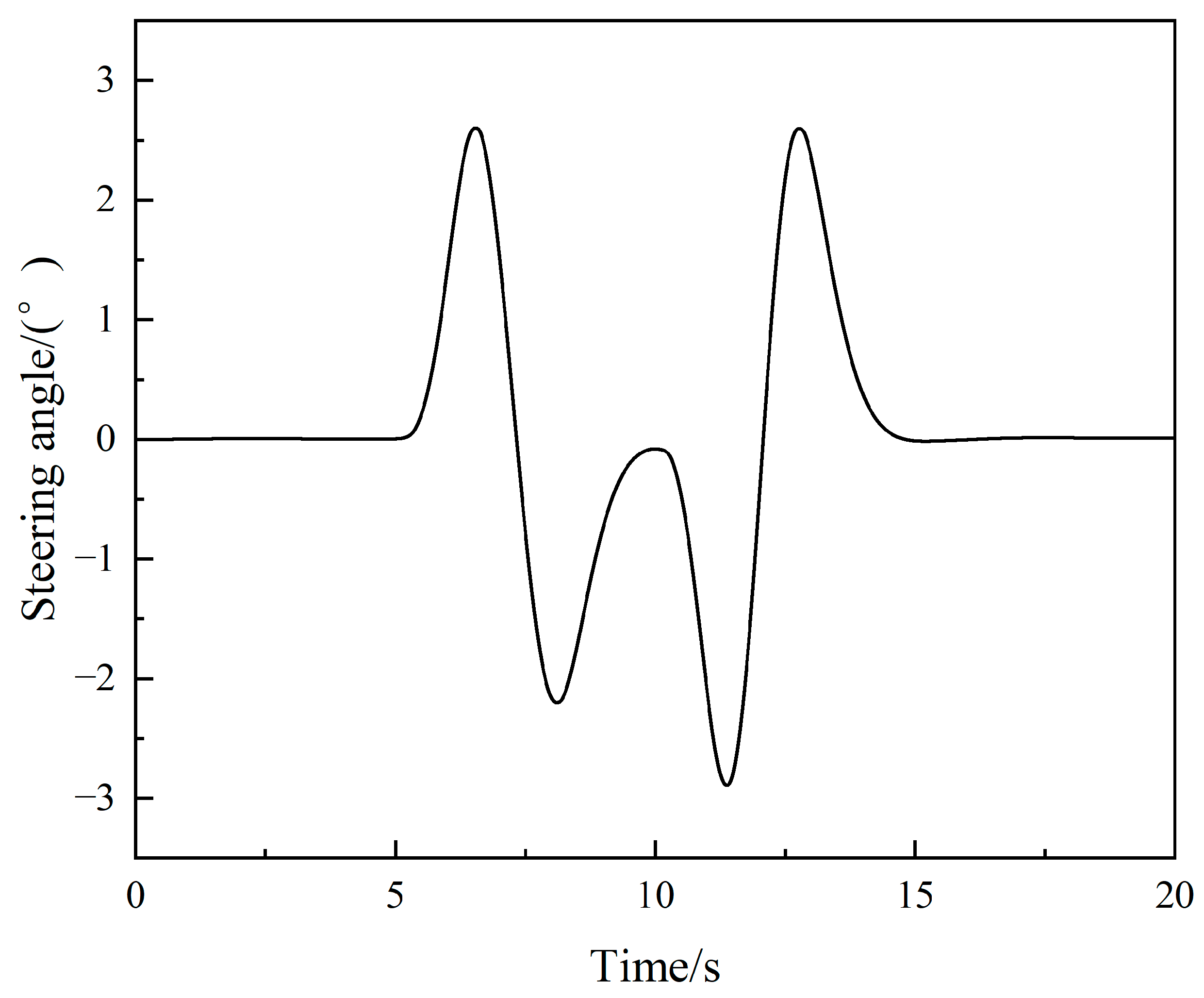
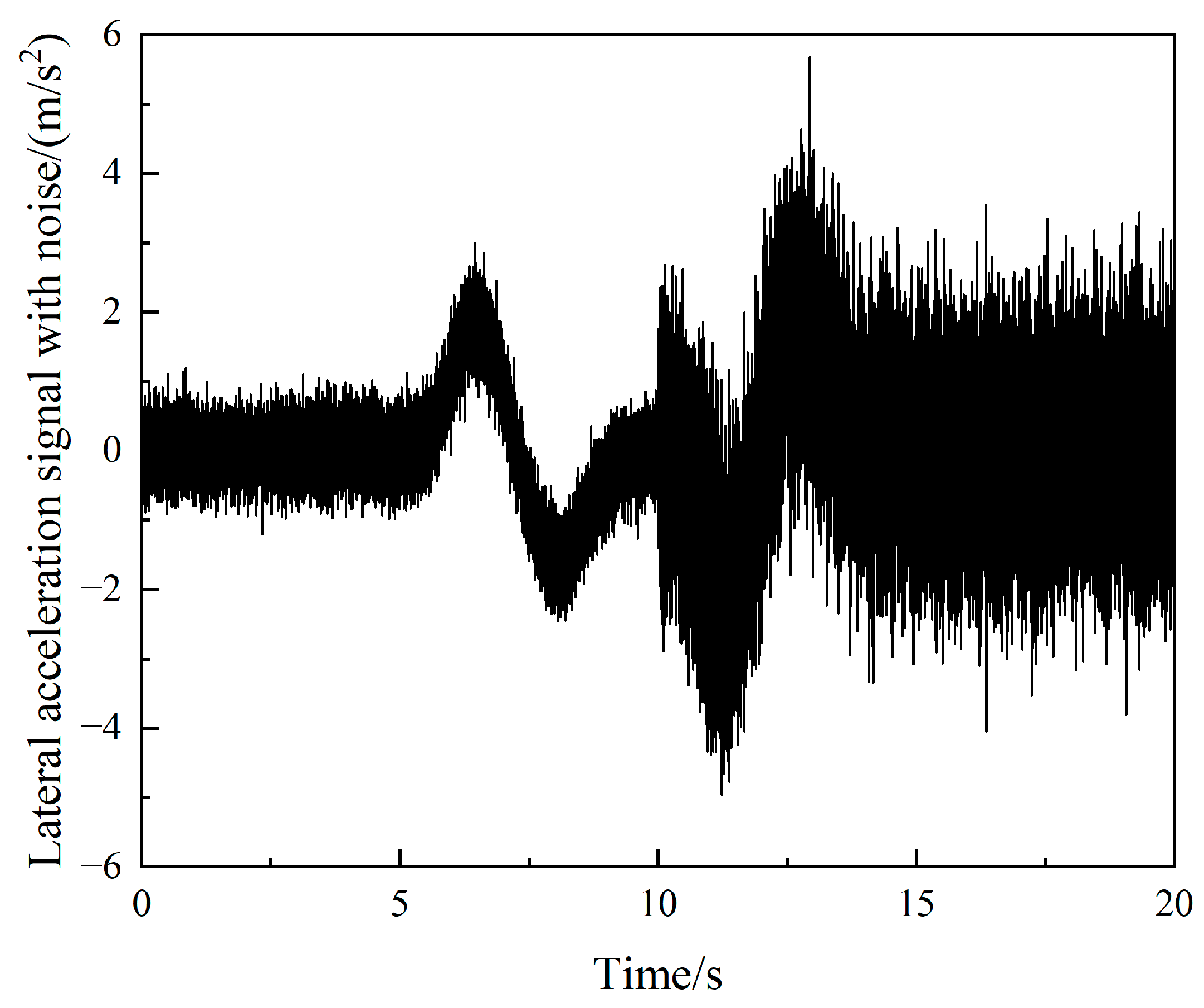
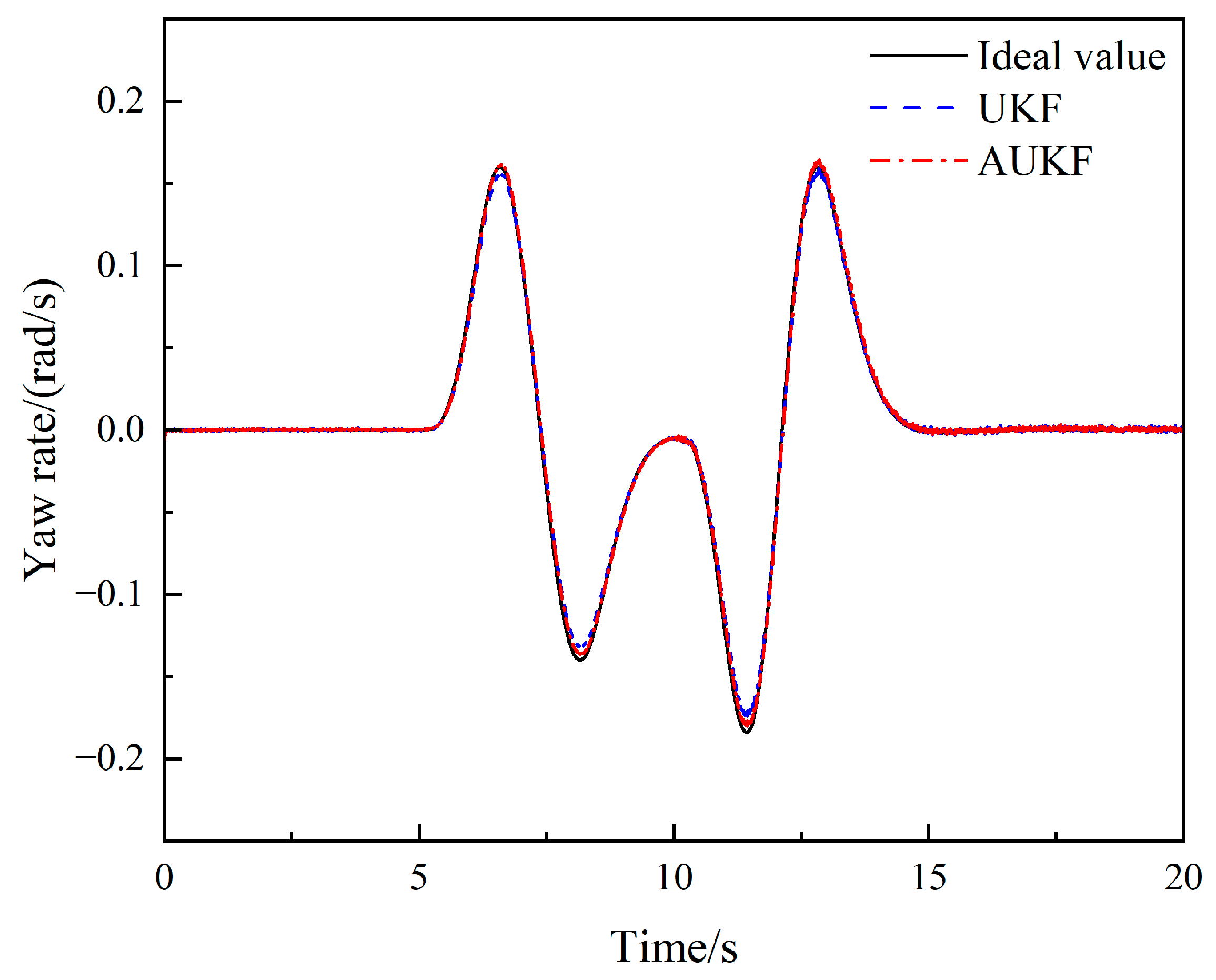
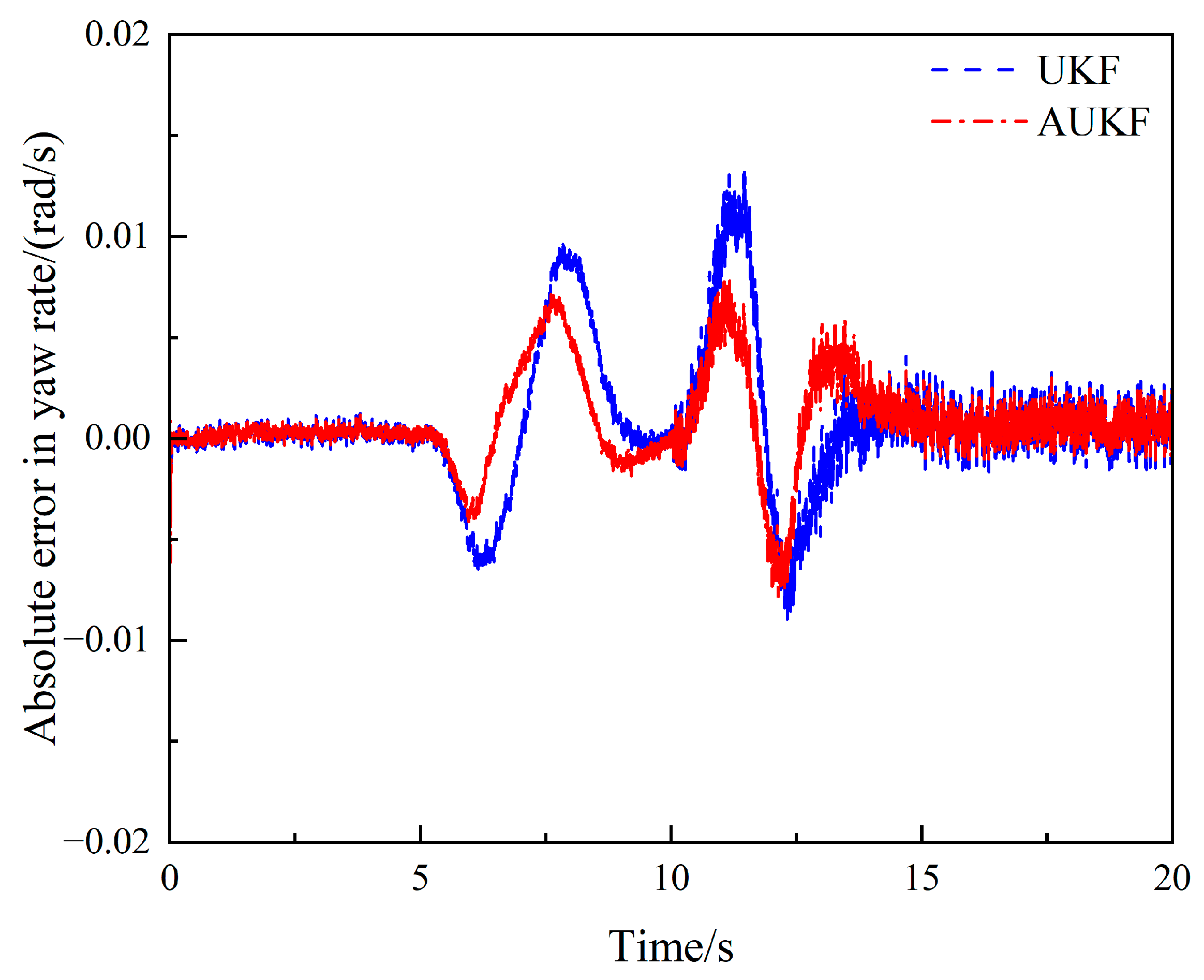
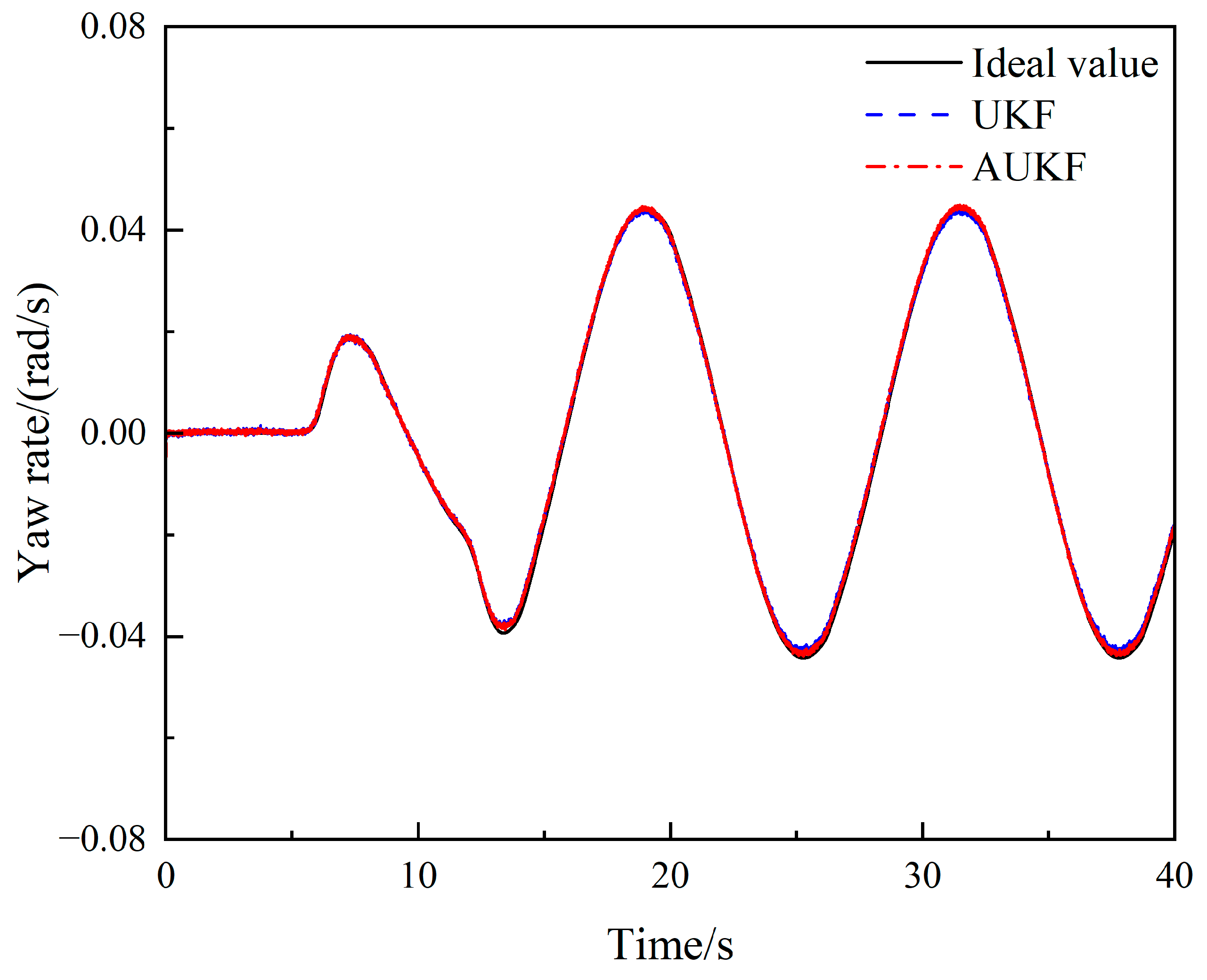
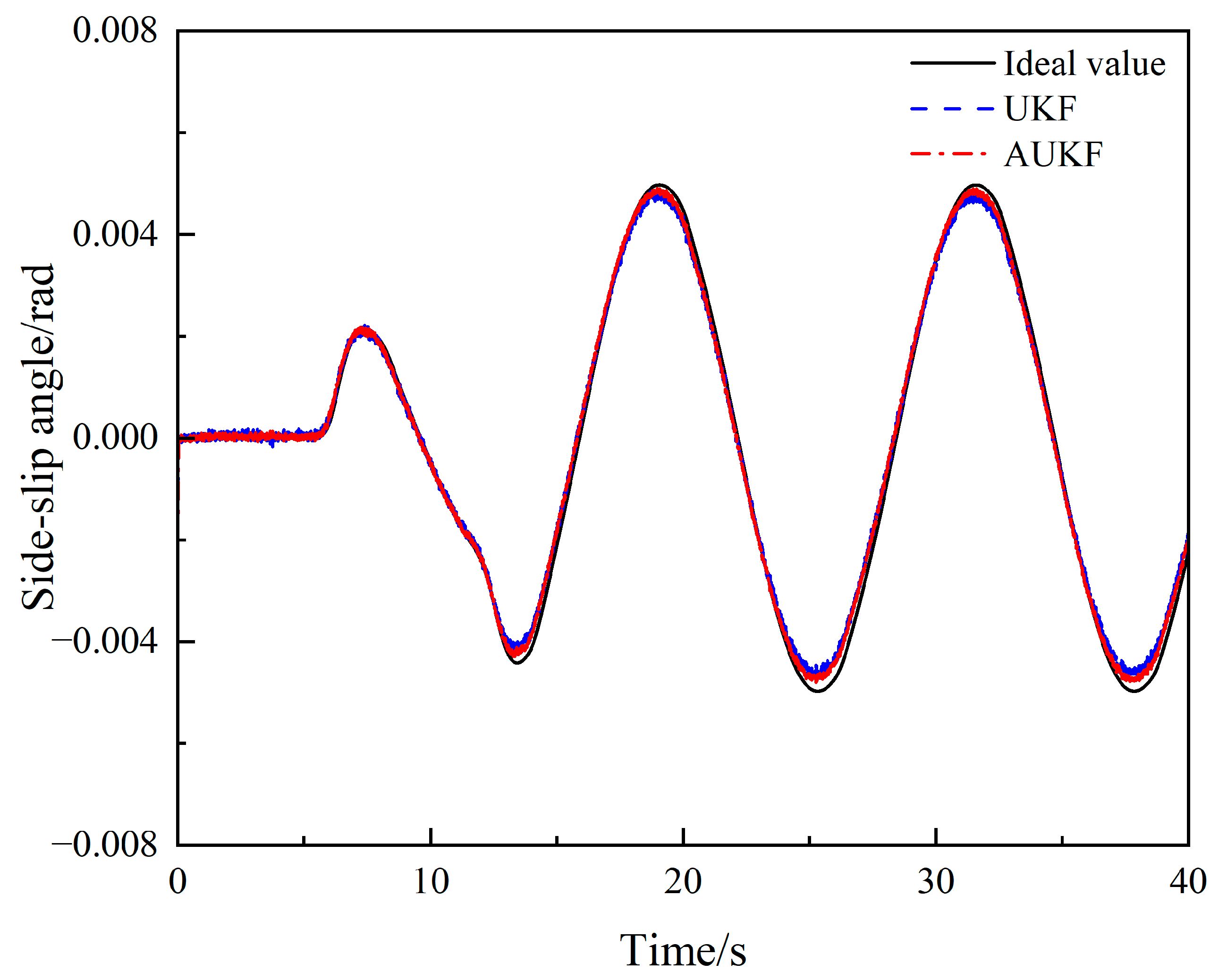
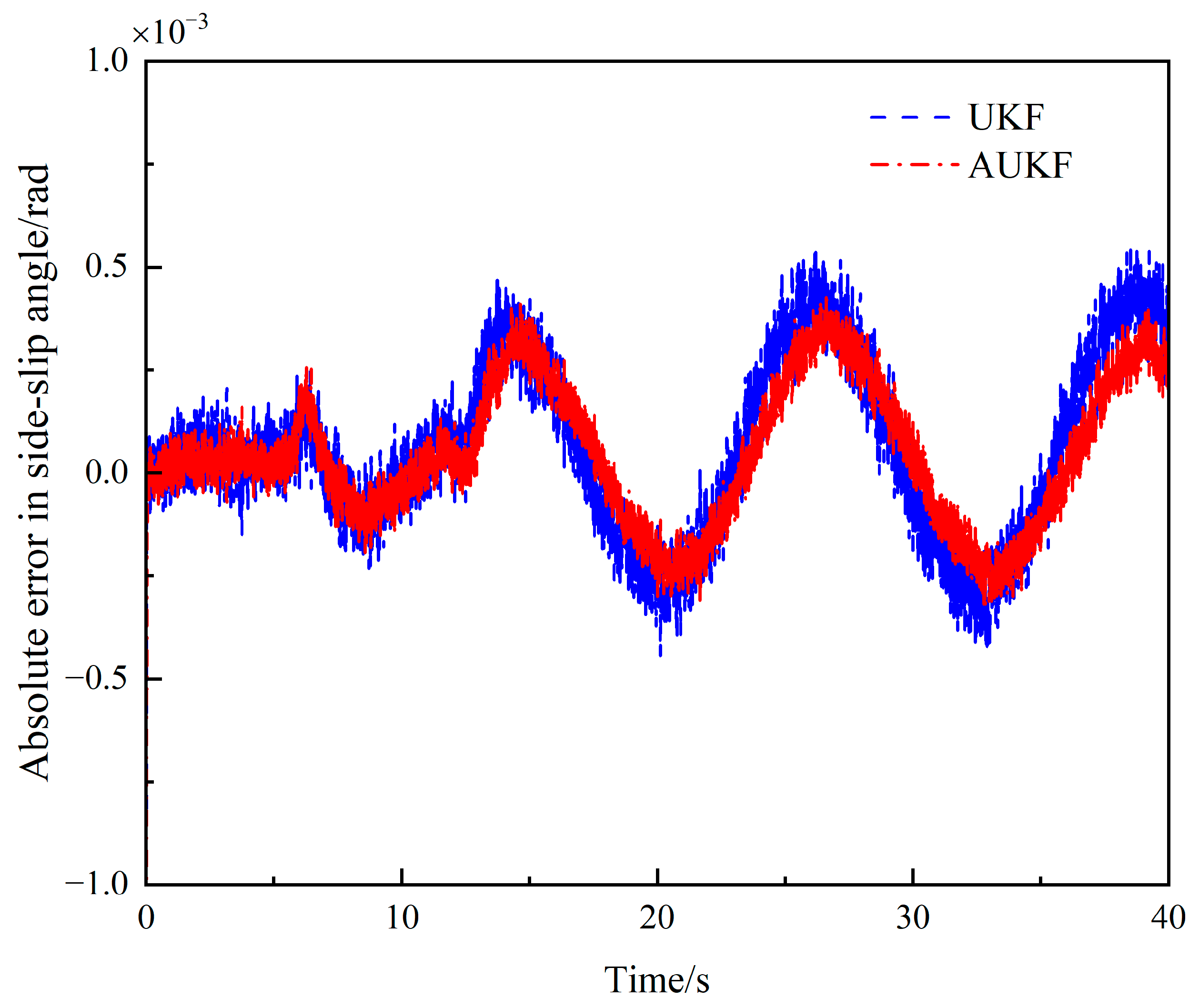
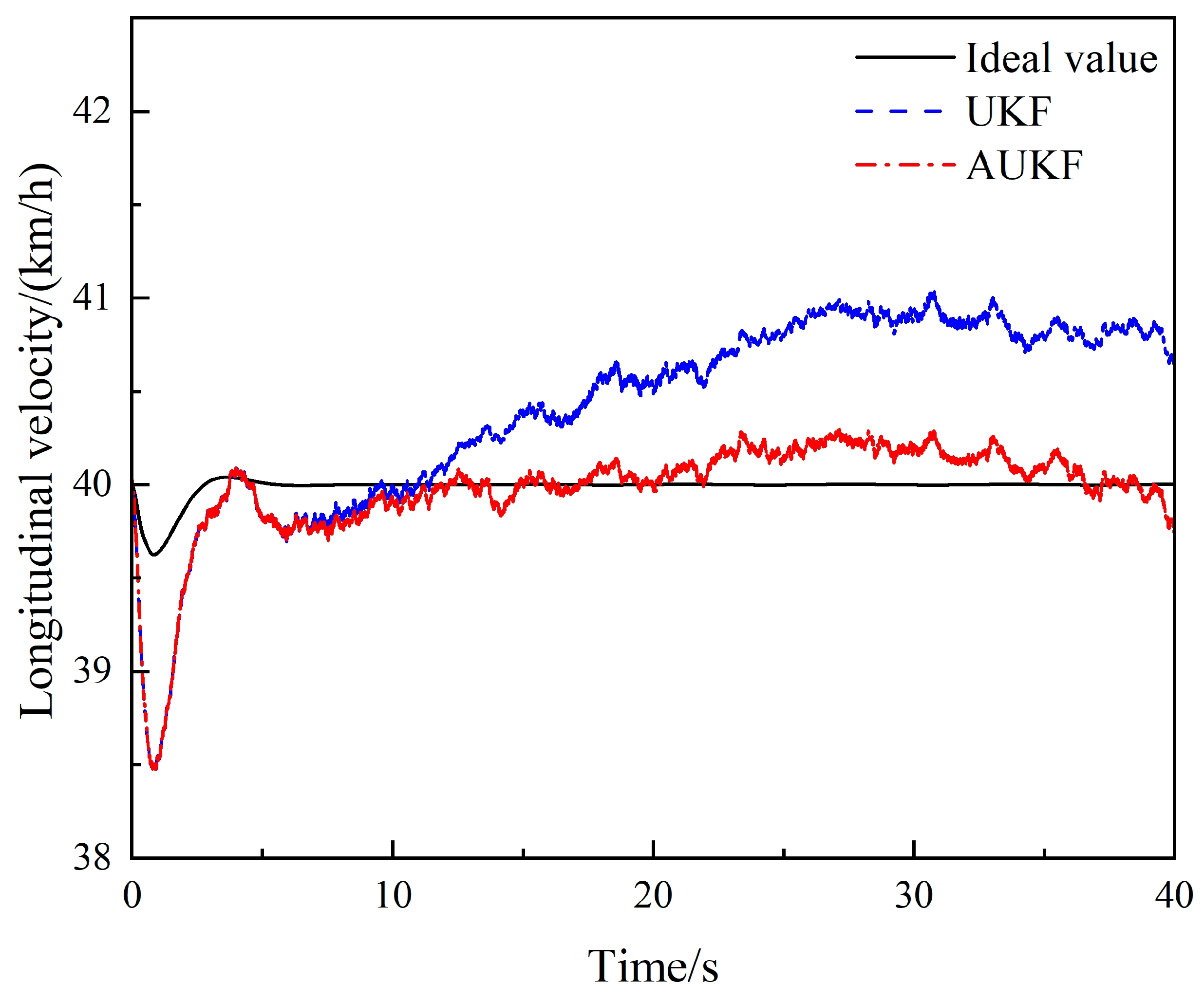
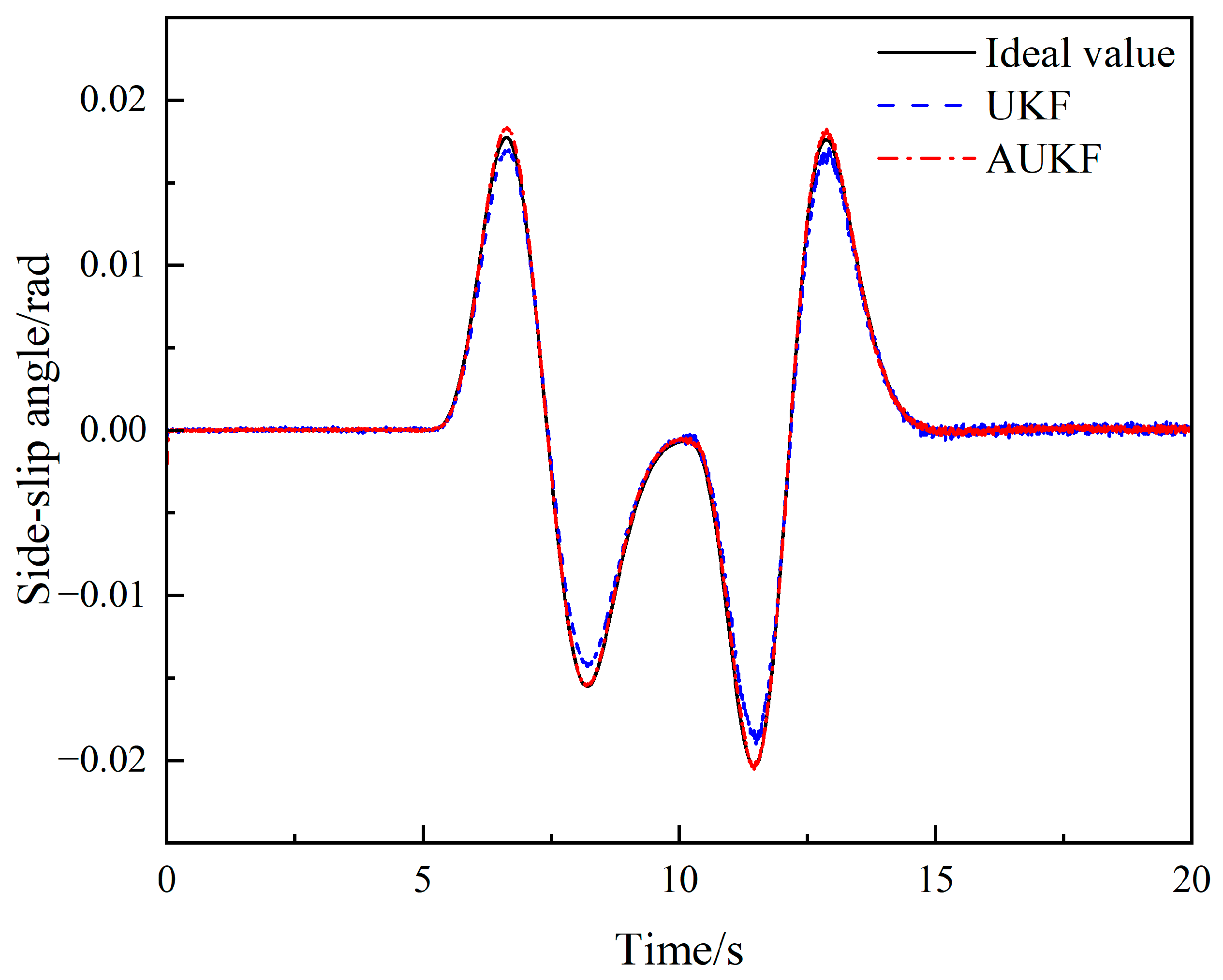
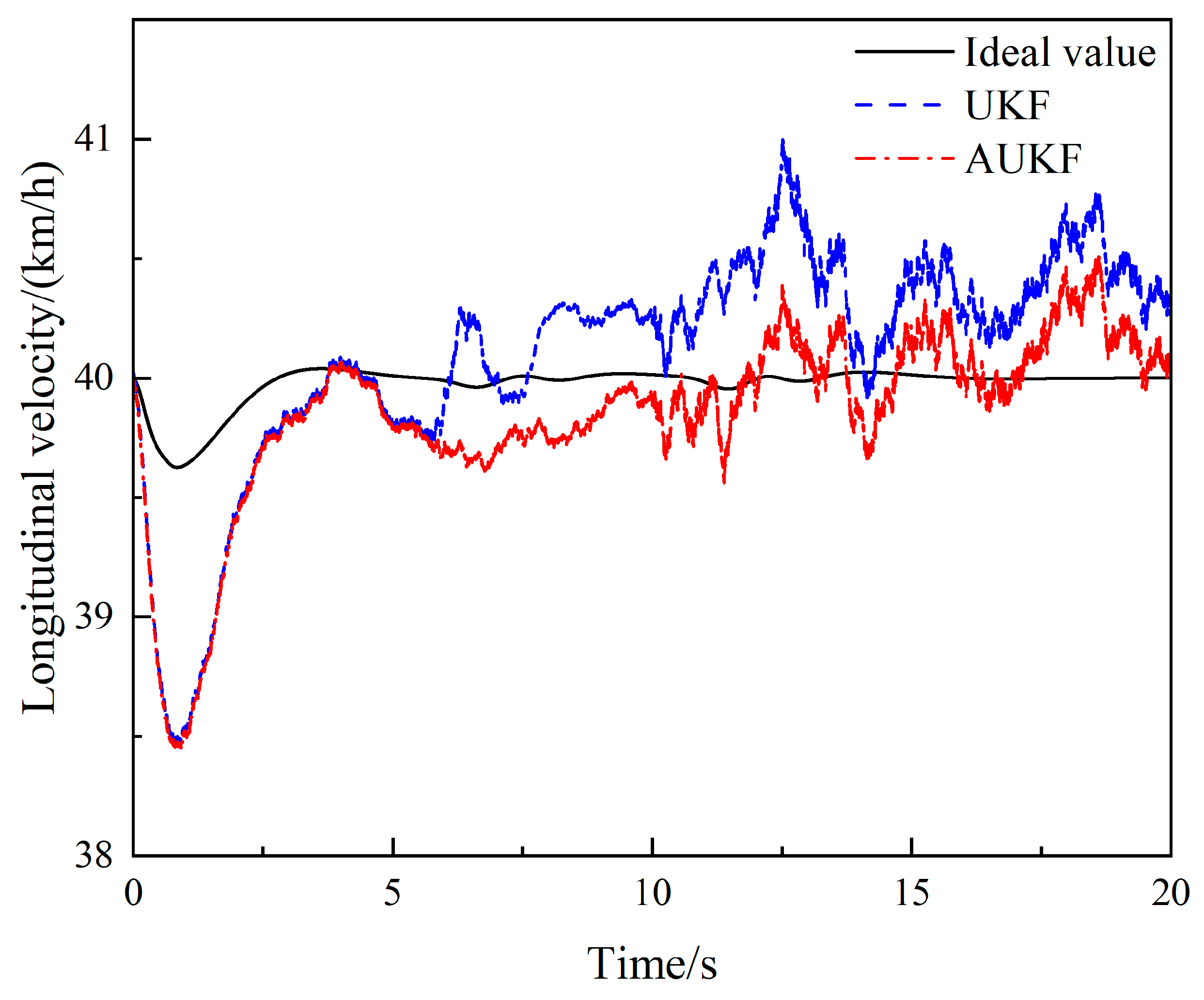
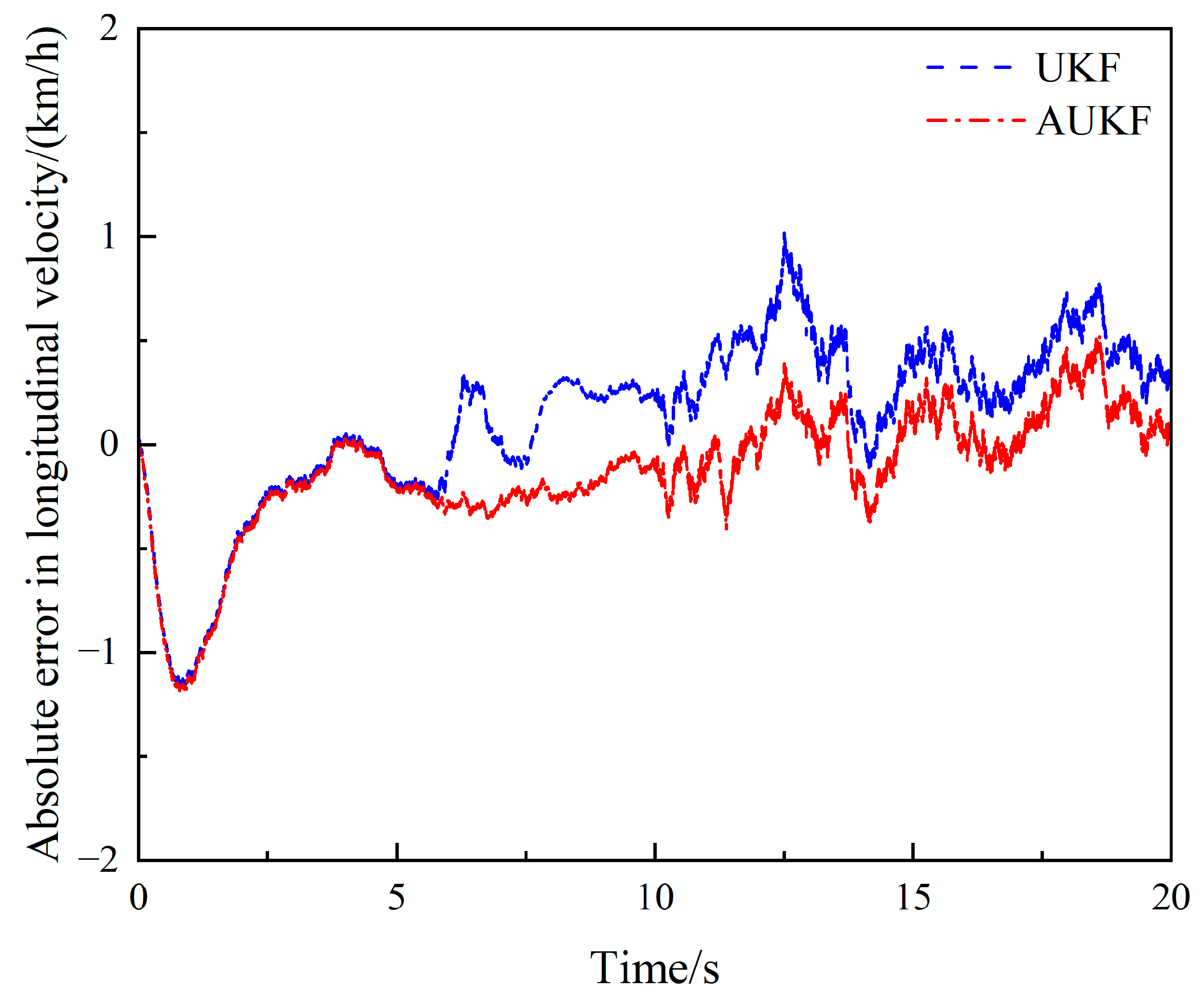
The simulation environment in Carsim is set to a typical steering angle step-input condition, sinusoidal steering condition, and double-lane change condition. These driving conditions can cover various situations in daily driving, such as turning, overtaking, and continuous overtaking. In addition, when the noise covariance matrix is time-varying, the algorithm’s performance is tested by altering the statistical properties of measurement noise under the double-lane change condition. The road adhesion coefficient is set to 0.85, the vehicle’s initial speed is 40 km/h, the transmission ratio of the steering wheel to the front wheel is 20, and the sampling time is 0.001 s. In Carsim, the car is chosen as a C-class hatchback with the fundamental parameters in

Table 1. Vehicle Parameter Settings.

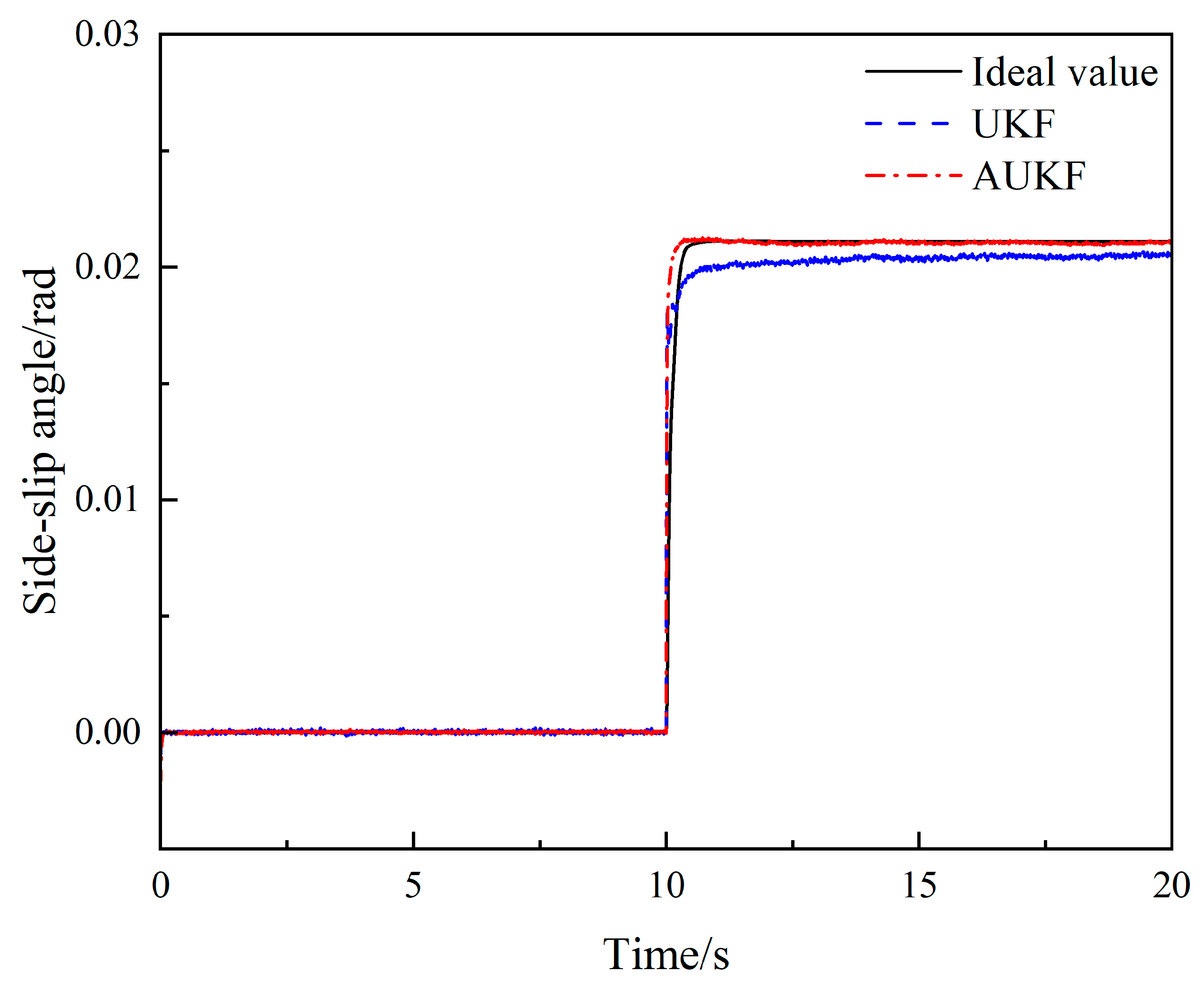
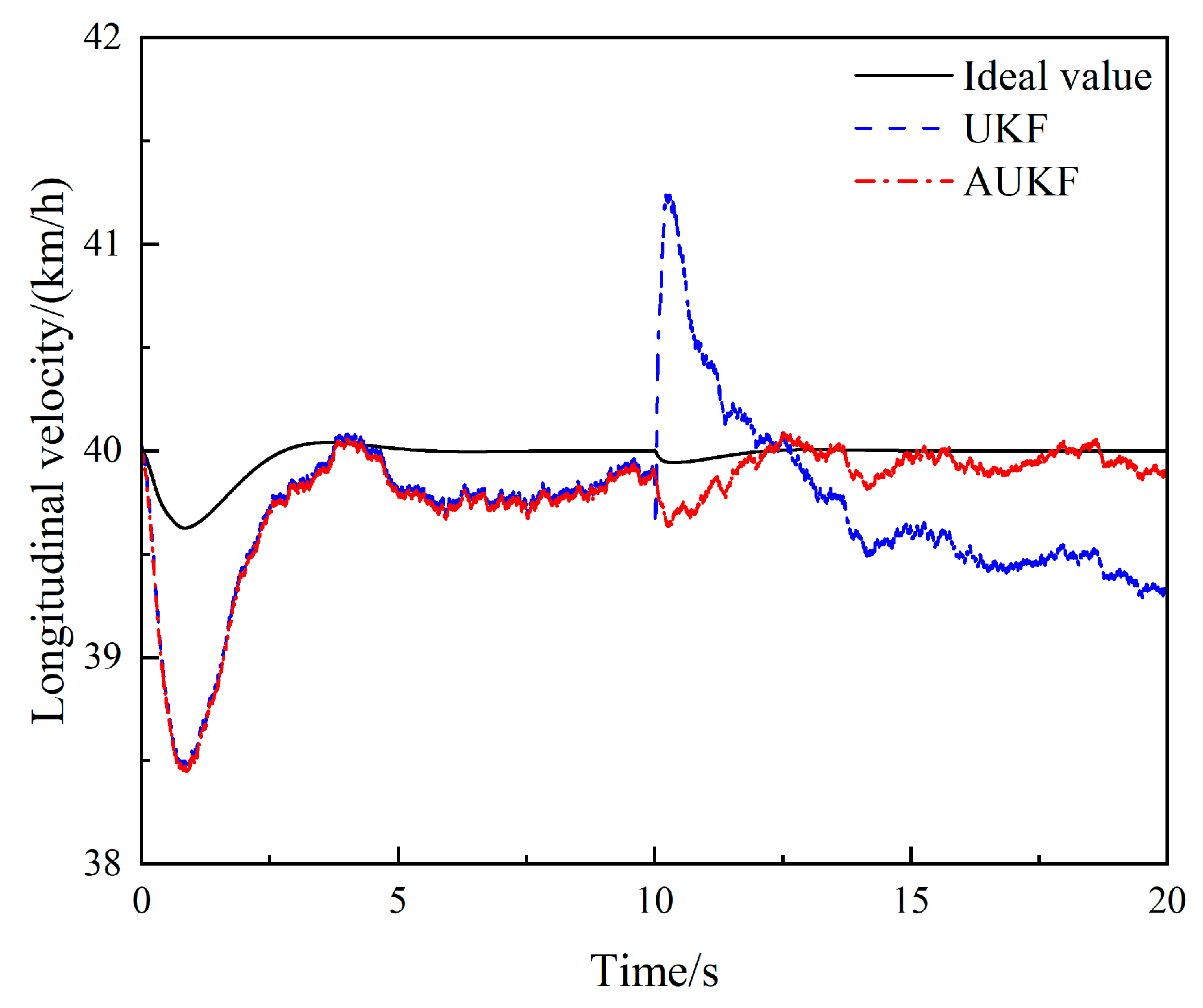
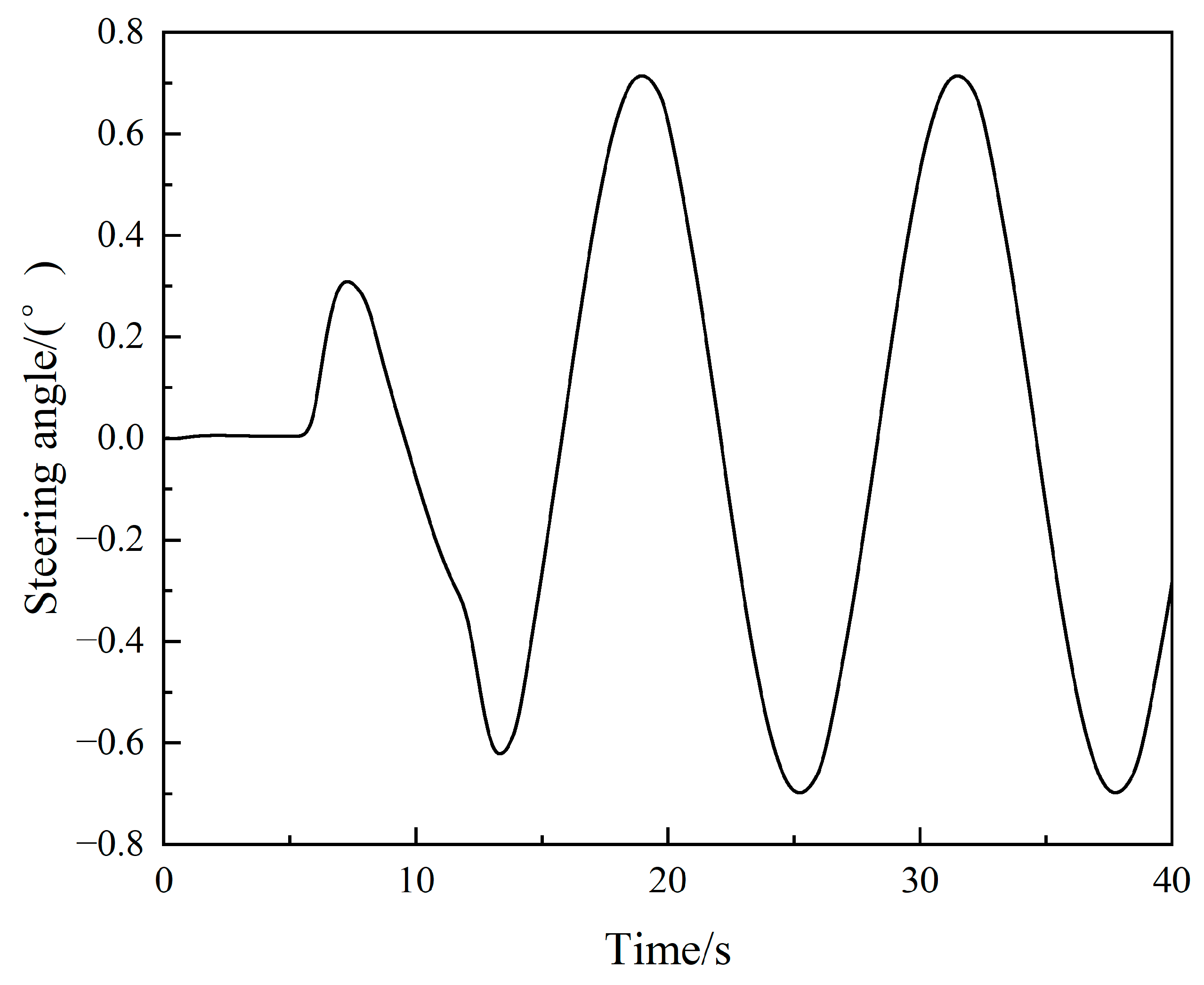
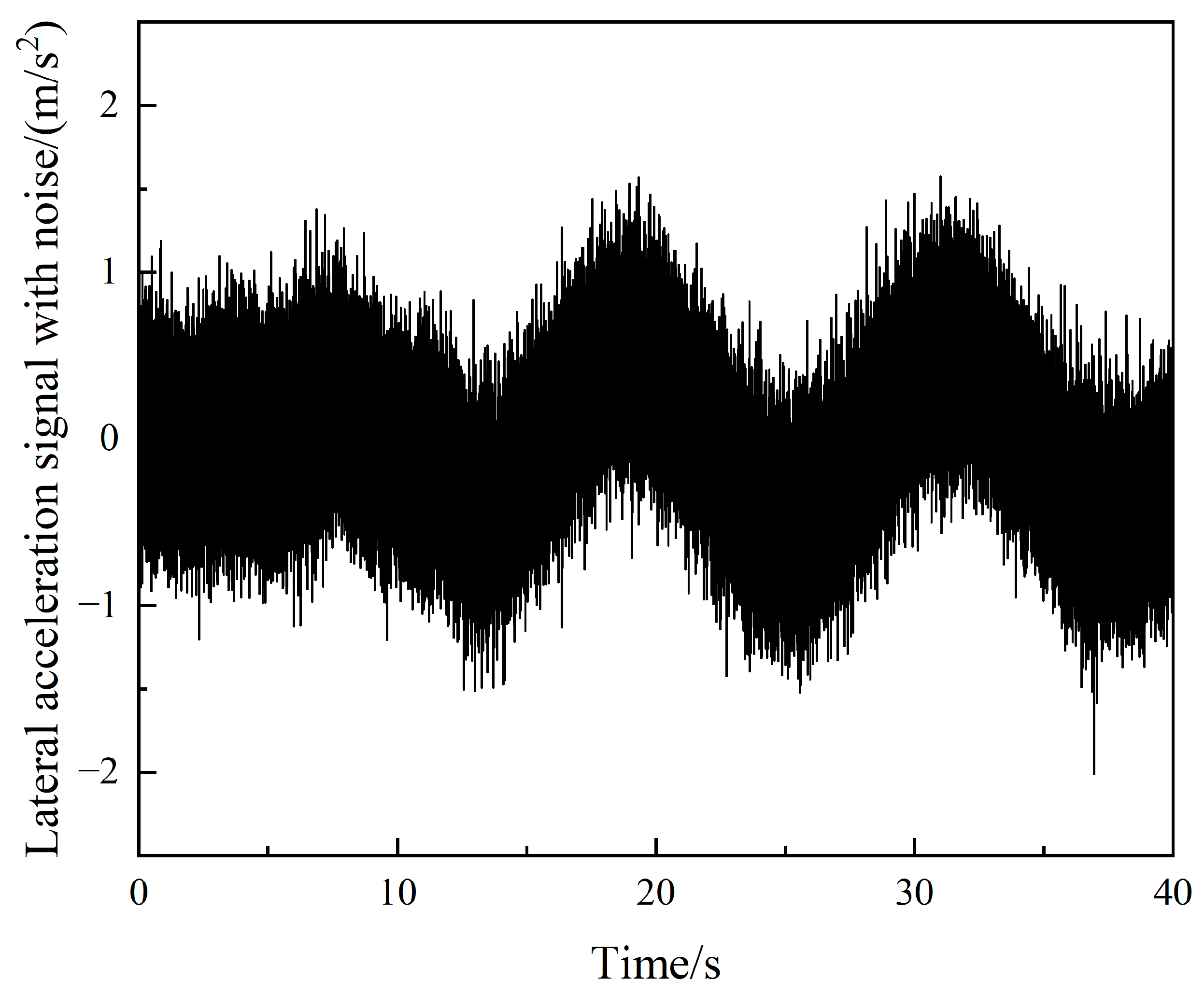
Parameter	Value
$m$	1410 kg
$a$	1.015 m
$b$	1.895 m
$k_1$	−122,540 N·rad−1
$k_2$	−100,500 N·rad−1
$I_z$	1536.7 kg·m2

.

Assigning the basic parameters of the algorithm, the initial value of the error covariance matrix $P$ is set to eye (3), the initial value of the system process noise covariance matrix $Q$ is set to eye (3) × 0.001, and the initial value of the measurement noise covariance matrix $R$ is set to 100.

4.1. Steering Angle Step-Input Condition

We set the initial value of the system-state vector $X(t_0)$ to [0, 0, 40/3.6]^T. The initial value of the system-input vector $u(t)$ is [$\delta$, $a_x$]^T, and its input waveform is shown in Figure 3. The observed quantity $Z$ is $a_y$, and the waveform after adding Gaussian white noise is shown in Figure 4.

Figure 5, Figure 6 and Figure 7 depict the simulation results, where Carsim’s output represents the ideal value, UKF and AUKF originating from the estimated values obtained by the UKF and AUKF algorithms, respectively. Figure 5 and Figure 6 show how the standard UKF estimation are significantly impacted when the steering wheel is twisted violently at 10 s. They demonstrate that UKF cannot be precisely predicted when there is unknown noise interference. The AUKF algorithm’s estimated value is more accurately calculated than the classic UKF algorithm and is roughly consistent with the ideal value, which can effectively lessen the influence of unidentified noise.

Figure 7 shows that there is a certain deviation in the estimation of UKF and AUKF within 0–3 s when calculating the longitudinal vehicle speed. Then, within 3–10 s, both UKF and AUKF are approaching the actual value. At 10 s, due to step input of the steering wheel, the input value of the observer undergoes a significant change in an instant, and the estimated value of UKF suddenly increases and deviates from the actual value. At the same time, AUKF is less affected and can still accurately estimate the longitudinal speed of the vehicle within 10–20 s.

The mean absolute error (MAE) and root mean square error (RMSE) are indicators used in this research to quantify further and examine the estimation values. The root means square error and means absolute error can be used to assess the precision and tracking abilities of the estimation results, respectively. The expressions are defined as

$$\mathrm{MAE}=\frac{1}{n}{\displaystyle \sum _{i=1}^n|y_i-{\widehat{y}}_i|}$$

(33)

$$\mathrm{RMSE}=\sqrt{\frac{1}{n}{\displaystyle \sum _{i=1}^n{\left(y_i-{\widehat{y}}_i\right)}^2}}$$

(34)

As shown in

Table 2. MAE between estimated value and true value under the steering angle step-input condition.

Algorithm	Yaw Rate (rad/s)	Side-Slip Angle (rad)	Longitudinal Velocity (km/h)
UKF	0.0012	0.000462	0.3726
AUKF	0.0009	0.000140	0.1982

and

Table 3. RMSE between estimated value and true value under the steering angle step-input condition.

Algorithm	Yaw Rate (rad/s)	Side-Slip Angle (rad)	Longitudinal Velocity (km/h)
UKF	0.0063	0.000907	0.4644
AUKF	0.0061	0.000821	0.3133

, the estimation accuracy and stability of the AUKF algorithm are better than those of the UKF algorithm in the MAE indicators and the RMSE indicators. The accuracy of yaw rate estimation under the steering angle step-input condition has been improved by 3.2%, the accuracy of side-slip angle estimation has been improved by 9.5%, and the estimation of longitudinal velocity has been improved by 32.5%.

4.2. Sinusoidal Steering Condition

We set the initial value of the system state vector $X(t_0)$ to [0, 0, 40/3.6]^T. The initial value of the system input vector $u(t)$ is [$\delta$, $a_x$]^T, and its input waveform is shown in Figure 8. The observed quantity $Z$ is $a_y$, and the waveform after adding Gaussian white noise is shown in Figure 9.

The simulation results are shown in Figure 10, Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15. Figure 10 and Figure 12 show that under the sinusoidal steering condition, the car changes lanes after 5 s. The original UKF deviates from the ideal value when the steering wheel angle experiences a quick shift, but the proposed AUKF algorithm can successfully track the ideal value. Figure 11 and Figure 13 show that the error and diffusion of AUKF are smaller than those of UKF, indicating that AUKF can better reduce the impact of unknown noise. It can be seen from Figure 14 and Figure 15 that the divergence of UKF is larger than AUKF because UKF cannot dynamically adjust the measurement noise covariance matrix. The error of UKF becomes larger and larger as time goes on, and the error of AUKF is relatively stable, which proves that the algorithm can effectively reduce the influence of unknown noise and curb the divergence of the filtering results.

As shown in

Table 4. MAE between estimated value and true value under the sinusoidal steering condition.

Algorithm	Yaw Rate (rad/s)	Side-Slip Angle (rad)	Longitudinal Velocity (km/h)
UKF	0.000726	0.000176	0.557
AUKF	0.000551	0.000141	0.154

and

Table 5. RMSE between estimated value and true value under the sinusoidal steering condition.

Algorithm	Yaw Rate (rad/s)	Side-Slip Angle (rad)	Longitudinal Velocity (km/h)
UKF	0.000916	0.000219	0.6434
AUKF	0.000689	0.000176	0.2356

, the accuracy of yaw rate estimation has been improved by 24.8%, the accuracy of side-slip angle estimation has been improved by 19.6%, and the estimation of longitudinal velocity by AUKF has been improved by 63.4% under the sinusoidal steering condition.

4.3. Double-Lane Change Condition

We set the initial value of the system state vector $X(t_0)$ to [0, 0, 40/3.6]^T. The initial value of the system input vector $u(t)$ is [$\delta$, $a_x$]^T, and its input waveform is shown in Figure 16. The observed quantity $Z$ is $a_y$, and the waveform after adding time-varying Gaussian white noise is shown in Figure 17, in which the statistical characteristics of the measurement noise becomes 10 times that of the first 10 s at 10–20 s, i.e., 10$R_k$.

The simulation results are shown in Figure 18, Figure 19, Figure 20, Figure 21, Figure 22 and Figure 23. Figure 18 and Figure 20 show that under the double-lane change condition, the car changes lanes between 5–15 s. The original UKF deviates from the ideal value when the steering wheel angle experiences a quick shift, but the proposed AUKF algorithm can successfully track the ideal value. Figure 19 and Figure 21 show that the error of AUKF is smaller than that of UKF, indicating that AUKF can better reduce the impact of unknown noise. And after 10 s, when the statistical characteristics of the measurement noise covariance increase by ten times, the divergence of UKF significantly increases, proving that UKF cannot accurately estimate state parameters when the noise covariance is time-varying. The fluctuation of AUKF is relatively small, and the error is within an acceptable range.

As shown in Figure 22, the estimates of UKF and AUKF are the same within 0–5 s, and both show some deviation. Whereas, after 5 s, when the driver starts to turn the steering wheel, the UFK is unable to provide real-time updates in calculating the longitudinal speed and deviates as the error increases. As can be seen in Figure 23, both UKF and AUKF are affected after the statistical characteristics of the noise is expanded by a factor of 10, but the fluctuation of AUKF is smaller than that of UKF, and the estimation results are still more accurate than those of UKF. The simulation results show that the proposed algorithm has a higher accuracy and can cope with the time-varying noise covariance characteristic values.

As shown in

Table 6. MAE between estimated value and true value under the double-lane change condition.

Algorithm	Yaw Rate (rad/s)	Side-Slip Angle (rad)	Longitudinal Velocity (km/h)
UKF	0.0020	0.000363	0.348
AUKF	0.0016	0.000116	0.234

and

Table 7. RMSE between estimated value and true value under the double-lane change condition.

Algorithm	Yaw Rate (rad/s)	Side-Slip Angle (rad)	Longitudinal Velocity (km/h)
UKF	0.0034	0.000578	0.4289
AUKF	0.0024	0.000177	0.3321

, the accuracy of yaw rate estimation has been improved by 29.4%, the accuracy of side-slip angle estimation has been improved by 69.3%, and the estimation of longitudinal velocity by AUKF has been improved by 22.5% under the double-lane change condition.

As shown in

Table 8. Comparison of algorithm complexity in steering angle step-input condition.

Algorithm	Total Running Time (s)	Single-Step Running Time (s)	Computational Complexity
UKF	23.433	0.00117	O(n2)
AUKF	24.026	0.00120	O(n2)

,

Table 9. Comparison of algorithm complexity in sinusoidal steering condition.

Algorithm	Total Running Time (s)	Single-Step Running Time (s)	Computational Complexity
UKF	52.716	0.00132	O(n2)
AUKF	56.439	0.00141	O(n2)

and

Table 10. Comparison of algorithm complexity in double-lane change condition.

Algorithm	Total Running Time (s)	Single-Step Running Time (s)	Computational Complexity
UKF	24.892	0.00124	O(n2)
AUKF	26.214	0.00131	O(n2)

, the AUKF algorithm has a longer single-step running time than the UKF algorithm. This is because the AUKF algorithm needs to calculate the weight factors and check whether the covariance matrix is positively definite. The computational complexity is higher than that of the UKF algorithm, and therefore, the total running time is longer.

5. Conclusions

When the vehicle is disturbed by uncertain noises, the traditional vehicle state estimation methods will appear to reduce the accuracy or even diverge. To solve this problem, an AUKF algorithm based on the Sage–Husa algorithm is proposed in this paper. By ignoring the update of the process noise covariance matrix $Q$ and adjusting the measurement noise covariance matrix $R$ online, the estimation of vehicle state parameters under unknown noise disturbance is solved.

This article uses Carsim and Matlab/Simulink for joint simulation to estimate the vehicle’s side-slip angle, yaw rate, and longitudinal speed. The simulation results show that the accuracy of the AUKF algorithm is improved by 3.2%, 9.5%, and 32.5% under the steering angle step-input condition, 24.8%, 19.6%, and 63.4% under the sinusoidal steering condition, and 29.4%, 69.3%, and 22.5% under the double-lane change condition. Compared with the UKF algorithm, although the single-step running time of the AUKF algorithm is slightly increased, its accuracy is greatly improved, which can effectively filter out unknown noise. In practical applications, the three working conditions proposed in this article can cover various situations in daily driving. The proposed method eliminates the need to obtain critical state parameters from high-precision sensors, reduces the cost of the vehicle, and can provide more accurate parameters for vehicle decision-making and control systems, which significantly helps to improve the vehicle’s handling characteristics.

However, when estimating the longitudinal speed of the vehicle, both UKF and AUKF have significant errors at the beginning. This may be caused by errors in the tire model. In our future research, we will build more accurate models to reduce the uncertainty error further and consider the vehicle state estimation under different road surface adhesion coefficients and road slopes. Then, we will improve our proposed algorithm by incorporating more complex working conditions verification and conduct a real-vehicle test.