Online Broadband Impedance Identification for Lithium-Ion Batteries Based on a Nonlinear Equivalent Circuit Model
Abstract
1. Introduction
2. Experimental Section
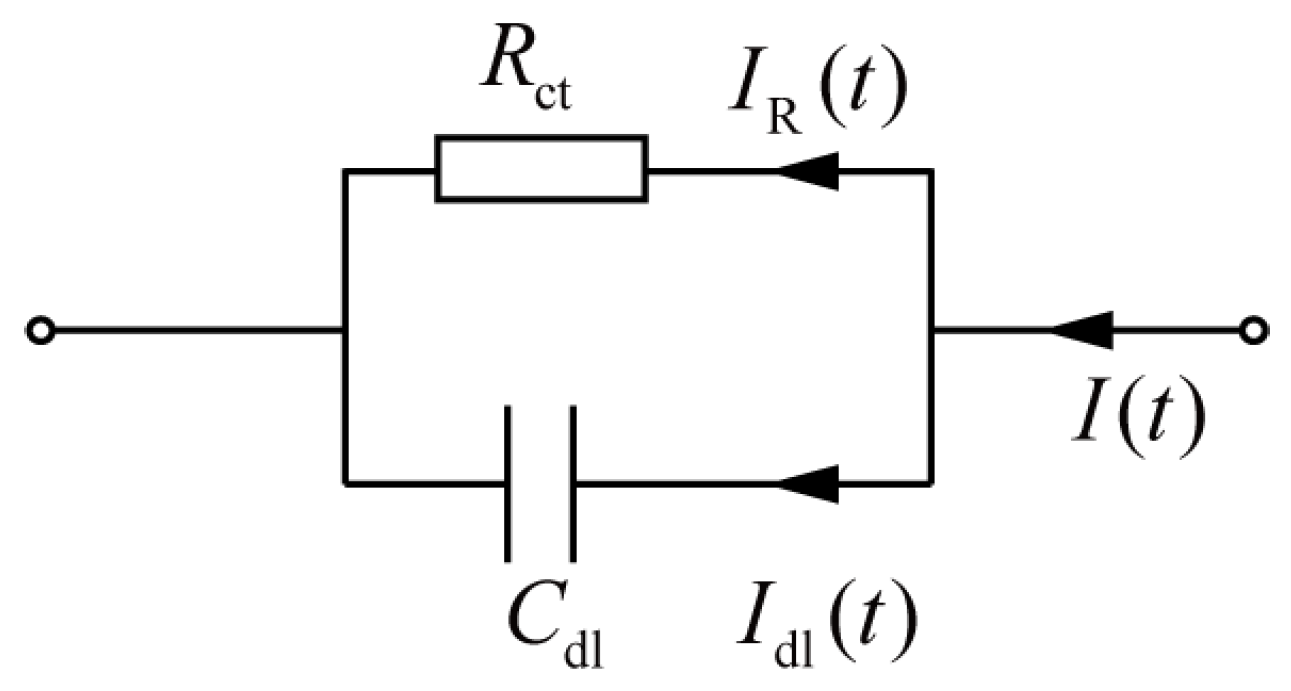
3. Modeling
4. Methodology
4.1. Discretization of Impedance Model
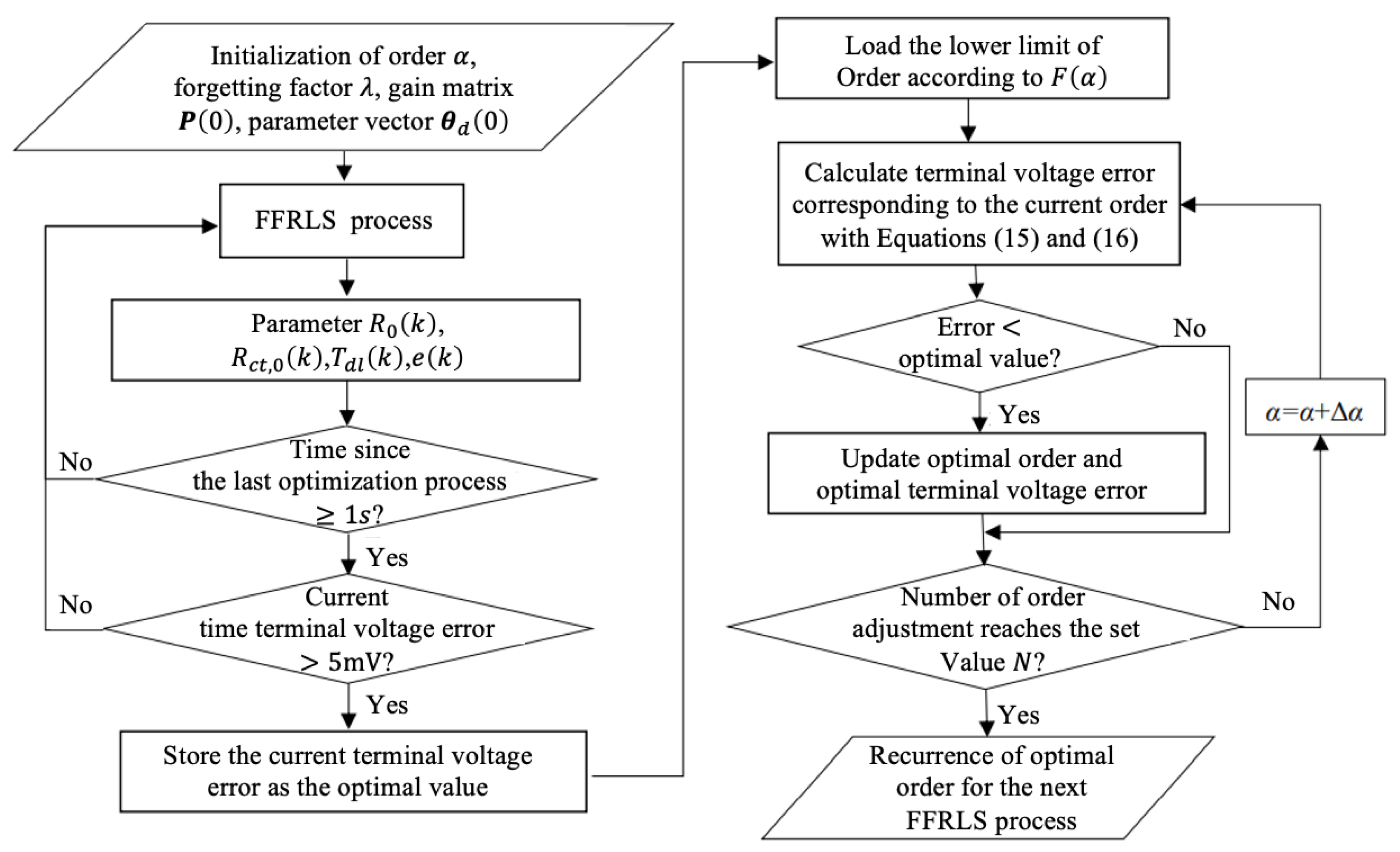
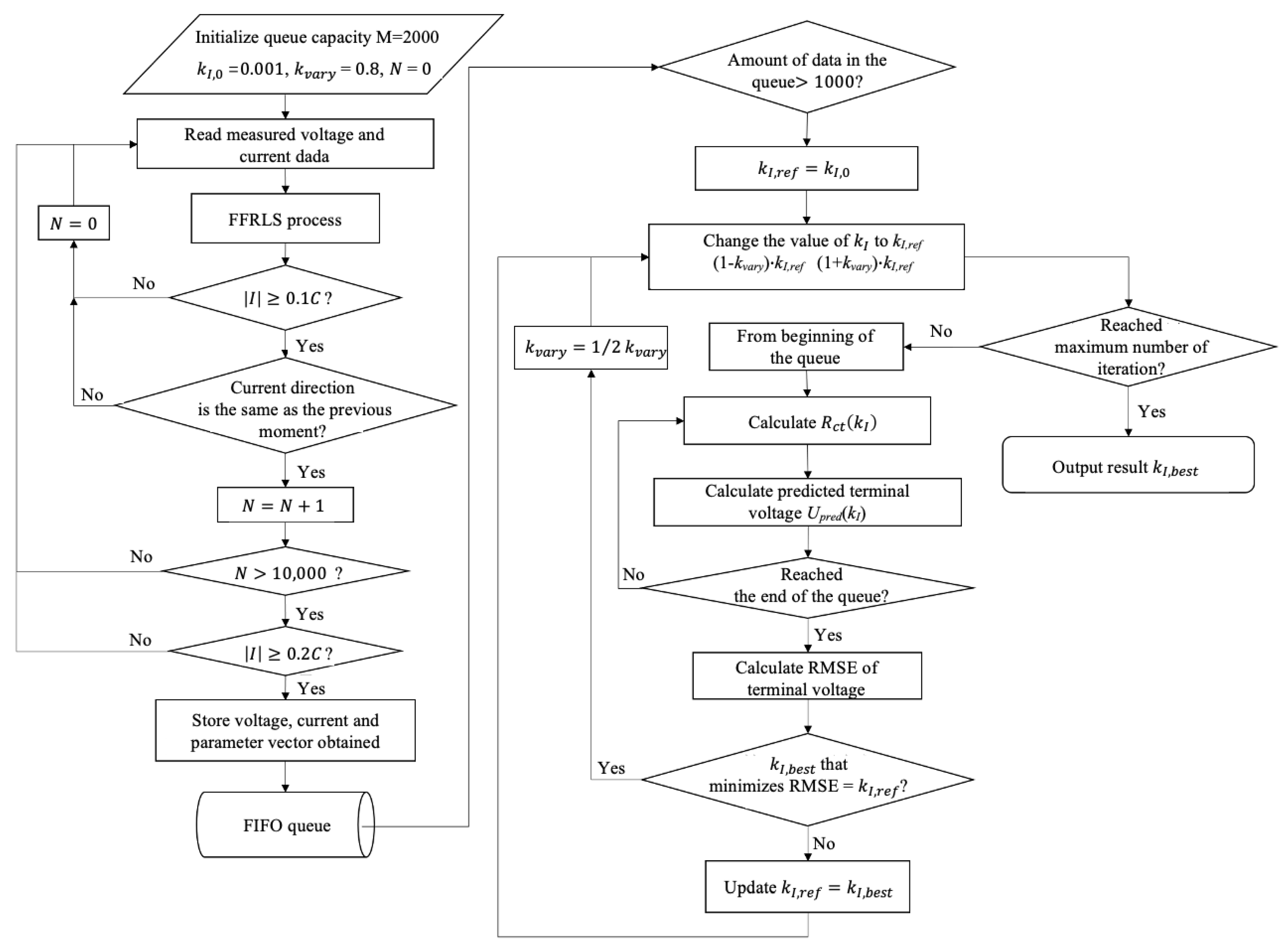
4.2. Online Identification Algorithm for Impedance Models
5. Results and Discussion
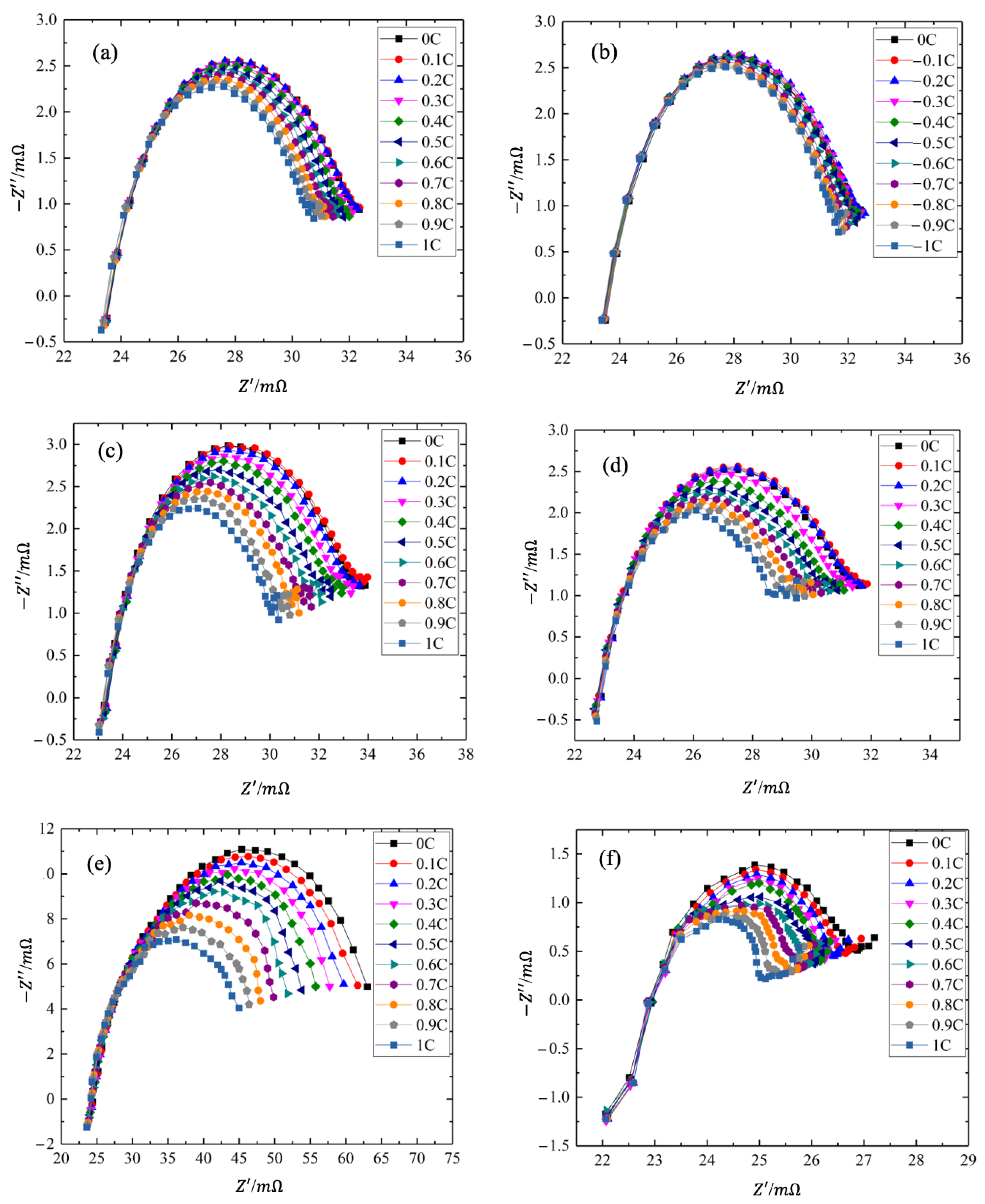
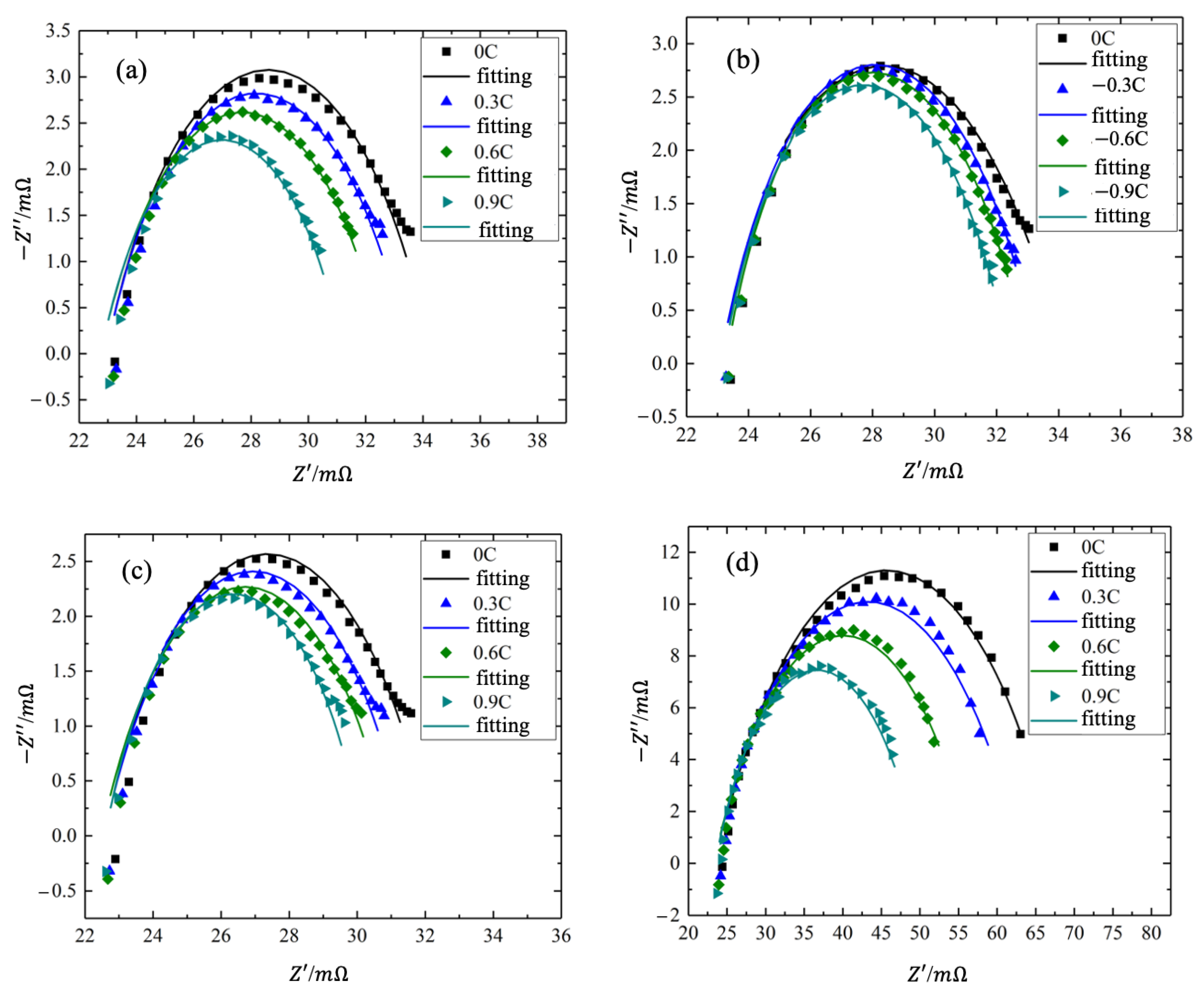
5.1. Verification of Impedance Model
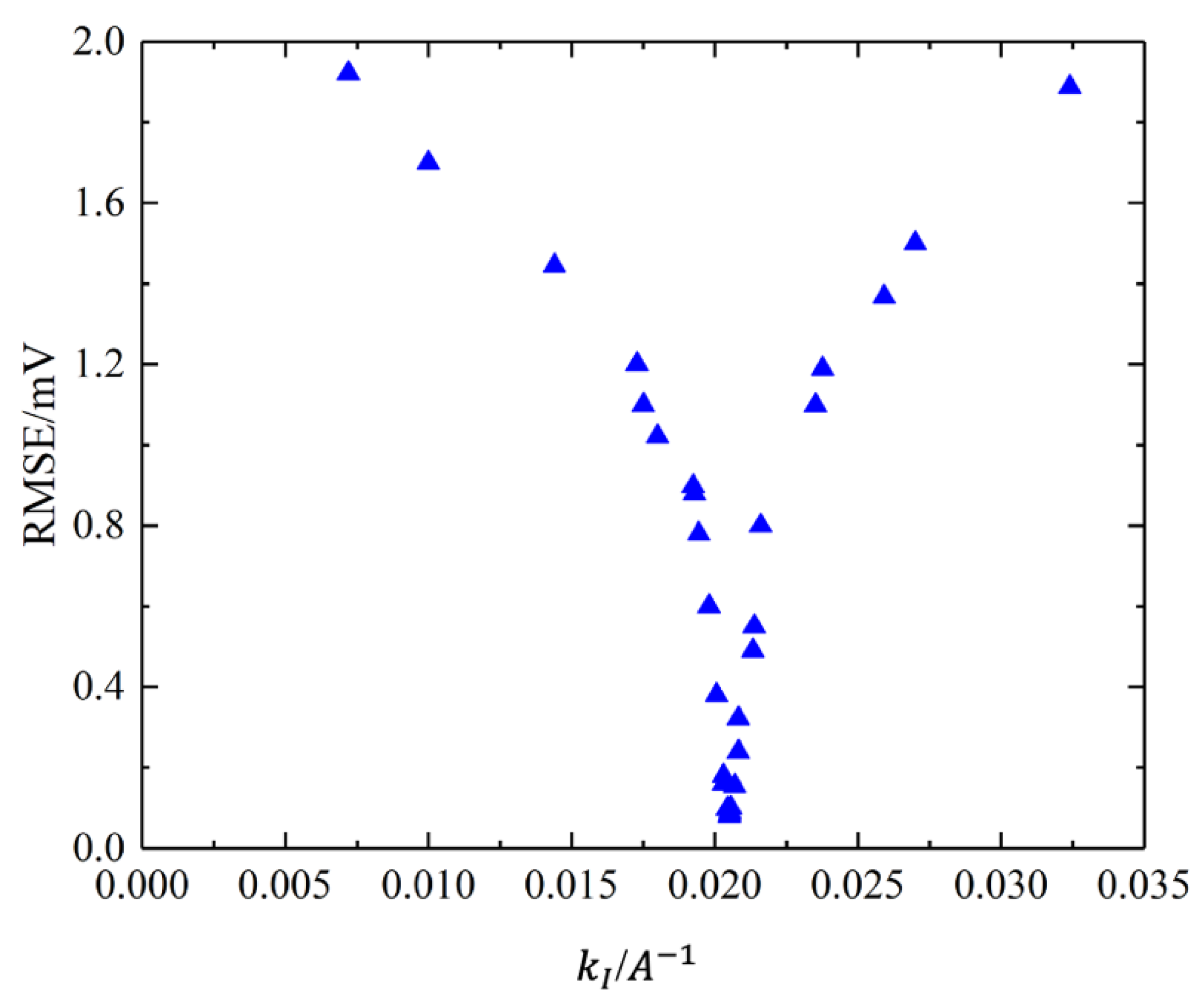
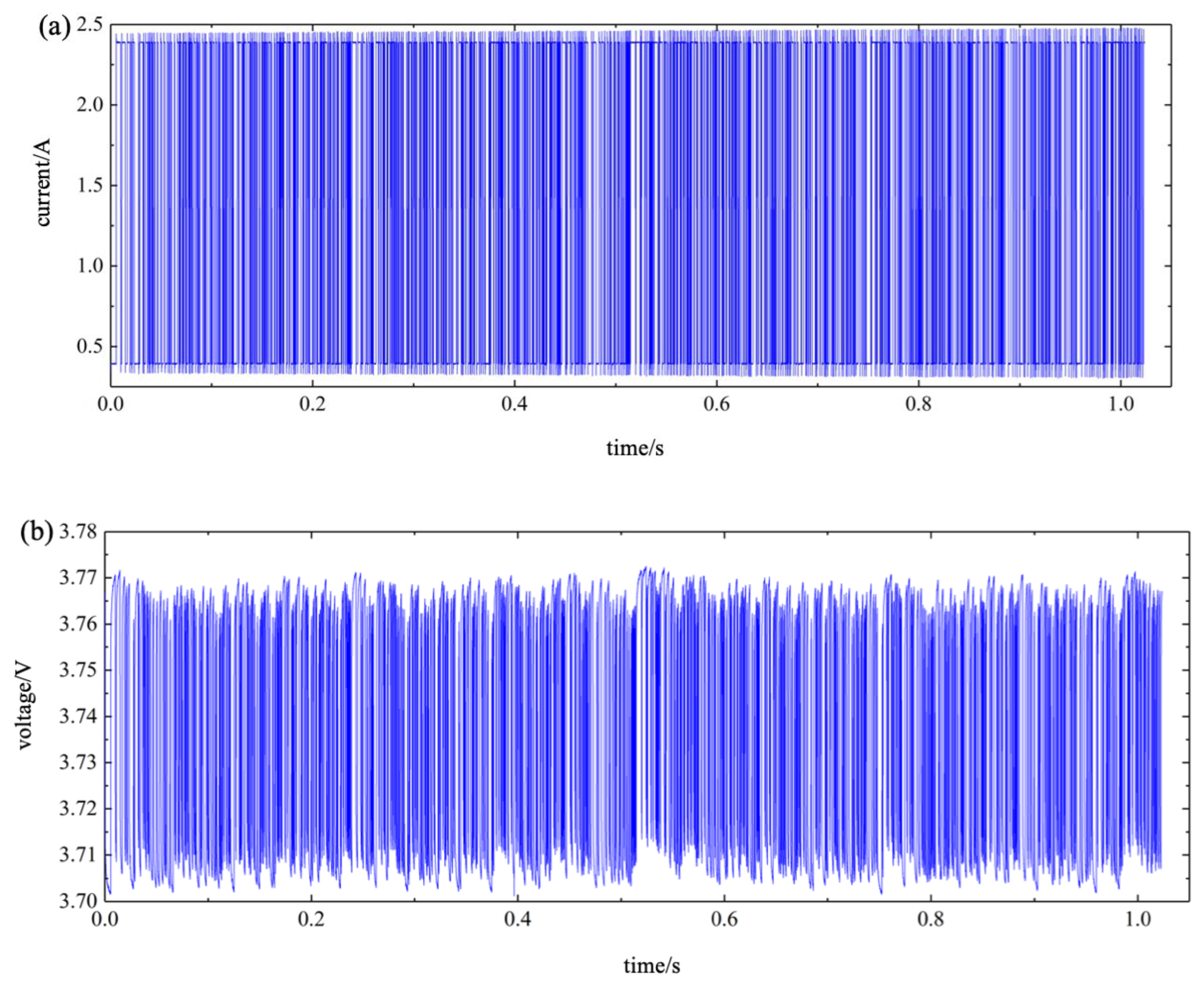
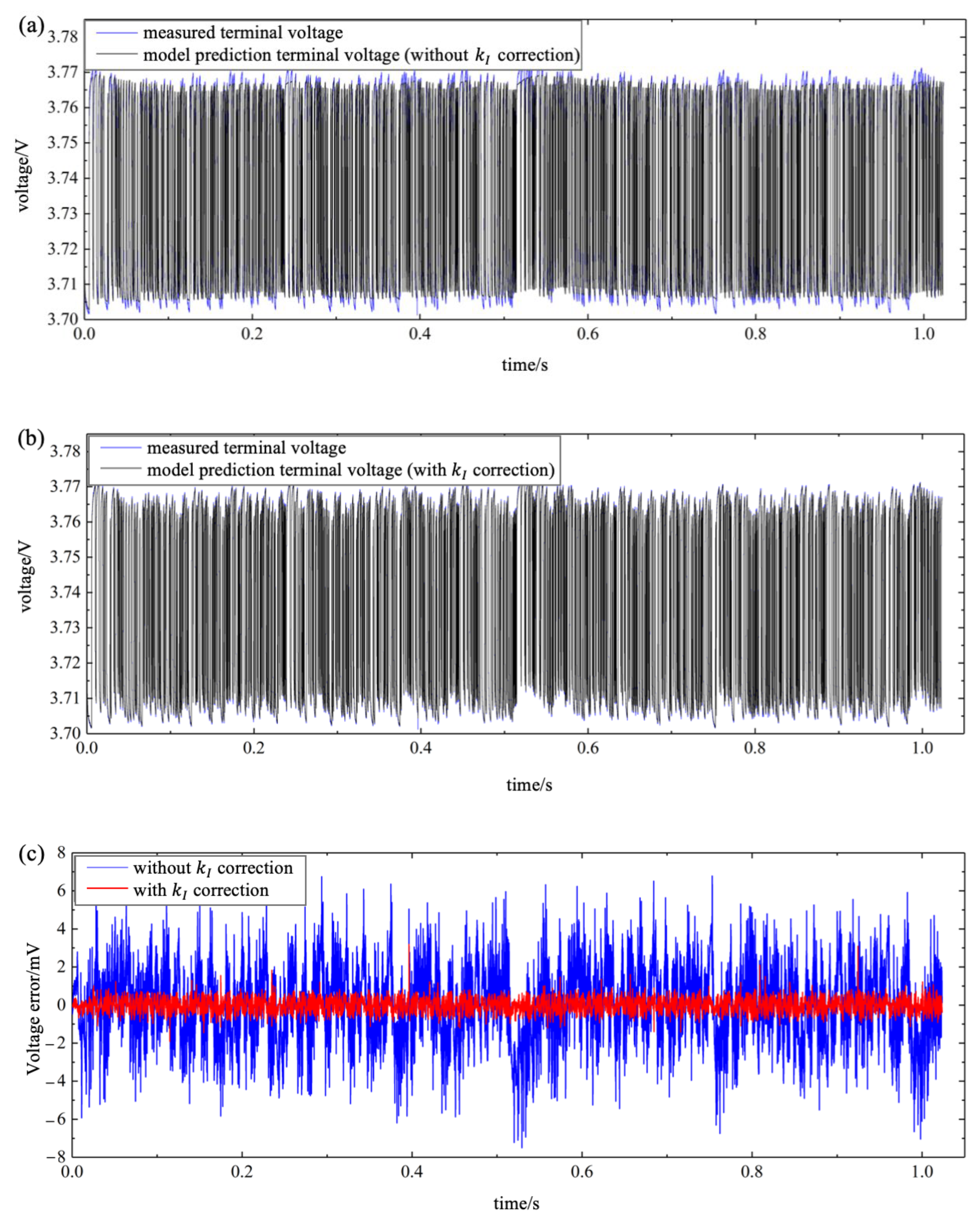
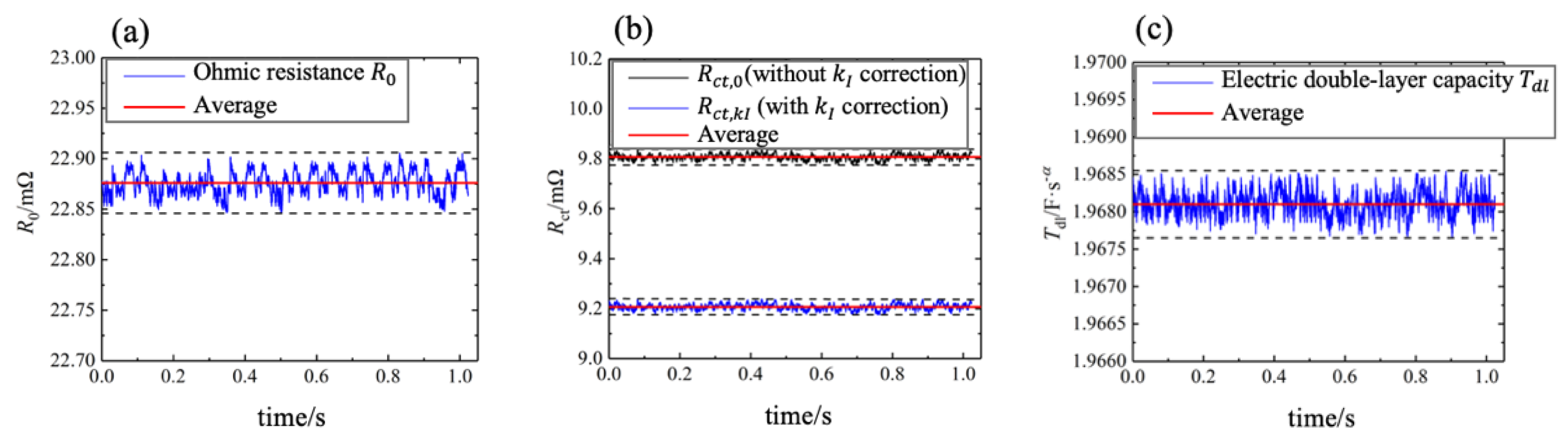
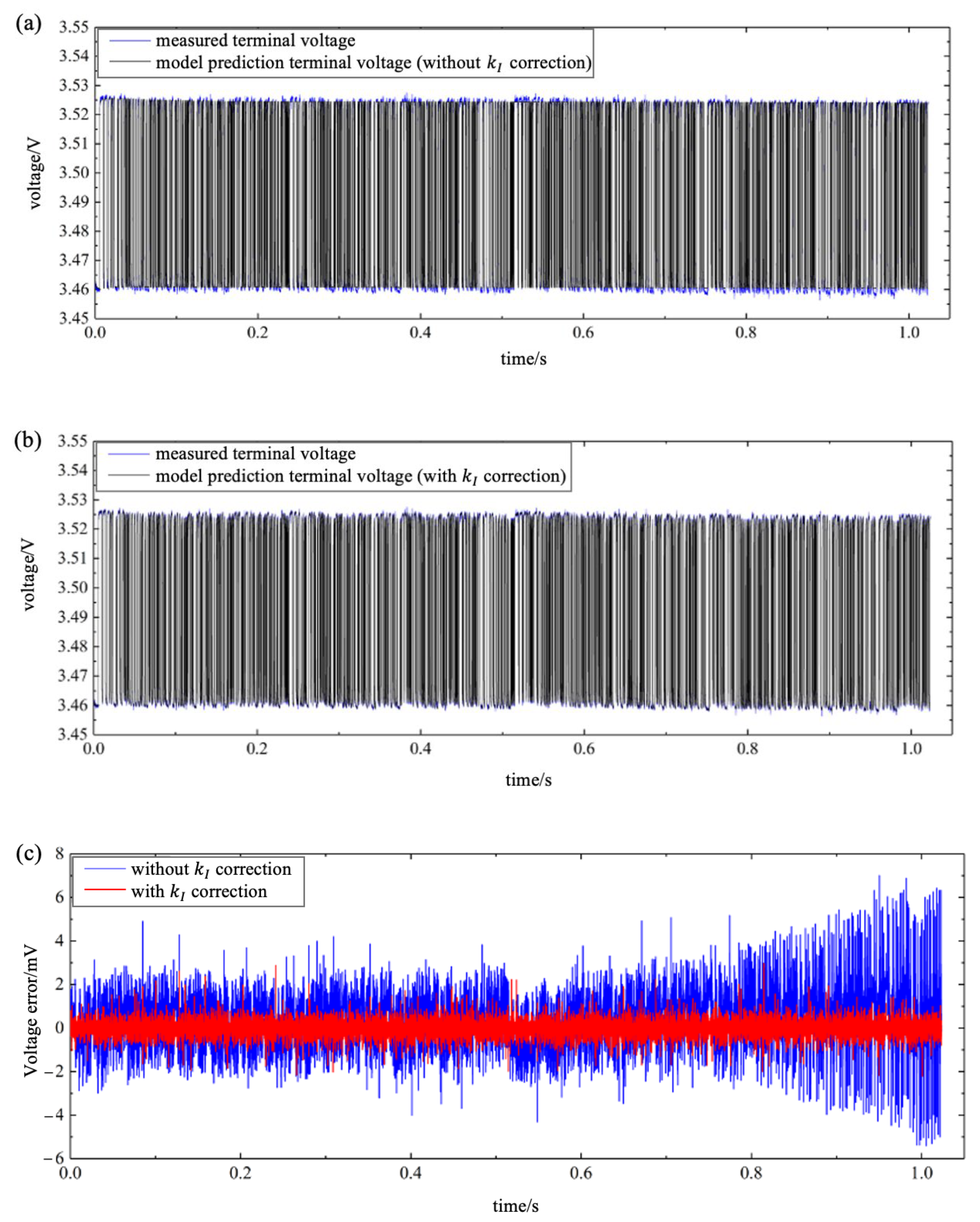
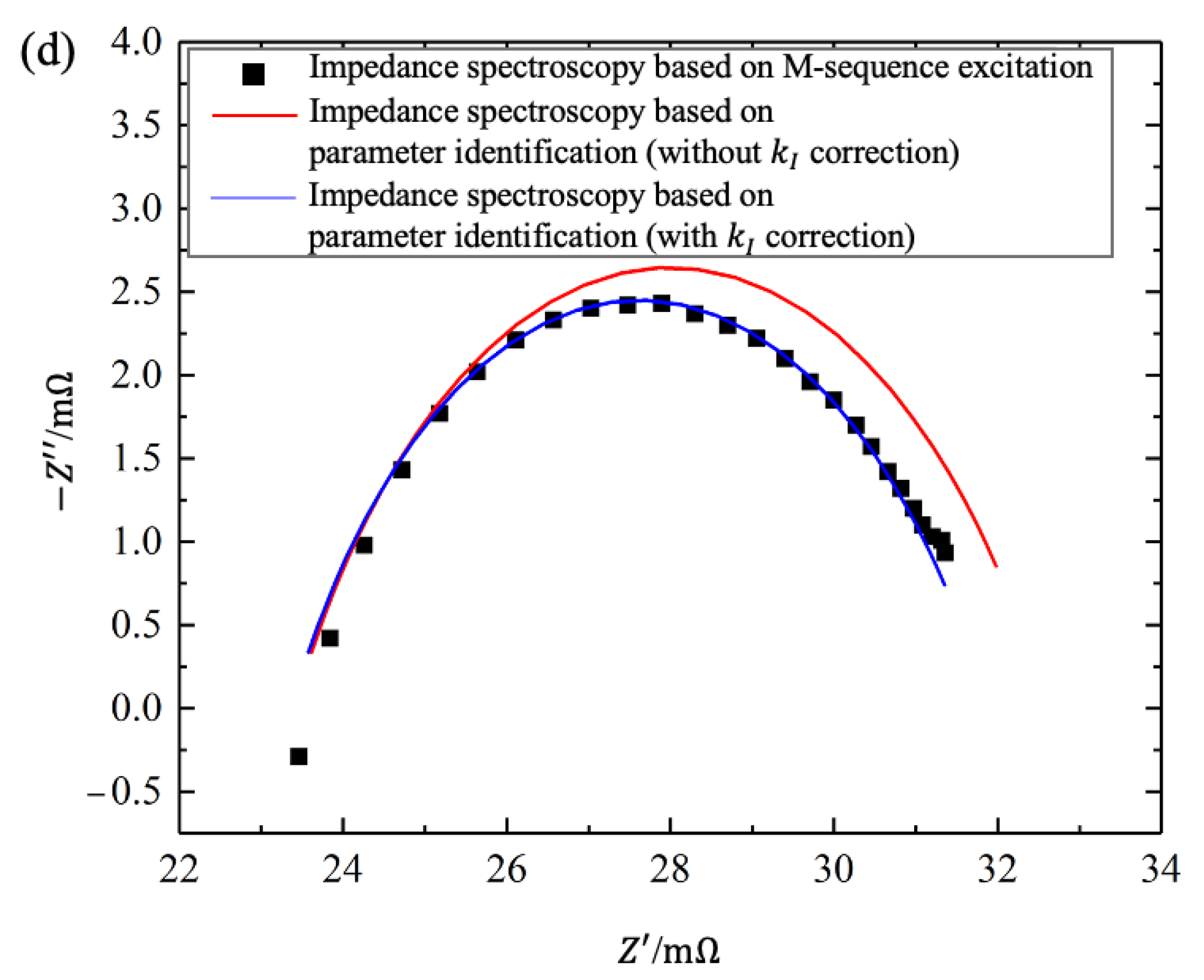
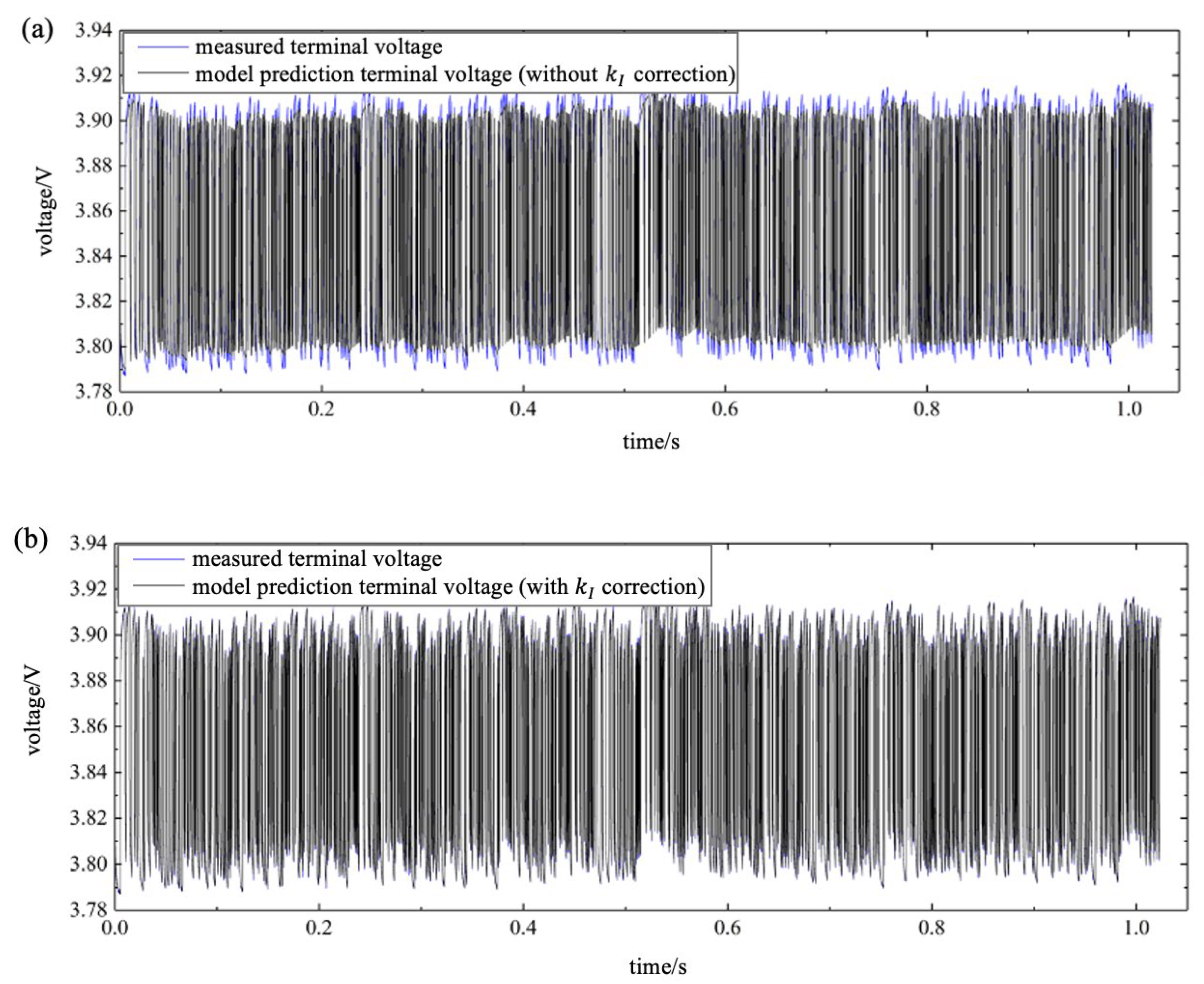
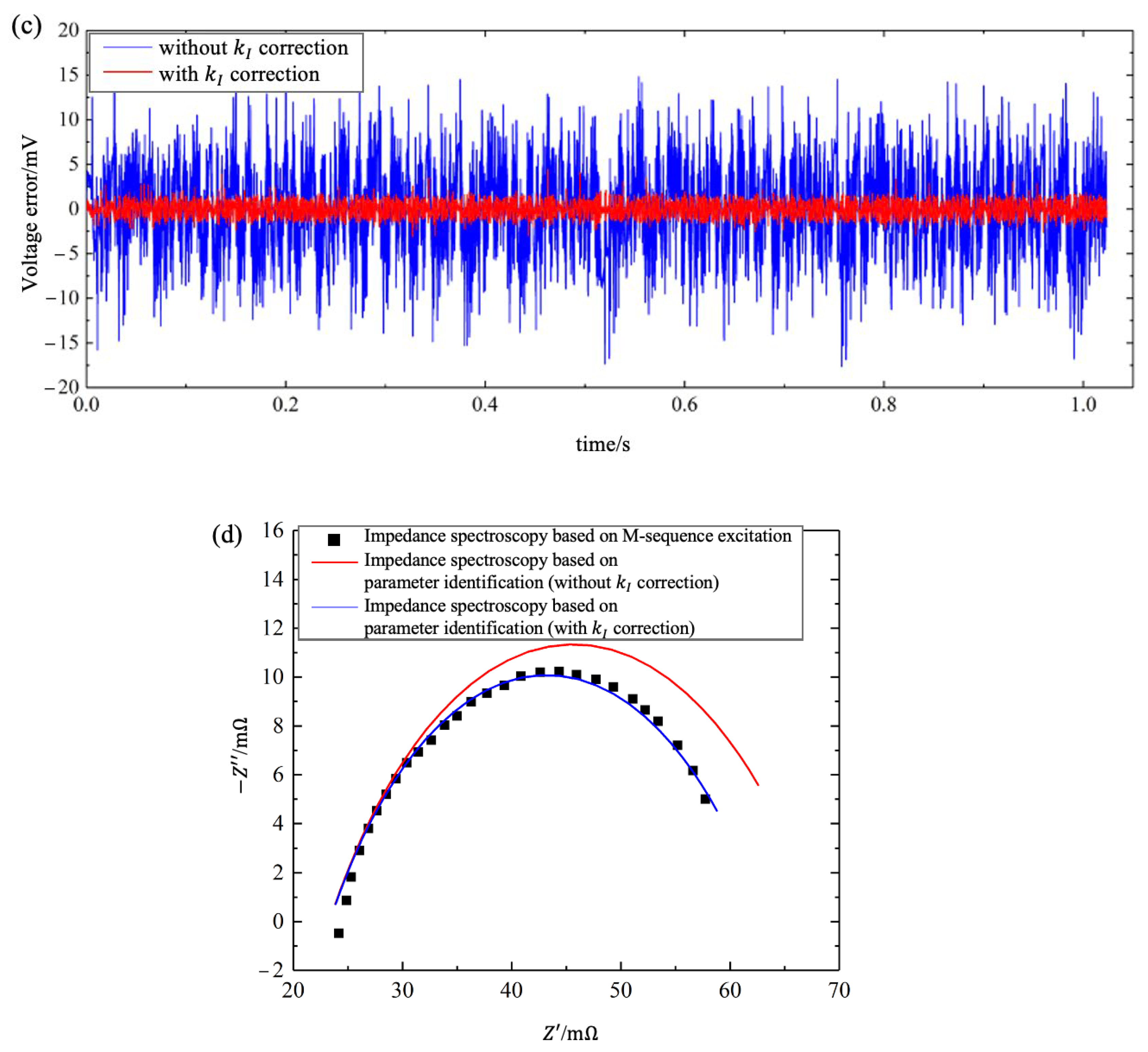
5.2. Verification of Parameter Identification Methods
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fuller, T.F.; Doyle, M.; Newman, J. Simulation and Optimization of the Dual Lithium Ion Insertion Cell. J. Electrochem. Soc. 1994, 141, 1–10. [Google Scholar] [CrossRef]
- Doyle, M.; Newman, J.; Gozdz, A.S.; Schmutz, C.N.; Tarascon, J.-M. Comparison of Modeling Predictions with Experimental Data from Plastic Lithium Ion Cells. J. Electrochem. Soc. 2019, 143, 1890. [Google Scholar] [CrossRef]
- Doyle, M.; Fuller, T.F.; Newman, J. Modeling of Galvanostatic Charge and Discharge of the Lithium/Polymer/Insertion Cell. J. Electrochem. Soc. 2019, 140, 1526–1533. [Google Scholar] [CrossRef]
- Santhanagopalan, S.; Guo, Q.; Ramadass, P.; White, R.E. Review of models for predicting the cycling performance of lithium ion batteries. J. Power Sources 2005, 156, 620–628. [Google Scholar] [CrossRef]
- Li, J.; Lotfi, N.; Landers, R.G.; Park, J. A Single Particle Model for Lithium-Ion Batteries with Electrolyte and Stress-Enhanced Diffusion Physics. J. Electrochem. Soc. 2017, 164, A874–A883. [Google Scholar] [CrossRef]
- Pajkossy, T. Impedance of rough capacitive electrodes. J. Electroanal. Chem. 1994, 364, 111–125. [Google Scholar] [CrossRef]
- Pauliukaite, R.; Ghica, M.E.; Fatibello-Filho, O.; Brett, C.M. Electrochemical impedance studies of chitosan-modified electrodes for application in electrochemical sensors and biosensors. Electrochim. Acta 2010, 55, 6239–6247. [Google Scholar] [CrossRef]
- Jacobsen, T.; West, K. Diffusion impedance in planar, cylindrical and spherical symmetry. Electrochim. Acta 1995, 40, 255–262. [Google Scholar] [CrossRef]
- Weydanz, W.; Jossen, A. Moderne Akkumulatoren Richtig Einsetzen; Cuvillier Verlag: Göttingen, Germany, 2019. [Google Scholar]
- Huang, J. Diffusion impedance of electroactive materials, electrolytic solutions and porous electrodes: Warburg impedance and beyond. Electrochim. Acta 2018, 281, 170–188. [Google Scholar] [CrossRef]
- Doyle, M.; Newman, J. The use of mathematical modeling in the design of lithium/polymer battery systems. Electrochim. Acta 1995, 40, 2191–2196. [Google Scholar] [CrossRef]
- Li, S.E.; Wang, B.; Peng, H.; Hu, X. An electrochemistry-based impedance model for lithium-ion batteries. J. Power Sources 2014, 258, 9–18. [Google Scholar] [CrossRef]
- Chu, Z.; Feng, X.; Lu, L.; Li, J.; Han, X.; Ouyang, M. Non-destructive fast charging algorithm of lithium-ion batteries based on the control-oriented electrochemical model. Appl. Energy 2017, 204, 1240–1250. [Google Scholar] [CrossRef]
- Klein, R.; Chaturvedi, N.A.; Christensen, J.; Ahmed, J.; Findeisen, R.; Kojic, A. Optimal charging strategies in lithium-ion battery. In Proceedings of the 2011 American Control Conference, San Francisco, CA, USA, 29 June–1 July 2011; pp. 382–387. [Google Scholar]
- Klein, R.; Chaturvedi, N.A.; Christensen, J.; Ahmed, J.; Findeisen, R.; Kojic, A. Electrochemical Model Based Observer Design for a Lithium-Ion Battery. Trans. Control. Syst. Technol. 2013, 21, 289–301. [Google Scholar] [CrossRef]
- Rahimian, S.K.; Rayman, S.C.; White, R.E. Maximizing the life of a lithium-ion cell by optimization of charging rates. Electrochem. Soc. 2010, 157, A1302–A1308. [Google Scholar] [CrossRef]
- Meng, J.; Yue, M.; Diallo, D. Nonlinear extension of battery constrained predictive charging control with transmission of Jacobian matrix. Int. J. Electr. Power Energy Syst. 2023, 146, 108762. [Google Scholar] [CrossRef]
- Randles, J.E.B. Kinetics of rapid electrode reactions. Discuss. Faraday Soc. 1947, 1, 11–19. [Google Scholar] [CrossRef]
- Eddine, A.N.; Huard, B.; Gabano, J.D.; Poinot, T. Initialization of a fractional order identification algorithm applied for Lithium-ion battery modeling in time domain. Commun. Nonlinear Sci. Numer. Simul. 2017, 59, 375–386. [Google Scholar] [CrossRef]
- Wang, B.; Li, S.E.; Peng, H.; Liu, Z. Fractional-order modeling and parameter identification for lithium-ion batteries. J. Power Sources 2015, 293, 151–161. [Google Scholar] [CrossRef]
- Troltzsch, U.; Kanoun, O.; Trankler, H.R. Characterizing aging effects of lithium ion batteries by impedance spectroscopy. Electrochim. Acta 2006, 51, 1664–1672. [Google Scholar] [CrossRef]
- Risse, S.; Cañas, N.A.; Wagner, N.; Härk, E.; Ballauff, M.; Friedrich, K.A. Correlation of capacity fading processes and electrochemical impedance spectra in lithium/sulfur cells. J. Power Sources 2016, 323, 107–114. [Google Scholar] [CrossRef]
- Rahman, A.; Anwar, S.; Izadian, A. Electrochemical model parameter identification of a lithium-ion battery using particle swarm optimization method. J. Power Sources 2016, 307, 86–97. [Google Scholar] [CrossRef]
- Rathmann, H.; Weber, C.; Benecke, W.; Eichholz, J.; Kaehler, D. Novel methode of state-of-charge estimation using in-situ impedance measurement: Single cells in-situ impedance measurement based state-of-charge estimation for LiFePO4—Li2TO3 Battery Cells with a real BMS. In Proceedings of the Conference of the IEEE Industrial Electronics Society, Dallas, TX, USA, 29 October–1 November 2014. [Google Scholar]
- Wei, Z.; Meng, S.; Xiong, B.; Ji, D.; Tseng, K.J. Enhanced online model identification and state of charge estimation for lithium-ion battery with a FBCRLS based observer. Appl. Energy 2016, 181, 332–341. [Google Scholar] [CrossRef]
- Zhang, C.; Allafi, W.; Dinh, Q.; Ascencio, P.; Marco, J. Online estimation of battery equivalent circuit model parameters and state of charge using decoupled least squares technique. Energy 2018, 142, 678–688. [Google Scholar] [CrossRef]
- Cai, M.; Chen, W.; Tan, X. Battery State-of-Charge Estimation Based on a Dual Unscented Kalman Filter and Fractional Variable-Order Model. Energies 2017, 10, 1577. [Google Scholar] [CrossRef]
- Wu, H.; Yuan, S.; Yin, C. A Lithium-Ion Battery Fractional Order State Space Model and Its Time Domain System Identification. In Proceedings of the FISITA 2012 World Automotive Congress, Berlin/Heidelberg, Germany, 27–30 November 2012; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Cai, J.; Zhang, L.; Wang, X.; Zhu, J.; Yuan, Y.; Wang, Y.; Wei, X.; Dai, H. Investigation of an M-Sequence based impedance spectrum acquisition method for lithium-ion batteries from the engineering application perspective. J. Energy Storage 2023, 59, 106428. [Google Scholar] [CrossRef]
- Heubner, C.; Schneider, M.; Michaelis, A. Investigation of charge transfer kinetics of Li-Intercalation in LiFePO 4. J. Power Sources 2015, 288, 115–120. [Google Scholar] [CrossRef]
- Salari, M.; Aboutalebi, S.H.; Chidembo, A.T.; Nevirkovets, I.P.; Konstantinov, K.; Liu, H.K. Enhancement of the electrochemical capacitance of TiO2 nanotube arrays through controlled phase transformation of anatase to rutile. Phys. Chem. Chem. Phys. 2012, 14, 4770–4779. [Google Scholar] [CrossRef]
- Huang, J.; Zhang, J.; Li, Z.; Song, S.; Wu, N. Exploring Differences between Charge and Discharge of LiMn2O4/Li Half-Cell with Dynamic Electrochemical Impedance Spectroscopy. Electrochim. Acta 2014, 131, 228–235. [Google Scholar] [CrossRef]
- Kuipers, M.; Schröer, P.; Nemeth, T.; Zappen, H.; Blömeke, A.; Sauer, D.U. An Algorithm for an Online Electrochemical Impedance Spectroscopy and Battery Parameter Estimation: Development, Verification and Validation. J. Energy Storage 2020, 30, 101517. [Google Scholar] [CrossRef]
- Waag, W.; Fleischer, C.; Sauer, D.U. On-line estimation of lithium-ion battery impedance parameters using a novel varied-parameters approach. J. Power Sources 2013, 237, 260–269. [Google Scholar] [CrossRef]
- Lai, X.; Huang, Y.; Gu, H. Remaining discharge energy estimation for lithium-ion batteries based on future load prediction considering temperature and ageing effects. Energy 2022, 238, 121754. [Google Scholar] [CrossRef]



| Temperature | SOC | Charge/Discharge Rate | RMSE/mΩ | Temperature | SOC | Charge/Discharge Rate | RMSE/mΩ |
|---|---|---|---|---|---|---|---|
| 25 °C | 50% | 0.3C | 0.425 | 25 °C | 70% | 0.3C | 0.458 |
| 0.6C | 0.478 | 0.6C | 0.427 | ||||
| −0.3C | 0.450 | 5 °C | 50% | 0.3C | 0.406 | ||
| −0.6C | 0.493 | 0.6C | 0.379 | ||||
| 30% | 0.3C | 0.462 | 35 °C | 0.3C | 0.495 | ||
| 0.6C | 0.397 | 0.6C | 0.484 |
| Temperature | SOC | Charge/ Discharge Rate | Terminal Voltage RMSE/mV | Impedance RMSE/mΩ |
|---|---|---|---|---|
| 25 °C | 50% | 0.5C | 0.228 | 0.358 |
| 1C | 0.154 | 0.324 | ||
| −0.5C | 0.286 | 0.426 | ||
| −1C | 0.215 | 0.379 | ||
| 30% | 0.5C | 0.239 | 0.361 | |
| 1C | 0.173 | 0.412 | ||
| 70% | 0.5C | 0.112 | 0.344 | |
| 1C | 0.237 | 0.466 | ||
| 5 °C | 50% | 0.5C | 0.258 | 0.438 |
| 1C | 0.279 | 0.435 | ||
| 35 °C | 50% | 0.5C | 0.281 | 0.472 |
| 1C | 0.292 | 0.493 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, H.; Wang, X.; Zhang, L.; Wang, R.; Dai, H.; Wei, X. Online Broadband Impedance Identification for Lithium-Ion Batteries Based on a Nonlinear Equivalent Circuit Model. World Electr. Veh. J. 2023, 14, 168. https://doi.org/10.3390/wevj14070168
Pan H, Wang X, Zhang L, Wang R, Dai H, Wei X. Online Broadband Impedance Identification for Lithium-Ion Batteries Based on a Nonlinear Equivalent Circuit Model. World Electric Vehicle Journal. 2023; 14(7):168. https://doi.org/10.3390/wevj14070168
Chicago/Turabian StylePan, Hongyu, Xueyuan Wang, Luning Zhang, Rong Wang, Haifeng Dai, and Xuezhe Wei. 2023. "Online Broadband Impedance Identification for Lithium-Ion Batteries Based on a Nonlinear Equivalent Circuit Model" World Electric Vehicle Journal 14, no. 7: 168. https://doi.org/10.3390/wevj14070168
APA StylePan, H., Wang, X., Zhang, L., Wang, R., Dai, H., & Wei, X. (2023). Online Broadband Impedance Identification for Lithium-Ion Batteries Based on a Nonlinear Equivalent Circuit Model. World Electric Vehicle Journal, 14(7), 168. https://doi.org/10.3390/wevj14070168








