Abstract
In this paper, we present the adaptation of the terminal component learning-based model predictive control (TC-LMPC) architecture for autonomous racing to the Formula Student Driverless (FSD) context. We test the TC-LMPC architecture, a reference-free controller that is able to learn from previous iterations by building an appropriate terminal safe set and terminal cost from collected trajectories and input sequences, in a vehicle simulator dedicated to the FSD competition. One major problem in autonomous racing is the difficulty in obtaining accurate highly nonlinear vehicle models that cover the entire performance envelope. This is more severe as the controller pushes for incrementally more aggressive behavior. To address this problem, we use offline and online measurements and machine learning (ML) techniques for the online adaptation of the vehicle model. We test two sparse Gaussian process regression (GPR) approximations for model learning. The novelty in the model learning segment is the use of a selection method for the initial training dataset that maximizes the information gain criterion. The TC-LMPC with model learning achieves a 5.9 s reduction (3%) in the total 10-lap FSD race time.
1. Introduction
Autonomous driving (AD) is an active field of research for academia and the industry. Autonomous driving cars are of growing importance nowadays, and this is expected to increase in the future. Most stakeholders aim at improving road safety [1], reducing traffic congestion and emissions [2], and deploying universal mobility. The applications span from personal vehicles, robotaxis, and delivery vehicles to long-haul trucks, shuttles, and mining vehicles [3,4,5,6].
This paper focuses on autonomous electric racing, a subfield of autonomous driving that aims to contribute to the broader problem by introducing innovations in autonomous technology through sport [7]. This type of synergy is well established between Formula One and Formula E and the automotive industry. In particular, we aim to contribute to the tasks of trajectory planning and control.
Paden et al. [8] surveyed planning and control algorithms for AD in the urban setting. Several controllers that resort to a kinematic bicycle model have been designed, e.g., the Stanley controller [9]. To handle more demanding driving manoeuvres, more complex controllers must be designed. Advances in computing hardware and mathematical programming have made model predictive control (MPC) feasible for real-time use in AD [10].
We target the 10-lap trackdrive event of the Formula Student Driverless (FSD) autonomous racing competition. Formula Student (www.formulastudent.de/about/concept/ (accessed on 20 April 2023)) is a student engineering competition where teams design and compete with a formula race car. The autonomous racing competition environment is controlled in the sense that no other agents, such as other vehicles or pedestrians, are near the track. The track is composed of blue and yellow cones on the left and right borders, respectively. The perception and decision modules in this setting are simpler than in urban AD. In contrast, the motion planning and control problem can be greater as teams aim to drive at the limits of handling [11,12].
Obtaining a sufficiently accurate vehicle model in these conditions without rendering the MPC computationally intractable is a challenging task. Moreover, the recursive feasibility of optimization-based problems is still a challenging issue with respect to their real-time implementation due to the limited computing capacity of processors [13,14]. To overcome this issue, machine learning (ML) techniques have been used to improve the formulation of the MPC using collected data. A recent survey of learning-based model predictive control (LMPC) applications [15] divides the field into the three following categories: (i) system dynamics learning, using ML techniques as a data-based adaptation of the prediction model or uncertainty description (also referred to as model learning); (ii controller design learning, which targets an MPC controller’s parameterization, e.g., the cost function or terminal components; (iii) MPC for safe learning, which concerns approaches where MPC is used as a safety filter for learning-based controllers.
A cautious LMPC that combines a nominal model with Gaussian process regression (GPR) techniques to model the unknown dynamics was presented in [16]. It has been applied to trajectory tracking with a robotic arm [17]. Alternatively, Bayesian linear regression (BLR) has been used to model the unknown dynamics [18]. The authors argue that this simple model is more accurate in estimating the mean behavior and model uncertainty than GPR and generalizes to novel operating conditions with little or no tuning. Further, they propose a framework that combines BLR model learning with cost learning [19]. However, the algorithm was tested on a slow-moving robot in off-road terrain. Therefore, the main challenge is related to changing dynamics throughout different parts of the terrain.
An LMPC for autonomous racing was applied to the AMZ Driverless FSD prototype [20]. The proposed formulation considers a nominal vehicle model where GPR models residual model uncertainty. The approach is based on model predictive contouring control (MPCC) [21] and cautious MPC [16]. However, the focus is placed only on learning a more accurate vehicle model. We augment this approach by also using the safe set.
The main contribution of this work is the adaptation of Rosolia et al.’s [22] terminal component LMPC (TC-LMPC) architecture to the full-sized autonomous electric racing FSD competition, shown in Figure 1. The same authors present an adaptation to the AD problem [23]; however, it was tested in a miniaturized 1/10 race car. The increased velocities of the full-sized application require a higher control frequency; for this reason, we implement a computationally efficient solution resorting to C++ and FORCESPRO [24,25]. Further, Rosolia et al.’s [23] approach considers tracks with segment-wise constant curvature, while the formulation here presented considers more complex tracks, such as those that we encounter in FSD competitions. Finally, with respect to vehicle modeling, in [23], a linear model is learned using a local linear regressor, while we use the nonlinear version of the bicycle model. Without these adaptations, the completion of a single lap in the full-sized racing application would not be possible. Moreover, we extend the TC-LMPC approach with GPR for model learning [26] by actively choosing the initial training set [27]. We call the combination of the TC-LMPC architecture with ML for model learning TC-LMPCML. We show that TC-LMPC reduces the best lap time by 10% for the 10-lap FSD race. In the work of Kabzan et al. [20], a 10% lap time reduction was also achieved. However, when we activate the model learning component, we show that a 10% lap time reduction can be sustained throughout the event but with a total race time reduction of 3% when compared to the TC-LMPC without the model learning part.

Figure 1.
FST10d—autonomous electric race car from FST Lisboa (©FSG—Cornelius Mosch).
This paper is organized as follows. In Section 2, we provide the theoretical background of the methods used in the LMPC architecture, including the original TC-LMPC formulation. In Section 3, we describe the TC-LMPC architecture for autonomous racing, which improves performance by learning the terminal components (safe set and terminal cost), as well as our adaptation to the full-sized autonomous electric racing FSD competition—controller design learning. Section 4 explains how the TC-LMPCML architecture uses GPR for system dynamics learning. Finally, we introduce the implementation details and show the simulation results for model learning and for both architectures in Section 5. Section 6 provides a summary of the main contributions and suggestions for future research directions.
2. Learning-Based Model Predictive Control
We use bold lowercase letters for vectors and bold capitalized letters for matrices , while scalars are non-bold.
2.1. Model Predictive Control
The idea of receding horizon control (RHC) is that an infinite-horizon sub-optimal controller can be designed by repeatedly solving finite-time constrained optimal control (FTCOC) problems in a receding horizon fashion [28]. At each sampling time, starting at the current state, an open-loop optimal control problem is solved over a finite horizon. The computed optimal input signal is applied to the process only during the following sampling interval . At the next time step , a new optimal control problem based on new measurements of the state is solved over a shifted horizon.
MPC is an RHC problem where the FTCOC problem with a prediction horizon of N is computed by solving online the following optimization problem:
where x is the state and u the control input. The subscript represents a given quantity in the prediction horizon with respect to time t. Equation (5) imposes the current system state to be the initial condition of the generic FTCOC problem. Equation (2) represents the discrete-time linear time-invariant system dynamics. State and input constraints are given by (3). The terminal constraint is given by (4), which forces the terminal state into some set . The stage and terminal cost are any arbitrary, continuous, strictly positive functions.
2.2. TC-LMPC—Terminal Component Learning
This work is based on the TC-LMPC architecture first proposed in [22]. This is a reference-free iterative control strategy able to learn from previous iterations. At each iteration, the initial condition, the constraints, and the objective function do not change. The authors show how to design a terminal safe set——and a terminal cost function—the Q-function—such that the following theoretical guarantees hold:
- Nonincreasing cost at each iteration;
- Recursive feasibility, i.e., state and input constraints are satisfied at iteration j if they were satisfied before;
- Closed-loop equilibrium is asymptotically stable.
Considering (1), the terminal cost is given by the Q-function: . Meanwhile, the terminal constraint corresponds to the terminal safe set : .
At the jth iteration, the inputs applied to the system and the corresponding state evolution are collected in the vectors given by (6) and (7), respectively.
The safe set , given by (8), is the collection of all state trajectories at iteration i for —the set of indexes k corresponding to the iterations that successfully steer the system to the final point .
The function, defined in (9), assigns to every point in the safe set the minimum cost-to-go along the trajectories therein.
where corresponds to the iteration that minimizes such a cost starting at the particular state x, and is the respective time of this state in this iteration.
The safe set works as a safe region given the shorter horizon N. For example, in autonomous racing, it can account for the shape of the track beyond the horizon. In this way, the controller is informed by past experimental data regarding how fast he can travel at a particular part of the track without having to compute the global optimal racing line.
2.3. Gaussian Processes Regression
Gaussian processes [29] are a non-parametric, probabilistic machine learning approach to learning in kernel machines. They provide a fully probabilistic predictive distribution, including estimates of the uncertainty of the predictions. Consider an unknown latent function that is identified from a collection of inputs and corresponding outputs .
where is independent and identically distributed Gaussian noise with diagonal variance . The set of n input and output data pairs form a dictionary :
Assuming a Gaussian prior on in each output dimension , such that they can be treated independently, the posterior distribution in dimension d at an evaluation point has a mean and variance given by Equations (12) and (13), respectively. Further, in this situation, one refers to as . In other words, there is a collection of n-dimensional vectors .
where is the Gramian matrix, i.e., , , , and corresponds to the kernel function used. The specification of the prior is important because it fixes the properties of the covariance functions considered for inference—in particular, the type of kernel function used and its hyperparameters.
The multivariate Gaussian process approximation is given by , where and .
2.4. Sparse Approximations for Gaussian Process Regression
The computational complexity of GPR strongly depends on the number of data points n. In particular, a computational cost of is incurred whenever a new training point is added to the dictionary . This is due to the need to invert in Equations (12) and (13), which is a matrix. Moreover, the evaluation of the mean and variance has a complexity cost of and , respectively.
Several sparse approximation techniques have been proposed to allow the application of GPR to large problems in machine learning [30]. An additional set of latent variables , which are called inducing variables or support points, are used to approximate (12) and (13). These are values of the Gaussian process evaluated at the inducing inputs . The latent variables are represented as rather than as they are not real observations, thus not including the noise variance.
The simplest sparse approximation method is the Subset of Data (SoD) approximation, i.e., it solves (12) and (13) by substituting by . It is often used as a baseline for sparse approximations. The computational complexity is reduced to for training and and for the mean and variance, respectively.
The Fully Independent Training Conditional approximation [31] assumes that all the training data points are independent. The computational complexity is initially and and per test case for the predictive mean and variance, respectively. FITC can be viewed as a standard GP with a particular non-stationary covariance function parameterized by the pseudo-inputs. The mean and variance are given by
where , is the information vector taken for each d sparse model, and .
3. Performance-Driven Controller Learning
3.1. Learning Terminal Components for Autonomous Racing
Learning terminal components is considered a sub-field of controller design learning for LMPC [15]. Rosolia and Borrelli first introduced in [23] the adaptation of the core TC-LMPC architecture to the autonomous racing problem. This is formulated as a minimum time problem, where an iteration j corresponds to a lap. Therefore, the stage cost is given as follows:
where is the set of points beyond the finish line. A slower trajectory contains more points until the finish line, thus having a greater cost associated.
The vehicle dynamics considers the states and input vector quantities in (17) and (18), respectively.
where collects states that describe the vehicle movement and is the vector of control inputs. s is the distance along the track centerline measured from the start line; and are the lateral distance and heading angle errors between the vehicle pose and the centerline, respectively. These quantities are given in the curvilinear abscissa reference frame -—see Figure 2—also known as the Frenet reference frame. A given track is defined by the curvature and maximum admissible lateral error along the track centerline. and are the longitudinal and lateral vehicle velocities, respectively, while r is the vehicle yaw rate. The inputs are the longitudinal acceleration a and the steering angle .
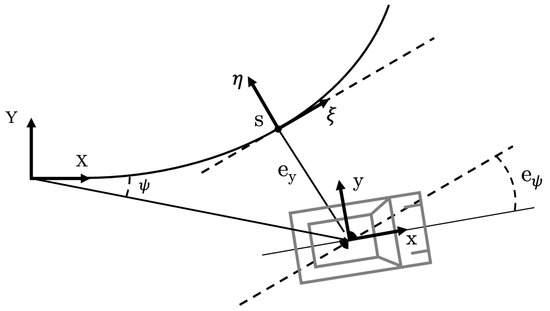
Figure 2.
Local and global vehicle frames.
Rosolia and Borrelli [32] further extended this architecture by proposing a local TC-LMPC that significantly reduced the computational burden by using a subset of the stored data. In particular, the local convex safe set is built around the candidate terminal state using the -nearest neighbours from each of the previous laps. Notice that . These points are collected in the matrix , defined in (19), which is updated at each time step. The candidate terminal state is the estimated value for , calculated at time . The approximation of the cost-to-go is computed using the costs associated with the selected states in .
3.2. TC-LMPC for Formula Student Driverless
The original TC-LMPC architecture represents the vehicle pose in the local coordinate frame, (17). However, the discretization method used, which assumes a constant track curvature within a sampling period, fails to properly describe tracks with rapidly changing curvatures. This issue was not taken into consideration in [26,32].
Therefore, we propose to change the vehicle model pose states to the global coordinate frame X–Y. In this case, s and are still calculated because these quantities provide immediate information regarding the track, but they are not used to characterize the vehicle pose dynamics. The longitudinal control input is , which represents a pedal setpoint. This corresponds to the normalized acceleration and brake pedal travel, i.e., the way in which the actual prototype is controlled both in simulation and reality. Thus, for our application, Equations (17) and (18), respectively, become
The adopted cost function is composed of five main parts and is given as follows:
First, the derivative terms apply a penalty on the squared change of a given quantity between consecutive steps along the prediction horizon, both for dynamic states and inputs. This enables us to obtain smooth trajectories. Second, a quadratic cost is applied on to act as a regularization cost, which forces the vehicle into its stable domain and helps convergence. Third, a quadratic cost is applied to the lag error, which measures the accuracy of the global to local coordinate transformation [21].
The fourth part concerns the soft constraints on the states. Bounds on the states are not implemented as hard constraints since one cannot exclude that the real system moves outside the constraint range due to, for instance, model mismatch, which would render the problem infeasible [28]. Thus, the bound on a given state is approximated by , where , and a term is added to the cost functional. It can be shown that with a sufficiently high u and ensures that no constraint violation occurs, provided that there exists a feasible input. The bounded states are and , where needs to be bounded to stay within the track width. Additionally, a velocity ellipse is implemented to ensure that the vehicle remains within its physical limits.
Finally, the last part of the cost functional in (22) contains two penalty terms on the terminal components of the MPC. A linear cost is applied to the product of —the coefficients of the local safe set convex hull—and —the cost-to-go of each point in the safe set, (9). Moreover, a quadratic penalty is applied to the error between the terminal state and the safe set points , i.e., , for each point i in the safe set. While this slack term ensures that the terminal state lies within the convex hull, the terminal cost favors points in the safe set that result in faster laps.
Bounds on both inputs’ maximum level and rate are applied. These bounds may be more restrictive than the actual physical limits imposed by the robotic platform.
The control actuation applied at the current sampling time corresponds to the previous sampling time solution shifted by one step, (23). This delay aims to achieve a constant control rate given the solver’s processing time—which is significant in real time and may be inconsistent across the experiment.
3.3. Formula Student Driverless Vehicle Model
The system dynamics in (2) results from the discretization of (24), which is the sum of an a priori physics-based model and a term to model the unknown dynamics , given as follows:
The pose dynamics are given by the following equations:
The dynamic part of the vehicle model is modeled by a dynamic bicycle model—Figure 3. This model is frequently used in automotive control algorithms [33] and is given as follows:
where m is the vehicle mass and is the rotational inertia about the vertical axis z. The front and rear axles are identified by the subscripts , respectively. is the distance between the vehicle center of gravity and the corresponding axle. The lateral force is given as
where the tire coefficients , , and are experimentally identified and the slip angle —the angle between the tire centerline and its velocity vector—is computed as follows:
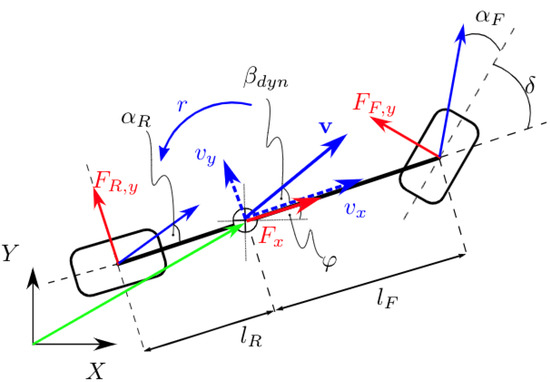
Figure 3.
Dynamic bicycle model (reprinted from [34]). The red arrows represent forces applied in the vehicle. The blue arrows represent both linear and angular velocities. The green arrows represents the position vector of the vehicle’s center of gravity with respect to the global coordinate frame.
The longitudinal force is given as follows:
where is the maximum available torque at each of the two rear-axle in-wheel motors. is the transmission gear ratio and is the roll resistance factor. Concerning the aerodynamic drag force, is the air density, is the vehicle frontal area used as a reference for the force calculation, and is the drag coefficient.
4. System Dynamics Learning
Gaussian process regression is used to predict the error between the vehicle model—Equations (25)–(28)—and the available measurements, i.e., estimate in Equation (24). We do not make use of the uncertainty prediction. Thus, Equations (13) and (15) are disregarded in our application.
We assume that the modeling error only affects the dynamic part of the first-principle model [20], i.e., the velocity states. Therefore, the training outputs—(10)—are given by the difference in the velocity components between the measurement and the nominal model prediction:
where —the Moore–Penrose pseudo-inverse of —is a selection matrix introduced to consider only the velocity components. Hence, GPR predicts the error in the three velocities: , and .
The GPR training input, i.e., the feature state, is . This is based on the assumption that the model errors are independent of the vehicle position. This disregards potential modeling shortcomings introduced by, for instance, segments of the track that have different traction conditions, e.g., due to puddles. Further, we removed as we identified a strong correlation between this quantity and r. This is not surprising as both quantities characterize the lateral movement of the vehicle. The removal of instead of r is justified by the fact that it is difficult to precisely estimate , while r is measured directly using a gyroscope. These approximations substantially reduce the learning problem’s dimensionality.
The covariance function— in (12) and (13)—used is the squared-exponential kernel with the independent measurement noise component :
Two sparse approximations have been explored: (i) SoD and (ii) FITC. The first approximation method is essentially a full GP that does not use all data available. This means that the computations for the error prediction in (24) are those of an exact GP given by (12). Meanwhile, for the second approach, the computations are those of (14).
The SoD approximation is often seen as naive as only a fraction of the available dataset is used. Hence, in order to improve the probability of good performance, rather than selecting the m points randomly, we use a technique to select points included in the active set that maximizes the information gain criterion [27].
Finally, it should be noted that some quantities can be pre-computed that otherwise could prevent real-time feasibility. In particular, in (12) only needs to be recomputed whenever the training data are changed—this is the training step. In the SoD offline learning case, it is only computed once before the controller is launched. Inference corresponds to the rest of the computation of (12).
In the FITC approximation, the training step corresponds to the determination of the information vector , which only requires recomputation when either the training dataset or the inducing points are changed. In our application, however, the inducing points are updated at each sampling time. They are equally distributed along the last sampling time’s shifted predicted trajectory. This is a sensible placement of the inducing points since the new test cases are expected to be near the preceding ones, as the trajectory does not change significantly at consecutive sampling times. This means that the online adaptation of the dictionary is immediately possible.
GPR is generally susceptible to outliers, which can hinder the model error learning performance [20]. Moreover, large and sudden changes in the GPR predictions can lead to erratic driving behavior. To attenuate these effects, we only include data points in the dictionary (both online and offline) whose measurements fall within predefined bounds , defined from physical considerations and empirical knowledge.
The hyperparameters are tuned offline based on pre-collected data. There are two main reasons that this is not done online. First, this optimization is not real-time feasible. Second, it is assumed that the general trend of the model error remains constant throughout the vehicle’s operation.
5. Implementation and Results
5.1. Implementation
Figure 4 exhibits the autonomous racing software architecture used by the FST Lisboa team. In the Trackdrive event, the entire control module in Figure 4 (green nodes) is substituted by the TC-LMPC algorithm.
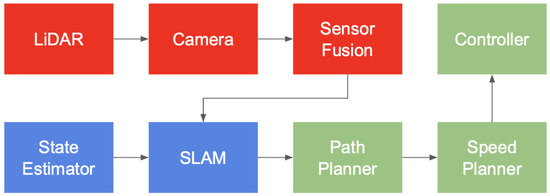
Figure 4.
FST10d autonomous racing software stack.
FSSIM (https://github.com/AMZ-Driverless/fssim (accessed on 20 April 2023)) is the vehicle simulator used. AMZ Driverless developed this vehicle simulator, dedicated to the FSD competition, and released it open-source to other teams. This team reported 1% lap time simulator accuracy compared with their actual FSG 2018 10-lap trackdrive run [34]. Due to real-time requirements, this simulator does not simulate raw sensor data, e.g., camera or LiDAR data. Instead, cone observations around the vehicle are simulated using a given cone sensor model. This means that, in simulation, the perception module in Figure 4 (red nodes) is not the same as in actual prototype testing.
We developed a custom ROS/C++ implementation of the TC-LMPC architecture using FORCESPRO [24,25]—a solver designed for the embedded solving of MPC—to solve the optimization problem. The computations associated with GPR model error prediction described in Section 4 resort to the C++ open-source albatross (https://swiftnav-albatross.readthedocs.io/en/latest/index.html (accessed on 20 April 2023)) library developed by Swift Navigation.
5.2. Model Learning Analysis
In this section, we investigate the performance of the sparse GPR approximations for the prediction of the model error. We use the compound average error to evaluate the overall model learning performance: is the average 2-norm error of the nominal model, i.e., , and is the corresponding error of the corrected dynamics, i.e., . The results shown here correspond to the average over 10 laps. To evaluate the effectiveness of the proposed solution, the results shown were collected using FST Lisboa’s—the FSD team from the University of Lisbon—autonomous vehicle parameters in the MPC dynamic vehicle model, while using the AMZ Driverless car model in the simulator.
For the SoD approximation, we use the active set selection method described in Section 4 to find the active set of different sizes for each model d from a dictionary of , collected over 10 different runs with changing parameters. Morever, we use the active set of the SoD approximation as the training set for the FITC approximation, i.e., .
Table 1 shows the model error prediction fitness for both sparse GPR approximations. For the SoD results, on the left, the horizontal dashed line separates the results of the offline (above) and online (below) schemes. For the online FITC results, on the right, the horizontal dashed line separates the results of (above) and (below) schemes.

Table 1.
Model learning performance analysis.
We conclude that there is a positive correlation between and the model error fitting ability. In the offline fashion, the 2-norm average error reduction, i.e., reduction from to , is 63.9% and 70.7% with and , respectively. The computation cost evolves linearly with m but, within this range, takes acceptable values given the current node rate of 20 Hz. Arguably, we could further increase but likely with negligible model learning improvements.
Instead, we should aim to adapt the training data online as this would enable adaptation to changing conditions or even simply the collection of data from dynamic maneuvers not included in the original dictionary. With a dictionary size of data points, the model error reduction is 65.4% and 75.7% for and , respectively. In particular, it enables more aggressive maneuvers toward the end of the event while keeping the corrected dynamics error relatively low.
In the online case, the model with performs significantly better than the model with . While the average node processing time is well within the limits, it too often breaks the real-time requirement.
As explained in Section 4, the FITC sparse approximation is a natural candidate to enable online learning. The best-performing model with yields model learning performance comparable to that of the SoD approximation. However, the corrected dynamics average error is 0.12, slightly above the SoD benchmark value of 0.09.
5.3. Simulation Results—Model Mismatch Influence
In Table 2, we show the lap times along the 10-lap trackdrive event and the average model error for the FSG track. The initial safe set was collected using a pure pursuit controller [35] following the track centerline. It is composed of four laps with lap times of around 28.80 s. If an initial safe set containing faster trajectories is collected, the initial laps would be faster but would eventually converge to approximately the same lap time. The controllers herein have a prediction horizon of , which corresponds to a look-ahead time of 1 s, unless stated otherwise. The TC-LMPC results prove the iterative improvement nature of the architecture. The first lap is immediately 33% faster compared to the path-following controller. Equivalently, the last lap is 39% faster. Furthermore, the last lap corresponds to a 10% improvement compared to the first TC-LMPC lap.

Table 2.
FSG lap times and model error.
Figure 5 shows the 10-lap FSG trackdrive trajectories using the TC-LMPC strategy. The finish line is at the origin and the vehicle runs clockwise. It can be seen that TC-LMPC exploits the track layout to improve the vehicle’s performance. Nevertheless, the third column of Table 2 shows a severe model mismatch, which causes the vehicle to violate the track constraint. See, for instance, the exit of the hairpin, where the trajectory is on top of the track boundary. This indicates that a cone was hit, since the trajectory corresponds to the center of mass. Furthermore, the approach to the slalom segment is not considered optimal by empirical vehicle dynamics standards. The vehicle brakes too late, which leads to a slower slalom with greater steering actuation required.

Figure 5.
TC−LMPC FSG trackdrive trajectory []. The grey arrow shows the track direction.
We now analyze the performance of the controller when the GPR model learning scheme is deployed. Table 2—TC-LMPCML—shows that the last lap is 41% and 10% faster when compared to the pre-collected path-following lap and the first lap, respectively. Furthermore, the total event time, 176.5 s, is 5.9 s faster than when using TC-LMPC, a 3% improvement. These results correspond to the online SoD model with . Figure 6 shows the corresponding 10-lap FSG trackdrive trajectories. It is clear that the reduced model mismatch prevented the vehicle from violating the track constraint. However, it seems that there is still room for improvement during the slalom segment.
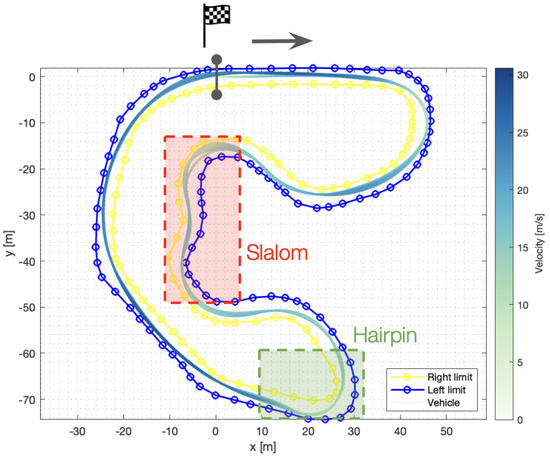
Figure 6.
TC−LMPCML FSG trackdrive trajectory []. The grey arrow shows the track direction.
5.4. Simulation Results—Prediction Horizon Influence
We subsequently tested TC-LMPCML with increasing prediction horizons. In Table 3, we display the lap times and modeling errors for two sets of controller gains with or a look-ahead time of 1.5 s. The results on the left correspond to the parameters used thus far in this section. For the controller on the right, we reduced some derivative costs and the regularization cost on and increased the Q-function-associated cost to promote greater track progress at each sampling time.

Table 3.
FSG lap times and model error [].
With a longer horizon, both controllers achieve optimal trajectories in the slalom segment and can safely navigate the vehicle around the track such that the safe set loses its relative importance. Specifically, the controllers are able to predict consistently until the slowest point on a given corner. In this way, the information conveyed by the safe set regarding the types of maneuvers that follow is not as valuable. The safety characteristic only applies when model learning is deployed. Otherwise, the severe model mismatch hinders the performance. This is substantiated by the fact that both controllers achieve small lap times in the first few laps and quickly converge to their steady-state lap times of around 16.75 s for the default controller and 16.16 s for the aggressive controller.
Both models used the offline version of the SoD approximation with . The model learning scheme is able to significantly reduce the model mismatch to enable safe aggressive racing. For the first case, with default parameters, the corrected dynamics model average error is around 0.08, which corresponds to a reduction of about 70% compared to the nominal model. Meanwhile, for the aggressive controller, the final model mismatch is on average 0.15, a reduction of 60%. The model learning scheme can achieve an acceptable value of corrected dynamics model mismatch, even in the case of offline model learning on the aggressive controller. It should be noted that such high nominal model errors were not present in the original training dataset.
6. Conclusions and Future Work
This paper presented the extension of the results of the TC-LMPC architecture to the autonomous electric racing FSD context. We have demonstrated that the TC-LMPC using a dynamic bicycle model with an appropriate terminal safe set and Q-function leads to safe iterative improvements. Despite the significant model mismatch, the best lap time is reduced by 10%, when compared to the first lap using the same controller, at the 10-lap FS event. When using GPR with the active training set selection method introduced for model learning, we are able to successfully predict the modeling error, which leads to a 5.9 s total time reduction for the 10-lap FSD event.
The main limitation of the proposed solution, inherent in the use of model-based controllers, is model mismatch. This can impact the feasibility of the solution, and the theoretical guarantees of the TC-LMPC listed above might not hold. The other major limitation is that this architecture requires pre-collected data, which requires a suboptimal but safe controller. Alternatively, replication of this work may be possible by resorting to manual data collection, which should be available in most practical applications.
These simulation results are promising for an experimental implementation on the full-sized FST10d electric racing prototype. An important focus of the research on learning model-based controllers has been on reducing model mismatch. An implementation of an online dictionary management procedure [20] is under study. Further, research work is underway to test the Automatic Relevance Determination GPR kernel and other ML techniques, such as the use of Bayesian linear regression or neural networks. The minimum-time stage cost for the TC-LMPC Q-function could be augmented such that points that yield long-term benefits are more favored. We are also studying the use of the state uncertainty measurement, which is inherent with the application of Gaussian processes, in a robust learning-based model predictive control framework with constraint tightening. Finally, the automatic adjustment of the MPC parameters using a reward function exploited by a reinforcement learning algorithm is also a future line of research.
Author Contributions
Conceptualization, J.P., G.C., P.U.L. and M.A.B.; methodology, J.P., G.C., P.U.L. and M.A.B.; software, J.P. and G.C.; validation, P.U.L. and M.A.B.; writing—original draft preparation, J.P.; writing—review and editing, P.U.L. and M.A.B.; visualization, J.P.; supervision, P.U.L. and M.A.B. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by the Portuguese Science and Technology Foundation (FCT), through IDMEC, under LAETA, project UID/EMS/50022/2020, and LARSyS strategic funding—FCT Project UID/50009/2020.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AD | Autonomous Driving |
| MPC | Model Predictive Control |
| FSD | Formula Student Driverless |
| ML | Machine Learning |
| LMPC | Learning-Based Model Predictive Control |
| GPR | Gaussian Process Regression |
| BLR | Bayesian Linear Regression |
| MPCC | Model Predictive Contouring Control |
| TC-LMPC | Terminal Component Learning-Based Model Predictive Control |
| FITC | Fully Independent Training Conditional |
| RHC | Receding Horizon Control |
| FTCOC | Finite-Time Constrained Optimal Control |
| SoD | Subset of Data |
References
- Scanlon, J.M.; Kusano, K.D.; Daniel, T.; Alderson, C.; Ogle, A.; Victor, T. Waymo simulated driving behavior in reconstructed fatal crashes within an autonomous vehicle operating domain. Accid. Anal. Prev. 2021, 163, 106454. [Google Scholar] [CrossRef]
- Stogios, C.; Kasraian, D.; Roorda, M.J.; Hatzopoulou, M. Simulating impacts of automated driving behavior and traffic conditions on vehicle emissions. Transp. Res. Part D Transp. Environ. 2019, 76, 176–192. [Google Scholar] [CrossRef]
- Bischoff, J.; Maciejewski, M. Simulation of City-wide Replacement of Private Cars with Autonomous Taxis in Berlin. Procedia Comput. Sci. 2016, 83, 237–244. [Google Scholar] [CrossRef]
- Srinivas, S.; Ramachandiran, S.; Rajendran, S. Autonomous robot-driven deliveries: A review of recent developments and future directions. Transp. Res. Part E Logist. Transp. Rev. 2022, 165, 102834. [Google Scholar] [CrossRef]
- Engholm, A.; Björkman, A.; Joelsson, Y.; Kristoffersson, I.; Pernestål, A. The emerging technological innovation system of driverless trucks. Transp. Res. Procedia 2020, 49, 145–159. [Google Scholar] [CrossRef]
- Kim, H.; Choi, Y. Autonomous Driving Robot That Drives and Returns along a Planned Route in Underground Mines by Recognizing Road Signs. Appl. Sci. 2021, 11, 10235. [Google Scholar] [CrossRef]
- Betz, J.; Wischnewski, A.; Heilmeier, A.; Nobis, F.; Stahl, T.; Hermansdorfer, L.; Lohmann, B.; Lienkamp, M. What can we learn from autonomous level-5 motorsport? In 9th International Munich Chassis Symposium 2018; Pfeffer, P., Ed.; Proceedings; Springer: Wiesbaden, Germany, 2019; pp. 123–146. [Google Scholar] [CrossRef]
- Paden, B.; Čáp, M.; Yong, S.; Yershov, D.; Frazzoli, E. A survey of motion planning and control techniques for self-driving urban vehicles. IEEE Trans. Intell. Veh. 2016, 1, 33–55. [Google Scholar] [CrossRef]
- Thrun, S.; Montemerlo, M.; Dahlkamp, H.; Stavens, D.; Aron, A.; Diebel, J.; Fong, P.; Gale, J.; Halpenny, M.; Hoffmann, G.; et al. Stanley: The robot that won the DARPA Grand Challenge. J. Field Robot. 2006, 23, 661–692. [Google Scholar] [CrossRef]
- Kim, E.; Kim, J.; Sunwoo, M. Model predictive control strategy for smooth path tracking of autonomous vehicles with steering actuator dynamics. Int. J. Automot. Technol. 2014, 15, 1155–1164. [Google Scholar] [CrossRef]
- Santos, S.D.; Azinheira, J.R.; Botto, M.A.; Valério, D. Path Planning and Guidance Laws of a Formula Student Driverless Car. World Electr. Veh. J. 2022, 13, 100. [Google Scholar] [CrossRef]
- Srinivasan, S.; Nicolas Giles, S.; Liniger, A. A Holistic Motion Planning and Control Solution to Challenge a Professional Racecar Driver. IEEE Robot. Autom. Lett. 2021, 6, 7854–7860. [Google Scholar] [CrossRef]
- Hosseinzadeh, M.; Sinopoli, B.; Kolmanovsky, I.; Baruah, S. Implementing Optimization-Based Control Tasks in Cyber-Physical Systems with Limited Computing Capacity. In Proceedings of the 2022 2nd International Workshop on Computation-Aware Algorithmic Design for Cyber-Physical Systems (CAADCPS), Milan, Italy, 3–6 May 2022; pp. 15–16. [Google Scholar] [CrossRef]
- Feller, C.; Ebenbauer, C. A stabilizing iteration scheme for model predictive control based on relaxed barrier functions. Automatica 2017, 80, 328–339. [Google Scholar] [CrossRef]
- Hewing, L.; Wabersich, K.P.; Menner, M.; Zeilinger, M.N. Learning-Based Model Predictive Control: Toward Safe Learning in Control. Annu. Rev. Control Robot. Auton. Syst. 2020, 3, 269–296. [Google Scholar] [CrossRef]
- Hewing, L.; Kabzan, J.; Zeilinger, M.N. Cautious Model Predictive Control Using Gaussian Process Regression. IEEE Trans. Control Syst. Technol. 2020, 28, 2736–2743. [Google Scholar] [CrossRef]
- Carron, A.; Arcari, E.; Wermelinger, M.; Hewing, L.; Hutter, M.; Zeilinger, M.N. Data-Driven Model Predictive Control for Trajectory Tracking with a Robotic Arm. IEEE Robot. Autom. Lett. 2019, 4, 3758–3765. [Google Scholar] [CrossRef]
- McKinnon, C.D.; Schoellig, A.P. Learn Fast, Forget Slow: Safe Predictive Learning Control for Systems With Unknown and Changing Dynamics Performing Repetitive Tasks. IEEE Robot. Autom. Lett. 2019, 4, 2180–2187. [Google Scholar] [CrossRef]
- McKinnon, C.D.; Schoellig, A.P. Context-aware Cost Shaping to Reduce the Impact of Model Error in Receding Horizon Control. In Proceedings of the IEEE International Conference on Robotics and Automation, Virtual Event, 31 May–31 August 2020; pp. 2386–2392. [Google Scholar] [CrossRef]
- Kabzan, J.; Hewing, L.; Liniger, A.; Zeilinger, M.N. Learning-Based Model Predictive Control for Autonomous Racing. IEEE Robot. Autom. Lett. 2019, 4, 3363–3370. [Google Scholar] [CrossRef]
- Liniger, A.; Domahidi, A.; Morari, M. Optimization-Based Autonomous Racing of 1:43 Scale RC Cars. Optim. Control Appl. Methods 2015, 36, 628–647. [Google Scholar] [CrossRef]
- Rosolia, U.; Borrelli, F. Learning model predictive control for iterative tasks. A data-driven control framework. IEEE Trans. Autom. Control 2018, 63, 1883–1896. [Google Scholar] [CrossRef]
- Rosolia, U.; Carvalho, A.; Borrelli, F. Autonomous racing using learning Model Predictive Control. In Proceedings of the 2017 American Control Conference (ACC), Seattle, WA, USA, 24–26 May 2017; pp. 5115–5120. [Google Scholar] [CrossRef]
- FORCES Professional. Available online: https://embotech.com/FORCES-Pro (accessed on 15 April 2023).
- Zanelli, A.; Domahidi, A.; Jerez, J.; Morari, M. FORCES NLP: An efficient implementation of interior-point methods for multistage nonlinear nonconvex programs. Int. J. Control 2020, 93, 13–29. [Google Scholar] [CrossRef]
- Xu, S. Learning Model Predictive Control for Autonomous Racing Improvements and Model Variation in Model Based Controller Examiner. Master’s Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2018. [Google Scholar]
- Lawrence, N.D.; Platt, J.C. Learning to Learn with the Informative Vector Machine. In Proceedings of the Twenty-First International Conference on Machine Learning, Banff, AB, Canada, 4–8 July 2004; p. 65. [Google Scholar] [CrossRef]
- Borrelli, F.; Bemporad, A.; Morari, M. Predictive Control for Linear and Hybrid Systems; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; The MIT Press: Cambridge, MA, USA, 2005. [Google Scholar] [CrossRef]
- Quiñonero-Candela, J.; Rasmussen, C.; Williams, C. Approximation methods for Gaussian process regression. In Large-Scale Kernel Machines; MIT Press: Cambridge, MA, USA, 2007. [Google Scholar]
- Snelson, E.; Ghahramani, Z. Sparse Gaussian Processes Using Pseudo-Inputs; MIT Press: Cambridge, MA, USA, 2005; pp. 1257–1264. [Google Scholar]
- Rosolia, U.; Borrelli, F. Sample-Based Learning Model Predictive Control for Linear Uncertain Systems. In Proceedings of the IEEE Conference on Decision and Control, Nice, France, 11–13 December 2019; pp. 2702–2707. [Google Scholar] [CrossRef]
- Jazar, R.N. Vehicle Dynamics: Theory and Applications; Springer US: New York, NY, USA, 2008; pp. 1–1015. [Google Scholar] [CrossRef]
- Kabzan, J.; Valls, M.; Reijgwart, V.; Hendrikx, H.; Ehmke, C.; Prajapat, M.; Bühler, A.; Gosala, N.; Gupta, M.; Sivanesan, R.; et al. AMZ Driverless: The full autonomous racing system. J. Field Robot. 2020, 37, 1267–1294. [Google Scholar] [CrossRef]
- Coulter, R. Implementation of the Pure Pursuit Path Tracking Algorithm. 1992. Available online: https://www.ri.cmu.edu/publications/implementation-of-the-pure-pursuit-path-tracking-algorithm/ (accessed on 20 April 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).