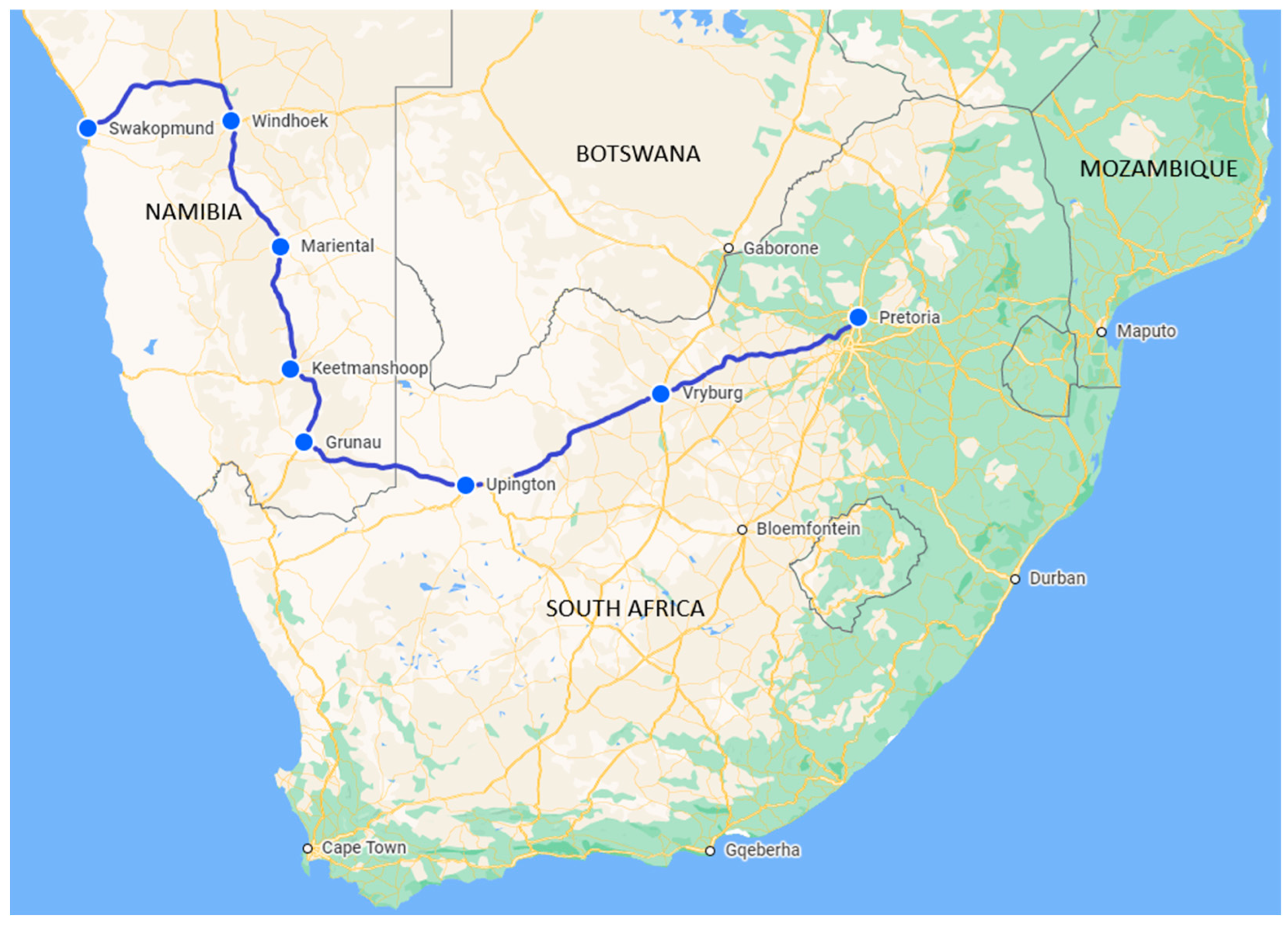
As discussed, the data collected during the road trip was split into two sections. Each of these two sections comprised merged data from three days of the trip. The three days of data were concatenated to form a larger data set. The two data sets are the data used for optimisation and the data used for validation. The data used for optimisation was used to determine the Cd and Cr values, and the data used for validation was used to determine if these coefficients are realistic. The percentage error between the real and modelled energies after validation confirmed how realistic the coefficients are.
As there were various conditions on each day, the data were split and merged into non-consecutive days to make the experiment as accurate as possible. This merger ensured that successive days’ conditions did not affect the results. Days 2, 4, and 6 were used for optimisation purposes, and Days 3, 5, and 7 were used for validation purposes. Day 1 was omitted from the research as there were errors in the data collection process on that day.
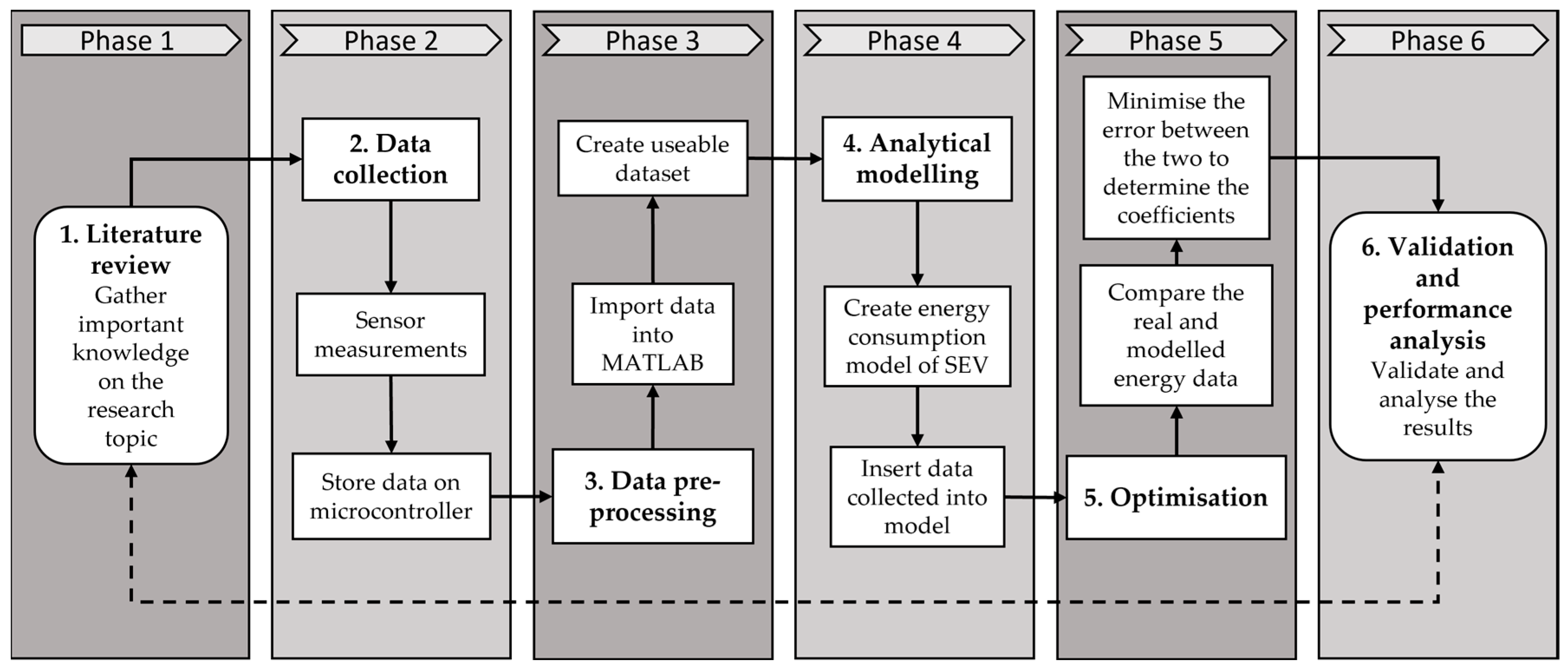
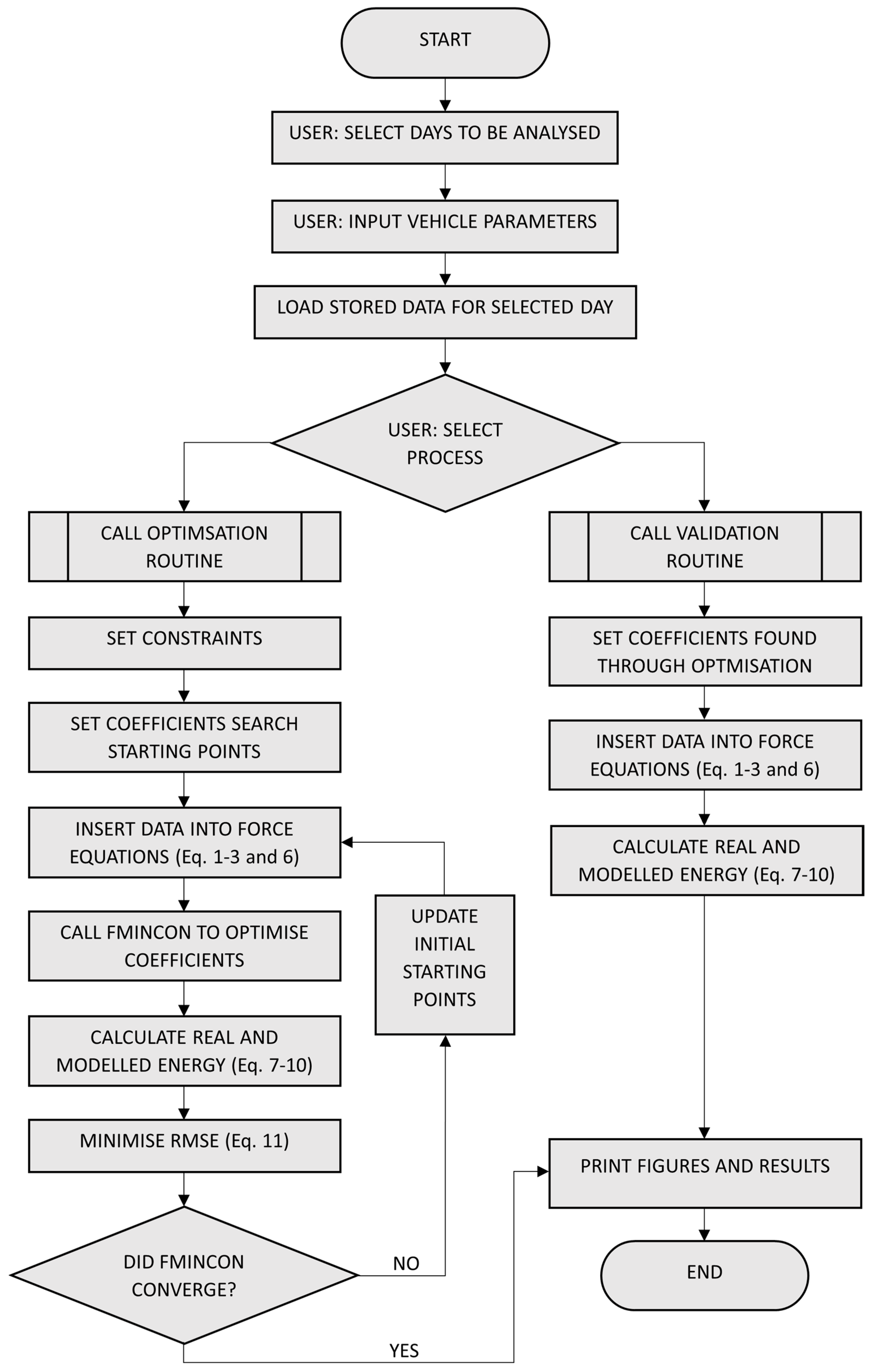
3.1. Calculating and Validating the Unknown Coefficients
The first step was to create a model of the SEV that was as accurate as possible. The creation of this model was performed in MATLAB. The energy consumption model was created using Equations (1)–(3), (6), (7) and (9). This model can be seen in Equation (8) and is validated by its use in other relevant research [
6,
7,
12,
13].
Noticeably, every variable in these equations is either a constant, a measured value, or a calculated value, except for the Cd and Cr components.
The optimisation process could then be attempted while using the modelled and real energies of the SEV.
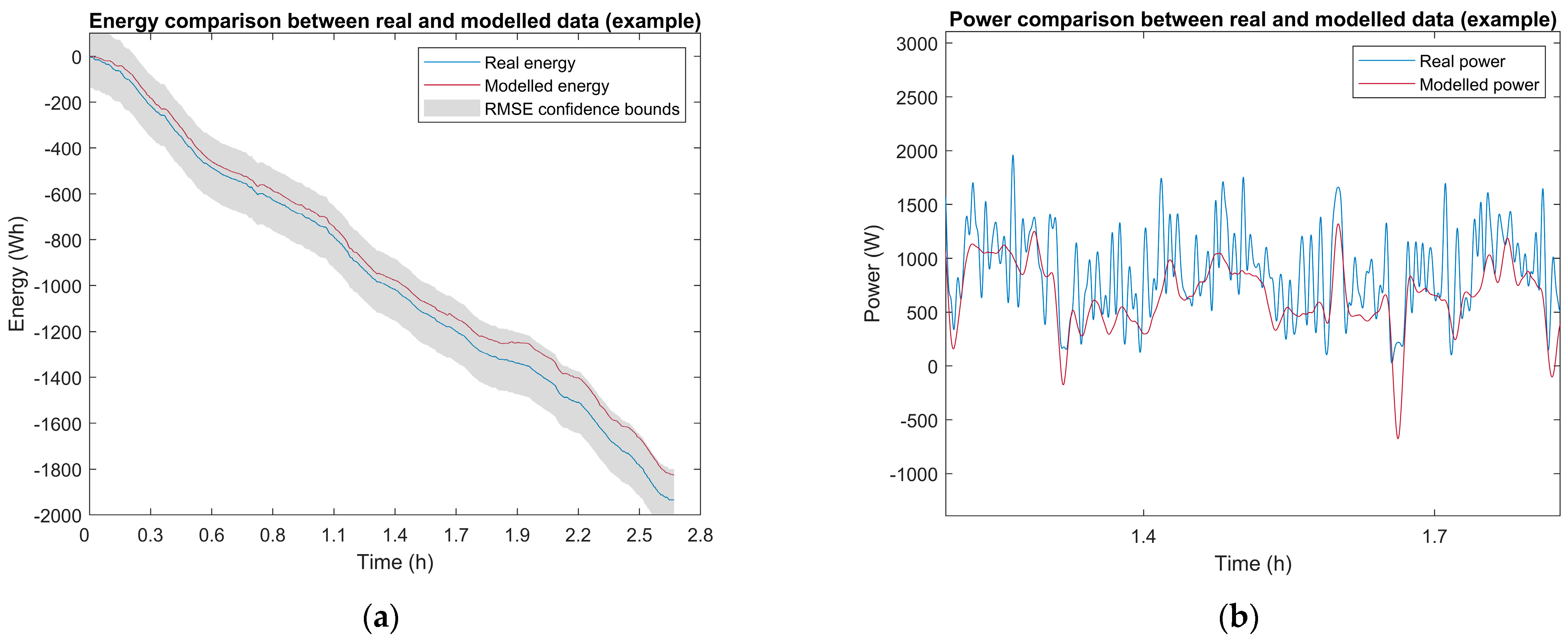
Figure 7a shows the results of the first test using the optimisation algorithm. Here, the energy calculated using the model (Equation (8)) and the real energy used by the SEV (Equation (10)) are plotted against each other. The
RMSE between the two energies was minimised and determined which values of the coefficients best fit this optimal error.
In
Figure 7a, the curves are very close together with an
RMSE of 88 Wh. This indicates a very good relationship between the modelled and real energies. The
Cd and
Cr values found from the minimisation process are 0.0044 and 0.0131, respectively. However, this shows that the coefficients are far off from what was expected according to typical values, as seen in
Table 6 and
Table 7. The
RMSE confidence bounds also show this. The final value of the modelled energy is outside the statistical mean forecasted error. There are a few factors at play here in the inaccuracy of the coefficients. Specifically, the non-dynamic model of the electric motor, different weights of the SEV drivers during the trip, variations in tyre pressure and bearing wear, crosswinds, road surface, and other unmodelled components contributed to this.
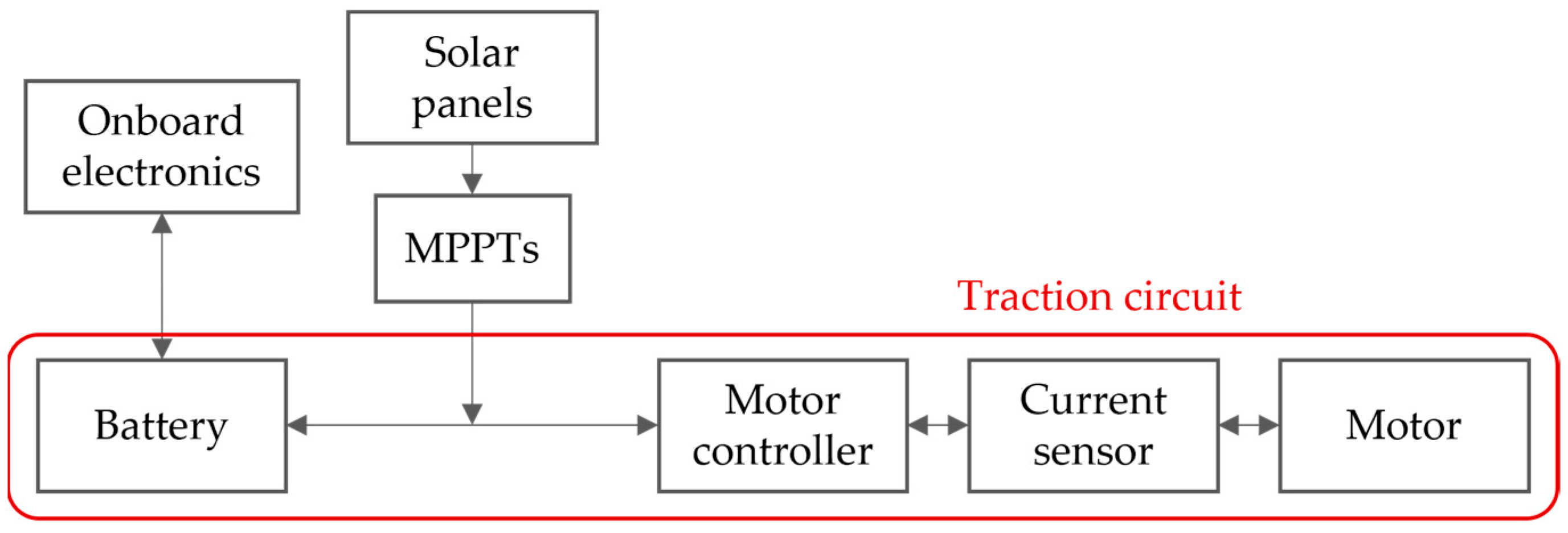
The first significant factor that influenced the undesirable results involved the modelling of the SEV’s electric motor. A complete dynamic model of the electric motor is required to determine its inefficiencies at different load and revolution-per-minute (RPM) rates. This is because the motor’s efficiency is determined by its torque and speed (RPM) at any given moment. Many factors (such as the inclination of the road) can change the torque and RPM of the motor. Since a dynamic efficiency map of the motor did not exist, the dynamic efficiency of the motor was not known at the time of this work. Therefore, a constant was chosen to represent the efficiency of the motor. The efficiency constant selected for the motor was 80%, as this was the value used for the same motor in a similar paper [
22], and it is the average motor efficiency as supplied by the motor manufacturer.
Another factor that affected the coefficient values was the mass of the driver. To reduce driver fatigue, two drivers were used throughout the trip. The mass of the first driver was 80 kg, and that of the second driver was 63 kg. As the SEV already had a low mass, this mass variation would have significantly affected the vehicle’s behaviour. Unfortunately, it was not recorded when each driver was driving the vehicle. This, therefore, added to the discrepancies in the coefficients found via the optimisation routine. The mass of the heavier driver was used in this research as a worst-case scenario.
Variations in tyre pressure and bearing wear also influenced the coefficients. Tyre pressure can fluctuate as a result of heat or road surface, affecting the Cr value. Bearing wear also plays a role.
Crosswinds and wind gusts could also affect the Cd parameter. Although wind was considered in creating the model, it was difficult to determine the full effects of these wind gusts and crosswinds. For example, during heavy cross winds, the amount of tyre scrub increased dramatically as the vehicle underwent micro-sliding from left to right rather than just forward or backward (as a result of the car’s lightweight design). The micro-sliding caused significant wear to the tyres and affected their rolling resistance forces.
The road surface was also important. A road trip over 2000 km through two countries means that different road development and maintenance standards existed throughout.
Many less significant factors were unmodelled, as it would have been challenging to incorporate them and they would have made computation unnecessarily complex.
A similar energy model has been shown to be accurate and has been tested extensively in other research [
13,
22]. These concluded that omitting similar unmodelled components would not affect the results significantly. Thus, the coefficients found via the optimiser without constraints include all of these unmodelled components as well as the actual values for
Cd and
Cr. The optimiser without constraints tried to compensate for all discrepancies in the energy comparison by manipulating the
Cd and
Cr values accordingly.
These coefficients were then used on the validation data to determine their accuracy. The validation data are a concatenation of Days 3, 5, and 7. The results can be seen in
Figure 7b. The validation of the unrealistic coefficients produced an
RMSE of 232 Wh, translating to a final error value of 7.25%. This error value means that using three days of data to optimise the coefficients results in a final error value of 7.25%, according to these data. The final error value is the error value found at the end of Day 7 (the end of the trip). This is the final deviation that the user of the vehicle would experience in the state of charge between what was predicted and what is seen at the end of a trip.
Because of the unrealistic coefficients, constraints were added to the optimisation process. The constraints would limit the values of the coefficients within a specific, realistic range. These constraints can be seen in Equation (11) and were chosen based on known realistic values for
Cd and
Cr, which can be seen in
Table 6 and
Table 7. The graph of the minimisation of the
RMSE between the two energies can be seen in
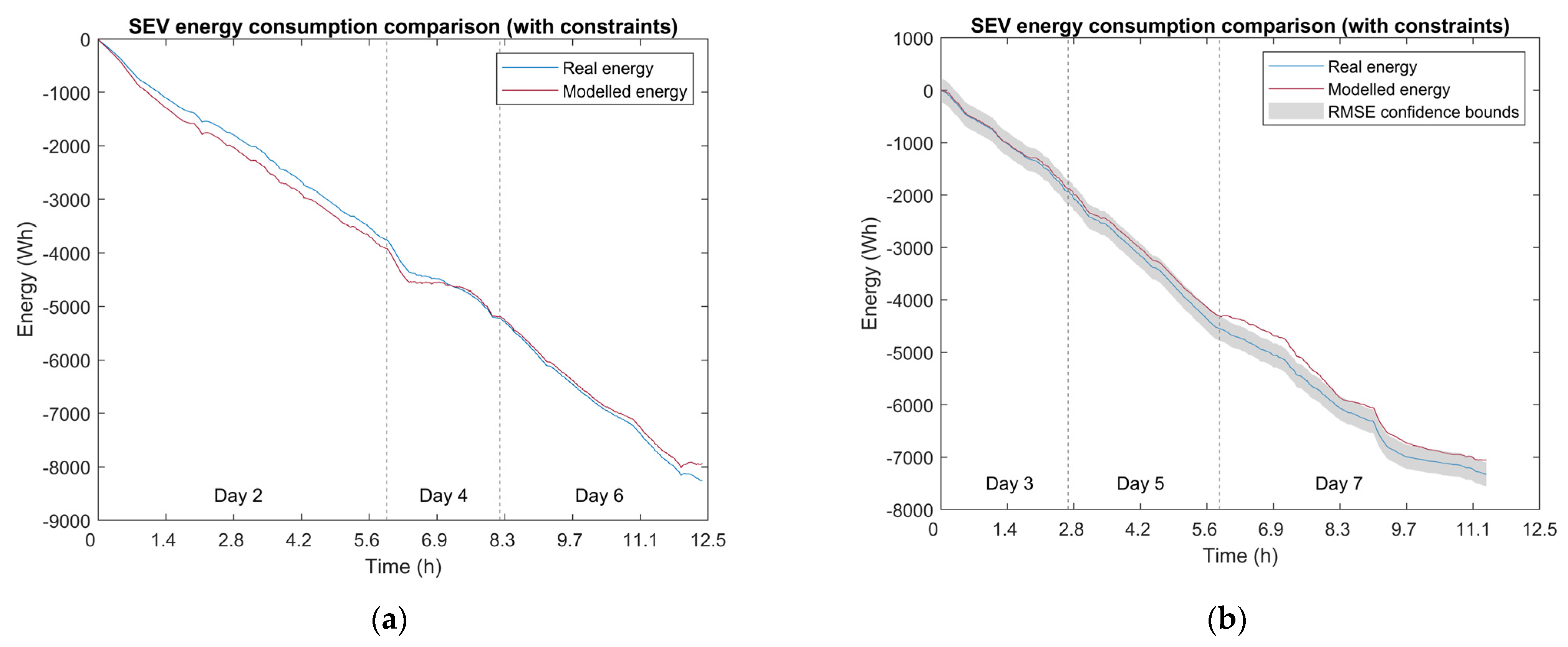
Figure 8a. This is from the same optimisation data set from Days 2, 4, and 6 used above.
Using constraints, the
RMSE increased, but the values for the coefficients were far more realistic. The
RMSE value was 161 Wh, and the
Cd and
Cr values were 0.13 and 0.0059, respectively. It can be noted that the value found for
Cd does reach the lower bound of its constraint. This is due to the fact that the optimisation algorithm was still attempting to minimise the error towards the
RMSE value found when no constraints were added. This is acceptable for this research as the lower bound of the constraint is a realistic value for
Cd. As confirmation of this, the lower bound coefficient value is justified by the results of a CFD analysis found for the same vehicle performed by the members of the TUT solar car team [
35]. A part of the modelled energy profile still exceeded the
RMSE confidence interval, most likely because of the unmodelled components, as discussed above. However, it still provides a statistical error range for consideration by the user (in this case, the energy manager, or when this method is applied to other EVs, it might be the vehicle driver). The confidence interval was intentionally omitted from the optimisation results (
Figure 8a), as visual error quantification is more applicable to the validation results.
With realistic values having been found for
Cd and
Cr using the optimisation data, it was then possible to test them on the validation data from Days 3, 5, and 7. The values of 0.13 for the
Cd component and 0.0059 for the
Cr component were inserted into the model of the SEV. With all model components known, the energy according to the model could be compared against the real (actual) energy. This was to validate the coefficients. The energy comparison can be seen in
Figure 8b.
The validation of the realistic coefficients produced an RMSE of 217 Wh, which translates to a final error value of 4.12%. This contrasts with the 7.25% found using the unrealistic coefficients when no constraints were added. This further confirms that using the optimisation constraints provides realistic results (with a lower final error value); therefore, optimisation cannot be performed without adequate constraints.
3.2. Discussion of the Parameters That Affect the Model’s Performance
Multiple areas of interest in
Figure 7 and
Figure 8 show where and why the energies diverged. These could be attributed to certain environmental conditions. The conditions for Days 2, 4, and 6 can be seen in
Figure 9.
Table 8 displays the time range and time spent driving each day. This table refers to the information found in
Figure 9 and represents Days 2, 4, and 6.
Day 2 is characterised by an initial road climb followed by a long descent. It was a warm day with a stable air density (
Figure 9c) and low humidity (
Figure 9d). Air density is affected by temperature, pressure, and humidity and plays an important role in a vehicle’s drag force, as seen in Equation (1). The high altitude (
Figure 9a) resulted in a lower drag force throughout the day. As the air density remained relatively constant, the drag force did not fluctuate as a result of the environmental conditions. Therefore, the gravity force affected the energy loss/gain the most. It can be seen in
Figure 8a that the energies diverged almost immediately as a result of the gravity force. The real amount of energy used was higher than what the model predicted. This is most likely due to the lack of a motor model, as the efficiency of a motor varies based on the road’s incline (torque demand). Day 4 is characterised by a sharp uphill followed by a sharp downhill. As the vehicle gained elevation, the air density dropped. This lowered the drag force as a result of the thinning of the air. The temperature profile of Day 4 (
Figure 9b) was very similar to Day 2. There was also very low humidity (
Figure 9d). The drag and gravity forces would have affected the total energy loss/gain. The effects of this sharp climb on Day 4 can be seen in
Figure 8a. The energy loss, according to the real and modelled data, showed the same trend. First, extra energy was consumed as the SEV ascended, followed by very little energy loss as the vehicle descended. Day 6 corresponds to a large and steady incline throughout the day. This took the SEV to the highest point of the trip. As in Day 4, when the elevation increased, the air density decreased. Therefore, the effects of the drag force decreased throughout the day, but there was a significant and stable gravitational force as a result of the increase in elevation. The lower temperature (
Figure 9b) and high humidity (
Figure 9d) also affected the air density (
Figure 9c). The sudden decrease in elevation at the end of the day is also visible in
Figure 8a. As the SEV decreased in altitude, its use of energy also decreased.
From looking at the elevation profiles (
Figure 9a), it can be seen that the divergence between the actual and modelled energies is mainly attributed to changes in elevation. Although the divergence between energies is directly correlated to elevation, this is not the reason for the separation. The blue curve in
Figure 7 and
Figure 8 shows the SEV’s real energy usage. The divergence, therefore, most likely comes from the inaccuracies of the modelled energy. This confirms a relationship between the divergence observed and the factors mentioned above. The main reason for this is most likely that there was no dynamic motor efficiency model. The motor efficiency was set at a constant 80%; however, this was not always the case, especially when considering elevation changes. A significant incline (seen in all the elevation profiles in
Figure 9) places a large amount of torque on a motor while speed (RPM) decreases or remains low. Most electric motors have a very low efficiency at high torque and low RPM. This is, therefore, not considered in the model as it results in visible deviations in the energies. The variations in driver mass also create inaccuracies as the gravity force will increase or decrease depending on this mass change.
There are also interesting areas in
Figure 7b and
Figure 8b. These represent the data from Days 3, 5, and 7.
Table 9 displays the time spent and the range of time driving on each day. This table refers to the information found in
Figure 10 and represents Days 3, 5, and 7.
Day 3 was relatively short as it included the border crossing into Namibia from South Africa. It can be seen from the elevation profile in
Figure 10a that the elevation jumped to a higher altitude instantaneously, in around 6000 s. This resulted from moving the SEV around 100 km on a trailer after the border post. As this day was relatively short, it did not have that much of an impact on the divergence between the energies. This means that the coefficients were a reasonably accurate prediction on Day 3. The altitude did not change much (
Figure 10a), and the air density (
Figure 10c) was quite constant. Therefore, the drag was relatively stable. This day was also characterised by the highest temperatures (
Figure 10b) of the trip and low humidity (
Figure 10d).
The elevation profile of Day 5 can be seen in
Figure 10a. It followed the same trend as Day 3. The air density (
Figure 10c) did not change much, with the elevation staying relatively constant and the humidity (
Figure 10d) staying low. However, the temperature (
Figure 10b) was slightly lower than it was on Day 3.
The elevation profile of Day 7 can be seen in
Figure 10a. This shows an overall descent across the day from the inland parts of Namibia down to sea level. As the vehicle approached sea level, the air density (
Figure 10c) and humidity (
Figure 10d) increased. This was expected, as air becomes denser at lower altitudes and humidity rises closer to the sea. The temperature (
Figure 10b) remained low throughout the day. This increase in air density played a role in the drag force, and the variable gravity force (no knowledge of which driver was in the vehicle at a time) from descending caused the energies to diverge, as seen in
Figure 8b. The efficiency of the motor is once again most likely the culprit for this divergence. At an incline or decline, the lack of a dynamic motor model makes the overall model less accurate. The model predicts less energy used than what was actually used.