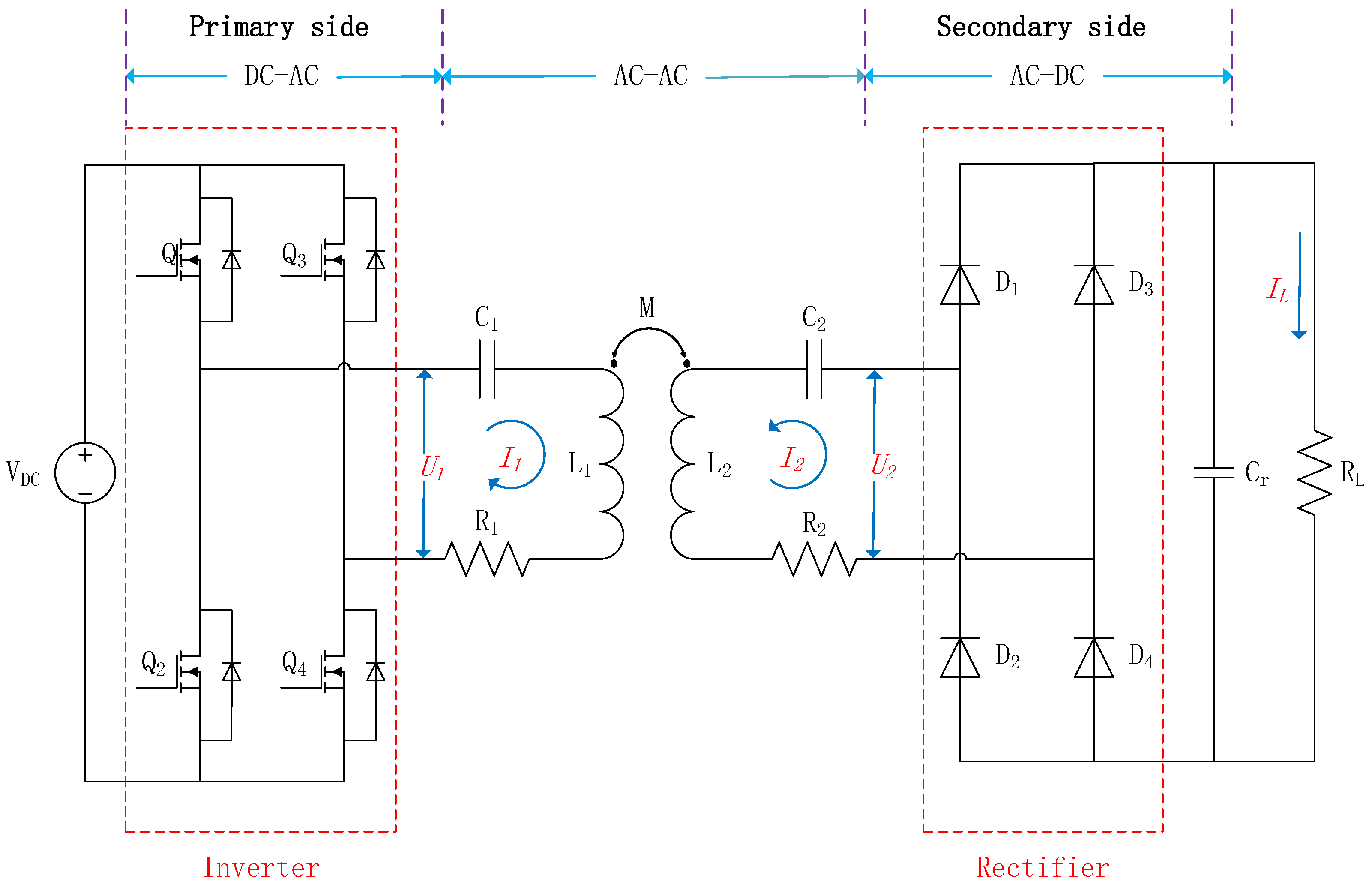1. Introduction
Electricity transmission is crucial for human production and daily life. Wireless power transfer (WPT) technology enables the transmission of electric energy from a power source to a load without direct electrical contact. WPT technology has rapidly developed with the advancements in modern industry and technology and is widely utilized in various fields, such as biomedical equipment, aerospace, consumer electronics, manufacturing facilities, and electric vehicles [
1,
2,
3,
4].
As a sustainable transportation option, electric vehicles (EVs) are becoming increasingly popular worldwide. With the increasing demand for electric vehicles, it is important to develop efficient and reliable charging techniques for their lithium-ion batteries. There are three commonly used charging methods: constant current–constant voltage (CC-CV) charging [
5], constant power charging [
6,
7], and pulse charging [
8,
9]. CC-CV charging involves controlling the charging current and voltage to keep the battery at a constant current or voltage during the charging process. Constant current charging can charge the battery faster in the early stages of charging, and constant voltage charging can fill the battery faster in the later stages of charging. Therefore, by combining constant current and constant voltage charging, charging efficiency and speed can be maximized. This charging method performs well in terms of charging speed and efficiency and can prevent overcharging and over-discharging, thereby extending the battery’s lifespan.
In contrast, constant power charging and pulse charging have faster charging speeds but are more prone to overcharging or over-discharging the battery, which can reduce its lifespan. Constant power charging involves continuously adjusting the charging current and voltage to maintain a constant charging power during the charging process. Pulse charging applies periodic high-voltage and high-current pulse signals to the battery during charging to increase the charging speed.
Although constant power charging and pulse charging allow faster charging speeds, they require more complex control strategies to avoid negative impacts on the battery. In comparison, CC-CV charging has a simpler and more reliable control strategy, can adapt to different types of batteries, and can effectively protect the battery.
Therefore, in many applications, CC-CV charging is still one of the most commonly used charging methods, especially in the electric vehicle and renewable energy storage fields. By accurately controlling the charging current and voltage, CC-CV charging can achieve efficient, safe, and reliable battery charging.
Over the years, electric vehicles known for their eco-friendliness and high efficiency have been increasingly replacing traditional fuel-based vehicles, leading to a surge in the interest in wireless charging technologies for electric vehicles. Lithium-ion batteries are now widely used as energy storage units in electric vehicles [
10].
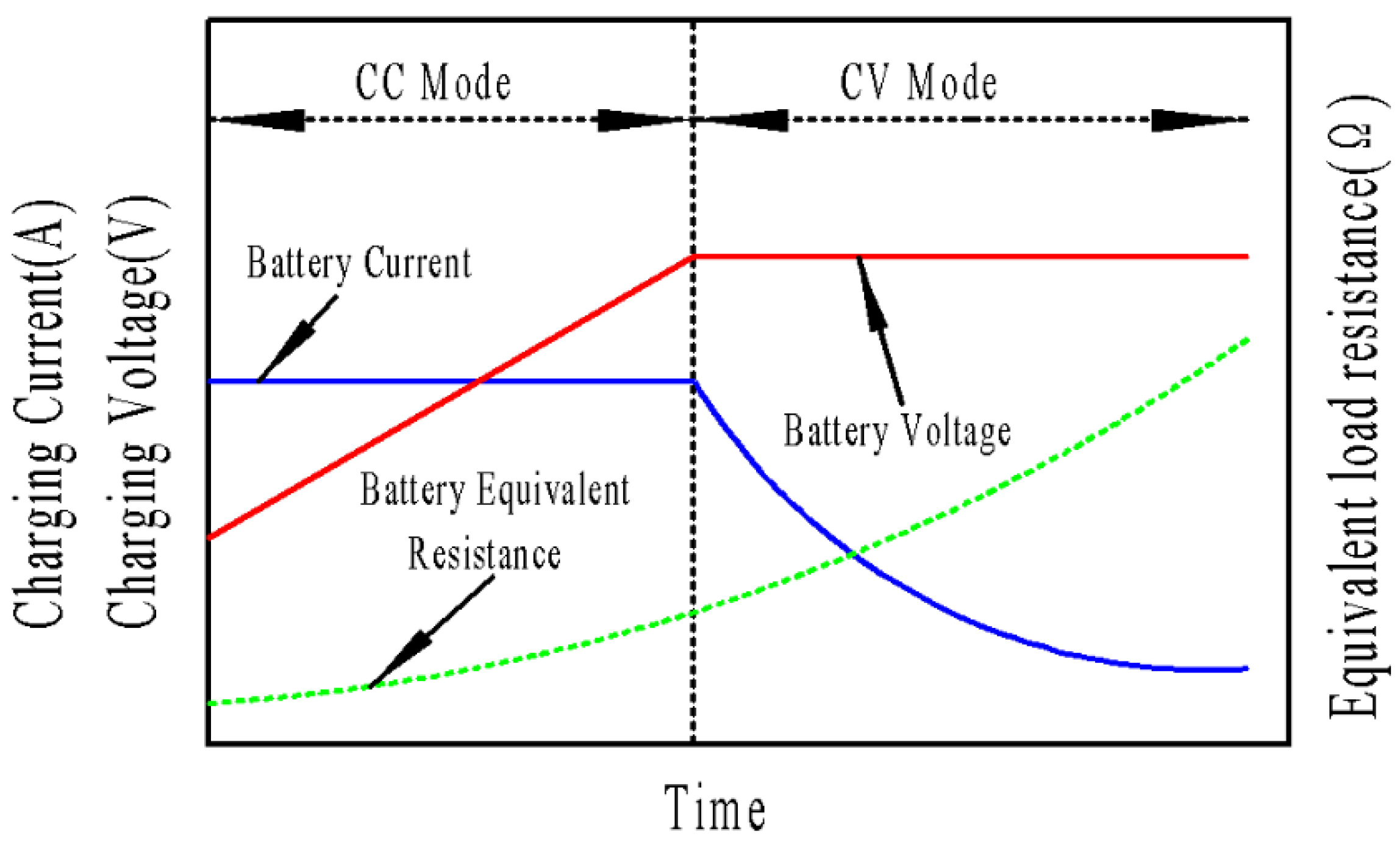
Figure 1 illustrates the charging process of a lithium battery, which begins with the CC mode and switches to the CV mode as the battery voltage increases [
11]. The dynamic changes in the equivalent load resistance of the battery during the charging process can affect the charging current, charging voltage, and system transmission efficiency. Hence, a closed-loop control scheme is crucial for achieving precise control of CC and CV charging in the wireless charging system [
12].
The output of a WPT system is influenced by compensation parameters, operating frequency, and load conditions. Typically, compensation parameters and operating frequency are constant, while the system output varies with load conditions. The use of DC-DC converter, a variable frequency or phase-shifted full-bridge inverter, or an impedance matching network are the main control methods for CC and CV wireless charging systems [
13,
14,
15]. Using a buck/boost converter for DC-DC conversion can potentially have a negative impact on the system transmission efficiency and may also result in increased weight or cost [
13]. If the operating frequency of the system deviates significantly from the optimal frequency, adjusting the frequency may result in a reduction in the system’s power transmission capacity [
14]. Phase-shift control is a technique that modifies the duty cycle of the inverter output voltage by varying the phase difference between the front and rear sections of the inverter, thereby adjusting the system output. This method is effective at compensating for the reactive power of the system when it operates at the resonant frequency. However, when using impedance matching, a large array of capacitors or inductors is required, which can increase the weight, size, and control complexity of the system [
15].
In two papers [
14,
15], the system in question utilizes a DC-DC converter on the primary side and employs frequency conversion or phase-shift control for the full bridge inverter on the primary side to achieve CV output through impedance-matching control. In another two studies [
16,
17], to achieve CV output, a chopper control link such as a buck or boost converter is added to the secondary circuit. While these systems have achieved good CV output, the addition of extra circuits reduces the transmission efficiency of the system and increases the control complexity. In the studies [
18,
19], phase shift control was utilized to achieve CV output, but the circuit may fail to meet the output voltage requirements when the load varies significantly. Another study [
20] utilized a PWM scheme with a phase-locked loop (PLL) control method. However, the circuit-input impedance needs to be inductive throughout the entire load variation range, which results in an increase in reactive power loss. In the studies [
21,
22], the system achieved CC and CV output through frequency-conversion control at two different operating frequencies. However, changing the frequency increases the complexity of hardware circuit design.
Many practical applications of WPT systems suffer from misalignment or variations in transmission distance between the transmitting and receiving coils. This can cause a significant change in the coupling coefficient, leading to instability in the output voltage and current. To address this issue, many researchers have investigated methods to identify the coupling coefficient. One such method proposed in [
23] uses a switched capacitor, but its implementation in practical applications is challenging. In [
24], a dynamic method that only requires parameters from the receiving end was analyzed, but its measurement complexity and uncertainty are high due to the high harmonics of the rectified current. In [
25], the coupling coefficient was estimated by analyzing the relationship between the duty cycle of the buck–boost circuit and the coupling-coefficient change. However, this method results in two solutions for the coupling coefficient, and obtaining the true value from the two solutions using the duty cycle of the buck circuit is inefficient. Another method proposed in [
26] identifies the coupling coefficient using the input impedance equation, which offers a single solution and avoids the double-solution problem encountered in [
25]. This paper proposes a method for estimating the coupling coefficient when the coil is misaligned or the transmission distance changes during charging, and designs a CC/CV output adaptive control flow based on the coupling-coefficient estimation.
The SPWM inverter is a type of inverter used to convert DC voltage into AC voltage. It works by generating a sequence of high-frequency pulses whose widths are modulated in such a way that the average voltage waveform obtained is a sine wave. This makes the SPWM inverter an ideal solution for applications that require a high-quality sine wave input. One of the main advantages of SPWM inverters over other types of inverters is that they provide a high-quality sine wave output with low harmonic distortion, which is essential for many electrical devices. Additionally, SPWM inverters are efficient, reliable, and can be easily controlled, making them ideal for use in various applications.
This paper proposes a WPT system based on SS compensation with an SPWM inverter circuit. To achieve CC/CV output, the modulation depth of the inverter circuit is controlled within a certain range as the load varies. Specifically, the system operates in CC mode with an output current of 0.75 A when the load voltage is below the maximum charging voltage of 12 V. Once the load voltage reaches 12 V, the system switches to CV mode, and charging ends when the load current is less than the charging end current. The contributions of this paper are as follows:
(1) A method to realize CC/CV output of WPT system under the control of SPWM inverter is proposed.
(2) A mathematical model between load voltage (and load current ) and the modulation depth of SPWM inverter was built.
(3) An adaptive control flow of CC/CV output was designed.
(4) A method for coupling-coefficient estimation during charging is proposed.
(5) A CC/CV adaptive output strategy for WPT systems with coupling-coefficient estimation was designed.
(6) An experimental circuit of WPT with S-S compensation with CC/CV output was built, and the proposed model and method were verified.
This paper is organized as follows.
Section 2 presents an analysis of the proposed WPT circuit, including the derivation of the relationship between modulation depth and CC/CV output condition, estimating coupling coefficients and the controlling scheme. In
Section 3, the proposed control scheme is validated through simulations.
Section 4 evaluates the effectiveness of the proposed method through experimental results. Finally,
Section 5 provides the conclusions of this study.
2. System Analysis
2.1. Theoretical Model of S-S WPT Circuit
The WPT system comprises a transmitter and a receiver, which are connected through magnetic coupling to transfer energy via an alternating magnetic field. The transmitter employs a full bridge inverter circuit to convert DC voltage to AC voltage, and the receiver uses a full bridge rectifier circuit to convert AC voltage back to DC voltage.
To efficiently transfer electrical energy in the WPT system using an alternating magnetic field, compensation elements (usually capacitors) are added to the transmitting and receiving coil ends to reduce reactive power [
11,
27,
28,
29,
30,
31,
32,
33,
34,
35]. The basic compensation topology of the WPT system can be classified into four types based on the series or parallel connection between the capacitor and the transmitting/receiving coil. These four types are: series–series (S-S), series–parallel (S-P), parallel–parallel (P-P), and parallel–series (P-S) [
27,
28,
29]. Among them, the S-S compensation circuit is widely used due to its simple structure, and the selection of capacitance is not affected by load and coupling conditions when the system operates at resonance frequency, hence the popularity of this circuit [
11,
29,
30,
31].
Figure 2 illustrates the typical circuit diagram of S-S WPT [
11,
29,
31], which consists of a full bridge inverter circuit (
), a transmission coil (
), a receiving coil (
), a full bridge rectifier circuit (
), and two compensation capacitors (
and
). The transmitter coil
and the compensation capacitor
form the primary-side resonant circuit, and the receiver coil
and the compensation capacitor
form the secondary-side resonant circuit.
M is the mutual inductance between the transmitter coil
and the receiver coil
.
and
are the rms values of the resonant current on the primary side and the secondary side, respectively.
and
are the internal resistance of the transmitter coil
and the receiver coil
, respectively, and
is the filter capacitor. The DC voltage
is the input voltage of the full-bridge inverter circuit.
is the rms value of the output voltage of the full-bridge inverter circuit.
is the rms value of the input voltage of full-bridge rectifier circuit.
is the load current.
is the load voltage.
The following equations can be derived based on Kirchhoff’s voltage law (KVL):
where
is the operating angle frequency of the system satisfying
.
is the operating frequency of the system.
and
are the equivalent impedances of the transmitting and the receiving, respectively:
Typically,
and
are complex numbers. However, when the system operates at the resonant frequency,
and
can be represented as pure resistance, with
, where
is the equivalent AC resistance between the rectifier bridge circuit and the DC load. According to the fundamental equivalent principle,
and
are satisfied with [
34]:
It can be intuitively inferred that if the DC load is known, the corresponding DC load voltage or current can be adjusted by controlling .
2.2. Analysis of SPWM Single-Phase Inverter Circuit
In the single-phase inverter circuit, PWM modulation is often used to control the switches (). There are square wave modulation and SPWM modulation among the PWM modulation methods. Although the square-wave modulation has a high DC utilization rate, the harmonic content of output voltage is also high. The output voltage waveform of the inverter circuit using SPWM modulation is a series of rectangular pulses with the same amplitude and unequal width. The pulse width varies according to the sine law. When it acts on the inertial component, the output is equivalent to a sine wave. Its benefits include a reduced level of harmonic distortion and a high degree of linearity in voltage regulation.
The SPWM single-phase inverter circuit is shown in
Figure 3. The SPWM signal is generated by comparing the sine wave of the modulation wave with the triangle wave of the carrier wave. In the part where the sine wave is larger than the triangle wave, the switches
and
are on. At the time where the sine wave is smaller than the triangle wave, the switching devices
and
are on. The output voltage
of the inverter circuit is continuously switched between positive and negative
as the switches turn on at carrier frequency.
When the amplitude of the sine wave is
, the amplitude of the triangle wave is
, the modulation depth is defined as
, and 0 <
≤ 1, then the output voltage of inverter circuit can be expressed as:
where
is the rms value of the voltage of the inverter circuit. It can be seen intuitively that the output voltage
of the inverter circuit can be adjusted by controlling the modulation depth
.
In practical applications, microcontrollers (such as stm32 series controllers) are usually used to generate a SPWM signal, and the external drive circuit drives the on–off of switches .
2.3. Analysis of CC/CV Output
When the WPT system operates in the resonant frequency, the impedance angle is zero—that is, the imaginary part of the impedance is zero. The impedance can be represented as pure resistance, with
. Therefore, the resonant frequency of the resonant circuits on the primary side and secondary side are designed to be same, and the system is operated at the resonant frequency
—that is:
When the WPT system is operated in CC mode, the relationship between load current
and modulation depth
in the SPWM inverter is:
Further, it can be expressed as follows:
where
is the output current required in CC mode, and
is the modulation depth in CC mode. From Equation (10), when the load
varies, the modulation depth
can be adjusted so that the system output current
tracks the output current
required by the CC mode, and
increases as
increases. When the coil internal resistance
and
are ignored, Equation (10) can be further simplified to:
It can be seen in Equation (11) that when the internal resistance of the coil is ignored and the system operates at resonant frequency, the WPT circuit with S-S compensation can realize CC charging independent of load [
32].
When the WPT system is operated in CV mode, the relationship between load voltage
and modulation depth
of SPWM inverter is as follows:
Further, it can be expressed as follows:
where
is the output voltage required in CV mode, and
is the modulation depth in CV mode. Similarly, when the coil’s internal resistances,
and
, are ignored, Equation (13) can be further simplified to:
From Equations (13) and (14), when the load varies, the modulation depth can be adjusted so that the system output voltage tracks the output voltage required by the CV mode, and decreases as increases.
The system’s load power is:
The system’s input power is:
The system’s transmission efficiency
can be expressed as:
If the coil internal resistances
and
are ignored, transmission efficiency,
, can be simplified as:
In Equation (18), the DC input voltage
, mutual inductance
M, and operating angle frequency
ω of the WPT system are fixed. Therefore, when the system operates in CC mode, the transmission efficiency
is determined by the modulation depth
and the system output current
, where
is constant. Equation (11) indicates that the modulation depth
is constant when the system operates in CC mode, resulting in an almost constant efficiency
. When the system operates in CV mode, the transmission efficiency
is determined by the modulation depth
m, the system output voltage
, and the load
, where
is constant. Taking partial derivatives of
with respect to
and
yields:
Compare the absolute values of two partial derivatives, yielding:
As is less than or equal to 1, and is typically greater than 1, Equation (21) is less than 1, which means . Therefore, dominates in the denominator of Equation (18). As a result, the efficiency in CV mode gradually decreases with an increase in .
2.4. Adaptive Control Strategy for CC-CV Output of WPT System
During battery charging, the WPT system operates in CC mode if the battery voltage is lower than the set voltage, causing the voltage to rise. Once the battery voltage reaches the preset level, the system switches from CC mode to CV mode, resulting in a decrease in charging current. Charging ends once the charging current falls below the preset end current. The equivalent load resistance of the battery changes over time during the charging process, which can affect the charging voltage or current. As noted in literature [
36], a properly designed WPT system should ensure output stability. Therefore, in the event of a variation in the equivalent load resistance, a well-designed WPT system should be capable of automatically adjusting the system’s parameters to enable the output current in CC mode to follow the required
and the output voltage in CV mode to follow the required
. In this study, the modulation depth
m of the SPWM inverter circuit is controlled to enable
to track
or
to track
. The closed-loop control structure is depicted in
Figure 4.
The ARM (Advanced RISC Machine) controller is a type of microcontroller based on the ARM architecture. The ARM processor is designed to be 32-bit, but it also supports a 16-bit instruction set. In addition, the ARM processor has advantages such as low power consumption, high performance, high reliability, easy development, and good flexibility. The STM32F103ZET6 is a microcontroller based on the ARM Cortex-M3 core, developed by ST Microelectronics. It has the advantages of high performance, low power consumption, high reliability, and easy development. The microcontroller has 512 KB of built-in flash memory and 64 KB of SRAM memory, and is equipped with multiple timers, an ADC, a DAC, and other modules. Therefore, in this study, the STM32F103ZET6 was chosen as the controller.
In
Figure 4, the ARM controller at the receiver calculates the load
by detecting the load current
and voltage
. Then, the
is fed back to the ARM controller at the transmitter through wireless communication. The transmitter ARM controller tracks the required output current
or the required output voltage
by calculating the modulation depth
m of SPWM inverter circuit through Equation (10) or Equation (13).
The flow of the control scheme proposed in this paper is shown in
Figure 5, including the following steps:
- (1)
Make the WPT circuit operate at the resonant frequency ;
- (2)
Detect whether < ; if < , start the control procedure. Otherwise, close the S-S WPT circuit.
- (3)
Detect and , and calculate .
- (4)
According to Equation (10), adjust the modulation depth m, so that = , and the control system operates in CC mode.
- (5)
Judge whether = is true; if it is true, execute step (6); if not true, repeat steps (3)–(4).
- (6)
Re-detect and , and calculate .
- (7)
According to Equation (13), adjust the modulation depth m, so that = , and the control system operates in CV mode.
- (8)
Repeat steps (6) and (7) until .
- (9)
When , the charging is completed, and close the S-S WPT circuit.
2.5. Coupling-Coefficient Estimation
The WPT system exhibits loose coupling, which means that variations in the alignment of the transmitting and receiving coils, or changes in transmission distance, can lead to significant fluctuations in the coupling coefficient
k. These fluctuations in k can directly impact the output voltage or current of the system, resulting in unstable performance. To maintain CC/CV output, it is essential to estimate the coupling coefficient
k. This section examines the method of estimating the coupling coefficient based on circuit parameters, utilizing
Figure 2 as a reference.
The rms value of voltage of receiving coil
can be derived as:
Assuming that is constant, and combined with Equation (4), it can be seen that is also constant. However, any changes in the mutual inductance M would cause a variation in the ratio of . Therefore, combining Equations (4) and (22) can estimate mutual inductance M.
can be calculated as:
Mutual inductance
M can be derived as:
Combining Equation (5) with Equation (6), it can be deduced that:
Substituting Equation (25) into Equation (24), mutual inductance
M can be further deduced as:
The relationship between mutual inductance
M and coupling coefficient
k is as follows:
Equation (27) reveals that the coupling coefficient
k is influenced by both the self-inductance of the transmitting and receiving coils and their mutual inductance. Specifically, the coupling coefficient
k is directly proportional to the mutual inductance
M and inversely proportional to the self-inductance
or
of the coils. Thus, when the sizes, dimensions, and numbers of turns of the transmitting and receiving coils are fixed, the coupling coefficient
k depends solely on the mutual inductance
M between the coils. In other words, as the mutual inductance
M increases, so does the coupling coefficient
k. Therefore, the coupling coefficient
k can be derived as:
When the coil is misaligned or the transmission distance changes, the CC/CV output of the WPT system can be achieved by utilizing the coupling coefficient k calculated using Equation (28).
If the internal resistances
and
of the transmitting and receiving coils are ignored, then one solution of Equations (26) and (28) is 0, and the other solution can be expressed as follows:
Thus, the sign “±” in Equations (26) and (28) should be interpreted as “+” instead.
2.6. Control Strategy Based on Coupling-Coefficient Estimation
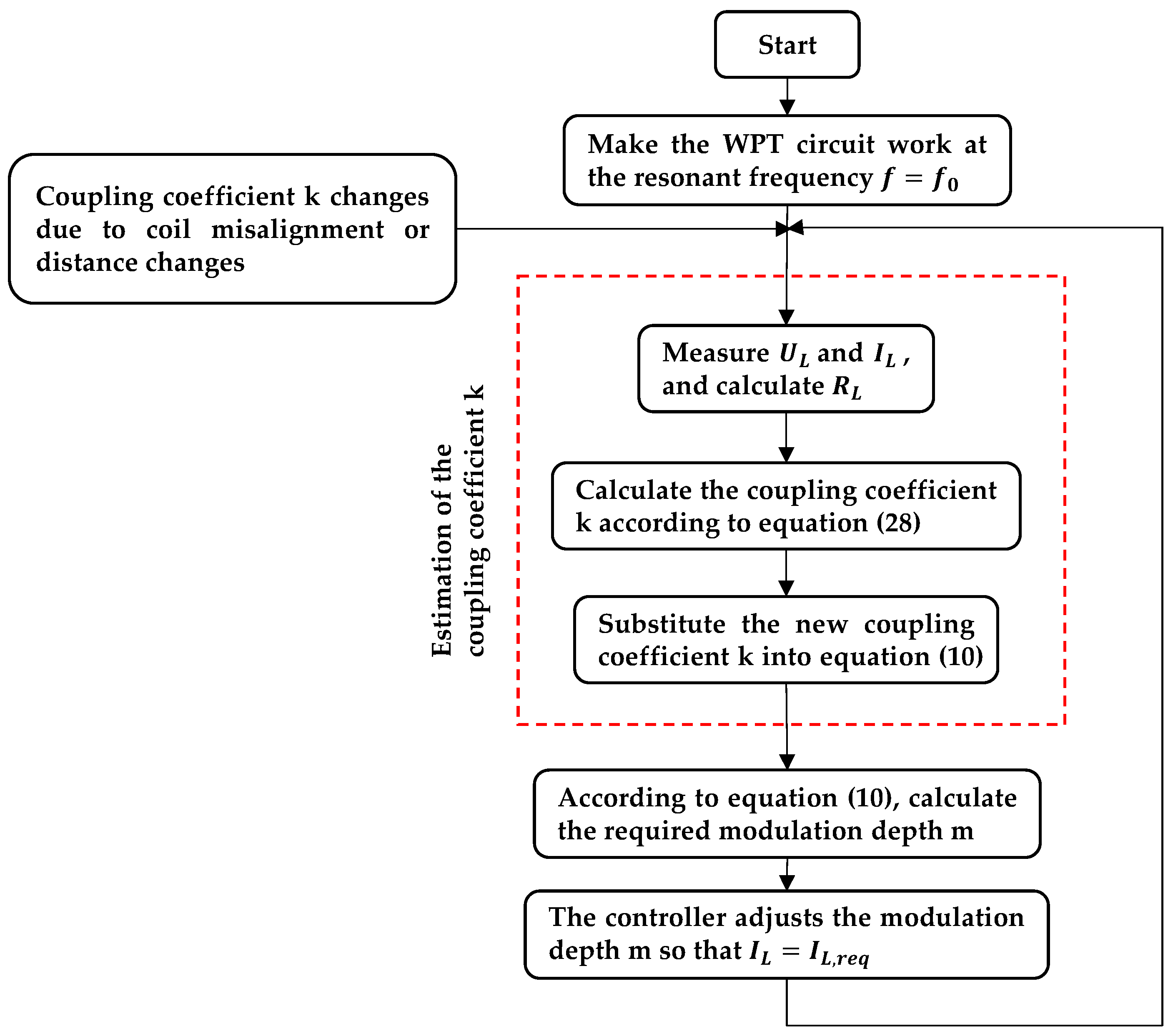
When the coils are misaligned or the transmission distance varies, the coupling coefficient k will change accordingly, making it impossible for the system to achieve CC/CV output. To address this issue, as depicted by Equation (28), we can estimate the coupling coefficient k by measuring the output parameters of the circuit and known system parameters, and then use this estimated value to adjust the desired modulation depth m for the CC/CV mode, as shown in Equation (10) or Equation (13) after substitution.
Figure 6 illustrates the CC/CV control process utilizing coupling-coefficient estimation. After establishing communication between the transmitter and receiver, the receiver controller calculates the load resistance
by measuring the load voltage
and the load current
, and also detects changes in
and
. Any changes detected are then fed back to the transmitter controller. Using Equation (28), the transmitter determines the coupling coefficient
k and subsequently determines the CC/CV modulation depth
m using Equation (10) or (13). The transmitter controller automatically adjusts
m to ensure that
tracks
or
tracks
.
Based on Equation (9), as the coupling coefficient k varies, the output current in CC mode also varies. Therefore, at this stage, the WPT system fails to achieve the required output current in CC mode. Equation (10) indicates that the system can achieve the required output current in CC mode by adjusting the modulation depth m. To adjust the modulation depth m, the first step is to estimate the coupling coefficient k of the system when the coils are misaligned or the transmission distance varies. Subsequently, by substituting the newly acquired coupling coefficient k into Equation (10), the modulation depth m that satisfies the requirement of the CC mode for the output current can be determined.
Figure 7 illustrates the process for adjusting the modulation depth
m in CC mode when there is a misalignment of the coil or a change in transmission distance. The circuit should be connected based on the ideal circuit, and when the coupling coefficient
k changes, measurements of the output voltage
, output current
, and input voltage
of the transmitting coil should be taken. From these measurements, the load
can be calculated. Using Equation (28), the coupling coefficient
k can be estimated. Next, the required modulation depth
m can be calculated using Equation (10), and the controller can adjust the modulation depth
m to ensure that the output current
tracks the required current
for CC mode.
Equation (12) implies that changes in the coupling coefficient k will cause a corresponding change in the output voltage in CV mode, making it impossible for the WPT system to meet the required output voltage in CV mode. However, Equation (13) shows that adjusting the modulation depth m can enable the system to satisfy the required output voltage in CV mode. To determine how to adjust the modulation depth m, the first step is to estimate the coupling coefficient k of the system when there is misalignment of the coils or variations in transmission distance. Then, this new coupling coefficient k can be substituted into Equation (13) to obtain the modulation depth m required to achieve the output voltage in CV mode.
Figure 8 illustrates the process for adjusting the modulation depth
m in CV mode when there is a misalignment or a change in transmission distance of the coil. The first step is to connect the circuit based on the ideal circuit. Then, when there is a change in the coupling coefficient
k, the output voltage
, output current
, and input voltage
of the transmitting coil are measured. Using the output voltage
and output current
, the load
is calculated, and the coupling coefficient
k is estimated at this time using Equation (28). Equation (13) is used to calculate the required modulation depth
m, and the controller adjusts the modulation depth
m to ensure that the output voltage
tracks the
required for the CV mode.
3. Simulation of the Wireless Charging System
The circuit model of the WPT system was established in MATLAB/Simulink, and the CC-CV charging was simulated under the condition of coupling coefficient
and the load
of 10–25 Ω. The system parameters are shown in
Table 1.
The MATLAB/Simulink model established includes an SPWM inverter circuit, a resonant circuit, a rectifier circuit, a sinusoidal signal generator, a triangular wave-signal generator, an amplitude comparator, and a signal inverter, as shown in
Figure 9. During the model operation, the CC output is conducted when the load
is 10–15 Ω and the required
is 0.75 A. When the
is 16–25 Ω, the
required for CV output is 12 V.
The amplitude of the triangle wave signal generator was set as unit 1. The amplitude of the sinusoidal signal generator was calculated by Equations (10) and (13) according to the value of the load . The signals generated by the sinusoidal signal generator and the triangle wave signal generator were compared by the amplitude comparator to generate the SPWM signal, which controlled the switches and . The signal reverser reverses the generated SPWM signal and controls the switches and . The DC power is first converted to high-frequency AC power by the SPWM inverter circuit. This high-frequency AC power is then fed into the transmitting coil via the compensation capacitor , which generates a high-frequency alternating magnetic field when excited. The receiving coil and compensation capacitor generate AC power through magnetic coupling induced by this high-frequency alternating magnetic field. The generated AC power is then rectified by the rectifier circuit, converting it to DC power. In this way, the wireless power transfer is achieved.
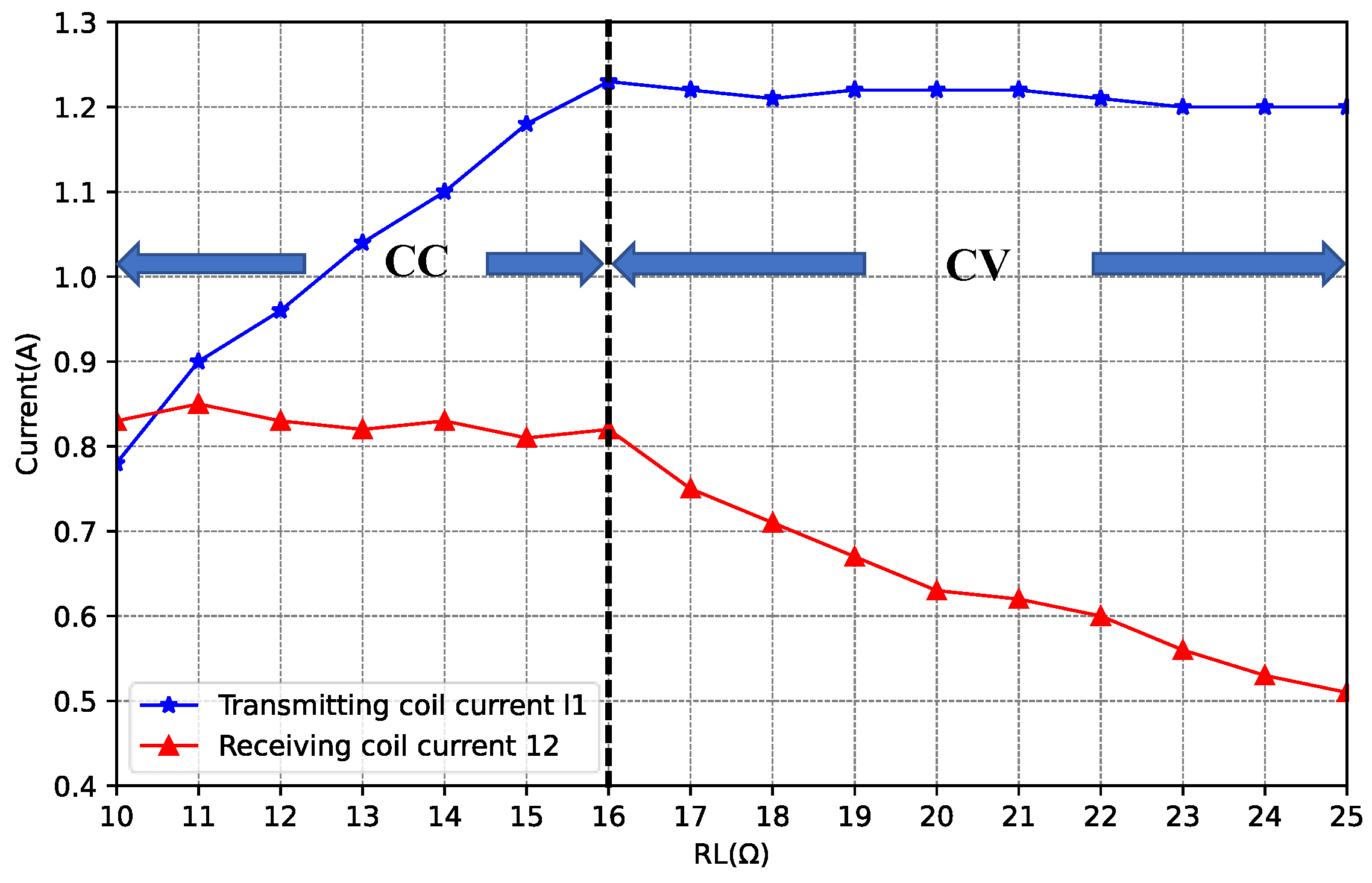
Figure 10 shows that the
increases from 10 to 25 Ω, and simulation results of
and
are compared with the theoretical values. The simulation results are in good agreement with the theoretical values, indicating that the system has good CC and CV output performance, which verifies the accuracy of the model and method. In CC mode,
tracks
, and
increases with increases of
. In CV mode,
tracks
, and
decreases as
increases. The simulation results of
and
are slightly lower than the theoretical values, because the impedance of the rectification bridge circuit and load is equivalent to a pure resistance, which will produce error in the design of system parameters. Overall, the error is within the acceptable range.