Abstract
Electric vehicles contain various types of light emitting diode (LED) devices. A significant twice-line-frequency ripple current is usually produced in a conventional offline LED driver with a high power factor. In this paper, a flicker-free LED driver based on isolated Cuk converter with integrated magnetic technique is proposed. Two inductors and power transformer are combined into one magnetic core to eliminate the wave current as much as possible. With time domain analysis in electrical circuit and magnetic circuit, the operation principle, operational waveforms, and transfer function are analyzed in detail. Finally, experimental results from a 30 W laboratory prototype supplied by a 220 V grid validate the effectiveness of proposed LED driver.
1. Introduction
Light emitting diodes (LEDs) have the advantages of long lifetime, high luminous efficiency, small size, energy saving, and environmental friendliness. It has gradually become the fourth generation of green light source following incandescent, fluorescent, and sodium lamps [1,2,3]. With the improvement of light efficiency and chromatic aberration, LED is widely used in electric vehicles, screen display, and other fields. LEDs require a constant DC current to produce stable lighting. Therefore, the LED driver is the most critical part of the entire LED lighting equipment, which determines the quality of the lighting and seriously affects the sales price of the entire lighting equipment, the use of expenditure and service life. High-quality LED driver is a guarantee for the development of the LED industry, which directly affects the performance of LED.
To satisfy the harmonic standard in IEC 61000-3-2 with AC power supply such as general lighting and large-screen display, a power factor correction (PFC) stage is required in LED driver. Generally, PFC stage can be Fly-back, Buck, Buck-Boost, SEPIC, et al. All of these single-stage LED drivers have only once power conversion, which has high efficiency, small size, and is controlled simply [4,5,6]. While the power conversion achieves unity power factor, the input current is in the same phase as the input voltage, and the instantaneous input power takes on twice-line-frequency, which results in pulsating current in LED [7]. For example, if the grid frequency is 50 Hz, the LED will contain current component with 100 Hz. Studies in recent years have found that long-term learning and working under the flickering light will lead to fatigue easily [8,9]. At the same time, the pulsating current generated by the LED driver can also affect the stability and efficiency of the overall system operation of electric vehicles powered by electricity.
The diodes in the circuit not only produce losses, but also reduce the power factor of the circuit. Because the rectifier bridge is composed of four uncontrollable ordinary diodes, each diode has a threshold voltage (generally 0.5 V for silicon, 0.2 V for germanium). The AC power passing through the diode rectifier bridge causes waveform distortion, which is no longer an ideal sine wave, and the voltage waveform is used as a reference for the back-end PFC control circuit to correct the input current, which makes the input current also occur over the zero distortion, the input power factor of the circuit is reduced, and the higher harmonics at the zero point of the input voltage are increased. In addition, while the PFC circuit works, the input current will flow through three semiconductor devices (two rectifier diodes and a switching tube or two rectifier tubes plus the renewal diode) at any given time, the circuit components experience large through-state losses, which are more pronounced in the case of low-voltage and high current diode through-state losses.
To eliminate AC components in offline LED drivers, scholars have focused on two main aspects: one is optimizing topology structure, the other is improving control strategy. In [10], a bidirectional Buck-Boost converter is connected in parallel between the fly-back converter and LED load. The bidirectional Buck-Boost converter provides a path for the AC component pulsating current with twice line frequency of the PFC converter to flow through, leaving a pure DC current to drive the LED load without flicker. The principle of the bidirectional converter is to absorb the second harmonic AC ripple current of the PFC converter [11]. But two switches are needed in this topology and the two control loops will increase the complexity of the design. The number of system components, cost, and size can be significantly reduced using schemes such as PSR [12].
In [13], a LED driving circuit based on Cuk with active ripple compensation is proposed. In this circuit, the active ripple compensation branch is used to replace the output filter’s electrolytic capacitor to offset the inductor ripple current, which provides the LED array with a constant DC and further with an ideal driving state. There are many strengths among the proposed LED driver, such as high reliability, suitable for a wide range of voltages, small volume by integrating compensation circuit and control circuit. But this method is only suitable for a low-power LED with a DC input voltage and requires a DC source for the transistor. In [14], electrolytic capacitors are also eliminated and a flyback three-port converter is used to make the driver smaller and the control strategy simpler.
In [15], a new control strategy is proposed to reduce the peak-to-average ratio of the instantaneous input power by injecting third and fifth harmonics in the input current. The variation of the duty cycle in a line period of fly-back converter is derived in a DCM mode and is further simplified for ease of implementation, requiring only the sensing of the input voltage. However, a drawback of the harmonic injection techniques is that two control loops are needed, which increases the complexity of the control structure compared with the conventional LED driver. On the other hand, if the capacitance value is reduced further, it is necessary to increase the amplitude of the harmonics, which will reduce the power factor [16]. Additional power processing circuitry at the converter output port is required to compensate for output current combined with voltage ripple to improve the power factor [17,18]. However, IEC 1000-3-2 requires that the maximum third harmonic amplitude should be less than 0.3 I*PF if the input power is larger than 25 W. Therefore, this method is only suitable for small power supply. Moreover, a complicated control approach, more stress on the semiconductor devices, and a high switching frequency, result in higher losses and poor efficiency.
According to the principle of luminescence of LED, a flicker-free offline LED driver based on Cuk converter with integrated magnetics is proposed in this paper. Two inductors and isolated transformer are integrated into one magnetic core so that a certain proportion of the voltage can supply to the two inductors. This approach allows a zero current ripple in theory by means of a proper design of inductors and transformer, thus resulting in low cost, small volume, and high power density.
The remaining of this paper is organized as follows. Section 2 introduces the principle of the Cuk converter with integrated magnetics. Section 3 presents the procedure of the small signal modeling and transfer function of the converter. In Section 4, the design of the circuit is shown. Section 5 presents simulation and experimental results according to the designed parameter. Finally, the conclusion of this work is detailed in Section 6.
2. Operating Principle
Figure 1 shows the circuit configuration of the proposed flicker-free LED driver based on isolated Cuk converter with integrated magnetic technique. The isolated Cuk converter includes switch Q1, inductors L1 and L2, the coupling capacitors C1 and C2 with large voltage ripple, diode D1, transformer Tr in which LP and LS are the primary and secondary inductance of the transformer, and LED load. The transformer Tr is introduced to separate the input and output. The two inductors and the transformer are wound on an EI magnetic core to achieve magnetic integration. In the proposed circuit, the transformer wire is wound around the center leg3, and two conductors’ wire are wound around the two side leg—leg1 and leg2 with a very small air gap. Mutual inductance exists between the two inductors by this method and ensures decoupling integration between the two inductors and the transformer. Due to the mutual inductance, the voltage can be shared and the voltage on the inductors can be reduced [19,20]. Then the twice-line-frequency LED current ripple of the LED driver based on the Cuk converter with integrated magnetics can be greatly reduced.
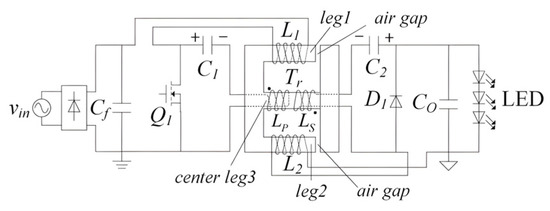
Figure 1.
Topology of the flicker-free LED driver with integrated magnetics.
Compared with Buck-Boost converter and SEPIC converter, Cuk converter has the following advantages.
- Both input and output are connected to inductors, making both input and output currents continuous and the pulsating currents of both are small, which is convenient for filtering at the input and output.
- The output voltage of Cuk converter can be larger or smaller than the input voltage, which increases the application range of the converter.
- The Cuk converter has better anti-interference performance because the switching tube short-circuits the interference at the input during the switching tube conduction and the diode short-circuits the interference at the input during the switching tube turn-off.
- If the input inductor and output inductor are integrated into one core, the output ripple can be reduced by half, and by choosing a suitable inductor value or increasing the operating frequency of the converter, the output current can theoretically achieve zero ripple.
The circuit operates in continuous conduction mode (CCM) because the Cuk CCM inverter has a medium power capacity, ability to step up or down, and low input/output current ripples [21]. The flicker-free LED driver is operated in two modes based on its operation principle: (1) Q1 switched on and D1 switched off and (2) Q1 turned off and D1 turned on. Figure 2 shows the equivalent circuit of proposed LED driver in each mode of operation. Figure 3 shows the key voltage and current waveforms.
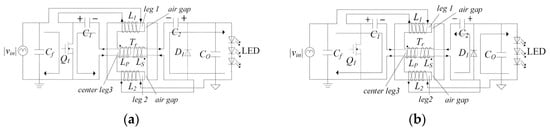
Figure 2.
The equivalent circuit of the proposed LED driver. (a) [t0–t1]. (b) [t1–t2].
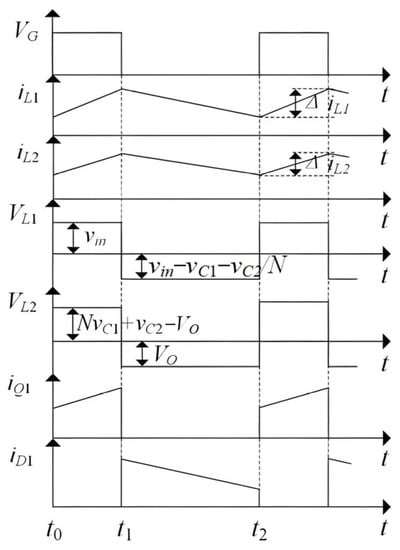
Figure 3.
The key waveforms of voltage and current.
To simplify the analysis process, the following assumptions are made:
- All electronic devices are ideal, ignoring their parasitic parameters.
- The switching frequency fS is much larger than the grid frequency fL, that is to say the input voltage is approximately constant over a switching period;
- Capacitors C1, C2, and CO are large enough to keep the voltage constant approximately;
- Since the decoupling integration mainly affects the volume and loss of the magnetic components, the influence on voltage and current is very small, the interaction between the inductors and the transformer can be neglected.
Mode1 [t0–t1]: At t0, the switch Q1 is turned on and diode D1 is turned off because of the reverse voltage. The equivalent circuit is shown in Figure 2a. The voltage on the inductor L1 is input voltage vin and it is charging during this period. The voltage on the primary winding NL is equal to the voltage of the capacitor C1. At the same time, the voltage induced by the secondary winding NS and capacitor C2 supplies to LED load together. The current flowing through L2 increases and L2 stores energy. According to Figure 2a, the equation can be expressed as
where VL1 and VL2 are the voltages on the L1 and L2 respectively, VC1 and VC2 are the voltages on the C1 and C2 respectively, M is the mutual inductance between L1 and L2, N = NS/NP is the transformer turns ratio.
Mode2 [t1–t2]: At t1, the switch Q1 was turned off and diode D1 was turned on to provide an afterflow for LS and L2. At this time, L1 is discharging and provides energy to C1. Meanwhile, the voltage induced by the secondary winding is charging C2 through D1. L2 provides energy to LED load through D1 as well. According to Figure 2b, the equation can be expressed as
According to the volt-second balance for the inductors (L1, L2) over a switching period TS, we can get
where D is the duty ratio of the switch Q1.
The relationship between the input and output voltage can be expressed by the equation
Substituting (1) and (3) into (4), the ripple currents can be derived as
where ΔiL1 and ΔiL2 are the increment of iL1 and iL2 from t0 to t1.
From Equation (5), it is shown that if M = NL1, the ripple current of the inductor L2 reaches zero, and the input current iL1 remains the same as the case of no coupling. Therefore, the output current ripple is only related to inductor L1, the mutual inductance M between two inductors, and the transformer turns ratio N. The mutual inductance M is an intrinsic parameter between the coils and related to the turns of the inductors, the dimension, the position, and the magnetic medium. Anyhow, the output current ripple can be much smaller than that of the discrete magnetics.
Therefore, according to the above working principle, the twice-line-frequency LED current ripple of the LED driver based on Cuk converter with integrated magnetics can be reduced greatly.
3. Critical Design Parameter
In this section, the critical design parameters of the proposed LED driver is discussed.
3.1. Inductors L1 and L2
As mentioned in Section 1, the LED driver is devised to operate in full CCM. Therefore, the design of the inductors L1 and L2 must ensure this operating condition so that all the relationships established in the theoretical analysis are valid. From (4), we have
In order to achieve high power factor, the maximum ratio of the current ripple through L1 is chosen as 20%. According to the increase of iL1 from t0 to t1, the expression is shown in (7)
where η is the efficiency of LED driver, PO is the power of LED, TS is the switching period of Q1 and TS = 1/fS.
Substitute (6) into (7) yields
The average current flowing through the filter capacitor CO is zero in a grid period, so the current flowing through the LED load is equal to the current flowing through L2 and the maximum ratio of the current ripple through L2 is chosen as 5%. The expression is shown in Equation (9)
Substitute (6) into (9) yields
3.2. Capacitors C1, C2, and CO
The charging and discharging current of the filter capacitor CO equal to the current ripple of L2, which results in the voltage ripple on CO. The equation of output voltage ripple is shown as (11).
The maximum voltage ripple on CO is 0.1 VCO
Combining (11) and (12), the restriction of design CO is obtained as
Capacitors C1 (is equal to C2) transfers energy from input to output and in order to balance the instantaneous input and output power, the maximum voltage ripple on C1 (or C2) is 0.5 VC1 (or 0.5 VC2). The computational procedure is same as CO.
In practical design, C1, C2, and CO are CBB capacitor because of low loss, low absorption coefficient, good frequency characteristic, good self- healing effect, and high reliability [22].
3.3. MOSFET Q1 and Diode D1
The maximum current flowing through Q1 is at the moment before Q1 is turned on and equals to the sum of IL1 and IC1. The calculation procedure of IQ is as follows.
The maximum voltage applied on the power switch transistor Q occurred at the moment after Q is turned on. The calculation procedure of VQ is as follows.
The design procedures of the current flowing through D1 and voltage applied on D1 are similar to that of transistor Q. According to the above analysis, the circuit specifications and parameters designed in this paper are listed in Table 1.

Table 1.
The key parameters of the proposed driver.
4. Small-Signal Analysis and Controller Design
While the steady-state analyses define the DC status of the proposed circuit, the small-signal analysis is helpful in understanding the dynamic behavior of the integrated magnetic technique in the LED driver, and therefore, in determining the design criteria for a suitable controller and compensator. The state-space averaging method is a typical small-signal modeling and analysis method for power converters [23]. Compared with magnetic path-electric circuit paring transformation and gyrator-capacitor equivalent model [24], the magnetic-electrical circuit synthesis time domain model has one state variable less than the above two modeling methods, which greatly simplifies the derivation process of solving the transfer function with multi-order determinant [25]. Therefore, magnetic-electrical circuit synthesis time-domain model is suitable for establishing a small signal model of the isolated Cuk converter with integrated magnetic technique.
There are various methods for modeling switching converters, such as current injection equivalent circuit method, state space averaging method, switching element averaging model method, and switching network averaging model method. Among them, the state-space averaging method is to select the voltage or current parameters of the nonlinear components to derive a model independent of the switching frequency, which provides more intuitive input and output characteristics and is more physically meaningful. Therefore, the state-space averaging method is selected for the derivation and analysis of the small-signal model in this paper.
The reluctance model of the Cuk converter with integrated magnetic is shown in Figure 4. The L1 is around the upper side leg1 with N1 turns of conductor, the magnetic flux is φ1, the reluctance is R1; the L2 is wound on the lower side leg2 with N2 turns of conductor, the magnetic flux is φ2, the reluctance is R2; the primary and secondary side of the transformer are wound in center leg3 with the magnetic flux φC and the reluctance RC. Thus, according to Ohm’s law based on the magnetic circuit, we can get the following equation:
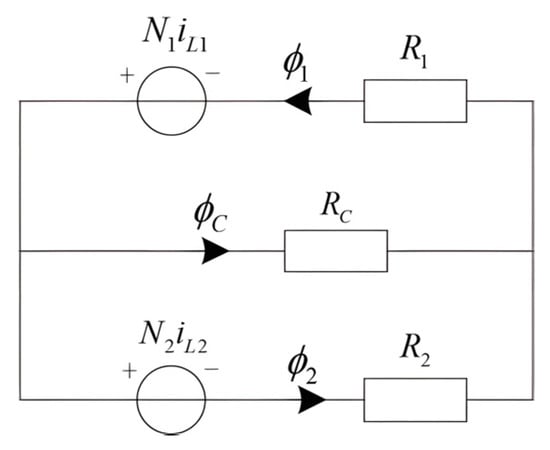
Figure 4.
Reluctance model of the proposed circuit.
According to the continuity of magnetic flux, φ1 = φ2 + φC, then (6) can be rewritten as
Select state vector x(t) in the proposed Cuk converter as [ϕ1(t) ϕ2(t) vO(t) vC1(t) vC2(t)]T, the input variable u(t) is [vin(t)]T, the state-space equation in mode 1 can be expressed as
The findi Rewrite (8) as = Ax(t) + Bu(t), then A1 and B1 can be expressed as follows ngs and their implications should be discussed in the broadest context possible. Future research directions may also be highlighted.
Similarly, the state-space equation in mode 2 can be expressed as
The corresponding matrix A2 and B2 are
Using the state-space averaging method, then we get the transfer function in the form of Laplasse transform and the small signal model is derived as follows:
where is the proportion of mode 2.
Based on the above small-signal model, the duty- ratio-to-output-voltage transfer function Gvd (s) can be expressed as
where the derived parameters ai(I = 1, 2, 3, 4) and bj(j = 1, 2, 3, 4, 5, 6) are omitted for brevity.
In the model, the reluctance R1 is 9.5 × 109 A·t/Wb, reluctance R2 is 1.27 × 1010 A·t/Wb, reluctance RC is 1.14 × 1010 A·t/Wb. Finally, we can calculate the Gvd(s) based on MATLAB with the parameters in Table 1. The Bode diagram of Gvd(s) is shown in Figure 5.
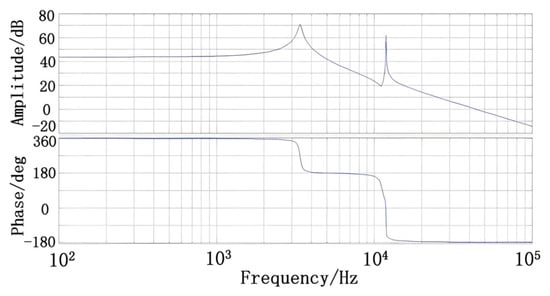
Figure 5.
Bode diagram of Gvd(s).
According to the Bode diagram, there are two low-frequency resonance points f1 = 3.2 kHz and f2 = 10.4 kHz and one zero resonance point f3 = 10.6 kHz. The zero resonance point at f3 balances the pole at f2, so there is no resonance peak in the Bode diagram, the circuit phase lags by 180 degree and its amplitude-frequency characteristic is declining by 40 dB/dec. Therefore, to make the circuit stable when wide range input voltage, phase compensation circuit should adopt the type II feedback network.
Figure 6 shows the circuit diagram of a typical type II feedback network. In order to realize quick regulation and high PF, the voltage-mode control is adopted. The compensator transfer function is
where , , .
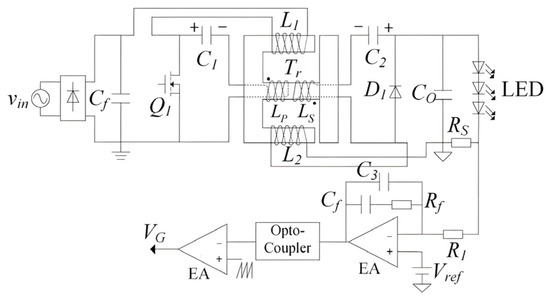
Figure 6.
Proposed circuit with type II feedback network.
In this compensator design, the circuit parameters are R1 = 51 kΩ, Rf = 270 kΩ, C3 = 680 pF, Cf = 470 nF.
According to classical control theory, an ideal control system should have the following characteristics.
- The low frequency band decreases at a slope of −20 dB/dec and has a certain height to ensure that the requirements of steady-state accuracy are met, followed by a slope of −40 dB/dec to increase the rapidity of the system.
- The middle frequency band should ensure that the cut-off frequency is large enough to meet the requirements of dynamic rapidity, and the amplitude-frequency characteristic curve at the 0 dB line should cross at −20 dB/dec and maintain a certain width to meet the requirements of the relative stability of the system.
- The amplitude-frequency characteristic curve of the high-frequency band should have a large negative slope, generally less than or equal to −40 dB/dec to improve the system’s ability to resist high-frequency interference.
Figure 7 shows the Bode diagrams of the proposed compensator. It can be observed that ratio is −20 dB/dec in low frequency, −40 dB/dec in medium frequency, and −20 dB/dec in high frequency, which are the key characteristic according to classical control theory.
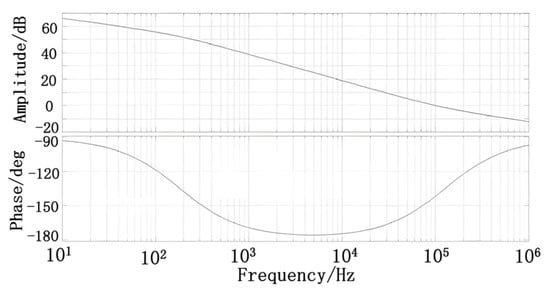
Figure 7.
Bode diagrams of the proposed compensator.
5. Simulation and Results Analysis of Proposed LED Driver
The Saber software was used to simulate the Cuk circuit with integrated magnetics. A resistance was used instead of the LED. The parameters are listed in Table 1. All the diodes are ideal.
The simulation results of the magnetic integrated circuit are shown in Figure 8. Figure 8a shows the waveforms of input voltage vin and input current iin. It can be seen that the input voltage and current are nearly in the same phase, so the driver achieves unity power factor. Figure 8b shows the waveforms of the inductor current iL1, iL2 and diode current iD1. It can be seen that the circuit works in CCM mode. Figure 8c gives the flux curves of the three legs. Obviously, φ1 + φ2 + φC = 0, which is exactly the same as the theory.
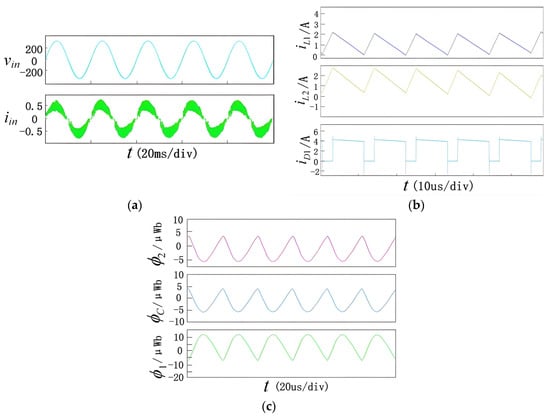
Figure 8.
Simulation results of Cuk circuit with integrated magnetics. (a) Waveforms of vin and iin. (b) Waveforms of iL1, iL2 and current iD1. (c) Waveforms of φ1, φ2 and φ3.
In order to verify the proposed flicker-free LED driver, a prototype has been built and tested in the laboratory. Beside the parameters listed in Table 1, other specification of the prototype is as follows: the load is three strings of 10 × 1 W LED, the core of transformer adopts the EI-shaped ferrite magnetic, power switch Q1:SPW20N60C3; free-wheeling diode D1: HFA25TB60S; control IC: UCC3844.
The bridgeless Cuk converter studied in this paper is a small to medium power circuit, and the switching tubes used are MOSFETs, whose maximum current withstand value occurs at the moment of transition from mode 1 to mode 2. At the same time, the switch tube withstand voltage value needs to be considered to leave twice the margin. The above selection conditions were combined to select the Infineon SPW20N60C3 model with a drain breakdown voltage of 650 V, on-state resistance, and continuous drain current of 20.5 A (25 °C). The voltage stress of the diode is the same as the voltage of the switching tube, so the actual circuit should be left with more than twice the margin, the comprehensive selection of the international rectifier company HFA25TB60S. The UC3842 is a high-performance fixed-frequency current-mode PWM integrated controller from TI that uses a minimum of external components to achieve PFC correction and an internal high-current totem pole output of ±1 A, making it an ideal device for driving power MOSFETs.
In addition, the filtering electrolytic capacitors required by the converter can be replaced by film capacitors or ceramic capacitors to some extent. Compared with electrolytic capacitors, film capacitors have the advantages of long life, high stability, good temperature characteristics, high voltage-withstanding capability, and low loss in high frequency, while ceramic capacitors have better high-frequency characteristics and can play the role of coupling, filtering, and oscillation in high-frequency circuits. Therefore, the use of film capacitors or ceramic capacitors can reduce the system loss and maintenance cost, while not affecting the size of the system.
Figure 9 shows the waveforms of input voltage vin and current iin. The input current follows the voltage change and achieves high power factor. The measured PF value is 0.982. Figure 10 shows the waveforms of switching signal VGS and the freewheeling diode current iD1. The switching frequency is presented as 100 kHz and the duty ratio D is 31%. The freewheel diode operates in CCM mode, which is exactly the same as the theoretical analysis. Figure 11 shows the waveforms of filter capacitor voltage VO and LED current IO. The filter capacitor voltage contains AC component with twice the line frequency, but the LED current is a pure DC current, thus it basically eliminates the LED flicker. Figure 12 shows a comparison of the system output current before and after the adoption of the magnetic integration technique. It can be seen that the system output current ripple is significantly reduced after adopting the integrated magnetic technology.
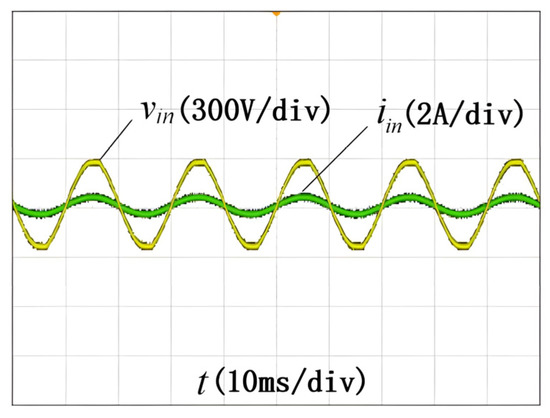
Figure 9.
Waveforms of vin and iin.
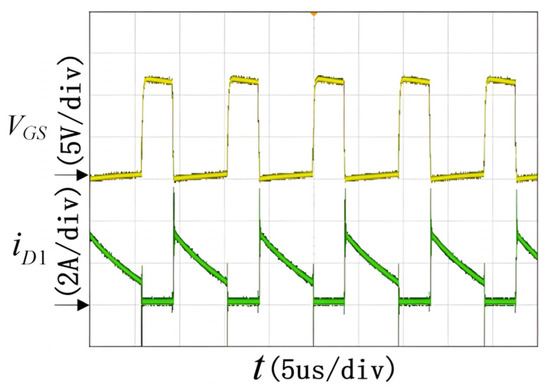
Figure 10.
Waveforms of VGS and iD1.
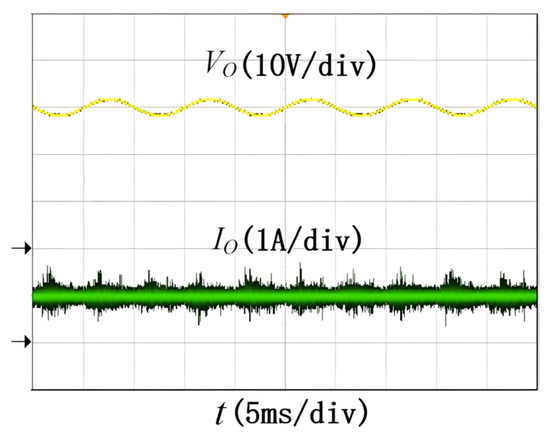
Figure 11.
Waveforms of filter capacitor voltage VO and LED current IO.
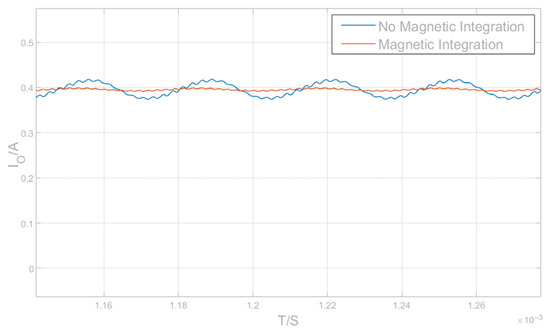
Figure 12.
Comparison of output current before and after adopting integrated magnetic technology.
Figure 13 shows the relationship between the PF value and the efficiency of the flicker-free LED driver with different input voltage, respectively. From Figure 13, it can be seen that the PF value is always above 0.95 and the maximum efficiency is 0.838 over the entire input voltage range. The difference between the theoretical prediction and the experimental results occurs mainly due to the efficiency of the converter, which varies according to the input voltage. Figure 14 illustrates the winding method of the coil and transformer to form an integrated magnetic element, and the pin-out figure of the element. Figure 15 shows the photo of the magnetic integrated inductance L1, L2 and transformer Tr. Figure 16 shows the system circuit diagram.
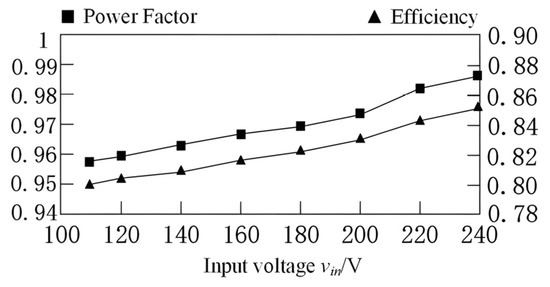
Figure 13.
PF and efficiency of the proposed LED driver.
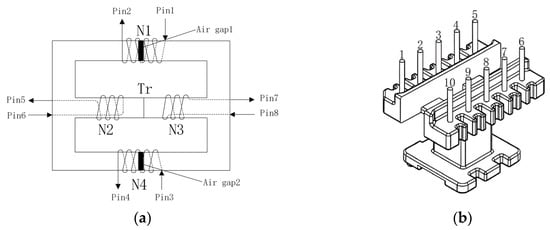
Figure 14.
(a) The winding method of the coil. (b) The pin-out figure of the element.
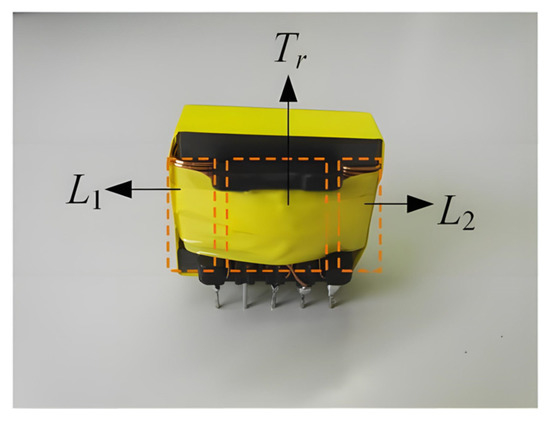
Figure 15.
Photo of the magnetic integrated inductance and transformer.
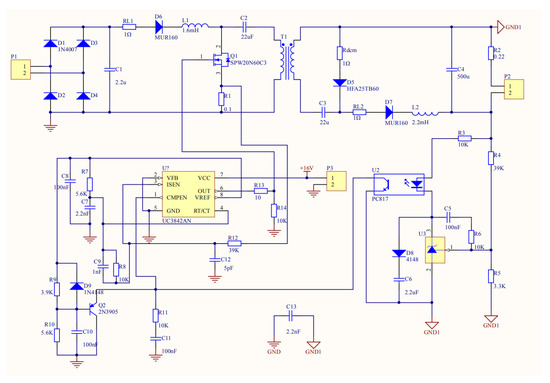
Figure 16.
System circuit diagram.
The LED driver proposed in this paper reduces the cost of the system mainly through the following two aspects. First, in terms of component selection, film capacitors or ceramic capacitors can be used instead of the commonly used filtering electrolytic capacitors, which not only improves the system operating performance, but also saves component turnover and reduces system maintenance costs. Second, most current pulsating current elimination methods need to rely on complex control loops or require the provision of additional DC power supplies, etc. These methods more or less enhance the cost of building LED drivers. This paper proposes to integrate two inductors and isolation transformers in one core, which can make the maximum working magnetic density of the integrated magnetic parts much smaller than the magnetic density of each discrete magnetic parts and thus achieve the purpose of reducing the cross-sectional area of the magnetic parts core and reducing the cost and volume of the magnetic parts. At the same time, this approach does not need to rely on the above-mentioned measures to enhance system cost to achieve zero current ripple.
The converter efficiency can be improved by means of improving the magnetic concentration elements. There are two main types of methods to improve the magnetic concentration element with the main purpose of improving efficiency. The first type is to cut the AC fluxes to each other in the common column, which largely reduces the alternating magnetic density and at the same time reduces the loss of the magnetic core. There are three main ways: (1) Changing the winding connection and changing the coupling of fluxes; (2) merging the windings according to the specific circuit; (3) splitting the windings with the source transfer equivalent transformation method. The second type is the mutual superposition of AC flux and DC flux, which can improve the core utilization.
6. Conclusions
This paper presents a 30 W flicker-free LED driver prototype that uses magnetic integration technique to eliminate stroboscopic effect in an isolated Cuk converter. The operation principle of Cuk converter with integrated magnetics is analyzed in detail using time domain analysis in electrical and magnetic circuits. The transfer function Gvd (s) is calculated and the Bode diagram is drawn. Based on simulation and experimental results, the flicker-free LED driver has a power factor of 0.982 and a maximum efficiency of 0.838 when the input voltage is 240 V and LED current is pure DC current. The proposed driver is small-sized and cost-effective due to the use of only one transformer core. Future research will focus on improving the efficiency by analyzing the loss distribution of the magnetic integrated LED driver and applying a soft switching circuit and improved magnetic integrated element.
Author Contributions
Conceptualization, Y.S. and J.X.; methodology, J.X.; software, C.C.; validation, J.X.; formal analysis, all authors; investigation, all authors; writing—original draft preparation, Y.S.; writing—review and editing, J.X. and C.C.; visualization, C.C.; project administration, Y.S. and J.X.; funding acquisition, Y.S. and J.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key R&D Program, grant number 2020YFB1711102.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicate.
Acknowledgments
The authors would like to thank all the anonymous reviewers for their insightful comments and constructive suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Liao, Z.; Ruan, X. Present status and developing trend of the semiconductor lighting. Trans. China Electrotech. Soc. 2006, 21, 106–111. [Google Scholar]
- Marty, C.; Howard, C.; Ken, M. Solid-state lighting: Rhe new normal in lighting. IEEE Trans. Ind. Appl. 2015, 51, 109–119. [Google Scholar]
- Sun, C.C.; Ma, S.H.; Nguyen, Q.K. Advanced LED Solid-state Lighting Optics. Crystals 2020, 10, 758. [Google Scholar] [CrossRef]
- Behzad, P.; Ehsan, A. Analysis of the integrated SEPIC-Flyback converter as a single stage single-switch power-factor-correction LED driver. IEEE Trans. Ind. Electron. 2016, 63, 3562–3570. [Google Scholar]
- Yan, T.; Xu, J.; Cao, T.; Zhou, G.; Gao, J. A flicker-free transformerless LED driving circuit based on quadratic Buck PFC converter. Trans. China Electrotech. Soc. 2015, 30, 512–519. [Google Scholar] [CrossRef]
- Soares, G.M.; Almeida, P.S.; Alonso, J.M.; Braga, H.A.C. Capacitance minimization in offline LED drivers using an active ripple compensation technique. IEEE Trans. Power Electron. 2017, 32, 3022–3033. [Google Scholar] [CrossRef]
- Peng, F.; Liu, Y.; Paresh, C. A flicker-free single-stage offline LED driver with high power factor. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 654–665. [Google Scholar] [CrossRef]
- Wilkins, A.; Veitch, J.; Lehman, B. LED lighting flicker and potential health concerns: IEEE standard PAR1789 updatep. IEEE Energy Convers. Congr. Expo. 2010, 171–178. [Google Scholar]
- Lehman, B.; Wilkins, A.J. Designing to mitigate effects of flicker in LED lighting: Redcuing risks to health and safety. IEEE Power Electron. Mag. 2014, 1, 18–26. [Google Scholar] [CrossRef]
- Wang, S.; Ruan, X.; Yao, K.; Tan, S.; Yang, Y.; Ye, Z. A flicker-free electrolytic capacitor-less AC-DC LED driver. IEEE Trans. Power Electron. 2012, 27, 4540–4548. [Google Scholar] [CrossRef]
- Udumula, R.; Beeramangalla, L. Single-stage electrolytic capacitor less non-inverting buck-boost PFC based AC-DC ripple free LED driver. IET Power Electron. 2017, 10, 38–46. [Google Scholar]
- Li, Y.; Chen, C. A novel primary-side regulation scheme for single-stage high-power-factor AC-DC LED driving circuit. IEEE Trans. Ind. Electron. 2013, 60, 4978–4986. [Google Scholar] [CrossRef]
- Tang, Z.; Wang, R.; Yang, X. Power supply driven by Cuk constant current with active ripple compensation for LED headlamp. J. S. China Univ. Technol. 2016, 44, 34–39. [Google Scholar]
- Wang, F.; Li, L.; Zhong, Y. An electrolytic capacitor-less LED driver with integrated dual flyback converter. IEEE Trans. Ind. Electron. 2017, 64, 5818–5827. [Google Scholar] [CrossRef]
- Lamar, D.G.; Sebastian, J.; Arias, M. On the limit of the output capacitor reduction in power-factor correctors by distorting the line input current. IEEE Trans. Power Electron. 2012, 27, 1168–1176. [Google Scholar] [CrossRef]
- Ma, H.; Zheng, C.; Yu, W.; Feng, Q. Electrolytic capacitor-less SEPIC-derived LED driver with valley fill cell. Electr. Mach. Control. 2012, 16, 13–20. [Google Scholar]
- Sun, L.; Han, Y. A Capacitorless and Low-optical-flicker AC Direct LED Driving IC and System Applied to Street Lighting. IEEE Trans. Electr. Electron. Eng. 2021, 16, 1013–1024. [Google Scholar] [CrossRef]
- Salazar-Perez, D.; Ponce-Silva, M.; Alonso, J.M.; Aqui-Tapia, J.A.; Cortes-Garcia, C. A Novel High-Power-Factor Electrolytic-Capacitor-Less LED Driver Based on Ripple Port. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 6248–6258. [Google Scholar] [CrossRef]
- Chen, Q.; Feng, Y.; Zhou, L.; Wang, J.; Ruan, X. Active forward converter with integrated magnetics and the minimum output ripple current. Proc. CSEE 2009, 29, 7–13. [Google Scholar]
- Khan, A.A.; Cha, H.; Kim, H.G. Magnetic Integration of discrete Coupled Inductors in Single-Phase Direct PWM AC-AC Converter. IEEE Trans. Power Electron. 2016, 31, 2129–2138. [Google Scholar] [CrossRef]
- Han, B.; Lee, J.S.; Kim, M. Repetitive controller with phase-lead compensation for Cuk CCM inverter. IEEE Trans. Ind. Electron. 2016, 65, 2356–2367. [Google Scholar] [CrossRef]
- Lam, J.; El-Taweel, N.; Abbasi, M. An output- current-dependent DC-link energy regulation scheme for a family of soft-switched AC/DC offline LED drivers without electrolytic capacitors. IEEE Trans. Ind. Electron. 2017, 64, 5838–5850. [Google Scholar] [CrossRef]
- Nabinejad, A.; Rajaei, A.; Mardaneh, M. A Systematic Approach to Extract State-Space Averaged Equations and Small-Signal Model of Partial-Power Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 2475–2483. [Google Scholar] [CrossRef]
- Chen, Q.; Ruan, X.; Yang, Y. The application of the magnetic-integration techniques in switching power supply. Trans. China Electrotech. Soc. 2004, 19, 1–8. [Google Scholar]
- Liu, Y.; Jiang, S.; Liang, W.; Wang, H.; Peng, J. Modeling and Design of the Magnetic Integration of Single- and Multi-stage EMI Filters. IEEE Trans. Power Electron. 2020, 35, 276–288. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).