PLUG: A City-Friendly Navigation Model for Electric Vehicles with Power Load Balancing upon the Grid
Abstract
:1. Introduction
2. Problem Statement
2.1. Problem
2.2. Pricing Policies
2.3. Paper Contribution
- Load awareness: The model is responsible for keeping up with the dynamic load changes in the city’s energy grids, and accordingly, it nominates those routes that help keep the grids’ load balanced.
- Incentive driven: The model adopts the RTP dynamic pricing mechanism that motivates choosing load-balancing routes by offering lower price units for the charging services over such nominated routes.
- Dynamically adaptive: The model’s routing process is adaptive to any dynamic updates happening at the nominated routes and their charging stations. It also adapts to the real-time status of the EV’s battery, and its driving mode changes.
- Shortest: In addition to choosing the load-balancing grid zone, it runs the Dijkstra Algorithm to find the shortest load-balanced routes that pass through those nominated less-loaded city zones.
- Autonomous: The model runs a navigation process for each EV in a way that matches its make, its model, the battery’s SoH, and the route preferences set by the driver via a weighted preference function.
- Cognitive: Where its chosen routes may differ from one EV to another, even for the same EV profile and trip coordinates, routes may vary according to the chosen driving preferences, time, and weather conditions.
3. Related Work
4. Problem Formulation
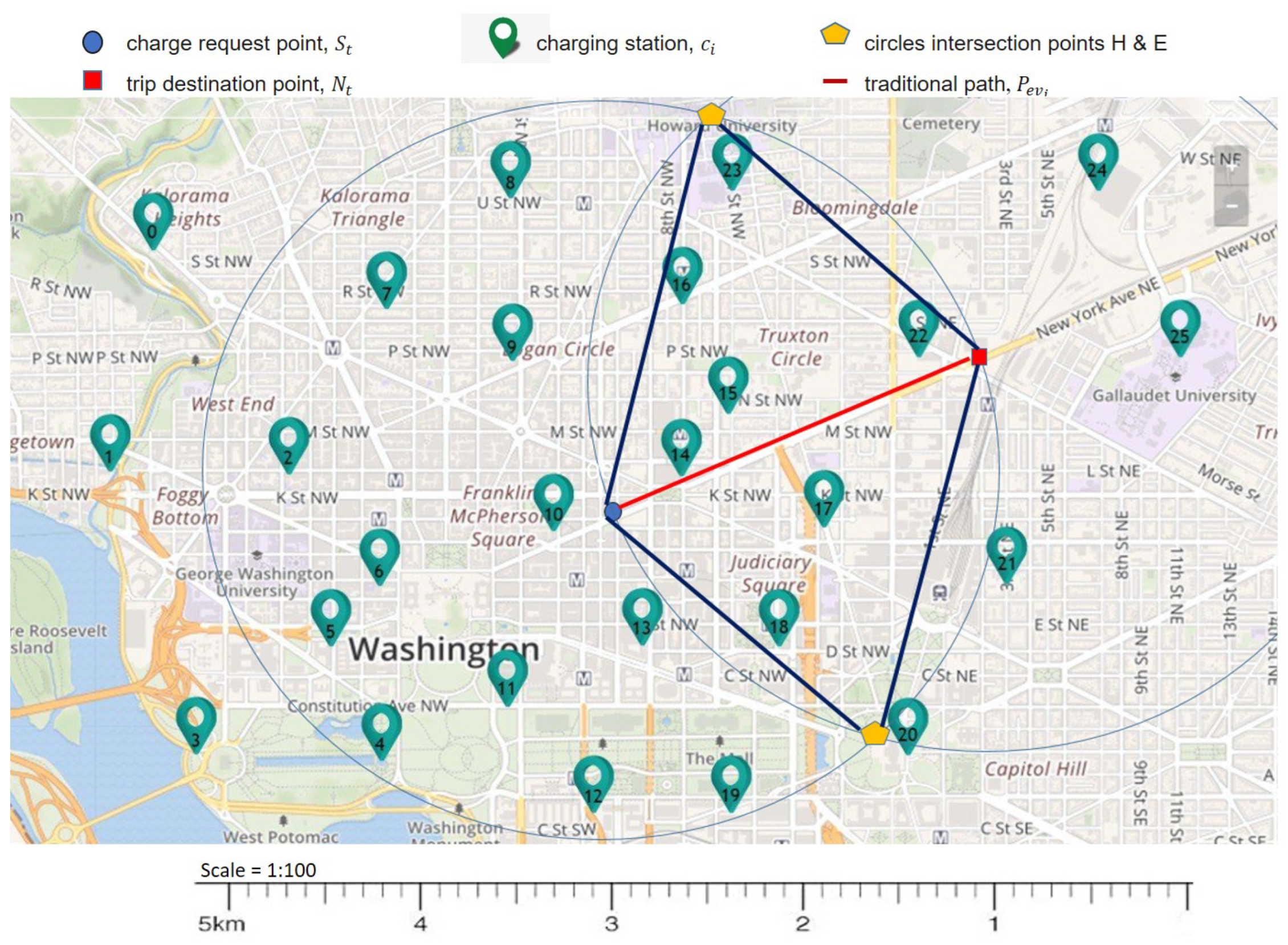
4.1. Benchmark Model
- Why did the model choose point S and the trip destination point P as a reference to create the charging area? What if we choose another reference point?
- How does the model guarantee the match state for those charging points located within the predefined search area? In other words, on which basis do we define a charging point as being addeda candidate charging point for an EV request or not?
- EVs come with different battery ranges and SoH values, so, has this been taken into account? A route that may suit an EV may not quite suit another.
- Does the model provide any guarantees that the chosen routes are the shortest navigation routes?
4.2. Shortest-Route, EV-Oriented Routing Model
4.2.1. Shortest-Route Navigation Methodology
| Algorithm 1 Shortest-route load-oblivious routing algorithm |
| 1: input: The model reads the EV make and model , its SoH, and the trip’s and points, |
| 2: the current driving mode of the vehicle , |
| 3: the battery charge status , |
| 4: the power consumption rate of the vehicle in , |
| 5: for each EV type , and the threshold value set by ; |
| 6: Find the range threshold value , and accordingly: from the point S, find the location of point J, |
| 7: Calculate the distance D, from the point S to point J; |
| 8: run the navigation model, list candidate charging points in L, and then |
| 9: while the list L is not empty, and there is at least a that is compatible with , then do; |
| 10: From the source , ∀ ∈ L, find the distances to all points, and accordingly: |
| 11: sort list L in an descending order, update L, |
| 12: select with the longest distance from , and accordingly, update the route in the navigation system, |
| 13: else; |
| 14: choose the next shortest route towards , |
| 15: find a new list L, |
| 16: get back to line 8 again, |
| 17: being charged in ; start from line 1 again. |
| 18: end |
4.2.2. Load-Oblivious Routing
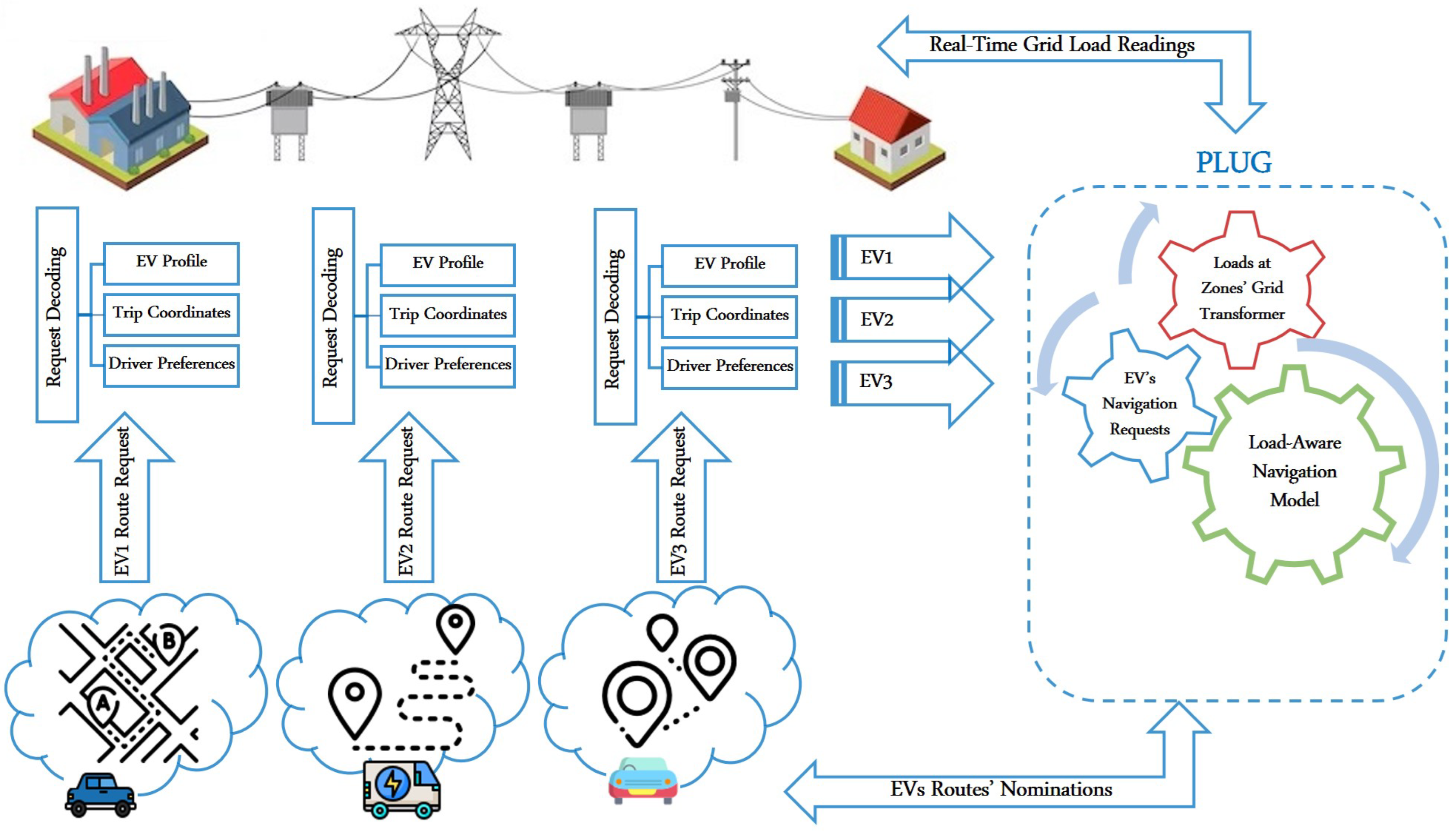
4.3. PLUG: A Load-Aware Shortest-Route Navigation
4.3.1. Communication Infrastructure Requirements
Model’s Requirement from EVs
Model’s Requirement from Charging Stations
4.3.2. Model’s Constraints
Trip’s Charge Requirements
Charge Points Distances
Charge Points Types
Complete Routes Only
Single Route Assignment Only
4.3.3. PLUG Load-Aware Shortest-Route Navigation Algorithm
| Algorithm 2 PLUG model: load-aware shortest-route navigation algorithm |
| 1: Input: PLUG model reads EV’s profile , trip , and finds: |
| 2: source and destination points (, ), |
| 3: EV battery charge status , |
| 4: EV power consumption rate , |
| 5: EV range threshold value , |
| 6: EV driver preference values: (, , ), |
| 7: read real-time grid’s loads of the city zones transformers, |
| 8: for points of (, and ), run Dijkstra, then: |
| 9: list the candidate routes in , and check for: |
| 10: One: no-charge requirement routes, |
| 11: update , |
| 12: Two: charge-points distance compatibility, |
| 13: update , |
| 14: Three: charge-points type compatibility, |
| 15: update to , |
| 16: Four: complete routes to , |
| 17: update to , |
| 18: Five: no duplicate routes for the same trip , |
| 19: for each route in , do: |
| 20: find the trip distance, , of the whole route, |
| 21: find the trip time, , of the whole route, |
| 23: update , |
| 24: define the charging points used by the whole route, and then, |
| 25: locate their city zones, and get their real-time price units, then, |
| 26: calculate the route’s charge service costs, , |
| 27: update , |
| 28: for each candidate route in : |
| 29: calculate the route’s weight value, |
| 30: update , |
| 31: sort the routes in in a descending according to their weight values, |
| 32: choose the first route in the list, |
| 33: add the expected charge loads to the nominated route’s charging stations, |
| 34: Start navigation, |
| 35: end |
5. Simulation Results
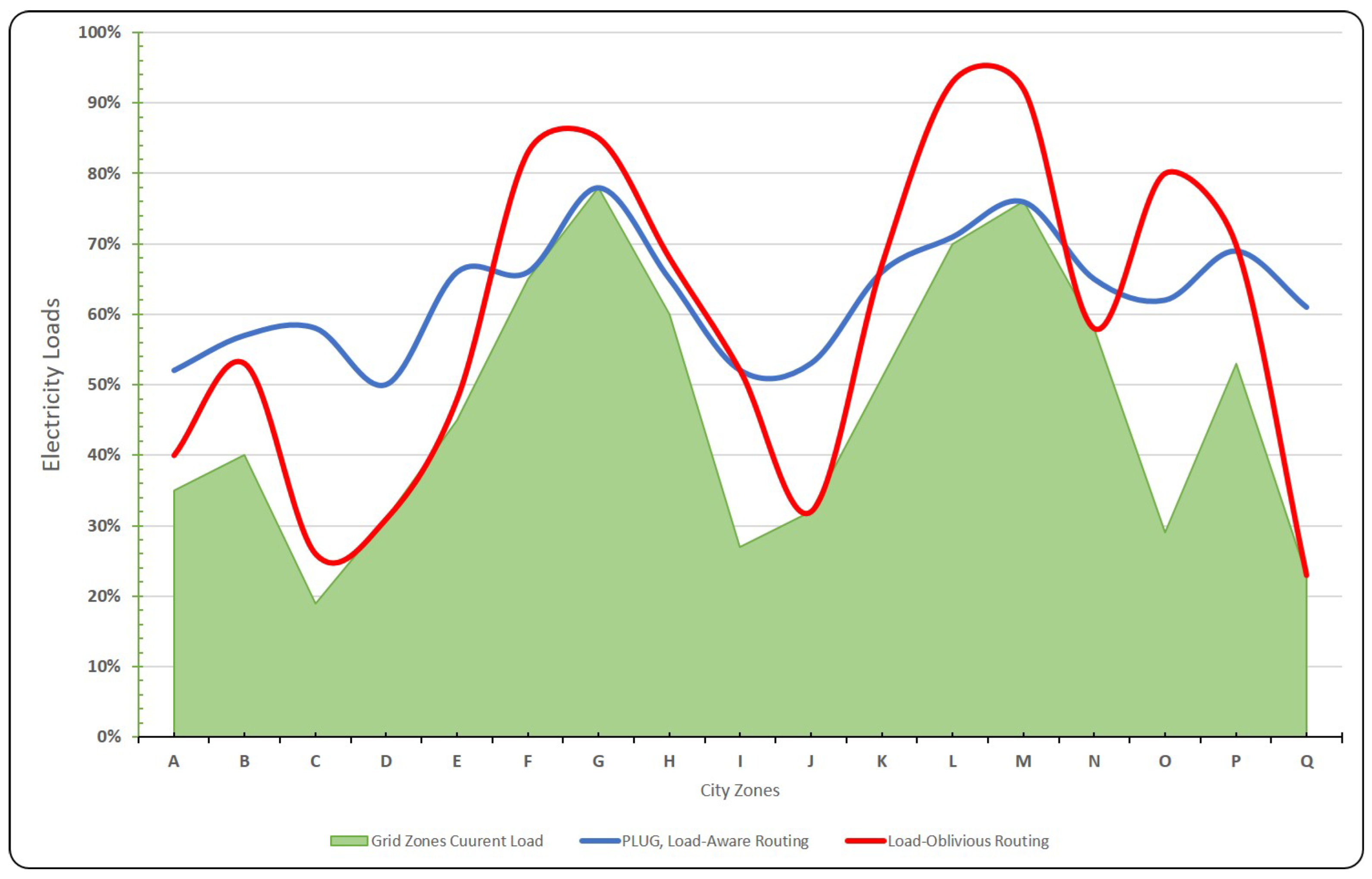
5.1. Discussion
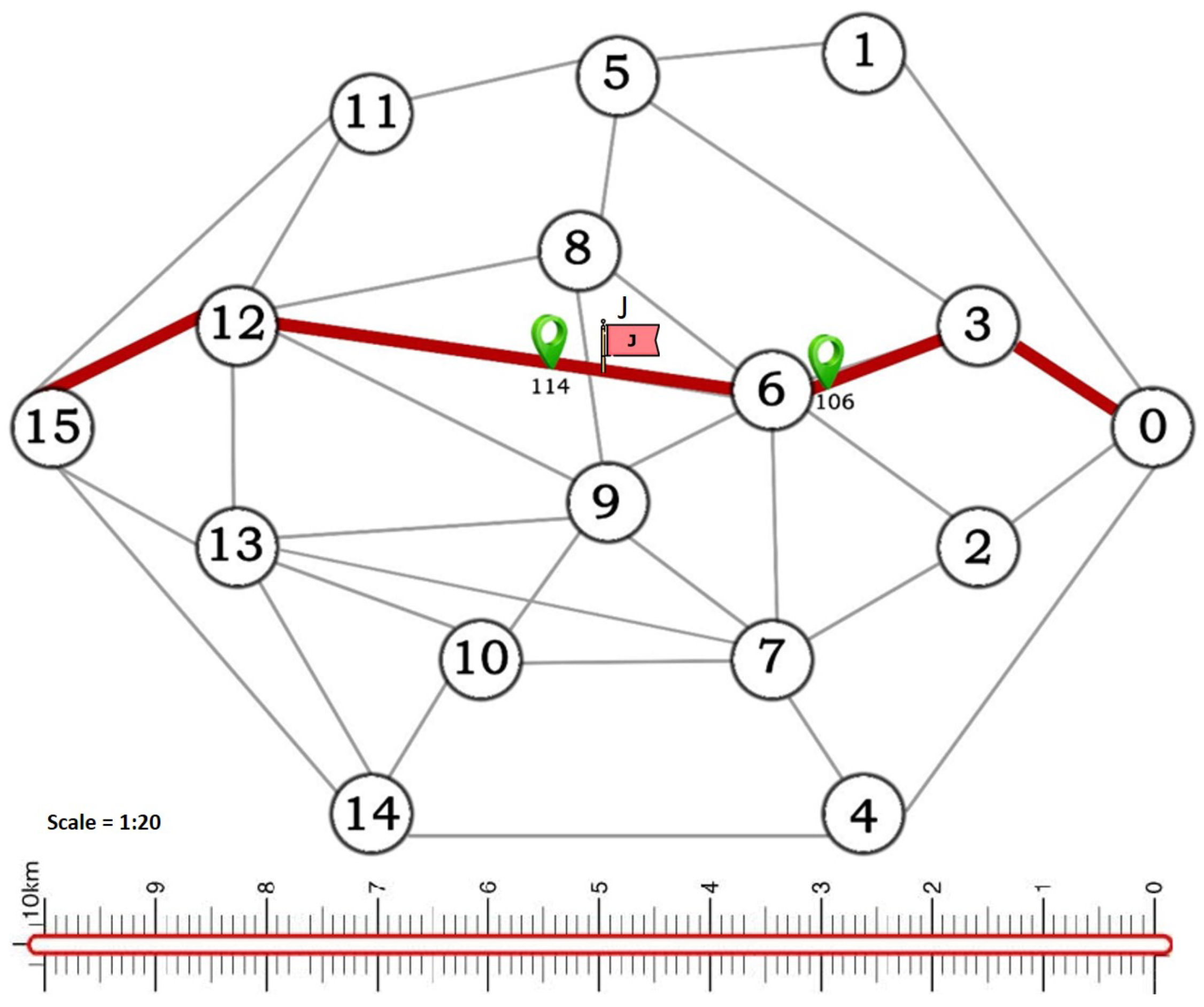
5.2. Load-Balanced Power Grid Zones
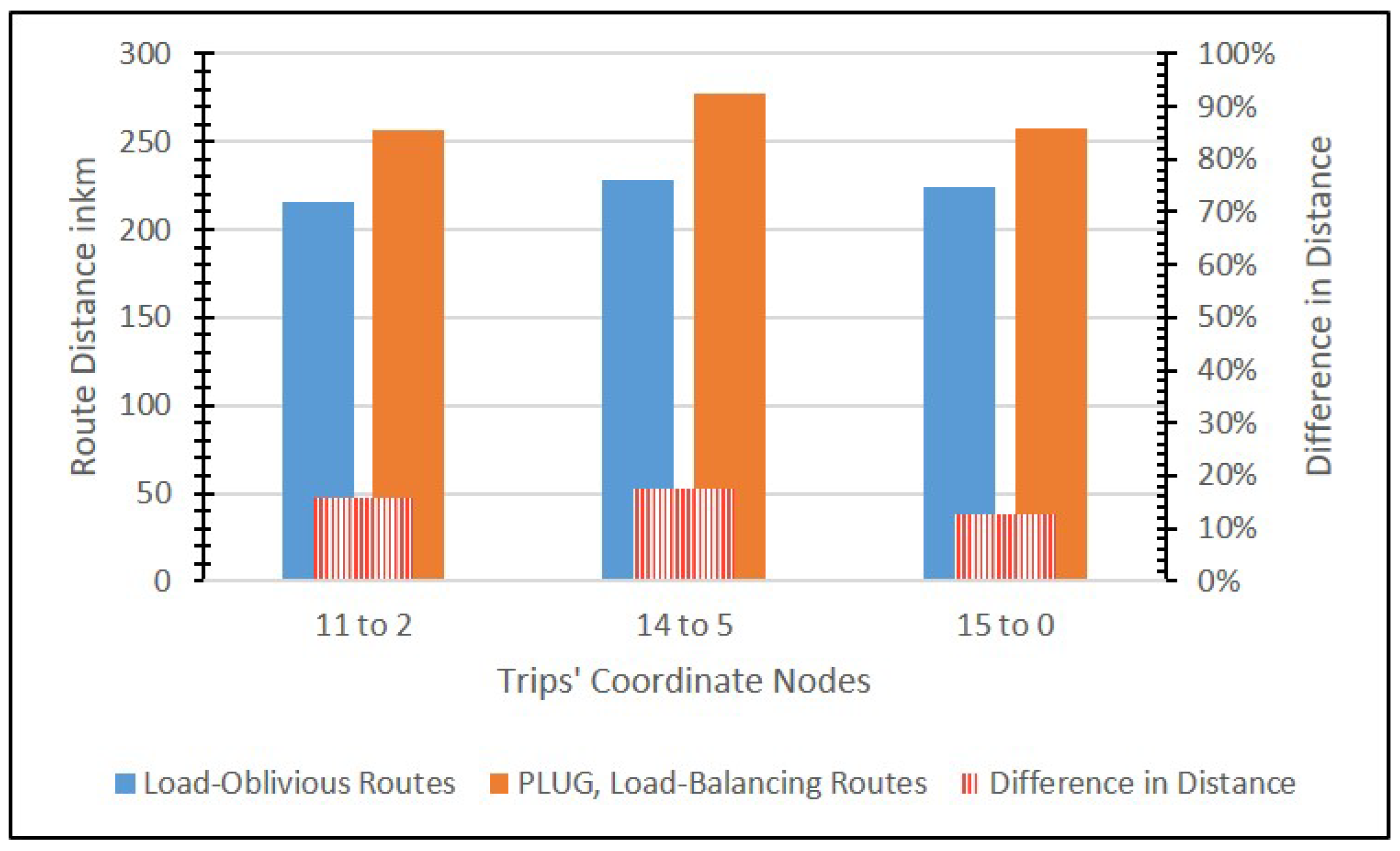
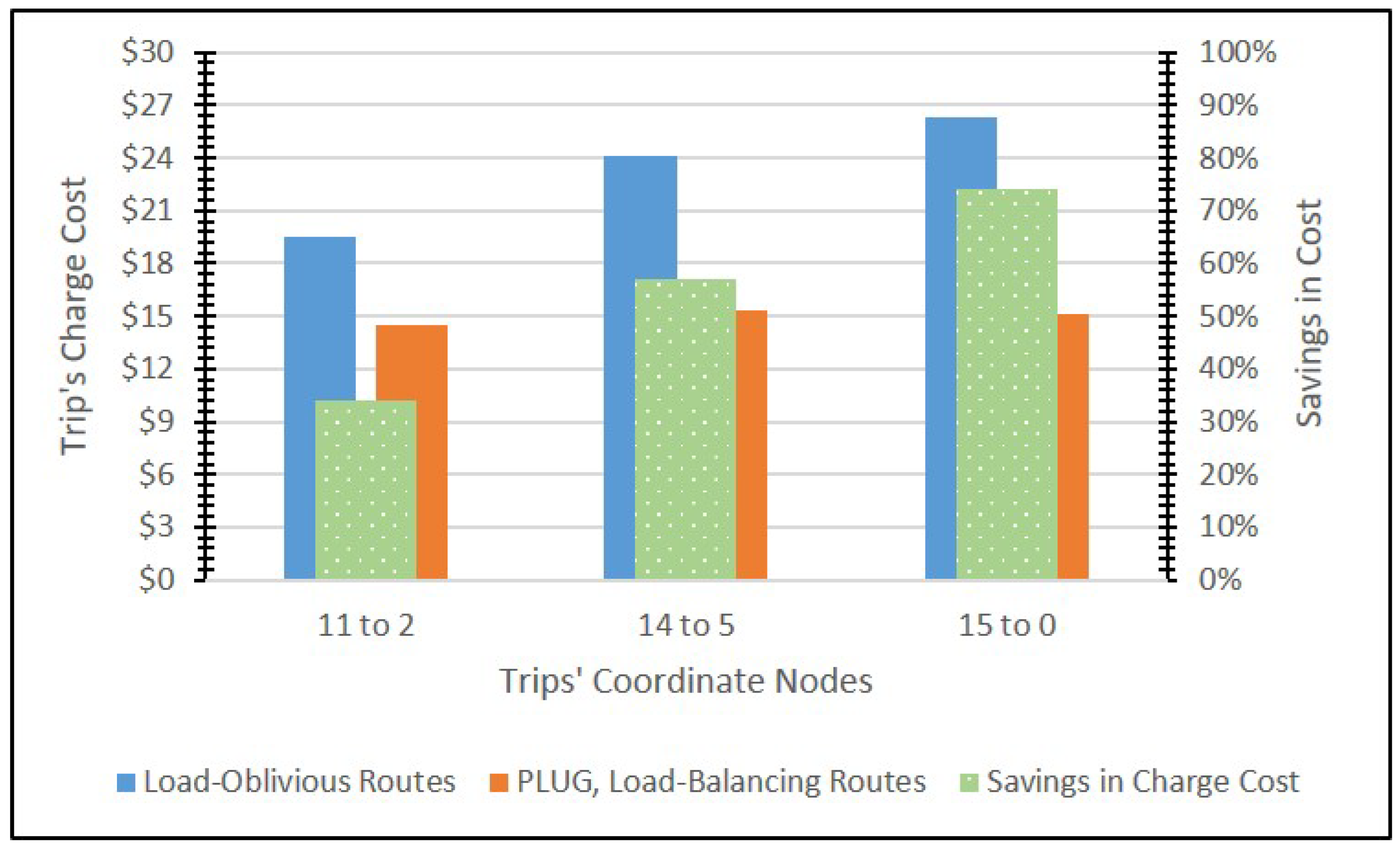
5.3. Route Samples
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.; Bi, J.; Lu, C.; Ding, C. Route Guidance Strategies for Electric Vehicles by Considering Stochastic Charging Demands in a Time-Varying Road Network. Energies 2020, 13, 2287. [Google Scholar] [CrossRef]
- Bonges, H.A.; Lusk, A.C. Addressing electric vehicle (EV) sales and range anxiety through parking layout, policy and regulation. Transp. Res. Part A Policy Pract. 2016, 83, 63–73. [Google Scholar] [CrossRef]
- Guo, F.; Yang, J.; Lu, J. The battery charging station location problem: Impact of users’ range anxiety and distance convenience. Transp. Res. Part A Policy Pract. 2018, 114, 1–18. [Google Scholar] [CrossRef]
- Lin, Z.P.; Wang, H.S.; Tsai, A.J. The Intelligent Charging Path Planning for Electric Vehicle. Int. J. Comput. Netw. Wirel. Mob. Commun. 2016, 6, 1–8. [Google Scholar]
- Amin, A.; Tareen, W.U.K.; Usman, M.; Ali, H.; Bari, I.; Horan, B.; Mekhilef, S.; Asif, M.; Ahmed, S.; Mahmood, A. A Review of Optimal Charging Strategy for Electric Vehicles under Dynamic Pricing Schemes in the Distribution Charging Network. Sustainability 2020, 12, 10160. [Google Scholar] [CrossRef]
- Siano, P. Demand response and smart grids—A survey. Renew. Sustain. Energy Rev. 2014, 30, 461–478. [Google Scholar] [CrossRef]
- Tan, J.; Wang, L. Real-time charging navigation of electric vehicles: A non-cooperative game approach. In Proceedings of the 2015 IEEE Power and Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015. [Google Scholar]
- Dutta, G.; Mitra, K. A literature review on dynamic pricing of electricity. J. Oper. Res. Soc. 2017, 68, 1131–1145. [Google Scholar] [CrossRef]
- Korolko, N.; Sahinoglu, Z. Robust Optimization of EV Charging Schedules in Unregulated Electricity Markets. IEEE Trans. Smart Grid 2017, 8, 149–157. [Google Scholar] [CrossRef]
- Latinopoulos, C.; Sivakumar, A.; Polak, J.W. Response of electric vehicle drivers to dynamic pricing of parking and charging services: Risky choice in early reservations. Transp. Res. Part C Emerg. Technol. 2017, 80, 175–189. [Google Scholar] [CrossRef]
- Bitencourt, L.A.; Bruno, S.B.; Renan, S.M.; Marcio, Z.F.; Ferreira, V.H. Optimal EV charging and discharging control considering dynamic pricing. In Proceedings of the 2017 IEEE Manchester PowerTech, Manchester, UK, 18–22 June 2017; pp. 1–6. [Google Scholar]
- Yin, Y.; Zhou, M.; Li, G. Dynamic decision model of critical peak pricing considering electric vehicles’ charging load. In Proceedings of the International Conference on Renewable Power Generation (RPG 2015), Beijing, China, 17–18 October 2015. [Google Scholar]
- Mohajeryami, S.; Schwarz, P.; Baboli, P.T. Including the behavioural aspects of customers in demand response model: Real time pricing versus peak time rebate. In Proceedings of the 2015 North American Power Symposium (NAPS), Charlotte, NC, USA, 4–6 October 2015. [Google Scholar]
- Abushnaf, J.; Rassau, A.; Górnisiewicz, W. Impact of dynamic energy pricing schemes on a novel multi-user home energy management system. Electr. Power Syst. Res. 2015, 125, 124–132. [Google Scholar] [CrossRef]
- Quttoum, A.N. AARM: An Autonomous Adaptive Routing Model for Electric-Vehicles. Procedia Comput. Sci. 2022, 210, 28–35. [Google Scholar] [CrossRef]
- Jeroen, S.; John, S.D. Transition Challenges for Alternative Fuel Vehicle and Transportation Systems. Environ. Plan. B Plan. Des. 2008, 35, 1070–1097. [Google Scholar]
- Schneider, M.; Stenger, A.; Goeke, D. The Electric Vehicle-Routing Problem with Time Windows and Recharging Stations. Transp. Sci. 2014, 48, 500–520. [Google Scholar] [CrossRef]
- Erdogan, S.; Hooks, E.M. A Green Vehicle Routing Problem. Transp. Res. Part E Logist. Transp. Rev. 2012, 48, 100–114. [Google Scholar] [CrossRef]
- Conrad, R.G.; Figliozzi, M.A. The Recharging Vehicle Routing Problem. In Proceedings of the 2011 Industrial Engineering Research Conference, Kuala Lumpur, Malaysia, 22–24 January 2011. [Google Scholar]
- He, F.; Yin, Y.; Lawphongpanich, S. Network equilibrium models with battery electric vehicles. Transp. Res. Part B Methodol. 2014, 67, 306–319. [Google Scholar] [CrossRef]
- Manshadi, S.; Mohammad, K.; AbdElghany, K.; Uster, H. Wireless Charging of Electric Vehicles in Electricity and Transportation Networks. IEEE Trans. Smart Grid 2018, 9, 4503–4512. [Google Scholar] [CrossRef]
- Yang, Z.; Huang, H.; Lin, F. Sustainable Electric Vehicle Batteries for a Sustainable World: Perspectives on Battery Cathodes, Environment, Supply Chain, Manufacturing, Life Cycle, and Policy. Adv. Energy Mater. 2022, 12, 2200383. [Google Scholar] [CrossRef]
- Zhang, L.; Gao, T.; Cai, G.; Hai, K.L. Research on electric vehicle charging safety warning model based on back propagation neural network optimized by improved gray wolf algorithm. Energy Storage 2022, 49, 104092. [Google Scholar] [CrossRef]
- Li, S.; Tong, L.; Xing, J.; Zhou, Y. The Market for Electric Vehicles: Indirect Network Effects and Policy Design. J. Assoc. Environ. Resour. Econ. 2017, 4, 89–133. [Google Scholar] [CrossRef]
- Mahardhika, S.P.; Putriani, O. A Review of Artificial Intelligence-Enabled Electric Vehicles in Traffic Congestion Management. In Proceedings of the First International Conference on Sustainable Engineering Development and Technological Innovation, ICSEDTI 2022, Tanjungpinang, Indonesia, 11–13 October 2022; European Alliance for Innovation: Bratislava, Slovakia, 2023. [Google Scholar]
- Hariri, A.O.; Esfahani, M.; Mohammed, O. A Cognitive Price-Based Approach for Real-time Management of En-route Electric Vehicles. In Proceedings of the 2018 IEEE Transportation Electrification Conference and Expo (ITEC), Long Beach, CA, USA, 13–15 June 2020. [Google Scholar]
- Etesami, S.; Saad, W.; Mandavam, N.; Poor, H. Smart Routing of Electric Vehicles for Load Balancing in Smart Grids. Automatica 2020, 120, 109148. [Google Scholar] [CrossRef]
- Cai, J.; Chen, D.; Jiang, S.; Pan, W. Dynamic-Area-Based Shortest-Path Algorithm for Intelligent Charging Guidance of Electric Vehicles. Sustainability 2020, 12, 7343. [Google Scholar] [CrossRef]
- Haider, Z.M.; Mehmood, K.K.; Khan, S.U.; Khan, M.O.; Wadood, A.; Rhee, S.-B. Optimal Management of a Distribution Feeder During Contingency and Overload Conditions by Harnessing the Flexibility of Smart Loads. IEEE Access 2021, 9, 40124–40139. [Google Scholar] [CrossRef]
- Xu, P.; Li, J.; Sun, X.; Zheng, W.; Liu, H. Dynamic Pricing at Electric Vehicle Charging Stations for Queueing Delay Reduction. In Proceedings of the 2017 IEEE 37th International Conference on Distributed Computing Systems (ICDCS), Atlanta, GA, USA, 5–8 August 2017; pp. 2565–2566. [Google Scholar]
- Mohsenian-Rad, A.H.; Leon-Garcia, A. Optimal Residential Load Control With Price Prediction in Real-Time Electricity Pricing Environments. IEEE Trans. Smart Grid 2010, 1, 120–133. [Google Scholar] [CrossRef]

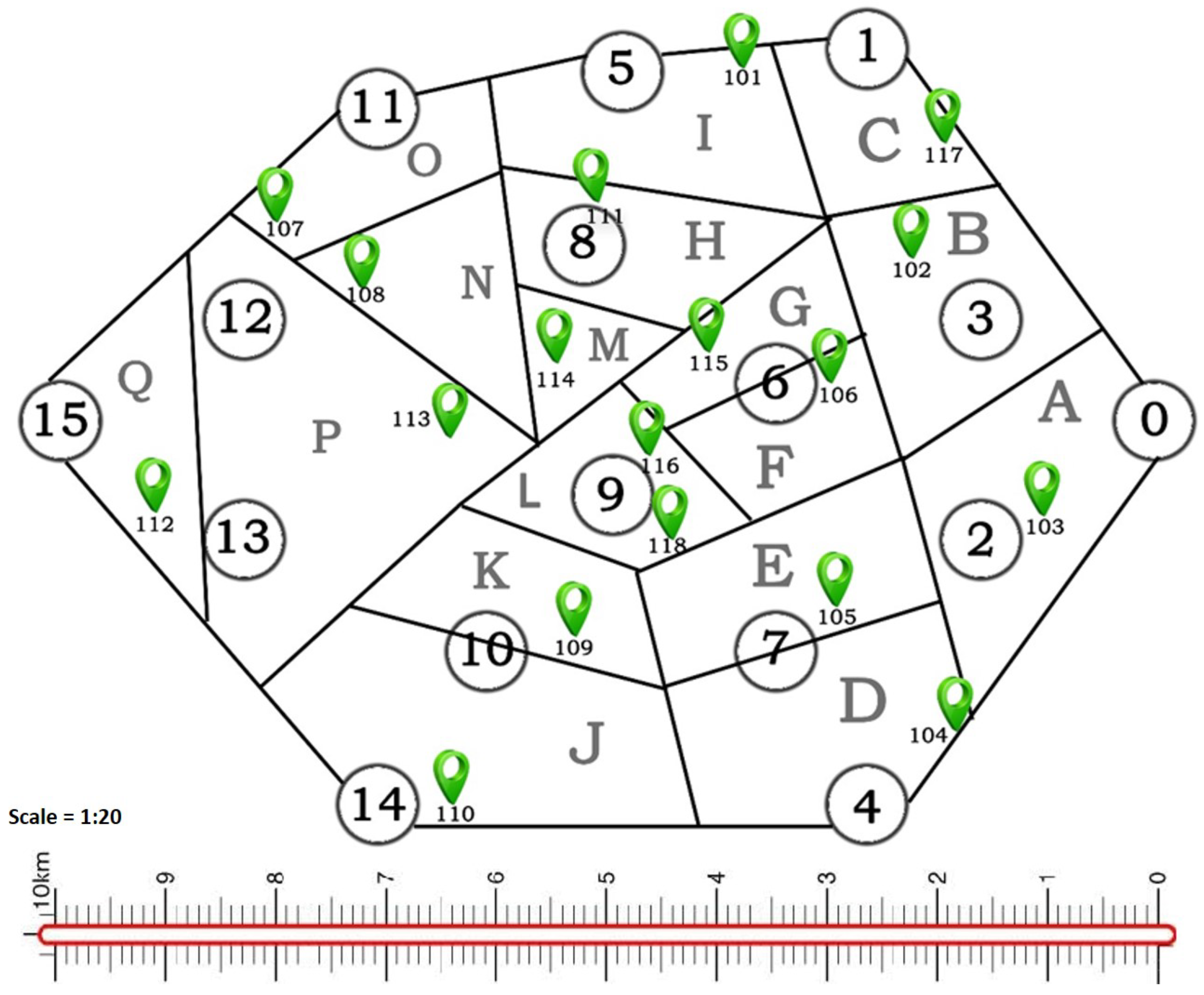
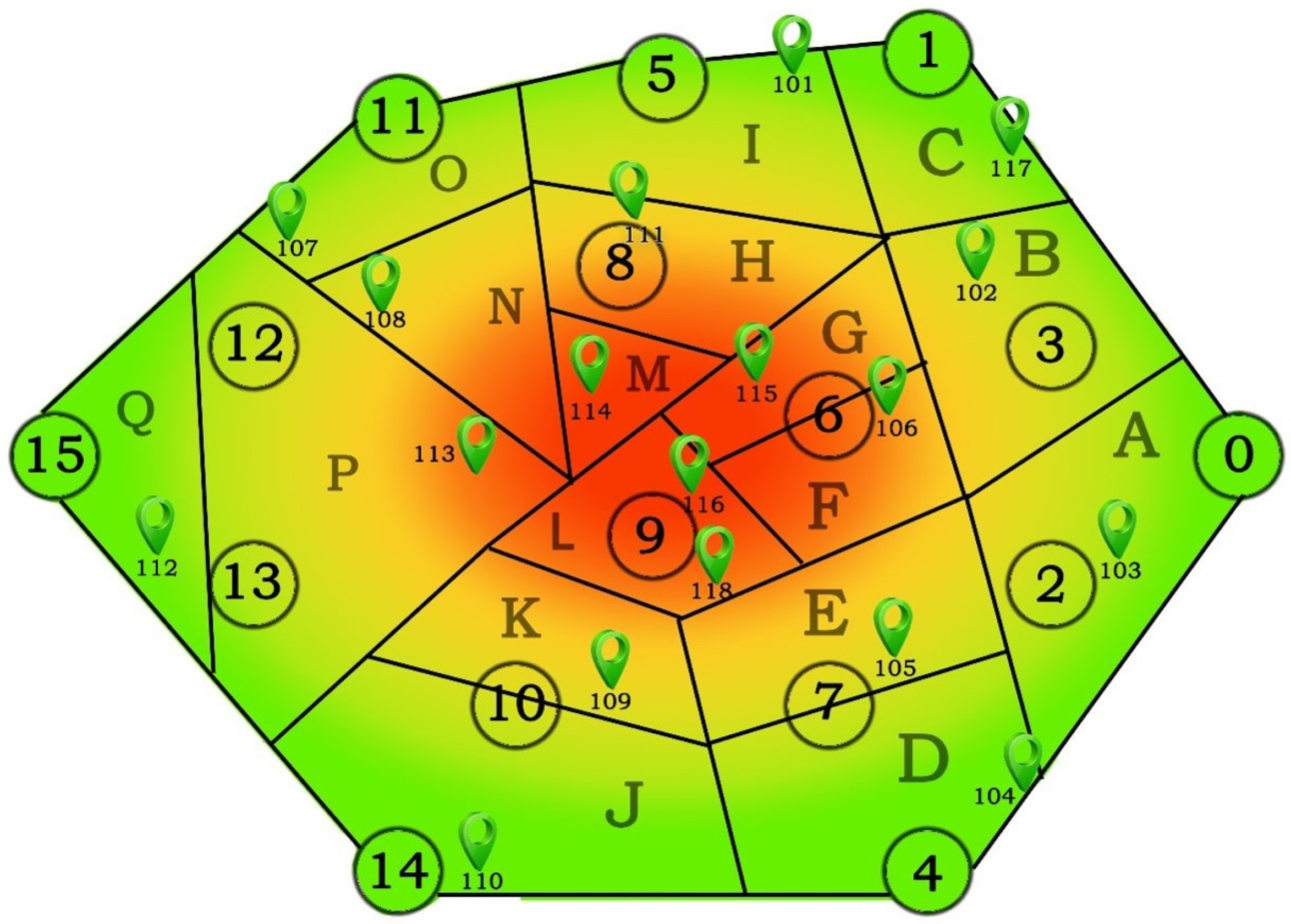



| Zone Name | Charging Station No. | Consumption Ratio | Availability Ratio | Corresponding Dynamic Price Unit |
|---|---|---|---|---|
| A | 103 | 40% | 60% | $0.36 |
| B | 102 | 45% | 55% | $0.42 |
| C | 117 | 20% | 80% | $0.16 |
| D | 104 | 35% | 65% | $0.33 |
| E | 105 | 52% | 48% | $0.48 |
| F | 106 | 75% | 25% | $0.78 |
| G | 115 | 88% | 12% | $0.94 |
| H | 111 | 70% | 30% | $0.69 |
| I | 101 | 30% | 70% | $0.27 |
| J | 110 | 35% | 65% | $0.33 |
| K | 109 | 57% | 43% | $0.54 |
| L | 116, 118 | 82% | 18% | $0.86 |
| M | 114 | 87% | 13% | $0.90 |
| N | 108 | 66% | 34% | $0.64 |
| O | 107 | 32% | 68% | $0.30 |
| P | 113 | 61% | 39% | $0.57 |
| Q | 112 | 25% | 75% | $0.24 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quttoum, A.N.; Alsarhan, A.; Aljaidi, M.; Alshammari, M. PLUG: A City-Friendly Navigation Model for Electric Vehicles with Power Load Balancing upon the Grid. World Electr. Veh. J. 2023, 14, 338. https://doi.org/10.3390/wevj14120338
Quttoum AN, Alsarhan A, Aljaidi M, Alshammari M. PLUG: A City-Friendly Navigation Model for Electric Vehicles with Power Load Balancing upon the Grid. World Electric Vehicle Journal. 2023; 14(12):338. https://doi.org/10.3390/wevj14120338
Chicago/Turabian StyleQuttoum, Ahmad Nahar, Ayoub Alsarhan, Mohammad Aljaidi, and Mohammed Alshammari. 2023. "PLUG: A City-Friendly Navigation Model for Electric Vehicles with Power Load Balancing upon the Grid" World Electric Vehicle Journal 14, no. 12: 338. https://doi.org/10.3390/wevj14120338
APA StyleQuttoum, A. N., Alsarhan, A., Aljaidi, M., & Alshammari, M. (2023). PLUG: A City-Friendly Navigation Model for Electric Vehicles with Power Load Balancing upon the Grid. World Electric Vehicle Journal, 14(12), 338. https://doi.org/10.3390/wevj14120338







