Integrated DC/DC Converter Topology Study for Fuel Cell Hybrid Vehicles with Two Energy Sources
Abstract
1. Introduction
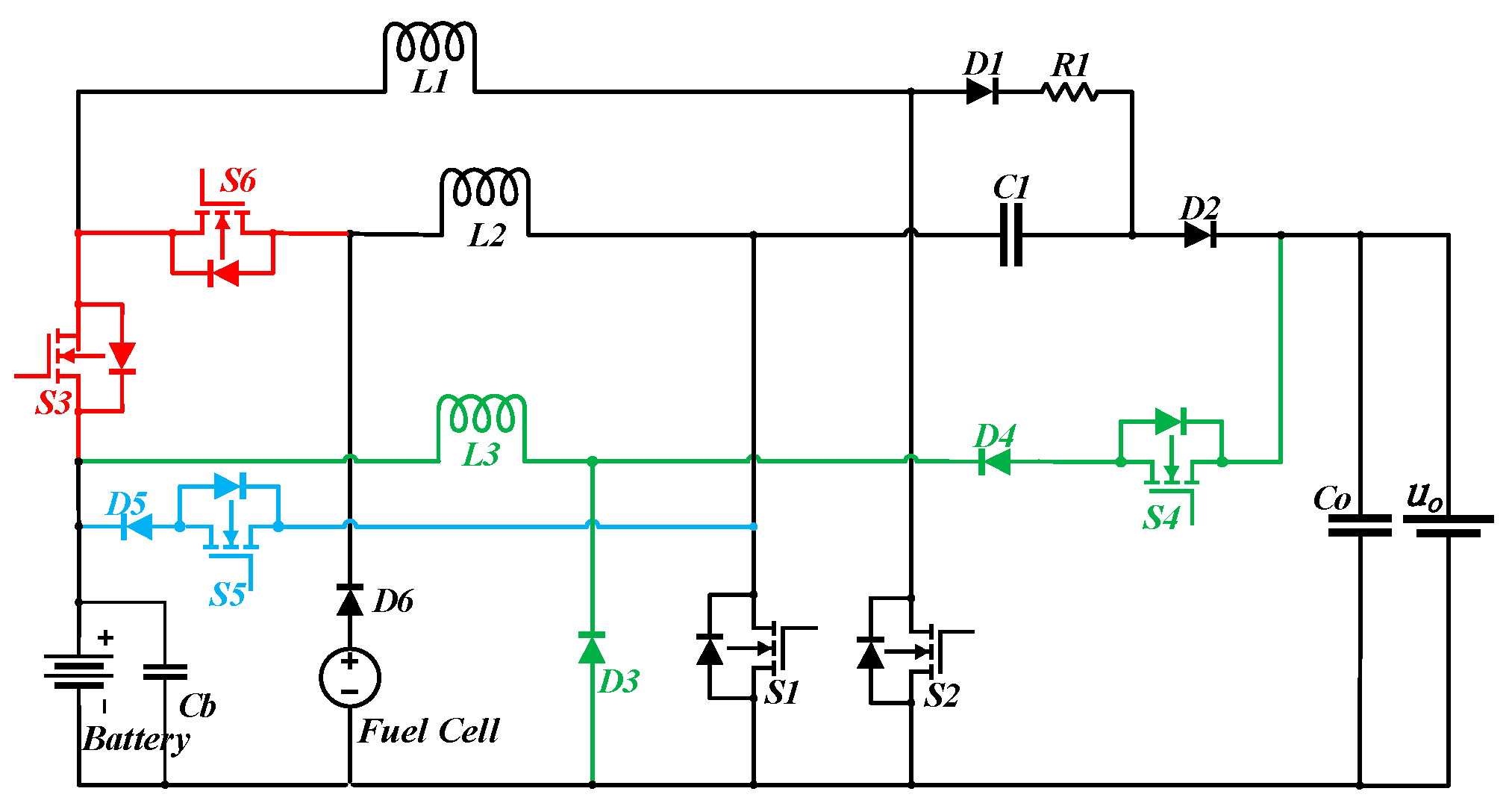
2. Improved Converter Topological Structure and Operating Principle
2.1. Topological Structure
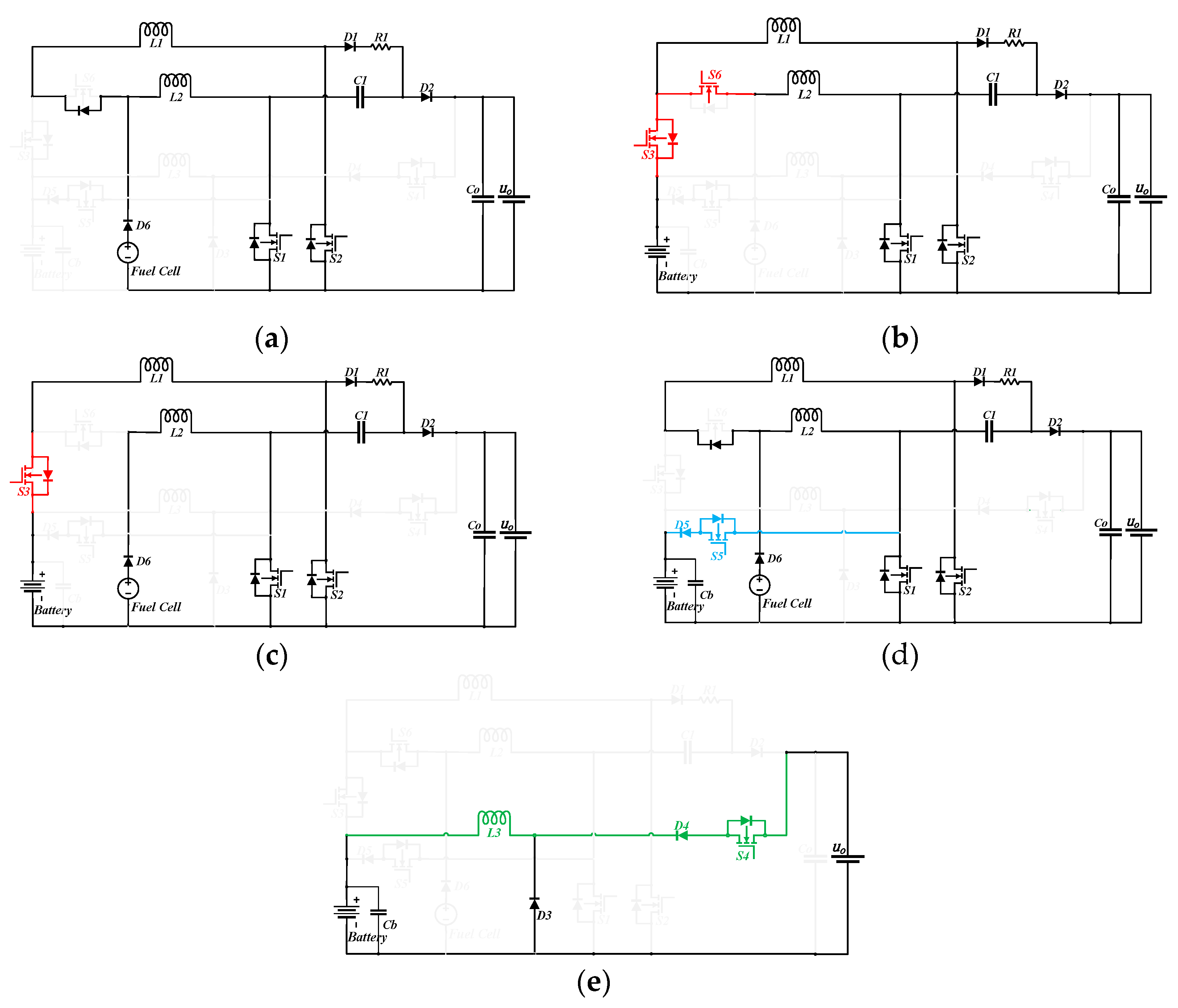
2.2. Operating Principle
- State 1:
- Mode 1:
- Mode 2:
- Mode 3:
- 2.
- State 2:
- 3.
- State 3:
- Mode 1:
- Mode 2:
- Mode 3:
- Mode 4:
- 4.
- State 4:
- Mode 1:
- Mode 2:
- Mode 3:
- 5.
- State 5:
- Mode 1:
- Mode 2:
3. Steady-State Analysis
3.1. Topology-Gain Analysis
3.1.1. State 1
3.1.2. State 2
3.1.3. State 3
3.1.4. State 4
3.1.5. State 5
3.2. Switching Capacitor Charge/Discharge Characteristics Analysis
3.3. Voltage and Current Analysis
- The average current of inductors is equal at state 1 and state 2, and the sum of the two is equal to the input current Iin. The system does not carry out power distribution at this time, thus:where Iin can be the input current of the fuel cell or battery, and D is the duty cycle of switches S1 and S2.
- Similarly, IL1 and IL2 are equal to the battery input current Ib and fuel cell input current Ifc, respectively, at state 3, so:or
- As mentioned before, the average current IL1 and IL2 is equal to the fuel cell input current Ifc1 and Ifc2 at state 4, so:
- When braking feedback, the average current IL3 of inductor IL3 is equal to the output current Ib, thus we can obtain:where ILoad is the braking feedback current.
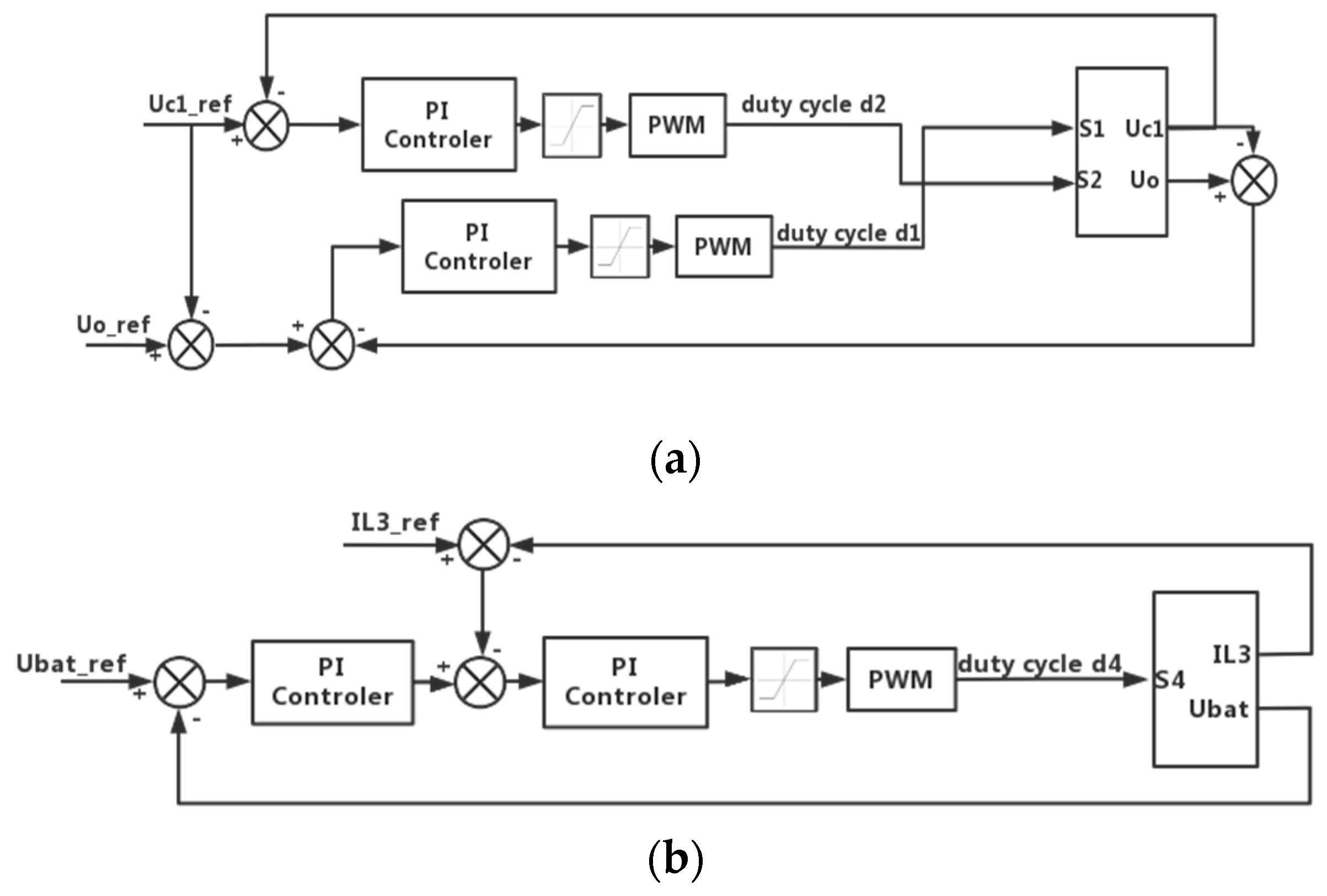
4. Topology Dynamic Modeling and Controller Solutions
5. Comparative Analysis of Related Converter Topologies
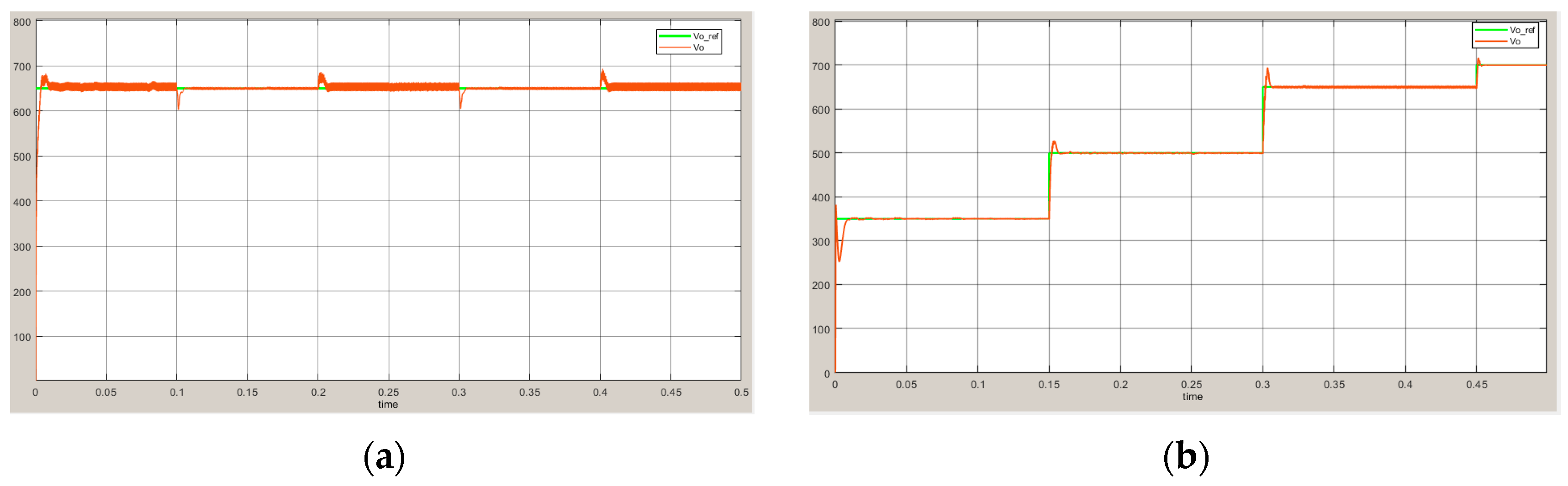
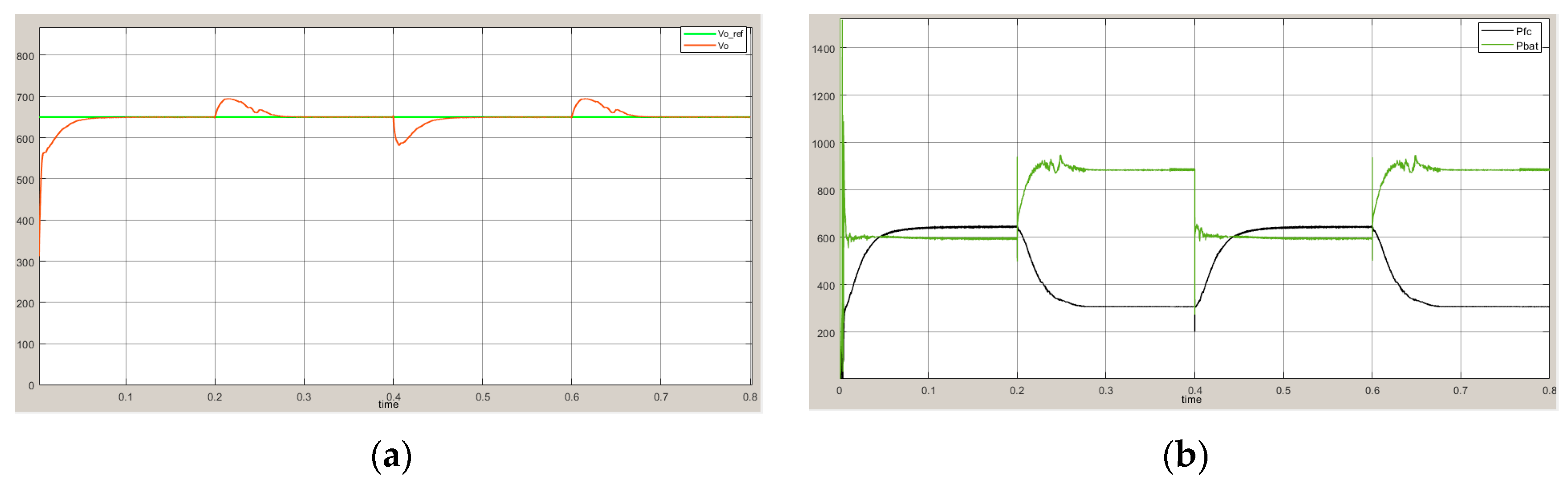
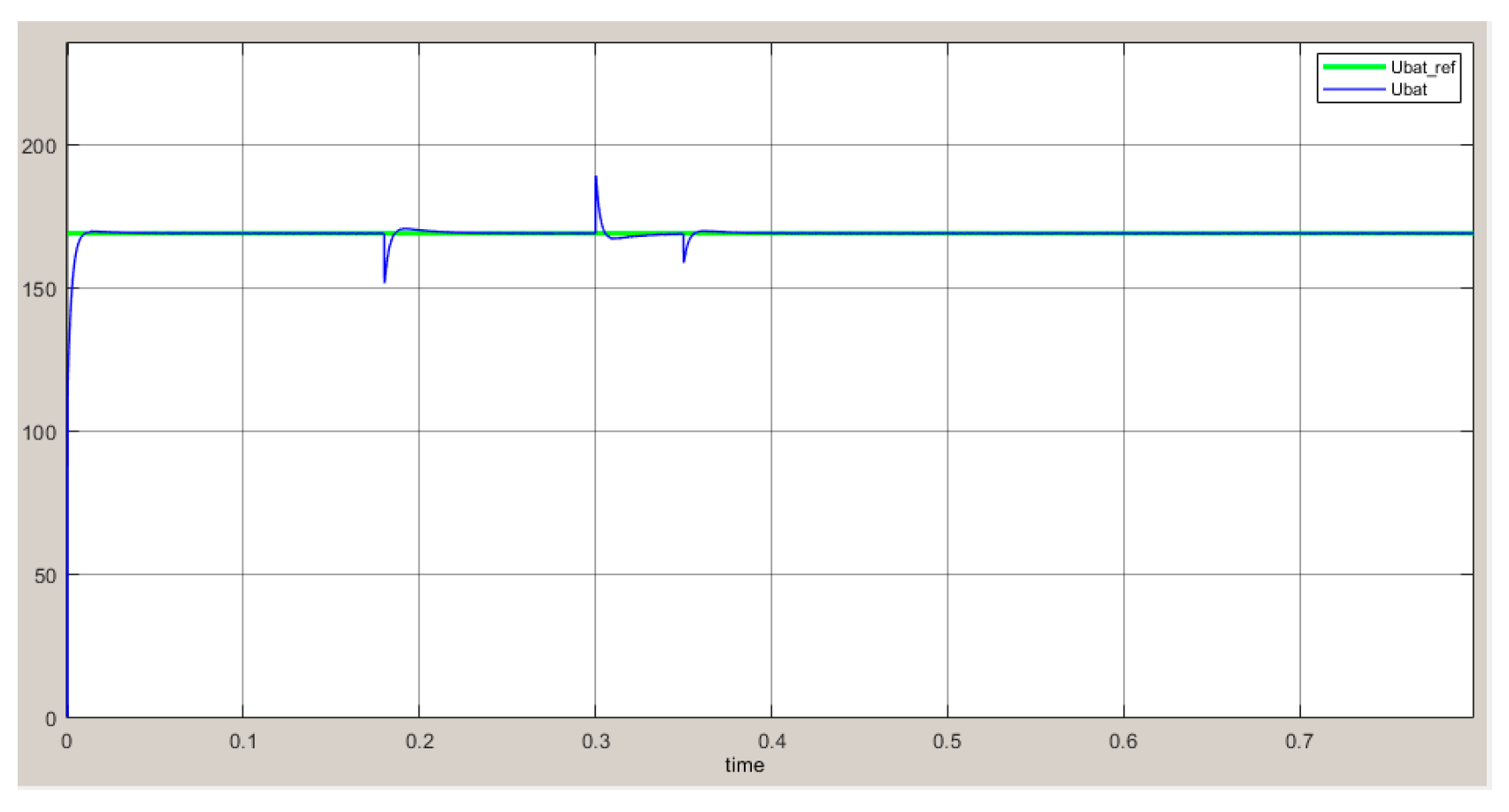
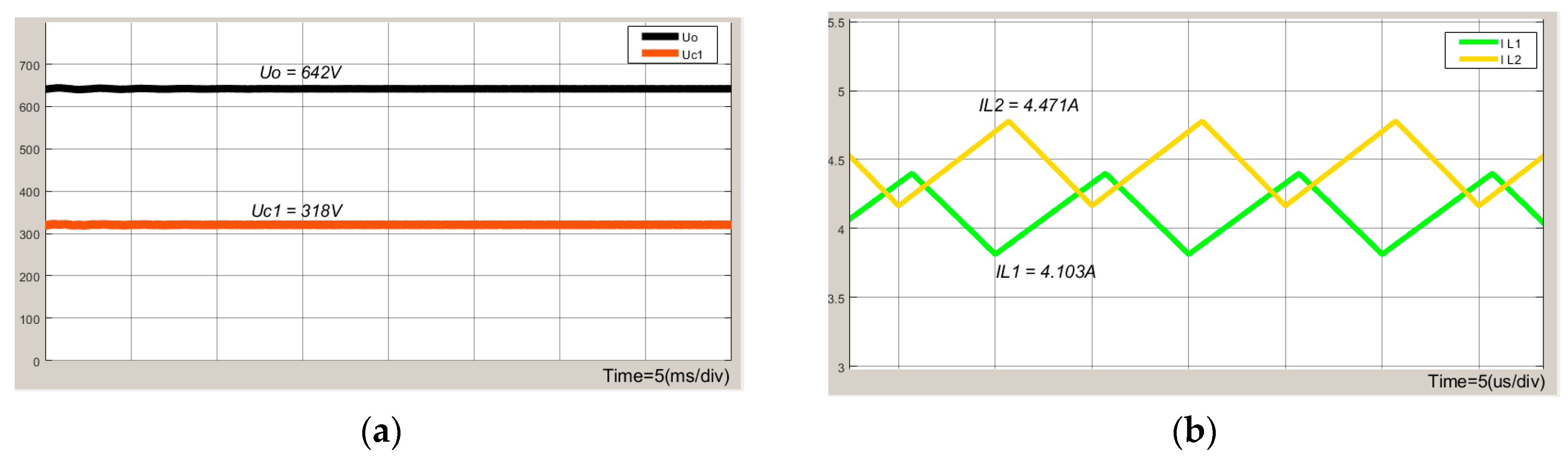
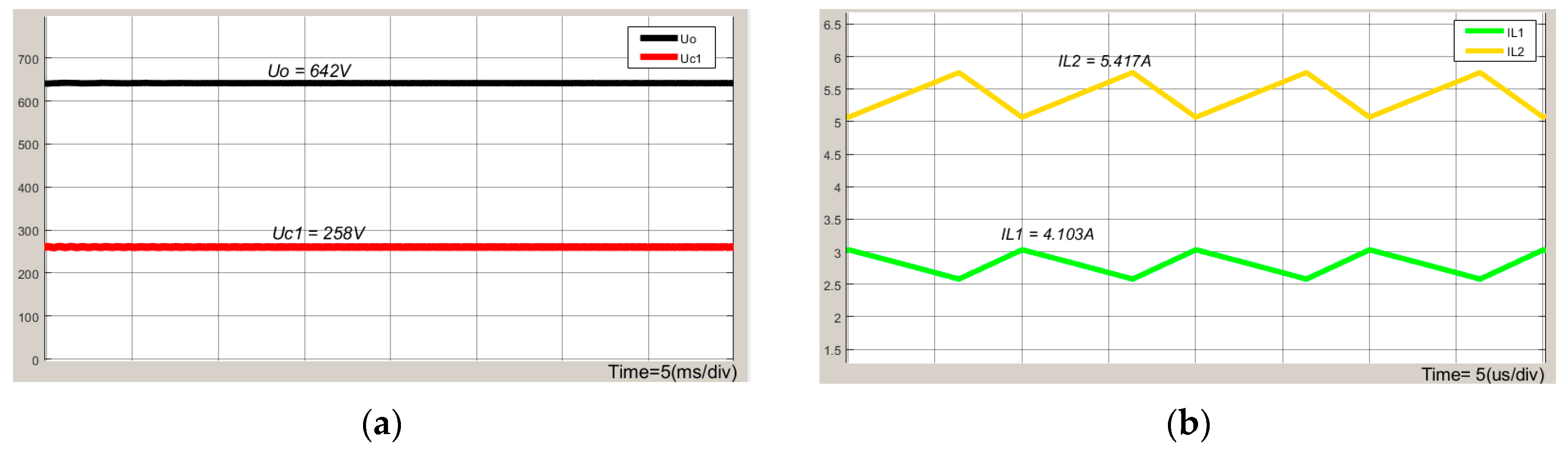
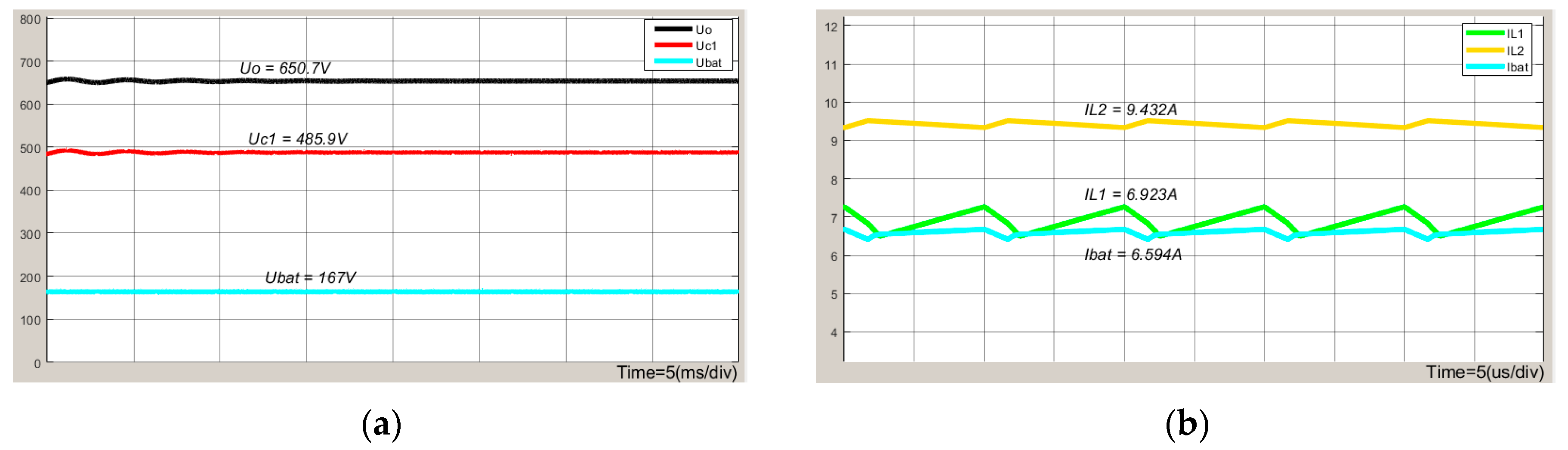
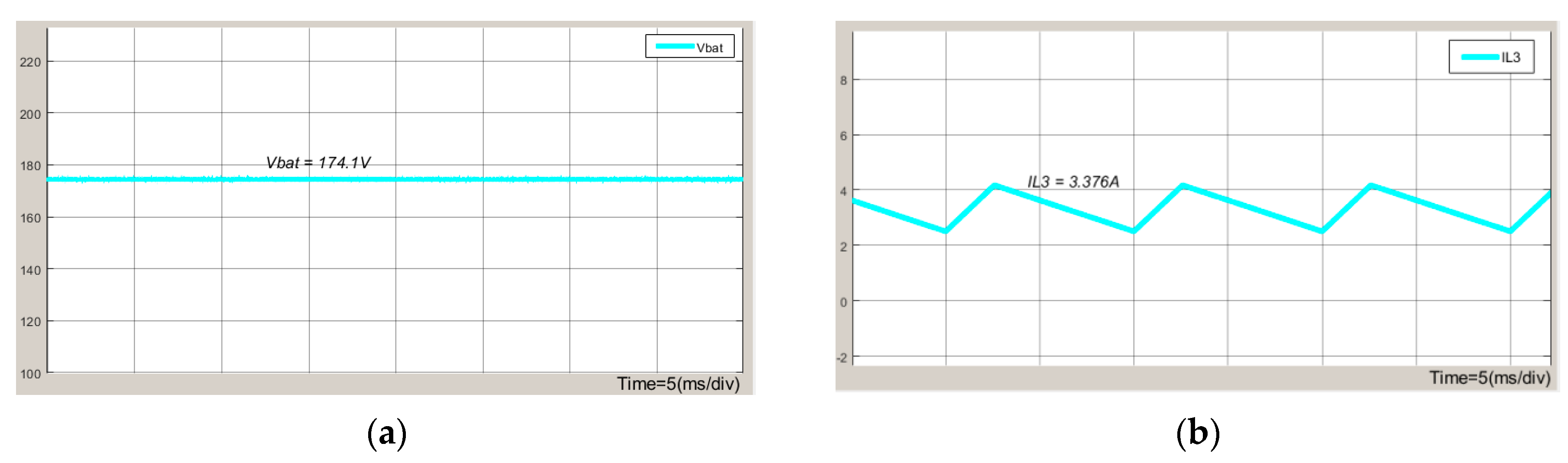
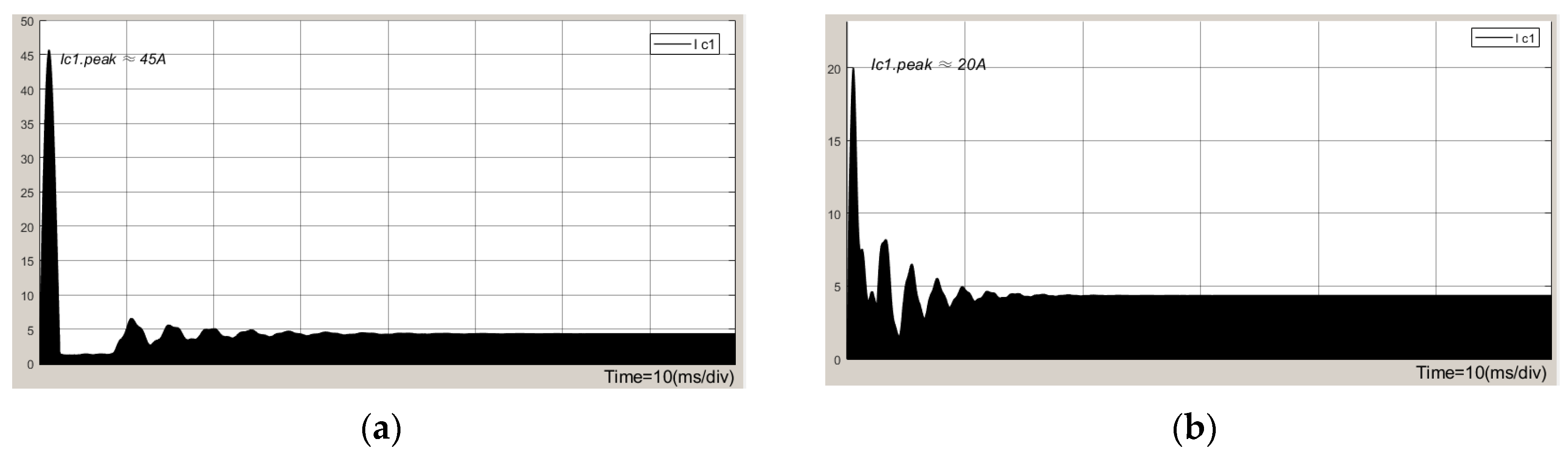
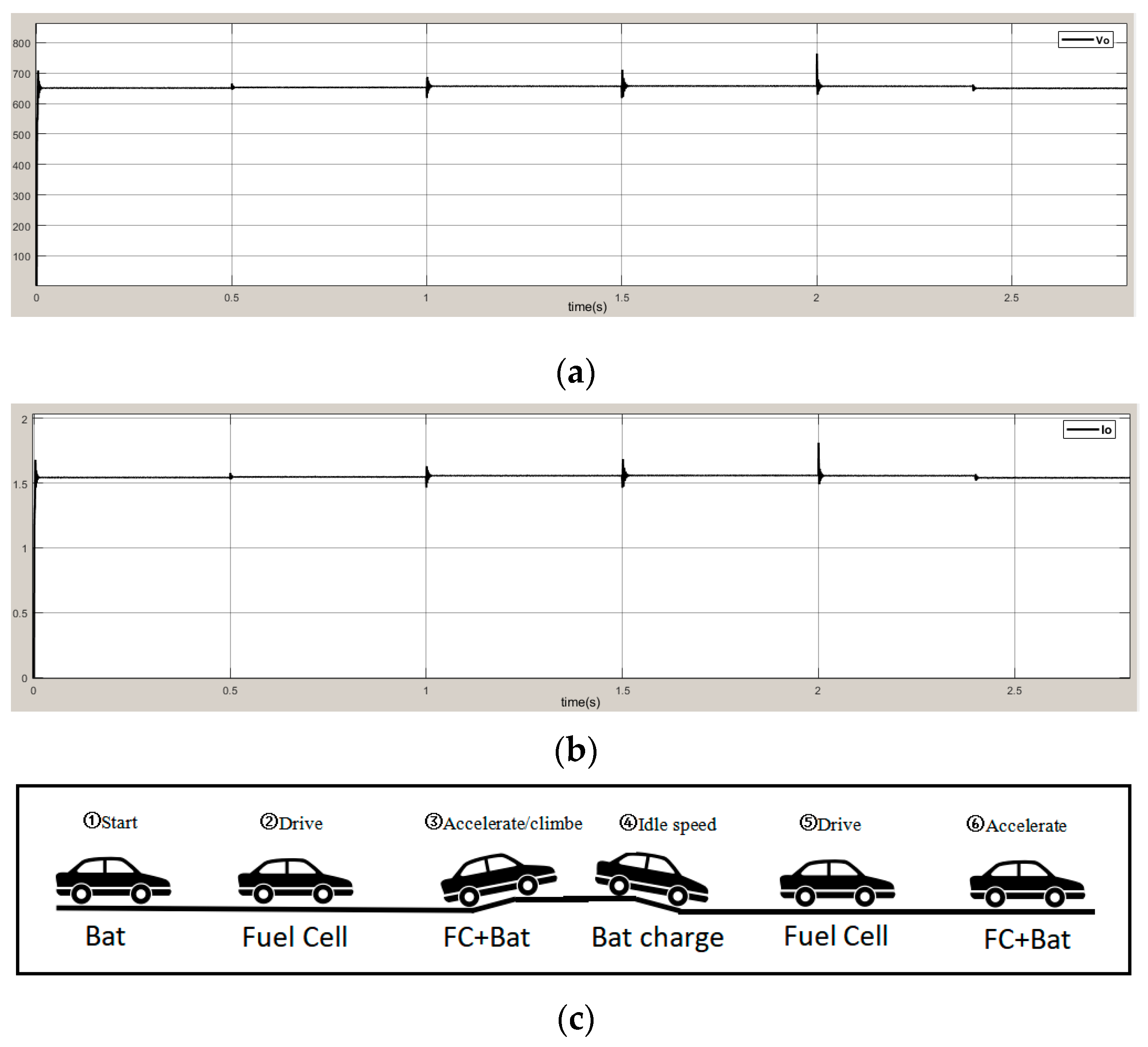
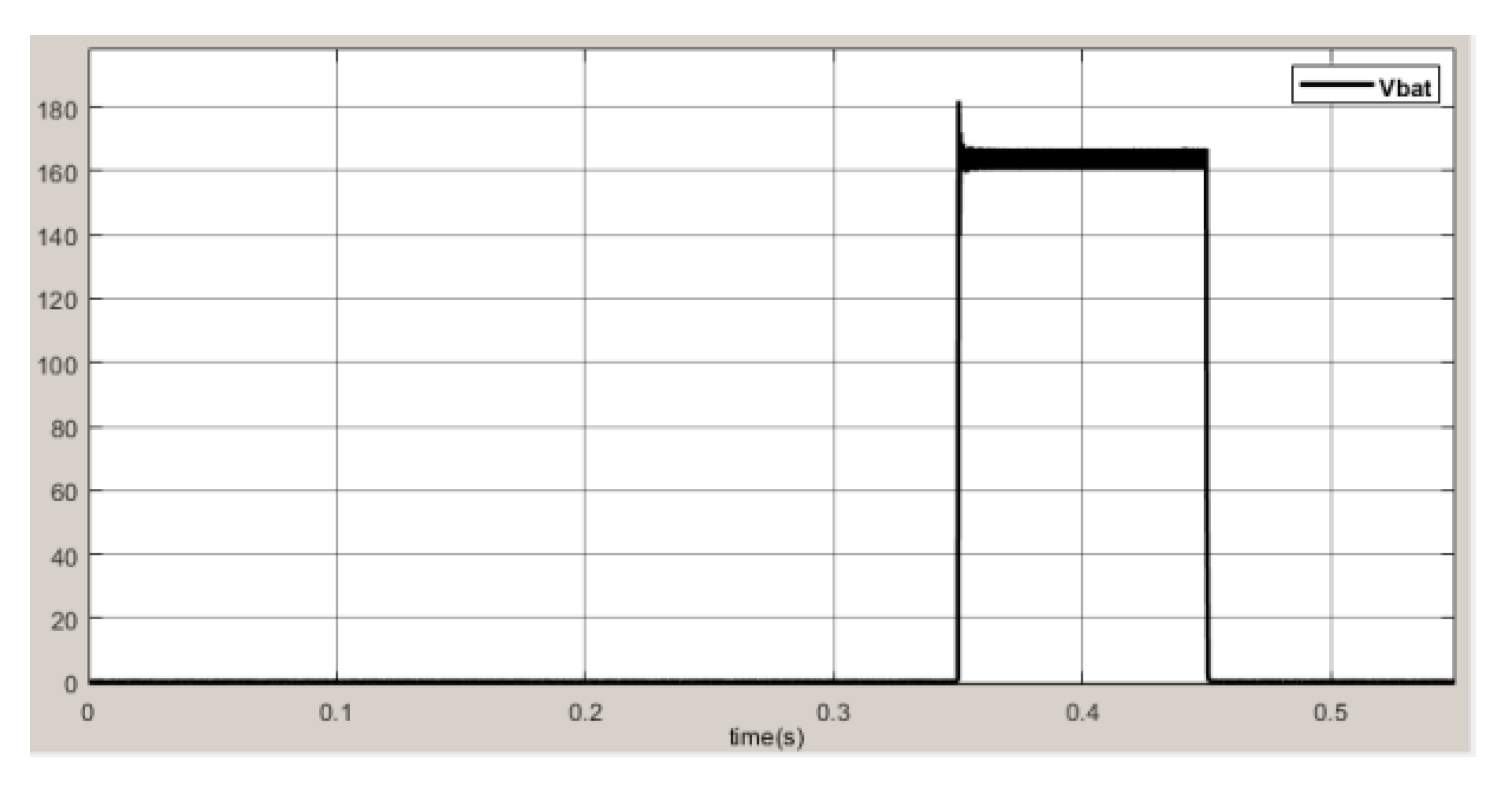
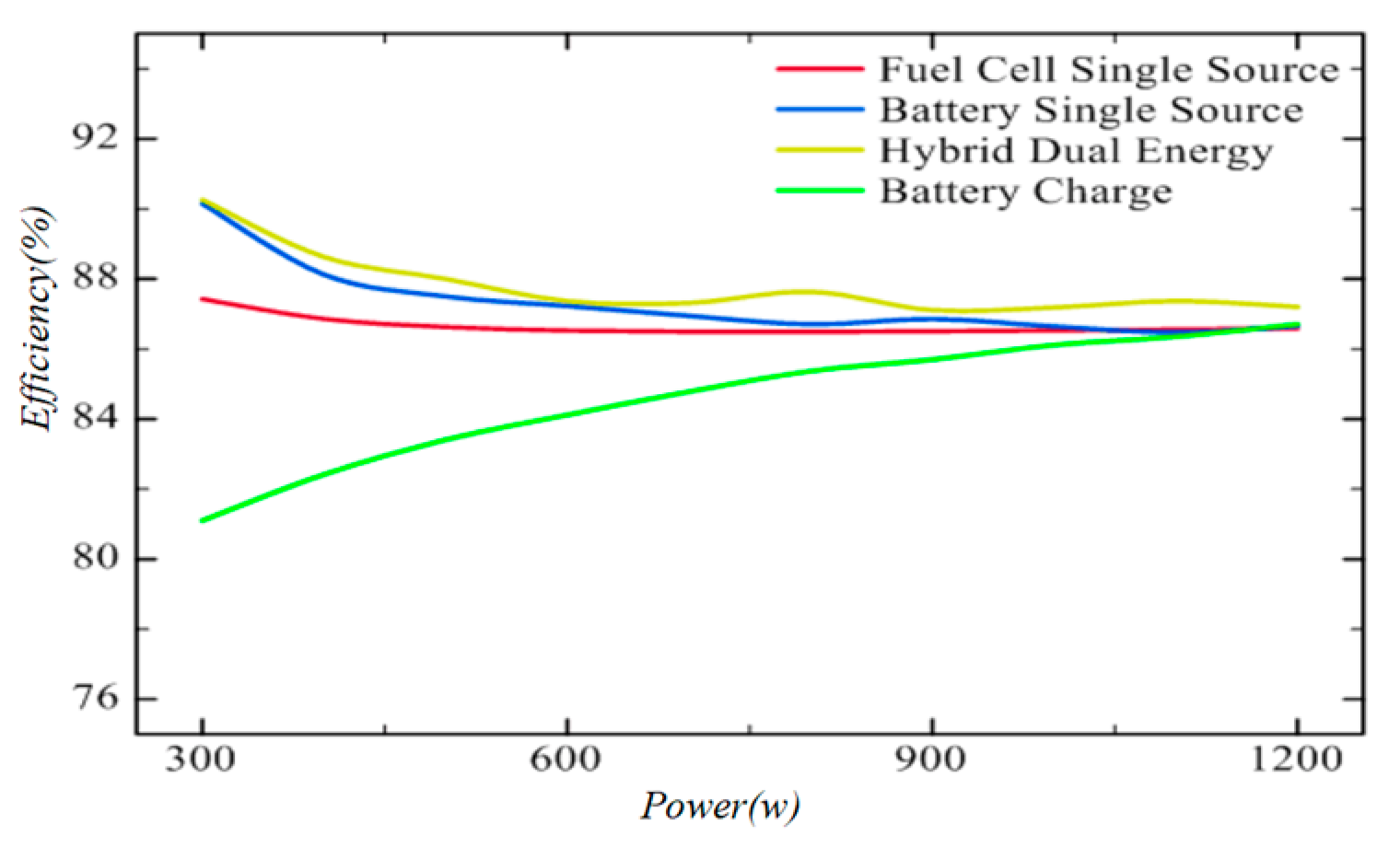
6. Simulation Experiments and Results Analysis
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gao, Z.; Li, X.; Liu, Z.; Rao, J. Research status and development trend of hydrogen fuel cell vehicles. Mater. Rep. 2022, 36, 74–81. [Google Scholar] [CrossRef]
- Guo, N.; Zhang, X.; Zou, Y.; Guo, L.; Du, G. Real-time predictive energy management of plug-in hybrid electric vehicles for coordination of fuel economy and battery degradation. Energy 2021, 214, 119070. [Google Scholar] [CrossRef]
- Feng, Y. Toyota Mirai hydrogen fuel cell vehicle analysis. Automot. Repair Maint. 2020, 8, 71–73. [Google Scholar]
- Babaei, E.; Sakhavati, S. An overview of different topologies of multi-port dc/dc converters for dc renewable energy source applications. In Proceedings of the 2016 13th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology, Chiang Mai, Thailand, 28 June–1 July 2016. [Google Scholar] [CrossRef]
- Vermulst, B.J.; Duarte, J.L.; Lomonova, E.A.; Wijnands, K.G. Scalable multi-port active-bridge converters: Modelling and optimised control. IET Power Electron. 2017, 10, 80–91. [Google Scholar] [CrossRef]
- Song, S.; Li, W.; Ni, K.; Xu, H.; Hu, Y.; Si, J. Modular Multi-Port Ultra-High Power Level Power Converter Integrated with Energy Storage for High Voltage Direct Current (HVDC) Transmission. Energies 2018, 11, 2711. [Google Scholar] [CrossRef]
- Wang, C.; Li, W.; Wang, Y.; Han, F.; Meng, Z.; Li, G. An Isolated Three-Port Bidirectional DC-DC Converter with Enlarged ZVS Region for HESS Applications in DC Microgrids. Energies 2017, 10, 446. [Google Scholar] [CrossRef]
- Li, W.; Wang, Y.; Han, F.; Chen, B. An isolated three-port bidirectional LCLC multiresonant DC converter. Trans. China Electrotech. Soc. 2018, 33, 3231–3244. [Google Scholar] [CrossRef]
- Peng, Y. Study of Input-Output Relationships of Four-Port DC Converters. Chin. LABAT Man 2018, 55, 18–22. [Google Scholar] [CrossRef]
- Wang, H.; Li, H.; Liu, J. A Wide-Range Soft-Switching High-Gain Bidirectional Multi-Port Converter. Power Electron. 2019, 53, 74–77+82. [Google Scholar]
- Akar, F.; Tavlasoglu, Y.; Ugur, E.; Vural, B.; Aksoy, I. A Bidirectional Nonisolated Multi-Input DC–DC Converter for Hybrid Energy Storage Systems in Electric Vehicles. IEEE Trans. Veh. Technol. 2016, 65, 7944–7955. [Google Scholar] [CrossRef]
- Wang, H.; Tian, Q.; Shen, Y.; Yu, T. Non-isolated three-port converter with wide operating range and low EMI characteristics. Sci. Technol. Vis. 2021, 3, 34–39. [Google Scholar] [CrossRef]
- Pourjafar, S.; Shayeghi, H.; Sedaghati, F.; Seyedshenava, S.; Blaabjerg, F. A bidirectional multiport DC-DC converter applied for energy storage system with hybrid energy sources. Int. J. Circ. Theor. Appl. 2021, 49, 2453–2478. [Google Scholar] [CrossRef]
- Shayeghi, H.; Pourjafar, S.; Hashemzadeh, S.M. A Switching Capacitor based Multi-Port Bidirectional DC-DC Converter. IET Power Electron. 2021, 14, 1622–1636. [Google Scholar] [CrossRef]
- Yi, W.; Ma, H.; Peng, S.; Liu, D.; Ali, Z.M.; Dampage, U.; Hajjiah, A. Analysis and implementation of multi-port bidirectional converter for hybrid energy systems. Energy Rep. 2022, 8, 1538–1549. [Google Scholar] [CrossRef]
- Suresh, K.; Bharatiraja, C.; Chellammal, N.; Tariq, M.; Chakrabortty, R.K.; Ryan, M.J.; Alamri, B. A Multifunctional Non-Isolated Dual Input-Dual Output Converter for Electric Vehicle Applications. IEEE Access 2021, 9, 64445–64460. [Google Scholar] [CrossRef]
- Zhang, J.; Wu, H.; Huang, J.; Xing, Y.; Ma, X. Research on Multi-port Bidirectional Buck-Boost Converter. Power Electron. 2021, 55, 129–135. [Google Scholar] [CrossRef]
- Jiang, L.; Fan, J.; Zhang, W.; He, D.; Liao, Z. Simulation Study of Three-Port DC/DC Converters. China Comput. Commun. 2021, 33, 1–4. [Google Scholar]
- Shao, Z. Analysis of a non-transformer isolated three-port converter with single input and dual output operation mode. J. Xuchang Univ. 2019, 38, 131–133. [Google Scholar]
- Moradisizkoohi, H.; Elsayad, N.; Mohammed, O.A. An Integrated Interleaved Ultrahigh Step-Up DC–DC Converter Using Dual Cross-Coupled Inductors With Built-In Input Current Balancing for Electric Vehicles. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 8, 644–657. [Google Scholar] [CrossRef]
- Kumar, A.; Sensarma, P. Ripple-Free Input Current High Voltage Gain DC-DC Converters With Coupled Inductors. IEEE Trans. Power Electron. 2019, 34, 3418–3428. [Google Scholar] [CrossRef]
- Faraji, R.; Farzanehfard, H. Soft-Switched Nonisolated High Step-Up Three-Port DC–DC Converter for Hybrid Energy Systems. IEEE Trans. Power Electron. 2018, 33, 10101–10111. [Google Scholar] [CrossRef]
- Kardan, F.; Alizadeh, R.; Banaei, M.R. A novel step-up multi-input DC-DC converter for hybrid electric vehicles application. IEEE Trans. Power Electron. 2017, 32, 3549–3561. [Google Scholar] [CrossRef]
- Kardan, F.; Alizadeh, R.; Banaei, M. A New Three Input DC/DC Converter for Hybrid PV/FC/Battery Applications. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 1771–1778. [Google Scholar] [CrossRef]
- Jalilzadeh, T.; Rostami, N.; Babaei, E.; Hosseini, S.H. Bidirectional Multi-Port DC-DC Converter with Low Voltage Stress on Switches and Diodes. IET Power Electron. 2020, 13, 1593–1604. [Google Scholar] [CrossRef]
- Liu, J.; Hu, R.; Zeng, J. Non-isolated three-port converter with high gain. Trans. China Electrotech. Soc. 2019, 34, 10. [Google Scholar] [CrossRef]
- Ma, S.; Pan, T. Switched-Capacitor Based Three-Port DC-DC Converters. J. Power Supply 2015, 13, 48–55. [Google Scholar] [CrossRef]
- Wang, H.; Chen, Y.; Zeng, Q.; Li, S.; Zhu, B. A Multi-Condition High Gain Multi-Port DC/DC Converter. Proc. CSEE 2019, 39, 2155–2166. [Google Scholar] [CrossRef]
- Fares, A.M.; Klumpner, C.; Sumner, M. A Novel Multiport DC-DC Converter for Enhancing the Design and Performance of Battery—Supercapacitor Hybrid Energy Storage Systems for Unmanned Aerial Vehicles. Appl. Sci. 2022, 12, 2767. [Google Scholar] [CrossRef]
- Santosh Kumar Reddy, P.; Obulesu, Y. Design and Development of a New Transformerless Multi-port DC-DC Boost Converter. J. Electr. Eng. Technol. 2022, 14, 23–38. [Google Scholar] [CrossRef]
- Suntiom, T.; Messo, T.; Puukko, J. Power Electronic Converters—Dynamics and Control in Conventional and Renewable Energy Applications; John Wiley & Sons: Weinheim, Germany, 2017. [Google Scholar] [CrossRef]
- Venkataramana, S. Small Signal Modeling of Non-Isolated High Gain DC-DC converter. In Proceedings of the 2020 International Conference for Emerging Technology (INCET), Belgaum, India, 5–7 June 2020. [Google Scholar] [CrossRef]
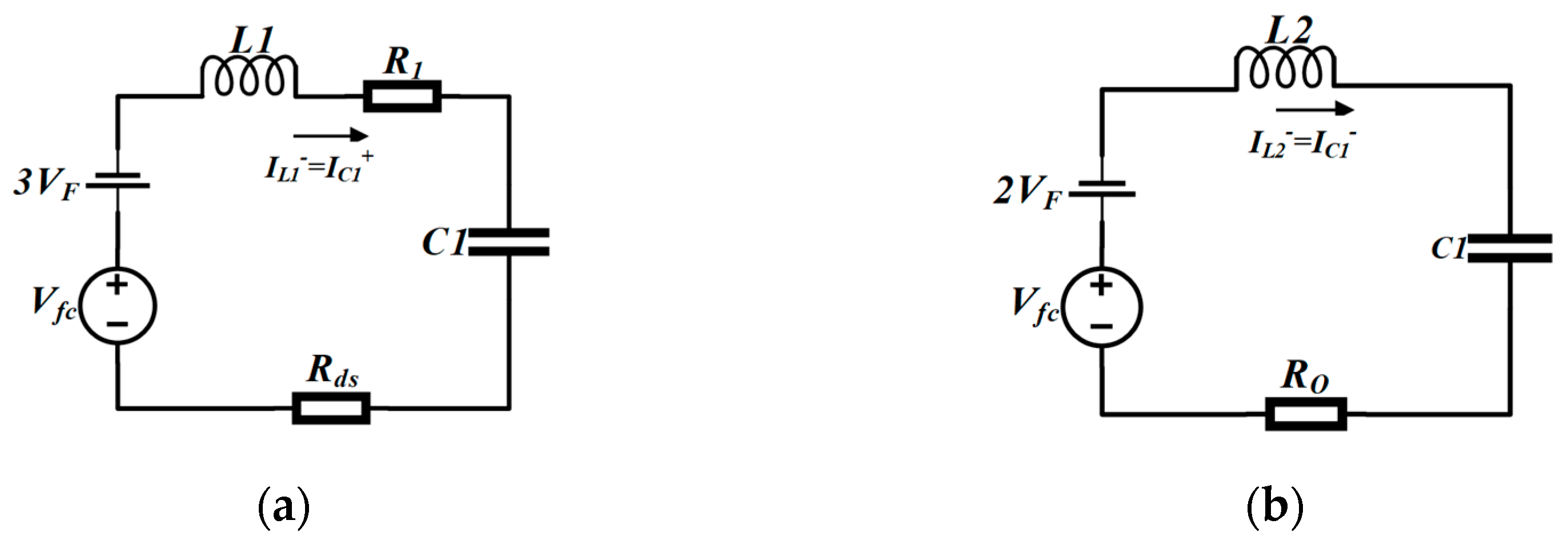


| Study Number | Number of Switches | Number of Inductors | Number of Capacitors | Boost Gain | Number of Applicable States | Bi-Directional Function | Power Distribution Function | Port Independently |
|---|---|---|---|---|---|---|---|---|
| [11] | 4 | 2 | 1 | 3 | √ | √ | × | |
| [14] | 3 | 2 | 3 | 2 | √ | × | × | |
| [16] | 3 | 2 | 3 | 5 | √ | × | √ | |
| [24] | 4 | 2 | 1 | 3 | × | × | × | |
| [27] | 3 | 3 | 3 | 5 | × | × | √ | |
| [28] | 5 | 2 | 2 | 4 | × | √ | √ | |
| Proposed | 6 | 3 | 2 | 5 | √ | √ | √ |
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Fuel cell voltage Vfc | 120 to 160 V | Inductor L1 | 1.28 × 10−3H |
| Battery voltage Vbat | 168 V | Inductor L2 | 1.28 × 10−3H |
| Load rated voltage uo | 650 V | Inductor L3 | 0.747 × 10−3H |
| Load port current Io | 1.5 A | Capacitor C1 | 4.8 × 10−6F |
| Battery port resistance Rbat | 25 Ω | Capacitor Co | 9.192 × 10−6F |
| Load port resistance Ro | 422 Ω | Frequency | 100 kHz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, W.; Luo, W.; Qin, Y. Integrated DC/DC Converter Topology Study for Fuel Cell Hybrid Vehicles with Two Energy Sources. World Electr. Veh. J. 2023, 14, 9. https://doi.org/10.3390/wevj14010009
Xie W, Luo W, Qin Y. Integrated DC/DC Converter Topology Study for Fuel Cell Hybrid Vehicles with Two Energy Sources. World Electric Vehicle Journal. 2023; 14(1):9. https://doi.org/10.3390/wevj14010009
Chicago/Turabian StyleXie, Weijin, Wenguang Luo, and Yongxin Qin. 2023. "Integrated DC/DC Converter Topology Study for Fuel Cell Hybrid Vehicles with Two Energy Sources" World Electric Vehicle Journal 14, no. 1: 9. https://doi.org/10.3390/wevj14010009
APA StyleXie, W., Luo, W., & Qin, Y. (2023). Integrated DC/DC Converter Topology Study for Fuel Cell Hybrid Vehicles with Two Energy Sources. World Electric Vehicle Journal, 14(1), 9. https://doi.org/10.3390/wevj14010009









