Abstract
Battery pack specific energy, which can be enhanced by minimising the mass of the battery thermal management system (BTMS), is a limit on electric fixed-wing flight applications. In this paper, the use of phase-change materials (PCMs) for BTMSs is numerically explored in the 3D domain, including an equivalent circuit battery model. A parametric study of PCM properties for effective thermal management is conducted for a typical one-hour flight. PCMs maintain an ideal operating temperature (288.15 K–308.15 K) throughout the entire battery pack. The PCM absorbs heat generated during takeoff, which is subsequently used to maintain cell temperature during the cruise phase of flight. In the control case (no BTMS), battery pack temperatures fall below the ideal operating range. We conduct a parametric study highlighting the insignificance of PCM thermal conductivity on BTMS performance, with negligible enhancement observed across the tested window (0.1–10 W m−1 K−1). However, the PCM’s latent heat of fusion is critical. Developers of PCMs for battery-powered flight must focus on enhanced latent heat of fusion, regardless of the adverse effect on thermal conductivity. In long-haul flight, an elongated cruise phase and higher altitude exasperate this problem. The unique characteristics of PCM offer a passive low-mass solution that merits further investigation for flight applications.
1. Introduction
1.1. Motivation
Global climate change and dwindling natural resources are currently two of the major challenges in the world. Aviation has had a significant impact on these problems; in the 21st century, civil aviation has contributed 2.5% of total anthropogenic emissions []. Consequently, electrification of aircraft propulsion systems has been proposed as a solution, and has been a focus of recent research. While progress is being made to commercialise electric aircraft, the limiting factor is battery pack specific energy. In the case of an electric car, the possibility of the battery pack running out of energy represents an inconvenience to the user. However, the result is much more catastrophic in the case of electric aircraft. In the very long term, solid-state battery technology may provide a solution to this problem; however, it cannot be relied upon as the aerospace industry is decarbonised in the coming decade. Smart engineering solutions are essential to enhance the specific energy of battery packs using existing lithium-ion cell chemistry.
One of the possible solutions is to develop a low-mass battery thermal management system considering the profile of flight-specific power demand. In certain phases of flights where high power level is demanded, such as take-off and landing, batteries generate significant amounts of heat (Figure 1) [,]. This consequently increases the temperature of a battery. For lithium-ion batteries (LIB), the operational temperature range specified by battery manufacturers is typically between −20 °C and 60 °C []. Above this range, catastrophic failures such as thermal runaway represent considerable risks, while below this range battery performance is severely hindered because battery resistance increases at low temperatures (itself a catastrophic failure in the context of powered flight). Safety risks must be avoided at all costs, especially when the battery provides power to flying objects. Further, battery pack designers aim to maintain a far narrower operating window for optimised performance, typically around 15–35 °C []. A failure to operate in this optimal range results in accelerated degradation and reduced performance [,]. For example, Ramadass et al. showed that an LIB cycled 800 times at 50 °C lost 60% of its initial energy storage capacity. In the same test run at 55 °C, the LIB lost 70% of its initial energy storage capacity after just 600 cycles []. Uneven distribution of temperature across a single LIB or an entire battery pack leads to imbalances and high localised loading of current flow, again contributing towards accelerated degradation [,].
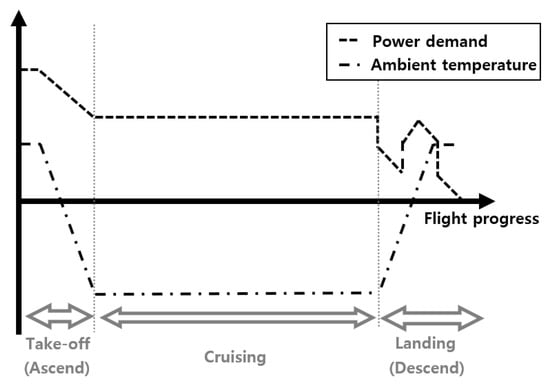
Figure 1.
Simplified profiles of power demand and ambient temperature for typical regional passenger flights.
Battery-powered flight is a particularly challenging thermal management problem because, away from take-off and landing, the LIBs are discharged at a lower rate (i.e., cruise phase), generating significantly less heat []. This characteristic is coupled with the very nature of flight; cruise occurs at a high altitude where ambient conditions are cooler than on the ground (sub-zero temperatures are commonly experienced) and at high speeds (implying high convective cooling rates). Figure 1 graphically presents a qualitative description of the typical operational characteristics for a flight. Conventional aircraft employ an Environmental Control System for climatic control and fresh air ventilation in the majority of the aircraft (cockpit, cabin, cargo and avionics room). This system uses the heat generated as a byproduct of thrust from the gas turbine engines []. This clearly is not possible for battery flight, leading to the conclusion that heat energy management must be very carefully considered and optimised for this emerging application. It is important both to keep batteries cool (especially during take-offs and landings) and warm (while cruising), requiring use of an effective battery thermal management system (BTMS). In general, the current BTMS techniques can be categorised based on their use of different heat transfer media: air, liquid, phase change material (PCM), or their combinations [].
1.2. Background Knowledge on PCM
This work investigates the use of solid-liquid PCMs for application in a BTMS. Uniquely, PCMs provide an opportunity to store heat energy rather than dissipate it, as with other BTMS designs. This is an avenue towards solving the problem introduced above. Further, PCMs can aid in the homogeneous distribution of temperature, and are designed to provide a significant thermal barrier against excessive temperature rise at the temperature of the user’s choosing (i.e., the melting temperature of the PCM). This enables efficient control of temperature and the capacity for fast thermal response from the BTMS []. The heat transfer medium can be categorised into three main classes, each with advantages and disadvantages for BTMS application, as can be seen in Table 1. The typical ranges of thermal properties of these PCM categories are listed in Table 2.

Table 1.
PCM categories and their details for BTMS application.

Table 2.
Typical values of thermal properties of each PCM category presented in Table 1.
PCMs absorb, store and release heat by undergoing a phase change from solid to liquid states or vice versa. During this transition, energy is stored in the form of latent heat at a near constant temperature (the melting temperature of the PCM), as shown in Figure 2. This characteristic of PCMs is beneficial for systems that experience large fluctuations in both ambient temperature and the heat generated by systems, such as space vehicles and buildings in desert areas [,].
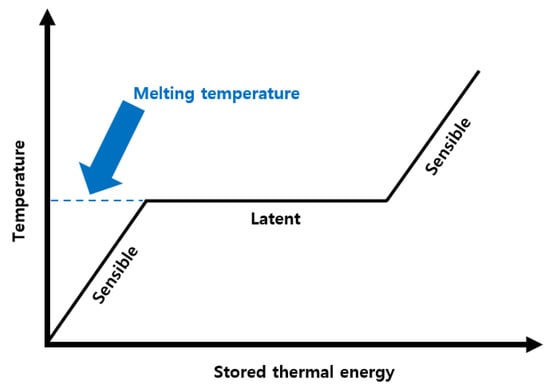
Figure 2.
PCM temperature as a function of thermal energy stored in a PCM.
Another such system is a battery pack. In particular, battery packs used for flights require high power output, thereby generating a significant amount of heat during take-off and landing. On the other hand, the rate of heat generation while cruising is relatively low. This is further coupled with the low temperatures at high altitudes. Consequently, a PCM-based BTMS absorbs and releases heat during take-off/landing and cruising, respectively. This means that PCM-based BTMS can be used for both the cooling and heating processes, instead of requiring two separate systems for each process, which potentially increases payload by reducing the mass of BTMS. Moreover, this passive BTMS can be favorable compared to active ones due to the fact that:
- No moving parts such as pumps and fans are required. Less frequent maintenance is required, meaning that it is less likely for the BTMS to malfunction.
- The BTMS is passive; it consumes little energy, reducing the parasitic demand on the battery pack and inherently increasing the energy available to power the flight.
However, any PCM adds mass to the system. In flight applications this is of critical importance, as the power demand is increased and the payload of the aircraft is reduced with the increased mass of the system. This is contrary to the automotive application of PCM-based BTMS, where the reduction in weight is less prioritised [].
Due to low thermal conductivity of PCM, highly thermal conductive materials such as ultrathin graphite sheets, carbon nanotubes, and expanded graphite can be added to create composite PCM (CPCM) [,]. Alternatively, instead of using these additives, the PCM can be combined with metal networks fitted around a heat generating system; examples of these include fins []. For the application of PCM to BTMS, especially, there have been attempts to develop flame retardant CPCM to account for global issues of battery explosions and fire []. However, a large amount of additives are required to sufficiently increase the thermal conductivity and flame retardancy by creating CPCM. Therefore, growth in these two properties is achieved only at the cost of reducing the latent heat of fusion for a given mass of CPCM. Accordingly, a trade-off has to be made between the two competing properties for a targeted application.
1.3. Objectives
The idea of PCM-based BTMS for application to electric vehicles (EV) has existed for a long time []. However, unlike the literature on EVs, there have been few studies on the aerospace applications of PCM-based BTMS.
The fundamental objective of this work is to test the practicality of a PCM-based BTMS for aviation applications. In particular, its application to regional passenger airplanes is tested. In addition, parametric studies for PCM properties are carried out in order to aid PCM selection in future studies. This study conducts a sensitivity analysis on the latent heat of fusion and thermal conductivity in order to contribute towards the optimised design of PCMs in the future (comparing the suitability of PCM and CPCM), and further investigates the effect of different PCM melting temperatures on overall BTMS and LIB performance. The methodology followed in the presented work is as follows:
- Battery Equivalent Circuit Model (ECM) parameters are extracted.
- These parameters are used to calculate the voltage response and heat generation rate of battery for thr power demand of regional passenger airplanes taken from the literature.
- A 3D numerical model of a part of a battery pack (composed of the BTMS and cells) is developed using STAR-CCM+.
- The output of the numerical model is used for feasibility and parametric studies of PCM-based BTMS for flight applications.
2. Methods
In this paper, a part of a battery pack in a regional passenger aircraft is numerically modelled. A battery pack refers to a system consisting of individual cells and a BTMS. Because a PCM-based BTMS is to be tested, the components in the numerical model include a lithium-ion cell, PCM, and insulation. STAR-CCM+ (Version 2020.3) was used to develop and run the model.
2.1. Battery Modeling/Properties
To model the dynamic behavior of a cell, the Thevenin equivalent circuit model (ECM) was adapted (Figure 3). This battery model was chosen over others such as electrochemical models due to its simplicity and low computational cost relative to the others []. The ECM of a cell is composed of several components:
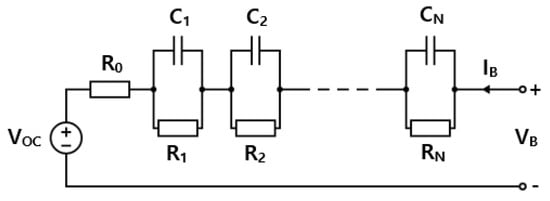
Figure 3.
Typical Thevenin-based ECM of a cell [].
- A voltage source emulating the open circuit voltage (OCV) of the cell.
- A resistor the representing internal resistance of the cell.
- The resistor–capacitor (RC) pairs, and , respectively, characterising the transient behaviour of the cell.
All of these ECM parameters are functions of battery temperature and state of charge (SOC), which is defined as
where t is time, is cell capacity in Ah, and is the current flowing through a cell.
These ECM parameters take current profiles as an input and provide the voltage response, which is given by
where N is the number of RC pairs (= 3 in this work) and is the voltage loss at each RC pair, given by
where t is time.
The same ECM parameters allow for calculating the internal heat generation. A general equation for this variable was developed by Bernardi et al. [], as follows:
where is the irreversible heat generation rate, defined as
and is the reversible heat generation rate, given as
where T is temperature, is the entropy coefficient, accounts for irreversibilities such as mass transfer limitations, charge-transfer overpotentials, and ohmic losses, and is related to entropy change. It should be noted here that other terms such as enthalpy-of-mixing and phase-change can be added to Equation 4 in order to put the equation in an exact form. However, when compared to and , these terms are negligible, and are omitted here [].
To find the temperature field, the heat transfer of the cell was modelled using the Three-Dimensional, Solid, and Implicit Unsteady models on STAR-CCM+. The energy source option was activated to include the battery internal heat generation rate using defined above. The ECM parameters were expressed in terms of SOC, assuming that parameter dependency on the cell temperature is insufficient to severely affect their quantities. This assumption is valid within the temperature ranges tested in the present study [,,]. Under this assumption, it is possible to eliminate a dimension of parameter determination that is necessary at every time step of the numerical simulation, making all ECM parameters functions of SOC alone. This significantly reduces the computational demand for the ECM within the CFD solver, enabling far greater resolution for the planned parametric study with four variables (thermal conductivity, latent heat of fusion, and battery pack initial and PCM melting temperatures).
A 5Ah high=power pouch cell manufactured by Kokam (SLPB11543140H5) was used in this work. Its material properties and dimensions are provided in Table 3. The ECM parameters and entropy coefficients determined and validated by Zhao et al. were used to develop the ECM in the present study []. Identical drive cycles to those used by Zhao et. al. were tested on the ECM for this investigation. Strong agreement between the data of Zhao et al. and the thermal and voltage responses from the present study’s ECM provided the validation for the present model. These ECM parameters were expressed as functions of SOC using high-order polynomial regression, with a unique function for each ECM parameter and the entropy coefficient. Each function was imported into the numerical model using STAR-CCM’s Field Functions module, allowing the parameters to be calculated at each time step for a given SOC.

Table 3.
Material properties and dimensions of the cell used.
2.2. PCM Modelling/Properties
To model the flow and heat transfer of PCM, the following assumptions were made:
- The flow of solid/liquid PCM is in a laminar regime and unsteady.
- The change in volume during liquid–solid (or vice versa) phase change is negligible.
- The density of PCM during liquid–solid (or vice versa) phase change changes linearly.
During the melting process of PCM, its volume change can move from 0 to around 20% depending on the nature of PCM []. This is significant, and must not be ignored in BTMS design. That said, the focus of this study is the performance of PCM as a thermal mass, and the mass of the PCM is unchanged throughout any change of state. To this end, this investigation does not go into great depth in proposing intuitive methods to contain a PCM during expansion or contraction, instead focusing on the thermal effects that result from the change of state. Under these assumptions, the STAR-CCM+ models listed in Table 4 were used. The PCM modeling techniques first validated by Dekhil et al. are used throughout the present study [,].

Table 4.
STAR-CCM+ models used for PCM modelling.
The PCMs used in the study were based on the properties of RT31, manufactured by Rubitherm, a leading manufacturer of PCMs. The exact properties used across the study are listed in Table 5. As evidenced, the range of thermal conductivity, latent heat of fusion, and melting temperature allows for a parametric study of these properties. It should be noted here that the ranges used in the present study do not relate directly to any one category of PCM listed in Table 1 (i.e., organic, inorganic, or eutectic), instead representing the broadest possible range of parameter magnitudes. This decision was made to ensure that the study covered all possible PCM types, rather than focusing on any one category without due consideration of others. The ranges used for both the thermal conductivity and latent heat of fusion were selected based upon the values reported in the relevant academic literature [,,]. Latent heat of fusion can be decreased by adding highly thermally conductive materials to enhance the thermal conductivity of the PCM. As such, a high value in one of the two variables generally corresponds to a low value in the other. To widen the relevance and enhance the impact of this study, the parametric study was extended beyond the state-of-the-art PCM material properties available today up to high values of the thermal conductivity and latent heat capacity. Thus, the results can aid designers of new PCMs in prioritising development to enhance those material properties that can boost performance most effectively. The range of melting temperatures used was decided such that they would be within the range of the ideal battery operating temperatures.

Table 5.
Tested PCM properties.
2.3. Insulation Modelling/Properties
Unlike the PCM modelling, no optional models are needed for insulation modelling. The Three-Dimensional, Solid, and Implicit Unsteady models were chosen to model the heat transfer within the insulation. The insulation properties are summarised in Table 6.

Table 6.
Insulation properties [].
2.4. Battery Pack Geometry and Boundary Conditions
A battery pack refers to a system consisting of multiple cells and a BTMS. Assuming adiabatic boundary conditions on the top and bottom surfaces of the pack, the domain can be reduced to a 2D cross-sectional view, as can be seen in Figure 4a. In this work, the modeled cells are entirely enclosed by the PCM, creating a conductive heat transfer interface on each of the four modeled interfaces between cell and PCM. This optimises the surface area to volume ratio of the PCM in order to maximise the effectiveness for thermal management purposes []. Symmetrical boundaries allow the modelled domain to be further reduced to just one-quarter of the full cell and the corresponding adjacent PCM. It is assumed that heat transfer in the x-direction across the pack is negligible when compared to that in the y-direction (Figure 4a), i.e., there is no heat transfer from one cell to the adjacent cell. This is justifiable for large battery packs, as would be expected for use in regional flight applications.
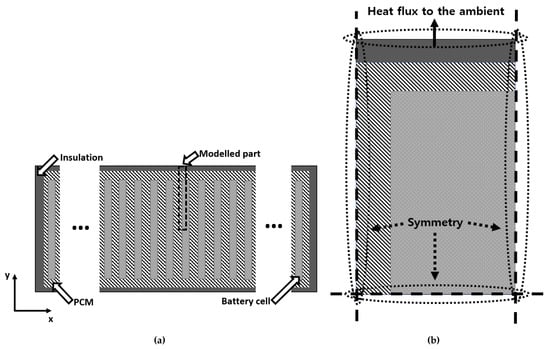
Figure 4.
(a) 2D cross-sectional view of the modeled battery pack and (b) boundary conditions of the modeled part of the battery pack.
Research among engineers in the battery industry has highlighted that a PCM contained within a BTMS for flight applications must be kept to a minimum, with 5% of the mass of the lithium-ion cells representing a reasonable circumstance. Minimising the mass of the BTMS is key for its application in electric flights, as this maximises the payload and efficiency of the aircraft. It is evident that the mass of the PCM used for an e-aircraft BTMS is always affected by the application, and powertrain requirements, and ambient conditions. For this reason, in order to maintain a generalised case and study that is relevant to the BTMS design of any future e-aircraft, this threshold value of 5% of the mass of the lithium-ion cells is used throughout the present study in order to calculate the thicknesses of the PCM. Where insulating material is used in place of the PCM to create the control case for the parametric study, the equivalent thickness of insulation is used.
The boundary conditions are shown in Figure 4b. This 2D cross-section was extended in the z-direction by the cell length (given in Table 3) to create the 3D geometry on STAR-CCM+.
In Figure 4b, the heat flux due to convection is modeled on the boundary of the insulation. This heat flux is defined as
where is the thermal resistance, is the ambient temperature, and is the temperature of the insulation at its interface with the environment. The profile of over a flight is discussed in the following subsection.
Here, represents the thermal resistance of the material which separates the lithium-ion cells from the ambient conditions, and is calculated as set out below:
where A is the heat transfer area, is the thickness of the sample, and is the estimated lumped thermal conductivity. A and were approximated based upon estimations of the dimensions of the battery pack (and its associated casing) found in the EcoPulse and E-fan manufactured by Airbus (, and [,]). To obtain , a weighted average was calculated based on the expected thickness and thermal conductivity of the constituent materials listed in Table 7. These materials can be considered as the casing of the physical battery pack, and are kept strictly 1D to ensure that the presented study retains relevance with any size and geometry of battery pack designed for a given application.

Table 7.
Assumed battery packaging materials [].
There is a lack of publicly released electric aircraft battery pack specifications. Consequently, the values listed in Table 7 and those used to calculate A and were taken from different aircraft prototypes. Figure 5 shows that the numerical model is not sensitive to ; when increased by five times, there is no discernible change to model outputted temperature rise. Therefore, was rounded to the nearest order of magnitude () and maintained as a constant throughout the investigation.
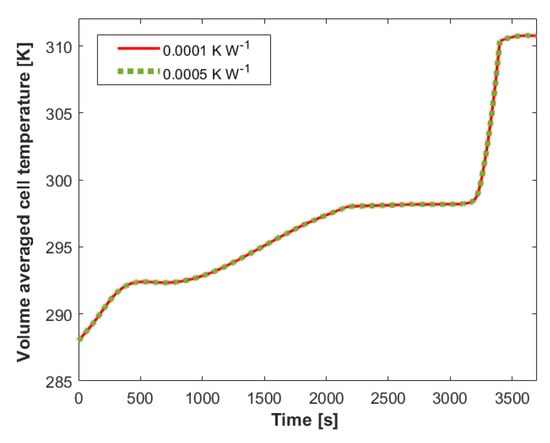
Figure 5.
Sensitivity test of R-value.
2.5. Flight Specific Profiles
In this study, a typical power profile for the flight of a regional passenger airplane was used. This profile was taken from the work by Jux et al. []. The normalised power profile can be seen in Figure 6a. In light of the assumption made earlier that ECM parameters can be expressed in terms of SOC alone, the current profile can be calculated for this power profile. Because power, current, voltage, and SOC are all interrelated, an iterative calculation method was employed using the Goal Seek function in Microsoft Excel. In this calculation process, a condition was introduced to ensure that the SOC at the end of the flight was 0% (i.e., fully discharged state).
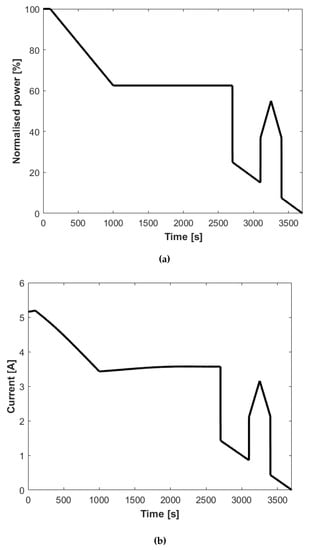
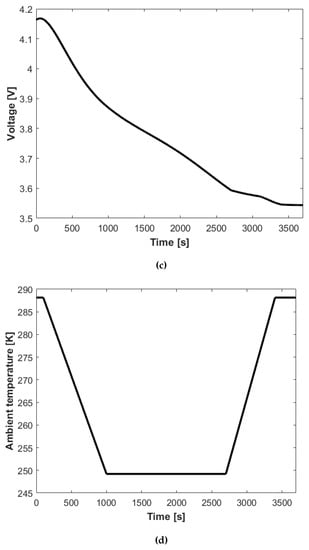
Figure 6.
Profiles of (a) normalised power, (b) current, (c) voltage, and (d) ambient temperature over a flight by a regional passenger airplane.
For the ambient temperature profile, a general case of 288.15 K on the ground and 249.2 K at a cruising altitude of 6000 m were taken from open-source data for a typical flight in North America []. The temperature variation between the ground and cruising altitudes was assumed to be linear, as can be seen in Figure 6d.
2.6. Discretisation Schemes
Mesh independence tests were carried out to ensure the accuracy of the numerical model. Testing began with the most coarse grid of 34,190 mesh elements. The base mesh element size of this case was then divided by two and four to create refined grids of 108,638 and 336,859 mesh elements, respectively. Figure 7 shows that the change in the simulation results when further increasing the number of mesh elements above 34,190 is negligible. Therefore, a mesh configuration with 34,190 mesh elements was chosen. The first-order implicit unsteady scheme was used for temporal discretisation, with a time step size of 0.02 s and maximum number of inner iterations of 15.
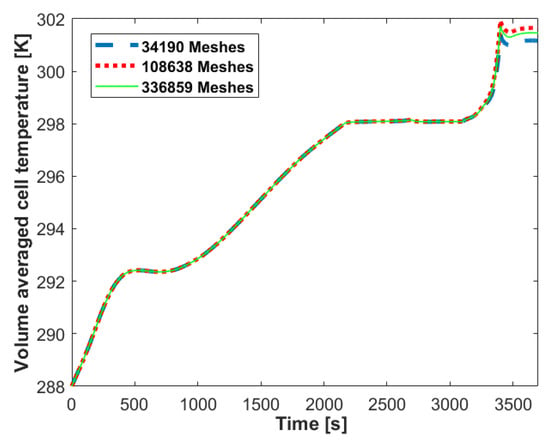
Figure 7.
Mesh independence test.
3. Results and Discussion
In this section, our simulation results are presented and discussed. To this end, it is important to remember the definitions of the operational and optimal operating temperature ranges, which are discussed in Section 1.1. The cell temperature must be kept within the operational temperature range for it to operate in the way it is designed to behave and to avoid any failures. This range is from 253.15 K to 333 K. On the other hand, the optimal operating range refers to the range within which the cell temperature should ideally be maintained in order to achieve its best performance and minimise the rate of degradation, which is between 288.15 K and 308.15 K.
3.1. Benchmark Cases
Before our feasibility and parametric study results are presented, three benchmark cases are discussed. This is to investigate whether PCM-based BTMS can be used to improve battery operating conditions. The cases are: (1) real flight conditions; (2) no heat generation assumed, and (3) perfect adiabatic conditions. Although the last two cases are not representative of realistic flight conditions, they help to provide insight into the previously mentioned objective.
It is important to discuss the effects of heat loss and generation (cases (2) and (3), respectively) separately, as the power and ambient temperature profiles used in this work are for the general case (as described in Section 2.5), and the effect of one can outweigh that of the other depending on the type of flight. As can be seen in Figure 8, case (2) shows that when only the heat loss is considered the averaged battery temperature drops to nearly 273.15 K, which is below the lower limit of the optimal battery operating temperature range. This highlights the concerns raised regarding the cruise phase of any flight profile. When the power demand from the powertrain is low, there is little heat generation and the overall temperature is expected to drop due to the low ambient temperatures and high convection cooling coefficients. On the other hand, when only heat generation is taken into account (case 3), the temperature crosses the upper limit. These two cases highlight the fact that thermal control of the battery pack is necessary; it cannot be entirely insulated to create an adiabatic system. This justifies the purpose of the presented investigation of PCM-based BTMS usage cases, as a correctly designed BTMS using a PCM is able to provide insulation as well as offering a heat sink from the system to maintain an ideal operating window.
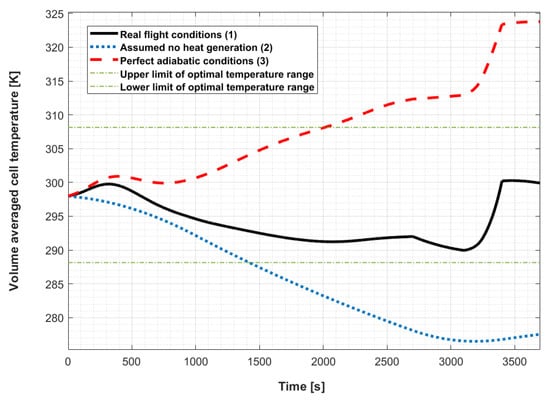
Figure 8.
Simulation results of the three benchmark cases.
Case (1) aims to be representative of real flight conditions, considering both heat loss and generation. The temperature profile shows that the effects of heat loss and generation balance each other out to keep the battery temperature within the optimal range. Nonetheless, it is important to note that flight conditions may vary depending on the date and route of flights, as previously discussed. For instance, unlike the regional flight modeled here, international flights with a longer cruising period experience cell temperatures dropping further, causing the curve to be closer to case (2). Therefore, use of a BTMS would allow flexibility in the operation of flights and provide an extra layer of safety in case of emergency or if unexpected actions need to be taken. In addition, the BTMS helps to achieve a uniform temperature distribution throughout the battery pack during those flight stages in which a sudden peak in power use is required, such as take-off. In this respect, a PCM-based BTMS can act as a passive thermal control mechanism, absorbing heat energy during moments of high discharge and releasing heat back into the battery during periods of low power demand.
3.2. Parametric Study of PCM Properties
In this subsection and the following one, parametric studies are conducted. As a performance indicator of the BTMS, the root mean squared difference (RMSD) is defined as
where is the number of time steps, n represents each time step, and is the volume averaged battery temperature in Kelvin. RMSD is simply a measure of how much is off the optimal battery temperature range (between 288.15 K and 308.15 K). Consequently, the lower RMSD is, the better performance the PCM-based BTMS is observed to deliver. It is noteworthy to emphasise that performance is inversely proportional to RMSD; thus, in this paper the level of BTMS performance is defined as follows:
Using the variable defined above, a parametric study on PCM properties is carried out in this subsection. More specifically, this study examines the latent heat of fusion and thermal conductivity of the PCM at fixed values of the initial and melting temperatures of the battery pack and PCM, respectively. For both temperatures, 298.15 K was used, which is the mid-point of the optimal temperature range. To allow the PCM to be in its complete solid form (i.e., remaining latent heat capacity is 100%) at the beginning of flight in a case where initial and melting temperatures are meant to be the same, the initial temperature was purposely lowered by 0.01 K. The effect of both temperatures is examined in the following subsection.
It can be observed from Figure 9a,b that increasing the thermal conductivity corresponds to improved performance of the BTMS. This is because heat is transformed across the battery pack, thereby removing the issue of the PCM partially melting near the cell surfaces. However, it is clear from Figure 9a that BTMS performance is far more sensitive to changes in the latent heat of fusion. Hence, it is logical to focus on the relationship between performance and latent heat of fusion.
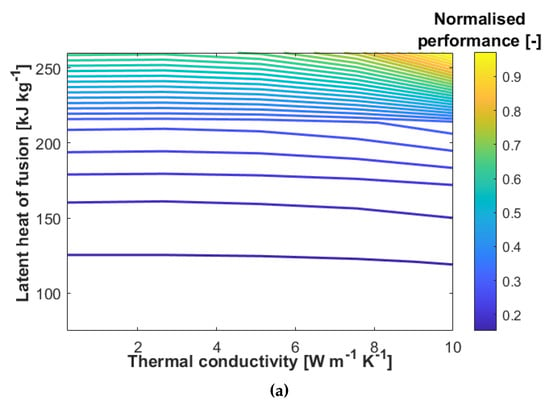
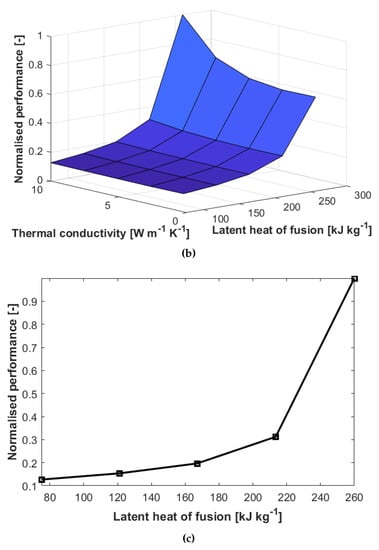
Figure 9.
(a) Contour plot of normalised performance of BTMS against latent heat of fusion and thermal conductivity of PCM; (b) surface plot of normalised performance against latent heat of fusion and thermal conductivity of PCM; (c) graph of normalised performance against latent heat of fusion.
Figure 9c suggests that the performance improves with increasing latent heat of fusion in a close to exponential manner. It should be remembered that in this study the mass of BTMS is set to be 5% of that of battery, which makes the thickness of the PCM layer quite small. With this in mind, the heat conduction rate across the thickness of the PCM layer is excellent, meaning even a very low thermal conductivity does not create a significant insulating layer of PCM from the perspective of the cell generating heat. On the other hand, because the volume of PCM used is consequently low, the PCM should be intrinsically able to capacitate a large amount of energy in the form of latent heat in order to effectively control the temperature of the pack. Hence, it is concluded that for the application of PCM-based BTMS to flights, increasing latent heat of fusion should be prioritised over increasing thermal conductivity. Thus, the data suggest that composite PCM (CPCM) is not suitable for battery flight applications; the mass of PCM that can be used to maintain a high battery pack specific energy means that adding conductive materials is unnecessary and wasteful with respect to the property that ultimately needs to be maximised, that is, thermal storage capacity.
3.3. Initial and Melting Temperatures
In this subsection, the temperature of the battery pack at the beginning of a flight and melting temperature of PCM are tested. These tests were conducted by considering the best PCM properties found in the previous subsection; the latent heat of fusion is set to be 260 kJ kg−1, which is the maximum value used in the previous parametric study. Three different melting temperatures of PCM are examined, selected to perform across the optimal temperature range at intervals of 10 K. Considering that at a given melting temperature the PCM maintains a constant temperature under a continuous heat supply, it is sensible to use a PCM with a melting temperature within the desired temperature range. For the initial temperatures, the cases of 288.15 K and 298.15 K are considered. An initial temperature equal to the upper limit of the optimal range is not considered in light of the fact that the average temperature increases during take-off, which would make the average temperature higher than the upper limit from the start.
In Figure 10a, for the case with a melting temperature of 288.15 K and initial temperature of 298.15 K, the temperature at the last phase of a flight passes beyond the upper limit. This is because at the start of a flight, the solid fraction of PCM is 0 (i.e., the PCM is fully melted because the temperature of the PCM is greater than the melting temperature), as shown in Figure 11a. This can be determined from the fact that the temperature does not maintain a constant temperature at any point of flight, which means that the PCM remains fully melted from the beginning of the flight. Hence, it can be said that this case is the one with the worst BTMS performance. This suggests that for PCM-based BTMS to effectively manage temperature of batteries on regional passenger airplanes, two conditions are necessary: (1) the melting temperature of the PCM is within the ideal temperature operating window of the battery and (2) the initial temperature of the battery pack is below the melting temperature of the PCM. The best case would be for the PCM to start a flight in its completely solid form.
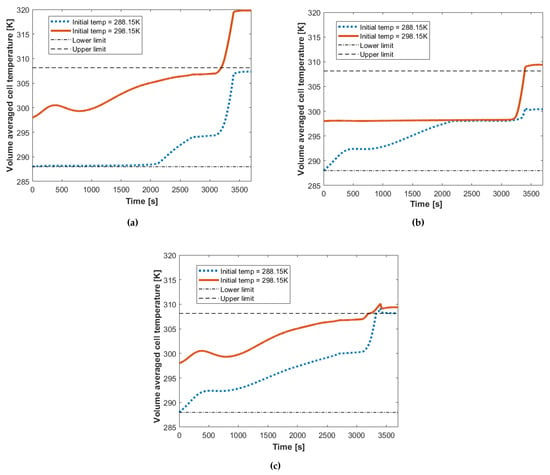
Figure 10.
Profiles of the average lithium-ion cell temperature throughout the progress of each modeled flight, where the initial temperature of the entire modeled domain (i.e., the battery pack including PCM and lithium-ion cells) is either 288.15 K or 298.15 K; (a) considers the case where the PCM melting temperature is 288.15 K, while (b) considers a melting temperature of 298.15 K and (c) considers a melting temperature of 308.15 K. The upper and lower limits refer to the optimal thermal conditions for the lithium-ion cells.
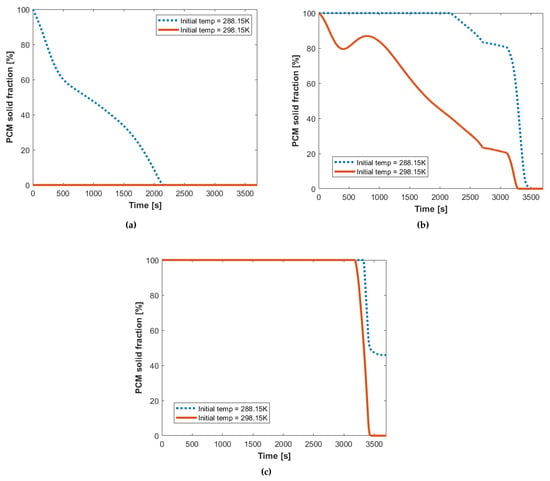
Figure 11.
Profiles of the solid fraction of the PCM throughout the progress of each modeled flight, where the initial temperature of the entire modeled domain (i.e., battery pack including PCM and lithium-ion cells) is either 288.15 K or 298.15 K; (a) considers the case where the PCM melting temperature is 288.15 K, while (b) considers a melting temperature of 298.15 K and (c) considers a melting temperature of 308.15 K.
For all the other cases, the temperature over the entire flight duration predominantly falls within the optimal range. However, the cases with melting temperature of 298.15 K in Figure 10b specifically provide performance superior to that of all other scenarios. This is because the full temperature window that these two cases span is small relative to those of cases with melting temperatures other than 298.15 K, as can be observed in Table 8. Moreover, this scenario spends a greater amount of time in the center of the ideal temperature operating window relative to all other scenarios. Taking the case with a melting temperature of 308.15 K as an example, Figure 11c shows that the PCM starts to melt at around the onset of the last quarter of the flight, and the cell temperature increases to reach the melting temperature before then, as can be seen in Figure 10c. This means that the case with a melting temperature of 298.15 K has relatively high tolerance to sudden variations of temperature due to unplanned events. Such events may include sharp changes in ambient temperature, expected adjustment of air routes owing to severe weather conditions, and emergency landings. Further, it can be noted that the temperature profile is maintained at the melting temperature for a longer period. Here, it is important to highlight that this melting procedure does not terminate before the end of take-off (as shown in Figure 11b), after which power usage and the resulting battery heat generation rate is relatively low. Thus, the BTMS is capable of absorbing all heat generated over the entire take-off phase. It then uses this stored heat to prevent the battery temperature from decreasing due to low ambient temperature during the cruise phase. The significance of this benefit is inherently enhanced as the flight duration increases (e.g., international flights), where the battery discharge rate is lower (i.e., lower heat generation rate) with the longer cruise phase and keeping the cells warm is the primary role of the thermal system.

Table 8.
Size of temperature span (represented in Figure 10) for each case of different PCM melting and initial temperatures.
Thus, having analysed all the cases with different PCM melting and initial temperatures, it is concluded that a PCM with a melting temperature of 298.15 K has the most promising characteristics for further investigation, for the reasons discussed above.
For the case without BTMS under real flight conditions, presented in Figure 8 in Section 3.1, the temperature falls and rises over the duration of the flight such that most of time the temperature remains in the centre of the optimal temperature operating window, which is ideal. On the other hand, with BTMS it can be seen that the temperature only increases, eventually reaching the upper limit of the range at the end of the flight. This stems from two factors. First, a thin layer of insulation was added to the outskirt of the BTMS. Second, the PCM has thermal conductivity, which can be as low as that of the insulation. These two factors mean that the effect of heat convection to the ambient temperature at a high cruising altitude is minimised by limiting the rate of heat transfer through conduction across the BTMS; this becomes significantly important for the application of prolonged flights as compared to the regional one-hour flight studied here, such as international flights, where the cruising phase (low ambient temperature and heat generation rate) accounts for the most of flight duration. This implies that the main role of the BTMS in such cases is to absorb and store the heat generated from the battery; it can be seen in Figure 11b,c that the BTMS is capable of doing this, reemphasising that the latent heat of fusion should take the highest priority among all of the PCM properties that need to be optimised.
4. Conclusions
A numerical model integrating a lumped ECM representing a lithium-ion cell with a model of solid-liquid PCM has been developed in this study to investigate the suitability of PCM-based BTMS for application in electric battery-powered regional passenger aircraft.
This model used the battery ECM parameters and power demand profile of the analysed flight type in order to calculate the heat generation of the battery. Coupled with this, a part of the battery pack was generated in STAR-CCM+ to model the heat transfer within the system and heat loss to the environment using a lumped model representing layers of materials between the battery pack and the outside of the aircraft body. The mass of the PCM was set to contribute just 5% of the total battery pack mass. Ideal operating bounds of the lithium-ion cells, outside which safety, lifetime, and performance are diminished, were set across the investigation to 288.15 K–308.15 K.
It was found that under idealised flight conditions of regional passenger airplanes, heat generation from the battery and ambient heat loss counteract one another to an extent, leading to a reasonable battery operating temperature being maintained throughout. However, it is apparent that deviation from such ideal conditions, an inevitability considering operation throughout the year and in various geographical locations, results in battery operating conditions outside of the bounds set by the investigation. In the case where the thermal resistance to the ambient conditions is eliminated, the battery temperature drops below the ideal temperature bounds, to 281.50 K, while in the adiabatic case (i.e., a perfectly insulated battery pack), the battery temperature increases outside the bounds, reaching 323.60 K, which is close to the safety limit. These findings can justify certain BTMS design considerations.
Our parametric study highlighted that the performance of a PCM-based BTMS increases exponentially with the latent heat of fusion of the PCM, while thermal conductivity has a negligible impact on performance. Increasing the latent heat of fusion must be prioritised over the thermal conductivity, making the PCM being more suitable than CPCM. Our study shows that PCMs must be in their solid state at the start of flight, highlighting the requirement for geographical and seasonal considerations in BTMS design. Pre-conditioning on the ground before a flight may be employed as well. In the case where the initial temperature was 298.15 K and the PCM melting temperature was 288.15 K, the battery pack temperature rose above the ideal bounds, as the energy absorbed by state changes was not harnessed. In all the other cases used to investigate the relationship between ambient temperature and PCM melting temperature, the results were positive, and the battery temperature did not exceed the thermal bounds. While this demonstrates that there is flexibility in the exact design of a PCM-based BTMS for battery flight, further optimisation of BTMS performance is possible. A PCM melting temperature in the centre of the ideal operating conditions (i.e., 298.15 K in this study) yields the best overall performance. Here, the PCM is able to work effectively both as a thermal mass to prevent overheating at any point in the battery pack, and conversely to prevent excessive heat loss during the cruise phase of flight. This design rule leads to the most robust BTMS design which is most capable of damping the adverse effects of unexpected operational and thermal conditions. The PCM-based BTMS has proven to be a viable technology for application to battery-powered regional passenger aircraft; moreover, PCM-based BTMS can be expected to become ever more viable as flight ranges are extended in the coming years.
Suggestions for Future Works
The purpose of this study was to test feasibility and find the trends of the optimal parameter values, and it is hoped that the conclusions of the present study can motivate researchers and leads to more detailed studies by helping to set the directions of future investigations. For more detailed studies specific to different flight types and further system improvements, the following possibilities are suggested for future works:
- Simulation with different batteries, ambient conditions, and power demand profiles.
- Experimental studies is to test the system under realistic physical conditions in order to assess any practical issues, such as PCM leakage.
- BTMS design optimisation by varying the mass of PCM to observe the enhanced temperature uniformity when more PCM is used, along with any offset in terms of reduced performance of the powertrain due to the additional mass.
Author Contributions
Conceptualization, D.K. and A.H.; Methodology, D.K. and S.A.; Software, D.K.; Formal Analysis, D.K.; Investigation, D.K.; Resources, G.B.; Writing—Original Draft Preparation, D.K.; Writing—Review and Editing, D.K. and A.H. and S.A. and G.B.; Visualization, D.K.; Supervision, A.H.; Project Administration, D.K. and A.H.; Funding Acquisition, A.H. All authors have read and agreed to the published version of the manuscript.
Funding
This was funded by the EPSRC Impact Acceleration Account (grant number: A109921) and the Royal Society (research grant: RGS-R1-221197).
Data Availability Statement
Not applicable.
Acknowledgments
This work was carried out using the computational facilities of the Advanced Computing Research Centre, University of Bristol (http://www.bristol.ac.uk/acrc/, accessed on 28 October 2022). We thank Yan Zhao et al. for the raw equivalent circuit model parameters originally presented in [], which we used for our study.
Conflicts of Interest
The authors declare no conflict of interest. The funding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| PCM | Phase change material |
| BTMS | Battery thermal management system |
| EV | Electric vehicle |
| CPCM | Composite phase change material |
| ECM | Equivalent circuit model |
| LIB | Lithium-ion battery |
| RC | Resistor–capacitor |
| RMSD | Root mean squared difference |
| SOC | State of charge |
References
- Grote, M.; Williams, I.; Preston, J. Direct carbon dioxide emissions from civil aircraft. Atmos. Environ. 2014, 95, 214–224. [Google Scholar] [CrossRef] [PubMed]
- Liu, G.; Ouyang, M.; Lu, L.; Li, J.; Han, X. Analysis of the heat generation of lithium-ion battery during charging and discharging considering different influencing factors. J. Therm. Anal. Calorim. 2014, 116, 1001–1010. [Google Scholar] [CrossRef]
- Zhang, L.; Fan, W.; Wang, Z.; Li, W.; Sauer, D.U. Battery heating for lithium-ion batteries based on multi-stage alternative currents. J. Energy Storage 2020, 32, 101885. [Google Scholar] [CrossRef]
- Ma, S.; Jiang, M.; Tao, P.; Song, C.; Wu, J.; Wang, J.; Deng, T.; Shang, W. Temperature effect and thermal impact in lithium-ion batteries: A review. Prog. Nat. Sci. Mater. Int. 2018, 28, 653–666. [Google Scholar] [CrossRef]
- Vetter, J.; Novák, P.; Wagner, M.R.; Veit, C.; Möller, K.C.; Besenhard, J.; Winter, M.; Wohlfahrt-Mehrens, M.; Vogler, C.; Hammouche, A. Ageing mechanisms in lithium-ion batteries. J. Power Sources 2005, 147, 269–281. [Google Scholar] [CrossRef]
- Situ, W.; Yang, X.; Li, X.; Zhang, G.; Rao, M.; Wei, C.; Huang, Z. Effect of high temperature environment on the performance of LiNi0. 5Co0. 2Mn0. 3O2 battery. Int. J. Heat Mass Transf. 2017, 104, 743–748. [Google Scholar] [CrossRef]
- Ramadass, P.; Haran, B.; White, R.; Popov, B.N. Capacity fade of Sony 18650 cells cycled at elevated temperatures: Part II. Capacity fade analysis. J. Power Sources 2002, 112, 614–620. [Google Scholar] [CrossRef]
- Abada, S.; Marlair, G.; Lecocq, A.; Petit, M.; Sauvant-Moynot, V.; Huet, F. Safety focused modeling of lithium-ion batteries: A review. J. Power Sources 2016, 306, 178–192. [Google Scholar] [CrossRef]
- Offer, G.; Patel, Y.; Hales, A.; Bravo Diaz, L.; Marzook, M. Cool metric for lithium-ion batteries could spur progress. Nature 2020, 582, 485–487. [Google Scholar] [CrossRef]
- Chen, K.; Unsworth, G.; Li, X. Measurements of heat generation in prismatic Li-ion batteries. J. Power Sources 2014, 261, 28–37. [Google Scholar] [CrossRef]
- Wright, S.; Dixon-Hardy, D.; Heggs, P.J. Aircraft air conditioning heat exchangers and atmospheric fouling. Therm. Sci. Eng. Prog. 2018, 7, 184–202. [Google Scholar] [CrossRef]
- Qin, P.; Sun, J.; Yang, X.; Wang, Q. Battery thermal management system based on the forced-air convection: A review. ETransportation 2021, 7, 100097. [Google Scholar] [CrossRef]
- Luo, J.; Zou, D.; Wang, Y.; Wang, S.; Huang, L. Battery thermal management systems (BTMs) based on phase change material (PCM): A comprehensive review. Chem. Eng. J. 2022, 430, 132741. [Google Scholar] [CrossRef]
- Hamut, H.S.; Javani, N.; Dinçer, I. Thermal Management of Electric Vehicle Battery Systems; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Waqas, A.; Din, Z.U. Phase change material (PCM) storage for free cooling of buildings—A review. Renew. Sustain. Energy Rev. 2013, 18, 607–625. [Google Scholar] [CrossRef]
- Konstantinidis, C.V. Integration of Thermal Energy Storage in Buildings. Ph.D. Thesis, The University of Texas, Austin, TX, USA, 2010. [Google Scholar]
- Fukai, J.; Kanou, M.; Kodama, Y.; Miyatake, O. Thermal conductivity enhancement of energy storage media using carbon fibers. Energy Convers. Manag. 2000, 41, 1543–1556. [Google Scholar] [CrossRef]
- Jaguemont, J.; Omar, N.; Van den Bossche, P.; Mierlo, J. Phase-change materials (PCM) for automotive applications: A review. Appl. Therm. Eng. 2018, 132, 308–320. [Google Scholar] [CrossRef]
- Mills, A.; Farid, M.; Selman, J.; Al-Hallaj, S. Thermal conductivity enhancement of phase change materials using a graphite matrix. Appl. Therm. Eng. 2006, 26, 1652–1661. [Google Scholar] [CrossRef]
- Choi, M.K. Phase Change Material for Temperature Control of Imager or Sounder on GOES Type Satellites in GEO. In Proceedings of the 44th International Conference on Environmental Systems, Tucson, AZ, USA, 13–17 July 2014. [Google Scholar]
- Pasupathy, A.; Athanasius, L.; Velraj, R.; Seeniraj, R. Experimental investigation and numerical simulation analysis on the thermal performance of a building roof incorporating phase change material (PCM) for thermal management. Appl. Therm. Eng. 2008, 28, 556–565. [Google Scholar] [CrossRef]
- Zhang, J.; Li, X.; Zhang, G.; Wu, H.; Rao, Z.; Guo, J.; Zhou, D. Experimental investigation of the flame retardant and form-stable composite phase change materials for a power battery thermal management system. J. Power Sources 2020, 480, 229116. [Google Scholar] [CrossRef]
- Chen, X.; Gao, H.; Tang, Z.; Dong, W.; Li, A.; Wang, G. Optimization strategies of composite phase change materials for thermal energy storage, transfer, conversion and utilization. Energy Environ. Sci. 2020, 13, 4498–4535. [Google Scholar] [CrossRef]
- Sun, Z.; Fan, R.; Yan, F.; Zhou, T.; Zheng, N. Thermal management of the lithium-ion battery by the composite PCM-Fin structures. Int. J. Heat Mass Transf. 2019, 145, 118739. [Google Scholar] [CrossRef]
- Weng, J.; Xiao, C.; Ouyang, D.; Yang, X.; Chen, M.; Zhang, G.; Yuen, R.K.K.; Wang, J. Mitigation effects on thermal runaway propagation of structure-enhanced phase change material modules with flame retardant additives. Energy 2022, 239, 122087. [Google Scholar] [CrossRef]
- Shen, Z.G.; Chen, S.; Liu, X.; Chen, B. A review on thermal management performance enhancement of phase change materials for vehicle lithium-ion batteries. Renew. Sustain. Energy Rev. 2021, 148, 111301. [Google Scholar] [CrossRef]
- Hossain, M.; Saha, S.; Haque, M.E.; Arif, M.T.; Oo, A.M.T. A parameter extraction method for the Thevenin equivalent circuit model of Li-ion batteries. In Proceedings of the 2019 IEEE Industry Applications Society Annual Meeting, Baltimore, MD, USA, 29 September–3 October 2019; pp. 1–7. [Google Scholar]
- Tian, J.; Xiong, R.; Shen, W. A review on state of health estimation for lithium ion batteries in photovoltaic systems. ETransportation 2019, 2, 100028. [Google Scholar] [CrossRef]
- Bernardi, D.; Pawlikowski, E.; Newman, J. A general energy balance for battery systems. J. Electrochem. Soc. 1985, 132, 5. [Google Scholar] [CrossRef]
- Nejad, S.; Gladwin, D.; Stone, D. A systematic review of lumped-parameter equivalent circuit models for real-time estimation of lithium-ion battery states. J. Power Sources 2016, 316, 183–196. [Google Scholar] [CrossRef]
- Hu, X.; Li, S.; Peng, H. A comparative study of equivalent circuit models for Li-ion batteries. J. Power Sources 2012, 198, 359–367. [Google Scholar] [CrossRef]
- Troxler, Y.; Wu, B.; Marinescu, M.; Yufit, V.; Patel, Y.; Marquis, A.J.; Brandon, N.P.; Offer, G.J. The effect of thermal gradients on the performance of lithium-ion batteries. J. Power Sources 2014, 247, 1018–1025. [Google Scholar] [CrossRef]
- Zhao, Y.; Patel, Y.; Zhang, T.; Offer, G.J. Modeling the effects of thermal gradients induced by tab and surface cooling on lithium ion cell performance. J. Electrochem. Soc. 2018, 165, A3169. [Google Scholar] [CrossRef]
- Hales, A.; Marzook, M.W.; Diaz, L.B.; Patel, Y.; Offer, G. The surface cell cooling coefficient: A standard to define heat rejection from lithium ion battery pouch cells. J. Electrochem. Soc. 2020, 167, 020524. [Google Scholar] [CrossRef]
- Hales, A.; Diaz, L.B.; Marzook, M.W.; Zhao, Y.; Patel, Y.; Offer, G. The cell cooling coefficient: A standard to define heat rejection from lithium-ion batteries. J. Electrochem. Soc. 2019, 166, A2383. [Google Scholar] [CrossRef]
- Cabeza, L.F.; Zsembinszki, G.; Martín, M. Evaluation of volume change in phase change materials during their phase transition. J. Energy Storage 2020, 28, 101206. [Google Scholar] [CrossRef]
- Dekhil, M.; Tala, J.S.; Bulliard-Sauret, O.; Bougeard, D. Numerical analysis of the solidification process of water used as PCM in a rectangular latent heat thermal storage unit. In Proceedings of the Journal of Physics: Conference Series, Coimbatore, India, 25–26 March 2021; Volume 2116, p. 012044. [Google Scholar]
- Dekhil, M.A.; Tala, J.V.S.; Bulliard-Sauret, O.; Bougeard, D. Numerical analysis of the performance enhancement of a latent heat storage shell and tube unit using finned tubes during melting and solidification. Appl. Therm. Eng. 2021, 192, 116866. [Google Scholar] [CrossRef]
- Chen, X.; Cheng, P.; Tang, Z.; Xu, X.; Gao, H.; Wang, G. Carbon-based composite phase change materials for thermal energy storage, transfer, and conversion. Adv. Sci. 2021, 8, 2001274. [Google Scholar] [CrossRef]
- Jebasingh, B.E.; Arasu, A.V. A comprehensive review on latent heat and thermal conductivity of nanoparticle dispersed phase change material for low-temperature applications. Energy Storage Mater. 2020, 24, 52–74. [Google Scholar] [CrossRef]
- Thermal Ceramics—SuperwoolTM 607TM MAX Blanket. Available online: http://www.lloyd-ris.co.uk/pdfs/datasheets/607%20MAX%20DATA%20Sheet.pdf (accessed on 3 October 2022).
- Wu, W.; Wu, W.; Wang, S. Thermal management optimization of a prismatic battery with shape-stabilized phase change material. Int. J. Heat Mass Transf. 2018, 121, 967–977. [Google Scholar] [CrossRef]
- Airbus’ High-Voltage Battery Technology Prepares for Ecopulse Flight Test and Beyond|Airbus. Available online: https://www.airbus.com/en/newsroom/news/2022-03-airbus-high-voltage-battery-technology-prepares-for-ecopulse-flight-test (accessed on 19 June 2022).
- Werfelman, L. Thin Skinned. In Aerosafety World 2011 Nov; Flight Safety Foundation: Alexandria, VA, USA, 2011; pp. 18–20. [Google Scholar]
- Carvill, J. Mechanical Engineer’s Data Handbook; Butterworth-Heinemann: Oxford, UK, 1994. [Google Scholar]
- Jux, B.; Foitzik, S.; Doppelbauer, M. A standard mission profile for hybrid-electric regional aircraft based on web flight data. In Proceedings of the 2018 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Madras, India, 18–21 December 2018; pp. 1–6. [Google Scholar]
- United States Committee on Extension to the Standard Atmosphere and United States. US Standard Atmosphere, 1962: ICAO Standard Atmosphere to 20 Kilometers; Proposed ICAO Extension to 32 Kilometers; Tables and Data to 700 Kilometers; US Government Printing Office: Washington, DC, USA, 1962. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).