A Model Predictive Control Method for Vehicle Drifting Motions with Measurable Errors
Abstract
:1. Introduction
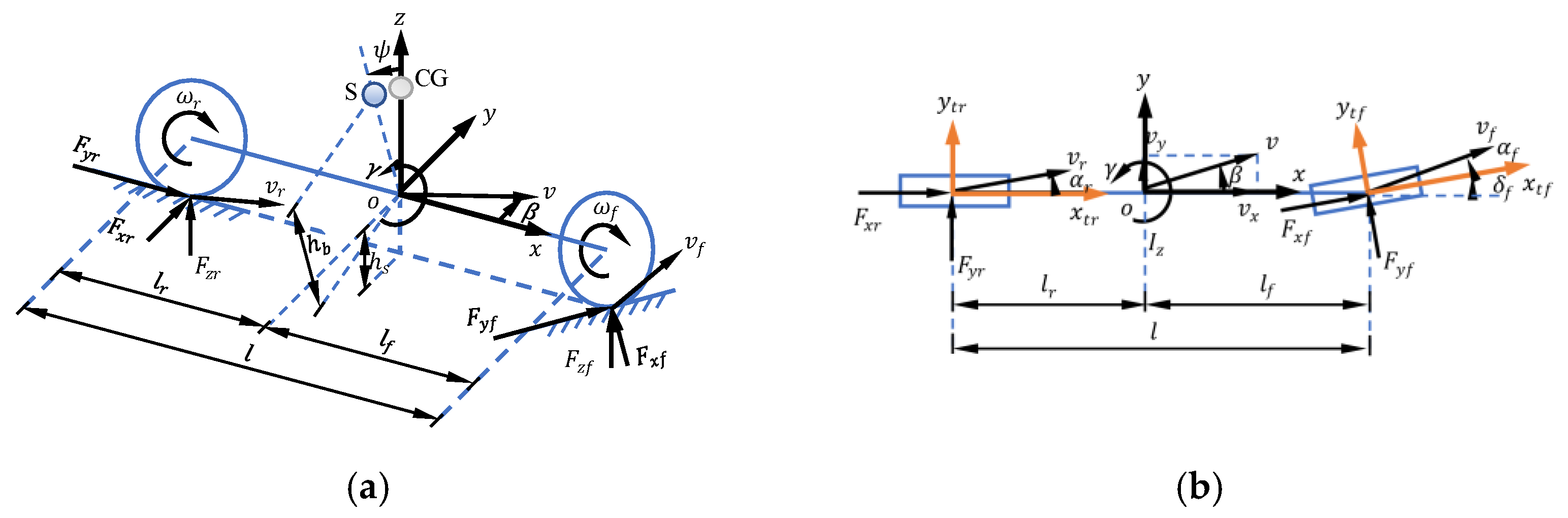
2. Vehicle Dynamics Model
2.1. Vehicle Dynamics Equations
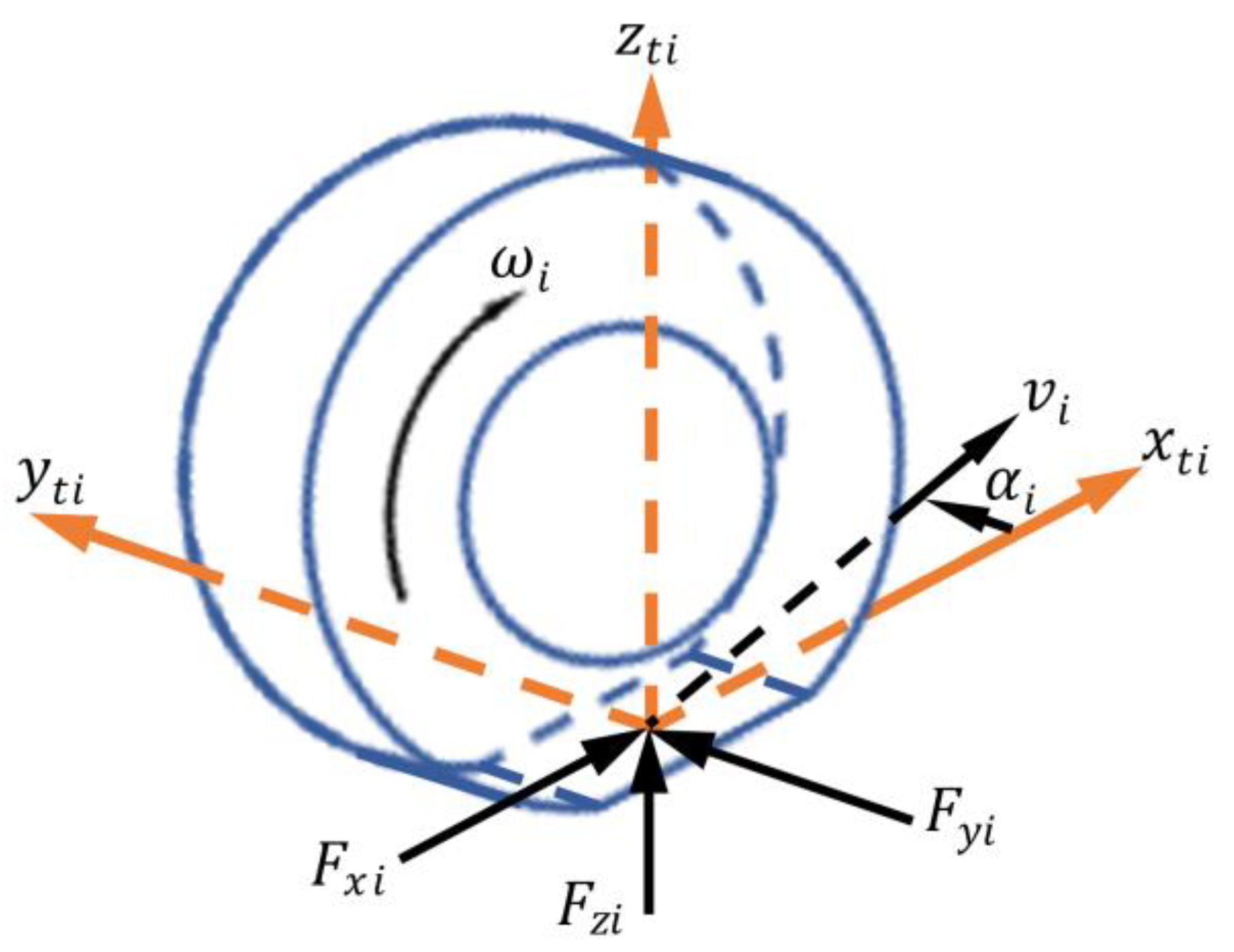
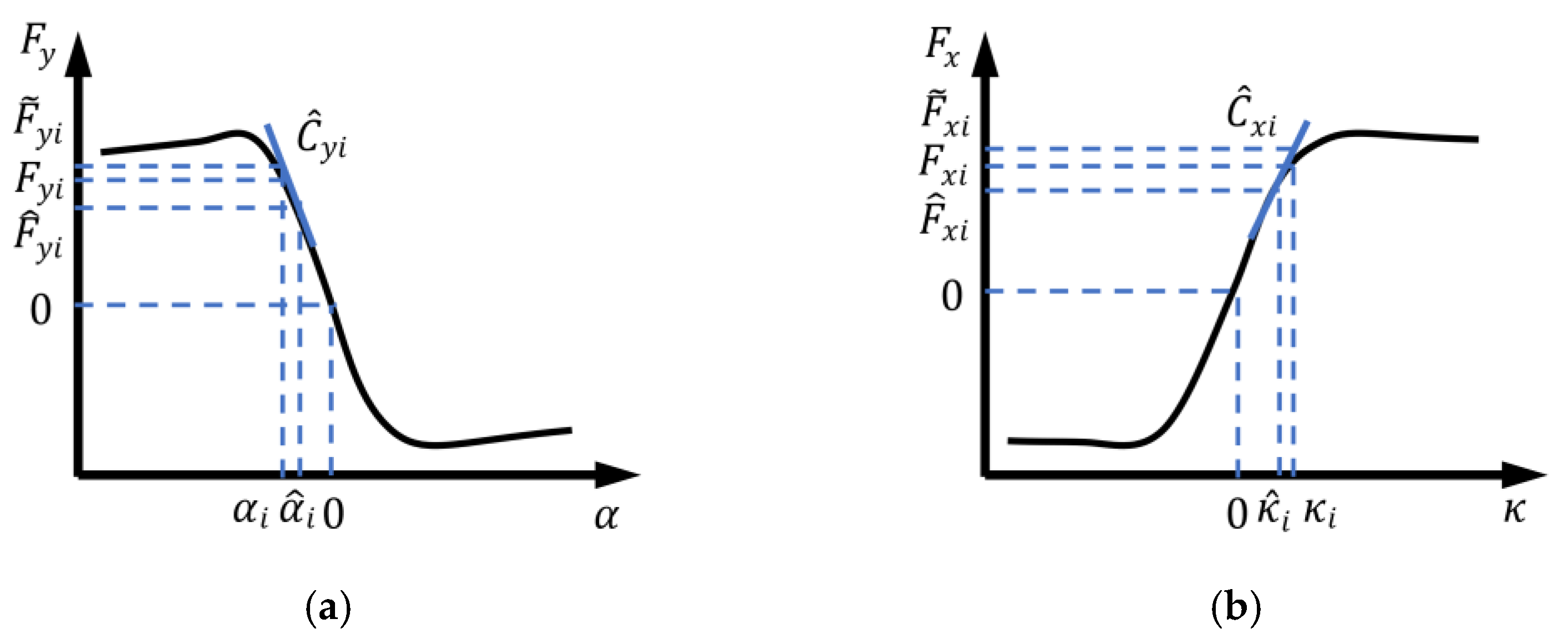
2.2. Tire Force
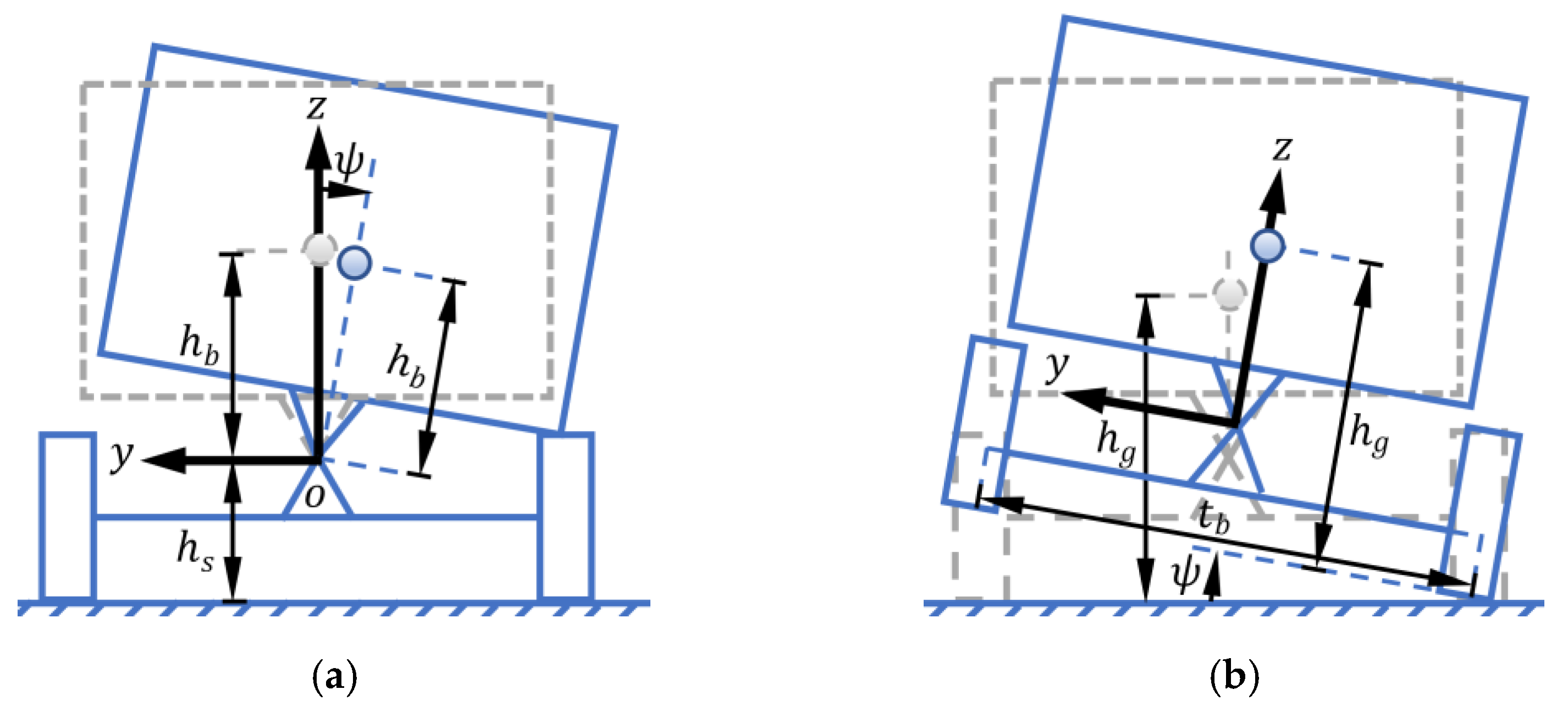
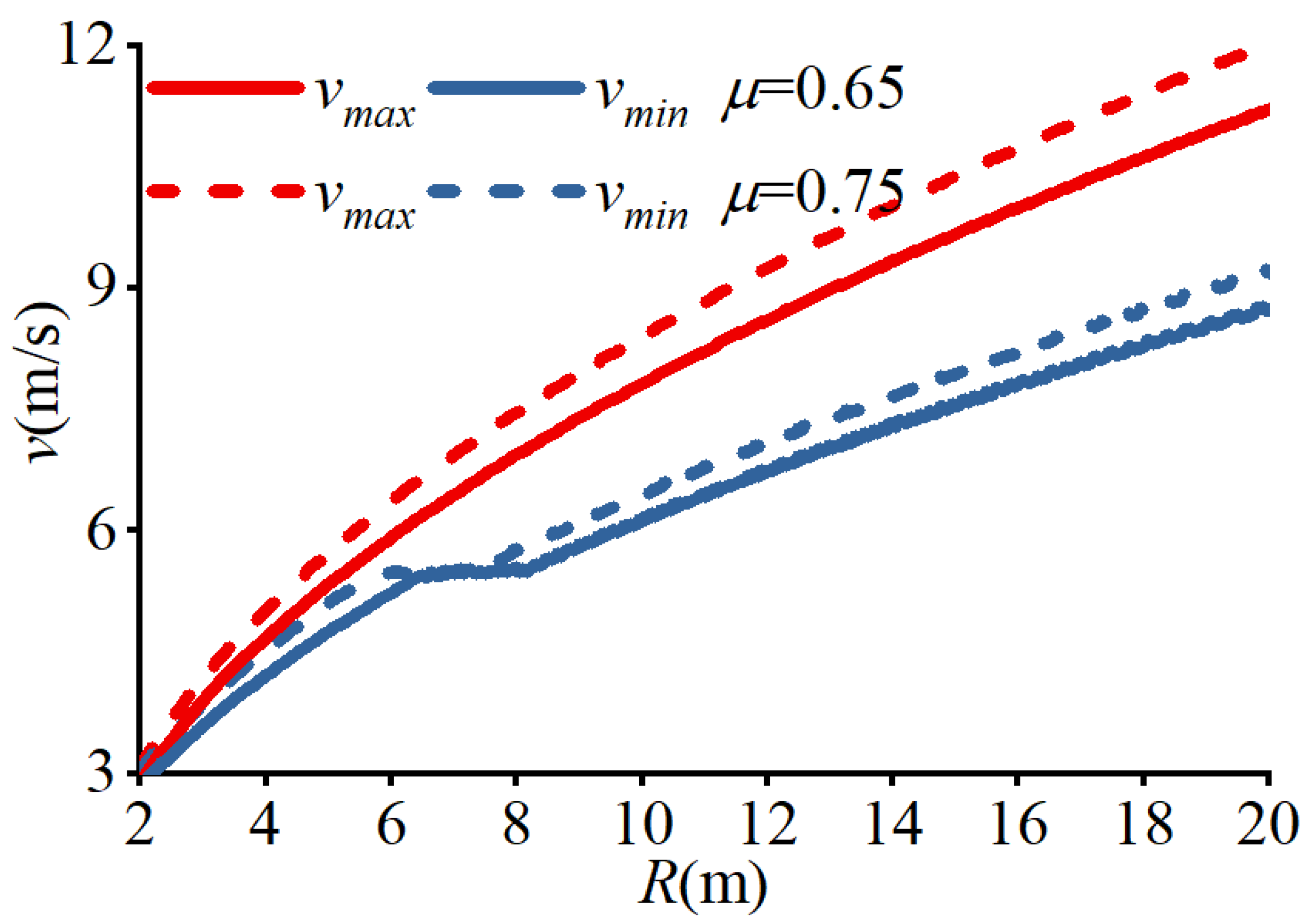
2.3. Roll Safety Analysis
3. Vehicle Drifting Based on Model Predictive Control
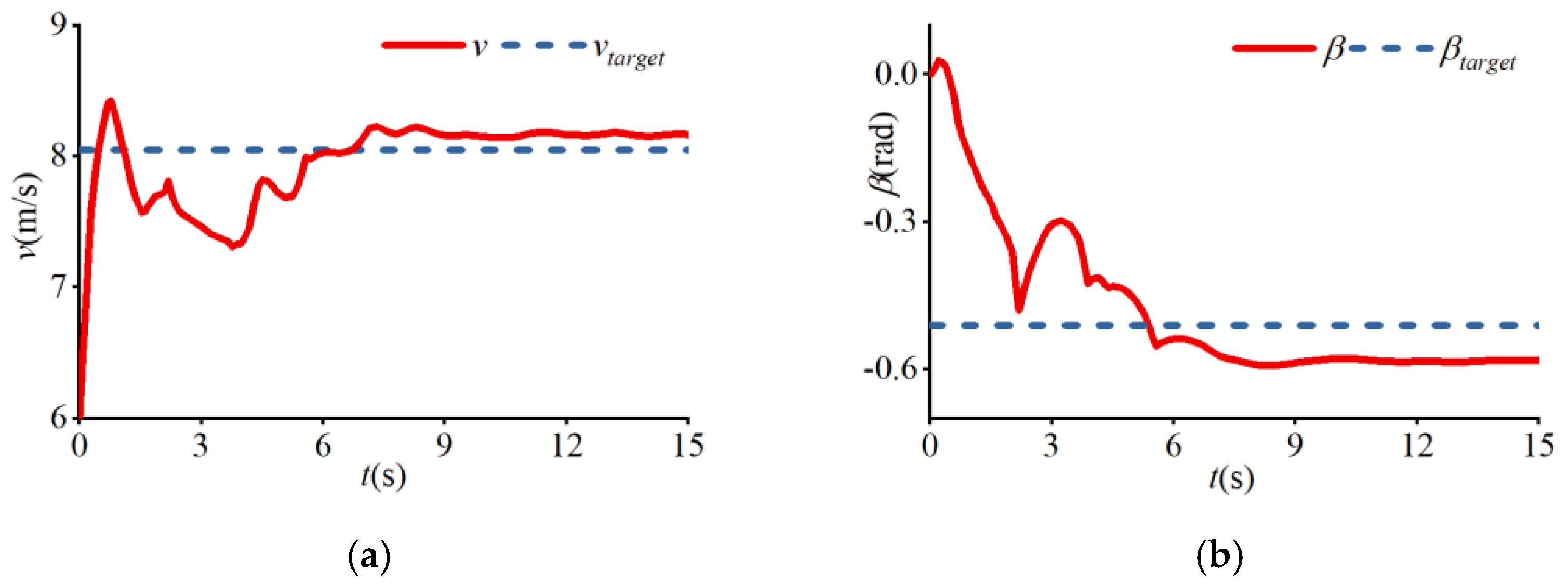
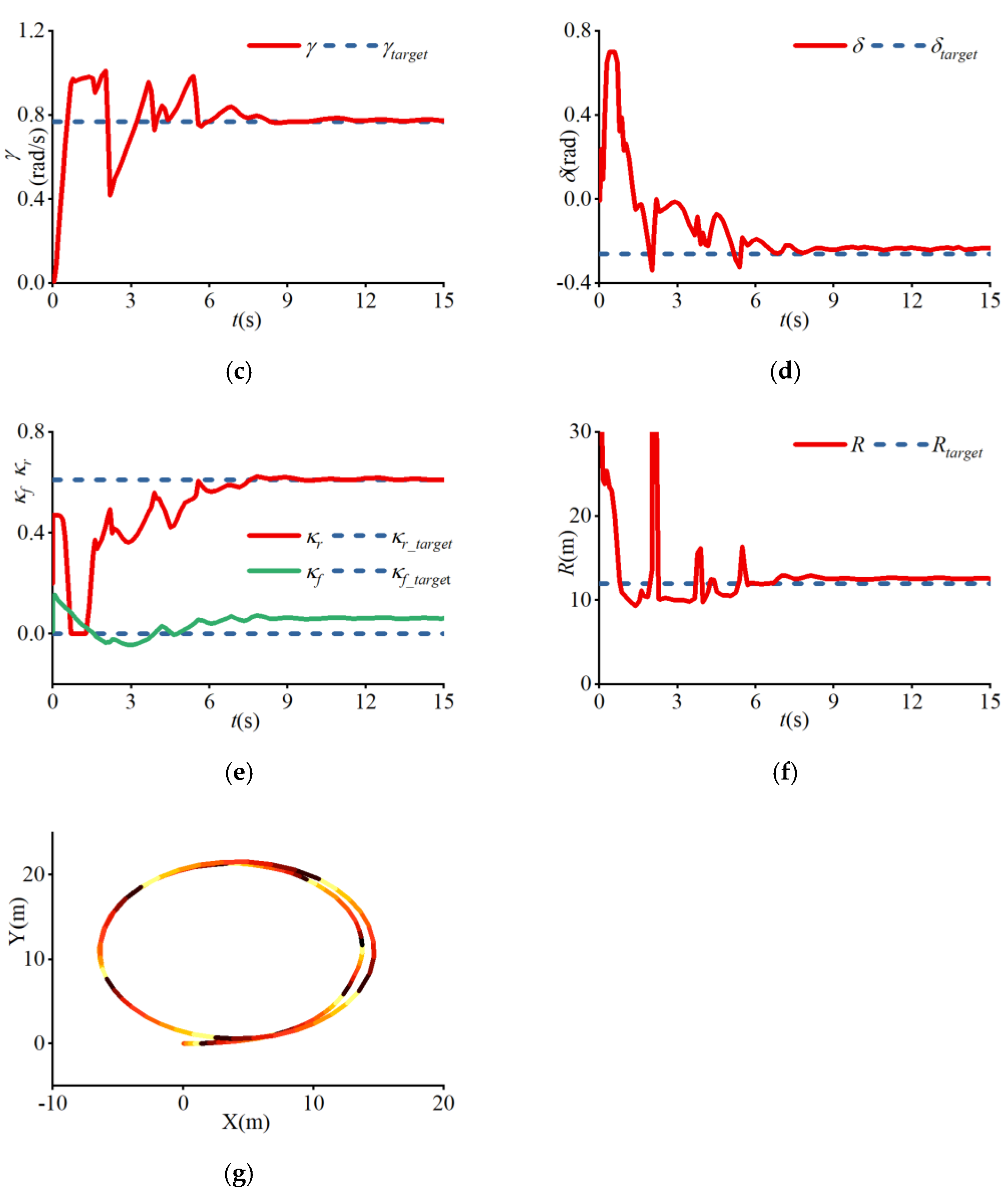
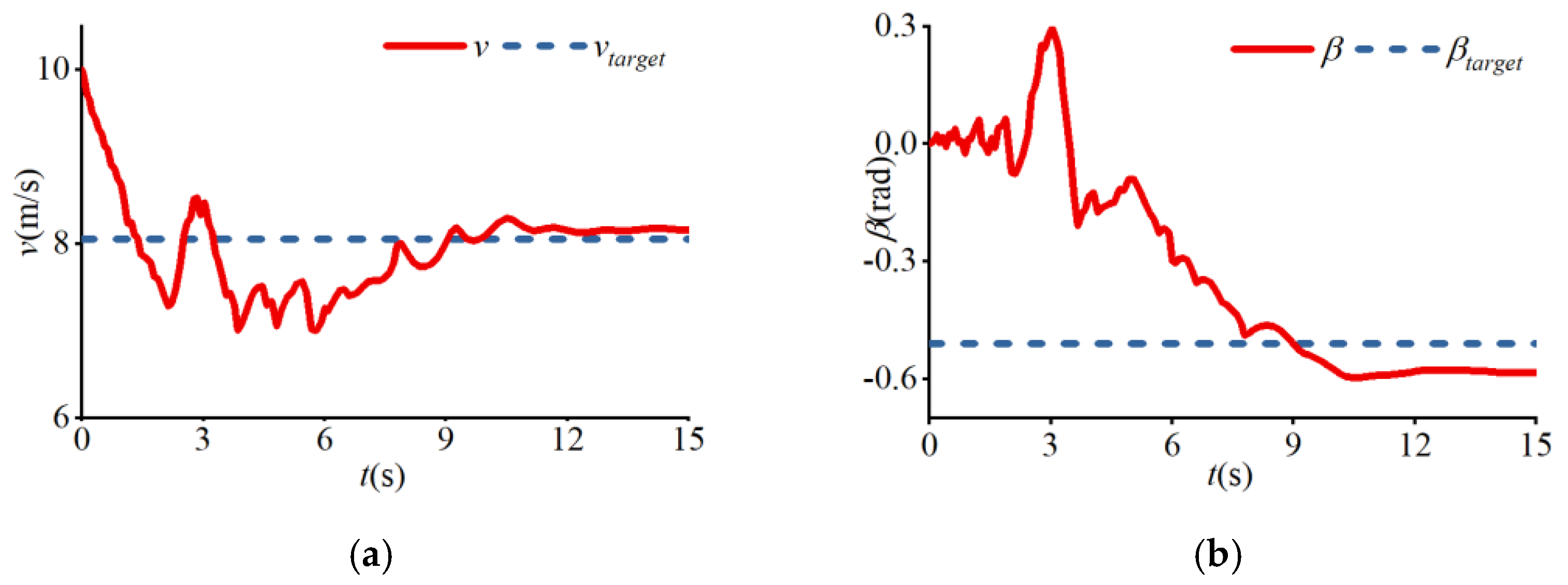
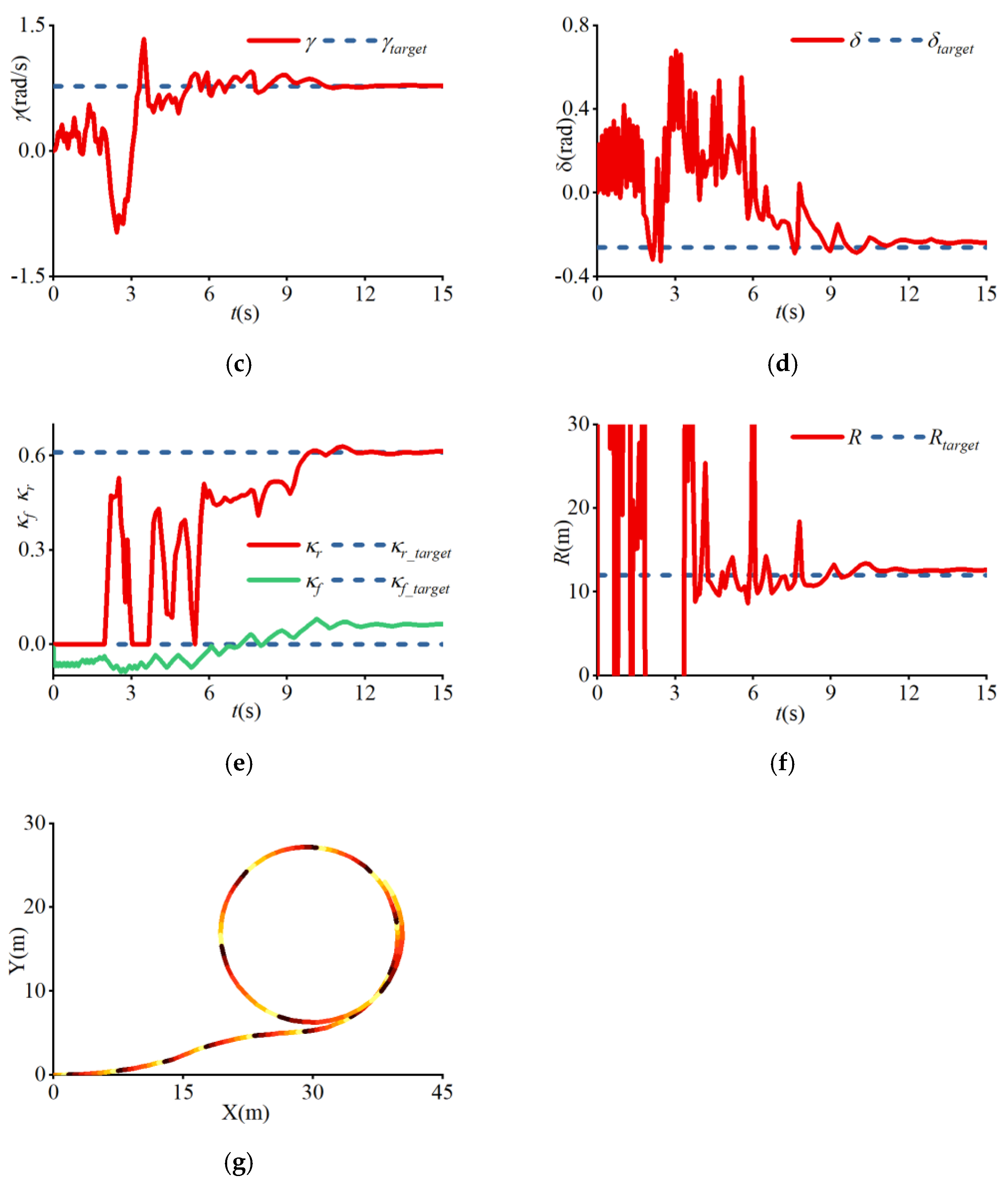
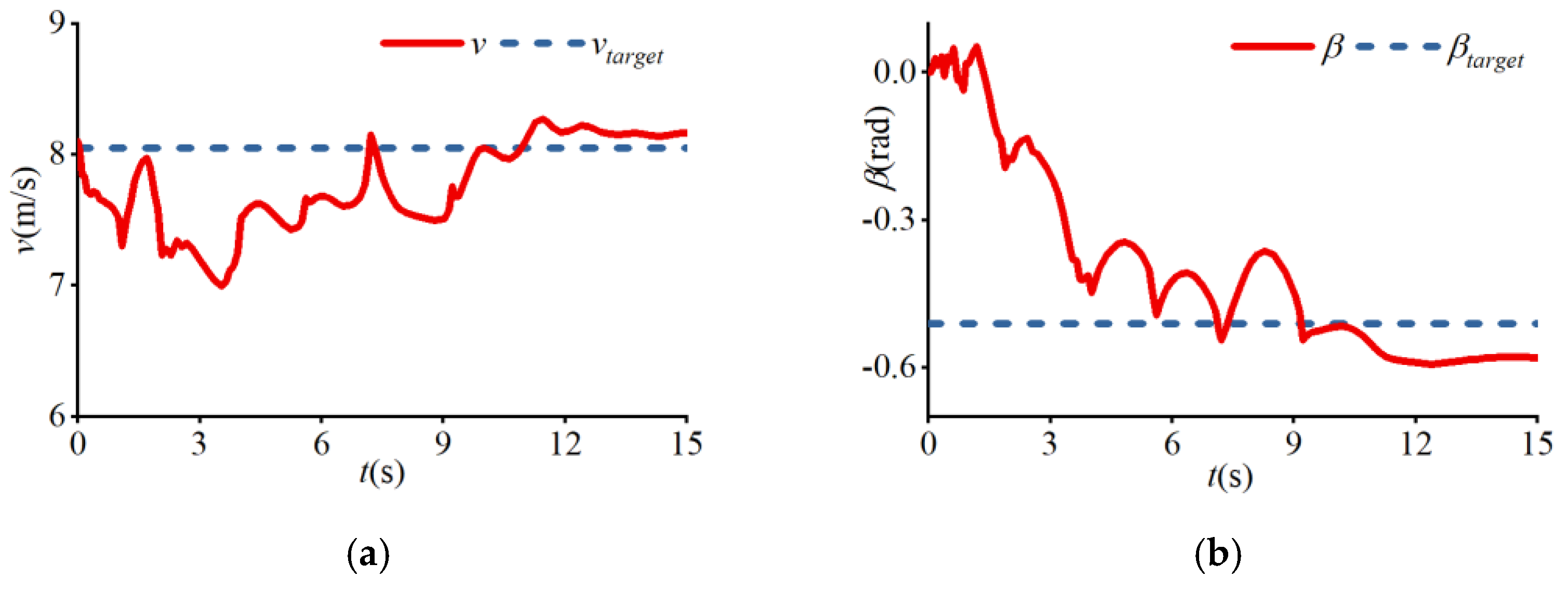
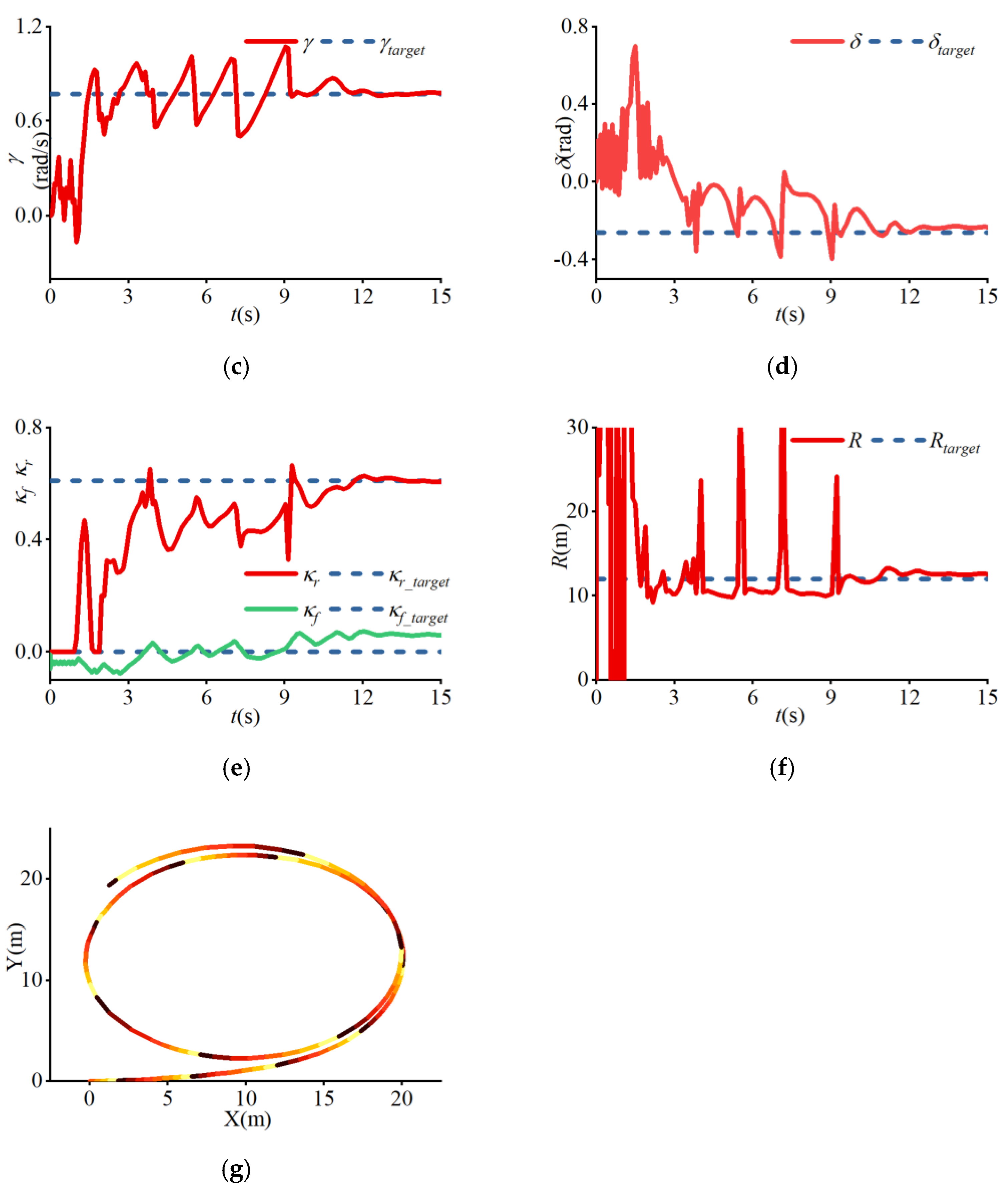
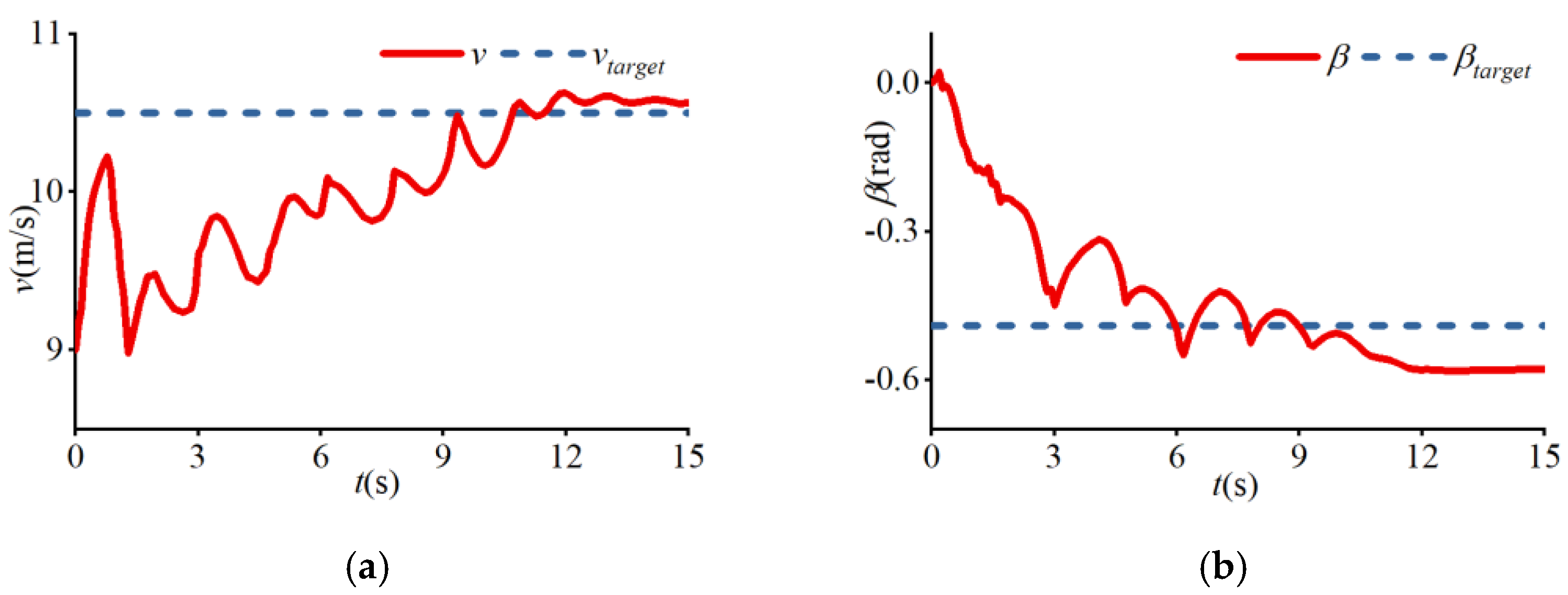
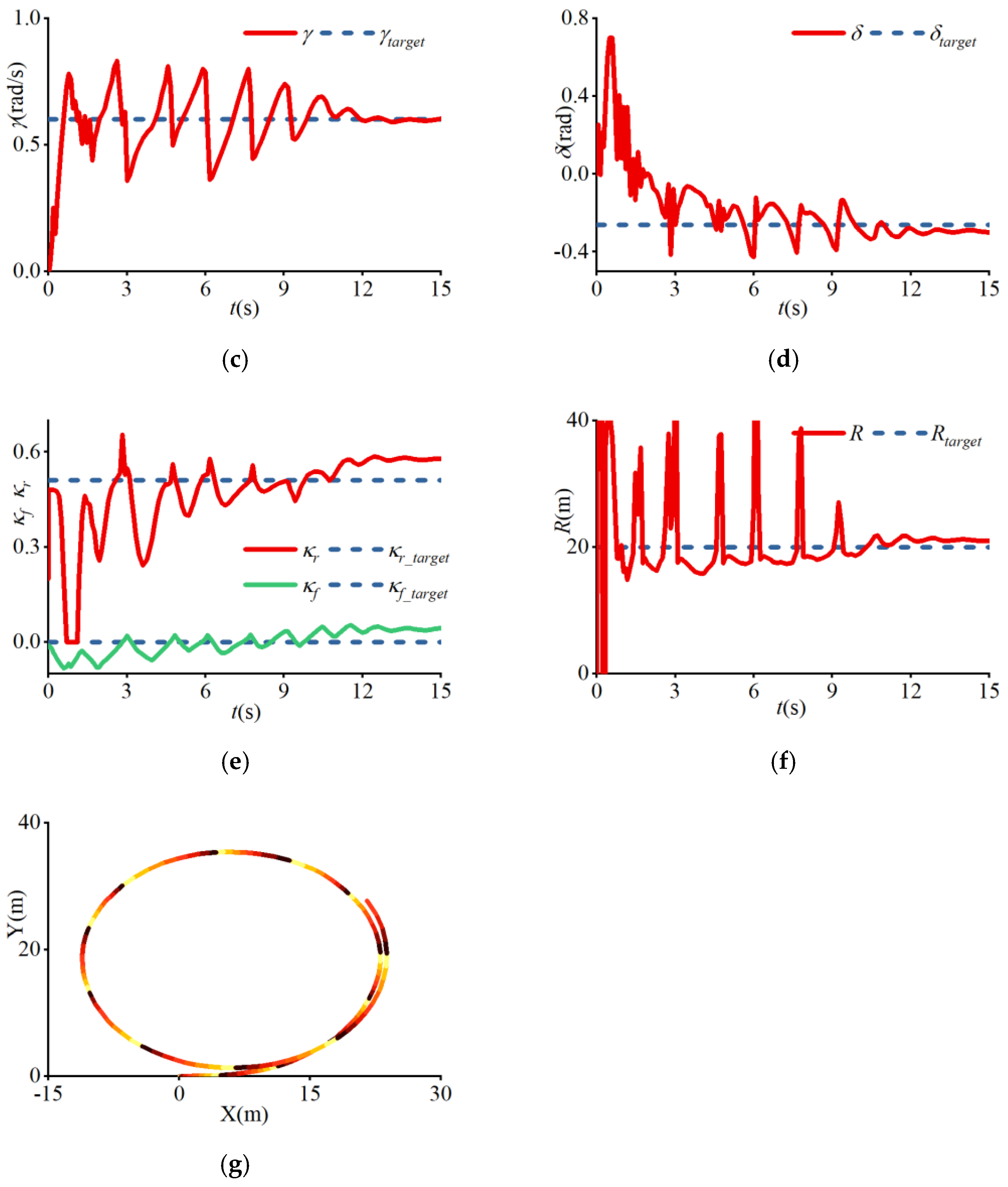
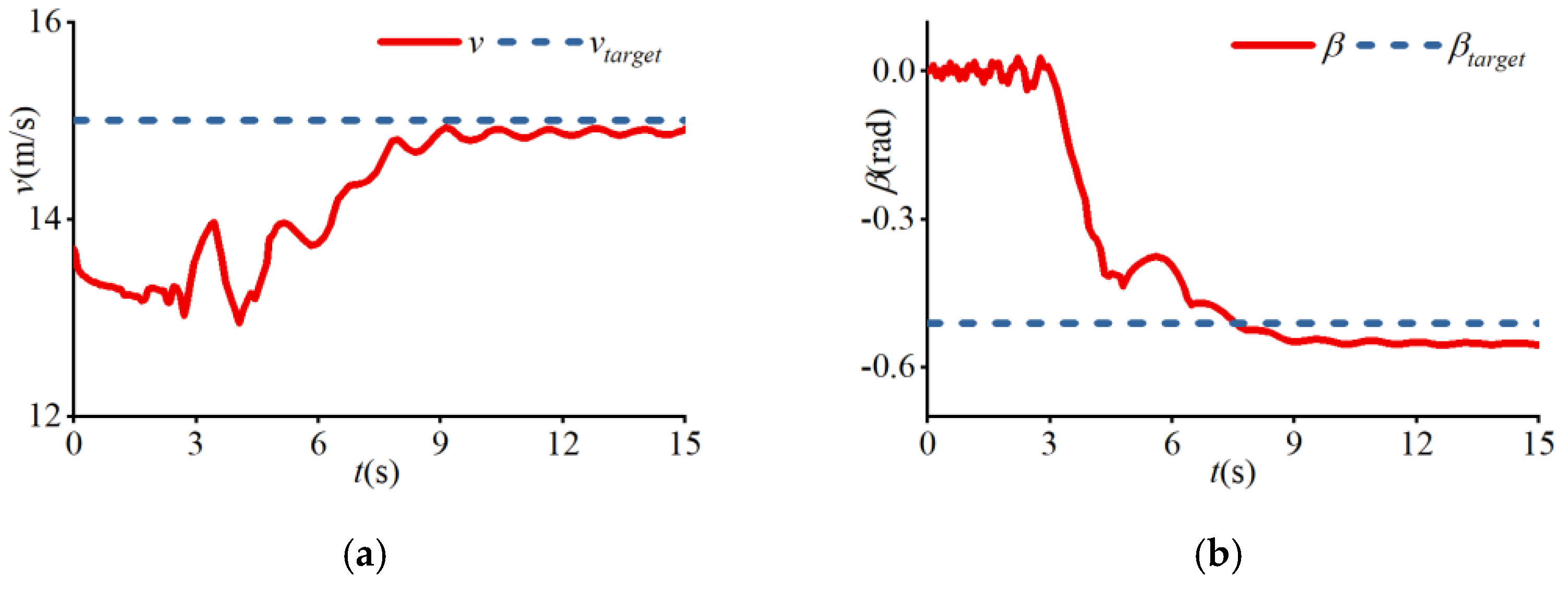
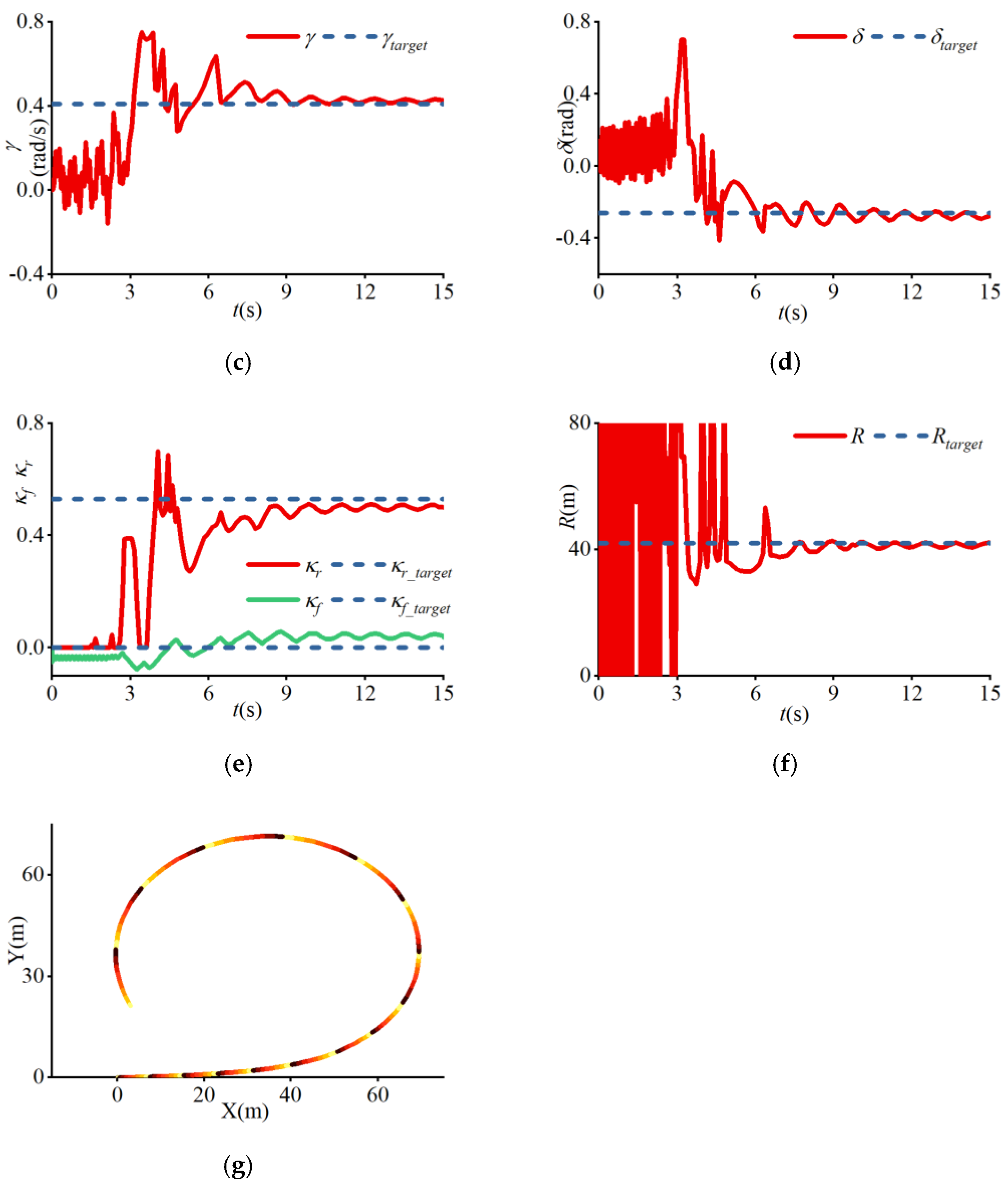
4. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Katzourakis, D.I.; Velenis, E.; Abbink, D.A.; Happee, R.; Holweg, E. Race-Car Instrumentation for Driving Behavior Studies. IEEE Trans. Instrum. Meas. 2012, 61, 462–474. [Google Scholar] [CrossRef]
- Spielberg, N.A.; Brown, M.; Kapania, N.R.; Kegelman, J.C.; Gerdes, J.C. Neural network vehicle models for high-performance automated driving. Sci. Robot. 2019, 4. [Google Scholar] [CrossRef] [PubMed]
- Acosta, M.; Kanarachos, S. Teaching a vehicle to autonomously drift: A data-based approach using Neural Networks. Knowl.-Based Syst. 2018, 153, 12–28. [Google Scholar] [CrossRef]
- Cai, P.; Mei, X.; Tai, L.; Sun, Y.; Liu, M. High-Speed Autonomous Drifting with Deep Reinforcement Learning. IEEE Robot. Au-Tom. Lett. 2020, 5, 1247–1254. [Google Scholar] [CrossRef] [Green Version]
- Jin, X.; Yin, G.; Wang, J. Robust fuzzy control for vehicle lateral dynamic stability via Takagi-Sugeno fuzzy approach. In Proceedings of the American Control Conference (ACC), Seattle, WA, USA, 24–26 May 2017. [Google Scholar]
- Nguyen, A.T.; Rath, J.; Guerra, T.M.; Palhares, R.; Zhang, H. Robust Set-Invariance Based Fuzzy Output Tracking Control for Vehicle Autonomous Driving Under Uncertain Lateral Forces and Steering Constraints. IEEE Trans. Intell. Transp. Syst. 2021, 22, 5849–5860. [Google Scholar] [CrossRef]
- Hindiyeh, R.Y.; Gerdes, J.C. Equilibrium analysis of drifting vehicles for control design. In Proceedings of the ASME 2009 Dynamic Systems and Control Conference, Los Angeles, CA, USA, 12–14 October 2009. [Google Scholar]
- Velenis, E.; Katzourakis, D.; Frazzoli, E.; Tsiotras, P.; Happee, R. Steady-state drifting stabilization of RWD vehicles. Control Eng. Pract. 2011, 19, 1363–1376. [Google Scholar] [CrossRef]
- Zhang, F.; Gonzales, J.; Li, K.; Borrelli, F. Autonomous Drift Cornering Mixed Open-loop and Closed-loop Control. IFAC Pap. 2017, 50, 1916–1922. [Google Scholar] [CrossRef]
- Khan, M.A.; Youn, E.; Youn, I.; Wu, L. Steady State Drifting Controller for Vehicles Travelling in Reverse Direction. In Proceedings of the 15th International Bhurban Conference on Applied Sciences and Technology (IBCAST), Islamabad, Pakistan, 9–13 January 2018. [Google Scholar]
- Zubov, I.; Afanasyev, I.; Gabdullin, A.; Mustafin, R.; Shimchik, I. Autonomous Drifting Control in 3D Car Racing Simulator. In Proceedings of the 9th International Conference on Intelligent Systems (IS), Funchal, Portugal, 25–27 September 2018. [Google Scholar]
- Vignati, M.; Sabbioni, E.; Cheli, F.A. Torque Vectoring Control for Enhancing Vehicle performance in Drifting. Electronics 2018, 7, 394. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Zuo, J.; Liu, S.; Zheng, W.; Wang, L. Model-free adaptive control of steady-state drift of unmanned vehicles. Control Theory Appl. 2021, 38, 23–32. [Google Scholar]
- Hrovat, D.; Di Cairano, S.; Tseng, H.E.; Kolmanovsky, I.V. The Development of Model Predictive Control in Automotive Industry: A Survey. In Proceedings of the IEEE International Conference on Control Applications (CCA), Dubrovnik, Croatia, 3–5 October 2012. [Google Scholar]
- Liu, M.; Leng, B.; Xiong, L.; Yu, Y.; Yang, X. Segment Drift Control with a Supervision Mechanism for Autonomous Vehicles. Actuators 2021, 10, 219. [Google Scholar] [CrossRef]
- Xu, D.; Wang, G.; Qu, L.; Ge, C. Robust Control with Uncertain Disturbances for Vehicle Drift Motions. Appl. Sci. 2021, 11, 4917. [Google Scholar] [CrossRef]
- Li, P.; Nguypen, A.T.; Du, H.; Wang, Y.; Zhang, H. Polytopic LPV approaches for intelligent automotive systems: State of the art and future challenges. Mech. Syst. Signal Process. 2021, 161, 107931. [Google Scholar] [CrossRef]
- Guo, K.; Lu, D. UniTire: Unified tire model for vehicle dynamic simulation. Veh. Syst. Dyn. Int. J. Veh. Mech. Mobil. 2007, 45, 79–99. [Google Scholar] [CrossRef]
- Guo, K.; Lu, D.; Chen, S.; Lin, W.; Lu, X. The UniTire model: A nonlinear and non-steady-state tyre model for vehicle dynamics simulation. Veh. Syst. Dyn. Int. J. Veh. Mech. Mobil. 2005, 43, 341–358. [Google Scholar] [CrossRef]
- Guo, K. UniTire: Unified Tire Model. J. Mech. Eng. 2016, 52, 90–99. [Google Scholar] [CrossRef]
- Yoon, J.; Kim, D.; Yi, K. Design of a rollover indexbased vehicle stability control scheme. Veh. Syst. Dyn. Int. J. Veh. Mech. Mobil. 2007, 45, 459–475. [Google Scholar] [CrossRef]
- Jia, G. The Research on Anti-Roll Control of Sport Utility Vehicle Based on Differential Braking. Master’s Thesis, Tsinghua University, Beijing, China, 2015. [Google Scholar]
- Chou, T.; Chu, T. An improvement in rollover detection of articulated vehicles using the grey system theory. Veh. Syst. Dyn. 2014, 52, 679–703. [Google Scholar] [CrossRef]
- Erlien, S.M.; Fujita, S.; Gerdes, J.C. Shared Steering Control Using Safe Envelopes for Obstacle Avoidance and Vehicle Stability. IEEE Trans. Intell. Transp. Syst. 2016, 17, 441–451. [Google Scholar] [CrossRef]
| Parameter Symbol | Unit | Value |
|---|---|---|
| kg | 1126.7 | |
| kg | 1111 | |
| kg·m2 | 2038 | |
| m | 1.265 | |
| m | 1.335 | |
| m | 0.136 | |
| m | 0.518 | |
| m2 | 1.6 | |
| N/kg | 9.8 | |
| 0.65 |
| (m) | (m/s) | (rad) | (rad/s) | |||
|---|---|---|---|---|---|---|
| (a) | 12 | 8.73 | −0.06 | 0.73 | 0.06 | 0.03 |
| (b) | 12 | 6.82 | −0.90 | 0.91 | −0.7 | 0.95 |
| (c) | 12 | 8.05 | −0.51 | 0.77 | −0.26 | 0.61 |
| (d) | 20 | 10.5 | −0.49 | 0.6 | −0.26 | 0.51 |
| (e) | 42 | 15 | −0.51 | 0.41 | −0.26 | 0.53 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, D.; Han, Y.; Ge, C.; Qu, L.; Zhang, R.; Wang, G. A Model Predictive Control Method for Vehicle Drifting Motions with Measurable Errors. World Electr. Veh. J. 2022, 13, 54. https://doi.org/10.3390/wevj13030054
Xu D, Han Y, Ge C, Qu L, Zhang R, Wang G. A Model Predictive Control Method for Vehicle Drifting Motions with Measurable Errors. World Electric Vehicle Journal. 2022; 13(3):54. https://doi.org/10.3390/wevj13030054
Chicago/Turabian StyleXu, Dongxin, Yueqiang Han, Chang Ge, Longtao Qu, Rui Zhang, and Guoye Wang. 2022. "A Model Predictive Control Method for Vehicle Drifting Motions with Measurable Errors" World Electric Vehicle Journal 13, no. 3: 54. https://doi.org/10.3390/wevj13030054
APA StyleXu, D., Han, Y., Ge, C., Qu, L., Zhang, R., & Wang, G. (2022). A Model Predictive Control Method for Vehicle Drifting Motions with Measurable Errors. World Electric Vehicle Journal, 13(3), 54. https://doi.org/10.3390/wevj13030054






