Soft Actor-Critic Algorithm-Based Energy Management Strategy for Plug-In Hybrid Electric Vehicle
Abstract
1. Introduction
1.1. Literature Review
1.2. Contribution
2. PHEV Powertrain Model
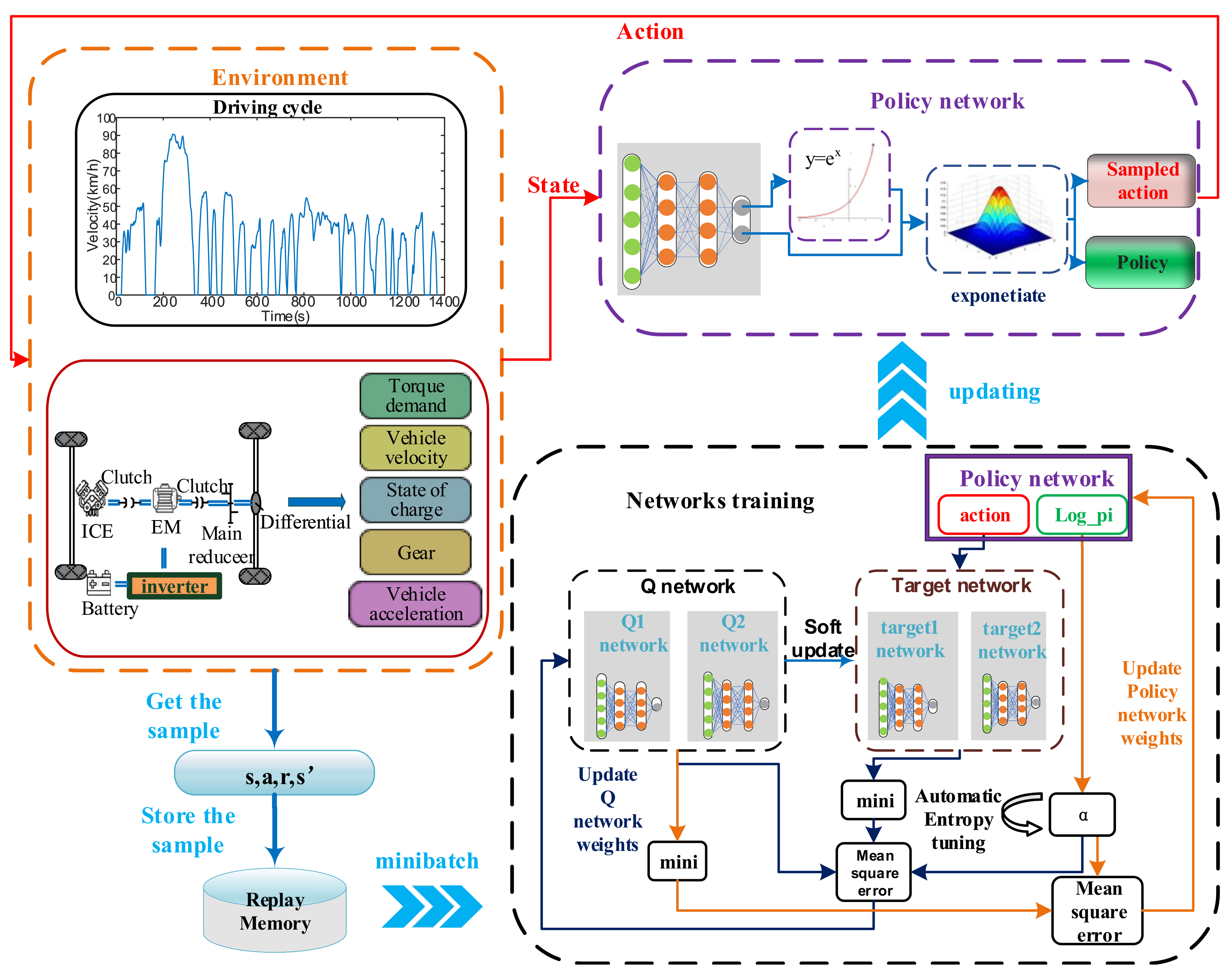
3. Energy Management Strategy Based on SAC Algorithm
3.1. SAC Algorithm
3.1.1. Soft Policy Iteration
3.1.2. Automatic Entropy Adjustment
3.2. Practical Algorithm
| Algorithm 1. Soft actor-critic DRL with automating entropy adjustment algorithm. |
|
3.3. Design of SAC Algorithm-Based EMS
3.3.1. State
3.3.2. Action
3.3.3. Reward
4. Simulation and Discussion
4.1. The Performance of SAC Algorithm-Based EMS for UDDS
4.2. Comparison of Different Strategies
4.3. The Adaptability of SAC Algorithm-Based EMS
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Deng, Z.; Weng, D.; Chen, J.; Liu, R.; Wang, Z.; Bao, J.; Zheng, Y.; Wu, Y. Airvis: Visual analytics of air pollution propagation. IEEE Trans. Vis. Comput. Graph. 2020, 26, 800–810. [Google Scholar]
- Djelailia, O.; Necaibia, S.; Kelaiaia, M.S.; Merad, F.; Labar, H.; Chouial, H. Optimal fuel consumption planning and energy management strategy for a hybrid energy system with pumped storage. In Proceedings of the 2019 1st International Conference on Sustainable Renewable Energy Systems and Applications (ICSRESA), Tébessa, Algeria, 4–5 December 2019; pp. 1–6. [Google Scholar]
- Ceraolo, M.; di Donato, A.; Franceschi, G. A general approach to energy optimization of hybrid electric vehicles. IEEE Trans. Veh. Technol. 2008, 57, 1433–1441. [Google Scholar] [CrossRef]
- Mahyiddin, S.H.; Mohamed, M.R.; Mustaffa, Z.; Khor, A.C.; Sulaiman, M.H.; Ahmad, H.; Rahman, S.A. Fuzzy Logic Energy Management System of Series Hybrid Electric Vehicle; IET Conference Publications: Kuala Lumpur, Malaysia, 2016; pp. 1–6. [Google Scholar]
- Zhang, F.; Hu, X.; Langari, R.; Cao, D. Energy management strategies of connected hevs and phevs: Recent progress and outlook. Prog. Energy Combust. Sci. 2019, 73, 235–256. [Google Scholar] [CrossRef]
- Liu, K.; Jiao, X.; Yang, C.; Wang, W.; Xiang, C.; Wang, W. Event-triggered intelligent energy management strategy for plug-in hybrid electric buses based on vehicle cloud optimisation. IET Intell. Transp. Syst. 2020, 14, 1153–1162. [Google Scholar] [CrossRef]
- Sierra, A.; Herrera, V.; González-Garrido, A.; Milo, A.; Gaztañaga, H.; Camblong, H. Experimental comparison of energy management strategies for a hybrid electric bus in a test-bench. In Proceedings of the 2018 Thirteenth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte-Carlo, Monaco, 5–7 May 2018; pp. 1–9. [Google Scholar]
- Ma, G.; Ghasemi, M.; Song, X. Integrated powertrain energy management and vehicle coordination for multiple connected hybrid electric vehicles. IEEE Trans. Veh. Technol. 2018, 67, 2893–2899. [Google Scholar] [CrossRef]
- Chen, H.; Xiong, R.; Lin, C.; Shen, W. Model predictive control based real-time energy management for hybrid energy storage system. CSEE J. Power Energy Syst. 2021, 7, 862–874. [Google Scholar]
- Zhang, Y.; Ma, R.; Zhao, D.; Huang, F.; Liu, W. A Novel Energy Management Strategy Based on Dual Reward Function Q-learning for Fuel Cell Hybrid Electric Vehicle. IEEE Trans. Ind. Electron. 2022, 69, 1537–1547. [Google Scholar] [CrossRef]
- Du, G.; Zou, Y.; Zhang, X.; Kong, Z.; Wu, J.; He, D. Intelligent energy management for hybrid electric tracked vehicles using online reinforcement learning. Appl. Energy 2019, 251, 113388. [Google Scholar] [CrossRef]
- Lian, R.; Tan, H.; Peng, J.; Li, Q.; Wu, Y. Cross-type transfer for deep reinforcement learning based hybrid electric vehicle energy management. IEEE Trans. Veh. Technol. 2020, 69, 8367–8380. [Google Scholar] [CrossRef]
- Wang, P.; Li, Y.; Shekhar, S.; Northrop, W.F. Actor-critic based deep reinforcement learning framework for energy management of extended range electric delivery vehicles. In Proceedings of the 2019 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Hong Kong, China, 8–12 July 2019; pp. 1379–1384. [Google Scholar]
- Qiu, L.; Qian, L.; Zomorodi, H.; Pisu, P. Global optimal energy management control strategies for connected four-wheel-drive hybrid electric vehicles. IET Intell. Transp. Syst. 2017, 11, 264–272. [Google Scholar] [CrossRef]
- Ostadian, R.; Ramoul, J.; Biswas, A.; Emadi, A. Intelligent energy management systems for electrified vehicles: Current status, challenges, and emerging trends. IEEE Open J. Veh. Technol. 2020, 1, 279–295. [Google Scholar] [CrossRef]
- Li, P.; Jiao, X.; Li, Y. Adaptive real-time energy management control strategy based on fuzzy inference system for plug-in hybrid electric vehicles. Control Eng. Pract. 2021, 107, 104703. [Google Scholar] [CrossRef]
- Zhou, S.; Chen, Z.; Huang, D.; Lin, T. Adaptive real-time energy management control strategy based on fuzzy inference system for plug-in hybrid electric vehicles. IEEE Trans. Power Electron. 2021, 36, 5926–5940. [Google Scholar] [CrossRef]
- Natella, D.; Mostacciuolo, E.; Baccari, S.; Vasca, F. A velocity-thresholds power splitting optimization for hybrid electric vehicles. In Proceedings of the 2019 18th European Control Conference (ECC), Naples, Italy, 25–28 June 2019; pp. 4148–4153. [Google Scholar]
- Hu, B.; Li, J. An adaptive hierarchical energy management strategy for hybrid electric vehicles combining heuristic domain knowledge and data-driven deep reinforcement learning. IEEE Trans. Transp. Electrif. 2022, 8, 3275–3288. [Google Scholar] [CrossRef]
- Zeng, X.; Wang, J. A parallel hybrid electric vehicle energy management strategy using stochastic model predictive control with road grade preview. IEEE Trans. Control Syst. Technol. 2015, 23, 2416–2423. [Google Scholar] [CrossRef]
- Zhang, F.; Hu, X.; Langari, R.; Wang, L.; Cui, Y.; Pang, H. Adaptive energy management in automated hybrid electric vehicles with flexible torque request. Energy 2021, 214, 118873. [Google Scholar] [CrossRef]
- Liu, T.; Zou, Y.; Liu, D.; Sun, F. Reinforcement learning of adaptive energy management with transition probability for a hybrid electric tracked vehicle. IEEE Trans. Ind. Electron. 2015, 62, 7837–7846. [Google Scholar] [CrossRef]
- Miro-Padovani, T.; Colin, G.; Ketfi-Chérif, A.; Chamaillard, Y. Implementation of an energy management strategy for hybrid electric vehicles including drivability constraints. IEEE Trans. Veh. Technol. 2016, 65, 5918–5929. [Google Scholar] [CrossRef]
- Park, S.; Ahn, C. Power management controller for a hybrid electric vehicle with predicted future acceleration. IEEE Trans. Veh. Technol. 2019, 68, 10477–10488. [Google Scholar] [CrossRef]
- Zhang, Y.; Chu, L.; Fu, Z.; Xu, N.; Guo, C.; Zhao, D.; Ou, Y.; Xu, L. Energy management strategy for plug-in hybrid electric vehicle integrated with vehicle-environment cooperation control. Energy 2020, 197, 117192. [Google Scholar] [CrossRef]
- Li, J.; Liu, Y.; Qin, D.; Li, G.; Chen, Z. Research on equivalent factor boundary of equivalent consumption minimization strategy for phevs. IEEE Trans. Veh. Technol. 2020, 69, 6011–6024. [Google Scholar] [CrossRef]
- Feng, T.; Yang, L.; Gu, Q.; Hu, Y.; Yan, T.; Yan, B. A supervisory control strategy for plug-in hybrid electric vehicles based on energy demand prediction and route preview. IEEE Trans. Veh. Technol. 2015, 64, 1691–1700. [Google Scholar]
- Borhan, H.; Vahidi, M.; Phillips, A.L.; Kuang, M.; Kolmanovsky, I.V.; Di Cairano, S. Mpc-based energy management of a power-split hybrid electric vehicle. IEEE Trans. Control Syst. Technol. 2012, 20, 593–603. [Google Scholar] [CrossRef]
- Uebel, S.; Murgovski, N.; Bäker, B.; Sjöberg, J. A two-level mpc for energy management including velocity control of hybrid electric vehicles. IEEE Trans. Veh. Technol. 2019, 68, 5494–5505. [Google Scholar] [CrossRef]
- Mariani, V.; Rizzo, G.; Tiano, F.; Glielmo, L. A model predictive control scheme for regenerative braking in vehicles with hybridized architectures via aftermarket kits. Control Eng. Pract. 2022, 123, 105142. [Google Scholar] [CrossRef]
- Tipaldi, M.; Iervolino, R.; Massenio, P.R. Reinforcement learning in spacecraft control applications: Advances, prospects, and challenges. Annu. Rev. Control 2022, in press. [CrossRef]
- Zhou, Q.; Li, J.; Shuai, B.; Williams, H.; He, Y.; Li, Z.; Xu, H.; Yan, F. Multi-step reinforcement learning for model-free predictive energy management of an electrified off-highway vehicle. Appl. Energy 2019, 255, 113755. [Google Scholar] [CrossRef]
- Xu, B.; Malmir, F.; Filipi, Z. Real-Time Reinforcement Learning Optimized Energy Management for a 48v Mild Hybrid Electric Vehicle; SAE Technical Papers 2019-01-1208; SAE: Warrendale, PA, USA, 2019. [Google Scholar]
- Chen, Z.; Hu, H.; Wu, Y.; Xiao, R.; Shen, J.; Liu, Y. Energy management for a power-split plug-in hybrid electric vehicle based on reinforcement learning. Appl. Sci. 2018, 8, 2494. [Google Scholar] [CrossRef]
- He, D.; Zou, Y.; Wu, J.; Zhang, X.; Zhang, Z.; Wang, R. Deep q-learning based energy management strategy for a series hybrid electric tracked vehicle and its adaptability validation. In Proceedings of the 2019 IEEE Transportation Electrification Conference and Expo (ITEC), Detroit, MI, USA, 19–21 June 2019; pp. 1–6. [Google Scholar]
- Arulkumaran, K.; Deisenroth, M.P.; Brundage, M.; Bharath, A.A. Deep reinforcement learning: A brief survey. IEEE Signal Process. Mag. 2017, 34, 26–38. [Google Scholar] [CrossRef]
- Wu, J.; He, H.; Peng, J.; Li, Y.; Li, Z. Continuous reinforcement learning of energy management with deep q network for a power split hybrid electric bus. Appl. Energy 2018, 222, 799–811. [Google Scholar] [CrossRef]
- Han, X.; He, H.; Wu, J.; Peng, J.; Li, Y. Energy management based on reinforcement learning with double deep q-learning for a hybrid electric tracked vehicle. Appl. Energy 2019, 254, 113708. [Google Scholar]
- Chen, Z.; Gu, H.; Shen, S.; Shen, J. Energy management strategy for power-split plug-in hybrid electric vehicle based on mpc and double q-learning. Energy 2022, 245, 123182. [Google Scholar] [CrossRef]
- Zou, R.; Fan, L.; Dong, Y.; Zheng, S.; Hu, C. Dql energy management: An online-updated algorithm and its application in fix-line hybrid electric vehicle. Energy 2021, 225, 120174. [Google Scholar] [CrossRef]
- Wu, Y.; Tan, H.; Peng, J.; Zhang, H.; He, H. Deep reinforcement learning of energy management with continuous control strategy and traffic information for a series-parallel plug-in hybrid electric bus. Appl. Energy 2019, 247, 454–466. [Google Scholar] [CrossRef]
- Li, Y.; He, H.; Khajepour, A.; Wang, H.; Peng, J. Energy management for a power-split hybrid electric bus via deep reinforcement learning with terrain information. Appl. Energy 2019, 255, 113762. [Google Scholar] [CrossRef]
- Yue, S.; Wang, Y.; Xie, Q.; Zhu, D.; Pedram, M.; Chang, N. Model-free learning-based online management of hybrid electrical energy storage systems in electric vehicles. In Proceedings of the IECON 2014-40th Annual Conference of the IEEE Industrial Electronics Society, Dallas, TX, USA, 29 October–1 November 2014; pp. 3142–3148. [Google Scholar]
- Qiu, C.; Hu, Y.; Chen, Y.; Zeng, B. Deep deterministic policy gradient (ddpg)-based energy harvesting wireless communications. IEEE Internet Things J. 2019, 6, 8577–8588. [Google Scholar] [CrossRef]
- Lian, R.; Peng, J.; Wu, Y.; Tan, H.; Zhang, H. Rule-interposing deep reinforcement learning based energy management strategy for power-split hybrid electric vehicle. Energy 2020, 197, 117297. [Google Scholar] [CrossRef]
- Henderson, P.; Islam, R.; Bachman, P.; Pineau, J.; Precup, D.; Meger, D. Deep reinforcement learning that matters. In Proceedings of the AAAI conference on artificial intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Yang, J.; Zhang, J.; Xi, M.; Lei, Y.; Sun, Y. A deep reinforcement learning algorithm suitable for autonomous vehicles: Double bootstrapped soft-actor-critic-discrete. IEEE Trans. Cogn. Dev. Syst. 2021, 1. [Google Scholar] [CrossRef]
- Nguyen, B.-H.; German, R.; Trovão, J.P.F.; Bouscayrol, A. Real-time energy management of battery/supercapacitor electric vehicles based on an adaptation of pontryagin’s minimum principle. IEEE Trans. Veh. Technol. 2019, 68, 203–212. [Google Scholar] [CrossRef]
- Haarnoja, T.; Zhou, A.; Ha, S.; Tan, J.; Tucker, G.; Levine, S. Learning to walk via deep reinforcement learning. arXiv 2018, arXiv:1812.11103. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. In Proceedings of the International Conference on Machine Learning 2018, Macau, China, 26–28 February 2018. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Hartikainen, K.; Tucker, G.; Ha, S.; Tan, J.; Kumar, V.; Zhu, H.; Gupta, A.; Abbeel, P.; et al. Soft actor-critic algorithms and applications. arXiv 2018, arXiv:1812.05905. [Google Scholar]
- Fu, F.; Kang, Y.; Zhang, Z.R.; Zhang, Z.; Yu, F.R.; Wu, T. Soft actor–critic drl for live transcoding and streaming in vehicular fog-computing-enabled iov. IEEE Internet Things J. 2021, 8, 1308–1321. [Google Scholar] [CrossRef]


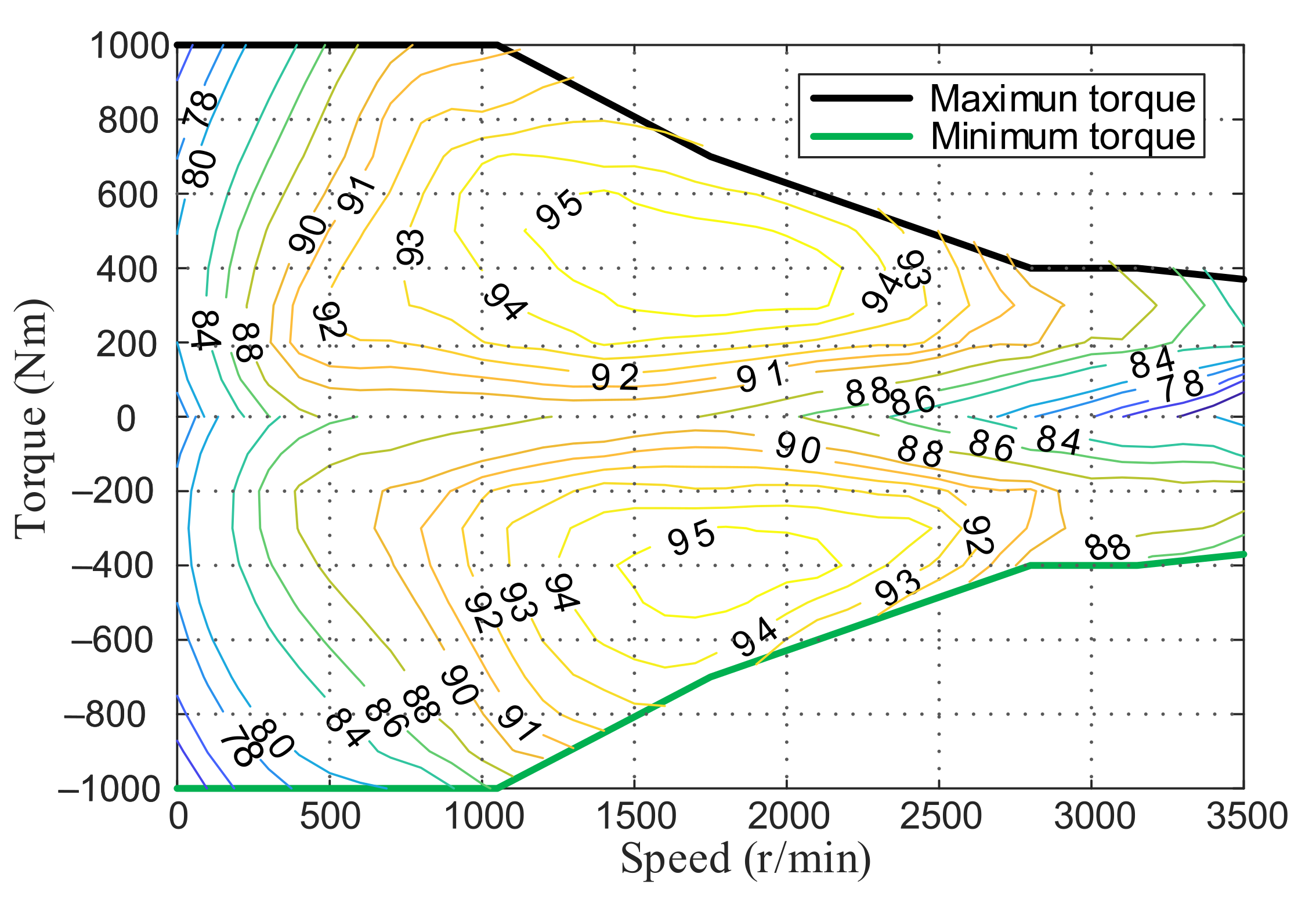














| Symbol | Parameters | Value |
|---|---|---|
| Vehicle | Curb weight | 10,500 kg |
| Rolling resistance coefficient | 0.015 | |
| Air resistance coefficient | 0.65 | |
| Frontal area | 6.75 m | |
| EM | Maximum power | 135 kW |
| Maximum torque | 1000 Nm | |
| Maximum speed | 3500 rpm | |
| ICE | Maximum power | 159 kW |
| Maximum torque | 904 Nm | |
| Maximum speed | 2300 rpm | |
| Battery | Voltage | 525 V |
| capacity | 96 Ah |
| Upshifting Velocity (km/h) | 0–10 | 10–20 | 20–32 | 32–50 | 50–66 | 66–95 |
| Downshifting Velocity (km/h) | 0–7 | 7–15 | 15–28 | 28–45 | 45–58 | - |
| Gear position | 1 | 2 | 3 | 4 | 5 | 6 |
| Gear ratio | 6.39 | 3.97 | 2.40 | 1.48 | 1 | 0.73 |
| Parameters | Value |
|---|---|
| discount factor | 0.99 |
| target smoothing coefficient | 0.005 |
| learning rate | 0.0003 |
| batch size | 256 |
| hidden size | 300 |
| replay size | 1,000,000 |
| entropy target | −3 |
| Algorithm | ICE Fuel Consumption (l/100 km) | Equivalent Fuel Consumption (l/100 km) | Saving Rate (%) | Final SOC |
|---|---|---|---|---|
| SAC (learned parameter) | 9.4283 | 23.5767 | 4.37 | 0.29 |
| DDPG | 9.5372 | 23.9056 | 3.04 | 0.28 |
| SAC (fixed parameter) | 10.6914 | 24.5879 | 0.26 | 0.31 |
| ECMS | 10.9499 | 24.6541 | - | 0.31 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, T.; Cui, W.; Cui, N. Soft Actor-Critic Algorithm-Based Energy Management Strategy for Plug-In Hybrid Electric Vehicle. World Electr. Veh. J. 2022, 13, 193. https://doi.org/10.3390/wevj13100193
Li T, Cui W, Cui N. Soft Actor-Critic Algorithm-Based Energy Management Strategy for Plug-In Hybrid Electric Vehicle. World Electric Vehicle Journal. 2022; 13(10):193. https://doi.org/10.3390/wevj13100193
Chicago/Turabian StyleLi, Tao, Wei Cui, and Naxin Cui. 2022. "Soft Actor-Critic Algorithm-Based Energy Management Strategy for Plug-In Hybrid Electric Vehicle" World Electric Vehicle Journal 13, no. 10: 193. https://doi.org/10.3390/wevj13100193
APA StyleLi, T., Cui, W., & Cui, N. (2022). Soft Actor-Critic Algorithm-Based Energy Management Strategy for Plug-In Hybrid Electric Vehicle. World Electric Vehicle Journal, 13(10), 193. https://doi.org/10.3390/wevj13100193






