Dual-Side Phase-Shift Control for Strongly Coupled Series–Series Compensated Electric Vehicle Wireless Charging Systems

Abstract

Wireless power transfer (WPT) for electric vehicles is an emerging technology and a future trend. To increase power density, the coupling coefficient of coils can be designed to be large, forming a strongly coupled WPT system, different from the conventional loosely coupled WPT system. In this way, the power density and efficiency of the WPT system can be improved. This paper investigates the dual-side phase-shift control of the strongly coupled series–series compensated WPT systems. The mathematical models based on the conventional first harmonic approximation and differential equations for the dual-side phase-shift control are built and compared. The dual-side phase-shift angle and its impact on the power transfer direction and soft switching are investigated. It is found that synchronous rectification at strong couplings can lead to hard switching because the dual-side phase shift in this case is over 90°. In comparison, a relatively high efficiency and soft switching can be realized when the dual-side phase shift is below 90°. The experimental results have validated the analysis.

1. Introduction

Compared with the conventional conductive power transfer, wireless power transfer (WPT) [1,2,3,4,5,6] has many advantages, such as safety, automation, convenience, and feasibility to various working environments, such as mining and underwater situations. Thus, WPT has broad application scenarios, such as wireless sensor networks, consumer electronics, implantable medical devices, domestic appliance, electric vehicles (EVs), electric vessels, and even space solar station. WPT via magnetic induction is the most popular WPT technology and has received tremendous attention both from academia and industry. Wireless charging for EVs based on magnetic induction is currently one of the research hot topics [7].

Power density is one of the key indicators for WPT systems. To increase power density, the coupling coefficient of the two coupled coils can be designed to be large, forming a strongly coupled WPT system, where the coupling coefficient is normally larger than 0.5. This system has a totally different feature from the conventional loosely coupled WPT systems, whose coupling coefficient is around 0.2. The current waveforms of the strongly coupled WPT systems are distorted and can be discontinuous [8], whereas in loosely coupled WPT systems the current waveforms are sinusoidal.

(1)

Synchronous rectification is normally conducted to the secondary-side rectifier of the loosely coupled WPT systems to improve efficiency [9,10]. However, it is found in strongly coupled WPT systems that this will result in the primary-side inverter working in hard switching, leading to decreasing efficiency and potential circuit failures. Additionally, in loosely coupled WPT systems, dual-side phase-shift control is seldomly used to regulate the secondary-side charging current due to the fact that too much reactive power will be introduced if the phase difference between the primary-side and secondary-side voltages is not 90°. However, in strongly coupled WPT systems, since the coupling coefficient is large, the efficiency can still be high even though the phase difference is not 90°. Thus, the secondary-side charging current and even bidirectional power flow can be easily regulated. The contributions of this paper include building the mathematical model of dual-side phase-shift control for strongly coupled WPT systems;

(2)

Investigating the performance of dual-side phase-shift control for strongly coupled WPT systems;

(3)

Revealing that synchronous rectification is not suitable for strongly coupled WPT system because soft switching can be lost;

(4)

Experimentally validating the model and analysis.

This paper studies the dual-side phase-shift control of the strongly coupled series–series compensated WPT systems. The mathematical models based on first harmonic approximation (FHA) and differential equations are built in Section 2. Experimental results are offered in Section 3 to validate the analysis. Section 4 concludes this paper.

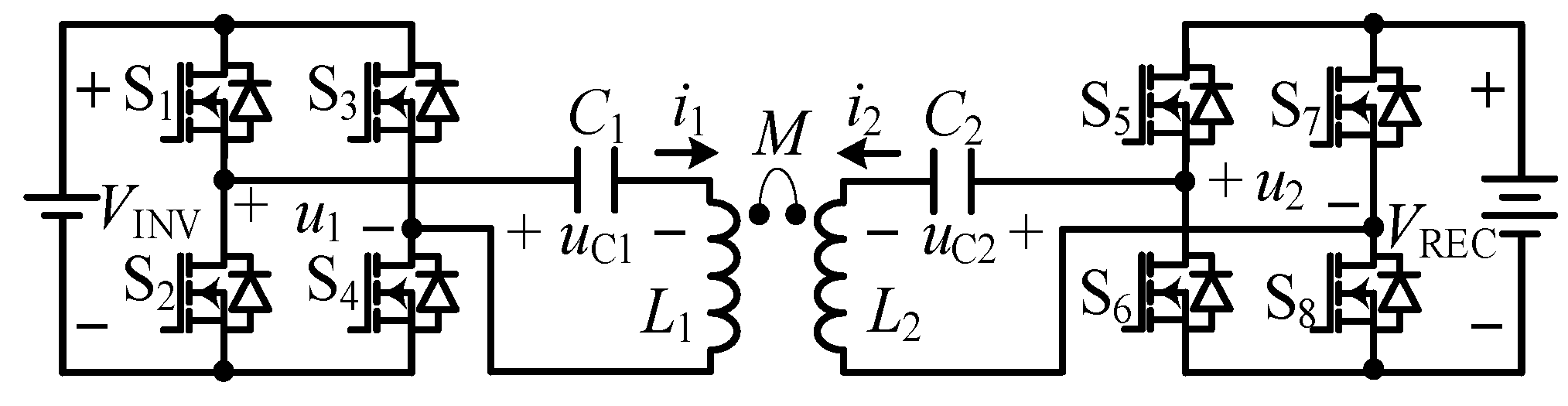
2. Mathematical Modelling

The topology of a series–series compensated EV wireless charging system with full-bridge converters is shown in Figure 1. S₁–S₈ are the active switches. V_INV (V_REC), u₁ (u₂), i₁ (i₂), L₁ (L₂), C₁ (C₂), u_C1 (u_C2) are the respective primary-side (secondary-side) dc voltage, ac voltage, ac current, self-inductance, capacitance, and capacitor voltage. M is the mutual inductance.

Figure 1. Topology of a series–series compensated WPT system for EV charging.

The load is modelled as a voltage-source load. The voltage gain of the WPT system G_V is defined as

$$G_V=\frac{V_{\mathrm{REC}}}{V_{\mathrm{INV}}}$$

(1)

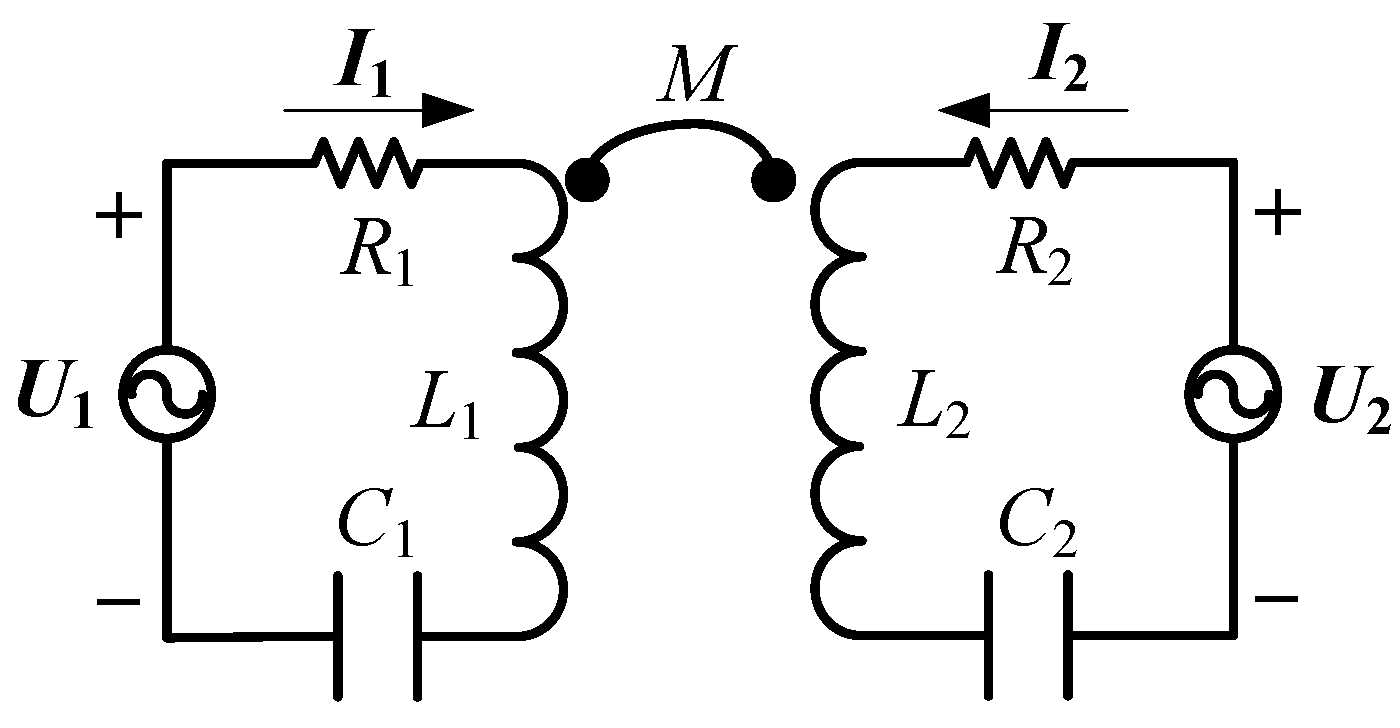
2.1. First Harmonic Approximation

FHA is normally utilized to model the WPT system. Based on FHA, the equivalent circuit is shown in Figure 2. U₁ (U₂) and I₁ (I₂) are the fundamental components of the inverter (rectifier) ac voltage and current, respectively. R₁ and R₂ are the equivalent resistance of the transmitter and receiver, respectively. With 180° phase shift within the legs of the inverter and the rectifier, we have

$$\{\begin{array}{l}{U}_1=\frac{2\sqrt{2}}{\pi }{V}_{\mathrm{INV}}\\ U_2=\frac{2\sqrt{2}}{\pi }{V}_{\mathrm{REC}}.\end{array}$$

(2)

Figure 2. Equivalent circuit of series–series compensated WPT system based on FHA.

The model in Figure 2 can be established as

$$\{\begin{array}{l}{\mathit{U}}_1=\left(R_1+\mathrm{j}\omega L_1+\frac{1}{\mathrm{j}\omega C_1}\right){\mathit{I}}_1+\mathrm{j}\omega M{\mathit{I}}_2\\ {\mathit{U}}_2=\left(R_2+\mathrm{j}\omega L_2+\frac{1}{\mathrm{j}\omega C_2}\right){\mathit{I}}_2+\mathrm{j}\omega M{\mathit{I}}_1,\end{array}$$

(3)

where ω is the working angular frequency and the parameters in bold represent the phasor quantities.

At resonance where

$$\omega ={\omega }_0=\frac{1}{\sqrt{L_1{C}_1}}=\frac{1}{\sqrt{L_2{C}_2}},$$

(4)

and ignoring R₁ and R₂ when their voltage drops are significantly smaller than U₁ and U₂, we have

$$\{\begin{array}{l}{I}_1=\frac{2\sqrt{2}}{\pi }\frac{V_{\mathrm{REC}}}{\omega M}\\ I_2=\frac{2\sqrt{2}}{\pi }\frac{V_{\mathrm{INV}}}{\omega M}.\end{array}$$

(5)

According to FHA, the transmitter and receiver currents are constant.

With the dual-side phase-shift angle of β, by which U₂ leads U₁, the phasor diagram is plotted in Figure 3 [11]. The rectifier dc current and the output power can be calculated as

$$I_{\mathrm{REC}\text{-}\mathrm{FHA}}=\frac{8}{{\pi }^2}\frac{V_{\mathrm{INV}}}{\omega M}\sin \beta$$

(6)

$$P_{\mathrm{out}\text{-}\mathrm{FHA}}=\frac{8}{{\pi }^2}\frac{V_{\mathrm{INV}}{V}_{\mathrm{REC}}}{\omega M}\sin \beta .$$

(7)

Figure 3. Phasor diagram of series–series compensated WPT system based on FHA.

I_REC and P_out change sinusoidally with the dual-side phase-shift angle β.

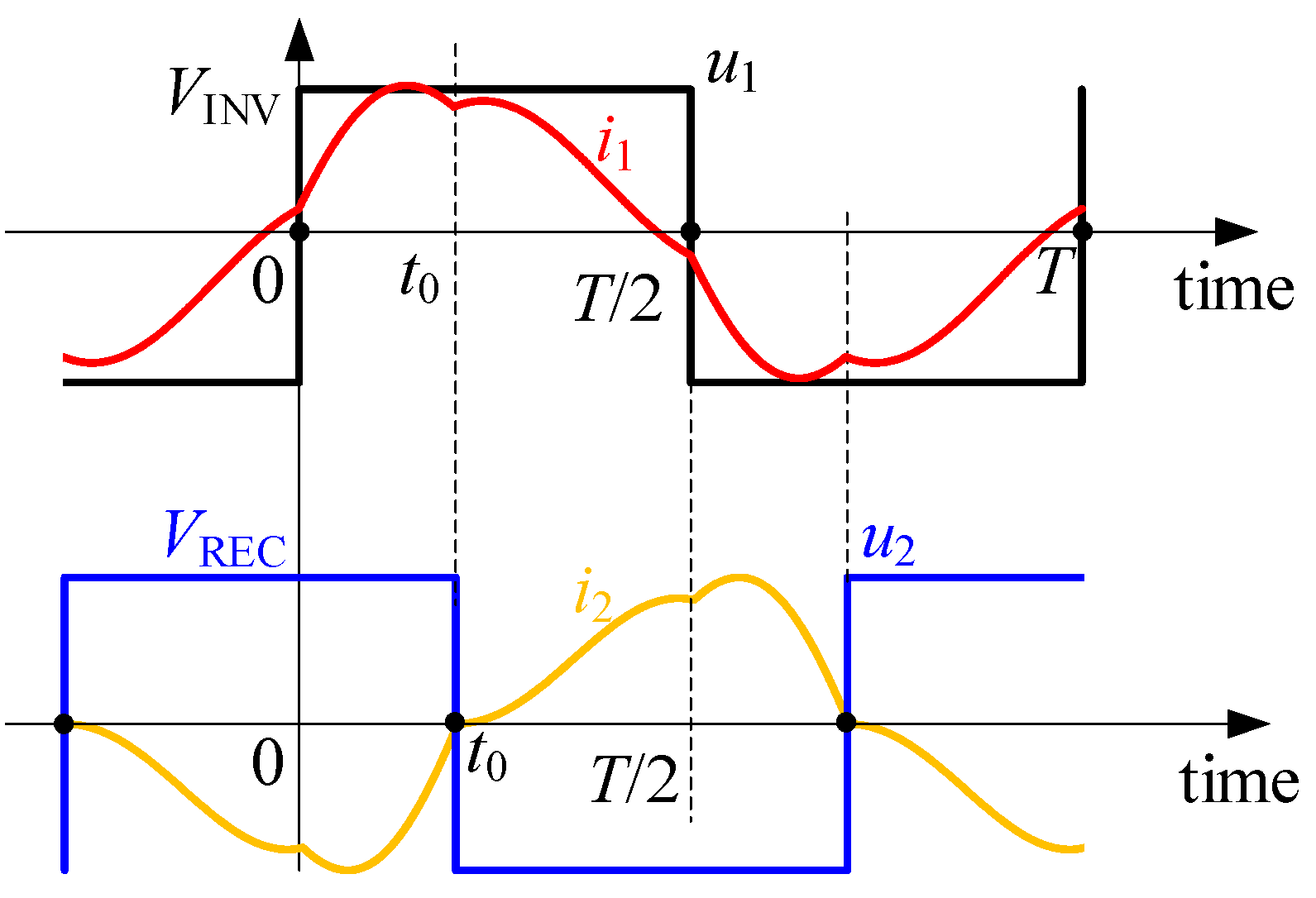
2.2. Time-Domain Modelling

The waveforms of the series–series compensated WPT system are distorted and can be discontinuous [10,12]. Therefore, FHA is no longer valid. Similar to [12], the time domain modelling based on differential equations is conducted. The typical waveforms are shown in Figure 4. Assume that the cycle is T. At t = 0, u₁ is rising, and at t₀, u₂ is falling. In the first half cycle, S₁ and S₄ are on and S₂ and S₃ are off. In the second half cycle, S₁ and S₄ are off and S₂ and S₃ are on. Due to symmetry, only the first half cycle is considered.

Figure 4. Typical waveforms of inverter and rectifier ac voltages and currents.

When 0 < t < t₀, S₁, S₄, S₅, and S₈ are all on, namely u₁ and u₂ are both positive, the differential equations can be given as

$$\{\begin{array}{l}{V}_{\mathrm{INV}}=u_{\mathrm{C}1-1}+L_1\frac{d{i}_{1-1}}{dt}+M\frac{d{i}_{2-1}}{dt}\\ V_{\mathrm{REC}}=u_{\mathrm{C}2-1}+M\frac{d{i}_{1-1}}{dt}+L_2\frac{d{i}_{2-1}}{dt}\\ i_{1-1}=C_1\frac{d{u}_{\mathrm{C}1-1}}{dt}\\ i_{2-1}=C_2\frac{d{u}_{\mathrm{C}2-1}}{dt},\end{array}$$

(8)

where the subscript “−1” denotes that the symbols are in the interval of 0 < t < t₀.

When t₀ < t < T/2, S₂, S₃, S₅, and S₈ are all on, namely u₁ is positive and u₂ is negative, the differential equations can be given as

$$\{\begin{array}{l}{V}_{\mathrm{INV}}=u_{\mathrm{C}1-2}+L_1\frac{d{i}_{1-2}}{dt}+M\frac{d{i}_{2-2}}{dt}\\ -V_{\mathrm{REC}}=u_{\mathrm{C}2-2}+M\frac{d{i}_{1-2}}{dt}+L_2\frac{d{i}_{2-2}}{dt}\\ i_{1-2}=C_1\frac{d{u}_{\mathrm{C}1-2}}{dt}\\ i_{2-2}=C_2\frac{d{u}_{\mathrm{C}2-2}}{dt},\end{array}$$

(9)

where the subscript “−2” denotes that the symbols are in the interval of t₀ < t < T/2.

With considerations of the boundary conditions, namely

$$\{\begin{array}{c}{i}_{1-1}\left(0\right)=-i_{1-2}\left(\frac{T}{2}\right)\\ i_{1-1}\left(t_0\right)=i_{1-2}\left(t_0\right)\\ i_{2-1}\left(0\right)=-i_{2-2}\left(\frac{T}{2}\right)\\ i_{2-1}\left(t_0\right)=i_{2-2}\left(t_0\right)\\ u_{\mathrm{C}1-1}\left(0\right)=-u_{\mathrm{C}1-2}\left(\frac{T}{2}\right)\\ u_{\mathrm{C}1-1}\left(t_0\right)=u_{\mathrm{C}1-2}\left(t_0\right)\\ u_{\mathrm{C}2-1}\left(0\right)=-u_{\mathrm{C}2-2}\left(\frac{T}{2}\right)\\ u_{\mathrm{C}2-1}\left(t_0\right)=u_{\mathrm{C}2-2}\left(t_0\right),\end{array}$$

(10)

the differential equations can be solved.

The rectifier dc current and the output power can be calculated as

$$I_{\mathrm{REC}\text{-}\mathrm{DE}}=\frac{V_{\mathrm{INV}}}{\pi \omega \sqrt{L_1{L}_2}}\left[\begin{array}{l}\frac{\cos \left(\frac{2\pi }{\sqrt{1+k}}\frac{t_0}{T}\right)+\cos \left(\frac{2\pi }{\sqrt{1+k}}\left(\frac{t_0}{T}-\frac{1}{2}\right)\right)}{1+\cos \left(\frac{\pi }{\sqrt{1+k}}\right)}\\ -\frac{\cos \left(\frac{2\pi }{\sqrt{1-k}}\frac{t_0}{T}\right)+\cos \left(\frac{2\pi }{\sqrt{1-k}}\left(\frac{t_0}{T}-\frac{1}{2}\right)\right)}{1+\cos \left(\frac{\pi }{\sqrt{1-k}}\right)}\end{array}\right]$$

(11)

$$P_{\mathrm{out}\text{-}\mathrm{DE}}=\frac{V_{\mathrm{INV}}{V}_{\mathrm{REC}}}{\pi \omega \sqrt{L_1{L}_2}}\left[\begin{array}{l}\frac{\cos \left(\frac{2\pi }{\sqrt{1+k}}\frac{t_0}{T}\right)+\cos \left(\frac{2\pi }{\sqrt{1+k}}\left(\frac{t_0}{T}-\frac{1}{2}\right)\right)}{1+\cos \left(\frac{\pi }{\sqrt{1+k}}\right)}\\ -\frac{\cos \left(\frac{2\pi }{\sqrt{1-k}}\frac{t_0}{T}\right)+\cos \left(\frac{2\pi }{\sqrt{1-k}}\left(\frac{t_0}{T}-\frac{1}{2}\right)\right)}{1+\cos \left(\frac{\pi }{\sqrt{1-k}}\right)}\end{array}\right],$$

(12)

where k is the coupling coefficient, defined as

$$k=\frac{M}{\sqrt{L_1{L}_2}}.$$

(13)

t₀ indicates the phase-shift instant when the secondary-side rectifier is switching. The relationship between t₀ and β is

$$\beta =2\pi \frac{t_0}{T}.$$

(14)

Thus, (11) and (12) are transformed into

$$I_{\mathrm{REC}\text{-}\mathrm{DE}}=\frac{V_{\mathrm{INV}}}{\pi \omega \sqrt{L_1{L}_2}}\left[\frac{\cos \frac{\beta }{\sqrt{1+k}}+\cos \frac{\beta -\pi }{\sqrt{1+k}}}{1+\cos \left(\frac{\pi }{\sqrt{1+k}}\right)}-\frac{\cos \frac{\beta }{\sqrt{1-k}}+\cos \frac{\beta -\pi }{\sqrt{1-k}}}{1+\cos \left(\frac{\pi }{\sqrt{1-k}}\right)}\right]$$

(15)

$$P_{\mathrm{out}\text{-}\mathrm{DE}}=\frac{V_{\mathrm{INV}}{V}_{\mathrm{REC}}}{\pi \omega \sqrt{L_1{L}_2}}\left[\frac{\cos \frac{\beta }{\sqrt{1+k}}+\cos \frac{\beta -\pi }{\sqrt{1+k}}}{1+\cos \left(\frac{\pi }{\sqrt{1+k}}\right)}-\frac{\cos \frac{\beta }{\sqrt{1-k}}+\cos \frac{\beta -\pi }{\sqrt{1-k}}}{1+\cos \left(\frac{\pi }{\sqrt{1-k}}\right)}\right].$$

(16)

For synchronous rectification, there should be one more boundary condition as i_2-1(t₀) = i_2-2(t₀) = 0, which is the natural zero crossing point of the receiver current. By solving this, the phase-shift angle between u₂ and the u₁ is larger than 90°. In this condition, i_1-1(0) is larger than 0, indicating that soft switching is lost.

2.3. Comparison of FHA and Model Based on Differential Equations

Dividing (15) by (6) yields the ratio of the rectifier dc current from the differential equations over that from FHA, namely

$$\frac{I_{\mathrm{REC}\text{-}\mathrm{DE}}}{I_{\mathrm{REC}\text{-}\mathrm{FHA}}}=\frac{k\pi }{8\sin \beta }\left[\frac{\cos \frac{\beta }{\sqrt{1+k}}+\cos \frac{\beta -\pi }{\sqrt{1+k}}}{1+\cos \left(\frac{\pi }{\sqrt{1+k}}\right)}-\frac{\cos \frac{\beta }{\sqrt{1-k}}+\cos \frac{\beta -\pi }{\sqrt{1-k}}}{1+\cos \left(\frac{\pi }{\sqrt{1-k}}\right)}\right].$$

(17)

The ratio of the rectifier dc currents in (17), varying with the phase difference between u₂ and u₁, namely β, is plotted in Figure 5. At strong couplings, the rectifier dc currents are larger than the predictions from FHA between the phase-shift angles of 60° and 120°, and smaller at other phase-shift angles. This shows the inaccuracy of FHA at strong couplings.

Figure 5. Ratio of I_REC in (17) varying with β.

In Figure 2 and Figure 3, the corresponding voltage and current (U₁ and I₁, U₂ and I₂) are defined in an associate reference direction. This means that when the active power of the voltage source is positive, the voltage source acts as an actual source and the active power is transferred from the voltage source to the outside circuit; when the active power of the voltage source is negative, the voltage source acts as a sink and the active power is transferred from the outside circuit to the voltage source. Thus, in Figure 3, when U₂ leads U₁ or β ∈ (0, 180°), active power is transferred from the primary side to the secondary side; when U₂ lags behind U₁ or β ∈ (−180°, 0), active power is transferred from the secondary side to the primary side. This is also true for strongly coupled cases.

Attention should be paid to the range of [0, 180°] where active power is transferred from the primary side to the secondary side. As can also be seen from Figure 3, when 0 < β < 90°, I₁ lags behind U₁, which means the input impedance is inductive. Thus, zero voltage switching (ZVS) can be achieved for both the primary-side inverter and secondary-side rectifier. When 90° < β < 180°, I₁ leads U₁, and zero current switching (ZCS) can be achieved for both the primary-side inverter and secondary-side rectifier. When MOSFETs are used, ZVS is preferred, indicating that the dual-side phase-shift angle should be in the range of [0, 90°]. The variations of the rectifier currents or output power with the dual-side phase-shift angle β are plotted in Figure 6.

Figure 6. Variation of I_REC or P_out with β.

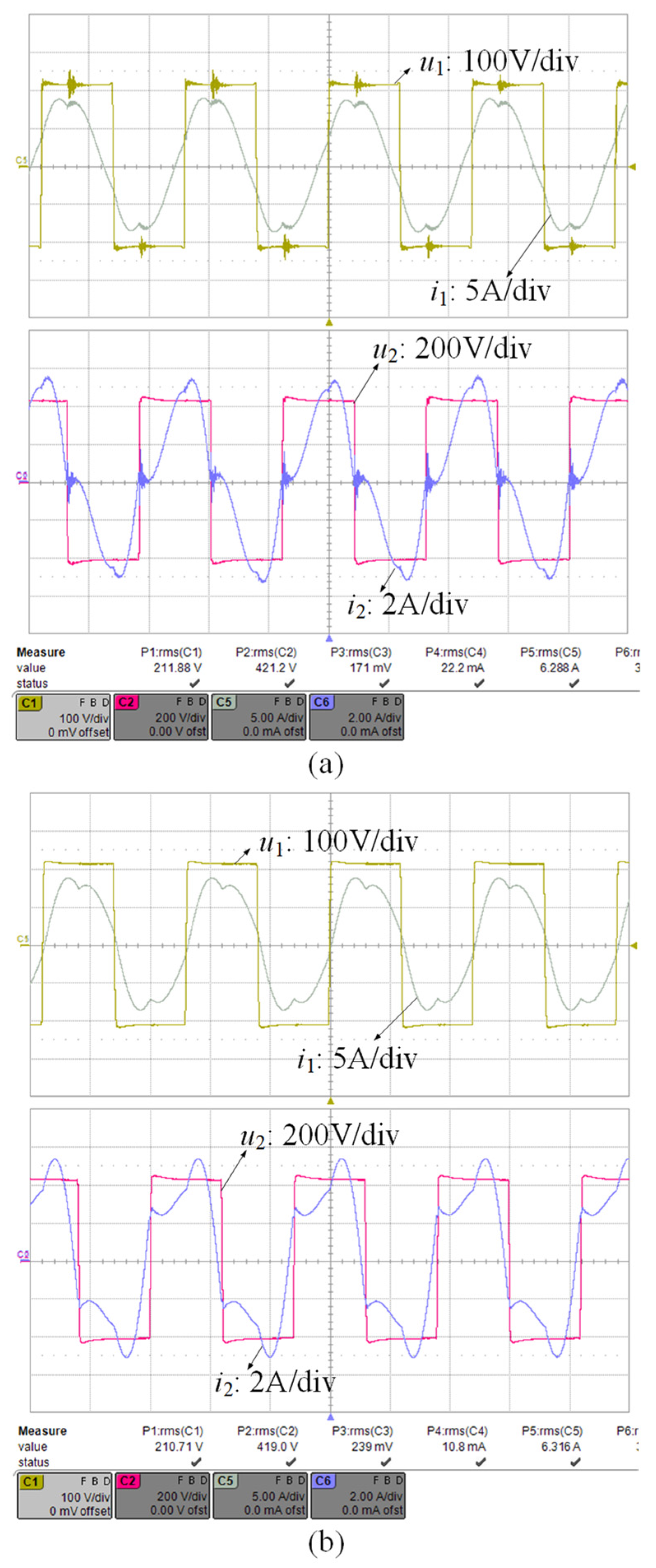
3. Experimental Validation

An experimental prototype is implemented to validate the analysis, as shown in Figure 7. The parameters of the experimental prototype are tabulated in Table 1. The prototype with the coupling coefficient of 0.64 is a typical strongly coupled WPT system. V_INV is set to 200 V. Three voltage gains are selected: 0.5, 1.0, and 2.0, with corresponding V_REC of 100 V, 200 V, and 400 V.

Figure 7. Photo of the experimental prototype.

Table 1. Parameters of experimental prototype.

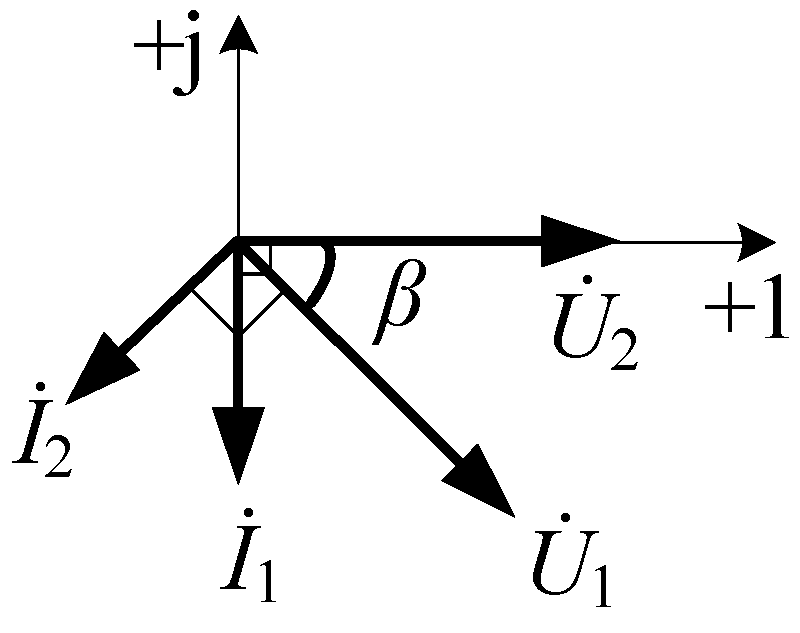
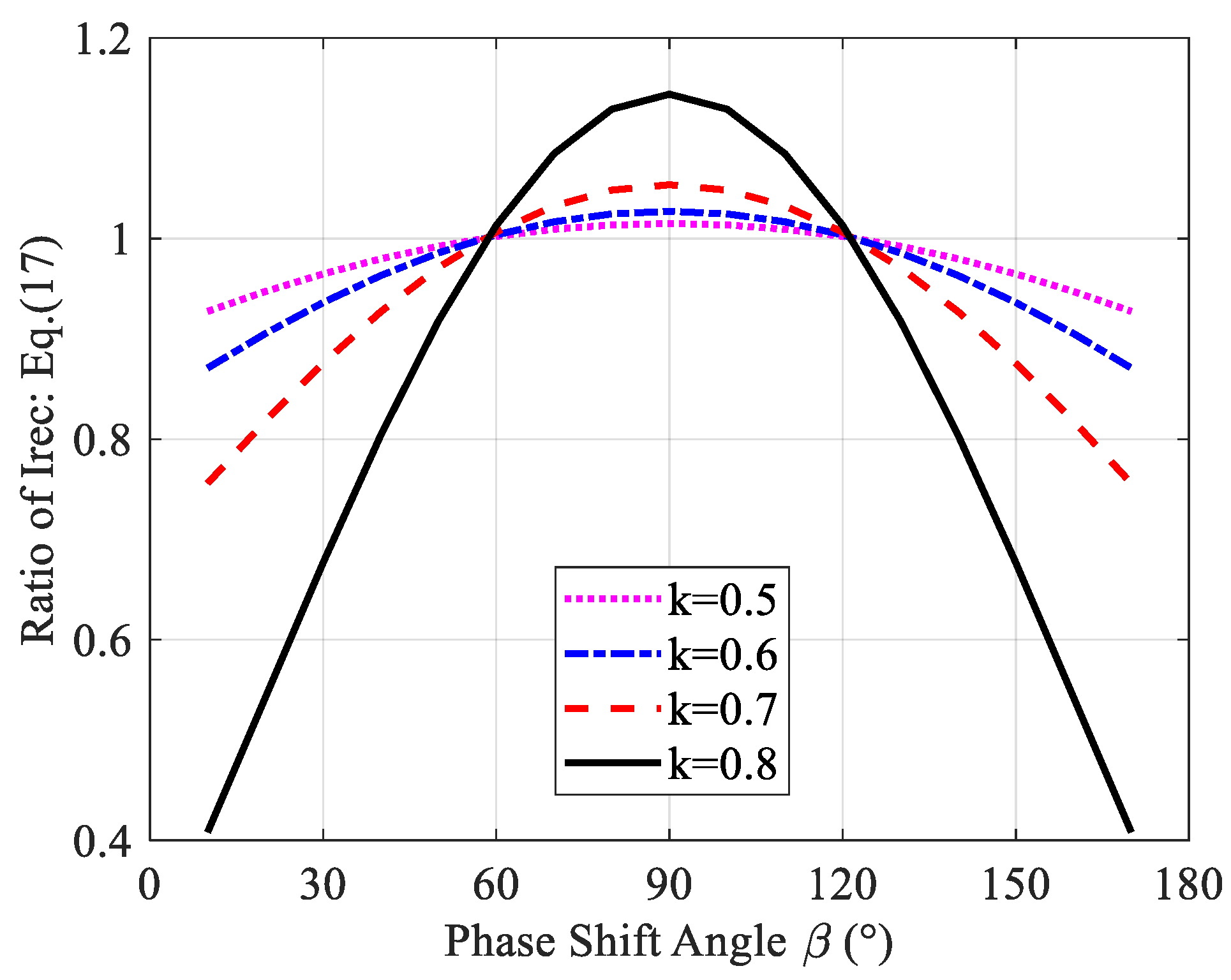
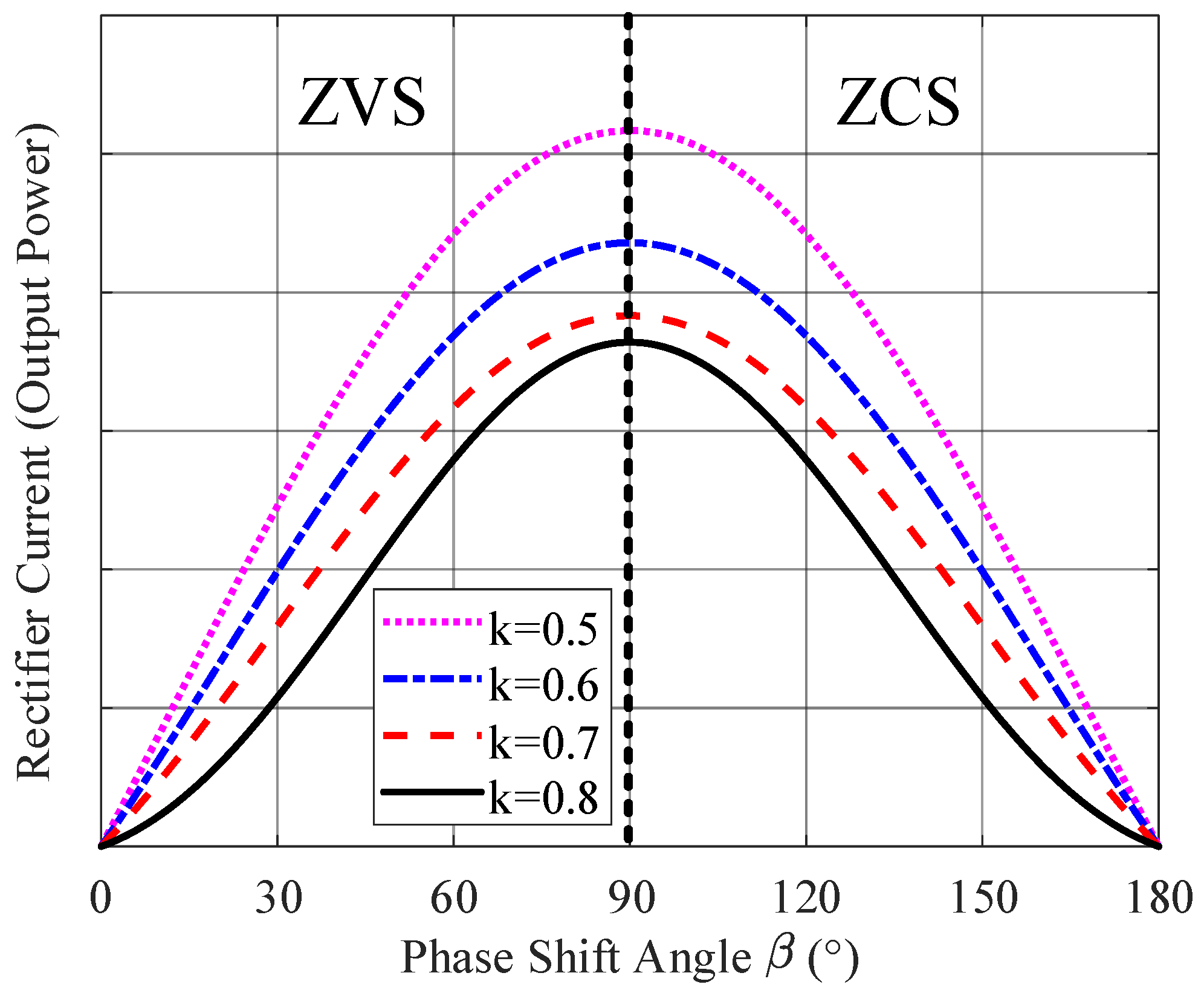
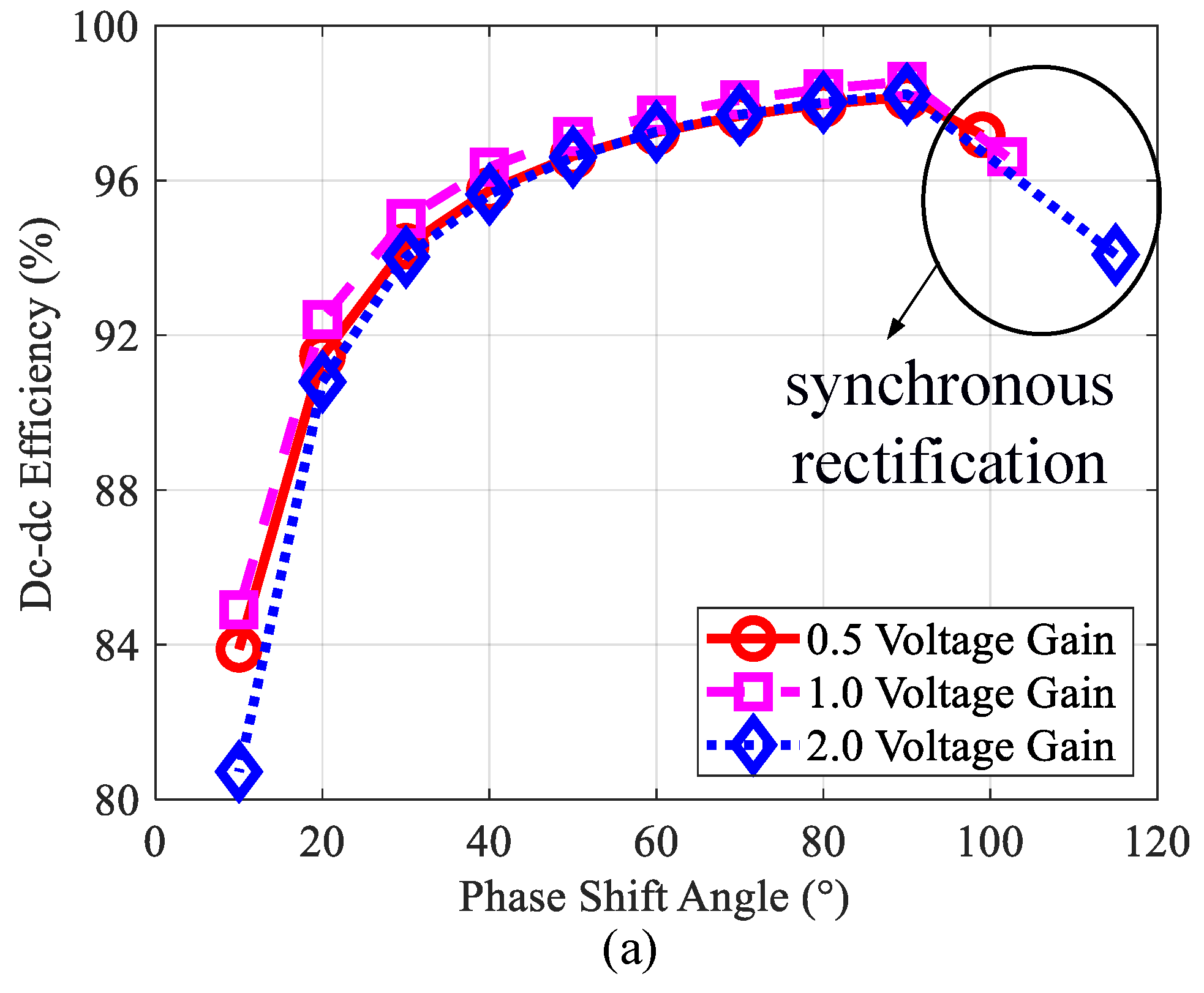
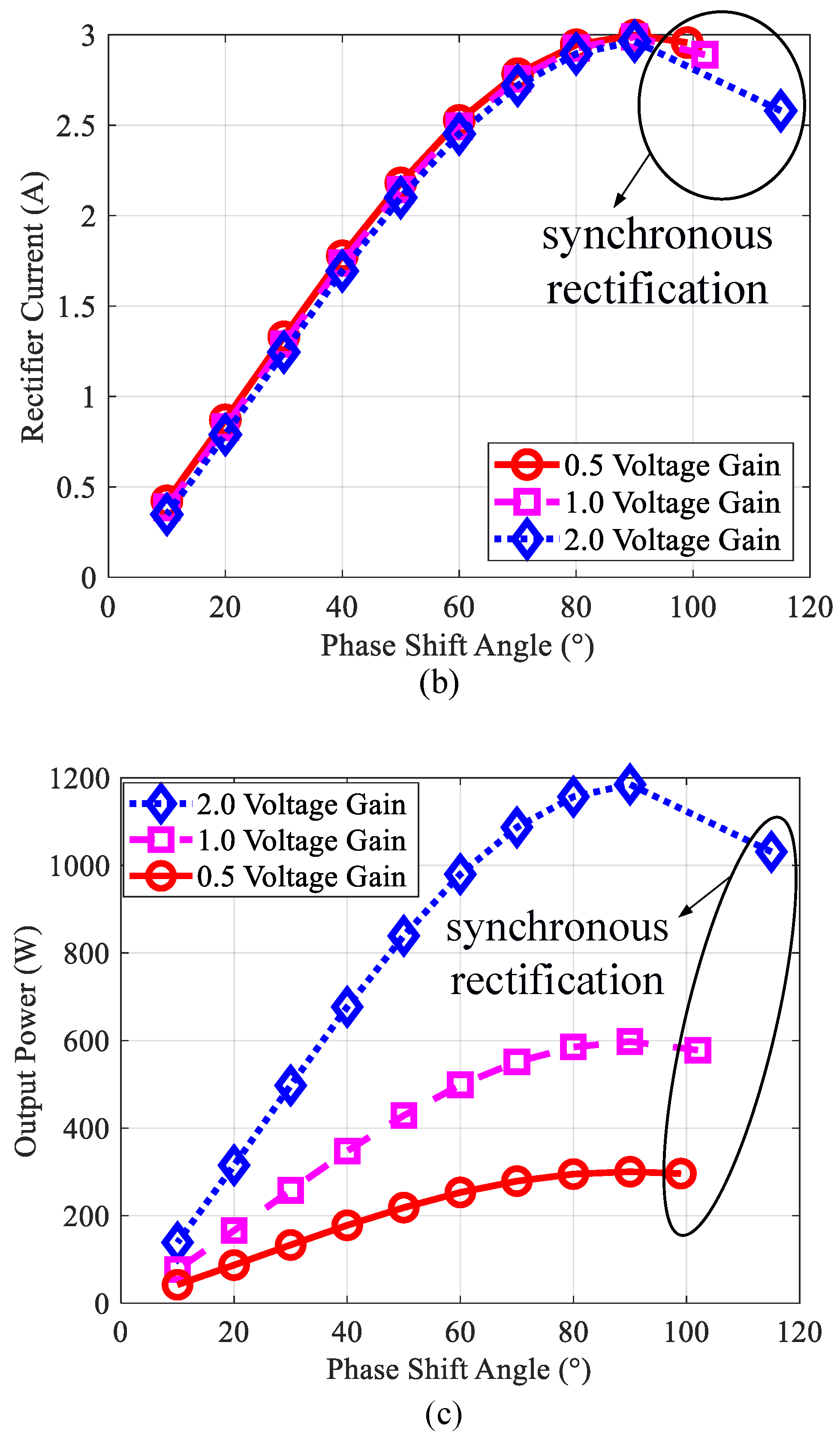
Parameters	Values
Airgap	40 mm
f0	83.3 kHz
L1	169.7 μH
L2	169.8 μH
C1	21.5 nF
C2	21.5 nF
k	0.64

The measured dc-dc efficiency, the rectifier current, and the output power under synchronous rectification and phase shift are illustrated in Figure 8. The data denoted as “synchronous rectification” indicate that synchronous rectification is achieved at these phase-shift angles, which are larger than 90° and locate at the range of ZCS, as shown in Figure 6. Thus, with synchronous rectification, soft switching is lost. By changing the phase shift angle between 0 and 90°, the output current, namely the rectifier current, can be easily regulated, as shown in Figure 8b. In the wide regulation range, the dc-dc efficiency can still be high, different from the loosely coupled wireless power transfer systems.

Figure 8. (a) Measured dc-dc efficiency, (b) rectifier current, and (c) output power under three voltage gains.

The experimental waveforms when the voltage gain is 2.0 are shown in Figure 9. With synchronous rectification in strongly coupled WPT systems, the phase-shift angles are always larger than 90°, and the dc-dc efficiency is smaller than that with a 90° phase shift. The inverter may work in hard switching, as shown in Figure 9a. With a 90° phase shift, this issue is solved, as shown in Figure 9b.

Figure 9. Experimental waveforms with 2.0 voltage gain: (a) synchronous rectification; (b) 90° phase shift.

4. Conclusions

This paper presented the modelling and dual-side phase-shift control of the strongly coupled series–series compensated WPT systems. There are issues with synchronous rectification in strongly coupled series–series compensated WPT systems: the efficiency is not the highest and the inverter may work in hard switching. In comparison, with a 90° phase shift, the inverter will always work in soft switching and the efficiency is the highest. Moreover, with dual-side phase-shift regulation in strongly coupled series–series compensated WPT systems, the output current can be easily regulated by changing the phase difference between the primary-side and the secondary-side converters with relatively high dc-dc efficiency over a wide regulation range, which is a different characteristic from the loosely coupled WPT systems.