Author Contributions
Conceptualization, S.P.S.; methodology, S.P.S. and D.W.; software, L.K.P.; validation, T.D. and D.W.; formal analysis, L.K.P. and S.P.S.; investigation, T.D. and D.W.; resources, T.D. and D.W.; data curation, L.K.P.; writing—original draft preparation, L.K.P.; writing—review and editing, S.P.S., T.D. and D.W.; visualization, L.K.P.; supervision, S.P.S., T.D., D.W.; project administration, S.P.S.; funding acquisition, S.P.S. All authors have read and agreed to the published version of the manuscript.
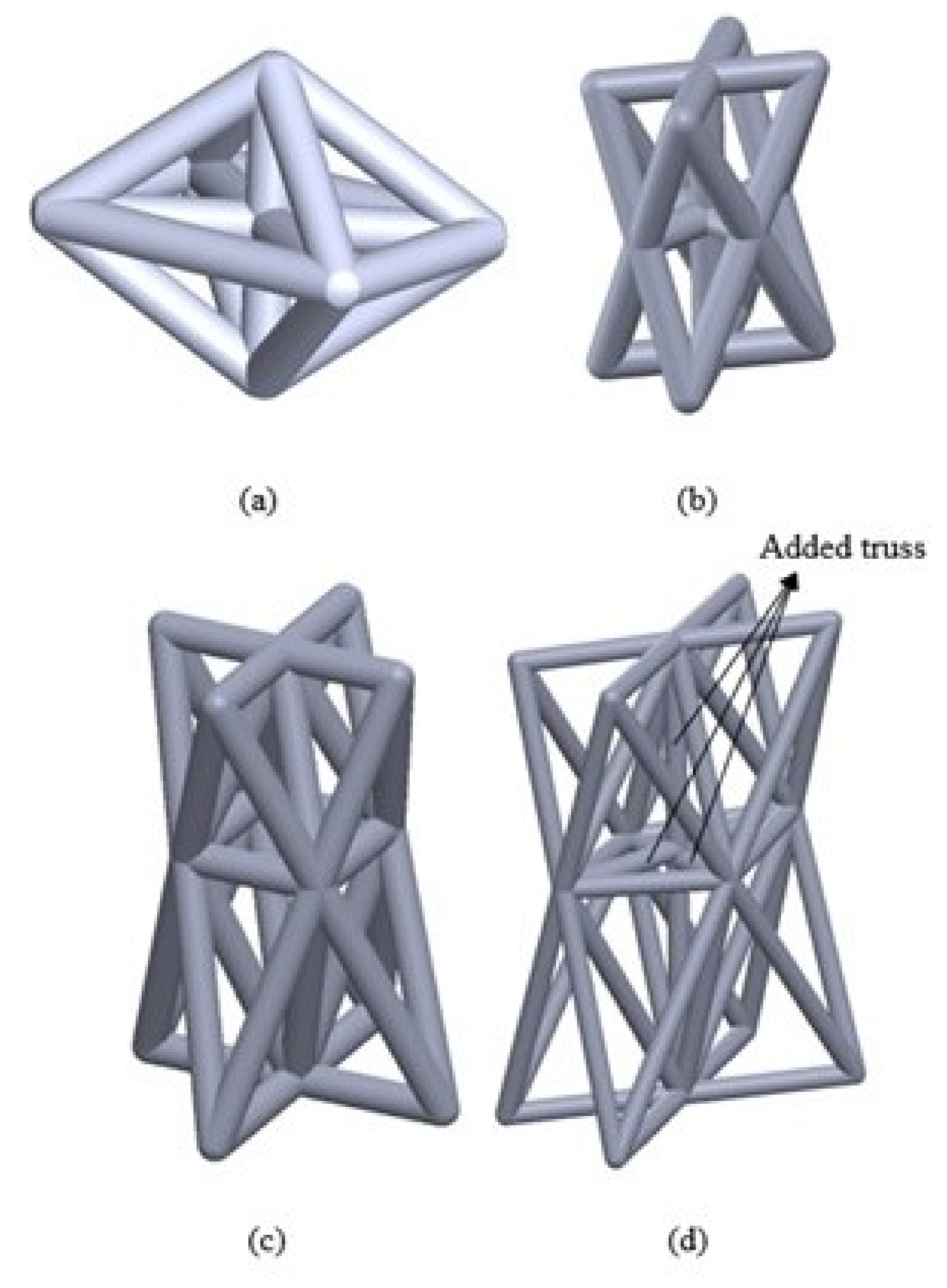
Figure 1.
Four Lattice Structure Cell Model: (a) Octahedron-Cross (OHC). (b) Octet-Cross (OC). (c) Octet-Truss (OT). (d) Octet-Truss-Modified.
Figure 1.
Four Lattice Structure Cell Model: (a) Octahedron-Cross (OHC). (b) Octet-Cross (OC). (c) Octet-Truss (OT). (d) Octet-Truss-Modified.
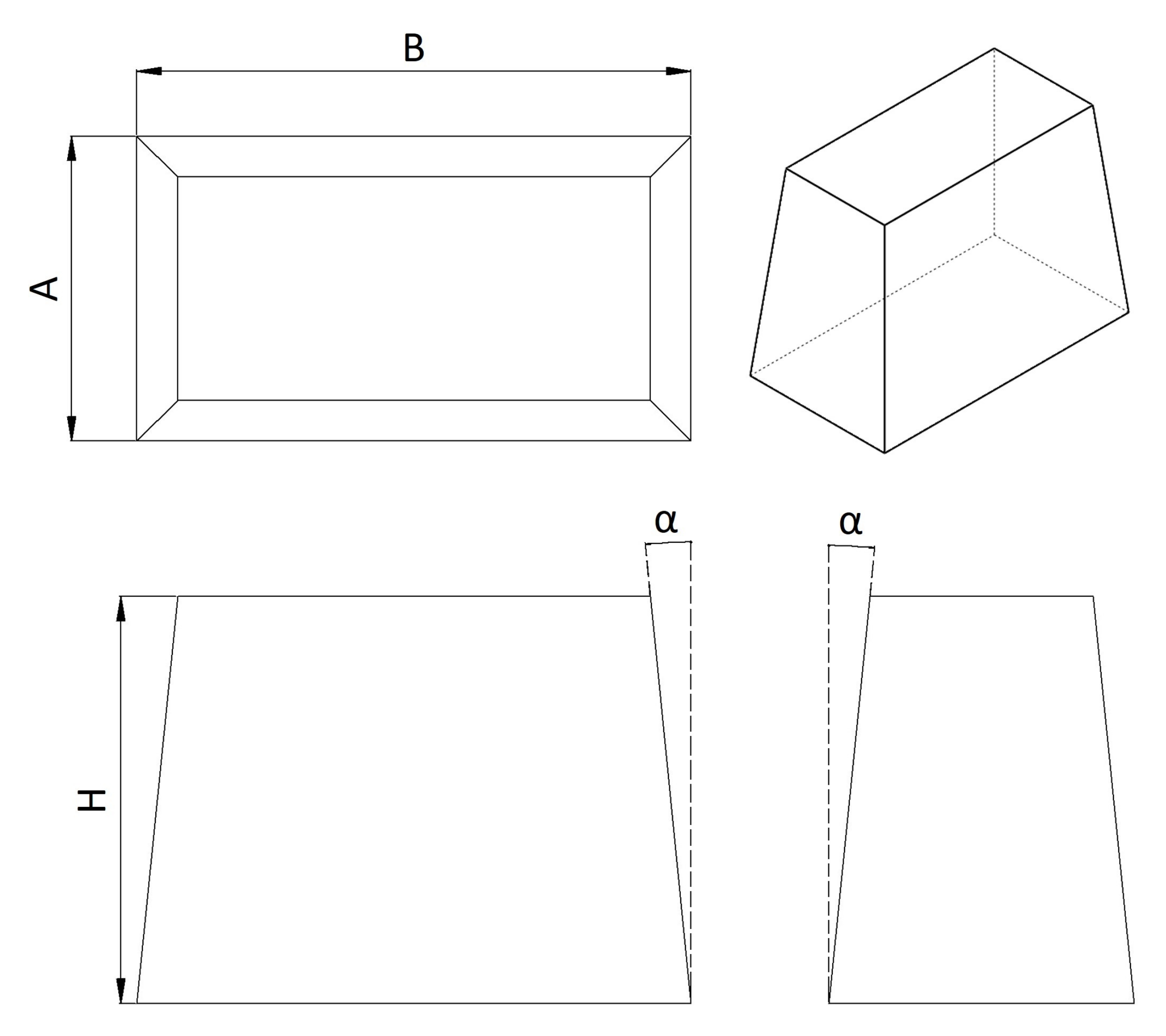
Figure 2.
Solid Cube Dimension Reference.
Figure 2.
Solid Cube Dimension Reference.
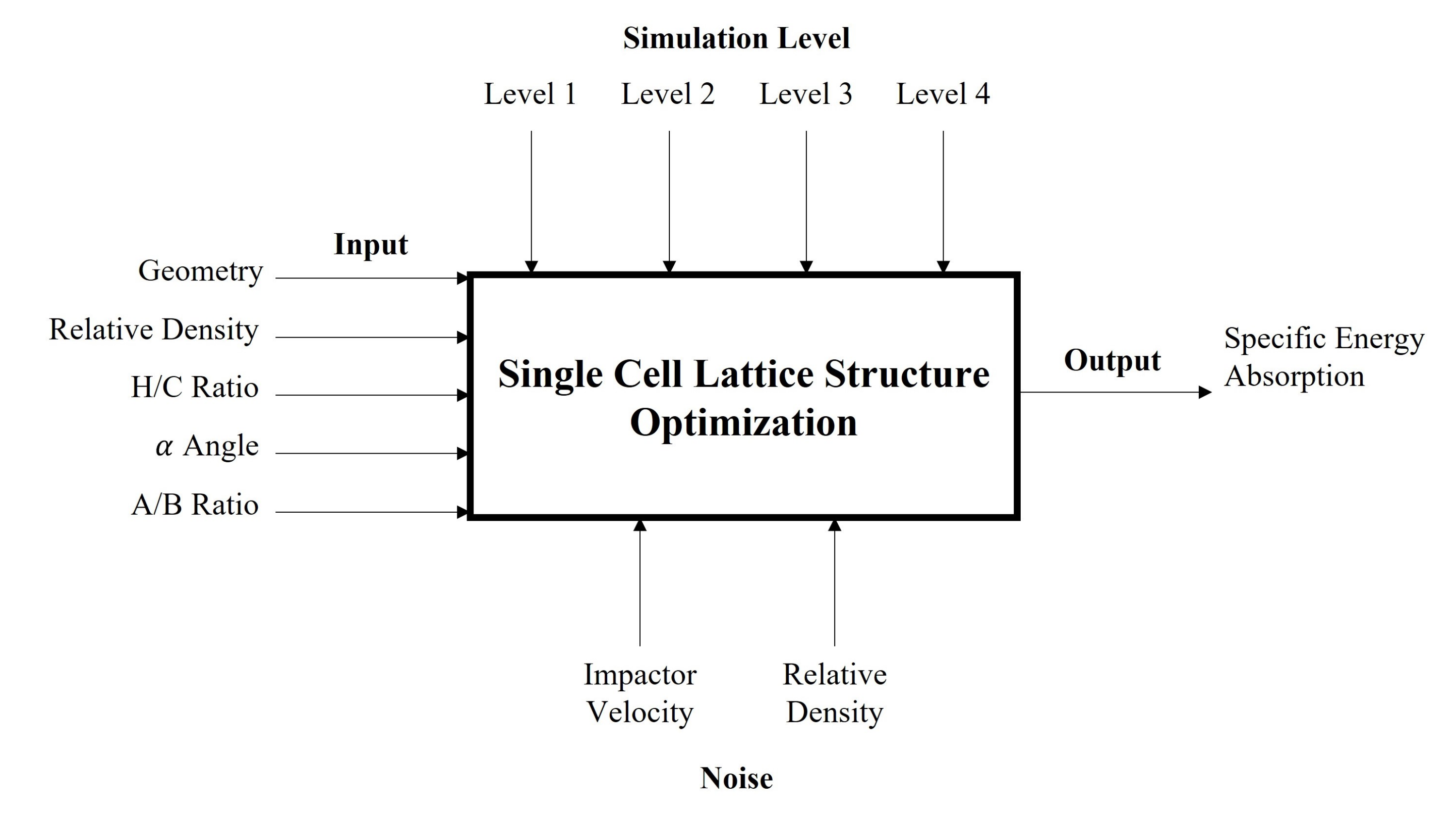
Figure 3.
Process Diagram of The Single-Cell Lattice Structure Simulation.
Figure 3.
Process Diagram of The Single-Cell Lattice Structure Simulation.
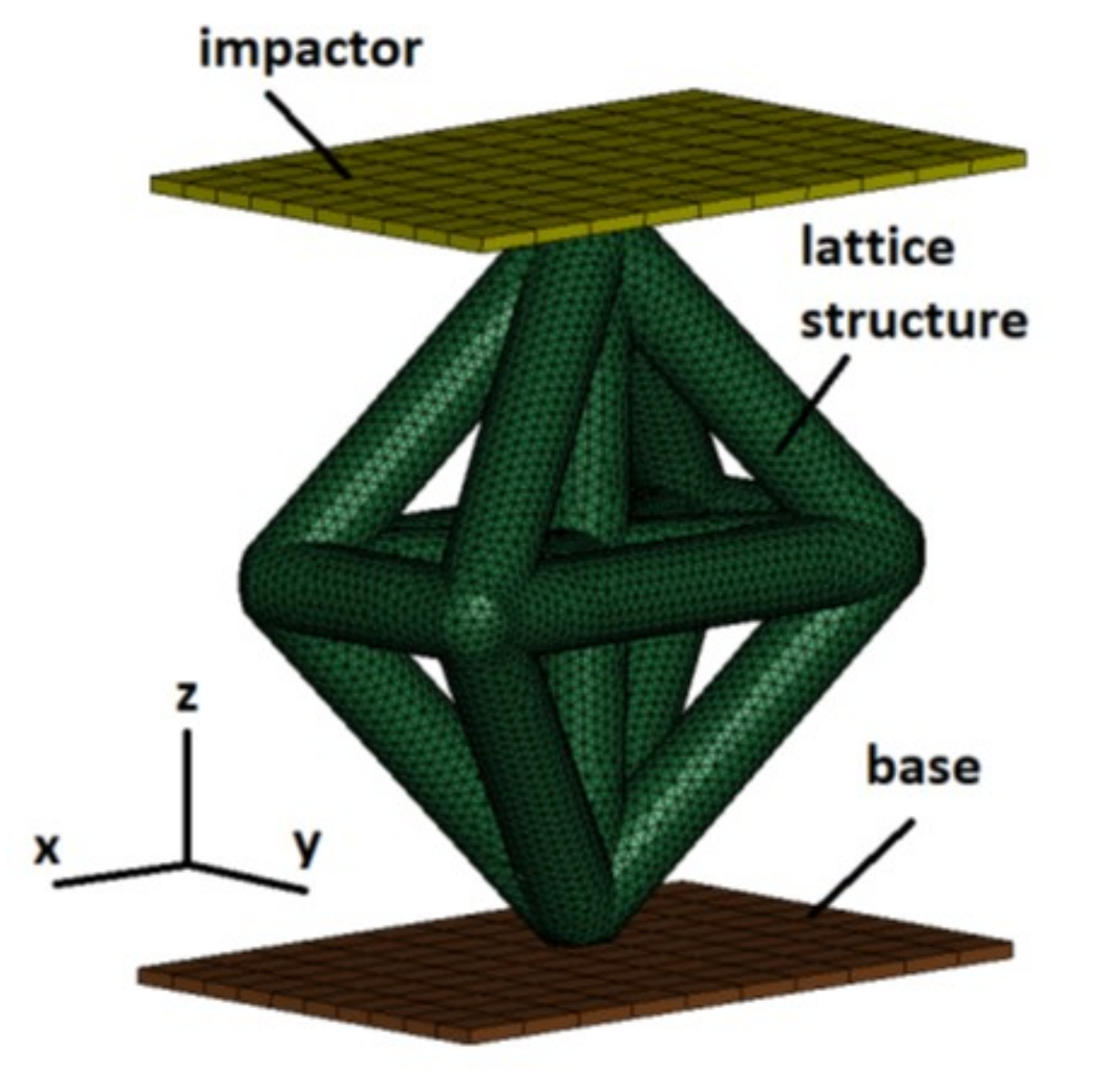
Figure 4.
Numerical Simulation Model.
Figure 4.
Numerical Simulation Model.
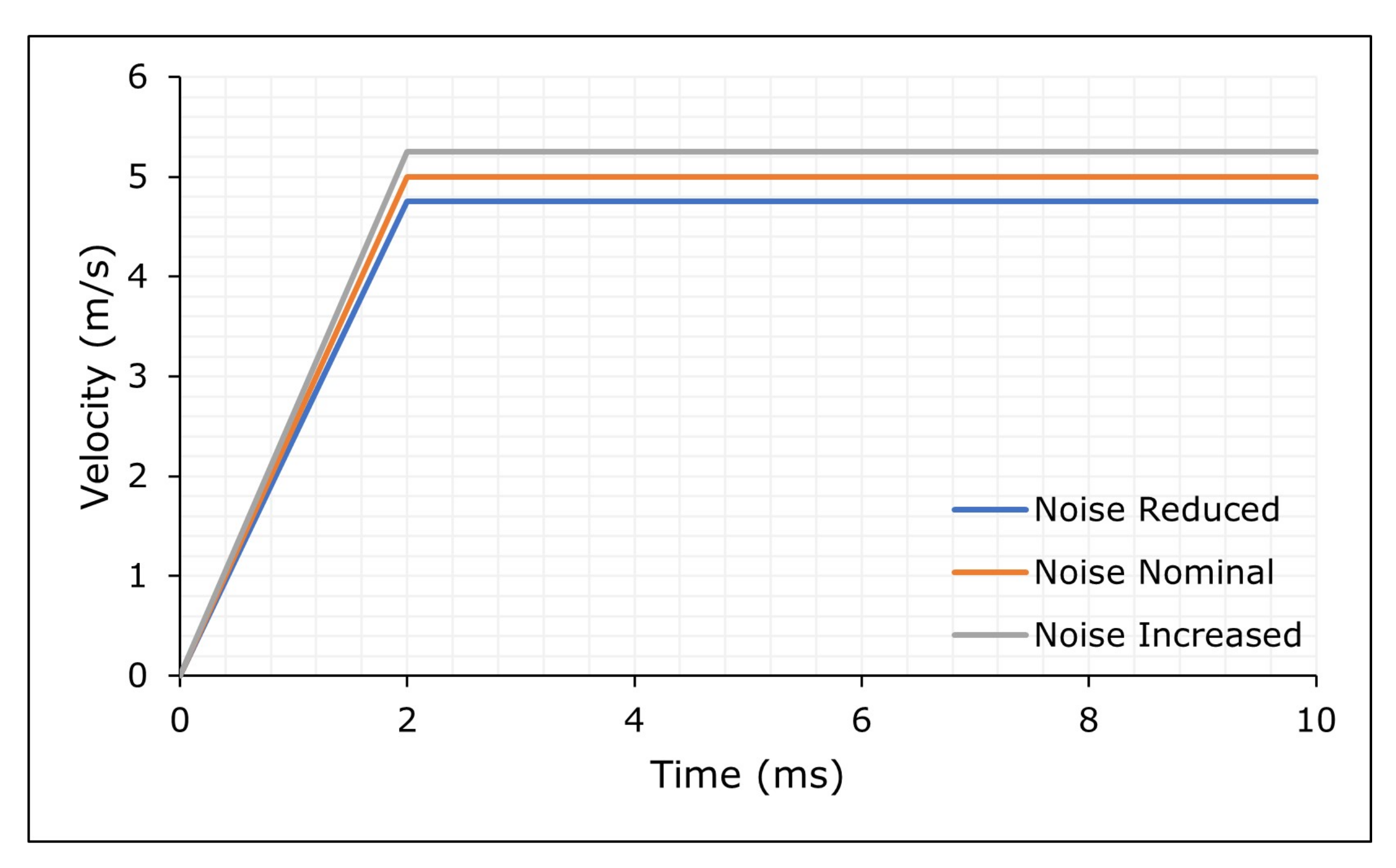
Figure 5.
Impactor’s Velocity Curve.
Figure 5.
Impactor’s Velocity Curve.
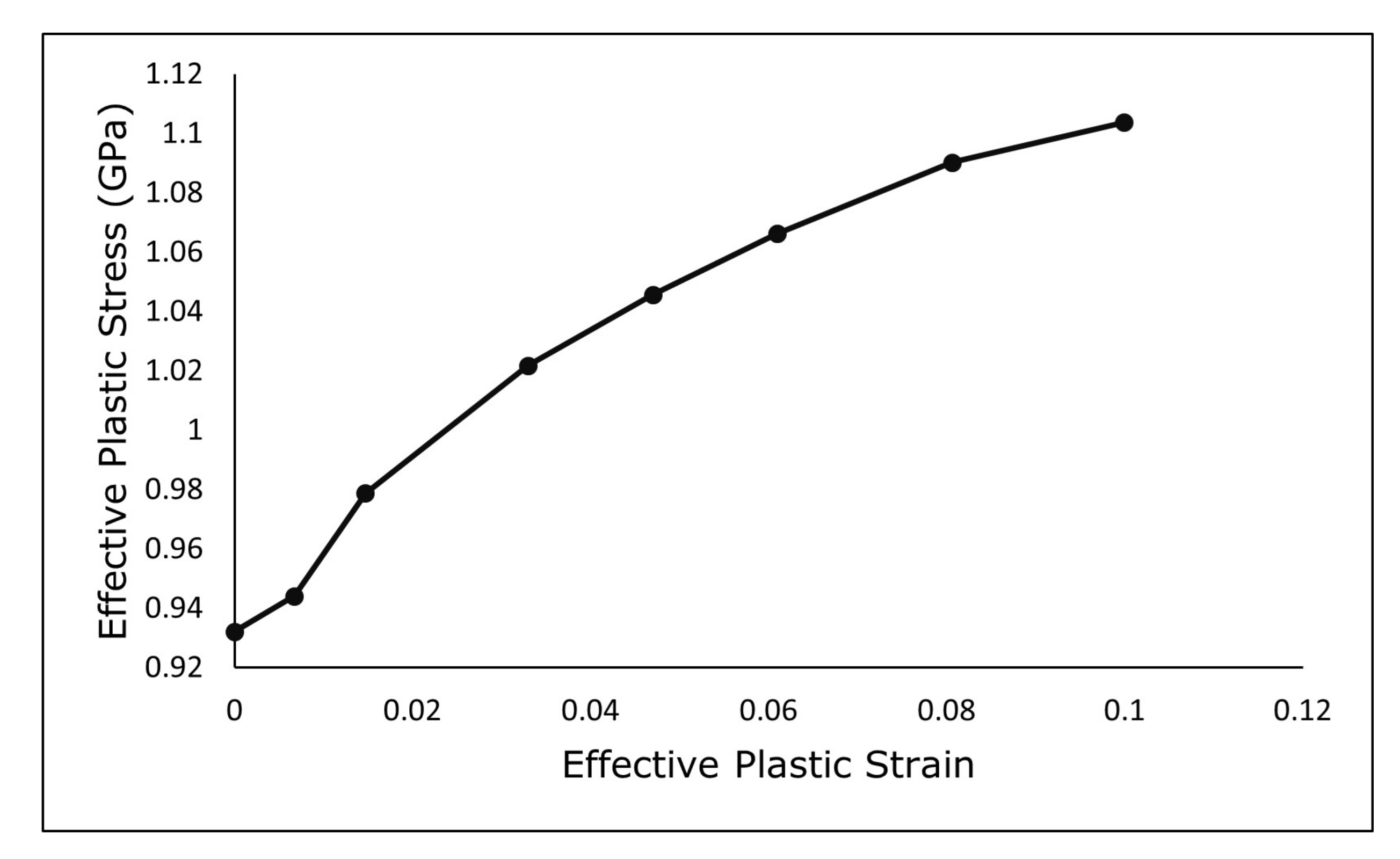
Figure 6.
Ti-6Al-4V Effective Plastic True Stress-Strain Curve [
26].
Figure 6.
Ti-6Al-4V Effective Plastic True Stress-Strain Curve [
26].
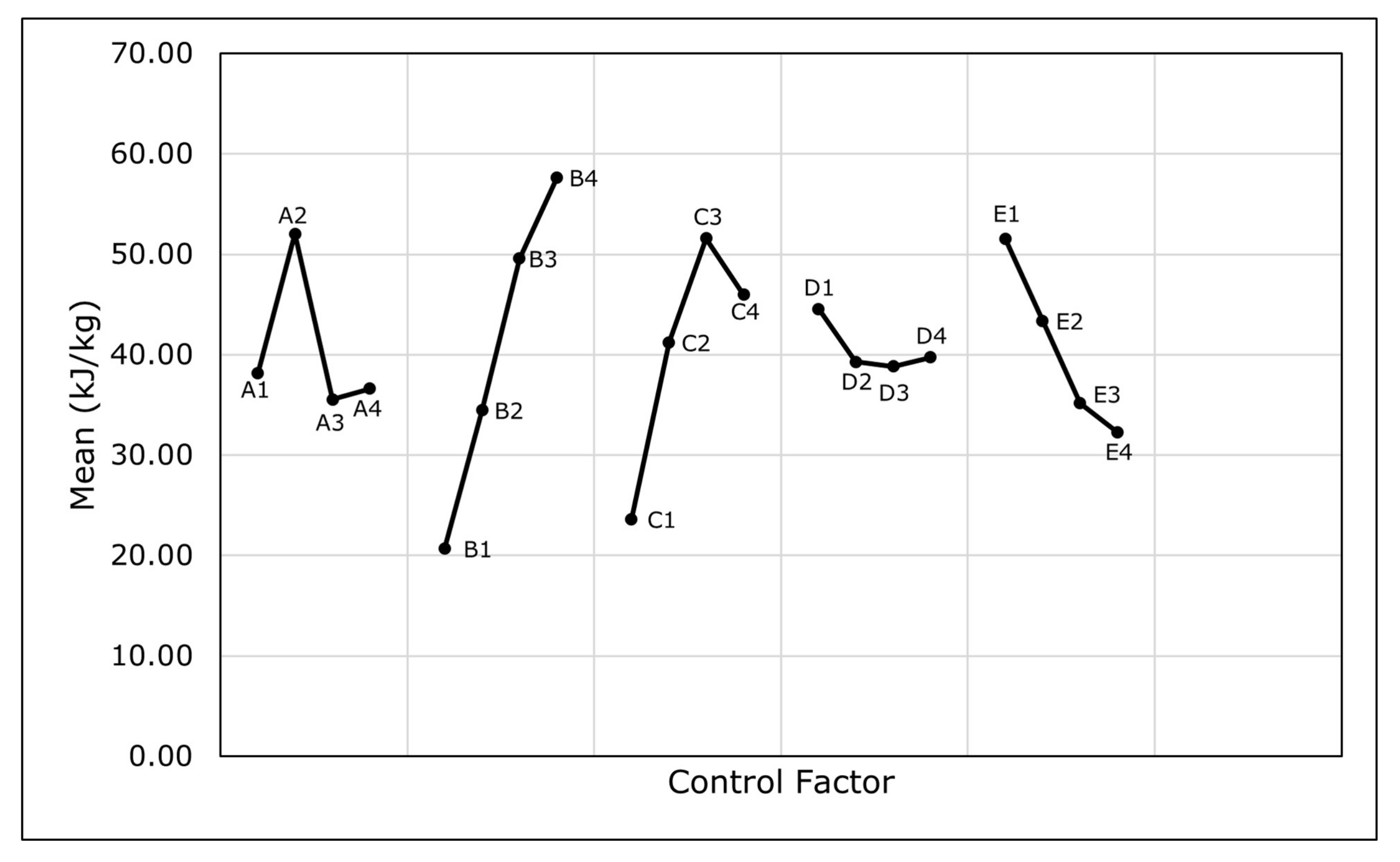
Figure 7.
Response Chart: Mean.
Figure 7.
Response Chart: Mean.
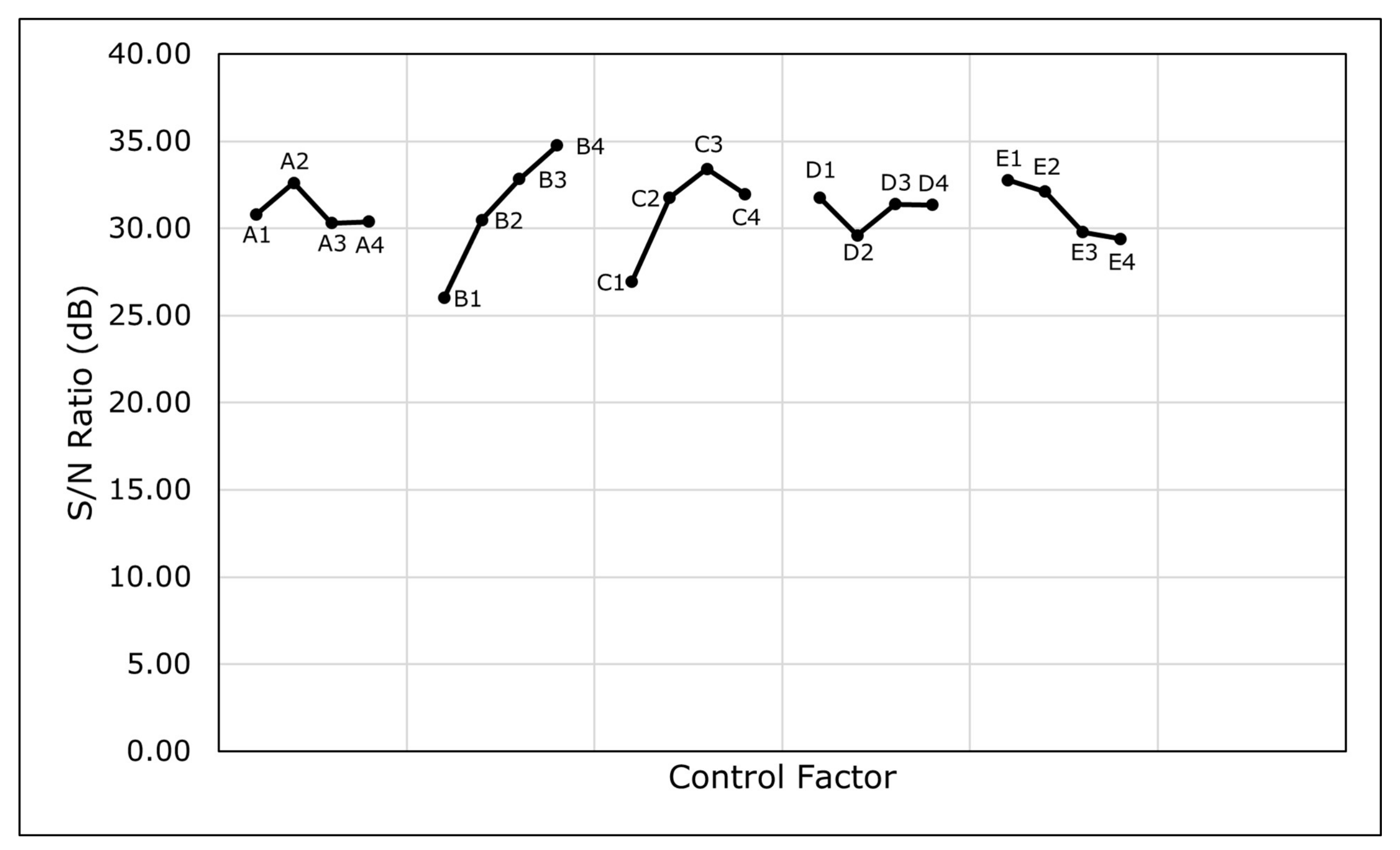
Figure 8.
Response Chart: S/N Ratio.
Figure 8.
Response Chart: S/N Ratio.
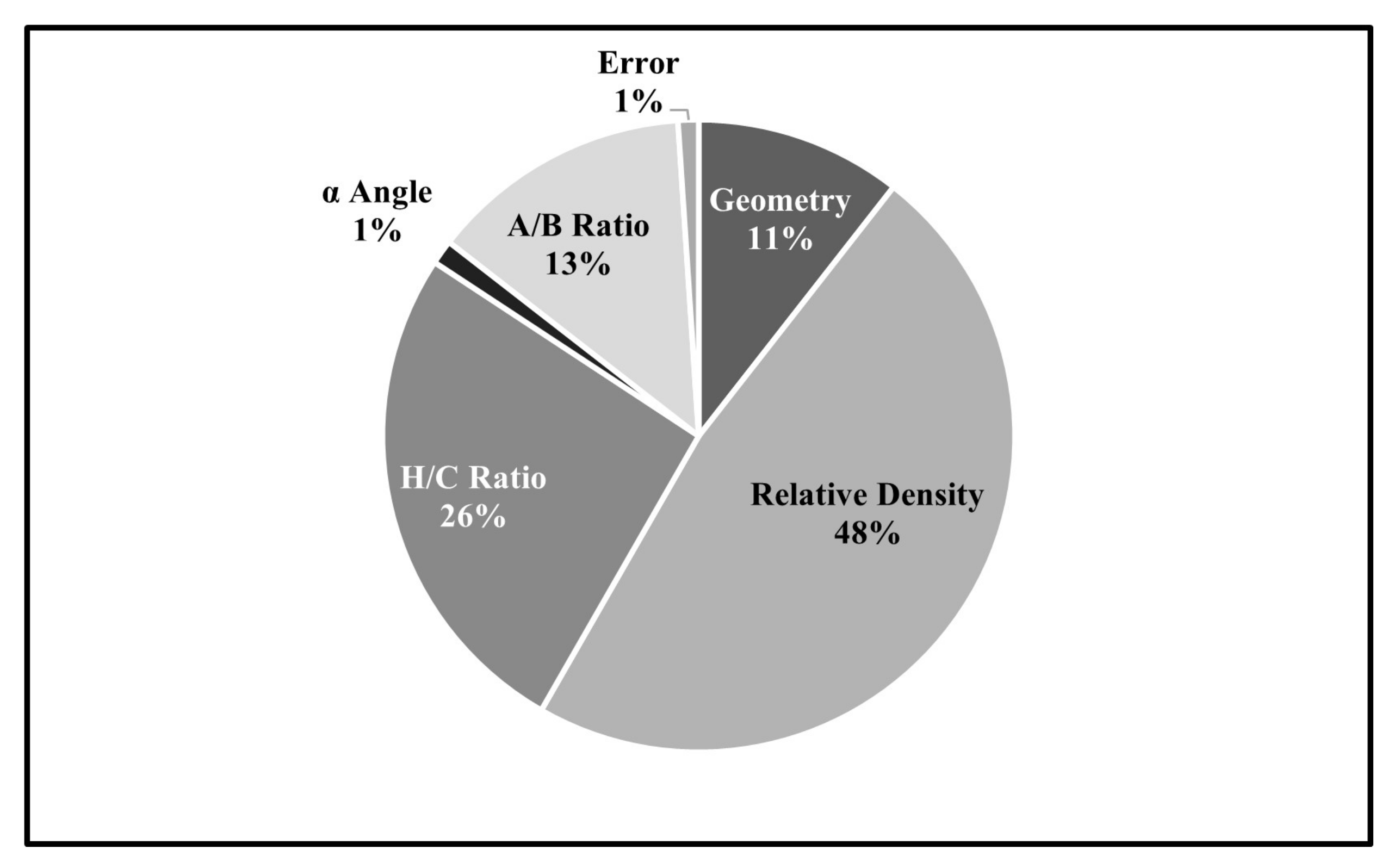
Figure 9.
Contributions of Each Control Factor.
Figure 9.
Contributions of Each Control Factor.
Figure 10.
Optimized Model Illustration.
Figure 10.
Optimized Model Illustration.
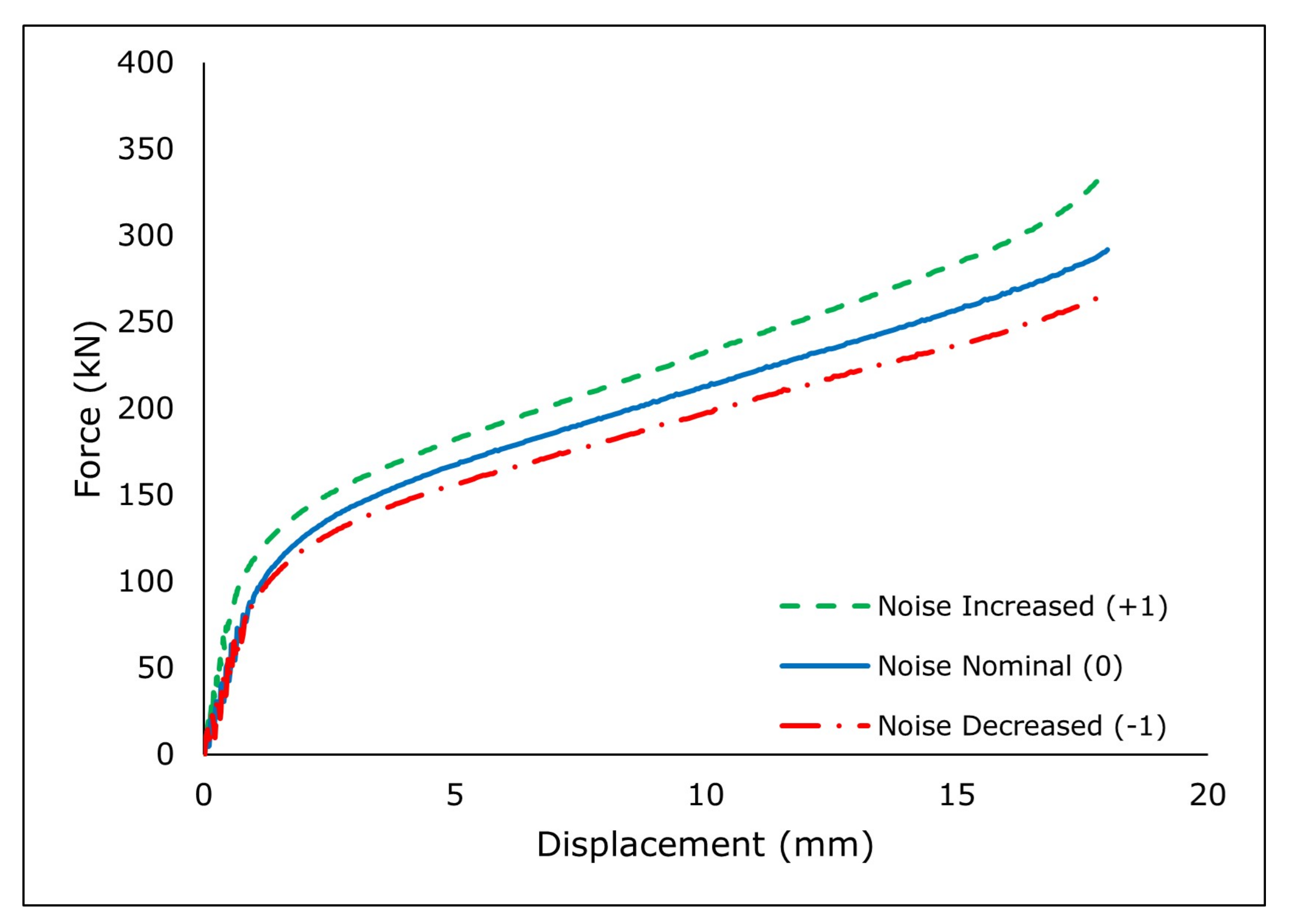
Figure 11.
Force-Displacement Curve of Optimum Model.
Figure 11.
Force-Displacement Curve of Optimum Model.
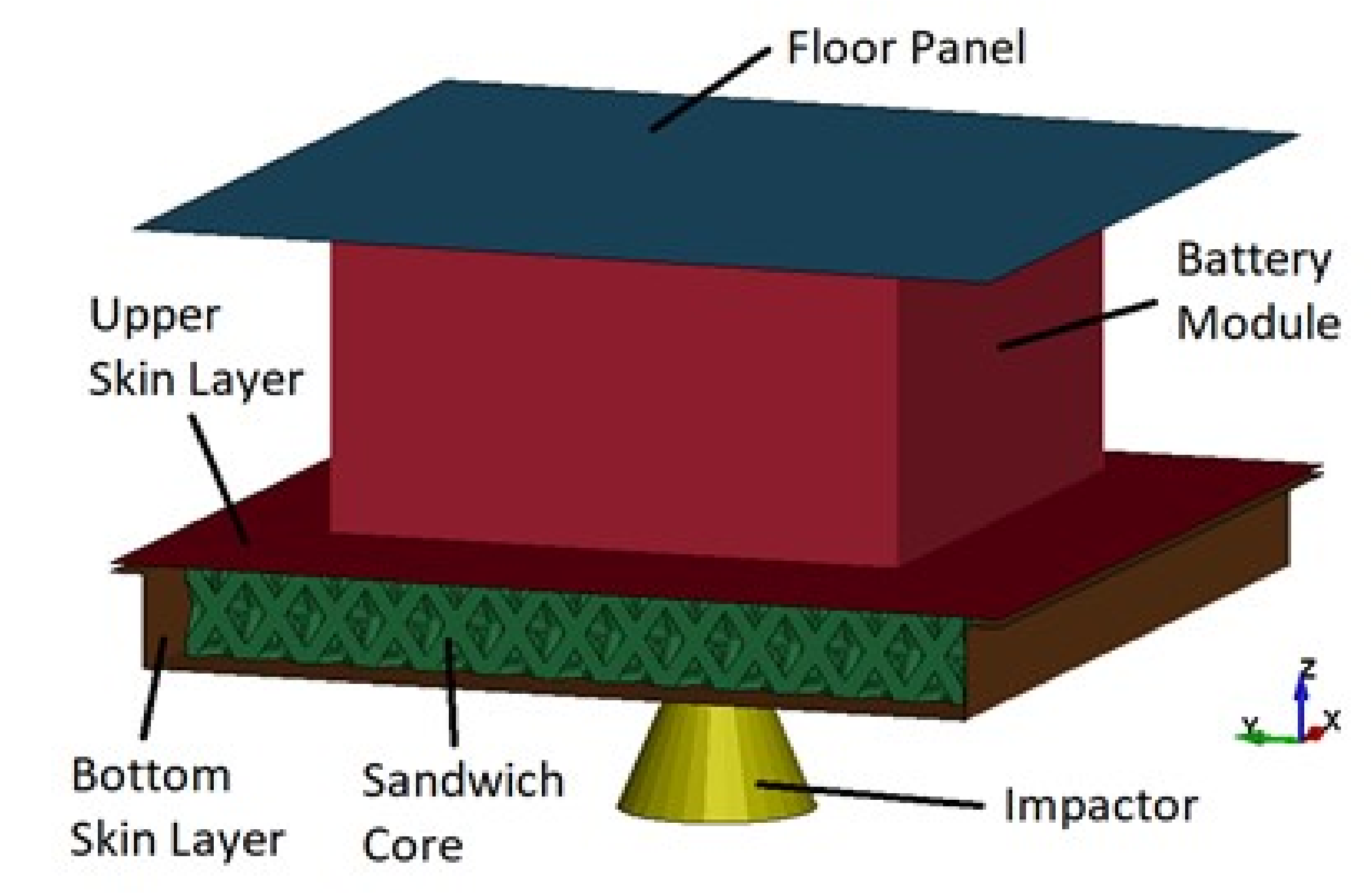
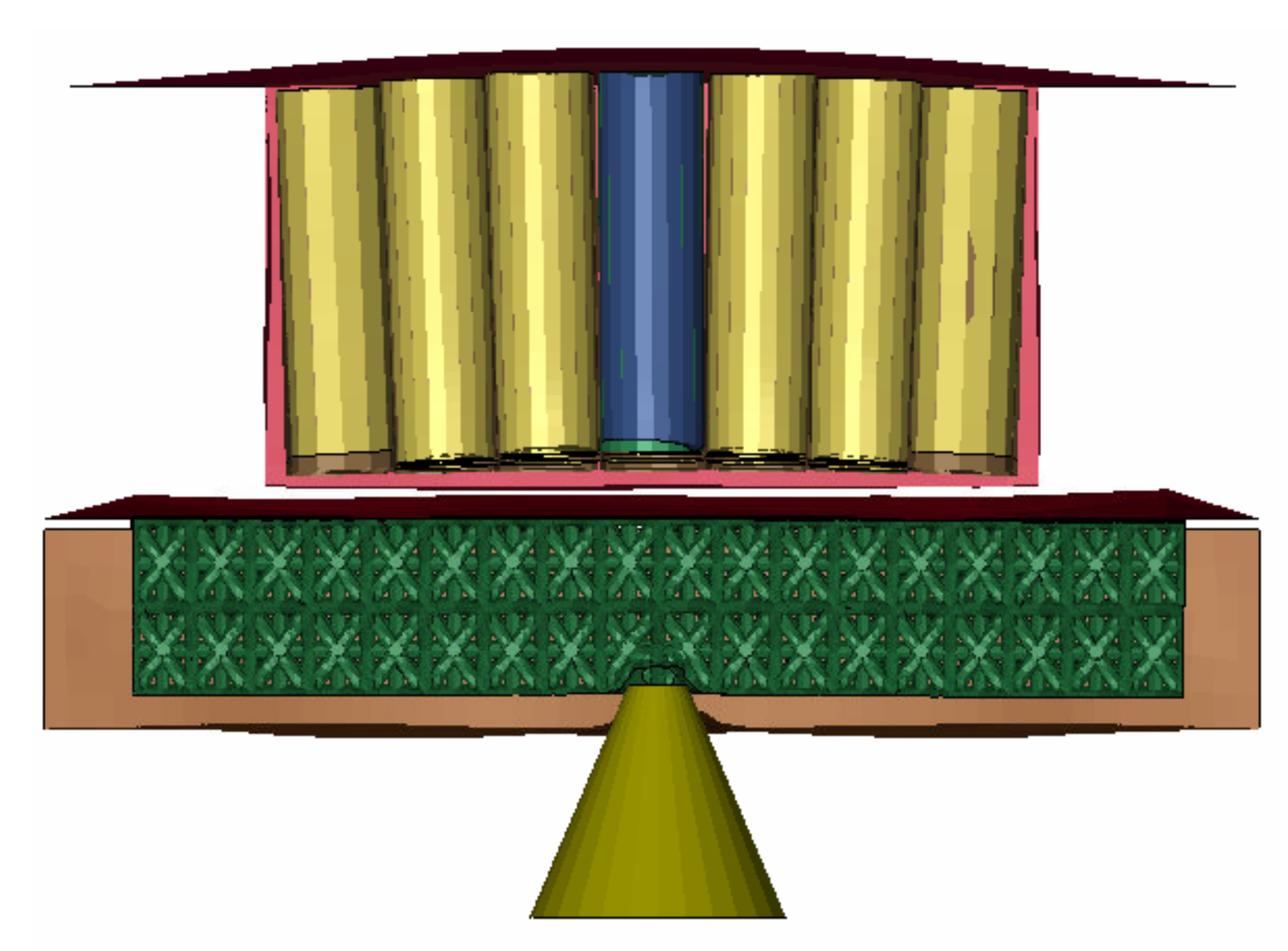
Figure 12.
Battery Protection Simulation Modelling Configuration.
Figure 12.
Battery Protection Simulation Modelling Configuration.
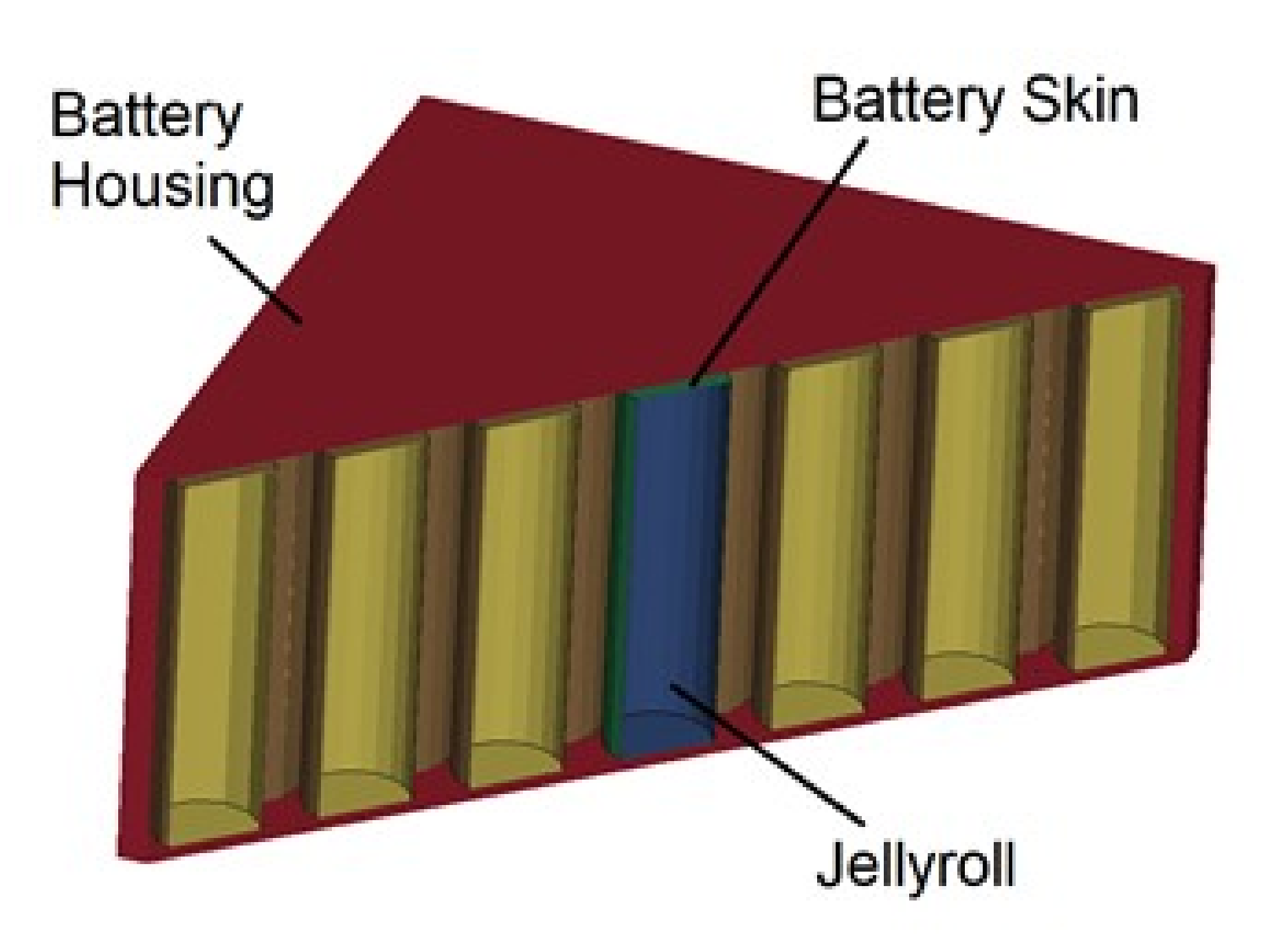
Figure 13.
Internal Configuration of Battery Module.
Figure 13.
Internal Configuration of Battery Module.
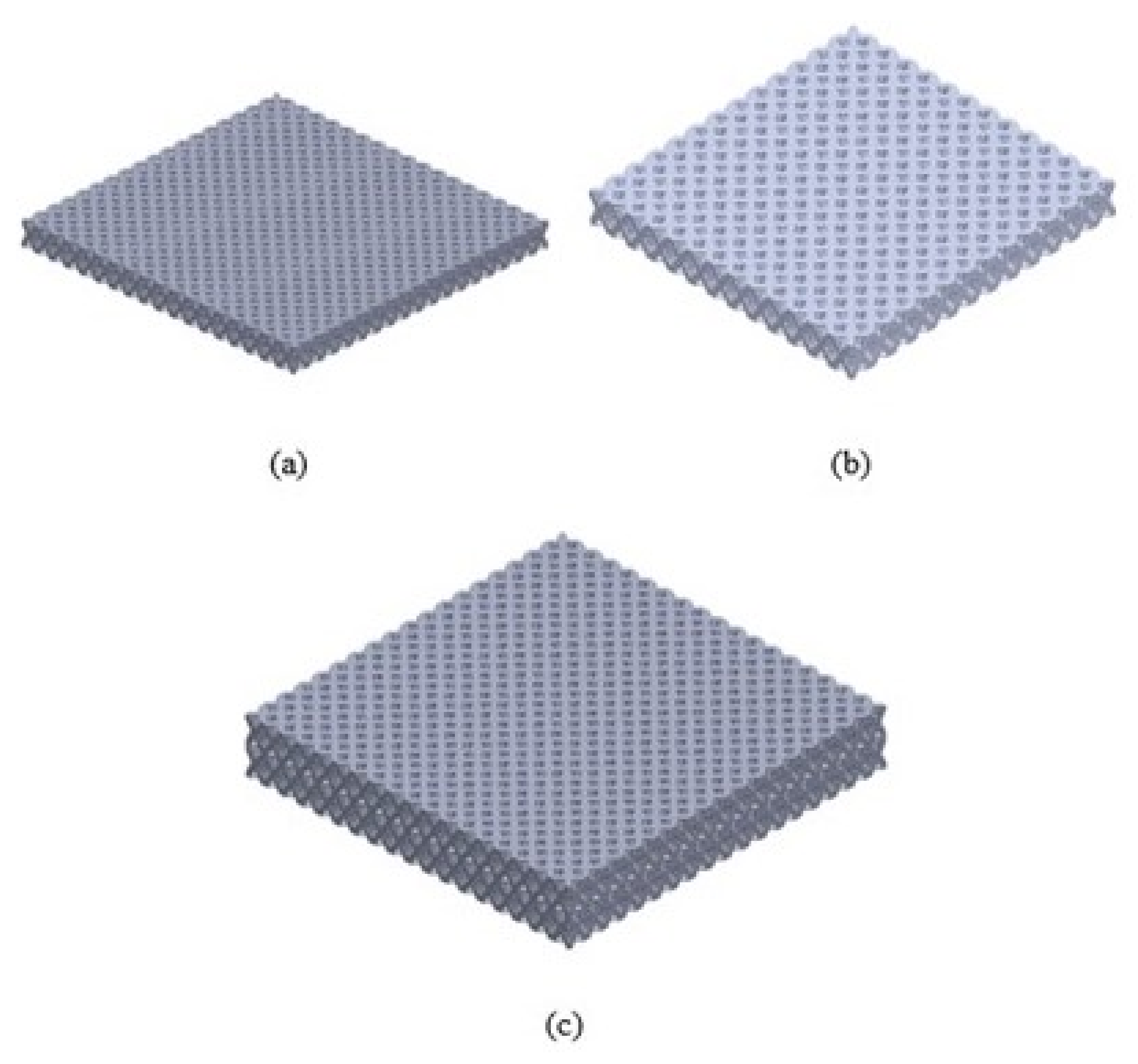
Figure 14.
Multicell Lattice Structure Configuration: (a) Configuration #1. (b) Configuration #2. (c) Configuration #3.
Figure 14.
Multicell Lattice Structure Configuration: (a) Configuration #1. (b) Configuration #2. (c) Configuration #3.
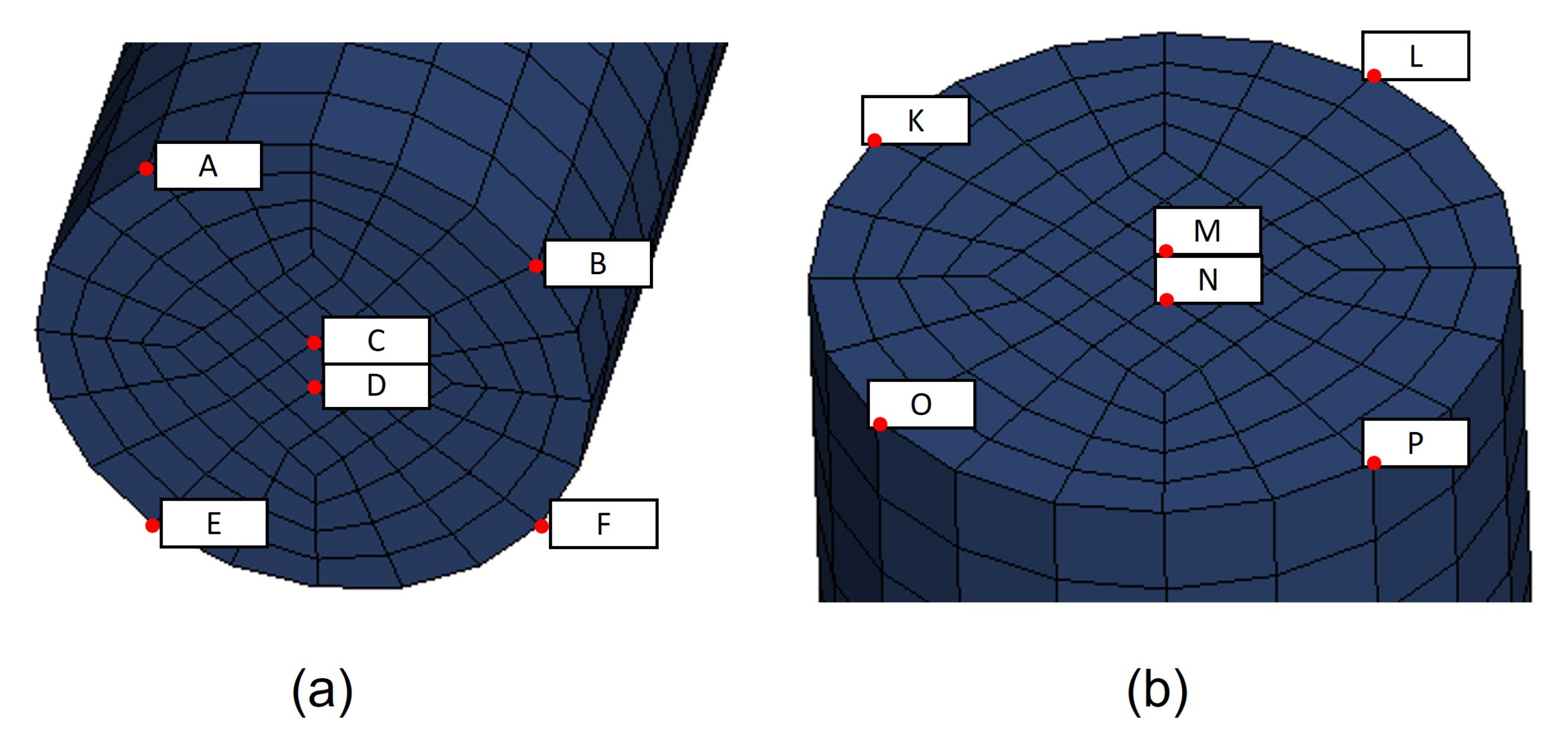
Figure 15.
Trackers Position: (a) Under The Jellyroll. (b) Above The Jellyroll.
Figure 15.
Trackers Position: (a) Under The Jellyroll. (b) Above The Jellyroll.
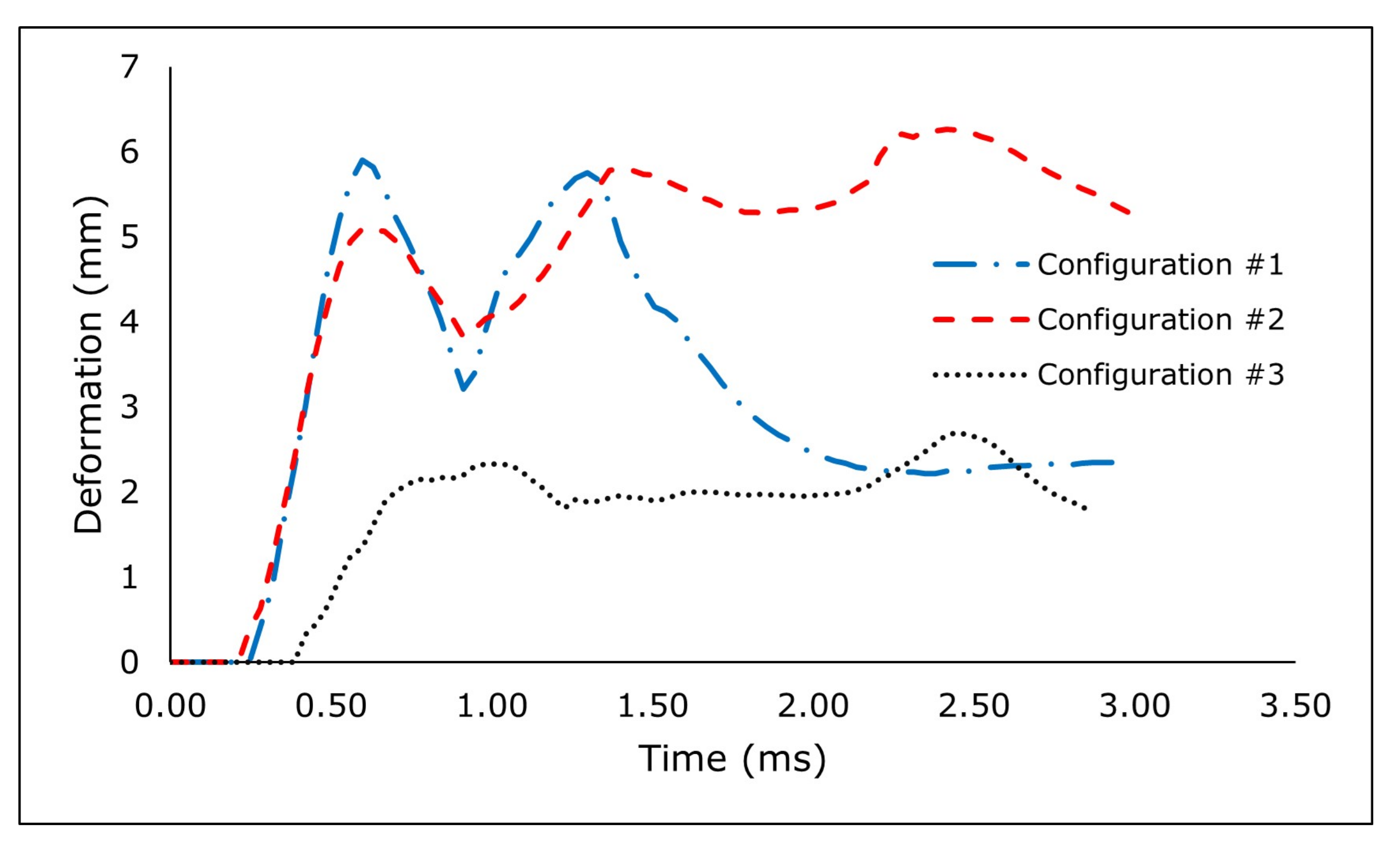
Figure 16.
Deformation Curve of The Battery for Each Lattice Configuration.
Figure 16.
Deformation Curve of The Battery for Each Lattice Configuration.
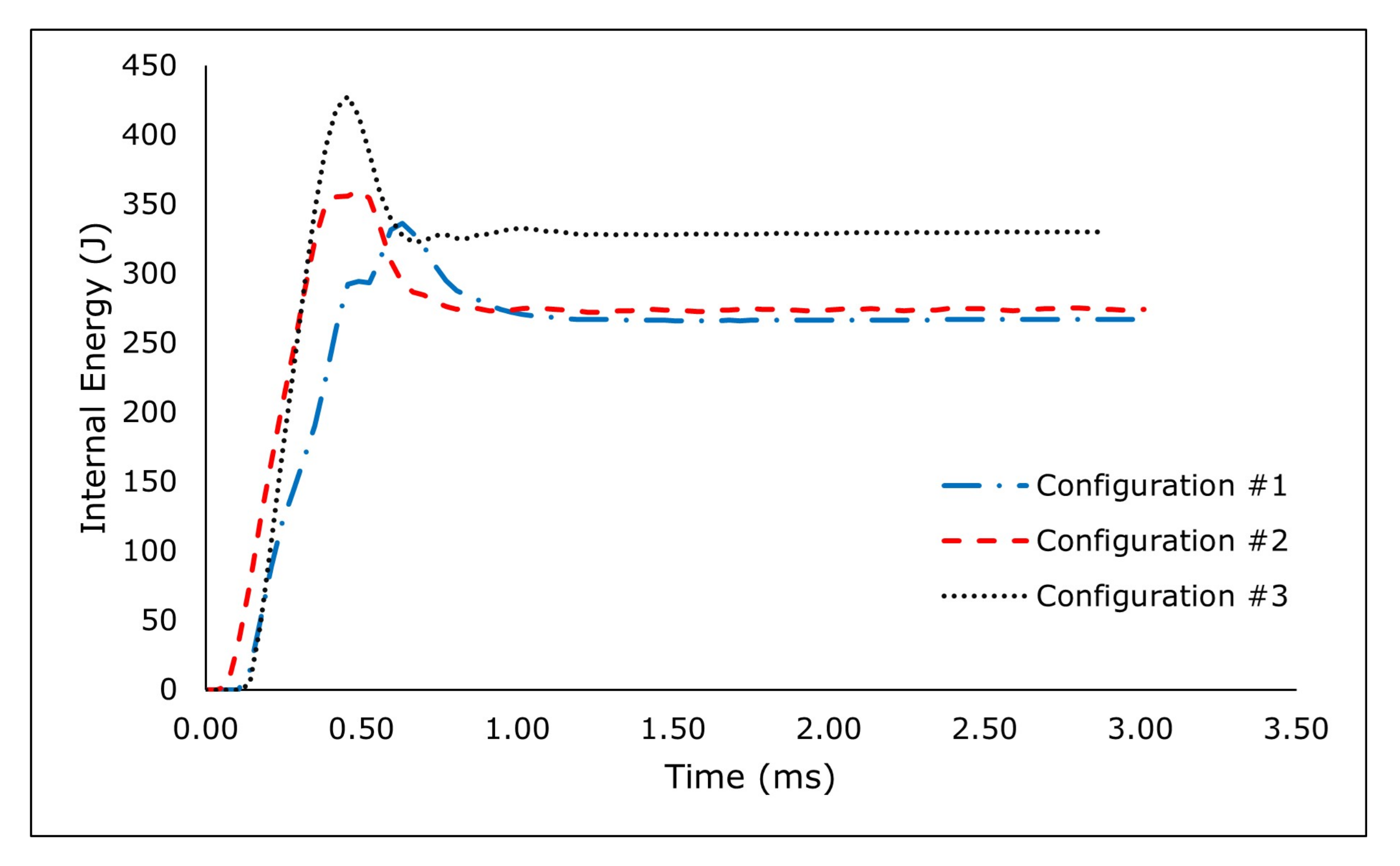
Figure 17.
Internal Energy Change of The Lattice Structure.
Figure 17.
Internal Energy Change of The Lattice Structure.
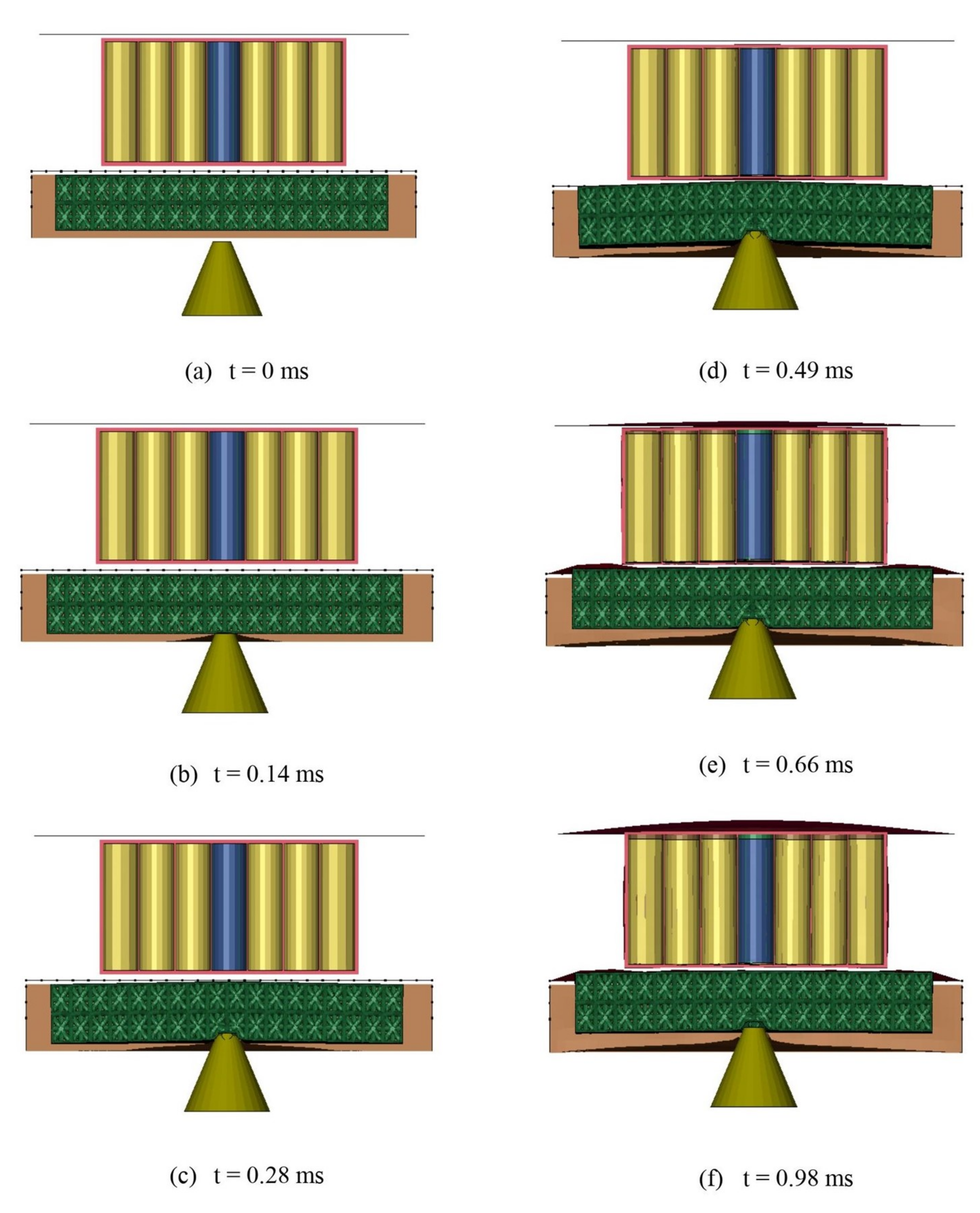
Figure 18.
Battery Protection System Response to Ground Impact.
Figure 18.
Battery Protection System Response to Ground Impact.
Figure 19.
Battery Protection System Response to Ground Impact.
Figure 19.
Battery Protection System Response to Ground Impact.
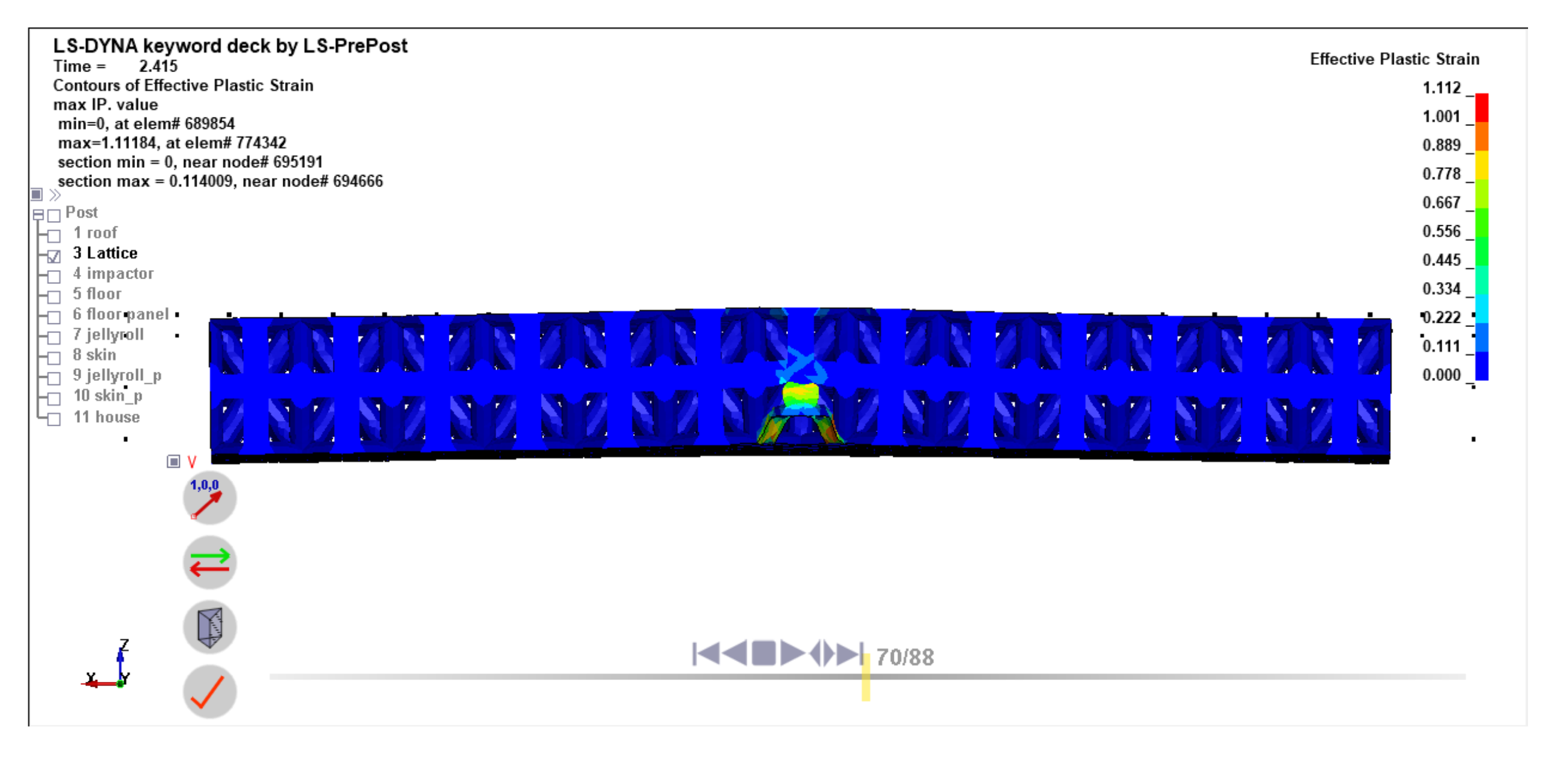
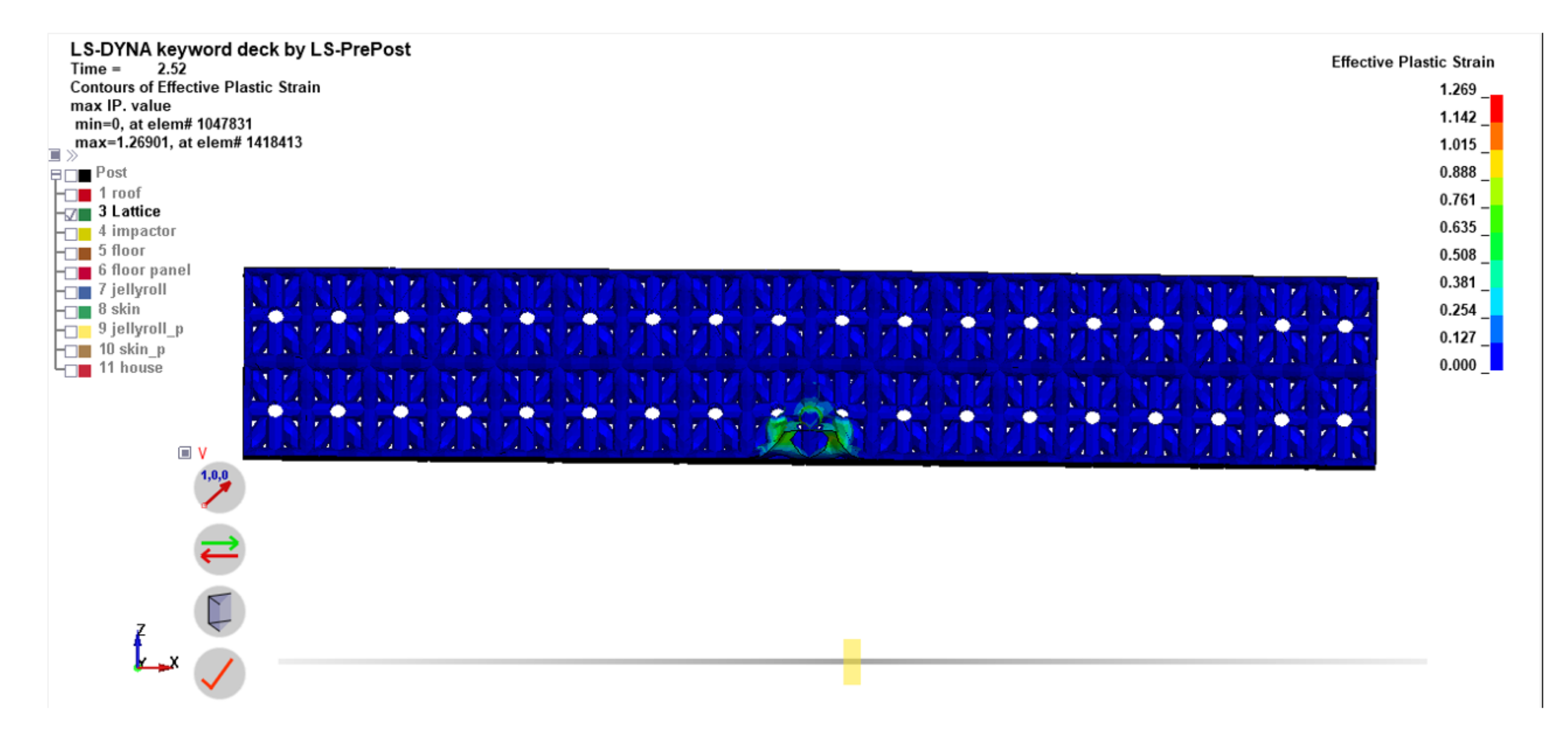
Figure 20.
Plastic Deformation of The Configuration #1 Lattice Structure.
Figure 20.
Plastic Deformation of The Configuration #1 Lattice Structure.
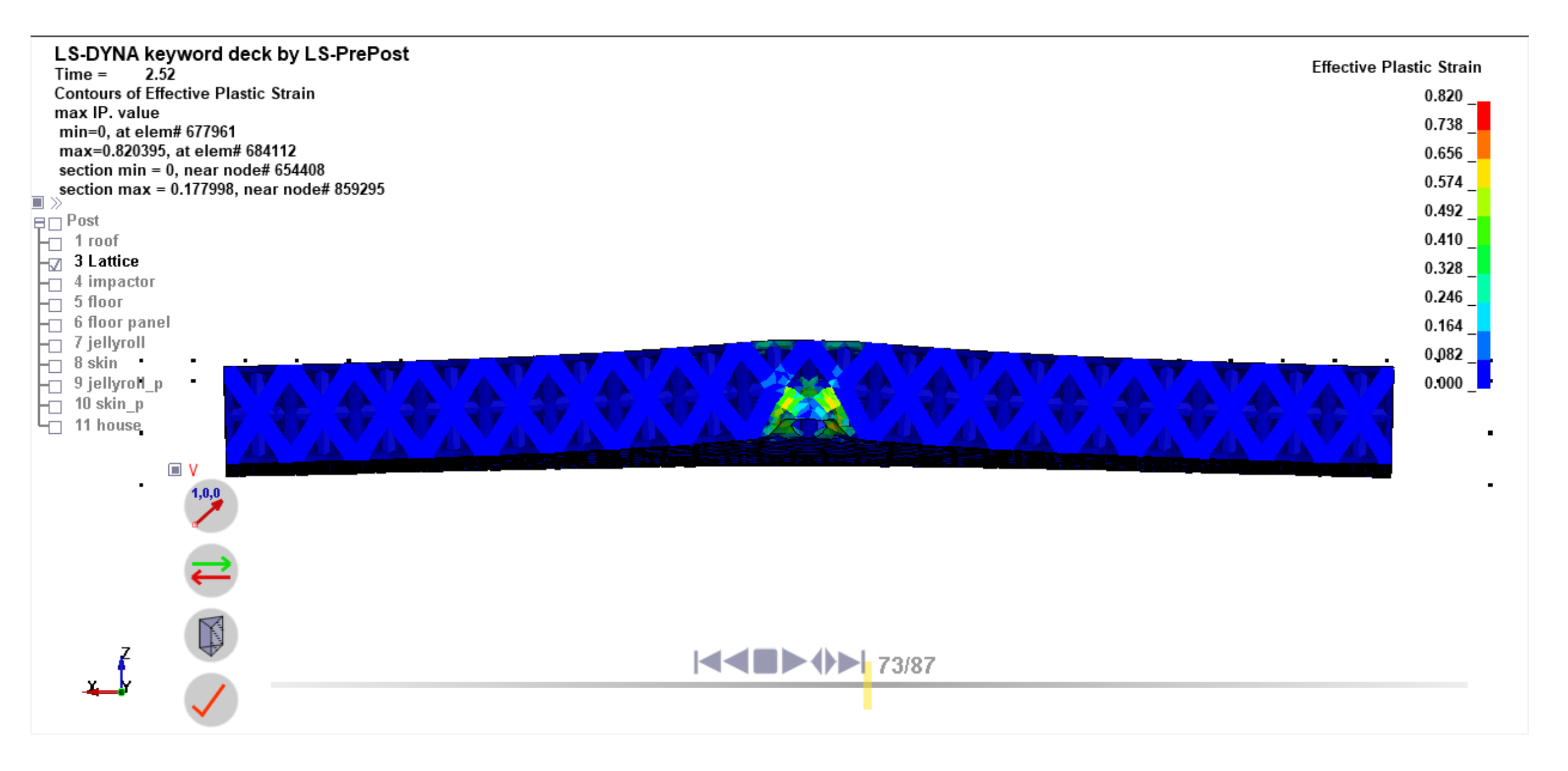
Figure 21.
Plastic Deformation of The Configuration #2 Lattice Structure.
Figure 21.
Plastic Deformation of The Configuration #2 Lattice Structure.
Figure 22.
Plastic Deformation of The Configuration #3 Lattice Structure.
Figure 22.
Plastic Deformation of The Configuration #3 Lattice Structure.
Table 1.
Lattice Structure Simulation Parameters.
Table 1.
Lattice Structure Simulation Parameters.
| Control Factors | Level |
|---|
| 1 | 2 | 3 | 4 |
|---|
| A | Geometry | OHC | OC | OT | OTM |
| B | | 10% | 20% | 30% | 40% |
| C | H/C Ratio | 0.5 | 1 | 1.5 | 2 |
| D | | 0 | 1.5 | 3 | 4.5 |
| E | A/B Ratio | 1 | 1.5 | 2 | 2.5 |
Table 2.
Complete Taguchi’s Design of Experiment.
Table 2.
Complete Taguchi’s Design of Experiment.
| Running No. | Control Factor |
|---|
| A (Geometry) | B () | C (H/C) | D () | E (A/B) |
|---|
| 1 | 1 | [OHC] | 1 | [10%] | 1 | [0.5] | 1 | [0] | 1 | [1] |
| 2 | 1 | [OHC] | 2 | [20%] | 2 | [1] | 2 | [1.5] | 2 | [1.5] |
| 3 | 1 | [OHC] | 3 | [30%] | 3 | [1.5] | 3 | [3] | 3 | [2] |
| 4 | 1 | [OHC] | 4 | [40%] | 4 | [2] | 4 | [4.5] | 4 | [2.5] |
| 5 | 2 | [OC] | 1 | [10%] | 2 | [1] | 3 | [3] | 4 | [2.5] |
| 6 | 2 | [OC] | 2 | [20%] | 1 | [0.5] | 4 | [4.5] | 3 | [2] |
| 7 | 2 | [OC] | 3 | [30%] | 4 | [2] | 1 | [0] | 2 | [1.5] |
| 8 | 2 | [OC] | 4 | [40%] | 3 | [1.5] | 2 | [1.5] | 1 | [1] |
| 9 | 3 | [OT] | 1 | [10%] | 3 | [1.5] | 4 | [4.5] | 2 | [1.5] |
| 10 | 3 | [OT] | 2 | [20%] | 4 | [2] | 3 | [3] | 1 | [1] |
| 11 | 3 | [OT] | 3 | [30%] | 1 | [0.5] | 2 | [1.5] | 4 | [2.5] |
| 12 | 3 | [OT] | 4 | [40%] | 2 | [1] | 1 | [0] | 3 | [2] |
| 13 | 4 | [OTM] | 1 | [10%] | 4 | [2] | 2 | [1.5] | 3 | [2] |
| 14 | 4 | [OTM] | 2 | [20%] | 3 | [1.5] | 1 | [0] | 4 | [2.5] |
| 15 | 4 | [OTM] | 3 | [30%] | 2 | [1] | 4 | [4.5] | 1 | [1] |
| 16 | 4 | [OTM] | 4 | [40%] | 1 | [0.5] | 3 | [3] | 2 | [1.5] |
Table 3.
Noise Applied in Finite Element Simulation.
Table 3.
Noise Applied in Finite Element Simulation.
| Variable | Noise |
|---|
| Increasing | Nominal | Reducing |
|---|
| Impactor velocity (m/s) | 5.25 | 5 | 4.75 |
| Relative Density | ρ × 1.05
| ρ | ρ × 0.95
|
Table 4.
Ti-6Al-4V Material Properties.
Table 4.
Ti-6Al-4V Material Properties.
| Variable | Value | Unit |
|---|
| Density [25] | 4428.79 | kg/m3 |
| Young’s Modulus [25] | 116.52 | GPa
|
| Yield Strength [26] | 932.22 | MPa
|
| Poisson’s Ratio [25] | 0.31 | |
| Cowper-Symonds Constant: D [27] | 200 | |
| Cowper-Symonds Constant: q [27] | 15 | |
Table 5.
SEA Results from Simulations Based on Taguchi Design of Experiment.
Table 5.
SEA Results from Simulations Based on Taguchi Design of Experiment.
| Running No. | Noise; SEA (kJ/kg) | Average (kJ/kg) | S/N Ratio (dB) |
|---|
| Increased | Nominal | Decreased |
|---|
| 1 | 16.42 | 16.19 | 16.02 | 16.21 | 24.19 |
| 2 | 35.28 | 34.15 | 33.04 | 34.15 | 30.66 |
| 3 | 53.32 | 51.24 | 48.24 | 50.93 | 34.12 |
| 4 | 55.63 | 50.30 | 48.34 | 51.42 | 34.18 |
| 5 | 23.60 | 22.49 | 21.94 | 22.68 | 27.10 |
| 6 | 23.31 | 22.77 | 21.82 | 22.63 | 27.08 |
| 7 | 79.77 | 73.49 | 66.03 | 73.10 | 37.20 |
| 8 | 91.99 | 89.63 | 87.56 | 89.73 | 39.05 |
| 9 | 29.76 | 28.83 | 26.99 | 28.53 | 29.08 |
| 10 | 46.60 | 42.54 | 42.73 | 43.96 | 32.84 |
| 11 | 19.66 | 18.08 | 16.07 | 17.94 | 24.99 |
| 12 | 53.40 | 52.12 | 49.52 | 51.68 | 34.25 |
| 13 | 16.38 | 15.39 | 14.18 | 15.32 | 23.66 |
| 14 | 39.65 | 37.89 | 33.83 | 37.13 | 31.34 |
| 15 | 57.87 | 56.24 | 54.87 | 56.33 | 35.01 |
| 16 | 39.80 | 37.65 | 35.65 | 37.70 | 31.50 |
| Total | 1948.30 | - | - |
Table 6.
Average and S/N Ratio for Each Control Factor and Level.
Table 6.
Average and S/N Ratio for Each Control Factor and Level.
| Variable | Index | Mean (kJ/kg) | S/N RAtio (dB) |
|---|
| A | 1 | 38.18 | 30.79 |
| 2 | 52.03 | 32.61 |
| 3 | 35.53 | 30.29 |
| 4 | 36.62 | 30.38 |
| B | 1 | 20.68 | 26.01 |
| 2 | 34.47 | 30.48 |
| 3 | 49.57 | 32.83 |
| 4 | 57.63 | 34.75 |
| C | 1 | 23.62 | 26.94 |
| 2 | 41.21 | 31.76 |
| 3 | 51.58 | 33.40 |
| 4 | 45.95 | 31.97 |
| D | 1 | 44.53 | 31.75 |
| 2 | 39.29 | 29.59 |
| 3 | 38.82 | 31.39 |
| 4 | 39.73 | 31.34 |
| E | 1 | 51.56 | 32.77 |
| 2 | 43.37 | 32.11 |
| 3 | 35.14 | 29.78 |
| 4 | 32.29 | 29.40 |
Table 7.
Optimum Lattice Structure Parameters.
Table 7.
Optimum Lattice Structure Parameters.
| Control Factor | Level | Description | Value |
|---|
| A | 2 | Geometry | Octet-Cross |
| B | 4 | ρ | 40% |
| C | 3 | H/C Ratio | 1.5 |
| D | 1 | α | 0° |
| E | 1 | A/B Ratio | 1 |
Table 8.
Analysis of Variance Result.
Table 8.
Analysis of Variance Result.
| Variable | DOF | SS | Contribution | MS | F | Significance |
|---|
| A | 3 | 2138.19 | 10.57% | 712.73 | 106.98 | Significant |
| B | 3 | 9659.32 | 47.73% | 3219.77 | 483.31 | Significant |
| C | 3 | 5254.40 | 25.96% | 1751.47 | 262.90 | Significant |
| D | 3 | 253.26 | 1.25% | 84.42 | 12.67 | Significant |
| E | 3 | 2718.77 | 13.43% | 906.26 | 136.03 | Significant |
| Error | 32 | 213.18 | 1.05% | 6.66 | | |
| Total | 47 | 20,237.12 | 100% | | | |
Table 9.
Performance of The Optimum Model.
Table 9.
Performance of The Optimum Model.
| Parameter | Noise |
|---|
| Increase | Nominal | Decrease |
|---|
| Volume (mm3) | 10,014.24 | 9473.54 | 8943.15 |
| Mass (g) | 44.36 | 41.97 | 39.62 |
| Total EA (J) | 3931.29 | 3553.12 | 3293.07 |
| SEA (kJ/kg) | 88.62 | 84.66 | 83.12 |
Table 10.
Verification of The Optimized Model Summary.
Table 10.
Verification of The Optimized Model Summary.
| Parameters | Existing Model | Estimated | Verification | Difference |
|---|
| Value | Gain | Value | Gain |
|---|
| Mean SEA (kJ/kg) | 40.59 | 94.97 | 54.38 | 85.47 | 44.88 | 9.51 |
| S/N Ratio (dB) | 31.02 | 41.21 | 10.19 | 38.63 | 7.61 | 2.58 |
Table 11.
Jellyroll Material Properties [
13].
Table 11.
Jellyroll Material Properties [
13].
| Variable | Value |
|---|
| Density | 2.721 × 10−6 kg/mm3 |
| Young’s Modulus | 0.5 GPa |
Table 12.
Lattice Structure Scaling Configuration.
Table 12.
Lattice Structure Scaling Configuration.
| Configuration | Dimension (mm × mm × mm) | Plies | Mass (g) |
|---|
| 1 | 10 × 10 × 15 | 1 | 861 |
| 2 | 14 × 14 × 21 | 1 | 1232 |
| 3 | 10 × 10 × 15 | 2 | 1722 |
Table 13.
Master and Slave Parts of Defined Contact Parameters.
Table 13.
Master and Slave Parts of Defined Contact Parameters.
| Master Part | Slave Part |
|---|
| Impactor | Top Sandwich Layer |
| Impactor | Lattice Core |
| Impactor | Bottom Sandwich Layer |
| Impactor | Battery Housing |
| Lattice Core | Lattice Core |
| Top Sandwich Layer | Lattice Core |
| Bottom Sandwich Layer | Lattice Core |
| Battery Skin | Battery Housing |
| Top Sandwich Layer | Battery Housing |
| Floor Panel | Battery Housing |
| Battery Jellyroll | Battery Skin |