Abstract
The software-in-the-loop and hardware-in-the-loop tests of a battery management system require a real-time compatible electro-thermal battery pack model. In our study, a numerically complex electrochemical-thermal model has been characterized from experimental data of a nickel-rich, silicon-graphite 18650-type lithium-ion cell. While it accurately represents the electro-thermal battery behavior, it is hardly suitable for real-time application due to its intensively numerical solving effort and related calculation time if no huge numerical efforts are applied to reduce the model. The objective of this paper is to present a simple method to derive a reduced-order electro-thermal cell model from the complex electrochemical-thermal cell model and build a real-time compatible battery pack model with the reduced-order cell model.
1. Introduction
The battery management system (BMS) is a critical component for electric vehicles. During the development of BMS, several types of test can be done in order to evaluate its performance: (1) Software-in-the-Loop (SiL) test to evaluate the BMS control algorithm; (2) Hardware-in-the-Loop (HiL) test to evaluate the real-time performance of the BMS; (3) test with real battery pack to finally validate the BMS performance. For the SiL and HiL tests, a battery pack model is needed to represent the electro-thermal behavior of the cells in the pack. The battery pack model consists of individual cell models which can be either characterized with experimental measurements or with simulated data from a complex model (e.g., electrochemical-thermal model). The battery pack model must have a good compromise of accuracy and simplicity to be real-time compatible for the SiL and HiL tests. In our study, the numerically intensive pseudo-two dimensional, electrochemical-thermal model for a lithium-ion battery [1] is considered and was parameterized and validated in a wide operating range in our previous work [2]. The problem to solve is to get a reduced-order electro-thermal cell model from the electrochemical-thermal model and build a battery pack model which is real-time compatible and ready for the SiL and HiL tests of BMS. The objective of this paper is to present a simple method to get a reduced-order electro-thermal cell model from a complex electrochemical cell model and then build a battery pack model with the reduced-order cell model.
The remaining part of this paper is organized as follows. Section 2 presents the electrochemical model. Section 3 describes the method to get the reduced-order electro-thermal model. It also presents the validation of the method by comparing the simulation results between the two models. Section 4 presents the battery pack model build from the reduced-order cell model in the simulation software Siemens Simcenter Amesim. Section 5 concludes the paper.
2. Electrochemical Model
In our study, the well-known pseudo-two dimensional (p2D) electrochemical-thermal model [1] has been used which is parameterized and validated at various temperatures and current loads for an 18650 nickel-rich, silicon-graphite lithium-ion cell of 3.35 Ah as presented in the work of Sturm et al. [2]. The p2D model used here simulates potentials and concentrations in the active materials and the electrolyte based on porous electrode theory and concentrated solution theory combined via electrode kinetics throughout the thickness of a single electrochemical cell unit containing an anode, separator and cathode [1]. Model reduction and implementation into MATLAB 2018a were applied to the p2D model used in this work according to previous works [3]. The Parabolic Profile approximation [4] for the approximation of the particle domain was used together with the finite difference method (FDM) for the remaining spatial discretization of the differential algebraic equation system. The Crank Nicolson [5] formulation was used for the time discretization, and an iterative Newton–Raphson scheme [6] was used for the overall solving process. No side reactions or multiple particle sizes were included in this p2D model.
While the complete electrochemical model presents many advantages such as giving detailed insight into the electrochemical process inside the battery cell, it is not suitable for real-time simulation due to its high computational cost. To simulate the electro-thermal behavior of a battery pack including many cells connected in series and parallel, a simplified cell model must be used and at the same time it must be able to represent accurately the electro-thermal behavior of the cell.
3. Reduced-Order Electro-Thermal Model
In the literature, several types of simplified models to represent the electro-thermal behavior of the battery have been proposed, such as the equivalent circuit model, the single particle (SP) model and black box model:
- Firstly, the equivalent circuit models are intensively studied in the literature. They commonly share a similar structure with electrical or electrochemical elements: (1) a voltage source to represent the open circuit voltage; (2) an ohmic resistance to represent the instantaneous voltage drop when a current is applied to the battery; (3) a diffusion impedance to capture the dynamic behavior related to the diffusion of lithium-ion inside the battery. The diffusion impedance can be represented by a network of RC circuits connected in series [7,8,9,10,11,12,13,14], by an electrochemical impedance such as the constant phase element (CPE) or Warburg impedance [15,16,17], or by other circuit structures including resistances and capacitors [11,18]. The equivalent circuit models are mostly calibrated with temporal test data. Frequency data from the electrochemical impedance spectroscopy (EIS) has also been used to identify the diffusion impedance [16,17]. The equivalent circuit models can be easily coupled with a simplified thermal model to estimate the temperature change during the battery operation [7,9,10,11,14]. The simplified thermal models reported in the literature commonly include one or several equivalent thermal capacitors to represent the specific heat of the battery cell, one or several equivalent thermal resistances to represent the heat conduction inside the cell and the heat convection with the ambient environment. The equivalent circuit models are compatible with aging modeling [19] and thermal runaway modeling [20]. These models have also been implemented in some of the simulation software, such as Simcenter Amesim which is a multi-physical simulation software of Siemens.
- Secondly, the single particle (SP) model, which is a simplified version of the p2D electrochemical model, is also widely studied in the literature [21,22,23]. The SP model shares many parameters with the p2D model. Compared to the equivalent circuit model, the SP model requires considerable effort in experimental tests and parameter identification. The computation cost of the SP model is higher than that of the equivalent circuit model.
- Finally, some black box models based on the neural network have been reported in the literature [24,25]. While they could capture the battery dynamic behavior, specific sets of data are needed to train the neural network model so that the model gives correct estimation in the expected operating range. Since the parameter values of the black box models do not have explicit physical meaning like in the equivalent circuit model and the electrochemical model, the black box models require higher effort to find out the exact reason when there is a significant difference between the model estimation and the battery test data.
In our study, an equivalent circuit model is chosen because it is simple, with a good compromise of accuracy/simplicity. In addition, the model has already been implemented in Simcenter Amesim [26], which allows for the fast construction of a battery pack model and ease integration of the pack model into a vehicle system simulation platform, as will be presented in Section 4.
3.1. Proposed Model
Figure 1 shows the reduced-order electro-thermal model used in our study. The electrical behavior of the cell is represented with an equivalent circuit model incorporating: (1) a voltage source to represent the open circuit voltage (OCV); (2) a resistance Rohm to represent the ohmic resistance responsible for the instantaneous voltage drop when the cell current changes; and (3) several RC circuits Rdff[i]/Cdiff[i] to represent the dynamic behavior of the cell mainly related to the diffusion of lithium-ion inside the battery cell. Different numbers of RC circuits were used in the literature, e.g., one in [7,10], two in [9] and five in [8]. Having more RC circuits helps to improve the model accuracy at the cost of complexity in parameter identification and higher calculation time [8,9]. The OCV is a function of the state of charge (SoC) and the temperature. Other elements in Figure 1 are functions of the SoC, the temperature and the current.
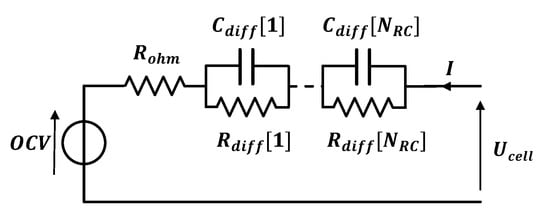
Figure 1.
Equivalent circuit model.
The SoC is determined by the coulomb counting as follows:
where SoCinit is the initial SoC; I is the current; Qcell is the cell capacity; ηcell is the faradic efficiency which is set to 1 in our study since the faradic efficiency of lithium-ion cells is very close to 1. However, for example the faradic efficiency for NiMH cells should not be neglected. The voltage of the cell is calculated by the following equation:
where:
- The OCV is calculated with the following equation to consider the hysteresis behavior of the OCV in battery:
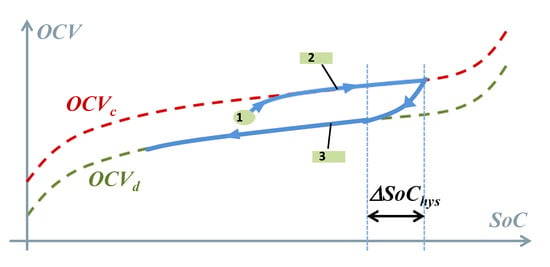
Figure 2.
Open Circuit Voltage (OCV) transition between its high and low boundaries.
- The ohmic voltage drop ΔUohm is calculated with equation:
- The voltage drop ΔUdiff_i for each of the RC circuits (i = 1, 2, …, NRC) is calculated with the following equation:
The heat generated by the cell (Hgen) during its operation includes the heat related to the entropic coefficient (), the hysteresis loss (), the ohmic loss () and the diffusion loss (). The heat generated is calculated with equations as follows:
The thermal behavior of the battery cell is represented with a simple thermal model consisted of different elements as shown in Figure 3: (1) a heat source to represent the heat generated by the cell; (2) a thermal capacity of the cell; (3) a thermal convection resistance; and (4) a temperature source to represent the ambient temperature Tamb. The cell temperature Tcell is calculated with equation:
where mcell is the cell mass and Cp is the cell specific heat. If the temperature gradient inside the battery cell needs to be considered, additional RC elements could also be added to the model in Figure 3 at the cost of increasing simulation time and calibration effort. For example, one additional set of RC elements could be added to the model in Figure 3 to take into account the heat capacity of the cell casing and the heat conduction between the cell core and the casing.
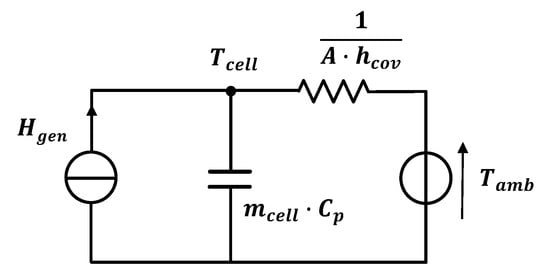
Figure 3.
Thermal model of the cell.
Table 1 summarizes the parameters needed for the model. The battery model in Simcenter Amesim also includes other features such as aging and thermal runaway modeling, which are not used in our study. Detailed information of the model can be found in the help documentation of Simcenter Amesim [26].

Table 1.
Parameters for the reduced-order circuit model.
3.2. Model Calibration
The reduced-order circuit model is calibrated with simulated data from the electrochemical model. Two types of test profile are used to generate the simulated data:
- Test 1: Pulses test. As shown in Figure 4a, this profile discharges the cell from 100% to 0% SoC. It includes several groups of short-duration (<2 s) charge and discharge pulses at different current levels. Between two groups of pulses, a long-duration discharge with a constant current is used to decrease 5% SoC of the cell. Two levels of current are used alternatively for the long-duration discharge (1 C and 0.5 C). Each long-duration discharge is followed by a long rest period (1800 s) to stabilize the cell voltage and temperature.
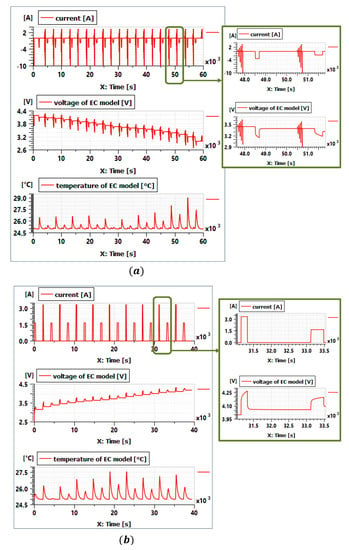 Figure 4. (a) Test 1: pulses test. (b) Test 2: charge test.
Figure 4. (a) Test 1: pulses test. (b) Test 2: charge test. - Test 2: Charge test. As shown in Figure 4b, this profile consists of long-duration charges with two levels of current used alternatively (1 C and 0.5 C) to charge the cell from 0% to 95% SoC. Each long-duration charge increases the SoC of the cell by 5% and is followed by a long rest period (1800 s).
These test profiles are designed on the one hand to facilitate the parameter identification with the Battery Identification Assistant tool in Simcenter Amesim [26]. On the other hand, the duration for the pulses and the current levels for the long-duration discharges or charges are chosen to minimize the temperature variation of the cell during the test. These profiles can be easily adapted to test other battery cells. In our study, the test profiles were applied to the electrochemical model at three ambient temperatures (5 °C, 25 °C and 45 °C). Figure 4 shows the examples of the simulated data from the electrochemical model at 25 °C for the two test profiles, respectively.
The parameters in Table 1 are identified with the Battery Identification Assistant tool in Simcenter Amesim as explained in the following paragraphs.
3.2.1. OCVd and OCVc
The OCVd and OCVc are identified with the relaxation phase after each long-duration discharge or charge. The value at the end of each relaxation after the long-duration discharge (Figure 4a is considered as the OCV value in discharge. Figure 5 shows an example of the OCVd identified at the three temperatures. The same process allows us to get the OCVc at the three temperatures by using the charge profile in Figure 4b. A temperature of 25 °C is chosen as the reference temperature in our study to calculate the open circuit voltage with Equation (3).
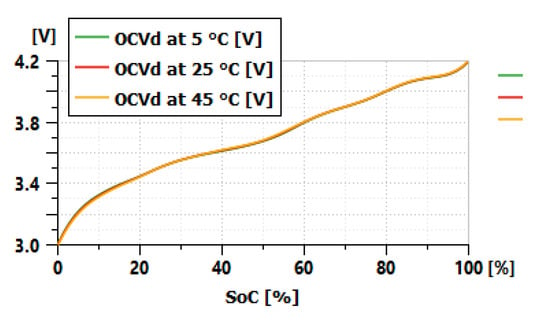
Figure 5.
OCVd identified at different temperatures.
3.2.2. ΔSoChys
Figure 6 shows the hysteresis between the OCVd and OCVc at 25 °C. The experimental test results of a Li-ion cell in [27] show that the state of charge variation (ΔSoChys) necessary for full charge/discharge OCV transition is from 15% to 25% in most of the case. In the absence of tests to identify ΔSoChys, its value is set arbitrarily to 15% in our study. For the future studies, it would be interesting to investigate several things in the hysteresis behavior for different battery chemistries, such as the impact of the temperature on the value of ΔSoChys, as well as a fast and simple method to identify the value of ΔSoChys from limited test data.
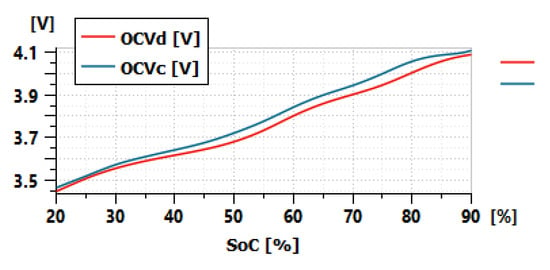
Figure 6.
Hysteresis between OCVd and OCVc at 25 °C.
3.2.3. dU/dT
The entropic coefficient curve can be calculated by using the OCV curves identified previously as follows:
where T1 and T2 are two different temperatures; OCVx can be OCVd or OCVc. In our case, the OCV is identified at three temperatures in discharge and in charge. There are therefore six possible combinations to calculate six curves of entropic coefficient as illustrated in Table 2. The average curve of the six entropic coefficient curves is the one to be used in the reduced-order circuit model. The average curve is shown in Figure 7.

Table 2.
Six combinations to calculate entropic coefficient.
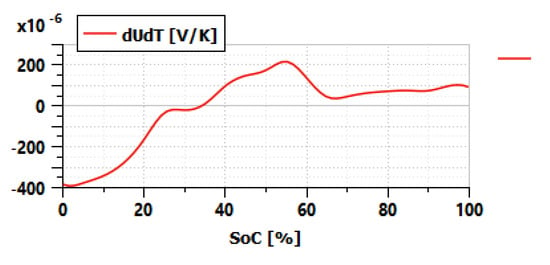
Figure 7.
dU/dT used in the reduced-order circuit model.
3.2.4. Rohm_d and Rohm_c
The instantaneous ohmic resistances are identified with the groups of short-duration pulses (Figure 4a). These pulses allow to get the ohmic resistance value at different SoCs, currents and temperatures. Figure 8 shows the result of the ohmic resistance identified at 25 °C.
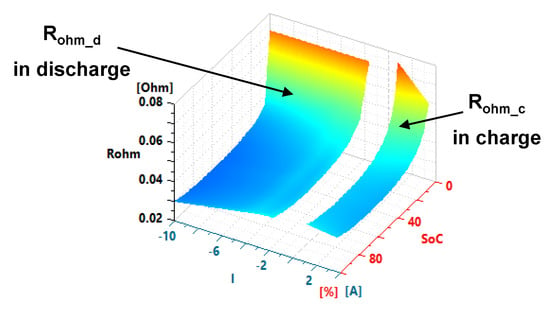
Figure 8.
Ohmic resistances at 25 °C.
3.2.5. RC Circuits
By using the long-duration discharge and charge pulses in Figure 4 which decrease or increase 5% SoC of the cell, the RC circuits Rdff[i]/Cdiff[i] are identified with the Battery Identification Assistant tool of Simcenter Amesim. Instead of identifying directly several RC circuits, the tool identifies a Warburg impedance represented by two parameters (a diffusion resistance Rss and a time coefficient Tc). The identification process of the Warburg impedance is similar to the ones in [15,16]. Once the Warburg impedance is identified, it can be easily approximated by a different number of RC circuits in the Simcenter Amesim battery model with the help of the RC transformation tool [26]. The parameters Rss and Tc of the Warburg impedance are identified at three different temperatures (5, 25 and 45 °C). Their values are in function of the current, the SoC and the temperature. Figure 9 shows the Rss and Tc identified at 25 °C.
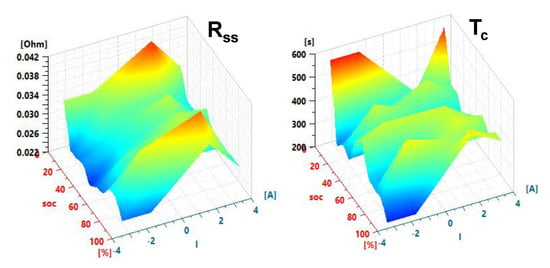
Figure 9.
Warburg impedance at 25 °C.
The values of each parameter are stored in a multi-dimensional data table. The calculation of the parameter value for an operating condition (defined by a current, a SoC and a temperature) is done by using the “strinitu” function [28] in the battery model of Simcenter Amesim. For a normal operating condition which is inside the characterization range of the data table, the value of the parameter is calculated via linear interpolation. For an operating condition outside of the characterization range of the data table, the extreme value is used to avoid meaningless extrapolation of the table data. The current is considered in the Rss and Tc in order to capture the eventual dependency of the battery dynamic behavior on the current amplitude and direction. However, the current dependency increases the complexity of the lookup table for the Rss and Tc, which results in a longer simulation time. Additional effort is also required to implement the high dimensional lookup table in the battery model if one needs to develop in-house battery model instead of using a dedicated simulation software such as Simcenter Amesim. Several further improvements in the Warburg impedance identification, which are not covered by this paper, could be carried out in the future studies to:
- Evaluate the possibility of removing the current dependency, so that faster simulation time and simpler lookup table implementation could be achieved;
- Include the relaxation phase after the current pulse into the parameter identification, so that the dynamic behavior during the relaxation phase could also be properly represented in case the battery dynamic behavior in the relaxation phase is significantly different from the one during the current pulse;
- Search for an optimal function, such as a polynomial used in [9], to represent the parameter value in function of the SoC or the current. It could help to guarantee smooth parameter value change along the SoC and current axis. The smooth parameter value change during the simulation has several benefits. It will allow to have faster model simulation. It will also minimize the risk of simulation failure due to the discontinuity issue in which there is a sharp change of the parameter value during the simulation [29].
3.2.6. Thermal Parameters
The parameter values of the thermal model are the same as the ones used in the electrochemical model as shown in Table 3.

Table 3.
Values of parameters for the thermal model.
3.3. Model Validation
Figure 10 shows the simulation sketch in Simcenter Amesim to evaluate the performance of the reduced-order circuit model. The sketch includes several elements, such as (A) the battery model which represents the electrical model in Figure 1; (B) a convective heat exchange component and a thermal mass to represent the thermal model in Figure 3; (C) a resistance to represent the connector resistance in the electrochemical model; (D) a virtual test bench to deliver current to the battery model and measure the voltage; (E) three tables which import the current, voltage and temperature data generated by the electrochemical model (EC model). This sketch allows us to compare the estimation of the two models on the battery voltage and temperature for the same current profile.
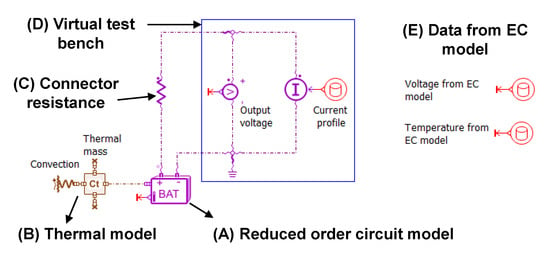
Figure 10.
Simulation sketch for model validation in Simcenter Amesim.
To evaluate the performance of the reduced-order circuit model, a validation test profile in Figure 11a has been applied to the reduced-order circuit model and the electrochemical model. The profile includes a constant current charge phase to represent fast charge situation; several long-duration discharges to set the cell at different SoCs; and several dynamic cycles at different SoCs to represent the situation during driving. As explained in Section 3.2.5, the number of the RC circuit can be easily set in the reduced-order model with the help of the RC transformation tool in Simcenter Amesim. Simulations with five different RC circuits (NRC = 1 to 5) have therefore been done. Figure 11b–d show the comparison of the two models on the estimation of battery voltage and temperature at respectively 5, 25 and 45 °C, with NRC = 1 in the reduced-order circuit model. These figures show that the reduced-order circuit model (ROC model) can reproduce correctly the voltage and temperature behavior of the electrochemical model (EC model).
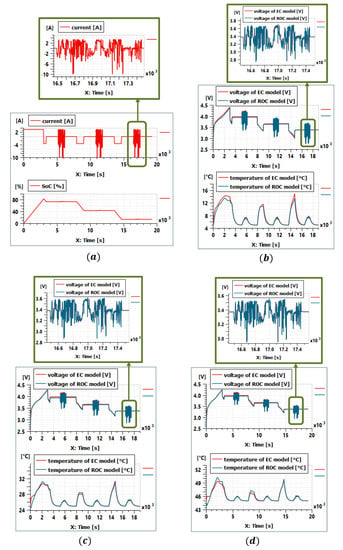
Figure 11.
(a) Validation current and SoC profiles. (b) Validation test at 5 °C. (c) Validation test at 25 °C. (d) Validation test at 45 °C.
To evaluate quantitatively the performance of the reduced-order circuit model, the RMS (root mean squared) errors for the voltage and temperature estimation are calculated by the equation as follows:
where VECM,k is the voltage or temperature of the electrochemical model; VROM,k is the voltage or temperature of the reduced-order circuit model; Ns is the number of the voltage or temperature data sample. Table 4 and Table 5 present the RMS errors of the voltage and temperature estimation according to the number of RC circuits used. The results show that the reduced-order circuit model with one RC circuit is sufficient to correctly simulate the electrochemical model. Adding additional RC circuits does not significantly improve the estimation precision. The RMS errors of the reduced-order circuit model are similar to the ones reported in other works in the literature [7,9].

Table 4.
Root mean squared (RMS) error for voltage estimation.

Table 5.
RMS error for temperature estimation.
4. Battery Pack Model
4.1. Battery Pack Model in a Virtual Test Bench
In our study, the battery pack model is composed of 16 modules in series; each module is composed of 12 groups in series and each group is composed of 20 cells in parallel (20P12S). There are 3840 cells in total. The battery pack, together with a BMS developed by another partner, will be implemented in an electric vehicle (Voltia eVan) in the future stage of our project. To evaluate the performance of the BMS before hardware implementation in the eVan, a real-time compatible battery pack model is needed for the SiL and HiL tests.
By using the reduced-order cell model descripted in Section 3, a battery pack model has been built in Simcenter Amesim. Figure 12 shows the simulation sketch of the electric vehicle including the battery pack model. The battery pack model includes 16 modules in series as the real pack. However, not every single cell is represented in each module of the battery pack model. To limit the number of components in the sketch, each module includes only four battery models in series. Each battery model is used to represent three groups of cells, which means 60 cells (20P3S) in total. All these 60 cells are considered to be identical, so only one battery model is enough to represent all of them by configuring the architecture of the battery model in Simcenter Amesim to be 20 in parallel and three in series (20P3S). By doing so, the battery pack is split into 48 battery models, which allows one to have access to, for example, 48 temperatures at different places in the battery pack. The battery pack casing is also modeled. The casing is divided into 16 parts and each part is represented by a thermal mass element. The thermal mass of each part of the casing is connected to the nearby module.
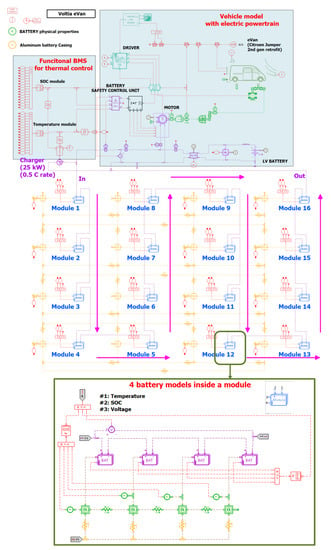
Figure 12.
Integration of the battery pack model in a virtual test bench of an electric vehicle in Simcenter Amesim.
The battery pack model is connected to the vehicle model of the Voltia eVan via the electric powertrain. Furthermore, a functional BMS is implemented in the simulation sketch to control the active air cooling of the battery pack via its casing. This functional BMS will be replaced by the real BMS function in the SiL environment and by the real BMS in the HiL environment.
4.2. Scenarios for Battery Pack Cooling
To illustrate the use of the battery pack model with a BMS, a case study is presented in Figure 13 to compare the electro-thermal behavior of the battery pack under two cooling scenarios: with and without the active air cooling. For the scenario with the active air cooling, the functional BMS is used to turn on the air cooling when one of the 48 battery models reaches 35 °C. In this case, the heat exchange of the casing with its environment will change from natural convection (with hconv equal to 20 W/m2/K) to forced convection (with hconv equal to 200 W/m2/K). The active air cooling is turned off when all the 48 temperatures are less than 30 °C. For both scenarios, the battery pack is charged during the first 2 h. Then the vehicle follows two WLTC (Worldwide harmonized Light-duty vehicles Test Cycles) driving cycles. The comparison of the simulation results for the two scenarios shows that the active cooling helps to increase the effective charge time and significantly decrease the battery cell temperatures.
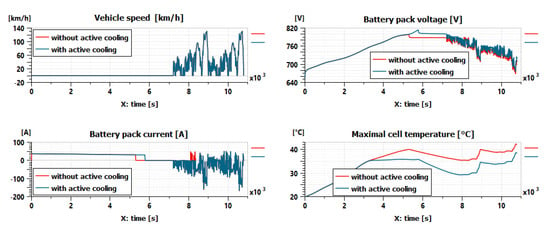
Figure 13.
Comparison of results between two cooling strategies.
4.3. Real-Time Capability
To use the battery pack model for the SiL and HiL tests, the simulation time of the battery pack model must be analyzed to confirm its real-time capability. Indeed, model in the SiL platform and especially in the HiL platform must be run with fixed step solver and must be faster than real time at each integration step. Figure 14 shows an analysis of the simulation time for the scenario with the active air cooling. The simulation sketch in Figure 12 was run with a fixed step solver by setting the integration time step to 0.002 s. The simulation was carried out on a laptop with Intel i7 2.6 GHz CPU, 16 GB RAM and a 512 GB SSD hard drive. The Euler method is used for the fixed step solver in the Simcenter Amesim. In Figure 14, the cumulative CPU time for the simulation is 801 s at the end of the simulation, which is 13 times faster than the duration of the scenario (10,800 s). The mean CPU time used per step (0.0001 s) is 20 times faster than the fixed time step value (0.002 s). The real-time capability of the model in Figure 12 is then validated.
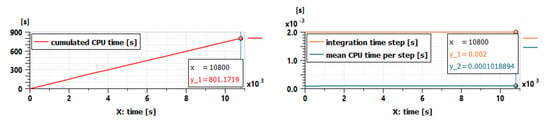
Figure 14.
Simulation time for the scenario with the active air cooling.
5. Conclusions
In this paper, a simple method is proposed to get a reduced-order electro-thermal cell model from a complex electrochemical cell model. The method requires only two tests per temperature to the electrochemical model to collect the simulated data of voltage and temperature. An equivalent circuit model is then identified from the simulated data. The method has been applied to get the reduced-order model from the electrochemical-thermal p2D model calibrated for a nickel-rich, silicon-graphite lithium-ion cell of 3.35 Ah. The reduced-order model can correctly reproduce the voltage and temperature behavior of the electrochemical model according to the validation tests. The method is generic so it can be applied with minor modification to any complex electrochemical models calibrated for other battery cells.
With the reduced-order model, a battery pack model has been created and integrated in the virtual test bench for an electric vehicle in Simcenter Amesim. The real-time capability of the pack model has been analyzed and validated via the simulation of a cooling scenario during vehicle normal operation with charging and driving cycles. The battery pack model is then ready to be used for the SiL and HiL tests of the BMS.
Author Contributions
Conceptualization, A.L., M.P. and J.S.; methodology, A.L., M.P. and J.S.; software, A.L. and M.P.; validation, A.L., M.P. and J.S.; writing—original draft preparation, A.L., M.P. and J.S.; writing—review and editing, A.L., M.P., J.S. and A.J.; supervision, A.J.; project administration, M.P. and A.J. All authors have read and agreed to the published version of the manuscript.
Funding
This work has received funding from the European Union’s Horizon 2020 research program under the grant “Electric Vehicle Enhanced Range, Lifetime and Safety through INGenious Battery Management” (EVERLASTING-713771).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Doyle, M.; Fuller, T.F.; Newman, J.S. Modeling of Galvanostatic Charge and Discharge of the Lithium/Polymer/Insertion Cell. J. Electrochem. Soc. 1993, 140, 1526–1533. [Google Scholar] [CrossRef]
- Sturm, J.; Rheinfeld, A.; Zilberman, I.; Spingler, F.B.; Kosch, S.; Frie, F.; Jossen, A. Modeling and Simulation of inhomogeneities in a 18650 nickel-rich, silicon-graphite lithium-ion cell during fast charging. J. Power Sources 2019, 412, 204–223. [Google Scholar] [CrossRef]
- Sturm, J.; Ennifar, H.; Erhard, S.; Rheinfeld, A.; Kosch, S.; Jossen, A. State estimation of lithium-ion cells using a physicochemical model based extended Kalman filter. Appl. Energy 2018, 223, 103–123. [Google Scholar] [CrossRef]
- Subramanian, V.R.; Diwakar, V.D.; Tapriyal, D. Efficient Macro-Micro Scale Coupled Modeling of Batteries. J. Electrochem. Soc. 2005, 152, A2002. [Google Scholar] [CrossRef]
- Thomas, K.E.; Newman, J.; Darling, R.M. Mathematical Modeling of Lithium Batteries. In Advances in Lithium-Ion Batteries; Van Schalkwijk, W.A., Scrosati, B., Eds.; Springer: Boston, MA, USA, 2002; pp. 345–392. [Google Scholar]
- Brenan, K.E.; Campbell, S.L.; Petzold, L.R. (Eds.) Numerical Solution of Initial-Value Problems in Differential-Algebraic Equations; Classics in Applied Mathematics; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1996; Volume 14. [Google Scholar]
- Mathew, M.; Mastali, M.; Catton, J.W.A.; Samadani, E.; Janhunen, S.; Fowler, M. Development of an Electro-Thermal Model for Electric Vehicles Using a Design of Experiments Approach. Batteries 2018, 4, 29. [Google Scholar] [CrossRef]
- Li, A.; Pelissier, S.; Venet, P.; Gyan, P. Fast Characterization Method for Modeling Battery Relaxation Voltage. Batteries 2016, 2, 7. [Google Scholar] [CrossRef]
- Lin, X.; Perez, H.E.; Mohan, S.; Siegel, J.B.; Stefanopoulou, A.G.; Ding, Y.; Castanier, M.P. A lumped-parameter electro-thermal model for cylindrical batteries. J. Power Sources 2014, 257, 1–11. [Google Scholar] [CrossRef]
- German, R.; Shili, S.; Sari, A.; Venet, P.; Bouscayrol, A. Characterization Method for Electrothermal Model of Li-Ion Large Cells. In Proceedings of the 2017 IEEE Vehicle Power and Propulsion Conference (VPPC), Belfort, France, 11–14 December 2017; pp. 1–6. [Google Scholar]
- Saldaña, G.; Martín, J.I.S.; Zamora, I.; Asensio, F.J.; Onederra, O. Analysis of the Current Electric Battery Models for Electric Vehicle Simulation. Energies 2019, 12, 2750. [Google Scholar] [CrossRef]
- Meng, J.; Luo, G.; Ricco, M.; Swierczynski, M.; Stroe, D.-I.; Teodorescu, R. Overview of Lithium-Ion Battery Modeling Methods for State-of-Charge Estimation in Electrical Vehicles. Appl. Sci. 2018, 8, 659. [Google Scholar] [CrossRef]
- Fotouhi, A.; Auger, D.J.; Propp, K.; Longo, S.; Wild, M. A review on electric vehicle battery modelling: From Lithium-ion toward Lithium–Sulphur. Renew. Sustain. Energy Rev. 2016, 56, 1008–1021. [Google Scholar] [CrossRef]
- Gao, Z.; Chin, C.S.; Woo, W.L.; Jia, J. Integrated Equivalent Circuit and Thermal Model for Simulation of Temperature-Dependent LiFePO4 Battery in Actual Embedded Application. Energies 2017, 10, 85. [Google Scholar] [CrossRef]
- Hafsaoui, J.; Scordia, J.; Sellier, P.; Aubret, P. Development of an Electrochemical battery model and Its Parameters Identification Tool. Int. J. Automot. Eng. 2012, 3, 27–33. [Google Scholar]
- Montaru, M.; Pelissier, S. Frequency and Temporal Identification of a Li-ion Polymer Battery Model Using Fractional Impedance. In Proceedings of the Proceedings in Advances in Hybrid Powertrains, Paris, France, 25–26 November 2008. [Google Scholar]
- Stroe, D.-I.; Swierczynski, M.J.; Stroe, A.-I.; Kær, S.K. Generalized Characterization Methodology for Performance Modelling of Lithium-Ion Batteries. Batteries 2016, 2, 37. [Google Scholar] [CrossRef]
- Urbain, M.; Hinaje, M.; Raël, S.; Davat, B.; Desprez, P. Energetical Modeling of Lithium-Ion Batteries Including Electrode Porosity Effects. IEEE Trans. Energy Convers. 2010, 25, 862–872. [Google Scholar] [CrossRef]
- Mesbahi, T.; Rizoug, N.; Bartholomeus, P.; Sadoun, R.; Khenfri, F.; Le Moigne, P. Dynamic Model of Li-Ion Batteries Incorporating Electrothermal and Ageing Aspects for Electric Vehicle Applications. IEEE Trans. Ind. Electron. 2018, 65, 1298–1305. [Google Scholar] [CrossRef]
- Petit, M.; Abada, S.; Mingant, R.; Bernard, J.; Desprez, P.; Perlo, P.; Biasiotto, M.; Introzzi, R.; Lecocq, A.; Marlair, G. Demobase project: Numerical simulation for seamless integration of battery pack in light electric vehicle. In Proceedings of the 32nd Electric Vehicle Symposium (EVS32), Lyon, France, 22 May 2019. [Google Scholar]
- Prada, E.; Di Domenico, D.; Creff, Y.; Bernard, J.C.; Sauvant-Moynot, V.; Huet, F. Simplified Electrochemical and Thermal Model of LiFePO4-Graphite Li-Ion Batteries for Fast Charge Applications. J. Electrochem. Soc. 2012, 159, A1508–A1519. [Google Scholar] [CrossRef]
- Bizeray, A.M.; Kim, J.-H.; Duncan, S.R.; Howey, D.A. Identifiability and Parameter Estimation of the Single Particle Lithium-Ion Battery Model. IEEE Trans. Control. Syst. Technol. 2019, 27, 1862–1877. [Google Scholar] [CrossRef]
- Chen, J.; Wang, R.; Li, Y.; Xu, M. A Simplified Extension of Physics-Based Single Particle Model for Dynamic Discharge Current. IEEE Access 2019, 7, 186217–186227. [Google Scholar] [CrossRef]
- Li, S.; Li, J.; He, H.; Wang, H. Lithium-ion battery modeling based on Big Data. Energy Procedia 2019, 159, 168–173. [Google Scholar] [CrossRef]
- Sarvi, M.; Masoum, M.A.S. A Neural Network Model for Ni-Cd Batteries. In Proceedings of the 43rd International Universities Power Engineering Conference, Padova, Italy, 1–4 September 2008. [Google Scholar]
- Siemens. Help Document of ESSBATCA01—Advanced Equivalent Circuit Model of Battery Cell; Simcenter Amesim V17; Siemens: Munich, Germany, 2018. [Google Scholar]
- Marongiu, A.; Nußbaum, F.G.W.; Waag, W.; Garmendia, M.; Sauer, D.U. Comprehensive study of the influence of aging on the hysteresis behavior of a lithium iron phosphate cathode-based lithium ion battery—An experimental investigation of the hysteresis. Appl. Energy 2016, 171, 629–645. [Google Scholar] [CrossRef]
- Siemens. Help Document of Strinitu Utility; Simcenter Amesim V17; Siemens: Munich, Germany, 2018. [Google Scholar]
- Siemens. Help Document of Discontinuity Handling—Impact of a Discontinuity on Simulation; Simcenter Amesim V17; Siemens: Munich, Germany, 2018. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).